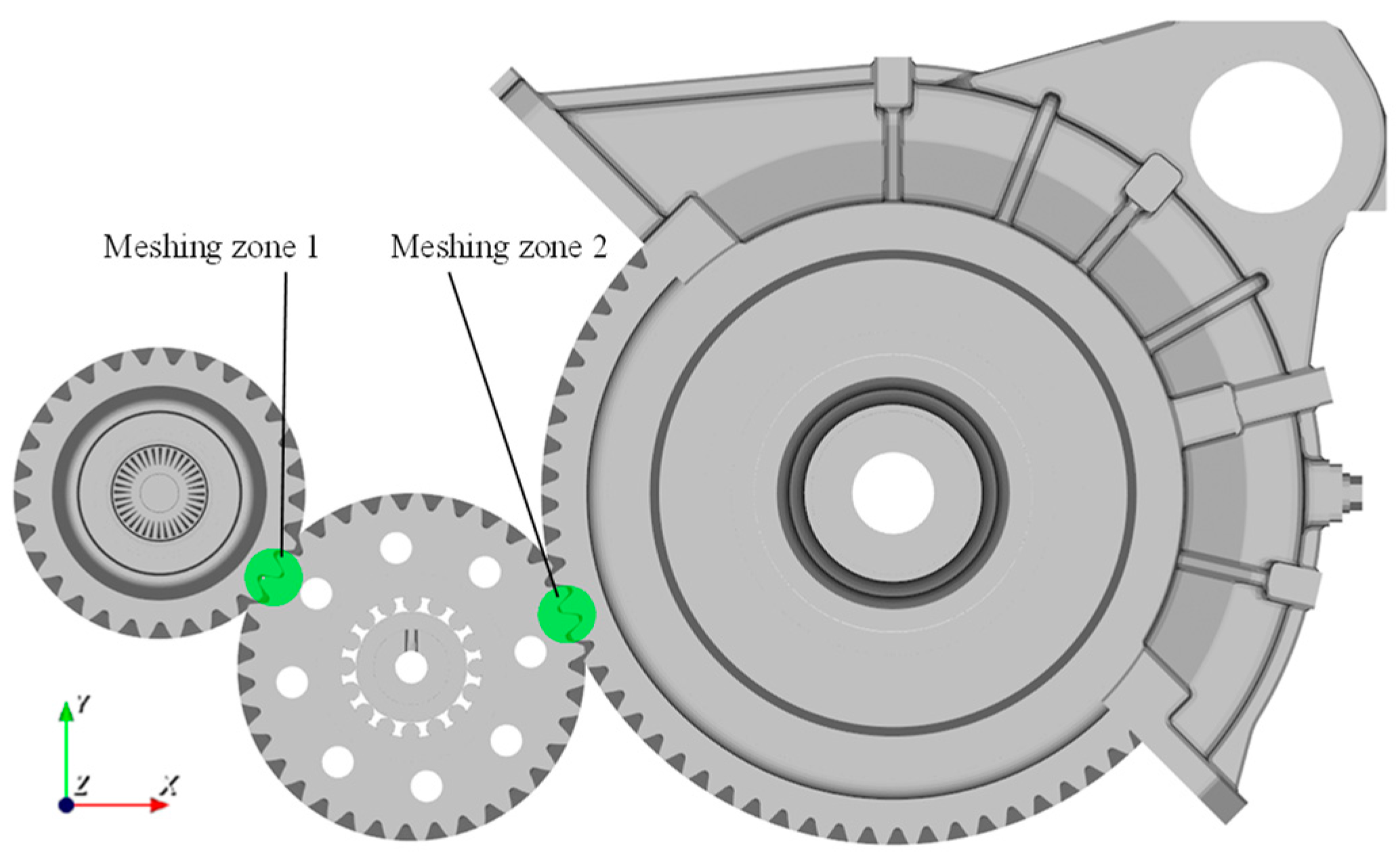
1. Introduction
High-speed train gearboxes serve in extreme environments for long durations, so it is particularly important to evaluate the lubrication state during their service. The temperature of bearings and lubricant is typically a key indicator for monitoring the operational state of the gearbox. When the temperature surpasses the predetermined safety threshold, the safety warning mechanism of the high-speed train will be triggered, and the train will have to slow down or stop. Effective lubrication minimizes friction and wear between components, absorbs shocks and vibrations, reduces noise, and dissipates heat, maintaining the gearbox at optimal temperatures. In contrast, inadequate lubrication increases friction and raises bearing temperatures sharply, potentially causing burnouts, gear pitting [
1], and scoring, as shown in
Figure 1, and significantly reducing gearbox lifespan and reliability. In order to ensure good lubrication of the gearbox and improve the reliability of the train operation, it is necessary to accurately evaluate the lubrication state of each component of the gearbox [
2,
3]. Hence, studying the lubrication characteristics and influencing factors of high-speed train gearboxes is highly significant.
Many scholars have applied numerical simulation methods to study the splash lubrication characteristics of gearboxes, and the finite volume method (FVM) is commonly adopted [
4]. Liu and colleagues established a computational fluid dynamics (CFD) model for the splash lubrication of FZG gearboxes based on the FVM and investigated the relationships between fluid distribution, churning power loss, gear rotating speed, and oil level [
5,
6]. Hildebrand et al. studied the interaction relationship between lubricant flow and power loss by introducing a guide plate [
7]. Mastrone et al. improved the mesh generation process of the FVM, and the proposed mesh partitioning algorithm can significantly reduce computational costs. The flow field structure of the CFD numerical model was validated by particle image velocimetry, and good consistency was achieved [
8]. Hu et al. [
9] and Jiang et al. [
10] conducted an array of investigations regarding the splash lubrication characteristics of bevel gear trains for helicopters. Nevertheless, there are many simplifications of the housing structure in their CFD models, all in order to ensure mesh quality. Mastrone et al. [
11] proposed a grid reconstruction method, which is believed to be applicable to multi-stage transmission systems. In CFD models based on the FVM, the moving grid technique is needed to generate the grid surrounding the gears to simulate rotational motion [
12,
13,
14]. If the clearance is too small, it is easy to cause severe mesh distortion in the meshing area, which can lead to non-convergence of the calculation. Excessive clearance will weaken the gear meshing effect and increase the calculation error. The moving grid used in helical gear transmission is more likely to diverge due to mesh distortion than that of spur gear transmission. The moving grid used in herringbone gear transmission needs to ensure the coordination and consistency of the two sets of meshes. However, for continuous transmission with the idle gear, many meshing techniques are no longer applicable.
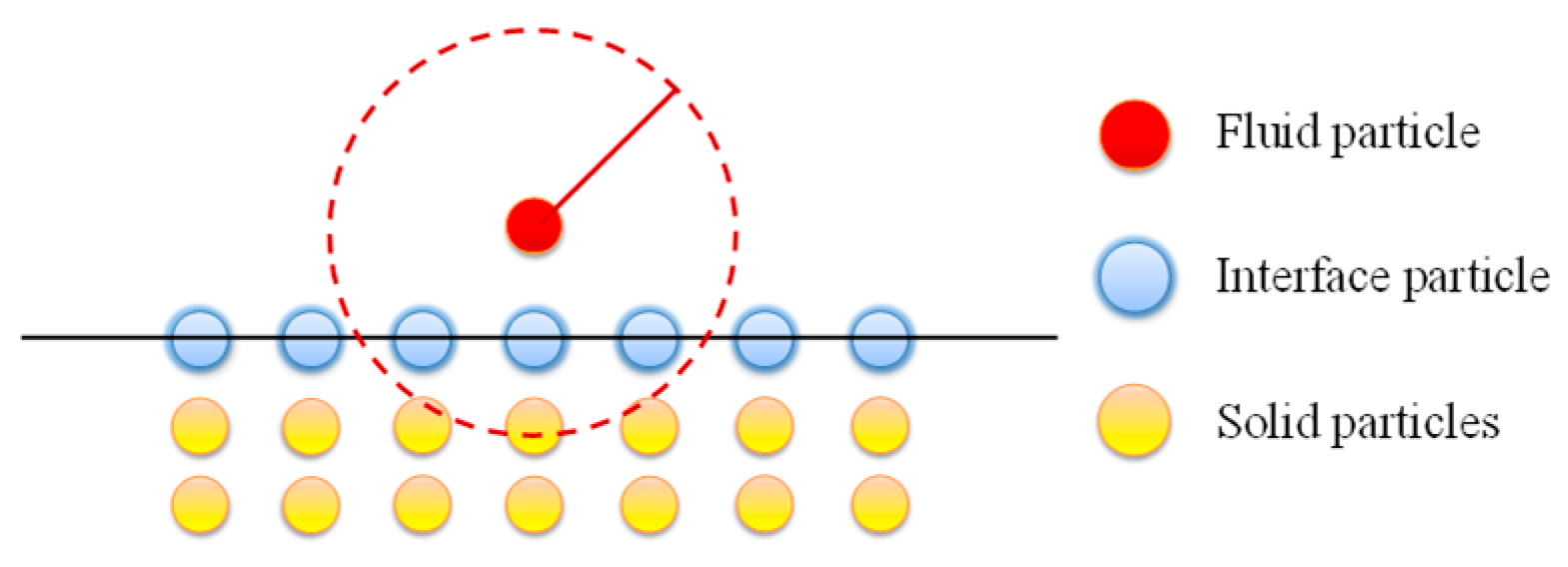
Compared to the grid-based CFD method, there is no fixed topology between the nodes in the particle-based CFD method, which avoids the complex process of grid distortion and old–new grid conversion in large deformation problems. It has obvious advantages in dealing with severe deformation issues such as free-surface flow. Liu et al. applied the smoothed particle hydrodynamics (SPH) approach to simulate and analyze the oil distribution of an FZG gearbox. The oil distribution captured by a fast frame camera showed that the SPH has a strong ability to predict oil distribution [
15]. Ji et al. employed this method to discretize air and oil in a gearbox and studied the aeration behavior during the churning process [
16]. Legrady et al. studied the churning loss in spiral bevel gear trains and found that the difference in churning loss was up to 30% using a 98% scaled gear geometry [
17]. One other widely available particle-based CFD method is the moving particle semi-implicit (MPS) approach. Liu et al. [
18] used MPS to simulate the CFD model established in reference [
14] and pointed out that MPS is more accurate than SPH in the prediction of churning torque. Guo et al. [
19] used an orthogonal experimental method to study the influence of geometric dimensions and working conditions on the churning power loss of a gear system and pointed out gear rotating speed as the mostly important influential parameter. Deng and others [
20,
21,
22] visualized the internal flow field of the single-stage transmission gearbox and screw reducer with MPS. Shao et al. [
23] further carried out a study on the impact of oil adjustment devices on the lubrication mechanism of high-speed train gearboxes. The CFD simulation models established in references [
20,
21,
22,
23] highly replicate the actual structure of the gearbox, demonstrating the significant superiority of MPS in visualizing the internal flow field of transmission systems with complex surfaces. However, their research focuses only on oil circulation, flow patterns, and churning losses, without studying the coverage of lubricants on component surfaces or the distribution characteristics of oil films on these surfaces.
Different types of lubricants are used in gearboxes, each with distinct advantages and disadvantages. Mineral oil is cost-effective and widely available but lacks thermal stability and longevity [
24]. Synthetic oil offers superior performance and durability but is expensive [
25]. High-viscosity-index oil ensures stable viscosity across temperature variations but is costly [
26]. Specialty oils provide enhanced protection for specific applications but may have compatibility issues and higher costs. Semi-synthetic oil, often considered the best option, balances cost and effectiveness, offering good performance at a reasonable price, and is therefore widely used in gear transmission systems [
27]. Additionally, adding suitable additives to lubricating oils can improve their frictional properties [
28].
The unique structural design of herringbone gears ensures more uniform interaction between the teeth, thereby reducing noise and vibration. The two helices of the herringbone gear are arranged on the opposite side, which can withstand both radial and axial forces simultaneously, while reducing load on the bearings and having stronger carrying capacity [
29,
30,
31]. The increasing speed of the high-speed train has led to higher requirements for the power that can be transmitted by the transmission system. And, at the same time, the continuous improvement in passenger comfort also puts forward higher requirements for noise control of the transmission system. Transmission systems with herringbone gears can better meet these requirements. The space under the high-speed train is very limited, and the structure of the bogies is very compact [
32,
33]. With a fixed transmission ratio, the fixed platform height limits the use of large gears in the transmission system. To ensure the power transmission distance, gearboxes with idle gears have been widely used. In this kind of transmission system, in order to meet the lubrication requirements, multiple gears are immersed in the lubricant, and the lubricant splash behavior is more complicated. The lubrication characteristics of gearboxes with an idle gear remain largely unstudied.
This study focuses on the herringbone gearbox used in high-speed trains, introducing a liquid film flow model to enhance the non-slip wall boundary conditions of MPS, so that MPS possesses the capability to forecast surface liquid film flow. The distribution characteristics of the liquid film on the inner wall of the casing are analyzed, and the influence of gear rotating speed, lubricant volume, and temperature on the lubrication performance of the gearbox are studied. The research findings offer a theoretical basis for optimizing the casing structure and improving the sealing effect and transmission efficiency of the gearbox.
4. Experiment Verification
Due to the limitation of the experimental conditions, the same geometric model as the gearbox in reference [
5] is established. The geometry dimensions of the gear pair are displayed in
Table 5. The gearbox dimensions are 274 × 56 × 175 mm. The CFD simulation model was created using the shonDy, with the lubricant physical properties and gear speeds set the same as in reference [
5], as detailed in
Table 6. Condition 1 is used to verify the oil distribution, while conditions 2~7 are used to verify the churning torque. A comparison of the experiment and simulation results is depicted in
Figure 6 and
Figure 7.
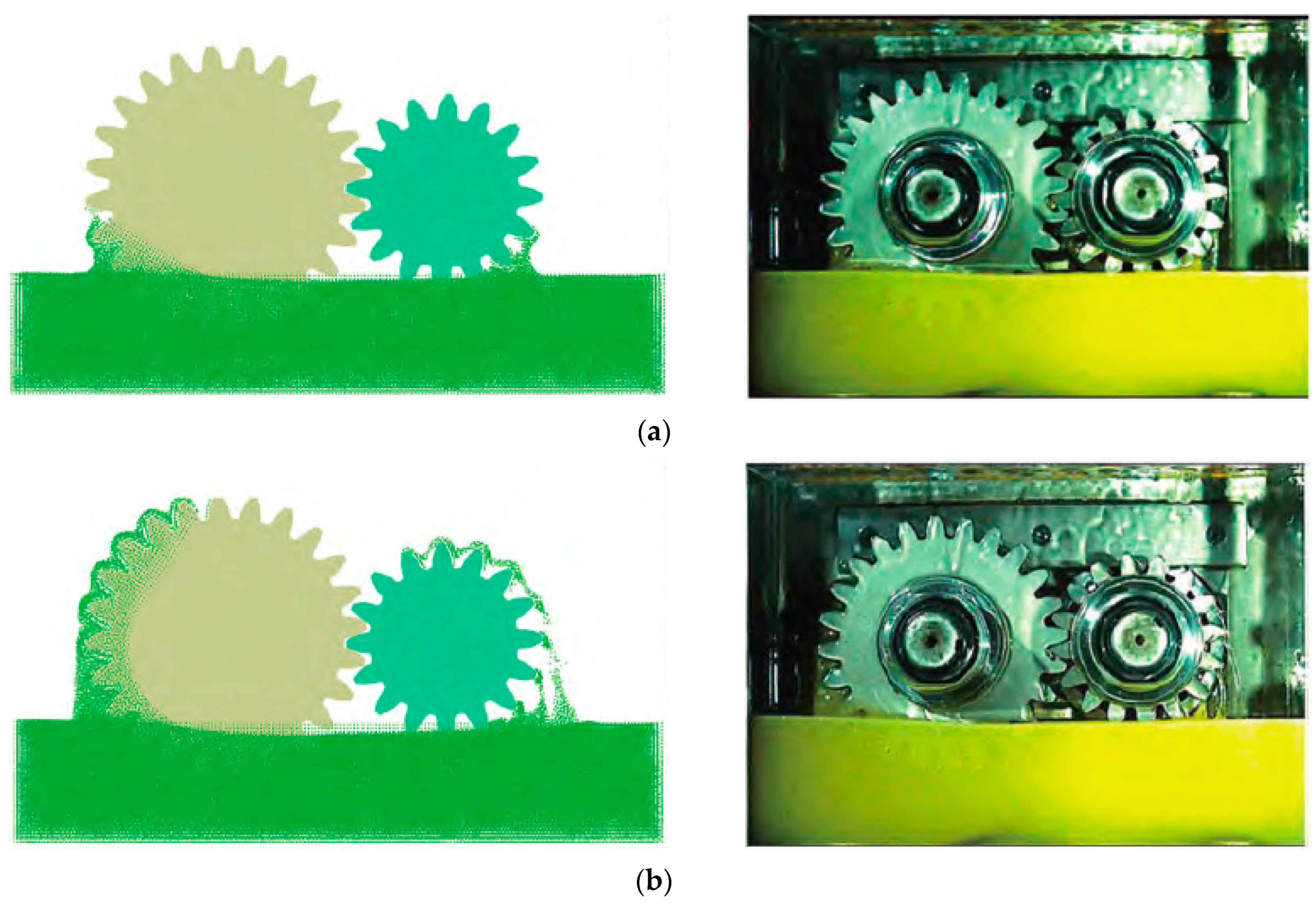
As seen in
Figure 6, when the pinion rotates 50°, the teeth initially immersed in the lubricant rotate three teeth. Due to the oil viscosity, a clear oil trail is formed. The gear rotates at a low speed and turns about two teeth. The lubricant churned up by the gear accumulates in the lower left of the gear, without forming a clear oil path. When the pinion rotates 100°, four oil trails form on the tooth side, with the outermost two almost overlapping. The centrifugal force acting on the lubricant churned up by the gear is about 2/3 that on the pinion. Due to the viscosity, the lubricant still accumulates in the lower left of the gear. The amount of lubricant churned up is also much more than when the pinion gear is rotated by 50°.
Figure 7 presents the simulated churning torque values predicted by MPS and the experiment churning torque values reported in reference [
5]. Overall, the churning torque predicted by MPS and the experiment values both indicate an increase in churning torque as the pitch line velocity of the gear rises. Although there is a numerical deviation of about 30% between the results predicted by MPS and the experiment data, the overall trend displayed by both is consistent. This may be due to differences in the material characteristics of the lubricant or numerical errors caused by using discrete lubricant particles instead of a continuous phase. At both high and low pitch line velocities, the churning torque estimated through MPS demonstrates satisfactory concurrence with the experimental results. The comparison shows a strong agreement between the oil distribution and churning torque predicted by MPS and the experimental measurements. This demonstrates the capability of MPS to accurately forecast the oil distribution and churning torque in a gearbox.
6. Conclusions and Future Work
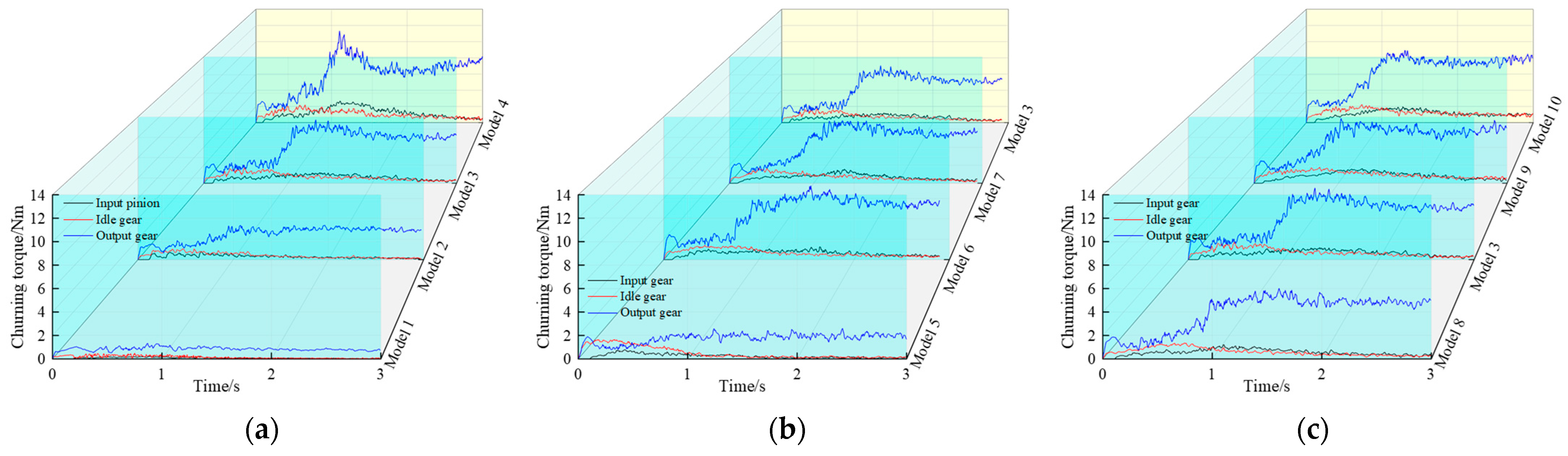
In this paper, 10 high-fidelity CFD simulation models of a herringbone gear transmission gearbox with an idle gear for a high-speed train are established. The effects of gear rotating speed, lubricant volume, and temperature on the lubrication characteristics, lubrication in the meshing zone, and churning power loss are studied with MPS. The major conclusions of the present study are the following:
(1) MPS is utilized for investigating the lubrication characteristics of a herringbone gear transmission gearbox with an idle gear. This offers a novel research approach for the lubrication study of continuous gear transmission and non-convectional gear transmission. The combination of a liquid film flow model and MPS expands the capability of MPS to forecast the distribution of a liquid film on the surface of components and provides new indicators for the evaluation of gearbox lubrication.
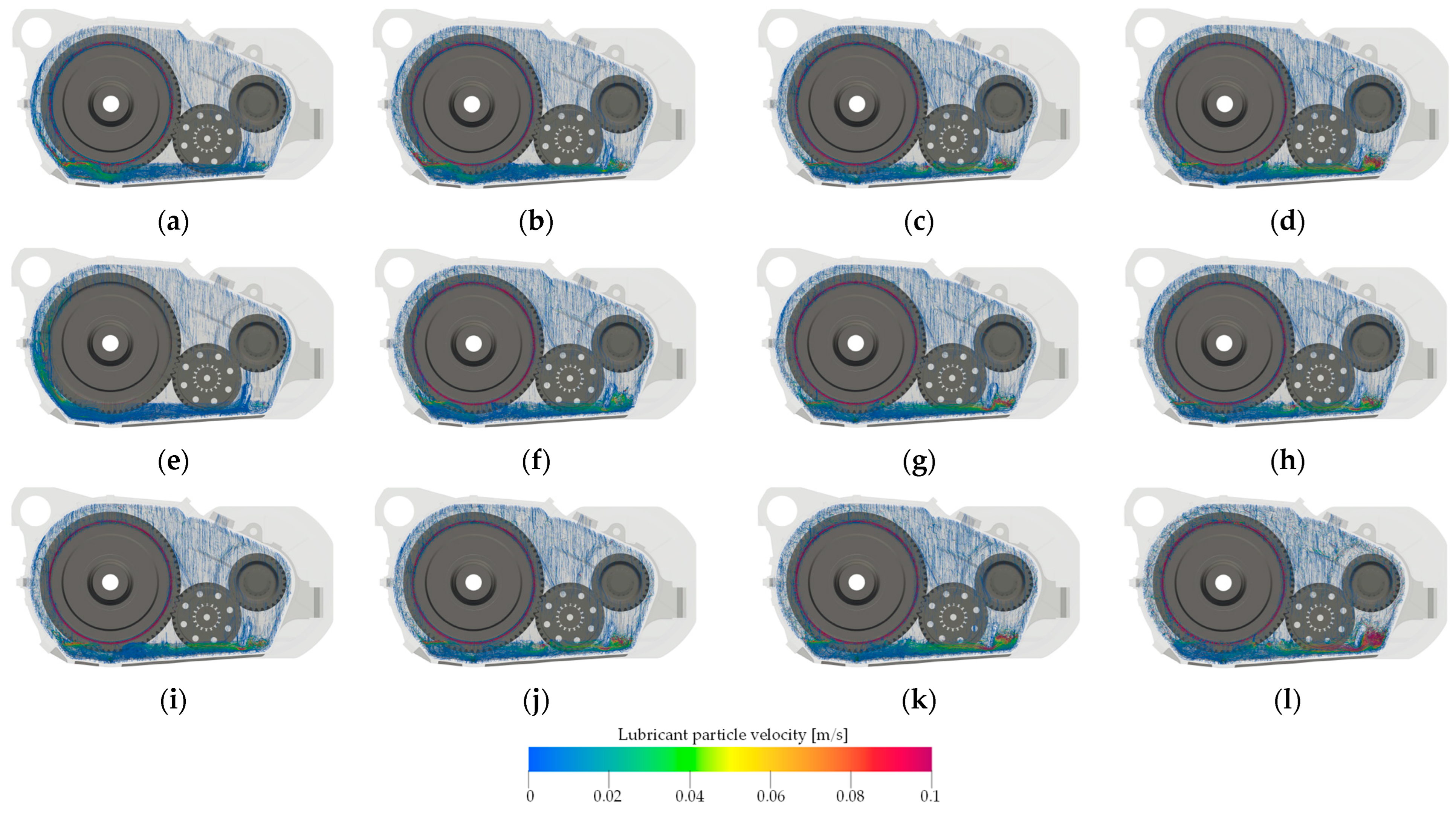
(2) The velocity field and lubricant pathline for CFD models are visualized. The results indicate that the lubrication characteristics depend on the splashing effect of rotating gears on the lubricant and the fluidity of the lubricant. Gear rotating speed is the main factor influencing the splashing effect of the lubricant, while the lubricant fluidity is significantly affected by temperature. Increasing the initial lubricant volume not only enhances the splashing effect but also improves the lubricant fluidity.
(3) The distribution of the lubricant film on the inner wall of the casing for each model was analyzed. The results suggest that fast rotating gears enhance the thickness and coverage of the lubricant film on the casing inner wall. The higher the lubricant temperature, the more uniform the lubricant film distribution. Increasing the initial lubricant volume has little effect on the distribution characteristics of the lubricant film but significantly increases its thickness. In this two-stage herringbone transmission gearbox, the distribution of the lubricant film on the inner wall of the casing primarily depends on the splashing effect of the output gear on the lubricant.
(4) The quantity of lubricant particles in the meshing zone correlates positively with gear rotating speed and initial lubricant volume. When the lubricant temperature is above 20 °C, the lubricant particles in the meshing zone are negatively correlated with temperature. If the temperature is too low, the quantity of lubricant particles in the meshing zone will also be minimal.
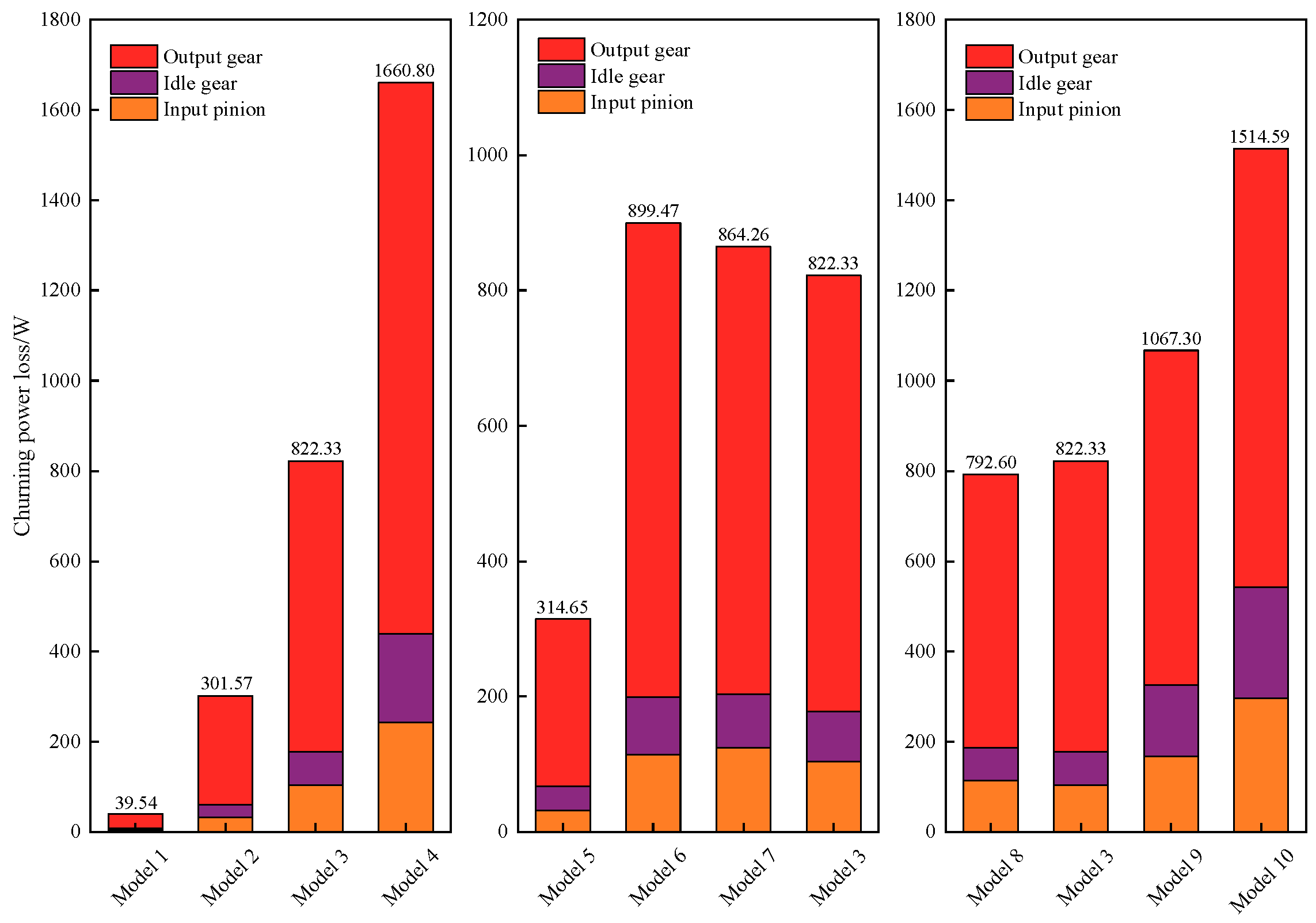
(5) The gear churning torque of each model is extracted, and the churning power loss is analyzed. This analysis reveals that most of the churning power loss primarily comes from the output gear. As the initial lubricant volume and gear rotating speed increase, the churning torque increases, leading to an increase in churning power loss. When the lubricant temperature is above 20 °C, with the increase in temperature, the viscosity decreases, resulting in a reduction in churning torque and churning power loss. However, low-temperature lubricants have high viscosity and poor fluidity, resulting in low churning power loss.
The MPS method provides an intuitive method for visualizing the flow field in high-speed train gearboxes. Reference [
50] employed the Taguchi optimization algorithm and a grey correlation analysis to optimize the parameters of the central gear of a planetary gearbox and evaluated the influence of modulus, tooth width, and material on the safety factor. This is very important to carry out parameter optimization of a high-speed train gearbox transmission system. Next, the State Key Laboratory of Rail Transit Vehicle System at Southwest Jiaotong University, in collaboration with CRRC Qingdao Sifang Co., Ltd., will conduct run-in tests on the high-speed train herringbone gearbox studied in this study. By opening transparent windows or arranging oil collection pipes at reasonable positions in the actual gearbox, the flow field characteristics of the gearbox can be analyzed. Torque sensors will be placed at the shaft ends of the output shaft to measure the resistance torque during gearbox operation. Run-in tests under multiple conditions will be conducted, and the simulation model will be corrected based on the measured data. The relationships between various parameters and churning power loss will be analyzed, and a mathematical model for directly calculating power loss will be derived using a dimensional analysis. In addition, long-term reliability experiments can be conducted to collect and analyze the data on the lubrication performance of gearboxes over time and to study the mechanisms of gear wear and lubricant degradation. This will help to gain a more comprehensive understanding of the performance of gearboxes under actual working conditions.