Advances in DFT-Based Computational Tribology: A Review
Abstract
1. Introduction
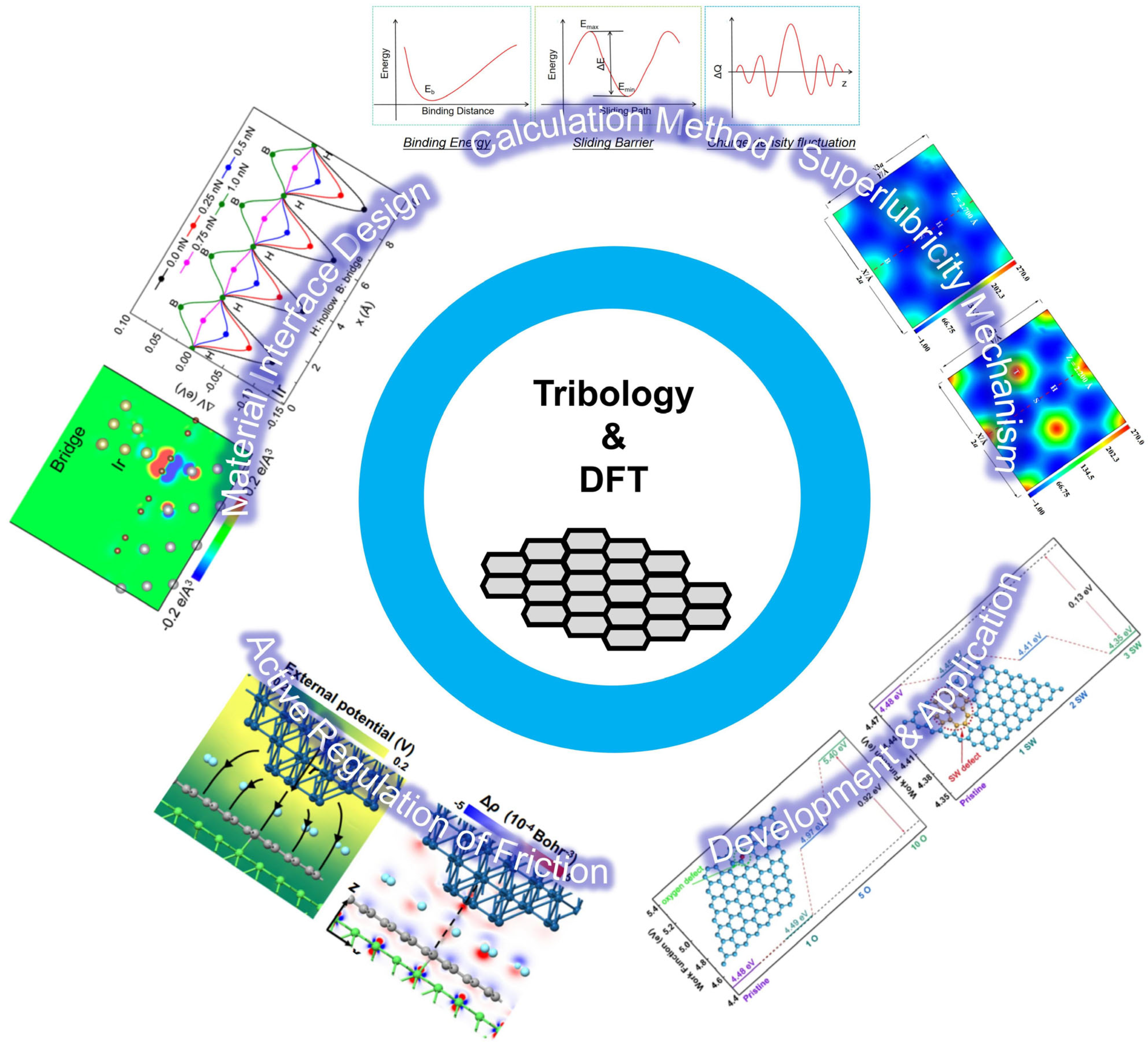
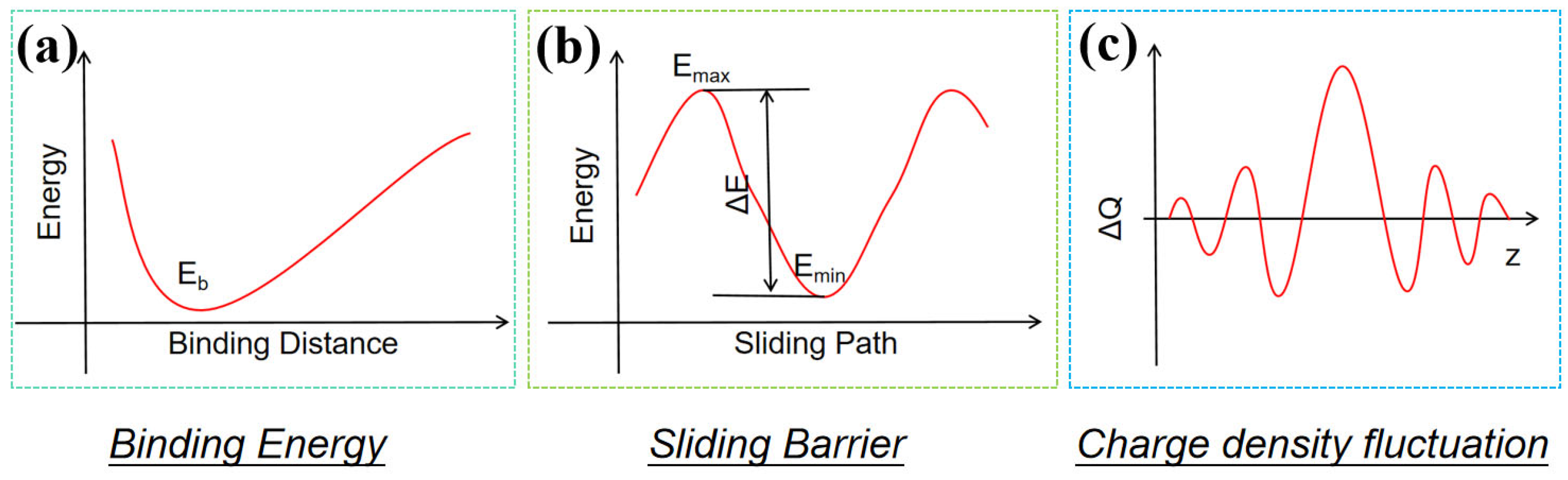
2. DFT-Based Methods for Analyzing Friction
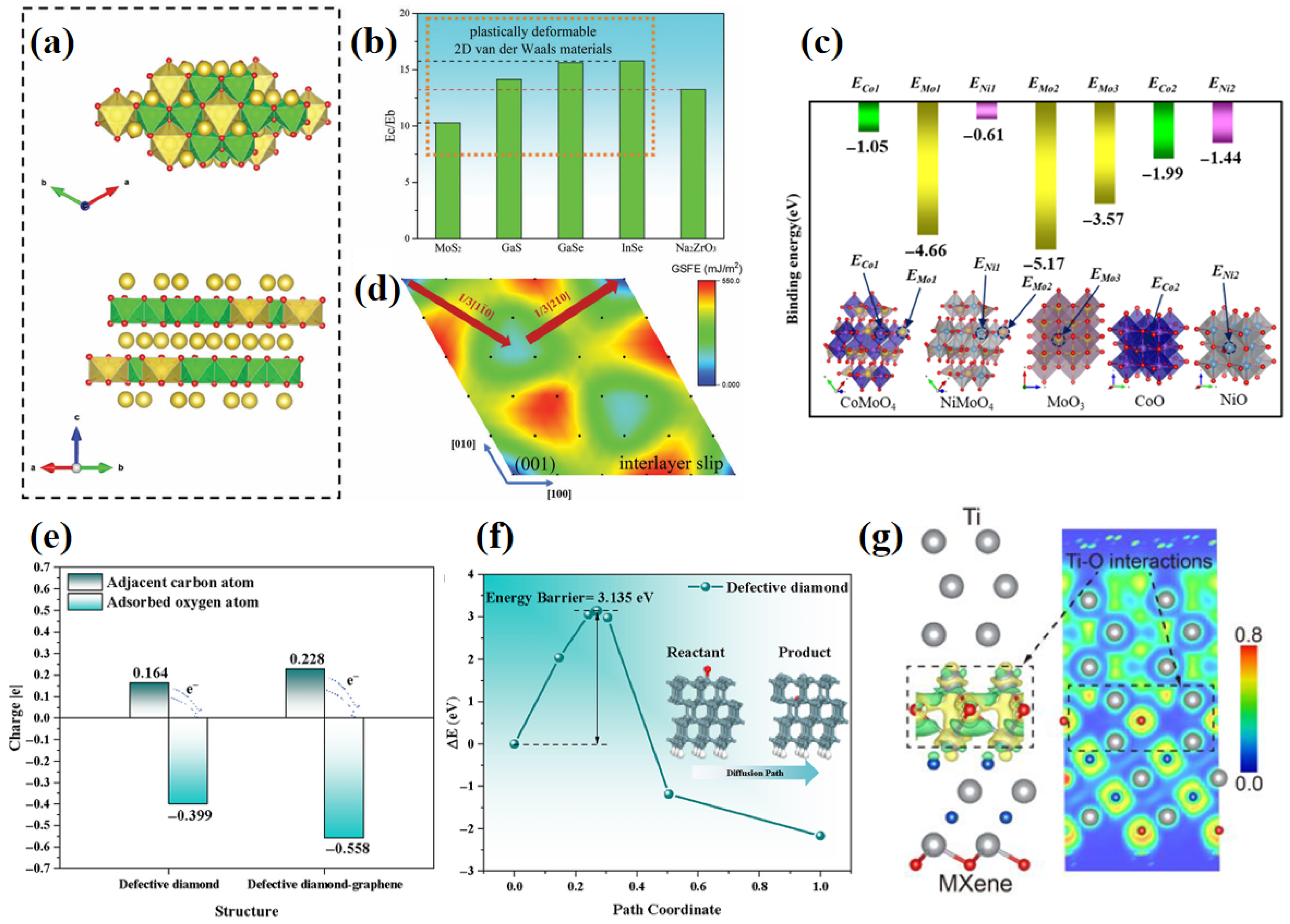
2.1. Binding Energy
2.2. Sliding Energy Barrier
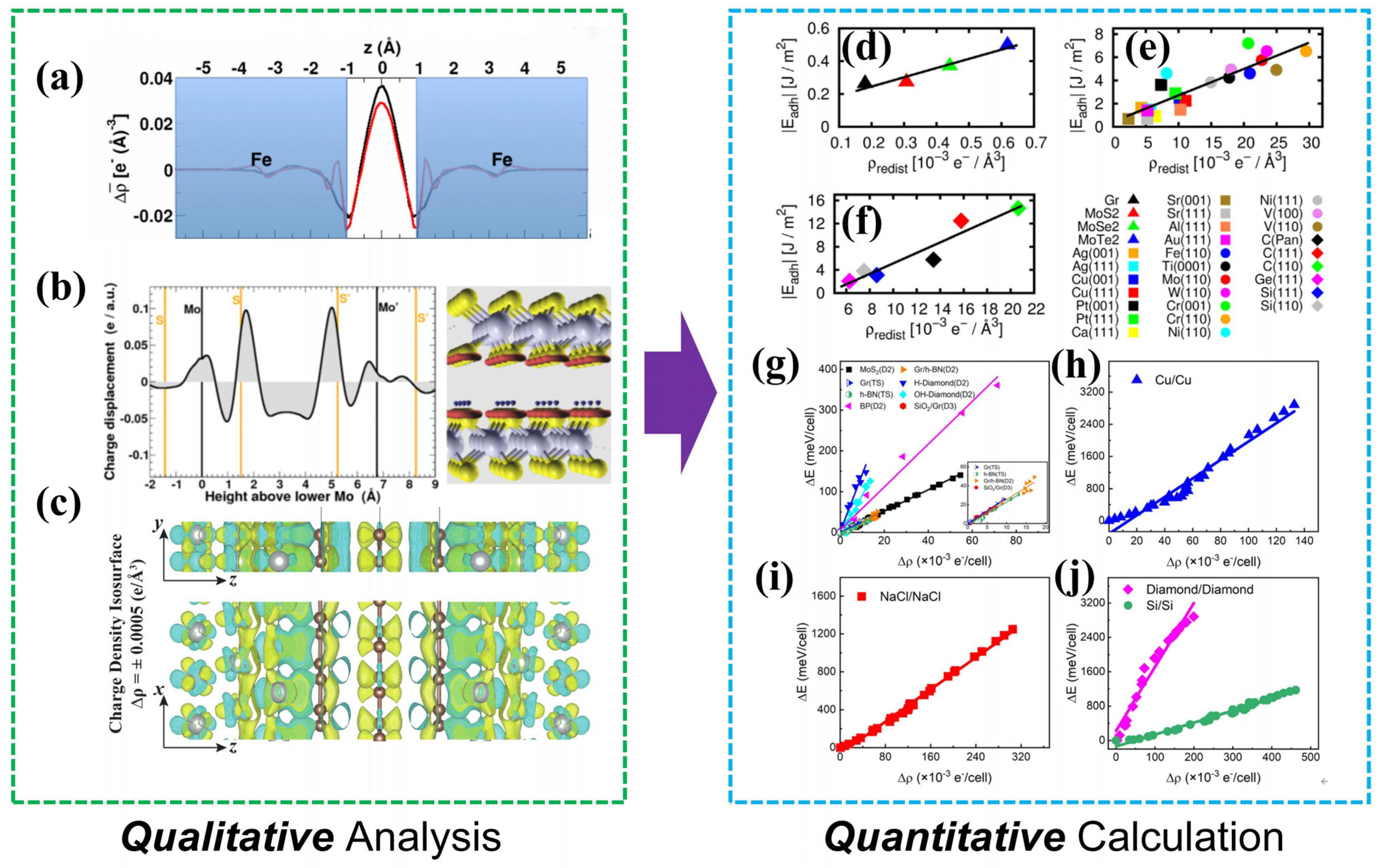
2.3. Charge Density
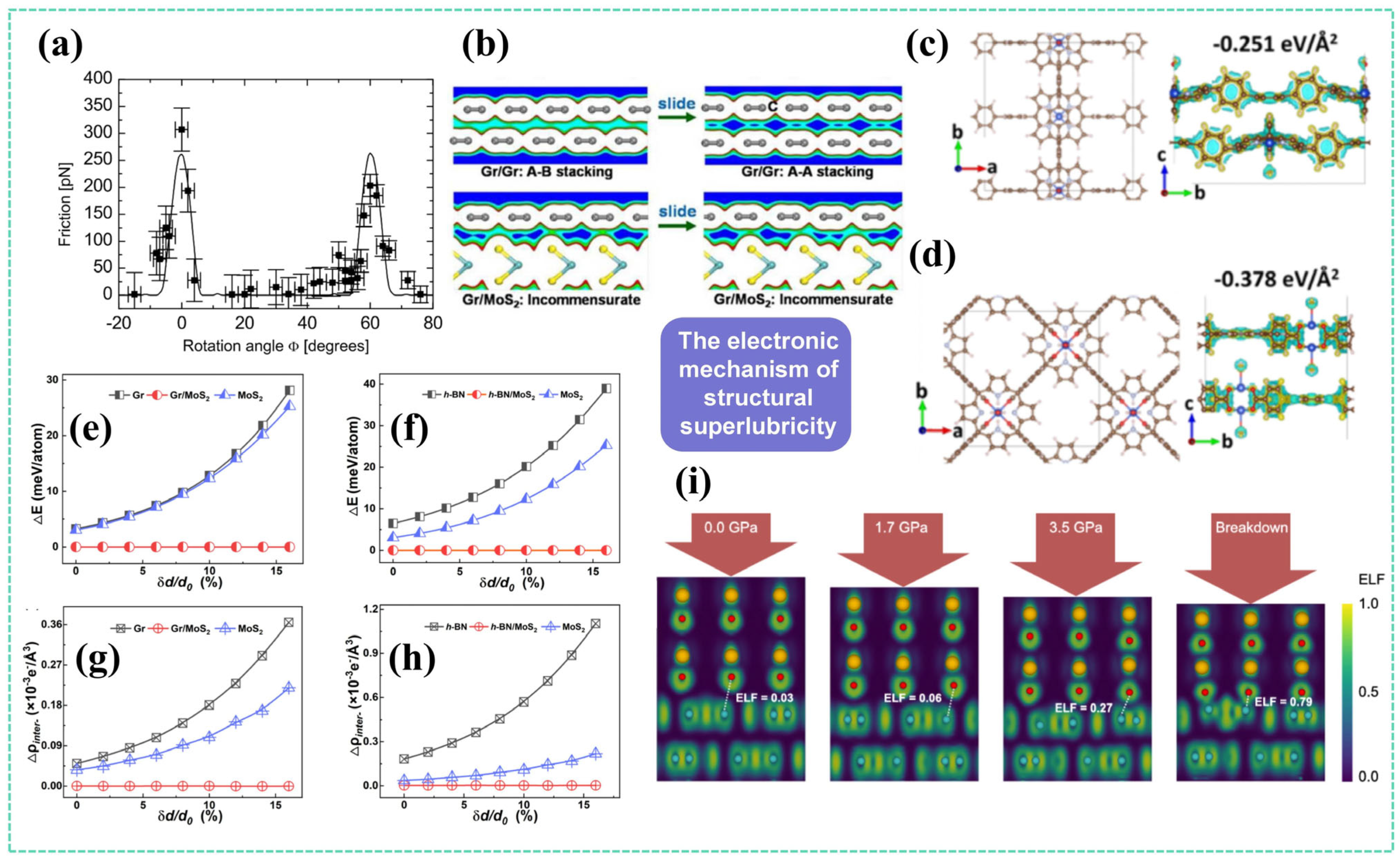
3. Superlubricity
3.1. Structural Superlubricity via Incommensurate Contact
3.2. Strain-Modulated Continuous Sliding
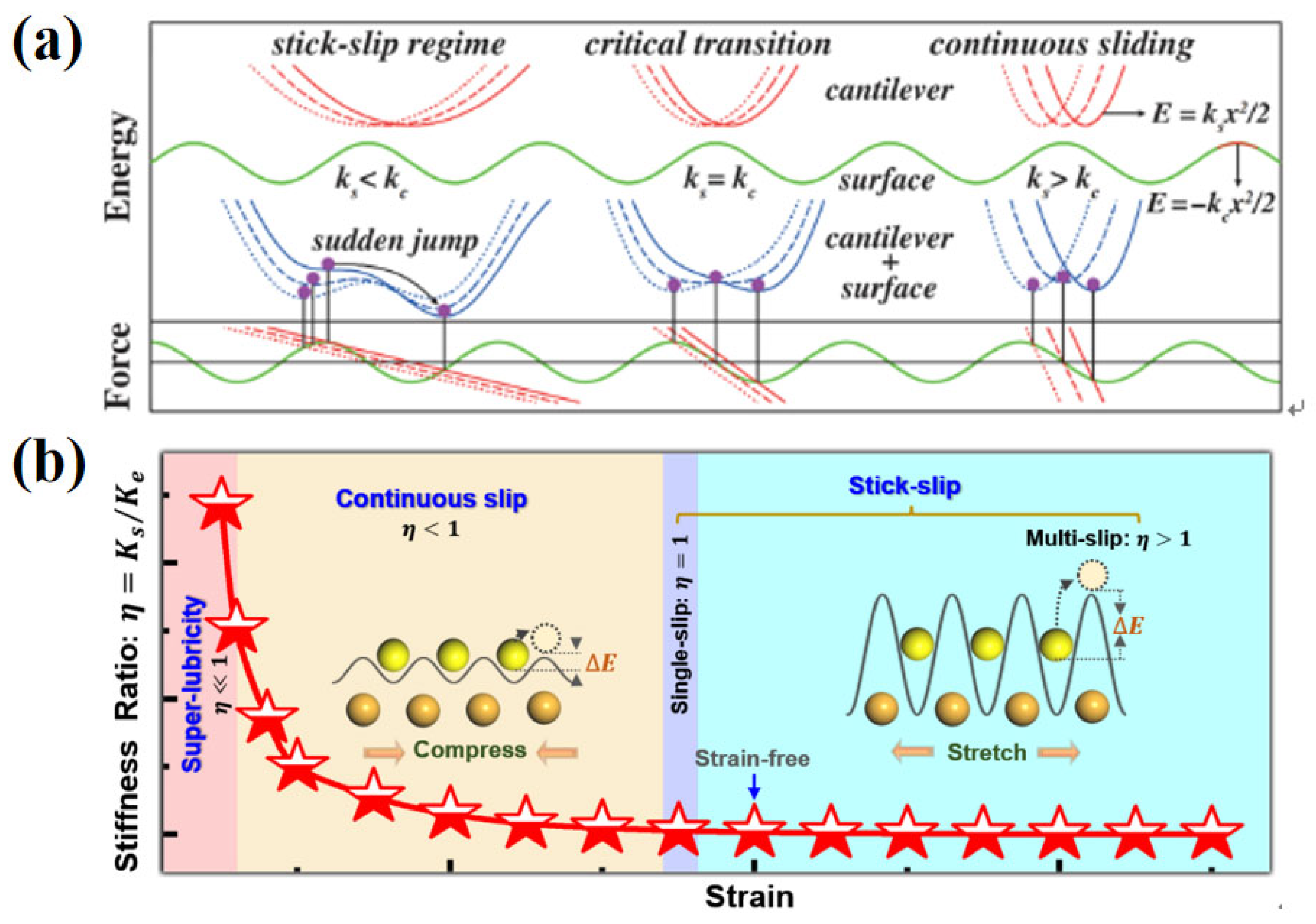
3.3. Critical Pressure Theory for Load-Induced Superlubricity
4. Design of Two-Dimensional Lubrication Interfaces
4.1. Screening of Intrinsic Material Properties
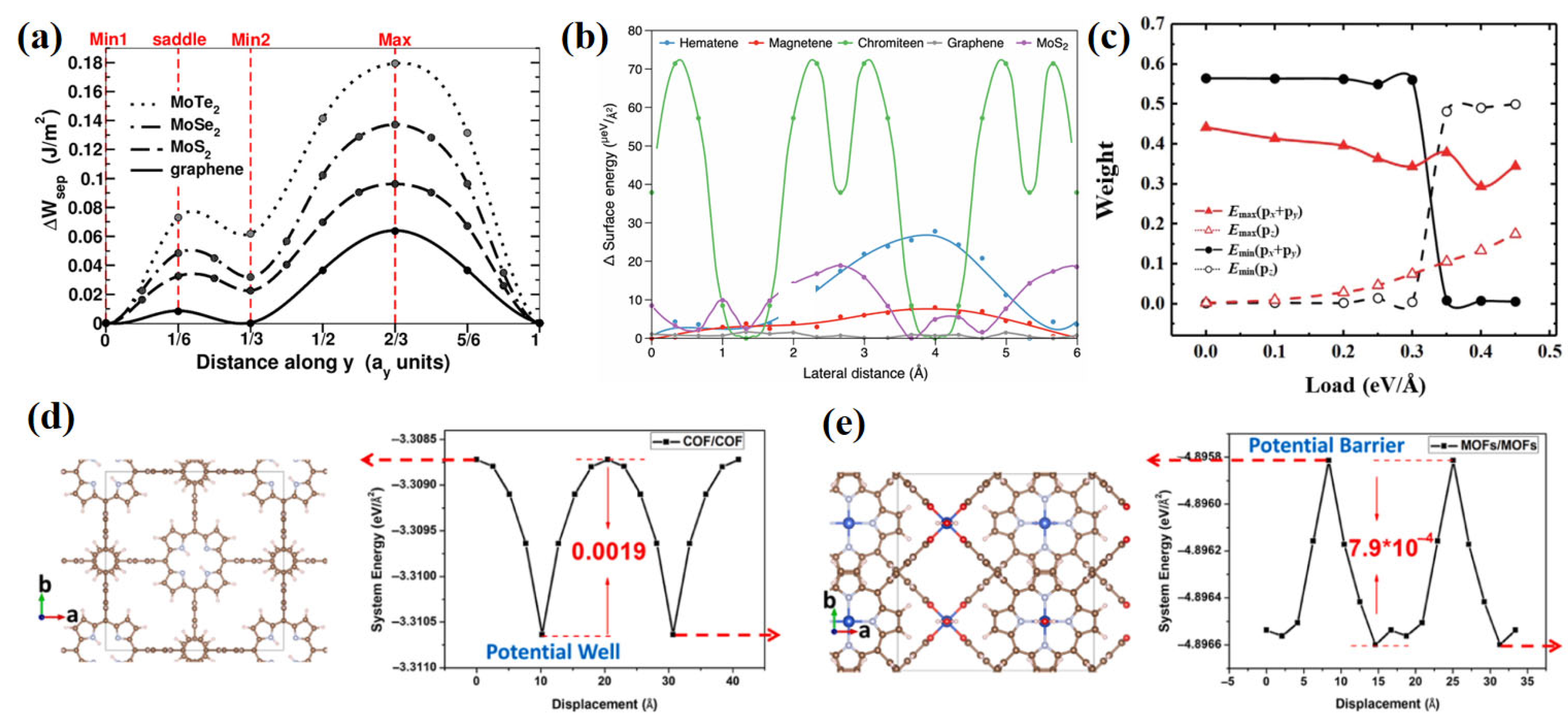
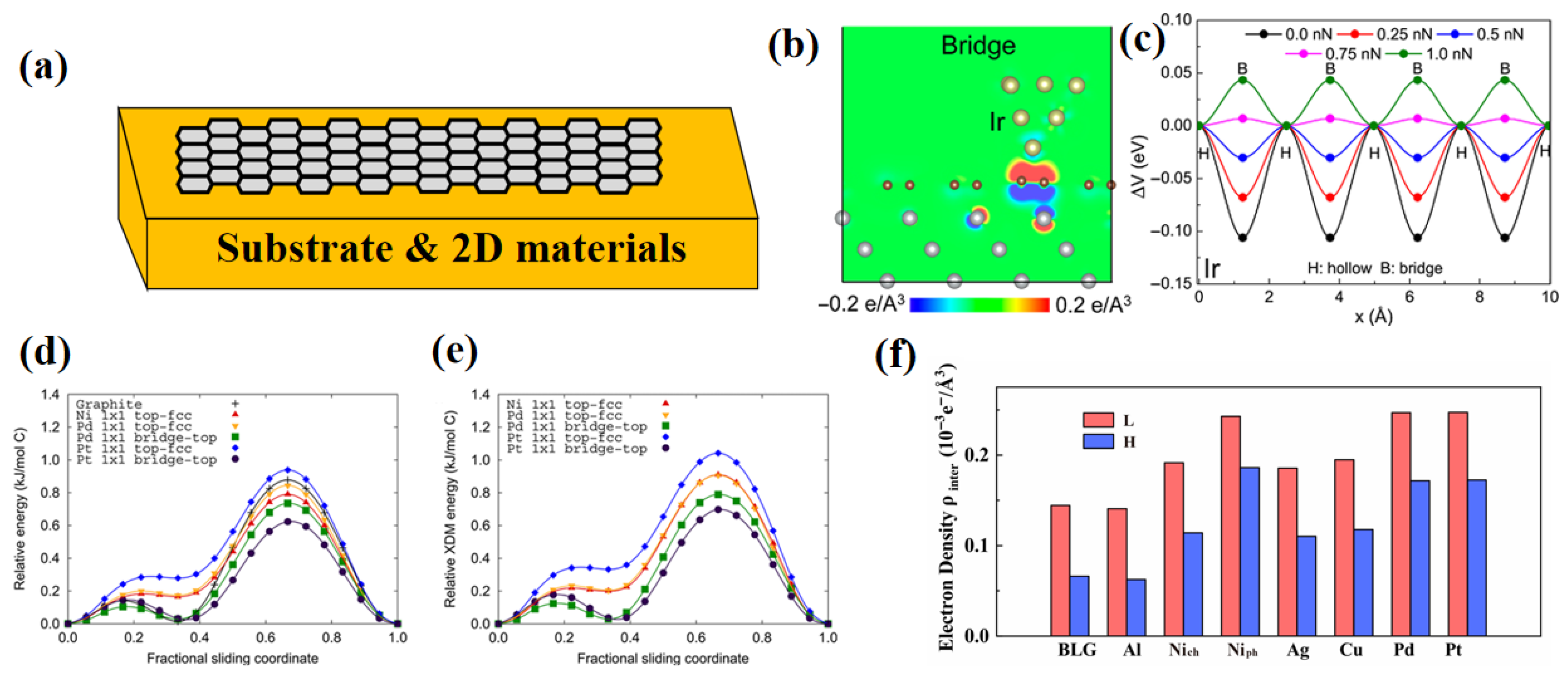
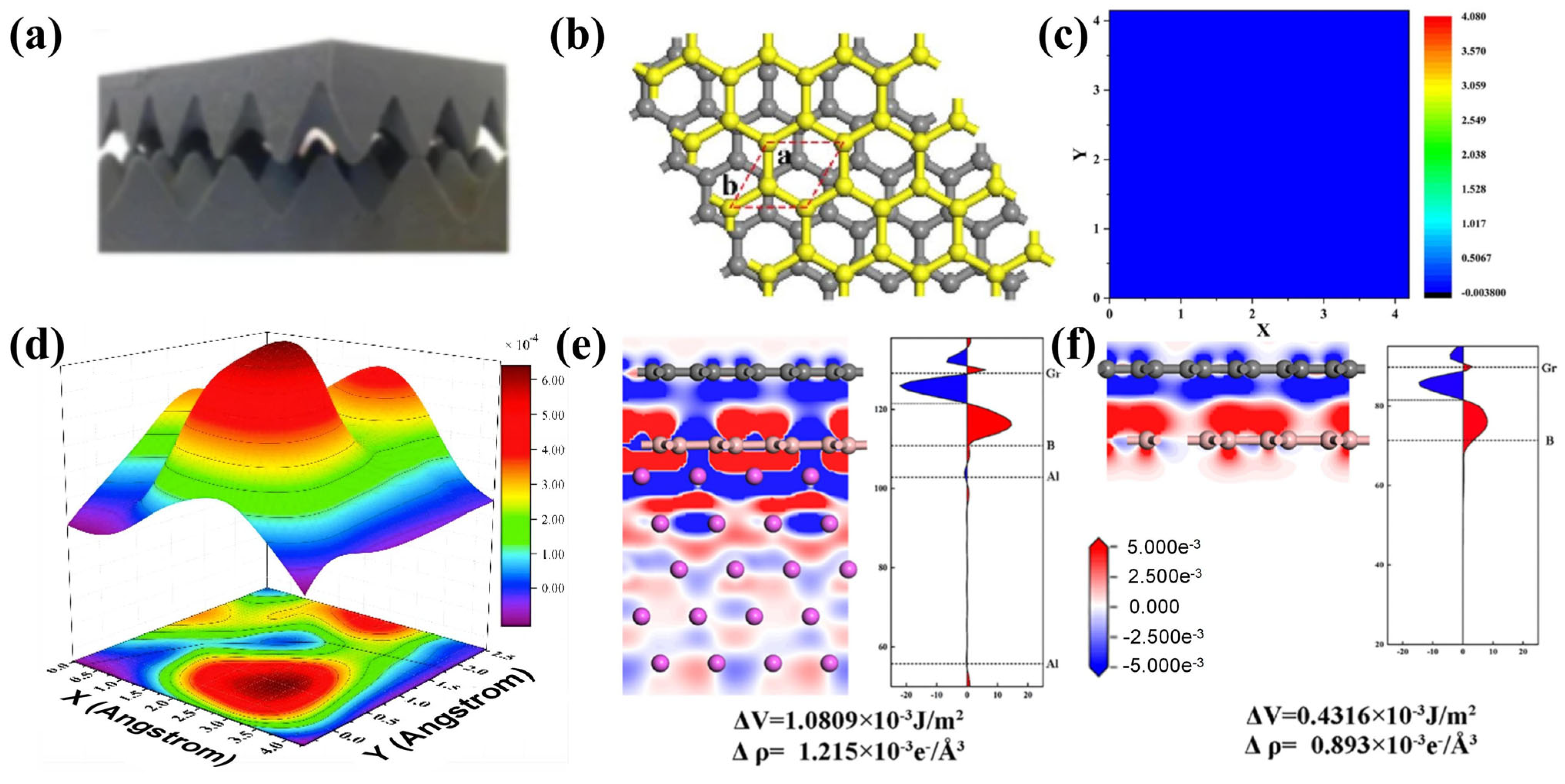
4.2. Metallic Substrate Modulation Mechanisms
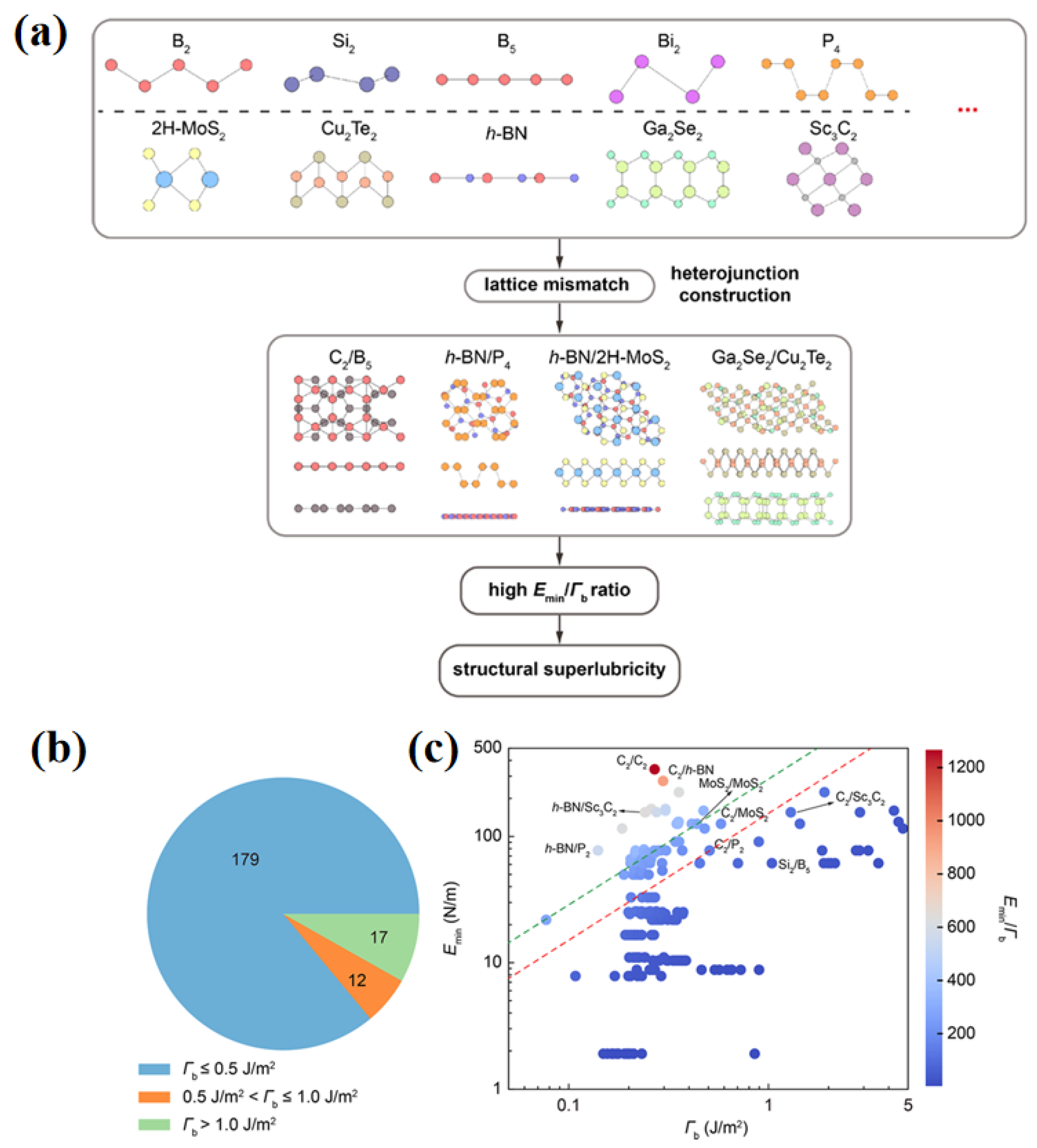
4.3. Heterointerface Design Strategies
5. Active Control of Nanofriction
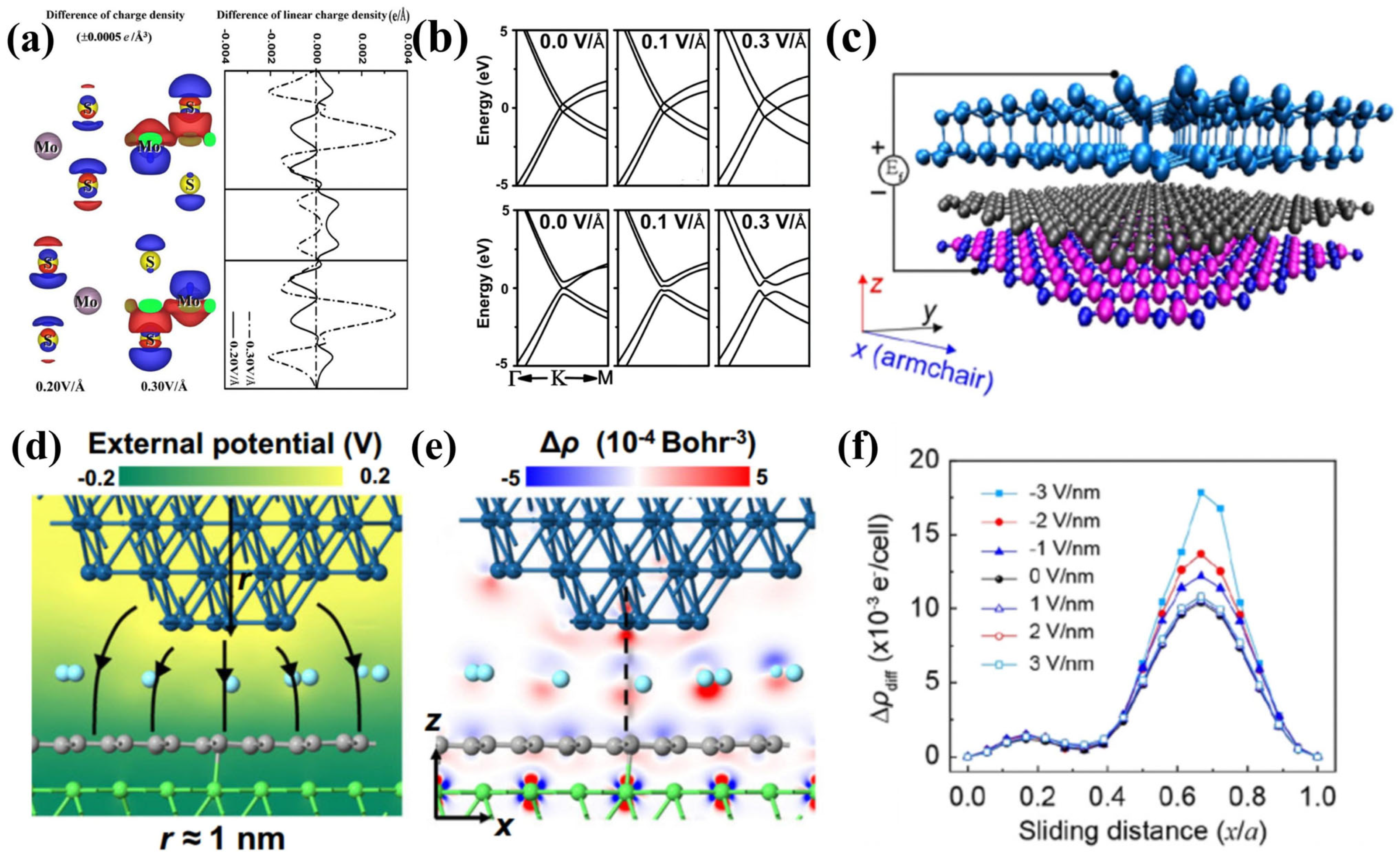
5.1. Electric Field Modulation of Interfacial Charge
5.2. Chemical Terminal Passivation
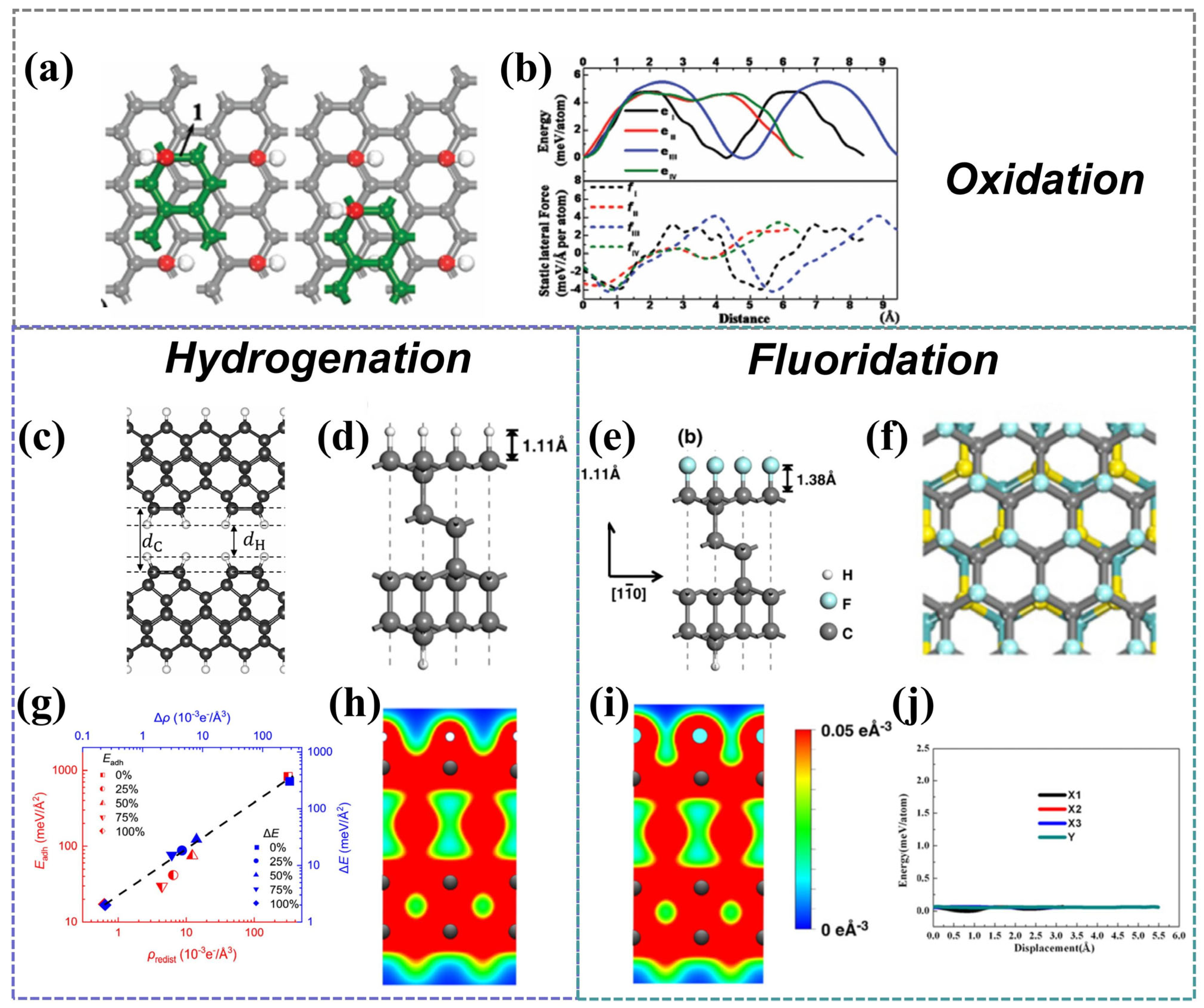
5.3. Doping Design and Defect Engineering

6. Development and Applications of DFT
6.1. DFT + Machine Learning
6.2. Analysis of Friction Coatings
6.3. Mechanisms of Nanoscale Triboelectric Generators

7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pitenis, A.A.; Dowson, D.; Gregory Sawyer, W. Leonardo da Vinci’s friction experiments: An old story acknowledged and repeated. Tribol. Lett. 2014, 56, 509–515. [Google Scholar] [CrossRef]
- Dienwiebel, M.; Verhoeven, G.S.; Pradeep, N.; Frenken, J.W.; Heimberg, J.A.; Zandbergen, H.W. Superlubricity of graphite. Phys. Rev. Lett. 2004, 92, 126101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Ning, Z.; Zhang, Y.; Zheng, Q.; Chen, Q.; Xie, H.; Zhang, Q.; Qian, W.; Wei, F. Superlubricity in centimetres-long double-walled carbon nanotubes under ambient conditions. Nat. Nanotechnol. 2013, 8, 912–916. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Smolyanitsky, A.; Li, Q.; Feng, X.-Q.; Cannara, R.J. Adhesion-dependent negative friction coefficient on chemically modified graphite at the nanoscale. Nat. Mater. 2012, 11, 1032–1037. [Google Scholar] [CrossRef] [PubMed]
- Gnecco, E.; Bennewitz, R.; Gyalog, T.; Loppacher, C.; Bammerlin, M.; Meyer, E.; Güntherodt, H.-J. Velocity dependence of atomic friction. Phys. Rev. Lett. 2000, 84, 1172. [Google Scholar] [CrossRef]
- Liu, B.; Wang, J.; Zhao, S.; Qu, C.; Liu, Y.; Ma, L.; Zhang, Z.; Liu, K.; Zheng, Q.; Ma, M. Negative friction coefficient in microscale graphite/mica layered heterojunctions. Sci. Adv. 2020, 6, eaaz6787. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Lu, Z.; Li, Q.; Xue, Q.; Du, S.; Pu, J.; Wang, L. Superlubricity enabled by pressure-induced friction collapse. J. Phys. Chem. Lett. 2018, 9, 2554–2559. [Google Scholar] [CrossRef]
- Prandtl, L. Ein Gedankenmodell zur kinetischen Theorie der festen Körper. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 1928, 8, 85–106. [Google Scholar] [CrossRef]
- Tomlinson, G.A. CVI. A molecular theory of friction. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1929, 7, 905–939. [Google Scholar] [CrossRef]
- Aubry, S.; Le Daeron, P.-Y. The discrete Frenkel-Kontorova model and its extensions: I. Exact results for the ground-states. Phys. D Nonlinear Phenom. 1983, 8, 381–422. [Google Scholar] [CrossRef]
- Gao, L.; Ma, Y.; Liu, Y.; Song, A.; Ma, T.; Hu, Y.; Su, Y.; Qiao, L. Anomalous frictional behaviors of Ir and Au tips sliding on graphene/Ni (111) substrate: Density functional theory calculations. J. Phys. Chem. C 2017, 121, 21397–21404. [Google Scholar] [CrossRef]
- Song, A.; Zhao, J.-X.; Tang, X.; Wu, H.-J.; Xu, Z.; Cao, J.; Liu, X.; Wang, H.; Li, Q.; Hu, Y.-Z.; et al. Tuning friction force and reducing wear by applying alternating electric current in conductive AFM experiments. Nat. Commun. 2025, 16, 4704. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Zhang, J.; Deng, Y.; Zhao, H.; Zhang, P.; Fu, S.; Xu, X.; Li, H. Defect-mediated work function regulation in graphene film for high-performing triboelectric nanogenerators. Nano Energy 2022, 99, 107411. [Google Scholar] [CrossRef]
- Luo, C.; Jiang, Y.; Liu, Y.; Wang, Y.; Sun, J.; Qian, L.; Chen, L. Role of interfacial bonding in tribochemical wear. Front. Chem. 2022, 10, 852371. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.J.; Hamilton, J. First-principles study of the solubility, diffusion, and clustering of C in Ni. Phys. Rev. B 2003, 68, 094105. [Google Scholar] [CrossRef]
- Baksi, M.; Toffoli, D.; Gulseren, O.; Ustunel, H. Nanotribological properties of the h-BN/Au (111) interface: A DFT study. J. Phys. Chem. C 2019, 123, 28411–28418. [Google Scholar] [CrossRef]
- De Barros Bouchet, M.-I.; Zilibotti, G.; Matta, C.; Righi, M.C.; Vandenbulcke, L.; Vacher, B.; Martin, J.-M. Friction of diamond in the presence of water vapor and hydrogen gas. Coupling gas-phase lubrication and first-principles studies. J. Phys. Chem. C 2012, 116, 6966–6972. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Ma, T.; Liu, D.; Gao, L.; Li, X.; Zhang, J.; Hu, Y.; Wang, H.; Dai, Y.; et al. Superlubricity of a graphene/MoS2 heterostructure: A combined experimental and DFT study. Nanoscale 2017, 9, 10846–10853. [Google Scholar] [CrossRef]
- Zhong, W.; Tománek, D. First-principles theory of atomic-scale friction. Phys. Rev. Lett. 1990, 64, 3054–3057. [Google Scholar] [CrossRef]
- Li, H.; Shi, W.; Guo, Y.; Guo, W. Nonmonotonic interfacial friction with normal force in two-dimensional crystals. Phys. Rev. B 2020, 102, 085427. [Google Scholar] [CrossRef]
- Leven, I.; Krepel, D.; Shemesh, O.; Hod, O. Robust superlubricity in graphene/h-BN heterojunctions. J. Phys. Chem. Lett. 2013, 4, 115–120. [Google Scholar] [CrossRef]
- Dong, Y.; Vadakkepatt, A.; Martini, A. Analytical models for atomic friction. Tribol. Lett. 2011, 44, 367–386. [Google Scholar] [CrossRef]
- Restuccia, P.; Righi, M.C. Tribochemistry of graphene on iron and its possible role in lubrication of steel. Carbon 2016, 106, 118–124. [Google Scholar] [CrossRef]
- Levita, G.; Cavaleiro, A.; Molinari, E.; Polcar, T.; Righi, M.C. Sliding properties of MoS2 layers: Load and interlayer orientation effects. J. Phys. Chem. C 2014, 118, 13809–13816. [Google Scholar] [CrossRef]
- Reguzzoni, M.; Fasolino, A.; Molinari, E.; Righi, M.C. Potential energy surface for graphene on graphene: Ab initioderivation, analytical description, and microscopic interpretation. Phys. Rev. B 2012, 86, 245434. [Google Scholar] [CrossRef]
- Cahangirov, S.; Ciraci, S.; Özçelik, V.O. Superlubricity through graphene multilayers between Ni(111) surfaces. Phys. Rev. B 2013, 87, 205428. [Google Scholar] [CrossRef]
- Wolloch, M.; Levita, G.; Restuccia, P.; Righi, M.C. Interfacial charge density and its connection to adhesion and frictional forces. Phys. Rev. Lett. 2018, 121, 026804. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, X.; Du, S.; Pu, J.; Wang, Y.; Yuan, Y.; Qian, L.; Francisco, J.S. Charge density evolution governing interfacial friction. J. Am. Chem. Soc. 2023, 145, 5536–5544. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, B.; An, X.; Lu, Z.; Zhang, G.; Ma, F.; Zhou, F. First-principles delimitation of the boundary between intralayer and interlayer in two-dimensional structures. J. Phys. Chem. C 2019, 123, 26912–26920. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Z.; Lv, Q.; Dong, X.; Niu, Y.; He, W.; Wang, Y.; Lu, Z. Potential negative friction coefficient predicted by first-principles calculations: A possible consequence of inaccurate computational models. Phys. Rev. B 2025, 111, 054109. [Google Scholar] [CrossRef]
- Cheng, Z.; Sun, J.; Zhang, B.; Lu, Z.; Ma, F.; He, Q.C. Superlubricity enabled by load-driven redistribution of electrons. Adv. Mater. Interfaces 2022, 9, 2101589. [Google Scholar] [CrossRef]
- Cheng, Z.; Feng, H.; Sun, J.; Lu, Z.; He, Q.C. Strain-Driven superlubricity of graphene/graphene in commensurate contact. Adv. Mater. Interfaces 2023, 10, 2202062. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, T.; Erdemir, A.; Li, Q. Tribology of two-dimensional materials: From mechanisms to modulating strategies. Mater. Today 2019, 26, 67–86. [Google Scholar] [CrossRef]
- Vanossi, A.; Bechinger, C.; Urbakh, M. Structural lubricity in soft and hard matter systems. Nat. Commun. 2020, 11, 4657. [Google Scholar] [CrossRef] [PubMed]
- Tabor, D. History of Tribology: D. Dowson; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Israelachvili, J.N. Adhesion, friction and lubrication of molecularly smooth surfaces. In Fundamentals of Friction: Macroscopic and Microscopic Processes; Springer: Dordrecht, The Netherlands, 1992; pp. 351–385. [Google Scholar]
- Hirano, M.; Shinjo, K. Atomistic locking and friction. Phys. Rev. B 1990, 41, 11837. [Google Scholar] [CrossRef]
- Müser, M.H. Structural lubricity: Role of dimension and symmetry. Europhys. Lett. (EPL) 2004, 66, 97–103. [Google Scholar] [CrossRef]
- Müser, M.H. Theoretical studies of superlubricity. In Fundamentals of Friction and Wear on the Nanoscale; Springer: Dordrecht, The Netherlands, 2015; pp. 209–232. [Google Scholar]
- Liu, L.; Li, Y.; Wang, H.; Yang, Z.; Wang, K.; Luo, J.; Liu, Y. The correlation between molecular structure and superlubricity in homojunctions of 2D materials. Mater. Sci. Eng. R Rep. 2024, 161, 100868. [Google Scholar] [CrossRef]
- Cheng, Z.; Feng, H.; Lu, Y.; Lu, Z.; He, Q.-C. Electron-scale origin of structural superlubricity. Tribol. Int. 2025, 202, 110294. [Google Scholar] [CrossRef]
- Sun, T.; Gao, E.; Jia, X.; Bian, J.; Wang, Z.; Ma, M.; Zheng, Q.; Xu, Z. Robust structural superlubricity under gigapascal pressures. Nat. Commun. 2024, 15, 5952. [Google Scholar] [CrossRef]
- Wang, L.; Ma, T.; Hu, Y.; Wang, H. Understanding the atomic-scale friction in graphene: The distinction in behaviors of interlayer interactions during sliding. J. Appl. Phys. 2016, 120, 205302. [Google Scholar] [CrossRef]
- Socoliuc, A.; Bennewitz, R.; Gnecco, E.; Meyer, E. Transition from stick-slip to continuous sliding in atomic friction: Entering a new regime of ultralow friction. Phys. Rev. Lett. 2004, 92, 134301. [Google Scholar] [CrossRef]
- Cahangirov, S.; Ataca, C.; Topsakal, M.; Sahin, H.; Ciraci, S. Frictional figures of merit for single layered nanostructures. Phys. Rev. Lett. 2012, 108, 126103. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Zhang, Y.; Sun, Q.; Jia, Y. Effect of strain on atomic-scale friction in layered MoS2. Tribol. Int. 2014, 77, 211–217. [Google Scholar] [CrossRef]
- Wang, K.; Ouyang, W.; Cao, W.; Ma, M.; Zheng, Q. Robust superlubricity by strain engineering. Nanoscale 2019, 11, 2186–2193. [Google Scholar] [CrossRef]
- Wu, S.; Meng, Z.; Tao, X.; Wang, Z. Superlubricity of molybdenum disulfide subjected to large compressive strains. Friction 2021, 10, 209–216. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, Y.; Li, S.; Liu, L.; Zhang, Z.; Feng, X.Q.; Li, Q. Tuning friction to a superlubric state via in-plane straining. Proc. Natl. Acad. Sci. USA 2019, 117, 6951. [Google Scholar] [CrossRef] [PubMed]
- Androulidakis, C.; Koukaras, E.N.; Paterakis, G.; Trakakis, G.; Galiotis, C. Tunable macroscale structural superlubricity in two-layer graphene via strain engineering. Nat. Commun. 2020, 11, 1595. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Sun, J.; Zhang, B.; Lu, Z.; Ma, F.; Zhang, G.; Xue, Q. Strain effects of vertical separation and horizontal sliding in commensurate two-dimensional homojunctions. J. Phys. Chem. Lett. 2020, 11, 5815–5822. [Google Scholar] [CrossRef]
- Righi, M.C.; Ferrario, M. Pressure induced friction collapse of rare gas boundary layers sliding over metal surfaces. Phys. Rev. Lett. 2007, 99, 176101. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Cheng, Z.; Yang, T.; Lu, Z.; He, Q.-C. Attraction-Induced superlubricity and its detection. Appl. Surf. Sci. 2023, 640, 158423. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Lu, Z.; Xue, Q.; Wang, L. Attraction induced frictionless sliding of rare gas monolayer on metallic surfaces: An efficient strategy for superlubricity. Phys. Chem. Chem. Phys. 2017, 19, 11026–11031. [Google Scholar] [CrossRef]
- Sun, J.; Chang, K.; Mei, D.; Lu, Z.; Pu, J.; Xue, Q.; Huang, Q.; Wang, L.; Du, S. Mutual identification between the pressure-induced superlubricity and the image contrast inversion of carbon nanostructures from AFM technology. J. Phys. Chem. Lett. 2019, 10, 1498–1504. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, C.; Liao, N.; Zhang, M. A DFT analysis on the superlubricity performance of structural superlubricity micro/nano-component on silicon-based surface. Tribol. Int. 2023, 189, 109005. [Google Scholar] [CrossRef]
- Levita, G.; Molinari, E.; Polcar, T.; Righi, M.C. First-principles comparative study on the interlayer adhesion and shear strength of transition-metal dichalcogenides and graphene. Phys. Rev. B 2015, 92, 085434. [Google Scholar] [CrossRef]
- Losi, G.; Restuccia, P.; Righi, M. Superlubricity in phosphorene identified by means of ab initio calculations. 2D Mater. 2020, 7, 025033. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Qiao, Y.; Tan, S.; Feng, S.; Ma, J.; Liu, Y.; Luo, J. 2D metal-organic frameworks with square grid structure: A promising new-generation superlubricating material. Nano Today 2021, 40, 101262. [Google Scholar] [CrossRef]
- Serles, P.; Arif, T.; Puthirath, A.B.; Yadav, S.; Wang, G.; Cui, T.; Balan, A.P.; Yadav, T.P.; Thibeorchews, P.; Chakingal, N. Friction of magnetene, a non–van der Waals 2D material. Sci. Adv. 2021, 7, eabk2041. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, J.; Zhao, X.; Zhu, Y.; Ren, X.; Shi, J.; Guo, Z.; Shan, C.; Liu, H.; Li, S. Negative differential friction coefficients of two-dimensional commensurate contacts dominated by electronic phase transition. Nano Res. 2022, 15, 5758–5766. [Google Scholar] [CrossRef]
- Zhang, L.; Tan, X.; Jiao, J.; Guo, D.; Luo, J. Interlayer friction behavior of molybdenum ditelluride with different structures. Nano Res. 2023, 16, 11375–11382. [Google Scholar] [CrossRef]
- Feng, H.; Cheng, Z.; Lu, Z.; He, Q.-C. Investigating lubrication capacities of novel 2D hexagonal materials by DFT simulations. Tribol. Int. 2025, 204, 110475. [Google Scholar] [CrossRef]
- Dong, S.; Shi, J.; Li, H.; Zhang, R.; Ma, X.; Yang, Y.; Cui, C.; Wang, W.; Li, J. Phytic acid-modified black phosphorus nanosheets achieve ultrahigh load bearing and rapid superlubrication on engineered steel surfaces. Adv. Funct. Mater. 2025, 35, 2500057. [Google Scholar] [CrossRef]
- Liu, L.; Wang, K.; Liu, Y. Interlayer superlubricity of layered Metal-organic frameworks and its heterojunctions enabled by highly oriented crystalline films. Chem. Eng. J. 2022, 450, 138249. [Google Scholar] [CrossRef]
- Munther, M.; Palma, T.; Beheshti, A.; Davami, K. Substrate-regulated nanoscale friction of graphene. Mater. Lett. 2018, 221, 54–56. [Google Scholar] [CrossRef]
- Qi, Y.; Liu, J.; Dong, Y.; Feng, X.-Q.; Li, Q. Impacts of environments on nanoscale wear behavior of graphene: Edge passivation vs. substrate pinning. Carbon 2018, 139, 59–66. [Google Scholar] [CrossRef]
- Zeng, X.; Peng, Y.; Lang, H. A novel approach to decrease friction of graphene. Carbon 2017, 118, 233–240. [Google Scholar] [CrossRef]
- Shi, B.; Gan, X.; Lang, H.; Zou, K.; Wang, L.; Sun, J.; Lu, Y.; Peng, Y. Ultra-low friction and patterning on atomically thin MoS 2 via electronic tight-binding. Nanoscale 2021, 13, 16860–16871. [Google Scholar] [CrossRef]
- Khomyakov, P.; Giovannetti, G.; Rusu, P.; Brocks, G.v.; Van den Brink, J.; Kelly, P.J. First-principles study of the interaction and charge transfer between graphene and metals. Phys. Rev. B—Condens. Matter Mater. Phys. 2009, 79, 195425. [Google Scholar] [CrossRef]
- Christian, M.S.; Johnson, E.R. Effect of a metal substrate on interlayer interactions in bilayer graphene. J. Phys. Chem. C 2018, 122, 8910–8918. [Google Scholar] [CrossRef]
- Feng, H.; Cheng, Z.; Long, D.; Yang, T.; Lu, Z.; He, Q. How Do Substrates Affect the Friction on Graphene at the Nanoscale? Lubricants 2023, 11, 465. [Google Scholar] [CrossRef]
- Hod, O.; Meyer, E.; Zheng, Q.; Urbakh, M. Structural superlubricity and ultralow friction across the length scales. Nature 2018, 563, 485–492. [Google Scholar] [CrossRef]
- Xu, Y.; Cheng, Z.; Zhu, X.; Lu, Z.; Zhang, G. Ultra-low friction of graphene/honeycomb borophene heterojunction. Tribol. Lett. 2021, 69, 44. [Google Scholar] [CrossRef]
- Jiang, X.; Lu, Z.; Zhang, R. The unusual tribological properties of graphene/antimonene heterojunctions: A first-principles investigation. Materials 2021, 14, 1201. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Cheng, Z.; Lu, Z.; He, W.; Zhang, G. A novel ultra-low friction heterostructure: Aluminum substrate-honeycomb borophene/graphene heterojunction. Comput. Mater. Sci. 2022, 205, 111236. [Google Scholar] [CrossRef]
- Sun, K.; Yu, S.; Wang, X.; Yao, L.; Xu, Y. Atomic-scale investigation of the tribological behaviors of black phosphorus/graphene heterostructures. Tribol. Int. 2025, 211, 110881. [Google Scholar] [CrossRef]
- Gao, E.; Wu, B.; Wang, Y.; Jia, X.; Ouyang, W.; Liu, Z. Computational prediction of superlubric layered heterojunctions. ACS Appl. Mater. Interfaces 2021, 13, 33600–33608. [Google Scholar] [CrossRef]
- Zhu, X.; Yuan, Q.; Zhao, Y.-P. Phase transitions of a water overlayer on charged graphene: From electromelting to electrofreezing. Nanoscale 2014, 6, 5432–5437. [Google Scholar] [CrossRef]
- Park, J.Y.; Ogletree, D.; Thiel, P.; Salmeron, M. Electronic control of friction in silicon pn junctions. Science 2006, 313, 186. [Google Scholar] [CrossRef]
- Lang, H.; Peng, Y.; Cao, X.a.; Zou, K. Atomic-scale friction characteristics of graphene under conductive AFM with applied voltages. ACS Appl. Mater. Interfaces 2020, 12, 25503–25511. [Google Scholar] [CrossRef]
- Lang, H.; Peng, Y.; Yu, K. Dynamic electron transfer for reducing nanofriction of graphene at electrified interfaces. Appl. Surf. Sci. 2020, 520, 146327. [Google Scholar] [CrossRef]
- Wang, C.; Chen, W.; Zhang, Y.; Sun, Q.; Jia, Y. Effects of vdW interaction and electric field on friction in MoS2. Tribol. Lett. 2015, 59, 7. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Li, C.; Cai, X.; Zhu, W.; Jia, Y. Tuning the nanofriction between two graphene layers by external electric fields: A density functional theory study. Tribol. Lett. 2016, 61, 4. [Google Scholar] [CrossRef]
- Li, Y.; Wu, B.; Ouyang, W.; Liu, Z.; Wang, W. Experimental decoding and tuning electronic friction of Si nanotip sliding on graphene. Nano Lett. 2024, 24, 1130–1136. [Google Scholar] [CrossRef]
- Wang, L.-F.; Ma, T.-B.; Hu, Y.-Z.; Wang, H. Atomic-scale friction in graphene oxide: An interfacial interaction perspective from first-principles calculations. Phys. Rev. B—Condens. Matter Mater. Phys. 2012, 86, 125436. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Li, J.; Sun, Q.; Yuan, P.; Jia, Y. Comparative study of friction properties for hydrogen-and fluorine-modified diamond surfaces: A first-principles investigation. Surf. Sci. 2013, 608, 74–79. [Google Scholar] [CrossRef]
- Wang, L.-F.; Ma, T.-B.; Hu, Y.-Z.; Wang, H.; Shao, T.-M. Ab initio study of the friction mechanism of fluorographene and graphane. J. Phys. Chem. C 2013, 117, 12520–12525. [Google Scholar] [CrossRef]
- Wang, L.-F.; Ma, T.-B.; Hu, Y.-Z.; Zheng, Q.; Wang, H.; Luo, J. Superlubricity of two-dimensional fluorographene/MoS2 heterostructure: A first-principles study. Nanotechnology 2014, 25, 385701. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Xiao, C.; Sun, J.; Li, J.; Qian, L. Electronic insight into ultralow friction in hydrogenated diamond. Tribol. Int. 2024, 193, 109410. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, G.; Cheng, Z.; Ma, F.; Lu, Z. Atomic-scale friction adjustment enabled by doping-induced modification in graphene nanosheet. Appl. Surf. Sci. 2019, 483, 742–749. [Google Scholar] [CrossRef]
- Wang, J.; Li, M.; Zhang, X.; Cai, X.; Yang, L.; Li, J.; Jia, Y. An atomic scale study of ultralow friction between phosphorus-doped nanocrystalline diamond films. Tribol. Int. 2015, 86, 85–90. [Google Scholar] [CrossRef]
- Du, C.-F.; Xue, Y.; Zeng, Q.; Wang, J.; Zhao, X.; Wang, Z.; Wang, C.; Yu, H.; Liu, W. Mo-doped Cr-Ti-Mo ternary o-MAX with ultra-low wear at elevated temperatures. J. Eur. Ceram. Soc. 2022, 42, 7403–7413. [Google Scholar] [CrossRef]
- Minkin, A.S.; Lebedeva, I.V.; Popov, A.M.; Knizhnik, A.A. Atomic-scale defects restricting structural superlubricity: Ab initio study on the example of the twisted graphene bilayer. Phys. Rev. B 2021, 104, 075444. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, Y.; He, M.; He, W.; Zhao, Z.; Lu, Z. Calculation and prediction of sliding energy barriers by first-principles combined with machine learning. Ceram. Int. 2023, 49, 24752–24761. [Google Scholar] [CrossRef]
- Li, H.; Guo, W.; Guo, Y. Impart of heterogeneous charge polarization and distribution on friction at water-graphene interfaces: A density-functional-theory based machine learning study. J. Phys. Chem. Lett. 2024, 15, 6585–6591. [Google Scholar] [CrossRef] [PubMed]
- Barik, R.K.; Woods, L.M. Frictional Properties of Two-Dimensional Materials: Data-Driven Machine Learning Predictive Modeling. ACS Appl. Mater. Interfaces 2024, 16, 40149–40159. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Zhang, Y.; Wang, P.; Zhao, Y.-M.; Zhou, J.; Yang, J.; Wang, X.; Shen, L. Machine learning assisted identification of homobilayer sliding ferroelectrics with large out-of-plane polarization and low sliding energy barriers. Phys. Rev. B 2025, 111, 094106. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, Y.; Cao, Y.; Liu, B.; Huang, Q.; Liu, Y. Superior self-lubricating coatings with heterogeneous nanocomposite structures on Ti–Nb–Zr–Ta–Hf refractory multi-principal element alloy. Adv. Funct. Mater. 2024, 34, 2405657. [Google Scholar] [CrossRef]
- Geng, Y.; Chen, H.; Luo, S.; Teng, Y.; He, Q.; Zhang, L.; Zhang, Z.; Yang, Z.; Shi, Y.; Wang, Q. In-Situ formed Titanium-MXene nanomembrane as ultrathin van-der-Waals lubricant. Mater. Today 2025, 88, 328–337. [Google Scholar] [CrossRef]
- Guo, D.; Jia, J.; Zhang, Z.; Yang, J.; Wang, J.; Jiao, X.; Shi, Y.; Cai, L.; He, N. High-temperature tribological characteristics and lubrication mechanisms of NiCrAlY-MoO3/CoO composite coatings: An experimental and DFT computation study. Surf. Coat. Technol. 2025, 496, 131701. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, H.; Xu, L.; Ji, L.; Wang, D.; Zheng, Y.; Feng, Y.; Sui, X.; Guo, Y.; Guo, W. Macro-superlubric triboelectric nanogenerator based on tribovoltaic effect. Matter 2022, 5, 1532–1546. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Vu, D.L.; Le, C.D.; Choi, W.M.; Ahn, K.-K. Tribo-hygro-electric generator: Harnessing mechanical energy with liquid-infused porous cellulose for multiple sensing and DC power generation. Nano Energy 2024, 132, 110353. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Van Tam, T.; Vu, D.L.; Ahn, J.H.; Choi, W.M.; Ahn, K.K. Ultrahigh current density DC triboelectric generator for energy harvesting and self-powered sensing. Nano Energy 2025, 143, 111291. [Google Scholar] [CrossRef]
- Hölscher, H.; Ebeling, D.; Schwarz, U.D. Friction at atomic-scale surface steps: Experiment and theory. Phys. Rev. Lett. 2008, 101, 246105. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, M.; Jin, L.; Li, L.; Mo, Y.; Su, G.; Li, X.; Zhu, H.; Tian, Y. Recent advances in friction and lubrication of graphene and other 2D materials: Mechanisms and applications. Friction 2019, 7, 199–216. [Google Scholar] [CrossRef]
- He, J.; Tang, H.; Wang, C. Advances of molecular dynamics simulation in tribochemistry and lubrication investigations: A review. J. Ind. Eng. Chem. 2023, 126, 1–19. [Google Scholar] [CrossRef]
- Tran, N.V.; Tieu, A.K.; Zhu, H. First-principles molecular dynamics study on the surface chemistry and nanotribological properties of MgAl layered double hydroxides. Nanoscale 2021, 13, 5014–5025. [Google Scholar] [CrossRef] [PubMed]
- Leriche, C.; Pedretti, E.; Kang, D.; Righi, M.C.; Weber, B. Passivation species suppress atom-by-atom wear of micro-crystalline diamond. Available at SSRN 5181990. [CrossRef]
- Restuccia, P.; Ferrario, M.; Righi, M. Monitoring water and oxygen splitting at graphene edges and folds: Insights into the lubricity of graphitic materials. Carbon 2020, 156, 93–103. [Google Scholar] [CrossRef]
- Peeters, S.; Charrin, C.; Duron, I.; Loehlé, S.; Thiebaut, B.; Righi, M. Importance of the catalytic effect of the substrate in the functionality of lubricant additives: The case of molybdenum dithiocarbamates. Mater. Today Chem. 2021, 21, 100487. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, H.; Cheng, Z.; Lu, Z.; He, Q. Advances in DFT-Based Computational Tribology: A Review. Lubricants 2025, 13, 483. https://doi.org/10.3390/lubricants13110483
Feng H, Cheng Z, Lu Z, He Q. Advances in DFT-Based Computational Tribology: A Review. Lubricants. 2025; 13(11):483. https://doi.org/10.3390/lubricants13110483
Chicago/Turabian StyleFeng, Haochen, Ziwen Cheng, Zhibin Lu, and Qichang He. 2025. "Advances in DFT-Based Computational Tribology: A Review" Lubricants 13, no. 11: 483. https://doi.org/10.3390/lubricants13110483
APA StyleFeng, H., Cheng, Z., Lu, Z., & He, Q. (2025). Advances in DFT-Based Computational Tribology: A Review. Lubricants, 13(11), 483. https://doi.org/10.3390/lubricants13110483



