Scuffing Calculation of Cylindrical Gears Facing Loss of Lubrication
Abstract
1. Introduction
2. Loss of Lubrication and Scuffing Safety Calculation
3. Scuffing Safety Calculation
3.1. Load-Dependent Gear Power Loss
3.2. Heat Transfer Coefficient and Bulk Temperature
3.3. Surface and Material Properties
3.4. Suggested Calculation Method
3.5. Validation
| Gear Geometry | Surface and Material Variant | ϑOil | Oil | Lubricant Factor XL | Scuffing Load Stage SLS | Oil Share Progression During LOL bOil|Ref | Gradient of Scuffing Temperature CS|Ref |
|---|---|---|---|---|---|---|---|
| Type Cmod,LOL | REF (ground) | 90 °C | AeroShell 500 | 0.8 | 7 ([6]) | −0.01 | 18 K/µs |
4. Results of Calculation Study
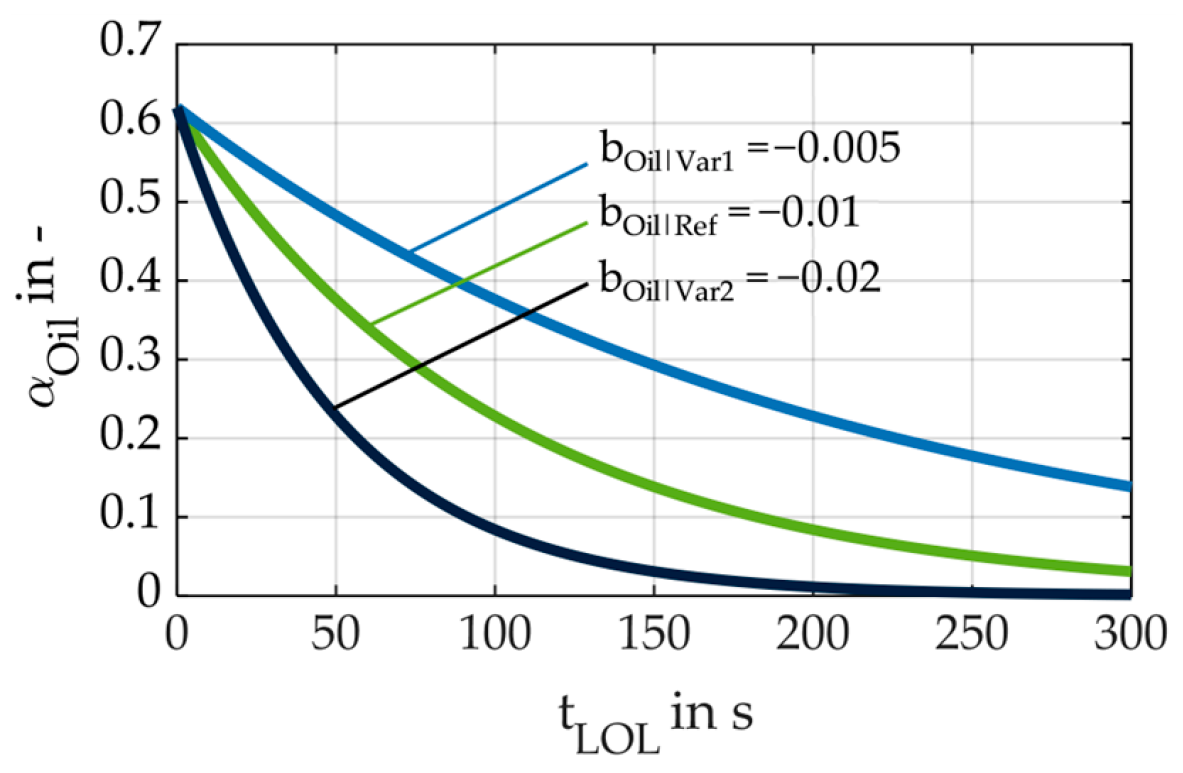
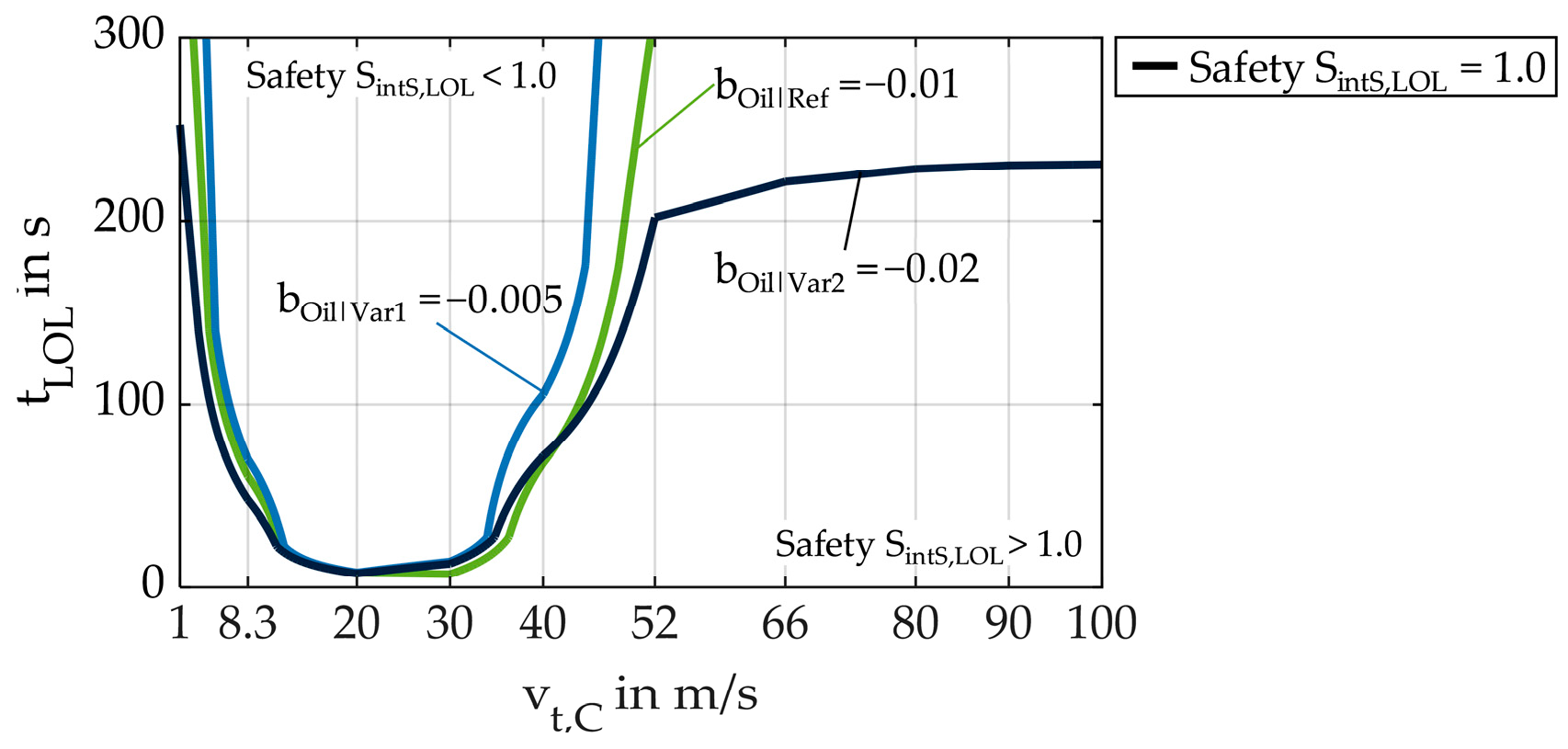
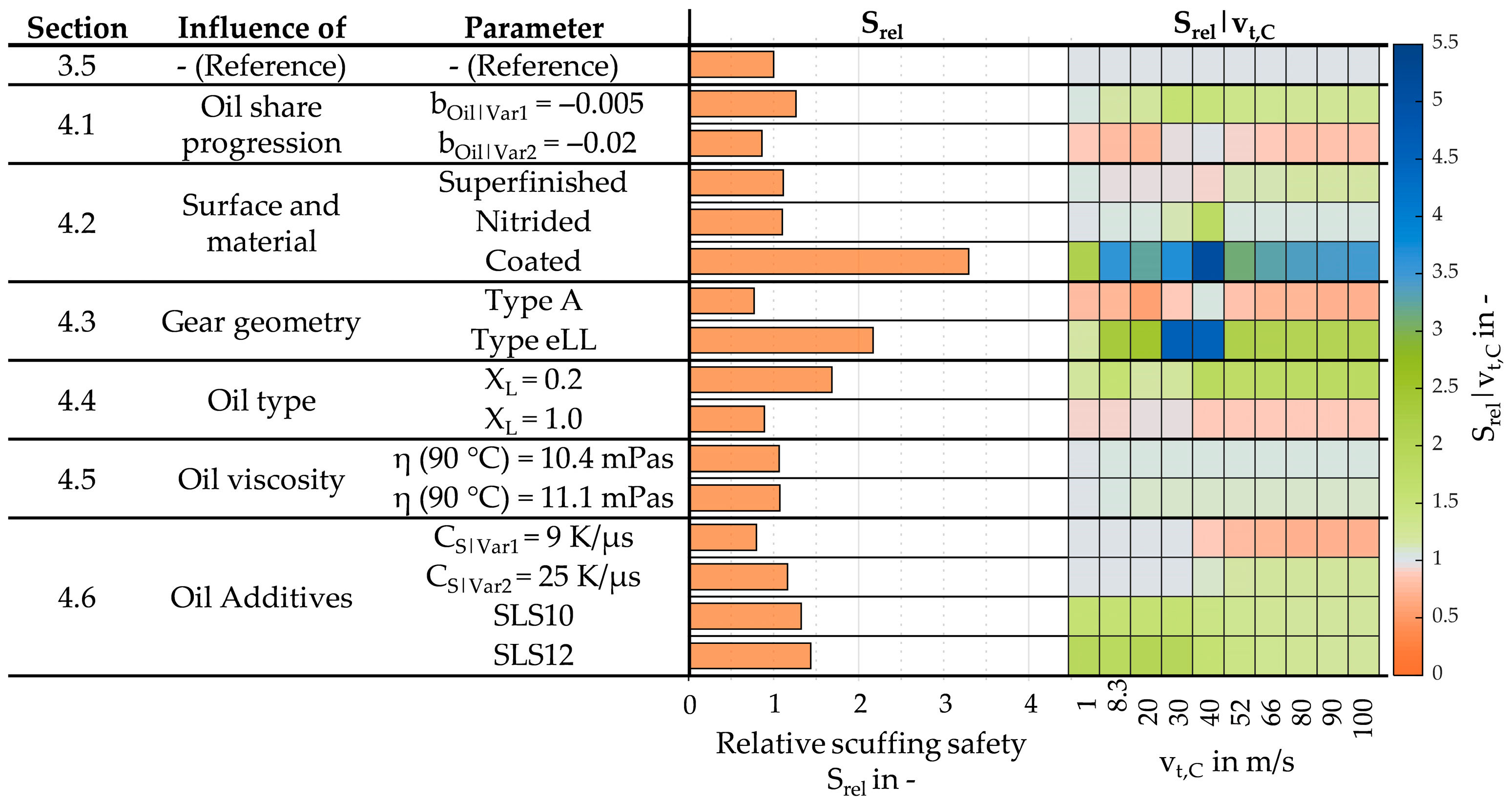
4.1. Influence of Oil Share Progression During LOL
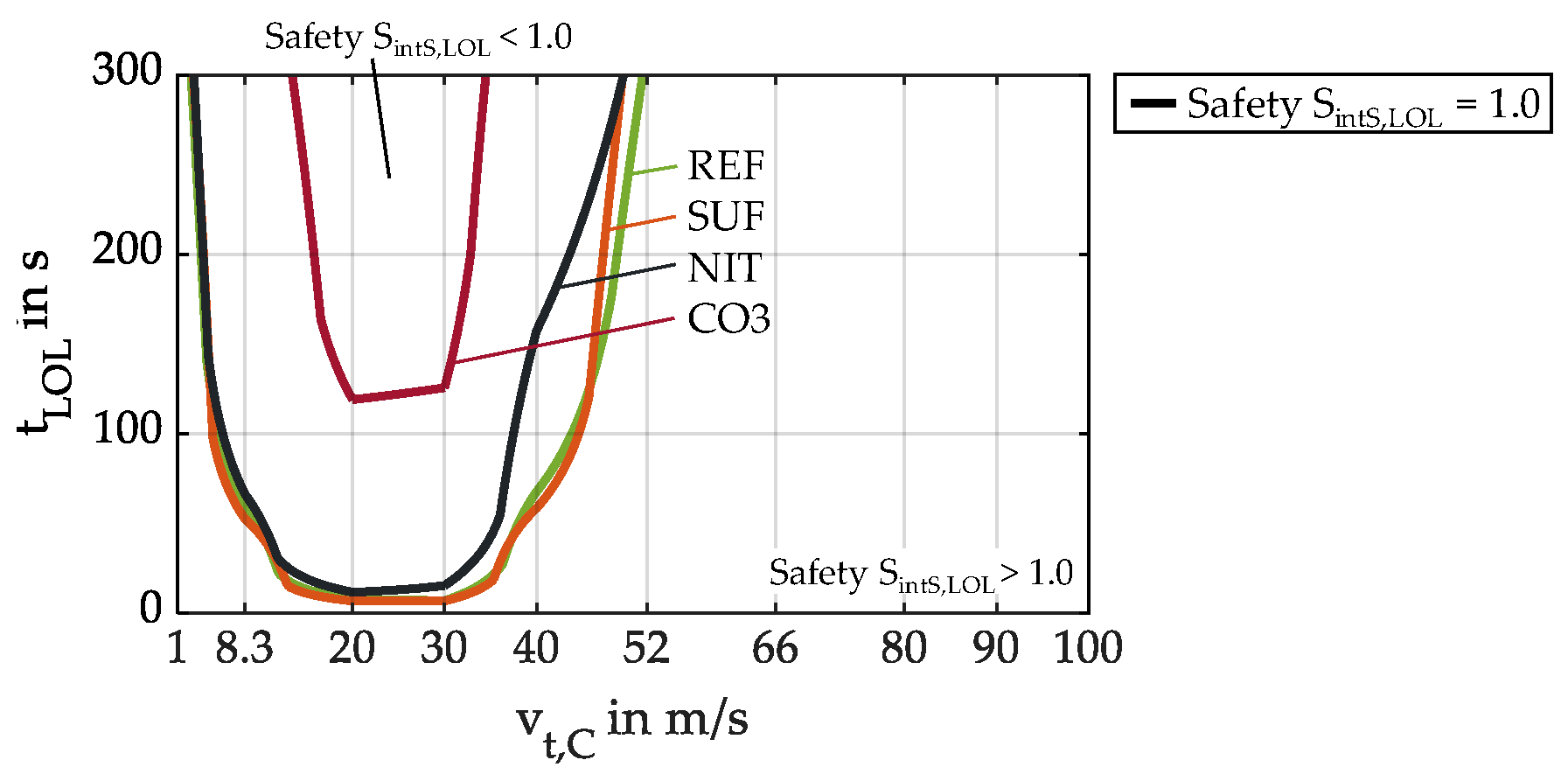
4.2. Influence of Gear Surface and Material
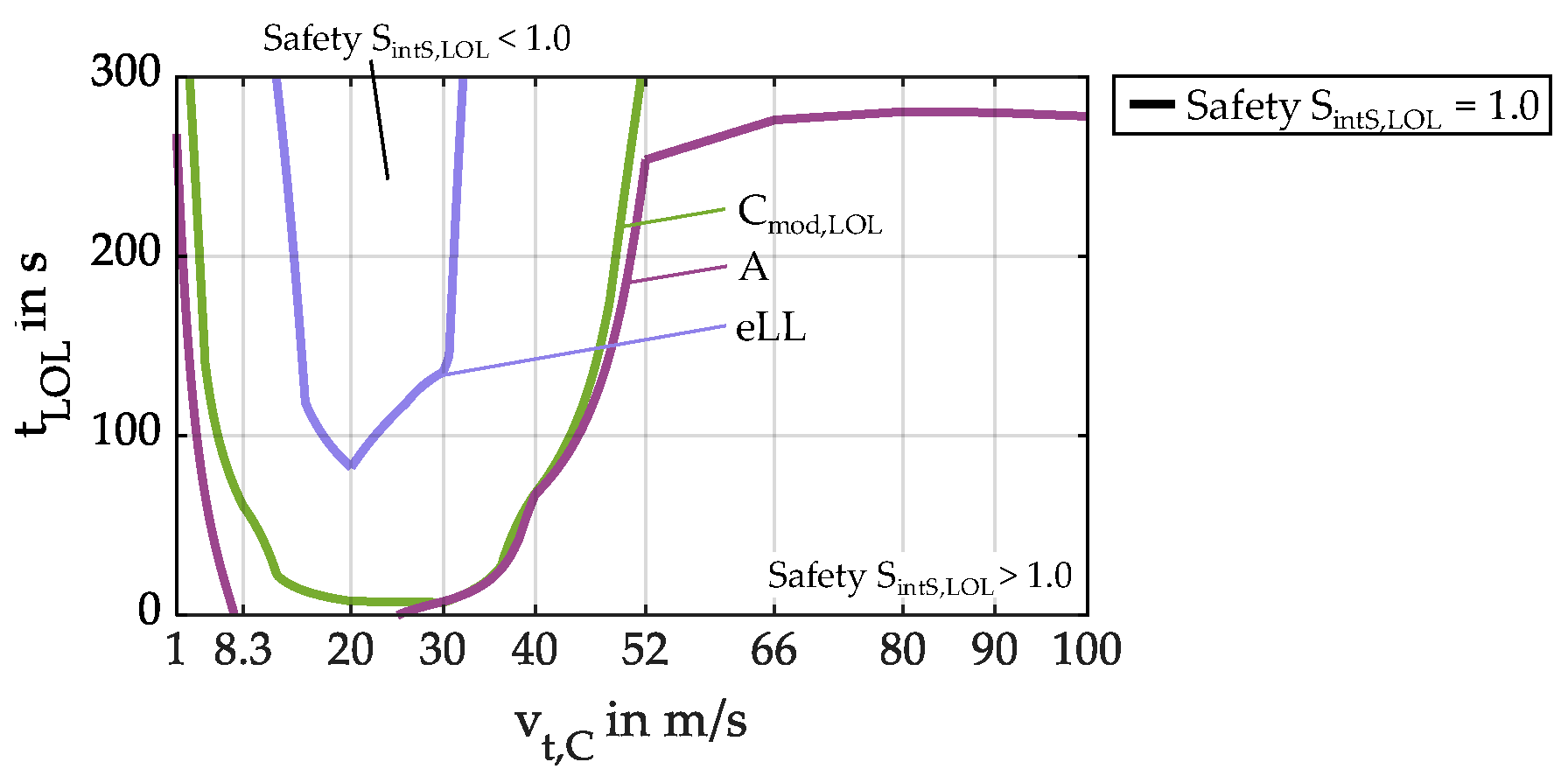
4.3. Influence of Gear Geometry
4.4. Influence of Oil Type
4.5. Influence of Oil Viscosity
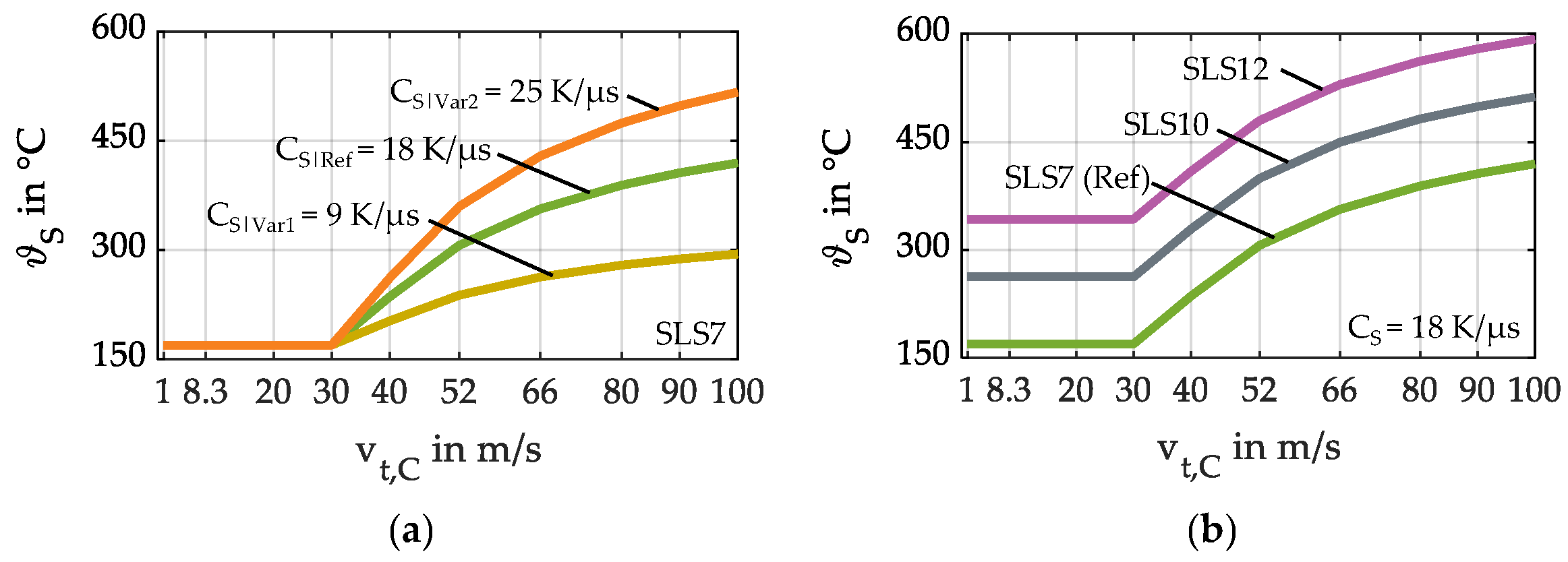
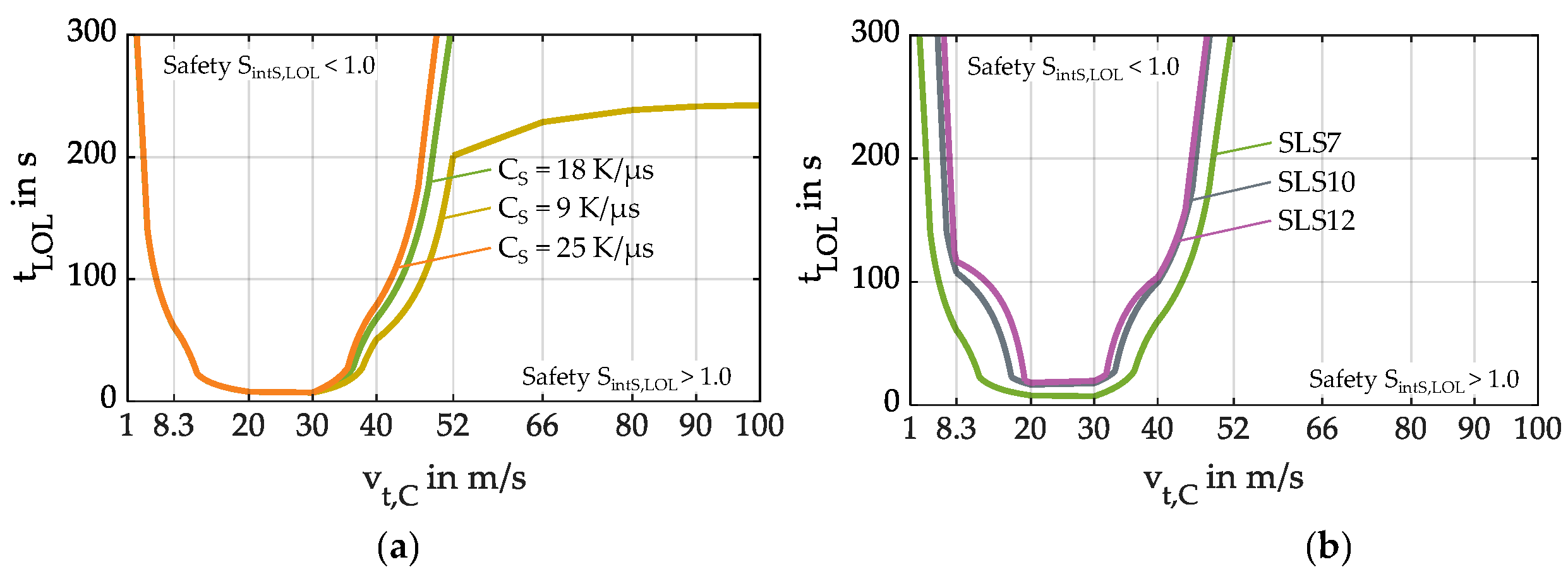
4.6. Influence of Oil Additives
5. Discussion
5.1. Classification of Influencing Factors on LOL Performance
5.2. Reflection
6. Conclusions
- The oil share during loss of lubrication should be kept at the highest possible level by taking constructive measures, as this increases the heat transfer and reduces bulk temperatures.
- DLC coatings offer the greatest potential for avoiding scuffing during loss of lubrication. However, the coating’s durability under design conditions must be ensured.
- A low-loss gear geometry is a promising solution for significantly improving the loss of lubrication performance, as sliding speeds are considerably reduced and scuffing safety is increased.
- The oil type can significantly influence the loss of lubrication performance when low friction is enabled. The viscosity itself has a subordinate influence.
- Oil additives can significantly increase loss of lubrication performance due to increased scuffing temperatures.
- A speed range of approx. 8 < vt,C < 40 m/s should be avoided, as the measures presented were unable to prevent a rapid decrease in scuffing safety within this speed range.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Center distance | mm |
| aMat | Material factor for loss of lubrication | - |
| aMat,REF | Material factor for loss of lubrication for case-hardened ground gears | - |
| aMat,SUF | Material factor for loss of lubrication for superfinished gears | - |
| aMat,CO3 | Material factor for loss of lubrication for coated gears | - |
| aMat,NIT | Material factor for loss of lubrication for nitrided gears | - |
| ap | Load factor for loss of lubrication | - |
| av | Speed factor for loss of lubrication | - |
| A | Starting point of meshing | - |
| b | Face width | mm |
| bOil | Factor for oil share decrease during LOL | - |
| B | Starting point of single tooth contact on driving gear | - |
| C | Pitch point | - |
| Ca | Tip relief | μm |
| CS | Gradient of the scuffing temperature | K/µs |
| C2 | Weighting factor | - |
| da1/2 | Tip diameter pinion/wheel | mm |
| db1/2 | Base diameter pinion/wheel | mm |
| dw1/2 | Pitch diameter pinion/wheel | mm |
| D | End point of single tooth contact point on driving gear | - |
| E | End point of meshing | - |
| Fbt | Tangential force at the base circle | N |
| FPi | Active surface of pinion | mm2 |
| FW | The tooth flank surface determining the heat transfer | mm2 |
| FWe | Active surface of wheel | mm2 |
| hc | Heat transfer coefficient | kcal/(mm2 s grd) |
| hmix | Heat transfer coefficient of oil air mixture | W/(m2 K) |
| hmix,LOL | Heat transfer coefficient of oil air mixture during LOL | W/(m2 K) |
| HV(L) | (Local) geometric tooth power loss factor | - |
| i | Transmission ratio | - |
| KBγ | Helical load factor | - |
| mn | Normal module | mm |
| pC | Hertzian pressure at the pitch point C | N/mm2 |
| pHm | Mean Hertzian pressure | kp/mm2 |
| Pin | Input power | W |
| PLGP | Load-dependent gear power loss | W (kcal/s for approach of Seitzinger [31]) |
| Pr | Prantl number | - |
| Q | Amount of lubricant (Volume flow rate) | L/min |
| q | Factor for heat transfer to the lubricant at the tooth flank surface and the face side | - |
| rC | Radius of pitch point C (wheel) | m |
| Ra | Arithmetic mean flank roughness | µm |
| Re | Reynolds number | - |
| SB | Scuffing safety factor (ISO/TS 6336-20) | - |
| SB,LOL | Scuffing safety factor for loss of lubrication based on ISO/TS 6336-20 | - |
| SintS | Scuffing safety factor (ISO/TS 6336-21) | - |
| SintS,LOL | Scuffing safety factor for loss of lubrication based on ISO/TS 6336-21 | - |
| SRef | Mean scuffing safety of the reference | - |
| SVar | Mean scuffing safety of variant | - |
| Srel | Relative scuffing safety | - |
| Srel|vt,C | Relative scuffing safety for discrete speeds vt,C | - |
| tC | Contact time | µs |
| tK | Contact time at the minimum of the scuffing speed curve | µs |
| Tin | Input torque | Nm |
| TLGP | Load-dependent gear torque loss | Nm |
| TLGP,LOL | Load-dependent gear torque loss during loss of lubrication | Nm |
| T1/T2 | Contact points of tangent (lines of engagement) at base circle | - |
| v | Reference line velocity | m/s |
| vgm | Mean sliding speed over the path of contact | m/s |
| vt,C | Circumferential speed at the pitch point C | m/s |
| v∑C | Sum speed at the pitch point C | m/s |
| wBt | Transverse unit load (ISO 6336-20)/ | N/mm |
| Specific tooth load (ISO 6336-21) | N/mm | |
| x1/2 | Profile shift coefficient | - |
| xi | Factor for the transmission ratio i | - |
| Xb | Factor for face width | - |
| XBE | Geometry factor at pinion tooth tip | - |
| XCa | Tip relief factor | - |
| XE | Run-in factor | - |
| XG | Geometry factor | - |
| XJ | Approach factor | - |
| XL | Lubricant factor | - |
| XLOL | Loss of lubrication factor | - |
| XM | Thermo-elastic factor (ISO 6336-20)/ | K∙N−3⁄4∙s1⁄2∙m−1⁄2∙mm/ |
| Themal flash factor (ISO 6336-21) | - | |
| XQ | Factor for the amount of oil/ | -/ |
| Approach factor (ISO 6336-21) | - | |
| XT | Factor considering the oil temperature (=1 for 90 °C) | - |
| XWrelT | Relative welding factor | - |
| Xαβ | Pressure angle ratio factor | - |
| XΓ | Load sharing factor | - |
| Xε | Contact ratio factor | - |
| z1/2 | number of teeth pinion/wheel | - |
Greek Symbols
| αn | Pressure angle | ° |
| αOil | Volumetric share of oil | - |
| αOil,Ref | Reference volumetric share of oil | - |
| αOil,Var1/2 | Volumetric share of oil of variant 1/2 | - |
| αsb | Working pressure angle | ° |
| β | Helix angle | ° |
| βg | Helix angle at base circle | ° |
| ε1/2 | Addendum contact ratio of the pinion/wheel | - |
| εα | Transverse contact ratio | - |
| εβ | Overlap ratio | - |
| η | Dynamic viscosity | mPas |
| ϑbmax | Maximum contact temperature | °C |
| ϑbmax,LOL | Maximum contact temperature for loss of lubrication | °C |
| ϑfl | Flash temperature | K |
| ϑfl,LOL | Flash temperature for loss of lubrication | K |
| ϑflaint | Mean flash temperature | K |
| ϑflaint,LOL | Mean flash temperature for loss of lubrication | K |
| ϑflaE | Flash temperature at pinion tooth tip when load sharing is neglected | K |
| ϑflaE,LOL | Flash temperature for loss of lubrication at pinion tooth tip when load sharing is neglected | K |
| ϑflmax | Maximum flash temperature | K |
| ϑflmax,LOL | Maximum flash temperature for loss of lubrication | K |
| ϑint | Integral temperature | °C |
| ϑint,LOL | Integral temperature for loss of lubrication | °C |
| ϑintS | Scuffing integral temperature | °C |
| ϑS | Scuffing temperature | °C |
| ϑSC | Constant scuffing temperature at long contact times | °C |
| ϑM | Bulk temperature | °C |
| ϑM,LOL | Bulk temperature during LOL | °C |
| ϑOil | Oil injection temperature | °C |
| ϑOver | Overtemperatuer | °C |
| λ | Thermal conductivity | W/(mK) |
| μmZ | Mean gear coefficient of friction | - |
| μmZ,LOL | Mean gear coefficient of friction during loss of lubrication | - |
| ν | Kinematic viscosity | mm2/s |
| ρredC | Relative curvature at the pitch point | mm |
| ρ | Density | kg/m3 |
| φavr | Physical properties of an averaged oil/air fluid flow | - |
| φavr,LOL | Physical properties of an averaged oil/air fluid flow during loss of lubrication | - |
| φoil/air | Physical properties of oil/air | - |
Abbreviations
| A | FZG test gear geometry “A” |
| CFD | Computational fluid dynamics |
| Cmod,LOL | FZG test gear geometry “Cmod,LOL” |
| eLL | FZG test gear geometry “extreme Low Loss” |
| EP | Extreme pressure |
| IL | Injection lubrication |
| ISO VG 46 | Oil “ISO VG 46” |
| LOL | Loss of lubrication |
| LS | Load stage |
| SLS | Scuffing load stage |
Appendix A
| Test Gear Geometry | Cmod,LOL [6] | A [52] | eLL [55] | |||
|---|---|---|---|---|---|---|
| Pinion | Wheel | Pinion | Wheel | Pinion | Wheel | |
| Number of teeth | 16 | 24 | 16 | 24 | 39 | 52 |
| Normal module mn in mm | 4.5 | 4.5 | 1.81 | |||
| Pressure angle αn in ° | 20 | 20 | 36 | |||
| Helix angle β in ° | - | - | 25 | |||
| Transverse contact ratio εα | 1.436 | 1.361 | 0.65 | |||
| Overlap ratio εβ | - | - | 2.08 | |||
| Face width b in mm | 14 | 20 | 28 | |||
| Center distance a in mm | 91.5 | 91.5 | 91.5 | |||
| Tip diameter da1/2 | 82.45 | 118.35 | 88.77 | 112.5 | 80.6 | 106.5 |
| Profile shift coefficient x1/2 | 0.182 | 0.171 | 0.853 | −0.5 | 0.183 | 0.168 |
| Tip relief Ca in μm | 35 | 35 | - | - | - | - |
| Geometric tooth power loss factor HV for LS7 | 0.195 | 0.302 | 0.066 | |||
| Arithmetic mean flank roughness Ra in µm | 0.29 | 0.29 | 0.29 | |||
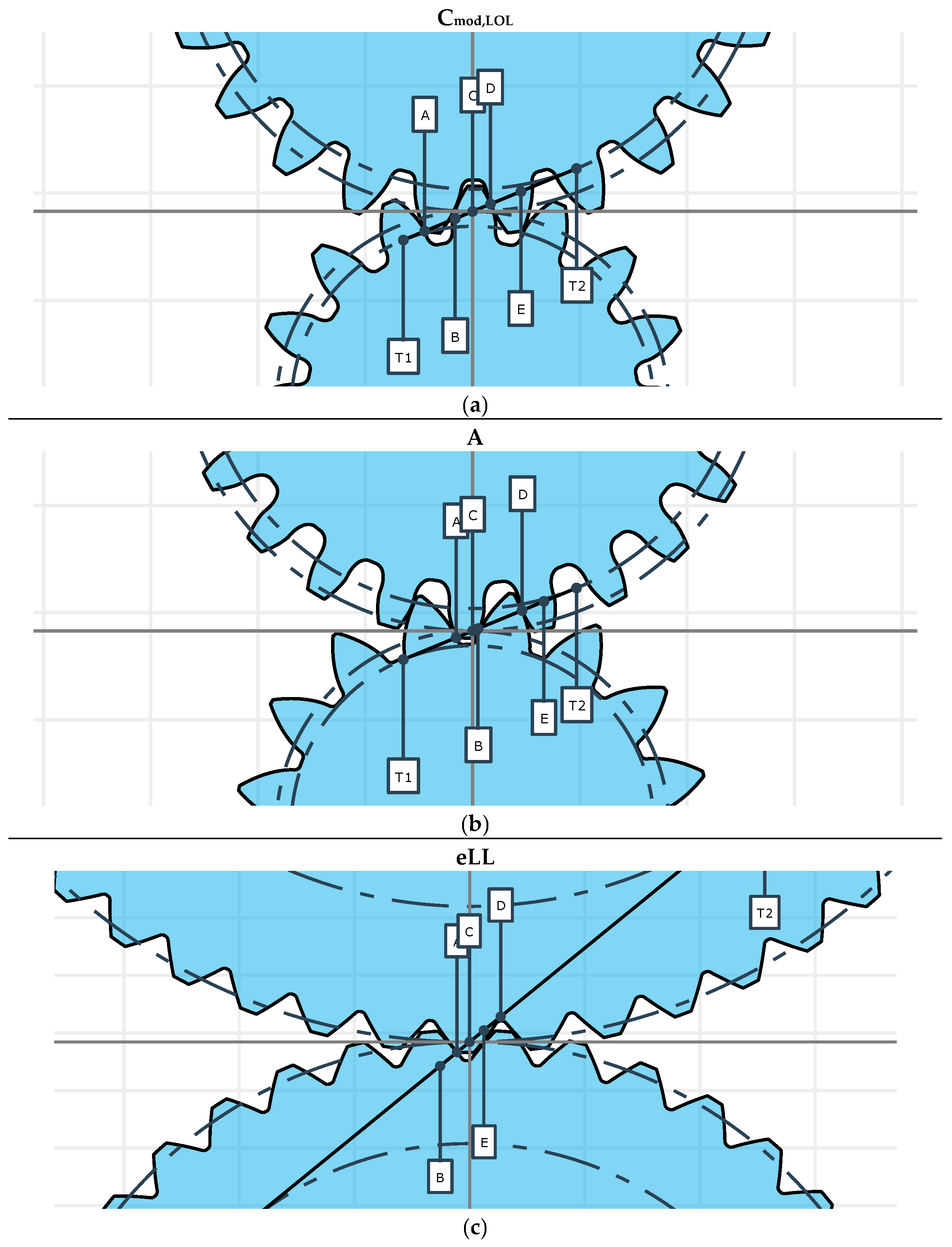
Appendix B
Appendix C
| Load Stage | Torque (Pinion) in Nm |
|---|---|
| 5 | 94.1 |
| 7 | 183.4 |
| 9 | 302.0 |
| 11 | 450.1 |
Appendix D
Appendix E

References
- Minister of Public Works and Government Services Canada. Aviation Investigation Report A09A0016: Main Gearbox Malfunction/Collision with Water; Transportation Safety Board of Canada: Gatineau, QC, Canada, 2010. [Google Scholar]
- Hudgins, W.A.; Schuetz, H.A. Loss-of-Lubrication of Helicopter Transmissions. Am. Helicopter Soc. 1982, 27, 3–10. [Google Scholar] [CrossRef]
- Faruck, A.A.M.; Hsu, C.-J.; Doerr, N.; Weigand, M.; Gachot, C. How lubricant formulations and properties influence the performance of rotorcraft transmissions under loss of lubrication conditions. Tribol. Int. 2020, 151, 106390. [Google Scholar] [CrossRef]
- Riggs, M.R.; Murthy, N.K.; Berkebile, S.P. Evaluation for Loss of Lubrication Performance of Black Oxide, Superfinished, and As-Ground Surfaces for Use in Rotorcraft Transmissions. US Army Research Laboratory ARL-TR-7815; Defense Technical Information Center: Fort Belvoir, VA, USA, 2016. [Google Scholar]
- Riggs, M.R.; Murthy, N.K.; Berkebile, S.P.; Korenyi-Both, A.L. Scuffing Resistance and Starved Lubrication Behavior in Helicopter Gear Steels Coated with Nanocomposite Surface Coatings with and without a Hard Sublayer. Tribol. Trans. 2020, 63, 610–620. [Google Scholar] [CrossRef]
- Morhard, B.; Paschold, C.; Lohner, T.; Stahl, K. Power Loss and Damage Behavior of Gears Operating under Loss of Lubrication. J. Tribol. 2024, 146, 072201. [Google Scholar] [CrossRef]
- Morhard, B.; Lohner, T.; Stahl, K. Influence of Surface and Material Technologies on the Loss of Lubrication Performance of Gears. J. Mater. Sci. Mater. Eng. 2024, 19, 1. [Google Scholar] [CrossRef]
- Morhard, B.; Lohner, T.; Stahl, K. Influence of high speeds on operating behavior of gears under loss of lubrication. Eng. Res. Forsch. Im Ingenieurwesen 2025, 89, 153. [Google Scholar] [CrossRef]
- ISO/TS 6336-21:2022; Calculation of Load Capacity of Spur and Helical Gears—Part 21: Calculation of Scuffing Load Capacity—Integral Temperature Method. International Organization for Standardization: Geneva, Switzerland, 2022.
- Alberti, J.; Lemanski, A. Oil-Starvation Test Program: Evaluation of VASCO-X2 Steel Spiral Bevel Gears; U.S. Army Air Mobility Research and Development Laboratory: Fort Rucker, AL, USA, 1972. [Google Scholar]
- Bartilotta, I.; Ciulli, E.; Manconi, S.; Toson, E. An experimental investigation on aerospace quality gears operating in loss of lubrication condition. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; Advanced Manufacturing Processes; Biomedical Engineering; Multiscale Mechanics of Biological Tissues; Sciences, Engineering and Education; Multiphysics; Emerging Technologies for Inspection and Reverse Engineering; Advanced Materials and Tribology. Volume 4. [Google Scholar] [CrossRef]
- AGMA 18FTM08; Oil-Off Characterization Method Using In-Situ Friction Measurement for Gears Operating Under Loss-of-Lubrication Conditions. American Gear Manufacturers Association Fall Technical Meeting: Detroit, MI, USA, 2018.
- Berkebile, S.; Murthy, N.; Radil, K.; Dykas, B.; Colon-Rivera, R.; Fetty, J. Experimental evaluation of transmission loss-of-lubrication technologies. In Proceedings of the 74th Annual Forum and Technology Display of the American Helicopter Society (AHS), Phoenix, AZ, USA, 14–17 May 2018. Annual Forum Proceedings—AHS International. [Google Scholar]
- Kozachyn, M.; McIntyre, S.; Robuck, M.; Isaacson, A.; Black, B.; Sahay, V. Loss of lubrication testing. In Proceedings of the 74th American Helicopter Society International Annual Forum and Technology Display 2018: The Future of Vertical Flight, Phoenix, AZ, USA, 14–17 May 2018; Annual Forum Proceedings—AHS International. Volume 2018-May. [Google Scholar]
- Murakawa, M.; Komori, T.; Takeuchi, S.; Miyoshi, K. Performance of a rotating gear pair coated with an amorphous carbon film under a loss-of-lubrication condition. Surf. Coat. Technol. 1999, 120–121, 646–652. [Google Scholar] [CrossRef]
- Murthy, N.; Rai, A.K.; Berkebile, S. Improved loss-of-lubrication performance with lubricants containing nano-graphene platelets and ionic liquids. Appl. Sci. 2020, 10, 7958. [Google Scholar] [CrossRef]
- Braumann, L.; Viteri, V.S.d.; Morhard, B.; Lohner, T.; Ochoa, J.; Amri, H. Tribology technologies for gears in loss of lubrication conditions: A review. J. Mater. Sci. Mater. Eng. 2025, 20, 29. [Google Scholar] [CrossRef]
- Handschuh, R.F.; Morales, W. Lubrication System Failure Baseline Testing on an Aerospace Quality Gear Mesh. In Proceedings of the ASME Design Engineering Technical Conference, Baltimore, ML, USA, 10–13 September 2000; Volume 6, pp. 739–745, 8th International Power Transmission and Gearing Conference. [Google Scholar] [CrossRef]
- Handschuh, R.F.; Polly, J.; Morales, W. Gear mesh loss-of-lubrication experiments and analytical simulation. In Proceedings of the 67th Annual Forum and Technology Display (Forum 67), Virginia Beach, VA, USA, 3–5 May 2011. [Google Scholar]
- Collenberg, H.F. Untersuchungen zur Fresstragfähigkeit schnelllaufender Stirnradgetriebe—Engl.: Investigations into the Scuffing Load Capacity of High-Speed Spur Gears. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1991. [Google Scholar]
- Bowman, W.F.; Stachowiak, G.W. A review of scuffing models. Tribol. Lett. 1996, 2, 113–131. [Google Scholar] [CrossRef]
- Brizmer, V.; Matta, C.; Nedelcu, I.; Morales-Espejel, G.E. The Influence of Tribolayer Formation on Tribological Performance of Rolling/Sliding Contacts. Tribol. Lett. 2017, 65, 57. [Google Scholar] [CrossRef]
- Lechner, G. Die Fress-Grenzlast bei Stirnrädern aus Stahl—Engl.: The Limit Scuffing Load for Spur Gears Made of Steel. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1966. [Google Scholar]
- Michaelis, K. Die Integraltemperatur zur Beurteilung der Fresstragfähigkeit von Stirnradgetrieben—Engl.: The Integral Temperature for Assessment of the Scuffing Load Capacity of Spur Gears. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1987. [Google Scholar]
- ISO/TS 6336-20:2022; Calculation of Load Capacity of Spur and Helical Gears—Part 20: Calculation of Scuffing Load Capacity—Flash Temperature Method. International Organization for Standardization: Geneva, Switzerland, 2022.
- Ziegltrum, A.; Emrich, S.; Lohner, T.; Michaelis, K.; Brodyanski, A.; Merz, R.; Kopnarski, M.; Hoehn, B.-R.; Stahl, K. Influence of tribofilms on failures and friction of gears with particular focus on running-in. Ind. Lubr. Tribol. 2019, 71, 1017–1026. [Google Scholar] [CrossRef]
- Wu, J.; Wei, P.; Liu, G.; Chen, D.; Zhang, X.; Chen, T.; Liu, H. A comprehensive evaluation of DLC coating on gear bending fatigue, contact fatigue, and scuffing performance. Wear 2024, 536–537, 205177. [Google Scholar] [CrossRef]
- Winter, H.; Michaelis, K. Scoring Tests of Aircraft Transmission Lubricants at High Speeds and High Temperatures. J. Synth. Lubr. 1986, 3, 121–135. [Google Scholar] [CrossRef]
- Winter, H.; Michaelis, K.; Collenberg, H.F. Investigations on the Scuffing Resistance of High-Speed Gears. AGMA Tech. Pap. 1990, 8, 1–14. [Google Scholar]
- Oster, P. Beanspruchung der Zahnflanken unter Bedingungen der Elastohydrodynamik—Engl.: Stress on the Tooth Flanks Under Elastohydrodynamic Conditions. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1982. [Google Scholar]
- Seitzinger, K. Die Erwärmung einsatzgehärteter Zahnräder als Kennwert für ihre Freßtragfähigkeit—Engl.: The Heating of Case-Hardened Gears as a Characteristic Value for their Scuffing Load Capacity. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1971. [Google Scholar]
- NASA/TM—2014-218396; Test Facility Simulation Results for Loss-of-Lubrication of Spur Gears. National Aeronautics and Space Administration: Washington, DC, USA, 2014.
- Handschuh, R.F. Thermal behavior of aerospace spur gears in normal and loss-of-lubrication conditions. Am. Helicopter Soc. Annu. Forum Technol. Disp. 2015, 4, 2292–2301. [Google Scholar] [CrossRef]
- Michaelis, K.; Höhn, B.-R.; Doleschel, A. Lubricant influence on gear efficiency. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 2009, San Diego, CA, USA, 30 August–2 September 2009. DETC2009. [Google Scholar] [CrossRef]
- Yilmaz, M.; Lohner, T.; Michaelis, K.; Stahl, K. Minimizing gear friction with water-containing gear fluids. Eng. Res. 2019, 83, 327–337. [Google Scholar] [CrossRef]
- Becker, K.M. Measurements of convective heat transfer from a horizontal cylinder rotating in a tank of water. Int. J. Heat Mass Transf. 1963, 6, 1053–1062. [Google Scholar] [CrossRef]
- Handschuh, R.F. Thermal Behavior of Spiral Bevel Gears; NASA Technical Memorandum 106518. Army Research Laboratory 1995, Technical Report ARL-TR-403; Case Western Reserve University: Cleveland, OH, USA, 1993. [Google Scholar]
- Lebeck, A.O. Principles and Design of Mechanical Face Seals, 1st ed.; Wiley-Interscience: New York, NY, USA, 1991; ISBN 978-0-471-51533-3. [Google Scholar]
- Long, H.; Lord, A.A.; Gethin, D.T.; Roylance, B.J. Operating temperatures of oil-lubricated medium-speed gears: Numerical models and experimental results. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2003, 217, 87–106. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Prediction of the Bulk Temperature in Spur Gears Based on Finite Element Temperature Analysis. ASLE Trans. 1977, 22, 25–36. [Google Scholar] [CrossRef]
- Hildebrand, L.; Genuin, S.; Lohner, T.; Stahl, K. Numerical Analysis of the Heat Transfer of Gears under Oil Dip Lubrication. Tribol. Int. 2024, 195, 109652. [Google Scholar] [CrossRef]
- Qiao, Z.; Zhou, C.; Su, J.; Jiang, X. A novel dynamic heat-flow coupled model under spray lubrication for high-speed gears: CFD simulation and experimental validation. Simul. Model. Pract. Theory 2024, 131, 102867. [Google Scholar] [CrossRef]
- Roda-Casanova, V.; Sanchez-Marin, F.; Martinez-Cuenca, R. Convective heat transfer modelling in dry-running polymer spur gears. Int. J. Mech. Sci. 2023, 241, 107927. [Google Scholar] [CrossRef]
- Zou, T.; Yan, Q.; Sui, T.; Zhao, Z.; Li, J.; An, Y. Key Parameters and Experimental Study of High-Speed Rotating Meshing Gear Injection Lubrication Based on Moving Particle Semi-Implicit Method. Lubricants 2023, 11, 366. [Google Scholar] [CrossRef]
- von Plehwe, F. Untersuchung des Wärmeübergangs durch Einspritzkühlung für ein Höchstleistungsgetriebe—Engl.: Investigation of Heat Transfer by Injection Cooling for a High Performance Gearbox. Ph.D. thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2022. [Google Scholar]
- Ohlendorf, H. Verlustleistung und Erwärmung von Stirnrädern—Engl.: Power Loss and Heat Generation in Cylindrical Gears. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1958. [Google Scholar]
- Michalczewski, R.; Szczerek, M.; Tuszyński, W.; Wulczyński, J.; Antonov, M. The effect of low-friction PVD coatings on scuffing and pitting resistance of spur gears. Tribologia 2013, 251, 5. [Google Scholar]
- Wimmer, J.A. Lastverluste von Stirnradverzahnungen: Konstruktive Einflüsse, Wirkungsgradmaximierung, Tribologie—Engl.: Load Losses of Spur Gears: Design Influences, Efficiency Maximization, Tribology. Ph.D. thesis, Technical University of Munich, Munich, Germany, 2006. [Google Scholar]
- Schlenk, L. Untersuchungen zur Freßtragfähigkeit von Großzahnrädern—Engl.: Investigations into the Scuffing Load Capacity of Large Gears. Ph.D. thesis, Technical University of Munich, Munich, Germany, 1995. [Google Scholar]
- Doleschel, A. Wirkungsgradberechnung von Zahnradgetrieben in Abhängigkeit vom Schmiertstoff—Engl.: Efficiency Calculation of Gearboxes in Dependency of the Lubricant. Ph.D. thesis, Technical University of Munich, Munich, Germany, 2003. [Google Scholar]
- ISO/TR 14179-1:2001-01; Gears -Thermal Capacity-Part 1: Rating Gear Drives with Thermal Equilibrium at 95 °C Sump Temperature. International Organization for Standardization: Geneva, Switzerland, 2001. Available online: https://www.iso.org/obp/ui/#iso:std:iso:tr:14179:-1:ed-1:v1:en (accessed on 21 October 2025).
- ISO 14635-1:2000; Gears—FZG Test Procedures-Part 1: FZG Test Method A/8,3/90 for Relative Scuffing Load-Carrying Capacity of Oils. International Organization for Standardization: Geneva, Switzerland, 2000.
- Dewinter, A.; Blok, H. Fling-Off Cooling of Gear Teeth. J. Eng. Ind. Trans. ASME 1974, 96, 60–70. [Google Scholar] [CrossRef]
- Blok, H. The Present Status of the Theory of Gear Lubrication; Laboratory for Machine Elements and Tribology, University of Technology: Delft, The Netherlands, 1968. [Google Scholar]
- Lohner, T.; Paschold, C. A Pathway Towards Energy Efficiency Classes for Gearboxes Related to Superefficiency. Eng. Res. Forsch. Im Ingenieurwesen 2025, 89, 2. [Google Scholar] [CrossRef]
- Shell. Technical Data Sheet—Turbine Oil 3: Mineral Lubricating Oil for Aircraft Turbine Engines; Shell PLC: London, UK, 2021. [Google Scholar]
- Hildebrand, L.; Lohner, T.; Stahl, K. A Mechanism-Based Characterization of the Load-Independent Power Loss of Dip-Lubricated Gears—Eingereicht. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2024, 239, 1382–1400. [Google Scholar] [CrossRef]
- Shell. Technical Data Sheet—AeroShell Turbine Oil 500: Synthetic Lubricating Oil for Aircraft Turbine Engines; Shell PLC: London, UK, 2021. [Google Scholar]
- EASTMAN. Technical Data Sheet—Easstman HALO 157: Synthetic Lubricating Oil for Aircraft Turbine Engines; Eastman: Kingsport, TN, USA, 2018. [Google Scholar]
- Exxon. Safety Data Sheet—Mobil Agl—Synthetic Aviation Gear Lubricant: Synthetic Lubricating Oil for Aircraft Turbine Engines; Exxon Mobil Corporation: Spring, TX, USA, 2002. [Google Scholar]
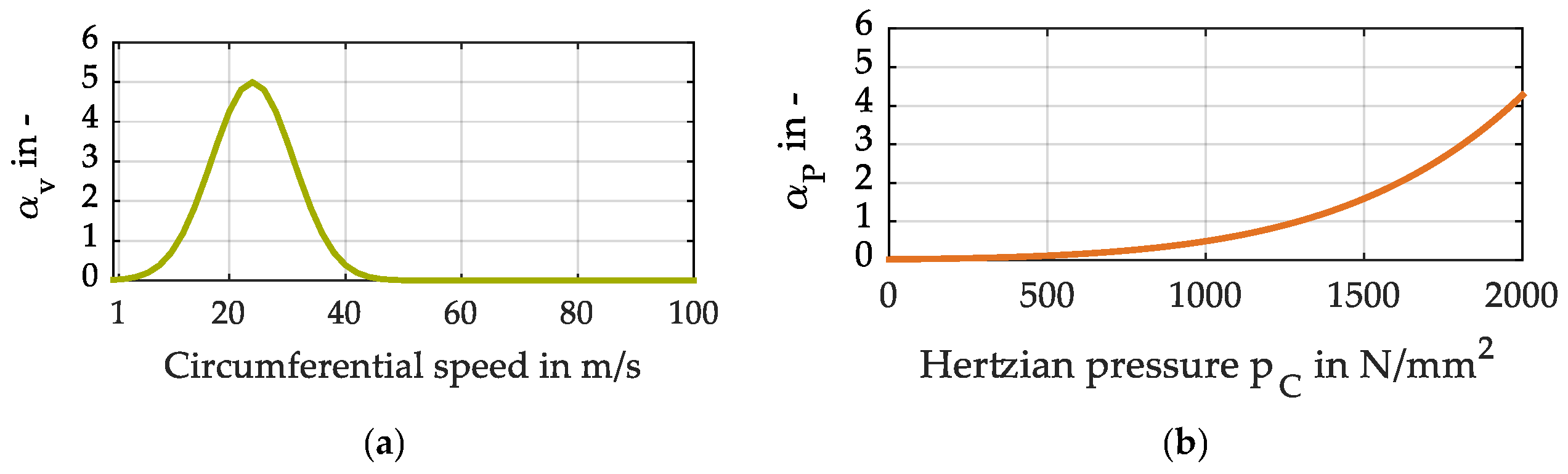
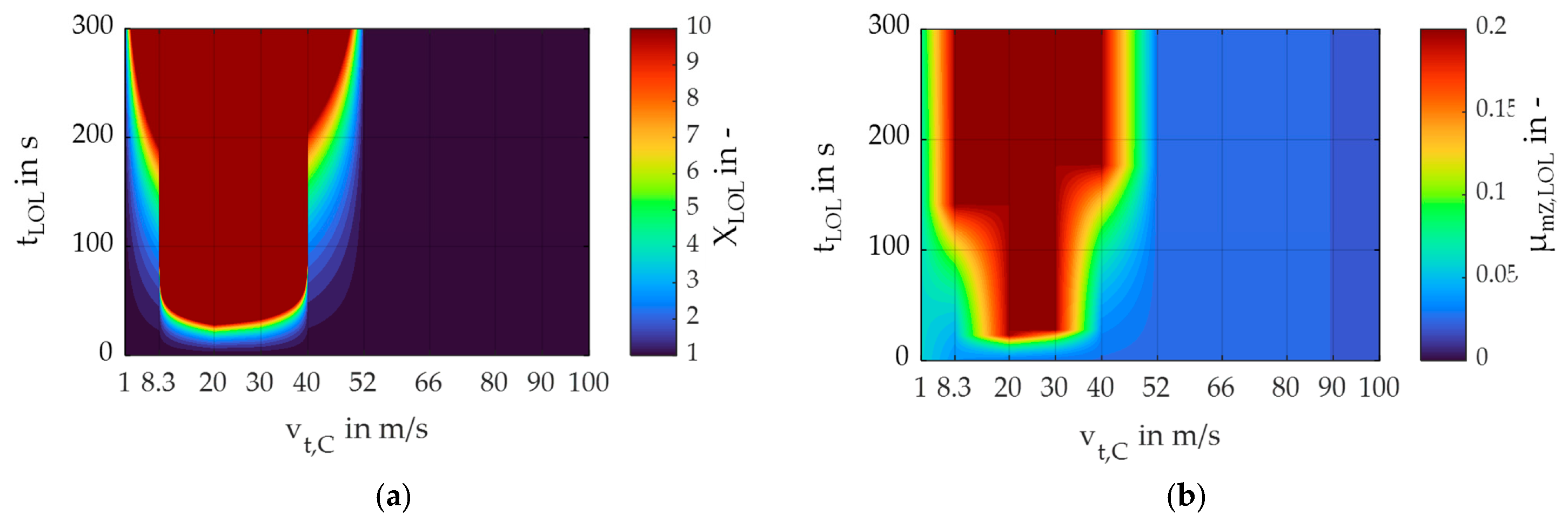
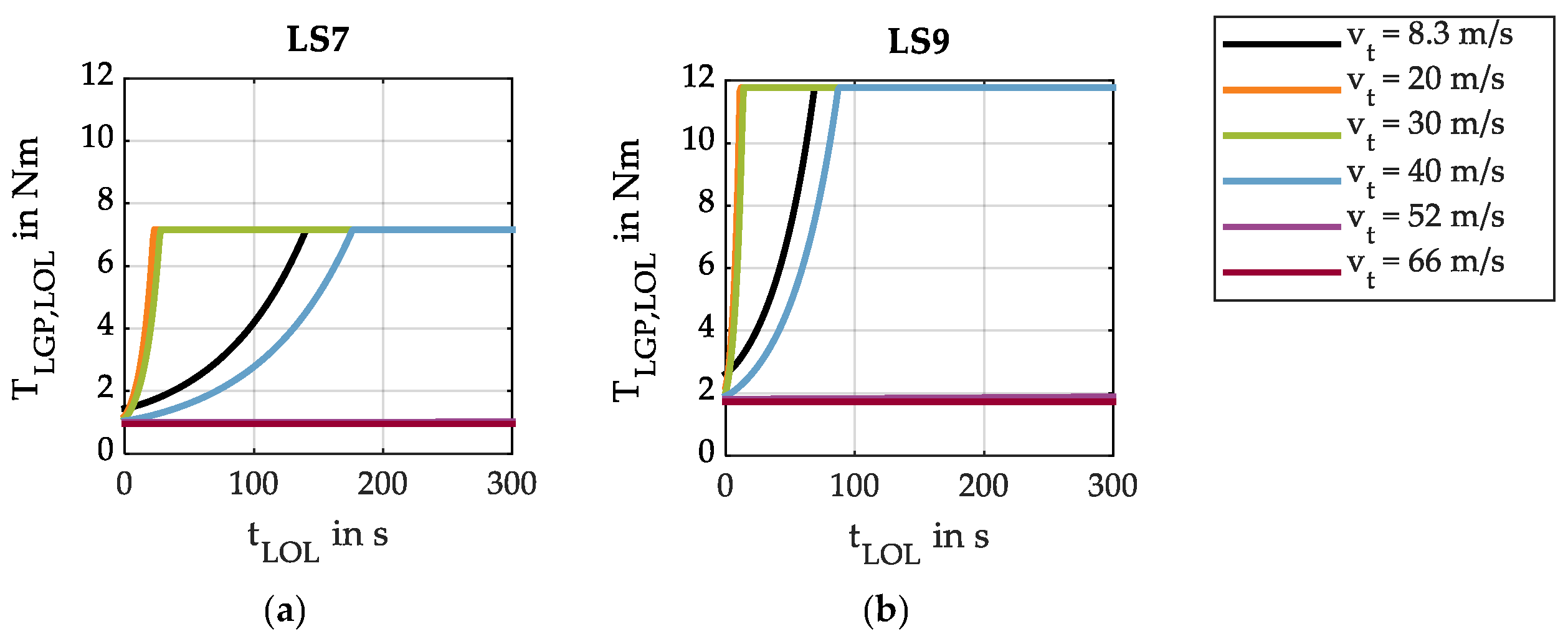

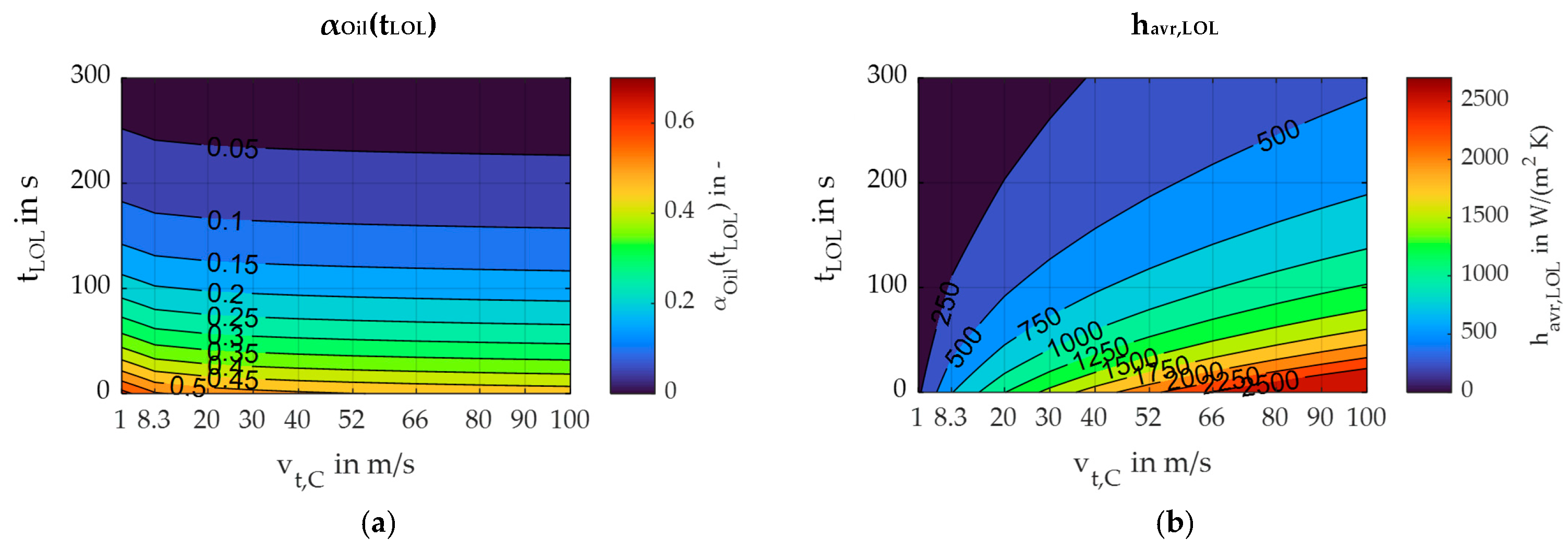

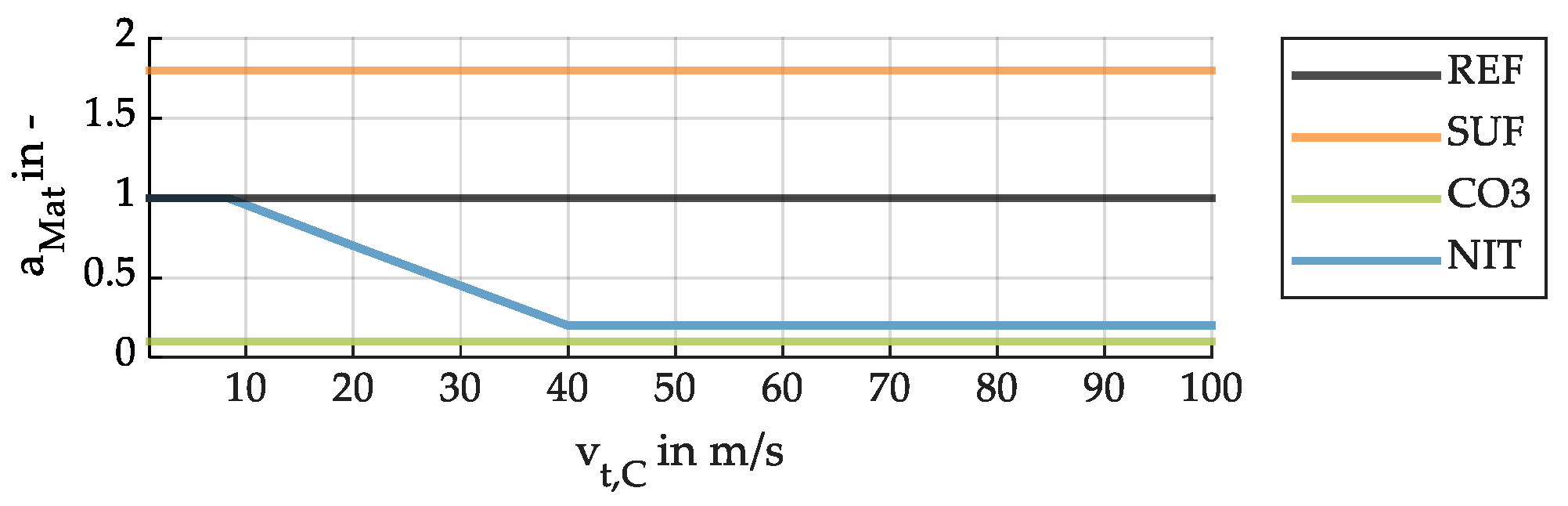
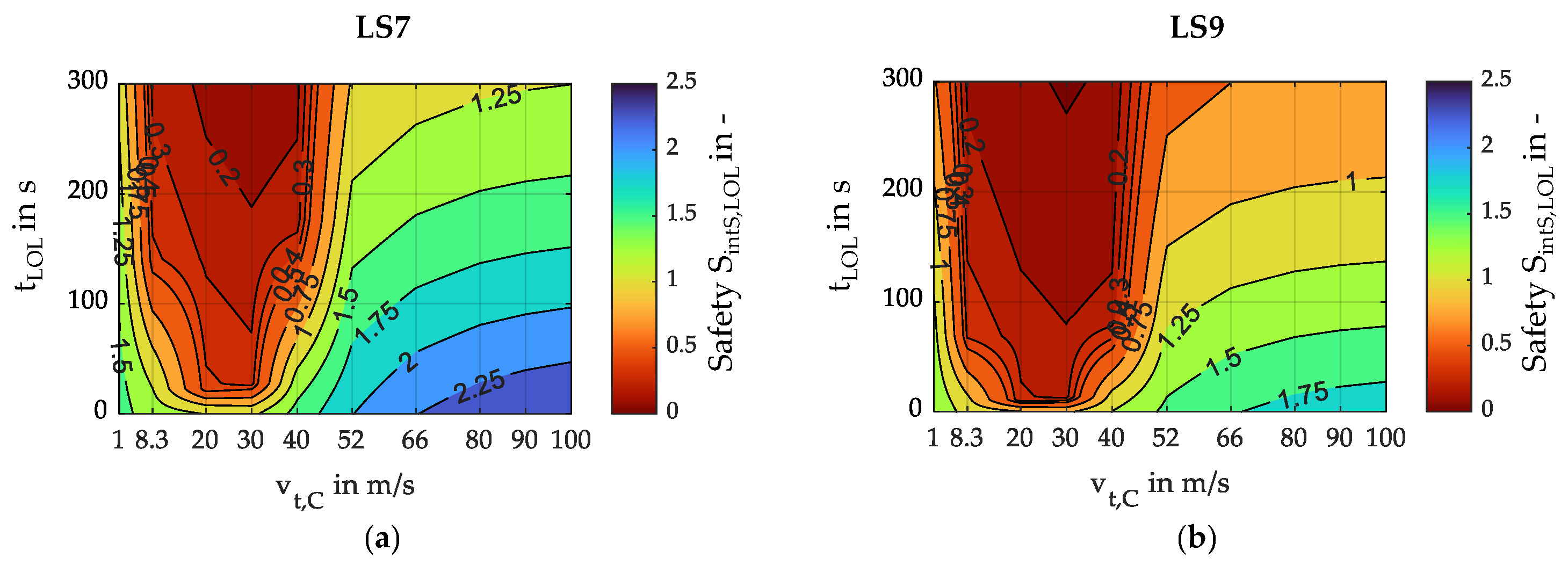
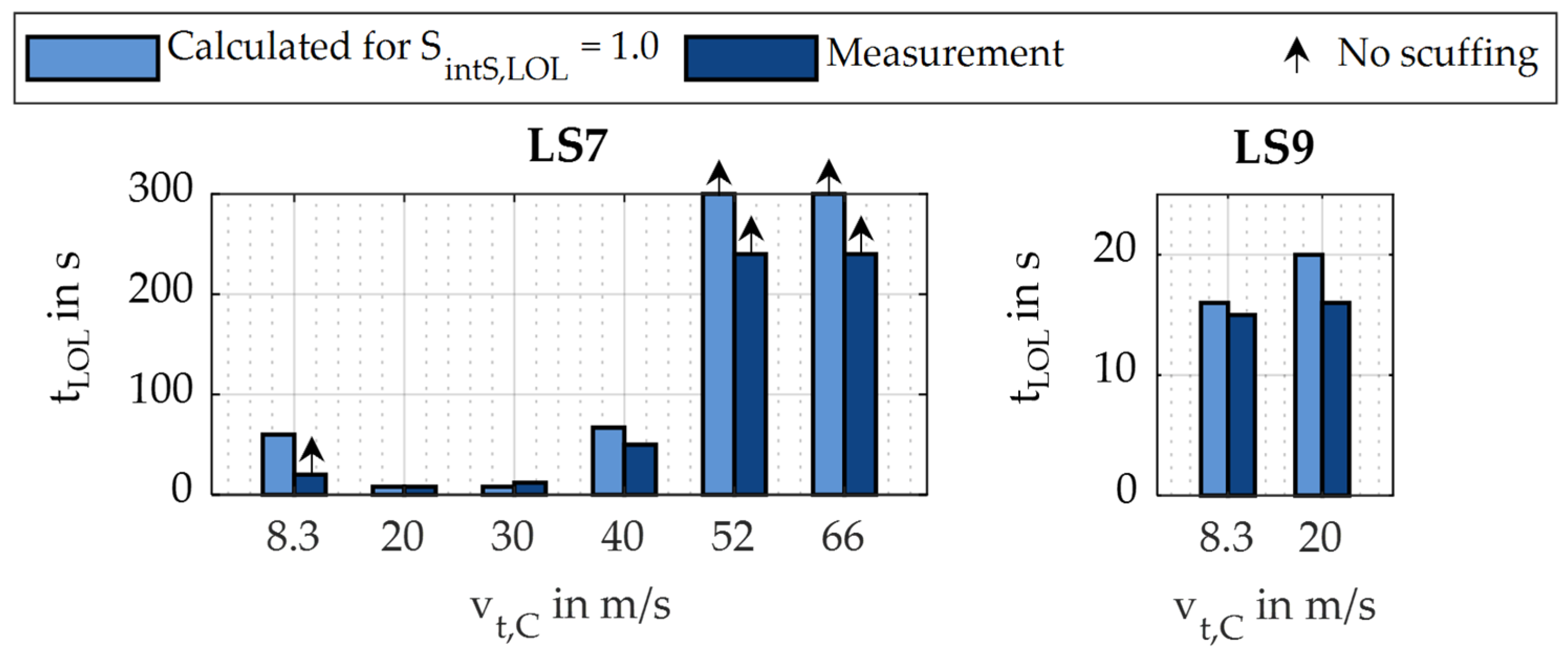


| vt,C in m/s | 1 | 8.3 | 20 | 30 | 40 | 52 | 66 | 80 | 90 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| aMat|REF in - | 1.0 | |||||||||
| aMat|SUF in - | 1.8 | |||||||||
| aMat|CO3 in - | 0.1 | |||||||||
| aMat|NIT in - | 1.0 | 1.0 | 0.7 | 0.45 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morhard, B.; Lohner, T.; Stahl, K. Scuffing Calculation of Cylindrical Gears Facing Loss of Lubrication. Lubricants 2025, 13, 484. https://doi.org/10.3390/lubricants13110484
Morhard B, Lohner T, Stahl K. Scuffing Calculation of Cylindrical Gears Facing Loss of Lubrication. Lubricants. 2025; 13(11):484. https://doi.org/10.3390/lubricants13110484
Chicago/Turabian StyleMorhard, Bernd, Thomas Lohner, and Karsten Stahl. 2025. "Scuffing Calculation of Cylindrical Gears Facing Loss of Lubrication" Lubricants 13, no. 11: 484. https://doi.org/10.3390/lubricants13110484
APA StyleMorhard, B., Lohner, T., & Stahl, K. (2025). Scuffing Calculation of Cylindrical Gears Facing Loss of Lubrication. Lubricants, 13(11), 484. https://doi.org/10.3390/lubricants13110484







