Machine Learning-Based Dynamic Modeling of Ball Joint Friction for Real-Time Applications
Abstract
1. Introduction
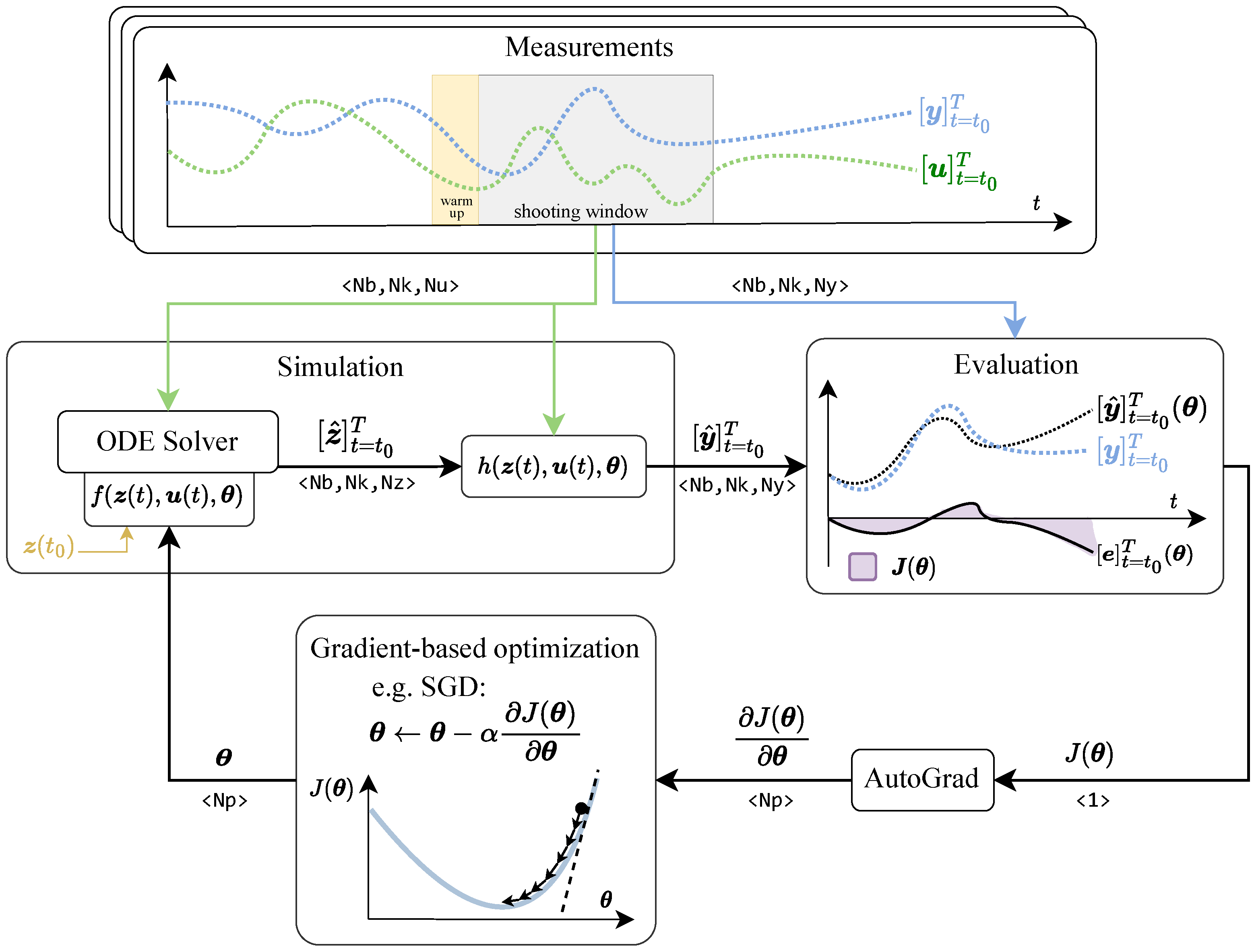
- We present a novel parameter estimation framework based on gradient-based optimization that enables the efficient learning of a wide range of dynamical systems, from white-box to black-box, discrete to continuous, using machine learning techniques.
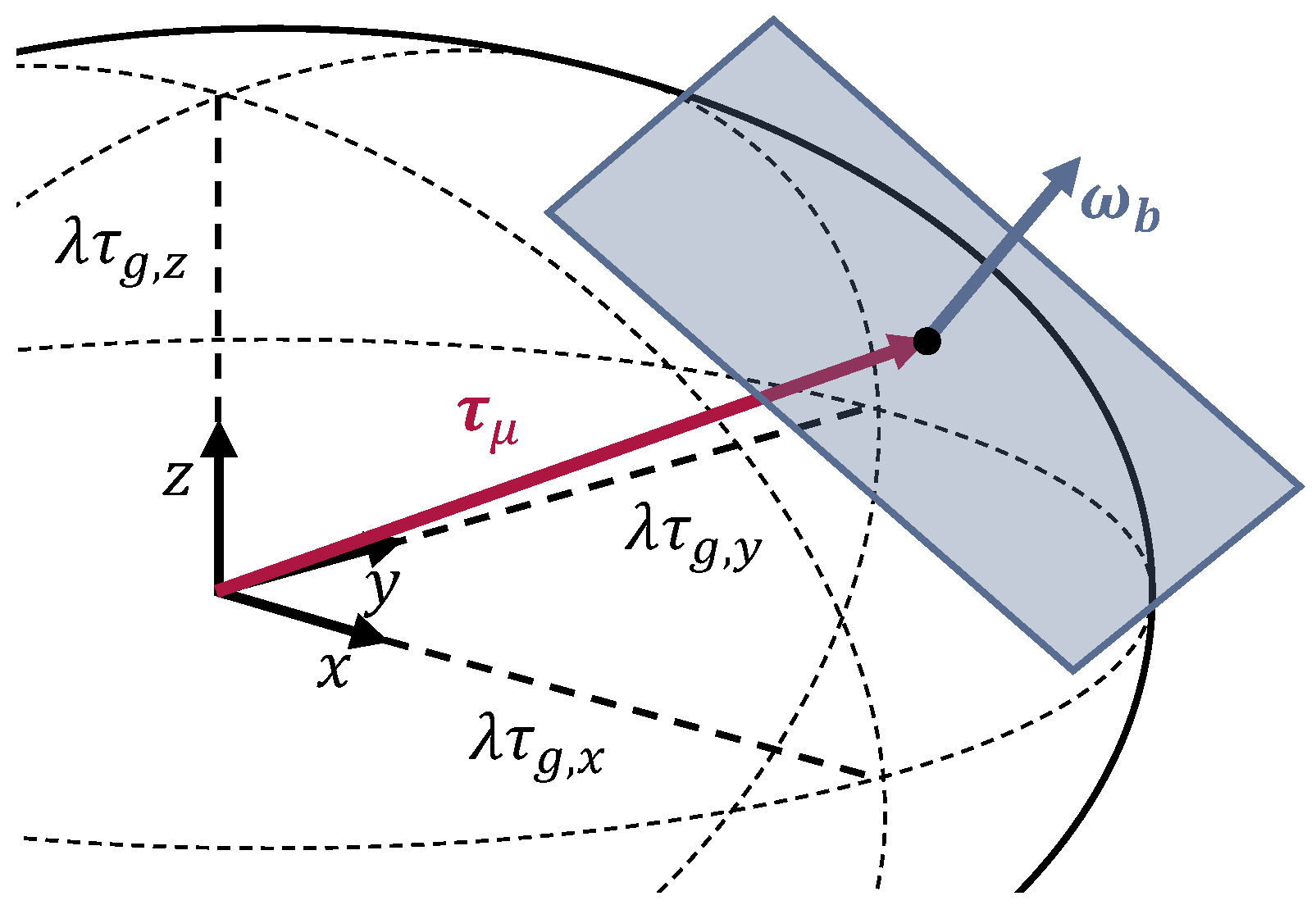
- We apply a three-dimensional LuGre model based on the approach by Velenis et al. [21] and the ideas from Pfitzer et al. [22] to phenomenologically capture ball joint friction at the macroscopic level, focusing on spherical contacts and properties derived from the Maximum Dissipation Principle. We compare this model to three alternatives and demonstrate that it is the most suitable for the given application case.
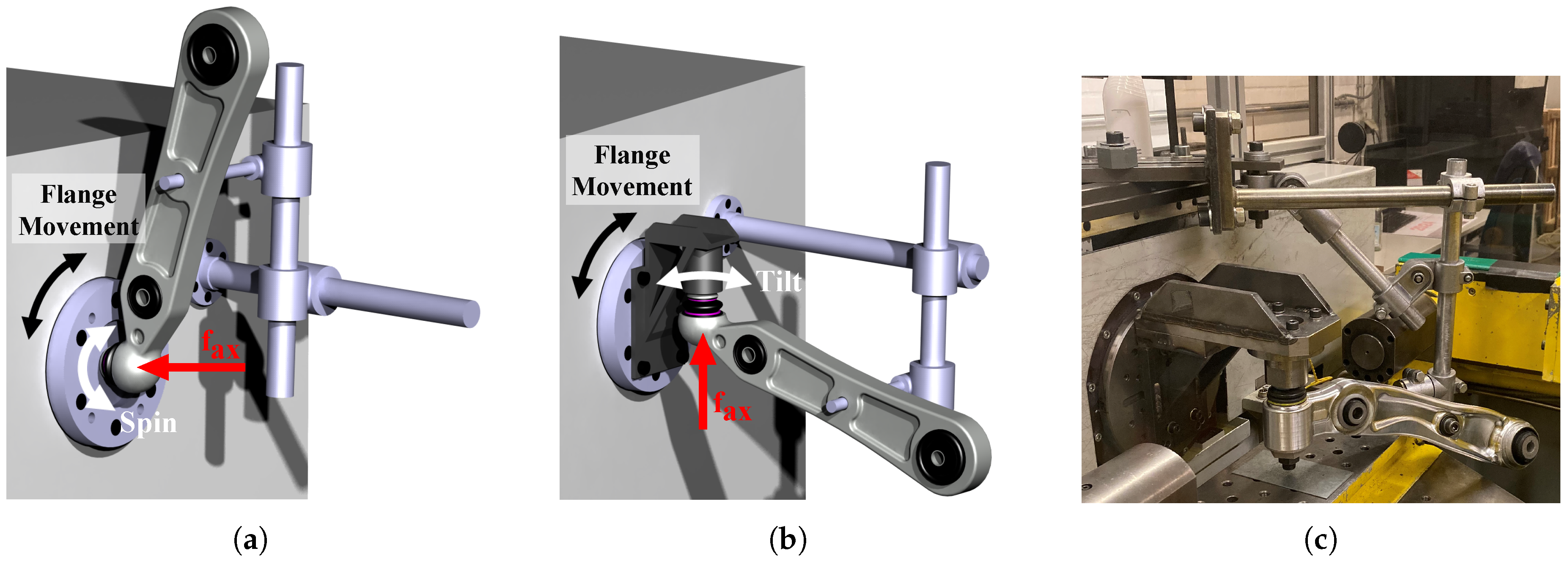
- We analyze the kinematic operating ranges of ball joints under real vehicle conditions. Based on these results, friction measurements are performed on a standardized component test bench, which is suitable for the standardized testing of ball joints according to AK-LH14 [33], in order to enable model parameter estimation.
2. Problem Statement
3. Related Work
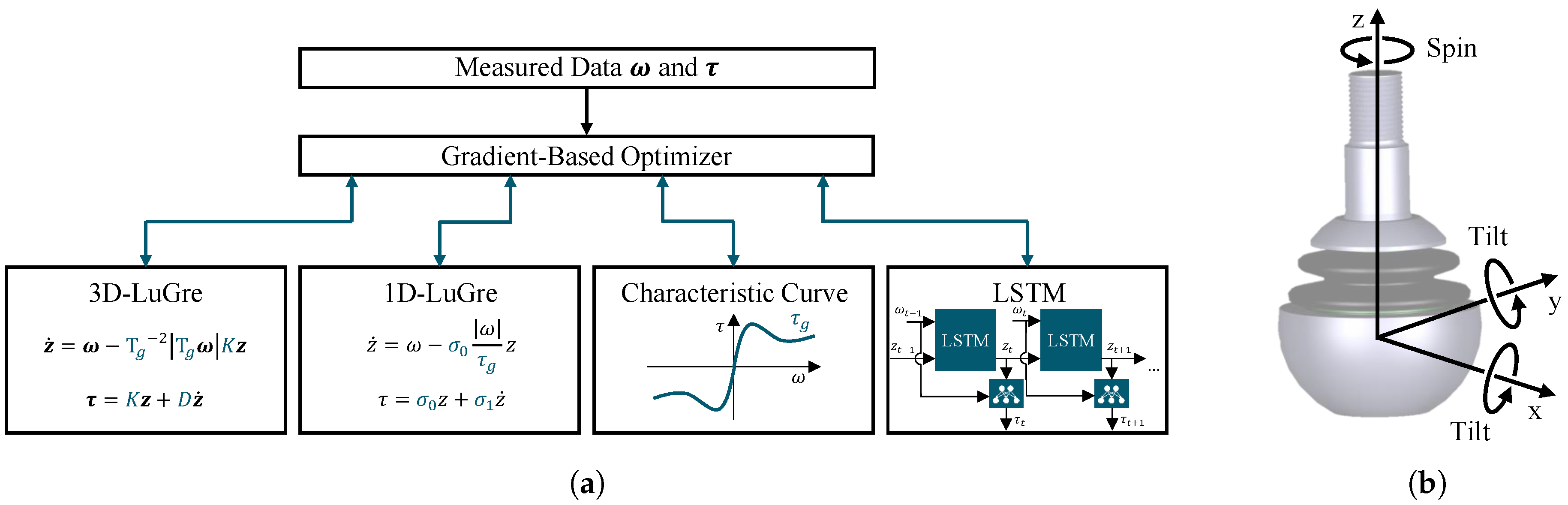
4. Model Learning
5. Ball Joint Friction Models
5.1. Three-Dimensional LuGre Model
| Algorithm 1: Neural network used to learn the functions of the three-dimensional LuGre model. |
 |
5.2. One-Dimensional LuGre Model
5.3. Characteristic Curves
| Algorithm 2: Neural network used to learn the functions of the characteristic curve. |
 |
5.4. LSTM Model
| Algorithm 3: Neural network used to calculate the torque from the LSTM states. |
 |
5.5. Model Summary
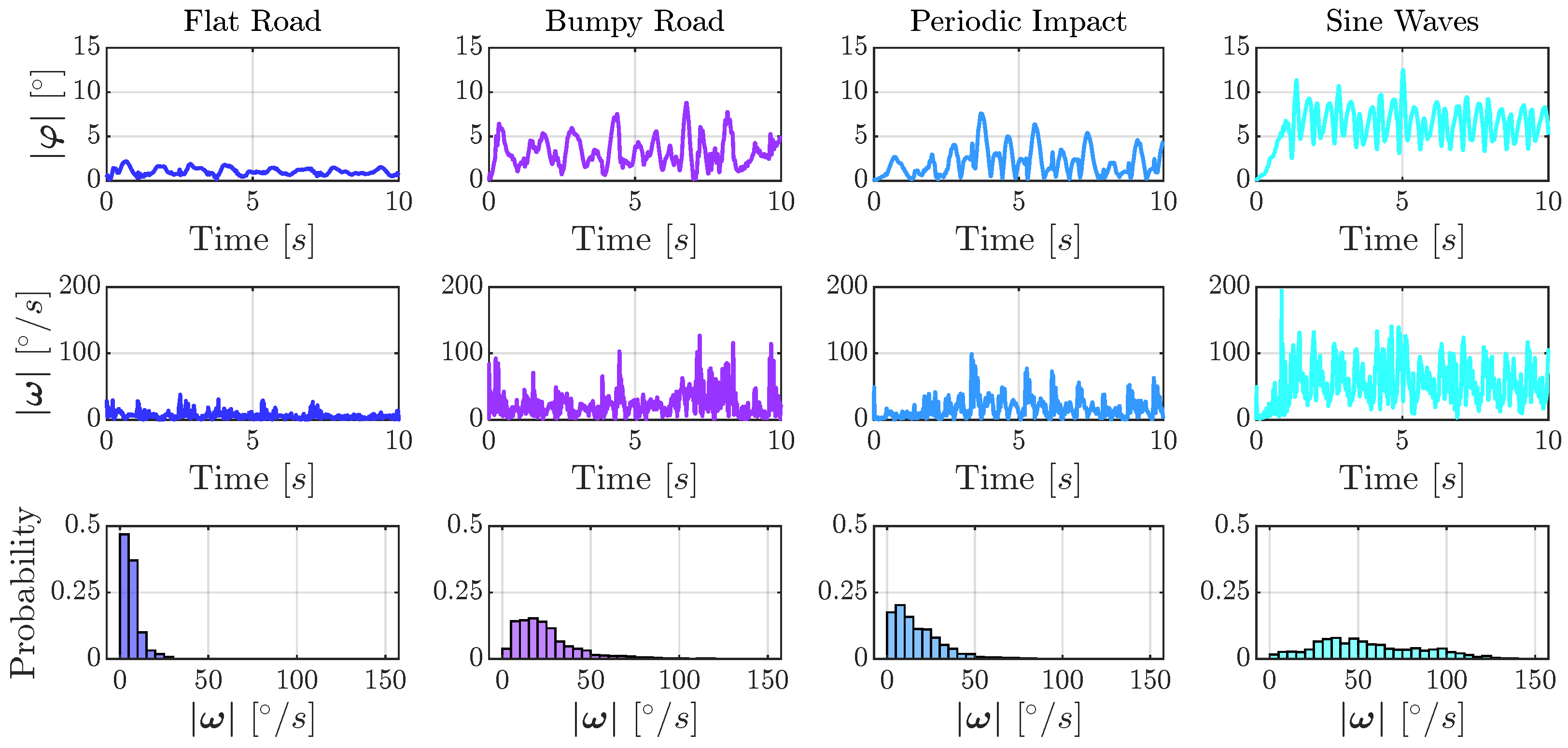
6. Operating Range Determination and Data Collection
6.1. Operating Range of Ball Joints
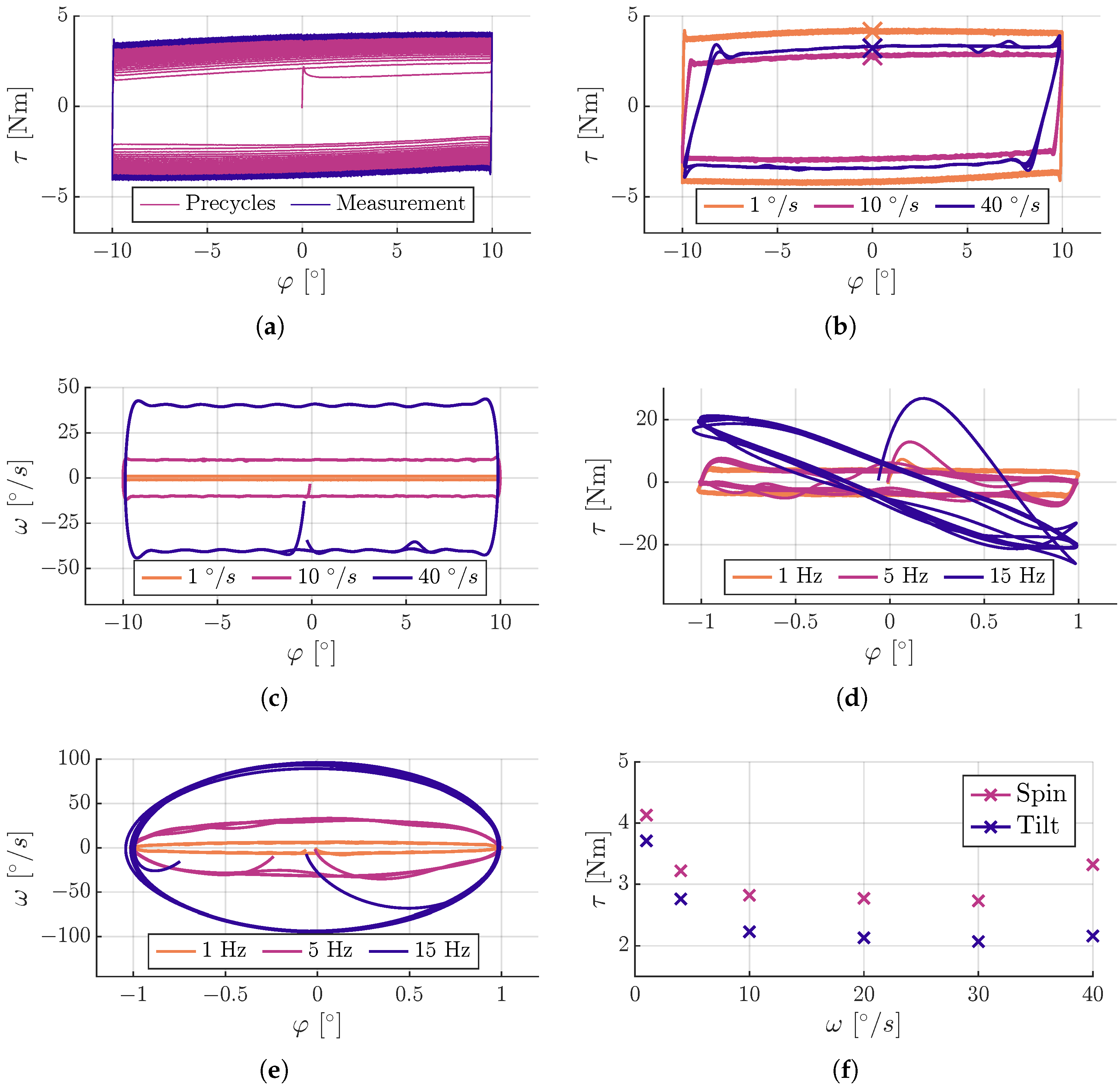
6.2. Measurement of Ball Joint Friction
6.3. Data Selection and Parameter Estimation
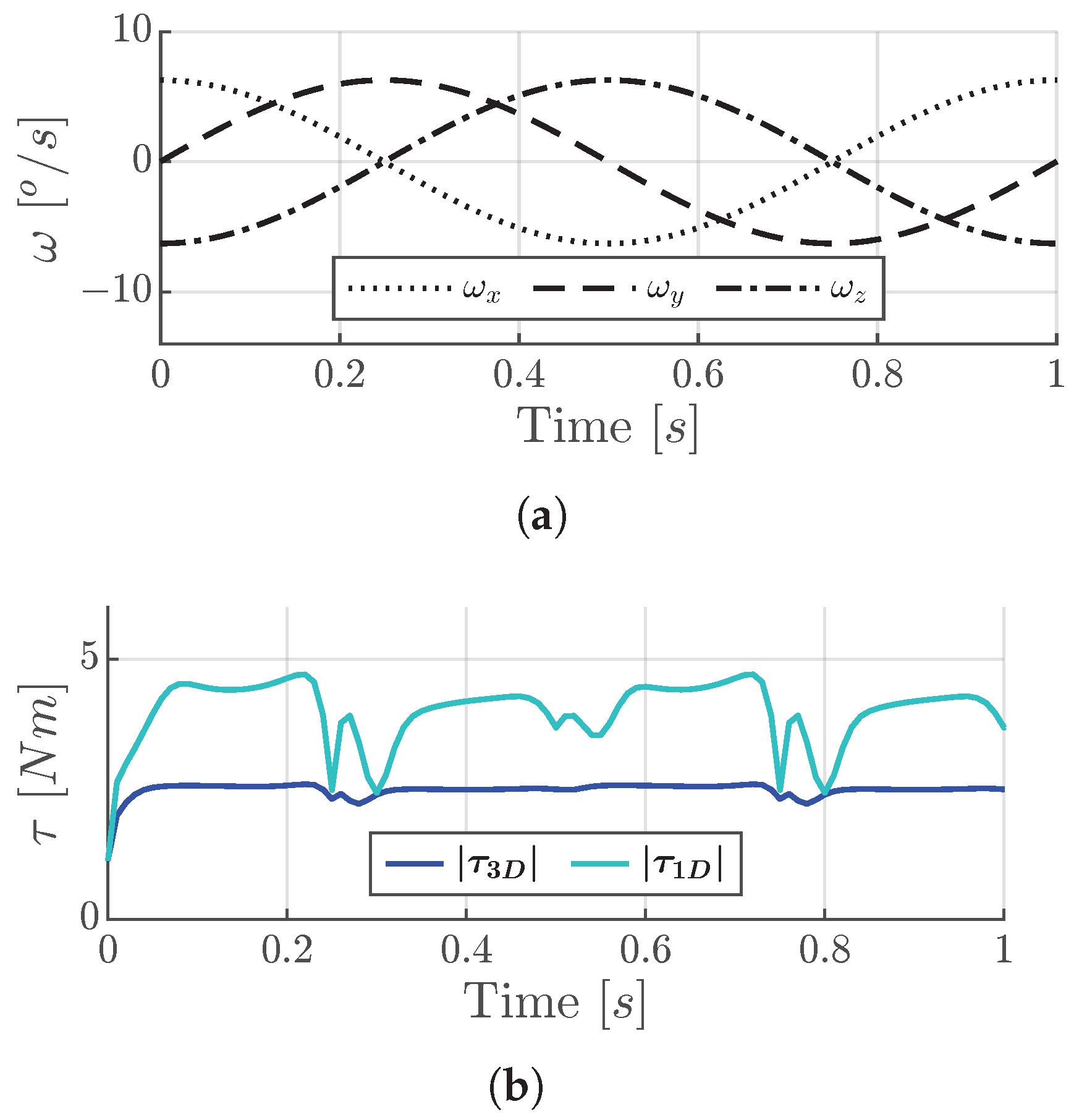
7. Results
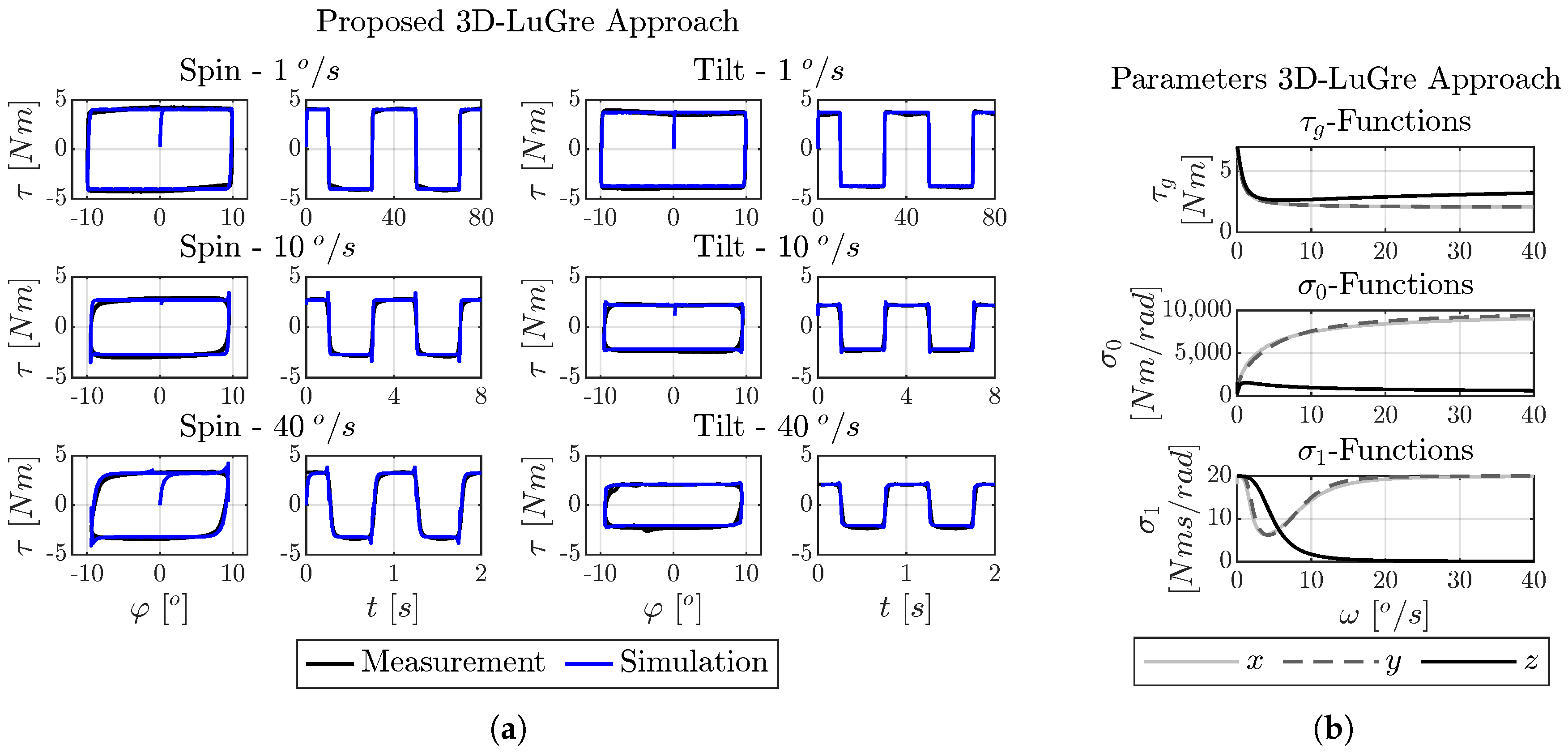
7.1. Fitting Results for Three-Dimensional LuGre Model
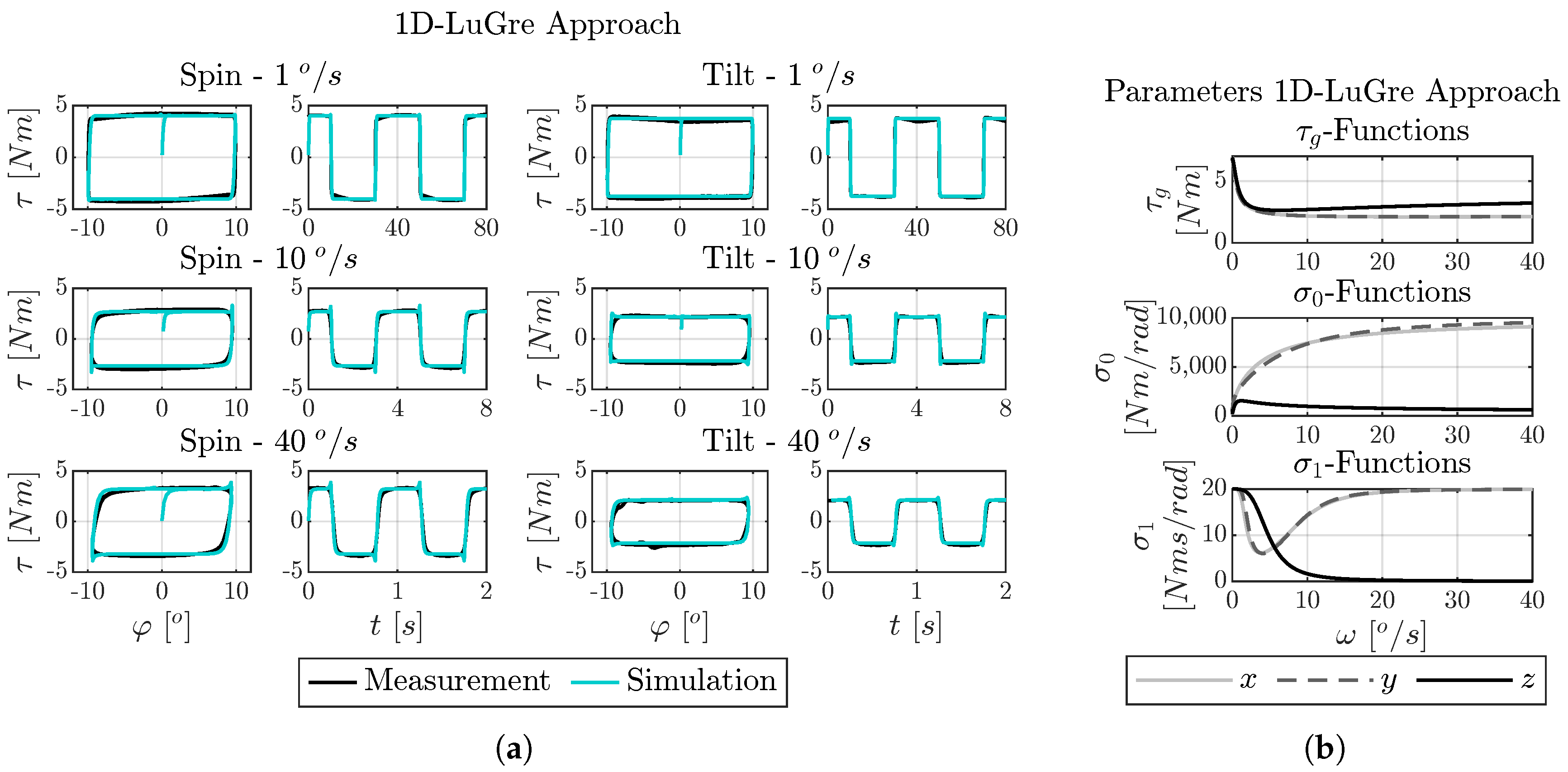
7.2. Fitting Results for the One-Dimensional LuGre Model
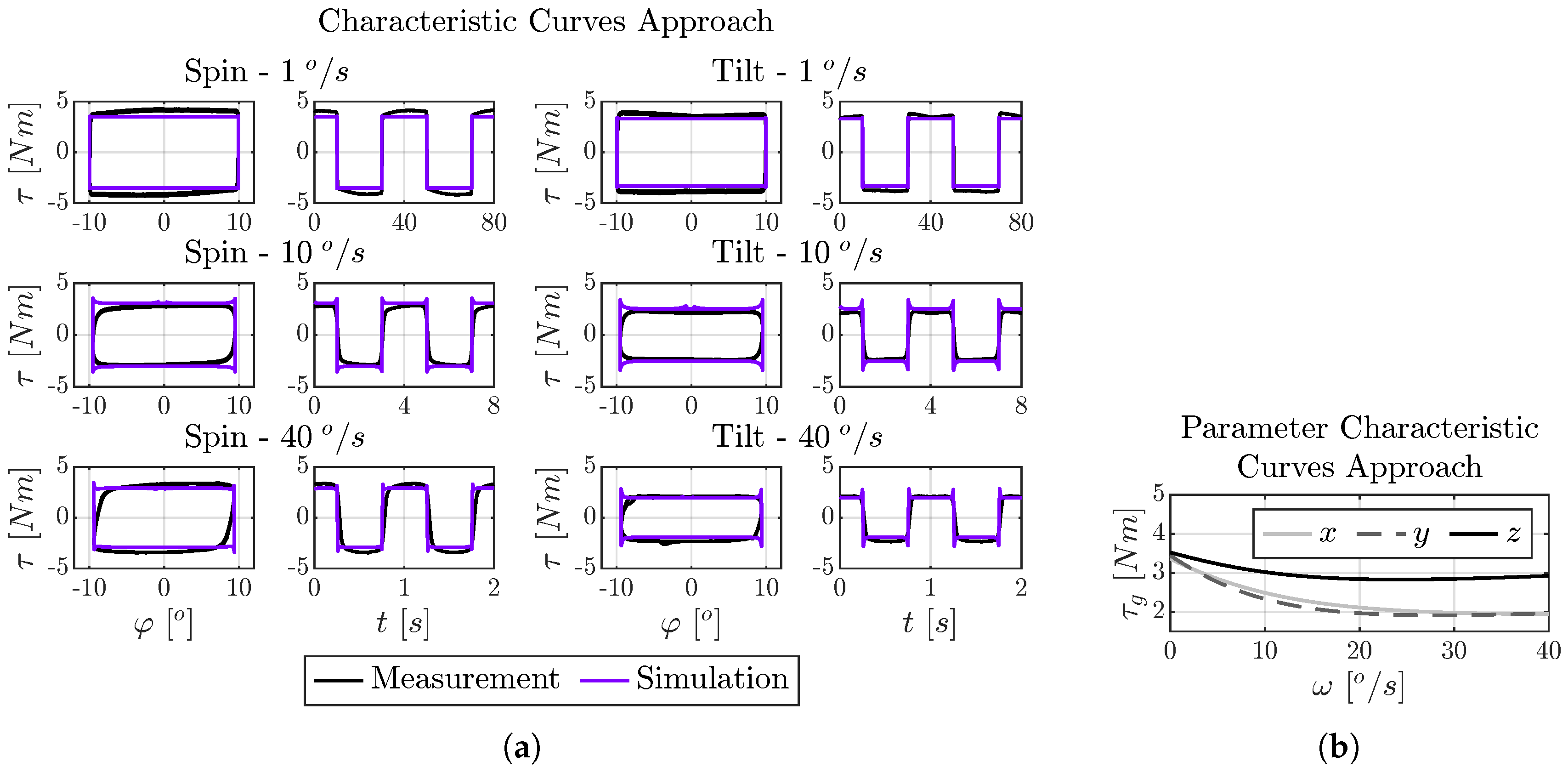
7.3. Fitting Results for the Characteristic Curves Model
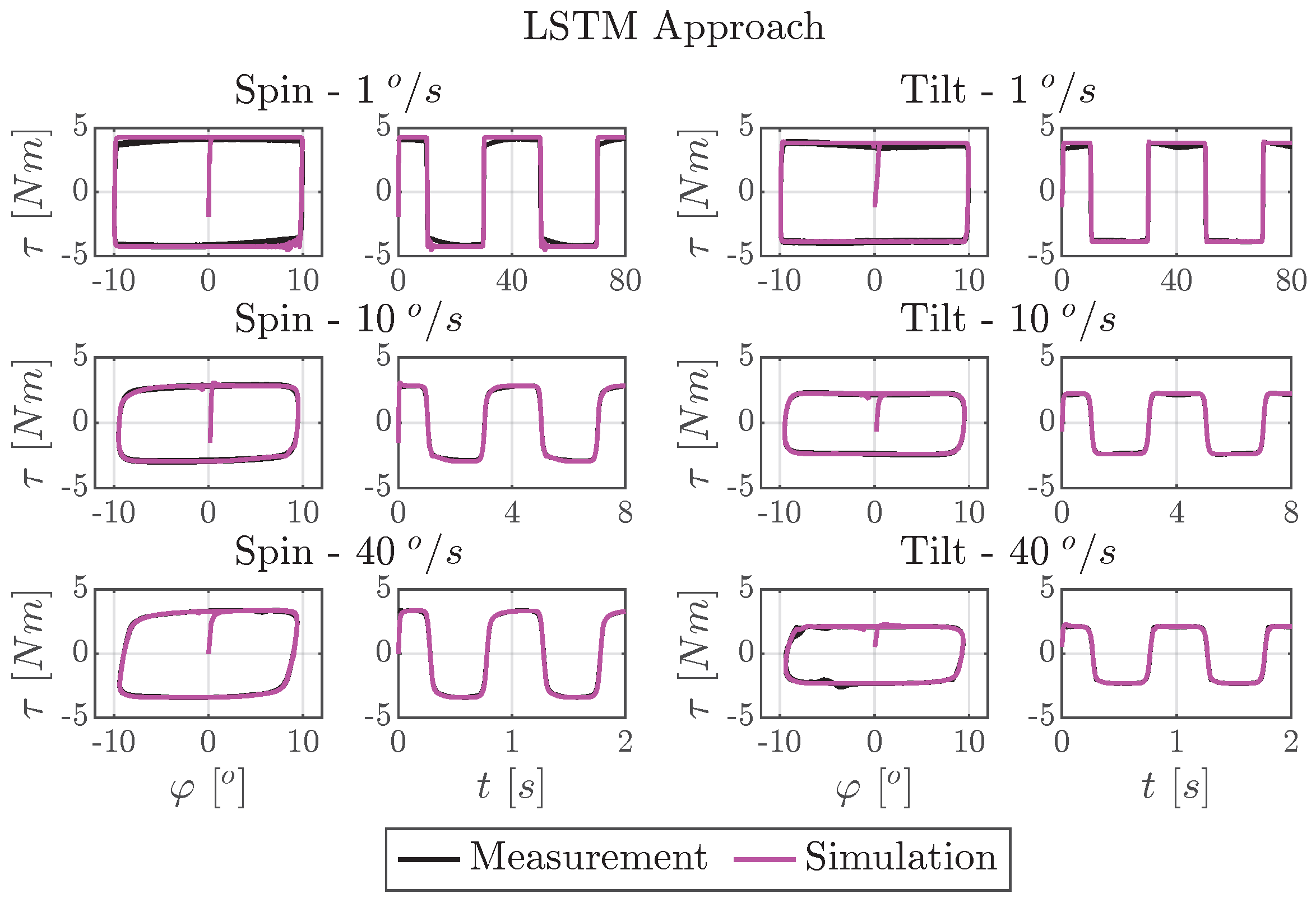
7.4. Fitting Results for the LSTM Model
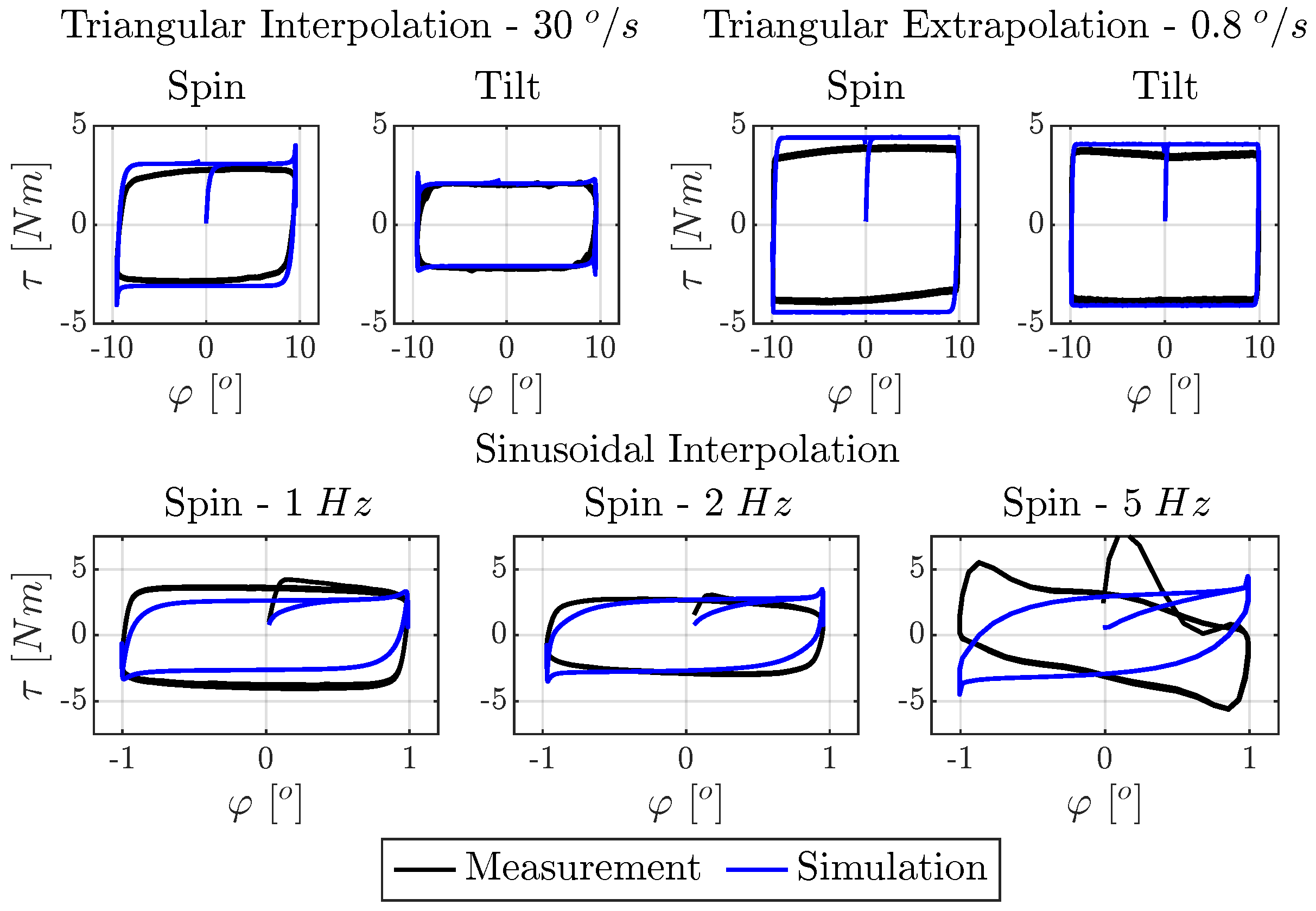
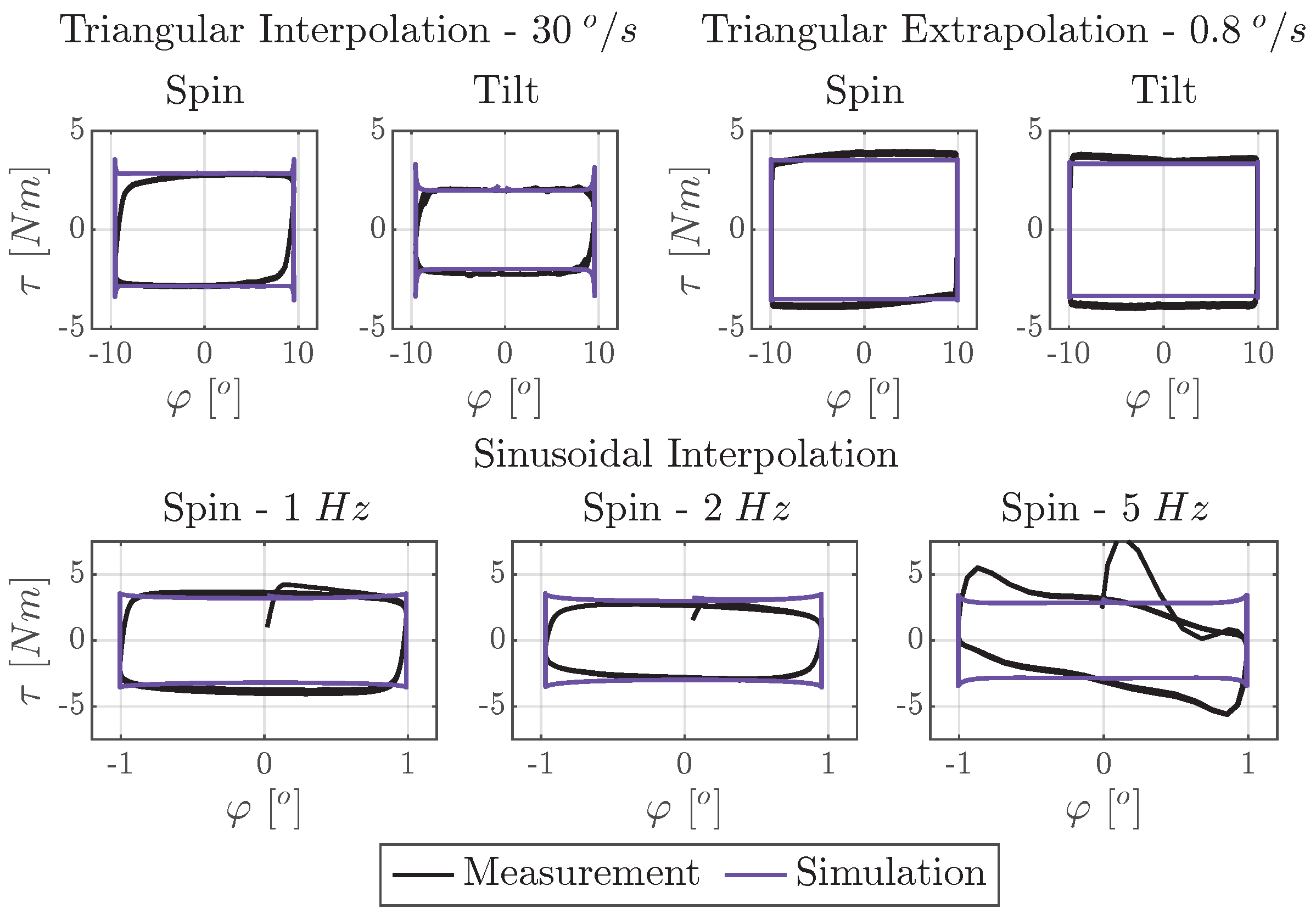
7.5. Synthetic Extrapolation of Model Approaches
7.5.1. Extrapolation for High Angular Velocities
7.5.2. Extrapolation for Fast and Small Excitations
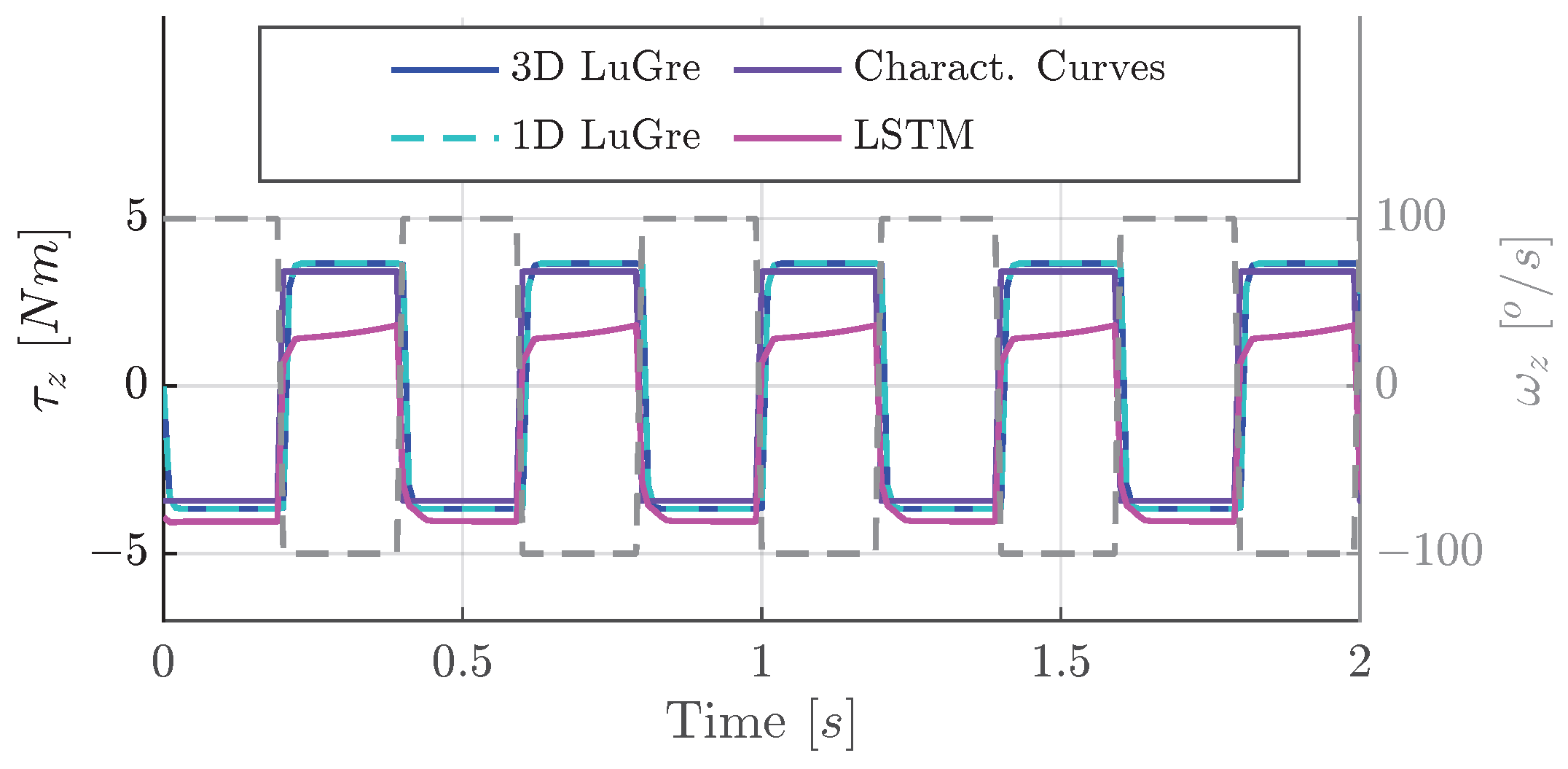
7.5.3. Model Behavior at Mixed Excitations
7.6. Discussion of Results
8. Conclusions
- A one-dimensional LuGre model;
- A static characteristic curve model; and
- A black-box long short-term memory (LSTM) model.
- Parameter Estimation Framework: The proposed method enables the efficient and reproducible identification of parameters in differentiable dynamic models. It supports the integration of both physically motivated and black-box model structures within a single optimization framework.
- Model Fitting Accuracy: The LSTM model achieved the highest numerical accuracy, showing an NRMSE of 0.0482 on the training dataset and 0.1887 on the test dataset. Both LuGre-based models followed closely, with NRMSE values near 0.13 for training data and 0.26 for test data. The static characteristic curve model showed the lowest performance with errors of 0.2711 on the training set and 0.3021 on the test set.
- Extrapolation Behavior and Robustness: While the LSTM model produced highly accurate results within the training domain, its behavior in extrapolated conditions was irregular, asymmetric, and physically implausible. This disqualifies it from use in real-time or safety-critical applications such as driving simulators.
- Numerical Stability of the Static Model: The characteristic curve model does not capture dynamic effects. As a result, it generates excessively large torque values under fast or small excitations, which can cause numerical instability in fixed-step simulations.
- Best Overall Performance—Three-Dimensional LuGre Model: Among the evaluated approaches, the three-dimensional LuGre model demonstrated the best balance between fitting accuracy, physical realism, and numerical robustness. Its ellipsoidal coupling of rotational degrees of freedom enables smooth and consistent torque behavior under multidimensional excitations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Performance Linearization
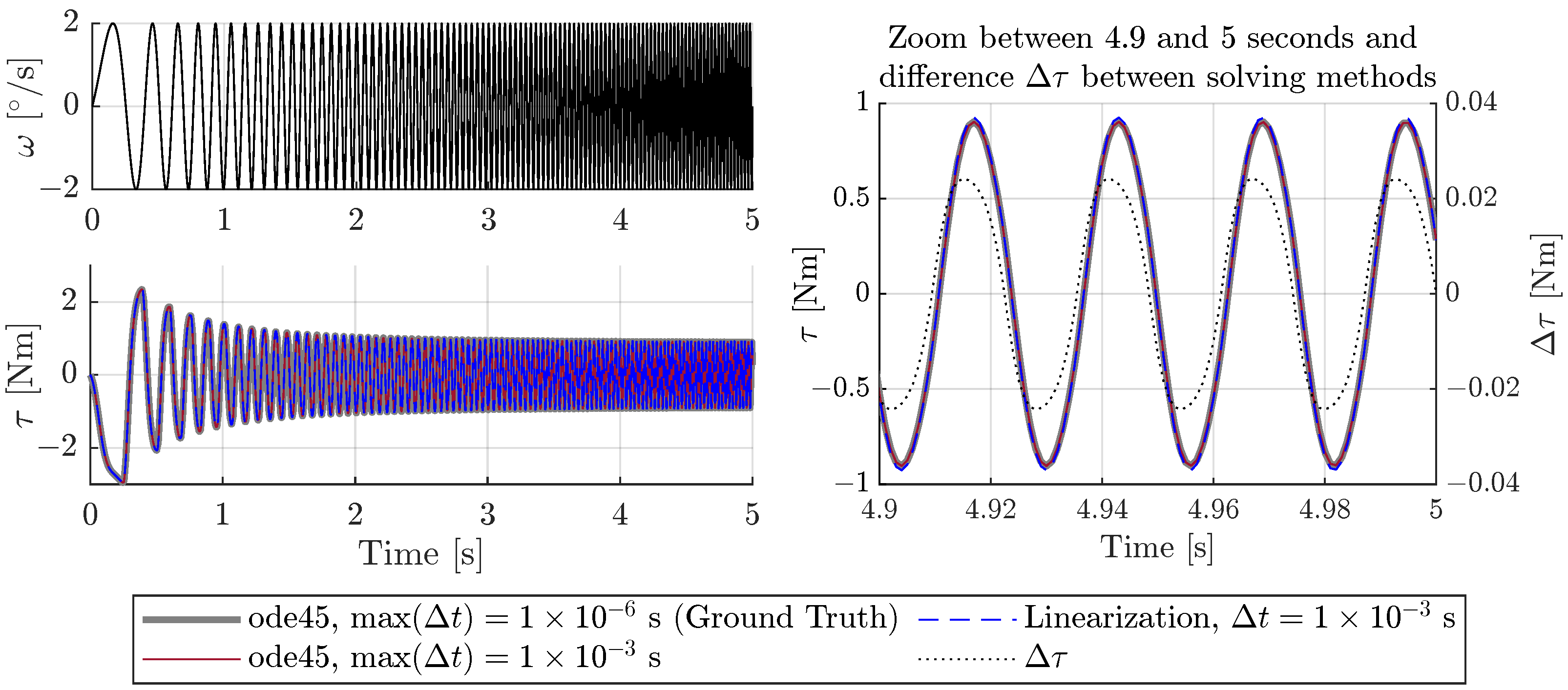
Appendix B. Sensor Specification
| Property | Strut Mount | Wheel Carrier |
|---|---|---|
| Type | Dytran Instruments 7556A1 | PCB 3713B1150G |
| Input Range | ±29.43 m/s2 | ±490.5 m/s2 |
| Frequency Range (PI) | 0–800 Hz | 0–1000 Hz |
Appendix C. NRMSE
Appendix D. Determination of Operation Ranges

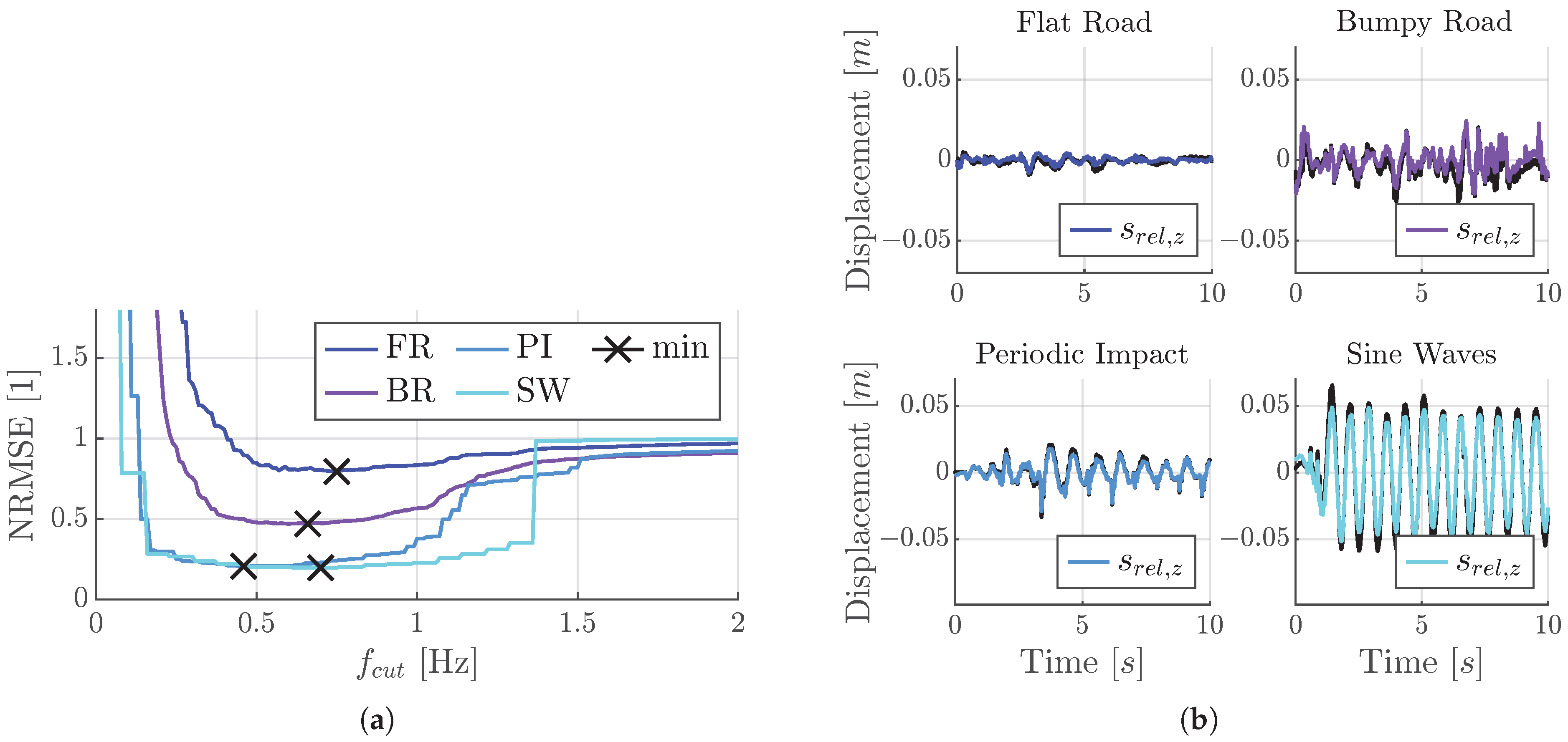
Appendix E. Specification of Tracks
| Track | Velocity | Description |
|---|---|---|
| Flat Road (FR) | 60 km/h | ISO 8608 Classification A |
| Bumpy Road (BR) | 80 km/h | ISO 8608 Classification C |
| Periodic Impact (PI) | 20 km/h | Concrete slabs with edges |
| Sine Waves (SW) | 60 km/h | Concrete modules with sinus shape |
Appendix F. Classification of the Flat Road
Appendix G. Measurement Program of the Component Test Bench
| Measurement in Spin and Tilt Direction | |||||
|---|---|---|---|---|---|
| Axial Preload of 5 kN | |||||
| Triangular Angle Signal | Sinusoidal Angle Signal | ||||
| Pos | Angle | Angular | Pos | Angle | Frequency |
| Velocity | |||||
| 1 | /s | 9 | |||
| 2 | /s | 10 | |||
| 3 | /s | 11 | |||
| 4 | /s | 12 | |||
| 5 | /s | 13 | |||
| 6 | /s | ||||
| 7 | /s | ||||
| 8 | /s | ||||
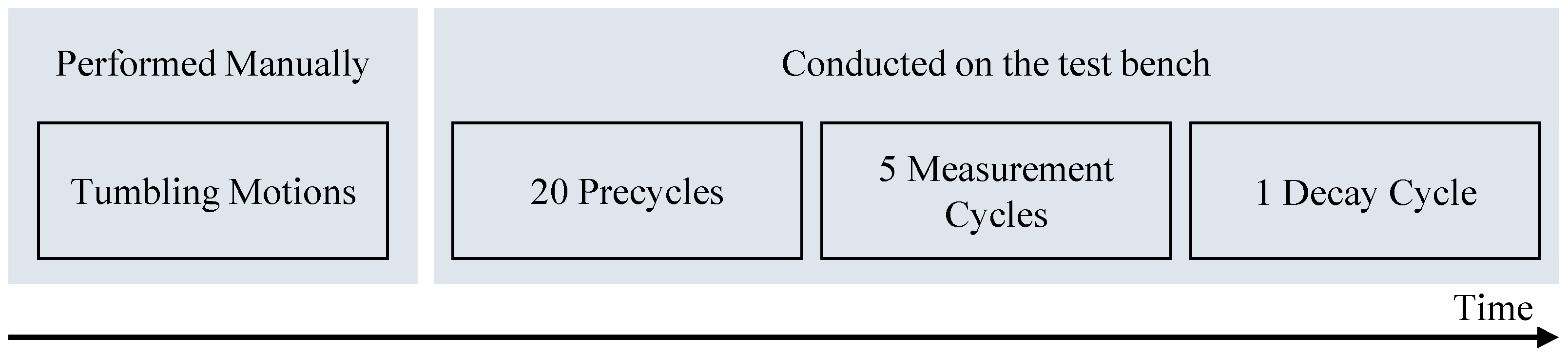
Appendix H. Preconditioning of Ball Joints
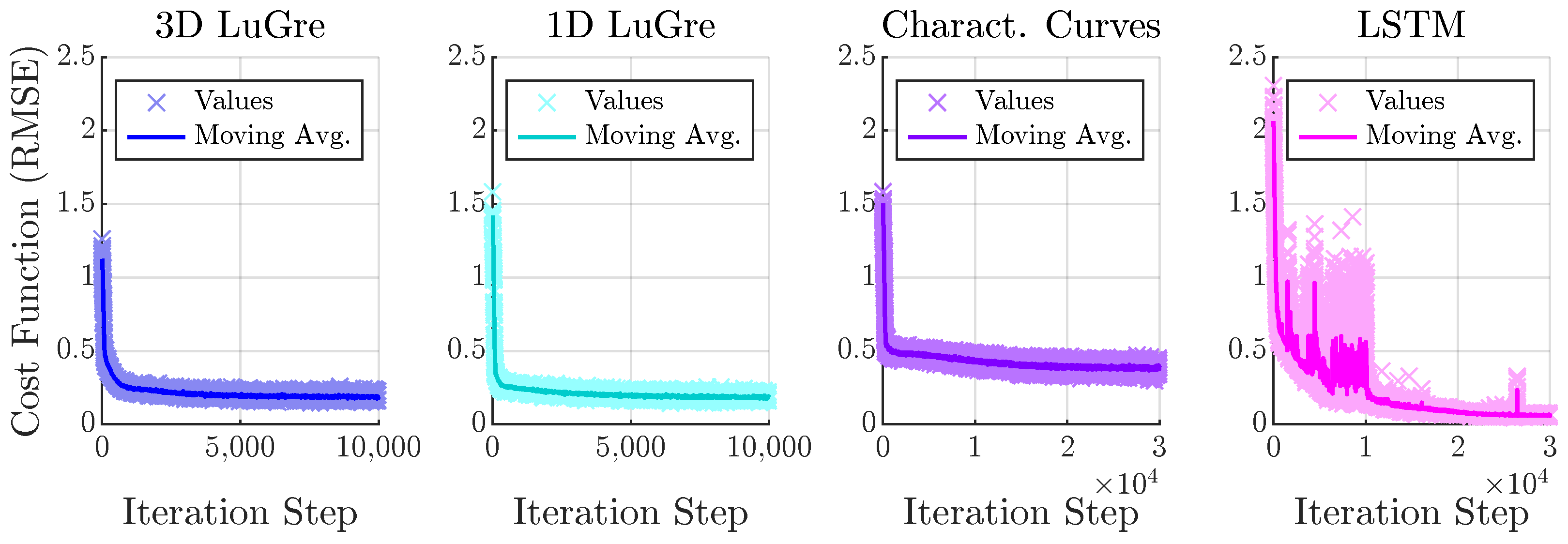
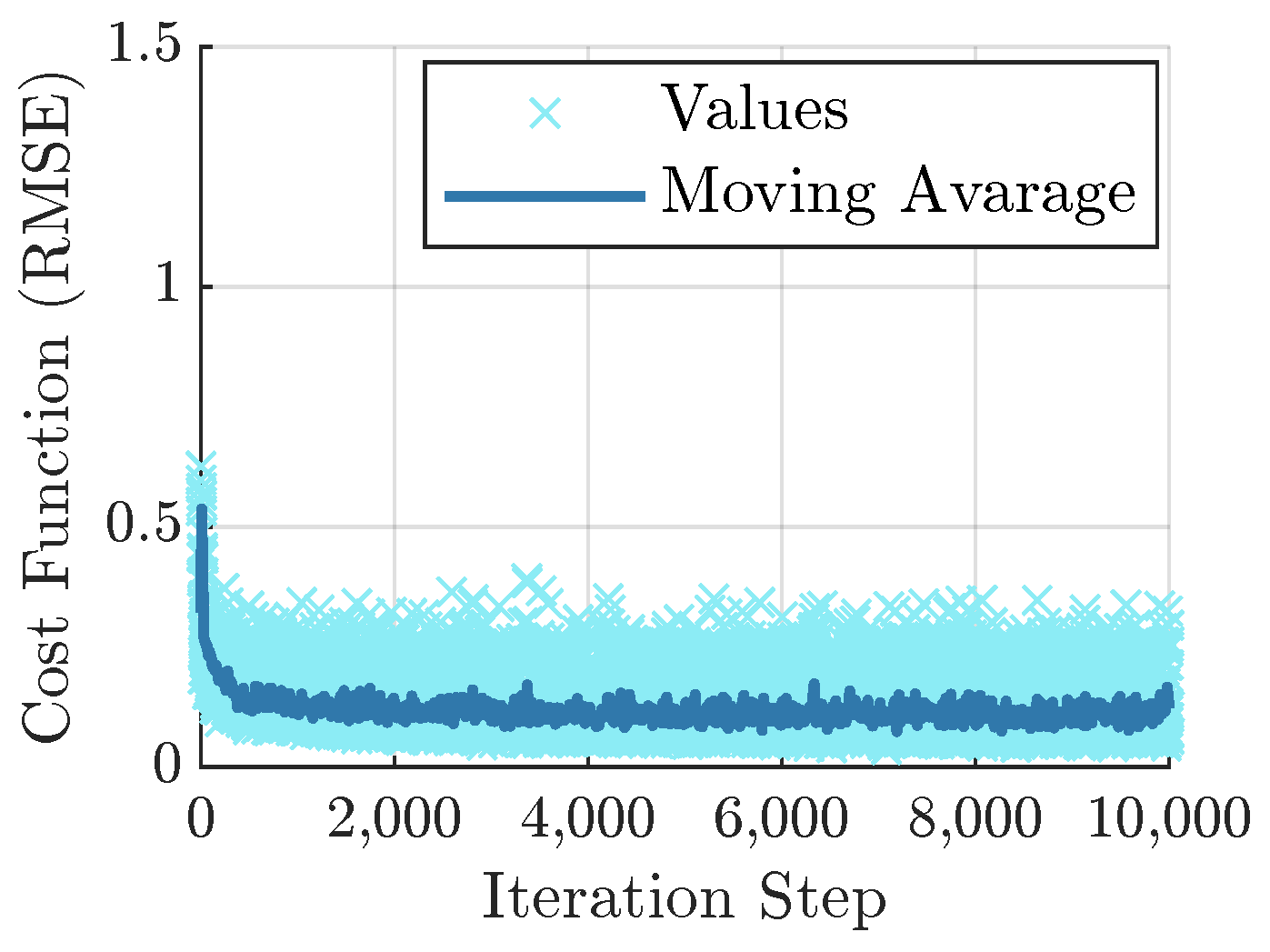
Appendix I. Parameter Estimation Performance over Iterations
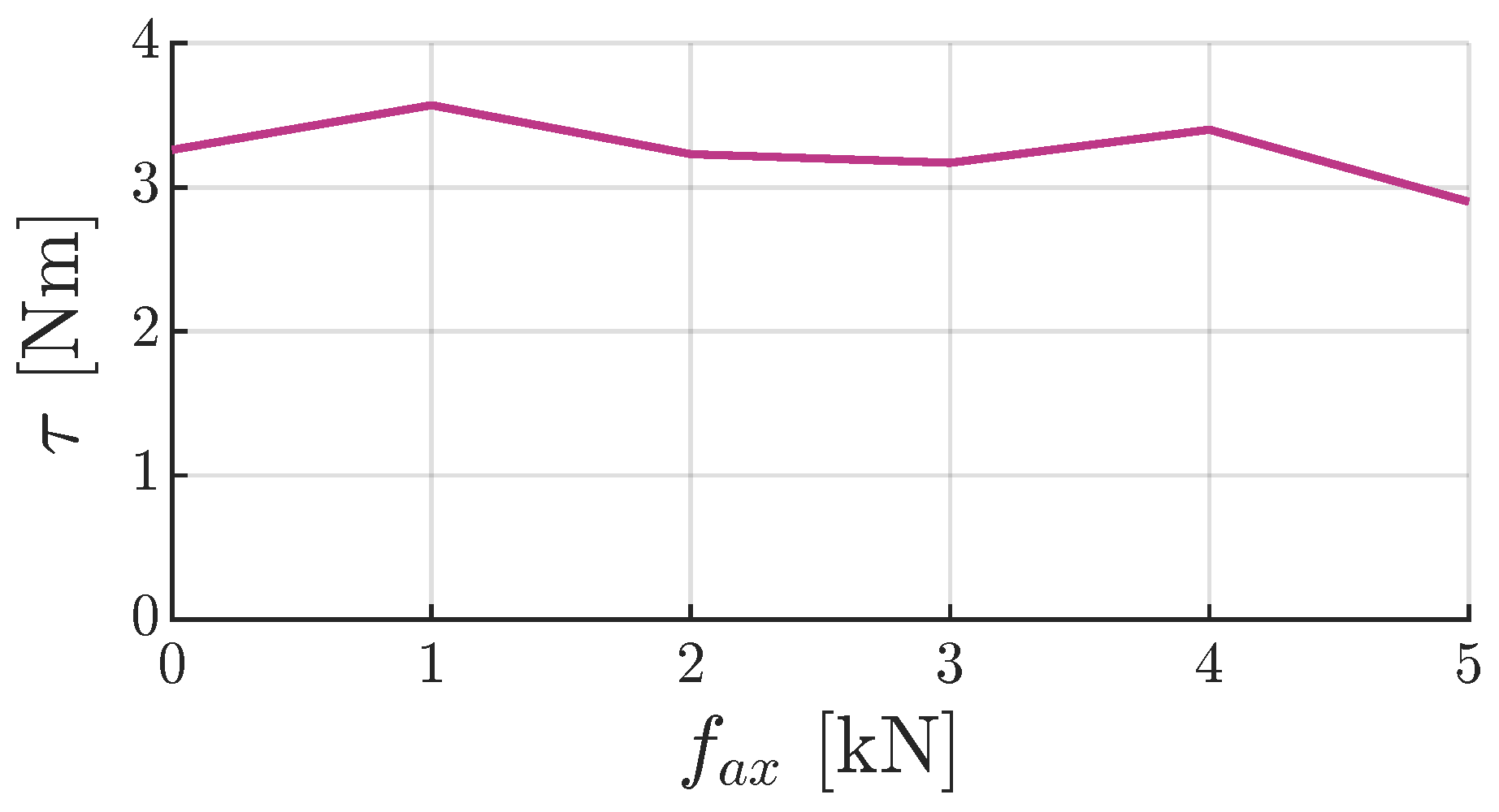
Appendix J. Influence of Load
Appendix K. Model Fitting with Constant σ0 and σ1

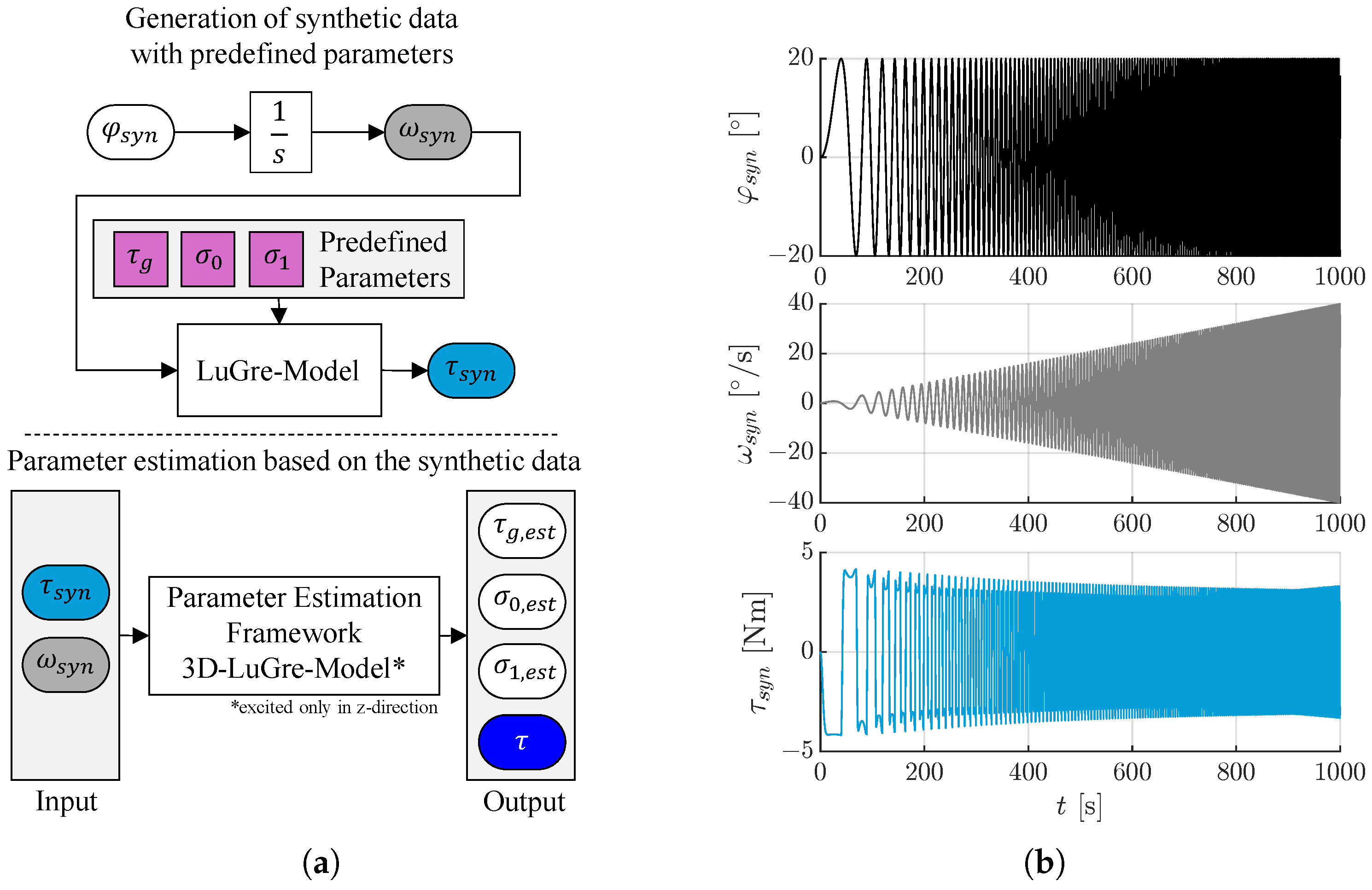
Appendix L. Reproduction of Predefined Parameters

References
- Schramm, D.; Hiller, M.; Bardini, R. Modellbildung und Simulation der Dynamik von Kraftfahrzeugen; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Huber, W. Industrie 4.0 in der Automobilproduktion; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2016. [Google Scholar] [CrossRef]
- Nan, J.; Ge, Z.; Ye, X.; Burke, A.F.; Zhao, J. Model predictive control for autonomous vehicle path tracking through optimized kinematics. Results Eng. 2024, 24, 103123. [Google Scholar] [CrossRef]
- Martin, S.; Schütte, J.; Bäumler, C.; Sextro, W.; Tröster, T. Identification of joints for a load-adapted shape in a body in white using steady state vehicle simulations. Forces Mech. 2022, 6, 100065. [Google Scholar] [CrossRef]
- Winner, H.; Hakuli, S.; Lotz, F.; Singer, C. Handbook of Driver Assistance Systems; Springer International Publishing: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Pech, D.; Dessort, R.; Prokop, G. Experimental parameter identification of scalable white and grey box jounce bumper models for ride comfort simulation. Veh. Syst. Dyn. 2024, 63, 1625–1648. [Google Scholar] [CrossRef]
- Troulis, M.; Gnadler, R.; Unrau, H.J. Übertragungsverhalten von Radaufhängungen für Personenwagen im komfortrelevanten Frequenzbereich. ATZ-Automob. Z. 2004, 106, 336–348. [Google Scholar] [CrossRef]
- Xuwang, W.; Chen, X.; Xu, P.; Zhang, Y. The Effect of Friction on Ride Comfort Simulation and Suspension Optimization; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Angrick, C.; Prokop, G.; Knauer, P.; Wagner, A. Improved prediction of ride comfort characteristics by considering suspension friction in the automotive development process. In 6th International Munich Chassis Symposium 2015: Chassis. Tech Plus; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2015; pp. 377–403. [Google Scholar] [CrossRef]
- Matheus, A.D.C.; De Oliveira, W.R.; Villani, E. A Safety-Oriented Motion Cueing Algorithm for a Serial Robotic Flight Simulator Using a Predictive Neural Network Reference Governor. IEEE Trans. Intell. Transp. Syst. 2024, 25, 15718–15731. [Google Scholar] [CrossRef]
- Official Journal of the European Union: Directive 2006/42/EC Annex IV. 2006. Available online: https://eur-lex.europa.eu/eli/dir/2006/42/oj/eng (accessed on 19 September 2025).
- Miller, S.; Wendlandt, J. Real-Time Simulation of Physical Systems Using Simscape™. In Real-Time Simulation Technologies; Series Title: Computational Analysis, Synarticle, & Design Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2012; Volume 13, pp. 581–598. [Google Scholar] [CrossRef]
- Stietz, T. Bewegungsverhalten von Kugelgelenken in Fahrzeugachsen im Akustisch Relevanten Frequenzbereich; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2018. [Google Scholar] [CrossRef]
- Smyrek, C. Simulation der Stillstandszeitabhängigen Losbrechkraft im Mischreibungskontakt Mittels Eines Viskoelastischen Ansatzes. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2021. [Google Scholar] [CrossRef]
- Wozniak, M.; Siczek, K.; Ozuna, G.; Kubiak, P. A Study on Wear and Friction of Passenger Vehicles Control Arm Ball Joints. Energies 2021, 14, 3238. [Google Scholar] [CrossRef]
- Dahl, P.R. A Solid Friction Model; The Aerospace Corporation: El Segundo, CA, USA, 1968. [Google Scholar] [CrossRef]
- De Wit, C.C.; Olsson, H.; Astrom, K.; Lischinsky, P. Dynamic Friction Models and Control Design. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; pp. 1920–1926. [Google Scholar] [CrossRef]
- Johanastrom, K.; Canudas-de Wit, C. Revisiting the LuGre friction model. IEEE Control Syst. 2008, 28, 101–114. [Google Scholar] [CrossRef]
- Kato, H. Friction model for planar two-dimensional motion. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 000220–000225. [Google Scholar] [CrossRef]
- Shao, R.; Wahle, M.; Zimmermann, M. A model for the dynamic friction behaviour of rubber-like materials. Tribol. Int. 2021, 164, 107220. [Google Scholar] [CrossRef]
- Velenis, E.; Tsiotras, P.; Canudas-de Wit, C. Extension of the lugre dynamic tire friction model to 2d motion. In Proceedings of the 10th IEEE Mediterranean Conference on Control and Automation-MED, Lisbon, Portugal, 9–12 July 2002. [Google Scholar]
- Pfitzer, K.; Rath, L.; Kolmeder, S.; Corves, B.; Prokop, G. A General Mechanical Formulation of Two-Dimensional Bristle Friction Models with a Focus on the Lugre Model and its Dynamics. SSRN 2025, preprint. [Google Scholar] [CrossRef]
- Ljung, L. System Identification. In Signal Analysis and Prediction; Procházka, A., Uhlíř, J., Rayner, P.W.J., Kingsbury, N.G., Eds.; Birkhäuser Boston: Boston, MA, USA, 1998; pp. 163–173. [Google Scholar] [CrossRef]
- Bradbury, J.; Frostig, R.; Hawkins, P.; Johnson, M.J.; Leary, C.; Maclaurin, D.; Necula, G.; Paszke, A.; VanderPlas, J.; Wanderman-Milne, S.; et al. JAX: Composable Transformations of Python+NumPy Programs. 2018. Available online: https://github.com/jax-ml/jax (accessed on 19 September 2025).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Trinh, M.; Pellenz, Y.; Gruendel, L.; Petrovic, O.; Becher, C. Modeling of Load-dependent Friction in Robot Joints Using Long Short-term Memory Networks. In Proceedings of the ISR Europe 2023: 56th International Symposium on Robotics, Stuttgart, Germany, 26–27 September 2023; pp. 46–53. [Google Scholar]
- Cortes, G.; Garcia-Suarez, J. Data-Driven Dynamic Friction Models based on Recurrent Neural Networks. arXiv 2025, arXiv:2402.14148. [Google Scholar] [CrossRef]
- Ozmen, A.; Hespanha, J.P.; Byl, K. Learning Transferable Friction Models and LuGre Identification via Physics Informed Neural Networks. arXiv 2025, arXiv:2504.12441. [Google Scholar] [CrossRef]
- Gupta, J.K.; Menda, K.; Manchester, Z.; Kochenderfer, M.J. A General Framework for Structured Learning of Mechanical Systems. arXiv 2019, arXiv:1902.08705. [Google Scholar] [CrossRef]
- Lutter, M.; Silberbauer, J.; Watson, J.; Peters, J. A Differentiable Newton Euler Algorithm for Multi-body Model Learning. arXiv 2020, arXiv:2010.09802. [Google Scholar] [CrossRef]
- Geist, A.R.; Trimpe, S. Structured learning of rigid-body dynamics: A survey and unified view from a robotics perspective. arXiv 2020, arXiv:2012.06250. [Google Scholar] [CrossRef]
- Lutter, M.; Peters, J. Combining Physics and Deep Learning to learn Continuous-Time Dynamics Models. arXiv 2023, arXiv:2110.01894. [Google Scholar] [CrossRef]
- Specification AK-LH14—Working committee of the following companies: Audi AG, Bayerische Motoren Werke AG, DaimlerChrysler AG, Porsche AG, Volkswagen AG. Unpublished work. 2004.
- Sage, R.M. The Mathematical Modelling of Ball-Joints with Friction; University of Leicester: Leicester, UK, 1987. [Google Scholar]
- Wu, J.; Li, W.; Xiong, Z. Identification of robot dynamic model and joint frictions using a baseplate force sensor. Sci. China Technol. Sci. 2021, 65, 30–40. [Google Scholar] [CrossRef]
- Trinh, M.; Schwiedernoch, R.; Gründel, L.; Storms, S.; Brecher, C. Friction Modeling for Structured Learning of Robot Dynamics. In Production at the Leading Edge of Technology; Springer: Cham, Switzerland, 2023; pp. 396–406. [Google Scholar] [CrossRef]
- Corrêa Do Lago, A.W.; Braz De Sousa, D.H.; Domingues, P.H.; Daneker, M.; Lu, L.; Hultmann Ayala, H.V. Physics-informed and black-box Identification of robotic actuator with a flexible joint. IFAC-PapersOnLine 2024, 58, 259–264. [Google Scholar] [CrossRef]
- Chen, S.; Cheng, G.; Pang, Y. Dynamic Analysis and Trajectory Tracking Control for a Parallel Manipulator with Joint Friction. Appl. Sci. 2022, 12, 6682. [Google Scholar] [CrossRef]
- Leguet, G.D.; Roche, J.F.; Hamdi, M.A.; Rachik, M. Investigation of ball joints under static and dynamic loads. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017; p. 14. [Google Scholar] [CrossRef]
- Kang, J. The onset condition of friction noise in ball joint under concentric loading. Appl. Acoust. 2015, 89, 57–61. [Google Scholar] [CrossRef]
- Kang, J. Theoretical Model for Friction-Induced Vibration of Ball Joint System under Mode-Coupling Instability. Tribol. Trans. 2015, 58, 807–814. [Google Scholar] [CrossRef]
- Kang, J. Nonlinear Vibration Induced by Friction in a Ball Joint System. Lubricants 2022, 10, 201. [Google Scholar] [CrossRef]
- Scholten, J. Theoretische und Experimentelle Untersuchungen zur Beanspruchungsermittlung Wartungsfreier Gelenklager; Ruhr University Bochum: Bochum, Germany, 2001. [Google Scholar]
- Haensel, H. Systemanalystische Betrachtung Sphärischer Tribomechanischer Systeme; Ruhr University Bochum: Bochum, Germany, 2004. [Google Scholar]
- Fuchs, H. Universale Ansätze zur Abbildung von Mangelschmierungseffekten in einer Tribomechanischen Bauteilsimulation; Ruhr University Bochum: Bochum, Germany, 2017. [Google Scholar]
- Weiss, C.; Morlock, M.M.; Hoffmann, N.P. Friction induced dynamics of ball joints: Instability and post bifurcation behavior. Eur. J.-Mech.-A/Solids 2014, 45, 161–173. [Google Scholar] [CrossRef]
- Neumann, D. Entwicklung einer Prognosemethode der beim “Parkieren im Stand” Auftretenden Zahnstangenkräfte für die Virtuelle Lenkungsauslegung. Ph.D. Thesis, Universität Duisburg-Essen, Essen, Germany, 2023. [Google Scholar] [CrossRef]
- Olsson, H.; Åström, K.; Canudas De Wit, C.; Gäfvert, M.; Lischinsky, P. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef]
- Stuhlenmiller, F.; Clos, D.; Rinderknecht, S.; Beckerle, P.; Font-Llagunes, J.M. Impact of friction and gait parameters on the optimization of series elastic actuators for gait assistance. Mech. Mach. Theory 2019, 133, 737–749. [Google Scholar] [CrossRef]
- Wojtyra, M.; Pękal, M.; Frączek, J. Utilization of the Moore-Penrose inverse in the modeling of overconstrained mechanisms with frictionless and frictional joints. Mech. Mach. Theory 2020, 153, 103999. [Google Scholar] [CrossRef]
- Stribeck, R. Die wesentlichen Eigenschaften der Gleit und Rollenlager. In Mitteilungen über Forschungsarbeiten auf dem Gebiete des Ingenieurwesens, Insbesondere aus den Laboratorien der Technischen Hochschulen; Springer: Berlin/Heidelberg, Germany, 1903. [Google Scholar]
- Lewis, R.; Olofsson, U. Wheel-Rail Interface Handbook; Woodhead Publishing in Mechanical Engineering; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Canudas De Wit, C.; Olsson, H.; Astrom, K.; Lischinsky, P. A new model for control of systems with friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- Swevers, J.; Al-Bender, F.; Ganseman, C.; Projogo, T. An integrated friction model structure with improved presliding behavior for accurate friction compensation. IEEE Trans. Autom. Control 2000, 45, 675–686. [Google Scholar] [CrossRef]
- Marques, F.; Wolinski, L.; Wojtyra, M.; Flores, P.; Lankarani, H.M. An investigation of a novel LuGre-based friction force model. Mech. Mach. Theory 2021, 166, 104493. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Marques, F.; Isaac, F.; Dourado, N.; Souto, A.P.; Flores, P.; Lankarani, H.M. A Study on the Dynamics of Spatial Mechanisms with Frictional Spherical Clearance Joints. J. Comput. Nonlinear Dyn. 2017, 12, 051013. [Google Scholar] [CrossRef]
- Sorine, M.; Szymanski, J. A New Dynamic Multi-DOF Tire-Model. IFAC Proc. Vol. 2000, 33, 549–554. [Google Scholar] [CrossRef]
- Liang, J.; Fillmore, S.; Ma, O. An extended bristle friction force model with experimental validation. Mech. Mach. Theory 2012, 56, 123–137. [Google Scholar] [CrossRef]
- Sorine, M. Applications of hysteresis models: Contact friction in tires, muscle contraction. In Proceedings of the IEEE CDC 98 Workshop, Tampa, FL, USA, 16 December 1998; Volume 2. [Google Scholar]
- Geist, A.R.; Trimpe, S. Structured Learning of Rigid-Body Dynamics: A Survey and Unified View. GAMM-Mitteilungen 2021, 44, e202100009. [Google Scholar] [CrossRef]
- Heiden, E.; Millard, D.; Sukhatme, G.S. Real2Sim Transfer using Differentiable Physics. In Proceedings of the R:SS Workshop on Closing the Reality Gap in Sim2real Transfer for Robotic Manipulation, New York, NY, USA, 27 June 2019. [Google Scholar]
- Heiden, E.; Millard, D.; Coumans, E.; Sheng, Y.; Sukhatme, G.S. NeuralSim: Augmenting Differentiable Simulators with Neural Networks. arXiv 2021, arXiv:2011.04217. [Google Scholar] [CrossRef]
- Heiden, E.; Denniston, C.E.; Millard, D.; Ramos, F.; Sukhatme, G.S. Probabilistic Inference of Simulation Parameters via Parallel Differentiable Simulation. arXiv 2021, arXiv:2109.08815. [Google Scholar]
- Deur, J.; Asgari, J.; Hrovat, D. A 3D Brush-type Dynamic Tire Friction Model. Veh. Syst. Dyn. 2004, 42, 133–173. [Google Scholar] [CrossRef]
- Holmes, M.H. Optimization: Descent Methods. In Introduction to Scientific Computing and Data Analysis; Series Title: Texts in Computational Science and Engineering; Springer International Publishing: Cham, Switzerland, 2023; Volume 13, pp. 411–474. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- ISO 8608:2016-11; Mechanical Vibration-Road Surface Profiles-Articleing of Measured Data. ISO: Genève, Switzerland, 2016.
- Gerlach, S. Zahlendarstellung und numerische Fehler. In Computerphysik; Springer: Berlin/Heidelberg, Germany, 2024; pp. 149–157. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals and Systems, 2nd ed.; Always learning; Pearson Education: London, UK, 2014. [Google Scholar]
- Hofmann, S. Numerische Integration von Beschleunigungssignalen. Mitteilungen Inst. Maschinenwesen Tech. Univ. Clausthal 2013, 38, 103–114. [Google Scholar]
- Albarbar, A.; Badri, A.; Sinha, J.K.; Starr, A. Performance evaluation of MEMS accelerometers. Measurement 2009, 42, 790–795. [Google Scholar] [CrossRef]
- Ersoy, M.; Gies, S. Fahrwerkhandbuch; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]




| 3D LuGre | 1D LuGre | Characteristic Curves | LSTM | |
|---|---|---|---|---|
| Velocity Dependent | x | x | x | x |
| Dependent Directions | x | |||
| Dynamic Behavior | x | x | x | |
| White Box | x | x | x | |
| Continuously | x | x | x |
| Excitations | ||
|---|---|---|
| Triangular | Sinusoidal | |
| Training Data | °/s, °/s, °/s | - |
| Test Data | °/s, °/s | 1 Hz, 2 Hz, 5 Hz |
| Hyperparameters | ||
|---|---|---|
| Nm | 10 Nm | |
| 100 Nm/rad | 10,000 Nm/rad | |
| Nms/rad | 20 Nms/rad | |
| 3D-LuGre | 1D-LuGre | Charact. Curves | LSTM | |
|---|---|---|---|---|
| NRMSE of training data | 0.1288 | 0.1281 | 0.2711 | 0.0482 |
| NRMSE of test data | 0.2596 | 0.2595 | 0.3021 | 0.1887 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pfitzer, K.; Rath, L.; Kolmeder, S.; Corves, B.; Prokop, G. Machine Learning-Based Dynamic Modeling of Ball Joint Friction for Real-Time Applications. Lubricants 2025, 13, 436. https://doi.org/10.3390/lubricants13100436
Pfitzer K, Rath L, Kolmeder S, Corves B, Prokop G. Machine Learning-Based Dynamic Modeling of Ball Joint Friction for Real-Time Applications. Lubricants. 2025; 13(10):436. https://doi.org/10.3390/lubricants13100436
Chicago/Turabian StylePfitzer, Kai, Lucas Rath, Sebastian Kolmeder, Burkhard Corves, and Günther Prokop. 2025. "Machine Learning-Based Dynamic Modeling of Ball Joint Friction for Real-Time Applications" Lubricants 13, no. 10: 436. https://doi.org/10.3390/lubricants13100436
APA StylePfitzer, K., Rath, L., Kolmeder, S., Corves, B., & Prokop, G. (2025). Machine Learning-Based Dynamic Modeling of Ball Joint Friction for Real-Time Applications. Lubricants, 13(10), 436. https://doi.org/10.3390/lubricants13100436






