Real-Time Prediction of Pressure and Film Height Distribution in Plain Bearings Using Physics-Informed Neural Networks (PINNs)
Abstract
1. Introduction
2. Materials and Methods
2.1. EHD Simulation
2.1.1. EHD Model for Radial Plain Bearing
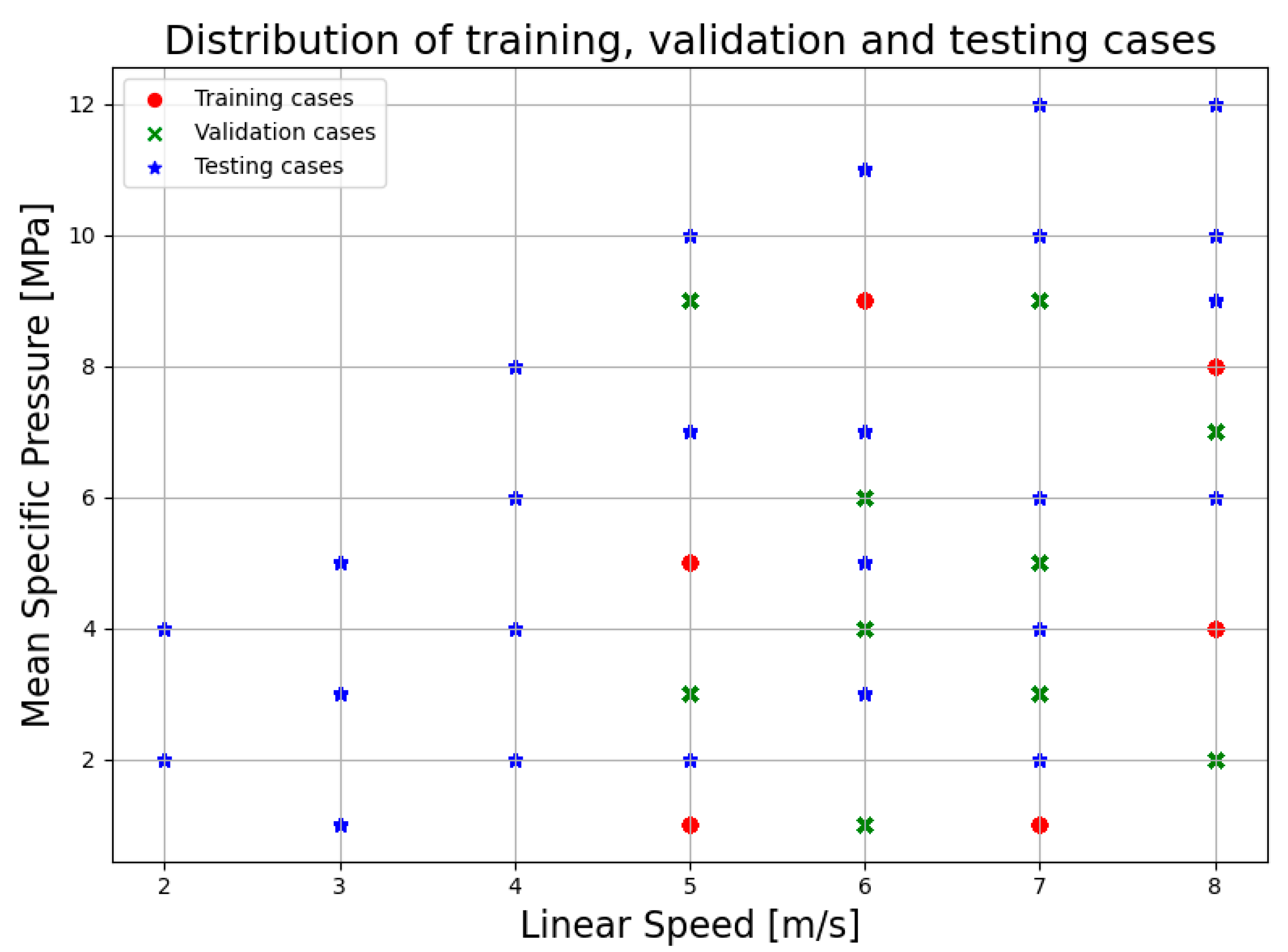
2.1.2. Training, Validation, and Testing Simulation Cases
2.2. PINN Framework
2.2.1. Loss Functions
2.2.2. Training Strategy
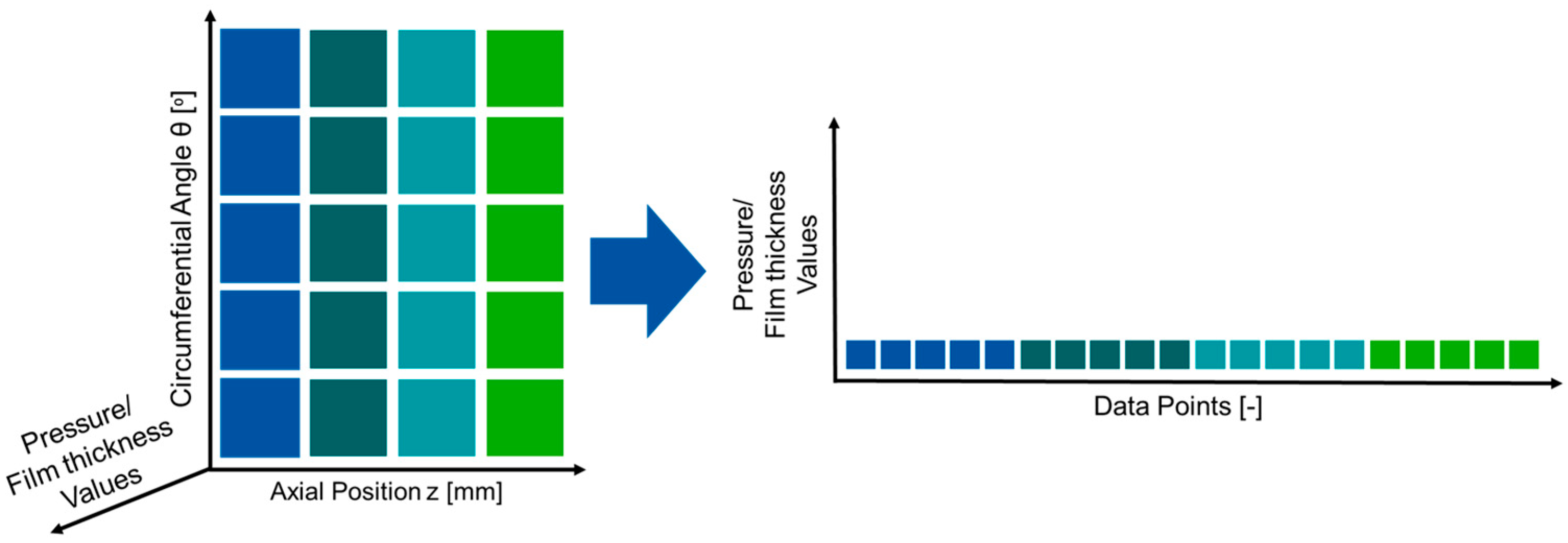
2.2.3. Training Points
3. Results and Discussion
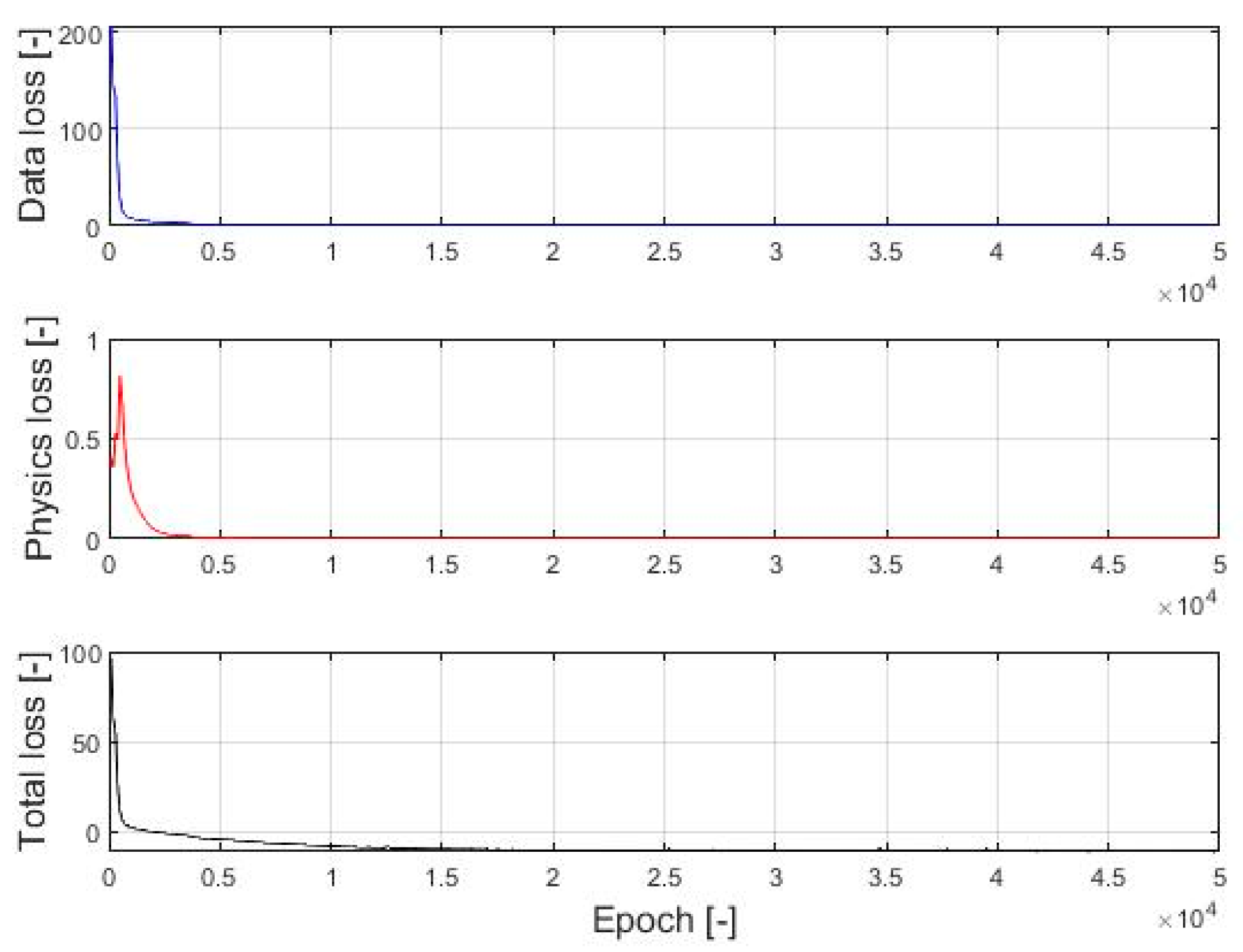
3.1. Model Behaviour and Validation Throughout Training
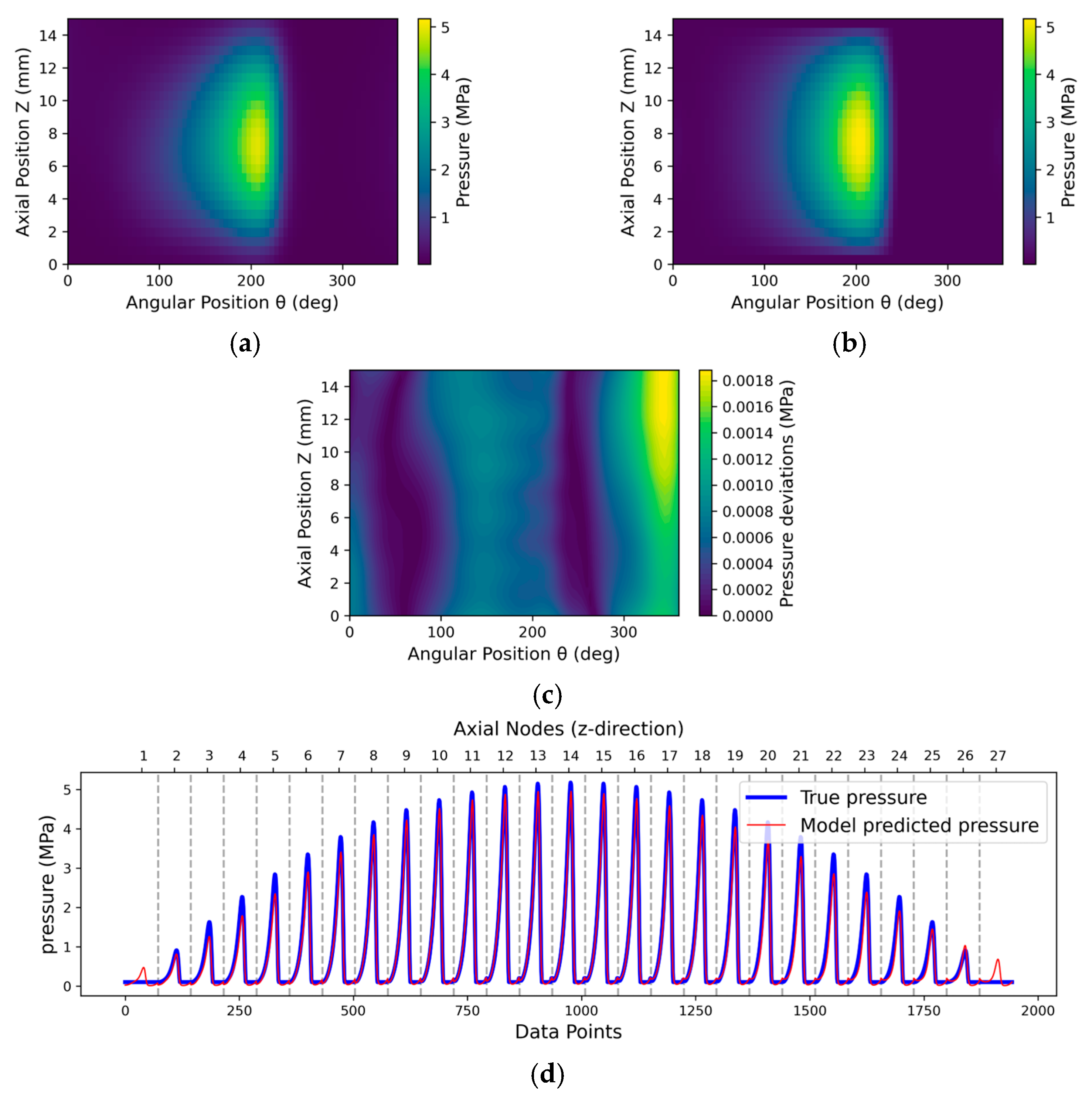
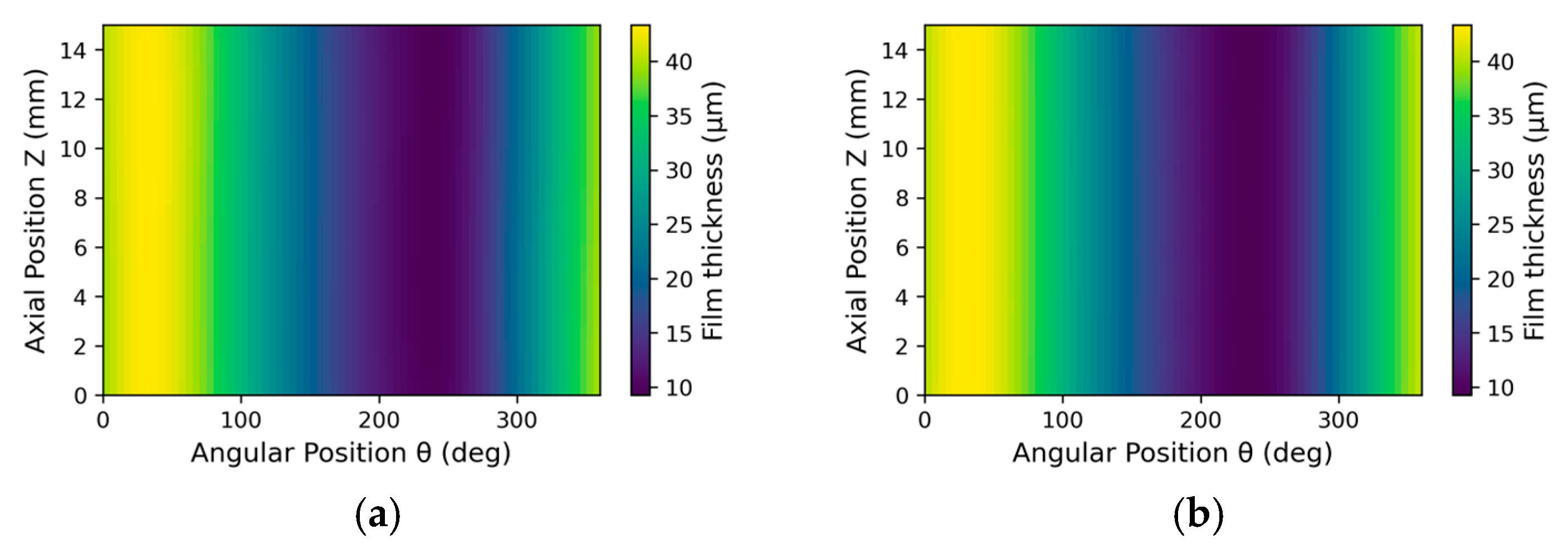
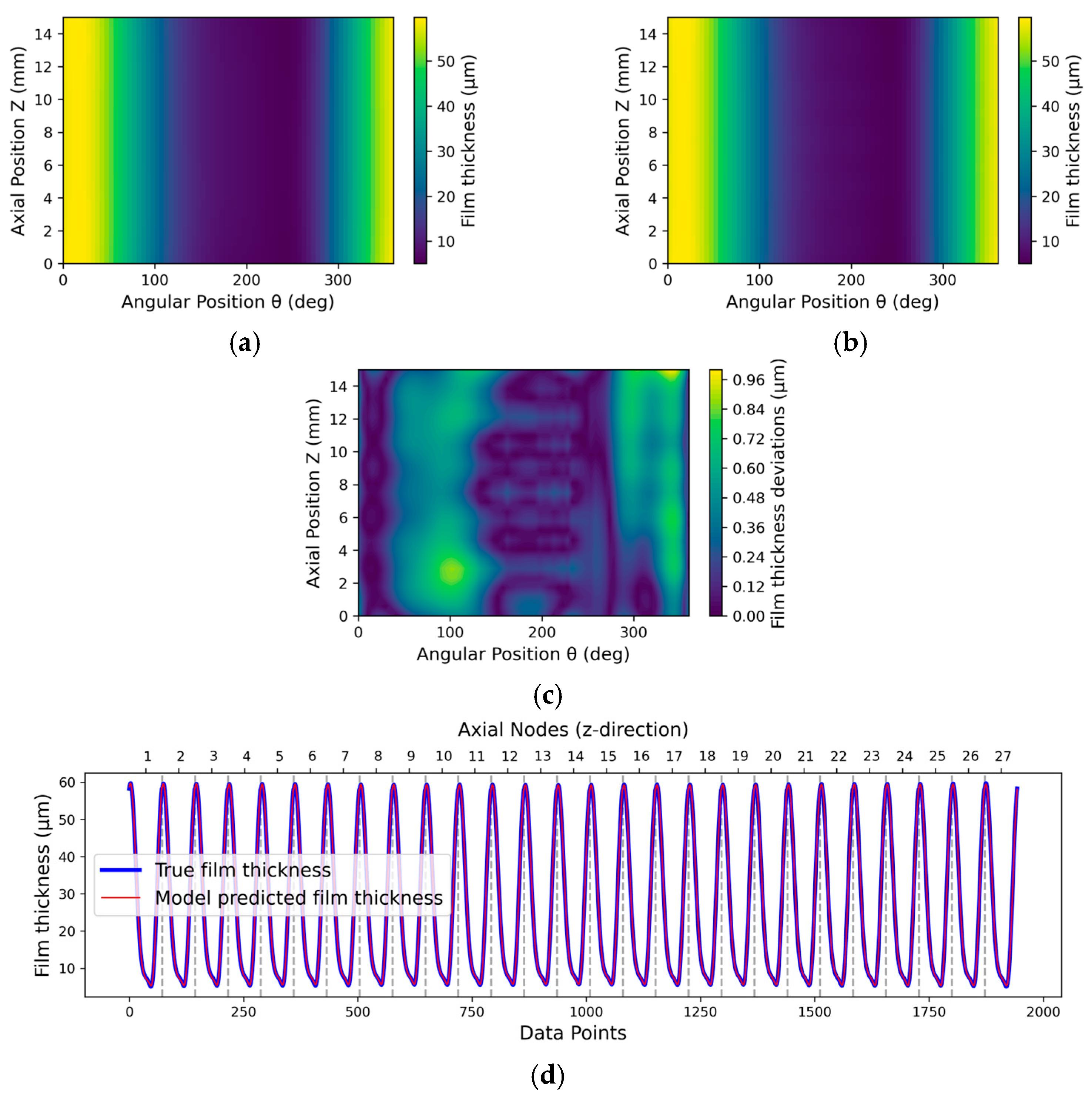
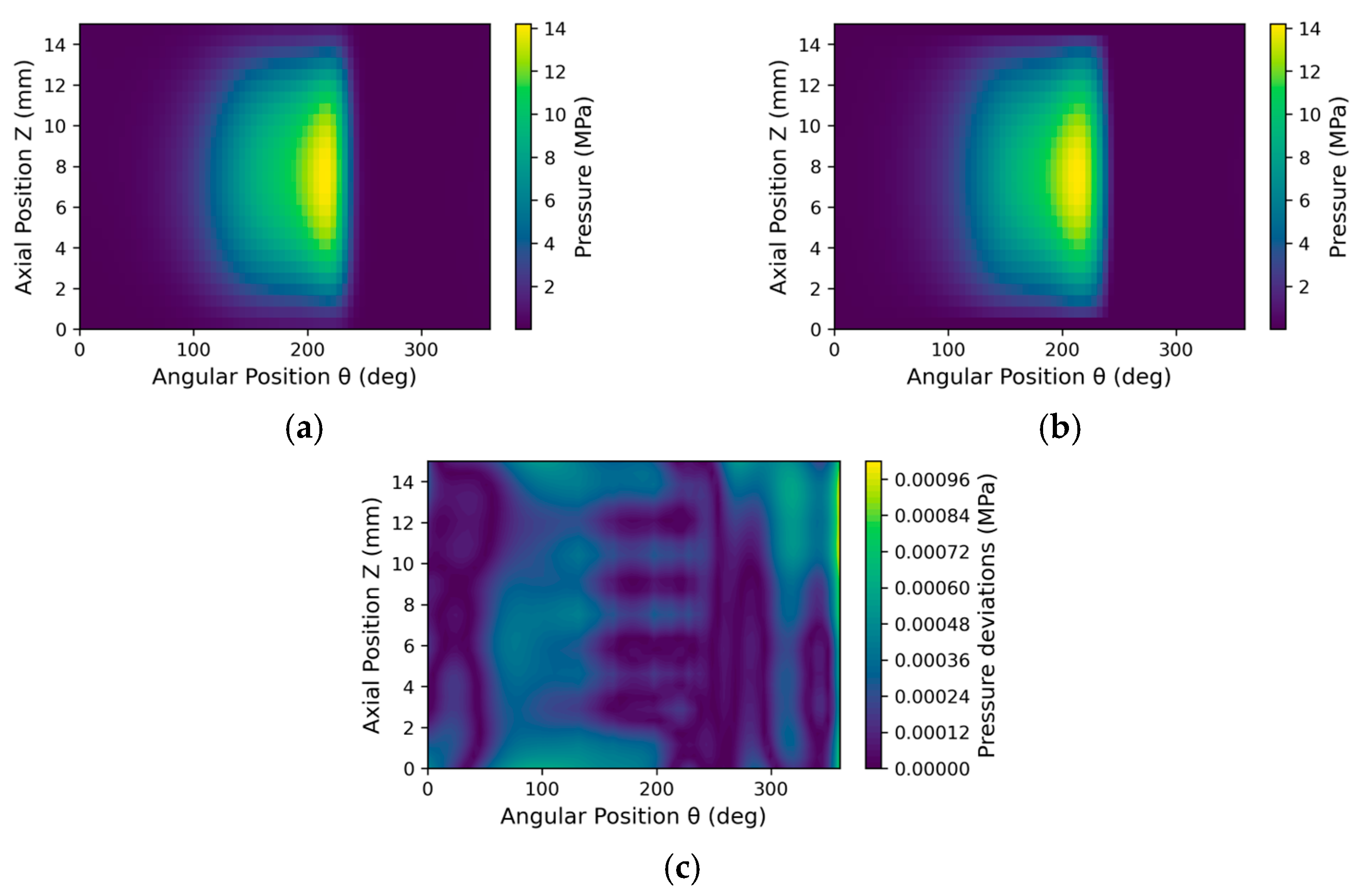
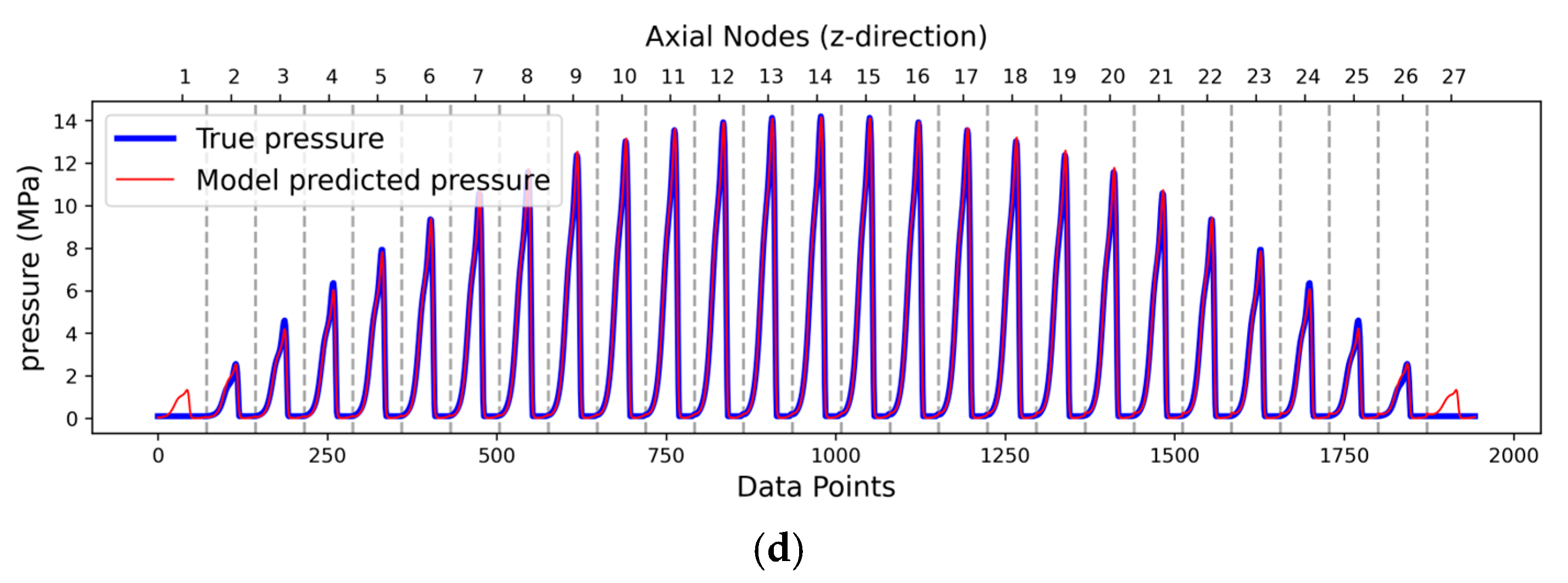
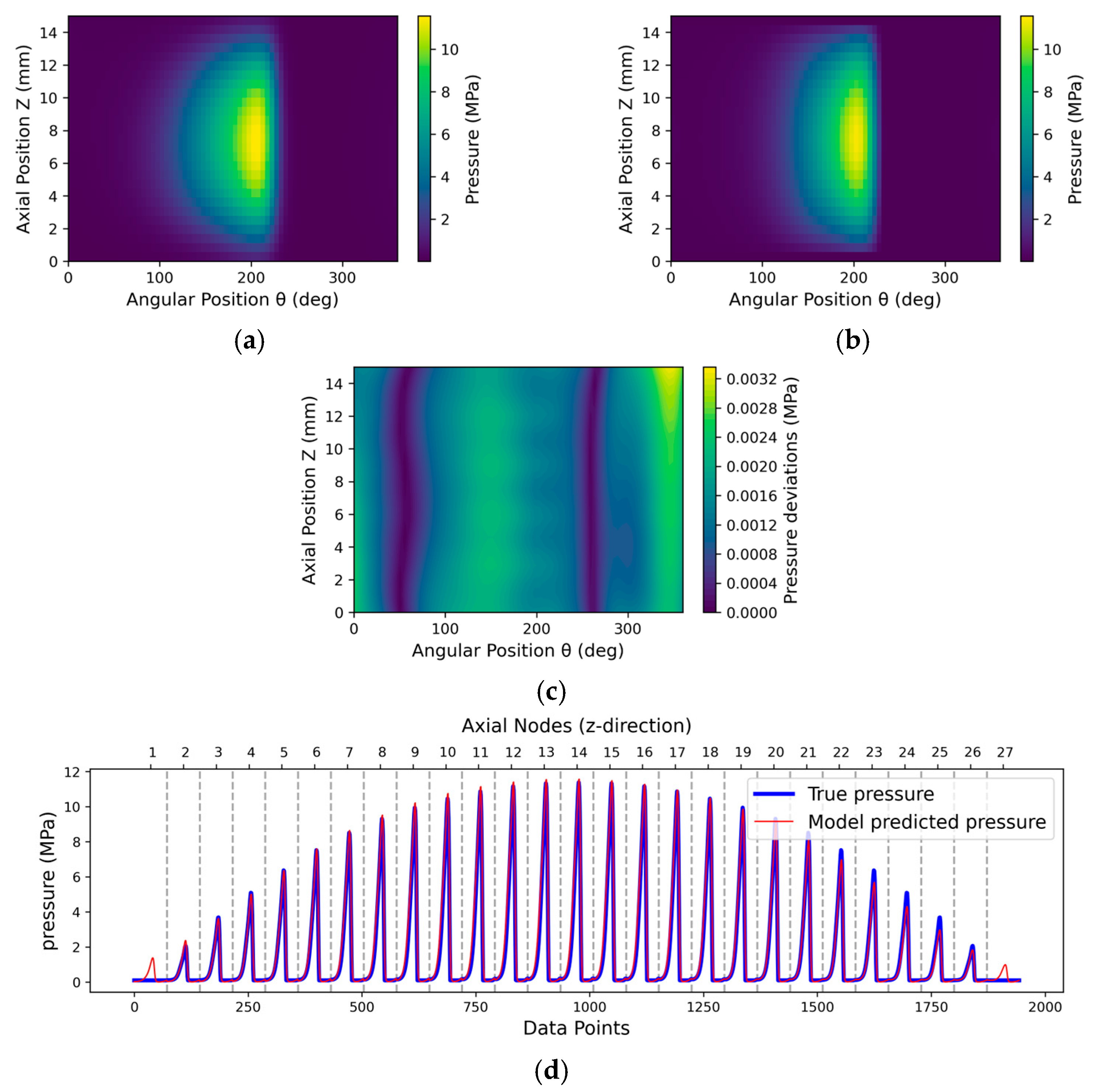
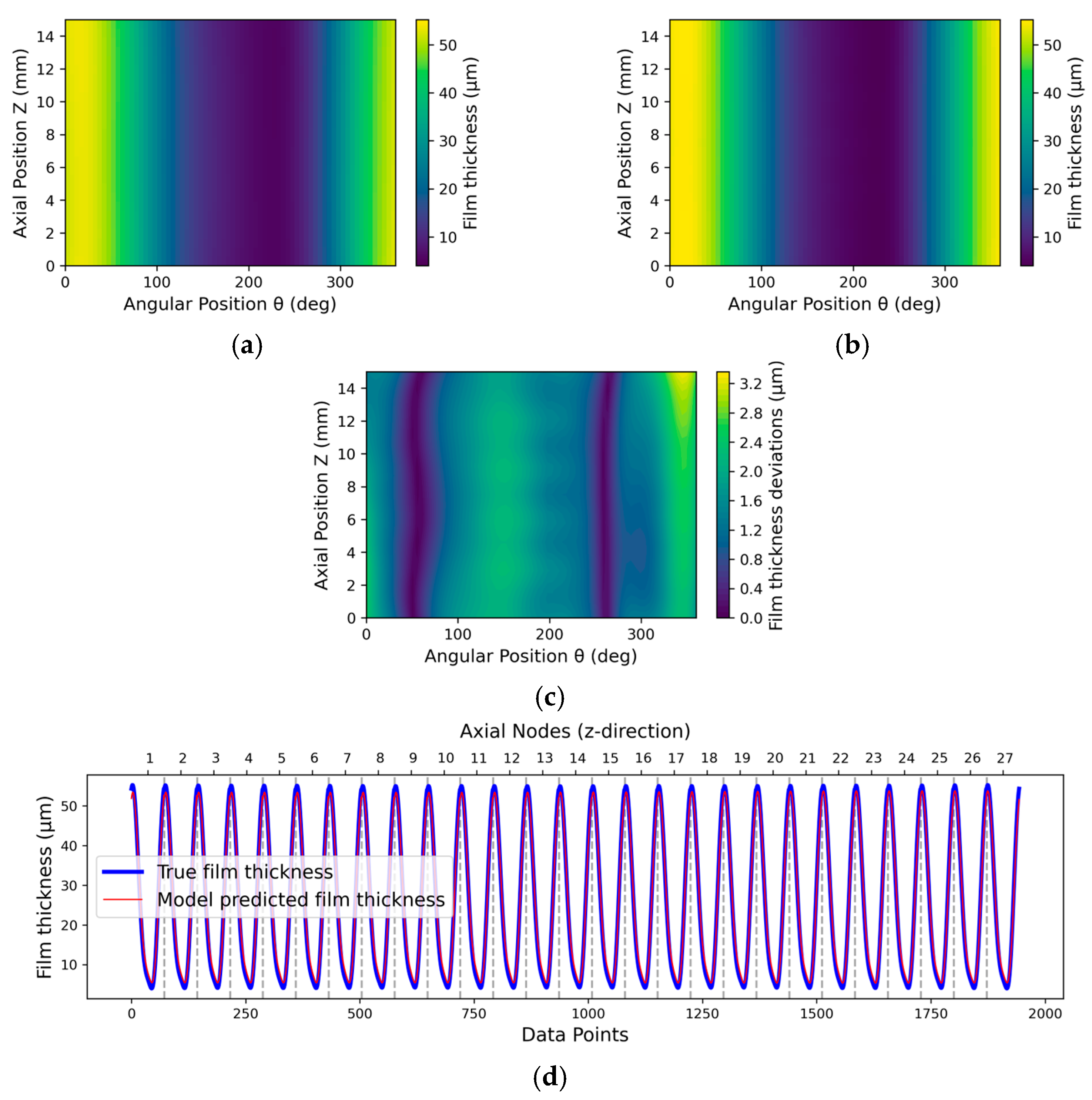
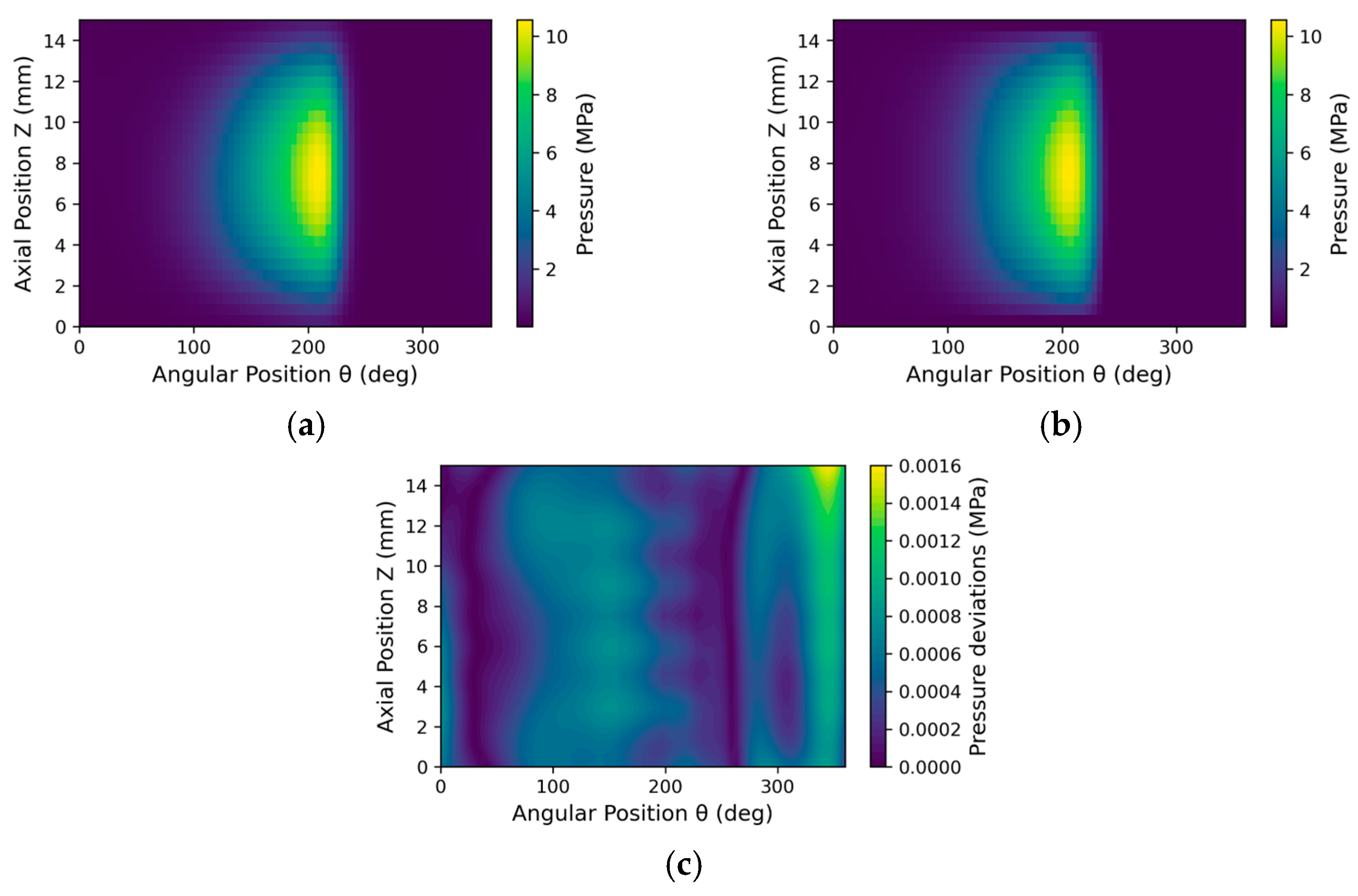
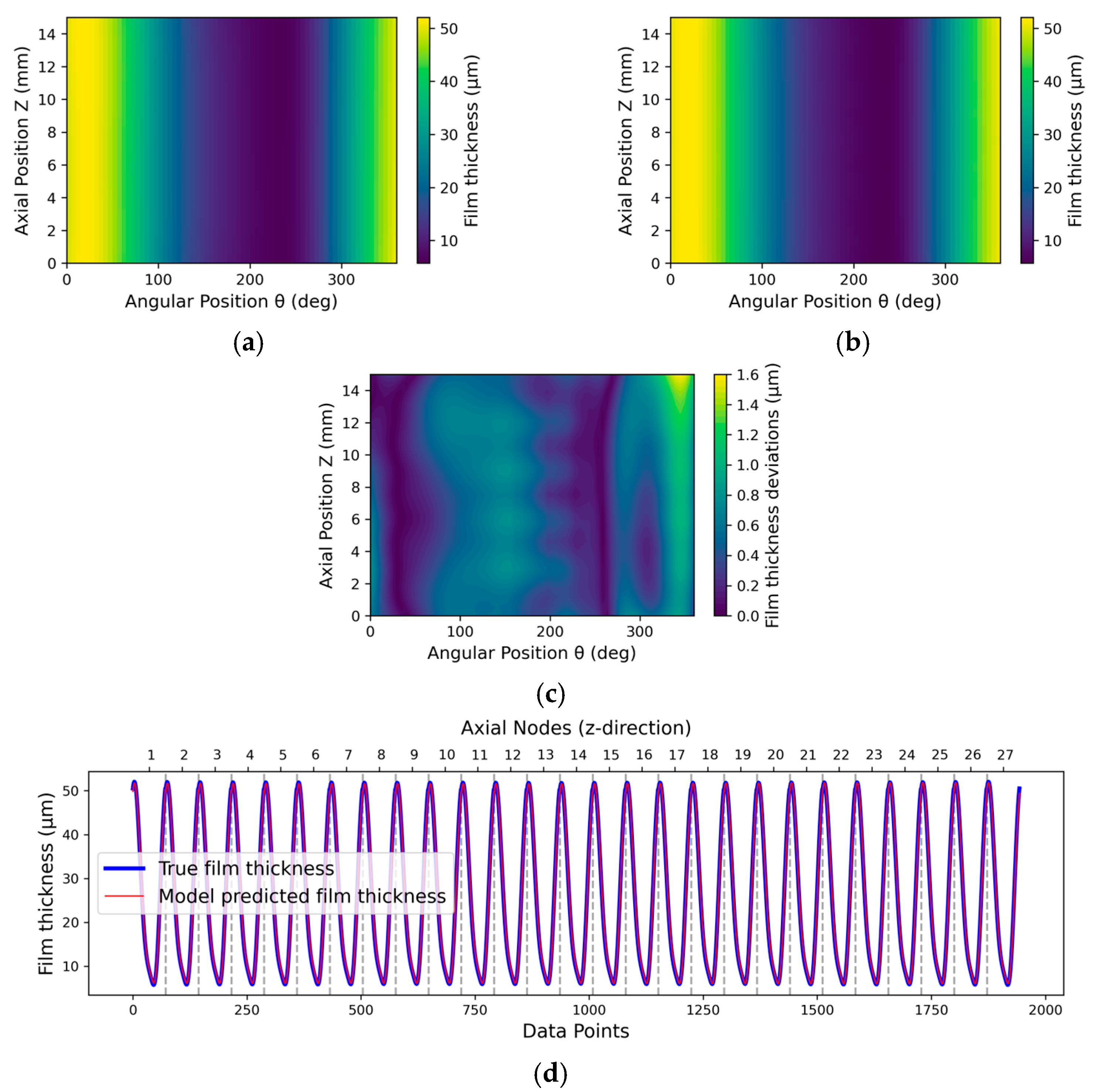
3.2. Post-Training Evaluation of Real-Time Model Behaviour
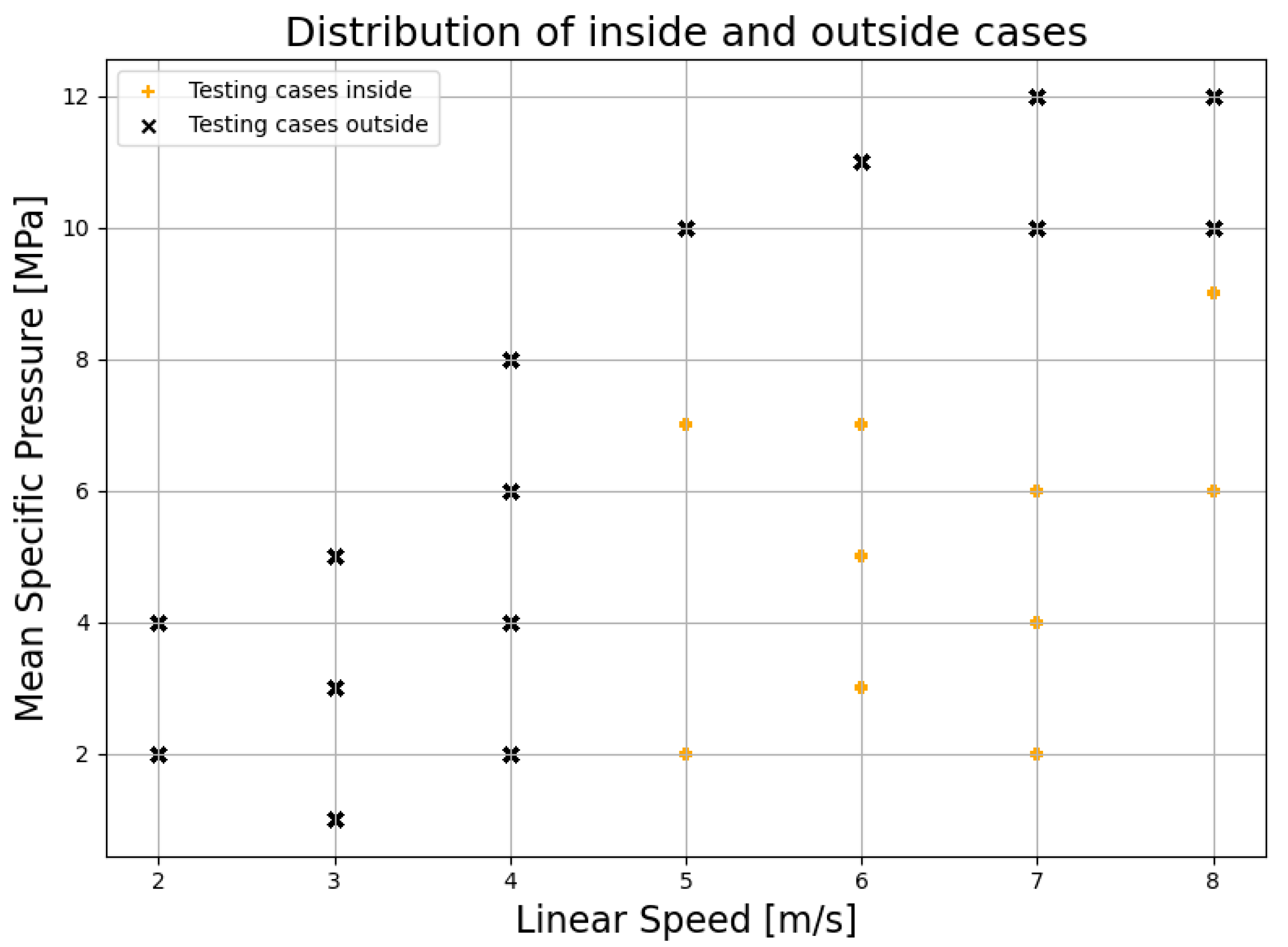
3.2.1. Inside Testing
3.2.2. Outside Testing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moder, J.; Bergmann, P.; Grün, F. Lubrication Regime Classification of Hydrodynamic Journal Bearings by Machine Learning Using Torque Data. Lubricants 2018, 6, 108. [Google Scholar] [CrossRef]
- Baszenski, T.; Kauth, K.; Kratz, K.-H.; Gutiérrez Guzmán, F.; Jacobs, G.; Gemmeke, T. Sensor integrating plain bearings: Design of an energy-autonomous, temperature-based condition monitoring system. Forsch. Im Ingenieurwesen 2023, 87, 441–452. [Google Scholar] [CrossRef]
- Gilges, M.; Saleh, A.; Bekker, A.; Jain, M.; Lehmann, B.; Jacobs, G. Influence of Propeller–Ice Loads on the Wear Development in Stern Tube Bearings of Marine Propulsion Systems and Identification of Critical Operating Conditions. J. Offshore Mech. Arct. Eng. 2024, 146, 061602. [Google Scholar] [CrossRef]
- Saleh, A.; Könekamp, M.; Jacobs, G.; Gilges, M.; Lehmann, B.; Lucassen, M. Evaluation of fatigue damage in stern tube sliding bearings of ship propulsion systems under ice impact. Forsch. Im Ingenieurwesen 2025, 89, 32. [Google Scholar] [CrossRef]
- Lucassen, M.; Jacobs, G.; Lehmann, B. Efficient dynamic simulations of planetary journal bearings in wind turbine gearboxes. Forsch. Im Ingenieurwesen 2025, 89, 20. [Google Scholar] [CrossRef]
- König, F.; Ouald Chaib, A.; Jacobs, G.; Sous, C. A multiscale-approach for wear prediction in journal bearing systems—From wearing-in towards steady-state wear. Wear 2019, 426, 1203–1211. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H. Starting and stopping behavior of worn journal bearings. Tribol. Int. 2018, 127, 478–488. [Google Scholar] [CrossRef]
- Koetz, F.; Schmitt, F.; Kirchner, E.; Zancul, E. Visualising the lubrication condition in hydrodynamic journal bearings using impedance measurement. Front. Mech. Eng. 2024, 10, 1456575. [Google Scholar] [CrossRef]
- Xu, F.; Ding, N.; Li, N.; Liu, L.; Hou, N.; Xu, N.; Guo, W.; Tian, L.; Xu, H.; Lawrence Wu, C.-M.; et al. A review of bearing failure Modes, mechanisms and causes. Eng. Fail. Anal. 2023, 152, 107518. [Google Scholar] [CrossRef]
- Scott, K.; Infield, D.; Barltrop, N.; Coultate, J.; Shahaj, A. Effects of Extreme and Transient Loads on Wind Turbine Drive Trains. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; p. 01092012, ISBN 978-1-60086-936-5. [Google Scholar]
- Abadi, N.M.M. Überwachung Hydrodynamischer Gleitlager Basierend auf der Körperschallanalyse. Master’s Dissertation, Technische Universität Berlin, Berlin, Germany, 2020. [Google Scholar]
- Brinkschulte, L.; Geimer, M. Real-time Estimation of the Remaining Lifetime of Components. ATZoffhighway Worldw. 2017, 10, 54–60. [Google Scholar] [CrossRef]
- Pagitsch, M.; Jacobs, G.; Bosse, D. Remaining Useful Life Determination for Wind Turbines. J. Phys. Conf. Ser. 2020, 1452, 12052. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. How to tell the difference between a model and a digital twin. Adv. Model. Simul. Eng. Sci. 2020, 7, 13. [Google Scholar] [CrossRef]
- Reynolds, O. IV. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. 1886, 177, 157–234. [Google Scholar] [CrossRef]
- AVL-List GmbH. EXCITE Power Unit User Manual (R2022.1); AVL-List GmbH: Graz, Austria, 2022. [Google Scholar]
- Cartwright, S.; Rothwell, B.C.; Figueredo, G.; Medina, H.; Eastwick, C.; Layton, J.; Ambrose, S. A machine learning-driven approach to predicting thermo-elasto-hydrodynamic lubrication in journal bearings. Tribol. Int. 2024, 196, 109670. [Google Scholar] [CrossRef]
- DIN 31652-1:2017-01; Gleitlager Hydrodynamische Radial-Gleitlager im stationären Betrieb—Teil 1: Berechnung von Kreiszylinderlagern. DIN Media, GmbH: Berlin, Germany, 2017.
- Vogelpohl, G. (Ed.) Beiträge zur Gleitlagerberechnung; Forschungsheft nr. 386; VDI: Düsseldorf, Germany, 1954. [Google Scholar]
- Kirk, R.G.; Gunter, E.J. Short Bearing Analysis Applied to Rotor Dynamics—Part I: Theory. J. Lubr. Technol. 1976, 98, 47–56. [Google Scholar] [CrossRef]
- DuBois, G.B.; Ocvirk, F.W. The Short Bearing Approximation for Plain Journal Bearings. J. Fluids Eng. 1955, 77, 1173–1178. [Google Scholar] [CrossRef]
- Faria, M.T.C. On the Hydrodynamic Long Journal Bearing Theory. In Proceedings of the World Congress on Engineering 2014, WCE 2014, London, UK, 2–4 July 2014; Volume II, ISBN 978-988-19253-5-0, ISSN 2078-0958 (Print)/2078-0966 (Online). [Google Scholar]
- Timbó, R.; Martins, R.; Bachmann, G.; Rangel, F.; Mota, J.; Valério, J.; Ritto, T. ROSS-Rotordynamic Open Source Software. J. Open Source Softw. 2020, 5, 2120. [Google Scholar] [CrossRef]
- Marian, M.; Bartz, M.; Wartzack, S.; Rosenkranz, A. Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review. Lubricants 2020, 8, 95. [Google Scholar] [CrossRef]
- Daniel, C. Simulation von gleit- und wälzgelagerten Systemen auf Basis eines Mehrkörpersystems für rotordynamische Anwendungen. Doctoral Dissertation, Otto-von-Guericke-Universität, Magdeburg, Germany, 2013. [Google Scholar]
- Gong, R.-Z.; Li, D.-Y.; Wang, H.-J.; Han, L.; Qin, D.-Q. Analytical solution of Reynolds equation under dynamic conditions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 416–427. [Google Scholar] [CrossRef]
- Mauro, F.; Kana, A.A. Digital twin for ship life-cycle: A critical systematic review. Ocean. Eng. 2023, 269, 113479. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S. Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants 2021, 9, 86. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S. Physics-Informed Machine Learning—An Emerging Trend in Tribology. Lubricants 2023, 11, 463. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Marian, M.; Profito, F.J.; Aragon, N.; Shah, R. The Use of Artificial Intelligence in Tribology—A Perspective. Lubricants 2021, 9, 2. [Google Scholar] [CrossRef]
- Sadık Ünlü, B.; Durmuş, H.; Meriç, C. Determination of tribological properties at CuSn10 alloy journal bearings by experimental and means of artificial neural networks method. Ind. Lubr. Tribol. 2012, 64, 258–264. [Google Scholar] [CrossRef]
- Hess, N.; Shang, L. Development of a Machine Learning Model for Elastohydrodynamic Pressure Prediction in Journal Bearings. J. Tribol. 2022, 144, 081603. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part II): Data-driven Discovery of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10566. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Rom, M. Physics-informed neural networks for the Reynolds equation with cavitation modeling. Tribol. Int. 2023, 179, 108141. [Google Scholar] [CrossRef]
- Markidis, S. The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Almqvist, A. Fundamentals of Physics-Informed Neural Networks Applied to Solve the Reynolds Boundary Value Problem. Lubricants 2021, 9, 82. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, L.; Wong, P.P.L. Application of physics-informed neural network in the analysis of hydrodynamic lubrication. Friction 2023, 11, 1253–1264. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Du, Q.; Liu, T.; Xie, Y. ReF-nets: Physics-informed neural network for Reynolds equation of gas bearing. Comput. Methods Appl. Mech. Eng. 2022, 391, 114524. [Google Scholar] [CrossRef]
- Cheng, Y.; He, Q.; Huang, W.; Liu, Y.; Li, Y.; Li, D. HL-nets: Physics-informed neural networks for hydrodynamic lubrication with cavitation. Tribol. Int. 2023, 188, 108871. [Google Scholar] [CrossRef]
- Xi, Y.; Deng, J.; Li, Y. A solution for finite journal bearings by using physics-informed neural networks with both soft and hard constrains. Ind. Lubr. Tribol. 2023, 75, 560–567. [Google Scholar] [CrossRef]
- Shutin, D.; Kazakov, Y.; Stebakov, I.; Savin, L. Data-driven and physics-informed approaches for improving the performance of dynamic models of fluid film bearings. Tribol. Int. 2024, 191, 109136. [Google Scholar] [CrossRef]
- Zhou, G.; Zhan, M.; Huang, D.; Lyu, X.; Yan, K. Enhanced PINNs with augmented Lagrangian method and transfer learning for hydrodynamic lubrication analysis. Ind. Lubr. Tribol. 2024, 76, 1246–1255. [Google Scholar] [CrossRef]
- Ramos, D.J.; Cunha, B.Z.; Daniel, G.B. Evaluation of physics-informed neural networks (PINN) in the solution of the Reynolds equation. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 568. [Google Scholar] [CrossRef]
- Brumand-Poor, F.; Bauer, N.; Plückhahn, N.; Thebelt, M.; Woyda, S.; Schmitz, K. Extrapolation of Hydrodynamic Pressure in Lubricated Contacts: A Novel Multi-Case Physics-Informed Neural Network Framework. Lubricants 2024, 12, 122. [Google Scholar] [CrossRef]
- Purcell, E.; Nejad, A.R.; Böhm, A.; Sapp, L.; Lund, J.; von Bock und Polach, F.; Nickerson, B.M.; Bekker, A.; Gilges, M.; Saleh, A.; et al. On Methodology for a Digital Twin of Ship Propulsion Under Harsh Environmental Conditions. In Volume 6: Polar and Arctic Sciences and Technology; CFD, FSI, and AI, Proceedings of ASME 2024 43rd International Conference on Ocean, Offshore and Arctic Engineering, Singapore, 9–14 June 2024; American Society of Mechanical Engineers: Little Falls, NJ, USA, 2024; p. 06092024. ISBN 978-0-7918-8784-4. [Google Scholar]
- Moseley, B.; Markham, A.; Nissen-Meyer, T. Finite basis physics-informed neural networks (FBPINNs): A scalable domain decomposition approach for solving differential equations. Adv. Comput. Math. 2023, 49, 62. [Google Scholar] [CrossRef]
- Allmaier, H.; Offner, G. Current Challenges and Frontiers for the EHD Simulation of Journal Bearings: A Review; SAE Technical Paper 2016-01-1856; SAE: Warrendale, PA, USA, 2016. [Google Scholar]
- Schmidt, J.H. An Efficient Solution Procedure for Elastohydrodynamic Contact Problems Considering Structural Dynamics; KIT Scientific Publishing: Karlsruhe, Germany, 2019; Volume 33. [Google Scholar]
- Nikolakopoulos, P.G.; Papadopoulos, C.A. Non-linearities in misaligned journal bearings. Tribol. Int. 1994, 27, 243–257. [Google Scholar] [CrossRef]
- Wei, W.; Guo, W.; Han, J.; Wu, X. A new method calculating load balance of sliding bearing by using neural network PID algorithm. Vibroeng. Procedia 2018, 21, 225–230. [Google Scholar] [CrossRef]
- König, F.; Sous, C.; Jacobs, G. Numerical prediction of the frictional losses in sliding bearings during start-stop operation. Friction 2021, 9, 583–597. [Google Scholar] [CrossRef]
- König, F.; Wirsing, F.; Singh, A.; Jacobs, G. Machine-Learning-Based Wear Prediction in Journal Bearings under Start–Stop Conditions. Lubricants 2024, 12, 290. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Chen, Y.; Koohy, S. GPT-PINN: Generative Pre-Trained Physics-Informed Neural Networks toward non-intrusive Meta-learning of parametric PDEs. arXiv 2023, arXiv:2303.14878. [Google Scholar] [CrossRef]
- Hosseini Dashtbayaz, N.; Farhani, G.; Wang, B.; Ling, C.X. Physics-Informed Neural Networks: Minimizing Residual Loss with Wide Networks and Effective Activations. arXiv 2024, arXiv:2405.01680. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. arXiv 2015, arXiv:1502.05767. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE international conference on computer vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Toscano, J.D.; Oommen, V.; Varghese, A.J.; Zou, Z.; Daryakenari, N.A.; Wu, C.; Karniadakis, G.E. From PINNs to PIKANs: Recent Advances in Physics-Informed Machine Learning. arXiv 2024, arXiv:2410.13228. [Google Scholar] [CrossRef]
- Xiang, Z.; Peng, W.; Liu, X.; Yao, W. Self-adaptive loss balanced Physics-informed neural networks. Neurocomputing 2022, 496, 11–34. [Google Scholar] [CrossRef]
- Song, C.; Kawai, R. Monte Carlo and variance reduction methods for structural reliability analysis: A comprehensive review. Probabilistic Eng. Mech. 2023, 73, 103479. [Google Scholar] [CrossRef]







| Authors | Activation Functions | Layer/Neuron Numbers | NN Family | Inputs | Output | Load Cases | Domains | Application |
|---|---|---|---|---|---|---|---|---|
| Almqvist [38] | Sigmoid | 1/10 | FF-NN | x | p | Static/single | 1D/rigid | Plain bearings |
| Zhao [39] | Sigmoid | 3/16 | FF-NN | x, y | p | Static/single | 2D/rigid | slider-on-disc test rig |
| Li [40] | Tanh | 10/10 | FF-NN | x, y, erel | p, h | Static/Single | 2D/rigid | Gas bearings |
| Rom [36] | Tanh | 6/20 | CNN | x, y, erel | p, θ | Static/Single | 2D/rigid | Plain bearings |
| Cheng [41] | ReLU-square, Tanh | 6/20 | FF-NN | x, y | p, θ | Static/single | 2D/rigid | Plain bearings |
| Shutin [43] | Tanh | 10/20 | FF-NN | x, y, V1, V2, X1, X2 | p, θ | Dynamic | 2D/rigid | Plain bearings |
| Brumand-Poor [46] | ReLU | 2/6 | FF-NN | x, ρ, η, h1, h2, h3, h4 | p | Static/single | 1D/rigid | Seals |
| Ramos [45] | Tanh | 6/15–60 | MLP | x, y, ε, φ, ėX, ėY | p | Dynamic | 2D/rigid | Plain bearings |
| Zhou [44] | Tanh | 3/32 | FF-NN | x, y | p | Static/single | 2D/rigid | Plain bearings |
| Fixed input parameter | Lubricant | FVA2 (additive-free mineral oil) |
| Kinematic viscosity at 40 °C | 32 mm2/s | |
| Diameter | 30 mm | |
| Width | 15 mm | |
| Radial clearance | 25 μm | |
| Bearing material | CuSn12Ni2-C | |
| Young’s modulus | 108 GPa | |
| Poisson ratio | 0.33 | |
| Oil temperature | 40 °C | |
| Variable input parameter | Radial load | 0.45–5.40 kN |
| Sliding speed | 2–8 m/s |
| Cases | Specific Pressure [MPa] | Liner Speed [m/s] | Hydrodynamic Pressure | Oil Film Thickness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 [-] | RMSE [MPa] | Peak True [MPa] | Peak Predicted [MPa] | Abs. Error [%] | R2 [-] | RMSE [μm] | Min. True [μm] | Min. Predicted [μm] | Abs. Error [%] | |||
| 1 | 4 | 6 | 0.9946 | 0.182 | 10.02 | 9.98 | 0.47 | 0.9997 | 0.245 | 7.048 | 6.919 | 1.82 |
| 2 | 6 | 6 | 0.9965 | 0.215 | 14.42 | 14.45 | 0.18 | 0.9998 | 0.243 | 5.603 | 5.638 | 0.62 |
| 3 | 3 | 7 | 0.9898 | 0.184 | 7.44 | 7.41 | 0.43 | 0.9989 | 0.424 | 8.845 | 8.739 | 1.20 |
| 4 | 5 | 7 | 0.9961 | 0.189 | 12.06 | 12.12 | 0.48 | 0.9999 | 0.179 | 6.731 | 6.644 | 1.30 |
| 5 | 7 | 8 | 0.9960 | 0.263 | 16.16 | 15.93 | 1.48 | 0.9991 | 0.543 | 5.519 | 6.072 | 10.0 |
| 6 | 3 | 5 | 0.9892 | 0.194 | 7.79 | 7.62 | 2.15 | 0.9981 | 0.605 | 7.497 | 7.519 | 0.29 |
| 7 | 9 | 5 | 0.9945 | 0.399 | 20.49 | 20.03 | 2.26 | 0.9998 | 0.263 | 3.9 | 4.21 | 7.97 |
| 8 | 1 | 6 | 0.9683 | 0.104 | 2.37 | 2.64 | 11.4 | 0.9997 | 0.127 | 13.95 | 13.619 | 2.37 |
| 9 | 9 | 7 | 0.9970 | 0.289 | 20.03 | 19.32 | 3.51 | 0.9998 | 0.247 | 4.693 | 4.884 | 4.06 |
| 10 | 2 | 8 | 0.9847 | 0.148 | 4.78 | 4,92 | 2.97 | 0.9972 | 0.529 | 11.523 | 11.788 | 2.29 |
| Cases | Specific Pressure [MPa] | Liner Speed [m/s] | Hydrodynamic Pressure | Oil Film Thickness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 [-] | RMSE [MPa] | Peak True [MPa] | Peak Predicted [MPa] | Abs. Error [%] | R2 [-] | RMSE [μm] | Min. True [μm] | Min. Predicted [μm] | Abs. Error [%] | |||
| 1 | 3 | 6 | 0.9890 | 0.195 | 7.6 | 7.44 | 2.01 | 0.9986 | 0.503 | 8.222 | 8.077 | 1.77 |
| 2 | 5 | 6 | 0.9962 | 0.187 | 12.25 | 12.33 | 0.68 | 0.9999 | 0.148 | 6.225 | 6.181 | 0.71 |
| 3 | 7 | 6 | 0.9966 | 0.243 | 16.39 | 16.43 | 0.26 | 0.9998 | 0.272 | 5.097 | 5.192 | 1.87 |
| 4 | 2 | 7 | 0.9815 | 0.165 | 4.88 | 4.85 | 0.53 | 0.9973 | 0.552 | 10.85 | 10.918 | 0.63 |
| 5 | 4 | 7 | 0.9945 | 0.182 | 9.82 | 9.87 | 0.51 | 0.9998 | 0.190 | 7.61 | 7.454 | 2.05 |
| 6 | 6 | 7 | 0.9967 | 0.207 | 14.2 | 14.16 | 0.27 | 0.9998 | 0.260 | 6.059 | 6.059 | 0.00 |
| 7 | 2 | 5 | 0.9768 | 0.190 | 5.17 | 4.95 | 4.33 | 0.9964 | 0.718 | 9.26 | 9.376 | 1.25 |
| 8 | 9 | 8 | 0.9959 | 0.339 | 19.85 | 19.03 | 4.13 | 0.9997 | 0.363 | 5.051 | 5.314 | 5.20 |
| 9 | 7 | 5 | 0.9946 | 0.311 | 16.67 | 16.79 | 0.72 | 0.9998 | 0.281 | 4.611 | 4.835 | 4.86 |
| 10 | 2 | 8 | 0.9960 | 0.226 | 14.01 | 14.04 | 0.21 | 0.9997 | 0.270 | 6.48 | 6.563 | 1.29 |
| Cases | Specific Pressure [MPa] | Liner Speed [m/s] | Hydrodynamic Pressure | Oil Film Thickness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 [-] | RMSE [MPa] | Peak True [MPa] | Peak Predicted [MPa] | Abs. Error [%] | R2 [-] | RMSE [μm] | Min. True [μm] | Min. Predicted [μm] | Abs. Error [%] | |||
| 1 | 2 | 2 | 0.9731 | 0.219 | 6.02 | 5.63 | 6.34 | 0.9819 | 2.016 | 5.796 | 7.597 | 31.07 |
| 2 | 4 | 2 | 0.9724 | 0.435 | 11.39 | 11.57 | 1.61 | 0.9931 | 1.531 | 3.975 | 5.324 | 33.94 |
| 3 | 1 | 3 | 0.9736 | 0.100 | 2.68 | 2.79 | 4.19 | 0.9950 | 0.757 | 10.215 | 10.884 | 6.55 |
| 4 | 3 | 3 | 0.9882 | 0.209 | 8.40 | 8.20 | 2.40 | 0.9946 | 1.155 | 5.779 | 6.562 | 13.55 |
| 5 | 5 | 3 | 0.985 | 0.386 | 13.14 | 13.59 | 3.47 | 0.9987 | 0.680 | 4.321 | 5.063 | 17.17 |
| 6 | 2 | 4 | 0.9779 | 0.187 | 5.38 | 5.08 | 5.58 | 0.9949 | 0.911 | 8.294 | 8.713 | 5.05 |
| 7 | 4 | 4 | 0.9939 | 0.197 | 10.51 | 10.57 | 0.58 | 0.9990 | 0.497 | 5.739 | 6.015 | 4.80 |
| 8 | 6 | 4 | 0.9911 | 0.348 | 14.88 | 15.37 | 3.29 | 0.9997 | 0.302 | 4.514 | 4.908 | 8.74 |
| 9 | 8 | 4 | 0.9888 | 0.510 | 18.75 | 18.96 | 1.13 | 0.9996 | 0.399 | 3.722 | 4.181 | 12.34 |
| 10 | 10 | 5 | 0.9935 | 0.479 | 22.20 | 21.18 | 4.60 | 0.9996 | 0.430 | 3.603 | 3.981 | 10.52 |
| 11 | 11 | 6 | 0.9923 | 0.565 | 23.58 | 21.84 | 7.36 | 0.9986 | 0.817 | 3.726 | 4.065 | 9.11 |
| 12 | 10 | 7 | 0.9953 | 0.405 | 21.71 | 20.56 | 5.30 | 0.9993 | 0.561 | 4.366 | 4.613 | 5.66 |
| 13 | 12 | 7 | 0.9847 | 0.865 | 25.15 | 22.43 | 10.82 | 0.9958 | 1.439 | 3.827 | 4.192 | 9.52 |
| 14 | 10 | 8 | 0.9934 | 0.475 | 21.58 | 20.33 | 5.76 | 0.9987 | 0.741 | 4.712 | 5.025 | 6.63 |
| 15 | 12 | 8 | 0.9815 | 0.951 | 25.00 | 22.30 | 10.78 | 0.9938 | 1.704 | 4.150 | 4.564 | 9.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleh, A.; Jacobs, G.; Katre, D.; Lehmann, B.; Lucassen, M. Real-Time Prediction of Pressure and Film Height Distribution in Plain Bearings Using Physics-Informed Neural Networks (PINNs). Lubricants 2025, 13, 360. https://doi.org/10.3390/lubricants13080360
Saleh A, Jacobs G, Katre D, Lehmann B, Lucassen M. Real-Time Prediction of Pressure and Film Height Distribution in Plain Bearings Using Physics-Informed Neural Networks (PINNs). Lubricants. 2025; 13(8):360. https://doi.org/10.3390/lubricants13080360
Chicago/Turabian StyleSaleh, Ahmed, Georg Jacobs, Dhawal Katre, Benjamin Lehmann, and Mattheüs Lucassen. 2025. "Real-Time Prediction of Pressure and Film Height Distribution in Plain Bearings Using Physics-Informed Neural Networks (PINNs)" Lubricants 13, no. 8: 360. https://doi.org/10.3390/lubricants13080360
APA StyleSaleh, A., Jacobs, G., Katre, D., Lehmann, B., & Lucassen, M. (2025). Real-Time Prediction of Pressure and Film Height Distribution in Plain Bearings Using Physics-Informed Neural Networks (PINNs). Lubricants, 13(8), 360. https://doi.org/10.3390/lubricants13080360





