Stability Analysis of the Output Speed in a Hydraulic System Powered by an Inverter-Fed Motor
Abstract
1. Introduction
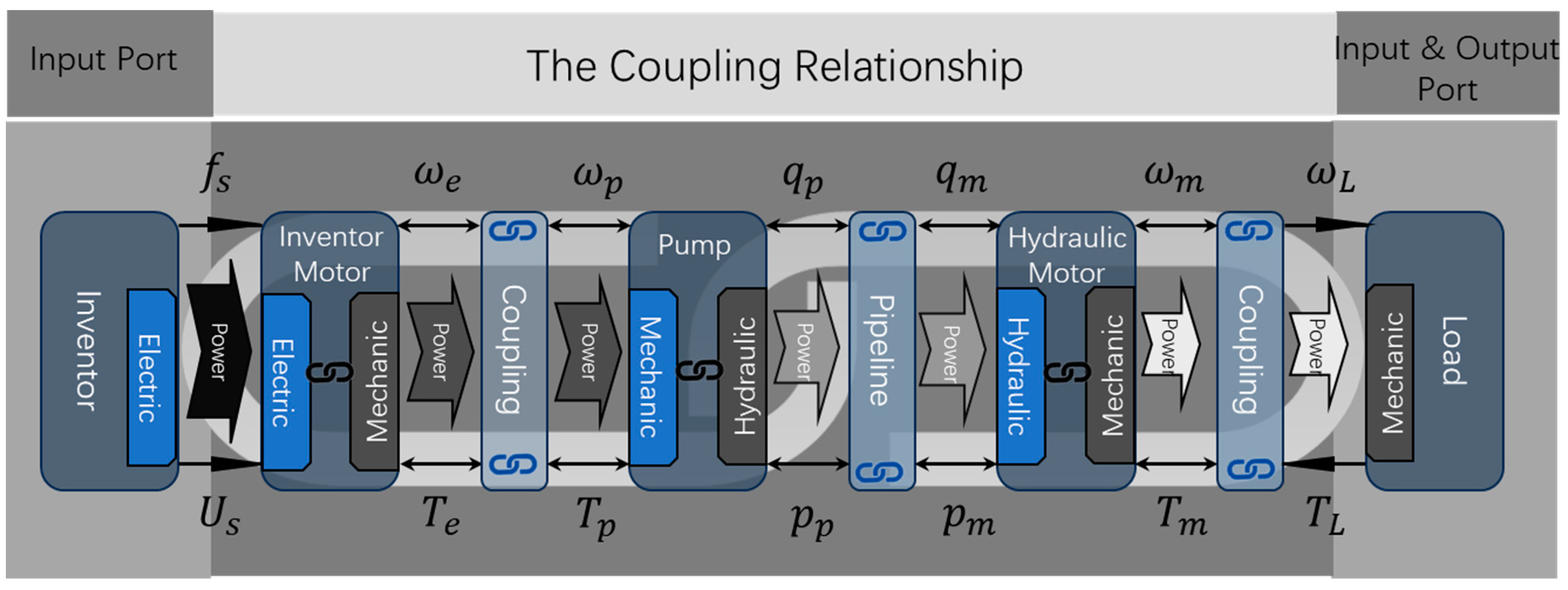
2. System Introduction
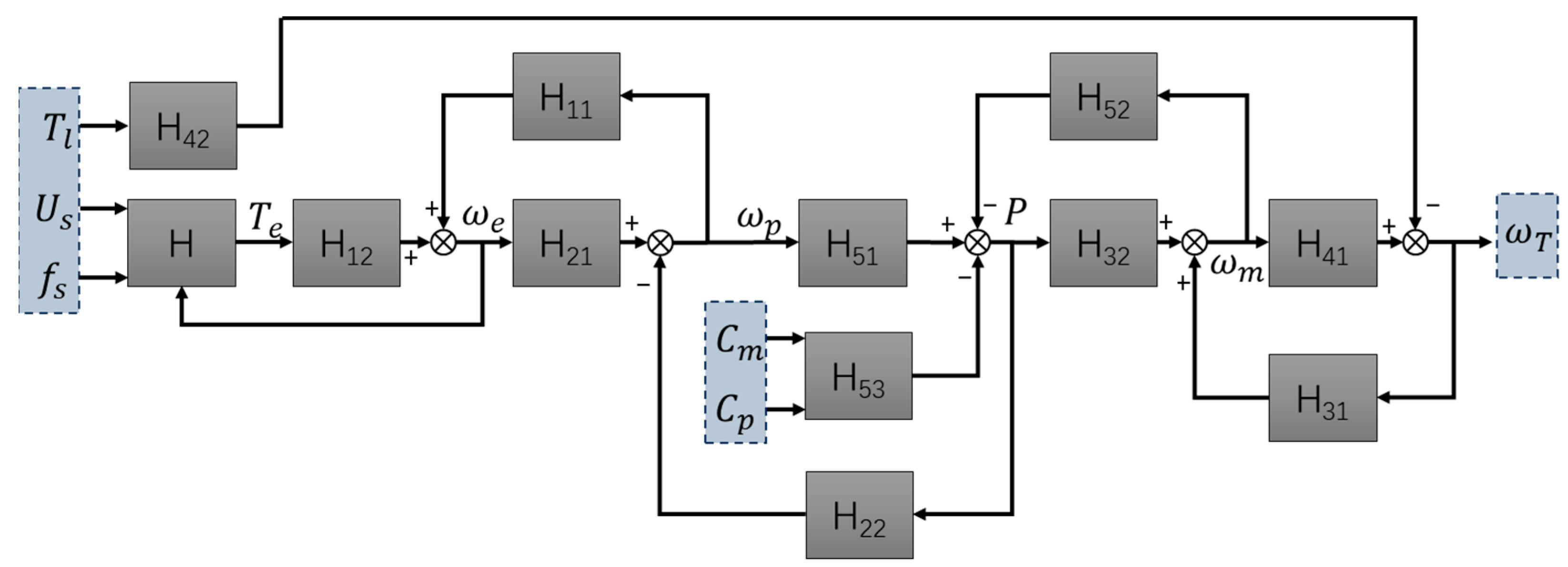
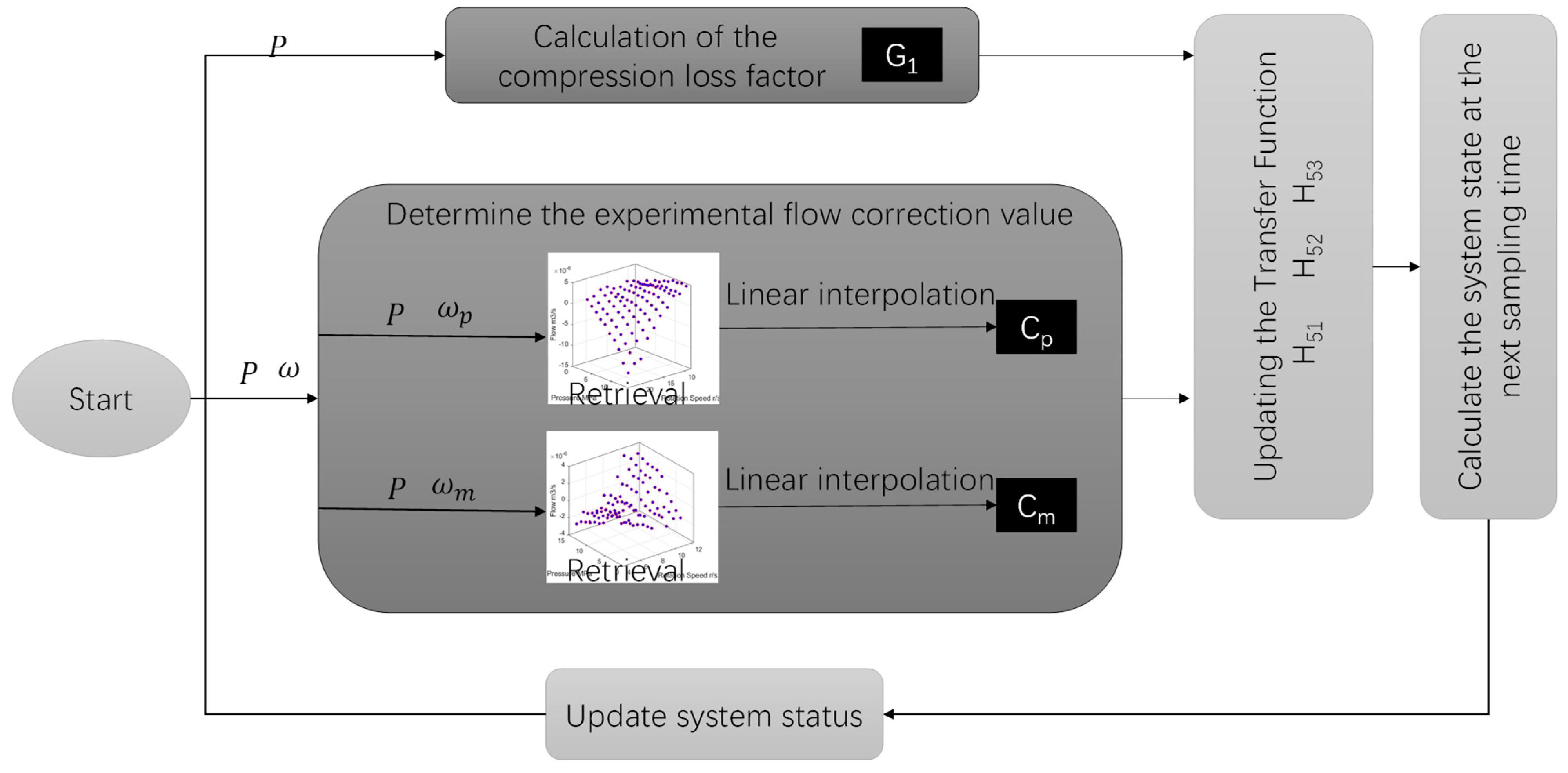
3. Mathematic Description of the IFMDH System
4. Parameter Identification
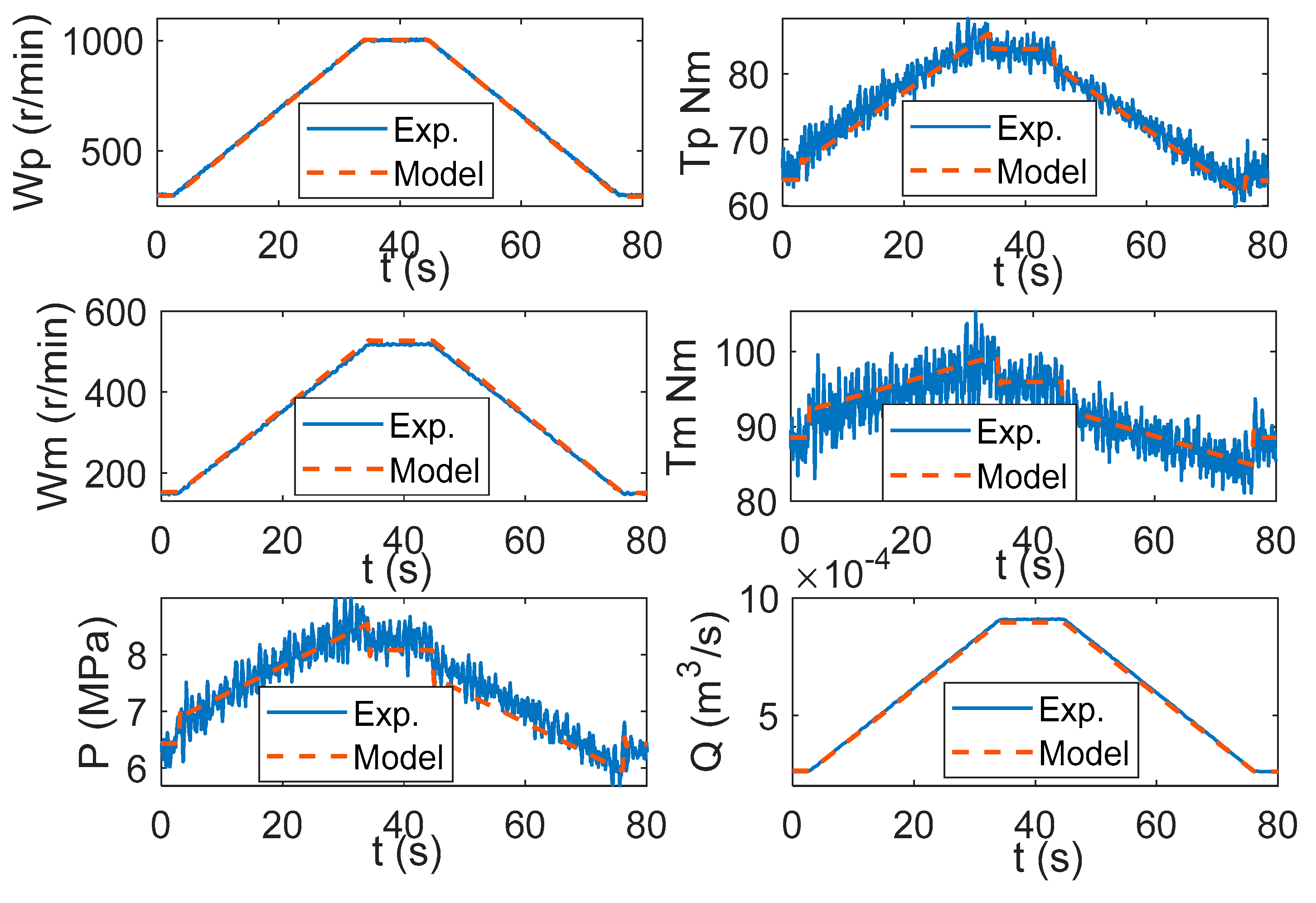
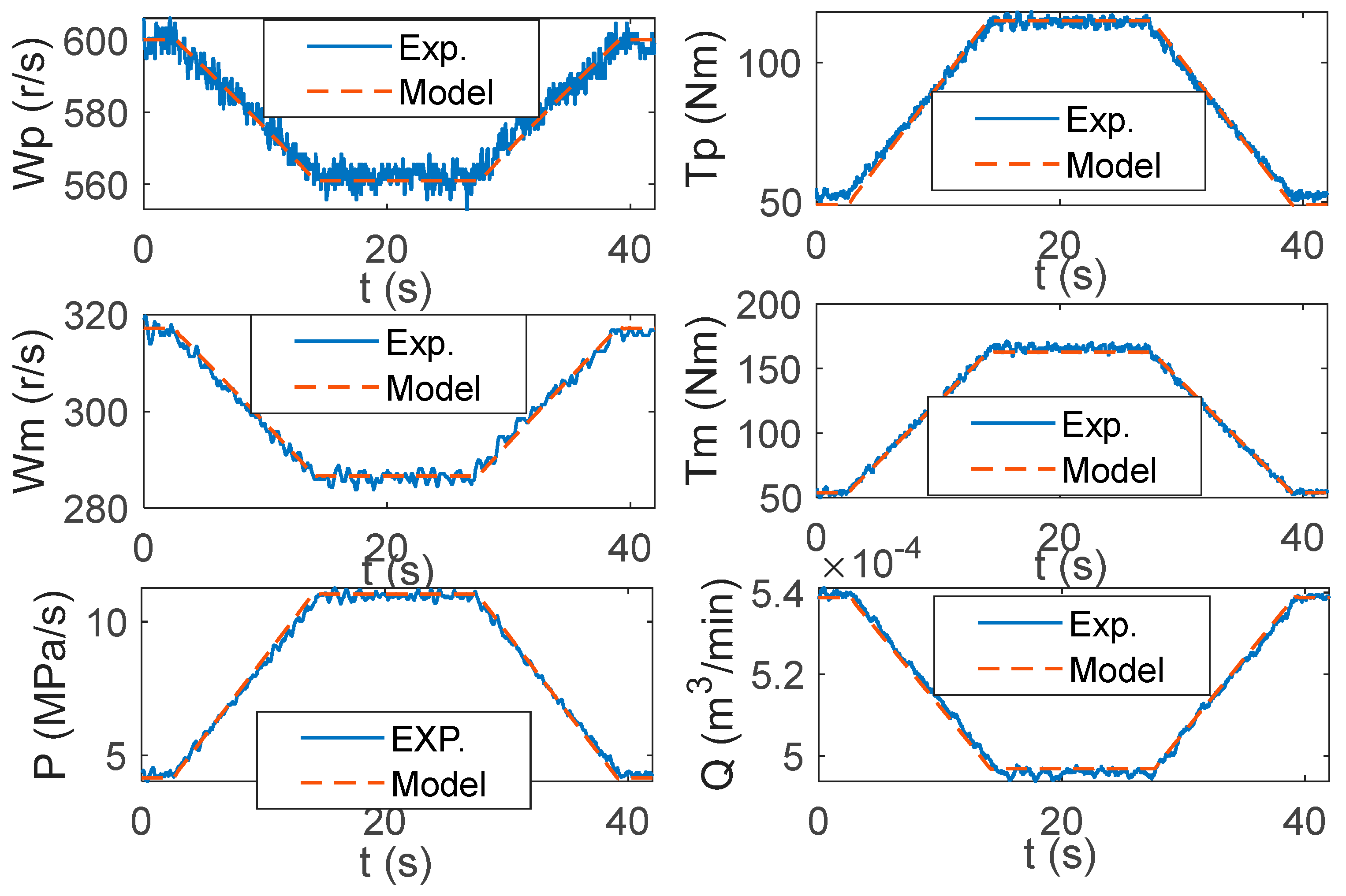
5. Simulation and Experimental Verification
6. Evaluation of System Output Speed Stability and Analysis of the Influencing Factors
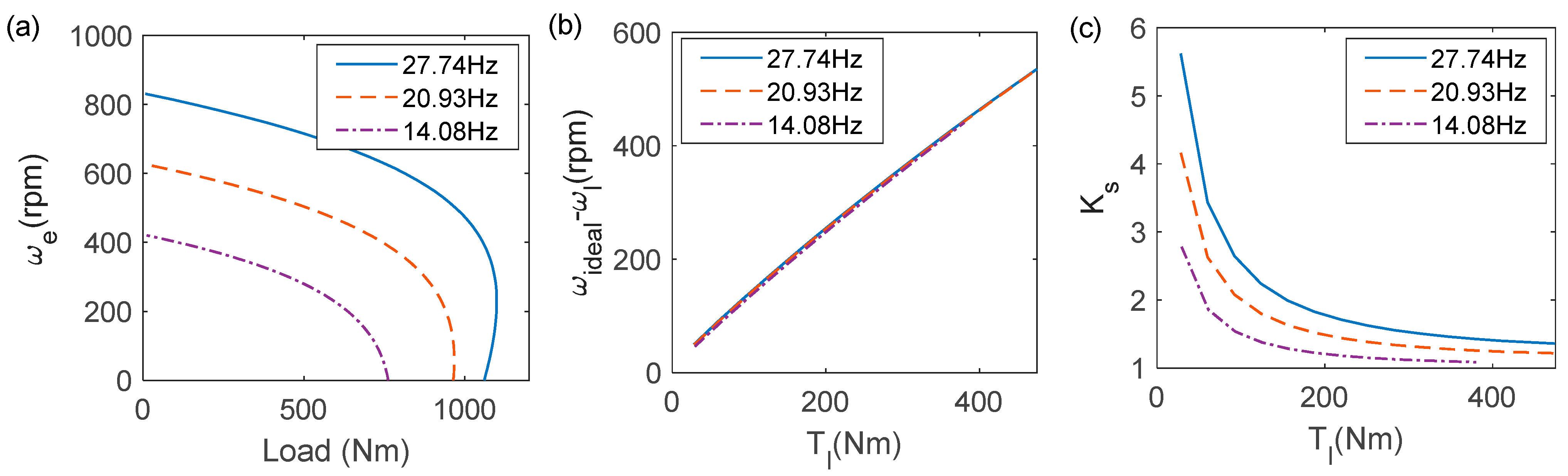
6.1. Evaluation of System Output Speed Stability
6.2. Analysis of Factors Affecting the Speed Stiffness of the System
6.3. Inference Verification
6.3.1. Effect of Motor Speed on the System Speed Stiffness
6.3.2. Effect of E-Motor Stiffness on the Speed Stiffness of the System
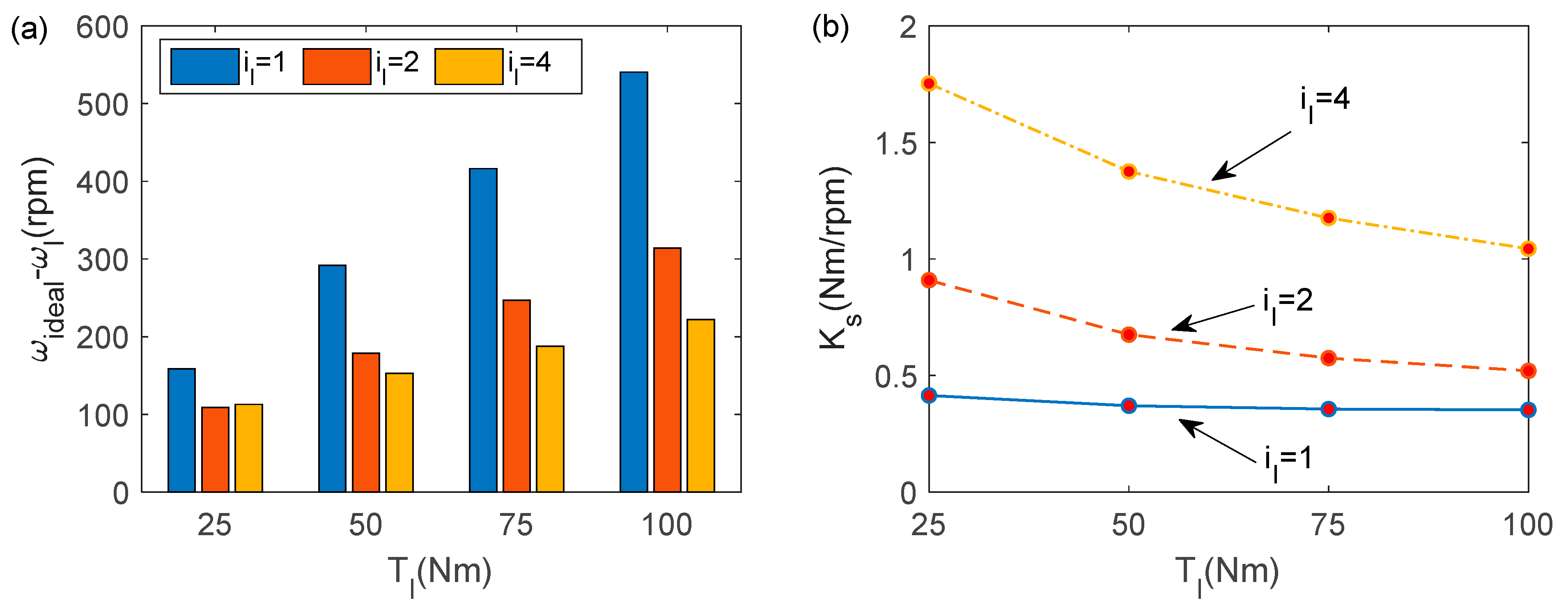
6.3.3. Influence of the Speed Ratio at the Output on the Speed Stiffness of the System
7. Discussion
8. Conclusions
- The coupling relationship of the IFMDH system is described by a mathematic model, and the proposed model decouples the coupling relationship between the variables of the system. The accuracy of the IFMDH system model is verified by experiments. This model can accurately describe the macro-nonlinear behaviours of the system over a wide range of speed regulations and a wide range of variable loads.
- Speed stiffness as an evaluation index can be used to monitor the working conditions of hydraulic components. When the wear of hydraulic components increases, the system leakage increases. The system shows a decrease in speed stiffness and degradation of system output performance. The redefined speed stiffness of the IFMDH system shows a good evaluation ability.
- Under the same load condition, the higher the rotational speed, the greater the speed stiffness. When the motor operating frequency is unchanged, the load increases and the system speed stiffness becomes smaller. Enhancing the mechanical characteristics of the motor and reducing the motor slip can enhance the system speed stiffness and improve the system output speed characteristics.
- The addition of a speed reducer at the output of the hydraulic system has the greatest effect on the system speed stiffness. The larger the reduction ratio, the higher the output stiffness. The system speed stiffness and the square of the deceleration ratio approximately satisfy the linear relationship.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbolic Variable | Parameters | Unit |
| The instantaneous rotational speed of the E-motor | rad/s | |
| The instantaneous rotational speed of the pump | rad/s | |
| The instantaneous rotational speed of the motor | rad/s | |
| The instantaneous rotational angular speed of the load | rad/s | |
| The E-motor damping | Nm·s/rad | |
| The pump rotational damping | Nm·s/rad | |
| The load rotational damping | Nm·s/rad | |
| The coefficients of hydraulic motor flow loss related to speed | m3·rad/s2 | |
| The coefficients of hydraulic motor flow loss related to pressure | m3/(Pa·s) | |
| The coefficients of piston pump flow loss related to speed | m3·rad/s2 | |
| The coefficients of piston pump flow loss related to pressure | m3/(Pa·s) | |
| The test flow correction of pump | m3/s | |
| The test flow correction of motor | m3/s | |
| The pump displacement | m3/s | |
| The motor displacement | m3/s | |
| The synchronous frequency | Hz | |
| G1 | The compression loss coefficient | m3/(rad·s) |
| G2 | The compression loss coefficient of oil | m3/Pa |
| The rotational inertia of the E-motor | kg·m2 | |
| The pump moment of inertia | kg·m2 | |
| The motor moment of inertia | kg·m2 | |
| The load rotational inertia | kg·m2 | |
| The elasticity coefficient of the elastic coupling between the motor and the pump | Nm/rad | |
| The elasticity coefficient of the coupling between the motor and the load | Nm/rad | |
| The number of pole pairs | - | |
| Electromagnetic torque | Nm | |
| Tl | The load torque | Nm |
| The stator voltage | V | |
| P | The system pressure | Pa |
References
- Quan, Z.; Quan, L.; Zhang, J. Review of energy efficient direct pump controlled cylinder electro-hydraulic technology. Renew. Sustain. Energy Rev. 2014, 35, 336–346. [Google Scholar] [CrossRef]
- Kalaiselvan, A.S.V.; Subramaniam, U.; Shanmugam, P.; Norbert, H. A comprehensive review on energy efficiency enhancement initiatives in centrifugal pumping system. Appl. Energy 2016, 181, 495–513. [Google Scholar]
- Xu, B.; Shen, J.; Liu, S.; Su, Q.; Zhang, J. Research and Development of Electro-hydraulic Control Valves Oriented to Industry 4.0: A Review. Chin. J. Mech. Eng. 2020, 33, 13–32. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Advanced Valves and Pump Coordinated Hydraulic Control Design to Simultaneously Achieve High Accuracy and High Efficiency. IEEE Trans. Control. Syst. Technol. 2021, 29, 236–248. [Google Scholar] [CrossRef]
- Quan, Z.; Ge, L.; Wei, Z.; Li, Y.W.; Quan, L. A Survey of Powertrain Technologies for Energy-Efficient Heavy-Duty Machinery. Proc. IEEE 2021, 109, 279–308. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, L.; Bo, X.; Zhang, C. Four-port Hydraulic Transformer with Inlet and Outlet Equal Flow and Its Efficiency Characteristics. Int. J. Fluid Mach. Syst. 2020, 13, 506–516. [Google Scholar] [CrossRef]
- Hoang, C.H.; Rangarajan, S.; Manaserh, Y.; Tradat, M.; Mohsenian, G.; Choobineh, L.; Ortega, A.; Schiffres, S.; Sammakia, B. A review of recent developments in pumped two-phase cooling technologies for electronic devices. IEEE Trans. Components, Packag. Manuf. Technol. 2021, 11, 1565–1582. [Google Scholar] [CrossRef]
- Un-Noor, F.; Wu, G.; Perugu, H.; Collier, S.; Yoon, S.; Barth, M.; Boriboonsomsin, K. Off-Road Construction and Agricultural Equipment Electrification: Review, Challenges, and Opportunities. Vehicles 2022, 4, 780–807. [Google Scholar] [CrossRef]
- Cheng, C.; Fu, J.; Su, H.; Ren, L. Recent Advancements in Agriculture Robots: Benefits and Challenges. Machines 2023, 11, 48. [Google Scholar] [CrossRef]
- Gu, L.; Yang, B. A Cooperation Analysis Method Using Internal and External Features for Mechanical and Electro-Hydraulic System. IEEE Access 2019, 7, 10491–10504. [Google Scholar] [CrossRef]
- Li, D.; Guo, F.; Xu, L.; Wang, S.; Yan, Y.; Ma, X.; Liu, Y. Analysis of Efficiency Characteristics of a Deep-Sea Hydraulic Power Source. Lubricants 2023, 11, 485. [Google Scholar] [CrossRef]
- Irizar, V.; Andreasen, C. Hydraulic pitch control system for wind turbines: Advanced modeling and verification of an hydraulic accumulator. Simul. Model. Pract. Theory 2017, 79, 1–22. [Google Scholar] [CrossRef][Green Version]
- Pourmovahed, A.; Beachley, N.; Fronczak, F. Modeling of a Hydraulic Energy Regeneration System: Part II—Experimental Program. Trans. ASME 1992, 114, 160–165. [Google Scholar] [CrossRef]
- Jeong, H. A novel performance model given by the physical dimensions of hydraulic axial piston motors-Model derivation. J. Mech. Sci. Technol. 2007, 21, 83–97. [Google Scholar] [CrossRef]
- Geng, B.; Gu, L.; Liu, J. Quasi-LPV system modeling and identification of a variable speed electro-mechanical and hydraulic MISO system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2022, 237, 291–304. [Google Scholar] [CrossRef]
- Kumar, A.; Dasgupta, K.; Das, J. Achieving constant speed of a hydrostatic drive using controlled operation of the pump and enhancing its energy efficiency. ISA Trans. 2019, 90, 189–201. [Google Scholar] [CrossRef]
- Vaezi, M.; Izadian, A. Piecewise Affine System Identification of a Hydraulic Wind Power Transfer System. IEEE Trans. Control. Syst. Technol. 2015, 23, 2077–2086. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, Y.; Wang, Q.; Yao, Z. Study on speed characteristics of hydraulic top drive under fluctuating load. J. Pet. Sci. Eng. 2018, 167, 277–286. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, Z.; Yu, S.; Li, X.; Huang, H.; Li, B. Analytical energy dissipation in large and medium-sized hydraulic press. J. Clean. Prod. 2015, 103, 908–915. [Google Scholar] [CrossRef]
- Kumar, N.; Dasgupta, K. Steady-state performance investigation of hydrostatic summation drive using bent-axis hydraulic motor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 3234–3251. [Google Scholar] [CrossRef]
- Kumar, N.; Dasgupta, K.; Ghoshal, S. Dynamic analysis of a closed-circuit hydrostatic summation drive using bent axis motors. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2015, 229, 761–777. [Google Scholar] [CrossRef]
- Gu, H.; Jiao, S. Investigation into speed stiffness form milling system of totally-hydraulic milling machine. Chin. J. Constr. Mach. 2010, 8, 14–16+34. [Google Scholar]
- Bing, X.; Hu, M.; Zhang, J.; Su, Q. Characteristics of volumetric losses and efficiency of axial piston pump with respect to displacement conditions. J. Zhejiang Univ. Sci. A 2016, 17, 186–201. [Google Scholar]
- Xie, H.; Tang, Y.; Shen, G.; Li, X.; Bai, D. Part I: Journal of Systems and Engineering, C.; Command filtered adaptive backstepping control for high-accuracy motion tracking of hydraulic systems with extended state observer. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2021, 236, 654–668. [Google Scholar]
- Gao, J.; Wang, X.; Li, F. Analysis of AC Machines and Their Systems, 2nd ed.; Tsinghua University Press: Beijing, China, 1993; pp. 318–327. [Google Scholar]
- Geng, B.; Gu, L.; Liu, J. Novel Methods for Modeling and Online Measurement of Effective Bulk Modulus of Flowing Oil. IEEE Access 2020, 8, 20805–20817. [Google Scholar] [CrossRef]
- Geng, B.; Gu, L.; Liu, J.; Shi, Y. Dynamic modeling of fluid nonlinear compression loss and flow loss oriented to fault diagnosis of axial piston pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. 2021, 235, 3236–3251. [Google Scholar] [CrossRef]
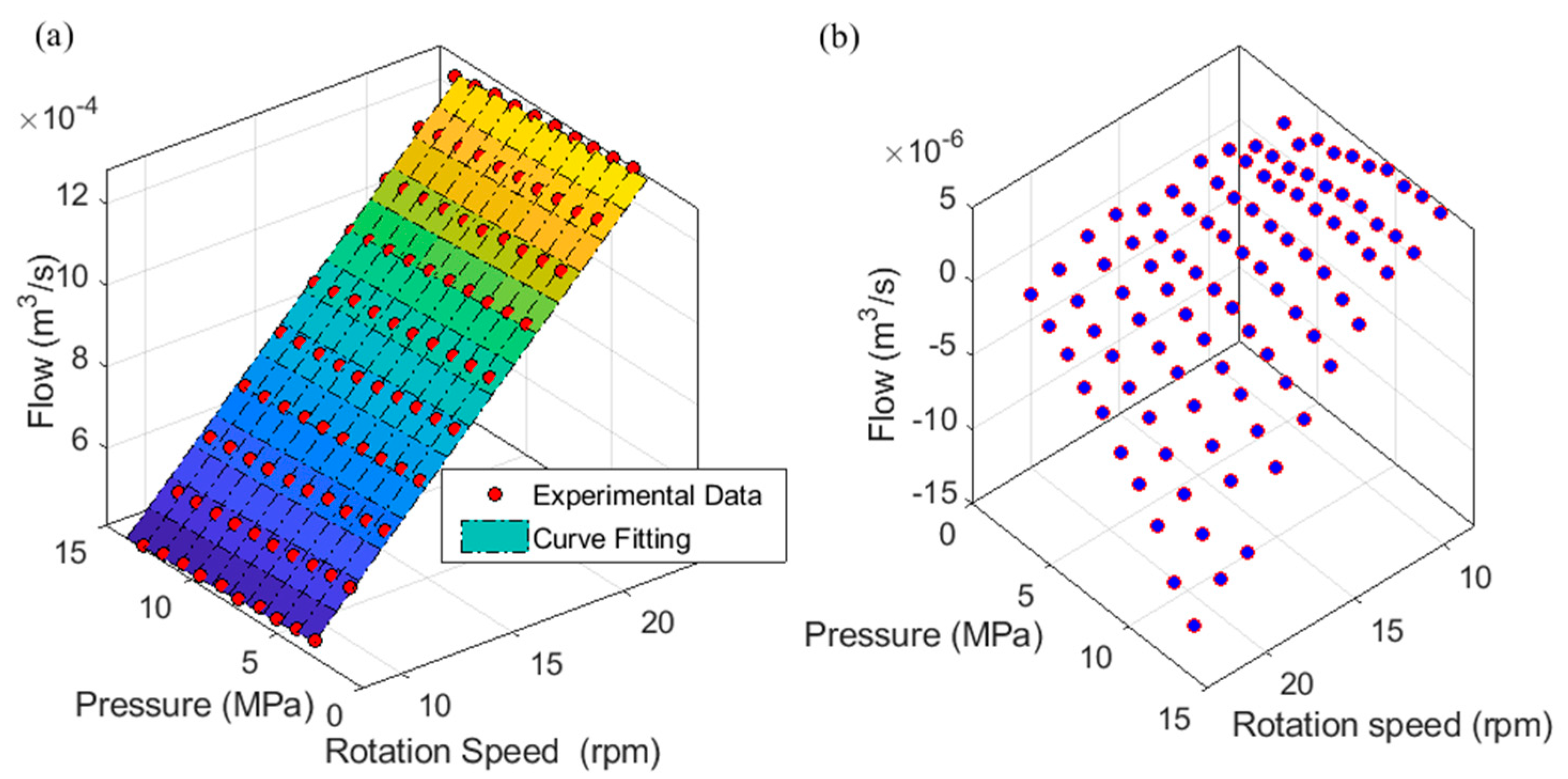
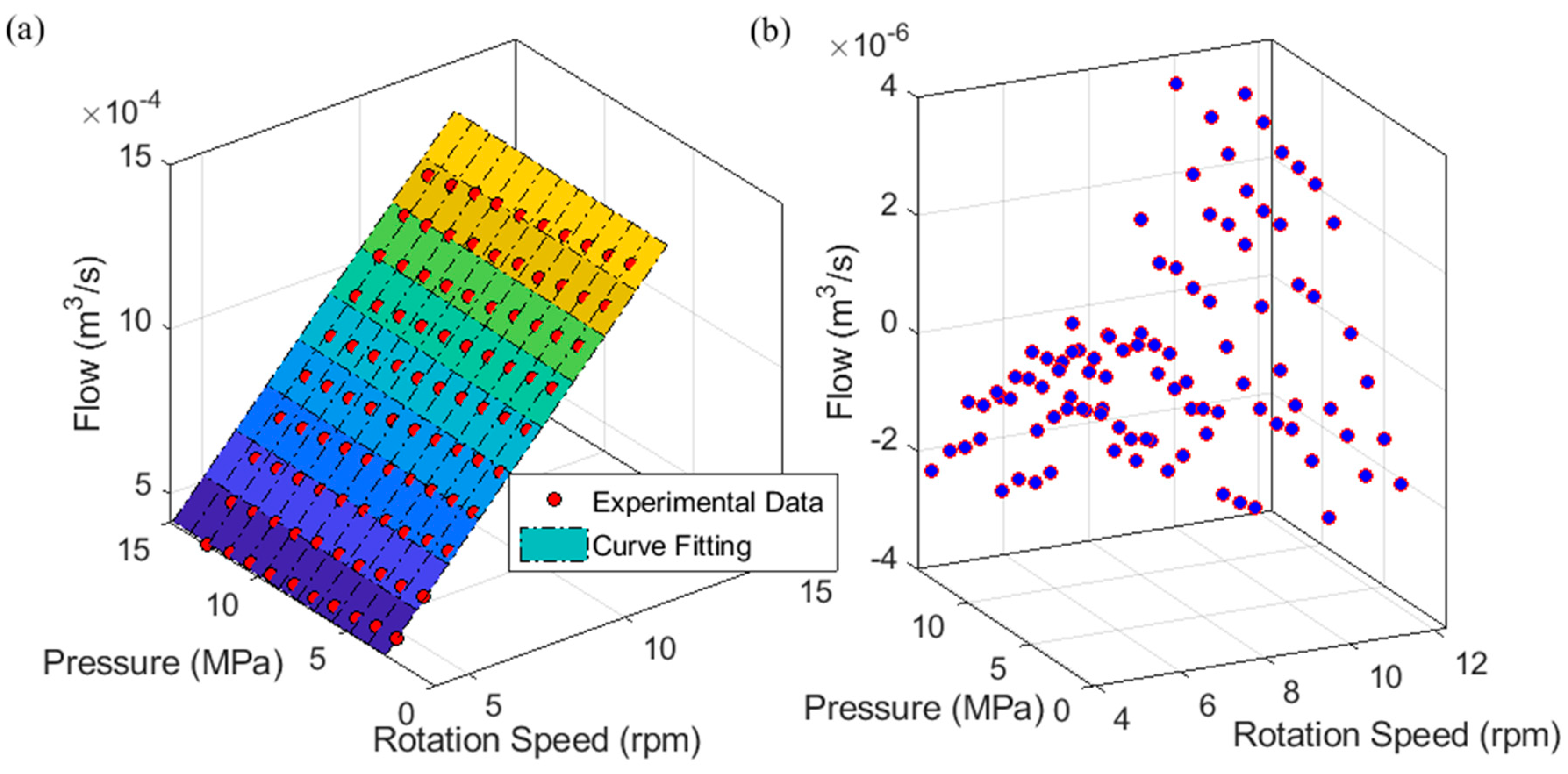



| Parameters | ||||
| Value | 4.236 × 10−7 | −3.392 × 10−12 | 3.121 × 10−6 | 8.214 × 10−13 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 55 mL | 49 mL | ||
| 0.0554 kg·m2 | 0.0644 kg·m2 | ||
| 0.524 kg·m2 | 1400 Nm/rad | ||
| 1400 Nm/rad | 0.041 Nm/rad | ||
| 0.039 Nm/rad | 0.043 Nm/rad |
| Key Component/Sensor | Technical Parameter | Content |
|---|---|---|
| Inverter-fed motor | Type | Siemens 1LG0206-4AA70-Z |
| Rated power | 30 KW | |
| Rated speed | 1470 r/min | |
| Hydraulic pump | Type | HPV55-02RE1X300E |
| Displacement | 0–55 mL | |
| Rated pressure | 42 MPa | |
| Maximum speed | 3300 r/min | |
| Hydraulic motor | Type | HMV105-02E1C |
| Displacement | 35–105 mL | |
| Rated pressure | 42 MPa | |
| Maximum speed | 3500 r/min | |
| Gear motor | Type | CBY4150-A3Fl |
| Displacement | 50 mL | |
| Rated pressure | 20 MPa | |
| Maximum speed | 2000 r/min | |
| Proportional relief valve | Type | ATOS AGMZO-TERS-PC-20/315/Y |
| Specification (diameter) | 20 | |
| Maximum regulating pressure /bar | 315 | |
| Linearity (% of maximum pressure) | ≤0.1 | |
| Repeat accuracy (% of maximum pressure) | ≤0.2 | |
| Flow sensor | Type | Karl BEM300 |
| Range | 0–150 L/min | |
| Maximum pressure | 25 MPa | |
| Pressure transducer | Type | HYDAC HDA4844-A-400-Y00 |
| Range | 0–60 MPa | |
| Overload pressure | 80 MPa | |
| Speed and torque sensor | Type | JCZ2 |
| Rated speed | 0–4000 rpm |
| No. | Operation | Experimental Description and Purposes |
|---|---|---|
| Case 1 | Varying speed operation | Keep the load input at 0.8 V. Vary the motor speed (including deceleration and acceleration) to check the accuracy of the model over a wide speed range. |
| Case 2 | Varying load operation | Keep the inverter input constant. Control the system input torque (both loaded and unloaded) by adjusting the load proportional valve voltage to vary continuously (0.4 V–0.8 V) to verify the accuracy of the model when the system load is operated over a wide range. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, B.; Jing, Q.; Wang, J.; Gu, L.; Lian, X.; Guo, J. Stability Analysis of the Output Speed in a Hydraulic System Powered by an Inverter-Fed Motor. Lubricants 2024, 12, 64. https://doi.org/10.3390/lubricants12030064
Geng B, Jing Q, Wang J, Gu L, Lian X, Guo J. Stability Analysis of the Output Speed in a Hydraulic System Powered by an Inverter-Fed Motor. Lubricants. 2024; 12(3):64. https://doi.org/10.3390/lubricants12030064
Chicago/Turabian StyleGeng, Baolong, Qian Jing, Jianji Wang, Lichen Gu, Xiao Lian, and Jinchang Guo. 2024. "Stability Analysis of the Output Speed in a Hydraulic System Powered by an Inverter-Fed Motor" Lubricants 12, no. 3: 64. https://doi.org/10.3390/lubricants12030064
APA StyleGeng, B., Jing, Q., Wang, J., Gu, L., Lian, X., & Guo, J. (2024). Stability Analysis of the Output Speed in a Hydraulic System Powered by an Inverter-Fed Motor. Lubricants, 12(3), 64. https://doi.org/10.3390/lubricants12030064





