Experimental Strategies for Studying Tribo-Electrochemical Aspects of Chemical–Mechanical Planarization
Abstract
1. Introduction
2. Tribo-Electrochemistry of CMP
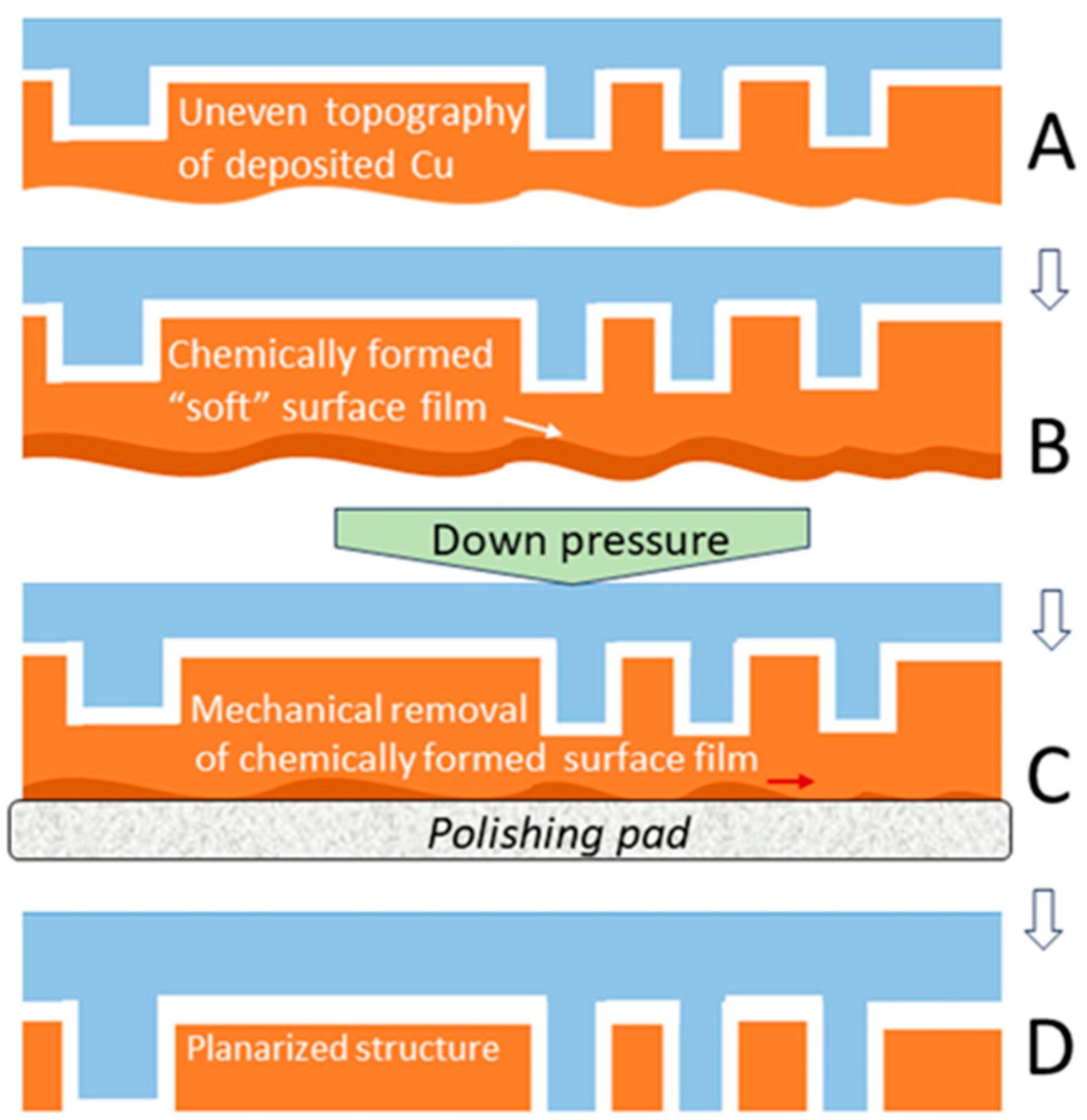
2.1. Corrosion-like Features of CMP-Enabling Reactions
2.2. Roles of Tribology and Slurry Chemistry
2.2.1. Roles of Down Pressure and Sliding Velocity
2.2.2. Controlling Down Pressure and Frictional Velocity for CMP
2.2.3. Slurry Delivery
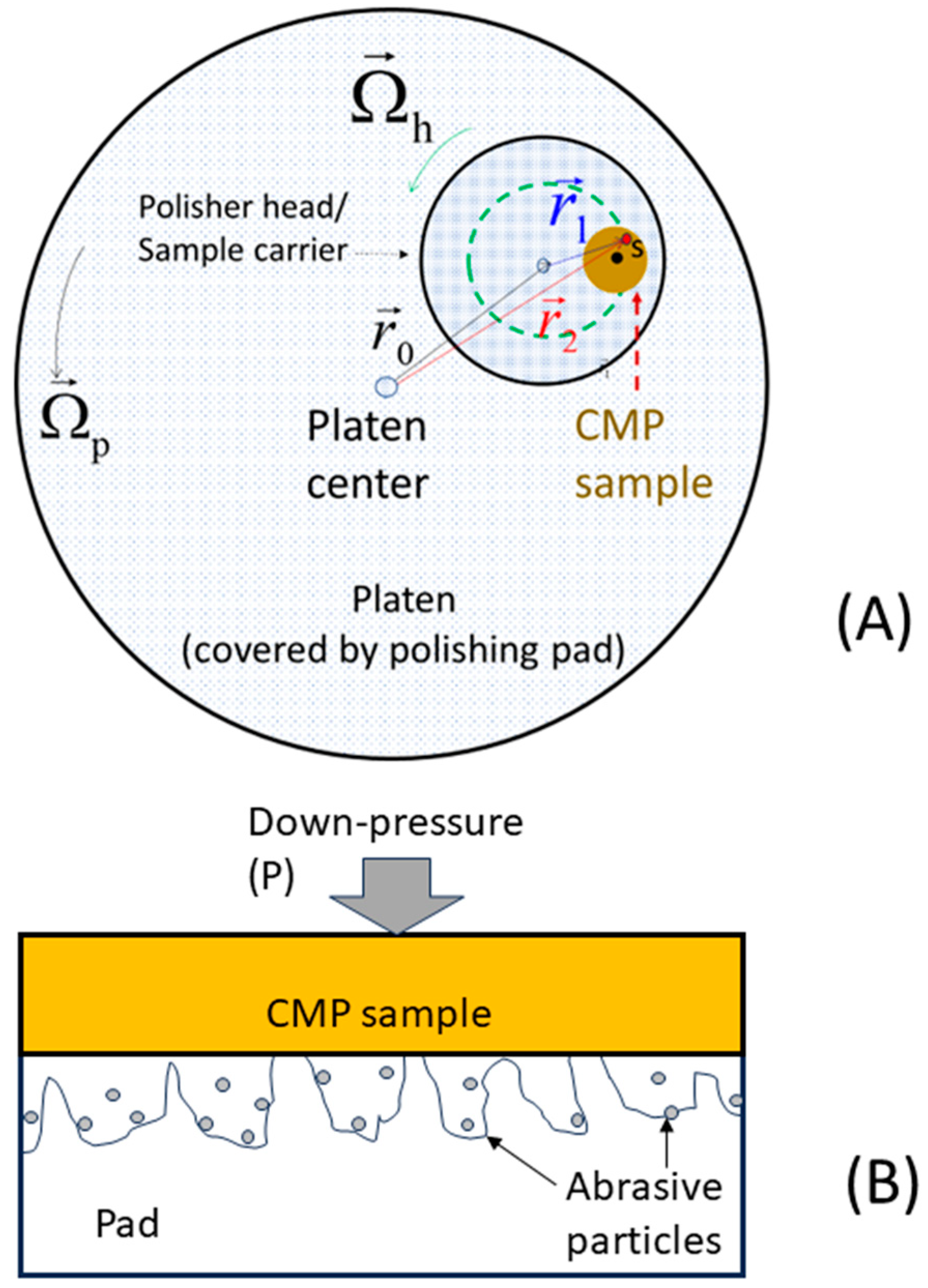
2.2.4. Pad–Sample Contact Area
2.2.5. Electrochemically Effective Area of a CMP Surface
2.2.6. Considerations of CMP Models
2.2.7. Tribological Effects on CMP Electrochemistry
3. Combining Electrochemical and Mechanical Features of CMP in Laboratory-Scale Measurements
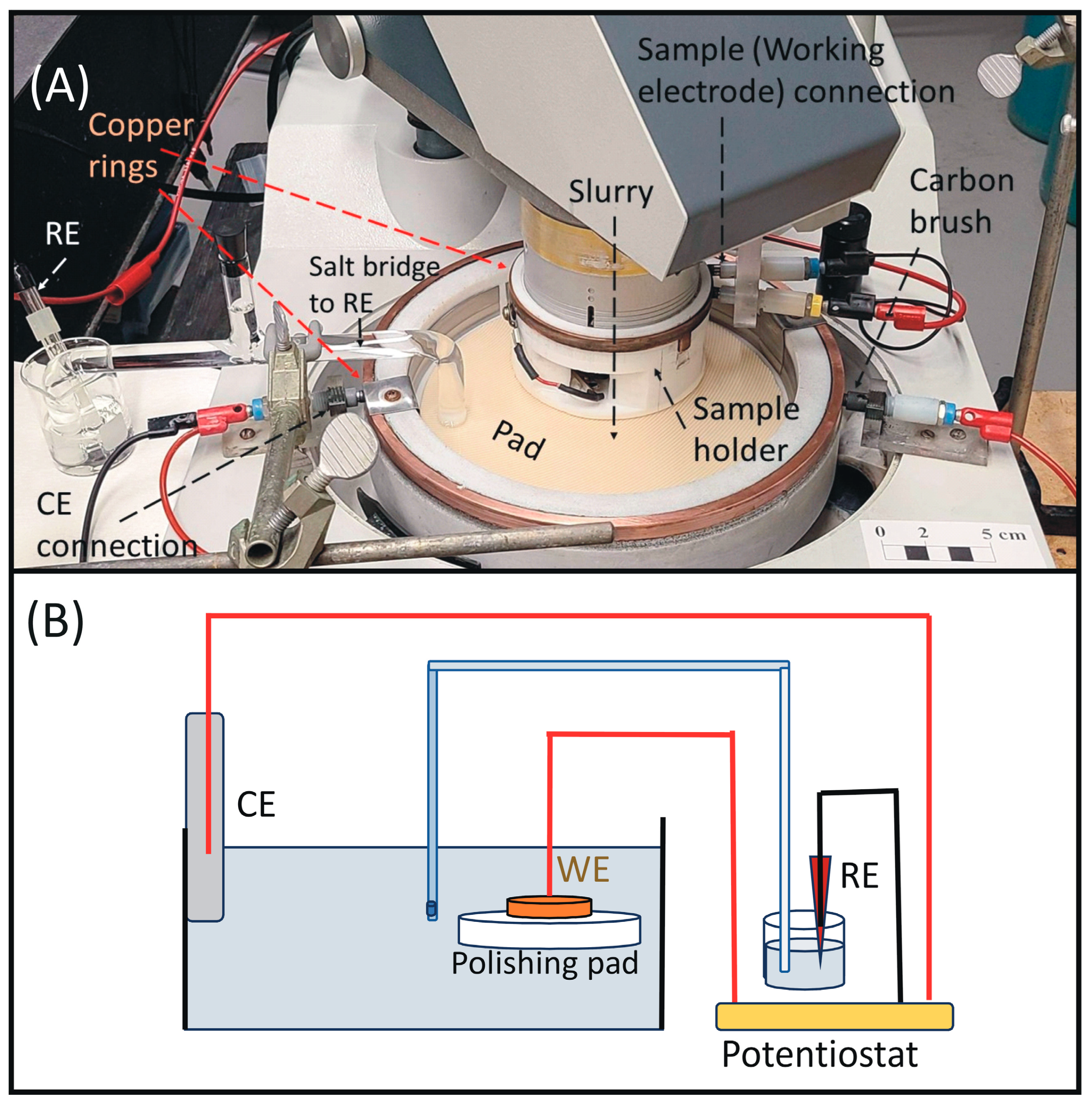
3.1. Instrumentation
3.2. Selection of Test Samples
3.3. Optimization of Experimental Systems to Enhance Signal Detection
4. Data Analysis Protocols and Theoretical Considerations
4.1. General Considerations for Data Analyses
4.2. Formulation of Corrosion Variables
5. Electrochemical Noise of CMP-Related Tribo-Corrosion
5.1. General Considerations
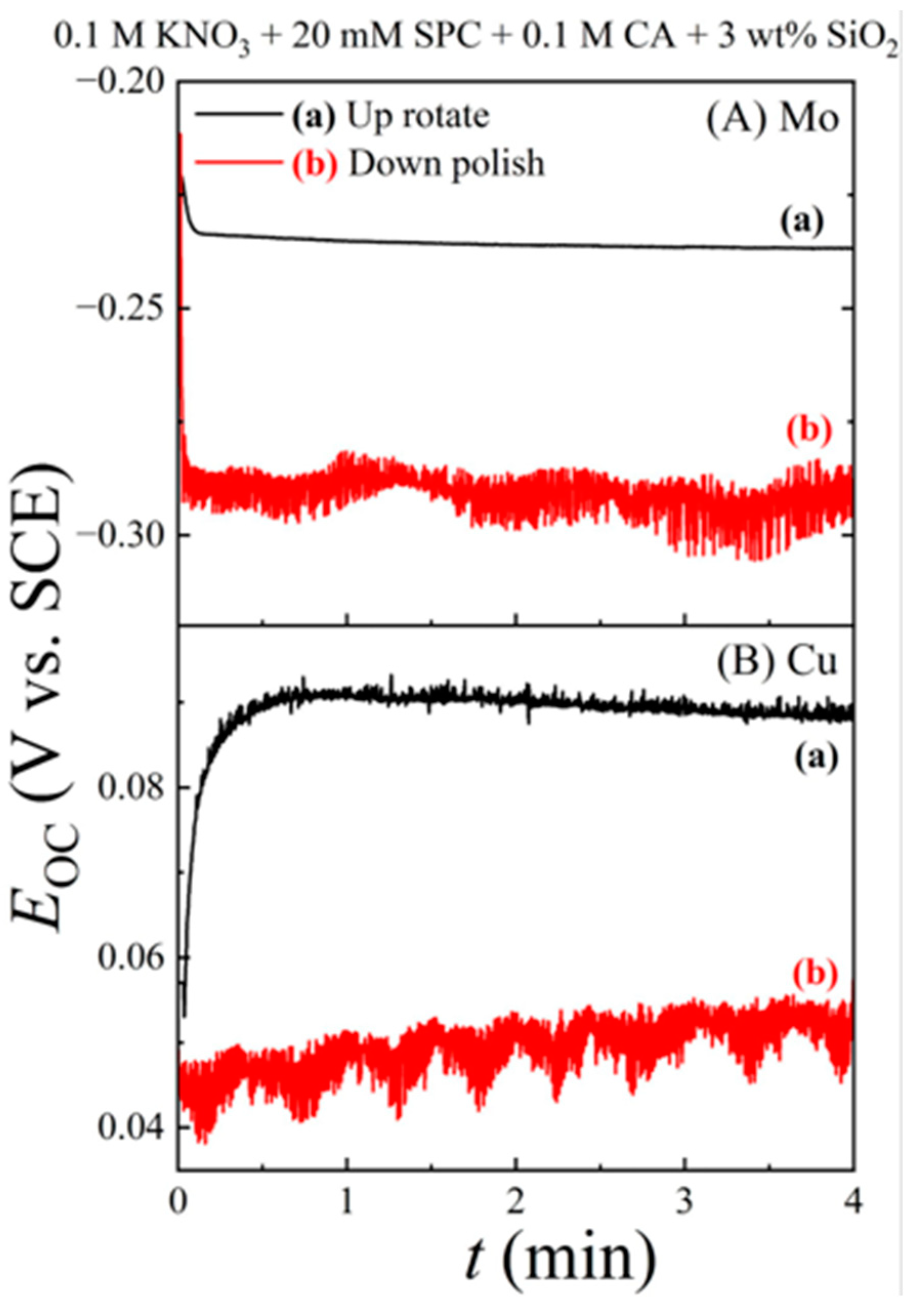
5.2. Tribo-Noise in Open-Circuit-Potential Measurements
5.3. Tribo-Noise in Potentiodynamic Polarization Measurements
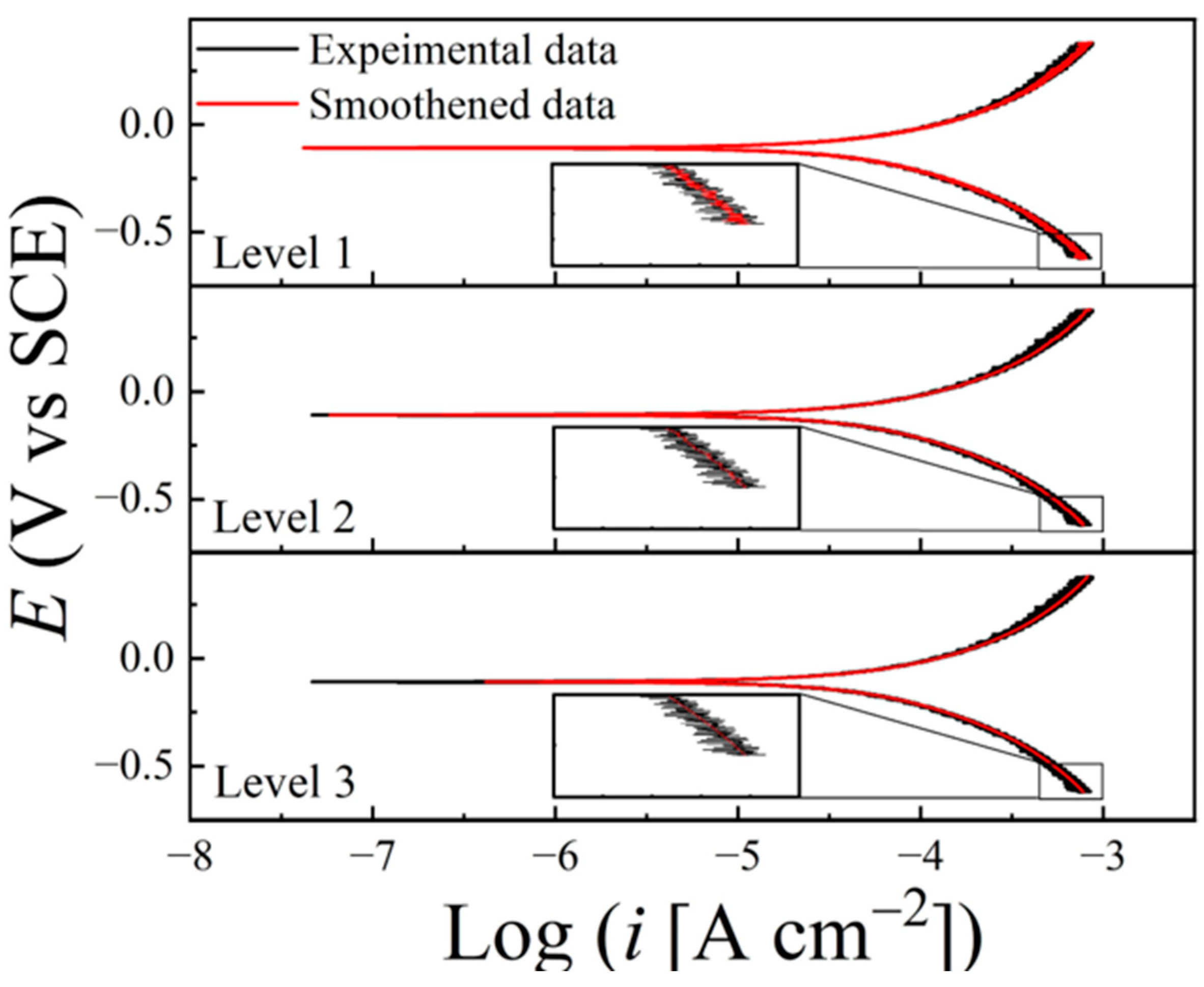
5.4. Processing of Tribo-Electrochemical Data for Systems Associated with Current Fluctuations
6. CMP-Specific Applications of Tribo-Electrochemical Measurements
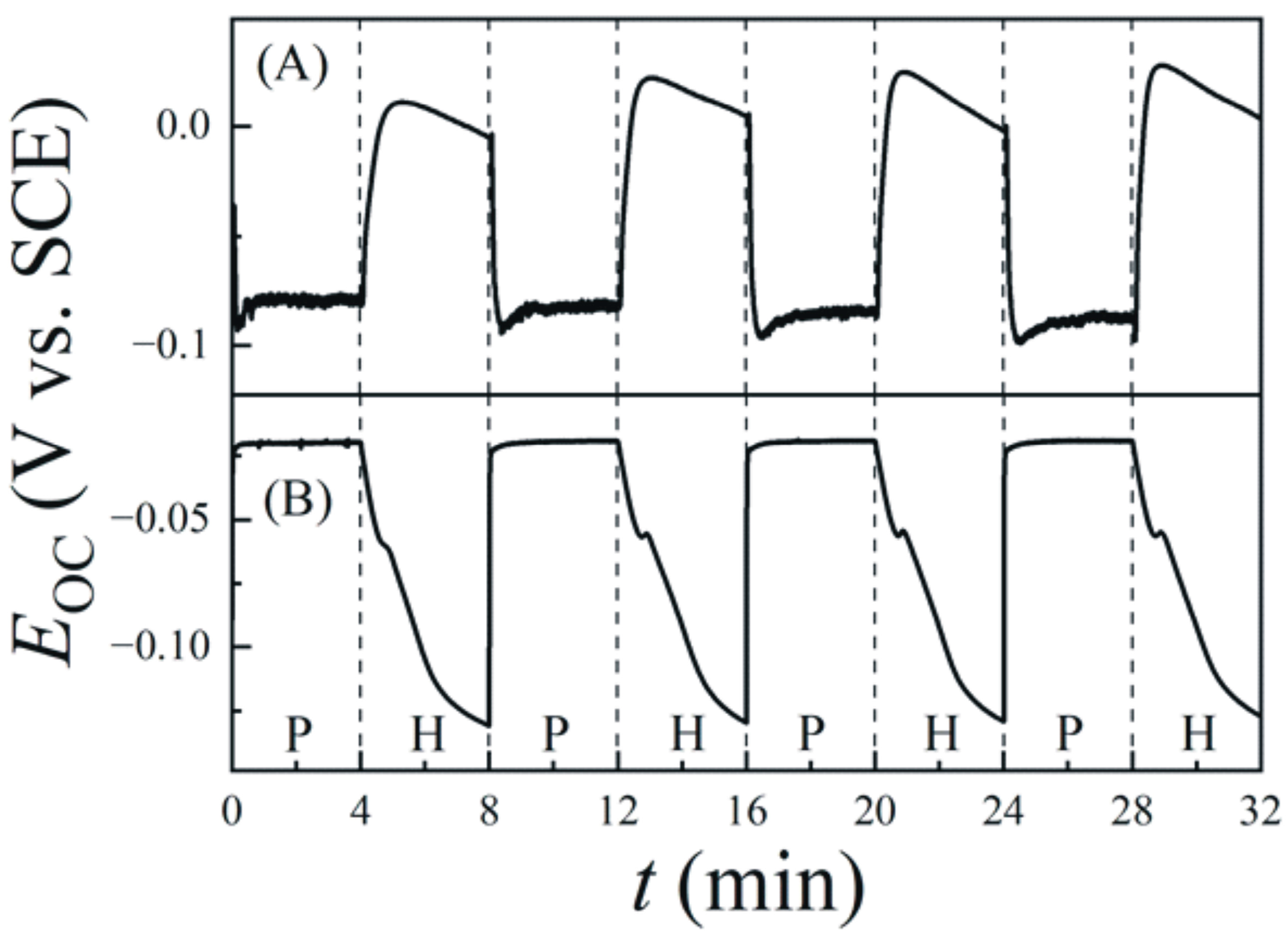
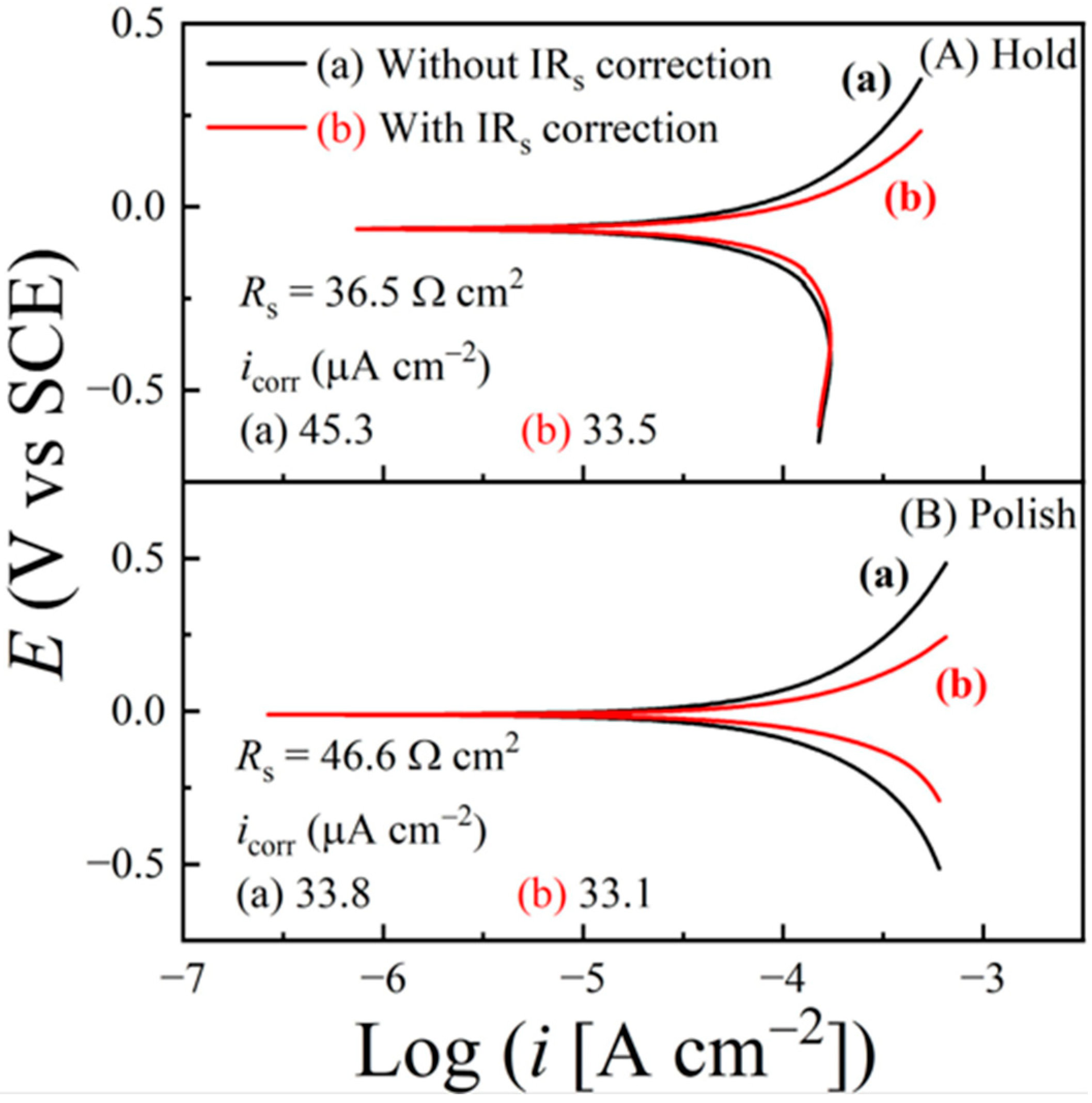
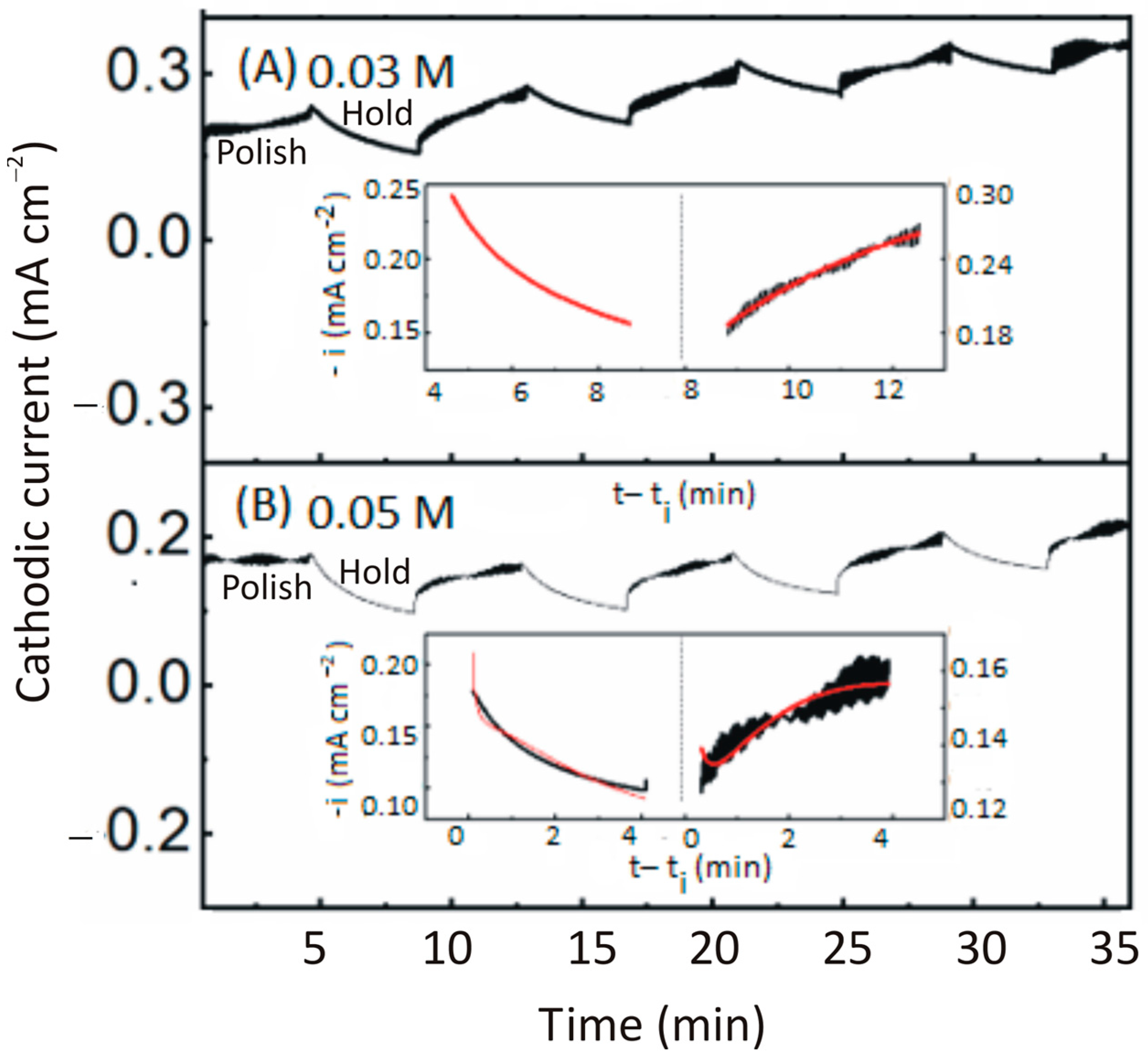
6.1. Intermittent Open-Circuit-Potential Transients under Polish and Hold Conditions
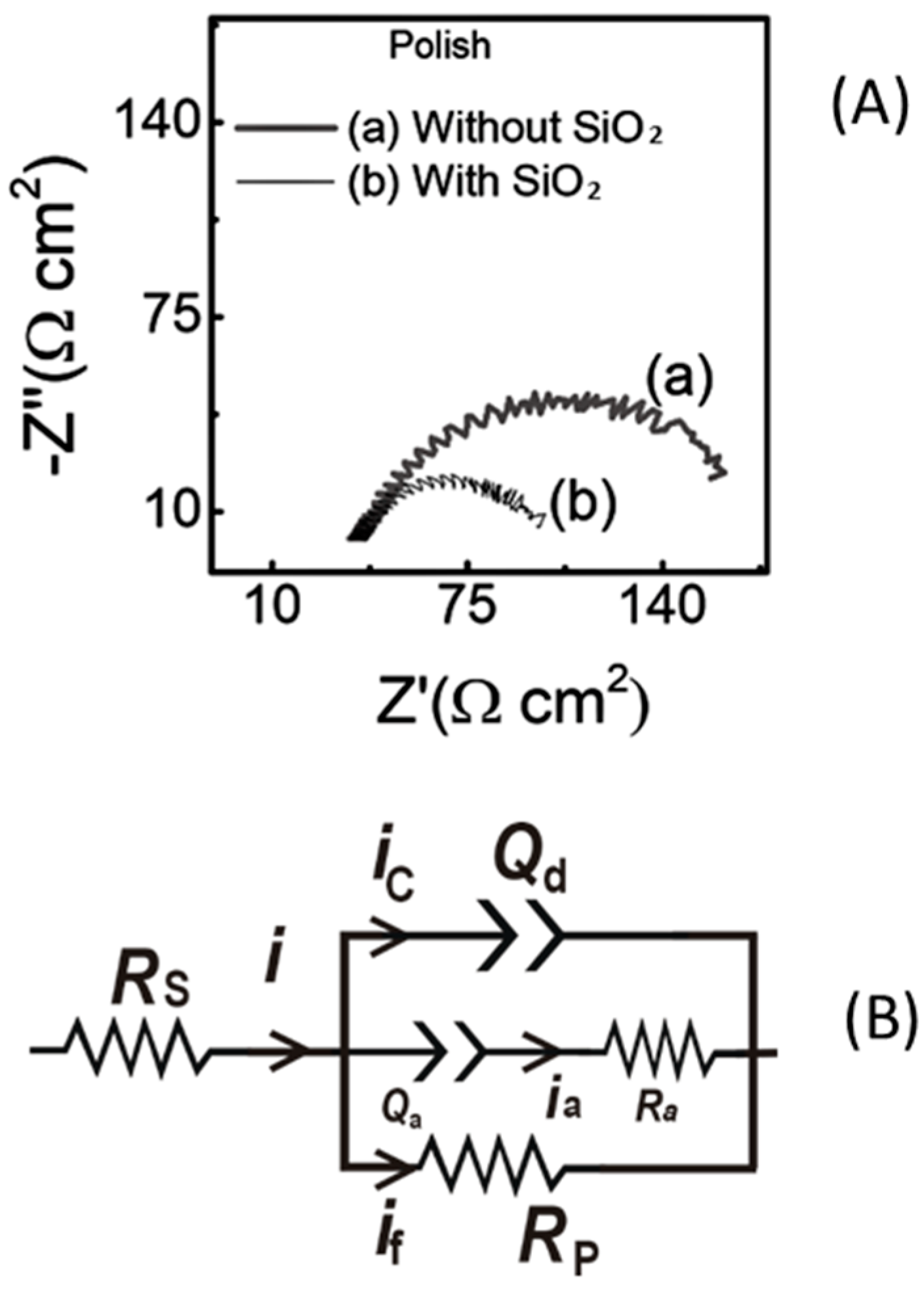
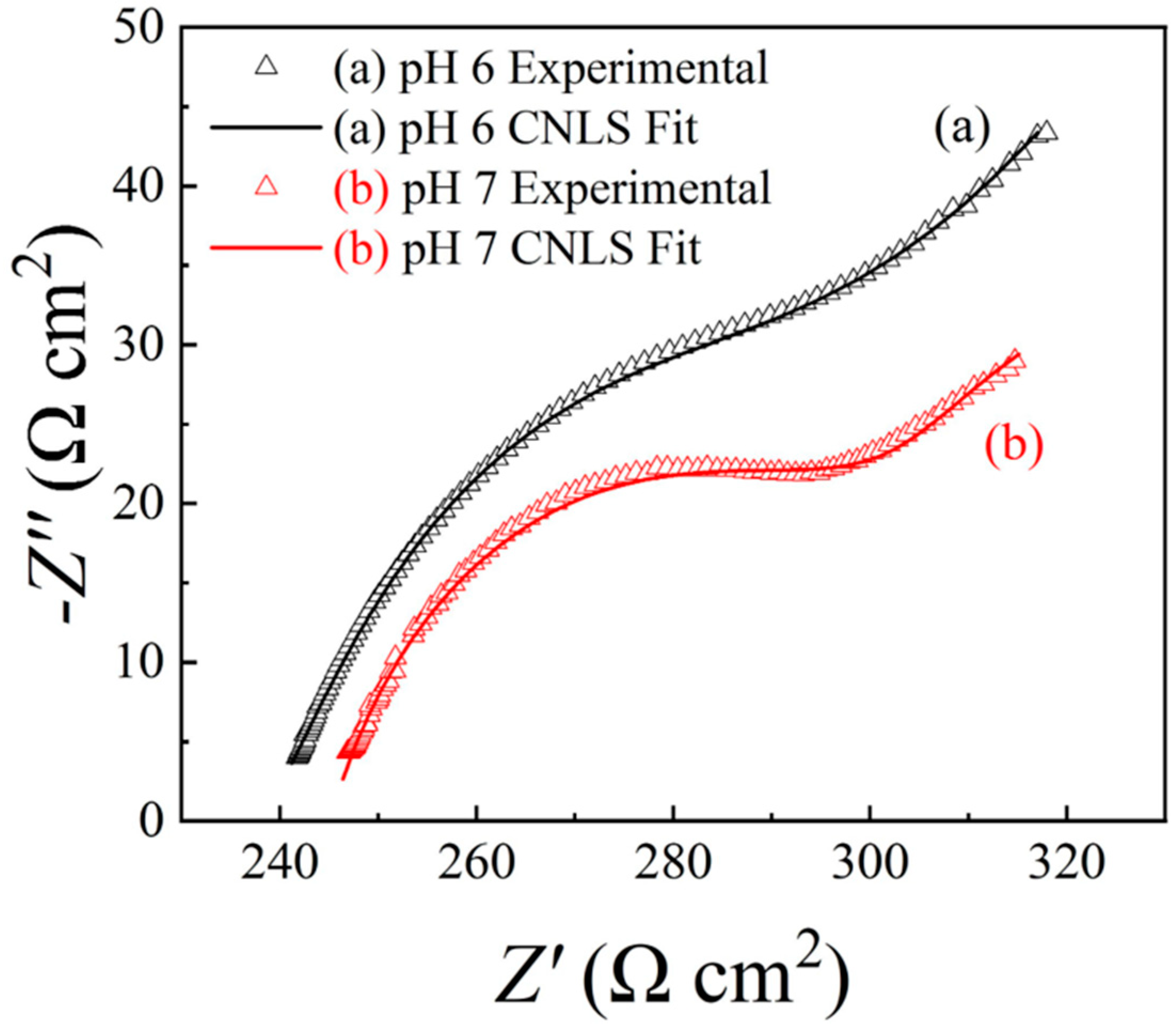
6.2. Electrochemical Impedance Spectroscopy
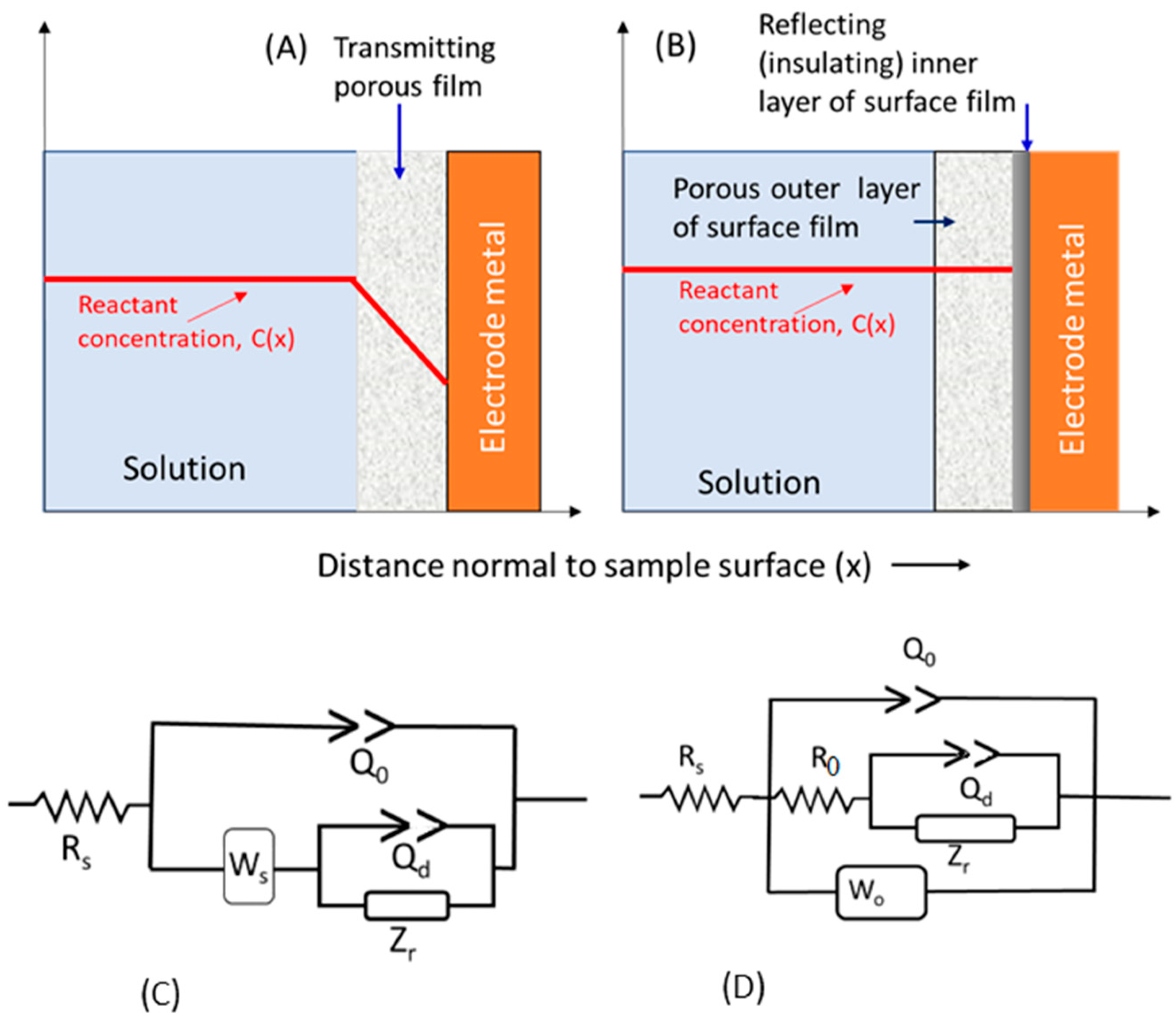
6.3. Detection and Analyses of Site-Blocking Surface Films
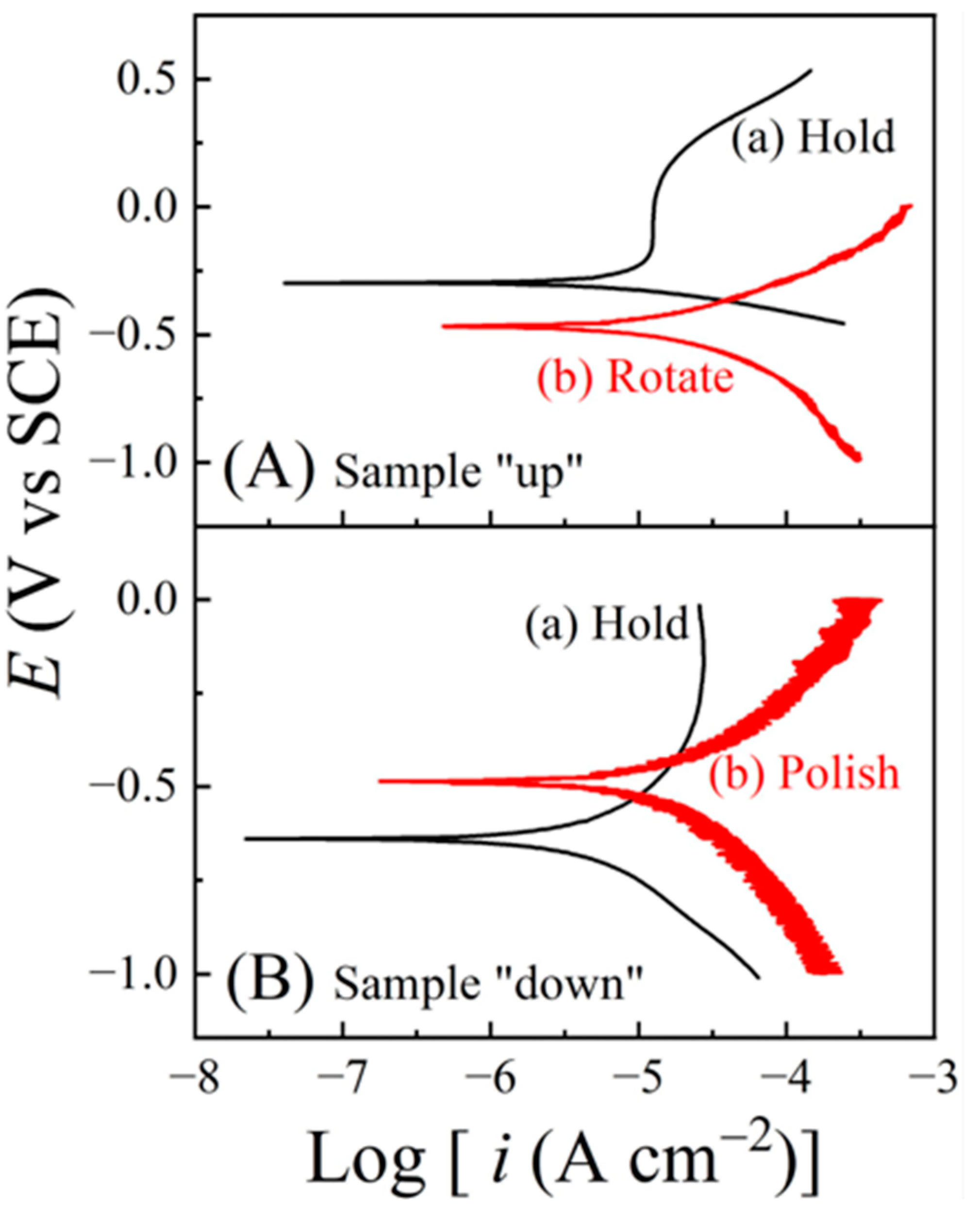
6.4. Tribo-Potentiodynamic Measurements
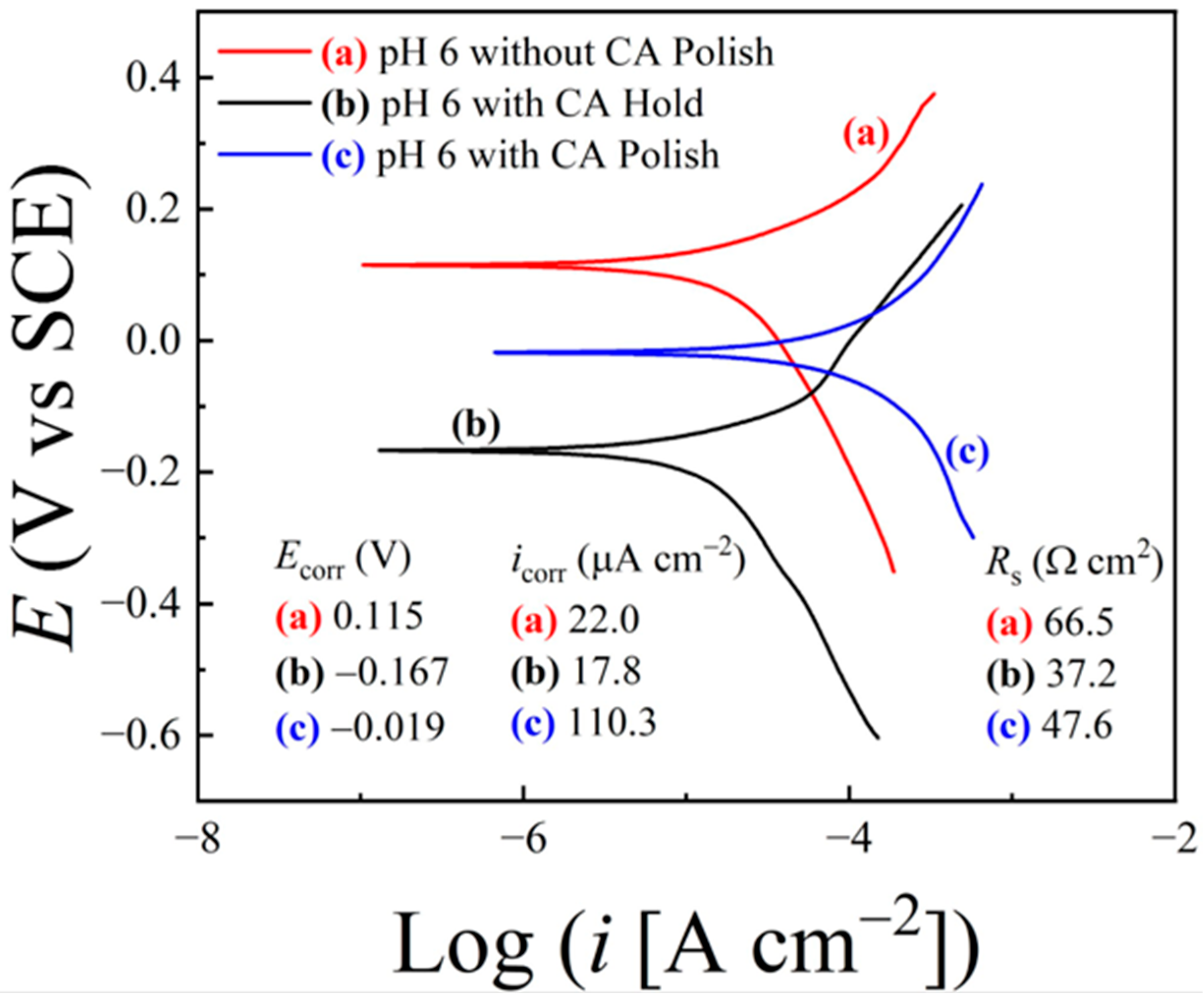
6.5. Tribology-Coupled Chronoamperometry
6.6. Tribology-Controlled Chronopotentiometry
7. Effects of Electrochemical Measurement Conditions on Corrosion Variables of Metal CMP Systems
7.1. General Considerations
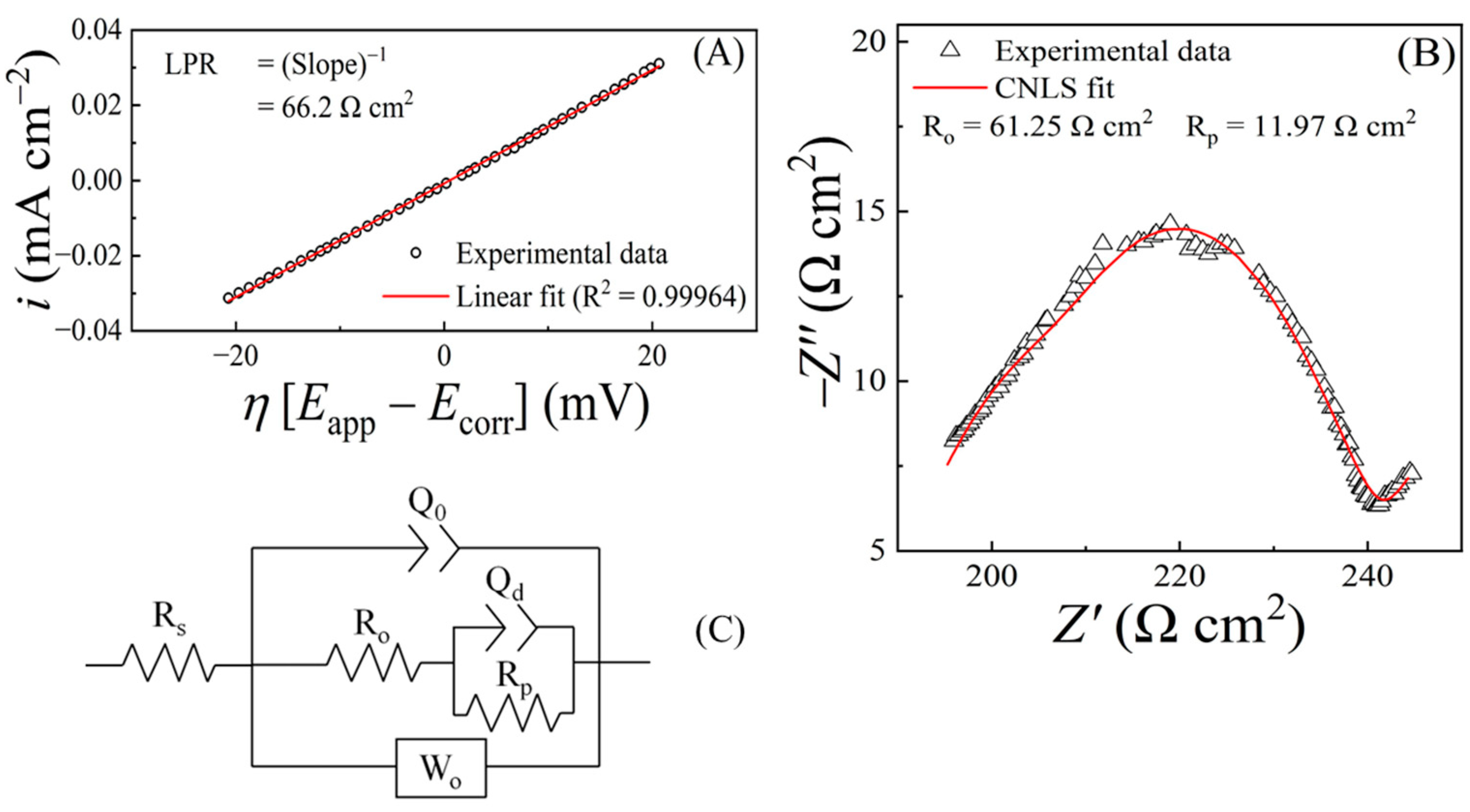
7.2. Comparing Polarization Resistances Measured with EIS and LPR
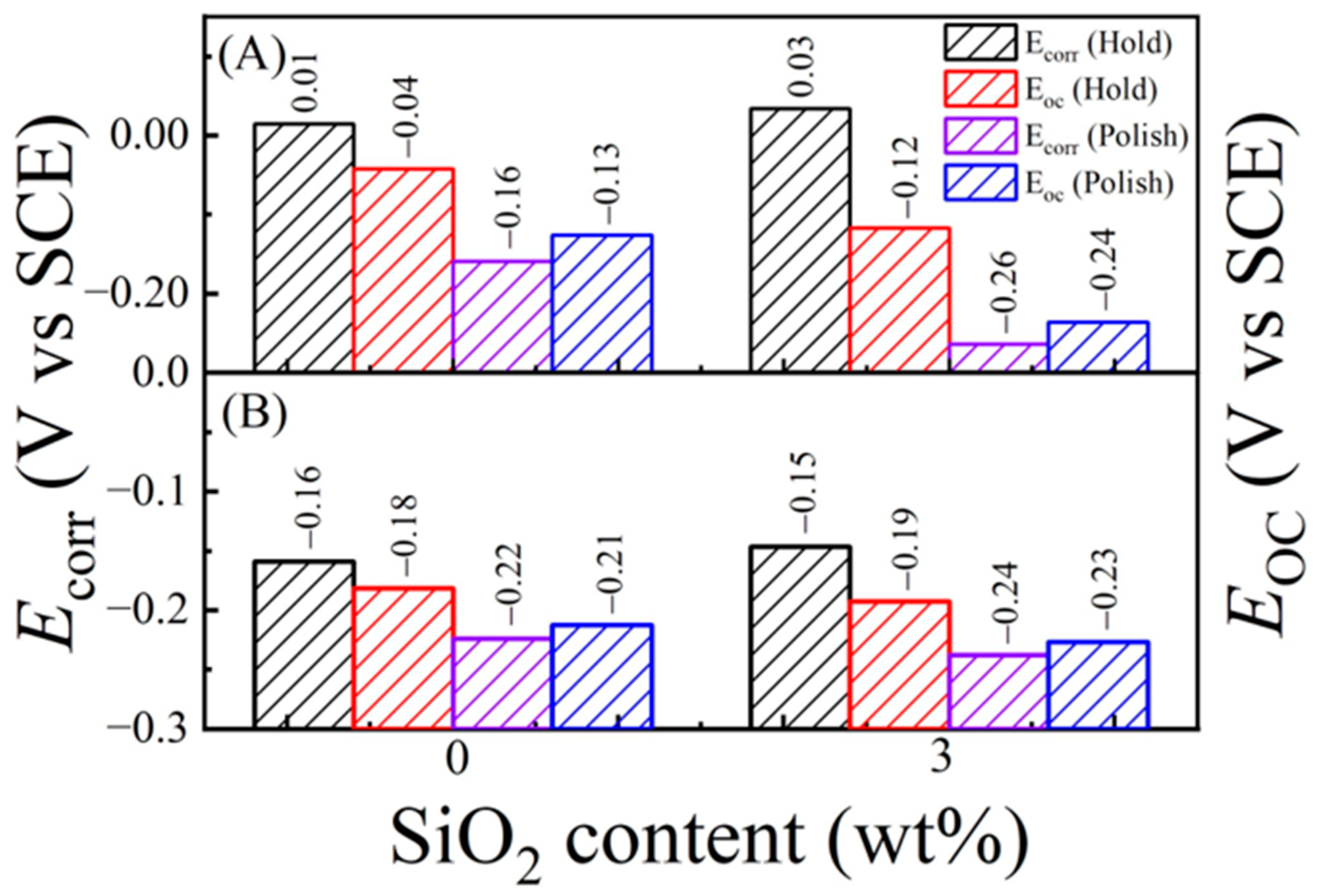
7.3. Comparing Open-Circuit Potentials and Corrosion Potentials
8. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| BE | Surface-binding energy of an adsorbed species |
| BEOL | Back end of line |
| BTA | Benzotriazole |
| CB | Carbon brush |
| CE | Counter electrode |
| CMP | Chemical–mechanical planarization |
| CNLS | Complex nonlinear least square |
| CPE | Constant phase element |
| CR | Corrosion rate |
| EEC | Electric equivalent circuit |
| EIS | Electrochemical impedance spectroscopy |
| FEOL | Front end of line |
| LOESS | Locally estimated scatterplot smoothing |
| LOWESS | Locally weighted scatterplot smoothing |
| LPR | Linear polarization resistance |
| LSV | Linear sweep voltammetry |
| MOL | Middle of line |
| MRR | Material removal rate |
| OCP | Open-circuit potential |
| PCMPC | Post-chemical–mechanical-planarization cleaning |
| PDP | Potentiodynamic polarization |
| PHT | Polish-vs.-hold transients |
| RE | Reference electrode |
| SB | Salt bridge |
| SCE | Saturated calomel electrode |
| SFR | Slurry flow rate |
| SPC | Sodium percarbonate |
| SWR | Specific wear rate |
| TCR | Tribo-corrosion rate |
| WE | Working electrode |
| WWNU | Within-wafer nonuniformity |
| Aa | Partial surface area of anodic oxidation reaction |
| Ac | Partial surface area of cathodic reduction reaction |
| Aeff | Effective area for electrochemical reactions |
| Af | Contact area of friction |
| ba | Anodic Tafel slope |
| bc | Cathodic Tafel slope |
| Cdeff | Effective double-layer capacitance |
| Ceff | Effective capacitance |
| D | Diffusion coefficient |
| E | Potential |
| Ea | External anodic potential |
| EB | Notation for surface-binding energy (BE) of an adsorbed species |
| Ec | External cathodic potential |
| Ecorr | Corrosion potential |
| Efr | Friction energy |
| Eoc | Open-circuit potential |
| Era | Reversible anodic Nernst potential |
| Erc | Reversible cathodic Nernst potential |
| F | Faraday constant |
| H | Material hardness |
| I | Current |
| i | Current density |
| Ia | Anodic current |
| ia | Area-normalized anodic current |
| Ic | Cathodic current |
| ic | Area-normalized cathodic current density |
| Icorr | Corrosion current |
| icorr | Corrosion current density |
| if | Faradaic current density |
| Ira | Reversible anodic Nernst current |
| ira | Reversible anodic Nernst current density |
| Irc | Reversible cathodic Nernst current |
| irc | Reversible cathodic Nernst current density |
| k0 | Equilibrium constant |
| Ka | Archard wear coefficient |
| kB | Boltzmann constant |
| KP | Preston coefficient |
| l | Effective film thickness or diffusion length of ions |
| Mm | Molecular weight of the CMP metal |
| P | Down pressure |
| p | Porosity of the film |
| Q0 | Surface film constant phase element |
| Qa | Constant phase element for nonfaradaic adsorption of anions |
| Qd | Double-layer constant phase element (CPE) |
| R | Gas constant |
| R0 | Diffusion resistance for a transmissive surface film |
| Ra | Resistance element for nonfaradaic adsorption of anions |
| Rb | Blocking resistance of a reflective surface film |
| RP | Polarization resistance |
| Rp’ | Modified polarization resistance in the presence of adsorption |
| Rs | Solution resistance |
| T | Temperature |
| V | Velocity maintained between pad and wafer |
| Ws | Short-circuit Warburg element |
| Yd, d | Frequency-independent constant-phase-element (CPE) parameters |
| z | Electron valency of mixed reaction |
| αa | Anodic transfer coefficient |
| αc | Cathodic transfer coefficient |
| βa | Anodic symmetry factor |
| βa | Cathodic symmetry factor |
| ΔEcorr | Corrosion potential difference between anode and cathode materials |
| ΔEr | Difference between reversible anodic and cathodic Nernst potentials |
| ηa | Anodic overpotential |
| ηc | Cathodic overpotential |
| θa | Potential-dependent fractional surface coverages of anodic intermediates (at Aa) |
| θc | Potential-dependent fractional surface coverages of cathodic intermediates (at Ac) |
| μeff | Effective coefficient of friction of a CMP interface |
| ρm | Density of the CMP metal |
| σp | Polarization conductance of CMP surface |
| ω | Applied frequency |
| ω0 | Frequency of diffusion |
| Ωh | Angular speed of sample holder |
| Ωp | Angular speed of rotating platen |
| eff | Effective time constant of the CMP test cell |
| Voltage scan rate |
References
- Seo, J. A review on chemical and mechanical phenomena at the wafer interface during chemical mechanical planarization. J. Mater. Res. 2020, 36, 235–257. [Google Scholar] [CrossRef]
- Peethala, C.B.; Kelly, J.J.; Canaperi, D.F.; Krishnan, M.; Nogami, T. Wet Chemical Processes for BEOL Technology. In Springer Handbook of Semiconductor Devices; Springer: Berlin/Heidelberg, Germany, 2022; pp. 219–257. [Google Scholar]
- Yan, H.; Niu, X.; Qu, M.; Luo, F.; Zhan, N.; Liu, J.; Zou, Y. A review: Research progress of chemical–mechanical polishing slurry for copper interconnection of integrated circuits. Int. J. Adv. Manuf. Technol. 2023, 125, 47–71. [Google Scholar] [CrossRef]
- Krishnan, M.; Nalaskowski, J.W.; Cook, L.M. Chemical Mechanical Planarization: Slurry Chemistry, Materials, and Mechanisms. Chem. Rev. 2009, 110, 178–204. [Google Scholar] [CrossRef]
- Thakurta, D.G.; Borst, C.L.; Schwendeman, D.W.; Gutmann, R.J.; Gill, W.N. Three-dimensional chemical mechanical planarization slurry flow model based on lubrication theory. J. Electrochem. Soc. 2001, 148, G207. [Google Scholar] [CrossRef]
- Zhou, P.; Kang, R.K.; Jin, Z.J.; Guo, D.M. Simulation of CMP process based on mixed elastohydrodynamic lubrication model with layered elastic theory. Adv. Mater. Res. 2012, 565, 330–335. [Google Scholar] [CrossRef]
- Higgs, C.F.; Ng, S.H.; Borucki, L.; Yoon, I.; Danyluk, S. A mixed-lubrication approach to predicting CMP fluid pressure modeling and experiments. J. Electrochem. Soc. 2005, 152, G193. [Google Scholar] [CrossRef]
- Liang, H. Chemical boundary lubrication in chemical–mechanical planarization. Tribol. Int. 2005, 38, 235–242. [Google Scholar] [CrossRef]
- Roy, D. Perspective—Electrochemical Assessment of Slurry Formulations for Chemical Mechanical Planarization of Metals: Trends, Benefits and Challenges. ECS J. Solid State Sci. Technol. 2018, 7, P209–P212. [Google Scholar] [CrossRef]
- Sulyma, C.M.; Goonetilleke, P.C.; Roy, D. Analysis of current transients for voltage pulse-modulated surface processing: Application to anodic electro-dissolution of copper for electrochemical mechanical planarization. J. Mater. Process. Technol. 2009, 209, 1189–1198. [Google Scholar] [CrossRef]
- Jeong, S.; Joo, S.; Kim, H.; Kim, S.; Jeong, H. Effect on two-step polishing process of electrochemical mechanical planarization and chemical–mechanical planarization on planarization. Jpn. J. Appl. Phys. 2009, 48, 066512. [Google Scholar] [CrossRef]
- Economikos, L. Planarization Technologies Involving Electrochemical Reactions. In Microelectronic Applications of Chemical Mechanical Planarization; John Wiley & Sons: Hoboken, NJ, USA, 2007; p. 319. [Google Scholar]
- Mohammad, A.E.K.; Wang, D. Electrochemical mechanical polishing technology: Recent developments and future research and industrial needs. Int. J. Adv. Manuf. Technol. 2016, 86, 1909–1924. [Google Scholar] [CrossRef]
- Kulkarni, M.; Gao, F.; Liang, H. Chemical-mechanical polishing (CMP): A controlled tribocorrosion process. In Tribocorrosion of Passive Metals and Coatings; Elsevier: Amsterdam, The Netherlands, 2011; pp. 498–518e. [Google Scholar]
- Kaufman, F.; Thompson, D.; Broadie, R.; Jaso, M.; Guthrie, W.; Pearson, D.; Small, M. Chemical-mechanical polishing for fabricating patterned W metal features as chip interconnects. J. Electrochem. Soc. 1991, 138, 3460. [Google Scholar] [CrossRef]
- Yagan, R.; Basim, G.B. A Fundamental Approach to Electrochemical Analyses on Chemically Modified Thin Films for Barrier CMP Optimization. ECS J. Solid State Sci. Technol. 2019, 8, P3118. [Google Scholar] [CrossRef]
- Choi, S.; Tripathi, S.; Dornfeld, D.A.; Doyle, F.M. Copper CMP modeling: Millisecond scale adsorption kinetics of BTA in glycine-containing solutions at pH 4. J. Electrochem. Soc. 2010, 157, H1153. [Google Scholar] [CrossRef]
- Paul, E. A model of chemical mechanical polishing. J. Electrochem. Soc. 2001, 148, G355. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, L.; Kim, S. A mathematical model for chemical–mechanical polishing based on formation and removal of weakly bonded molecular species. Wear 2003, 254, 332–339. [Google Scholar] [CrossRef]
- Beverskog, B.; Puigdomenech, I. Revised Pourbaix diagrams for nickel at 25–300 °C. Corros. Sci. 1997, 39, 969–980. [Google Scholar] [CrossRef]
- Barney, J.E.; Argersinger, W.J., Jr.; Reynolds, C. A Study of Some Complex Chlorides and Oxalates by Solubility Measurements1. J. Am. Chem. Soc. 1951, 73, 3785–3788. [Google Scholar] [CrossRef]
- Stojadinović, J.; Bouvet, D.; Mischler, S. Prediction of removal rates in chemical–mechanical polishing (CMP) using tribocorrosion modeling. J. Bio-Tribo-Corros. 2016, 2, 8. [Google Scholar] [CrossRef][Green Version]
- Datta, D.; Rai, H.; Singh, S.; Srivastava, M.; Sharma, R.K.; Gosvami, N.N. Nanoscale tribological aspects of chemical mechanical polishing: A review. Appl. Surf. Sci. Adv. 2022, 11, 100286. [Google Scholar] [CrossRef]
- Zhong, Z.-W. Recent developments and applications of chemical mechanical polishing. Int. J. Adv. Manuf. Technol. 2020, 109, 1419–1430. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.; Jeong, H. Mechanical aspects of the chemical mechanical polishing process: A review. Int. J. Precis. Eng. Manuf. 2016, 17, 525–536. [Google Scholar] [CrossRef]
- Luo, J.; Dornfeld, D.A. Material removal mechanism in chemical mechanical polishing: Theory and modeling. IEEE Trans. Semicond. Manuf. 2001, 14, 112–133. [Google Scholar]
- Wu, C.; Liao, X. Lubrication in Chemical and Mechanical Planarization; IntechOpen: London, UK, 2016. [Google Scholar]
- Kasai, T.; Bhushan, B. Physics and tribology of chemical mechanical planarization. J. Phys. Condens. Matter 2008, 20, 225011. [Google Scholar] [CrossRef]
- Joo, S.; Liang, H. Tribology in Chemical–Mechanical Planarization. In Tribology for Scientists and Engineers: From Basics to Advanced Concepts; Springer: Berlin/Heidelberg, Germany, 2013; pp. 747–782. [Google Scholar]
- Hong Liang, D.C. Tribology in Chemical-Mechanical Planarization; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Luo, J.; Dornfeld, D.A. Integrated Modeling of Chemical Mechanical Planarization for Sub-Micron IC Fabrication: From Particle Scale to Feature, Die and Wafer Scales; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Jairath, R.; Pant, A.; Mallon, T.; Withers, B.; Krusell, W. Linear planarization for CMP. Solid State Technol. 1996, 39, 107–112. [Google Scholar]
- Tseng, W.T.; Chin, J.H.; Kang, L.C. A comparative study on the roles of velocity in the material removal rate during chemical mechanical polishing. J. Electrochem. Soc. 1999, 146, 1952. [Google Scholar] [CrossRef]
- Philipossian, A.; Olsen, S. Fundamental tribological and removal rate studies of inter-layer dielectric chemical mechanical planarization. Jpn. J. Appl. Phys. 2003, 42, 6371. [Google Scholar] [CrossRef]
- Kwon, T.-Y.; Ramachandran, M.; Cho, B.-J.; Busnaina, A.A.; Park, J.-G. The impact of diamond conditioners on scratch formation during chemical mechanical planarization (CMP) of silicon dioxide. Tribol. Int. 2013, 67, 272–277. [Google Scholar] [CrossRef]
- Luo, Q.; Ramarajan, S.; Babu, S. Modification of the Preston equation for the chemical–mechanical polishing of copper. Thin Solid Film. 1998, 335, 160–167. [Google Scholar] [CrossRef]
- Wallburg, F.; Kuna, M.; Budnitzki, M.; Schoenfelder, S. A material removal coefficient for diamond wire sawing of silicon. Wear 2022, 504, 204400. [Google Scholar] [CrossRef]
- Zhao, B.; Shi, F. Chemical mechanical polishing in IC processes: New fundamental insights. In Proceedings of the Proceedings of the Fourth International Chemical Mechanical Planarization for ULSI Multilevel Interconnection Conference, Santa Clara, CA, USA, 11–12 February 1999. [Google Scholar]
- Park, B.; Jeong, S.; Lee, H.; Kim, H.; Jeong, H.; Dornfeld, D.A. Experimental investigation of material removal characteristics in silicon chemical mechanical polishing. Jpn. J. Appl. Phys. 2009, 48, 116505. [Google Scholar] [CrossRef]
- Choi, W.; Abiade, J.; Lee, S.-M.; Singh, R.K. Effects of slurry particles on silicon dioxide CMP. J. Electrochem. Soc. 2004, 151, G512. [Google Scholar] [CrossRef]
- Noh, K.; Lai, J.-Y.; Saka, N.; Chun, J.-H. Mechanics, Mechanisms and Modeling of the Chemical Mechanical Polishing Process. DSpace@MIT. 2002. Available online: https://dspace.mit.edu/handle/1721.1/4032 (accessed on 10 November 2023).
- Hashimoto, Y.; Furumoto, T.; Sato, T.; Suzuki, N.; Yasuda, H.; Yamaki, S.; Mochizuki, Y. Novel method to visualize Preston’s coefficient distribution for chemical mechanical polishing process. Jpn. J. Appl. Phys. 2022, 61, 116502. [Google Scholar] [CrossRef]
- Johnson, C.; Wei, S.; Roy, D. An Alkaline Slurry Design for Co-Cu CMP Systems Evaluated in the Tribo-Electrochemical Approach. ECS J. Solid State Sci. Technol. 2018, 7, P38–P49. [Google Scholar] [CrossRef]
- Kim, H.; Jeong, H. Effect of process conditions on uniformity of velocity and wear distance of pad and wafer during chemical mechanical planarization. J. Electron. Mater. 2004, 33, 53–60. [Google Scholar] [CrossRef]
- Zhao, D.; He, Y.; Wang, T.; Lu, X. Effect of kinematic parameters and their coupling relationships on global uniformity of chemical-mechanical polishing. IEEE Trans. Semicond. Manuf. 2012, 25, 502–510. [Google Scholar] [CrossRef]
- Patrick, W.J.; Guthrie, W.L.; Standley, C.L.; Schiable, P.M. Application of Chemical Mechanical Polishing to the Fabrication of VLSI Circuit Interconnections. J. Electrochem. Soc. 1991, 138, 1778–1784. [Google Scholar] [CrossRef]
- Hocheng, H.; Tsai, H.; Tsai, M. Effects of kinematic variables on nonuniformity in chemical mechanical planarization. Int. J. Mach. Tools Manuf. 2000, 40, 1651–1669. [Google Scholar] [CrossRef]
- Ilie, F.; Minea, I.-L.; Cotici, C.D.; Hristache, A.-F. The Effects of Friction and Temperature in the Chemical–Mechanical Planarization Process. Materials 2023, 16, 2550. [Google Scholar] [CrossRef]
- Zhao, D.; He, Y.; Wang, T.; Lu, X.; Luo, J. Effects of the polishing variables on the wafer-pad interfacial fluid pressure in chemical mechanical polishing of 12-inch wafer. J. Electrochem. Soc. 2012, 159, H342. [Google Scholar] [CrossRef]
- Tucker, T. Equipment used in cmp processes. In Chemical-Mechanical Planarization of Semiconductor Materials; Springer: Berlin/Heidelberg, Germany, 2004; pp. 133–165. [Google Scholar]
- Philipossian, A.; Mitchell, E. Slurry utilization efficiency studies in chemical mechanical planarization. Jpn. J. Appl. Phys. 2003, 42, 7259. [Google Scholar] [CrossRef]
- Jo, H.; Lee, D.S.; Jeong, S.H.; Lee, H.S.; Jeong, H.D. Hybrid CMP slurry supply system using ionization and atomization. Appl. Sci. 2021, 11, 2217. [Google Scholar] [CrossRef]
- Fujita, T.; Watanabe, J. Slurry supply mechanism utilizing capillary effect in chemical mechanical planarization. ECS J. Solid State Sci. Technol. 2019, 8, P3069. [Google Scholar] [CrossRef]
- Cho, Y.; Liu, P.; Jeon, S.; Lee, J.; Bae, S.; Hong, S.; Kim, Y.H.; Kim, T. Simulation and Experimental Investigation of the Radial Groove Effect on Slurry Flow in Oxide Chemical Mechanical Polishing. Appl. Sci. 2022, 12, 4339. [Google Scholar] [CrossRef]
- Mu, Y.; Zhuang, Y.; Sampurno, Y.; Wei, X.; Ashizawa, T.; Morishima, H.; Philipossian, A. Effect of pad groove width on slurry mean residence time and slurry utilization efficiency in CMP. Microelectron. Eng. 2016, 157, 60–63. [Google Scholar] [CrossRef]
- Borucki, L.; Charns, L.; Philipossian, A. Analysis of frictional heating of grooved and flat CMP polishing pads. J. Electrochem. Soc. 2004, 151, G809. [Google Scholar] [CrossRef]
- Liau, L.C.-K.; Lin, K.-M. Effect of slurry flow rates on tungsten removal optimization in chemical mechanical planarization. Microelectron. Reliab. 2023, 146, 115021. [Google Scholar] [CrossRef]
- Mudhivarthi, S.; Gitis, N.; Kuiry, S.; Vinogradov, M.; Kumar, A. Effects of slurry flow rate and pad conditioning temperature on dishing, erosion, and metal loss during copper CMP. J. Electrochem. Soc. 2006, 153, G372. [Google Scholar] [CrossRef]
- Zhou, C.; Shan, L.; Hight, J.R.; Ng, S.; Danyluk, S. Fluid pressure and its effects on chemical mechanical polishing. Wear 2002, 253, 430–437. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, D.; He, Y.; Lu, X. Effect of slurry injection position on material removal in chemical mechanical planarization. Int. J. Adv. Manuf. Technol. 2013, 67, 2903–2908. [Google Scholar] [CrossRef]
- Li, J.; Lu, X.; He, Y.; Luo, J. Modeling the chemical-mechanical synergy during copper CMP. J. Electrochem. Soc. 2010, 158, H197. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, X. Chemical mechanical polishing: Theory and experiment. Friction 2013, 1, 306–326. [Google Scholar] [CrossRef]
- Sun, T.; Zhuang, Y.; Borucki, L.; Philipossian, A. Characterization of pad–wafer contact and surface topography in chemical mechanical planarization using laser confocal microscopy. Jpn. J. Appl. Phys. 2010, 49, 066501. [Google Scholar] [CrossRef]
- Gray, C.; White, R.; Manno, V.P.; Rogers, C.B. Simulated effects of measurement noise on contact measurements between rough and smooth surfaces. Tribol. Lett. 2008, 29, 185–192. [Google Scholar] [CrossRef]
- White, R.D.; Mueller, A.J.; Shin, M.; Gauthier, D.; Manno, V.P.; Rogers, C.B. Measurement of microscale shear forces during chemical mechanical planarization. J. Electrochem. Soc. 2011, 158, H1041. [Google Scholar] [CrossRef]
- Schumacher-Härtwig, H. Characterization of Pad–Wafer Contact Area and Distance in Chemical-Mechanical Polishing. ECS J. Solid State Sci. Technol. 2023, 12, 074002. [Google Scholar] [CrossRef]
- Castillo-Mejia, D.; Beaudo, S. A Locally Relevant Prestonian Model for Wafer Polishing. J. Electrochem. Soc. 2004, 150, G96–G102. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Huang, P.-Y. Impact of abrasive particles on the material removal rate in CMP: A microcontact perspective. Electrochem. Solid-State Lett. 2004, 7, G40. [Google Scholar] [CrossRef]
- Zhao, Y.; Chang, L. A micro-contact and wear model for chemical–mechanical polishing of silicon wafers. Wear 2002, 252, 220–226. [Google Scholar] [CrossRef]
- Keddam, M.; Ponthiaux, P.; Vivier, V. Tribo-electrochemical impedance: A new technique for mechanistic study in tribocorrosion. Electrochim. Acta 2014, 124, 3–8. [Google Scholar] [CrossRef]
- Trasatti, S.; Petrii, O. Real surface area measurements in electrochemistry. Pure Appl. Chem. 1991, 63, 711–734. [Google Scholar] [CrossRef]
- Connor, P.; Schuch, J.; Kaiser, B.; Jaegermann, W. The determination of electrochemical active surface area and specific capacity revisited for the system MnOx as an oxygen evolution catalyst. Z. Phys. Chem. 2020, 234, 979–994. [Google Scholar] [CrossRef]
- Abdelbary, A.; Chang, L. 2—Properties and characteristics of tribo-surfaces. In Principles of Engineering Tribology; Abdelbary, A., Chang, L., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 33–75. [Google Scholar]
- Wei, S.; Johnson, C.; Roy, D. Probing the Mechanisms of Metal CMP Using Tribo-Electroanalytical Measurements: Results for a Copper/Malonate System. ECS J. Solid State Sci. Technol. 2021, 10, 034001. [Google Scholar] [CrossRef]
- Shi, X.; Simpson, D.; Roy, D. Tribo-electrochemical characterization of Ru, Ta and Cu CMP systems using percarbonate based solutions. ECS J. Solid State Sci. Technol. 2015, 4, P5058. [Google Scholar] [CrossRef]
- Thakurta, D.G.; Borst, C.L.; Schwendeman, D.W.; Gutmann, R.J.; Gill, W.N. Pad porosity, compressibility and slurry delivery effects in chemical-mechanical planarization: Modeling and experiments. Thin Solid Film. 2000, 366, 181–190. [Google Scholar] [CrossRef]
- Sundararajan, S.; Thakurta, D.G.; Schwendeman, D.W.; Murarka, S.P.; Gill, W.N. Two-dimensional wafer-scale chemical mechanical planarization models based on lubrication theory and mass transport. J. Electrochem. Soc. 1999, 146, 761. [Google Scholar] [CrossRef]
- Tichy, J.; Levert, J.A.; Shan, L.; Danyluk, S. Contact mechanics and lubrication hydrodynamics of chemical mechanical polishing. J. Electrochem. Soc. 1999, 146, 1523. [Google Scholar] [CrossRef]
- Tsai, H.; Jeng, Y.; Huang, P. An improved model considering elastic—Plastic contact and partial hydrodynamic lubrication for chemical mechanical polishing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 761–770. [Google Scholar] [CrossRef]
- Vlassak, J. A model for chemical–mechanical polishing of a material surface based on contact mechanics. J. Mech. Phys. Solids 2004, 52, 847–873. [Google Scholar] [CrossRef]
- Feng, C.; Yan, C.; Tao, J.; Zeng, X.; Cai, W. A contact-mechanics-based model for general rough pads in chemical mechanical polishing processes. J. Electrochem. Soc. 2009, 156, H601. [Google Scholar] [CrossRef][Green Version]
- Zhou, P.; Dong, Z.; Kang, R.; Jin, Z.; Guo, D. A mixed elastohydrodynamic lubrication model for simulation of chemical mechanical polishing with double-layer structure of polishing pad. Int. J. Adv. Manuf. Technol. 2015, 77, 107–116. [Google Scholar] [CrossRef]
- Terrell, E.J.; Higgs, C.F., III. A particle-augmented mixed lubrication modeling approach to predicting chemical mechanical polishing. J. Tribol. 2009, 131, 012201. [Google Scholar] [CrossRef]
- Jeng, Y.-R.; Huang, P.-Y.; Pan, W.-C. Tribological analysis of CMP with partial asperity contact. J. Electrochem. Soc. 2003, 150, G630. [Google Scholar] [CrossRef]
- McAllister, J.; Mariscal, J.C.; Dadashazar, H.; Sampurno, Y.; Philipossian, A. Effect of Abrasive Nanoparticle Concentration on the Tribological, Thermal and Kinetic Attributes of Tungsten Chemical Mechanical Planarization. ECS J. Solid State Sci. Technol. 2020, 9, 024014. [Google Scholar] [CrossRef]
- Borucki, L.J.; Sun, T.; Zhuang, Y.; Slutz, D.; Philipossian, A. Pad Topography, Contact Area and Hydrodynamic Lubrication in Chemical-Mechanical Polishing. MRS Online Proc. Libr. 2009, 1157, E1101–E1102. [Google Scholar] [CrossRef]
- Zhang, Y.; Biboulet, N.; Venner, C.; Lubrecht, A. Prediction of the Stribeck curve under full-film Elastohydrodynamic Lubrication. Tribol. Int. 2020, 149, 105569. [Google Scholar] [CrossRef]
- Levert, J.A.; Korach, C.S.; Mooney, B.; Lynam, F. Model of particle contact area for friction in oxide chemical mechanical polishing. ECS J. Solid State Sci. Technol. 2019, 8, P787. [Google Scholar] [CrossRef]
- Rosales-Yeomans, D.; Lee, H.; Suzuki, T.; Philipossian, A. Effect of concentric slanted pad groove patterns on slurry flow during chemical mechanical planarization. Thin Solid Film. 2012, 520, 2224–2232. [Google Scholar] [CrossRef]
- Lu, J.; Rogers, C.; Manno, V.P.; Philipossian, A.; Anjur, S.; Moinpour, M. Measurements of Slurry Film Thickness and Wafer Drag during CMP. J. Electrochem. Soc. 2004, 151, G241–G247. [Google Scholar] [CrossRef]
- Wang, Y.-S.; Chen, K.-W.; Cheng, M.-Y.; Lee, W.-H.; Wang, Y.-L. Effects of (002) β-Ta barrier on copper chemical mechanical polishing behavior. Thin Solid Film. 2013, 529, 435–438. [Google Scholar] [CrossRef]
- Seo, E.-B.; Bae, J.-Y.; Kim, S.-I.; Choi, H.-E.; Son, Y.-H.; Yun, S.-S.; Park, J.-H.; Park, J.-G. Interfacial Chemical and Mechanical Reactions between Tungsten-Film and Nano-Scale Colloidal Zirconia Abrasives for Chemical-Mechanical-Planarization. ECS J. Solid State Sci. Technol. 2020, 9, 054001. [Google Scholar] [CrossRef]
- Chen, K.-S.; Wu, S.-L.; Yeh, H.-M. Modeling of chemical mechanical polishing processes by cellular automata and finite element/matlab integration methods. Microsyst. Technol. 2015, 21, 1879–1892. [Google Scholar] [CrossRef]
- Rock, S.E.; Crain, D.J.; Zheng, J.P.; Pettit, C.M.; Roy, D. Electrochemical investigation of the surface-modifying roles of guanidine carbonate in chemical mechanical planarization of tantalum. Mater. Chem. Phys. 2011, 129, 1159–1170. [Google Scholar] [CrossRef]
- Lee, H.; Park, B.; Jeong, H. Mechanical effect of process condition and abrasive concentration on material removal rate profile in copper chemical mechanical planarization. J. Mater. Process. Technol. 2009, 209, 1729–1735. [Google Scholar] [CrossRef]
- Bozkaya, D.; Müftü, S. A Material Removal Model for CMP Based on the Contact Mechanics of Pad, Abrasives, and Wafer. J. Electrochem. Soc. 2009, 156, H890–H902. [Google Scholar] [CrossRef]
- Paul, E. A model of chemical mechanical polishing: II. Polishing pressure and speed. J. Electrochem. Soc. 2002, 149, G305. [Google Scholar] [CrossRef]
- Brugnoli, L.; Miyatani, K.; Akaji, M.; Urata, S.; Pedone, A. New Atomistic Insights on the Chemical Mechanical Polishing of Silica Glass with Ceria Nanoparticles. Langmuir 2023, 39, 5527–5541. [Google Scholar] [CrossRef] [PubMed]
- Steigerwald, J.M.; Murarka, S.P.; Gutmann, R.J. Chemical Mechanical Planarization of Microelectronic Materials; Wiley-VCH: Wineheim, Germany, 2004. [Google Scholar]
- Rock, S.; Crain, D.; Pettit, C.; Roy, D. Surface-complex films of guanidine on tantalum nitride electrochemically characterized for applications in chemical mechanical planarization. Thin Solid Film. 2012, 520, 2892–2900. [Google Scholar] [CrossRef]
- Echavarri Otero, J.; de la Guerra Ochoa, E.; Chacon Tanarro, E.; del Río López, B. Friction coefficient in mixed lubrication: A simplified analytical approach for highly loaded non-conformal contacts. Adv. Mech. Eng. 2017, 9, 1687814017706266. [Google Scholar] [CrossRef]
- Lee, H.; Joo, S.; Jeong, H. Mechanical effect of colloidal silica in copper chemical mechanical planarization. J. Mater. Process. Technol. 2009, 209, 6134–6139. [Google Scholar] [CrossRef]
- Brocks, W. Cohesive strength and separation energy as characteristic parameters of fracture toughness and their relation to micromechanics. Struct. Durab. Health Monit. 2005, 1, 233. [Google Scholar]
- Santefort, D.; Gamagedara, K.; Roy, D. Tribo-Electroanalytical Evaluation of CMP Slurries and Post-CMP Cleaning Solutions. In Proceedings of the ICPT Conference, Portland, OR, USA, 29 September 2022; pp. 1–8. [Google Scholar]
- Chen, Y.; Renner, P.; Liang, H. A review of current understanding in tribochemical reactions involving lubricant additives. Friction 2023, 11, 489–512. [Google Scholar] [CrossRef]
- Jeong, S.; Jeong, K.; Choi, J.; Jeong, H. Analysis of correlation between pad temperature and asperity angle in chemical mechanical planarization. Appl. Sci. 2021, 11, 1507. [Google Scholar] [CrossRef]
- Kim, H.J.; Ahn, S.-G.; Qin, L.; Koli, D.; Govindarajulu, V.; Moon, Y. Effects of pad temperature on the chemical mechanical polishing of tungsten. ECS J. Solid State Sci. Technol. 2014, 3, P310. [Google Scholar] [CrossRef]
- Gutman, E. Mechanochemistry of Metals and Corrosion Protection; Cambridge International Science Publishing: Cambridge, UK, 1998; p. 212. [Google Scholar]
- Kaleli, H. New Universal Tribometer as Pin or Ball-on-Disc and Reciprocating Pin-on-Plate Types. Tribol. Ind. 2016, 38, 235. [Google Scholar]
- Alkan, S.; Gök, M.S. Effect of sliding wear and electrochemical potential on tribocorrosion behaviour of AISI 316 stainless steel in seawater. Eng. Sci. Technol. Int. J. 2020, 24, 524–532. [Google Scholar] [CrossRef]
- Vats, V.; Baskaran, T.; Arya, S.B. Tribo-corrosion study of nickel-free, high nitrogen and high manganese austenitic stainless steel. Tribol. Int. 2018, 119, 659–666. [Google Scholar] [CrossRef]
- López-Ortega, A.; Arana, J.; Bayón, R. Tribocorrosion of passive materials: A review on test procedures and standards. Int. J. Corros. 2018, 2018, 7345346. [Google Scholar] [CrossRef]
- Jackson, C.L.; Mosley, D.W. Model friction studies of chemical mechanical planarization using a pin-on-disk tribometer. Tribol. Lett. 2019, 67, 81. [Google Scholar] [CrossRef]
- Lee, W.-J.; Park, H.-S. Development of novel process for Ru CMP using ceric ammonium nitrate (CAN)-containing nitric acid. Appl. Surf. Sci. 2004, 228, 410–417. [Google Scholar] [CrossRef]
- Stein, D.J.; Hetherington, D.; Guilinger, T.; Cecchi, J.L. In Situ Electrochemical Investigation of Tungsten Electrochemical Behavior during Chemical Mechanical Polishing. J. Electrochem. Soc. 1998, 145, 3190–3196. [Google Scholar] [CrossRef]
- Fang, Y.; Raghavan, S. Electrochemical Investigations during the Abrasion of Aluminum/Titanium Thin-Film Stacks in Iodate-Based Slurry. J. Electrochem. Soc. 2004, 151, G878–G881. [Google Scholar] [CrossRef]
- Aksu, S.; Wang, L.; Doyle, F.M. Effect of Hydrogen Peroxide on Oxidation of Copper in CMP Slurries Containing Glycine. J. Electrochem. Soc. 2003, 150, G718–G723. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, T.; Chai, Z.; Lu, X. Tribocorrosion study of copper during chemical mechanical polishing in potassium periodate-based slurry. Tribol. Lett. 2015, 58, 8. [Google Scholar] [CrossRef]
- Shima, S.; Fukunaga, A.; Tsujimura, M. Effects of Liner Metal and CMP Slurry Oxidizer on Copper Galvanic Corrosion. ECS Trans. 2007, 11, 285–295. [Google Scholar] [CrossRef]
- Hu, L.; Pan, G.; Zhang, X.; He, P.; Wang, C. Inhibition effect of TT-LYK on Cu corrosion and galvanic corrosion between Cu and Co during CMP in alkaline slurry. ECS J. Solid State Sci. Technol. 2019, 8, P437. [Google Scholar] [CrossRef]
- Turk, M.; Walters, M.; Roy, D. Tribo-electrochemical investigation of a slurry composition to reduce dissolution and galvanic corrosion during chemical mechanical planarization of Cu-Ru interconnects. Mater. Chem. Phys. 2017, 201, 271–288. [Google Scholar] [CrossRef]
- Turk, M.C.; Shi, X.; Gonyer, D.A.J.; Roy, D. Chemical and Mechanical Aspects of a Co-Cu Planarization Scheme Based on an Alkaline Slurry Formulation. ECS J. Solid State Sci. Technol. 2016, 5, P88–P99. [Google Scholar] [CrossRef]
- McGrath, J.; Davis, C. Polishing pad surface characterisation in chemical mechanical planarisation. J. Mater. Process. Technol. 2004, 153–154, 666–673. [Google Scholar] [CrossRef]
- Charns, L.; Sugiyama, M.; Philipossian, A. Mechanical properties of chemical mechanical polishing pads containing water-soluble particles. Thin Solid Film. 2005, 485, 188–193. [Google Scholar] [CrossRef]
- Jiang, L.; He, Y.; Li, Y.; Luo, J. Effect of ionic strength on ruthenium CMP in H2O2-based slurries. Appl. Surf. Sci. 2014, 317, 332–337. [Google Scholar] [CrossRef]
- Surisetty, C.; Peethala, B.; Roy, D.; Babu, S. Utility of oxy-anions for selective low pressure polishing of Cu and Ta in chemical mechanical planarization. Electrochem. Solid-State Lett. 2010, 13, H244–H247. [Google Scholar] [CrossRef]
- Yadav, K.; Manivannan, R.; Victoria, S.N. Chemical Mechanical Planarization of Ruthenium Using Sodium Hypochlorite Based Titania Slurry. ECS J. Solid State Sci. Technol. 2017, 6, P879–P885. [Google Scholar] [CrossRef]
- Jiang, L.; He, Y.; Li, J.; Luo, J. Passivation Kinetics of 1, 2, 4-Triazole in Copper Chemical Mechanical Polishing. ECS J. Solid State Sci. Technol. 2016, 5, P272–P279. [Google Scholar] [CrossRef]
- Choi, S.; Doyle, F.M.; Dornfeld, D.A. Material Removal Mechanism during Copper Chemical Mechanical Planarization Based on Nano-Scale Material Behavior. ECS J. Solid State Sci. Technol. 2017, 6, P235–P242. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, T.; Lu, X. Galvanic Corrosion Inhibitors for Cu/Ru Couple during Chemical Mechanical Polishing of Ru. ECS J. Solid State Sci. Technol. 2017, 6, P62–P67. [Google Scholar] [CrossRef]
- Qu, X.-P.; Yang, G.; He, P.; Feng, H. Chemical Mechanical Polishing of Mo Using H2O2 as Oxidizer in Colloidal Silica Based Slurries. ECS J. Solid State Sci. Technol. 2017, 6, P470–P476. [Google Scholar] [CrossRef]
- Jiang, L.; He, Y.; Liang, H.; Li, Y.; Luo, J. Effect of Potassium Ions on Tantalum Chemical Mechanical Polishing in H2O2-Based Alkaline Slurries. ECS J. Solid State Sci. Technol. 2016, 5, P100–P111. [Google Scholar] [CrossRef]
- Nair, R.R.; Gupta, A.; Victoria, S.N.; Manivannan, R. Chemical mechanical planarization of germanium using oxone® based silica slurries. Wear 2017, 376, 86–90. [Google Scholar] [CrossRef]
- Yang, G.; He, P.; Qu, X.-P. Inhibition effect of glycine on molybdenum corrosion during CMP in alkaline H2O2 based abrasive free slurry. Appl. Surf. Sci. 2018, 427, 148–155. [Google Scholar] [CrossRef]
- Carlton, C.; Ferreira, P. What is behind the inverse Hall–Petch effect in nanocrystalline materials? Acta Mater. 2007, 55, 3749–3756. [Google Scholar] [CrossRef]
- Amanapu, H.P.; Sagi, K.V.; Teugels, L.G.; Babu, S.V. Role of Guanidine Carbonate and Crystal Orientation on Chemical Mechanical Polishing of Ruthenium Films. ECS J. Solid State Sci. Technol. 2013, 2, P445–P451. [Google Scholar] [CrossRef]
- Feng, H.-P.; Lin, J.-Y.; Cheng, M.-Y.; Wang, Y.-Y.; Wan, C.-C. Behavior of Copper Removal by CMP and Its Correlation to Deposit Structure and Impurity Content. J. Electrochem. Soc. 2008, 155, H21–H25. [Google Scholar] [CrossRef]
- Sagi, K.; Teugels, L.; van der Veen, M.; Struyf, H.; Babu, S. Chemical Mechanical Polishing and Planarization of Mn-Based Barrier/Ru Liner Films in Cu Interconnects for Advanced Metallization Nodes. ECS J. Solid State Sci. Technol. 2017, 6, P259–P264. [Google Scholar] [CrossRef]
- Ponthiaux, P.; Wenger, F.; Drees, D.; Celis, J.-P. Electrochemical techniques for studying tribocorrosion processes. Wear 2004, 256, 459–468. [Google Scholar] [CrossRef]
- Wu, P.-Q.; Celis, J.-P. Electrochemical noise measurements on stainless steel during corrosion–wear in sliding contacts. Wear 2004, 256, 480–490. [Google Scholar] [CrossRef]
- Stemp, M.; Mischler, S.; Landolt, D. The effect of mechanical and electrochemical parameters on the tribocorrosion rate of stainless steel in sulphuric acid. Wear 2003, 255, 466–475. [Google Scholar] [CrossRef]
- Huo, J.I.J.A. Electrochemistry in ECMP. Microelectronic Applications of Chemical Mechanical Planarization; John Wiley & Sons: Hoboken, NJ, USA, 2007; p. 295. [Google Scholar]
- Totolin, V.; Göcerler, H.; Rodríguez Ripoll, M.; Jech, M. Tribo-electrochemical study of stainless steel surfaces during chemical–mechanical polishing. Lubr. Sci. 2016, 28, 363–380. [Google Scholar] [CrossRef]
- Kneer, E.; Raghunath, C.; Mathew, V.; Raghavan, S.; Jeon, J.S. Electrochemical measurements during the chemical mechanical polishing of tungsten thin films. J. Electrochem. Soc. 1997, 144, 3041. [Google Scholar] [CrossRef]
- Roy, D. Electrochemical techniques and their applications for CMP of metal films. In Advances in Chemical Mechanical Planarization (CMP); Elsevier: Amsterdam, The Netherlands, 2022; pp. 51–94. [Google Scholar]
- Lee, D.; Lee, H.; Jeong, H. Slurry components in metal chemical mechanical planarization (CMP) process: A review. Int. J. Precis. Eng. Manuf. 2016, 17, 1751–1762. [Google Scholar] [CrossRef]
- Jemmely, P.; Mischler, S.; Landolt, D. Electrochemical modeling of passivation phenomena in tribocorrosion. Wear 2000, 237, 63–76. [Google Scholar] [CrossRef]
- Papageorgiou, N.; Mischler, S. Electrochemical Simulation of the Current and Potential Response in Sliding Tribocorrosion. Tribol. Lett. 2012, 48, 271–283. [Google Scholar] [CrossRef]
- Angst, U.; Büchler, M. On the Applicability of the Stern–Geary Relationship to Determine Instantaneous Corrosion Rates in Macro-Cell Corrosion. Mater. Corros. 2015, 66, 1017–1028. [Google Scholar]
- Power, G.P.; Ritchie, I.M. Mixed potential measurements in the elucidation of corrosion mechanisms—1. Introductory theory. Electrochim. Acta 1981, 26, 1073–1078. [Google Scholar] [CrossRef]
- Gray, D.; Cahill, A. Theoretical Analysis of Mixed Potentials. J. Electrochem. Soc. 1969, 116, 443–447. [Google Scholar] [CrossRef]
- Calvo, E.J. Fundamentals. The-basics of electrode reactions. In Electrode Kinetics: Principles and Methodology; Bamford, C.H., Compton, R.G., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1986; Volume 26, p. 1. [Google Scholar]
- Akrout, H.; Bousselmi, L.; Triki, E.; Maximovitch, S.; Dalard, F. Adsorption mechanism of non-toxic organic inhibitors on steel in solutions at pH 8 determined by electrochemical quartz crystal microbalance measurements. Mater. Corros. 2005, 56, 185–191. [Google Scholar] [CrossRef]
- Habashi, F.; Bas, A.D. Evidence of the existence of cathodic and anodic zones during the leaching of minerals and metals. Hydrometallurgy 2014, 144–145, 148–150. [Google Scholar] [CrossRef]
- Ateya, B.G.; Pickering, H.W. The distribution of anodic and cathodic reaction sites during environmentally assisted cracking. Corros. Sci. 1995, 37, 1443–1453. [Google Scholar] [CrossRef]
- Jüttner, K.; Lorenz, W.J.; Kendig, M.W.; Mansfeld, F. Electrochemical Impedance Spectroscopy on 3-D Inhomogeneous Surfaces: Corrosion in Neutral Aerated Solutions. J. Electrochem. Soc. 1988, 135, 332–339. [Google Scholar] [CrossRef]
- Cao, C. On electrochemical techniques for interface inhibitor research. Corros. Sci. 1996, 38, 2073–2082. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods Fundamentals and Applications; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Buchanan, R.A.; Stansbury, E.E. 4—Electrochemical Corrosion. In Handbook of Environmental Degradation of Materials, 2nd ed.; Kutz, M., Ed.; William Andrew Publishing: Oxford, UK, 2012; pp. 87–125. [Google Scholar]
- Yang, L.J. Wear Coefficient Equation for Aluminum-Based Matrix Composites Against Steel Disc. Wear 2003, 255, 579–592. [Google Scholar] [CrossRef]
- . Sagi, K.V.; Amanapu, H.P.; Teugels, L.G.; Babu, S.V. Investigation of Guanidine Carbonate-Based Slurries for Chemical Mechanical Polishing of Ru/TiN Barrier Films with Minimal Corrosion. ECS J. Solid State Sci. Technol. 2014, 3, P227–P234. [Google Scholar] [CrossRef]
- Walter, G.W. Corrosion Rates of Zinc, Zinc Coatings and Steel in Aerated Slightly Acidic Chloride Solutions Calculated from Low Polarization Data. Corros. Sci. 1976, 16, 573–586. [Google Scholar] [CrossRef]
- Stansbury, E.E.; Buchanan, R.A. Fundamentals of Electrochemical Corrosion; ASM International: Materials Park, OH, USA, 2000. [Google Scholar]
- Huet, F.; Nogueira, R.; Ponthiaux, P.; Wenger, F.; Deforge, D. Electrochemical Noise Analysis of Tribo-Corrosion Processes under Steady-State Friction Regime. Corrosion 2005, 62, 514–521. [Google Scholar]
- Hudson, J.L.; Tsotsis, T. Electrochemical reaction dynamics: A review. Chem. Eng. Sci. 1994, 49, 1493–1572. [Google Scholar] [CrossRef]
- Cottis, R. Interpretation of electrochemical noise data. Corrosion 2001, 57, 265–285. [Google Scholar] [CrossRef]
- Jamali, S.S.; Mills, D.J. A critical review of electrochemical noise measurement as a tool for evaluation of organic coatings. Prog. Org. Coat. 2016, 95, 26–37. [Google Scholar] [CrossRef]
- Berradja, A.; Déforge, D.; Nogueira, R.; Ponthiaux, P.; Wenger, F.; Celis, J.-P. An electrochemical noise study of tribocorrosion processes of AISI 304 L in Cl− and media. J. Phys. D Appl. Phys. 2006, 39, 3184. [Google Scholar] [CrossRef]
- Wood, R.J.K. Tribo-Corrosion of Coatings: A review. J. Phys. D: Appl. Phys. 2007, 40, 5502–5521. [Google Scholar] [CrossRef]
- Mischler, S.; Munoz, A.I. Tribocorrosion, Encyclopedia of Interfacial Chemistry: Surface Science and Electrochemistry, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Zuo, Y.; Li, T.; Jiang, X.; Wu, M.; Zhang, Y.; Chen, F. Tribocorrosion behavior of Ca–P MAO coatings on Ti6Al4V alloy at various applied voltages. J. Mater. Res. 2020, 35, 444–453. [Google Scholar] [CrossRef]
- Bailey, R. Tribocorrosion response of surface-modified Ti in a 0.9% NaCl solution. Lubricants 2018, 6, 86. [Google Scholar] [CrossRef]
- Schlegel, J.M.; Paretti, R.F. An electrochemical oscillator: The mercury/chloropentammine cobalt (III) oscillator. J. Electroanal. Chem. 1992, 335, 67–74. [Google Scholar] [CrossRef]
- Lizama-Tzec, F.; Canché-Canul, L.; Oskam, G. Electrodeposition of copper into trenches from a citrate plating bath. Electrochim. Acta 2011, 56, 9391–9396. [Google Scholar] [CrossRef]
- Rode, S.; Henninot, C.; Vallières, C.; Matlosz, M. Complexation chemistry in copper plating from citrate baths. J. Electrochem. Soc. 2004, 151, C405–C411. [Google Scholar] [CrossRef]
- Tasdemir, M.; Alsaran, A. Tribocorrosion behaviour of porous anatase and rutile phases formed on surface of anodised Ti45Nb alloy. Lubr. Sci. 2020, 32, 192–201. [Google Scholar] [CrossRef]
- Yan, C.; Zeng, Q.; Xu, Y.; He, W. Microstructure, phase and tribocorrosion behavior of 60NiTi alloy. Appl. Surf. Sci. 2019, 498, 143838. [Google Scholar] [CrossRef]
- Wei, S.; Roy, D. Galvanodynamic probing of tribologically assisted material removal under chemical control: A cobalt/copper case study for application in chemical mechanical planarization. Tribol. Int. 2023, 179, 108185. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Ponthiaux, P.; Wenger, F.; Celis, J.-P. Tribocorrosion: Material behavior under combined conditions of corrosion and mechanical loading, Corrosion Resistance. Corros. Resist. 2012, 1, 81–106. [Google Scholar]
- Tamilmani, S.; Huang, W.; Raghavan, S. Galvanic Corrosion Between Copper and Tantalum under CMP Conditions. J. Electrochem. Soc. 2006, 153, F53–F59. [Google Scholar] [CrossRef]
- Wei, S.; Roy, D. Electrochemical Studies of CMP Related Metals and Slurry Solutions. Clarkson University, Potsdam, NY, USA. 2021; Unpubl. Results. [Google Scholar]
- Priya, R.; Ningshen, S. The Tribocorrosion Behaviour and its Mechanisms of Type 304L Stainless Steel in Nitric Acid Media. J. Mater. Eng. Perform. 2023, 32, 5261–5272. [Google Scholar] [CrossRef]
- Liu, E.; Zhang, Y.; Zhu, L.; Zeng, Z.; Gao, R. Effect of strain-induced martensite on the tribocorrosion of AISI 316L austenitic stainless steel in seawater. Rsc Adv. 2017, 7, 44923–44932. [Google Scholar] [CrossRef]
- Berlanga-Labari, C.; Claver, A.; Biezma-Moraleda, M.V.; Palacio, J.F. Study of Effect of Nickel Content on Tribocorrosion Behaviour of Nickel–Aluminium–Bronzes (NABs). Lubricants 2023, 11, 43. [Google Scholar] [CrossRef]
- Diomidis, N.; Mischler, S.; More, N.; Roy, M. Tribo-electrochemical characterization of metallic biomaterials for total joint replacement. Acta Biomater. 2012, 8, 852–859. [Google Scholar] [CrossRef]
- Jun, C.; Zhang, Q.; Li, Q.-a.; Fu, S.-l.; Wang, J.-z. Corrosion and tribocorrosion behaviors of AISI 316 stainless steel and Ti6Al4V alloys in artificial seawater. Trans. Nonferrous Met. Soc. China 2014, 24, 1022–1031. [Google Scholar]
- Zeng, L.; Chen, G.; Chen, H. Comparative study on flow-accelerated corrosion and erosion–corrosion at a 90 carbon steel bend. Materials 2020, 13, 1780. [Google Scholar] [CrossRef]
- Lotz, U.; Heitz, E. Flow-dependent corrosion. I. Current understanding of the mechanisms involved. Mater. Corros. 1983, 34, 454–461. [Google Scholar] [CrossRef]
- Pokhmurskii, V.; Zin, I.; Pokhmurska, H.; Vynar, V. Electrochemical investigations of aluminium alloys tribocorrosion. Int. J. Corros. Scale Inhib. 2014, 3, 129–136. [Google Scholar] [CrossRef]
- Souza, M.E.P.; Ariza, E.; Ballester, M.; Rocha, L.A.; Freire, C. Comparative behaviour in terms of wear and corrosion resistance of galvanized and zinc-iron coated steels. Matéria 2007, 12, 618–623. [Google Scholar] [CrossRef]
- Argibay, N.; Sawyer, W. Frictional voltammetry with copper. Tribol. Lett. 2012, 46, 337–342. [Google Scholar] [CrossRef]
- Gracia-Escosa, E.; García, I.; Sánchez-López, J.; Abad, M.D.; Mariscal, A.; Arenas, M.; de Damborenea, J.; Conde, A. Tribocorrosion behavior of TiBxCy/aC nanocomposite coating in strong oxidant disinfectant solutions. Surf. Coat. Technol. 2015, 263, 78–85. [Google Scholar] [CrossRef]
- Hu, L.; Pan, G.; Li, C.; Zhang, X.; Liu, J.; He, P.; Wang, C. Potassium tartrate as a complexing agent for chemical mechanical polishing of Cu/Co/TaN barrier liner stack in H2O2 based alkaline slurries. Mater. Sci. Semicond. Process. 2020, 108, 104883. [Google Scholar] [CrossRef]
- Johnson, C.; Liu, J.; White, M.L.; Roy, D. Tribo-Electrochemistry of Post-CMP Cleaning: Results for Co and Cu Wafer Films Brushed in Different Solutions. ECS J. Solid State Sci. Technol. 2021, 10, 054005. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, T.; Pan, J.; Lu, X. Corrosion investigations of ruthenium in potassium periodate solutions relevant for chemical mechanical polishing. J. Electron. Mater. 2016, 45, 4067–4075. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Pan, Y.; Lu, X. Chemical roles on Cu-slurry interface during copper chemical mechanical planarization. Appl. Surf. Sci. 2014, 293, 287–292. [Google Scholar] [CrossRef]
- Wang, L.; Snihirova, D.; Deng, M.; Vaghefinazari, B.; Höche, D.; Lamaka, S.V.; Zheludkevich, M.L. Revealing physical interpretation of time constants in electrochemical impedance spectra of Mg via Tribo-EIS measurements. Electrochim. Acta 2022, 404, 139582. [Google Scholar] [CrossRef]
- Geringer, J.; Normand, B.; Alemany-Dumont, C.; Diemiaszonek, R. Assessing the tribocorrosion behaviour of Cu and Al by electrochemical impedance spectroscopy. Tribol. Int. 2010, 43, 1991–1999. [Google Scholar] [CrossRef][Green Version]
- Chiu, S.-Y.; Wang, Y.-L.; Liu, C.-P.; Lan, J.-K.; Ay, C.; Feng, M.-S.; Tsai, M.-S.; Dai, B.-T. The application of electrochemical metrologies for investigating chemical mechanical polishing of Al with a Ti barrier layer. Mater. Chem. Phys. 2003, 82, 444–451. [Google Scholar] [CrossRef]
- Turk, M.C.; Walters, M.J.; Roy, D. Experimental considerations for using electrochemical impedance spectroscopy to study chemical mechanical planarization systems. Electrochim. Acta 2017, 224, 355–368. [Google Scholar] [CrossRef]
- Szekeres, K.J.; Vesztergom, S.; Ujvári, M.; Láng, G.G. Methods for the Determination of Valid Impedance Spectra in Non-stationary Electrochemical Systems: Concepts and Techniques of Practical Importance. ChemElectroChem 2021, 8, 1233–1250. [Google Scholar] [CrossRef]
- Wei, S.; Roy, D. Tribo-electrochemical studies of metal CMP systems. Clarkson University, Potsdam, NY, USA. 2021; Unpubl. Results. [Google Scholar]
- Wu, L.; Zhang, K.; Zhou, Z.; Wang, G.; Zhang, X. Two-step post treatment to improve corrosion resistance and friction performance of Fe-based metallic glasses/crystalline dual-phase coatings. J. Non-Cryst. Solids 2023, 609, 122268. [Google Scholar] [CrossRef]
- Kuo, H.-S.; Tsai, W.-T. Effects of alumina and hydrogen peroxide on the chemical-mechanical polishing of aluminum in phosphoric acid base slurry. Mater. Chem. Phys. 2001, 69, 53–61. [Google Scholar] [CrossRef]
- Yilma, H.B.; Zekarias, M.T.; Rao, G.N. Chemical Speciation Studies of Malonic Acid Complexes of Co(II), Cu(II), Ni(II) and Zn(II) in Dioxan-Water Mixtures. Pharma Chem. 2012, 4, 655–663. [Google Scholar]
- Lazanas, A.C.; Prodromidis, M.I. Electrochemical Impedance Spectroscopy—A Tutorial. ACS Meas. Sci. Au 2023, 3, 162–193. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, J.; Mirza-Rosca, J. Study of the corrosion behavior of titanium and some of its alloys for biomedical and dental implant applications. J. Electroanal. Chem. 1999, 471, 109–115. [Google Scholar] [CrossRef]
- Barik, R.; Wharton, J.; Wood, R.; Stokes, K.; Jones, R. Corrosion, erosion and erosion–corrosion performance of plasma electrolytic oxidation (PEO) deposited Al2O3 coatings. Surf. Coat. Technol. 2005, 199, 158–167. [Google Scholar] [CrossRef]
- Su, C.; Wu, W.; Li, Z.; Guo, Y. Prediction of film performance by electrochemical impedance spectroscopy. Corros. Sci. 2015, 99, 42–52. [Google Scholar] [CrossRef]
- Mansfeld, F. Electrochemical impedance spectroscopy (EIS) as a new tool for investigating methods of corrosion protection. Electrochim. Acta 1990, 35, 1533–1544. [Google Scholar] [CrossRef]
- Bisquert, J. Theory of the Impedance of Electron Diffusion and Recombination in a Thin Layer. J. Phys. Chem. B 2001, 106, 325–333. [Google Scholar] [CrossRef]
- Jindal, A.; Babu, S.V. Effect of pH on CMP of Copper and Tantalum. J. Electrochem. Soc. 2004, 151, G709–G716. [Google Scholar] [CrossRef]
- Stojadinović, J.; Mendia, L.; Bouvet, D.; Declercq, M.; Mischler, S. Electrochemically controlled wear transitions in the tribocorrosion of ruthenium. Wear 2009, 267, 186–194. [Google Scholar] [CrossRef]
- Turk, M.; Rock, S.; Amanapu, H.; Teugels, L.; Roy, D. Investigation of percarbonate based slurry chemistry for controlling galvanic corrosion during CMP of ruthenium. ECS J. Solid State Sci. Technol. 2013, 2, P205. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, T.; Wang, J.; Liu, Y.; Lu, X. Effects of KIO4 concentration and pH values of the solution relevant for chemical mechanical polishing of ruthenium. Microelectron. Eng. 2016, 151, 30–37. [Google Scholar] [CrossRef]
- Cui, H.; Park, J.-H.; Park, J.-G. Study of Ruthenium Oxides Species on Ruthenium Chemical Mechanical Planarization Using Periodate-Based Slurry. J. Electrochem. Soc. 2012, 159, H335–H341. [Google Scholar] [CrossRef]
- Fangteng, S.; Charles, E.A. A theoretical approach to galvanic corrosion, allowing for cathode dissolution. Corros. Sci. 1988, 28, 649–655. [Google Scholar] [CrossRef]
- Mansfeld, F. Area relationship in galvanic corrosion. Corrosion 1971, 27, 436–442. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Wang, T.; Lu, X.; Luo, J. Electrochemical investigation of copper passivation kinetics and its application to low-pressure CMP modeling. Appl. Surf. Sci. 2013, 265, 764–770. [Google Scholar] [CrossRef]
- Tripathi, S.; Doyle, F.M.; Dornfeld, D.A. Fundamental mechanisms of copper CMP–passivation kinetics of copper in CMP Slurry Constituents. MRS Online Proc. Libr. 2009, 1157, E1102–E1106. [Google Scholar] [CrossRef]
- Lingane, P.J.; Peters, D.G. Chronopotentiometry. CRC Crit. Rev. Anal. Chem. 1971, 1, 587–634. [Google Scholar] [CrossRef]
- Macdonald, D.D. Transient Techniques in Electrochemistry; Springer: Boston, MA, USA, 1977. [Google Scholar]
- Bard, A.J. Effect of Electrode Configuration and Transition Time in Solid Electrode Chronopotentiometry. Anal. Chem. 1961, 33, 11–15. [Google Scholar] [CrossRef]
- Gabrielli, C.; Keddam, M.; Takenouti, H.; Quang Kinh, V.; Bourelier, F. The relationship between the impedance of corroding electrode and its polarization resistance determined by a linear voltage sweep technique. Electrochim. Acta 1979, 24, 61–65. [Google Scholar] [CrossRef]
- Babić, R.; Metikoš-Huković, M. Spectroelectrochemical studies of protective surface films against copper corrosion. Thin Solid Film. 2000, 359, 88–94. [Google Scholar] [CrossRef]
- Scully, J.R. Polarization resistance method for determination of instantaneous corrosion rates. Corrosion 2000, 56, 200–218. [Google Scholar] [CrossRef]
- Stojadinović, J.; Bouvet, D.; Declercq, M.; Mischler, S. Effect of electrode potential on the tribocorrosion of tungsten. Tribol. Int. 2009, 42, 575–583. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Z.H.; Yao, Z.P.; Song, Y.; Wu, Z.D. Effects of scan rate on the potentiodynamic polarization curve obtained to determine the Tafel slopes and corrosion current density. Corros. Sci. 2009, 51, 581–587. [Google Scholar] [CrossRef]
- Cai, S.-y.; Wen, L.; Jin, Y. A comparative study on corrosion kinetic parameter estimation methods for the early stage corrosion of Q345B steel in 3.5 wt% NaCl solution. Int. J. Miner. Metall. Mater. 2017, 24, 1112–1124. [Google Scholar] [CrossRef]
- Tahmasebi, S.; Hossain, M.A.; Jerkiewicz, G. Corrosion Behavior of Platinum in Aqueous H2SO4 Solution: Part 1—Influence of the potential scan rate and the dissolved gas. Electrocatalysis 2018, 9, 172–181. [Google Scholar] [CrossRef]
- Rocchini, G. The influence of the potential sweep rate on the shape of polarization curves. Corros. Sci. 1998, 40, 1753–1768. [Google Scholar] [CrossRef]
- Ohtsuka, T.; Nishikata, A.; Sakairi, M.; Fushimi, K. Electrochemical Measurement of Wet Corrosion. In Electrochemistry for Corrosion Fundamentals; Springer: Berlin/Heidelberg, Germany, 2018; pp. 17–39. [Google Scholar]
- Lewandowski, D.; Bajerlein, D.; Schroeder, G. Adsorption of hydrogen peroxide on functionalized mesoporous silica surfaces. Struct. Chem. 2014, 25, 1505–1512. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamagedara, K.; Roy, D. Experimental Strategies for Studying Tribo-Electrochemical Aspects of Chemical–Mechanical Planarization. Lubricants 2024, 12, 63. https://doi.org/10.3390/lubricants12020063
Gamagedara K, Roy D. Experimental Strategies for Studying Tribo-Electrochemical Aspects of Chemical–Mechanical Planarization. Lubricants. 2024; 12(2):63. https://doi.org/10.3390/lubricants12020063
Chicago/Turabian StyleGamagedara, Kassapa, and Dipankar Roy. 2024. "Experimental Strategies for Studying Tribo-Electrochemical Aspects of Chemical–Mechanical Planarization" Lubricants 12, no. 2: 63. https://doi.org/10.3390/lubricants12020063
APA StyleGamagedara, K., & Roy, D. (2024). Experimental Strategies for Studying Tribo-Electrochemical Aspects of Chemical–Mechanical Planarization. Lubricants, 12(2), 63. https://doi.org/10.3390/lubricants12020063




