Analysis of Coefficient of Friction of Deep-Drawing-Quality Steel Sheets Using Multi-Layer Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Material
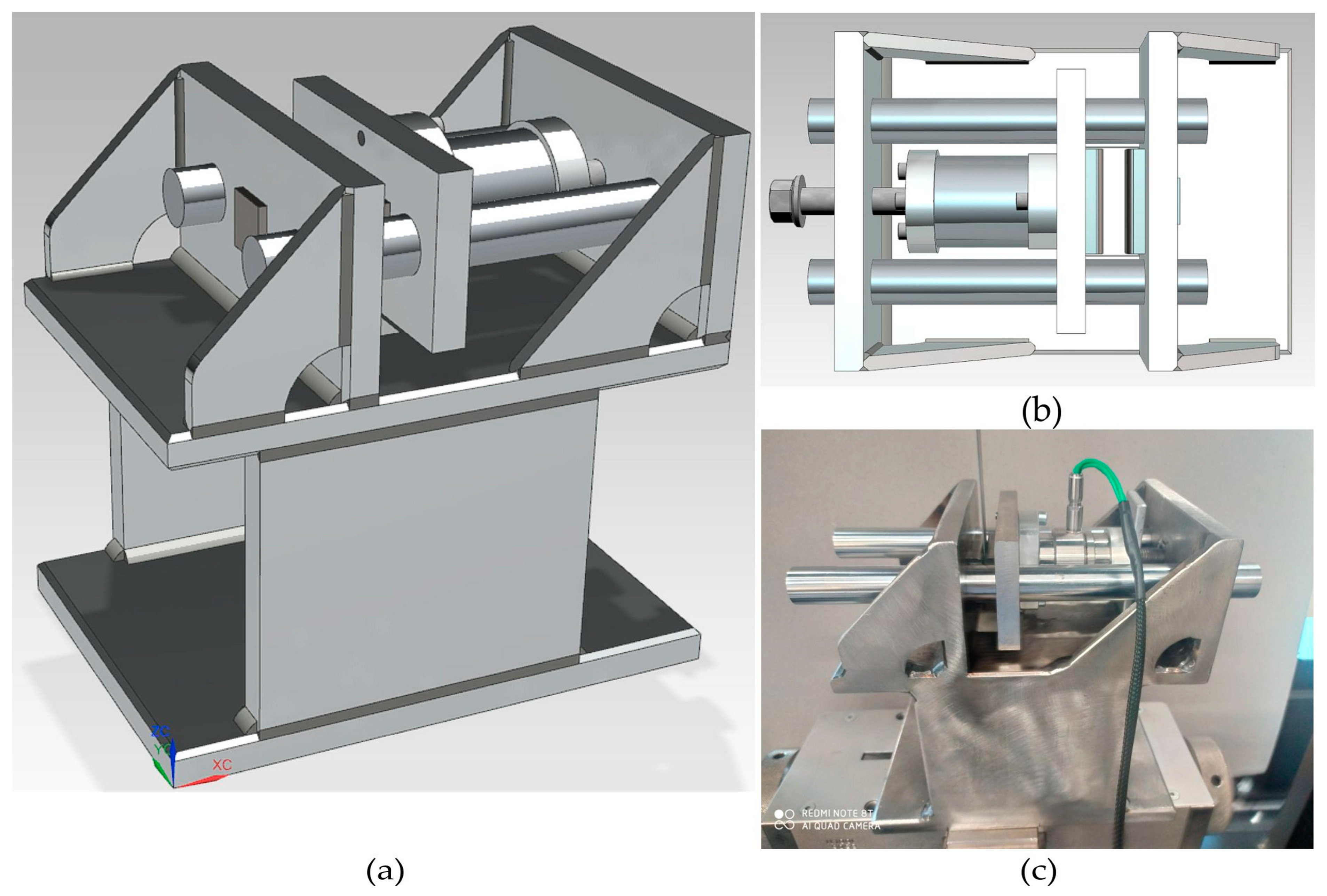
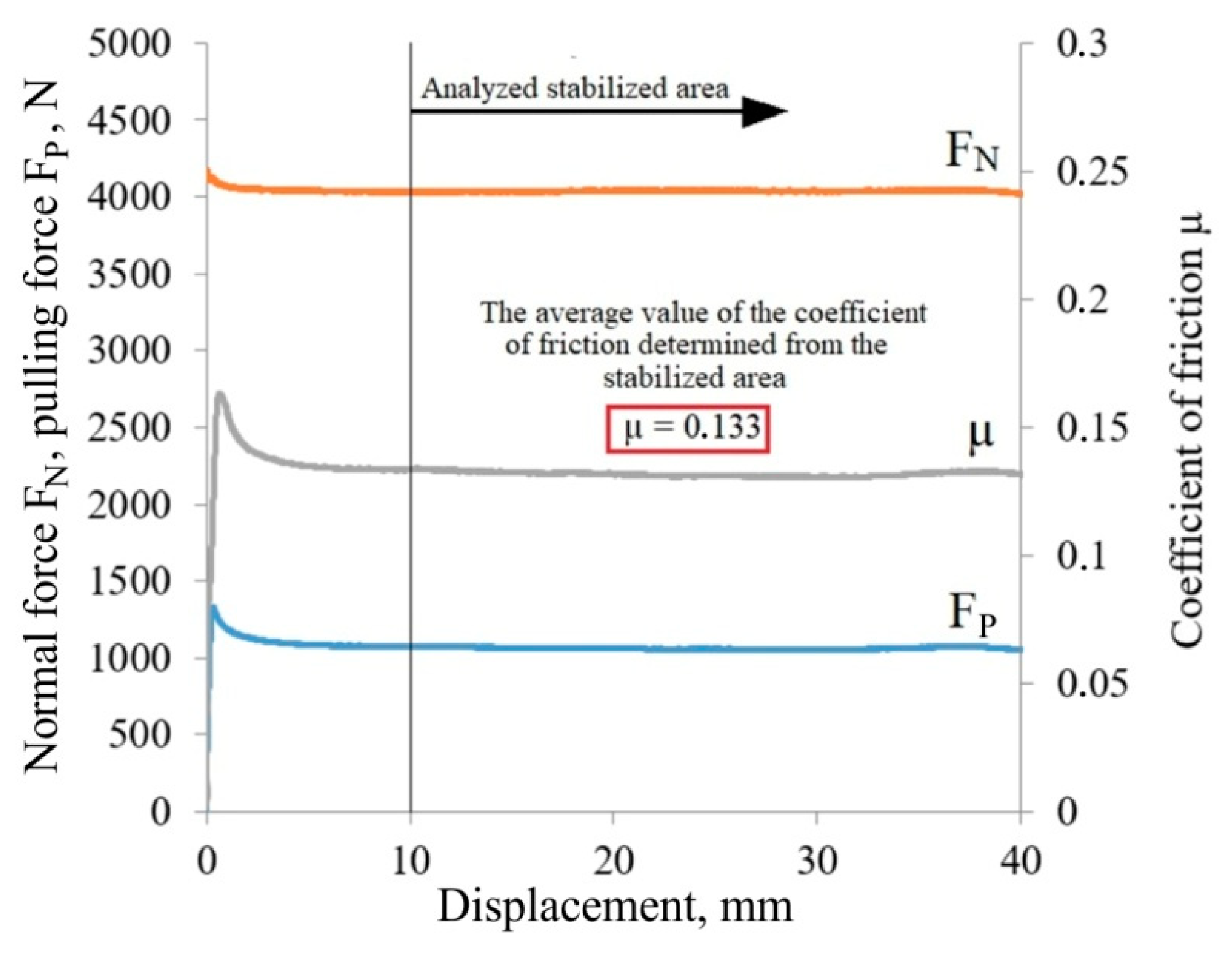
2.2. Experimental Procedure
2.3. Artificial Neural Networks
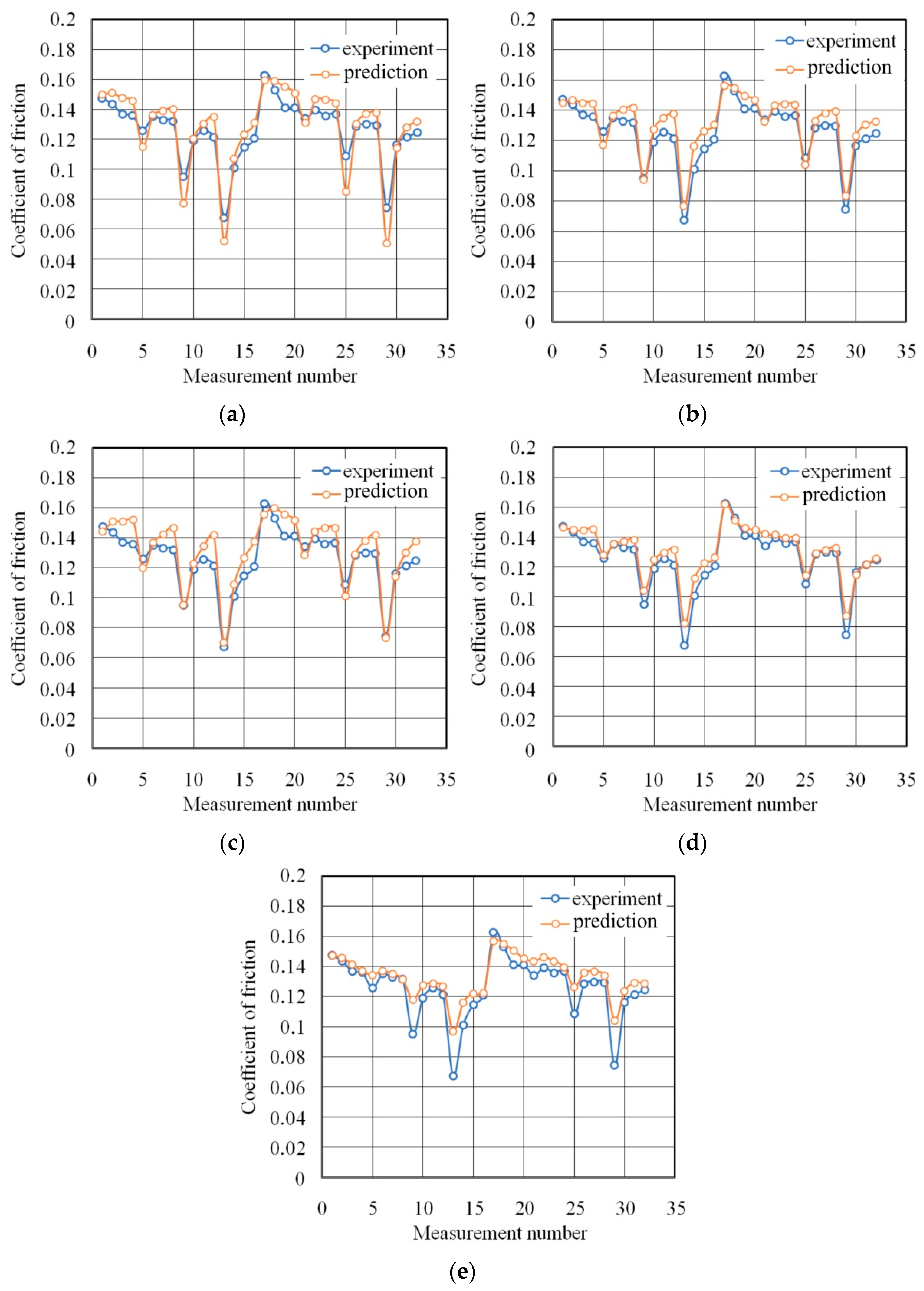
3. Results and Discussion
4. Conclusions
- To ensure a high performance of ANN prediction, it is necessary to simultaneously take into account all the considered roughness parameters (Sa, Ssk and Sku). Removing even one of these parameters from consideration reduces the quality of prediction of the multi-layer ANN.
- The predictive quality of the ‘best’ network (MLP-10-12-1) determined by the coefficient of determination for the validation set was greater than R2 = 0.96. The coefficient of determination for the test set was greater than 0.98.
- The lubricant pressure had the greatest impact on the COF. Increasing the value of lubricant pressure reduced the value of the COF.
- As the contact pressure increases, the mechanical interaction of the surface roughness peaks increases, and under these conditions, the beneficial effect of the pressurized lubricant is limited. Therefore, to obtain the optimal COF value, the simultaneous effect of contact pressure and oil pressure should be considered.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Recklin, V.; Groche, P. Strain induced surface change in sheet metal forming: Numerical prediction, influence on friction and tool wear. J. Manuf. Mater. Process. 2021, 5, 29. [Google Scholar] [CrossRef]
- Krasowski, B.; Kubit, A. Effect of the lubrication on the friction characteristics of EN AW-2024-T3 aluminium alloy sheets. Adv. Mech. Mater. Eng. 2022, 39, 23–35. [Google Scholar] [CrossRef]
- Wilson, W. Lubrication and friction in sheet metal forming. SAE Tech. Pap. 1992, 920911. [Google Scholar] [CrossRef]
- Szpunar, M.; Trzepieciński, T.; Żaba, K.; Ostrowski, R.; Zwolak, M. Effect of lubricant type on the friction behaviours and surface topography in metal forming of Ti-6Al-4V titanium alloy sheets. Materials 2021, 14, 3721. [Google Scholar] [CrossRef]
- Nielsen, C.V.; Bay, N. Review of friction modeling in metal forming processes. J. Mater. Process. Technol. 2018, 255, 234–241. [Google Scholar] [CrossRef]
- Szewczyk, M.; Szwajka, K. Assessment of the tribological performance of bio-based lubricants using analysis of variance. Adv. Mech. Mater. Eng. 2023, 40, 31–38. [Google Scholar] [CrossRef]
- Schell, L.; Seller, E.; Massold, M.; Groche, P. Tribology in warm and hot aluminum sheet forming: Transferability of strip drawing tests to forming trials. Adv. Eng. Mater. 2023, 25, 2201900. [Google Scholar] [CrossRef]
- Hasan, M.S.; Nosonovsky, M. Triboinformatics: Machine learning algorithms and data topology methods for tribology. Surf. Innov. 2022, 10, 229–242. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Chen, X.; Wu, C.; Cui, Z.; Niu, C. Fuzzy modelling of surface scratching in contact sliding. IOP Conf. Ser. Mater. Sci. Eng. 2020, 967, 012022. [Google Scholar] [CrossRef]
- Wei, L.; Yuying, Y. Multi-objective optimization of sheet metal forming process using Pareto-based genetic algorithm. J. Mater. Process. Technol. 2008, 208, 499–506. [Google Scholar] [CrossRef]
- Kumar, A.; Das, A. A nonlinear process monitoring strategy for a metal forming process. Mater. Today Proc. 2022, 59, 368–372. [Google Scholar] [CrossRef]
- Yin, N.; Xing, Z.; He, K.; Zhang, Z. Tribo-informatics approaches in tribology research: A review. Friction 2023, 11, 1–22. [Google Scholar] [CrossRef]
- Otero, J.E.; De La Guerra Ochoa, E.; Chacón Tanarro, E.; Lafont Morgado, P.; Díaz Lantada, A.; Munoz-Guijosa, J.M.; Muñoz Sanz, J.L. Artificial neural network approach to predict the lubricated friction coefficient. Lubr. Sci. 2014, 26, 141–162. [Google Scholar] [CrossRef]
- Tijani, I.B.; Wahyudi, M.; Talib, H. Adaptive neuro-fuzzy inference system (ANFIS) for friction modelling and compensation in motion control system. Int. J. Model. Simul. 2011, 31, 32–41. [Google Scholar] [CrossRef]
- Baboukani, B.S.; Ye, Z.; Reyes, K.G.; Nalam, P.C. Prediction of nanoscale friction for two-dimensional materials using a machine learning approach. Tribol. Lett. 2020, 68, 57. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Marian, M.; Profito, F.J.; Aragon, N.; Shah, R. The use of artificial intelligence in tribology—A perspective. Lubricants 2021, 9, 2. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2016. [Google Scholar]
- Sose, A.T.; Joshi, S.; Kunche, L.K.; Wang, F.; Deshmukh, S.A. A review of recent advances and applications of machine learning in tribology. Phys. Chem. Chem. Phys. 2023, 25, 4408–4443. [Google Scholar] [CrossRef]
- Bhaumik, S.; Mathew, B.R.; Datta, S. Computational intelligence-based design of lubricant with vegetable oil blend and various nano friction modifiers. Fuel 2019, 241, 733–743. [Google Scholar] [CrossRef]
- Bhaumik, S.; Pathak, S.D.; Dey, S.; Datta, S. Artificial intelligence based design of multiple friction modifiers dispersed castor oil and evaluating its tribological properties. Tribol. Int. 2019, 140, 105813. [Google Scholar] [CrossRef]
- Humelnicu, C.; Ciortan, S.; Amortila, V. Artificial neural network-based analysis of the tribological behavior of vegetable oil-diesel fuel mixtures. Lubricants 2019, 7, 32. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M. Application of artificial neural networks to the analysis of friction behaviour in a drawbead profile in sheet metal forming. Materials 2022, 15, 9022. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.S.; Kardijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Triboinformatic modeling of dry friction and wear of aluminum base alloys using machine learning algorithms. Tribol. Int. 2021, 161, 107065. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Szpunar, M. Assessment of the effectiveness of lubrication of Ti-6Al-4V titanium alloy sheets using radial basis function neural networks. Acta Polytech. 2021, 61, 489–496. [Google Scholar] [CrossRef]
- Najm, S.M.; Trzepieciński, T.; Kowalik, M. Modelling and parameter identification of coefficient of friction for deep-drawing quality steel sheets using the CatBoost machine learning algorithm and neural network. Int. J. Adv. Manuf. Technol. 2023, 124, 2229–2259. [Google Scholar] [CrossRef]
- Najjar, I.M.R.; Sadoun, A.M.; Ibrahim, A.; Ahmadian, H.; Fathy, A. A modified artificial neural network to predict the tribological properties of Al-SiC nanocomposites fabricated by accumulative roll bonding process. J. Compos. Mater. 2023, 57, 3433–3445. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Xie, H.B.; Wang, Z.J.; Qin, N.; Du, W.H.; Qian, L.M. Prediction of friction coefficients during scratch based on an integrated finite element and artificial neural network method. J. Tribol. 2020, 142, 021703. [Google Scholar] [CrossRef]
- Boidi, G.; da Silva, M.R.; Profito, F.J.; Machado, I.F. Using machine learning radial basis function (RBF) method for predicting lubricated friction on textured and porous surfaces. Surf. Topogr. Metrol. Prop. 2020, 8, 044002. [Google Scholar] [CrossRef]
- Korfanty, K.; Żaba, K.; Szwachta, G.; Seibt, P.; Puchlerska, S. Selection of the tool materials, lubrications and self-lubricating coatings for the rotary forming process of nickel superalloys sheets. In Proceedings of the METAL 2016—25th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 25–27 May 2016; pp. 421–426. [Google Scholar]
- Korfanty, K.; Żaba, K.; Kwiatkowski, M.; Nowak, S. Selection of the optimum conditions of friction and lubrication for the needs of the rotary forming process of nickel superalloys. In Proceedings of the AMPT 2015 Conference: Advances in Materials & Processing Technologies, Madrid, Spain, 14–17 December 2015. [Google Scholar]
- Argatov, I. Artificial neural networks (ANNs) as a novel modeling technique in tribology. Front. Mech. Eng. 2019, 5, 30. [Google Scholar] [CrossRef]
- Puturi, U.M.R.; Palakurthy, S.T.; Reddy, N.S. The role of machine learning in tribology: A systematic review. Arch. Comput. Methods Eng. 2022, 30, 1345–1397. [Google Scholar] [CrossRef]
- Marian, M.; Tremmel, S. Current trends and applications of machine learning in tribology—A review. Lubricants 2021, 9, 86. [Google Scholar] [CrossRef]
- Paszkowski, M. Some Aspects of Grease Flow in Lubrication Systems and Friction Nodes. In Tribology—Fundamentals and Advancements; Gegner, J., Ed.; IntechOpen: Rijeka, Croatia, 2013; pp. 77–106. [Google Scholar]
- EN 10130:2006; Cold rolled low carbon steel flat products for cold forming—Technical delivery conditions. European Committee for Standardization: Brussels, Belgium, 2006.
- Trzepieciński, T.; Szwajka, K.; Szewczyk, M. A Device for Determining the Coefficient of Friction, Especially for Sheet. Metals. Patent Application P.444834, 10 May 2023. [Google Scholar]
- Erbel, S.; Kuczyński, K.; Marciniak, Z. Cold Plastic Working; PWN: Warsaw, Poland, 1975. [Google Scholar]
- Prakash, V.; Kumar, D.R. Performance evaluation of bio-lubricants in strip drawing and deep drawing of an aluminium alloy. Adv. Mater. Process. Technol. 2022, 8, 1044–1057. [Google Scholar] [CrossRef]
- Sedlaček, M.; Vilhena, L.M.S.; Podgornik, B.; Vižintin, J. Surface topography modelling for reduced friction. Stroj. Vestn. J. Mech. Eng. 2011, 57, 674–680. [Google Scholar] [CrossRef]
- Boniecki, P.; Raba, B.; Pilarska, A.A.; Sujak, A.; Zaborowicz, M.; Pilarski, K.; Wojcieszak, D. Neural Reduction of Image Data in Order to Determine the Quality of Malting Barley. Sensors 2021, 21, 5696. [Google Scholar] [CrossRef]
- Doreswamy; Vastrad, C.M. Performance analysis of neural network models for oxazolines and oxazoles derivatives descriptor dataset. Int. J. Inf. Sci. Tech. 2013, 3, 1–15. [Google Scholar]
- Palacios-Santander, J.; Jiménez-Jiménez, A.; Cubillana-Aguilera, L.; Naranjo-Rodríguez, I.; Hidalgo-Hidalgo-de-Cisneros, J.L. Use of Artificial Neural Networks, Aided by Methods to Reduce Dimensions, to Resolve Overlapped Electrochemical Signals. A Comparative Study Including other Statistical Methods. Microchim. Acta 2003, 142, 27–36. [Google Scholar] [CrossRef]
- Root Mean Square Error (RMSE). Available online: https://c3.ai/glossary/data-science/root-mean-square-error-rmse/ (accessed on 31 January 2024).
- Pathmasiri, T.K.K.S.; Perera, G.I.P. Potential of using polyethylene as viscosity enhancer of palm oil to use as a lubricating oil. Adv. Mech. Eng. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Dowson, D.; Whomes, T.L. Paper 8: Side-leakage factors for a rigid cylinder lubricated by an isoviscous fluid. Proc. Institition Mech. Eng. Conf. Proc. 1966, 181, 165–176. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Hector, L.G., Jr. Hydrodynamic lubrication in axisymmetric stretch forming-part 1: Theoretical analysis. J. Tribol. 1991, 113, 659–666. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Q.; Zheng, Y.; Liu, X.; Politis, D.; El Fakir, O.; Wang, L. Investigation of the friction coefficient evolution and lubricant breakdown behaviour of AA7075 aluminium alloy forming processes at elevated temperatures. Int. J. Extrem. Manuf. 2021, 3, 025002. [Google Scholar] [CrossRef]
- Sutcliffe, M.P.F. Surface asperity deformation in metal forming processes. Int. J. Mech. Sci. 1988, 11, 847–868. [Google Scholar] [CrossRef]
- Kalin, M.; Zugelj, B.; Lamut, M.; Hamouda, K. Elastic and plastic deformation of surface asperities and their load-carrying mechanisms during the formation of a real contact area. Tribol. Int. 2023, 178, 108067. [Google Scholar] [CrossRef]
- Sheu, S.; Wilson, W.R.D. Flattening of workpiece surface asperities in metal forming. In Proceedings of the 11th North American Manufacturing Research Conference, Madison, WI, USA, 24–26 May 1983; pp. 172–178. [Google Scholar]
- Li, H.J.; Jiang, Z.Y.; Wei, D.B.; Han, J.T.; Tieu, A.K. Study on surface asperity flattening during uniaxial planar compression. Wear 2011, 271, 1778–1784. [Google Scholar] [CrossRef]
- Azushima, A.; Igarashi, K. Development of a New Sheet Metal Forming Simulator Contralled by Computer. In Proceedings of the Japanese Spring Conference on Technology of Plasticity, Beijing, China, 19–24 September 1993; pp. 79–82. [Google Scholar]
- Vollertsen, F.; Hu, Z. Tribological size effects in sheet metal forming measured by a strip drawing test. Ann. CIRP 2006, 55, 291–294. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Wang, Z.; Hua, M.; Wei, X. A study on variable friction model in sheet metal forming with advanced high strength steels. Tribol. Int. 2016, 93, 17–28. [Google Scholar] [CrossRef]

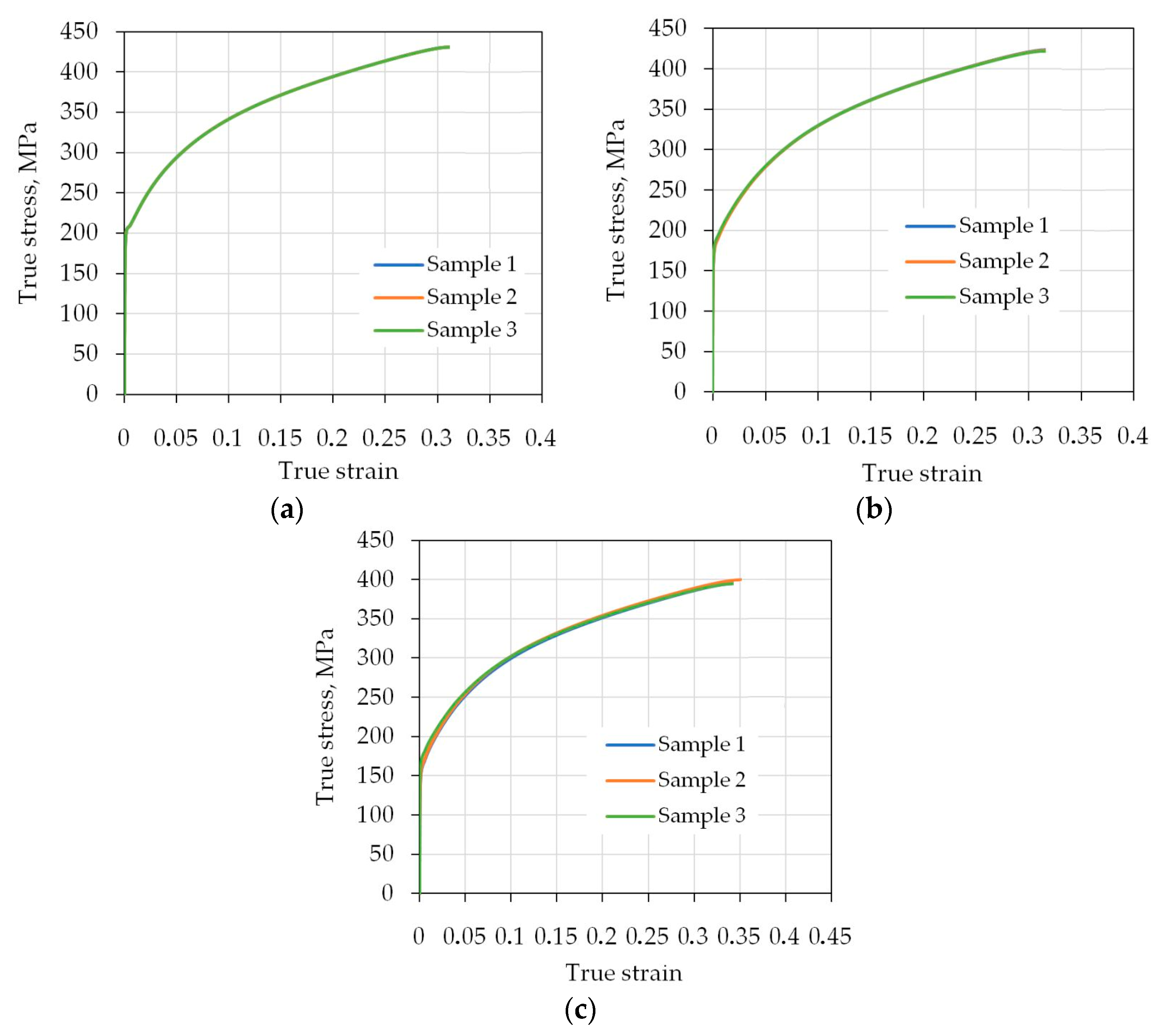

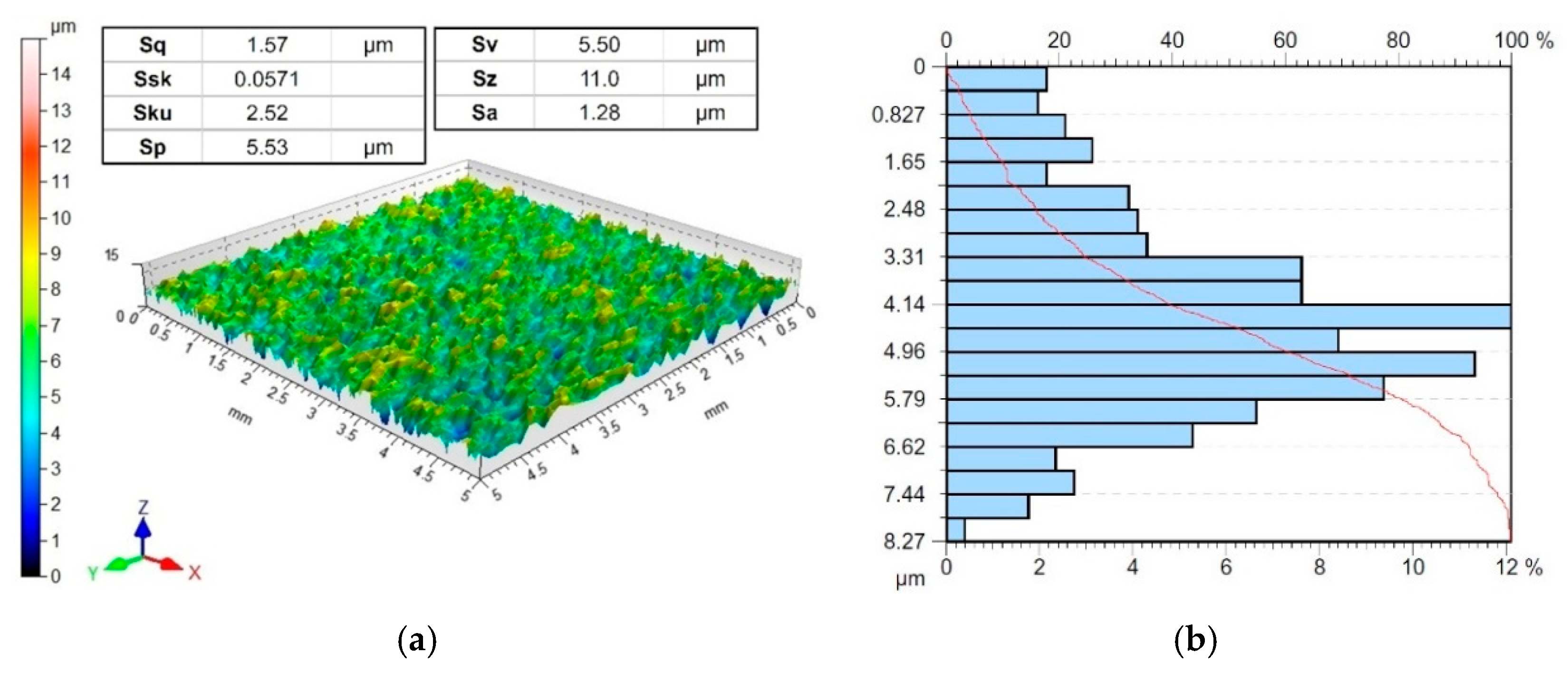








| Material | Sheet Thickness tsh, mm | Ultimate Tensile Stress Rm, MPa | Yield Stress Rp0.2, MPa | Young’s Modulus E, GPa | Elongation A50, % |
|---|---|---|---|---|---|
| DC03 | 1.2 | 322.7 | 203.9 | 165.8 | 23.9 |
| DC04 | 1.25 | 315.4 | 180.2 | 176.9 | 24.7 |
| DC05 | 1.25 | 289.1 | 162.5 | 163.2 | 25.9 |
| Measurement Number | Lubricant Type | Contact Pressure pc, MPa | Lubricant Pressure poil, MPa |
|---|---|---|---|
| 1 | S100+ | 2 | 0 |
| 2 | S100+ | 4 | 0 |
| 3 | S100+ | 6 | 0 |
| 4 | S100+ | 8 | 0 |
| 5 | S100+ | 2 | 0.6 |
| 6 | S100+ | 4 | 0.6 |
| 7 | S100+ | 6 | 0.6 |
| 8 | S100+ | 8 | 0.6 |
| 9 | S100+ | 2 | 1.2 |
| 10 | S100+ | 4 | 1.2 |
| 11 | S100+ | 6 | 1.2 |
| 12 | S100+ | 8 | 1.2 |
| 13 | S100+ | 2 | 1.8 |
| 14 | S100+ | 4 | 1.8 |
| 15 | S100+ | 6 | 1.8 |
| 16 | S100+ | 8 | 1.8 |
| 17 | S300 | 2 | 0 |
| 18 | S300 | 4 | 0 |
| 19 | S300 | 6 | 0 |
| 20 | S300 | 8 | 0 |
| 21 | S300 | 2 | 0.6 |
| 22 | S300 | 4 | 0.6 |
| 23 | S300 | 6 | 0.6 |
| 24 | S300 | 8 | 0.6 |
| 25 | S300 | 2 | 1.2 |
| 26 | S300 | 4 | 1.2 |
| 27 | S300 | 6 | 1.2 |
| 28 | S300 | 8 | 1.2 |
| 29 | S300 | 2 | 1.8 |
| 30 | S300 | 4 | 1.8 |
| 31 | S300 | 6 | 1.8 |
| 32 | S300 | 8 | 1.8 |
| ANN Denotation | Oil Viscosity, mm2/s | Contact Pressure, MPa | Oil Pressure, MPa | Ultimate Tensile Stress, MPa | Yield Stress, MPa | Young’s Modulus, GPa | Elongation, % | Sa, μm | Ssk | Sku |
|---|---|---|---|---|---|---|---|---|---|---|
| ANN-1–ANN-5 | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● |
| ANN-6.1 | ● | ● | ● | ● | ● | ● | ● | – | ● | ● |
| ANN-6.2 | ● | ● | ● | ● | ● | ● | ● | ● | – | ● |
| ANN-6.3 | ● | ● | ● | ● | ● | ● | ● | ● | ● | – |
| ANN Denotation | Hidden Layer | Output Layer |
|---|---|---|
| ANN-1 | tanh function (hyperbolic tangent) | tanh function (hyperbolic tangent) |
| ANN-2 | logistic activation function | exponential linear unit function |
| ANN-3 | exponential linear unit function | exponential linear unit function |
| ANN-4 | exponential linear unit function | tanh function (hyperbolic tangent) |
| ANN-5 | tanh function (hyperbolic tangent) | exponential linear unit function |
| ANN Denotation | ANN Structure | Correlation | Error | ||||
|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | Training | Validation | Testing | ||
| ANN-1 | MLP 10-5-1 | 0.9898 | 0.9877 | 0.9922 | 0.000004 | 0.000005 | 0.000005 |
| ANN-2 | MLP 10-12-1 | 0.9923 | 0.9673 | 0.9915 | 0.000003 | 0.000009 | 0.000006 |
| ANN-3 | MLP 10-6-1 | 0.9885 | 0.9805 | 0.9947 | 0.000005 | 0.000005 | 0.000005 |
| ANN-4 | MLP 10-12-1 | 0.9936 | 0.9619 | 0.9877 | 0.000003 | 0.000011 | 0.000009 |
| ANN-5 | MLP 10-10-1 | 0.9804 | 0.9576 | 0.9870 | 0.000008 | 0.000011 | 0.000009 |
| ANN Denotation | ANN Structure | Correlation | Error | ||||
|---|---|---|---|---|---|---|---|
| Training | Validation | Testing | Training | Validation | Testing | ||
| ANN-6.1 | MLP 9-12-1 | 0.9803 | 0.9304 | 0.9394 | 0.000008 | 0.000043 | 0.000037 |
| ANN-6.2 | MLP 9-12-1 | 0.9926 | 0.9072 | 0.9709 | 0.000003 | 0.000043 | 0.000022 |
| ANN-6.3 | MLP 9-12-1 | 0.9881 | 0.9595 | 0.9861 | 0.000005 | 0.000012 | 0.000009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trzepieciński, T.; Szwajka, K.; Szewczyk, M. Analysis of Coefficient of Friction of Deep-Drawing-Quality Steel Sheets Using Multi-Layer Neural Networks. Lubricants 2024, 12, 50. https://doi.org/10.3390/lubricants12020050
Trzepieciński T, Szwajka K, Szewczyk M. Analysis of Coefficient of Friction of Deep-Drawing-Quality Steel Sheets Using Multi-Layer Neural Networks. Lubricants. 2024; 12(2):50. https://doi.org/10.3390/lubricants12020050
Chicago/Turabian StyleTrzepieciński, Tomasz, Krzysztof Szwajka, and Marek Szewczyk. 2024. "Analysis of Coefficient of Friction of Deep-Drawing-Quality Steel Sheets Using Multi-Layer Neural Networks" Lubricants 12, no. 2: 50. https://doi.org/10.3390/lubricants12020050
APA StyleTrzepieciński, T., Szwajka, K., & Szewczyk, M. (2024). Analysis of Coefficient of Friction of Deep-Drawing-Quality Steel Sheets Using Multi-Layer Neural Networks. Lubricants, 12(2), 50. https://doi.org/10.3390/lubricants12020050







