Analyzing the Efficacy of Nickel Plating Coating in Hydraulic Pipeline Drag Reduction
Abstract
1. Introduction
2. Drag Reduction Experiment with Nickel Plating Coating
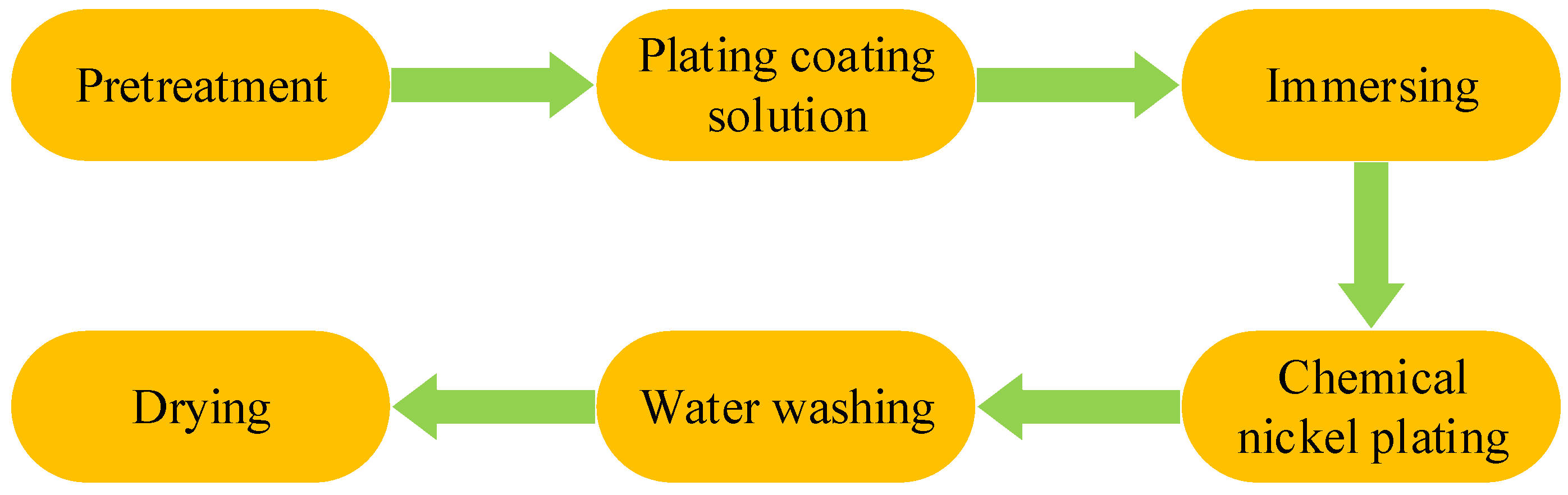
2.1. Preparation of Nickel Plating Coating
2.2. Drag Reduction Experiment with Nickel Plating Coating
3. Experiment Results and Drag Reduction Mechanism
3.1. Experiment Results
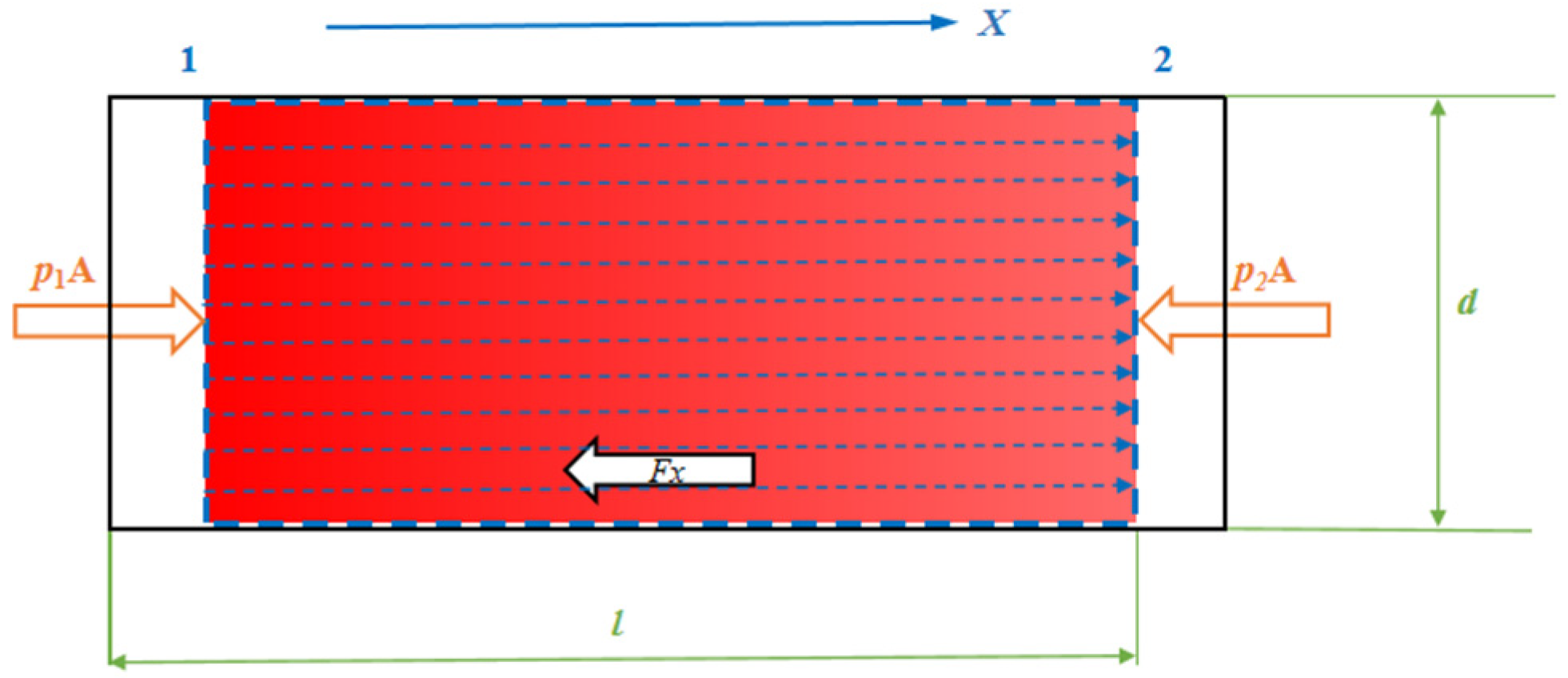
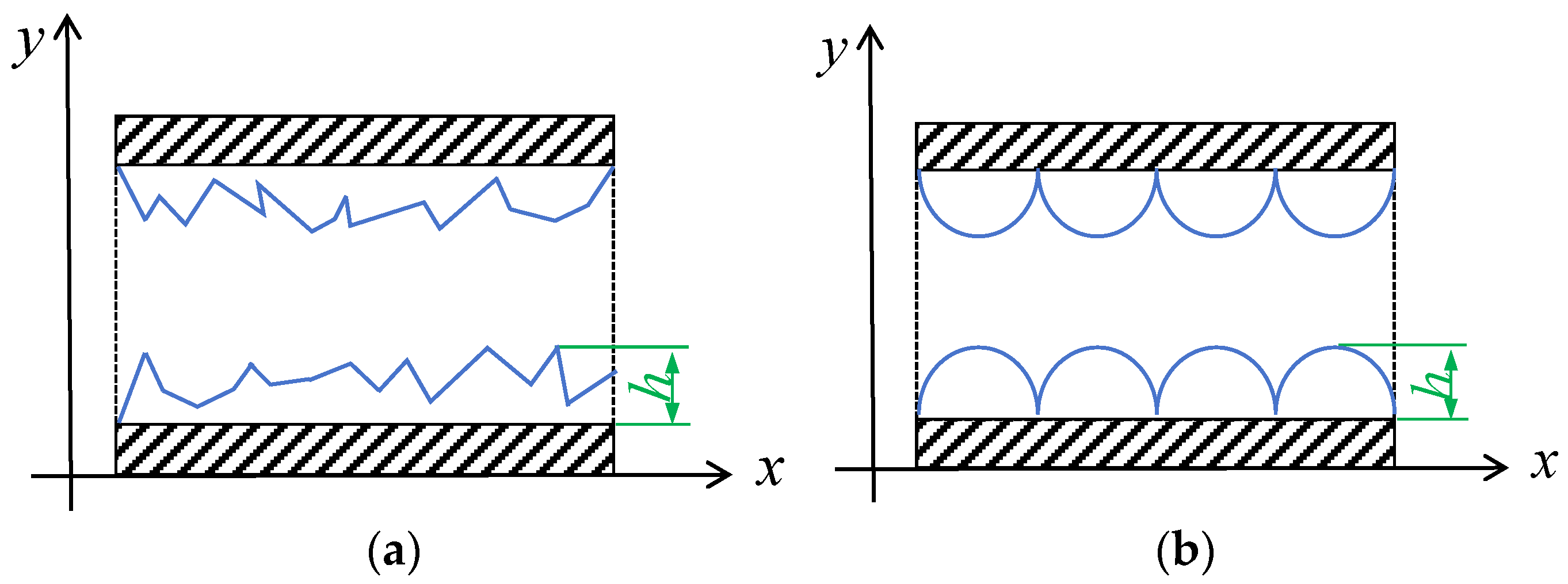
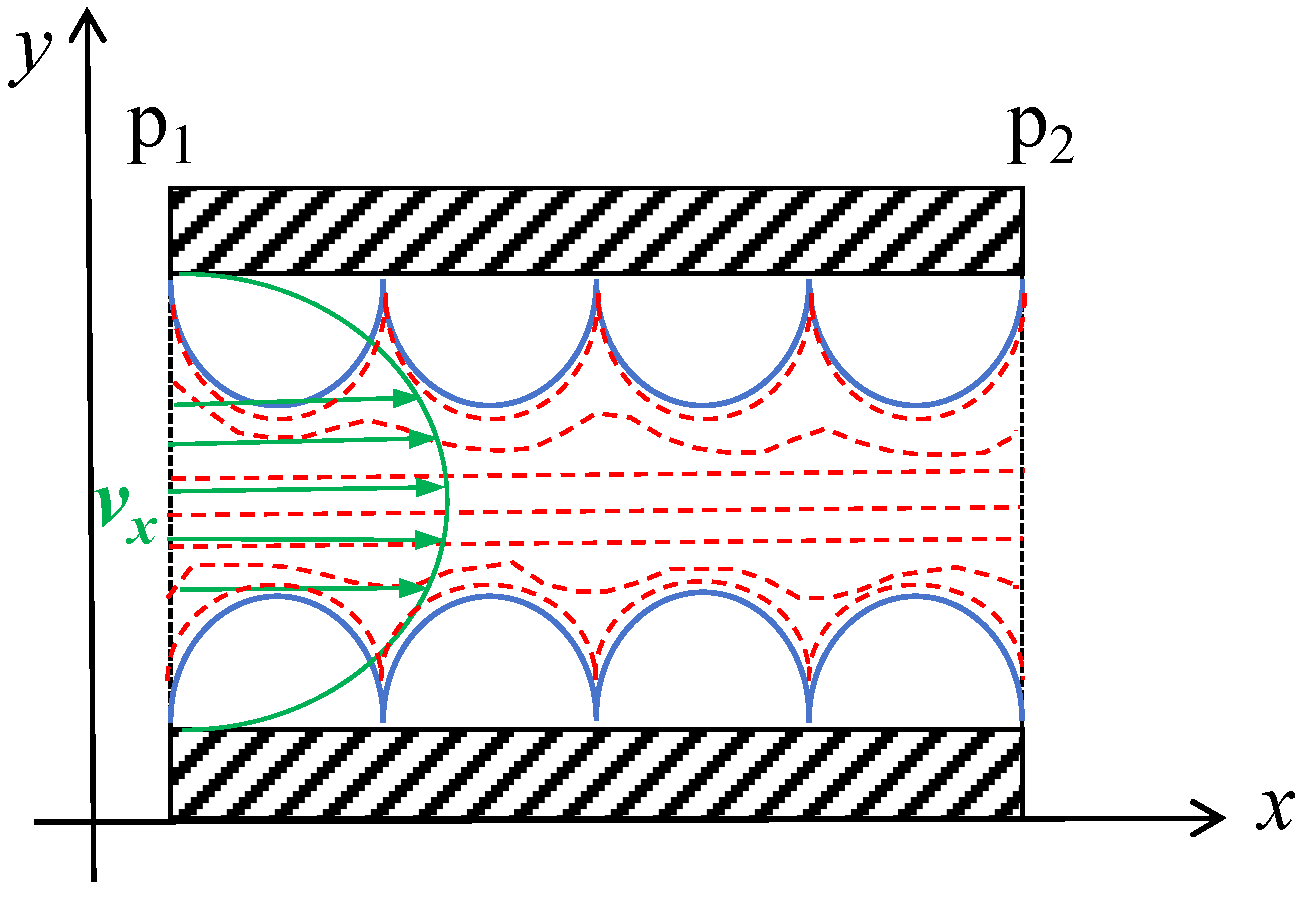
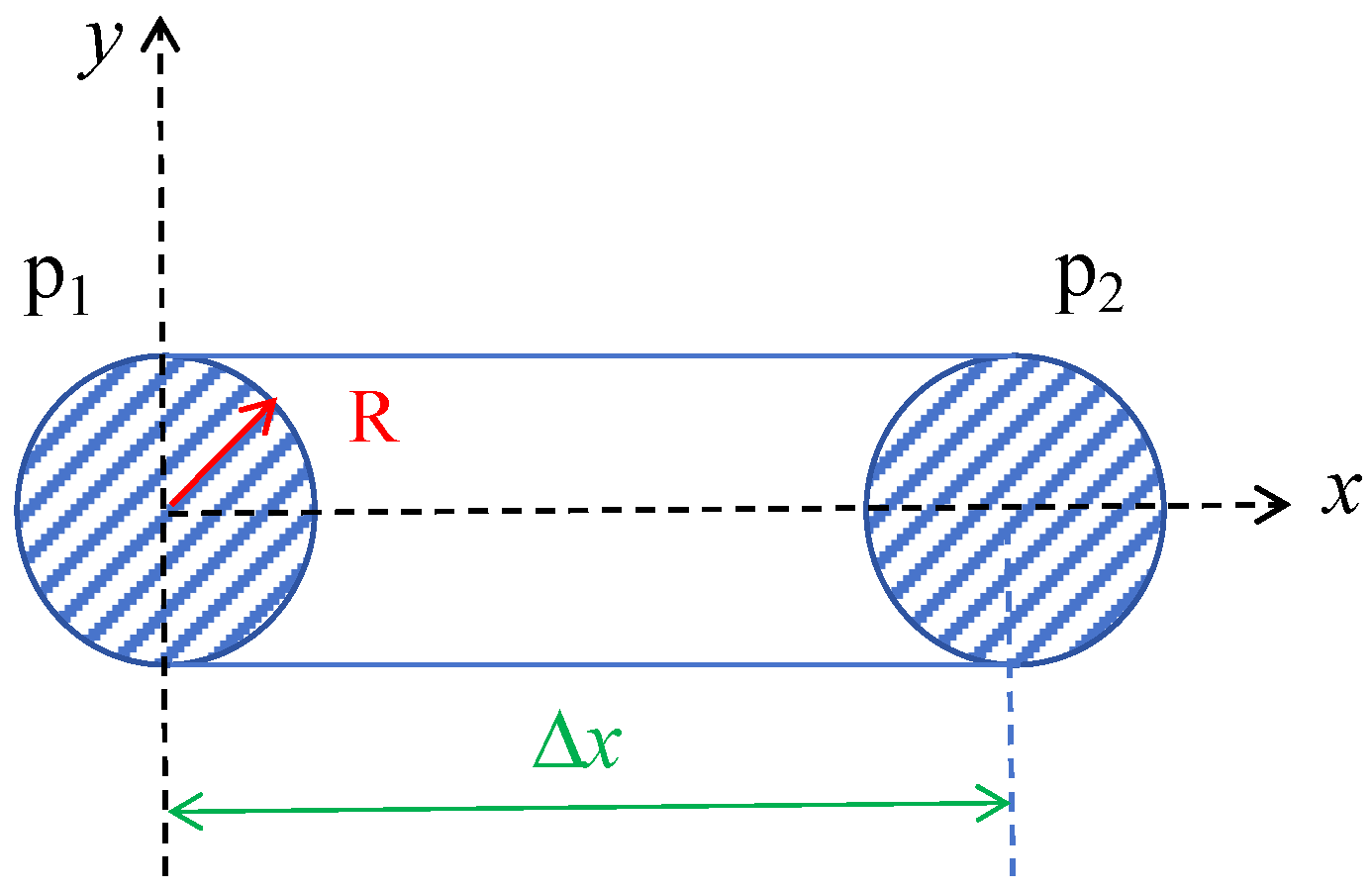
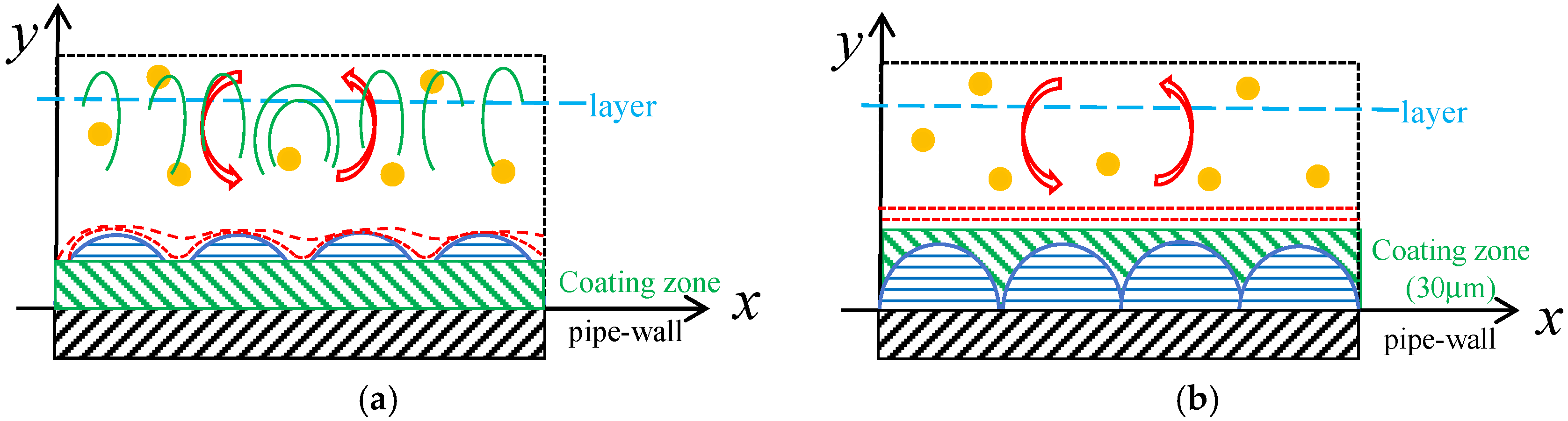
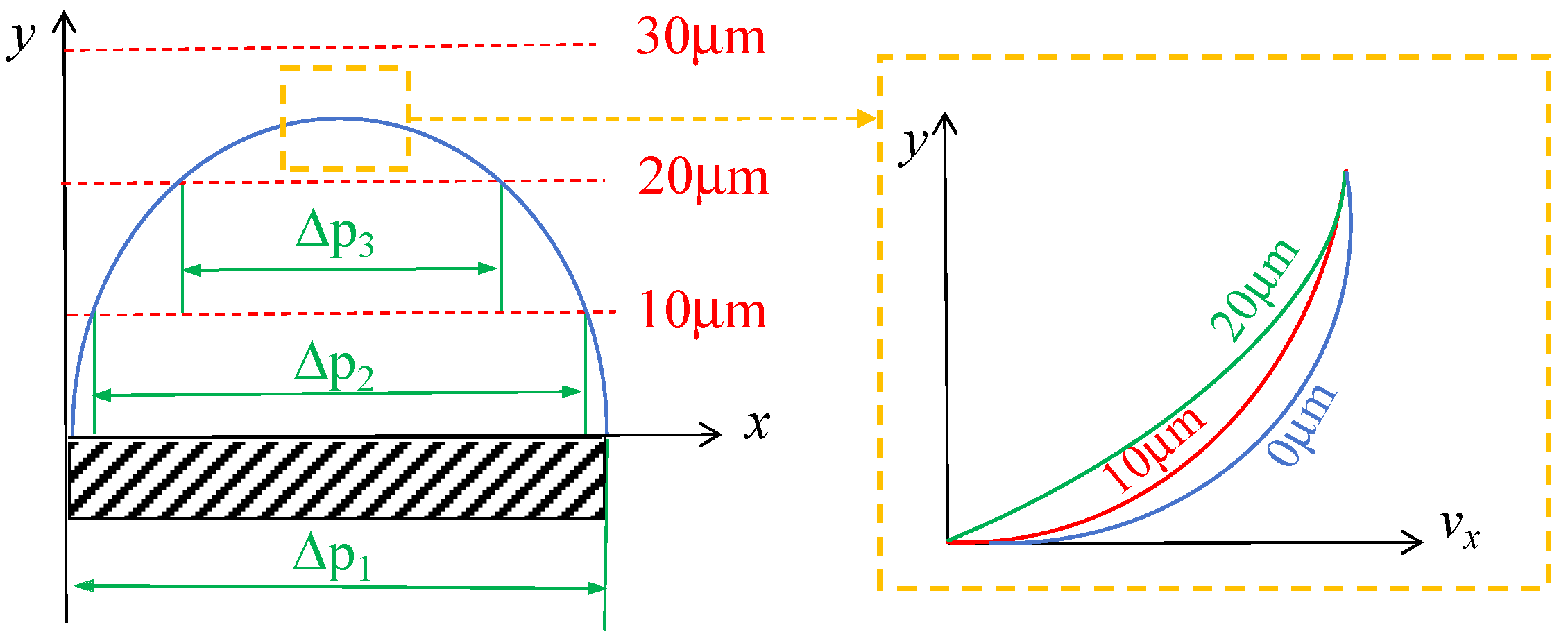
3.2. Analysis of the Drag Reduction Mechanism
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Burger, E.D.; Chorn, L.G.; Perkins, T.K. Perkins. Studies of drag reduction conducted over a broad range of pipeline conditions when flowing prudhoe bay crude oil. J. Rheol. 1980, 24, 603–626. [Google Scholar] [CrossRef]
- Golda, J. Hydraulic transport of coal in pipes with drag reducing additives. Chemical Eng. Commun. 1986, 43, 53–67. [Google Scholar] [CrossRef]
- Yunqing, G.; Junjun, Z.; Songwei, Y.; Chengqi, M.; Zhou, L.; Chendong, H.; Denghao, W.; Jiegang, M.; Yun, R. Unsteady numerical simulation method of hydrofoil surface cavitation. Int. J. Mech. Sci. 2022, 228, 107490. [Google Scholar]
- Vakarelski, I.U.; Kamoliddinov, F.; Jetly, A.; Thoroddsen, S.T. When superhydrophobicity can be a drag: Ventilated cavitation and splashing effects in hydrofoil and speed-boat models tests. Colloids Surf. A Physicochem. Eng. 2021, 628, 127344. [Google Scholar] [CrossRef]
- Hnativ, R.; Verbovskiy, O. Distribution of local velocities in a circular pipe with accelerating fluid flow. East. Eur. J. Enterp. Technol. 2019, 2, 58–63. [Google Scholar] [CrossRef]
- Li, Y.Z.; Woo, Y.; Manoj, S.; Srikanth, N.; Dong, Z.L. Effect of nano-titanium dioxide contained in titania-polyurea coating on marina biofouling and drag reduction. J. Biomed. Nanotechnol. 2021, 16, 1530–1541. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Jeon, K.H.; Lee, S.B.; Park, H.; Lee, I. Evaluation of in-service speed performance improvement by means of FDR-AF (frictional drag reducing anti-fouling) marine coating based on ISO19030 standard. Sci. Rep. 2021, 11, 1062. [Google Scholar] [CrossRef] [PubMed]
- Saadatbakhsh, M.; Asl, S.J.; Kiani, M.J.; Nouri, N.M. Slip length measurement of pdms/hydrophobic silica superhydrophobic coating for drag reduction application. Surf. Coat. Technol. 2020, 404, 126428. [Google Scholar] [CrossRef]
- Rose, J.B. Interfacial slip-and-drag reduction by superhydrophobic polymer coating. In Superhydrophobic Polymer Coatings; Elsevier: Amsterdam, The Netherlands, 2019; pp. 299–319. [Google Scholar]
- Yunqing, G.; Longbiao, M.; Muhan, Y.; Chendong, H.; Junjun, Z.; Jiegang, M.; Denghao, W.; Yun, R. Strategies for improving friction behavior based on carbon nanotube additive materials. Tribol. Int. 2022, 176, 107875. [Google Scholar]
- Bellemare, J.; Laliberté-Riverin, S.; Ménard, D.; Brochu, M.; Sirois, F. Coating density as the key factor behind hydrogen embrittlement of cadmium-plated 4340 steel. J. Appl. Electrochem. 2020, 50, 1045–1058. [Google Scholar] [CrossRef]
- Mawignon, F.J.; Qin, L.; Kouediatouka, A.N.; Lu, S.; Yang, H.; YEO, K.F.H.; Dong, G. Highly strong bio-inspired ZnO/PDMS superhydrophobic surface with drag reduction and antibacterial properties. Tribol. Int. 2023, 189, 109003. [Google Scholar] [CrossRef]
- Hansen, R.J.; Hunston, D.L. An experimental study of turbulent flows over compliant surfaces. J. Sound Vib. 1974, 34, 297–308. [Google Scholar] [CrossRef]
- Li, L.C.; Liu, B.; Hao, H.L.; Li, L.Y.; Zeng, Z.X. Investigation of the drag reduction performance of bionic flexible coating. Phys. Fluids 2020, 32, 084103. [Google Scholar] [CrossRef]
- Lv, X.S.; Qin, Y.; Liang, H.; Zhao, B.; Cui, X. A facile method for constructing a superhydrophobic zinc coating on a steel surface with anti-corrosion and drag-reduction properties. Appl. Surf. Sci. 2021, 562, 150192. [Google Scholar] [CrossRef]
- Rowin, W.A.; Asha, A.B.; Narain, R.; Ghaemi, S. A novel approach for drag reduction using polymer coating. Ocean Eng. 2021, 240, 109895. [Google Scholar] [CrossRef]
- Ott, J.O.; Lazalde, M.T.; Gu, G.X. Algorithmic-driven design of shark denticle bioinspired structures for superior aerodynamic properties. Bioinspiration Biomim. 2020, 15, 026001. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Yu, S.; Mou, J. Research progress on the collaborative drag reduction effect of polymers and surfactants. Materials 2020, 13, 444. [Google Scholar] [CrossRef]
- Wang, Y.H.; Zhang, Z.B.; Xu, J.K. One-step method using laser for large-scale preparation of bionic superhydrophobic & drag-reducing fish-scale surface—ScienceDirect. Surf. Coat. Technol. 2021, 409, 126801. [Google Scholar]
- Zhu, Y.; Yang, F.C.; Guo, Z.G. Bioinspired surfaces with special micro-structures and wettability for drag reduction: Which surface design will be a better choice? Nanoscale 2021, 13, 6. [Google Scholar] [CrossRef]
- Bonin, B.V.; Delaunois, F. Replacement of Lead stabilizer in electroless Nickel-Boron baths: Synthesis and characterization of coatings from bismuth stabilized bath. Sustain. Mater. Technol. 2020, 23, e00130. [Google Scholar] [CrossRef]
- Azli, N.N.; Amin, N.F.; Oluhende, S.T.; Mohamad, S.Z.; Fadil, N.A. Electroless deposited black nickel-phosphorous solar absorber coatings on carbon steel: Effect of plating bath pH. Mater. Today Proc. 2020, 39, 1071–1076. [Google Scholar] [CrossRef]
- Wu, W.; Huang, J.; Nther, J.; Omar, N.A.; Kster, F. Texture orientation, morphology and performance of nanocrystalline nickel coatings electrodeposited from a Watts-type bath: Effects of H3BO3 concentration and plating time. Surf. Coat. Technol. 2021, 424, 127648. [Google Scholar] [CrossRef]
- Yue, B.W.; Zhu, G.M.; Wang, Y.W.; Song, J.B.; Chang, Z. Uncertainty analysis of factors affecting coating thickness distribution during nickel electrodeposition. J. Electroanal. Chem. 2021, 891, 115274. [Google Scholar] [CrossRef]
- Güler, O.; Varol, T.; Alver, Ü.; Biyik, S. The wear and arc erosion behavior of novel copper based functionally graded electrical contact materials fabricated by hot pressing assisted electroless plating. Adv. Powder Technol. 2021, 32, 2873–2890. [Google Scholar] [CrossRef]
- Chen, M.; Dong, W.; Qin, C. A Method for Electroless Nickel Plating on Aluminum Alloy Surface. Eng. Sci. 2020, 5, 33. [Google Scholar] [CrossRef]
- Salicio-Paz, A.; Grande, F.; Pellicer, E.; Sort, J.; Fornell, J. Monolayered versus multilayered electroless NiP coatings: Impact of the plating approach on the microstructure, mechanical and corrosion properties of the coatings. Surf. Coat. Technol. 2019, 368, 138–146. [Google Scholar] [CrossRef]
- Fu, H.; Lu, Y.; Liang, H.R.; Wang, S.; Ling, K.G. Diagnosis of the single leakage in the fluid pipeline through experimental study and CFD simulation. J. Pet. Sci. Eng. 2020, 193, 107437. [Google Scholar] [CrossRef]
- White, F. Fluid Mechanics; McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
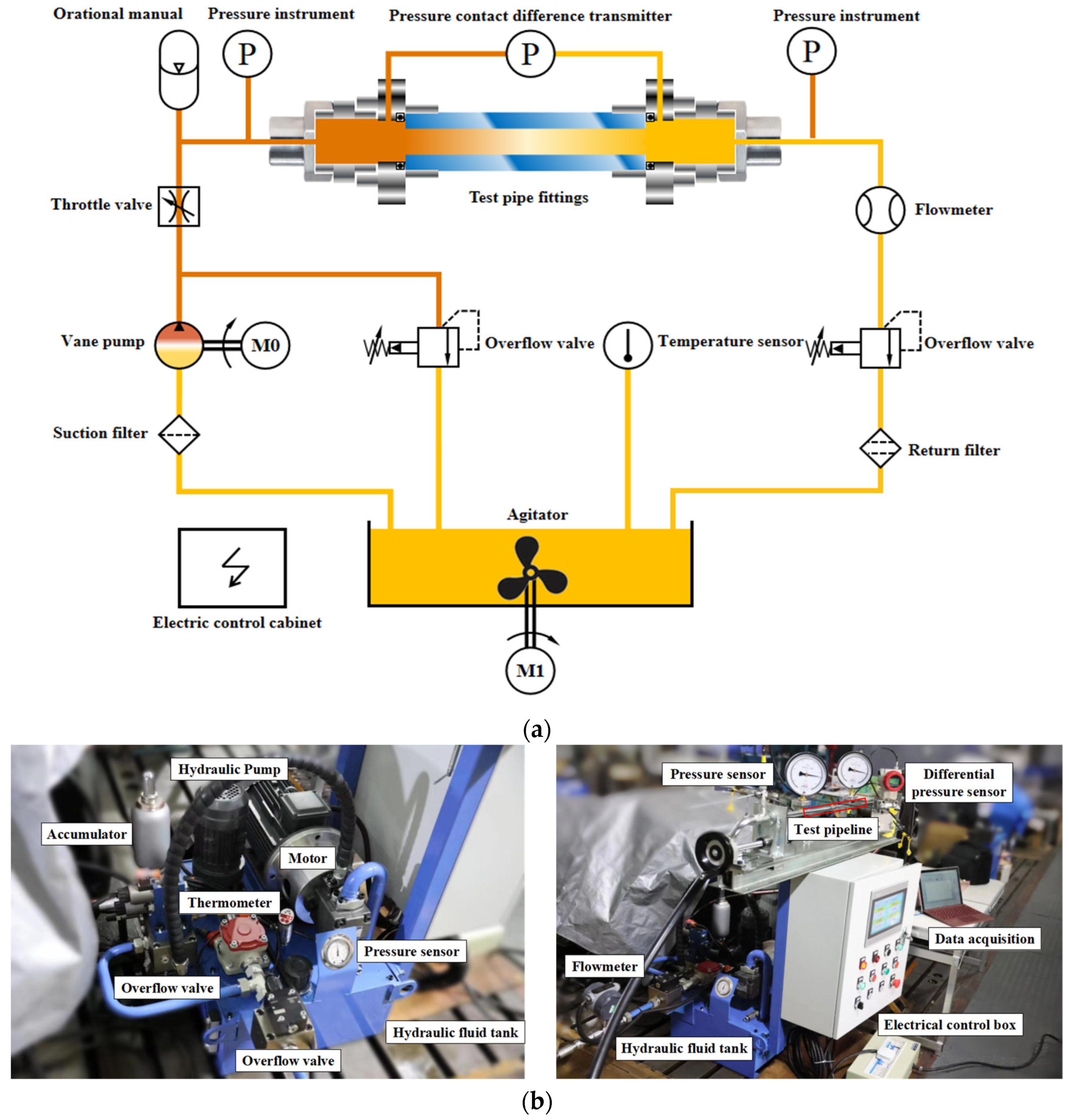
| Control and Data Acquisition System | Motor | Hydraulic Pump | |||||
|---|---|---|---|---|---|---|---|
| Pressure Sensor | Differential Pressure Sensor | Flowmeter | Power | Pressure | Pump Volume | ||
| pmax/MPa | Measurement accuracy | pmax/MPa | Measurement accuracy | Qmax/(m3/h) | PN/kW | pmax/MPa | Vpmax/(mL/r) |
| 6 | 0.4% FS | 250 | 0.075% FS | 40 | 3 | 16 | 16.3 |
| d | 8 mm | 9 mm | 10 mm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| δ | Coating Free | 10 µm | 20 µm | 30 µm | Coating Free | 10 µm | 20 µm | 30 µm | Coating Free | 10 µm | 20 µm | 30 µm | ||
| Δp (kPa) | ||||||||||||||
| v | ||||||||||||||
| 5 m/s | 113.31 | 110.76 | 108.51 | 109.13 | 91.24 | 88.91 | 86.88 | 87.62 | 73.47 | 70.79 | 69.78 | 70.33 | ||
| 4 m/s | 90.40 | 88.58 | 87.21 | 88.12 | 71.45 | 69.77 | 68.21 | 68.83 | 59.98 | 58.23 | 57.06 | 57.54 | ||
| 3 m/s | 68.24 | 66.89 | 65.86 | 66.70 | 54.18 | 53.01 | 51.87 | 52.32 | 43.74 | 42.66 | 41.74 | 42.07 | ||
| d | 8 mm | 9 mm | 10mm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| δ | Coating Free | 10 µm | 20 µm | 30 µm | Coating Free | 10 µm | 20 µm | 30 µm | Coating Free | 10 µm | 20 µm | 30 µm | ||
| η | ||||||||||||||
| v | ||||||||||||||
| 5 m/s | 2.25% | 4.24% | 3.69% | 2.55% | 4.78% | 3.97% | 3.65% | 5.02% | 4.27% | 2.25% | 4.24% | 3.69% | ||
| 4 m/s | 2.01% | 3.53% | 2.52% | 2.35% | 4.53% | 3.67% | 2.92% | 4.87% | 4.07% | 2.01% | 3.53% | 2.52% | ||
| 3 m/s | 1.98% | 3.49% | 2.26% | 2.16% | 4.26% | 3.43% | 2.47% | 4.57% | 3.82% | 1.98% | 3.49% | 2.26% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhou, J.; Yao, B.; Liao, W. Analyzing the Efficacy of Nickel Plating Coating in Hydraulic Pipeline Drag Reduction. Lubricants 2024, 12, 37. https://doi.org/10.3390/lubricants12020037
Wang X, Zhou J, Yao B, Liao W. Analyzing the Efficacy of Nickel Plating Coating in Hydraulic Pipeline Drag Reduction. Lubricants. 2024; 12(2):37. https://doi.org/10.3390/lubricants12020037
Chicago/Turabian StyleWang, Xue, Junjie Zhou, Bowen Yao, and Wenbo Liao. 2024. "Analyzing the Efficacy of Nickel Plating Coating in Hydraulic Pipeline Drag Reduction" Lubricants 12, no. 2: 37. https://doi.org/10.3390/lubricants12020037
APA StyleWang, X., Zhou, J., Yao, B., & Liao, W. (2024). Analyzing the Efficacy of Nickel Plating Coating in Hydraulic Pipeline Drag Reduction. Lubricants, 12(2), 37. https://doi.org/10.3390/lubricants12020037




