The Utilization of a Damping Structure in the Development of Self-Adaptive Water-Lubricated Stern Bearings
Abstract
1. Introduction
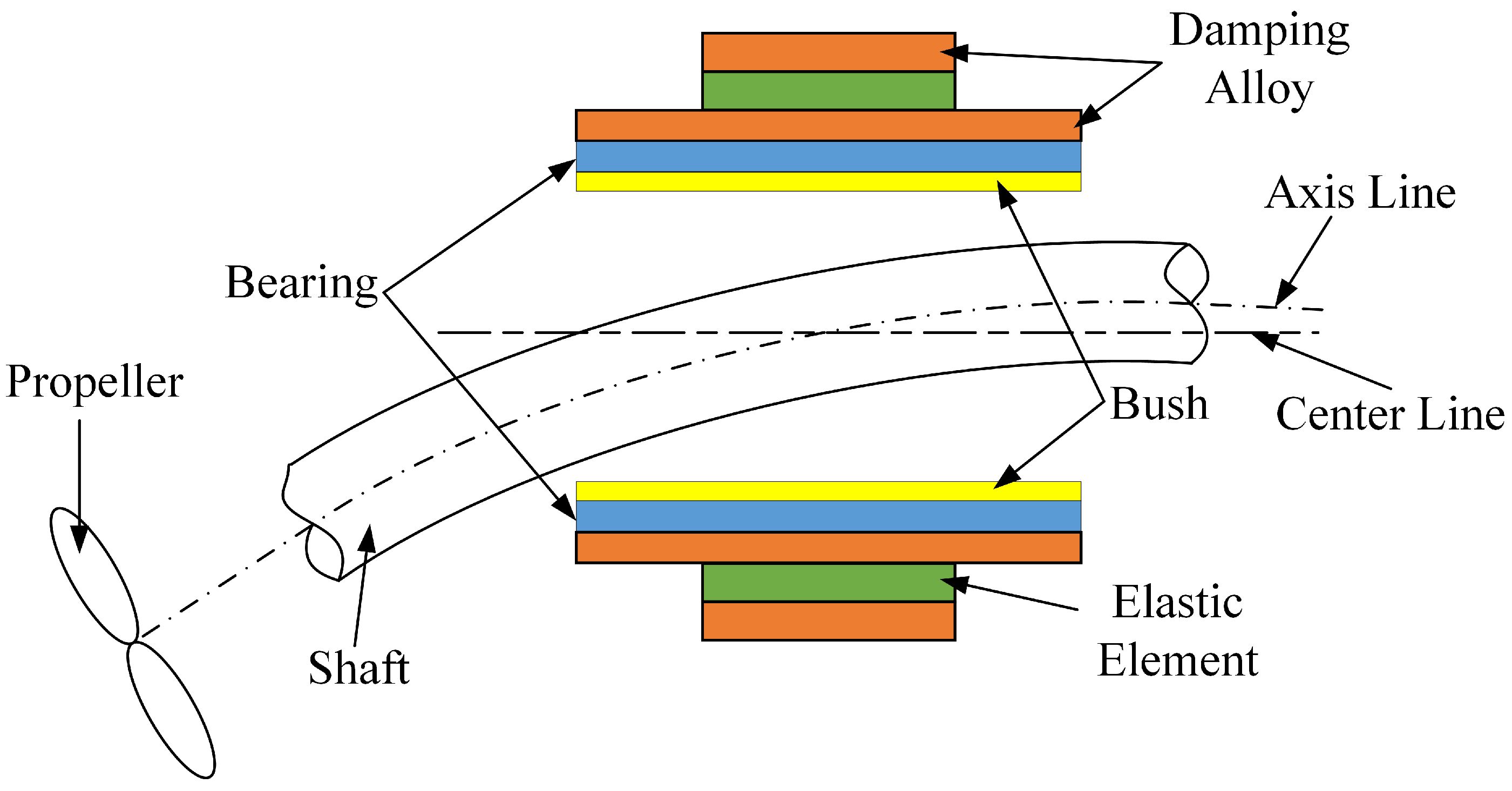
2. Adaptive Vibration-Damping Structure Design
2.1. Structure Design
Adaptive Damping Structure
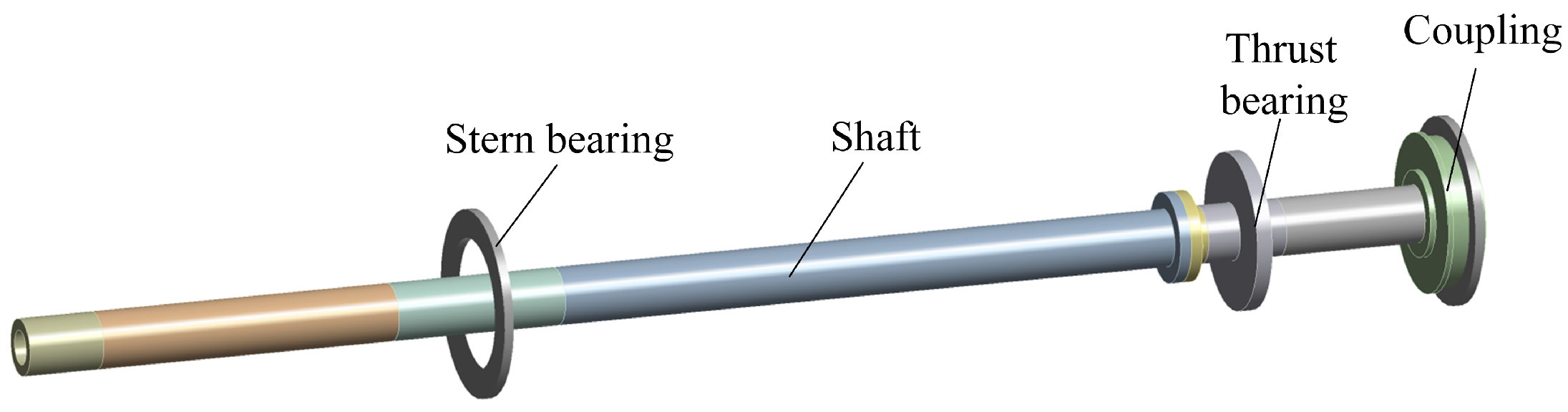
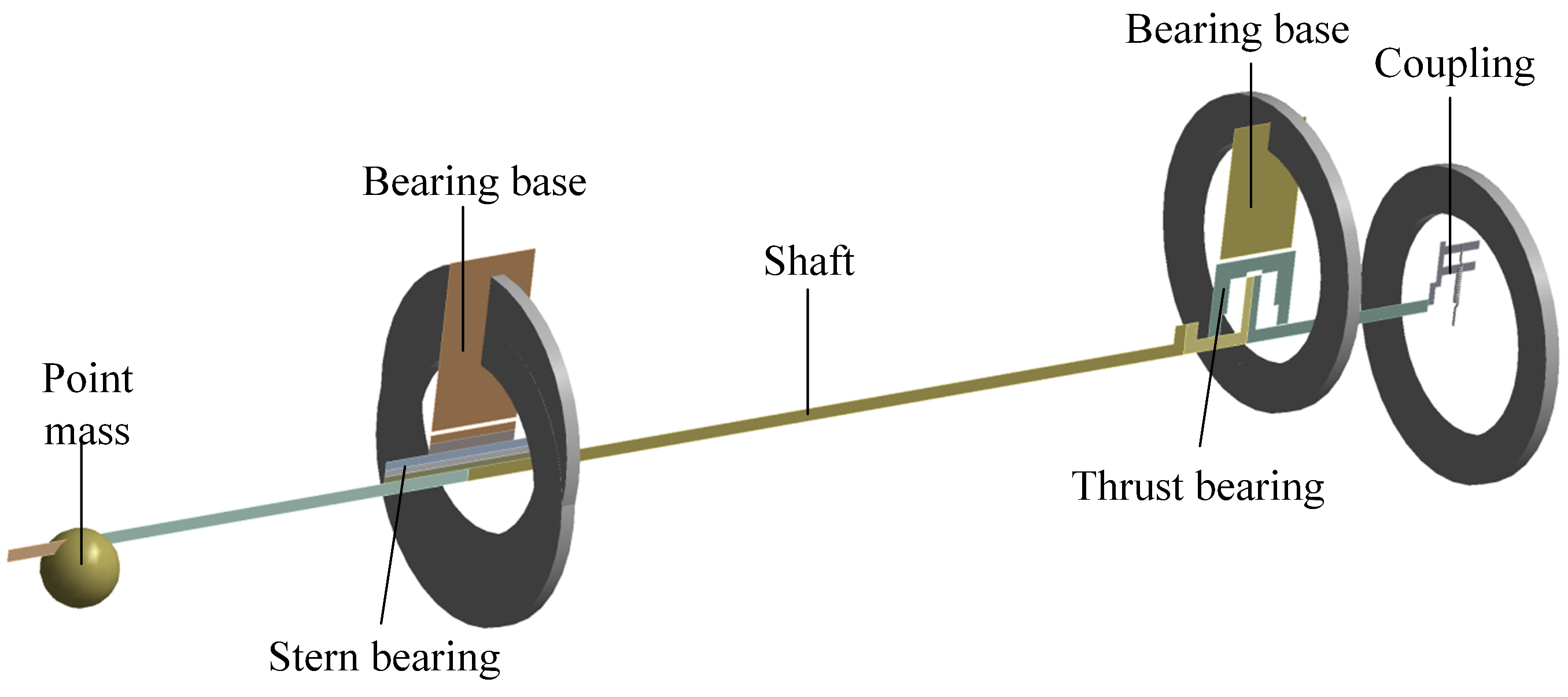
2.2. Configuration of Propulsion System
3. Static Performance Analysis
3.1. Finite Element Simulation
3.1.1. Finite Element Model
3.1.2. Shafting Connection and Boundary Conditions
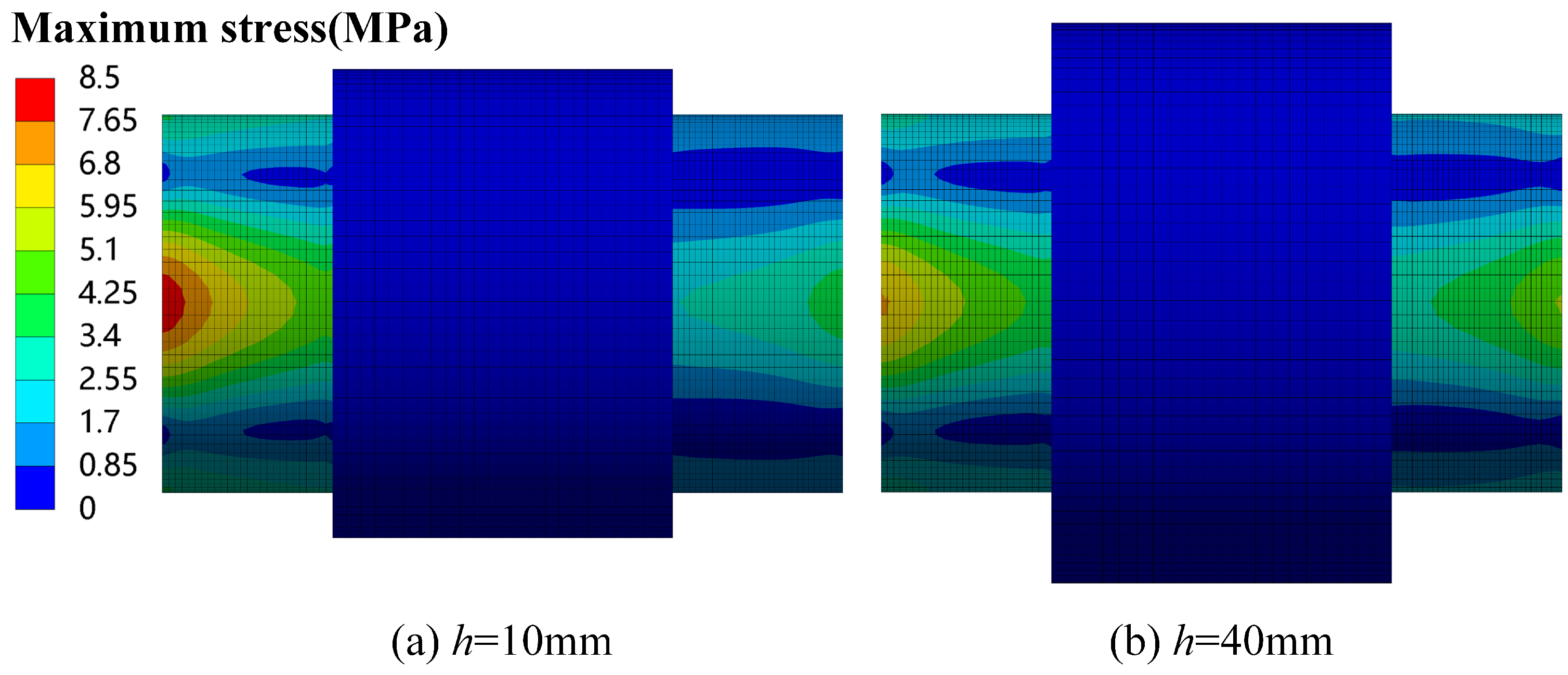
3.2. Influence of Thickness
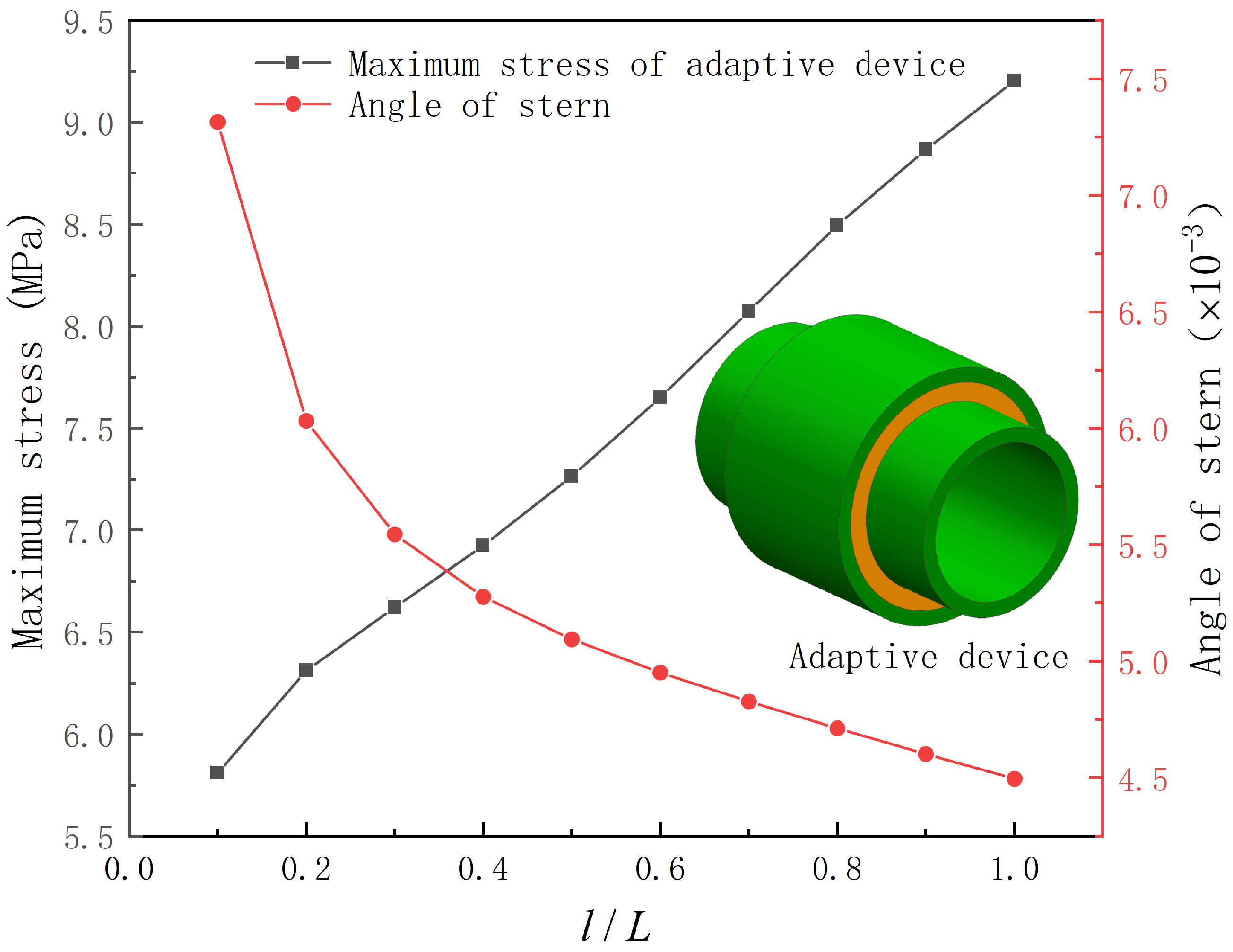
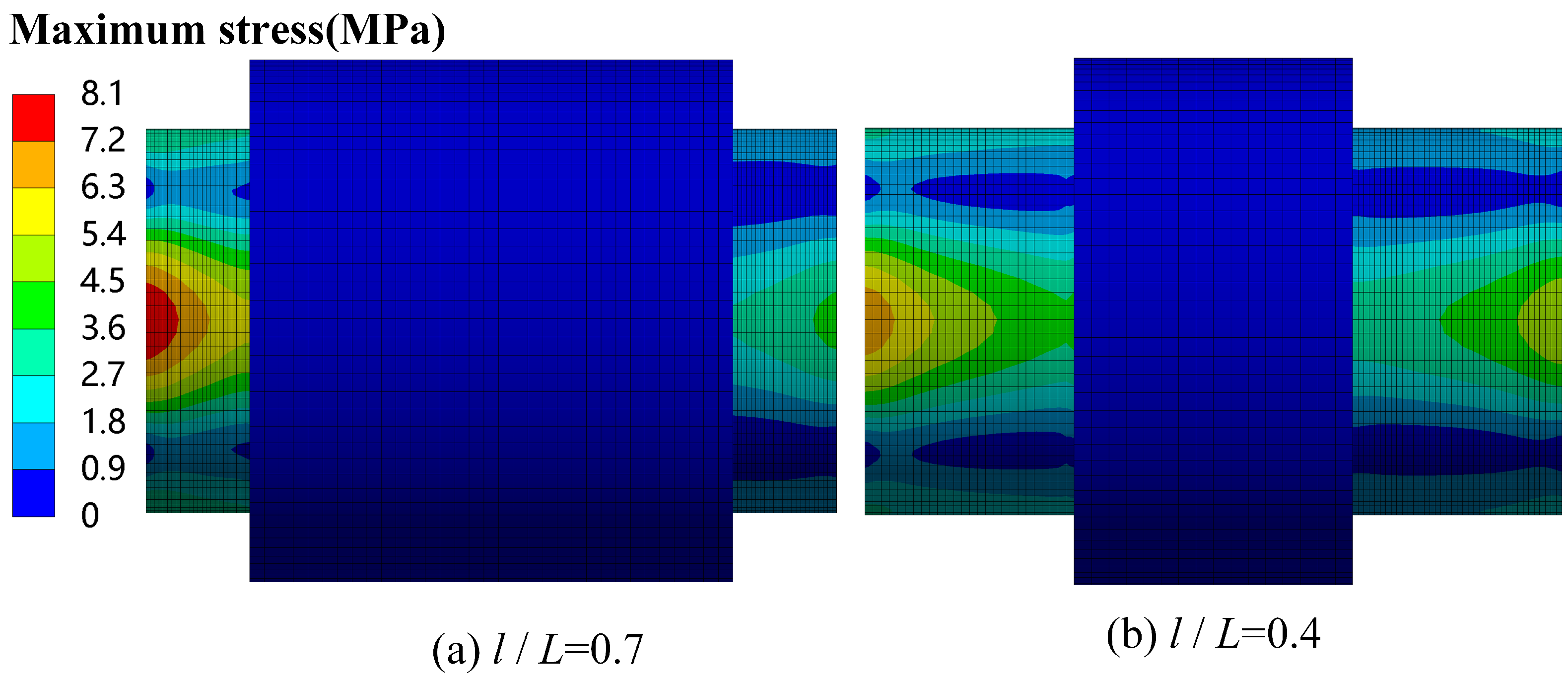
3.3. Influence of Length
4. Vibration Reduction Performance Analysis
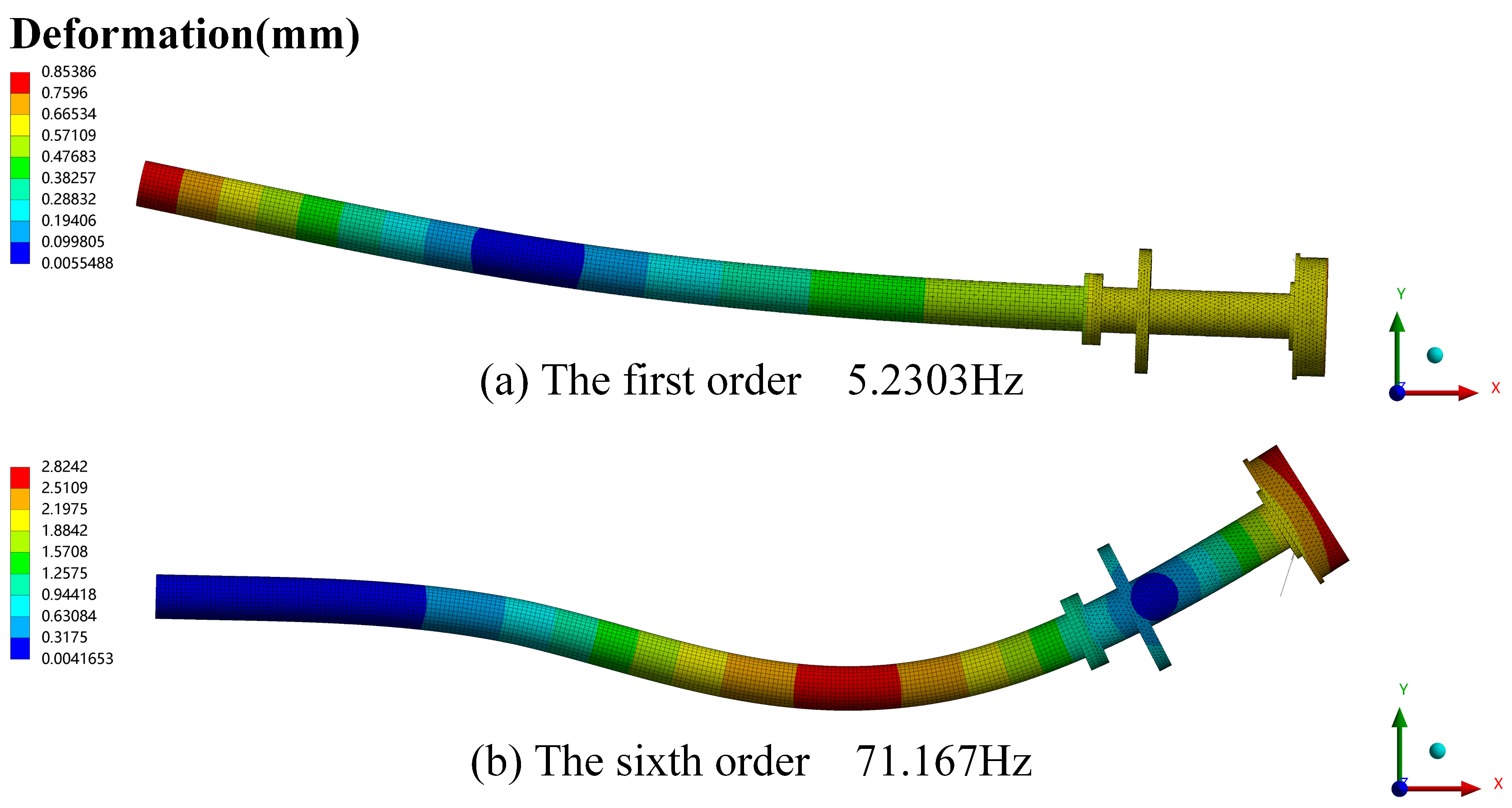
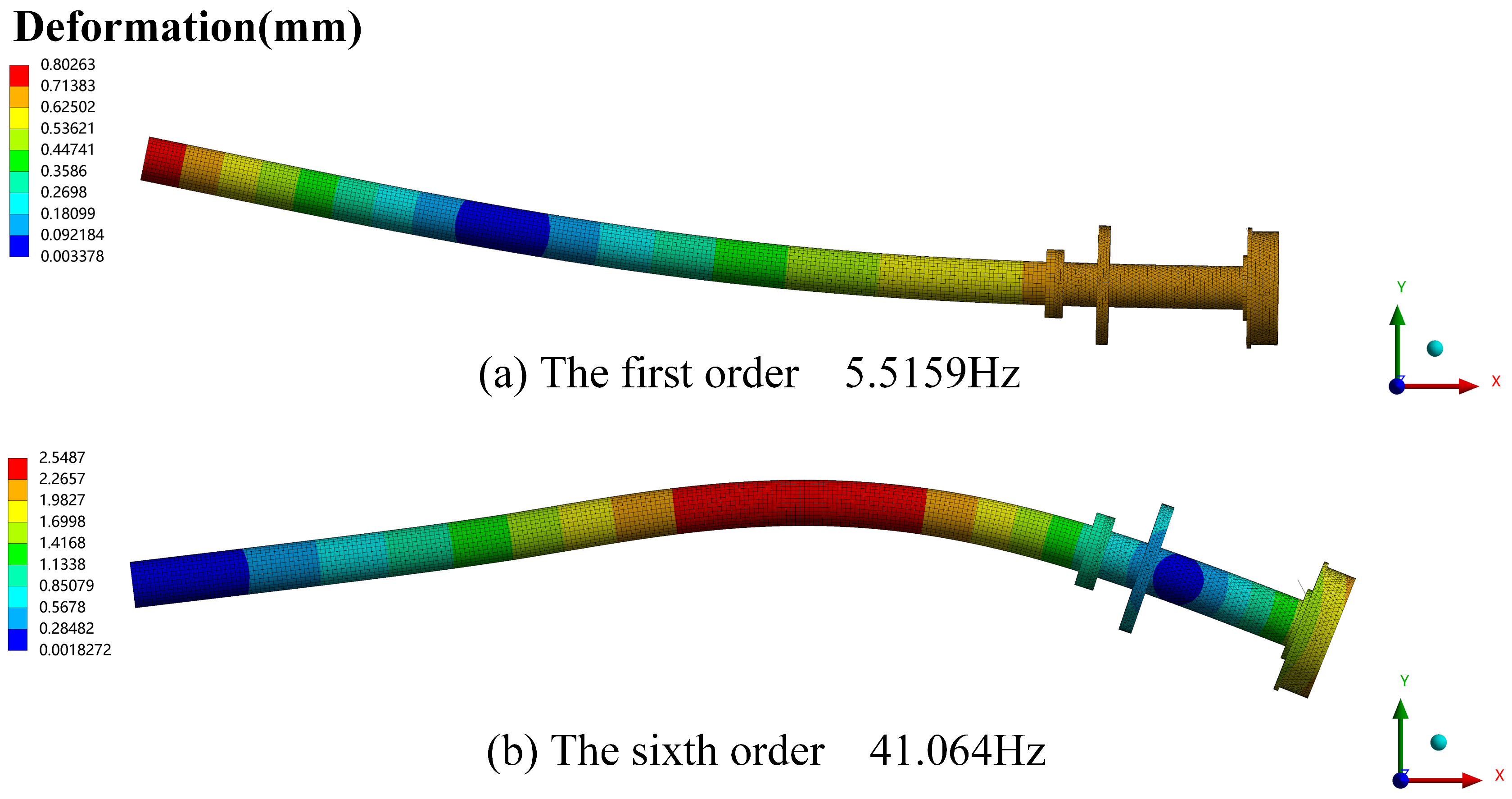
4.1. Modal Analysis
4.2. Harmonic Response Analysis
5. Discussion
6. Conclusions
- The adaptive stern bearing vibration-damping device comprises elastic elements and damping alloy layers. Notably, augmenting the thickness and length of the elastic element and damping alloy serves to enhance the bearing load-balancing and angle compensation capabilities, thereby mitigating bearing wear.
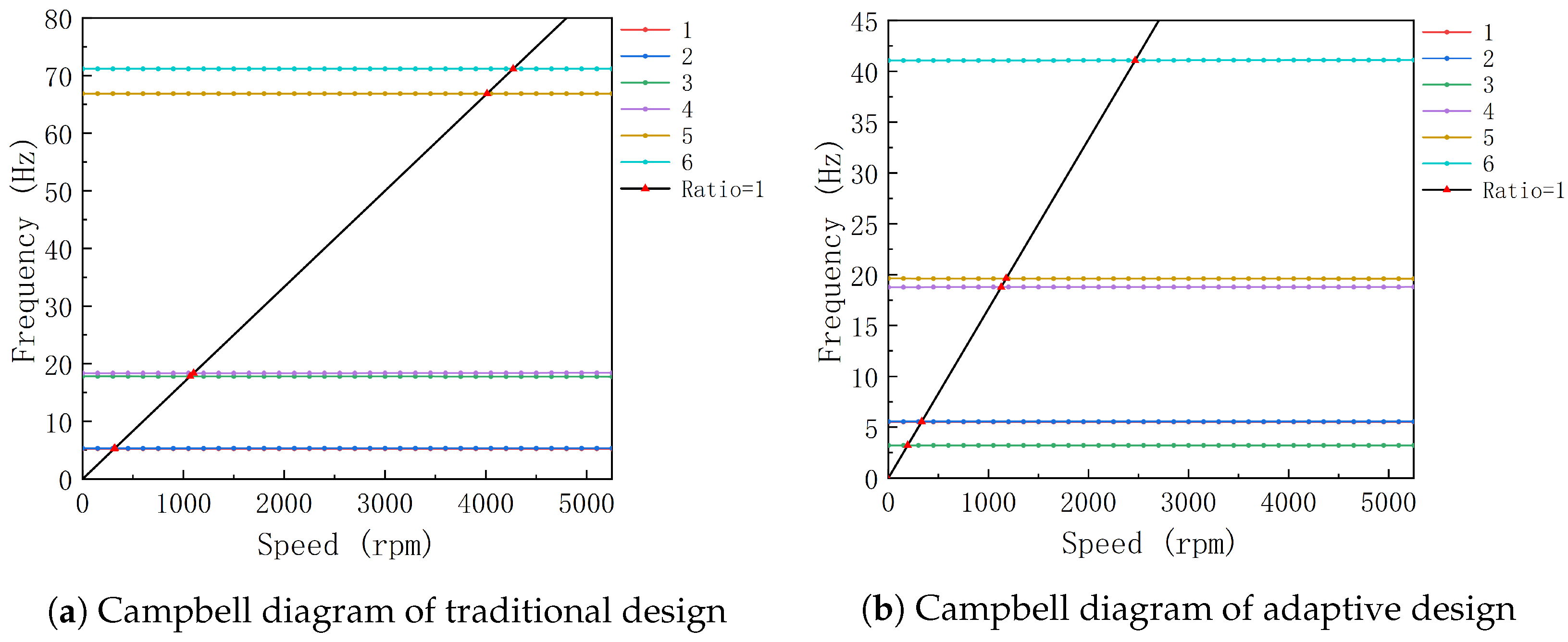
- The modal analysis calculations and comparative evaluations reveal a 5.46% increase in the first-order critical speed of the self-adaptive vibration-damping device for the propeller bearing shafting system in comparison to traditional shafting systems. Importantly, this adaptive device has minimal impact on critical speed.
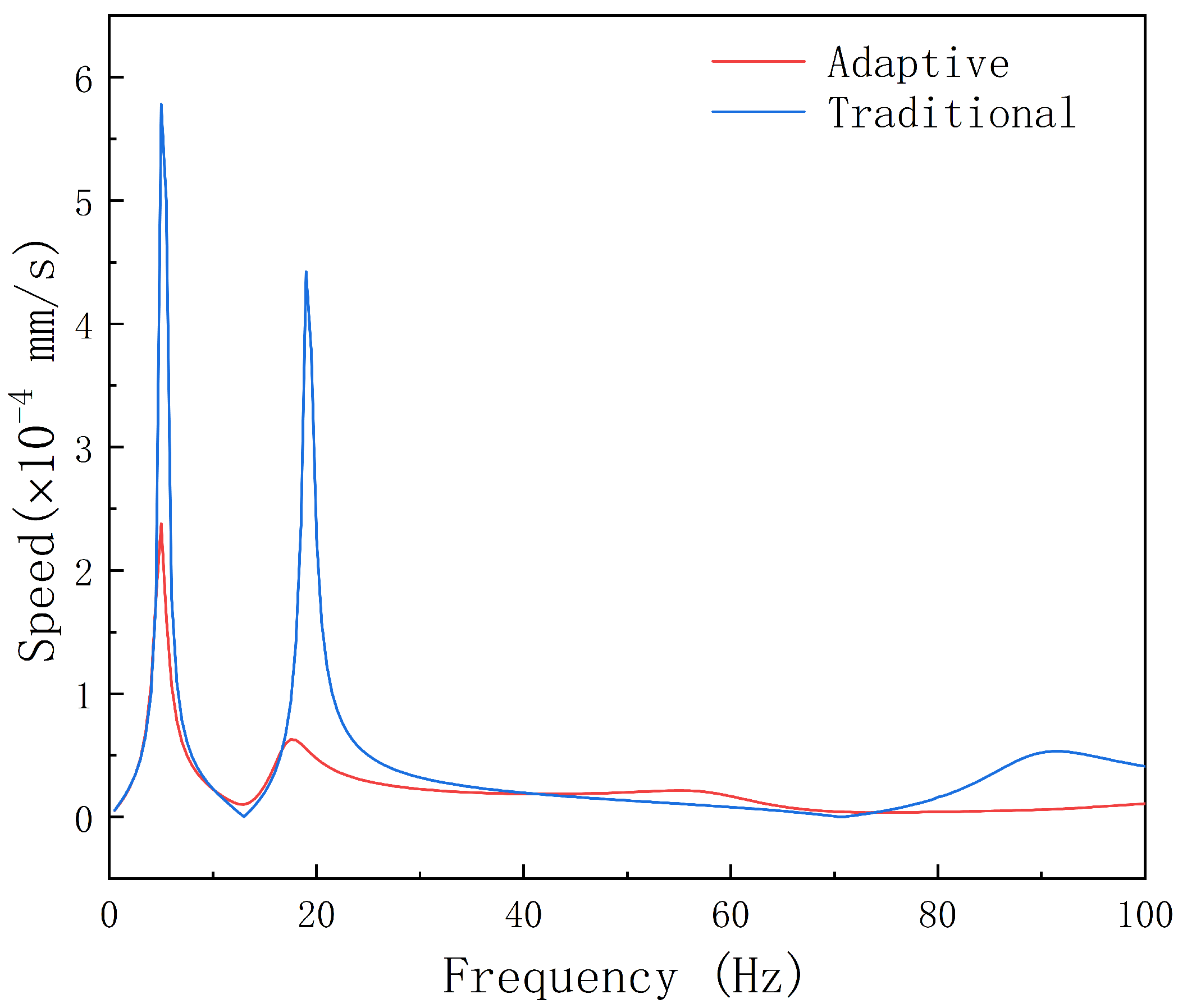
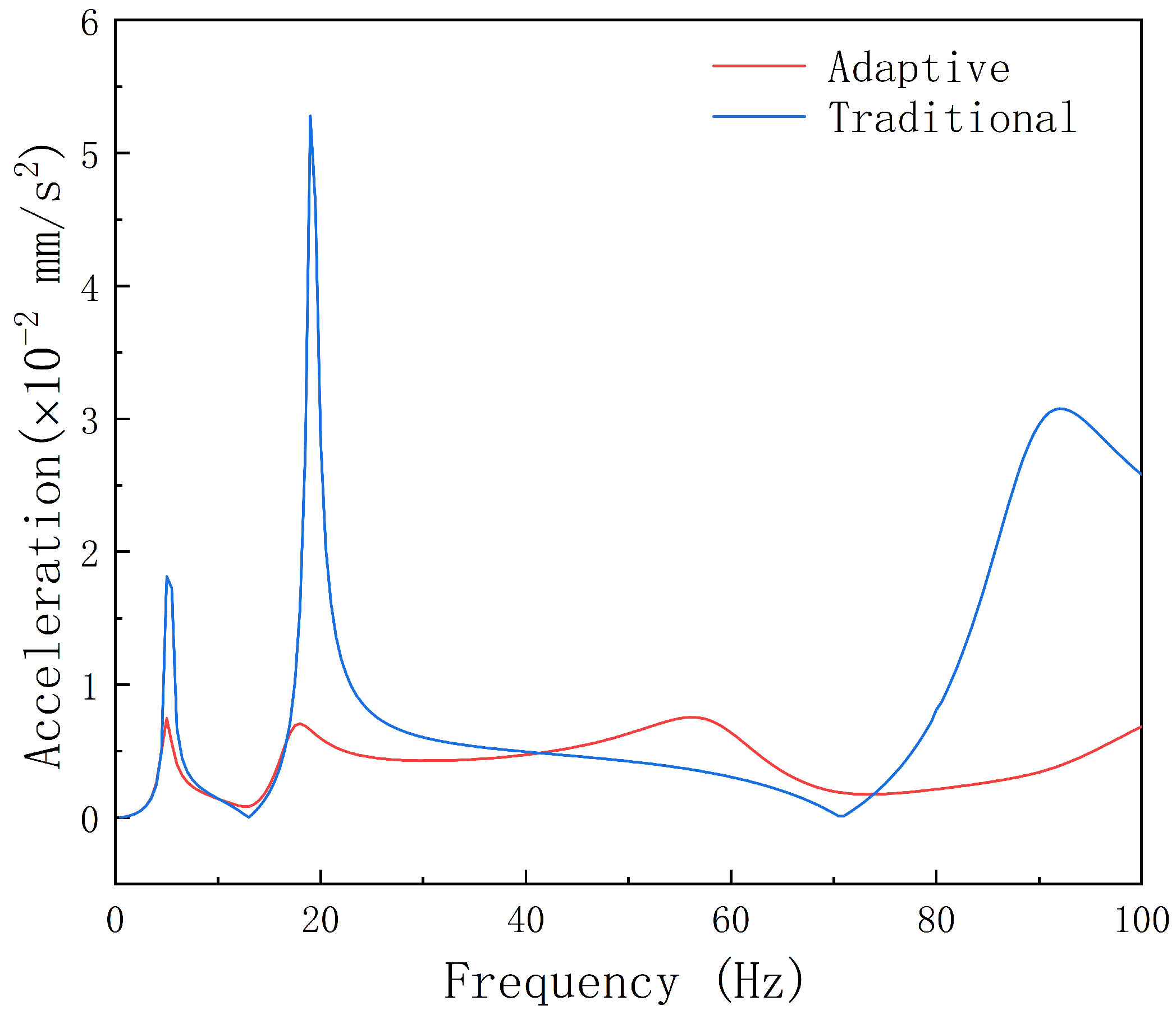
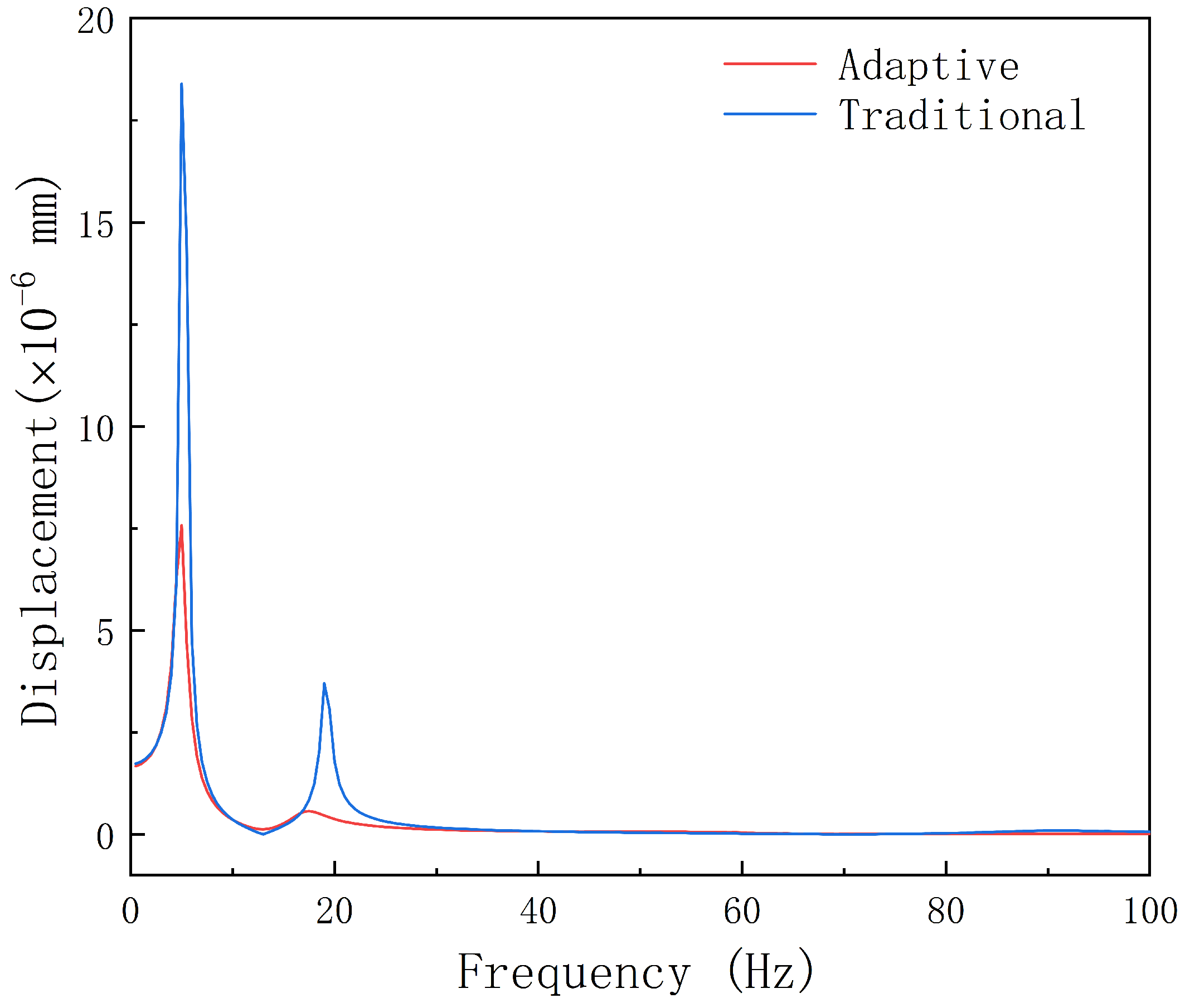
- The in-depth comparative analyses highlight the primary influence of the self-adaptive vibration-damping device on the first-order shaft frequency. Adoption of this self-adaptive structure results in a substantial 58.82% reduction in the velocity response at the first-order natural frequency, a commensurate 58.90% reduction in the acceleration response, and a noteworthy 58.86% reduction in the displacement response. This collective reduction effectively curtails the transmission of vibrations to the hull through the stern bearing.
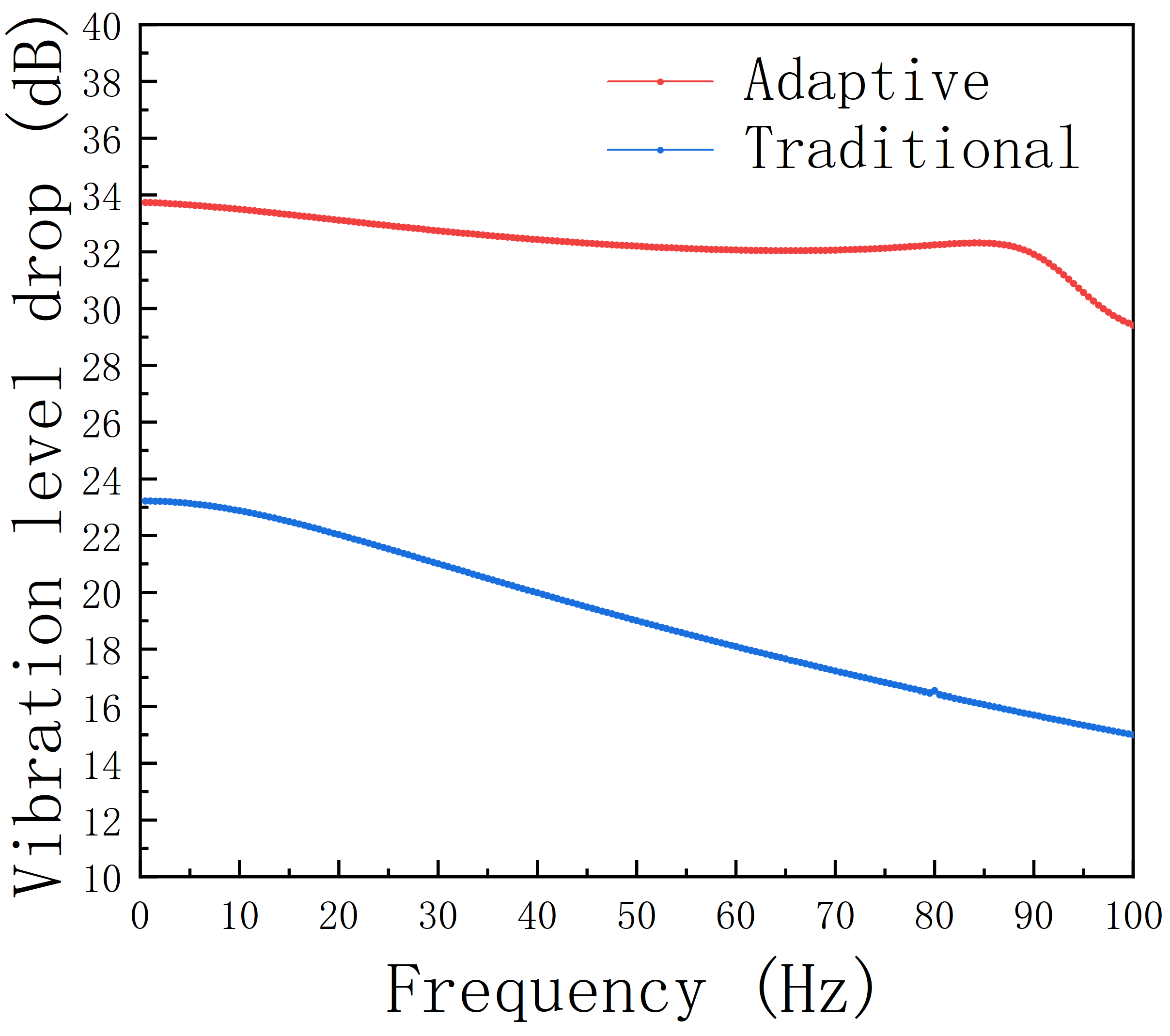
- Further comparative analyses demonstrate a conspicuous increase in the vibration level drop of the adaptive vibration-damping device compared to traditional designs when subjected to a transverse unit force at the propeller’s center of gravity within the 1~100 Hz frequency range. This heightened effect underscores the increased efficacy of the vibration damping provided by the adaptive device.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Gu, Z.; Liu, S. Research on MDO of Ship Propulsion Shafting Dynamics Considering the Coupling Effect of a Propeller-Shafting-Hull System. Pol. Marit. Res. 2023, 30, 86–97. [Google Scholar] [CrossRef]
- Xing, P.; Lu, L.; Li, G.; Wang, X.; Gao, H.; Song, Y.; Zhang, H. A Multi-Method Approach to Identify the Natural Frequency of Ship Propulsion Shafting under the Running Condition. J. Mar. Sci. Eng. 2022, 10, 1432. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.; Xing, P.; Gao, H.; Song, Y. A review of stochastic finite element and nonparametric modelling for ship propulsion shaft dynamic alignment. Ocean. Eng. 2023, 286, 115656. [Google Scholar] [CrossRef]
- Su, Z.; Zheng, Z.; Huang, X.; Hua, H. Research on dynamic vibration absorber with negative stiffness for controlling longitudinal vibration of propulsion shafting system. Ocean. Eng. 2022, 264, 112375. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, N.; Lin, C.; Hua, H. Coupled dynamic analysis of a heavily-loaded propulsion shafting system with continuous bearing-shaft friction. Int. J. Mech. Sci. 2020, 172, 105431. [Google Scholar] [CrossRef]
- Jose Legaz, M.; Amat, S.; Busquier, S. Marine Propulsion Shafting: A Study of Whirling Vibrations. J. Ship Res. 2021, 65, 55–61. [Google Scholar] [CrossRef]
- Jin, Y.; Lu, J.; Ouyang, W.; Liu, Z.; Lao, K. Vibration Reduction Performance of Damping-Enhanced Water-Lubricated Bearing Using Fluid-Saturated Perforated Slabs. Chin. J. Mech. Eng. 2020, 33, 92. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Yang, K.; Zhang, H. A state-of-art review on the water-lubricated bearing. Tribol. Int. 2023, 180, 108276. [Google Scholar] [CrossRef]
- Lai, G.J.; Jiang, Z.L.; Liu, J.L.; Ma, R.F.; Zeng, F.M. Influence of propeller hydrodynamic force on alignmentcharacteristics of a motor driving shafting system. J. Ship Mech. 2023, 27, 294–301. [Google Scholar]
- Boedo, S.; Booker, J.F. Classical Bearing Misalignment and Edge Loading: A Numerical Study of Limiting Cases. J. Tribol. 2004, 126, 535–541. [Google Scholar] [CrossRef]
- Peng, E.; Huang, R. Tribology investigation in marine rubber stern tube bearing with consideration of friction-induced vibration. Proc. Inst. Mech. Eng. Part-J. Eng. Tribol. 2016, 230, 376–388. [Google Scholar] [CrossRef]
- Kim, Y.G.; Kim, U.K. Design and analysis of the propulsion shafting system in a ship with single stern tube bearing. J. Mar. Sci. Technol. 2020, 25, 536–548. [Google Scholar] [CrossRef]
- Li, S.; Dong, C.; Yuan, C.; Bai, X. Effects of TiO2 nano-particles on wear-resistance and vibration-reduction properties of a polymer for water-lubricated bearing. Wear 2023, 522, 204713. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H.; Priebsch, H.H.; Reich, F.M.; Witt, M.; Skiadas, A.; Knaus, O. Edge loading and running-in wear in dynamically loaded journal bearings. Tribol. Int. 2015, 92, 395–403. [Google Scholar] [CrossRef]
- Bhushan, B. Stick-Slip Induced Noise Generation in Water-Lubricated Compliant Rubber Bearings. J. Lubr. Technol. 1980, 102, 201–210. [Google Scholar] [CrossRef]
- Krauter, A.I. Generation of Squeal/Chatter in Water-Lubricated Elastomeric Bearings. J. Lubr. Technol. 1981, 103, 406–412. [Google Scholar] [CrossRef]
- Yao, S.; Yang, J.; Zhang, X.; Wang, J.; Rao, Z. Vibration and noise mechanism analysis and tests for water-lubrication rubber bearings. J. Vib. Shock 2011, 30, 214–216. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, G.; Wang, J.X. Analysis of Frictional Noise for Water Lubricated Rubber Bearings System. Adv. Mater. Res. 2010, 156–157, 607–610. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, X.; Yan, Z.; Liu, Z.; Zhao, X. Rubber/UHMWPE composites for stern tube bearings and its properties. Ordnance Mater. Sci. Eng. 2014, 37, 23–27. [Google Scholar] [CrossRef]
- Qin, W. Investigation on Friction Characteristics of the Water-Lubricated Rubber Bearings and the Induced Vibration of the Propeller Shafting Systems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2017. [Google Scholar]
- Wang, S.T.; Ou, Y.W.; Jin, Y.; Wang, L.; Deng, T.Y. Analysis of static characteristics of wave bearings considering elastic deformation. J. Ship Mech. 2020, 24, 1443–1541. [Google Scholar]
- Ouyang, W.; Yan, Q.; Kuang, J.; Jin, Y.; Peng, W. Simulation and experimental investigations on water-lubricated squeeze film damping stern bearing. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 54. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Wrona, S. The fluid-structure interaction lubrication performances of a novel bearing: Experimental and numerical study. Tribol. Int. 2023, 179, 108151. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H.P.; Yang, H.; Dai, L.; He, T. Analysis of tribology and dynamics performance of self-adaptationwater-lubricated stern bearing. Ship Sci. Technol. 2022, 44, 66–70. [Google Scholar]
- He, T.; Xie, Z.; Tao, X.; Yang, K.; Jiao, J.; Huang, M.; Ma, W. Analysis of the Tribological and Dynamic Performance of the Self-Adapting Water-Lubricated Stern Bearing. Lubricants 2022, 10, 245. [Google Scholar] [CrossRef]
- He, T.; Wang, J.; Yao, S.W.; Shi, J.H.; Zhang, Q.C.; Xu, H.Z.; Zhao, B. Tribological and Dynamic Performances of Composite Water Lubricated Bearing with Magnetic Support. J. Propuls. Technol. 2022, 43, 200401. [Google Scholar] [CrossRef]
- Ji, X.; Chen, Y.; Liu, H.; Yu, H.; Wei, C.; Yan, Z. Experimental Investigation on the Vibration And Noise Characteristics of the Vibration Damping Alloy Material. In Proceedings of the ASME International Mechanical Engineering Congress And Exposition, Pittsburgh, PA, USA, 9–15 November 2018; Volume 11. [Google Scholar]
- Alaneme, K.K.; Ubah, T.J.; Aikulola, E.O. On the material characteristics of Ni modified Cu32Zn10Sn shape memory alloys: Mechanical and damping behaviour in consideration. Mater. Today-Proc. 2022, 62, S73–S78. [Google Scholar] [CrossRef]
- Xiao, P.; Yang, W.; Jiang, K.; Yang, J.; Shi, W. Study on Vibration Reduction Performance of Gear Pairs Made by a High-Strength Fe-Mn Damping Alloy. Appl. Sci. 2022, 12, 3925. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, C.; Jiang, S.; Gao, Y.; Wan, Y.; Chen, Z. Tailoring good combinations among strength, ductility and damping capacity in a novel Mg-1.5Gd-1Zn damping alloy via hot extrusion. Mater. Sci. Eng.-Struct. Mater. Prop. Microstruct. Process. 2023, 871, 144827. [Google Scholar] [CrossRef]
- Kam, M.; Saruhan, H.; Ipekci, A. Experimental investigation of vibration damping capabilities of 3D printed metal/polymer composite sleeve bearings. J. Thermoplast. Compos. Mater. 2023, 36, 2505–2522. [Google Scholar] [CrossRef]
- Fang, C.; Liang, D.; Zheng, Y.; Lu, S. Seismic performance of bridges with novel SMA cable-restrained high damping rubber bearings against near-fault ground motions. Earthq. Eng. Struct. Dyn. 2022, 51, 44–65. [Google Scholar] [CrossRef]
- Huang, S.K.; Zhou, D.C.; Liu, J.H.; Teng, J.; Li, N. Amplitude Frequency Response Characteristics of Fe-based Damping Alloy Simple Beams under Forced Vibrations. Adv. Mater. Res. 2011, 328–330, 1072. [Google Scholar] [CrossRef]
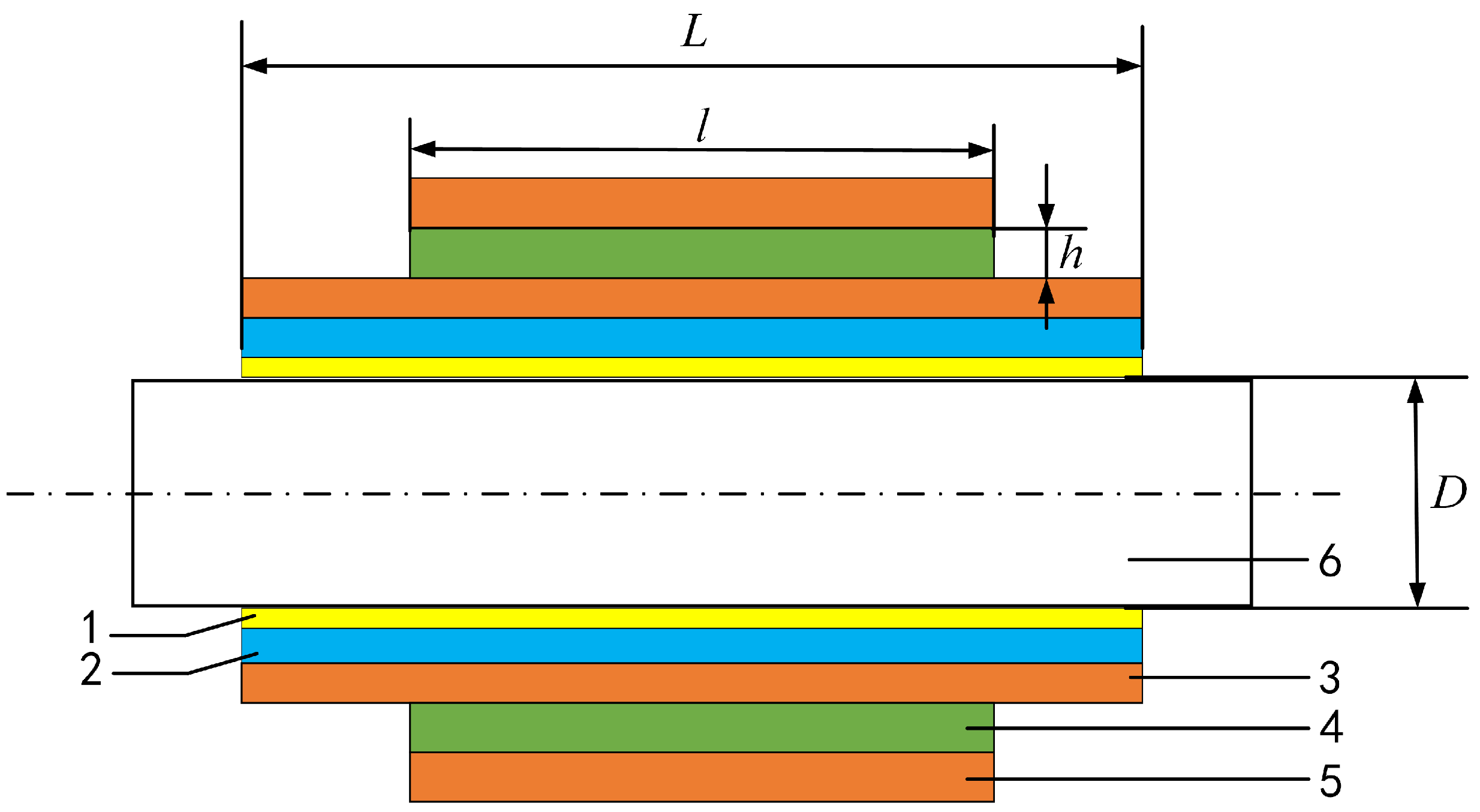



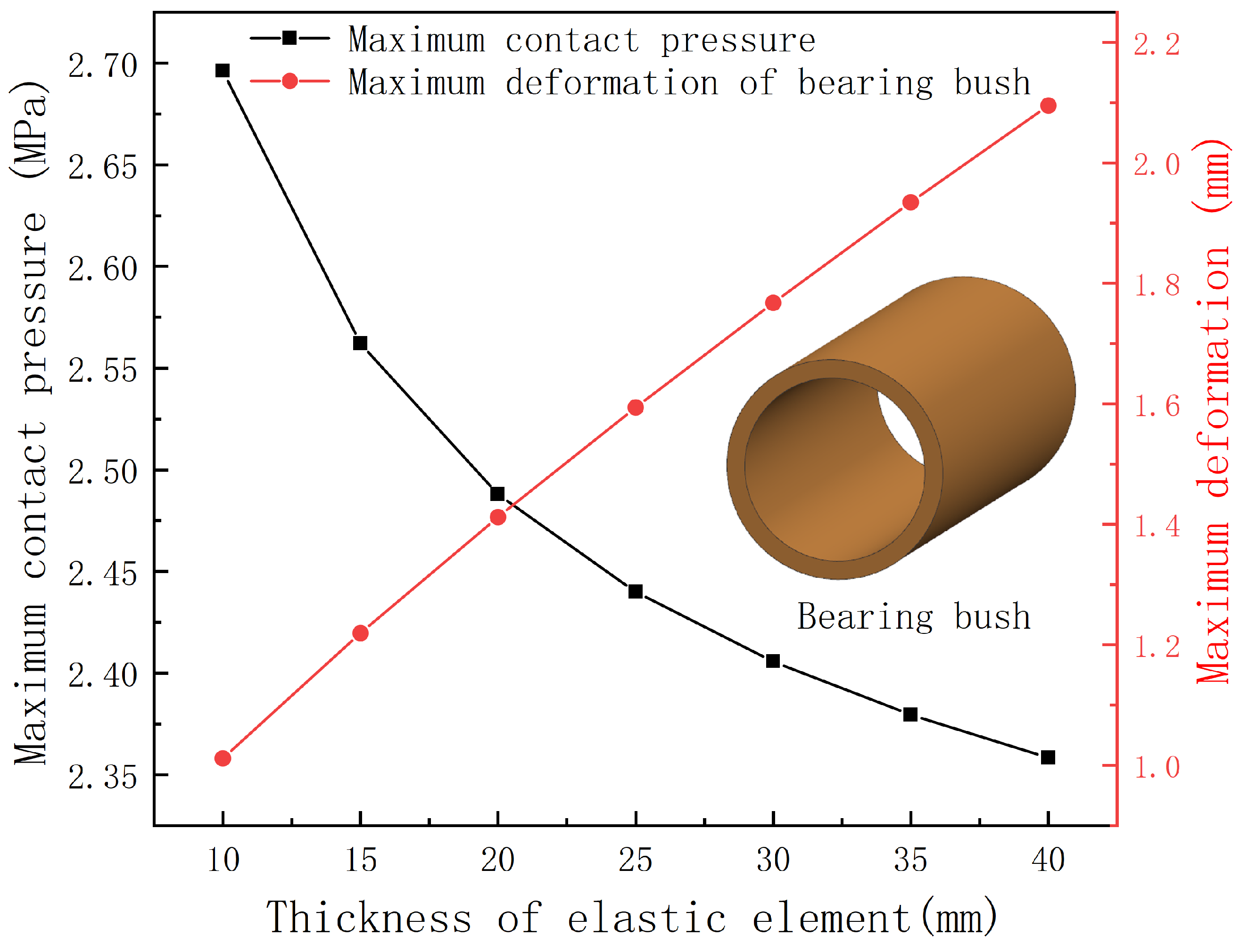
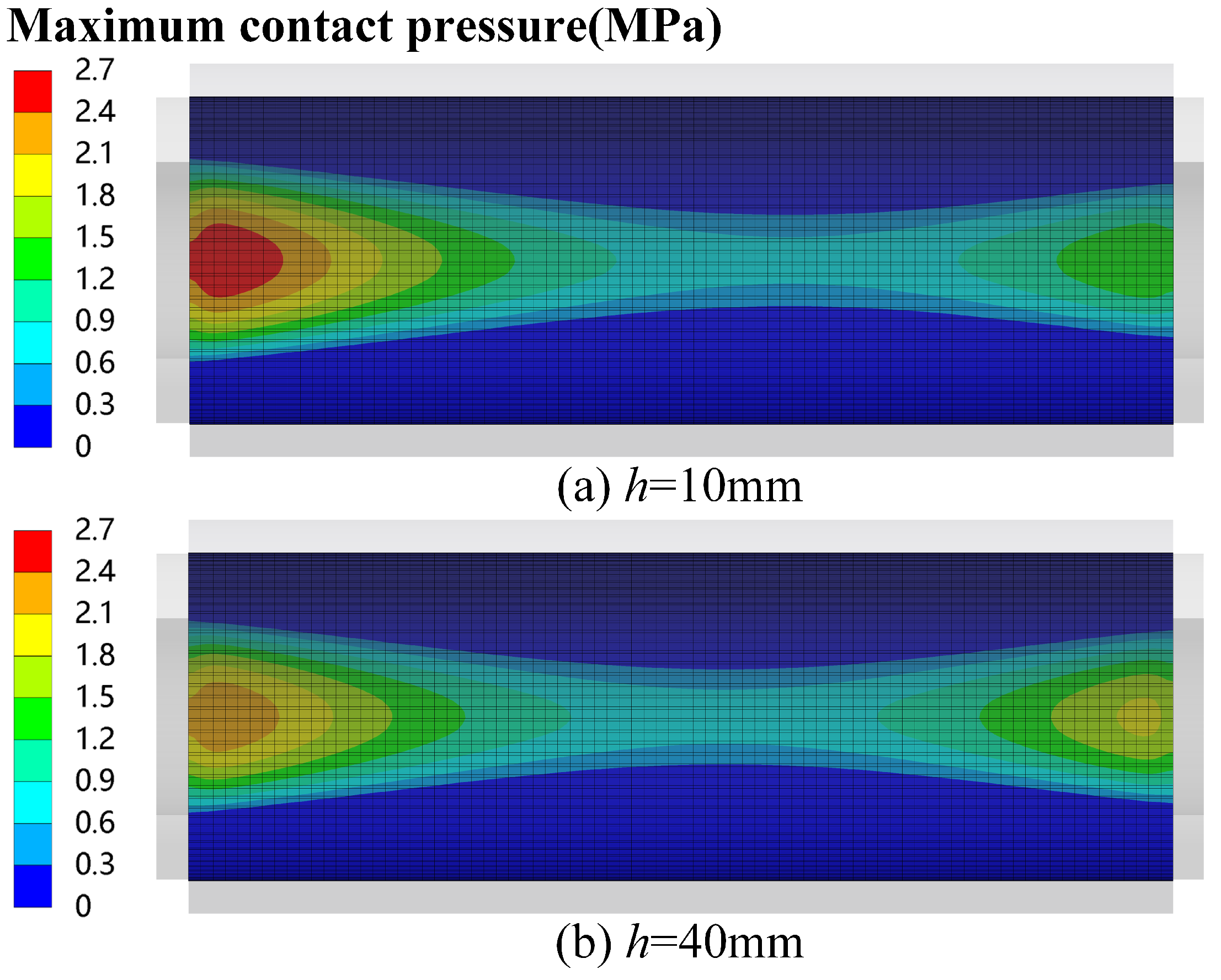



| Structure | Material | Young’s Modulus (MPa) | Poisson Ratio | Density (kg/m3) |
|---|---|---|---|---|
| Shaft | 35CrMo | 210,000 | 0.3 | 7850 |
| Bearing bush | Synthetic rubber | 305 | 0.37 | 2200 |
| Bearing | Structural steel | 200,000 | 0.3 | 7850 |
| Damping alloy | Modulated Mu-Cu alloy | 90,000 | 0.27 | 7330 |
| Elastic element | Composite silicone rubber | 6 | 0.27 | 1000 |
| Rank | Traditional Design | Adaptive Design |
|---|---|---|
| Positive Rotation | Positive Rotation | |
| 1 | 313.82 | 330.97 |
| 2 | 320.13 | 333.05 |
| 3 | 1068.2 | 192.65 |
| 4 | 1101.7 | 1127 |
| 5 | 4011.6 | 1177.4 |
| 6 | 4270.5 | 2465.1 |
| Speed (mm/s) | Acceleration (mm/s2) | Displacement (mm) | |
|---|---|---|---|
| Adaptive Design | |||
| Traditional Design | |||
| Reduction | 58.82% | 58.90% | 58.86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhou, Y.; He, T.; Xia, Y. The Utilization of a Damping Structure in the Development of Self-Adaptive Water-Lubricated Stern Bearings. Lubricants 2024, 12, 32. https://doi.org/10.3390/lubricants12020032
Liu Y, Zhou Y, He T, Xia Y. The Utilization of a Damping Structure in the Development of Self-Adaptive Water-Lubricated Stern Bearings. Lubricants. 2024; 12(2):32. https://doi.org/10.3390/lubricants12020032
Chicago/Turabian StyleLiu, Yong, Yingzhi Zhou, Tao He, and Yang Xia. 2024. "The Utilization of a Damping Structure in the Development of Self-Adaptive Water-Lubricated Stern Bearings" Lubricants 12, no. 2: 32. https://doi.org/10.3390/lubricants12020032
APA StyleLiu, Y., Zhou, Y., He, T., & Xia, Y. (2024). The Utilization of a Damping Structure in the Development of Self-Adaptive Water-Lubricated Stern Bearings. Lubricants, 12(2), 32. https://doi.org/10.3390/lubricants12020032






