Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity
Abstract
1. Introduction
2. Modeling and Verification for Lubrication Flow Field
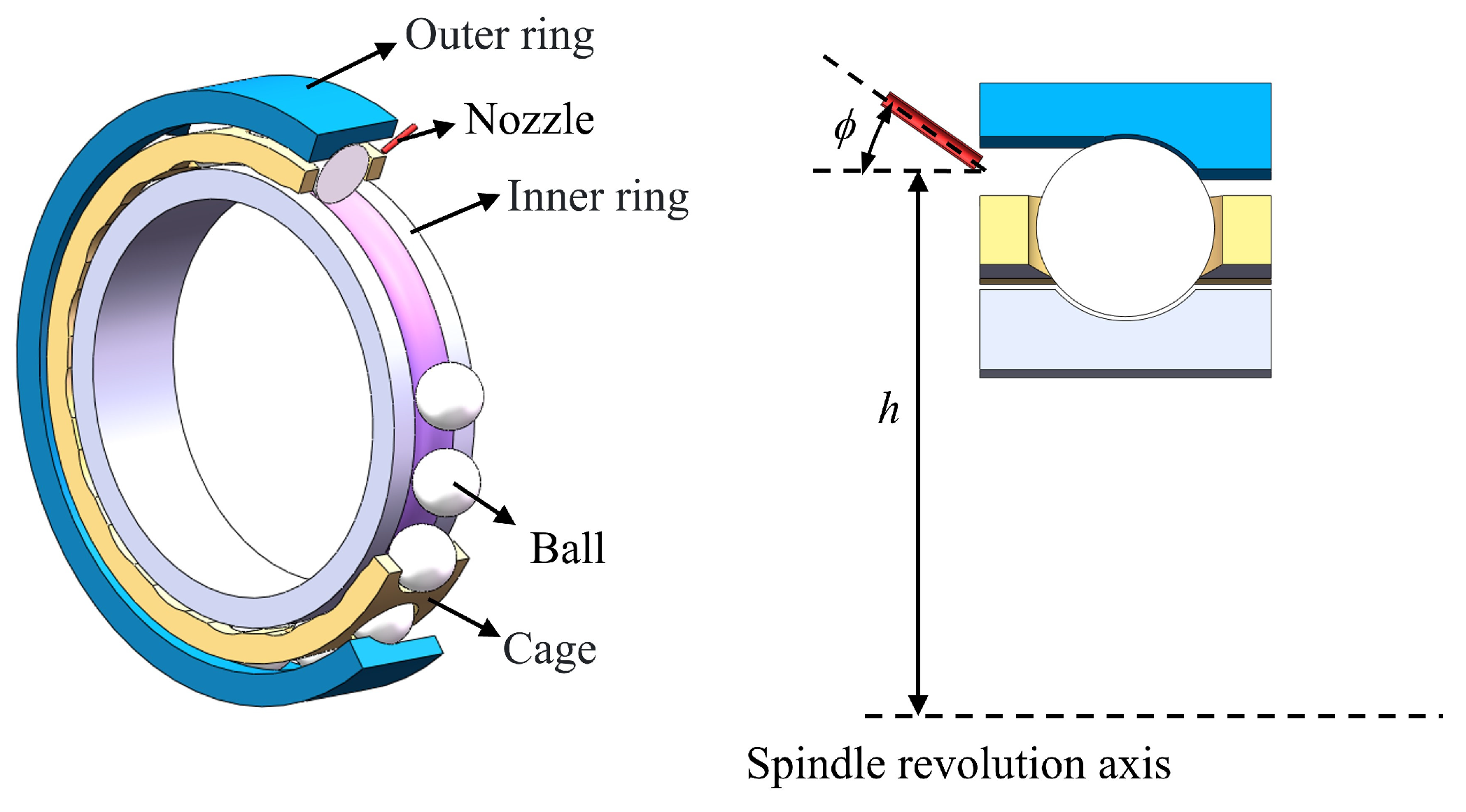
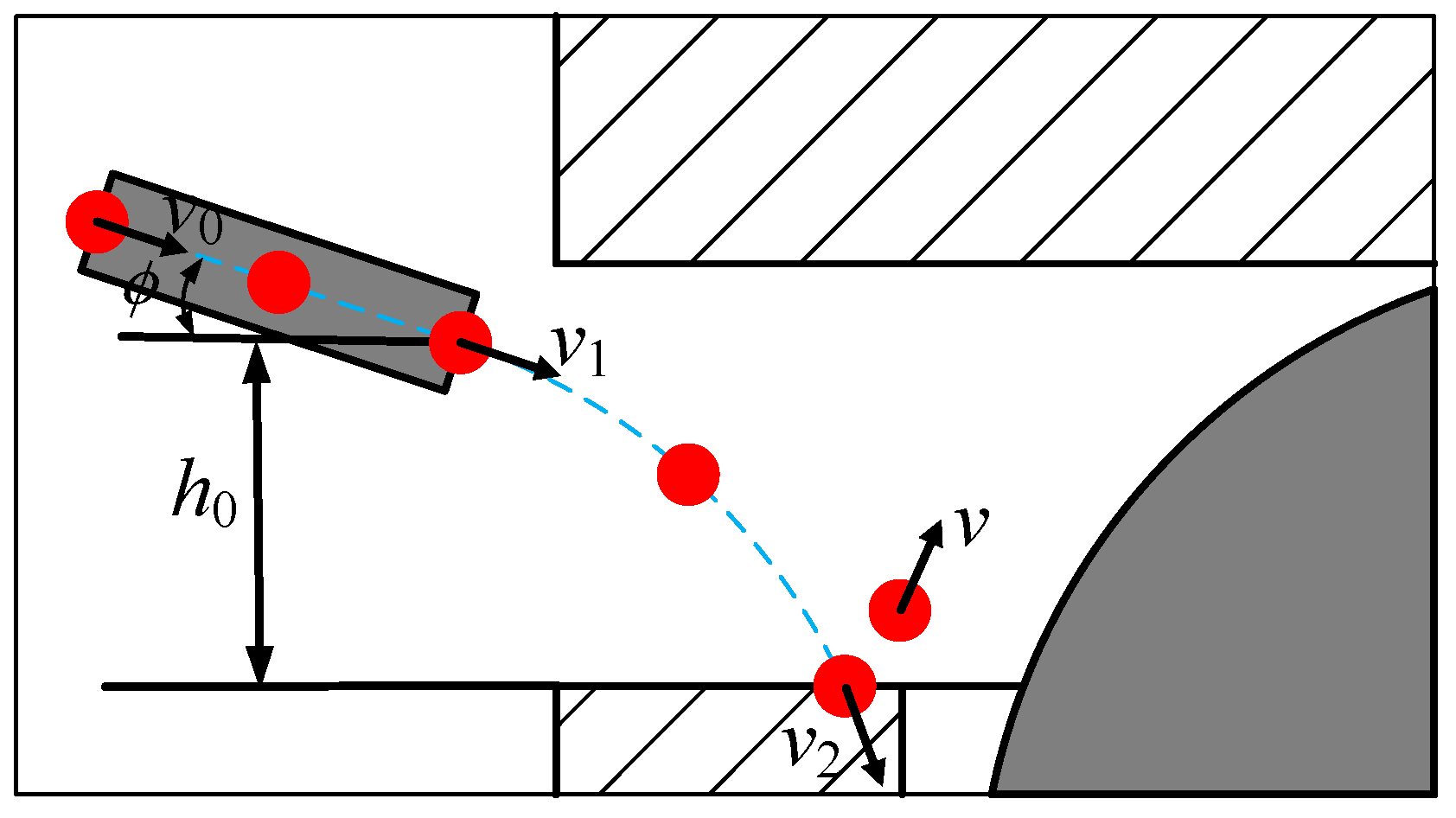
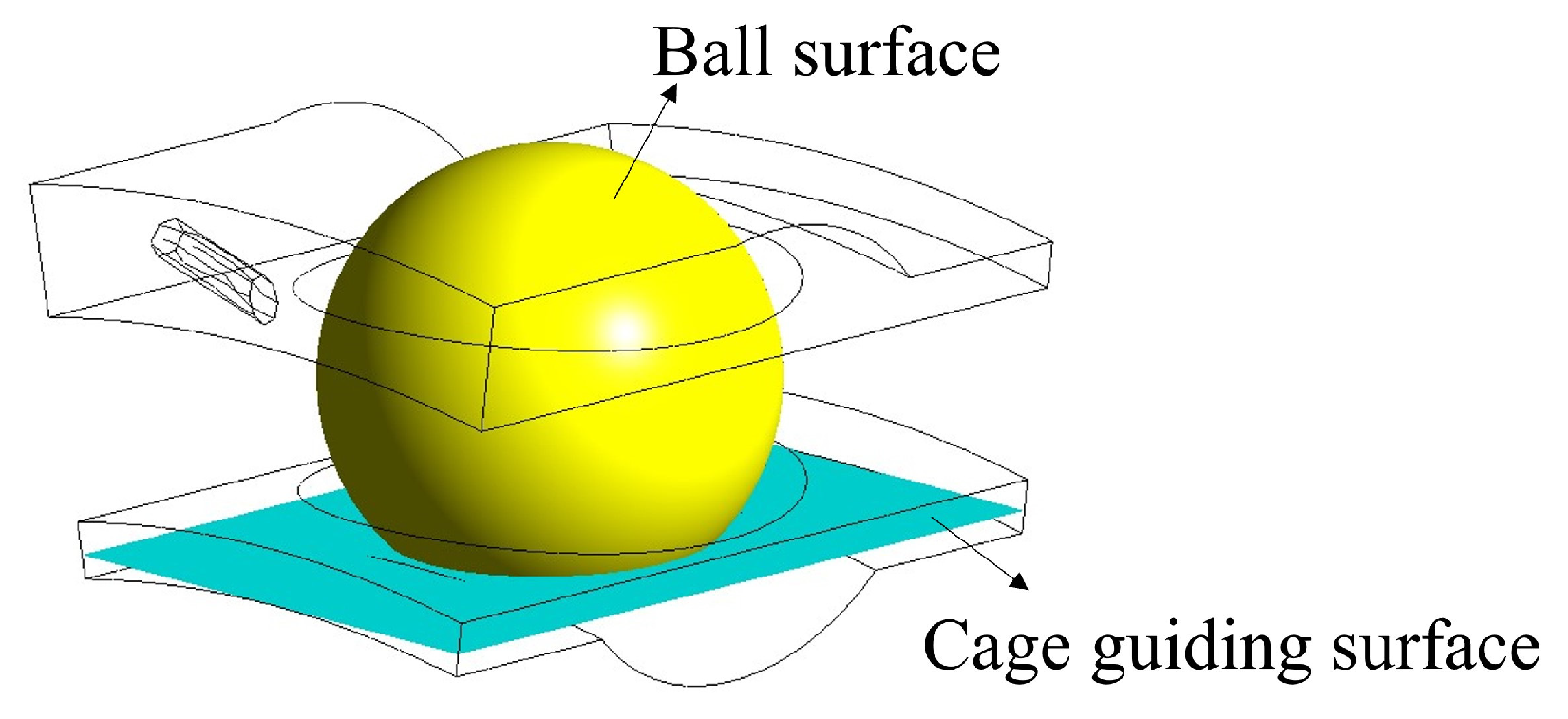
2.1. Oil-Jet Lubricated Ball Bearing and Its Motion Relationship
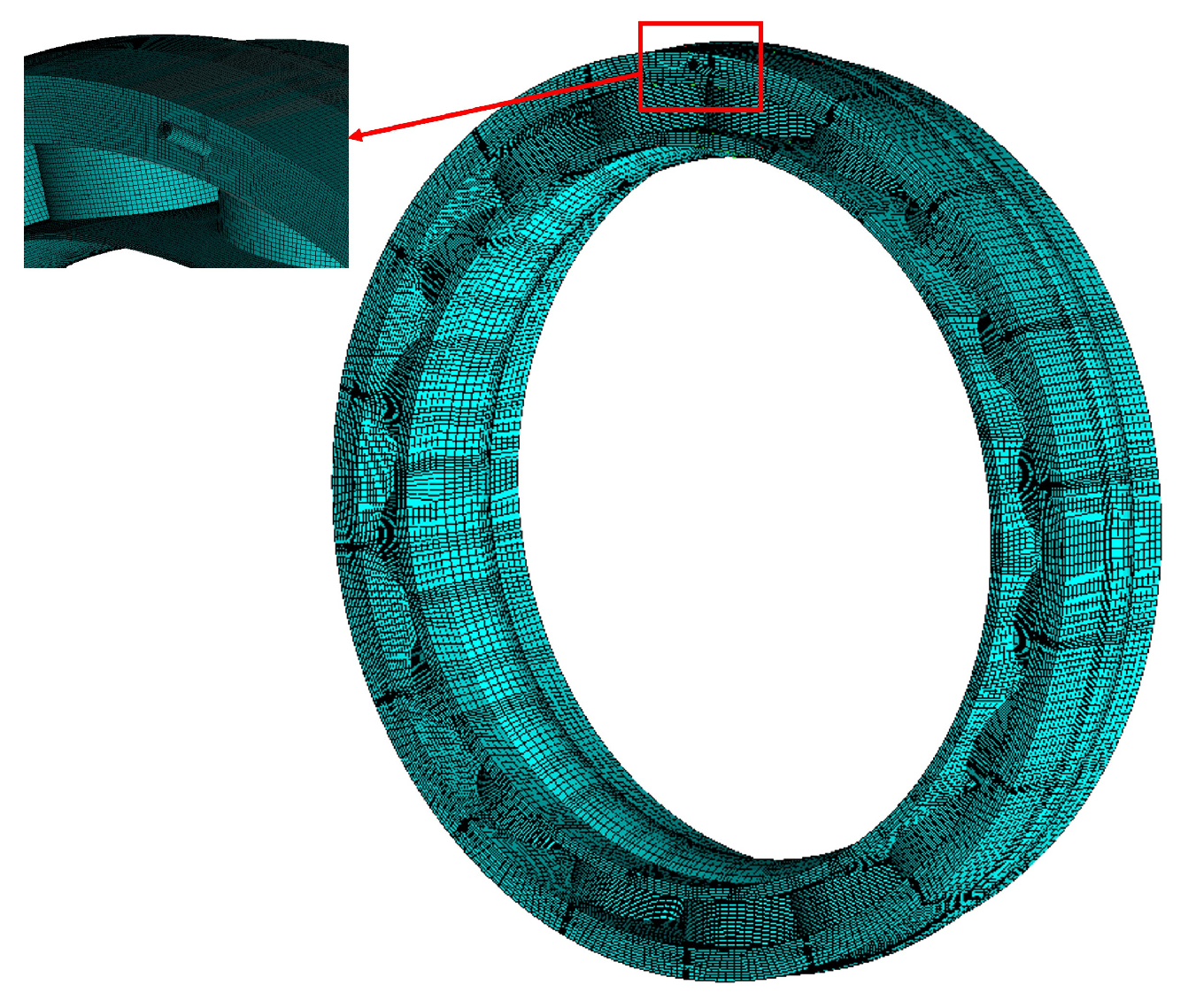
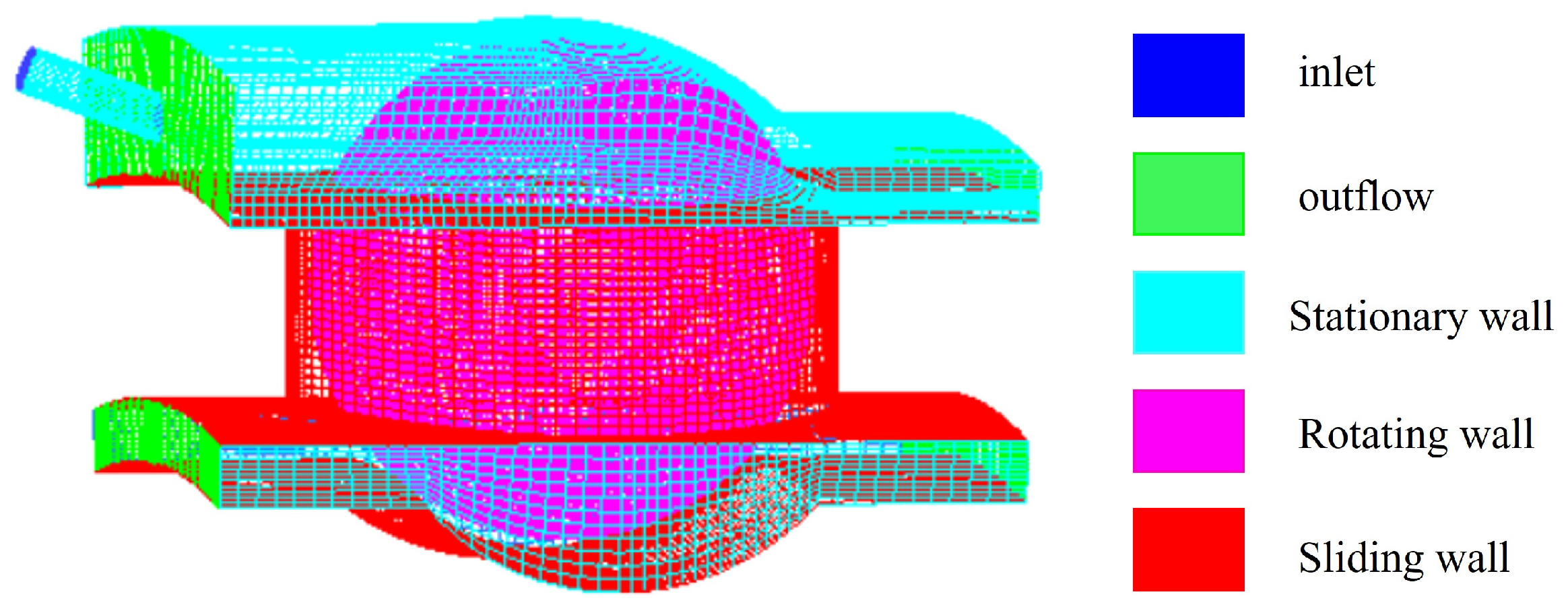
2.2. CFD Model of the Bearing Cavity Considering the Characteristics of Nozzle Position
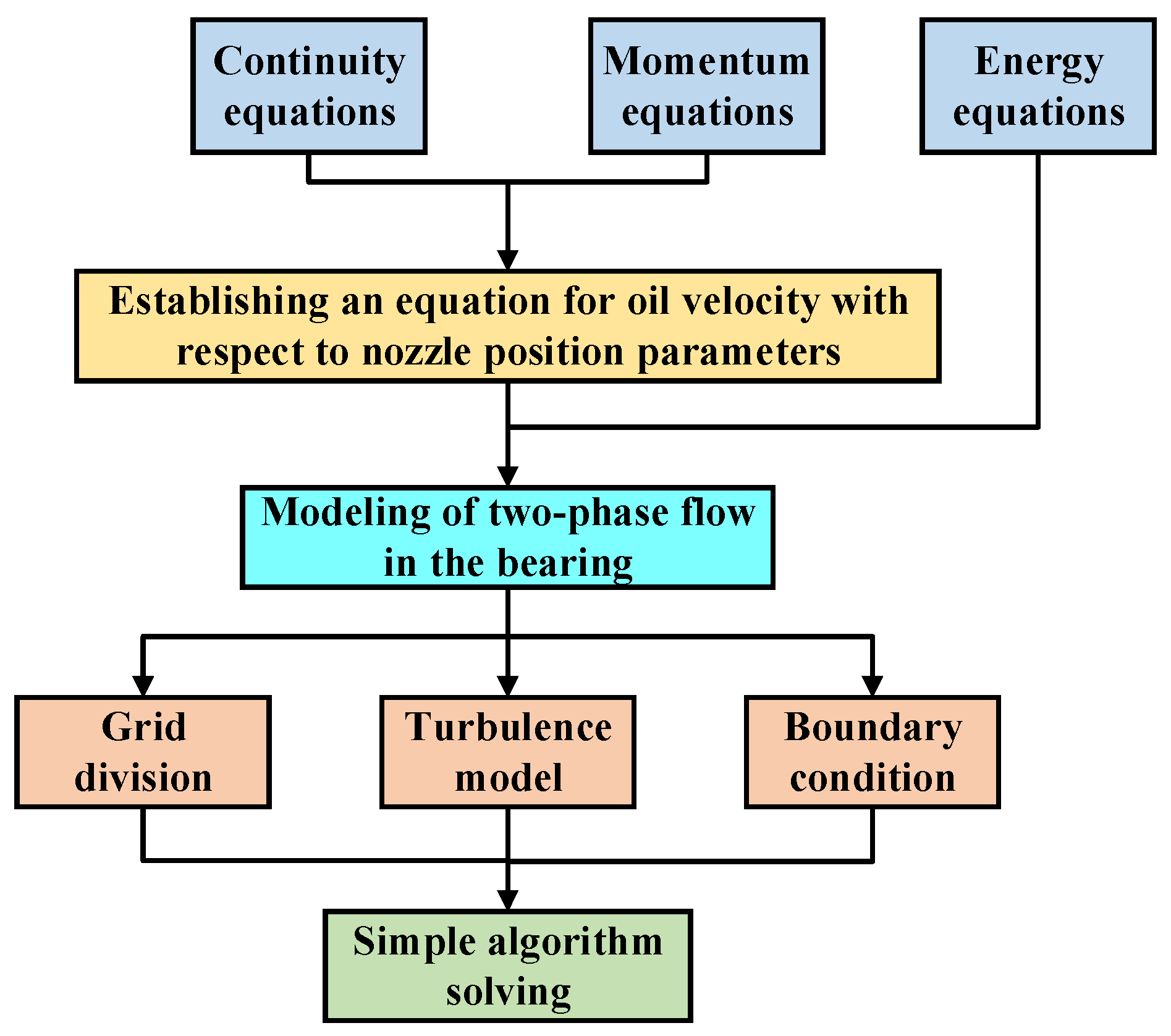
2.2.1. The Two-Phase Flow Model
2.2.2. Solution Method
2.3. Test Rig for Investigating the Lubricant Distribution in the Angular Contact Ball Bearing Cavity
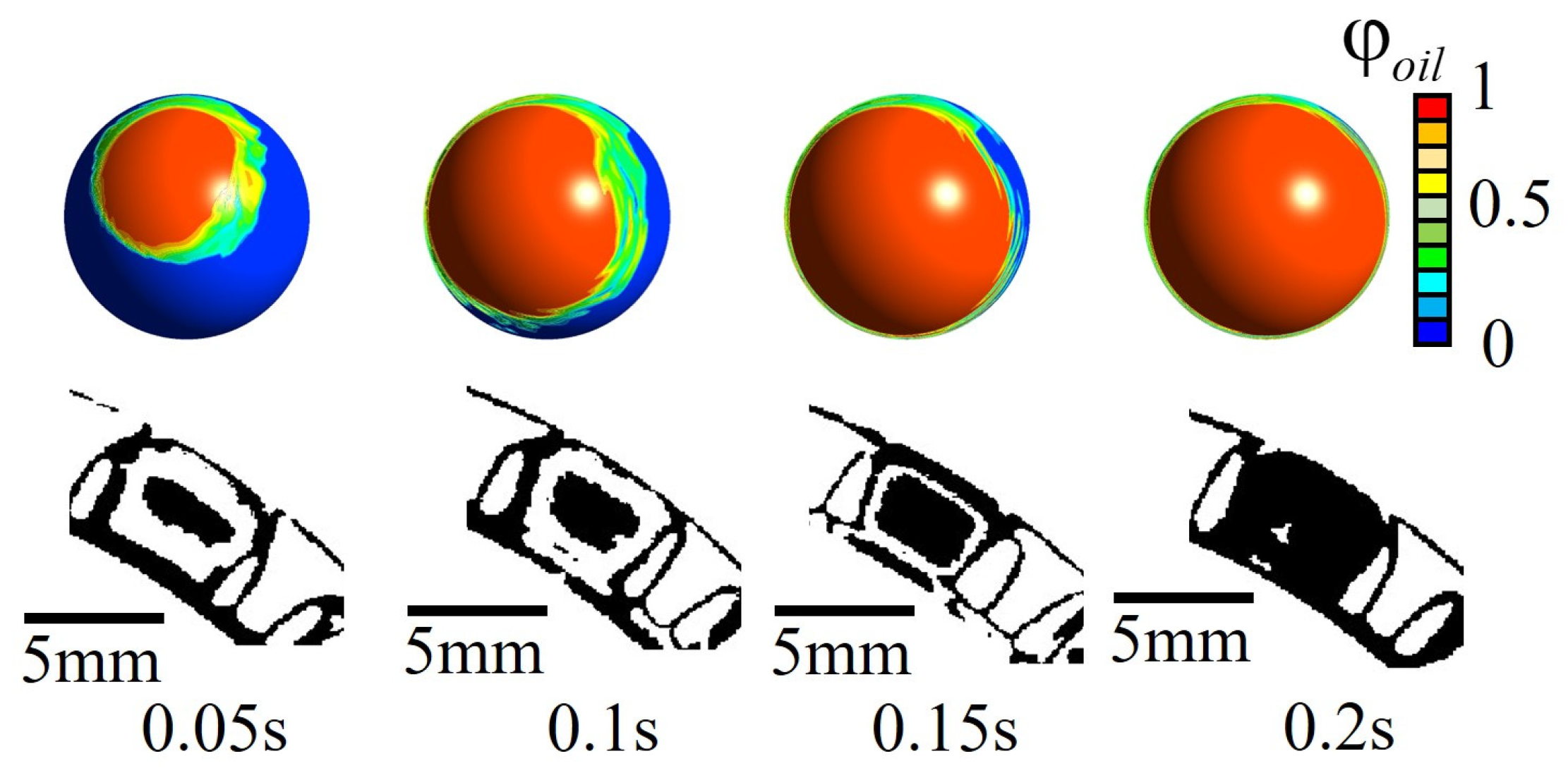
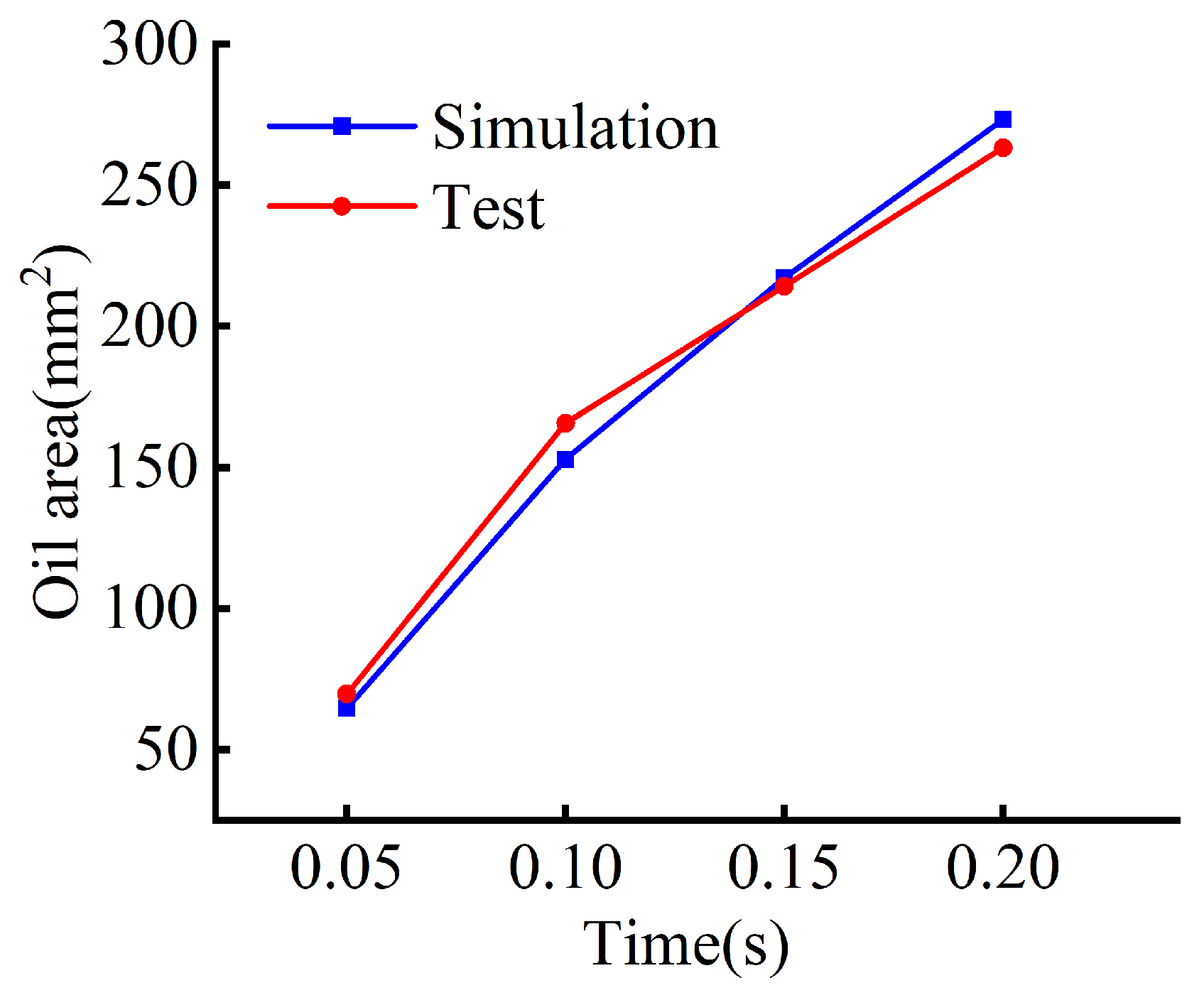
2.4. Comparative Verification
3. Influence of Nozzle Positions on Lubricant Distribution and Its Optimization
3.1. Influence of Nozzle Positions on Lubricant Distribution
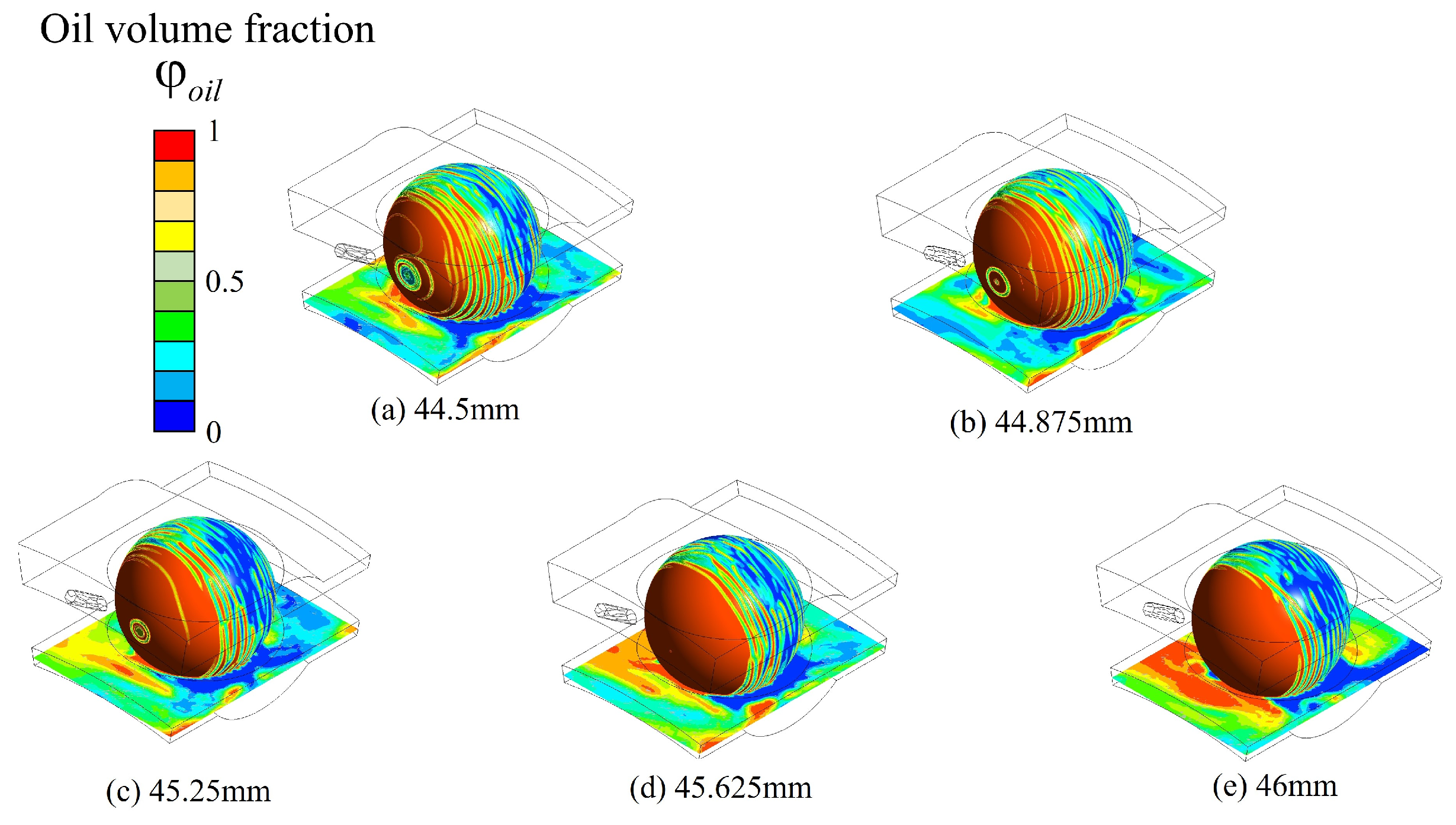
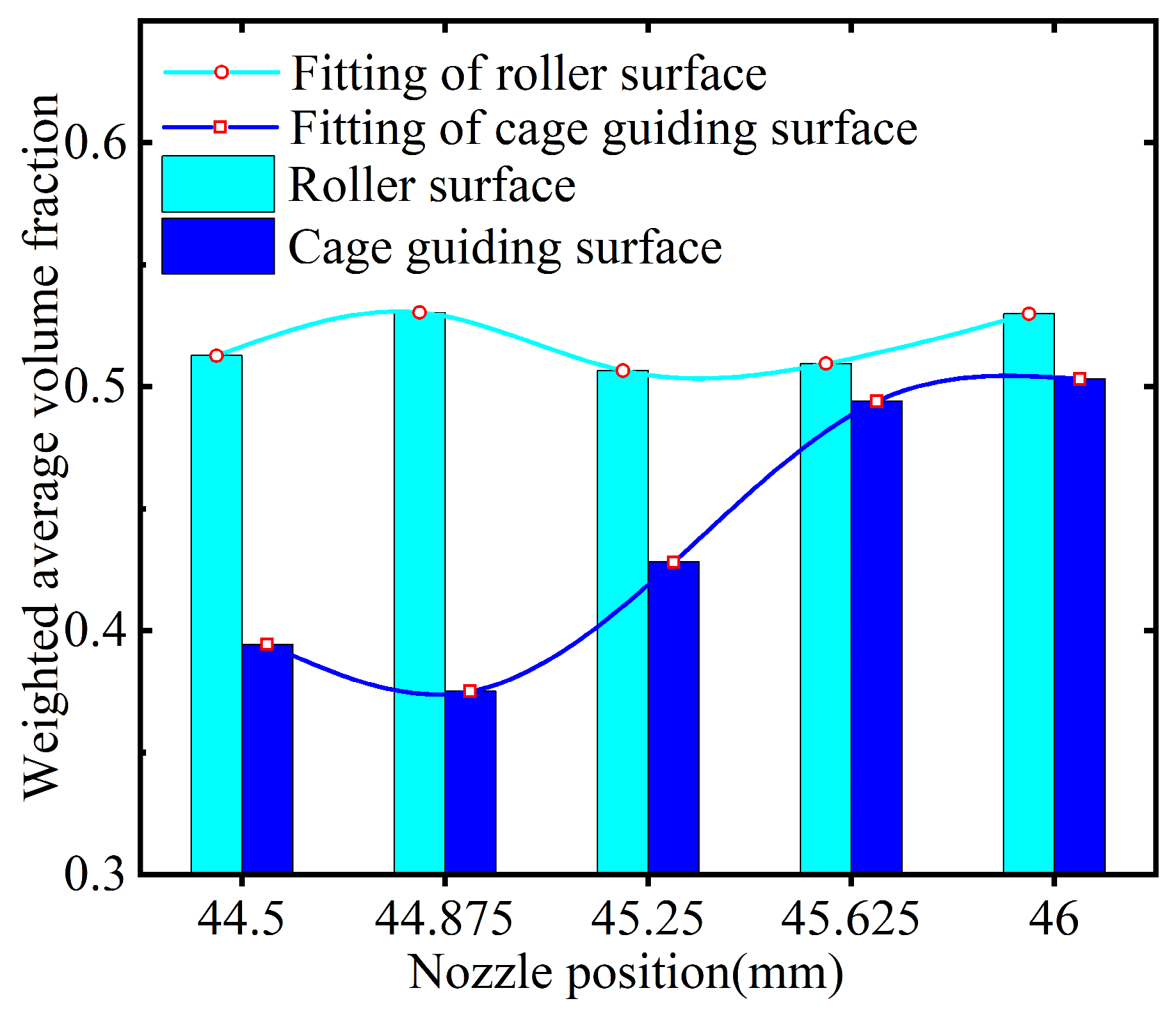
3.1.1. Influence of Nozzle Height on Lubricant Distribution
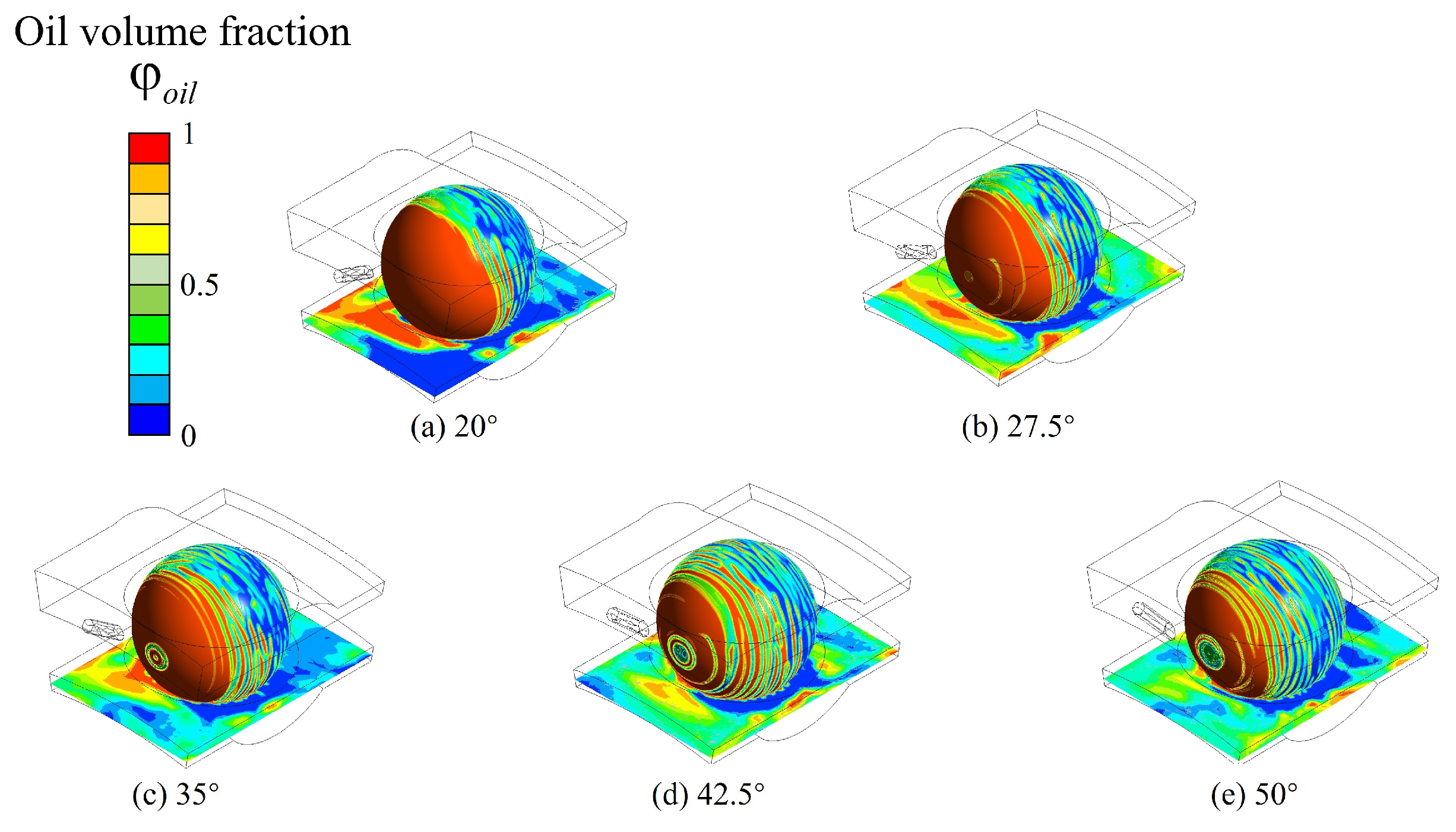
3.1.2. Influence of Nozzle Angle on Lubricant Distribution
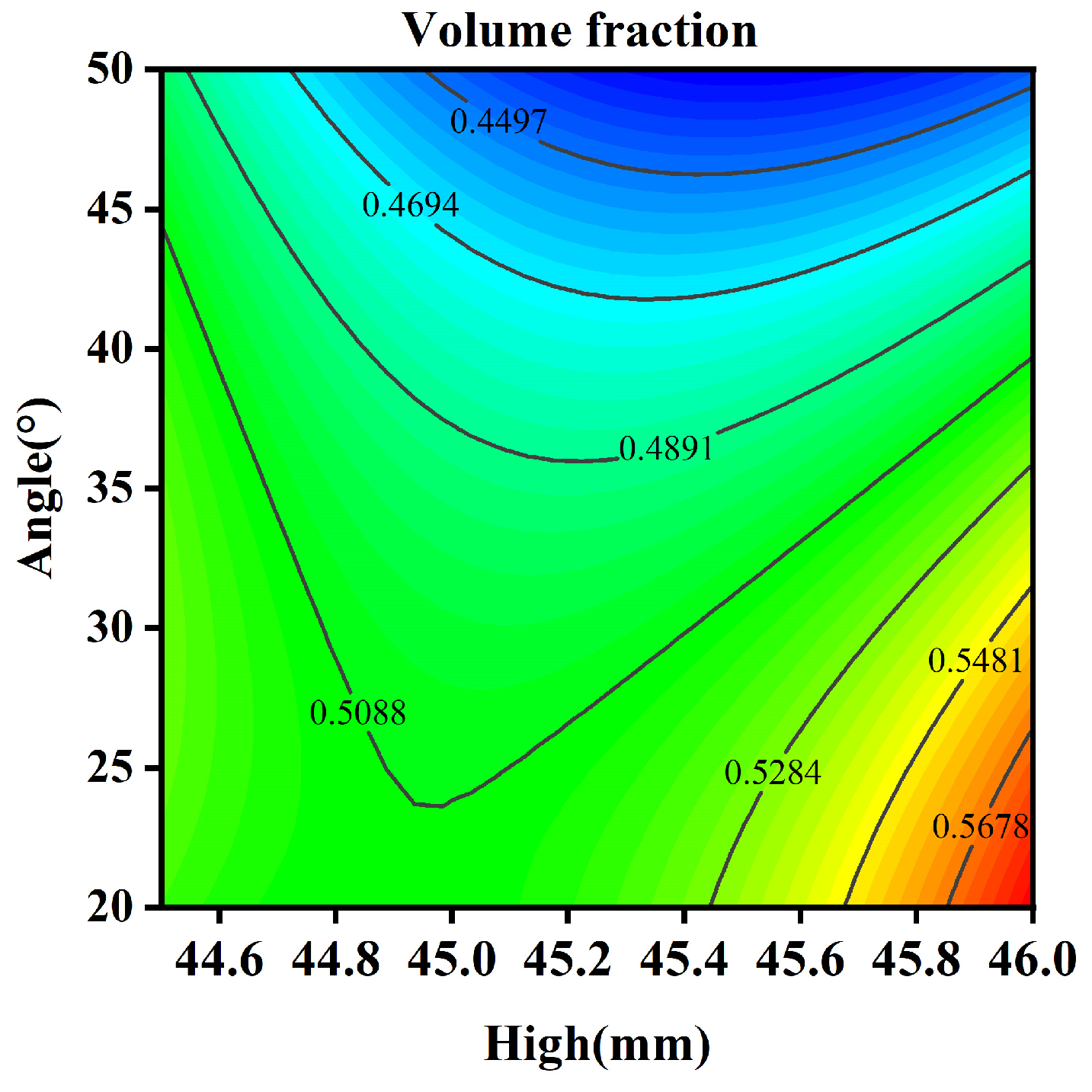
3.2. Optimization of the Nozzle Position with the Response Surface Methodology
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, W.; Nelias, D.; Li, K.; Liu, Z.; Lyu, Y. A multiphase computational study of oil distribution inside roller bearings with under-race lubrication. Tribol. Int. 2019, 140, 105862. [Google Scholar] [CrossRef]
- Yan, K.; Wang, Y.; Zhu, Y.; Hong, J.; Zhai, Q. Investigation on heat dissipation characteristic of ball bearing cage and inside cavity at ultra high rotation speed. Tribol. Int. 2016, 93, 470–481. [Google Scholar] [CrossRef]
- Yan, B.; Dong, L.; Yan, K.; Chen, F.; Zhu, Y.; Wang, D. Effects of oil-air lubrication methods on the internal fluid flow and heat dissipation of high-speed ball bearings. Mech. Syst. Signal Process. 2021, 151, 107409. [Google Scholar] [CrossRef]
- Bao, H.; Hou, X.; Lu, F. Analysis of Oil-Air Two-Phase Flow Characteristics inside a Ball Bearing with Under-Race Lubrication. Processes 2020, 8, 1223. [Google Scholar] [CrossRef]
- Ge, L.; Yan, K.; Wang, C.; Zhu, Y.; Hong, J. A novel method for bearing lubrication enhancement via the inner ring groove structure. J. Phys. Conf. Ser. 2021, 1820, 012092. [Google Scholar] [CrossRef]
- Chen, H.; Liang, H.; Wang, W.; Zhang, S. Investigation on the oil transfer behaviors and the air-oil interfacial flow patterns in a ball bearing under different capillary conditions. Friction 2022, 11, 228–245. [Google Scholar] [CrossRef]
- Shan, W.; Chen, Y.; Huang, J.; Wang, X.; Han, Z.; Wu, K. A multiphase flow study for lubrication characteristics on the internal flow pattern of ball bearing. Results Eng. 2023, 20, 101429. [Google Scholar] [CrossRef]
- Oh, I.-S.; Kim, D.; Hong, S.-W.; Kim, K. Three-dimensional air flow patterns within a rotating ball bearing. Adv. Sci. Lett. 2013, 19, 2180–2183. [Google Scholar] [CrossRef]
- Liu, J.; Ni, H.; Xu, Z.; Pan, G. A simulation analysis for lubricating characteristics of an oil-jet lubricated ball bearing. Simul. Model. Pract. Theory 2021, 113, 102371. [Google Scholar] [CrossRef]
- Peterson, W.; Russell, T.; Sadeghi, F.; Berhan, M.T. Experimental and analytical investigation of fluid drag losses in rolling element bearings. Tribol. Int. 2021, 161, 107106. [Google Scholar] [CrossRef]
- Aidarinis, J.; Missirlis, D.; Yakinthos, K.; Goulas, A. CFD modeling and LDA measurements for the air-flow in an aero engine front bearing chamber. J. Eng. Gas Turbines Power 2011, 133, 082504. [Google Scholar] [CrossRef]
- Maccioni, L.; Chernoray, V.G.; Mastrone, M.N.; Bohnert, C.; Concli, F. Study of the impact of aeration on the lubricant behavior in a tapered roller bearing: Innovative numerical modelling and validation via particle image velocimetry. Tribol. Int. 2022, 165, 107301. [Google Scholar] [CrossRef]
- Maccioni, L.; Chernoray, V.G.; Bohnert, C.; Concli, F. Particle Image Velocimetry measurements inside a tapered roller bearing with an outer ring made of sapphire: Design and operation of an innovative test rig. Tribol. Int. 2022, 165, 107313. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, Y.; Wang, W. Influence of the cage on the migration and distribution of lubricating oil inside a ball bearing. Friction 2021, 10, 1035–1045. [Google Scholar] [CrossRef]
- Arya, U.; Peterson, W.; Sadeghi, F.; Meinel, A.; Grillenberger, H. Investigation of oil flow in a ball bearing using Bubble Image Velocimetry and CFD modeling. Tribol. Int. 2023, 177, 107968. [Google Scholar] [CrossRef]
- Wen, B.; Li, Y.; Wang, M.; Yang, Y. Measurement for Lubricant Distribution in an Angular Contact Ball Bearing and Its Influence Investigation. Lubricants 2023, 11, 63. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Liang, H.; Ge, X. Observation of the oil flow in a ball bearing with a novel experiment method and simulation. Tribol. Int. 2022, 174, 107731. [Google Scholar] [CrossRef]
- Noda, T.; Shibasaki, K.; Miyata, S.; Taniguchi, M. X-Ray CT Imaging of Grease Behavior in Ball Bearing and Numerical Validation of Multi-Phase Flows Simulation. Tribol. Online 2020, 15, 36–44. [Google Scholar] [CrossRef]
- Kazumi, S.; Yusuke, A.; Yoshimu, I.; Nobuharu, K.; Yoshihiro, M. Observation of Grease Fluidity in a Ball Bearing Using Neutron Imaging Technology. Tribol. Online 2021, 16, 146–150. [Google Scholar]
- Franken, M.J.Z.; Chennaoui, M.; Wang, J. Mapping of Grease Migration in High-Speed Bearings Using a Technique Based on Fluorescence Spectroscopy. Tribol. Trans. 2017, 60, 789–793. [Google Scholar] [CrossRef]
- Sánchez-González, R.; North, S.W. Nitric oxide laser-induced fluorescence imaging methods and their application to study high-speed flows. In Frontiers and Advances in Molecular Spectroscopy; Elsevier: Amsterdam, The Netherlands, 2018; pp. 599–630. [Google Scholar]
- Meinhart, C.D.; Wereley, S.T.; Santiago, J.G. PIV measurements of a microchannel flow. Exp. Fluids 1999, 27, 414–419. [Google Scholar] [CrossRef]
- Mastrone, M.N.; Hartono, E.A.; Chernoray, V.; Concli, F. Oil distribution and churning losses of gearboxes: Experimental and numerical analysis. Tribol. Int. 2020, 151, 106496. [Google Scholar] [CrossRef]
- Hu, J.; Xun, B.; Zhang, X.-M.; Zhang, Q.-Y.; Li, G.-W. Design and research of new-type nozzle structure based on oil–air lubrication. Meccanica 2023, 59, 1–18. [Google Scholar] [CrossRef]
- Yan, K.; Zhang, J.; Hong, J.; Wang, Y.; Zhu, Y. Structural optimization of lubrication device for high speed angular contact ball bearing based on internal fluid flow analysis. Int. J. Heat Mass Transf. 2016, 95, 540–550. [Google Scholar] [CrossRef]
- Li, S.; Deng, G.; Hu, Y.; Yu, M.; Ma, T. Optimization of structural parameters of pilot-operated control valve based on CFD and orthogonal method. Results Eng. 2024, 21, 101914. [Google Scholar] [CrossRef]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S. Jet cooling for rolling bearings: Flow visualization and temperature distribution. Appl. Therm. Eng. 2016, 105, 217–224. [Google Scholar] [CrossRef]
- Wu, W.; Hu, J.; Yuan, S.; Hu, C. Numerical and experimental investigation of the stratified air-oil flow inside ball bearings. Int. J. Heat Mass Transf. 2016, 103, 619–626. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, J.; Hong, J.; Liu, C. A comparative study on simulation and experiment of oil-air lubrication unit for high speed bearing. Ind. Lubr. Tribol. 2016, 68, 325–335. [Google Scholar] [CrossRef]
- Samokhinv, N. Mathematical Models in Boundary Layer Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Liu, J.; Ni, H.; Zhou, R.; Li, X.; Xing, Q.; Pan, G. A Simulation Analysis of Ball Bearing Lubrication Characteristics Considering the Cage Clearance. J. Tribol. 2023, 145, 044301. [Google Scholar] [CrossRef]
- Hu, J.; Wu, W.; Wu, M.; Yuan, S. Numerical investigation of the air–oil two-phase flow inside an oil-jet lubricated ball bearing. Int. J. Heat Mass Transf. 2014, 68, 85–93. [Google Scholar] [CrossRef]
- Kaur, H.; Rahi, D.K. Response surface methodology-based optimisation of chitin production and its antioxidant activity from Aspergillus niger. Heliyon 2024, 10, e25646. [Google Scholar] [CrossRef] [PubMed]
- Rao, B.R.; Tiwari, R.J. Optimum design of rolling element bearings using genetic algorithms. Mech. Mach. Theory 2007, 42, 233–250. [Google Scholar]



| Item | Symbol | Unit | Value |
|---|---|---|---|
| Diameter of inner ring | d | mm | 65 |
| Diameter of outer ring | D | mm | 100 |
| Diameter of ball | mm | 11 | |
| Number of balls | Z | No. | 18 |
| Contact angle | ° | 15 | |
| Width of ring | B | mm | 18 |
| Parameter | Symbol | Unit | Value |
|---|---|---|---|
| temperature | t | K | 313.15 |
| density | kg/m3 | 876 | |
| Kinematic viscosity | 30 | ||
| Specific heat | c | 1.96 |
| Factors | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Nozzle height h/mm | 44.5 | 45.25 | 46 |
| Nozzle angle /° | 20 | 35 | 50 |
| Number | Factors | The Weighted Average of the Oil Phase Volume Fraction on the Ball Surface | The Weighted Average of the Oil Phase Volume Fraction on the Cage Guiding Surface | |
|---|---|---|---|---|
| h | ||||
| 1 | 44.5 | 20 | 0.52566 | 0.48531 |
| 2 | 44.5 | 35 | 0.51269 | 0.39439 |
| 3 | 44.5 | 50 | 0.4991 | 0.30932 |
| 4 | 45.25 | 20 | 0.50794 | 0.41052 |
| 5 | 45.25 | 35 | 0.50656 | 0.42806 |
| 6 | 45.25 | 50 | 0.43067 | 0.29146 |
| 7 | 46 | 20 | 0.59107 | 0.37645 |
| 8 | 46 | 35 | 0.52987 | 0.50311 |
| 9 | 46 | 50 | 0.44649 | 0.33966 |
| Source | Sum of Squares | df | Mean Square | F | p-Value |
|---|---|---|---|---|---|
| Model | 0.016 | 3 | 5.441 × 10−3 | 23.05 | 0.0023 |
| 0.010 | 1 | 0.010 | 43.57 | 0.0012 | |
| 3.482 × 10−3 | 1 | 3.482 × 10−3 | 14.75 | 0.0121 | |
| h2 | 2.557 × 10−3 | 1 | 2.557 × 10−3 | 10.83 | 0.0217 |
| Residual | 1.180 × 10−3 | 5 | 2.360 × 10−4 | ||
| Cor Total | 0.018 | 8 |
| Source | Sum of Squares | df | Mean Square | F | p-Value |
|---|---|---|---|---|---|
| Model | 0.035 | 5 | 7.049 × 10−3 | 2.87 | 0.2073 |
| h | 1.520 × 10−4 | 1 | 1.520 × 10−4 | 0.062 | 0.8196 |
| 0.018 | 1 | 0.018 | 7.47 | 0.0717 | |
| 4.844 × 10−3 | 1 | 4.844 × 10−3 | 1.97 | 0.2548 | |
| h2 | 1.220 × 10−3 | 1 | 1.220 × 10−3 | 0.5 | 0.5318 |
| 0.011 | 1 | 0.011 | 4.35 | 0.1284 | |
| Residual | 7.369 × 10−3 | 3 | 2.456 × 10−3 | ||
| Cor Total | 0.043 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, B.; Li, Y.; Li, Y.; Wang, M.; Zhai, J. Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity. Lubricants 2024, 12, 419. https://doi.org/10.3390/lubricants12120419
Wen B, Li Y, Li Y, Wang M, Zhai J. Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity. Lubricants. 2024; 12(12):419. https://doi.org/10.3390/lubricants12120419
Chicago/Turabian StyleWen, Baogang, Yuanyuan Li, Yemin Li, Meiling Wang, and Jingyu Zhai. 2024. "Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity" Lubricants 12, no. 12: 419. https://doi.org/10.3390/lubricants12120419
APA StyleWen, B., Li, Y., Li, Y., Wang, M., & Zhai, J. (2024). Influence and Optimization of Nozzle Position on Lubricant Distribution in an Angular Contact Ball Bearing Cavity. Lubricants, 12(12), 419. https://doi.org/10.3390/lubricants12120419





