On the Nucleation Rate of Confinement-Induced Liquidlike-to-Solidlike Phase Transitions
Abstract
1. Introduction
2. Simulation Details
3. Nucleation Rate Calculations
3.1. Mean First-Passage Time (MFPT) Method
3.2. Direct Observation Method (DOM)
3.3. Yasuoka–Matsumoto (YM) Method
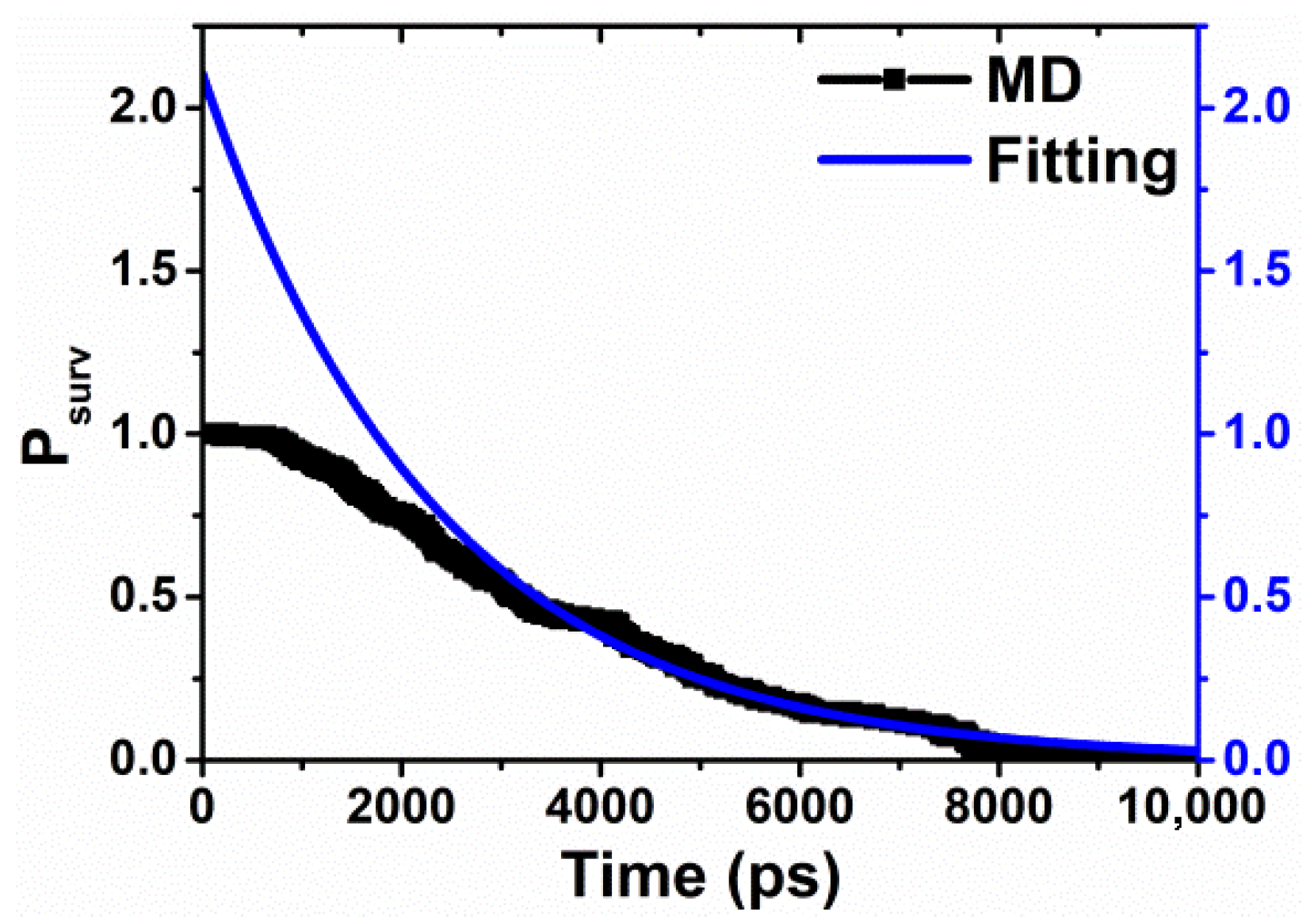
4. Survival Probability (SP) Method
5. Estimation of the Free Energy Profile of Solidification
6. Summary and Further Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Israelachvili, J.N.; McGuiggan, P.M.; Homola, A.M. Dynamic properties of molecularly thin liquid films. Science 1988, 240, 189–191. [Google Scholar] [CrossRef] [PubMed]
- Van Alsten, J.; Granick, S. Molecular tribometry of ultrathin liquid films. Phys. Rev. Lett. 1988, 61, 2570. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.; Kumacheva, E. Confinement-induced phase transitions in simple liquids. Science 1995, 269, 816–819. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.; Kumacheva, E. Simple liquids confined to molecularly thin layers. I. Confinement-induced liquid-to-solid phase transitions. J. Chem. Phys. 1998, 108, 6996–7009. [Google Scholar] [CrossRef]
- Schoen, M.; Diestler, D.; Cushman, J. Fluids in micropores. I. Structure of a simple classical fluid in a slit-pore. J. Chem. Phys. 1987, 87, 5464–5476. [Google Scholar] [CrossRef]
- Thompson, P.A.; Robbins, M.O. Origin of stick-slip motion in boundary lubrication. Science 1990, 250, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Luedtke, W.; Landman, U. Layering transitions and dynamics of confined liquid films. Phys. Rev. Lett. 1997, 79, 705. [Google Scholar] [CrossRef]
- Cui, S.; Cummings, P.; Cochran, H. Molecular simulation of the transition from liquidlike to solidlike behavior in complex fluids confined to nanoscale gaps. J. Chem. Phys. 2001, 114, 7189–7195. [Google Scholar] [CrossRef]
- Lei, Y.; Leng, Y. Force oscillation and phase transition of simple fluids under confinement. Phys. Rev. E 2010, 82, 040501. [Google Scholar] [CrossRef]
- Xu, R.-G.; Xiang, Y.; Papanikolaou, S.; Leng, Y. On the shear dilation of polycrystalline lubricant films in boundary lubricated contacts. J. Chem. Phys. 2020, 152, 104708. [Google Scholar] [CrossRef]
- Xu, R.-G.; Leng, Y. Squeezing and stick–slip friction behaviors of lubricants in boundary lubrication. Proc. Natl. Acad. Sci. USA 2018, 115, 6560–6565. [Google Scholar] [CrossRef] [PubMed]
- Chkonia, G.; Wölk, J.; Strey, R.; Wedekind, J.; Reguera, D. Evaluating nucleation rates in direct simulations. J. Chem. Phys. 2009, 130, 064505. [Google Scholar] [CrossRef] [PubMed]
- Wedekind, J.; Reguera, D. Kinetic reconstruction of the free-energy landscape. J. Phys. Chem. B 2008, 112, 11060–11063. [Google Scholar] [CrossRef] [PubMed]
- Wedekind, J.; Chkonia, G.; Wölk, J.; Strey, R.; Reguera, D. Crossover from nucleation to spinodal decomposition in a condensing vapor. J. Chem. Phys. 2009, 131, 114506. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.-G.; Rao, Q.; Xiang, Y.; Bian, M.; Leng, Y. Computational Simulations of Nanoconfined Argon Film through Adsorption–Desorption in a Uniform Slit Pore. Coatings 2021, 11, 177. [Google Scholar] [CrossRef]
- Xu, R.-G.; Xiang, Y.; Zhang, G.; Rao, Q.; Leng, Y. Nucleation of Frank Dislocation during the Squeeze-Out Process in Boundary Lubrication: A Molecular Dynamics Study. Materials 2022, 15, 997. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Wedekind, J.; Strey, R.; Reguera, D. New method to analyze simulations of activated processes. J. Chem. Phys. 2007, 126, 134103. [Google Scholar] [CrossRef] [PubMed]
- Julin, J.; Napari, I.; Vehkamäki, H. Comparative study on methodology in molecular dynamics simulation of nucleation. J. Chem. Phys. 2007, 126, 224517. [Google Scholar] [CrossRef] [PubMed]
- Yasuoka, K.; Matsumoto, M. Molecular dynamics of homogeneous nucleation in the vapor phase. I. Lennard-Jones fluid. J. Chem. Phys. 1998, 109, 8451–8462. [Google Scholar] [CrossRef]
- Yasuoka, K.; Matsumoto, M. Molecular dynamics of homogeneous nucleation in the vapor phase. II. Water. J. Chem. Phys. 1998, 109, 8463–8470. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, S.; Wang, L.; Li, Y.; Wu, W.; Duan, Y.; Li, H. Heterogeneous nucleation of Al melt in symmetrical or asymmetrical confined nanoslits. Nanoscale 2016, 8, 12339–12346. [Google Scholar] [CrossRef] [PubMed]
- Pérez, A.; Rubio, A. A molecular dynamics study of water nucleation using the TIP4P/2005 model. J. Chem. Phys. 2011, 135, 244505. [Google Scholar] [CrossRef]
- Leoni, F.; Shi, R.; Tanaka, H.; Russo, J. Crystalline clusters in mW water: Stability, growth, and grain boundaries. J. Chem. Phys. 2019, 151, 044505. [Google Scholar] [CrossRef]
- Goswami, Y.; Vasisht, V.V.; Frenkel, D.; Debenedetti, P.G.; Sastry, S. Thermodynamics and kinetics of crystallization in deeply supercooled Stillinger–Weber silicon. J. Chem. Phys. 2021, 155, 194502. [Google Scholar] [CrossRef]
- Song, H.; Sun, Y.; Zhang, F.; Wang, C.-Z.; Ho, K.-M.; Mendelev, M. Nucleation of stoichiometric compounds from liquid: Role of the kinetic factor. Phys. Rev. Mater. 2018, 2, 023401. [Google Scholar] [CrossRef]
- Saika-Voivod, I.; Romano, F.; Sciortino, F. Nucleation barriers in tetrahedral liquids spanning glassy and crystallizing regimes. J. Chem. Phys. 2011, 135, 124506. [Google Scholar] [CrossRef]
- Braun, O.; Manini, N. Dependence of boundary lubrication on the misfit angle between the sliding surfaces. Phys. Rev. E. 2011, 83, 021601. [Google Scholar] [CrossRef]
- Lutsko, J.F. Recent developments in classical density functional theory. Adv. Chem. Phys. 2010, 144, 1. [Google Scholar]
- Lutsko, J.F. How crystals form: A theory of nucleation pathways. Sci. Adv. 2019, 5, eaav7399. [Google Scholar] [CrossRef]
- Hu, T.; Wang, H.; Gomez, H. Direct van der Waals simulation (DVS) of phase-transforming fluids. Sci. Adv. 2023, 9, eadg3007. [Google Scholar] [CrossRef]
- Gallo, M.; Magaletti, F.; Georgoulas, A.; Marengo, M.; De Coninck, J.; Casciola, C.M. A nanoscale view of the origin of boiling and its dynamics. Nat. Commun. 2023, 14, 6428. [Google Scholar] [CrossRef]
- Wu, W.; Montiel, D.; Guyer, J.E.; Voorhees, P.W.; Warren, J.A.; Wheeler, D.; Gránásy, L.; Pusztai, T.; Heinonen, O.G. Phase field benchmark problems for nucleation. Comput. Mater. Sci. 2021, 193, 110371. [Google Scholar] [CrossRef]




| Z | |||
|---|---|---|---|
| 3763.1 | 0.02576 | 30 | 2.87 |
| 30 | 45 | 60 | 75 | 90 | |
| 2246 ± 113 | 3040 ± 148 | 3540 ± 171 | 3638 ± 172 | 3661 ± 172 | |
| 5.95 | 4.40 | 3.77 | 3.68 | 3.65 |
| 15 | 30 | 60 | 120 | |
| 4.04 | 4.04 | 4.07 | 4.08 |
| MFPT | DOM | YM | SP | |
|---|---|---|---|---|
| 2.87 | 3.77 | 4.07 | 5.71 |
| MFPT | DOM | YM | SP | |
|---|---|---|---|---|
| Need a predefined threshold size | N | Y | Y | Y |
| Provide a complete set of information of nucleation | Y | N | N | N |
| Reconstruct the free energy landscape | Y | N | N | N |
| Large system with low free energy barrier | High cost | Best | ||
| System with a very low free energy barrier | N | N | N | N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.-G.; Zhang, G.; Liu, T.; Xiang, Y.; Leng, Y. On the Nucleation Rate of Confinement-Induced Liquidlike-to-Solidlike Phase Transitions. Lubricants 2024, 12, 420. https://doi.org/10.3390/lubricants12120420
Xu R-G, Zhang G, Liu T, Xiang Y, Leng Y. On the Nucleation Rate of Confinement-Induced Liquidlike-to-Solidlike Phase Transitions. Lubricants. 2024; 12(12):420. https://doi.org/10.3390/lubricants12120420
Chicago/Turabian StyleXu, Rong-Guang, Gunan Zhang, Tianchen Liu, Yuan Xiang, and Yongsheng Leng. 2024. "On the Nucleation Rate of Confinement-Induced Liquidlike-to-Solidlike Phase Transitions" Lubricants 12, no. 12: 420. https://doi.org/10.3390/lubricants12120420
APA StyleXu, R.-G., Zhang, G., Liu, T., Xiang, Y., & Leng, Y. (2024). On the Nucleation Rate of Confinement-Induced Liquidlike-to-Solidlike Phase Transitions. Lubricants, 12(12), 420. https://doi.org/10.3390/lubricants12120420





