Abstract
In this study, a novel gas-extruded membrane bearing was developed, and an optimization algorithm was applied to solve a Reynolds equation that describes the load-bearing characteristics of this bearing. This was effective in improving the solution rate of the Reynolds equation, significantly reducing the difficulty of obtaining a solution, avoiding high programming difficulty, and achieving a high solution accuracy. Through a comparative analysis, the error in the accuracy of the alternating implicit difference method was addressed, and the traditional finite element method for solving the same model was verified, with an average error of 2% reached to verify its applicability. The algorithm was also used to analyze the load-bearing capacity of the gas-extruded membrane bearing. This revealed not only a positive correlation of the average load-bearing capacity of the gas-extruded membrane bearing with the frequency and amplitude of vibration but also a negative correlation with radial clearance, with the cut-off frequency reaching 19 Khz. The load-bearing capacity of the gas-extruded membrane bearing proposed in this paper reached 1.28 N, which indicated an error of 3.28% with the theoretical approach. To sum up, this research provides an important reference for the design and manufacture of novel gas-extruded membrane bearings.
1. Introduction
As a new type of non-contact bearing, a gas-extruded membrane bearing relies on the squeeze effect of a gas film to control the gas flow and pressure distribution for the smooth operation of the bearing [1]. It demonstrates advantages such as low friction, high precision, the capacity for self-lubrication, and environmentally friendly status, which make it widely applicable to high-speed rotation and precision motion applications in settings such as wind turbine power generation [2], aerospace engineering [3], precision machine tooling [4,5], automotive fuel cells [6], micro-gas compressors [7,8,9,10], and more.
With respect to gas-extruded membrane bearings, the key to achieving gas film support and bearing stability is to control the gas flow, and the Reynolds equation is the basic equation used to describe the gas flow behavior of gas-extruded membrane bearings [11,12]. The mainstream methods used to solve the Reynolds equation mainly include analytical and numerical solutions, but the gas Reynolds equation is a transient, second-order, nonlinear, partial differential equation [13]. When the equivalent squeeze number is small, or the amplitude cannot be treated as an insignificant disturbance, the analytical method will be unfit to accurately describe the distribution of pressure in the squeeze film, as it is usually only applicable to the special case of simplification. In practice, the numerical solution is often used to approximate the solution of the gas Reynolds equation.
As one of the most widely used methods to calculate complex fluid, the finite element method (FEM) [14,15] has been used by many scholars to solve the Reynolds equation numerically for more accurate results, which are needed to effectively describe the Reynolds number, gas film thickness, bearing parameters, etc. Ma W et al. [16] used the Galliukin weighted residual method to discretize the gas Reynolds equation and solve it using the finite element method to determine the relationship between the thickness of a gas film and the acceleration of the bearing motion. Chen C T et al. [17] discretized the gas Reynolds equation through the variational and weighted margin method and then applied the finite element method to solve it for determining the relationship between the eccentricity, bearing clearance, and influence of the load-bearing capacity, with the error caused during the experiment found to be less than 5%. However, the process of manually writing an FEM program is complicated and computationally intensive. Moreover, the final matrix equation obtained after the Reynolds equation is simplified as a nonlinear system of equations, which is difficult to solve, incurs great time costs, and is hard to converge during the calculation process.
The finite difference method (FDM) is a commonly used numerical solution method for solving nonlinear partial differential equations. There are explicit and implicit difference formats for FDM. The explicit difference format has strict limitations on the choice of time step and is less frequently used in practice. Liu Y et al. [18] used the finite difference method and Newton iteration method to solve the air film Reynolds equation. Li H et al. [19] and Shou T et al. [20] used the Crank–Nicolson implicit difference format to solve the equation numerically. However, the implicit difference method needs to solve a large-scale system of linear algebraic equations, which is computationally intensive; thus, the alternating direction implicit method was proposed.
In recent years, the alternating direction implicit method has been widely adopted to solve the numerical approximate solutions of complex and computationally difficult, nonlinear, partial differential equations in various fields, like fluid heat transfer and electromagnetic wave applications [21,22,23,24]. The alternating direction implicit (ADI) method has also commonly been used to solve partial differential equations, in which difference approximation is performed in alternation according to the temporal and spatial terms included [25]. The numerical algorithm achieves secondary accuracy [26]. In each time step, the difference in the half time step is determined in the direction of x and then y, followed by the difference in the half time step in the direction of y and then x. In this way, the solution of the two-dimensional problem can be decomposed into two one-dimensional partial differential equations, which significantly reduces the difficulty in finding the solution. The ADI method is effective in reducing the impact of discretization on computational efficiency, with greater robustness to computational errors [27,28]. Moreover, it outperforms the finite element method in terms of convergence speed and computational efficiency. Therefore, to address the high computational complexity and low computational efficiency of the gas Reynolds equation for complex fluids, the alternating direction implicit method, which is commonly used in fluid heat transfer and electromagnetic wave applications, was proposed to solve the Reynolds equation of the gas-extruded membrane bearing designed in this study. In addition, the gas-extruded membrane bearing was developed, the gas squeeze film Reynolds equation was established, and the approximate solution of the pressure distribution was obtained through simplified programming in Matlab. The effects of excitation frequency and amplitude on the load-bearing capacity of the extruded membrane bearing was analyzed in comparison with the results of simulation calculations obtained through the commonly used finite element software ANSYS. The alternating implicit check method was also adopted to solve the Reynolds equation, and the load-bearing capacity of the extruded membrane bearing was verified through experimentation.
2. The Reynolds Equation for Gas Extrusion Film Is Established and Solved with the Implicit Difference Method
2.1. Design of Gas Extrusion Membrane Bearing Structure
As a novel type of non-contact bearing reliant on the gas pressure film lubrication effect produced by the vibration squeeze [29] to bear load, the gas-extruded membrane bearing shows diversity in structure. In this paper, a piezoelectric-driven radially inclusive gas extrusion membrane bearing is developed, as shown in Figure 1. The body of this bearing is a cylindrical shell, and the suspended object is a cylindrical rotor. The shell is circumferentially distributed with three axial ribs spaced at 120°, and the ribs divide the whole shell into three vibration regions, each of which is pasted with a piezoelectric ceramic sheet, as shown in Figure 1a,b.
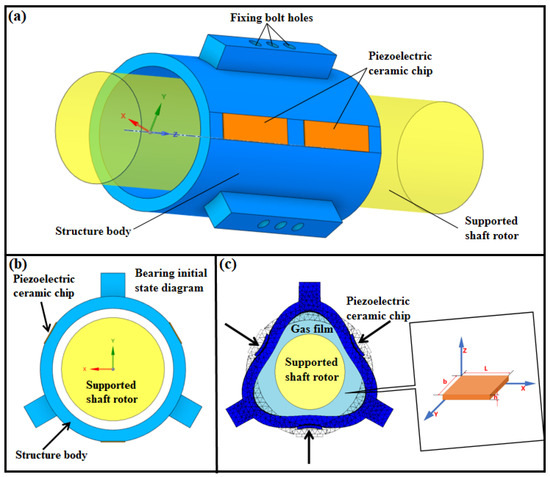
Figure 1.
(a) Schematic diagram of the structure; (b) schematic diagram of the structure in the initial state; (c) schematic diagram of the structure subjected to the maximum deformation.
When the signal of excitation voltage is applied to the upper and lower electrodes of the piezoelectric sheet, the piezoelectric ceramic sheet polarized along the thickness direction induces periodic tensile deformation in the length direction. Meanwhile, the elastic metal cylinder is driven to cause vibration, which leads to periodic tensile deformation along the axial direction with periodic radial squeezing motion, as shown in Figure 1c. The inner surface of the bearing sleeve and the cylindrical surface of the shaft rotor can be approximated as two extrusion surfaces, and an extrusion film is formed by the air between the extrusion shell and the cylindrical surface of the shaft. The thickness of the squeeze film is particularly small, generally ranging from a few microns to tens of microns. Compared with the squeeze film in other directions, it has a smaller characteristic size by several orders of magnitude, and the height of bearing clearance is much smaller than the radius of curvature on the journal surface. In the radial bearing calculation, the curvature of the fluid film is not considered to expand the gas film of the cylindrical gas bearing into a rectangular gas film as shown in Figure 1c. As shown in Figure 1c, the simplified gas film model of the gas-extruded membrane bearing is constructed by establishing the right-angle coordinate system in the gas film, which will be analyzed in detail in the following subsections.
The gas extrusion film bearing prototype as proposed in this paper is machined out of a whole brass substrate, which is processed by wire-cutting technology to minimize the effect of processing stress on the dimensions of the bearing. Since the combination of piezoelectric sheet and metal cylinder tightness has an immediate effect on the performance of the bearing, this study adopts the two-component acrylic structural adhesive with an excellent performance in temperature resistance and shock vibration resistance as the adhesive, and the piezoelectric ceramic sheet is made to adhere onto the outer surface of the metal cylinder. As the acrylic structural adhesive is not conductive, the piezoelectric piece of negative lead directly through the conductive silver adhesive bonded to the outer surface of the metal cylinder and piezoelectric ceramic piece when the glue was mixed with a certain proportion of nano-conductive silver powder made of conductive silver glue. Different from the conventional process of welding wires directly to the negative pole of the piezoelectric sheet, this new process significantly reduces the gap between the piezoelectric sheet and the substrate. Finally, after the acrylic structural adhesive is fully cured, the positive lead wire is soldered to the positive surface of the piezoelectric ceramic sheet. The above fabrication process plays a role in ensuring the durability of the structure.
2.2. Establishment of Reynolds Equation for Gas-Extrusion Film
Unlike the lubricated bearings containing a liquid medium, the basic equation used for gas extrusion film lubrication is highly complex. The relationship between velocity, temperature, density, and pressure is a nonlinear one, and all of them are the functions of coordinates and time. Therefore, it is necessary to solve the equation of motion, continuity equation, and state equation for determining the parameters such as velocity, density, pressure, and temperature of the gas film. In viscous fluid dynamics, the lubricant gas is considered as a compressible Newtonian fluid by associating the Navier–Stokes equation with the continuity equation of the gas [30].
In the simplest case, the fluid is assumed as a Newtonian fluid, the state of which is laminar. Additionally, the motion of this fluid is considered as an isothermal process, with the inertial and bulk forces of the fluid ignored. Since the characteristic size in other directions is much larger than the thickness of the gas film, the change of pressure in the direction of gas film thickness is negligible, and the velocity gradient is satisfied.x,y.
The Reynolds equation of gas lubrication is expressed in general as follows:
where p—absolute gas pressure (Pa);
- η—gas viscosity coefficient (Pa·s);
- u1, u2—the velocity component of the upper and lower surfaces of the gas film in the x direction (m/s);
- w1, w2—the velocity component of the upper and lower surfaces of the gas film in the z direction (m/s).
It is assumed that no tangential motion occurs on the surface of the two moving passes of the gas extrusion film studied in this paper, or the velocity of tangential motion is much lower than that of the extrusion motion, which means that the pressure in the gas film is largely determined by the extrusion motion between the moving pass.
In Equation (1), u1, u2, w1, w2 ≈ 0. After simplification and dimensionless processing, the dimensionless form of the Reynolds equation for compressible gas is obtained as follows:
Let H be a function of X and Y, so that Equation (2) can be further expressed as
By typing in capital letters and dimensionless parameters including , , , , , and , h represents the film thickness function related to coordinates, indicates the initial film thickness, denotes the environmental pressure, r refers to the gas film width, for extrusion.
2.3. Discrete Solution of Reynolds Equation for Gas Extruded Film
The finite difference method is purposed to discretize the differential equation in the computational domain and express the differential term of the equation by means of difference approximation, with the equation transformed into an algebraic equation to find the solution. There are both explicit and implicit difference schemes. The explicit difference scheme applies strict restrictions on the selection of time step, and it is difficult to converge for the calculation of stability difference. Although the implicit difference takes a more complex form than the explicit difference, it performs better in computational accuracy and stability. In this paper, an unconditional stable alternating direction implicit method is used to discretely solve the Reynolds equation. The gas film solution domain in Figure 1c is divided into a certain number of grids, as shown in Figure 2a.
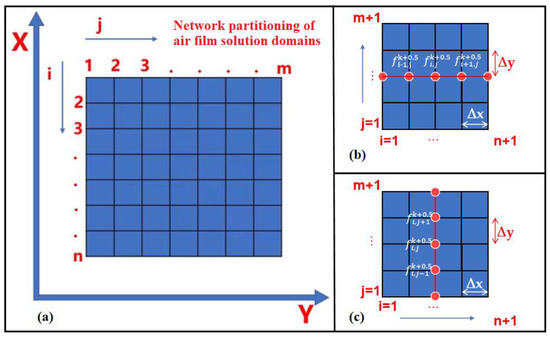
Figure 2.
(a) The solution domain is meshed; (b) the x-direction is implicit, and the y-direction is explicit; (c) the y-direction is implicit and the x-direction is explicit.
Considering the dimensionless boundary conditions, the pressure at all places of the air film at the initial moment of vibration is set as equal to the ambient atmospheric pressure, , the boundary of the air film is always the ambient atmospheric pressure during vibration, and .
Unlike the full implicit difference, which solves the k + 1 time layer directly from the k time layer, alternating direction implicit method inserts a transition time layer k + 0.5 between the k and k + 1 time layer, with k to k + 0.5 solved in only one direction. Additionally, it is solved in the other direction from k plus 0.5 to k plus 1, as shown in Figure 2b,c. By following the above ideas, the Reynolds equation firstly solves in the X direction from the time layer k to k + 0.5, with the first-order and second-order quantities in Equation (3) differentiated as follows:
By substituting it back into Formula (3), it can be obtained that
To sort out
where
It can be seen from above that a multivariate quadratic nonlinear equation can be obtained when i is valued. For each j, let i traverse from 1 to m, simultaneously obtain all the corresponding equations of i values, and consider the boundary conditions at the same time to obtain a multivariate quadratic nonlinear system of equations.
Since the initial pressure value of the nonlinear equations is known, the matrix comprising the nonlinear equations is denoted as F (p0):
Then, the initial matrix B0 can be expressed as
When λ = 0, and , calculation accuracy (ε1 and ε2) is set to calculate the .
To examine whether the calculation is accurate is to judge whether Equation (9) is true:
If Equation (9) is untrue, let
The following variables are reassigned as
Then, each variable obtained after reassignment is calculated and substituted into Equation (9) for calculating whether accuracy is achieved. Otherwise, the above process continues to repeat itself. If the accuracy of calculation is reached, the loop is jumped out of at the end of iteration, so that
represents the approximate value of the pressure at the desired node, so that the pressure distribution of the whole column of nodes corresponding to the coordinate of point j on the time layer k + 0.5 can be obtained. Let j traverse from 1 to n, and n nonlinear equations can be obtained. By solving these n equations, the pressure distribution of all nodes in the time layer k + 0.5 can be determined, which is equivalent to solving a one-dimensional problem. Then, the solution in the Y direction is performed. The final value obtained from the last iteration is treated as the initial value for solution in the time layer from k + 0.5 to k + 1. The difference scheme is reconstructed as follows:
The formula can be obtained as
Similarly, when j is evaluated, a multivariate quadratic nonlinear equation is obtained. For each i, let j traverse from 1 to n, simultaneously obtain all the corresponding equations of j point values, and consider the boundary conditions at the same time to obtain a multivariate quadratic nonlinear system of equations.
Similarly, the quasi-Newton iteration method (Equations (7)–(10)) as introduced above is used to solve the m nonlinear equations obtained in this time layer, and the pressure distribution of each node at k + 1 is determined. The above process leads to a set of discrete pressure values, which approximately represents the pressure distribution in the gas film. At the same time, the load-bearing capacity of the gas film at any time can be determined through the area integral of pressure at all nodes in the solution domain.
The above calculation process is converted into the flow chart of calculating the Reynolds equation used to solve the alternating direction implicit, as shown in Figure 3.
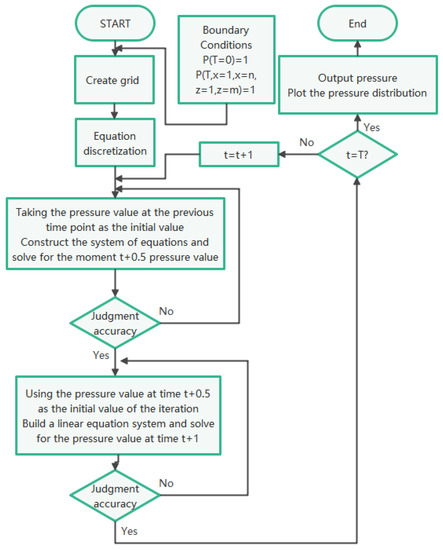
Figure 3.
Alternating direction implicit method for solving Reynolds equation computational procedure.
In ANSYS software, FLUID136 fluid unit is selected to simulate the effect of extrusion, a rectangular extruded film is modeled, and the Reynolds equation satisfied by the model is expressed as
where = − and refer to the surface pressure. The discretized structure is used to mesh the solution domain of the gas film, with the initial gap of the squeezed film and the boundary condition of the gas film set to h0 and the ambient background pressure, respectively. By assuming that the oscillator of the squeezed gas film shows simple harmonic vibration, the squeezed gas film oscillator model is established with hexahedral cells, with restrictions imposed on the nodal degrees of freedom in the x-axis and y-axis directions of the oscillator. Additionally, the nodal displacement of the sinusoidal function is applied in the z-axis, so that the film thickness equation can be expressed as
where represents the dimensionless amplitude, , a indicates the amplitude, and h0 denotes the initial film thickness, i.e., the extrusion gap.
3. Results and Discussion
3.1. Harmonic Response Analysis of Gas Extruded Film Bearing Modal Analysis
The modal analysis of the extruded film bearing is purposed to determine the characteristics of inherent vibration for the piezoelectric-driven gas extruded film bearing under the condition of free vibration, including the resonance frequency and vibration pattern of the bearing structure. Additionally, the modal analysis conducted by using ANSYS software lays a foundation for harmonic response analysis. The amplitude-frequency characteristic curve of the bearing structure can be drawn through the harmonic response analysis of the extruded membrane bearing structure model, while the amplitude-frequency characteristic curve of the bearing structure can be used to determine the intrinsic frequency of the structure. The vibration-induced deformation of the bearing structure is maximized when the operating frequency of the load-bearing cylinder is equal to the intrinsic frequency. In the present study, the piezoelectrically driven gas extruded membrane bearing is first modeled using ANSYS APDL. Then, finite element modal analysis and harmonic response analysis are carried out through a command flow approach to determine the appropriate vibration characteristic parameters of the bearing. Prior to the modal analysis, it is necessary to set suitable boundary conditions. The gas extruded film bearing under study in this paper is intended mainly for use in air at room temperature, and there are no other constraints imposed on the position of the bearing than that on circuit state. As indicated by the relevant parameters to the piezoelectric sheet, the voltage that can be withstood by the piezoelectric sheet used in engineering works is affected by the thickness of the piezoelectric sheet, the piezoelectric sheet used for modeling in this paper is 0.5 mm in thickness, and a 75 V AC power supply is applied between the upper and lower electrode surfaces of the piezoelectric ceramic sheet. The type of analysis module is determined through modal analysis, and the Block Lanczos method is adopted for computation. The number of modes depends on the degree of freedom in the node, the modal analysis load step is set, and the solver is used to determine the mode of gas extrusion membrane bearing vibration. The results are viewed in a general purpose post-processor, including the information on the mode shapes, deformation maps, and vibration frequencies for each order of modes of the extruded membrane bearing. When ANSYS harmonic response analysis is performed by means of modal analysis, it is necessary to determine the appropriate damping coefficient in the first place. Depending on the exact model, the damping ratio is set to 0.02. The type of analysis is selected as harmonic response analysis, and the full-order method is applied to solve the problem. The range of load frequency is set to 10~30 kHz, and 20 load sub-steps are divided in the selected frequency range for simulation calculation. The calculation results are viewed through the post-processor, and the curves of amplitude-frequency variation at the center point of the bearing cylinder wall along the x and y directions are drawn, as shown in Figure 4a,b.
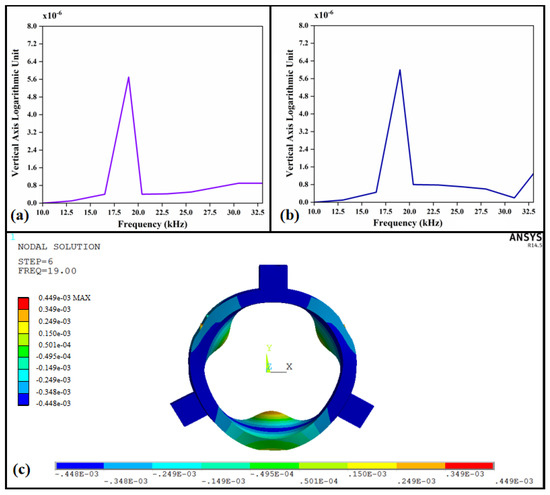
Figure 4.
(a) The amplitude-frequency variation curve of vibration in the x-direction; (b) the amplitude-frequency variation curve of vibration in the y-direction; (c) the cloud diagram of vibration deformation occurring to the gas-extruded membrane bearing.
It can be seen from the curve that the amplitude reaches its maximum at the center of the bearing cylinder wall given the excitation frequency of 19 kHz, and the vibration displacement along the x and y directions is basically identical. Figure 4c shows the dynamic deformation cloud diagram of the extracted frequency of 19 kHz in the modal analysis. Considering the working principle of the gas-extruded membrane bearing, it can be found that the gas-extruded membrane bearing in the rectangular piezoelectric ceramic sheet is in the direction of expansion and contraction of the vibration mode of extrusion and the shaft gap in the formation of air extrusion lubrication gas film. That is to say, for the structure at a frequency of 19 kHz, the bearing in the axial direction of the overall bending, and the radial “triangle” symmetrical contraction, the vibration of the bearing ends of the deformation is supposed to be radial uniform contraction to prevent the overflow of air in the gap. The bearing at the resonant frequency of 19 kHz meets the requirements on the vibration of the bearing for the formation of its extruded air film.
3.2. Comparative Analysis
In order to assess the accuracy of the Reynolds equation solved by the alternating direction implicit method proposed in the previous paper, the alternating direction implicit and the finite element software ANSYS are used for the hypothetical air film calculations, respectively in this section, with the calculation results obtained through the two methods compared. It is assumed that the length of air film is 40 mm, the width of air film is 20 mm, the thickness of air film is 50 μm, the vibration amplitude is 5 μm, and the vibration frequency is 19 kHz.
For the purpose of calculation, the alternating direction implicit procedure is written in Matlab according to the procedure shown in Figure 3. Based on the assumption that all points of the extruded air film show the simple harmonic vibration of equal amplitude, the dimensionless air film thickness function is expressed as sinT. The ambient pressure is 1 × 105 Pa, and the dynamic viscosity of the gas is 17.9 × 10−6 Pa∙s. With eight time nodes set in one vibration cycle, the instantaneous distribution of pressure at each time node is shown in Figure 5a. It can be seen from this figure that the maximum and minimum pressures are applied at the center of the air film within one vibration cycle. Among the above eight time points are the following: T = 2, the minimum value of pressure is obtained at the center of the air film; T = 6, the maximum value of pressure is obtained at the center of the air film, which leads to the best outcome of observation for comparison. Therefore, T = 6 is also used for comparison when ANSYS is used.
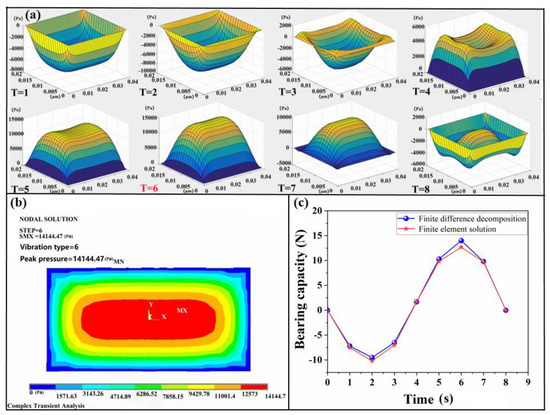
Figure 5.
(a) Instantaneous distribution of pressure at each node of the alternating implicit difference method; (b) finite element method T = 6 pressure instantaneous distributions; (c) comparison of bearing capacity values between the two methods in one cycle.
In order to transfer the squeezing motion of the oscillator to the gas region, it is necessary to ensure the consistence of point contact between the corresponding nodes in the solid and fluid regions of the oscillator. The displacement function, which involves parameters such as amplitude and vibration frequency, is applied to the vibrating surface with a sinusoidal variation over time. The distribution of the gauge pressure pq (i.e., pressure increment) on the air film in the gap in space and time is determined by selecting a suitable time step, with the transient solution method used to calculate the solution of the finite element model of the extruded air film. The generalized post-processor POST1 is used to view the pressure cloud of the air film at each time point. Figure 5b shows the cloud plot of the instantaneous pressure distribution at T = 6, corresponding to the maximum pressure in the air film. It can be observed that the gas film pressure is positive, with the maximum pressure occurring at the center of the gas film, forming a stable pressure platform. The pressure gradient decreases towards the edge of the gas film and approaches the ambient background pressure. These findings are consistent with the pressure distribution law obtained using the previous implicit difference method. To further evaluate the accuracy of the alternating direction implicit method, the air film pressure data collected at each time point in ANSYS are exported and then factored into Matlab for integration calculation within the solution domain. This allows the change in load-bearing capacity within one cycle to be determined. Additionally, the air film pressure, as calculated using the implicit difference method at each time node, is integrated over the solution domain to reveal the change in instantaneous load-bearing capacity within a cycle, and the average value of the obtained instantaneous load carrying capacity can be averaged to obtain the average load carrying capacity of the air film within a cycle. Finally, the finite difference decomposition and finite element solution of the intra-cycle bearing capacity change are compared, the results of which are shown in Figure 5c. When the initial state position of the structure body is taken as the starting position, the load-bearing capacity is 0. The negative load-bearing capacity in the figure is defined as the load-bearing capacity of the sleeve in the negative direction along the radial direction, and the positive load-bearing capacity is identical. It can be seen from the figure that the error is 0.02% when the alternating direction implicit reaches the minimum and the finite element software solution is obtained for calculating the gas film pressure through the same gas film parameters. Additionally, the error is 1.03% when the maximum value is reached, and the average error in one cycle is 2%. It is implied that the alternating direction implicit method proposed in this paper to solve the Reynolds equation meets the requirements on accuracy and effectiveness.
3.3. Analysis of the Load-Bearing Characteristics of Gas Extruded Membrane Bearings
The gas-extruded membrane bearing consists mainly of a cylinder stator and a cylindrical rotor. It is assumed that there is no rotational eccentricity when the bearing operates, and the cylindrical rotor is always suspended in the center of the cylinder stator. The sought suspension force of the gas film represents the load-bearing capacity of the bearing under static suspension, and the thickness of the gas squeeze film is determined by the radial clearance of the bearing. In this circumstance, amplitude a, radial clearance H0, and vibration frequency f are the three main influencing factors for the size of the load-bearing air film. Thus, the analysis of these three parameters is crucial to exploring the load-bearing capacity characteristics of the extruded film bearing. In this section, the effect of a, H0, f on the load carrying capacity of the extruded film bearing is analyzed using the numerical calculation method described in Section 3, given the air film area and other parameters.
When a = 5 μm and H0 = 50 μm, the instantaneous load-bearing capacity of air film during vibration frequency is 0–40 kHz, respectively. The effect of vibration frequency f on the load-bearing capacity is shown in Figure 6, and from the figure can be seen that the instantaneous load-bearing capacity of the air film within one cycle is small when the vibration frequency is low, and the load-bearing capacity of the extruded film is limited at this time. As the vibration frequency rises, the difference between the positive and negative instantaneous load-bearing capacity increases, and the peak positive load-bearing capacity in one cycle is obviously larger than the peak negative load-bearing capacity. At this time, the gas squeeze film effect is obvious, and a strong bearing effect is produced to achieve the stable suspension of the load. By calculating the average load-bearing capacity in cycles at different vibration frequencies as shown in Figure 6a, the relationship between the average load-bearing capacity and vibration frequency is determined, as shown in Figure 6b.
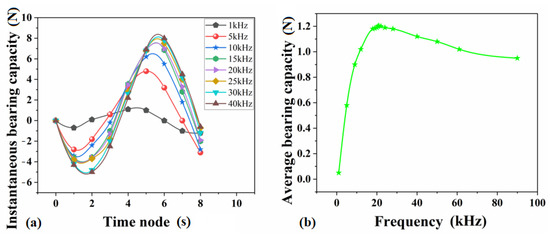
Figure 6.
(a) The effect of vibration frequency on the instantaneous load-bearing capacity; (b) the effect of vibration frequency on the average load-bearing capacity.
The average load-bearing capacity improves with the increase of vibration frequency. When the vibration frequency increases to 19 kHz, the average load-bearing capacity reaches the maximum of 1.22 N. At a greater vibration frequency than 19 kHz, the average load-bearing capacity changes less significantly or even decreases. The working principle of the gas extrusion membrane bearing is used for analysis. As the gas in the bearing gap is subject to viscous force, the gas cannot be synchronized with the vibration of the extruded surface during the process of inhaling and squeezing in and out of the gap. When the frequency is either too low or too high, there is a large difference in the transient load-bearing capacity at the beginning of the vibration cycle and at the end of this cycle, and the load-bearing capacity characteristics of the gas film cannot be restored at the end of the vibration cycle, thus affecting the stable output of the load-bearing capacity of the gas film in several consecutive vibration cycles. This causes the irregular oscillation of the gas in the gas film, making it difficult to achieve stability. Alternatively, the pressure film effect between the two extruded surfaces can be viewed as a result of the elastic force of the air film interacting with the damping force on the second plate under extrusion. When the two amplitudes of force are equal, the vibration squeeze frequency f is referred to as the cutoff frequency, at which the squeeze effect is optimal. Therefore, given the above analytical results, it is necessary to restrict the piezoelectric excitation frequency of the squeeze film bearing to a reasonable range for ensuring that the pressure distribution of the squeeze film remains smooth over several consecutive cycles, and the suspension load-bearing capacity is maximized. In the above example, 19 kHz is taken as the cut-off frequency of the squeeze film bearing when a = 5 μm and H0 = 50 μm.
When H0 = 50 μm, the effect of amplitude change on the average load-bearing capacity and cut-off frequency is investigated, and the instantaneous load-bearing capacity of the air film is calculated for a period during which the amplitude ranges from 0 to 7μm. The results are further analyzed to find out the law of how increasing amplitude affects the average load-bearing capacity, as shown in Figure 7. From the figure, it can be seen that given a certain thickness of the film, the larger the amplitude of the bearing extrusion motion is, the higher the extrusion efficiency of the film and the more significant the extrusion effect are. Thus, the average load-bearing capacity of the film also improves.
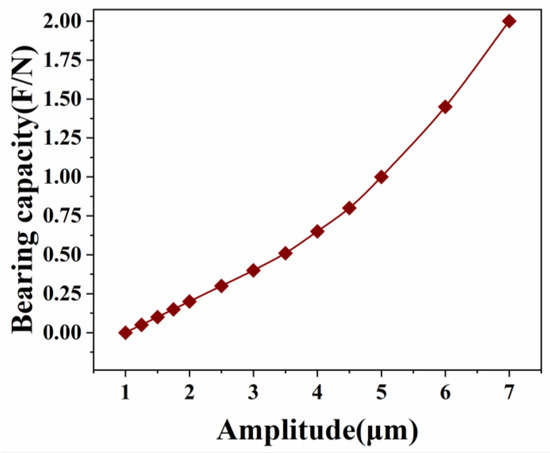
Figure 7.
Effect of amplitude variation on average load-bearing capacity.
For the radially inclusive structure of the squeeze film bearing, ideally, the cylindrical rotor is suspended at the center of the cylindrical stator when the bearing functions well. At this time, the maximum thickness of the air film is determined by the radial initial fit clearance of the bearing. By assuming that the amplitude a is constant, the effect of radial gap change on the average load-bearing capacity is investigated, with the results of multiple calculations shown in Figure 8a. Figure 8b is obtained by sorting out the relationship between the initial clearance change at the cutoff frequency and the maximum average carrying capacity.
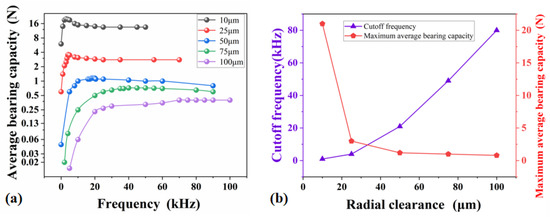
Figure 8.
(a) The load-bearing capacity with different radial clearances; (b) the impact of radial clearance change on both cut-off frequency and load-bearing capacity.
Given a certain amplitude, the larger the radial clearance of the bearing is, the smaller the ratio of bearing amplitude and air film thickness are, which is equivalent to reducing the amplitude in practice. Therefore, the average load-bearing capacity decreases when the radial clearance of the bearing increases. In case of a small radial clearance of the bearing, the volume of the gas film is lower, and it is easier for the gas in the gap to produce irregular oscillation, which reduces the cut-off frequency. When the radial clearance of the bearing increases, the volume of the gas in the gap increases, as do the volume and thickness of the gas film. Thus, the stiffness and damping of the gas film increase, showing a greater stability, which makes it less likely to produce irregular oscillation. Additionally, the cut-off frequency of the bearing rises.
3.4. Tests on the Load-Bearing Capacity Characteristics of Gas Extruded Film Bearings
In order to verify the effect caused by the load-bearing capacity of the gas extrusion die bearing as designed using the optimization algorithm in this paper, three groups of gas extrusion membrane bearing mechanism were produced, as shown in Table 1. Additionally, Figure 9a,b shows three groups of gas extrusion membrane suspension bearings.

Table 1.
Ultrasonic suspension bearing prototype in terms of size-related parameters.
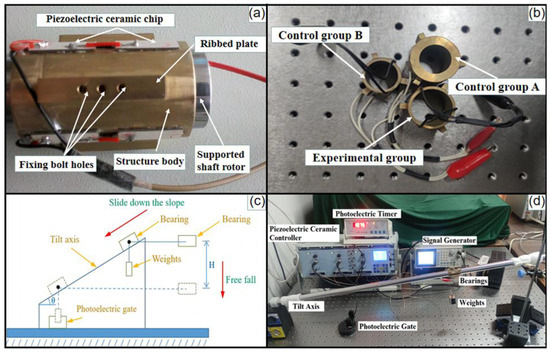
Figure 9.
(a) The prototype of gas extrusion membrane bearing; (b) three groups of gas extrusion membrane bearings; (c) the experimental principle of levitation force test; (d) the diagram of experimental setup.
Based on the assumption that the shaft is stationary when the bearing functions, it is difficult to determine whether the bearing is completely separated from the shaft surface due to the small thickness of the air film produced using the prototype generally at the micrometer level. As a result, it is a challenge to accurately measure the maximum force of radial levitation in the bearing. For this reason, a force measurement experimental bench was developed to indirectly measure the bearing force by observing and measuring the state of friction between the bearing and the inclined surface. During the experiment, the angle between the tilting axis and the horizontal plane was adjusted constantly. When the positive pressure applied by the bearing on the tilting axis is equal in magnitude and opposite in direction to the levitation force, it can be considered that the bearing achieves frictionless levitation. In this case, the acceleration of the sliding bearing is approximately equal to the acceleration of gravity. The downward acceleration of the bearing can be measured with a photoelectric timer, the mass of the bearing and the magnitude of load can be measured with precision balance, and the positive pressure applied by the bearing on the tilting axis can be calculated with the gravity of the bearing and load, as well as the angle between the tilting axis and the horizontal plane. The principle of conducting measurements on the test bench is shown in Figure 9c. During the experiment, the bearing cylinder is first allowed free fall with a vertical distance of H*, and a measurement is performed to determine the instantaneous velocity v1 of the bearing cylinder falling to the position of H*. Then, with the cylinder mounted on the tilting axis, a photoelectric gate is placed under the tilting axis to measure the instantaneous velocity of the cylinder passing through the photoelectric gate. The release position of the cylinder and the position of the photogate are adjusted to ensure that the cylinder slides down the tilt axis at a vertical height of H*. With the sleeve released from rest, the instantaneous velocity v2 of the bearing cylinder is measured as it slides down to the H* position, thus determining if v1v2 holds. If not, the inclination angle of the tilting axis θ* is constantly changed. The above process is repeated until v1v2 holds. At this time, it can be considered that the movement of the cylinder conforms to the conservation of mechanical energy. That is to say, there is no contact friction arising between the cylinder and the shaft cylindrical surfaces, which implies that the pressure exerted by the extrusion membrane can be induced by the bearing cylinder in the radial direction of the axial levitation up. The weight of the vibrator and the tilt angle θ* are known. According to the results of force analysis, it is perpendicular to the axis of gravity component—that is, the air membrane bearing force FN. According to the principle followed through the bearing force measurement, we build a force test bench as shown in Figure 9d:
In order to measure the load-bearing capacity of the gas squeeze film, a weight was attached to one end of a thin wire while the other end of the wire was bolted to the longitudinal ribs of the load-bearing cylinder in the experiment. The photoelectric timer was zeroed to measure the instantaneous velocity mode, and the photoelectric gate was placed as appropriate in the vertical direction. The bearing was released at a certain height from rest in the vertical direction and allowed free fall. Then, the photoelectric timer was used to measure the instantaneous velocity v1 at the end position, with the falling height H* recorded. The signal generator was adjusted, the frequency of the AC voltage signal was set to the same as the resonance frequency of the bearing structure—that is, 19 kHz—and the output sinusoidal AC voltage signal was amplified by the piezoelectric ceramic controller and connected to the piezoelectric ceramic piece on the outer surface of the bearing cylinder. At this time, the bearing vibrated under the action of the sinusoidal AC signal with the AC voltage of 75 V and the frequency of 19 kHz. The normal vibration of the gas extrusion membrane bearing occurred on the cylindrical slide at the initial position of the stationary. The photoelectric timer was set to measure the instantaneous speed mode, and the photoelectric gate was placed in a way to maintain a vertical distance from the height of the drop for H*. The bearing was released under the action of gravity from rest along the slide and weighted through the photoelectric gate to read the instantaneous speed v2 of the photoelectric timer. When v1v2 measurement was performed to record the vertical height of the bearing sliding down the H* and the slide rail tilt angle, the tilt angle of the slide rail θ* and the load subjected to the force of gravity G were used to calculate the positive pressure perpendicular to the slide FN = G∙cosθ*, and FN was numerically equal to the radial load-bearing capacity of the bearing. The experimental results of radial levitation force as measured by tilting the shaft down for three sets of bearings are shown in Table 2.

Table 2.
Experimental results of radial levitation force measurement.
By measuring the radial suspension force of the sliding amount of the inclined shaft of the bearing through the experiment when the bearing load mass is 165 g and the tilt angle of the inclined shaft is 36°, the radial suspension force is 1.28 N., and the theoretical case of 1.22 N error is only 4.68%. Thus, the feasibility of applying the alternating implicit differential method is verified.
4. Conclusions
In this paper, the alternating direction implicit method is used to discretize and solve the Reynolds equation of gas extrusion membrane for the design of the load-bearing structure of a gas extrusion membrane. Furthermore, the approximate solution of gas extrusion die pressure distribution is obtained through simplified programming in Matlab and then compared with the finite element method in the unified case. In comparison with the classical finite element method, its calculation accuracy reaches 0.02% under the minimum gas film pressure and 1.03% under the maximum gas film pressure. By changing the parameters of the gas-extruded membrane bearing arithmetic, the effects of amplitude at radial clearance H0 and vibration frequency f on the load-bearing capacity characteristics are explored. Through comparative analysis, it is concluded that when the radial clearance is fixed, the average load-bearing capacity improves with the increase in amplitude. Given a certain amplitude, the larger the radial clearance is, the lower the average load-bearing capacity and the higher the cut-off frequency are. Given certain parameters, there is a cut-off frequency for the extruded air film, at which the optimal extrusion effect is achieved, and the average load-bearing capacity is maximized. For example, when the amplitude a = 5 μm and the radial clearance H0 = 50 μm, the cut-off frequency of the bearing is 19 kHz, and the average load-bearing capacity is 1.22 N. A gas extruded film bearing with a 40 l/mm length, a 20 r/mm diameter, and a 2 h/mm wall thickness is produced. Three sets of gas-extruded film bearings were fabricated, and controlled experiments were carried out considering the actual process conditions. The radial levitation force obtained at a tilting angle of 36° of the tilting axis was 1.28 N for a fixed radial clearance of H0 = 50 μm, a set frequency of 19 kHz, and a mass of 165 g for the bearings and the load. In this paper, the experimental and theoretical analysis of the gas-extruded membrane bearing designed has an error of 4.68% compared with the theoretical case.
Author Contributions
Conceptualization, D.L. and R.M.; methodology, D.L. and R.M.; software, R.M. and Z.S.; validation, D.L. and R.M.; formal analysis, D.L. and R.M.; investigation, W.G. and R.M.; resources, D.L. and F.W.; data curation, W.G. and Z.S.; writing—original draft preparation, R.M.; writing—review and editing, K.Z. and R.M.; visualization, K.Z.; supervision, F.W. and K.Z.; project administration, D.L. and F.W.; funding acquisition, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Liaoning Provincial Department of Education Program Projects, grant number L991689” and “Dalian Science and Technology Innovation Fund, grant number 2018J12GX040”.
Data Availability Statement
The datasets used or analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| h | Coordinate-dependent film thickness function |
| Number of extrusions | |
| k | Time Layer |
| F() | Non-linear equations into a matrix |
| B0 | Initial Matrix |
| ε1,ε2 | Calculation accuracy |
| θ | Dimensionless amplitude |
| H | Dimensionless air film thickness |
| T | Vibration period |
| v1,v2 | Instantaneous speed |
| p | Absolute gas pressure (Pa) |
| η | Gas viscosity coefficient (Pa∙s) |
| u1,u2 | Velocity components of the upper and lower surfaces of the air film in the x-direction (m/s) |
| w1,w2 | Velocity components of the upper and lower surfaces of the air film in the z-direction (m/s) |
| h0 | Initial film thickness () |
| p0 | Ambient pressure (Pa) |
| r | Air film width () |
| P* | Nodal pressure approximation (Pa) |
| F | Air film bearing capacity (N) |
| Pq | Surface pressure (Pa) |
References
- Powell, J.W. A review of progress in gas lubrication. Rev. Phys. Technol. 1970, 1, 96. [Google Scholar] [CrossRef]
- Barnett, M.A.; Silver, A. Application of Air Bearings to High-Speed Turbomachinery; SAE Technical Paper; SAE: Warrendale, PA, USA, 1970. [Google Scholar]
- Kumar, N.; Satapathy, R.K. Bearings in Aerospace, Application, Distress, and Life: A Review. J. Fail. Anal. Prev. 2023, 23, 915–947. [Google Scholar] [CrossRef]
- Gao, Q.; Chen, W.; Lu, L.; Huo, D.; Cheng, K. Aerostatic bearings design and analysis with the application to precision engineering: State-of-the-art and future perspectives. Tribol. Int. 2019, 135, 1–17. [Google Scholar] [CrossRef]
- Abele, E.; Altintas, Y.; Brecher, C. Machine tool spindle units. CIRP Ann. 2010, 59, 781–802. [Google Scholar] [CrossRef]
- Colombo, F.; Lentini, L.; Raparelli, T.; Trivella, A. Gas Bearings Applications in Automotive Fuel Cell Technology. In Proceedings of the I4SDG Workshop 2023: IFToMM for Sustainable Development Goals, Bilbao, Spain, 22–23 June 2023; Springer Nature: Cham, Switzerland, 2023; pp. 307–314. [Google Scholar]
- De Koning, R. Conceptual Design of a Novel Small-Scale CO2 Compressor: Based on Gas Bearing Technology. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2021. [Google Scholar]
- Zhang, X.; Ziviani, D.; Braun, J.; Groll, E. Numerical analysis of gas bearings in oil-free linear compressors. IOP Conf. Ser. Mater. Sci. Eng. 2019, 604, 011008. [Google Scholar] [CrossRef]
- Bulat, P.V.; Volobuev, I.A.; Levikhin, A.A. Optimum Compression in a Wave Compressor with Hybrid Gas Bearings. Russ. Aeronaut. 2019, 62, 512–516. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, X.H.; Peng, N.; Zheng, L.W.; Ke, C.L.; Li, K.R.; Liang, Y.W.; Xiong, L.Y.; Dong, B.; Li, J.; et al. Mathematic prediction and experimental research of gas thrust bearing for high-speed turbo-expander involving hydrogen, helium, nitrogen and air working fluids. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1240, 012059. [Google Scholar] [CrossRef]
- Chasalevris, A.; Sfyris, D. Evaluation of the finite journal bearing characteristics, using the exact analytical solution of the Reynolds equation. Tribol. Int. 2013, 57, 216–234. [Google Scholar] [CrossRef]
- Dowson, D. A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Zaouter, T.; Lasseux, D.; Prat, M. Gas slip flow in a fracture: Local Reynolds equation and upscaled macroscopic model. J. Fluid Mech. 2018, 837, 413–442. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Barkanov, E. Introduction to the Finite Element Method. Available online: http://103.62.146.201:8081/jspui/bitstream/1/469/1/Book.pdf (accessed on 19 July 2023).
- Ma, W.; Kong, X.L.; Xu, Y. Mechanism and test of air hammer instability of aerostatic bearing based on phase-induced vibration. Opt. Precis. Eng. 2020, 28, 1101–1108. [Google Scholar]
- Chen, C.T. Structure Performance Analysis of High Speed Aerobearing and Its Experiment Research. Ph.D. Thesis, Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing, China, 2014. [Google Scholar]
- Liu, Y.; Sun, X.; Sepahvand, K.K.; Marburg, S. Theoretical analysis on the static and dynamic performances of a squeeze film air journal bearing with three separate pads structure. Int. J. Mech. Sci. 2021, 200, 106442. [Google Scholar] [CrossRef]
- Li, H.; Quan, Q.Q.; Hua, Y.X.; Deng, Z.Q. An ultrasonic levitating bearing supporting radial and axial loads. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 769–775. [Google Scholar]
- Shou, T.; Yoshimoto, S.; Stolarski, T. Running performance of an aerodynamic journal bearing with squeeze film effect. Int. J. Mech. Sci. 2013, 77, 184–193. [Google Scholar] [CrossRef]
- EL-Kabeir, S.M.; El-Zahar, E.R.; Rashad, A.M. Effect of chemical reaction on heat and mass transfer by mixed convection flow of casson fluid about a sphere with partial slip. J. Comput. Theor. Nanosci. 2016, 13, 5218–5226. [Google Scholar] [CrossRef]
- Ali, N.; Khan, S.U.; Sajid, M.; Abbas, Z. Flow and heat transfer of hydromagnetic Oldroyd-B fluid in a channel with stretching walls. Nonlinear Eng. 2016, 5, 73–79. [Google Scholar]
- Wang, Y.; Wang, J.; Yao, L.; Yin, W.-Y. EMI analysis of multiscale transmission line network using a hybrid FDTD method. IEEE Trans. Electromagn. Compat. 2021, 63, 1202–1211. [Google Scholar] [CrossRef]
- Feng, D.S.; Chen, C.S.; Dai, Q.W. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chin. J. Geophys. 2010, 53, 2484–2496. (In Chinese) [Google Scholar]
- Birkhoff, G.; Varga, R.S.; Young, D. Alternating direction implicit methods. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 1962; Volume 3, pp. 189–273. [Google Scholar]
- Yan, R.; Yang, X.; Sun, S. A class of explicit–implicit alternating parallel difference methods for the two-dimensional Black–Scholes equation. Int. J. Comput. Math. 2021, 98, 1112–1129. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F. Implicit difference approximation for the time fractional diffusion equation. J. Appl. Math. Comput. 2006, 22, 87–99. [Google Scholar] [CrossRef]
- Namiki, T. A new FDTD algorithm based on alternating-direction implicit method. IEEE Trans. Microw. Theory Tech. 1999, 47, 2003–2007. [Google Scholar] [CrossRef]
- Pierart, F.G.; Santos, I.F. Active lubrication applied to radial gas journal bearings. Part 2: Modelling improvement and experimental validation. Tribol. Int. 2016, 96, 237–246. [Google Scholar] [CrossRef]
- Khots, B. Observability and Mathematics: Fluid Mechanics, Solutions of Navier-Stokes Equations, and Modeling; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).