Key Technologies and Design Methods of Ultra-Precision Aerostatic Bearings

Abstract

Precision measurement technology and instruments are the basis for high-quality development in modern industry. With the specialization of supporting facilities, ultra-precision motion guidance has become a core technology to achieve ultra-precision measurement. Aerostatic bearings have the advantages of low friction and high precision, and are gradually playing an irreplaceable role in precision measurement and instruments. This paper summarizes and puts forward two contradictions for improving the loading capacity of aerostatic bearings, and investigates how to solve them via structural design. This paper analyzes the characteristics of the engineering calculation method, the gauge pressure ratio method, the gas resistance calculation method, and the AFVM (adaptive finite volume method) proposed. Finally, this paper summarizes the application scope of each method, gives solutions to the core problems, and outlines the developing trends.

1. Introduction

Precise measurement is the basis of advanced manufacturing and has become the basic technology used to strengthen the country with respect to science, manufacturing, and quality. Aerostatic guideways, aerostatic cushions/sliders, and other kinds of aerostatic bearing have the advantages of low friction and high precision. Therefore, aerostatic technology is playing an irreplaceable role in precision measurement and instruments. Recently, the continuous development of ultra-precision machining and computer-aided design have also been promoting the development of aerostatic technology. Many kinds of advanced equipment, such as high-velocity motorized aerostatic spindles, are used in high-end equipment manufacturing, measurement, transmission, and many other fields.

But gaseous lubricants are more easily compressed and result in poor loading capacity, compared with most grease lubricants. The key to improving the carrying performance of aerostatic bearings is to improve the average pressure of the film between the friction pairs, called the air film. Depending on the formation of the air film, there are three types of gas lubricant technology [1]: aerostatic, aerodynamic, and squeeze-film technology. Aerostatic bearings have fewer restrictions and wider application than both aerodynamic and squeeze-film ones. In the aerostatic field, there has been a large amount of correlational research in the past two decades, but each method has certain limitations in its use. This paper will help to find a fast design method for different applications and statuses.

2. Contradiction and Unification in Methodology of Aerostatic Bearings

There are two technical problems that can be solved to improve aerostatic bearing performance.

According to the forming principle of air film, improving the loading capacity will weaken the stability.

According to the structural limitation of the throttle, improving the loading capacity is contradictory to miniaturization.

The model of stiffness damping and compressible fluid dynamics could explain the contradictions in principle. But to solve the restriction and improve the loading capacity practically, there are two schools of thought. Some scholars try to suppress vibration under medium-high pressure, such as Ma [2] and Zhang [3]. Some others prefer to optimize the structure under medium-low pressure, such as Gao [4] and Wen [5].

These two schools of thought differ considerably in their working principles, objective functions, and constraint conditions, but reach similar conclusions in a few performance examples. In this section, we will mainly analyze the advantages and disadvantages of these two schools of thought.

2.1. Aerostatic Vibration and Suppression

For aerostatic bearings, the dynamic characteristics of air film vibration include three types: static unstable vibration, dynamic unstable vibration, and micro-vibration.

(1)

Static unstable vibration is a classic self-excited vibration caused by the compressibility of air, pressure change hysteresis, and inertial coupling.

(2)

Dynamic unstable vibration, called “whirl vibration”, usually occurs when the bearing resonates at a self-excited frequency.

(3)

Micro-vibration is caused by turbulent flow and has an amplitude of tens of nanometers with barely any impact on micrometer accuracy.

Therefore, static vibration is the main factor affecting the accuracy of aerostatic bearings and is most worth researching and suppressing. The fundamental reason for static vibration is that the thickness of the air film changes with a little delay after internal and external disturbances. If the compressibility of the gas is considered, the changing volume of the air film must be considered at the same time. But in a variable volume, the mass flow cannot reach equilibrium in an instant, and it needs to wait for a certain time to flow in or out. When the lag time meets the frequency conditions of the system, static vibration will occur, which sounds like a sharp howl.

At present, the research methods for static vibration mainly include the stability criterion, illustration, dynamic stiffness-damping, and the experimental method.

2.1.1. Stability Criterion Method

The stability criterion method introduces continuity conditions to small parameter perturbation. According to the Routh–Hurwitz stability criterion [6], the self-excitation stability condition of an air hammer for an aerostatic system is:

$$\left\{\begin{array}{l}\alpha +\beta >0,\eta >0,q>0,s>0\\ \frac{s}{q}>\frac{\eta }{\alpha +\beta }\end{array}\right.$$

(1)

$$\mathrm{where} \alpha =-\frac{d{M}_{in}}{d{p}_d},\beta =\frac{d{M}_{out}}{d{p}_d},\eta =\frac{d{M}_{out}}{dh},q=\frac{dM}{d{p}_d},s=\frac{dM}{dh}$$

In these equations, M_in is the mass flow at the inlet, M_out is the mass rate at the outlet, M is the mass flow rate after throttling, p_d is the pressure at the orifice outlet, and h is the thickness of the air film. In this method, the air film is regarded as a closed-loop stable system. If the real part of the solution of the characteristic equations is negative, it indicates that the system is stable.

Therefore, the stability criterion method can skip motion equation solving and directly judge whether air hammer vibration will be generated or not. However, this method was found to ignore structural details [3] and cannot easily estimate the impact of its weight and external loading on vibration.

2.1.2. Illustration Method

The illustration method is a manifestation of the time-domain analysis methods, in which the solution of the vibration differential equations is transformed into the relationship between time and displacement. The air film can be compressed along the thickness direction, so the direction of self-excited vibration is perpendicular to the air film. We express the displacement of vibration as a function of time. According to system characteristics, a vibration model can be established according to Equation (2). Therefore, the question can be transformed into solving the initial value of the ordinary differential equation of time.

$$\ddot{x}=f(x,\dot{x},t)$$

(2)

$$\mathrm{where} x=x(t)$$

In this research direction, Belforte [7] used a step response method and established the function of the vibration amplitude with regard to supply pressure, orifice diameter, and air film thickness. Chen [8] plotted a curve of the air film vibrations of different structures, which was in agreement with Belfort’s results. Colombo [9] used a graphical method that reflects stability by displacement. But this kind of method is not suitable for designing small structural parameters and lacks practical use in precision instruments.

2.1.3. Dynamic Stiffness-Damping Method

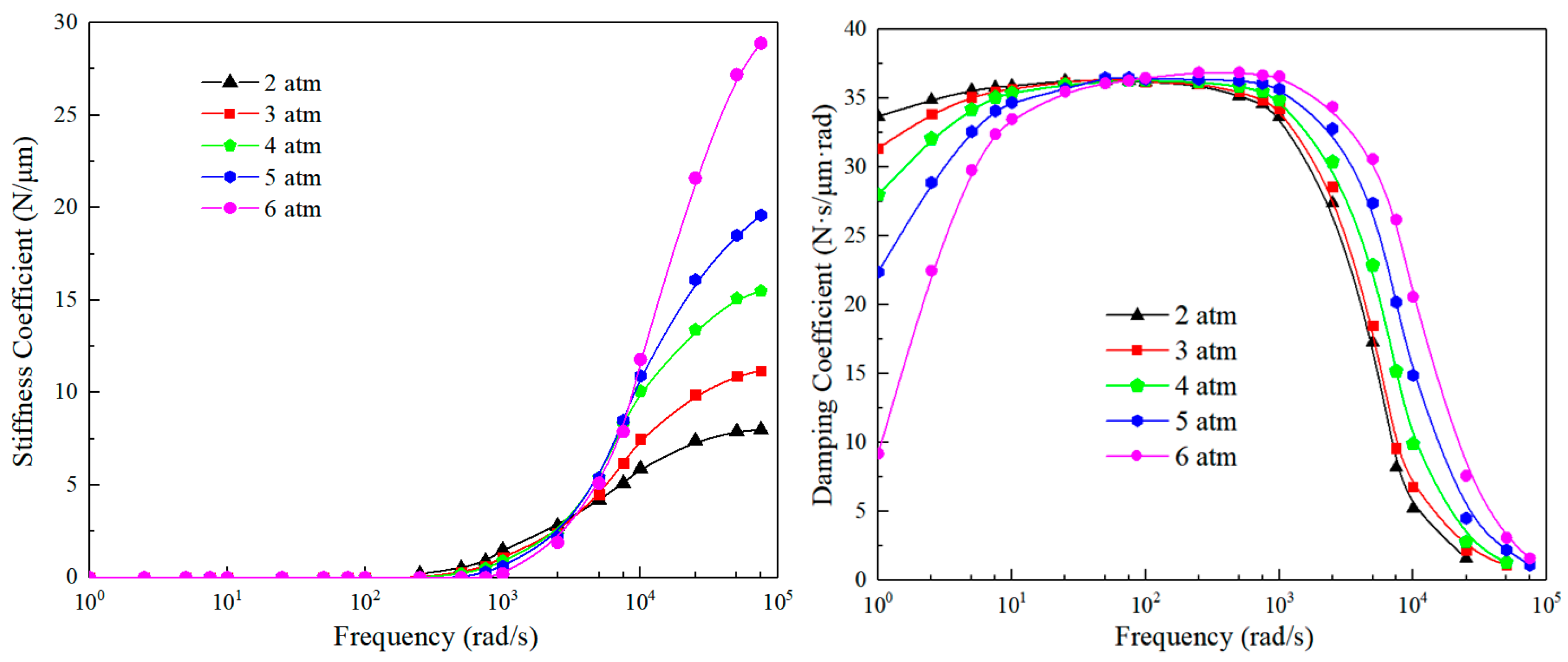
The dynamic stiffness-damping method considers the static vibration as a small harmonic motion near the equilibrium position. The integration of the real parts of the dynamic pressure in the entire air film is considered stiffness, and the integration of imaginary parts is considered damping. Therefore, this method is also called the frequency-domain method, which firstly involves Reynolds equation linearization; secondly, expresses the dynamic characteristic coefficients in plural; and lastly, uses pressure perturbation to replace the loading capacity perturbation, shown as Formulas (3) and (4). At low speed, the air inside can be compressed/expanded in enough time to prevent/promote relative movement. Therefore, the air film exhibits damping behavior. At a high speed, the air film cannot follow the kinematic pair in time, but generates an opposite force because of air viscosity.

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r{h}_0^3\frac{\partial P_0^2}{\partial r}\right)+\frac{1}{r^2}\frac{\partial }{\partial \theta }\left(r{h}_0^3\frac{\partial P_0^2}{\partial \theta }\right)+24\mu RT\frac{Q_0}{rdrd\theta }=0$$

(3)

$$\frac{\partial P_A}{\partial r^2}+\frac{1}{r}\frac{\partial P_A}{\partial r}+\frac{1}{r^2}\frac{{\partial }^2{P}_A}{\partial {\theta }^2}+12\mu RT\frac{\left(\phi P_A-Q_0{P}_0\right)}{P_0{h}_0^{3}rdrd\theta }=-\frac{12\mu \omega P_A}{P_0{h}_0^2}$$

(4)

This method can easily obtain the vibration characteristics in the frequency domain, and is suitable for quantitative research on dynamic performance at high speed, as shown in Figure 1. But [10] indicates that this method cannot intuitively judge whether vibration has occurred or not. Although the influence of frequency can be obtained via graphical analysis, it is difficult to determine the threshold of vibration and provide clear guidance for structural design.

2.1.4. Experimental Method

The experimental method [11,12,13] is the most direct and effective way to obtain the vibration characteristics and distinguish the static unstable vibration, the dynamic unstable vibration, and the micro-vibration. When the ratio of the micro-structure volume of the thrust bearing to the total air film volume is more than 2~10%, or that of the radial bearing is more than 5~15%, gas hammer vibration will occur.

2.2. Throttling Structure and Performance

The methods mentioned above improve the performance by preventing air hammer vibration and increasing the upper limit of inlet pressure. But the “structural school” is focused on optimizing the structure and micro-structure and improving the carrying performance without affecting critical stability. According to classical theory, it is unable to achieve both miniaturization of the structure and the maximization of performance. Thus, various forms of throttling structure have been studied.

The throttling structures include an orifice restrictor, slit restrictor, new material restrictor, and compound restrictor, as shown in

Table 1. The classification of aerostatic throttling structures based on throttle mechanisms.

Restrictor Type	Structure Characteristics	Bearing Capacity	Stability	Consumption of Gas	Difficulty in Manufacturing	Applicability
Orifice restrictor		Large	Poor	Low	Easy	Medium
		Medium	Medium	Medium	Easy	High
Slit restrictor		Medium	Medium	High	Difficult	Low
Porous restrictor		Medium	Good	Low	Difficult	High
Compound restrictor		Large	Good	Medium	Medium	Medium

. Their common principle is to increase the effective throttling area, increase throttling efficiency, or increase throttling pressure, and the common goal is to improve the carrying performance.

2.2.1. Orifice Restrictor

The essence of throttling involves forming a de Laval nozzle, by contracting first, and then, expanding. During this, the potential energy of the inlet air is converted into kinetic energy, and then, into potential energy of the air film. The throttled air is hindered in the following narrow film and results in a reduction in pressure and velocity. Thus, the pressure is homogenized in the air film and provides carrying capacity. However, different orifice restrictors have different throttling and homogenizing effects.

Wang [14] and Guo [15] established analytic models and tested them on two types of orifice restrictor, namely, a cross section and a cylindrical section, and determined the similarities and differences in their carrying performance. Ma [2], Cheng [16], and Zhang [17], respectively, used the finite element method, the finite difference method, and the separation of variables method to study the influence of restrictors and form their own design methods.

However, only the for orifice restrictor is it difficult to eclectically solve the contradiction between carrying performance and structural miniaturization. Gao [4] and Yu [18] optimized an orifice structure, which has the advantages of large carrying capacity, high stiffness, and low mass flow. Its shortcomings lie in the large eddy current and low damping of the air film.

2.2.2. Slit Restrictor

Slit throttling uses narrow and long gaps as restrictors. It is an ideal linear gas supplement with minimal lateral flow and jet impact within the gas film. Slit throttling has a better throttling effect and pressure homogenization effect. But it has higher gas consumption, difficult machining and assembling, and a complex technique, and is easier to block and difficult to clean. In order to solve these problems, the slit throttling structure has evolved into a groove in practical applications. Liu Tun and Du Jianjun [19] proposed a compatible transformation condition for the basic equation of an aerostatic bearing with a slit restrictor, used a weighted residual method to discretize the partial differential equation, and finally, used finite element analysis to analyze the flow field parameters of the bearing.

2.2.3. Porous Restrictor

Porous throttling is performed using special materials, through which a air film with uniform pressure can be formed [20,21]. Due to the uniform distribution of numerous micropores on the porous surface, and the throttling and homogenization effects are better, so the bearing capacity, stiffness, and stability are improved. In recent years, with the maturation of the CFD method, the design of porous throttling aerostatic bearings has been simplified, so the research focus has shifted to material manufacturing and secondary machining.

2.2.4. Compound Restrictor

Compound throttling [5] uses small structures such as recesses and grooves to induce secondary or multi-throttling on the aerostatic working surface, in order to improve throttling efficiency. Earlier research about compound throttling involved reducing the lateral flow and enhancing pressure homogenization using simple structures, such as connected grooves. In the 21st century, the electron beam, ion beam, and laser beam etching techniques, micro-EDM, and electrochemical machining technologies have been gradually improved, and could meet the requirements for the morphology and roughness of micro-, long, narrow structures on an aerostatic working surface, and could promote the development of micro-orifice throttling, recesses-assisted throttling, and groove compound throttling.

2.3. Contradictions and Unification of Methodologies

Both the “structural school” and the “control school” have a consistent purpose: to improve the carrying performance of aerostatic bearing. However, a single technology cannot easily meet the gradually increasing demand for indicators. Thus, the advantages of integrated technologies such as dynamic–static coupling, micro-structure compound throttling, and new material throttling are gradually reflected. Therefore, integrated technologies weaken the inherent contradiction of the two schools in the aspects of both structure and methodology. Taking dynamic–static coupling technology as an example, the main problem is determining how to achieve a stable transition between the pure static pressure state and the dynamic–static pressure coupling state when the speed changes during the start and stop process. Therefore, the solution is to combine new structures and methods to reduce the critical velocity and solve the issue of pressure coupling.

3. Design Methods and Scope of Application

Common methods for aerostatic bearing design include the engineering calculation method, gauge pressure ratio method, gas resistance calculation method, numerical calculation method, etc. These methods have different design ideas, resulting in differences in performance calculations for the same structure.

3.1. Engineering Calculation Method

The engineering design method is usually used for low precision requirements and the initial design stage. The most representative research achievement is from Wang [22]. This method is based on engineering experiences and experiments. It summarizes the relationship between the main parameters and performance, and simplifies the design and analysis process, but is only applicable to specific structure forms and throttling types. On the basis of the engineering design method, performance curves under established conditions can also be drawn, and the design and correction of parameters can be carried out as well. Therefore, the engineering design method is also called the chart design method, and the most representative research achievement in this area is from Powell [23].

The engineering method can be used to quickly design the external dimensions of aerostatic bearings, and estimate their loading capacity. Essentially, it is a simplified analytical calculation method. This kind of method comes from experiences and cannot easily explain changes in the law in principle. Especially for small characteristic changes, the theory may contradict the actual situation. Therefore, the engineering design method is generally used to design structures for large volumes and low precision requirements, such as aerostatic platforms, aerostatic bearings, and other mechanisms.

3.2. Gauge Pressure Ratio Method

The traditional analytical design method is based on a one-dimensional flow model, and uses gas motion equations, continuity equations, and boundary conditions for simultaneous calculation. The gauge pressure ratio is the ratio of local pressure to gas supply pressure (or standard atmospheric pressure), and is one of the key parameters. It affects the performance of aerostatic bearings, and can be used to establish the functions about structural parameters. Thus, the gauge pressure ratio method is a complete analytical method. This method can accurately evaluate the performance of aerostatic bearings and is suitable for various types. The most representative research achievement in this area is from Liu Tun [24].

The gauge pressure ratio method has been fully verified in the development of aerostatic technology and is widely applied. However, using many simplifications (such as dimensionless Reynolds equations) and assumptions (such as the assumption of uniform flow between restrictors), the analysis results show reasonable but undesired deviations from the actual situation. Therefore, a large safety margin is frequently used to compensate for calculation deviation and ensure reliability. Thus, this method is not suitable for situations of limited size and high characteristic requirements.

3.3. Gas Resistance Calculation Method

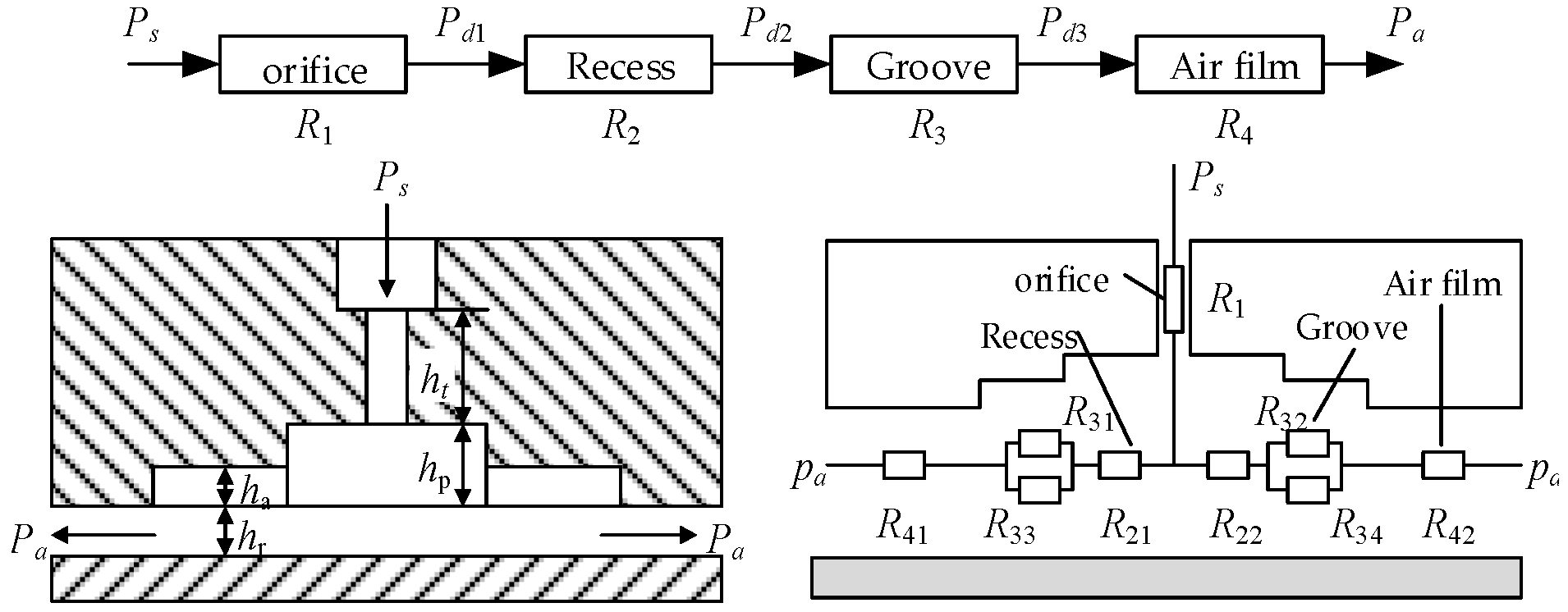
When high-pressure gas flows through restrictors, micro-structures, and gas films, it produces various degrees of airflow resistance, due to factors such as gas viscosity and channel changes. Similar to Ohm’s law in circuits, the gas resistance law also exists in aerostatic bearing calculation. In Equation (5), R_ex is the gas resistance, q is the volumetric flow passing through the region, and Δp is the pressure difference between the gas outlet and inlet in the region. When calculating, the nodes are first set according to the structure, and the pressure and impedance relationships of each node are represented in Figure 2. Then, the pressure distribution is calculated between each node and the pressure integrated to calculate the bearing capacity, stiffness, and other performance metrics. This method can be used for aerostatic bearings with complex and dispersed micro-structures. The most representative research achievement in this area is from Li [25].

$$R_{\mathrm{ex}}=\frac{\mathsf{\Delta }p}{q}$$

(5)

3.4. Numerical Calculation Method

The more complex the aerostatic structure, the larger the deviation between the simplified analytical model and actual one. In contrast, the numerical [26,27] and CFD [28,29,30] methods have fewer calculations of assumptions and simplifications. In order to solve the problem of non-convergence in the finite volume numerical solution of the compound throttling global flow field, we propose an adaptive finite volume method (AFVM) to capture and subdivide the mesh near the wall [5,31].

As shown in Formula (6), the dimensionless velocity u⁺ is modified as a mixed function of the linear law, which is associated with laminar flow, and of the logarithmic law, which is associated with turbulent flow. Then, the corrected u⁺ is incorporated into Equation (6) to obtain a new first grid height y_min, as shown in Formula (7).

According to y_min, the mesh is generated and used for finite volume calculation. Finally, the above steps are repeated until the grid height of the viscous bottom layer reaches y⁺ < 5, and the logarithmic law layer reaches y⁺ < 60.

$$u^{+}=e^{\mathsf{\Gamma }}{u}_{lam}^{+}+e^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathsf{\Gamma }$}\right.}{u}_{turb}^{+}$$

(6)

$$\mathrm{where} \mathsf{\Gamma }=-\frac{C_a{\left(y^{+}\right)}^4}{1+C_b{y}^{+}}, C_a=0.01, C_b=5$$

$$y_{min}=y_{min}^{+}\mu /\rho u\sqrt{\frac{0.058R{e}^{-\frac{1}{5}}}{2}}$$

(7)

$$\mathrm{where} u^{+}=\frac{u}{u_{\tau }},y^{+}=\frac{u_{\tau }}{\mu }y$$

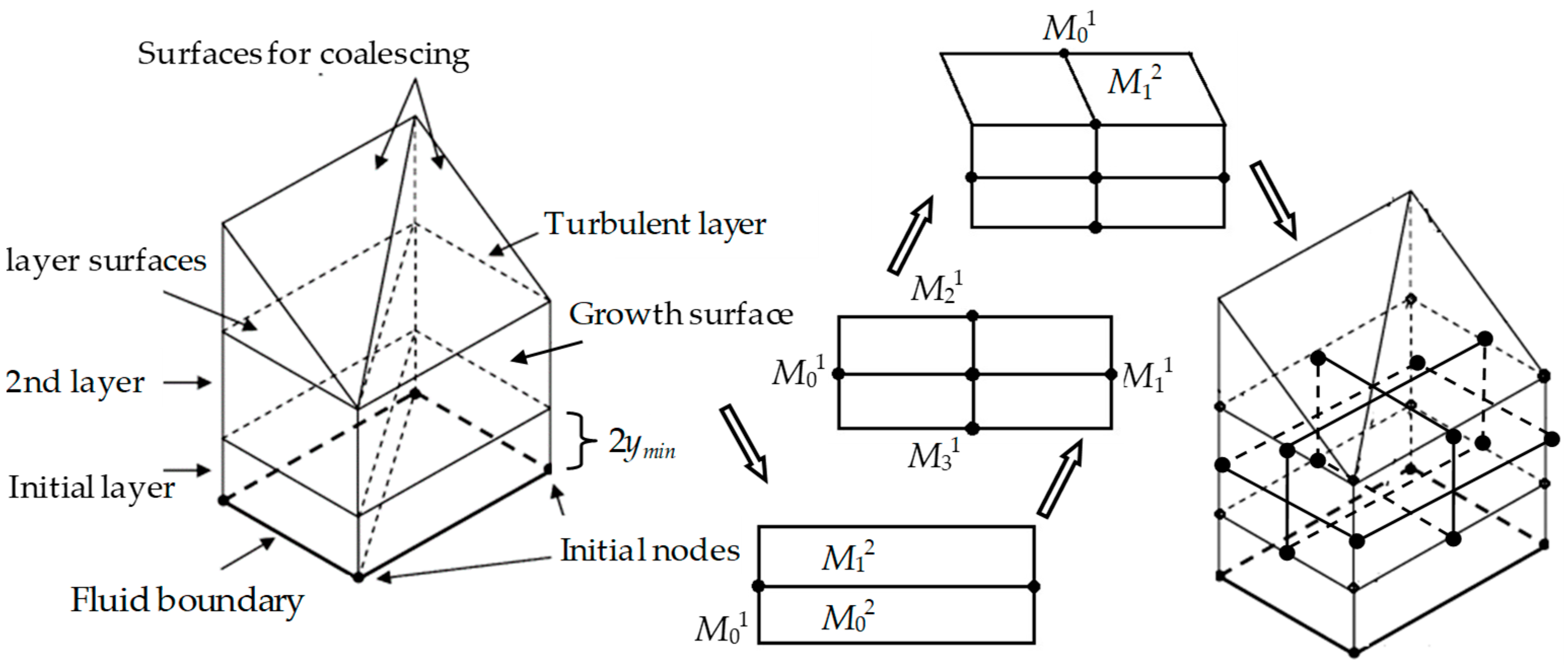
The adaptive method for the boundary layer is shown in Figure 3. The initial thickness of the layer is strictly divided according to 2y_min. The surface along the thickness direction is the growth surface, so each hexahedron grid is composed of four growth surfaces and two layer surfaces. Firstly, the subdivision starts from the initial nodes at the boundary of the computational domain, and the nodes are set according to an aspect ratio of less than 5:1.

Then, the growth surface is first symmetrically segmented along the thickness direction of the layer, that is, the line M₀¹ subdivides the original growth surface into two parts, M₁² and M₀². To keep the aspect ratio, the growth surface is symmetrically segmented along the normal direction of the computational domain boundary, with lines M₀¹, M₁¹, M₂¹, and M₃¹ dividing the original growth surface into four parts, M₀², M₁², M₂², and M₃². Finally, the subdivided grid will move the position of the initial node up one layer for further subdivision.

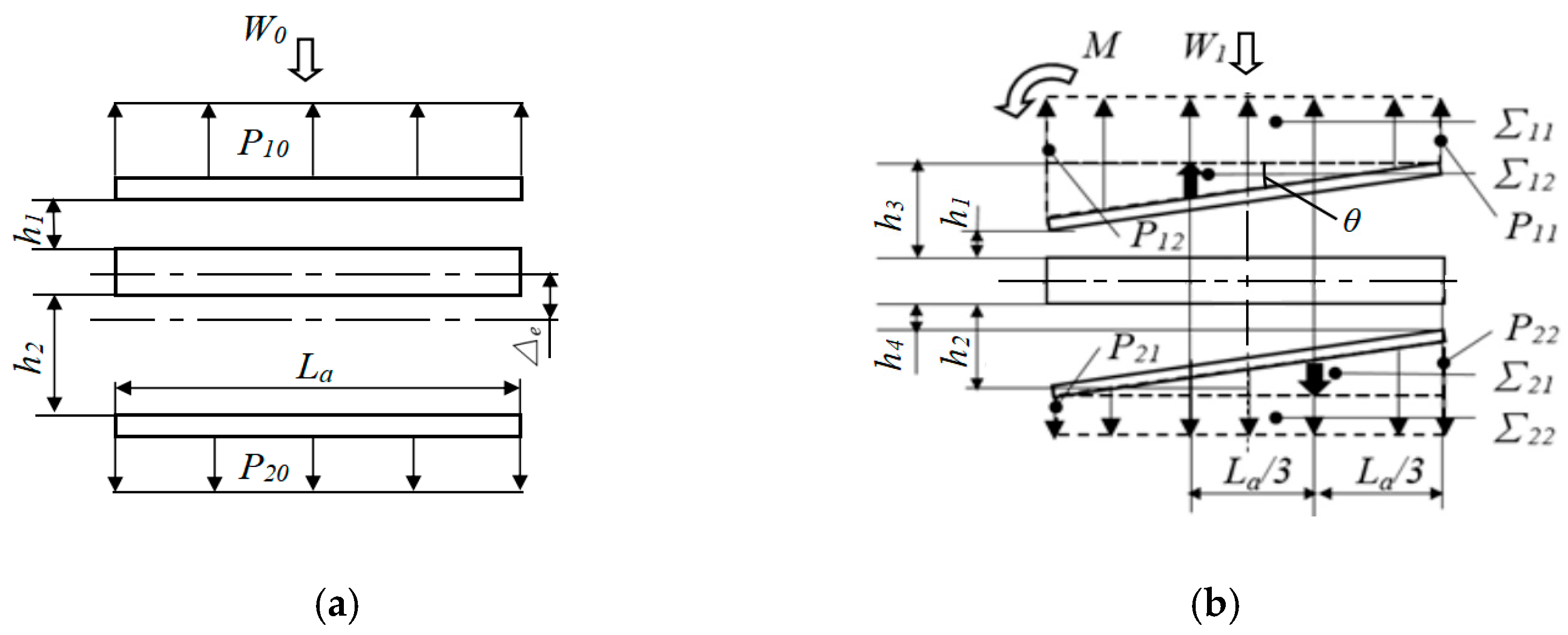
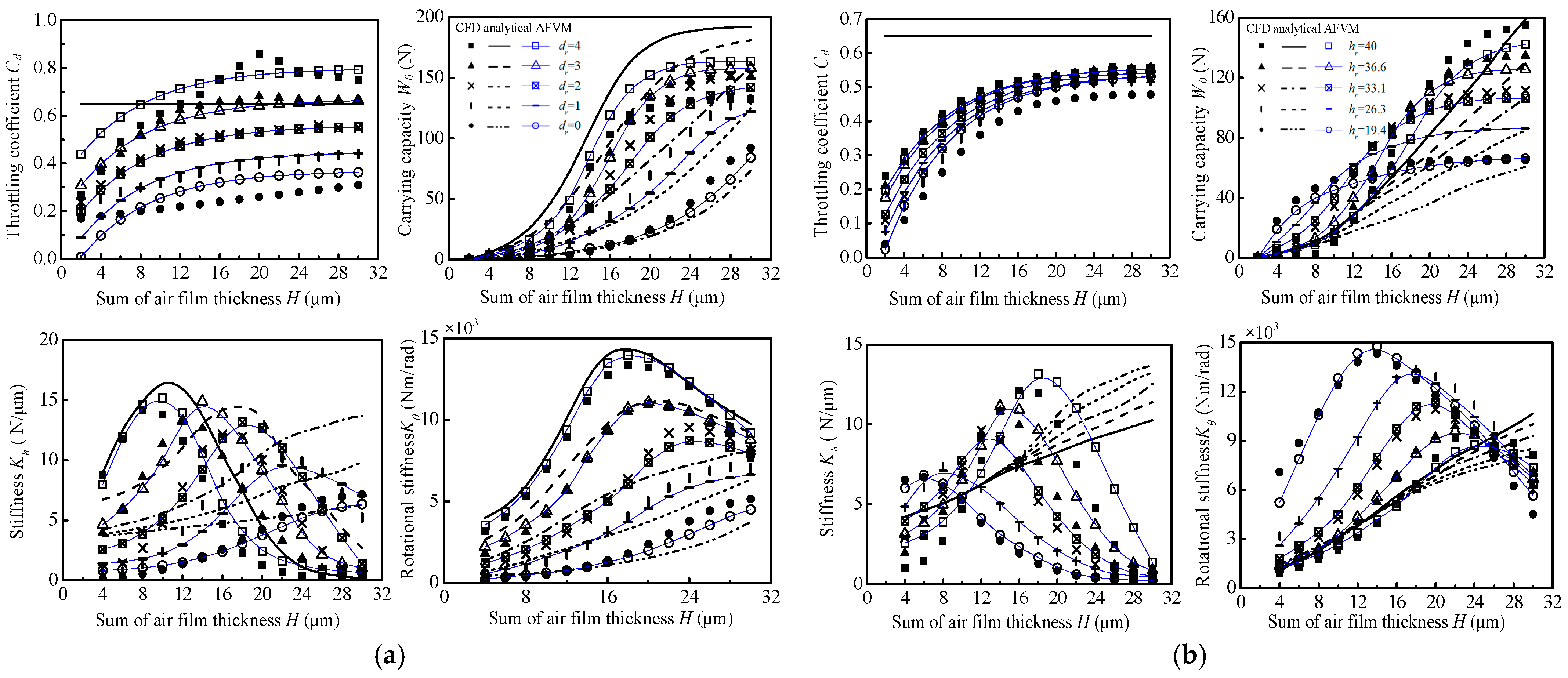
Using the AFVM method, we studied the effects of recess diameter and recess depth on the throttling coefficient, carrying capacity, stiffness, and rotational stiffness of the aerostatic guideway. As shown in Figure 4, the important variables in the design process, such as the sum of air film thickness H, which means h₁ + h₂, are also studied. The guideway with both upper and lower air films has greater stiffness and rotational stiffness, but loses some of loading capacity. In order to balance these performance indicators, we established a mathematical model for mechanical properties, as shown in Formulas (8)–(10).

$$W_0=P_{10}°L_a{L}_b-P_{20}°L_a{L}_b=L_a{L}_b(P_{10}-P_{20})$$

(8)

$$W_1={\displaystyle {\sum }_{11}+}{\displaystyle {\sum }_{12}-}{\displaystyle {\sum }_{21}-}{\displaystyle {\sum }_{22}=}{L}_a{L}_b(P_{11}-P_{21})$$

(9)

$$M={\displaystyle {\sum }_{12}\times \left(\frac{L_a}{2}-\frac{L_a}{3}\right)+}{\displaystyle {\sum }_{21}\times \left(\frac{L_a}{2}-\frac{L_a}{3}\right)}=\frac{1}{3}{L}_a{\displaystyle {\sum }_{21}}$$

(10)

$$\mathrm{where} {\displaystyle {\sum }_{21}=}\frac{1}{2}{L}_a{L}_b(P_{22}-P_{21})=\frac{1}{2}{L}_a{L}_b(\frac{W_0}{L_a{L}_b}-P_{12}+P_{22})=\frac{1}{2}{W}_0-\frac{1}{2}{L}_a{L}_b(P_{11}-P_{21})=\frac{1}{2}\left(W_0-W_1\right)$$

Using the model above, W₀ and W₁ can be obtained through AFVM. The derivative of W₁ at air film thickness h and tilt θ are stiffness K_h and rotational stiffness K_θ. As shown in Figure 5, the result indicates that AFVM can accurately characterize the impact of micro-structure changes at the micron level on throttling coefficient and carrying performance.

The result shows that throttling coefficient C_d is a function of H, d_r, and d_r. Previously, C_d could only be estimated through experience or experiments, but the AFVM method can obtain the regular pattern of C_d. Therefore, we used a large amount of data to fit the function of C_d, as in Formula (11). Figure 5 shows that the extreme point and corresponding H can be obtained if the stiffness or rotational performance is an optimization item. Thus, suggestions for d_r, and the selection of d_r with stiffness as the optimization target, are also provided in Formulas (12) and (13). This method has been used in the design of numerous small aerostatic guideways for photolithography machines [32].

$$C_d=(0.01h_{ri}-0.88)e^{-0.14H}+0.11d_{ri}+0.32$$

(11)

$$d_{ri}=1000\times \left(-0.58H+12.7\right)$$

(12)

$$h_{ri}=0.58H+11.4$$

(13)

To verify the design law via AFVM at multiple applications and statuses, it is still necessary to compare it with other methods under different requirements and structures.

4. Characteristics and Application Scope of Different Methods

In order to compare the characteristics of the methods above, the carrying performance of two guideways and two bearings are calculated, as shown in

Table 2. Comparison of bearing capacity and experimental results of four types of aerostatic structure calculated using four methods.

Guideways	Guideway A	Guideway B	Guideway C	Guideway D
Parameters (same parts)	Aerosurface: 84 mm × 20 mm Number of restrictors: 14 Gas supply pressure: 0.4 MPa Film thickness: 10 μm Orifice diameter: 0.2 mm Recess diameter: 2 mm		Aerosurface diameter: 40 mm Number of restrictors: 3 Gas supply pressure: 0.4 MPa Film thickness: 15 μm Orifice diameter: 0.3 mm Recess diameter: 4 mm
Parameters (different parts)	Consistent recess depth: 40 μm	Gradient recess depth: 10–40 μm	No equalizing groove	Groove width: 0.7 mm Groove depth: 10 μm
Experiment	42.8 N [33]	63.4 N [33]	Approximately 85 N [11]	Approximately 120 N [11]
Engineering method [23]	100.8 N	100.8 N	113 N	113 N
Gauge pressure ratio method [24]	58.6 N	82.7 N	107.6 N	107.6 N
Gas resistance method [25]	42.5 N	81.7 N	80.2 N	133.1 N
AFVM	47.9 N	62.6 N	83.2 N	128.8 N

.

The result shows that the engineering design method cannot easily reflect the impact of recesses and grooves on bearing performance, and the calculated values are too large. Therefore, using this method requires a large safety margin and is suitable for situations with large structures, thick gas films, and low precision requirements (such as D). The gauge pressure ratio method can reflect the impact of recesses on bearing performance, but it adopts the assumption of uniform flow, making it difficult to reflect the impact of pressure equalization grooves on bearing performance. It is suitable for structures with good self-pressure homogenization characteristics (such as A, D). The air resistance method can reflect the impact of recesses and equalizing grooves on bearing performance, and can be used to judge trends in micro-structure changes, or to design aerostatic devices without micro-structures (such as C).

AFVM is theoretically suitable for calculating all types of aerostatic structure, with high design precision but low efficiency. It is suitable for calculating complex or asymmetric compound throttling structures (such as B).

In summary, for slightly larger aerostatic equipment, the engineering design method can be used for low precision requirements or the pre-design stage. For aerostatic equipment with a medium size, good symmetry, recesses, and equalizing grooves, the gauge pressure ratio calculation method can be used. For situations where there are extreme requirements for bearing, stiffness, and rotational stiffness performance, when designing special micro-structures, the air resistance method is suitable for the law exploration stage. Additionally, the AFVM is suitable for performance calculation at the stage of the final structure.

In addition, regardless of the design method used, the performance of bearings is calculated more precisely than the performance of guideways, which is due to the symmetry of the bearings making the assumption of uniform flow closer to reality.

5. Key Technology and Development Trends

In order to solve the contradiction between mechanical performance, air film stability, and structural miniaturization, there are currently three key technologies: the coupling of aerostatic and aerodynamic bearings, micro-structure optimization, and new material throttling.

Aerostatic and aerodynamic coupling technology combines the throttling effect with the pumping effect to provide higher air film support. Therefore, changing the critical speed of the aerodynamic effect through new structures and control methods is the main developing trend for this technology.

Micro-structure optimization is an important technology to achieve multi throttling. We used AFVM to solve the high-speed near-wall flow field, theoretically and experimentally studied the influence of micro-structure parameters on the mechanical performance of the aerostatic guideway, corrected the flow coefficient, and obtained a calculation model.

Porous material throttling is a kind of technology that heavily relies on new materials with high surface hardness, good wear resistance, and uniform porosity. Currently, the core problems are the material manufacturing method and the secondary machining technology.