A Hydraulic Reciprocating Rod Seal’s Life Evaluation Method Incorporating Failure Mechanism Analysis and Test Observation Data
Abstract
1. Introduction
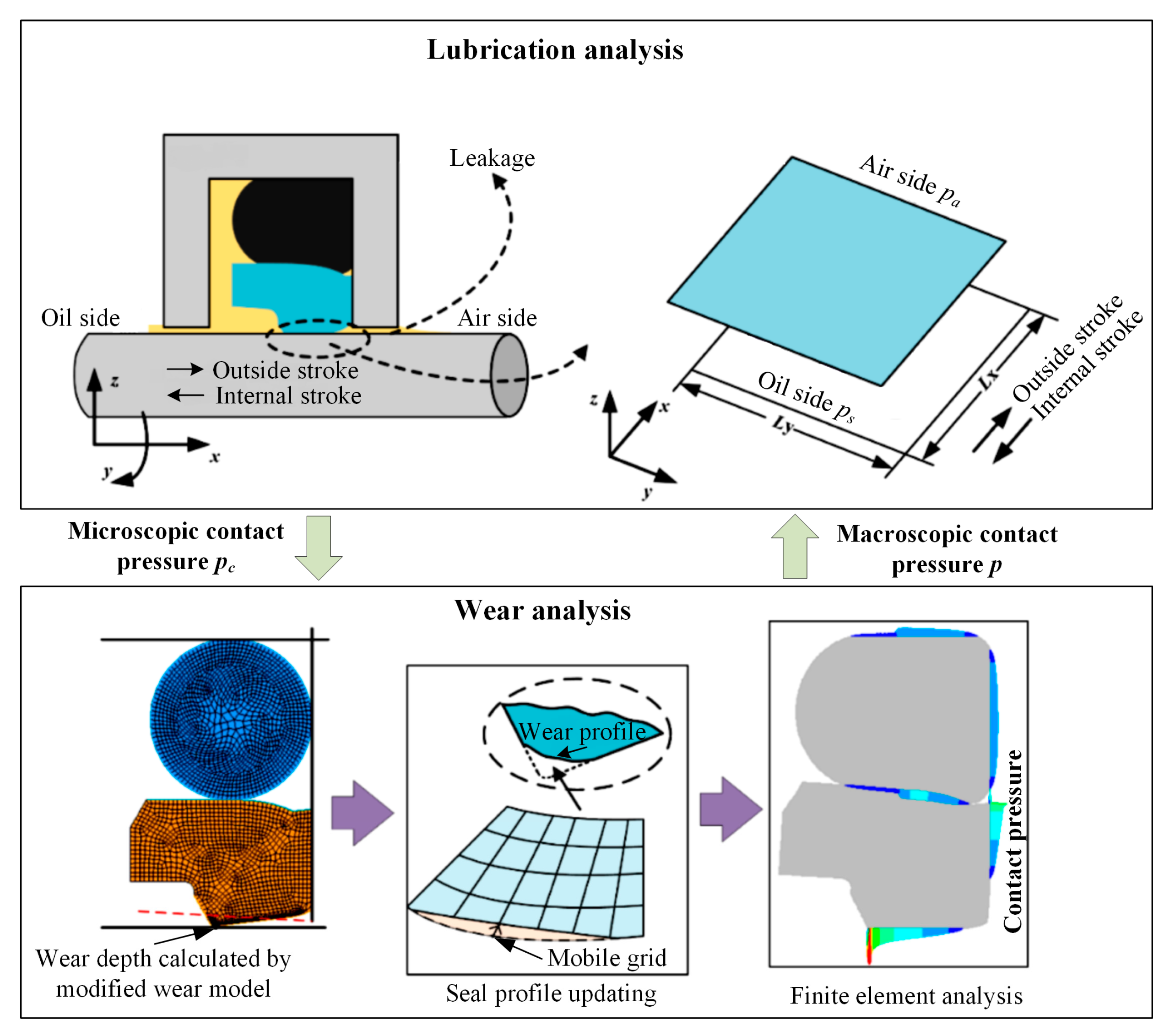
2. System Description
3. Wiener Process-Based Degradation Model with Measurement Error
3.1. Wiener Process Degradation Model
- (1)
- X(t) has independent increments, when t4 > t3 > t2 > t1, X(t4) − X(t3) and X(t2) − X(t1) are independent from each other;
- (2)
- The independent increment obeys the normal distribution, , where .
3.2. Measurement Error Analysis
4. Degradation Mean Function for Reciprocating Rod Seal
5. Remaining Life Prediction
5.1. Parameter Estimation
5.2. Random Parameter Update
5.3. Lifetime Prediction
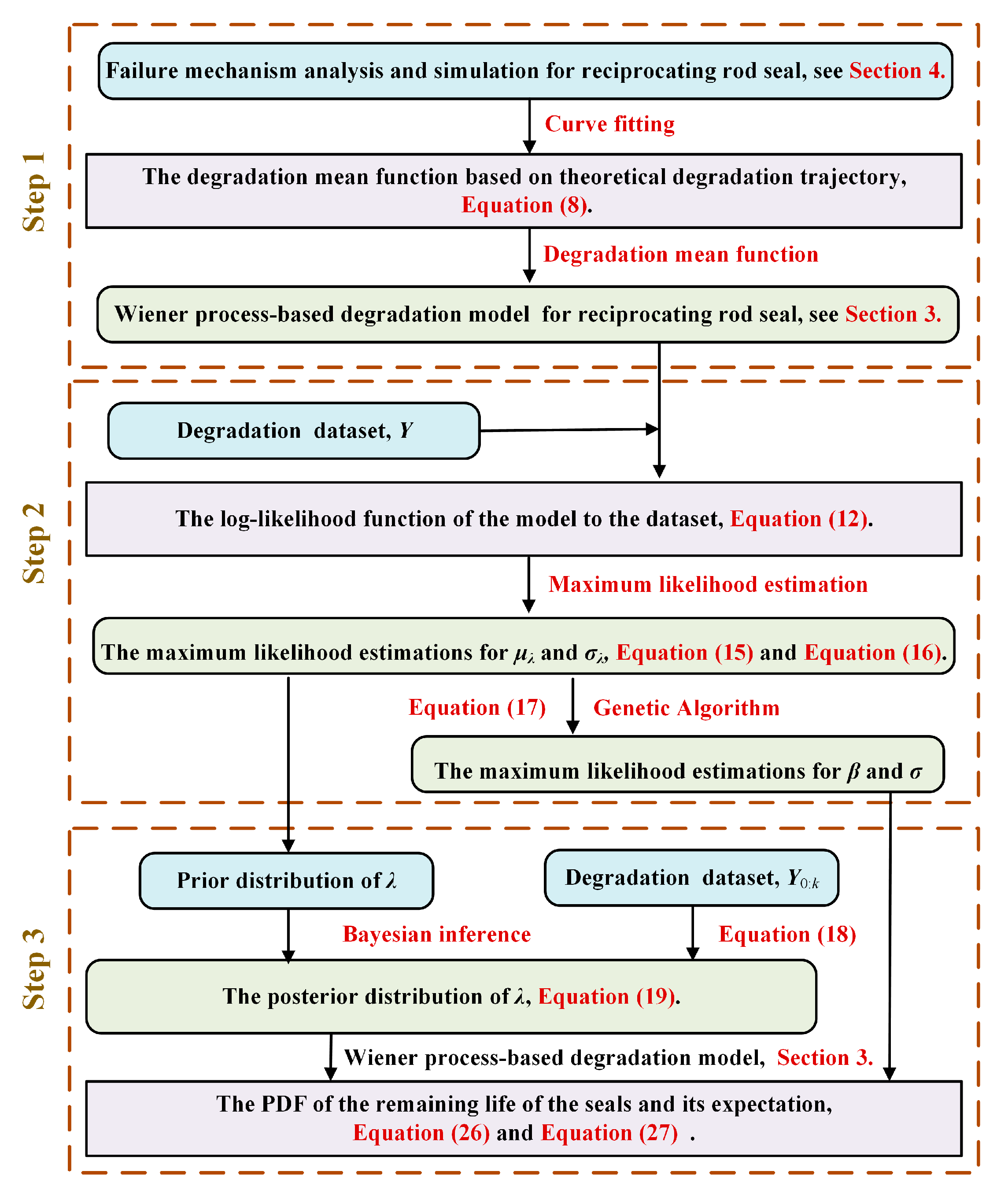
6. The Proposed Framework
7. Experimental Study
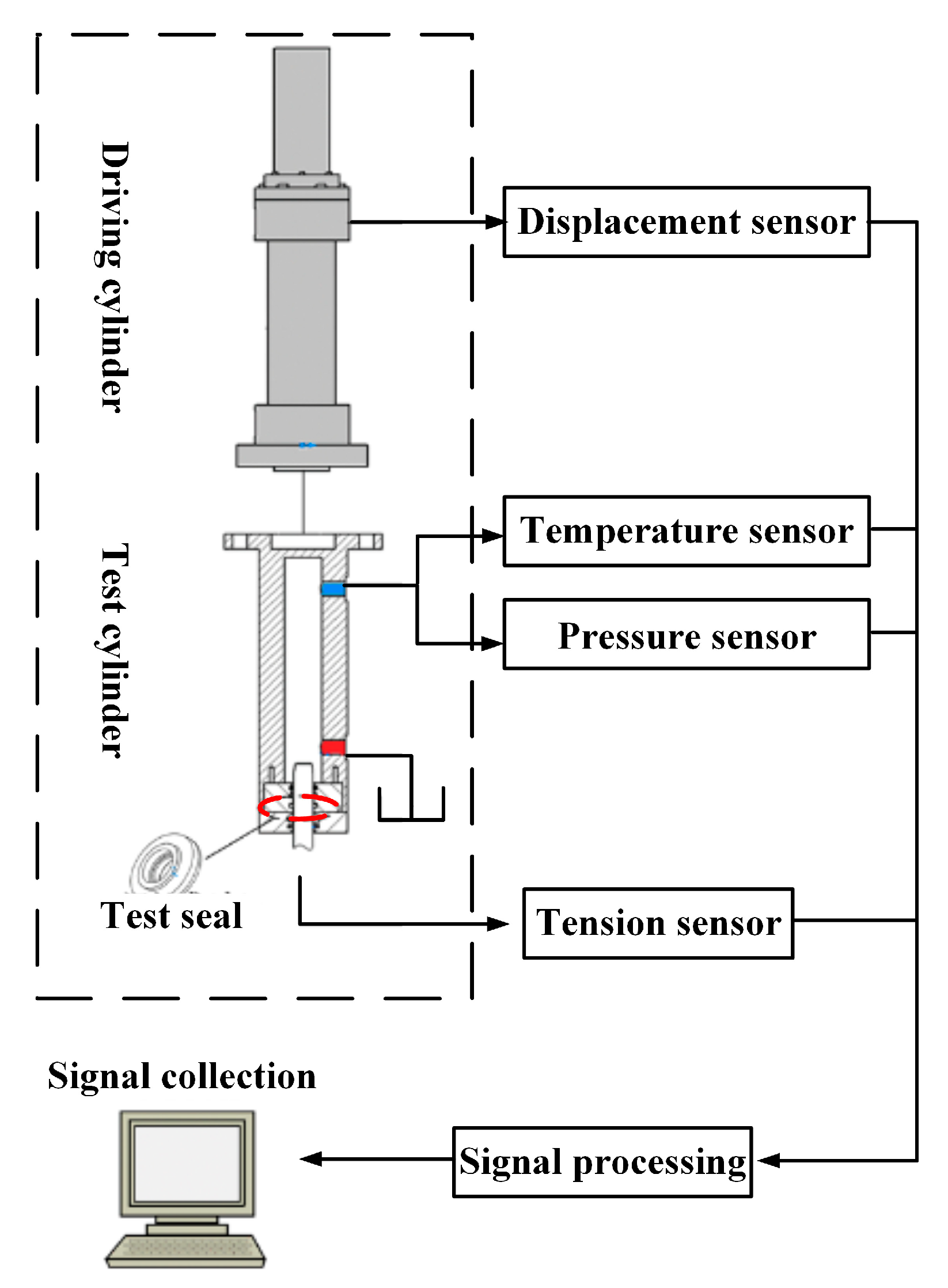
7.1. Experimental Approach
7.2. Discussions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| AIC | Akaike Information Criterion |
| B(•) | standard Brownian |
| FEA | Finite Element Analysis |
| FEM | Finite Element Model |
| GA | Genetic Algorithm |
| M0 | The model proposed in this paper |
| M1 | The nonlinear degenerate model without considering measurement error |
| N | The number of seals for degradation measurement |
| N(•) | Normal distribution |
| Probability density function | |
| PI | Performance Index |
| PTFE | Poly-Tetra-Fluoro-Ethylene |
| TL | First reach-time |
| X(t) | True degradation process |
| Xi | True amount of degradation at ti |
| Degradation increment of a degradation process X(t) | |
| Y(t) | Observed degradation process |
| Y0,k | The degenerate quantity observation vector for the seals from instants t0 to tk |
| Yi | The measured amount of degradation at ti |
| Yn | The vector of observed value of the degradation of the n-th seal |
| The vector of observed degradation increment | |
| The observed degradation increment of i-th sample | |
| f(ε) | Probability density function of ε |
| The number of parameters to be estimated in the model | |
| r(t) | The degradation rate |
| t | Time |
| ti | Degradation time |
| w | The failure threshold |
| The degradation trajectory | |
| (•) | Gamma function |
| β | Diffusion coefficient |
| ε | Measurement error |
| λ | Drift coefficient |
| Parameter vector | |
| g(θ) | The log-likelihood function |
| Positive definite tridiagonal matrix |
References
- Gu, Y.Q. Fluid Dynamic Seals; Petroleum University Press: Dongying, China, 1990. [Google Scholar]
- Zhang, S.J. Hydraulic Seals; Chemical Industry Press: Beijing, China, 2012. [Google Scholar]
- Paige, J.; Stephens, L.S. Surface characterization and experimental design for testing of a radial lip seal. Tribol. Trans. 2004, 47, 341–355. [Google Scholar] [CrossRef]
- Li, W.; Stephens, L.S.; Wenk, J.F. Experimental benchmarking of the numerical model of a radial lip seal with a surface textured shaft. Tribol. Trans. 2013, 56, 75–87. [Google Scholar] [CrossRef]
- Kanakasabai, V.; Warren, K.H.; Stephens, L.S. Surface analysis of the elastomer in lip seals run against shafts manufactured with micro-cavity patterns. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 723–736. [Google Scholar] [CrossRef]
- Horve, L. The correlation of rotary shaft radial lip seal service reliability and pumping ability to wear track roughness and microasperity formation. SAE Trans. 1991, 100, 620–627. [Google Scholar]
- Békési, N.; Váradi, K. Wear simulation of a reciprocating seal by global remeshing. Period. Polytech. Mech. Eng. 2010, 54, 71–175. [Google Scholar] [CrossRef]
- Békési, N.; Váradi, K.; Felhős, D. Wear simulation of a reciprocating seal. J. Tribol. 2011, 133, 031601. [Google Scholar] [CrossRef]
- Sui, H.; Pohl, H.; Schomburg, U.; Upper, G.; Heine, S. Wear and friction of PTFE seals. Wear 1999, 224, 175–182. [Google Scholar] [CrossRef]
- Wang, Z.; Draper, D.; Hodapp, T. Radial lip seal simulation using ANSYS non-standard procedures. In Proceedings of the International ANSYS Conference, Pittsburgh, PA, USA, 22–26 October 2006; pp. 1–12. [Google Scholar]
- Li, X.; Peng, G.L.; Li, Z. Prediction of seal wear with thermal-structural coupled finite element method. Finite Elem. Anal. Des. 2014, 83, 10–21. [Google Scholar]
- Angerhausen, J.; Woyciniuk, M.; Murrenhoff, H.; Schmitz, K. Simulation and experimental validation of translational hydraulic seal wear. Tribol. Int. 2019, 134, 296–307. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.P.; Shi, J. Mixed elastohydrodynamic lubrication model of rotary lip seal with non-Gaussian surfaces: Experimentation verification and numerical analysis on effects of sealed pressure. Sci. Progress 2021, 104, 00368504211017010. [Google Scholar] [CrossRef]
- Peng, C.; Guo, S.R.; Ouyang, X.P.; Zhou, Q.H.; Yang, H.Y. Mixed Lubrication Modeling of Reciprocating Seals Based on a Developed Multiple-Grid Method. Tribol. Trans. 2018, 61, 1151–1161. [Google Scholar] [CrossRef]
- Day, K.; Salant, R.F. Thermal elastohydrodynamic model of a radial lip seal, part I-analysis and base results. J. Tribol. 1999, 121, 1–10. [Google Scholar] [CrossRef]
- Guo, F.; Jia, X.; Huang, L.; Salant, R.F. The effect of aging during storage on the performance of a radial lip seal. Polym. Degrad. Stab. 2013, 98, 2193–2200. [Google Scholar] [CrossRef]
- Guo, F.; Jia, X.; Lv, M.; Wang, L.; Salant, R.F.; Wang, Y. The effect of aging in oil on the performance of a radial lip seal. Tribol. Int. 2014, 78, 187–194. [Google Scholar] [CrossRef]
- Guo, F.; Jia, X.; Wang, L.K.; Salant, R.F. The effect of wear on the performance of a rotary lip seal. J. Tribol. 2014, 136, 041703. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.P.; Zhang, C. A multiscale wear simulation method for rotary lip seal under mixed lubricating conditions. Tribol. Int. 2018, 121, 190–203. [Google Scholar] [CrossRef]
- Shao, Y.H.; Kang, R. A life prediction method for O-ring static seal structure based on physics of failure. In Proceedings of the Prognostics and System Health Management Conference, Zhangjiajie, China, 24–27 August 2014; pp. 16–21. [Google Scholar]
- Sun, J.J.; Gu, B.Q.; Wei, L.; Feng, X.; Liu, Q.H. Predicting seal life for contact mechanical seals. J. Chem. Ind. Eng. 2008, 12, 3095–3100. [Google Scholar]
- Zhou, J.F.; Gu, B.Q. Lifetime Prediction of Mechanical Seal Based on Artificial Neural Networks. Fluid Mach. 2006, 34, 19–23. [Google Scholar]
- Liu, D.; Wang, S.P.; Tomovic, M.M. Degradation modeling method for rotary lip seal based on failure mechanism analysis and stochastic process. Eksploat. Niezawodn. Maint. Reliab. 2020, 22, 381–390. [Google Scholar] [CrossRef]
- Zhang, C.H.; Lu, X.; Tan, Y.; Wang, Y. Reliability demonstration methodology for products with Gamma Process by optimal accelerated degradation testing. Reliab. Eng. Syst. Safe 2015, 142, 369–377. [Google Scholar] [CrossRef]
- Peng, C.Y. Inverse Gaussian processes with random effects and explanatory variables for degradation data. Technometrics 2015, 57, 100–111. [Google Scholar] [CrossRef]
- Peng, W.; Li, Y.F.; Yang, Y.J.; Mi, J.; Huang, H.Z. Bayesian Degradation Analysis with Inverse Gaussian Process Models Under Time-Varying Degradation Rates. IEEE Trans. Reliab. 2017, 66, 84–96. [Google Scholar] [CrossRef]
- Peng, W.; Li, Y.F.; Yang, Y.J.; Huang, H.Z.; Zuo, M.J. Inverse Gaussian process models for degradation analysis: A Bayesian perspective. Reliab. Eng. Syst. Saf. 2014, 130, 175–189. [Google Scholar] [CrossRef]
- Qin, H.; Zhang, S.; Zhou, W. Inverse Gaussian process-based corrosion growth modeling and its application in the reliability analysis for energy pipelines. Front. Struct. Civil Eng. 2013, 7, 276–287. [Google Scholar] [CrossRef]
- Ye, Z.S.; Tsui, K.L.; Wang, Y.; Tsui, K.L.; Pecht, M. Degradation data analysis using wiener processes with measurement errors. IEEE Trans. Reliab. 2013, 62, 772–780. [Google Scholar] [CrossRef]
- Ran, H.L.; Wang, S.P.; Liu, D. A multiscale wear model for reciprocating rod stepseal under mixed lubricating conditions based on linear elasticity. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 161–180. [Google Scholar] [CrossRef]
- Tang, S.J.; Guo, X.S.; Yu, C.Q.; Zhou, Z.J.; Zhou, Z.F.; Zhang, B.C. Real time remaining useful life prediction based on nonlinear Wiener based degradation processes with measurement errors. J. Cent. South Univ. 2014, 21, 4509–4517. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Chen, Y.X.; Guo, J.S.; Wang, Z.Z.; Deng, L. Residual life prediction of devices considering measurement errors and random effects. Syst. Eng. Electron. Technol. 2019, 41, 1658–1664. [Google Scholar]
- Si, X.S.; Wang, W.B.; Hu, C.H.; Zhou, D.H.; Pecht, M.G. Remaining useful life estimation based on a nonlinear diffusion degradation process. IEEE Trans. Reliab. 2012, 61, 50–67. [Google Scholar] [CrossRef]

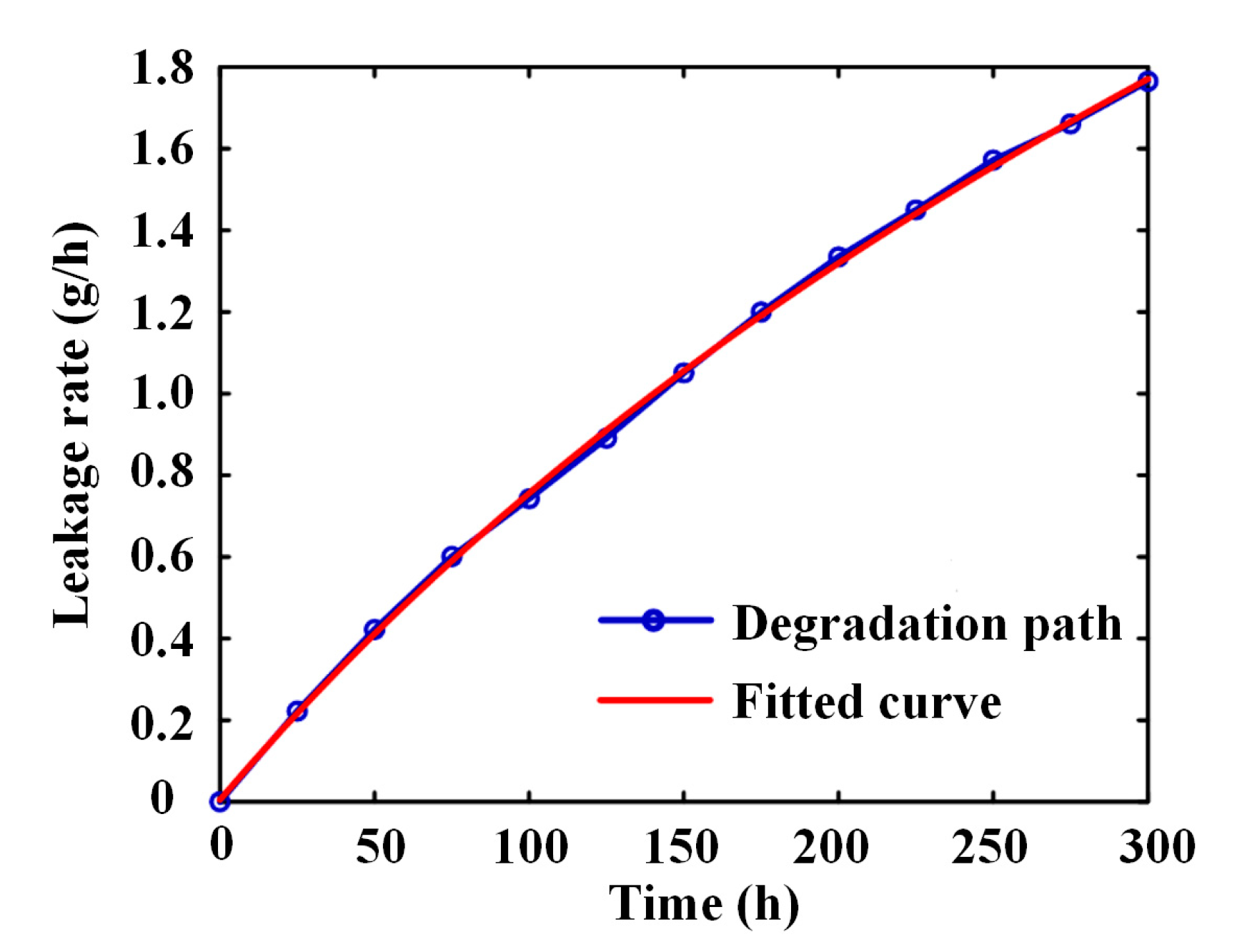

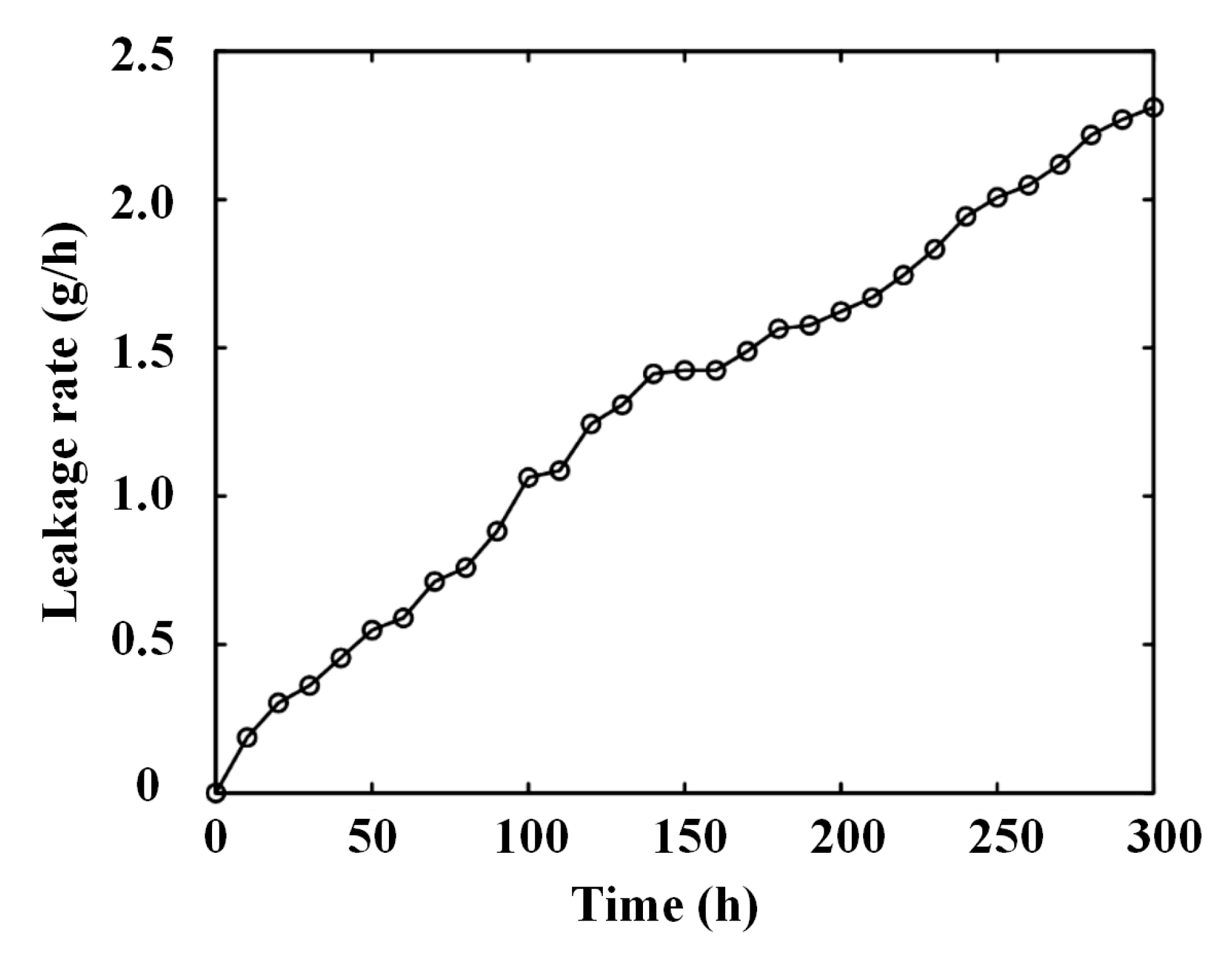

| Time (hours) | 10 | 20 | 30 | 40 | 50 |
| Observation (g/h) | 0.183 | 0.292 | 0.351 | 0.453 | 0.548 |
| Time (hours) | 60 | 70 | 80 | 90 | 100 |
| Observation (g/h) | 0.592 | 0.701 | 0.760 | 0.869 | 1.059 |
| Time (hours) | 110 | 120 | 130 | 140 | 150 |
| Observation (g/h) | 1.089 | 1.251 | 1.292 | 1.403 | 1.427 |
| Time (hours) | 160 | 170 | 180 | 190 | 200 |
| Observation (g/h) | 1.431 | 1.490 | 1.563 | 1.578 | 1.621 |
| Time (hours) | 210 | 220 | 230 | 240 | 250 |
| Observation (g/h) | 1.665 | 1.746 | 1.833 | 1.950 | 2.001 |
| Time (hours) | 260 | 270 | 280 | 290 | 300 |
| Observation (g/h) | 2.052 | 2.111 | 2.205 | 2.271 | 2.315 |
| Candidate Models | Measurement Error |
|---|---|
| M0 | √ |
| M1 | x |
| Parameters | μλ | β2 | σ2 | g | AIC | |
|---|---|---|---|---|---|---|
| M0 | 1.3126 | 1.5435 × 10−4 | 1.5420 × 10−4 | 1.2017 × 10−4 | 51.0560 | −94.1120 |
| M1 | 1.3125 | 1.7801 × 10−4 | 1.7798 × 10−4 | - | 50.9767 | −95.9534 |
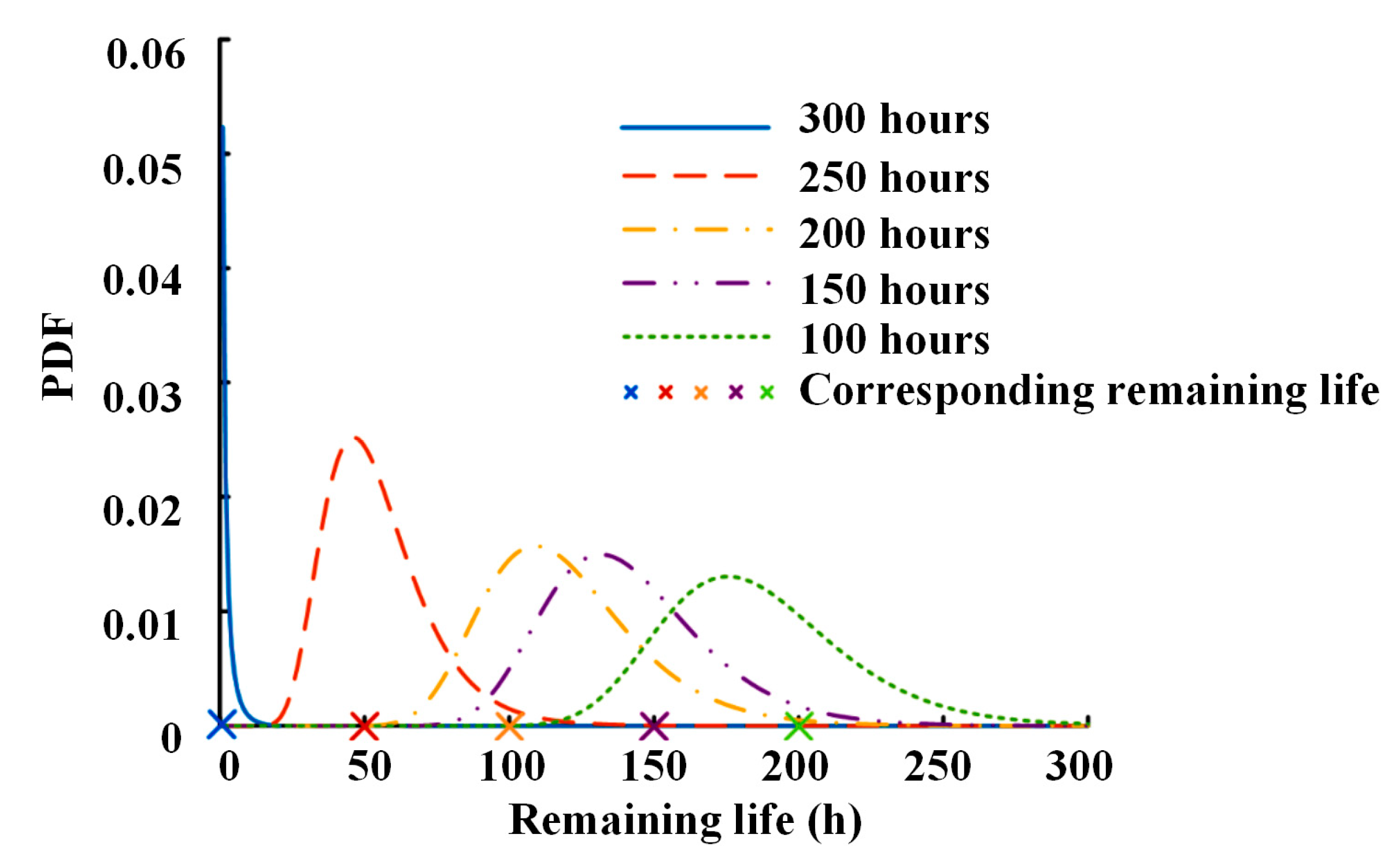
| Observation Time | Remaining Life Expectation | Actual Remaining Life | Error |
|---|---|---|---|
| 300 h | 0.2 h | 0 h | - |
| 250 h | 53.2 h | 50 h | 6.4% |
| 200 h | 116.2 h | 100 h | 16.2% |
| 150 h | 137.8 h | 150 h | 8.1% |
| 100 h | 180.4 h | 200 h | 9.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Liu, D.; Wang, S.; Shang, Y. A Hydraulic Reciprocating Rod Seal’s Life Evaluation Method Incorporating Failure Mechanism Analysis and Test Observation Data. Lubricants 2023, 11, 319. https://doi.org/10.3390/lubricants11080319
Duan X, Liu D, Wang S, Shang Y. A Hydraulic Reciprocating Rod Seal’s Life Evaluation Method Incorporating Failure Mechanism Analysis and Test Observation Data. Lubricants. 2023; 11(8):319. https://doi.org/10.3390/lubricants11080319
Chicago/Turabian StyleDuan, Xiaochuan, Di Liu, Shaoping Wang, and Yaoxing Shang. 2023. "A Hydraulic Reciprocating Rod Seal’s Life Evaluation Method Incorporating Failure Mechanism Analysis and Test Observation Data" Lubricants 11, no. 8: 319. https://doi.org/10.3390/lubricants11080319
APA StyleDuan, X., Liu, D., Wang, S., & Shang, Y. (2023). A Hydraulic Reciprocating Rod Seal’s Life Evaluation Method Incorporating Failure Mechanism Analysis and Test Observation Data. Lubricants, 11(8), 319. https://doi.org/10.3390/lubricants11080319






