The establishment of the digital twin of the pin-on-disk tribometer consisted of two parts which are elaborated upon in the following subsections. The first part describes how the virtual geometry was reconstructed in the macroscopic and microscopic roughness scales from the post-test topographies of the real-life pin and disk. The second part highlights the fundamentals of the solver that was used to simulate the Stribeck curve acquisition.
2.2.1. Virtual Geometry Reconstruction
The macro- and microscopic post-test topographies were first processed with the software Gwyddion
© to correct the measurement defects through interpolation with the Laplace equation, rotate the topography towards its mean plane as an initial levelling guess, set the zero-height mark to the mean plane and limit the height range to 20 µm. In case of the macroscopic pin topography, the points belonging to the area surrounding the pin were excluded in the computation of the mean plane. Furthermore, a Gaussian filter was applied to both the macroscopic pin and disk topographies to remove roughness information and measurement noise by smoothing the profiles. The size of the Gaussian filter was parametrised by its full width at half maximum of the Gaussian distribution. The microscopic roughness topographies, on the other hand, did not require any filtering since their measured profiles were sufficiently smooth due to the higher resolution. The remaining processing was performed with MATLAB
©. On both the macro- and microscopic scale, the disk topography was flipped above the pin and the topographies were aligned such that the
axis pointed in the same direction as the velocity of the disk
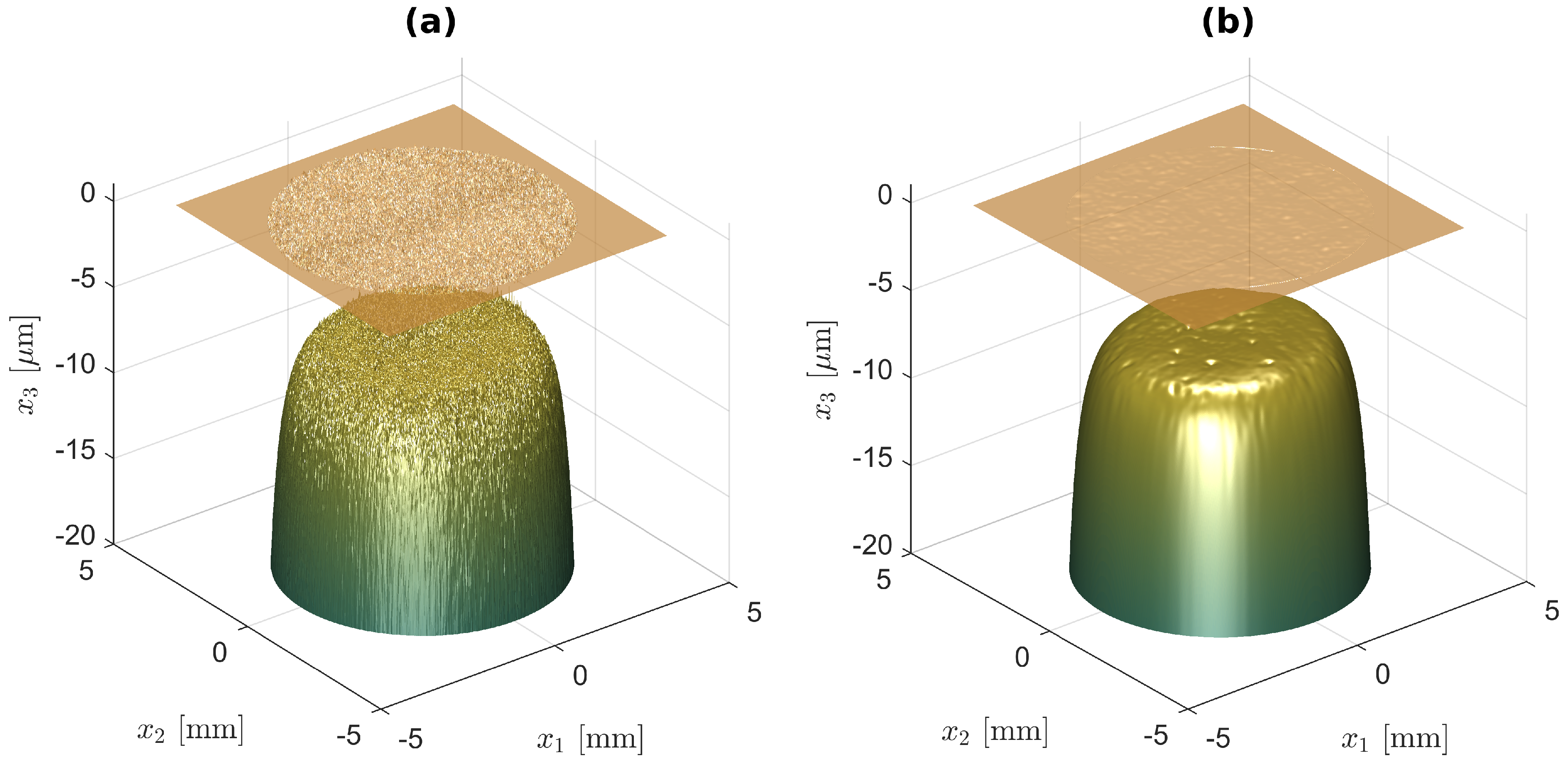
U. In the case of the macroscopic topographies, the origin of the coordinate system was also aligned with the centre of the pin. For the macroscopic pin, the pin height of 1 mm was set relative to its zero-height mark. Since any profile variations in the disc and the pin holder were assumed to be negligible in comparison to the overall pin height, the profiles of the disc and the pin holder around the pin were set to be perfectly smooth. Lastly, the resolution of the macroscopic profiles was adjusted by interpolation. For the roughness topographies, a subdomain of 256 × 256 pixel was extracted without interpolation from the original topography. The effect of the filtering on the resulting macroscopic virtual geometry of test 2.1 is depicted in
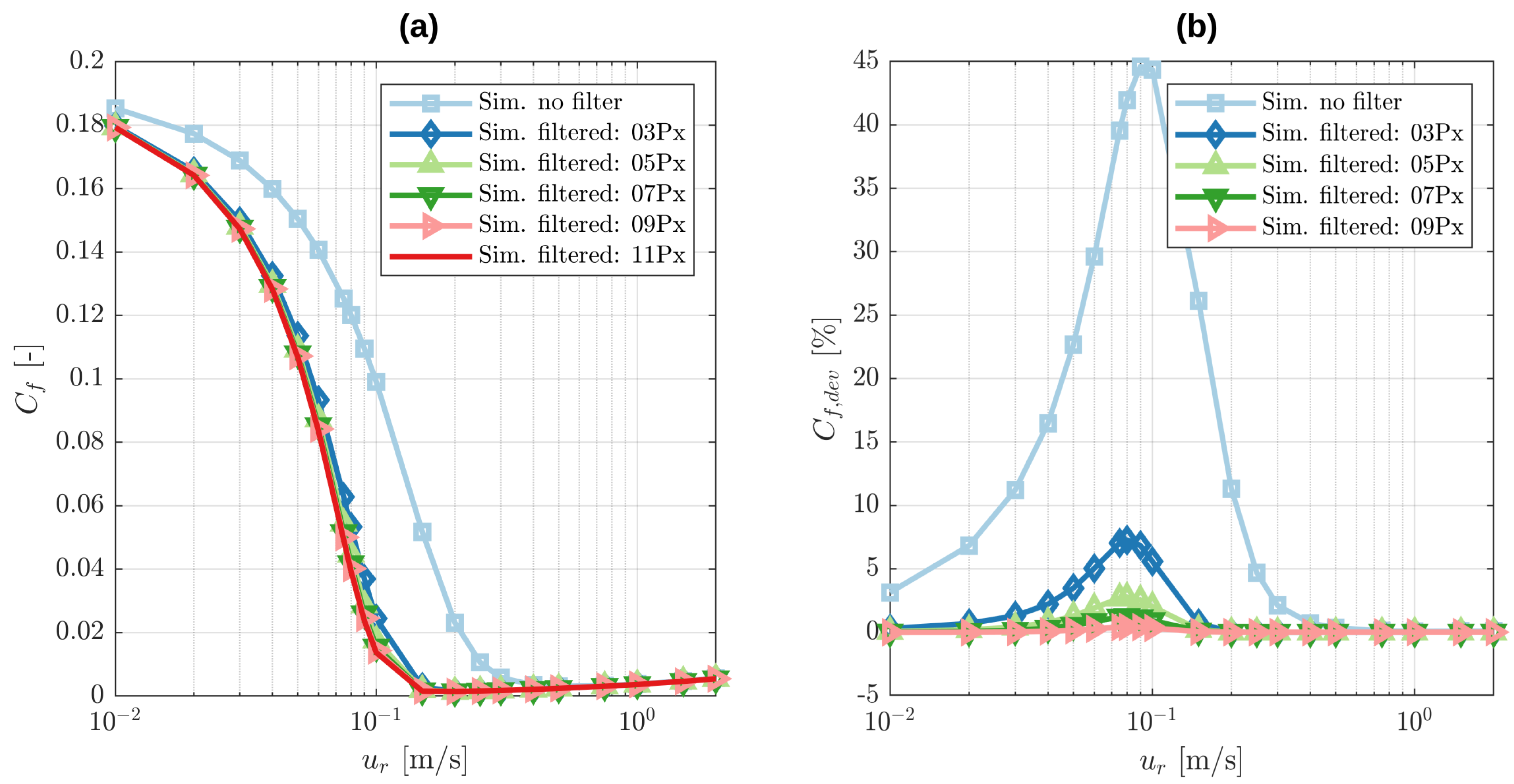
Figure 2 for an exemplary rigid body displacement of 10 µm and resolutions of 500 × 500 pixel, where unfiltered topographies are used in (a) and a 9 pixel Gaussian filter is used in (b).
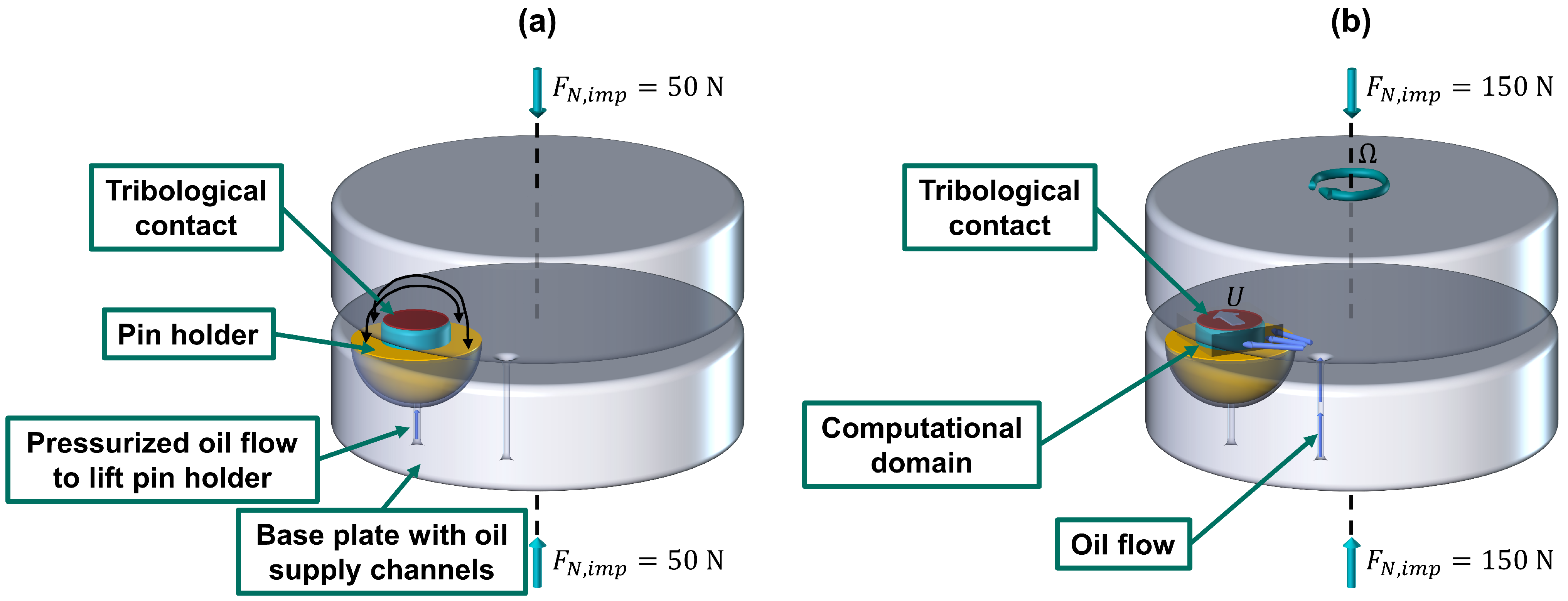
In order to simulate the alignment of the pin against the disk at an imposed normal load of
N as shown in
Figure 1a, a dry contact solver for non-periodic problems was coupled with the torque balance equation. The dry contact solver is based on the conjugate gradient-fast Fourier transform (CG-FFT) algorithm described by Polonsky and Keer [
13] and Sainsot and Lubrecht [
14]. During inner iterations, the code computes the equilibrium of elastic deformation and dry contact pressure for an imposed normal load while using linear convolutions with the kernel function derived from the elastic half-space theory when constant pressure over rectangular discretisation cells is assumed [
15] (Ch. 3.3), [
16]. Young’s modulus
E and the Poisson ratio
of the upper and lower surfaces are considered in the kernel function. Within the contact region, the dry contact pressure can take values between zero as a lower limit and the hardness
H of the material as a maximum limit [
17]. Outside of the contact zone, the pressure is set to zero. Once the dry contact solver delivers a converged dry contact pressure field
, this field is used in outer iterations to evaluate the resulting torques
and
around the
and
axes by summing up over all of the
grid points of size
:
The dimensionless residuals of the torque balances are computed at each outer iteration
n as:
As long as these residuals are larger than a prescribed tolerance of
, angles
and
are adjusted by a PID controller with its coefficients
,
and
:
Afterwards, the new pin profile
is computed by altering the unlevelled pin profile
and the loop is repeated:
Note, however, that
mm is enforced for the area around the pin because there, the levelling is assumed to be negligible in comparison to the pin height. The described levelling process is performed for each of the virtual macroscopic gap geometries. The employed values of the solver parameters are summarised in
Table 4.
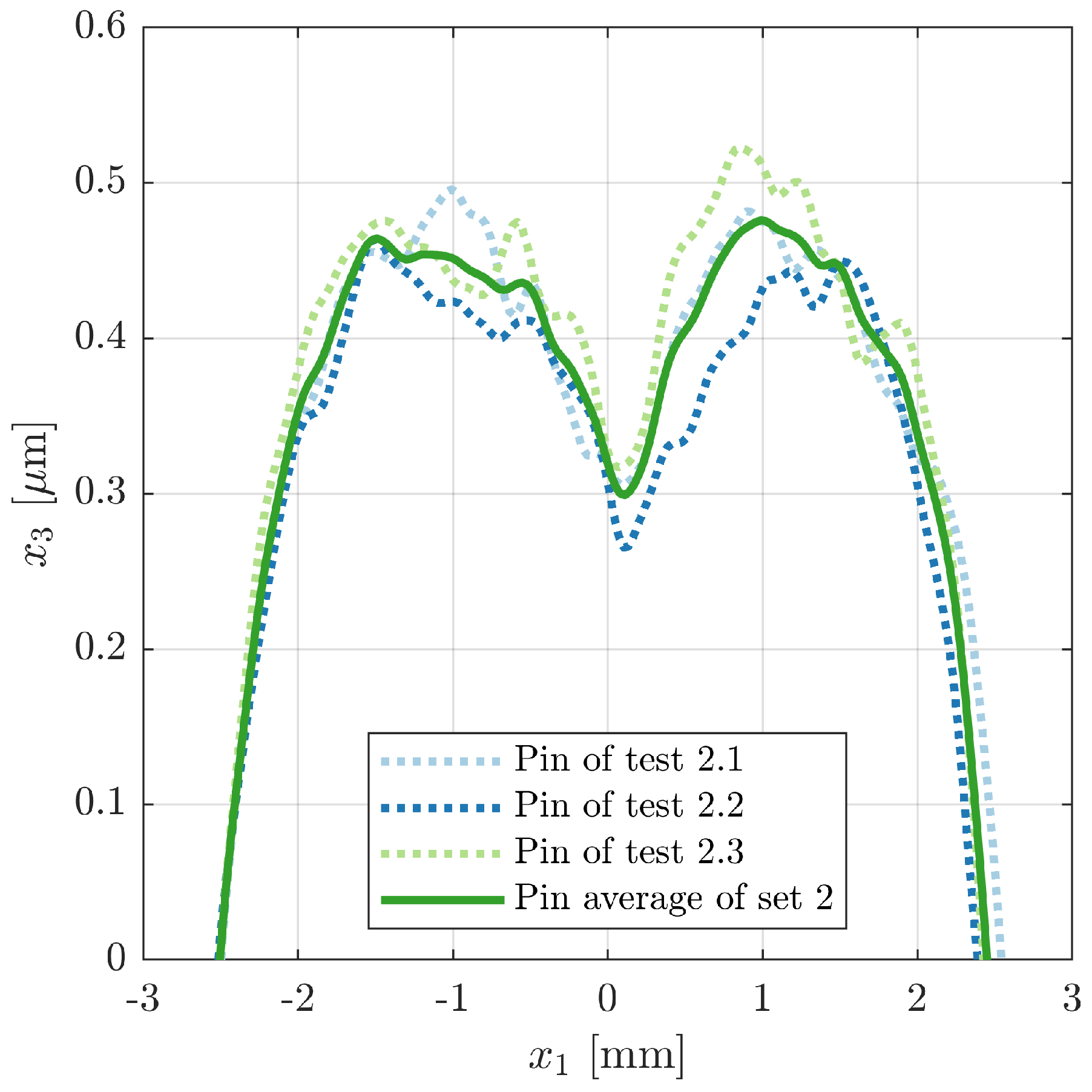
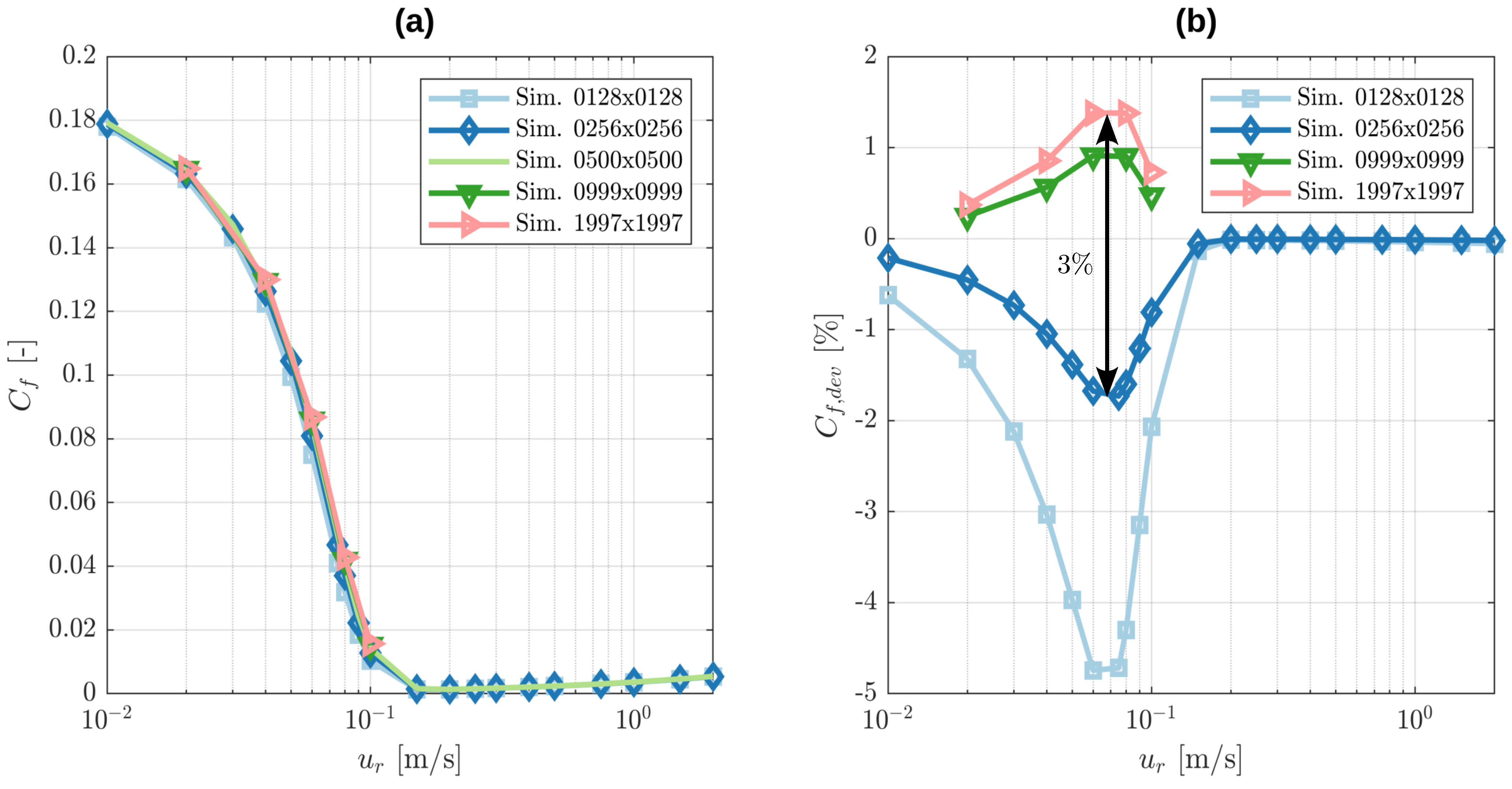
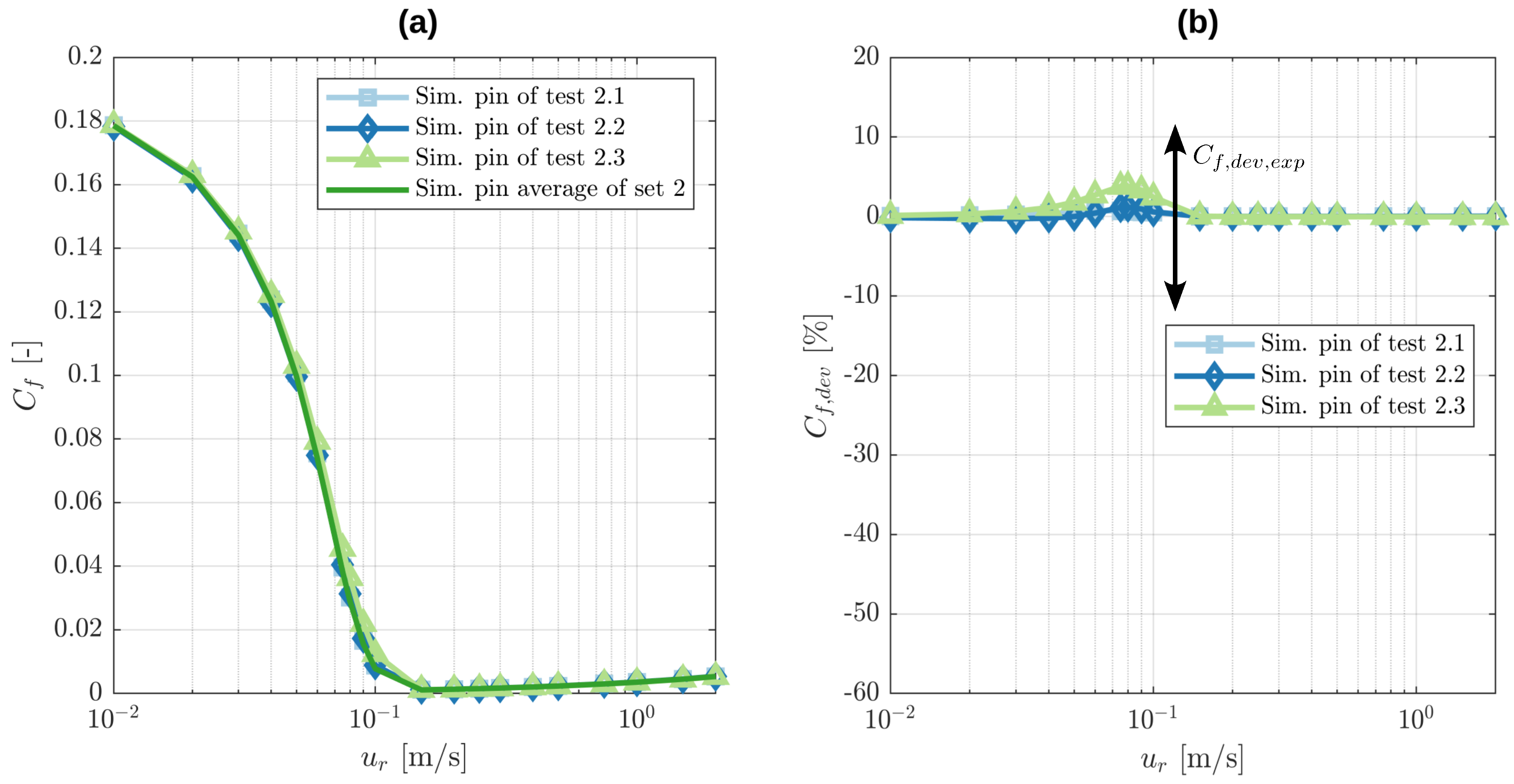
Before the profiles are averaged, the mean plane of each levelled pin profile within a radius of 3 mm from its centre is used to define its new zero-height mark. This is important to reduce the effect of the pin rim on the mean plane which could otherwise distort the following averaging by over-weighting certain pin topographies. For the disks, the zero-height mark remains unchanged. Once this is done for all of the tests within a set, the geometries are interpolated on a new grid on which the set average is determined for pin and disk. Below a truncation height of
µm, the pin height of
mm is enforced again. Finally, the obtained averaged geometry is levelled again. The centre lines of the resulting virtual macroscopic pin topographies of set 2 in the exemplary case of perfectly smooth macroscopic disk topographies as counter bodies are displayed in
Figure 3.
Similarly to some concepts in the literature [
18,
19,
20,
21], the microscopic geometries are used to compute the mean contact pressures, mean gap heights and homogenisation factors for 100 distinct rigid body displacements on the roughness scale
in an exponentially spaced range between
µm and
µm. The averaging is performed over the periodic roughness domain lengths
and
and the periodic roughness time length
. For each rigid body displacement,
discrete time steps are used to periodically move the roughness profile of the disk in the
direction once over the roughness profile of the pin. At each time
t, the asperity contact pressure
and deformed gap height distributions
h are computed at each spatial position (
,
) with a dry contact solver for periodic problems. It is of CG-FFT type and its algorithm is mainly based on the description by Akchurin et al. [
22]. The code computes the equilibrium of elastic deformation and asperity contact pressure for the imposed
while using cyclic convolutions with the kernel function derived from the elastic half-space theory when constant pressure over rectangular discretisation cells is assumed [
15] (Ch. 3.3), [
16]. The Young’s modulus
E and Poisson ratio
of the upper and lower surfaces are considered in the kernel function. Within the contact region, the asperity contact pressure can take values between zero as a lower limit and the hardness
H of the material as a maximum limit [
17]. Outside of the contact zone, the pressure is set to zero. The employed values of Young’s modulus, Poisson ratio and hardness are the same as those used for the levelling solver in
Table 4.
The obtained gap height distribution
h is truncated below 1 nm and used to compute solutions
,
and
of the unsteady local problems:
For the first time step, the steady problem is solved by neglecting the unsteady term. The local problems are discretised with the finite volume method (FVM). Second-order central schemes are used for the spatial derivatives, while the first-order Euler implicit scheme is used for the temporal derivative. Periodic boundary conditions are employed. One point of the domain is used for the Dirichlet condition
. The value of the Dirichlet condition can be chosen arbitrarily and does not influence the final homogenisation factors since they are only a function of the gradients of
,
and
. Furthermore, the discretised form of Equation (
8) becomes independent of
by setting the time step size to
, thus cancelling out
in the final expression. Once all time steps are solved for, their average is computed to obtain the mean contact pressure
, mean gap height
and the homogenisation factors
,
,
and
:
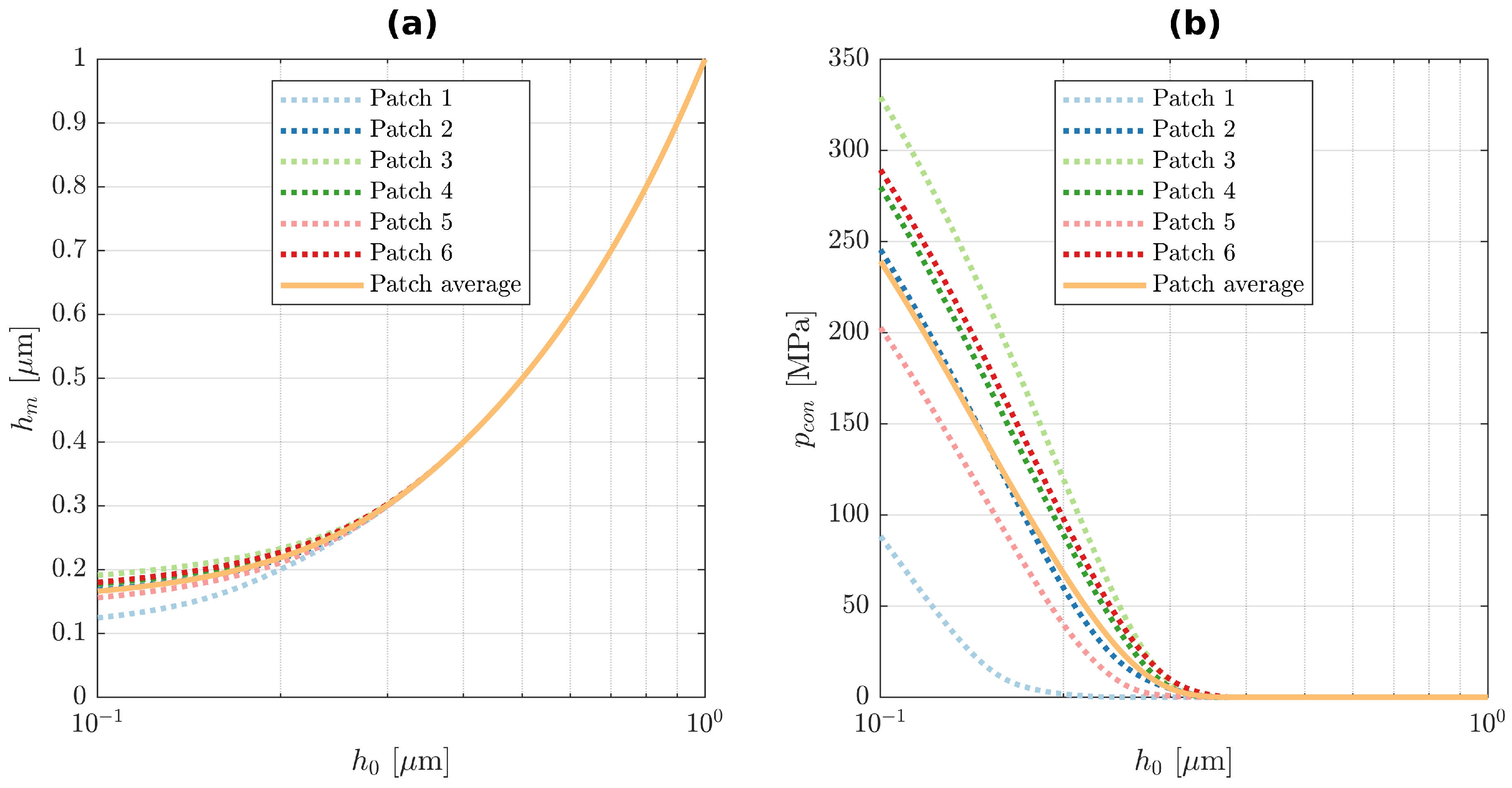
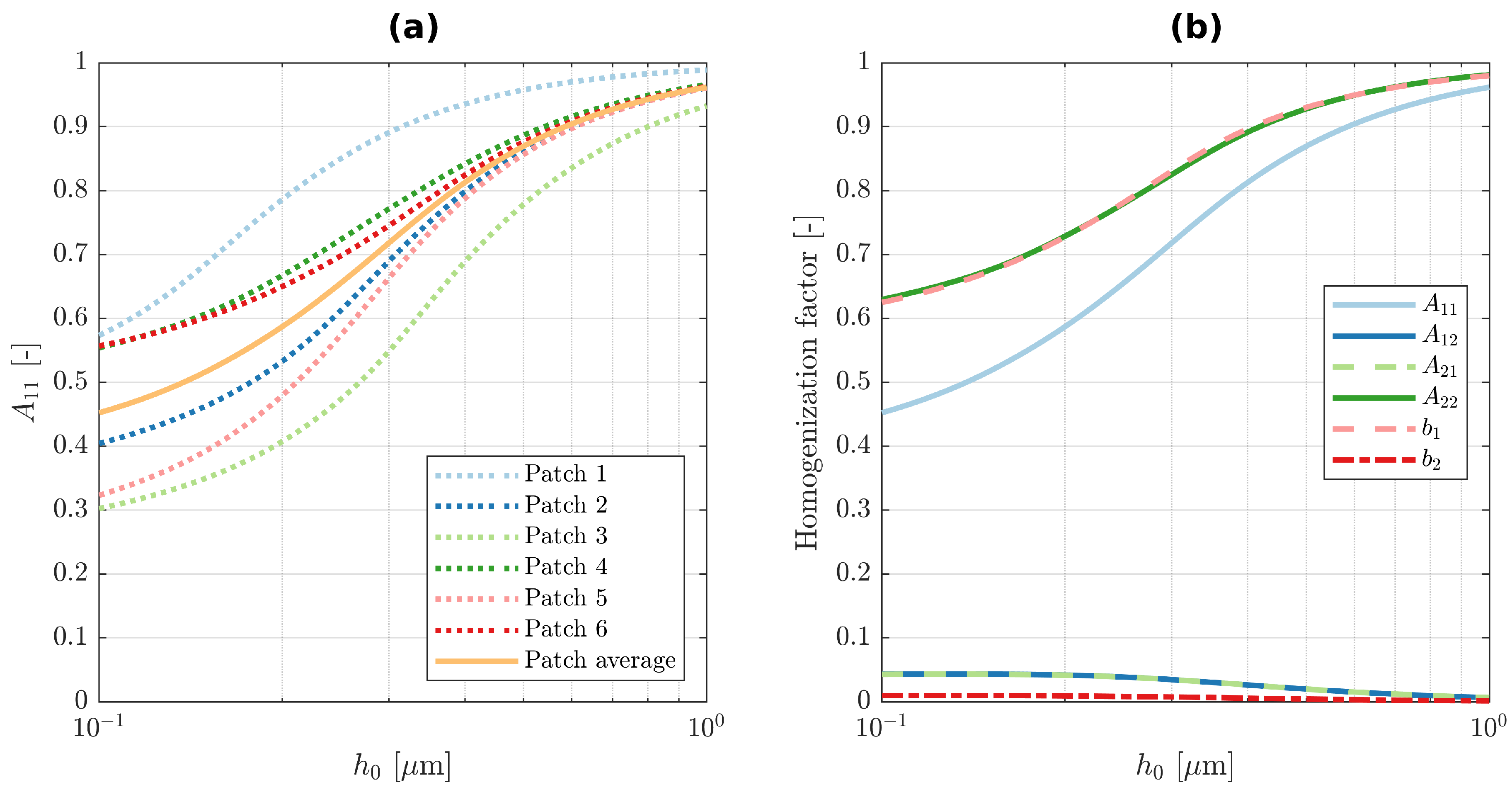
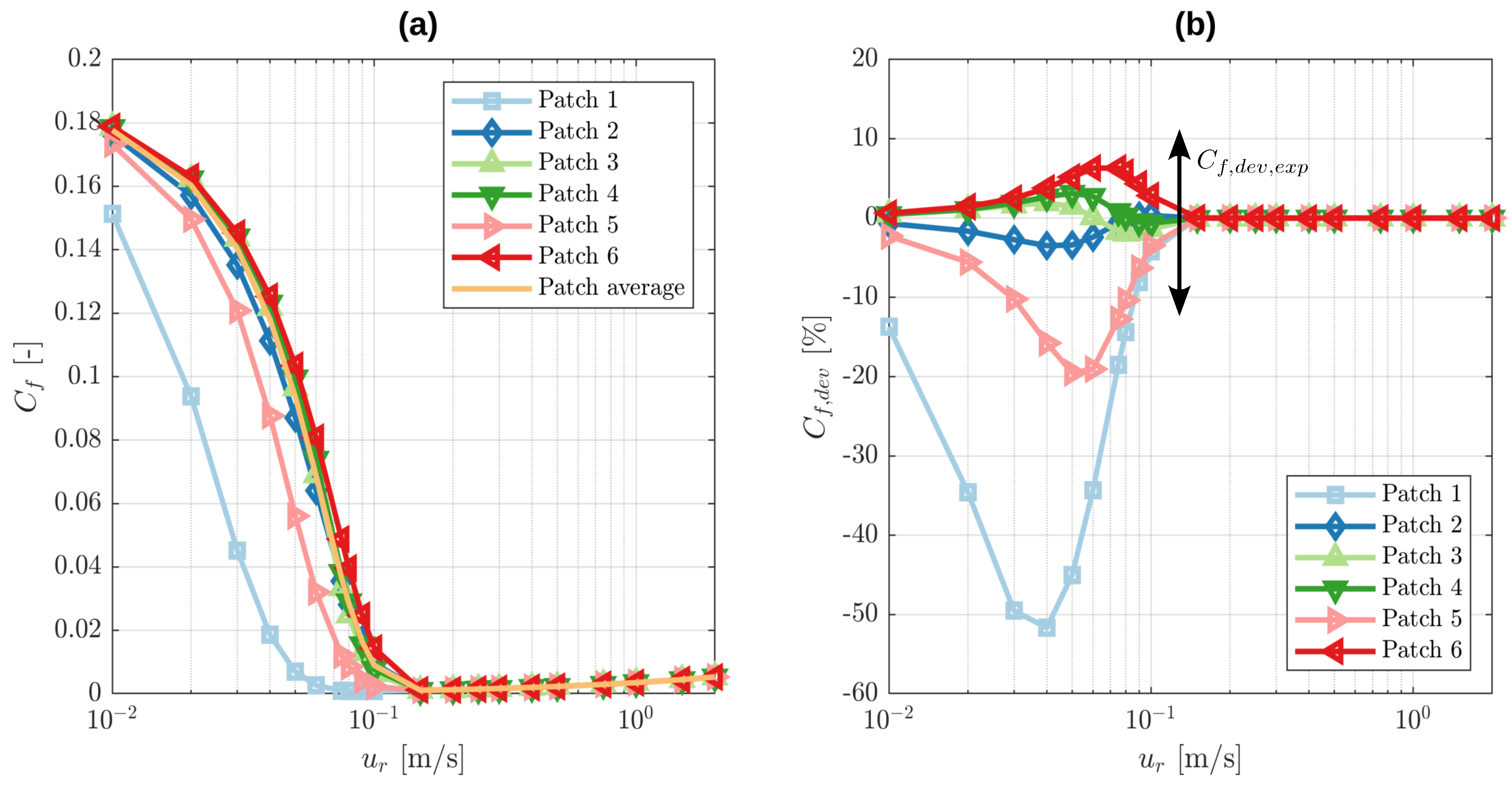
Once these factors are computed for several different roughness patches of a single post-test pin and disk specimen combination, the test average is computed. The results of six different pin and disk patches of test 2.1 and their average are displayed for the mean gap height
in
Figure 4a, the mean contact pressure
in
Figure 4b and the homogenisation factor
in
Figure 5a. The averages of the homogenisation factors
and
over the six patches are depicted in
Figure 5b. The root-mean-square values of the roughness topography of each patch are provided in
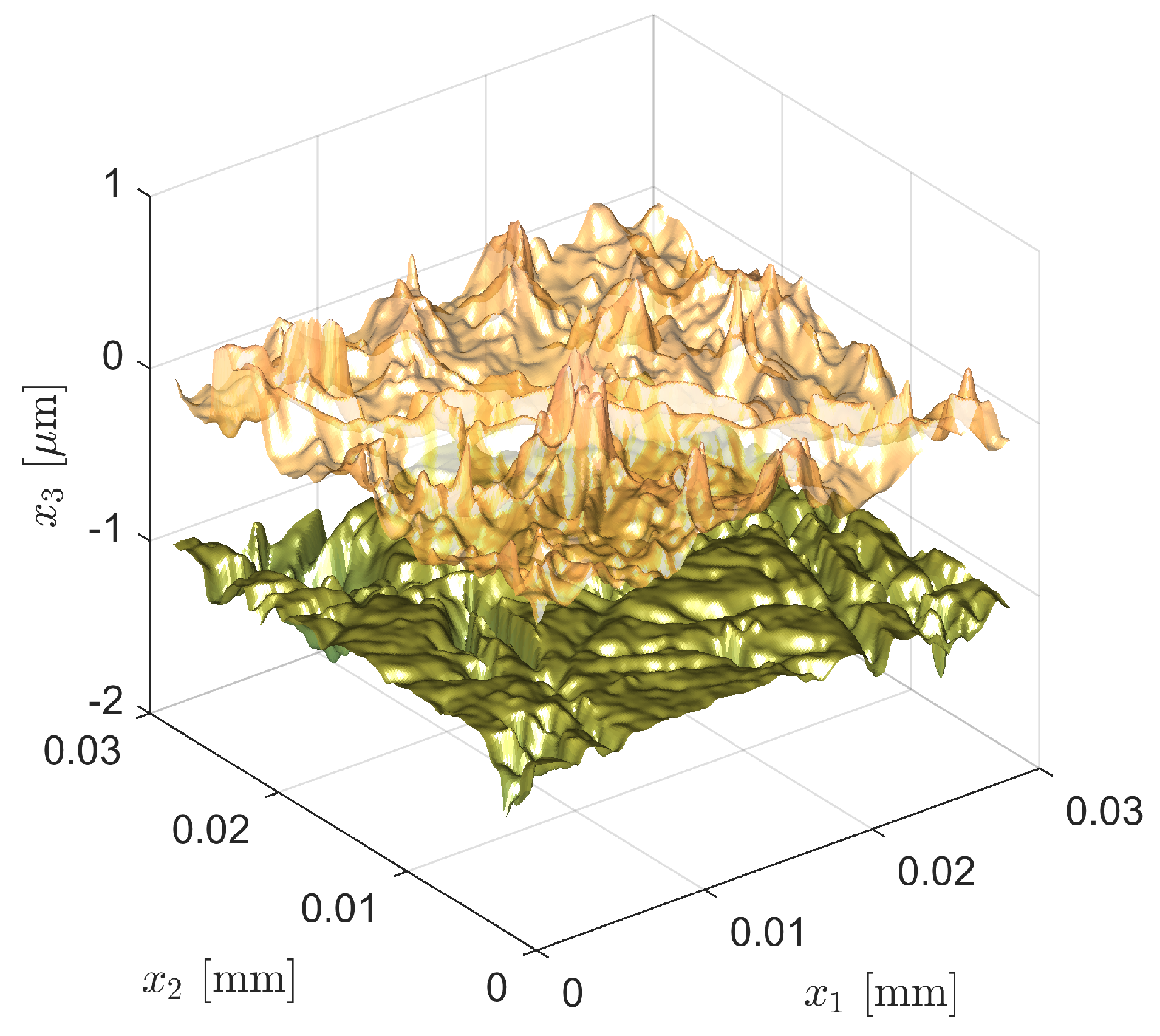
Table 5. The reconstructed microscopic virtual geometry of patch 4 of test 2.1 is exemplarily shown in
Figure 6 for a rigid body displacement of 1 µm.
2.2.2. Simulation of the Stribeck Curve Acquisition
In order to simulate the conditions within the macroscopic scale of the lubrication flow during the Stribeck curve acquisition depicted in
Figure 1b, a homogenised mixed elasto-hydrodynamic lubrication Fischer–Burmeister–Newton–Schur (HMEHL-FBNS) solver implementation in MATLAB
© was employed. It is an extension of the EHL-FBNS solver presented in an earlier work [
23]. The homogenised Reynolds equation is discretised with the finite volume method (FVM), where the Poiseuille terms are discretised with a second-order central scheme and the Couette term with a first-order upwind scheme. The fundamental equations incorporated in the extended solver are summarised in the following.
The difference between the hydrodynamic pressure
and cavitation pressure
is called relative pressure
. The cavity fraction
is defined as
, where
is the mixture density of the flow and
is the density of the liquid phase.
p and
are determined at each position
on the macroscopic scale with the steady homogenised Reynolds equation and the complementary cavitation constraint:
where the dynamic viscosity of the liquid phase
, mean velocity
, mean gap height
and homogenisation factors
and
are incorporated. For the pin-on-disk tribometer, the mean velocity is
, where
U is the velocity of the disk above the tribological contact.
and the homogenisation factors
and
are functions of the rigid body displacement on the roughness scale
. Their values and the mean contact pressure
can be interpolated at each position
on the macroscopic scale by realising that the macroscopic gap height is the same as the rigid body displacement on the roughness scale
. If
is larger than the
during the interpolation process described in
Section 2.2.1, then
is set equal to
, the mean contact pressure is set to 0 and the homogenisation factors are set to their value at
, thus being close to either 0 or 1 depending on the factor. On the macroscopic scale,
can be determined as:
where
denotes the rigid body displacement between the upper and lower macrogeometries,
is the gap height variation due to the rigid macrogeometries and
describes the combined elastic deformation of the macrogeometries. Using the elastic-half space assumption,
is found to be:
where the total pressure
is a superposition of the hydrodynamic pressure
and the mean contact pressure
within the domain of size
. Using Young’s modulus
E and Poisson ratio
of the upper and lower surfaces as described by the subscripts
and
, respectively, the reduced elastic modulus is expressed as:
Considering the validity of the half-space assumption, Zhang et al. [
24] investigated whether the free ends of the geometry should be considered or can be neglected in the modelling of the elastic deformation. They found that, for heavily loaded roller bearings under EHL conditions, neglecting the free ends delivers noticeable errors in the resulting deformation and pressure fields. However, these operating conditions differ fundamentally from those of the only lightly loaded conformal contact in the pin-on-disk tribometer. Even though there are free ends at rim of the pin, another work [
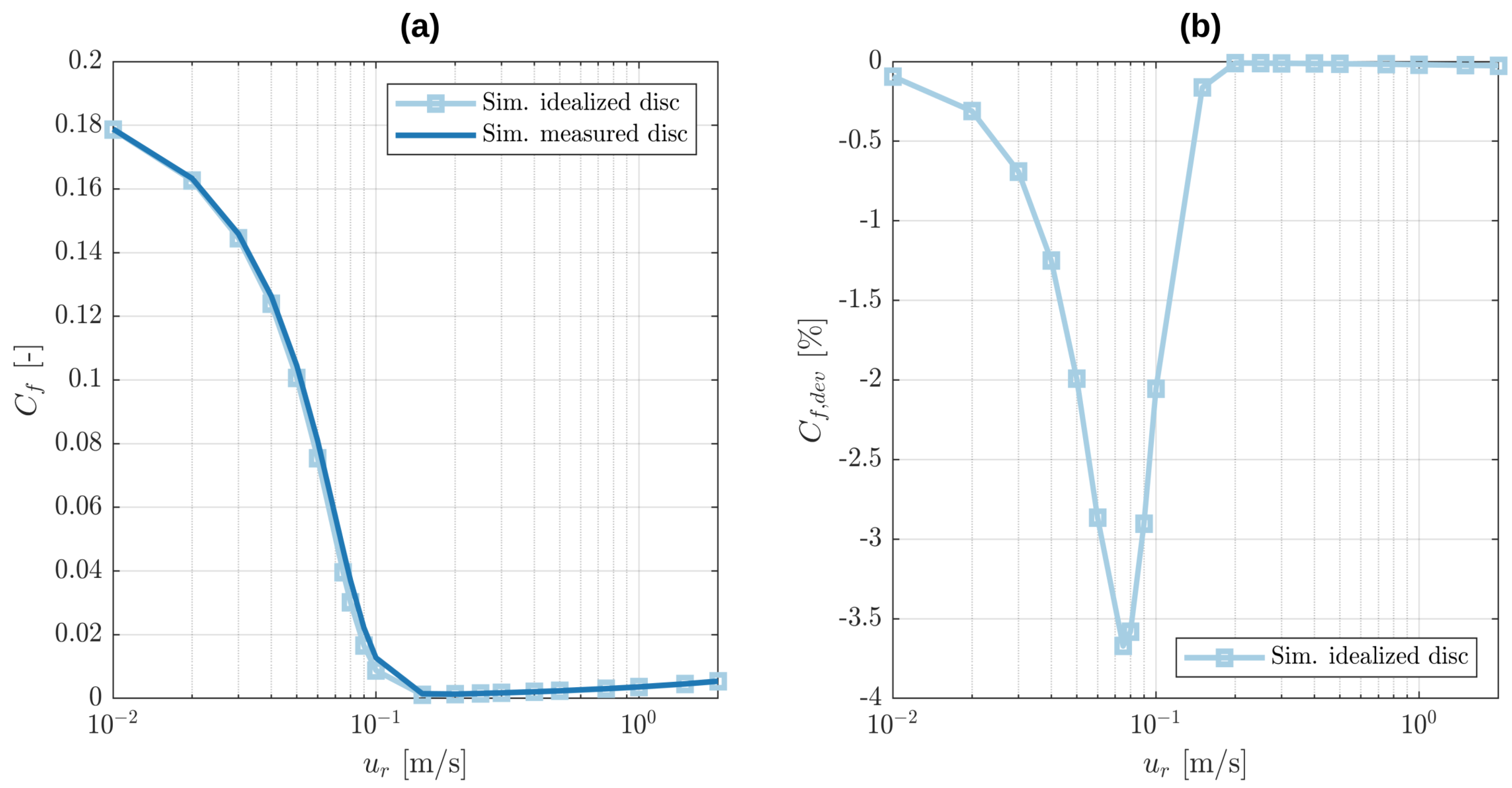
7] indicated that they introduce only small deviations in the Stribeck curve for simulations with an imposed normal load and neglecting their effect on the elastic deformation is therefore legit.
Piezoviscosity of the liquid phase is incorporated with the Roelands equation:
where
describes the pressure viscosity index,
is the pressure viscosity coefficient,
denotes a constant in the Roelands equation and
is the dynamic viscosity of the liquid phase at ambient pressure. The compressibility of the liquid phase is considered with the Dowson–Higginson model:
where
is the density of the liquid phase at ambient pressure and
and
are constants. In summary, the consequences of the employed models for the dynamic viscosity and density are as follows: while each simulation for itself is isothermal, the lubricant’s dependence upon temperature is still considered by the corresponding value of
at 24 and 50
C. The density is treated analogously. However, unlike
, the value of
can actually be eliminated from the Reynolds Equation (
17), because it appears in each single term. Consequently, the temperature dependence of
does not need any special consideration in the employed model. Lastly, one estimate of the magnitude of
is still necessary for the underlying EHL-FBNS solver described in [
23] to create the non-dimensional equation system. Nonetheless, piezoviscous and compressible effects are considered by Equations (
23) and (
24). They allow for the dynamic viscosity and density to change throughout the simulation domain according to the hydrodynamic pressure field.
Then, how the mean contact pressure is added to the already published EHL-FBNS algorithm is described [
23]. At each iteration
n, the update of the mean contact pressure is computed as:
where
is the expected mean contact pressure according to
and
describes the mean contact pressure of the previous iteration. For stability reasons, this update is applied with an underrelaxation coefficient
to obtain the mean contact pressure at iteration
n:
At the end of each iteration,
is used to compute
according to Equation (
21). Furthermore, the residual of
is computed as:
This residual is added to [
23] (Equation (
28)) when the convergence of the whole algorithm is checked against a tolerance. Moreover, the load balance equation taking the ambient pressure
into account reads:
In the solver, the rigid body displacement between the upper and lower macroscopic geometries
is adjusted through an incremental PID controller with its coefficients
,
and
:
This was performed at each iteration until a prescribed tolerance was met by the residual between the resulting normal load
and the imposed normal load
N:
Lastly, the hydrodynamic shear stresses on the pin surface are computed with the homogenised shear stress equation:
where
and
are homogenisation factors and
is the relative velocity between the upper and lower surfaces. For the pin-on-disk tribometer,
holds. The mean contact shear stress is determined as:
where
is an estimate for the boundary friction coefficient. It is set to
, which is a value theoretically derived by Bowden and Tabor [
25], Ch. V for the dry friction of metals under pure shearing, which serves as an unambiguous and uniquely defined upper limit for the boundary friction coefficient [
7]. The total shear stress
is computed by superposition and used to determine the resulting friction force
:
Eventually the friction coefficient is evaluated as:
The parameter values used in the simulations are summarised in
Table 6. The dynamic viscosity of the liquid phase
at ambient pressure was set according to
Table 3. The Dirichlet boundary conditions of ambient pressure
were employed for the hydrodynamic pressure
at the domain boundaries. Furthermore, the Dirichlet boundary condition of
was used at the domain inlet, whereas Neumann conditions were used for the cavity fraction at the remaining boundaries. A tolerance of
was used as a threshold for the residuals.