Abstract
Tilting pad journal bearings (TPJBs) are widely applied in the high-speed rotor system whose working speed is higher than its critical speed due to excellent hydrodynamic lubrication and stability. Pivot stiffness is one of the key design parameters of TPJBs compared to other journal bearings and has become particularly important for optimizing the performance of TPJB-rotor systems. In order to improve the vibration and critical characteristics of rotor systems, the transient dynamic characteristic of a TPJB-rotor system passing through the critical speed is investigated considering different pivot stiffness ratios. A time-varying dynamics model of a symmetrical single-disc rotor supported by four-pad TPJBs is established considering constant acceleration conditions and nonlinear hydrodynamic bearing force. The disc vibration characteristic, journal vibration characteristic, pad vibration characteristic, and hydrodynamic bearing force are analyzed by using Bode plot, shaft center orbit, pad phase orbit, waterfall plot, and time history. The results show that the pivot stiffness plays a major role in the suppression of resonance amplitude and working amplitude of a TPJB-rotor system, without changing the frequency characteristic of the system. This study provides a theoretical basis for the pivot stiffness design of TPJBs and the vibration suppression of rotor systems.
1. Introduction
With excellent hydrodynamic lubrication and stability, tilting pad journal bearings (TPJBs) are widely applied in the high-speed rotor system whose working speed is higher than its first-order critical speed, such as steam turbines, gas turbines, and turbopumps. The rotor system experiences resonance at the critical speed, and bearings as rotor support and control elements have a positive effect on improving the dynamic characteristic of the rotor system.
The pivot plays an important role in supporting the pad and providing sufficient stiffness for TPJBs. Kirk and Reedy [1] presented the equations for pivot stiffness of typical TPJBs considering the Hertzian contact stress and deformation theory and illustrated the necessity of pivot stiffness included in TPJB computer programs. Yan et al. [2] presented an analytical complete model for calculating the dynamic characteristics of TPJBs considering the pivot stiffness and damping and they showed that suitable pivot stiffness and damping could enhance the stability of bearing-rotor systems. San Andres and Tao [3] investigated the role of pivot stiffness on the dynamic force coefficients of TPJBs. Their results showed that the bearing impedance varied dramatically with frequency when the pivot stiffness was 0.1 to 10 times the fluid film stiffness, especially as the excitation frequency grew above the synchronous speed. Dimond et al. [4] investigated the modal frequency response of the TPJB with spherical pivots, finite pivot stiffness, and different pad preloads. Mehdi et al. [5] investigated the effect of pivot flexibility on the TPJB performance by comparing a rigid pivot model with a soft pivot model and they showed that soft pivot model predictions were closer to the test data. Dang et al. [6] investigated the influence of pivot stiffness on the dynamic force coefficients of rocker-backed pivot and spherical pivot TPJBs. Their results showed that the pivot flexibility had a significant effect on the clearance profile, shaft locus, and dynamic coefficients. Jin et al. [7] proposed an adjustable elastic pivot TPJB for vertical rotors and revealed the nonlinear dynamic performance of the bearing for different pivot stiffness, pre-tightening force, and preload factors. Shi et al. [8,9] investigated the influence of pivot design and pivot stiffness on the nonlinear dynamic characteristics of vertical and horizontal rotors supported by TPJBs and they showed that the bearing performance had an extremum in a wide range of pivot stiffness. Zhang et al. [10] investigated the influence of pivot stiffness on the dynamic characteristics of TPJBs and the stability of a vertical rotor-bearing system and they showed that the influence was obvious. Ciulli et al. [11] determined the stiffness of a ball-and-socket pivot by an experimental method and showed significant differences compared with Hertz formula.
The research on the dynamic behavior of journal bearings has developed from linear to nonlinear behavior and from hydrodynamic behavior to tribo-dynamic behavior. Hei et al. [12] investigated the nonlinear dynamic behavior of a rod fastening rotor-journal bearing system and revealed the complex nonlinear phenomena of the system. Maharshi et al. [13] investigated the stochastic dynamic behavior of hydrodynamic journal bearings considering random variabilities in eccentricity and surface roughness. They observed that the stochasticity had a significant influence on the bearing performance. Cui et al. [14] investigated the dynamic contact behavior of hydrodynamic journal bearings during start-up and clarified the effects of the relative clearance and acceleration time. Ma et al. [15] showed the effects of rough surface parameters and operating conditions on the resonant vibrations of hydrodynamic journal bearings and clarified the excitation mechanism induced by the tribofilm–asperity interaction. Chen et al. [16] investigated the effect of an imperfect journal with the amplitude and waviness of journal errors on the tribo-dynamic behavior of a water-lubricated bearing during start-up. Xiang et al. [17] investigated the effects of thermal effect and friction force on the transient nonlinear dynamic behavior of water-lubricated bearings under the mixed thermoelastohydrodynamic condition. Sayed and El-Sayed [18] investigated the nonlinear dynamic behavior and stability of a flexible rotor supported on two journal bearings using the second order stiffness and damping coefficients. Xie et al. [19] investigated the nonlinear dynamic behavior of a new journal bearing lubricated by high temperature liquid lead–bismuth solution through theoretical and experimental analysis. The above studies are concerned with fixed pad journal bearings. In the area of the dynamic behavior of TPJBs, Abu-Mahfouz and Adams [20] presented two instability mechanisms in TPJB-rotor systems and showed the subharmonic, quasi-periodic and chaotic motions for certain parameters. Okabe and Cavalca [21] investigated the influence of turbulence on the rotordynamic behavior of a Jeffcott/Laval rotor supported by TPJBs and they showed that turbulence could generate higher hydrodynamic force. Ying et al. [22] compared the rotordynamic response in TPJBs with and without the pad inertia effect. Their results showed that the pad inertia increased the complexity of dynamic characteristics of rotor-bearing systems. Hei et al. [23] analyzed the nonlinear dynamic behaviors and bifurcation of a rod fastening rotor supported by fixed-tilting pad journal bearings and they revealed that the rod fastening rotor system was more stable than the integral rotor system. Cha and Glavatskih [24] investigated the nonlinear dynamic behaviors of vertical and horizontal rotors in compliant liner TPJBs and discussed some bearing design parameters to control the journal orbit size. Tofighi-Niaki et al. [25] investigated the nonlinear dynamics of a flexible rotor supported by TPJBs due to the rub-impact effect and presented strongly nonlinear vibration phenomenon. Zhao et al. [26] measured the vibration and critical characteristics of a rotor supported by large TPJBs and proposed a non-excitation identification method for the critical speed. Kim and Palazzolo [27] investigated the nonlinear rotordynamic response with bifurcation considering the pad-pivot friction effect and they showed that pad-pivot friction played an important role in the stability of rotor systems. Jin et al. [28] investigated the nonlinear dynamic behaviors of a water-lubricated TPJB-Jeffcott rotor system considering the turbulent and thermal effects. They demonstrated the importance of flow regime and the negligibility of temperature rise in the analysis of water-lubricated bearings. Hojjati et al. [29] investigated the nonlinear vibration of a rigid rotor supported on TPJBs under the harmonic excitation and they showed that the system could have hardening or softening behaviors under different working conditions. Li et al. [30] investigated the dynamic behavior and bifurcation of a tilting pad aerodynamic bearing-rotor system under different rotational speeds.
However, previous research on pivot stiffness mostly focused on (i) pivot stiffness modeling; (ii) pivot stiffness effect on the dynamic coefficients of TPJBs, and (iii) pivot stiffness effect on the steady-state unbalance response of TPJB-rotor systems. There is little research on the transient dynamic characteristic of the system. The contribution of this paper is to develop a nonlinear time-varying dynamics model of a TPJB-rotor system considering the pivot stiffness effect and to clarify the effect of pivot stiffness on the transient dynamic behavior of the system experiencing resonance region. In this paper, a time-varying dynamics model of a symmetrical single-disc rotor supported by four-pad TPJBs under constant acceleration and nonlinear hydrodynamic force is established. The disc vibration characteristic, journal vibration characteristic, pad vibration characteristic, and hydrodynamic bearing force are analyzed from multiple perspectives including time domain, frequency domain and space domain. This study provides a theoretical basis for the pivot stiffness design of TPJBs and the vibration suppression of rotor systems.
2. Modeling
The bearing-rotor system model adopted is a symmetrical flexible rotor with a central disc supported by two TPJBs in the ends of the rotor, as shown in Figure 1a. The TPJB model adopted is a four-pad TPJB with the static load between pads, as shown in Figure 1b.
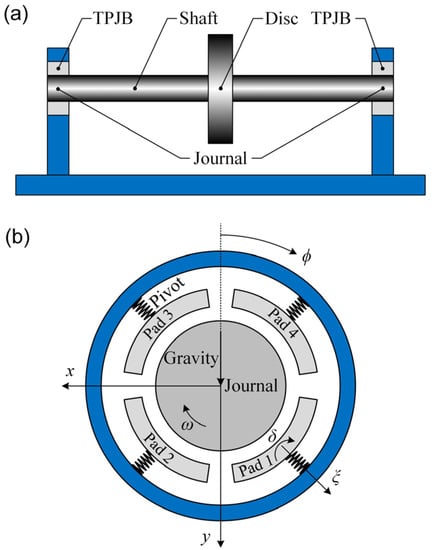
Figure 1.
Model of (a) TPJB-rotor system and (b) four-pad TPJB.
2.1. Hydrodynamic Lubrication Model of TPJB
The lubricant is modeled by the Reynolds equation considering the turbulent and unsteady flow. The hydrodynamic pressure of isoviscous and incompressible fluid film on each pad can be determined by:
where R is journal radius, p is fluid film pressure, h is fluid film thickness, μ is dynamic viscosity, ω is rotational angular speed, t is time, ϕ is circumferential coordinate, z is axial coordinate, and kϕ and kz are turbulence correction factors.
The film thickness distribution for a rigid pad aligned with the journal is written as:
where cp is radial pad clearance, cb is radial bearing clearance, ξi is radial pad displacement, βi is pivot position angle, xj and yj are horizontal and vertical journal displacements, respectively, and δi is pad tilt angle.
Ng and Pan’s turbulence correction factors for dominant Couette flow [31] can be represented by:
where Re is effective Reynolds number and it is dependent on the magnitude of the mean Reynolds number Rem and the critical Reynolds numbers: 800 and 1500 [32]. For the laminar flow (), . For the turbulent flow (), , where ρ is fluid density. For the transitional flow (), Re is determined through a third-order polynomial that ensures the continuity of Re and its first derivative at the beginning and end of the transitional zone.
The hydrodynamic force of fluid film between a pad and the journal is obtained by integrating the pressure:
where Fxi and Fyi are horizontal and vertical hydrodynamic force acting on the journal, respectively, Fξi is radial hydrodynamic force acting on the pad, L is bearing length, and ϕb and ϕe are the beginning and end angles of fluid film, respectively.
The total hydrodynamic force acting on the journal is:
where N is the number of pads. In this paper, .
The hydrodynamic force moment on the pad about its pivot is:
2.2. Transient Dynamic Model of TPJB-Rotor System
With the lumped mass method, the motion equation of the rotor under the excitation of disc imbalance can be written in the following form:
where is the lumped mass at the single journal, m1 is shaft mass, is the lumped mass at the disc, m2 is disc mass, xd and yd are horizontal and vertical disc displacements, respectively, is shaft stiffness, E is Young’s modulus, l is the distance between the two TPJBs, is the second moment of area, D is shaft diameter, c is shaft damping, g is gravitational acceleration, eu is unbalanced mass eccentricity, γ is phase angle, and the dot (·) represents time derivative.
The rotor mass is formed by the superposition of the shaft mass and disc mass:
where ρr is rotor density, Rd is disc radius, and d is disc thickness.
Considering that the rotational speed increases linearly with time, that is, the angular acceleration is constant, the following acceleration model is established:
where ω0 is initial angular speed, and a is angular acceleration.
The motion equation of each pad has two degrees of freedom and it can be written as:
where Ip is pad moment of inertia, mp is pad mass, and kp is pivot stiffness.
The shaft misalignment in the above model is reflected in two aspects. One is the misalignment of the disc center and the journal center due to the shaft flexibility, and the other is the misalignment of the journal center and the bearing center due to the bearing clearance. It is combined with the bearing deformation through the fluid film force variation caused by the journal center movement.
3. Solving Method
Since the rotational speed is expressed as a function of time, it would take a lot of time to solve the Reynolds equation under varying speeds using traditional numerical methods. In order to significantly improve the calculation efficiency, the analytical method [33] instead of numerical methods is adopted to solve the Reynolds equation. Equation (1) is solved by the method of separation of variables under the dynamic Gümbel boundary condition. The fluid film pressure is supposed to be separated into a multiplicative form of infinitely long bearing pressure in the circumferential direction and hyperbolic cosine pressure in the axial direction. Complete analytical expressions for the nonlinear hydrodynamic bearing force and moment are obtained. Equations (7) and (10) are solved numerically by the explicit Euler method. For the time-varying speed analysis (), the initial value of the motion equations is the equilibrium of the system at the initial rotational speed. For the constant speed analysis (), the initial value of the motion equations is set to zero. The nonlinear transient method is used to calculate the equilibrium of the disc, journal and pads synchronously, which is a stable value of the time history of the system without unbalance excitation. The time step is set as 1 × 10−7 s. Given a set of parameters of the TPJB-rotor system, the results for a desired speed range could be obtained within 5 min using MATLAB software (version R2022b) on the computer with Intel Core i9-10900K CPU at 3.70 GHz (sourced from Intel, Santa Clara, CA, USA).
The lubrication model is verified by comparing the calculated film pressure and film thickness with Taniguchi’s experiment data [34], as shown in Figure 2. It can be seen that our calculated results are in good agreement with their experimental results. The reason for the slight difference is that the thermoelastic effect is not taken into account in our model. The rotor model is verified by comparing the calculated critical speed with Zhang’s results from Campbell diagram [35], as shown in Table 1. It is observed that results from our model are very close to published data, and our model is more applicable to the flexible rotor analysis.
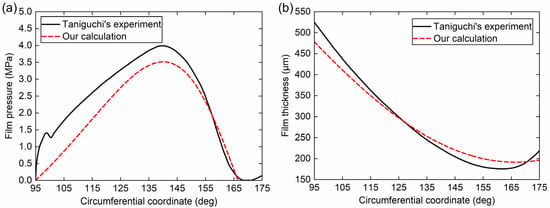
Figure 2.
Validations of (a) film pressure and (b) film thickness of TPJB.

Table 1.
Validation of critical speed of rotor system.
4. Results and Discussion
The specification of the TPJB-rotor system is presented in Table 2. According to the rotor parameters, it can be calculated that the shaft stiffness is 1 × 107 N/m, and the critical speed is 10,676 r/min. The shaft damping is set as zero. The ratio of pivot stiffness to shaft stiffness is defined as pivot stiffness ratio (kp/k), and the parameter value is varied in the course of the analysis to show its effect on the transient dynamic characteristic of the TPJB-rotor system. The minimum value of kp/k is chosen as 0.5, if this value is too small, it will lead to spragging of upper pads. The maximum value of kp/k is infinity, that is, a rigid pivot. Figure 3 shows the time-varying rotational speed and unbalanced load during rotor acceleration. The rotational speed increases linearly from 2000 r/min to 20,000 r/min in three seconds. The amplitude of unbalanced load gradually increases with time, and the maximum value is 175 N at the end of the calculation.

Table 2.
Specification of the TPIB-rotor system.
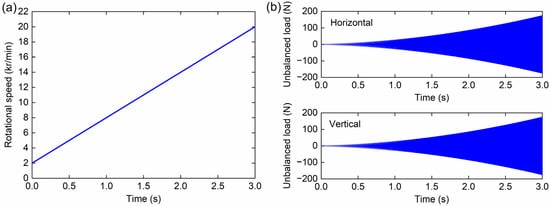
Figure 3.
(a) Rotational speed and (b) unbalanced load as a function of time during rotor acceleration.
The following numerical cases are performed to analyze the effect of pivot stiffness on the disc vibration characteristic, journal vibration characteristic, pad vibration characteristic, and hydrodynamic bearing force.
Firstly, the effect of pivot stiffness on the disc vibration characteristic is investigated. The peak-to-peak amplitude of the disc is obtained by the difference between the upper and lower envelopes of the disc displacement response, as shown in Figure 4. It is observed that the amplitude of the disc is consistent in both horizontal and vertical directions, and this characteristic is also applicable to the journal amplitude (see Figure 7). This is because the support stiffness of the rotor is the same in these two directions, which is a typical property of four-pad TPJBs with the static load between pads. It is also found that the critical speed and maximum amplitude of the rotor disc both decrease with the decrease of pivot stiffness ratios due to the decreasing system stiffness and increasing system damping, which indicates that properly reducing the pivot stiffness is beneficial for flexible rotors to suppress the resonance of the disc and prevent the working speed from approaching the critical speed. For example, the critical speed could decrease from 10,315 r/min to 8316 r/min (−19%), and the maximum amplitude could decrease from 60.6 μm to 24.1 μm (−60%) by reducing the pivot stiffness ratio from infinity to 0.5. In addition, when the working speed is lower than the critical speed, that is, for a rigid rotor, the disc amplitude is decreased with the increase of pivot stiffness ratios due to the increasing system stiffness; when the working speed is higher than the critical speed, that is, for a flexible rotor, the disc amplitude is decreased with the decrease of pivot stiffness ratios due to the increasing system damping. The system damping ratio increases from 0.085 in the case of rigid pivot to 0.281 in the case of kp/k = 0.5, which is obtained by the half-power bandwidth method, as shown in Table 3. The half-peak amplitude spectrum of the horizontal displacement response of the disc is analyzed by using the short-time Fourier transform (STFT), and the waterfall plot obtained is shown in Figure 5. A significant synchronous vibration caused by rotational frequency (1×) and a slight super-synchronous vibration with 2 times (2×) rotational frequency caused by the nonlinear hydrodynamic force are presented in the figure. Since no component below 1× frequency appears in the spectrum, it indicates that the rotor system is stable during acceleration.
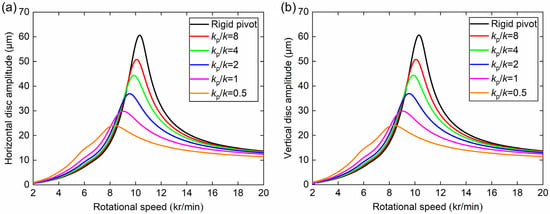
Figure 4.
(a) Horizontal and (b) vertical amplitudes (peak to peak) of the disc displacement response under different pivot stiffness ratios.

Table 3.
Damping ratio of the TPJB-rotor system under different pivot stiffness ratios.
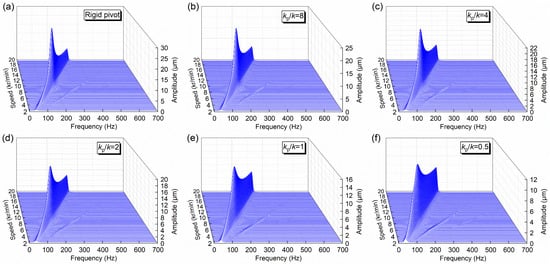
Figure 5.
STFT amplitude spectrum (half-peak) for horizontal displacement response of the disc under different pivot stiffness ratios.
Figure 6 presents the stable disc center orbits at the rotational speeds of 5000 r/min and 20,000 r/min for various pivot stiffness ratios. In this figure, as the pivot stiffness ratio decreases, the disc center orbit gradually moves away from the bearing center due to the decrease of load capacity of TPJBs, and the journal center orbit in Figure 9 also shows the same rule. The pivot stiffness variation could affect the rotor eccentricity due to the bearing load capacity variation, but not affect the rotor attitude angle. The rotor attitude angle equal to zero is a typical characteristic of four-pad TPJBs with the static load between pads, because the horizontal resultant force of fluid film in the bearing is equal to zero. Therefore, the pivot stiffness variation linearly affects the rotor center movement. When the working speed is 5000 r/min, the disc orbit size could be reduced by increasing the pivot stiffness, as shown in Figure 6a. Specifically, the orbit amplitude decreases from 9.36 μm to 4.59 μm (−51%) with the pivot stiffness ratio increasing from 0.5 to infinity. When the working speed is 20,000 r/min, the disc orbit size could be reduced by decreasing the pivot stiffness, as shown in Figure 6b. Specifically, the orbit amplitude decreases from 13.7 μm to 11.4 μm (−17%) with the pivot stiffness ratio decreasing from infinity to 0.5.
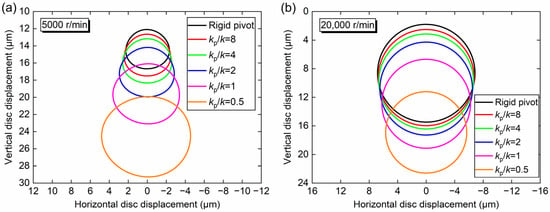
Figure 6.
Disc center orbit of the rotor system at (a) 5000 r/min and (b) 20,000 r/min under different pivot stiffness ratios.
Secondly, the effect of pivot stiffness on the journal vibration characteristic is investigated. The peak-to-peak amplitude of the journal is obtained by the difference between the upper and lower envelopes of the journal displacement response, as shown in Figure 7. In this figure, the maximum journal amplitude could be reduced by increasing the pivot stiffness, which is contrary to the variation of the maximum disc amplitude. This could be explained in two ways. On the one hand, the TPJB stiffness connected in series by pivot stiffness and fluid film stiffness increases with the increasing pivot stiffness. On the other hand, the increased TPJB stiffness allows the reduced resonance energy from journal to be transferred to the disc for release due to the conservation of energy in the rotor system. To be specific, when the pivot stiffness ratio increases from 0.5 to infinity, the maximum journal amplitude decreases from 13.7 μm to 12.2 μm (−11%). Figure 8 shows the half-peak amplitude spectrum of the horizontal displacement response of the journal for various pivot stiffness ratios. In addition to the main 1× frequency, 2× and 3× frequency components are slightly presented in all the cases.
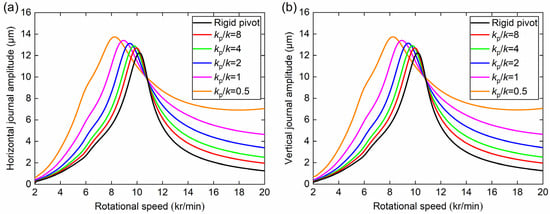
Figure 7.
(a) Horizontal and (b) vertical amplitudes (peak to peak) of the journal displacement response under different pivot stiffness ratios.
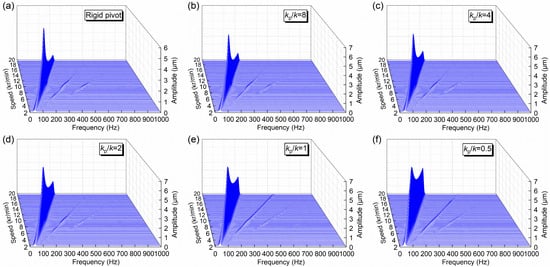
Figure 8.
STFT amplitude spectrum (half-peak) for horizontal displacement response of the journal under different pivot stiffness ratios.
Figure 9 presents the stable journal center orbits at the rotational speeds of 5000 r/min and 20,000 r/min for various pivot stiffness ratios. It is found that the journal orbit size could be reduced by increasing the pivot stiffness. When the pivot stiffness ratio increases from 0.5 to infinity, the orbit amplitude decreases from 5.87 μm to 1.80 μm (−69%) at 5000 r/min and from 7.07 μm to 1.25 μm (−82%) at 20,000 r/min.
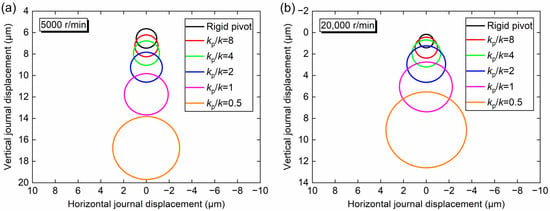
Figure 9.
Journal center orbit of the rotor system at (a) 5000 r/min and (b) 20,000 r/min under different pivot stiffness ratios.
Next, the effect of pivot stiffness on the pad vibration characteristic is investigated. Figure 10 presents the peak-to-peak amplitudes of the pads in the tilting and radial directions for various pivot stiffness ratios. It is found that the maximum pad amplitudes in both tilting and radial directions could be reduced by increasing the pivot stiffness, which is the same as the effect of pivot stiffness on the maximum journal amplitude. This is because the pivot deformation would increase the fluid film thickness and reduce the fluid film stiffness acting directly on the journal and the pads, thus affecting their vibration characteristics simultaneously. For example, when the pivot stiffness ratio increases from 0.5 to infinity, the maximum tilting amplitude could be decreased from 0.0368 deg to 0.0211 deg (−43%) for pad 1, from 0.0366 deg to 0.0213 deg (−42%) for pad 2, from 0.0322 deg to 0.0204 deg (−37%) for pad 3 and from 0.0327 deg to 0.0205 deg (−37%) for pad 4, and the maximum radial amplitude could be decreased by 8.58 μm for pad 1 and pad 2 and 6.38 μm for pad 3 and pad 4. Figure 11 shows the half-peak amplitude spectrum of the tilting angle response of pad 2 for various pivot stiffness ratios. Similar to the frequency characteristic of the journal vibration, slight super-synchronous harmonic components with 2× and 3× frequencies are found in this figure, and even a short 4× frequency component is observed, indicating a more significant effect of nonlinear hydrodynamic force on the journal and pads. Combining Figure 5, Figure 8, and Figure 11, it can be seen that the higher the frequency order, the more transient the harmonics appear, and the higher order harmonics are mainly concentrated in the critical speed region.
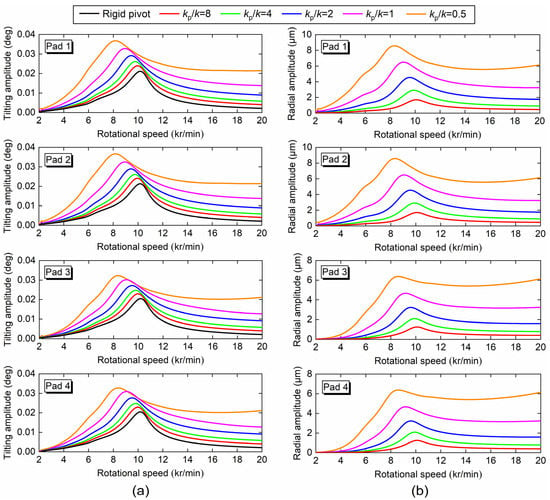
Figure 10.
(a) Tilting and (b) radial amplitudes (peak to peak) of the pad vibration response under different pivot stiffness ratios.
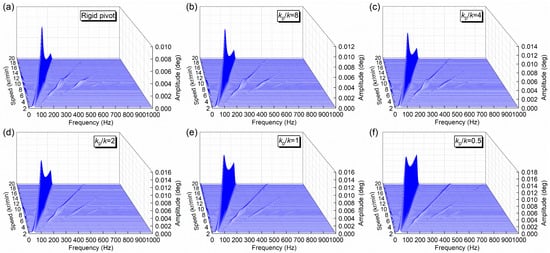
Figure 11.
STFT amplitude spectrum (half-peak) for tilting angle response of pad 2 under different pivot stiffness ratios.
Figure 12 presents the stable phase orbit of pad 2 at the rotational speeds of 5000 r/min and 20,000 r/min for various pivot stiffness ratios. The pad phase orbit reflects comprehensive information such as pad amplitude, pivot deformation, and pad stability. In this figure, the pad amplitude and pivot deformation could be reduced by increasing the pivot stiffness. When the pivot stiffness ratio increases from 0.5 to infinity, the tilting amplitude decreases from 0.0138 deg to 0.00315 deg (−77%), the radial amplitude decreases by 3.40 μm, and the maximum pivot deformation decreases by 10.2 μm for the working speed of 5000 r/min; the tilting amplitude decreases from 0.0214 deg to 0.00213 deg (−90%), the radial amplitude decreases by 6.15 μm, and the maximum pivot deformation decreases by 18.7 μm for the working speed of 20,000 r/min.
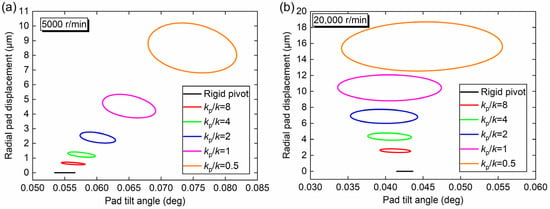
Figure 12.
Pad phase orbit of rotor system at (a) 5000 r/min and (b) 20,000 r/min under different pivot stiffness ratios (Pad 2).
Finally, the effect of pivot stiffness on the hydrodynamic bearing force is investigated. Figure 13 shows the envelopes of the hydrodynamic bearing force response in both the horizontal and vertical directions for various pivot stiffness ratios. In this figure, the horizontal and vertical responses have constant mean envelopes of 0 and 51.3 N, respectively. The mean envelope reflects the hydrodynamic force of a single TPJB under the static condition, where the vertical hydrodynamic force is equal in magnitude to the static load. In addition, it is found that the maximum hydrodynamic force and its amplitude decrease as the pivot stiffness ratio decreases. This is because the decrease in pivot stiffness leads to an increase in bearing clearance, which in turn weakens the squeezing effect of fluid film. To be specific, when the pivot stiffness ratio decreases from infinity to 0.5, the maximum hydrodynamic bearing force could be decreased from 137 N to 35 N (−74%) in the horizontal direction and from 189 N to 87 N (−54%) in the vertical direction.
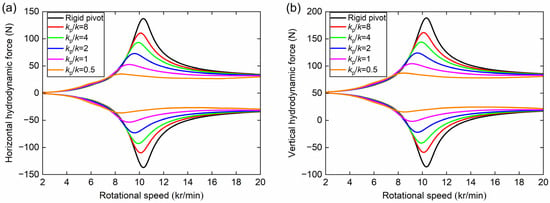
Figure 13.
Envelope of (a) horizontal and (b) vertical hydrodynamic bearing force response under different pivot stiffness ratios.
Figure 14 presents the stable response of hydrodynamic bearing force at the rotational speeds of 5000 r/min and 20,000 r/min for various pivot stiffness ratios. As the pivot stiffness ratio decreases, it is found that the maximum hydrodynamic force and amplitude render an opposite trend before and after the critical speed of the system, increasing at 5000 r/min and decreasing at 20,000 r/min. From the case of rigid pivot to that of kp/k = 0.5 specifically, the maximum hydrodynamic force in the vertical direction increases from 59.3 N to 62.0 N (+5%) at 5000 r/min and decreases from 85.6 N to 81.0 N (−5%) at 20,000 r/min.
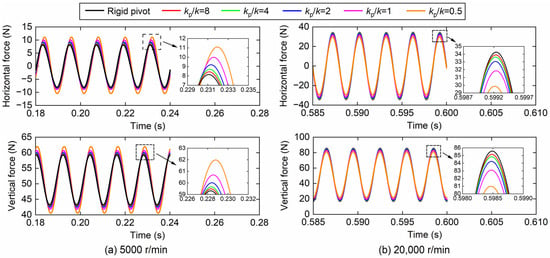
Figure 14.
Hydrodynamic bearing force response of the rotor system at (a) 5000 r/min and (b) 20,000 r/min under different pivot stiffness ratios.
5. Conclusions
The present research has demonstrated that the pivot stiffness has a significant effect on the transient dynamic characteristic of a TPJB-rotor system passing through the critical speed, which could be applied to the design of pivot stiffness of TPJBs to achieve the suppression of the resonance amplitude and working amplitude of the bearing-rotor system. Several conclusions can be summarized as follows:
- For a rigid rotor with working speed below the critical speed, the working amplitude of the rotor disc, journal, and pads and the maximum hydrodynamic force in the TPJB could be reduced by increasing the pivot stiffness.
- For a flexible rotor with working speed above the critical speed, the resonance amplitude, working amplitude, and critical speed of the rotor disc and the maximum hydrodynamic force in the TPJB could be reduced by decreasing the pivot stiffness, which helps the rotor system to pass through the critical speed safely and avoid its working speed adjacent to the critical speed. At the same time, the amplitude of the journal and pads would increase accordingly.
- The pivot stiffness has little effect on the vibrational frequency characteristic of a stable TPJB-rotor system passing through the critical speed. Due to the nonlinear hydro-dynamic bearing force, there are super-synchronous harmonic components with minor amplitudes in the system: 2× rotational frequency is found in the disc vibration; 2× and 3× rotational frequencies are found in the journal and pad vibrations.
Author Contributions
Conceptualization, Y.J.; methodology, X.Y.; software, Q.N.; validation, Y.Q.; formal analysis, X.Y.; investigation, Y.J.; resources, X.Y.; data curation, Y.Q.; writing—original draft preparation, Q.N.; writing—review and editing, Y.Q.; visualization, Q.N.; supervision, X.Y.; project administration, Y.J.; funding acquisition, Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 12202090, and the Fundamental Research Funds for the Central Universities, grant number 3132022116.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kirk, R.G.; Reedy, S.W. Evaluation of pivot stiffness for typical tilting-pad journal bearing designs. J. Vib. Acoust. Stress Reliab. Des. 1988, 110, 165–171. [Google Scholar] [CrossRef]
- Yan, Z.Y.; Lu, Y.; Zheng, T.S. An analytical complete model of tilting-pad journal bearing considering pivot stiffness and damping. J. Tribol. 2011, 133, 011702. [Google Scholar] [CrossRef]
- San Andres, L.; Tao, Y.J. The role of pivot stiffness on the dynamic force coefficients of tilting pad journal bearings. J. Eng. Gas Turbines Power 2013, 135, 112505. [Google Scholar] [CrossRef]
- Dimond, T.; Younan, A.A.; Allaire, P.; Nicholas, J. Modal frequency response of a four-pad tilting pad bearing with spherical pivots, finite pivot stiffness, and different pad preloads. J. Vib. Acoust. 2013, 135, 041101. [Google Scholar] [CrossRef]
- Mehdi, S.M.; Jang, K.E.; Kim, T.H. Effects of pivot design on performance of tilting pad journal bearings. Tribol. Int. 2018, 119, 175–189. [Google Scholar] [CrossRef]
- Dang, P.V.; Chatterton, S.; Pennacchi, P. The effect of the pivot stiffness on the performances of five-pad tilting pad bearings. Lubricants 2019, 7, 61. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Chen, F.; Zhang, F.; Yuan, X.Y. Nonlinear dynamic performance of tilting-pad journal bearing with adjustable elastic pivot design. Tribol. Int. 2019, 136, 533–547. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Jin, Y.Z.; Yuan, X.Y. Influence of pivot design on nonlinear dynamic analysis of vertical and horizontal rotors in tilting pad journal bearings. Tribol. Int. 2019, 140, 105859. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Jin, Y.Z.; Yuan, X.Y.; Chen, R.L. Effect of pivot stiffness on nonlinear dynamic characteristics of tilting pad journal bearings. Tribol. Int. 2020, 146, 106222. [Google Scholar] [CrossRef]
- Zhang, F.; Yin, P.; Liu, Y.Y.; Wang, J.M. Numerical and experimental study on dynamic characteristics of tilting-pad journal bearings considering pivot stiffness in a vertical rotor system. Ind. Lubr. Tribol. 2021, 73, 1275–1285. [Google Scholar] [CrossRef]
- Ciulli, E.; Forte, P.; Antonelli, F.; Minelli, R.; Panara, D. Tilting pad journal bearing ball and socket pivots: Experimental determination of stiffness. Machines 2022, 10, 81. [Google Scholar] [CrossRef]
- Hei, D.; Lu, Y.J.; Zhang, Y.F.; Liu, F.X.; Zhou, C.; Muller, N. Nonlinear dynamic behaviors of rod fastening rotor-hydrodynamic journal bearing system. Arch. Appl. Mech. 2015, 85, 855–875. [Google Scholar] [CrossRef]
- Maharshi, K.; Mukhopadhyay, T.; Roy, B.; Roy, L.; Dey, S. Stochastic dynamic behaviour of hydrodynamic journal bearings including the effect of surface roughness. Int. J. Mech. Sci. 2018, 142, 370–383. [Google Scholar] [CrossRef]
- Cui, S.H.; Gu, L.; Wang, L.Q.; Xu, B.; Zhang, C.W. Numerical analysis on the dynamic contact behavior of hydrodynamic journal bearings during start-up. Tribol. Int. 2018, 121, 260–268. [Google Scholar] [CrossRef]
- Ma, J.J.; Zhang, H.; Lou, S.; Chu, F.L.; Shi, Z.Q.; Gu, F.S.; Ball, A.D. Analytical and experimental investigation of vibration characteristics induced by tribofilm-asperity interactions in hydrodynamic journal bearings. Mech. Syst. Signal Proc. 2021, 150, 107227. [Google Scholar] [CrossRef]
- Chen, S.A.; Xiang, G.; Fillon, M.; Guo, J.; Wang, J.X.; Cai, J.L. On the tribo-dynamic behaviors during start-up of water lubricated bearing considering imperfect journal. Tribol. Int. 2022, 174, 107685. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, J.X.; Han, Y.F.; Yang, T.Y.; Dai, H.M.; Yao, B.W.; Zhou, C.D.; Wang, L.W. Investigation on the nonlinear dynamic behaviors of water-lubricated bearings considering mixed thermoelastohydrodynamic performances. Mech. Syst. Signal Proc. 2022, 169, 108627. [Google Scholar] [CrossRef]
- Sayed, H.; El-Sayed, T.A. Nonlinear dynamics and bifurcation analysis of journal bearings based on second order stiffness and damping coefficients. Int. J. Non-Linear Mech. 2022, 142, 103972. [Google Scholar] [CrossRef]
- Xie, Z.L.; Jiao, J.; Yang, K.; He, T.; Chen, R.G.; Zhu, W.D. Experimental and numerical exploration on the nonlinear dynamic behaviors of a novel bearing lubricated by low viscosity lubricant. Mech. Syst. Signal Proc. 2023, 182, 109349. [Google Scholar] [CrossRef]
- Abu-Mahfouz, I.; Adams, M.L. Numerical study of some nonlinear dynamics of a rotor supported on a three-pad tilting pad journal bearing (TPJB). J. Vib. Acoust. 2005, 127, 262–272. [Google Scholar] [CrossRef]
- Okabe, E.P.; Cavalca, K.L. Rotordynamic analysis of systems with a non-linear model of tilting pad bearings including turbulence effects. Nonlinear Dyn. 2009, 57, 481–495. [Google Scholar] [CrossRef]
- Ying, J.Y.; Jiao, Y.H.; Chen, Z.B. Nonlinear dynamics analysis of tilting pad journal bearing-rotor system. Shock Vib. 2011, 18, 45–52. [Google Scholar] [CrossRef]
- Hei, D.; Lu, Y.J.; Zhang, Y.F.; Lu, Z.Y.; Gupta, P.; Muller, N. Nonlinear dynamic behaviors of a rod fastening rotor supported by fixed-tilting pad journal bearings. Chaos Solitons Fractals 2014, 69, 129–150. [Google Scholar] [CrossRef]
- Cha, M.; Glavatskih, S. Nonlinear dynamic behaviour of vertical and horizontal rotors in compliant liner tilting pad journal bearings: Some design considerations. Tribol. Int. 2015, 82, 142–152. [Google Scholar] [CrossRef]
- Tofighi-Niaki, E.; Asgharifard-Sharabiani, P.; Ahmadian, H. Nonlinear dynamics of a flexible rotor on tilting pad journal bearings experiencing rub-impact. Nonlinear Dyn. 2018, 94, 2937–2956. [Google Scholar] [CrossRef]
- Zhao, Z.M.; Ji, F.; Guan, Y.S.; Yuan, X.Y. Vibration and critical characteristics of the tilting pads journal bearing-rotor system. Ind. Lubr. Tribol. 2019, 71, 295–300. [Google Scholar] [CrossRef]
- Kim, S.; Palazzolo, A.B. Pad-pivot friction effect on nonlinear response of a rotor supported by tilting-pad journal bearings. J. Tribol. 2019, 141, 091701. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Shi, Z.Y.; Zhang, X.J.; Yuan, X.Y. Rapid solution for analysis of nonlinear fluid film force and dynamic behavior of a tilting-pad journal bearing-rotor system with turbulent and thermal effects. Friction 2020, 8, 343–359. [Google Scholar] [CrossRef]
- Hojjati, M.; Navazi, H.M.; Haddadpour, H. Nonlinear vibrations of a rotor on nonlinear tilting-pad-journal-bearings. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 168. [Google Scholar] [CrossRef]
- Li, S.; Lu, Y.J.; Zhang, Y.F.; Zhao, X.W.; Luo, H.B.; Meng, J.C. Modeling and analysis of dynamic behaviors for a flexible rotor system supported in tilting pad aerodynamic bearings. Appl. Math. Model. 2022, 110, 262–284. [Google Scholar] [CrossRef]
- Taylor, C.M.; Dowson, D. Turbulent lubrication theory—Application to design. J. Lubr. Technol. 1974, 96, 36–46. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Chen, F.; Xu, J.M.; Yuan, X.Y. Nonlinear dynamic analysis of low viscosity fluid-lubricated tilting-pad journal bearing for different design parameters. Friction 2020, 8, 930–944. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Yuan, X.Y. Analytical method for hydrodynamic force in finite-length tilting-pad journal bearing including turbulence effect. J. Tribol. 2020, 142, 091802. [Google Scholar] [CrossRef]
- Taniguchi, S.; Makino, T.; Takeshita, K.; Ichimura, T. A thermohydrodynamic analysis of large tilting-pad journal bearing in laminar and turbulent-flow regimes with mixing. J. Tribol. 1990, 112, 542–548. [Google Scholar] [CrossRef]
- Zhang, S.L.; Xing, Y.; Xu, H.; Pei, S.Y.; Zhang, L. An experimental study on vibration suppression of adjustable elliptical journal bearing-rotor system in various vibration states. Mech. Syst. Signal Proc. 2020, 141, 106477. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).