Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques
Abstract
1. Introduction
2. Theory
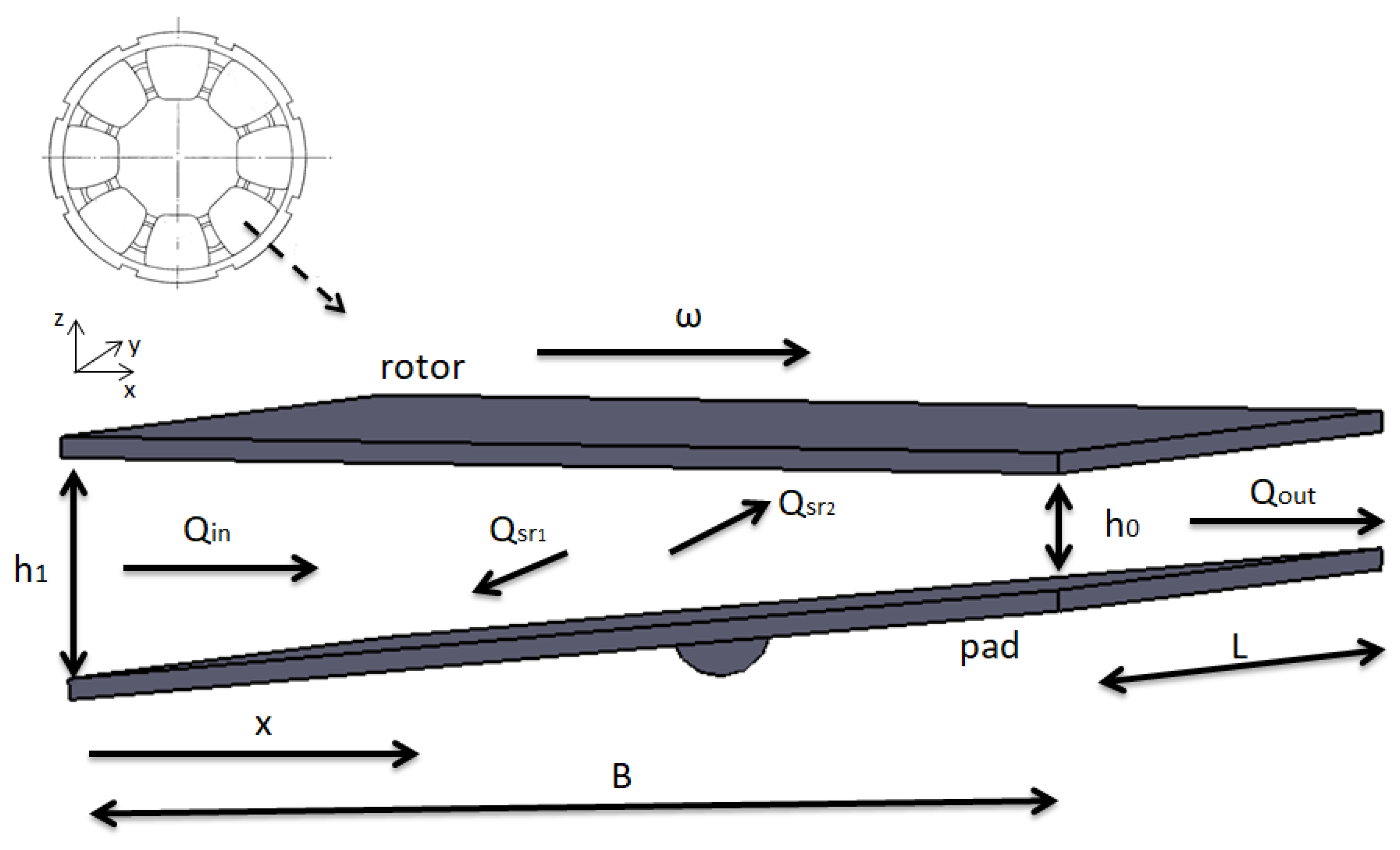
2.1. Hydrodynamic Lubrication Model
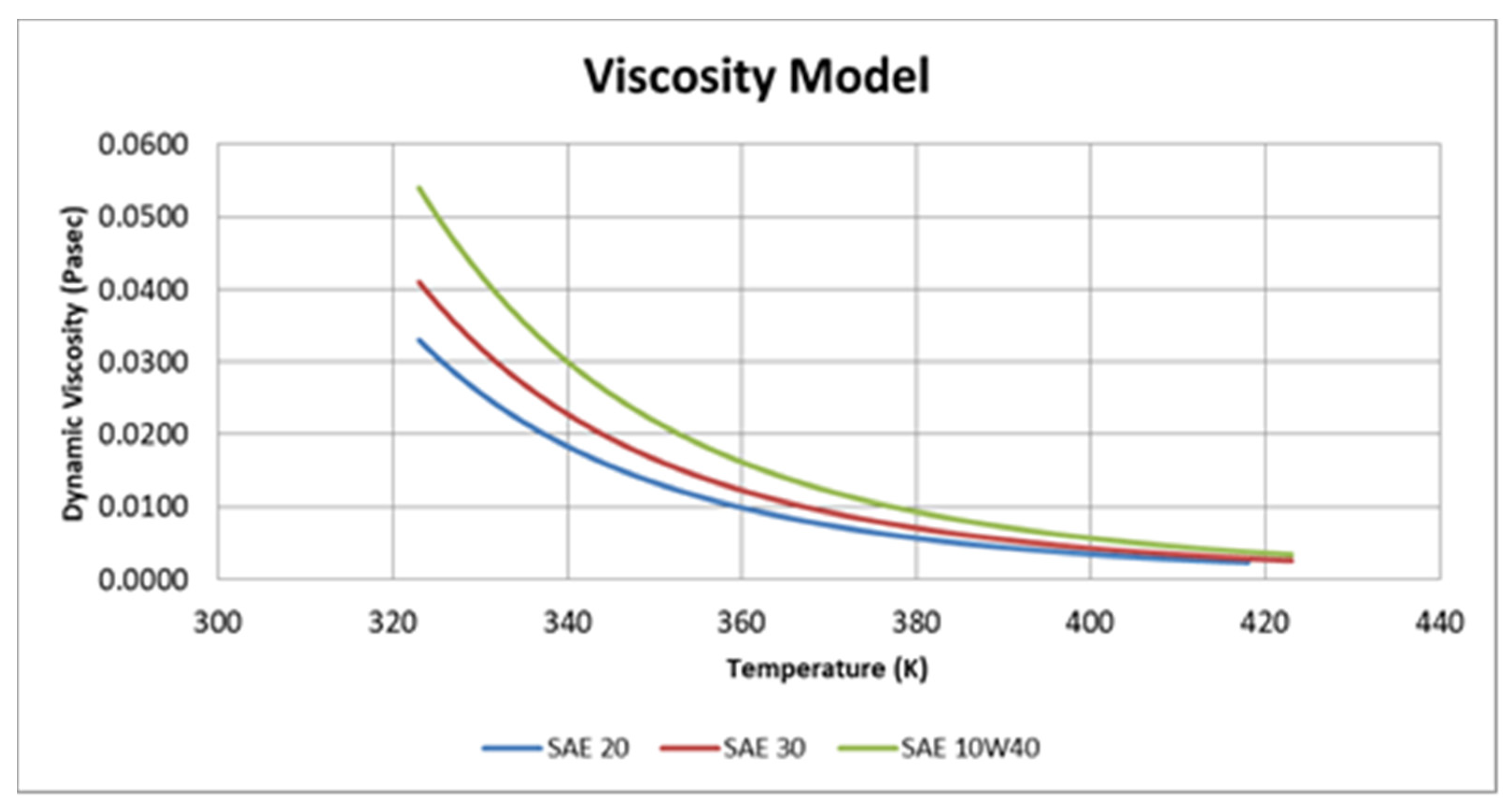
2.2. Viscosity Model
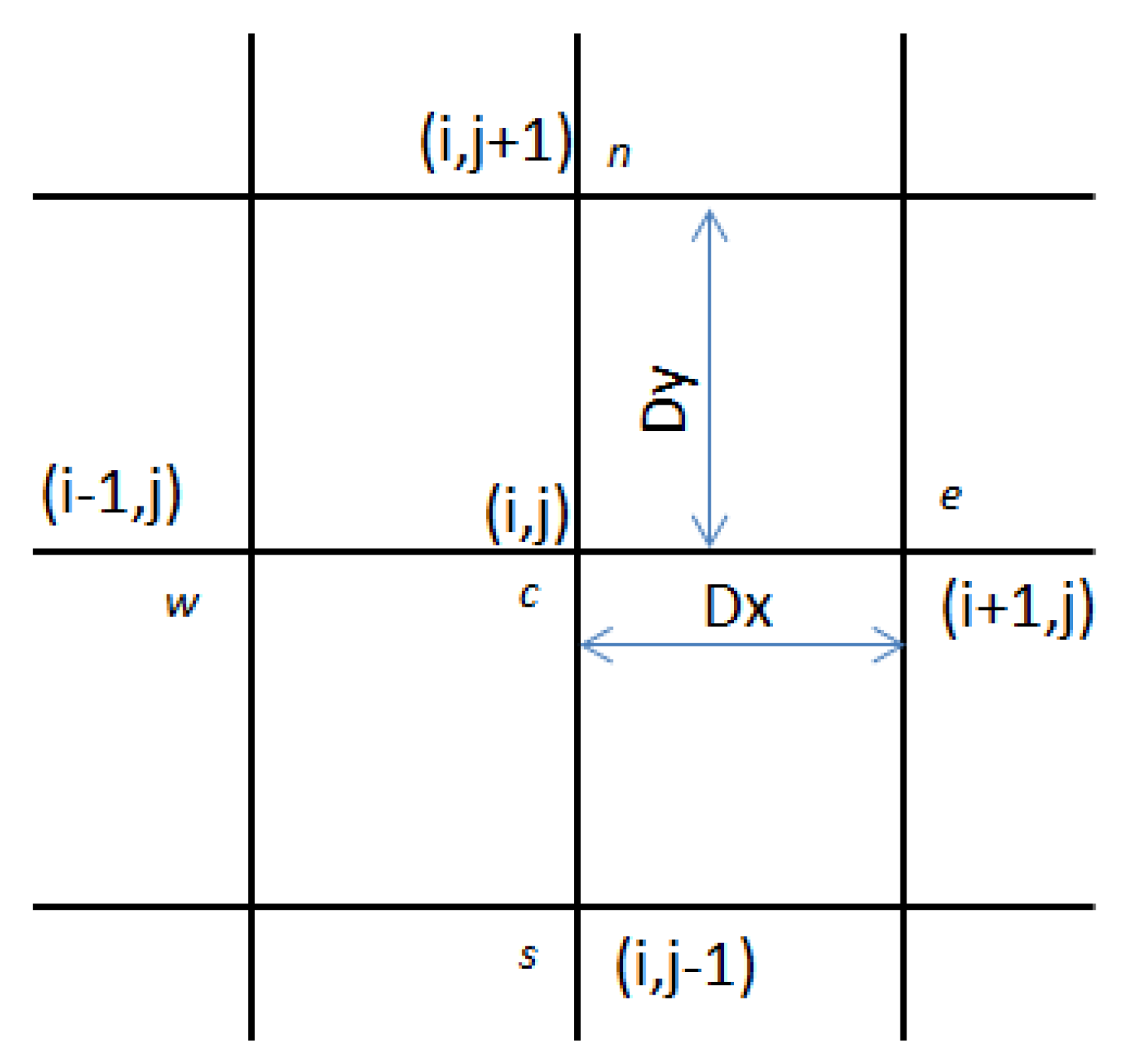
2.3. Numerical Analysis
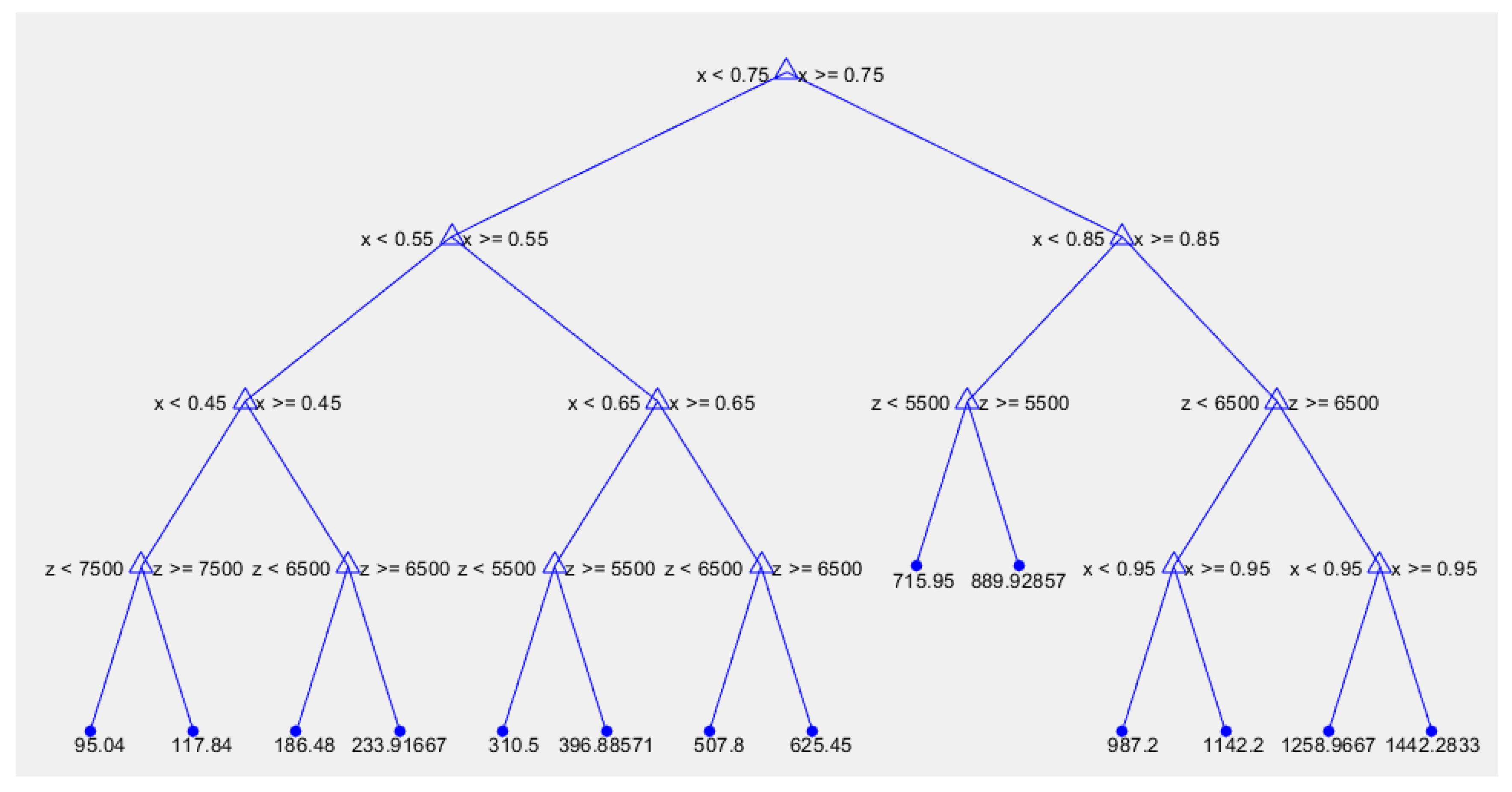
2.4. Machine-Learning
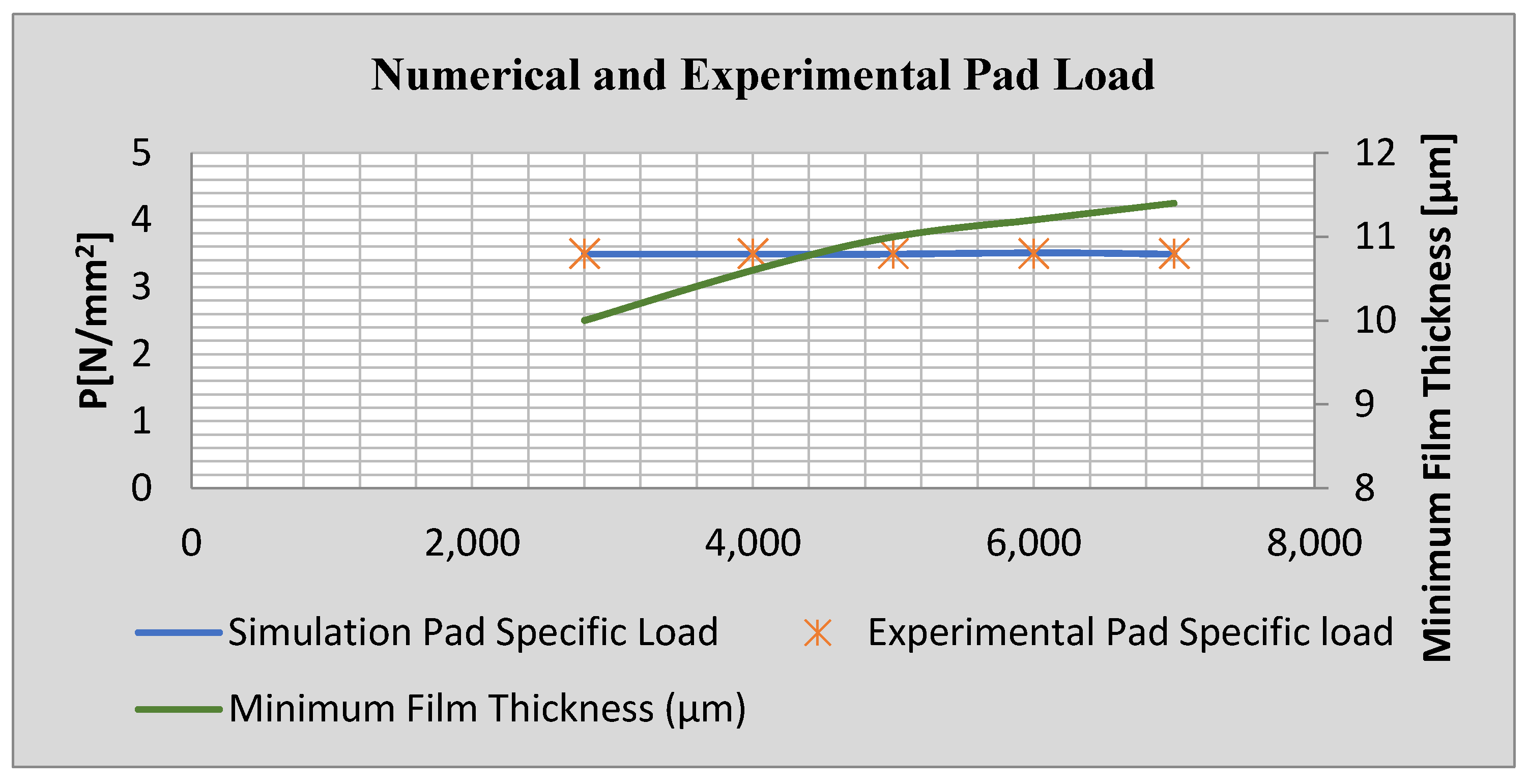
3. Results
4. Conclusions
- ▪
- As less oil covers the pad’s surface, the load-carrying capacity drops up to 93% for 40% of inlet oil coverage.
- ▪
- The load-carrying capacity of the pad is affected by the position of the oil film incompleteness. The lack of lubricant on the outer area of the pad, profile A, shows the worst load-carrying capacity results, while the case study C profile, with symmetrical lack of lubricant, presents up to 15% better performance.
- ▪
- From the studied lubricants, SAE 10W40 shows up to 135% better performance for the worst studied conditions of 12,000 rpm and 40% inlet oil coverage.
- ▪
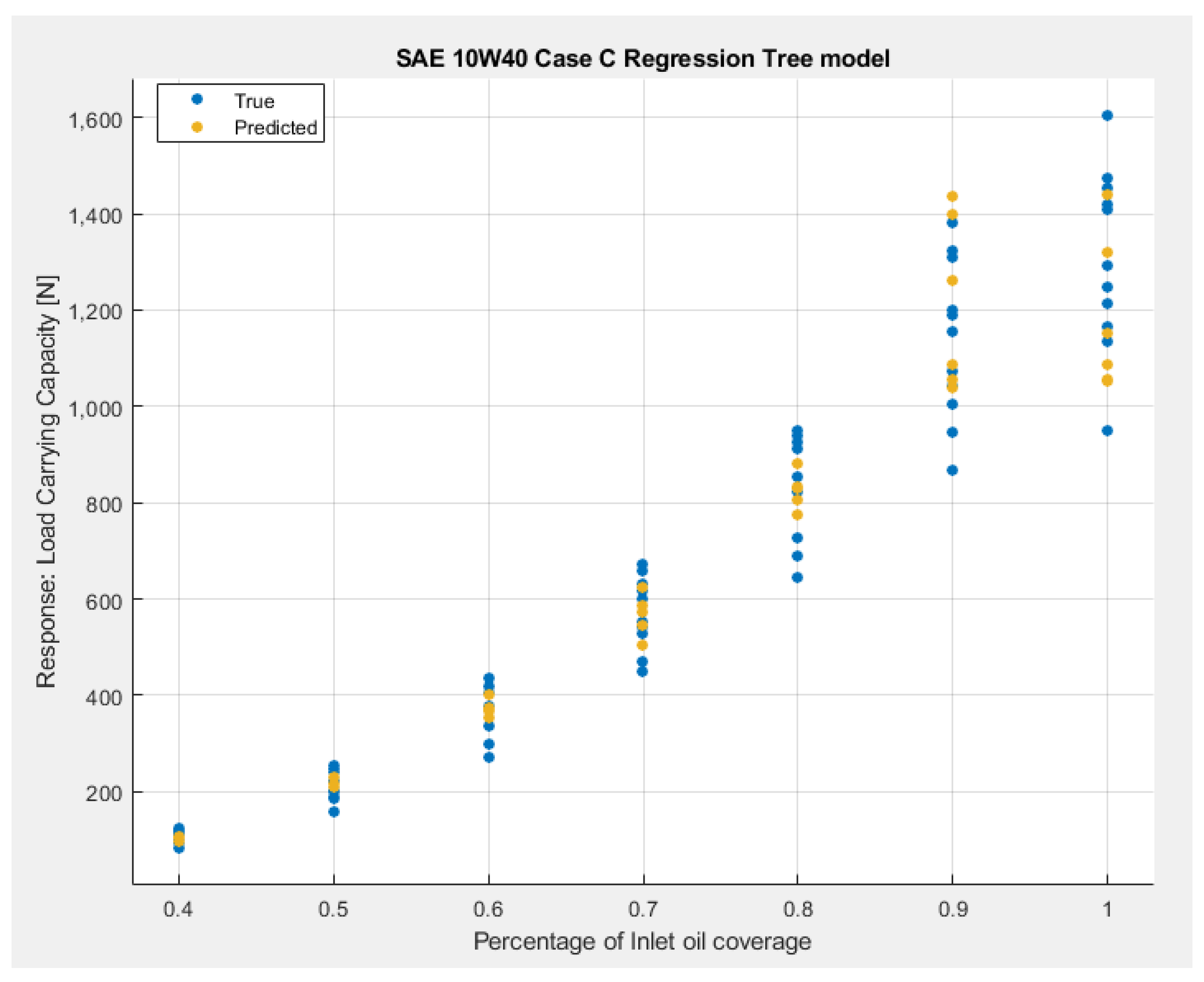
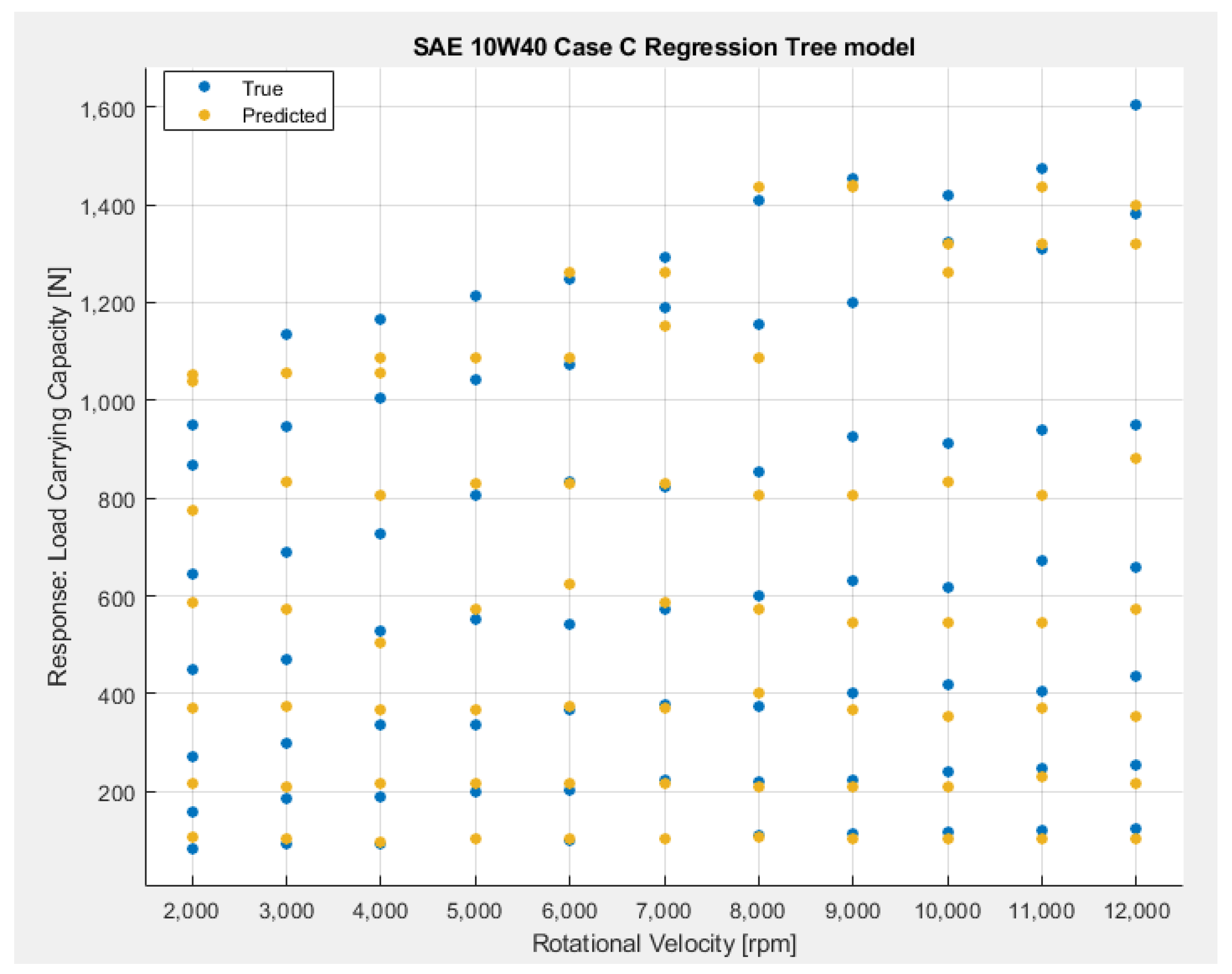
- All the machine-learning models have a good accuracy in predicting the load-carrying capacity of the pad, since all R2 values are higher than 0.95.
- ▪
- Finally, the Quadratic Polynomial Regression ML model shows 1% better accuracy compared to the Quadratic SVM model, and 4% better accuracy when compared to the Regression Tree ML model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| total area of bearing pads [m2] | |
| pad length in x-direction [m] | |
| first viscosity coefficient—absolute temperature at which μ = μν (323 K) | |
| second viscosity coefficient according to Sutherland’s law = 3800 | |
| third viscosity coefficient according to Sutherland’s law = 30,000 | |
| constants for each neighbor node | |
| film thickness [m] | |
| outlet, inlet film thickness [m] | |
| minimum film thickness [m]: | |
| convergence ratio: | |
| empirical constant = 0.8 [21] | |
| pad’s width in y-direction [m] | |
| absolute pressure [Pa] | |
| absolute nodal pressure [Pa] | |
| lubricant flow [m3/h] | |
| lubricant flow in inlet and outlet area of the pad [m3/h] | |
| lubricant outflow from the sides of the pad [m3/h] | |
| temperature [K] | |
| linear rotor velocity [m/s] | |
| dynamic viscosity coefficient [Pas] | |
| nominal dynamic viscosity | |
| independent variable of length along pad’s width side [m] | |
| rotational velocity [rpm] |
References
- Ettles, C. The Development of a Generalized Computer Analysis for Sector Shaped Tilting Pad Thrust Bearings. ASLE Trans. 1976, 19, 153–163. [Google Scholar] [CrossRef]
- Markin, D.; McCarthy, D.; Glavatskih, S. A FEM approach to simulation of tilting-pad thrust bearing assemblies. Tribol. Int. 2003, 36, 807–814. [Google Scholar] [CrossRef]
- Dadouche, A.; Fillon, M.; Dmochowski, W. Performance of a Hydrodynamic Fixed Geometry Thrust Bearing: Comparison between Experimental Data and Numerical Results. Tribol. Trans. 2006, 49, 419–426. [Google Scholar] [CrossRef]
- Papadopoulos, C.I.; Kaiktsis, L.; Fillon, M. CFD Thermohydrodynamic Analysis of 3-D Sector-Pad Thrust Bearings with rectangular dimples. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, GT2013, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Wasilczuk, M. Friction and Lubrication of Large Tilting-Pad Thrust Bearings. Lubricants 2015, 3, 164–180. [Google Scholar] [CrossRef]
- Fouflias, D.G.; Charitopoulos, A.G.; Papadopoulos, C.I.; Kaiktsis, L.; Fillon, M. Performance comparison between textured, pocket, and tapered-land sector-pad thrust bearings using computational fluid dynamics thermohydrodynamic analysis. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 229, 376–397. [Google Scholar] [CrossRef]
- Gropper, D.; Harvey, T.J.; Wang, L. A numerical model for design and optimization of surface textures for tilting pad thrust bearings. Tribol. Int. 2018, 119, 190–207. [Google Scholar] [CrossRef]
- Katsaros, K.; Bompos, D.A.; Nikolakopoulos, P.G.; Theodossiades, S. Thermal-Hydrodynamic Behavior of Coated Pivoted Pad Thrust Bearings: Comparison between Babbitt, PTFE and DLC. Lubricants 2018, 6, 50. [Google Scholar] [CrossRef]
- Etsion, I.; Barkon, I. Analysis of a Hydrodynamic Thrust Bearing with Incomplete Film. J. Lubr. Technol. 1981, 103, 355–359. [Google Scholar] [CrossRef]
- Heshmat, H.; Artiles, A.; Pinkus, O. Paper IV(ii) Parametric study and optimization of starved thrust bearings. Tribol. Ser. 1987, 11, 105–112. [Google Scholar] [CrossRef]
- Artiles, A.; Heshmat, H. Analyis of Starved Thrust Bearings Including Temperature Effects. J. Tribol. 1987, 109, 395–401. [Google Scholar] [CrossRef]
- Moosavian, A.; Ahmadi, H.; Tabatabaeefar, A.; Khazaee, M. Comparison of Two Classifiers; K-Nearest Neighbor and Artificial Neural Network, for Fault Diagnosis on a Main Engine Journal-Bearing. Shock. Vib. 2013, 20, 263–272. [Google Scholar] [CrossRef]
- Alves, D.S.; Daniel, G.B.; de Castro, H.F.; Machado, T.H.; Cavalca, K.L.; Gecgel, O.; Dias, J.P.; Ekwaro-Osire, S. Uncertainty quantification in deep convolutional neural network diagnostics of journal bearings with ovalization fault. Mech. Mach. Theory 2020, 149, 103835. [Google Scholar] [CrossRef]
- Poddar, S.; Tandon, N. Classification and detection of cavitation, particle contamination and oil starvation in journal bearing through machine learning approach using acoustic emission signals. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2137–2143. [Google Scholar] [CrossRef]
- Lorza, R.L.; Garcia, R.E.; Martinez, R.F.; Cueva, M.I.; MacDonald, B.J. Using the finite element method and data mining techniques as an alternative method to determine the maximum load capacity in tapered roller bearings. J. Appl. Log. 2016, 24, 4–14. [Google Scholar] [CrossRef]
- Katsaros, K.P.; Nikolakopoulos, P.G. On the tilting-pad thrust bearings hydrodynamic lubrication under combined numerical and machine learning techniques. Lubr. Sci. 2021, 33, 153–170. [Google Scholar] [CrossRef]
- Moschopoulos, M.; Rossopoulos, G.N.; Papadopoulos, C.I. Journal Bearing Performance Prediction Using Machine Learning and Octave-Band Signal Analysis of Sound and Vibration Measurements. Pol. Marit. Res. 2021, 28, 137–149. [Google Scholar] [CrossRef]
- Zavos, A.; Katsaros, K.P.; Nikolakopoulos, P.G. Optimum Selection of Coated Piston Rings and Thrust Bearings in Mixed Lubrication for Different Lubricants Using Machine Learning. Coatings 2022, 12, 704. [Google Scholar] [CrossRef]
- Aurelian, F.; Patrick, M.; Mohamed, H. Wall slip effects in (elasto) hydrodynamic journal bearings. Tribol. Int. 2011, 44, 868–877. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Fillon, M. A numerical investigation of both thermal and texturing surface effects on the journal bearings static characteristics. Tribol. Int. 2015, 90, 228–239. [Google Scholar] [CrossRef]
- Stachowiak, G.W.; Batchelor, A.W. Thermal Effects in Bearings. In Engineering Tribology; Paragraph 4.6; Butterworth-Heinemann Elsevier Ltd.: Oxford, UK, 2014; Chapter 4. [Google Scholar]
- Bielec, M.K.; Leopard, A.J. Paper 13: Tilting Pad Thrust Bearings: Factors Affecting Performance and Improvements with Directed Lubrication. Proc. Inst. Mech. Eng. Conf. Proc. 1969, 184, 93–102. [Google Scholar] [CrossRef]

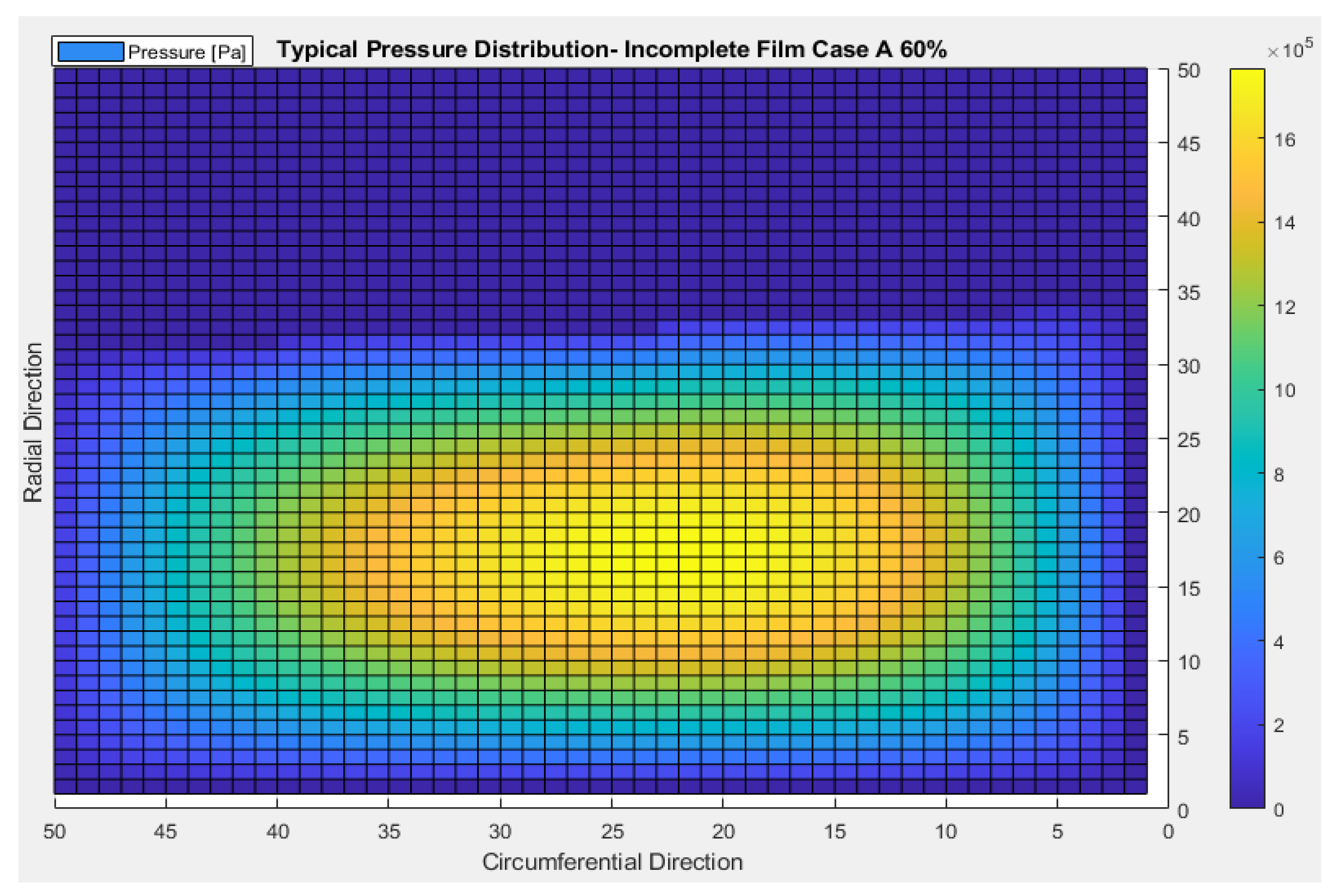



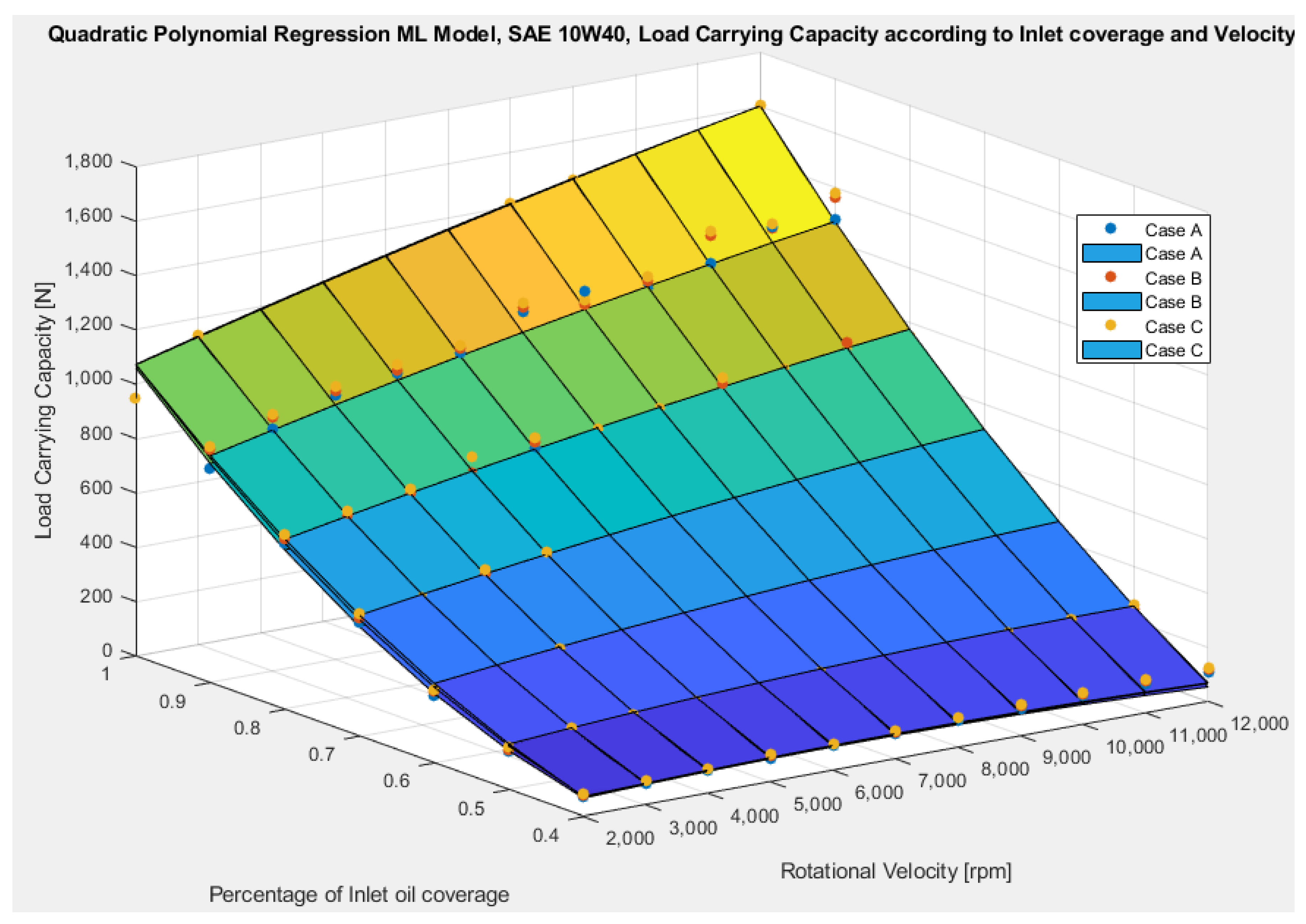
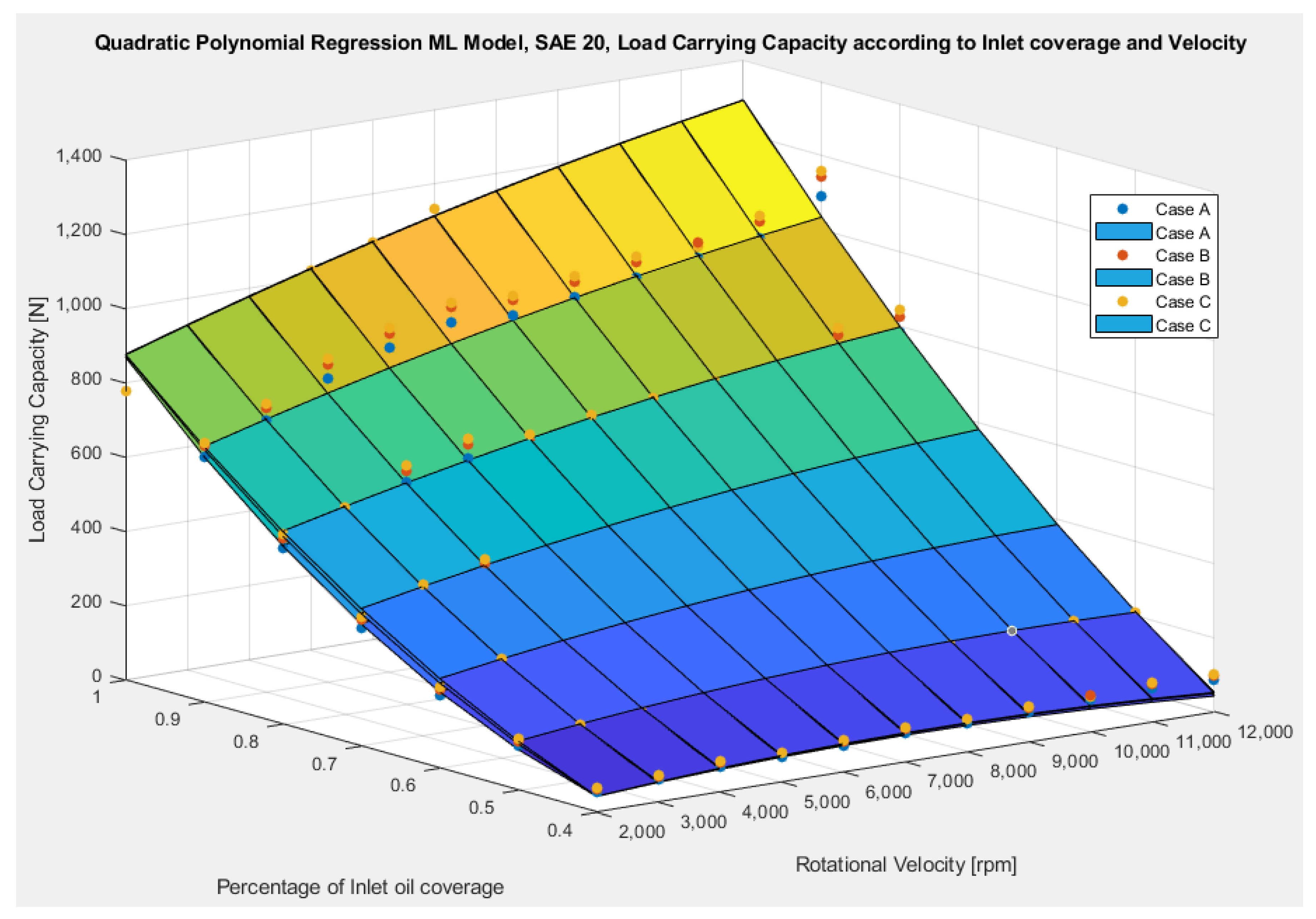

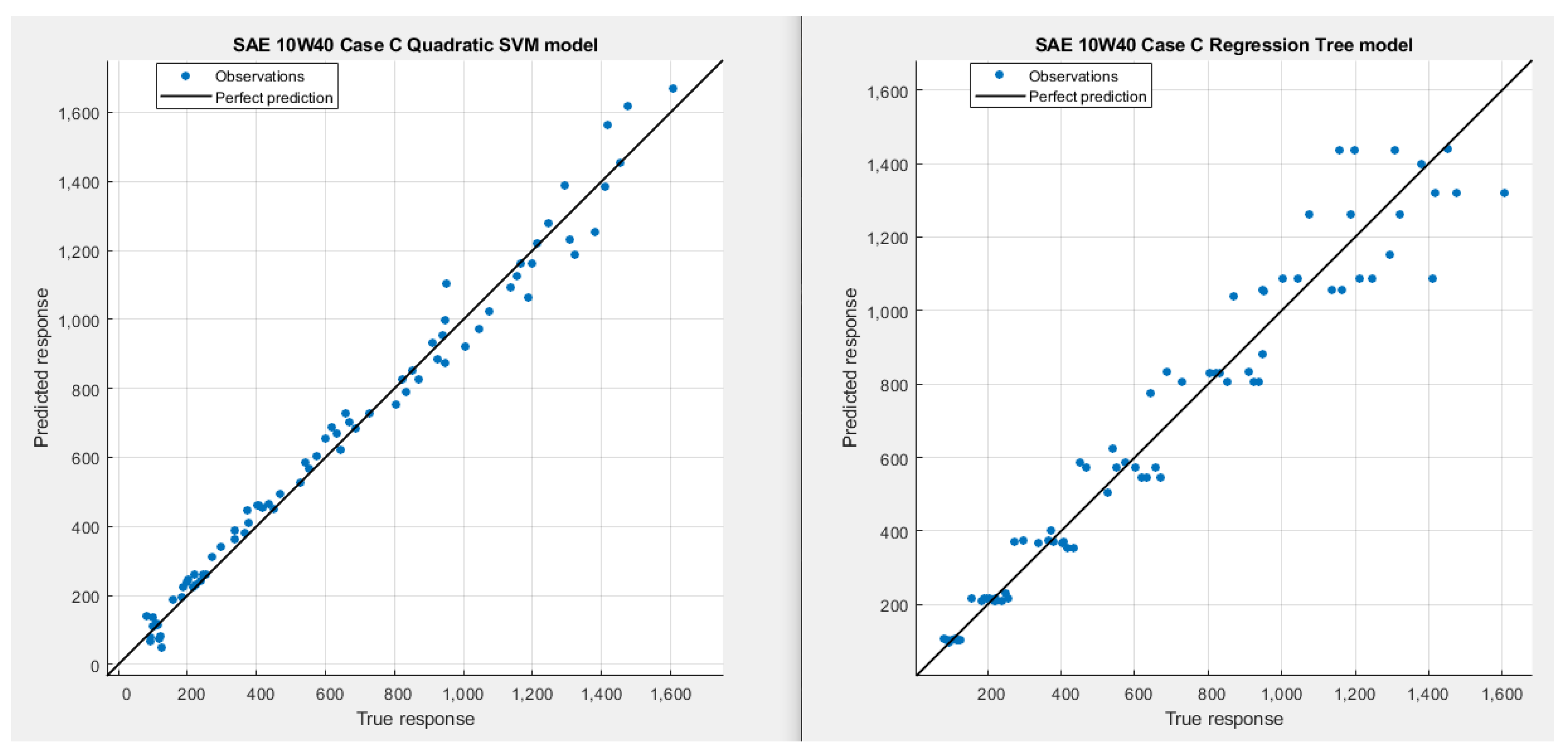


| Pad’s Length | 32 | mm |
| Pad’s Width | 28 | mm |
| Pad’s Outer Radious | 62 | mm |
| Pad’s Inclination | 0.1 | |
| Pad’s Pivot | center | |
| Rotational Velocity | 2000–12,000 | rpm |
| Percentage of Inlet Oil Coverage | 0.4–1 | |
| SAE 20 dynamic viscosity @50 °C | 0.033 | Pasec |
| SAE 30 dynamic viscosity @50 °C | 0.046 | Pasec |
| SAE 10W40 dynamic viscosity @50 °C | 0.054 | Pasec |
| SAE 20 density @40 °C | 861 | Kg/m3 |
| SAE 20 specific heat capacity | 2021 | J/kgK |
| SAE 30 density @40 °C | 869 | Kg/m3 |
| SAE 30 specific heat capacity | 1950 | J/kgK |
| SAE 10W40 density @40 °C | 851 | Kg/m3 |
| SAE 10W40 specific heat capacity | 1980 | J/kgK |
| Lubricant’s Inlet Temperature | 323 | K |
| Case Study | ML Model | R2 |
|---|---|---|
| SAE 30 Case A | 0.99 | |
| SAE 30 Case B | 0.99 | |
| SAE 30 Case C | 0.99 | |
| SAE 10W40 Case A | 0.99 | |
| SAE 10W40 Case B | 0.99 | |
| SAE 10W40 Case C | 0.99 | |
| SAE 20 Case A | 0.99 | |
| SAE 20 Case B | 0.99 | |
| SAE 20 Case C | 0.99 |
| Case Study | R2 |
| SAE 30 Quadratic SVM ML model | 0.98 |
| SAE 30 Regression Tree ML model | 0.95 |
| SAE 10W40 Quadratic SVM ML model | 0.98 |
| SAE 10W40 Regression Tree ML model | 0.95 |
| SAE 20 Quadratic SVM ML model | 0.98 |
| SAE 20 Regression Tree ML model | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsaros, K.P.; Nikolakopoulos, P.G. Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques. Lubricants 2023, 11, 113. https://doi.org/10.3390/lubricants11030113
Katsaros KP, Nikolakopoulos PG. Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques. Lubricants. 2023; 11(3):113. https://doi.org/10.3390/lubricants11030113
Chicago/Turabian StyleKatsaros, Konstantinos P., and Pantelis G. Nikolakopoulos. 2023. "Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques" Lubricants 11, no. 3: 113. https://doi.org/10.3390/lubricants11030113
APA StyleKatsaros, K. P., & Nikolakopoulos, P. G. (2023). Performance Prediction Model for Hydrodynamically Lubricated Tilting Pad Thrust Bearings Operating under Incomplete Oil Film with the Combination of Numerical and Machine-Learning Techniques. Lubricants, 11(3), 113. https://doi.org/10.3390/lubricants11030113






