Thickening Properties of Carboxymethyl Cellulose in Aqueous Lubrication
Abstract
1. Introduction
2. Materials and Methods
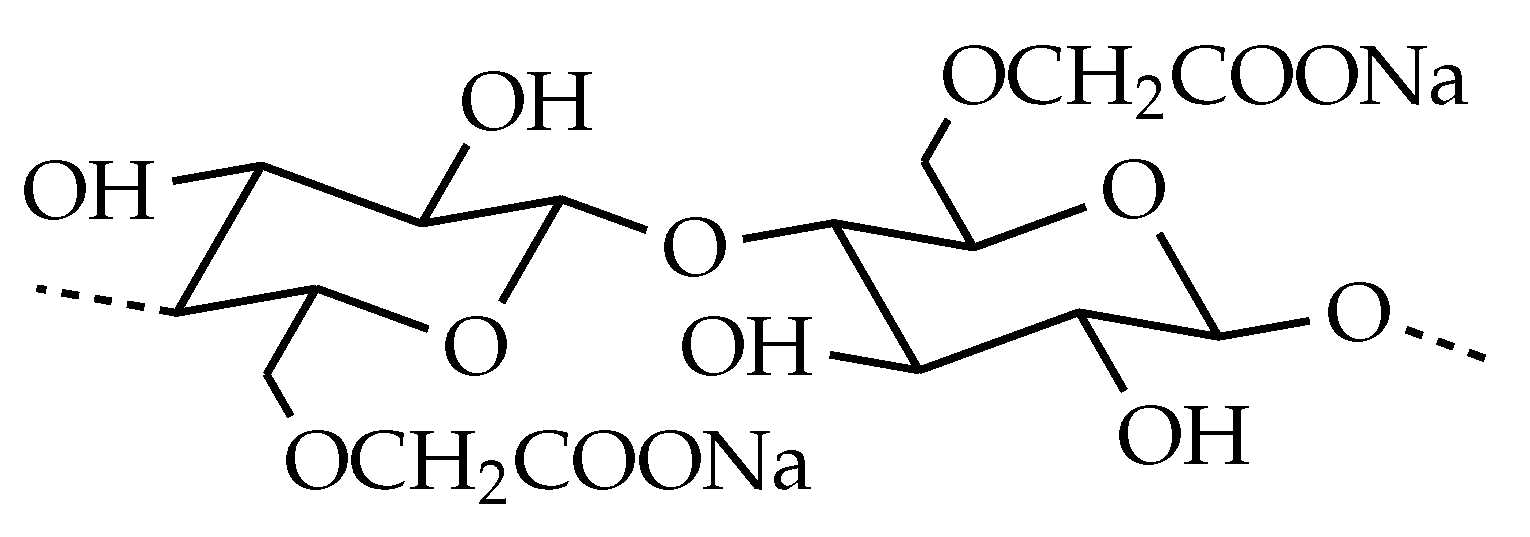
2.1. Materials
2.2. Flow Behavior and Critical Concentration
2.3. Influence of Pressure
2.4. Influence of Temperature
2.5. Tribological Investigations
2.6. Shear Stability—Permanent Viscosity Loss
3. Results and Discussion
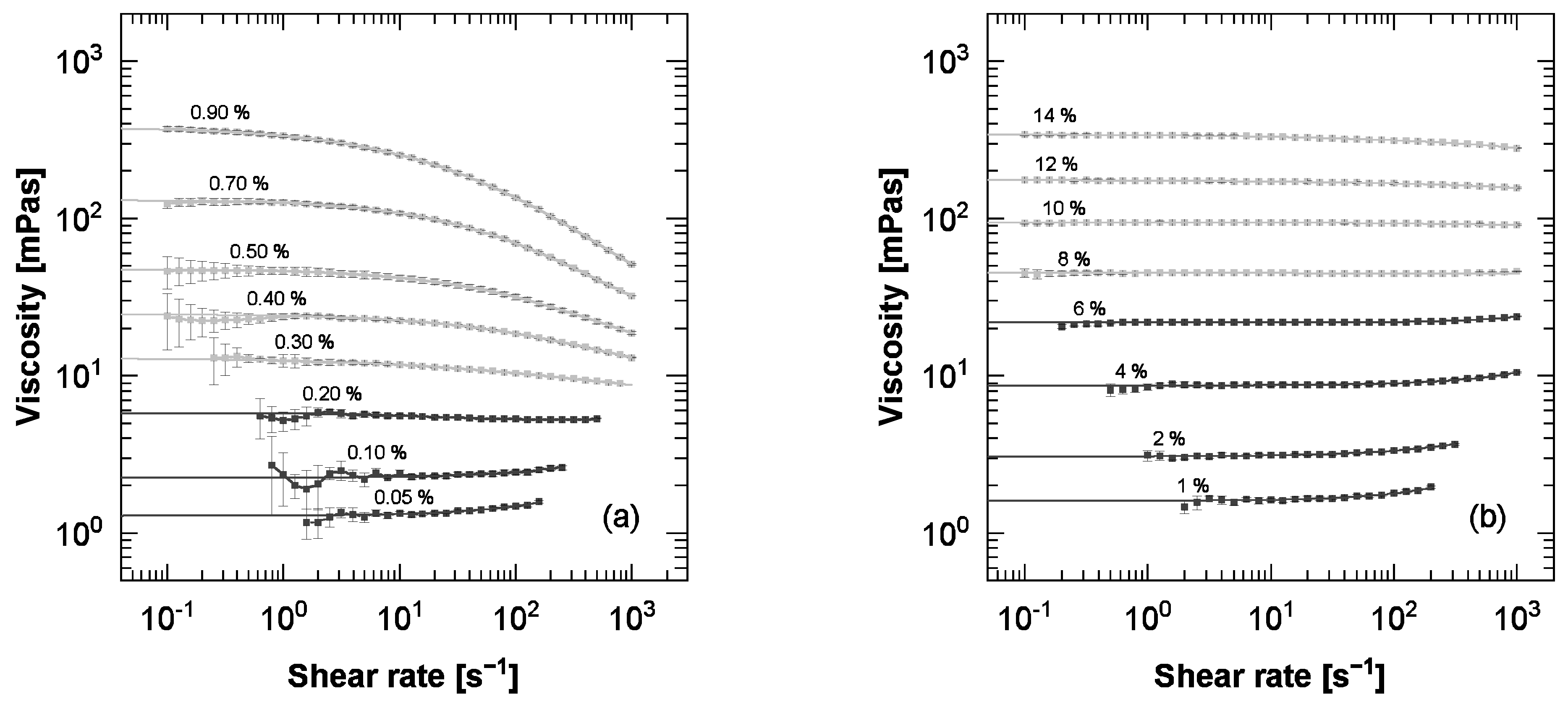
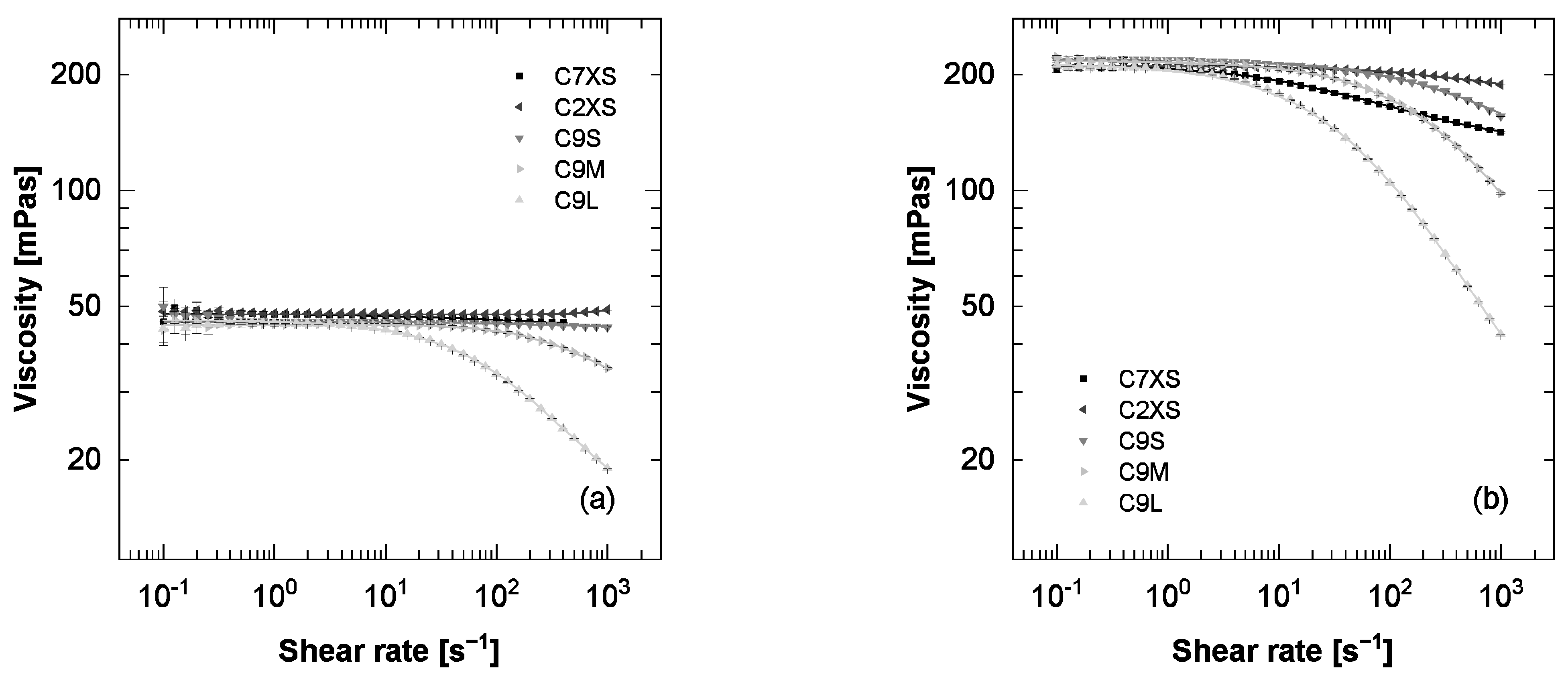
3.1. Viscosity-Concentration Relationship
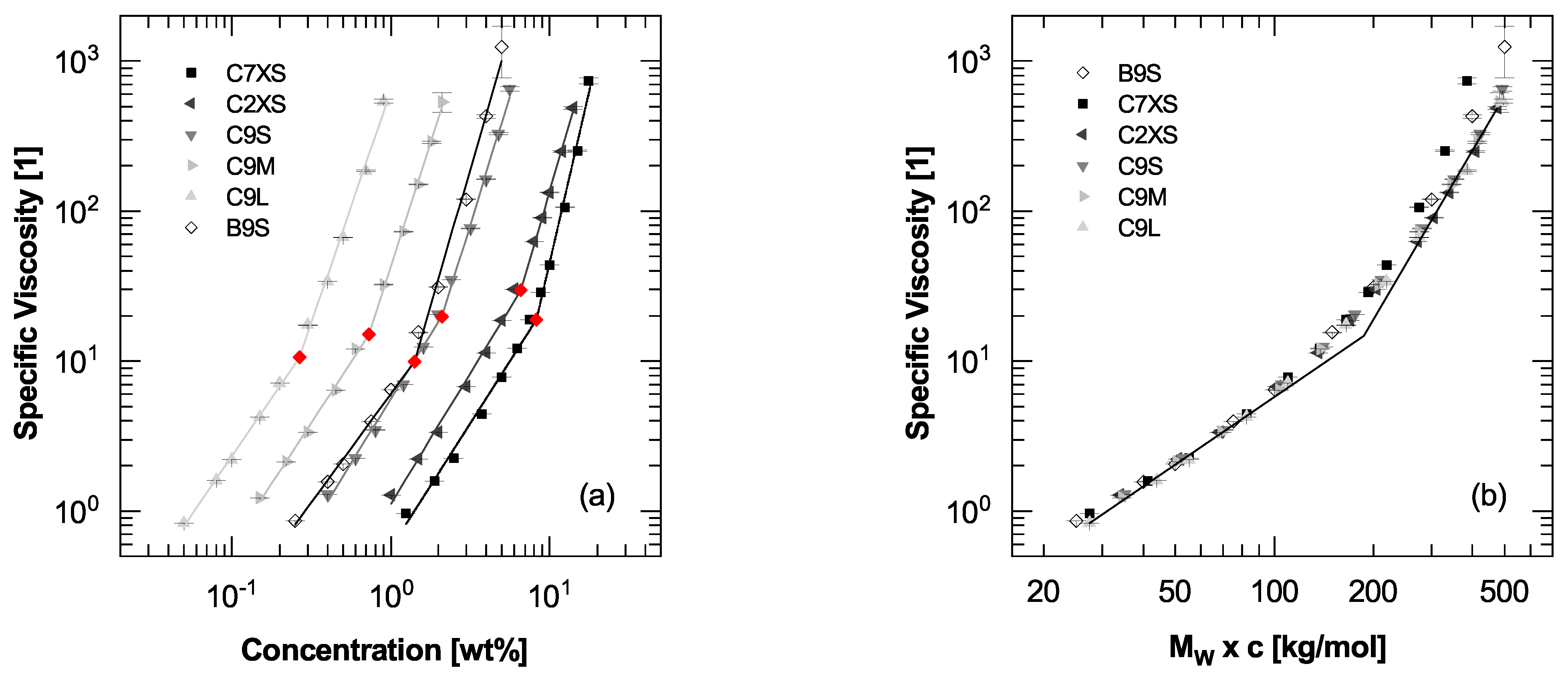
3.2. Critical Concentration
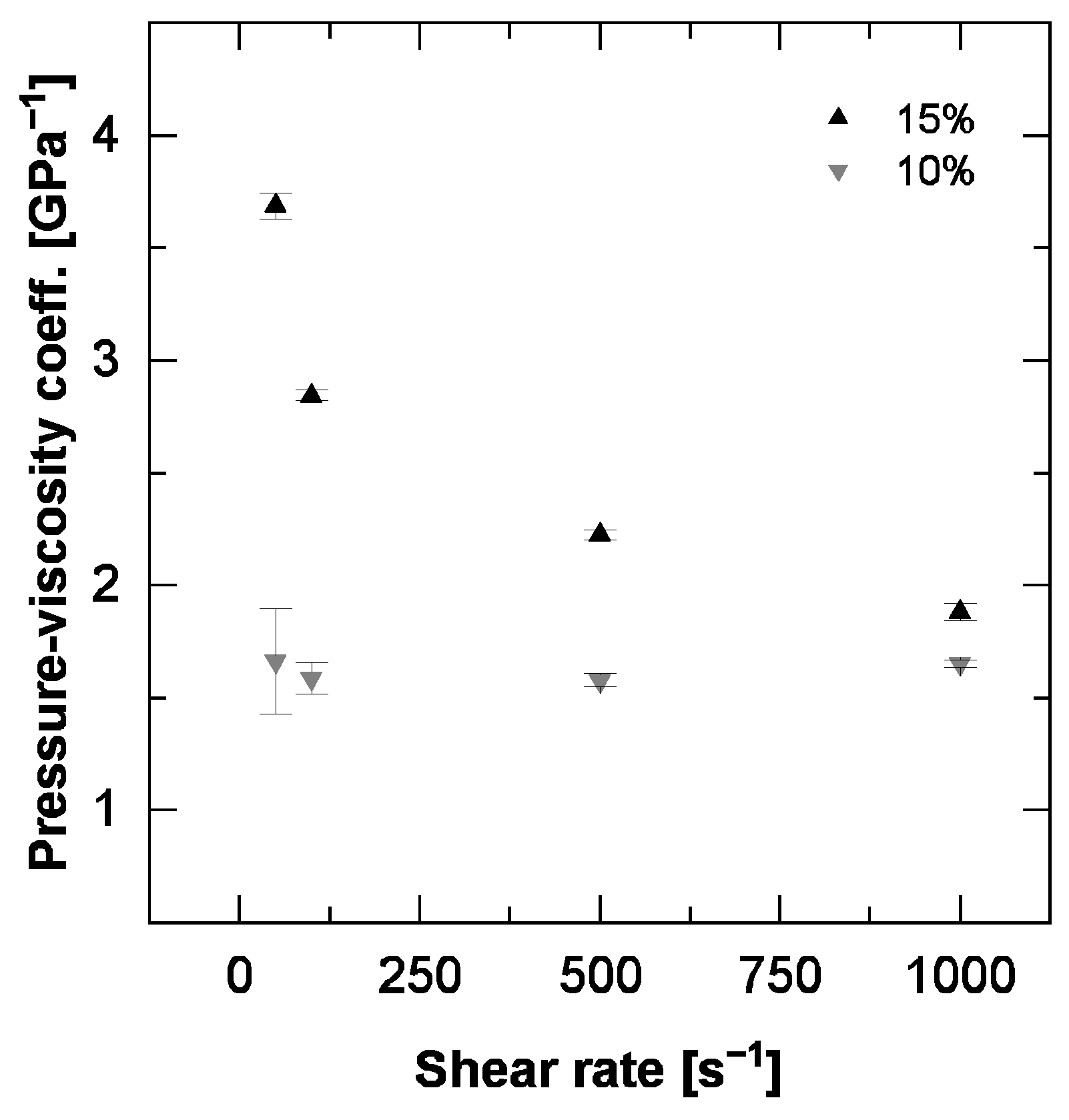
3.3. Viscosity-Pressure-Relationship
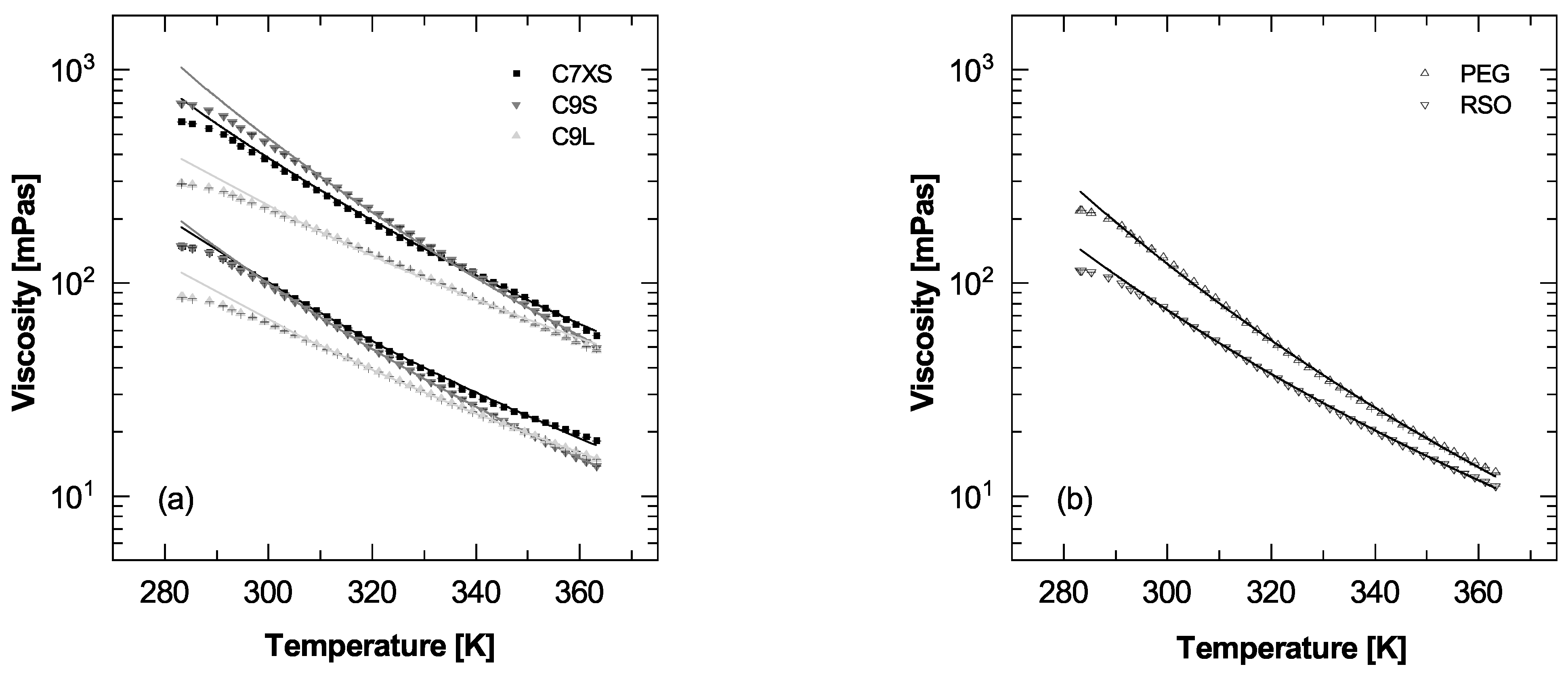
3.4. Viscosity-Temperature Relationship
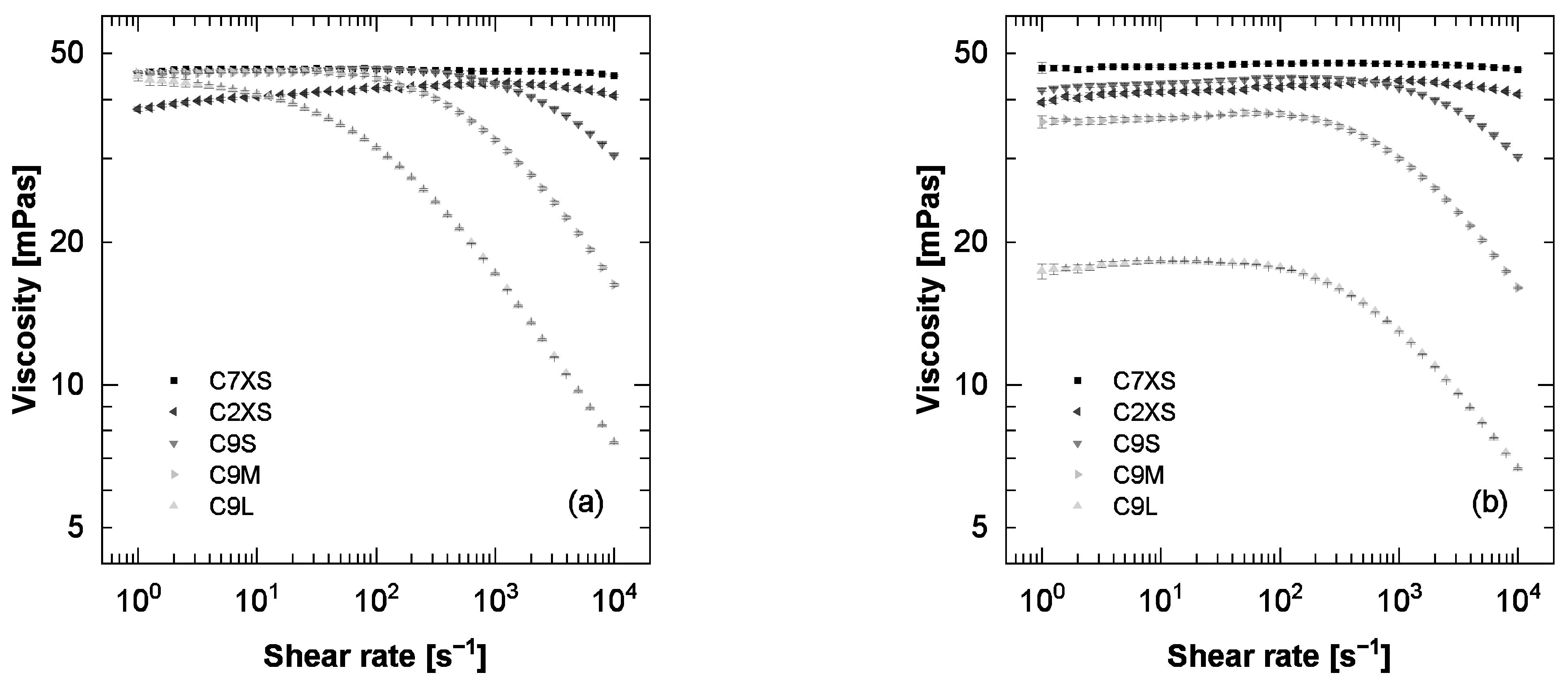
3.5. Temporary Viscosity Loss
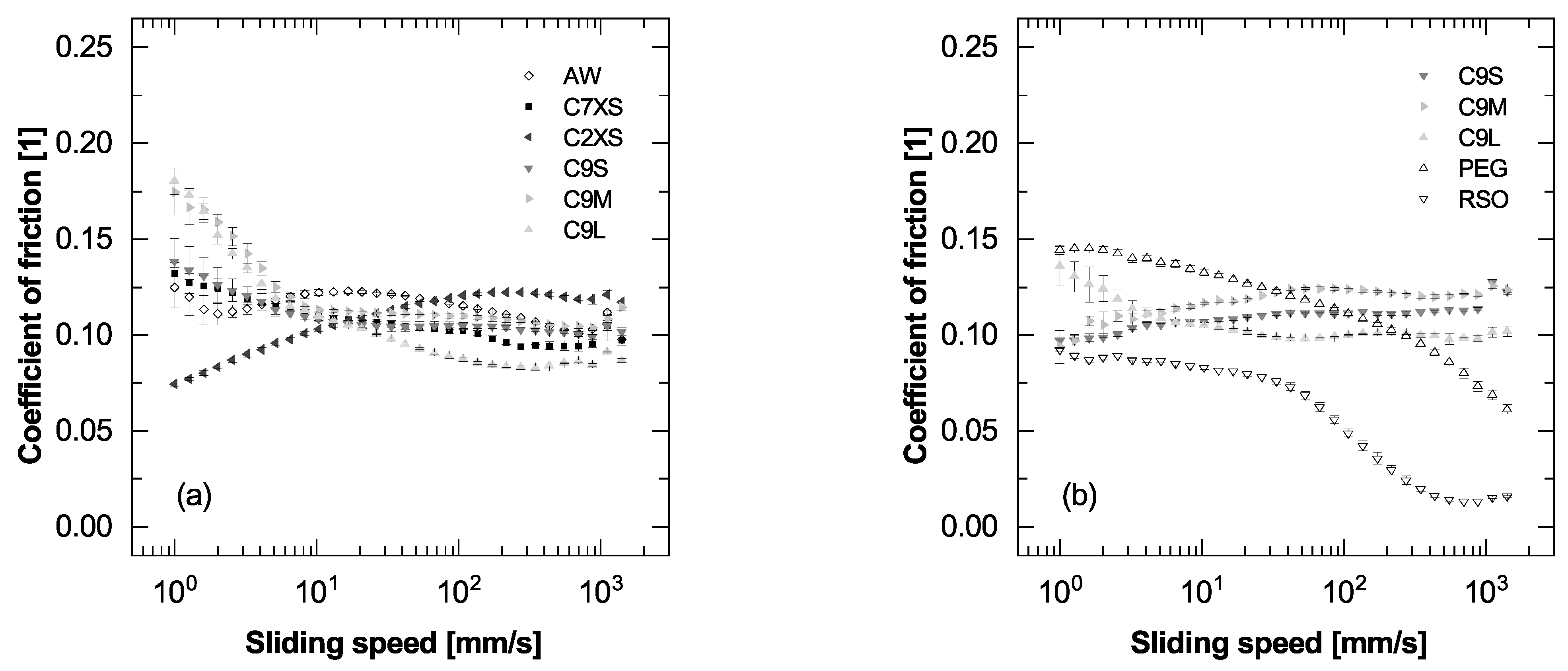
3.6. Lubricating Performance under Sliding Conditions
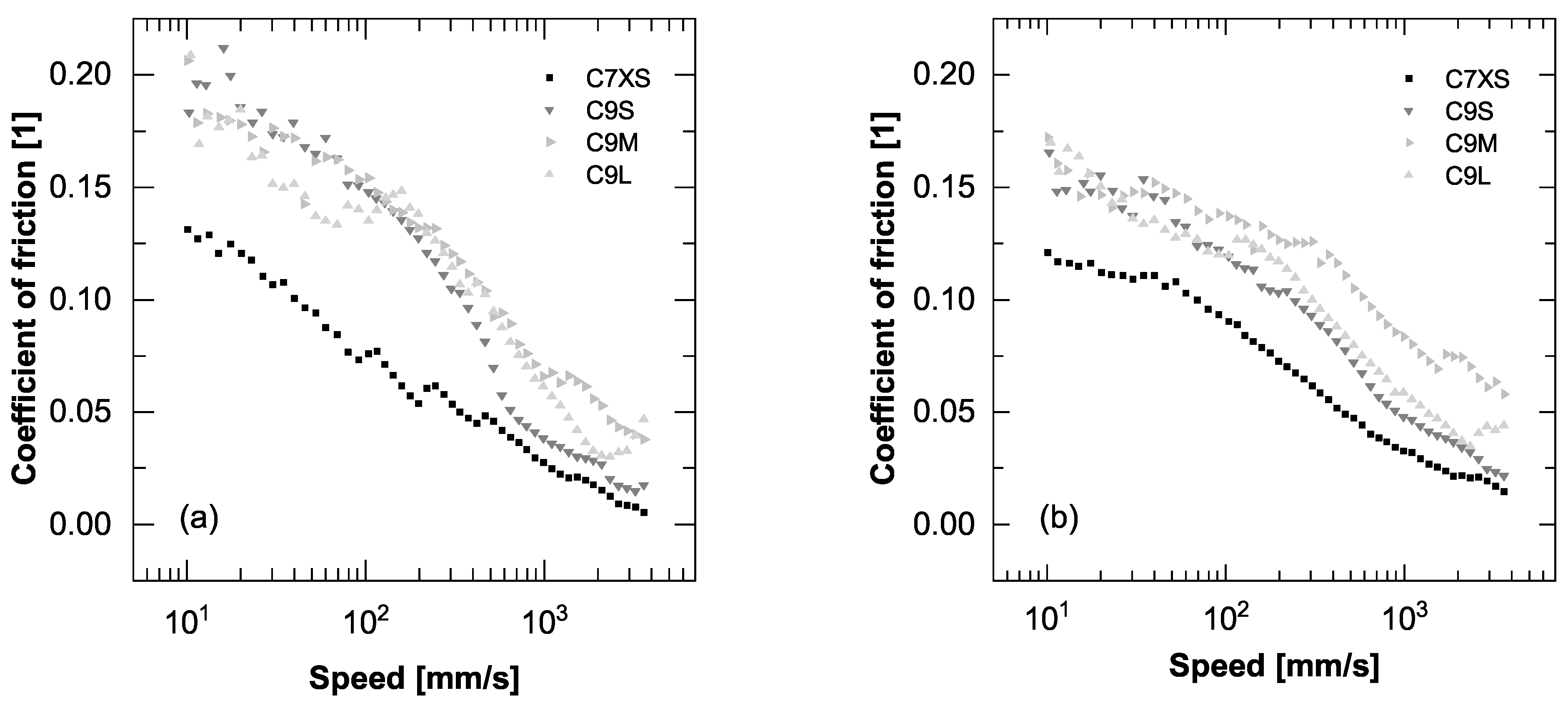
3.7. Lubricating Performance under Rolling Conditions
3.8. Permanent Viscosity Loss
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AW | Additivated Water |
| COF | Coefficient of Friction |
| CMC | Sodium Carboxymethyl Cellulose |
| DS | Degreee of Substitution |
| MTM | Mini Traction Machine |
| PEG | Polyethylene Glycol 400 |
| PVL | Permanent Viscosity Loss |
| RSO | Rapeseed Oil |
| SRR | Slide-Roll Ratio |
| TVL | Temporary Viscosity Loss |
| VM | Viscosity Modifier |
| WSD | Wear Scar Diameter |
| ZSVG | Zero-Shear Viscosity Grade |
References
- Ma, L.; Zhang, C.; Liu, S. Progress in experimental study of aqueous lubrication. Chin. Sci. Bull. 2012, 57, 2062–2069. [Google Scholar] [CrossRef]
- Yilmaz, M.; Mirza, M.; Lohner, T.; Stahl, K. Superlubricity in EHL contacts with water-containing gear fluids. Lubricants 2019, 7, 46. [Google Scholar] [CrossRef]
- Yilmaz, M.; Lohner, T.; Michaelis, K.; Stahl, K. Minimizing gear friction with water-containing gear fluids. Forsch. Ing. 2019, 83, 327–337. [Google Scholar] [CrossRef]
- Sagraloff, N.; Dobler, A.; Tobie, T.; Stahl, K.; Ostrowski, J. Development of an oil free water-based lubricant for gear applications. Lubricants 2019, 7, 33. [Google Scholar] [CrossRef]
- Rahman, M.H.; Warneke, H.; Webbert, H.; Rodriguez, J.; Austin, E.; Tokunaga, K.; Rajak, D.K.; Menezes, P.L. Water-based lubricants: Development, properties, and performances. Lubricants 2021, 9, 73. [Google Scholar] [CrossRef]
- Martin, J.M.; De Barros-Bouchet, M.I. Water-like lubrication of hard contacts by polyhydric alcohols. In Aqueous Lubrication; IISc Research Monographs Series; Co-Published with Indian Institute of Science (IISc): Bangalore, India, 2011; Volume 3, pp. 219–235. [Google Scholar]
- Martini, A.; Ramasamy, U.S.; Len, M. Review of viscosity modifier lubricant additives. Tribol. Lett. 2018, 66, 58. [Google Scholar] [CrossRef]
- Spencer, N.D. Aqueous lubrication with poly(ethylene glycol) brushes. Tribol. Online 2014, 9, 143–153. [Google Scholar] [CrossRef]
- Sagraloff, N.; Winkler, K.J.; Tobie, T.; Stahl, K.; Folland, C.; Asam, T. Investigations on the scuffing and wear characteristic performance of an oil free water-based lubricant for gear applications. Lubricants 2021, 9, 24. [Google Scholar] [CrossRef]
- Zhang, Z.; Ye, Z.; Hu, F.; Wang, W.; Zhang, S.; Gao, L.; Lu, H. Double-network polyvinyl alcohol composite hydrogel with self-healing and low friction. J. Appl. Polym. Sci. 2022, 139, 51563. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, J.; Zhang, M.; Jiang, Z.; Zhou, C.; Ma, X. Study on the tribological behaviour of nanolubricants during micro rolling of copper foils. Materials 2022, 15, 2600. [Google Scholar] [CrossRef]
- Dhakal, N.; Shi, Y.; Emami, N. Tribological behaviour of UHMWPE composites lubricated by polyvinylpyrrolidone-modified water. Lubr. Sci. 2022, 34, 42–53. [Google Scholar] [CrossRef]
- Naik, S.C.; Pittman, J.F.T.; Richardson, J.F.; Lansdown, A.R. Evaluation of hydroxyethyl cellulose ether as a thickener for aqueous lubricants or hydraulic fluids. Wear 1978, 50, 155–168. [Google Scholar] [CrossRef]
- Han, T.; Yi, S.; Zhang, C.; Li, J.; Chen, X.; Luo, J.; Banquy, X. Superlubrication obtained with mixtures of hydrated ions and polyethylene glycol solutions in the mixed and hydrodynamic lubrication regimes. J. Colloid Interface Sci. 2020, 579, 479–488. [Google Scholar] [CrossRef]
- Branch, D.W.; Wheeler, B.C.; Brewer, G.J.; Leckband, D.E. Long-term stability of grafted polyethylene glycol surfaces for use with microstamped substrates in neuronal cell culture. Biomaterials 2001, 22, 1035–1047. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Kim, C.; Kwon, D. Thermal degradation of poly(ethyleneglycol). Polym. Degrad. Stab. 1995, 47, 203–208. [Google Scholar] [CrossRef]
- Chen, W.; Amann, T.; Kailer, A.; Rühe, J. Thin-film lubrication in the water/octyl β-D-glucopyranoside system: Macroscopic and nanoscopic tribological behavior. Langmuir 2019, 35, 7136–7145. [Google Scholar] [CrossRef]
- Chen, W.; Amann, T.; Kailer, A.; Rühe, J. Macroscopic friction studies of alkylglucopyranosides as additives for water-based lubricants. Lubricants 2020, 8, 11. [Google Scholar] [CrossRef]
- George, A.; Sanjay, M.R.; Srisuk, R.; Parameswaranpillai, J.; Siengchin, S. A comprehensive review on chemical properties and applications of biopolymers and their composites. Int. J. Biol. Macromol. 2020, 154, 329–338. [Google Scholar] [CrossRef]
- Wüstenberg, T. Cellulose und Cellulosederivate: Grundlagen, Wirkungen und Applikationen; Behr’s GmbH: Hamburg, Germany, 2013. [Google Scholar]
- Wolfs, J.; Nickisch, R.; Wanner, L.; Meier, M.A.R. Sustainable one-pot cellulose dissolution and derivatization via a tandem reaction in the DMSO/DBU/CO2 switchable solvent system. J. Am. Chem. Soc. 2021, 143, 18693–18702. [Google Scholar] [CrossRef]
- Jain, S.; Sandhu, P.S.; Malvi, R.; Gupta, B. Cellulose derivatives as thermoresponsive polymer: An overview. J. Appl. Pharm. Sci. 2013, 3, 139–144. [Google Scholar]
- Gelinski, S.; Winter, M.; Wichmann, H.; Bock, R.; Herrmann, C.; Bahadir, M. Development and testing of a novel glycerol/chitosan based biocide-free hydraulic fluid. J. Clean. Prod. 2016, 112, 3589–3596. [Google Scholar] [CrossRef]
- Rahman, M.S.; Hasan, M.S.; Nitai, A.S.; Nam, S.; Karmakar, A.K.; Ahsan, M.S.; Shiddiky, M.J.A.; Ahmed, M.B. Recent developments of carboxymethyl cellulose. Polymers 2021, 13, 1345. [Google Scholar] [CrossRef]
- Heinze, T.; Pfeiffer, K. Studies on the synthesis and characterization of carboxymethylcellulose. Die Angew. Makromol. Chem. 1999, 266, 37–45. [Google Scholar] [CrossRef]
- Casaburi, A.; Montoya Rojo, U.; Cerrutti, P.; Vázquez, A.; Foresti, M.L. Carboxymethyl cellulose with tailored degree of substitution obtained from bacterial cellulose. Food Hydrocoll. 2018, 75, 147–156. [Google Scholar] [CrossRef]
- Elliot, J.H.; Ganz, A.J. Some rheological properties of sodium carboxymethylcellulose solutions and gels. Rheol. Acta 1974, 13, 670–674. [Google Scholar] [CrossRef]
- Lopez, C.G.; Rogers, S.E.; Colby, R.H.; Graham, P.; Cabral, J.T. Structure of sodium carboxymethyl cellulose aqueous solutions: A SANS and rheology study. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 492–501. [Google Scholar] [CrossRef]
- Xiquan, L.; Tingzhu, Q.; Shaoqui, Q. Kinetics of the carboxymethylation of cellulose in the isopropyl alcohol system. Acta Polym. 1990, 41, 220–222. [Google Scholar] [CrossRef]
- Kulicke, W.M.; Kull, A.H.; Kull, W.; Thielking, H.; Engelhardt, J.; Pannek, J.B. Characterization of aqueous carboxymethylcellulose solutions in terms of their molecular structure and its influence on rheological behaviour. Polymer 1996, 37, 2723–2731. [Google Scholar] [CrossRef]
- Kono, H.; Oshima, K.; Hashimoto, H.; Shimizu, Y.; Tajima, K. NMR characterization of sodium carboxymethyl cellulose: Substituent distribution and mole fraction of monomers in the polymer chains. Carbohydr. Polym. 2016, 146, 1–9. [Google Scholar] [CrossRef]
- Holtzapple, M.T.; Caballero, B. Cellulose. In Encyclopedia of Food Sciences and Nutrition, 2nd ed.; Academic Press: Oxford, UK, 2003; pp. 998–1007. [Google Scholar]
- Mondal, M.I.H.; Yeasmin, M.S.; Rahman, M.S. Preparation of food grade carboxymethyl cellulose from corn husk agrowaste. Int. J. Biol. Macromol. 2015, 79, 144–150. [Google Scholar] [CrossRef]
- Abdelrahim, K.A.; Ramaswamy, H.S.; Doyon, G.; Toupin, C. Effects of concentration and temperature on carboxymethylcellulose rheology. Int. J. Food Sci. Technol. 1994, 29, 243–253. [Google Scholar] [CrossRef]
- Abdelrahim, K.A.; Ramaswamy, H.S. High temperature/pressure rheology of carboxymethyl cellulose (CMC). Food Res. Int. 1995, 28, 285–290. [Google Scholar] [CrossRef]
- Guan, W.; Ke, G.; Tang, C.; Liu, Y. Study on Lubrication Properties of Carboxymethyl Cellulose as a Novel Additive in Water-Based Stock; Technical Report; American Society of Mechanical Engineers: New York, NY, USA, 2005; Volume 42010. [Google Scholar]
- Kulicke, W.M.; Clasen, C.; Lohman, C. Characterization of water-soluble cellulose derivatives in terms of the molar mass and particle size as well as their distribution. Macromol. Symp. 2005, 223, 151–174. [Google Scholar] [CrossRef]
- Morris, E.R. Assembly and rheology of non-starch polysaccharides. In Advanced Dietary Fibre Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2001; pp. 30–41. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Zeitschrift 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Ostwald, W. Ueber die rechnerische Darstellung des Strukturgebietes der Viskosität. Kolloid-Zeitschrift 1929, 47, 176–187. [Google Scholar] [CrossRef]
- Barus, C. Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, s3–s45, 87–96. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. FüR Phys. Chem. 1889, 4U, 226–248. [Google Scholar] [CrossRef]
- Habig, K.H.; Knoll, G. Schmierung. In Tribologie-Handbuch: Tribometrie, Tribomaterialien, Tribotechnik; Czichos, H., Habig, K.H., Eds.; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2020; pp. 209–229. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal elastohydrodynamic lubrication of point contacts: Part III–Fully flooded results. J. Lubr. Tech. 1977, 99, 264–275. [Google Scholar] [CrossRef]
- Stambaugh, R.L. Viscosity index improvers and thickeners. In Chemistry and Technology of Lubricants; Mortier, R.M., Orszulik, S.T., Eds.; Springer: Boston, MA, USA, 1992; pp. 124–159. [Google Scholar]
- Glass, J.E.; Schulz, D.N.; Zukoski, C.F. Polymers as Rheology Modifiers. In Polymers as Rheology Modifiers; ACS Symposium Series; Schulz, D.N., Glass, J.E., Eds.; American Chemical Society: Washington, DC, USA, 1991; Volume 462, pp. 2–17. [Google Scholar]
- Miehle, E.; Bader-Mittermaier, S.; Schweiggert-Weisz, U.; Hauner, H.; Eisner, P. Effect of physicochemical properties of carboxymethyl cellulose on diffusion of glucose. Nutrients 2021, 13, 1398. [Google Scholar] [CrossRef]
- Morris, E.R.; Cutler, A.N.; Ross-Murphy, S.B.; Rees, D.A.; Price, J. Concentration and shear rate dependence of viscosity in random coil polysaccharide solutions. Carbohydr. Polym. 1981, 1, 5–21. [Google Scholar] [CrossRef]
- Clasen, C.; Kulicke, W.M. Determination of viscoelastic and rheo-optical material functions of water-soluble cellulose derivatives. Prog. Polym. Sci. 2001, 26, 1839–1919. [Google Scholar] [CrossRef]
- Wagoner, T.B.; Çakır Fuller, E.; Drake, M.; Foegeding, E.A. Sweetness perception in protein-polysaccharide beverages is not explained by viscosity or critical overlap concentration. Food Hydrocoll. 2019, 94, 229–237. [Google Scholar] [CrossRef]
- Charpentier, D.; Mocanu, G.; Carpov, A.; Chapelle, S.; Merle, L.; Müller, G. New hydrophobically modified carboxymethylcellulose derivatives. Carbohydr. Polym. 1997, 33, 177–186. [Google Scholar] [CrossRef]
- Arinaitwe, E.; Pawlik, M. Dilute solution properties of carboxymethyl celluloses of various molecular weights and degrees of substitution. Carbohydr. Polym. 2014, 99, 423–431. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.H.; Zhu, W.L. Viscosity properties of sodium carboxymethylcellulose solutions. Cellulose 2007, 14, 409–417. [Google Scholar] [CrossRef]
- Lopez, C.G.; Colby, R.H.; Graham, P.; Cabral, J.T. Viscosity and scaling of semiflexible polyelectrolyte NaCMC in aqueous salt solutions. Macromolecules 2017, 50, 332–338. [Google Scholar] [CrossRef]
- Barba, C.; Montané, D.; Farriol, X.; Desbrières, J.; Rinaudo, M. Synthesis and characterization of carboxymethylcelluloses from non-wood pulps II. Rheological behavior of CMC in aqueous solution. Cellulose 2002, 9, 327–335. [Google Scholar] [CrossRef]
- Benchabane, A.; Bekkour, K. Rheological properties of carboxymethyl cellulose (CMC) solutions. Colloid Polym. Sci. 2008, 286, 1173. [Google Scholar] [CrossRef]
- Cook, R.L.; King, H.E.J.; Peiffer, D.G. High-pressure viscosity of dilute polymer solutions in good solvents. Macromolecules 1992, 25, 2928–2934. [Google Scholar] [CrossRef]
- Shi, Y.; Minami, I.; Grahn, M.; Björling, M.; Larsson, R. Boundary and elastohydrodynamic lubrication studies of glycerol aqueous solutions as green lubricants. Tribol. Int. 2014, 69, 39–45. [Google Scholar] [CrossRef]
- Sequeira, M.C.; Pereira, M.F.; Avelino, H.M.; Caetano, F.J.; Fareleira, J.M. Viscosity measurements of poly(ethyleneglycol) 400 (PEG 400) at temperatures from 293 K to 348 K and at pressures up to 50 MPa using the vibrating wire technique. Fluid Phase Equilibria 2019, 496, 7–16. [Google Scholar] [CrossRef]
- Joseph, G.G.; Hunt, M.L. Oblique particle-wall collisions in a liquid. J. Fluid Mech. 2004, 510, 71–93. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Li, J.; Luo, J. Investigation of superlubricity achieved by polyalkylene glycol aqueous solutions. Adv. Mater. Interfaces 2016, 3, 1600531. [Google Scholar] [CrossRef]
- Wan, G.T.Y.; Spikes, H.A. The elastohydrodynamic lubricating properties of water-polyglycol fire-resistant fluids. ASLE Trans. 1984, 27, 366–372. [Google Scholar] [CrossRef]
- Wan, G.T.Y.; Kenny, P.; Spikes, H.A. Elastohydrodynamic properties of water-based fire-resistant hydraulic fluids. Tribol. Int. 1984, 17, 309–315. [Google Scholar] [CrossRef]
- Dowson, D. Elastohydrodynamic and micro-elastohydrodynamic lubrication. Wear 1995, 190, 125–138. [Google Scholar] [CrossRef]
- Dowson, D. Paper 10: Elastohydrodynamics. Proc. Inst. Mech. Eng. Conf. Proc. 1967, 182, 151–167. [Google Scholar] [CrossRef]
- Arnšek, A.; Vižintin, J. Lubricating properties of rapeseed-based oils. J. Synth. Lubr. 2000, 16, 281–296. [Google Scholar] [CrossRef]
- Mobarak, H.M.; Niza Mohamad, E.; Masjuki, H.H.; Kalam, M.A.; Al Mahmud, K.A.H.; Habibullah, M.; Ashraful, A.M. The prospects of biolubricants as alternatives in automotive applications. Renew. Sustain. Energy Rev. 2014, 33, 34–43. [Google Scholar] [CrossRef]
- Attia, N.K.; El-Mekkawi, S.A.; Elardy, O.A.; Abdelkader, E.A. Chemical and rheological assessment of produced biolubricants from different vegetable oils. Fuel 2020, 271, 117578. [Google Scholar] [CrossRef]
- Hutter, C.; Wang, Y.; Chubarenko, I. Phenomenological coefficients of water. In Physics of Lakes; Springer: Berlin/Heidelberg, Germany, 2011; pp. 389–418. [Google Scholar]
- Lyytikäinen, J.; Laukala, T.; Backfolk, K. Temperature-dependent interactions between hydrophobically modified ethyl(hydroxyethyl)cellulose and methyl nanocellulose. Cellulose 2019, 26, 7079–7087. [Google Scholar] [CrossRef]
- Wilson, B. Lubricants and functional fluids from renewable sources. Ind. Lubr. Tribol. 1998, 50, 6–15. [Google Scholar] [CrossRef]
- Barton, W.R.S.; Payne, J.; Baker, M.; O’Connor, B.; Qureshi, F.; Huston, M.; Knapton, D. Impact of viscosity modifiers on gear oil efficiency and durability. SAE Int. J. Fuels Lubr. 2012, 5, 470–479. [Google Scholar] [CrossRef]
- Veltkamp, B.; Jagielka, J.; Velikov, K.; Bonn, D. Lubrication with non-newtonian fluids. Phys. Rev. Appl. 2023, 19, 014056. [Google Scholar] [CrossRef]
- Campen, S.; Green, J.; Lamb, G.; Atkinson, D.; Spikes, H. On the increase in boundary friction with sliding speed. Tribol. Lett. 2012, 48, 237–248. [Google Scholar] [CrossRef]
- Liu, S.; Guo, D.; Xie, G. Nanoscale lubricating film formation by linear polymer in aqueous solution. J. Appl. Phys. 2012, 112, 104309. [Google Scholar] [CrossRef]
- Chatterjee, A.; Das, B. Radii of gyration of sodium carboxymethylcellulose in aqueous and mixed solvent media from viscosity measurement. Carbohydr. Polym. 2013, 98, 1297–1303. [Google Scholar] [CrossRef]
- Vengudusamy, B.; Grafl, A.; Novotny-Farkas, F.; Schöfmann, W. Comparison of frictional properties of gear oils in boundary and mixed lubricated rolling-sliding and pure sliding contacts. Tribol. Int. 2013, 62, 100–109. [Google Scholar] [CrossRef]
- Antti, G.; Pentti, P.; Hanna, K. Ultrasonic degradation of aqueous carboxymethylcellulose: Effect of viscosity, molecular mass, and concentration. Ultrason. Sonochem. 2008, 15, 644–648. [Google Scholar] [CrossRef] [PubMed]
- Almeida, N.; Rakesh, L.; Zhao, J. Phase behavior of concentrated hydroxypropyl methylcellulose solution in the presence of mono and divalent salt. Carbohydr. Polym. 2014, 99, 630–637. [Google Scholar] [CrossRef] [PubMed]
- Schweiger, R.G. New cellulose sulfate derivatives and applications. Carbohydr. Res. 1979, 70, 185–198. [Google Scholar] [CrossRef]



| Trade Name | Abbr. | Viscosity at 25 °C [mPas] | DS |
|---|---|---|---|
| Blanose 7ULC | C7XS | 10–20 (6%) | 0.65–0.90 |
| Ambergum 1221 | C2XS | 10–20 (5%) | 1.15–1.45 |
| Walocel CRT 30 G | C9S | 20–40 (2%) | 0.82–0.95 |
| Blanose 9CLF | B9S | 25–50 (2%) | 0.80–0.95 |
| Walocel CRT 1000 PA | C9M | 550–800 (2%) | 0.82–0.95 |
| Walocel CRT 10000 PA | C9L | 900–1500 (1%) | 0.82–0.95 |
| Derivative | [kg/mol] | DS | [wt%] | [mPas] | [1] | [1] |
|---|---|---|---|---|---|---|
| C7XS | 24 * | 0.7 | 8.25 | 13.95 | 1.66 | 4.59 |
| C2XS | 35 * | 1.2 | 6.60 | 21.67 | 1.74 | 3.64 |
| C9S | 88 * | 0.9 | 2.10 | 14.60 | 1.71 | 3.44 |
| B9S | 100 | 0.9 | 1.41 | 7.71 | 1.45 | 3.64 |
| C9M | 240 * | 0.9 | 0.73 | 11.27 | 1.62 | 3.30 |
| C9L | 520 * | 0.9 | 0.27 | 8.17 | 1.54 | 3.10 |
| C7XS | C2XS | C9S | C9M | C9L | PEG | RSO | |
|---|---|---|---|---|---|---|---|
| Q at ZSVG 46 | 0.203 | 0.170 | 0.160 | 0.178 | 0.252 | 0.123 | 0.168 |
| Q at ZSVG 220 | 0.170 | 0.141 | 0.124 | 0.139 | 0.234 |
| Derivative | cCMC | TVL | WSD | ||||
|---|---|---|---|---|---|---|---|
| [wt%] | [mPas] | [mPas] | [%] | [µm] | [nm] | [1] | |
| C7XS | 11.670 | 47.90 ± 0.06 | 41.49 ± 1.20 | 13.38 | 482 | 32.10 | 0.76 |
| 15.740 | 213.60 ± 0.75 | 129.80 ± 1.69 | 39.23 | 1593 | 74.32 | 1.75 | |
| C2XS | 8.210 | 47.63 ± 0.02 | - | 0 | 497 | 35.26 | 0.83 |
| 12.940 | 210.06 ± 0.04 | 181.30 ± 6.42 | 13.69 | 1592 | 93.28 | 2.20 | |
| C9S | 3.060 | 45.70 ± 0.02 | 43.08 ± 0.03 | 5.73 | 328 | 32.93 | 0.78 |
| 4.990 | 219.80 ± 0.20 | 97.89 ± 0.83 | 55.46 | 357 | 61.35 | 1.45 | |
| C9M | 1.090 | 44.89 ± 0.02 | 27.70 ± 0.56 | 38.29 | 372 | 24.39 | 0.57 |
| 1.870 | 217.19 ± 0.20 | 25.98 ± 1.92 | 88.04 | 547 | 24.89 | 0.59 | |
| C9L | 0.415 | 46.07 ± 0.07 | 12.30 ± 0.19 | 73.30 | 301 | 14.04 | 0.33 |
| 0.750 | 213.73 ± 0.43 | 14.18 ± 0.69 | 93.37 | 332 | 16.49 | 0.39 | |
| AW | 0.77 ± 0.00 | 347 | |||||
| RSO | 32.64 ± 0.05 | 352 | |||||
| PEG | 45.42 ± 0.01 | 233 |
| Derivative | [kg/mol] | [mPas] | [mPas] | PVL [%] | cCMC [wt%] |
|---|---|---|---|---|---|
| C7XS | 24 * | 46.44 | 47.68 | - | 10.68 |
| C2XS | 35 * | 43.21 | 43.75 | - | 7.94 |
| C9S | 88 * | 45.70 | 42.86 | 6.21 | 3.30 |
| C9M | 240 * | 45.64 | 37.10 | 18.71 | 1.17 |
| C9L | 520 * | 45.81 | 18.89 | 58.76 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michaelis, J.U.; Kiese, S.; Amann, T.; Folland, C.; Asam, T.; Eisner, P. Thickening Properties of Carboxymethyl Cellulose in Aqueous Lubrication. Lubricants 2023, 11, 112. https://doi.org/10.3390/lubricants11030112
Michaelis JU, Kiese S, Amann T, Folland C, Asam T, Eisner P. Thickening Properties of Carboxymethyl Cellulose in Aqueous Lubrication. Lubricants. 2023; 11(3):112. https://doi.org/10.3390/lubricants11030112
Chicago/Turabian StyleMichaelis, Jan Ulrich, Sandra Kiese, Tobias Amann, Christopher Folland, Tobias Asam, and Peter Eisner. 2023. "Thickening Properties of Carboxymethyl Cellulose in Aqueous Lubrication" Lubricants 11, no. 3: 112. https://doi.org/10.3390/lubricants11030112
APA StyleMichaelis, J. U., Kiese, S., Amann, T., Folland, C., Asam, T., & Eisner, P. (2023). Thickening Properties of Carboxymethyl Cellulose in Aqueous Lubrication. Lubricants, 11(3), 112. https://doi.org/10.3390/lubricants11030112





