Improvement of Generative Adversarial Network and Its Application in Bearing Fault Diagnosis: A Review

Abstract

A small sample size and unbalanced sample distribution are two main problems when data-driven methods are applied for fault diagnosis in practical engineering. Technically, sample generation and data augmentation have proven to be effective methods to solve this problem. The generative adversarial network (GAN) has been widely used in recent years as a representative generative model. Besides the general GAN, many variants have recently been reported to address its inherent problems such as mode collapse and slow convergence. In addition, many new techniques are being proposed to increase the sample generation quality. Therefore, a systematic review of GAN, especially its application in fault diagnosis, is necessary. In this paper, the theory and structure of GAN and variants such as ACGAN, VAEGAN, DCGAN, WGAN, et al. are presented first. Then, the literature on GANs is mainly categorized and analyzed from two aspects: improvements in GAN’s structure and loss function. Specifically, the improvements in the structure are classified into three types: information-based, input-based, and layer-based. Regarding the modification of the loss function, it is sorted into two aspects: metric-based and regularization-based. Afterwards, the evaluation metrics of the generated samples are summarized and compared. Finally, the typical applications of GAN in the bearing fault diagnosis field are listed, and the challenges for further research are also discussed.

1. Introduction

Rotating machinery has many applications in practical engineering, in which bearing is one of the critical components [1,2,3]. Since bearings usually work in an extremely harsh environment, they are prone to wear, cracks, and other defects, affecting the equipment’s normal operation and even leading to huge economic losses and casualties. Therefore, detecting and diagnosing the bearing fault in time is very important.

Bearing fault diagnosis means determining the health status of the bearing based on monitoring data. Commonly used monitoring data include vibrations signal [1], temperature signal [4], current signal [5], stray flux [6], acoustic emission [7], and oil film condition [8]. Among them, the vibration signal is the most widely used in bearing fault diagnosis as it has many advantages, such as low cost, high sensitivity, good robustness, almost no response lag, and it is easy to install [1]. Traditional bearing fault diagnosis is a knowledge-driven approach in which experienced engineers use signal processing techniques to analyze vibration signals and determine the health status of bearings. Therefore, traditional methods are entirely human-dependent and challenging for online fault diagnosis. The advent of the industrial Internet has made massive data monitoring a reality. As a result, data-driven fault diagnosis methods ensue. Many researchers have successfully applied machine learning (ML) theory to bearing fault diagnosis and established diagnostic models to realize the automatic detection and identification of bearing faults. This field is also known as intelligent fault diagnosis [9]. When using traditional ML methods such as k-nearest neighbor (kNN), artificial neural network (ANN), and support vector machine (SVM) for bearing fault diagnosis, the diagnostic model can establish a link between the bearing fault characteristics and bearing health status, thereby automatically identifying the health status of the bearing by calculating the fault characteristics of the input data [10]. Technically, the traditional ML methods still require the manual extraction and selection of valid fault features from the collected data. Deep learning (DL), a branch of ML, enables automatic feature extraction from the collected data, linking the raw monitoring data directly to the health status of the bearing. Commonly used DL networks include convolutional neural network (CNN), stacked autoencoder (AE), long short-term memory (LSTM), deep belief network (DBN), and recurrent neural networks (RNNs). To date, DL has been massively studied in prognostics and health management (PHM) [11,12,13]. The success of the aforementioned data-driven fault diagnosis approaches is based on the premise that there are sufficient labeled data to train the diagnostic model. However, this assumption is usually unrealistic in practical engineering scenarios. For example, bearings operate under normal conditions for most of their life cycle, with a small percentage of fault conditions. Therefore, most bearing monitoring data are health data. The lack of fault data leads to two main problems. The first is the small sample problem, which refers to the small sample size of the fault data. The second is the data imbalance problem, which means the imbalanced distribution of sample size among measurement data from different bearing health states. Both of these two problems will lead to low diagnostic accuracy. Therefore, bearing fault diagnosis under small samples and imbalanced datasets is a very significant and promising research topic.

Data augmentation is an effective solution to address the small sample problem and the data imbalance problem. Commonly used bearing fault data augmentation methods are divided into oversampling techniques, data transformations, and generative models. As a generative model, GAN is one of the most popular methods for fault data augmentation. This paper will review the aforementioned fault data augmentation methods focusing on GANs. GANs are initially utilized to generate images in the field of computer vision. Liu et al. [14] first introduced GAN to bearing fault diagnosis. In recent years, many researchers improved the training technique and evaluation method of GAN to better apply it to bearing fault data augmentation. Based on our review of existing literature and our experience, we divide these improvements into three categories: improvements in the network structure, improvements in the loss function, and improvements in the evaluation of generated data.

Although there have been several review papers published related to data-driven machinery fault diagnosis, they focus on the whole artificial intelligence technology in mechanical fault diagnosis [1,9,11]. These papers cover both traditional machine learning methods and deep learning and have a wide range of study objects, including bearings, gearboxes, induction motors, and wind turbines. Furthermore, they focus on the improvements in the diagnostic model. As one of the key techniques to improve the accuracy of fault diagnostic models, data augmentation, especially data synthesis using GAN, has developed rapidly in recent years. Therefore, it is necessary to review the research in the field of bearing fault data generation, summarize the existing outcomes, and give possible prospects for future exploration.

The motivation of the study is to provide a systematic review of GAN, including theory, development, problems, and prospect. As presented in Figure 1, the rest of the review is organized. The research methodology and initial analysis are described in Section 2. Section 3 introduces three common methods for data augmentation. Section 4 focuses on the improvements and applications of GAN in the field of bearing fault diagnosis. Specifically, the improvements in GAN are categorized into structure improvement and loss function improvement. The evaluation metrics for the sample generation quality of GAN are also discussed in this section. Finally, the conclusions and prospects are given in Section 5.

2. Research Methodology and Initial Analysis

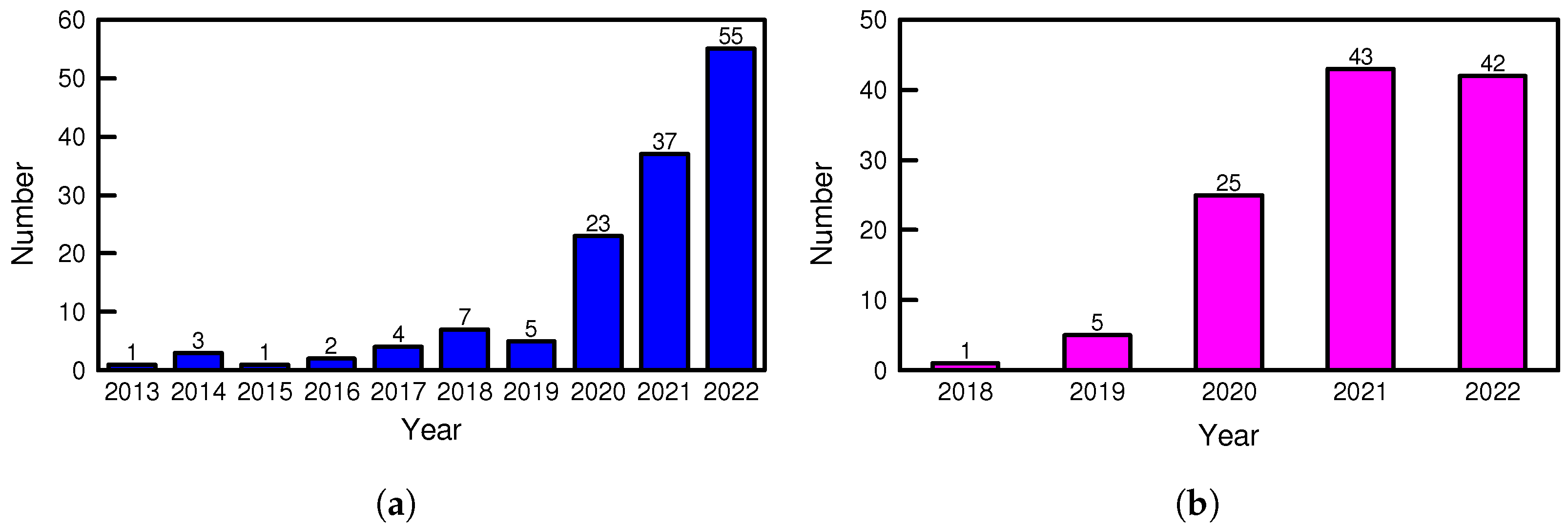
2.1. Research Methodology

To ensure the quality of the literature, the Web of Science Core Collection database was selected for the literature search in this paper. Using the topic keywords “bearing fault diagnosis AND (data augmentation OR data synthesis OR data generation)”, we initially obtained a total of 160 English journal and conference articles [15], as shown in Figure 2a. The search results include research articles published up to October 2022. To collect the literature as comprehensively as possible, the topic keywords “bearing fault diagnosis AND oversampling” and “bearing fault diagnosis AND generative adversarial network” were adopted to supplement our search results. The search results [16] of the latter are shown in Figure 2b. In addition, several relevant articles were found and included in our analysis after citation analysis. We first skimmed all the articles for the literature analysis to filter out the irrelevant ones. The remaining articles were further analyzed and categorized for study.

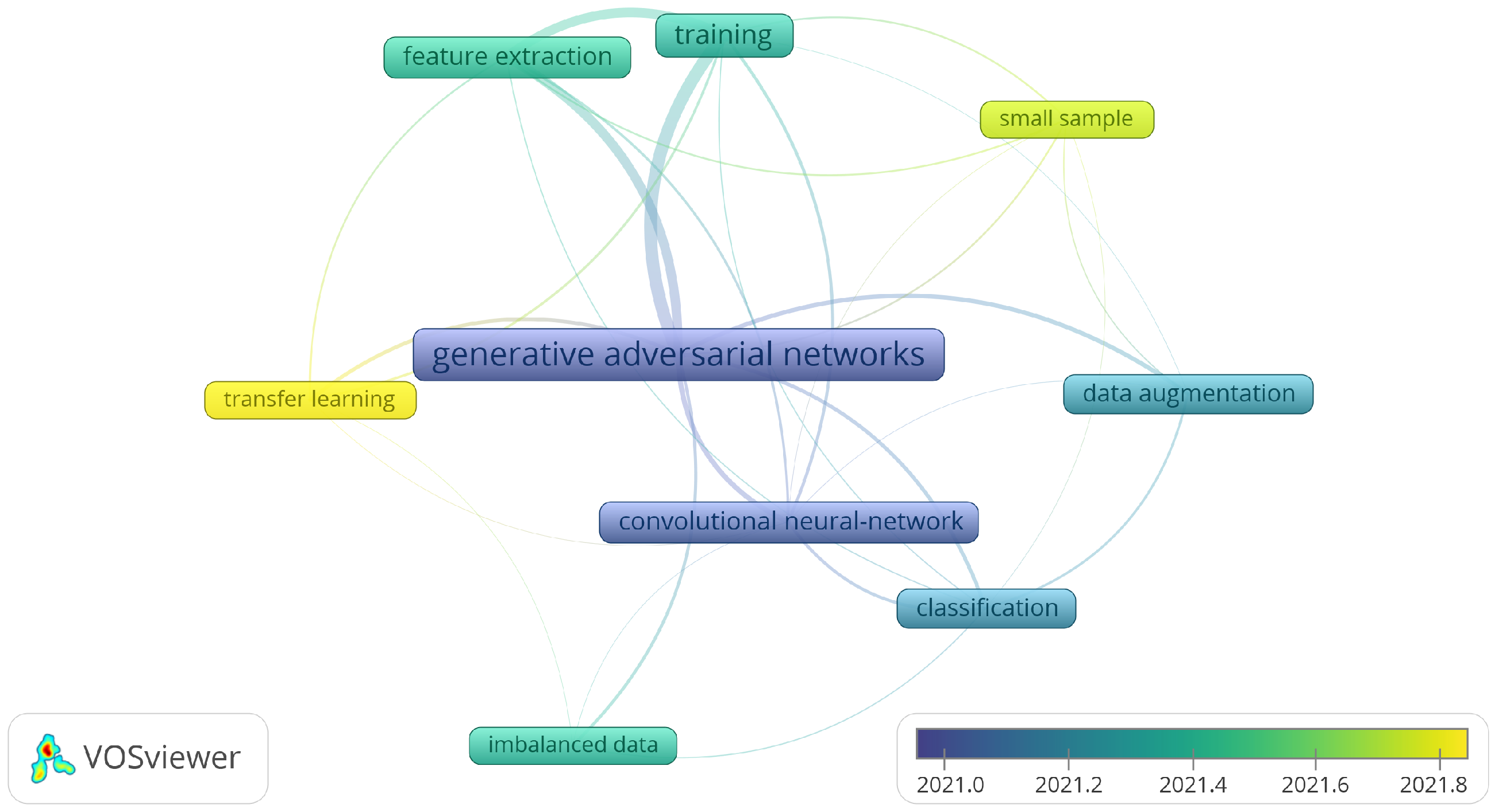
2.2. Initial Literature Analysis

Figure 2a shows that there has been an increasing number of studies on data augmentation for bearing fault diagnosis in the last decade. This reflects the fact that there is a lack of fault data in practice and the necessity to address this problem. According to Figure 2b, research on bearing fault diagnosis and GANs started in 2018 and rapidly became a research hotspot. From 2018 to 2022, the number of publications per year has grown substantially. Keyword co-occurrence analysis was performed using VOSviewer [17]. As shown in Figure 3, the initial research hotspot for GAN is the combination with CNN. At this time, the popular DCGAN was applied to bearing fault diagnosis. On the other hand, CNNs were commonly used as fault classification models. The next hot topic was the application of GAN as a data augmentation technique to generate fault data to address the small sample and imbalanced data problems, with fault classification problems being the most studied application scenario. Another preferred research direction was improving the training process for GANs. In recent years, transfer learning (TL) has become a popular research issue related to GAN.

3. Data Augmentation Methods for Bearing Fault Diagnosis

Training bearing fault diagnosis models require a large amount of fault data. However, fault data are usually lacking in practical engineering. Using data augmentation techniques to generate fault data is an effective solution. Data augmentation is the process of creating new similar samples for the original dataset, which can discover the unexplored space of the input data. This helps reduce overfitting when training a machine learning or deep learning model and enhances the generalization performance. Based on our analysis of the existing literature, the data augmentation methods for bearing fault diagnosis are divided into oversampling techniques, data transformations, and GANs. In the following, the introduction of these three data augmentation methods will be presented.

3.1. Data Augmentation Using Oversampling Techniques

Oversampling is a simple and effective method for data augmentation. The most basic oversampling method is random oversampling [18], in which new samples are generated by randomly replicating the samples of the minority class. However, this method does not increase the amount of information in the dataset and may increase the risk of overfitting. To overcome this problem, Chawla et al. [19] further proposed the synthetic minority over-sampling technique (SMOTE), which generates new samples by linear interpolation between two original samples. However, this method does not consider the probability distribution of the original data. Therefore, adding generated samples to the original dataset may lead to a change in its distribution. In addition, the new dataset may not involve real fault information. Although the two above methods can generate samples of the minority class, the synthetic samples cannot provide more fault information. Consequently, they are not feasible in bearing fault diagnosis. Usually, researchers use the two methods as benchmarks to demonstrate the superiority of their new methods [20].

SMOTE is a pioneer oversampling method, based on which many new oversampling techniques have been proposed and successfully improved bearing fault diagnosis accuracy. Jian et al. [21] presented a novel sample information-based synthetic minority oversampling technique (SI-SMOTE). It evaluates the sample information based on the Mahalanobis distance, thereby identifying informative minority samples. The original SMOTE is merely utilized to generate new samples of informative minority classes. Hao et al. [22] proposed the K-means synthetic minority oversampling technique (K-means SMOTE) based on the clustering distribution. This uses the K-means algorithm to filter out target clusters. As a result, only the samples of selected clusters are synthesized.

In addition, researchers have developed other oversampling methods that have proven effective in bearing fault diagnosis. For example, Razavi-Far et al. [23] developed a novel imputation-based oversampling technique to generate new synthetic samples of the minority class. Their approach generates a set of incomplete samples representative of the minor classes and uses the expectation maximization (EM) algorithm to produce new synthetic samples of the minor classes. To overcome the problem of multi-class imbalanced fault diagnosis, Wei et al. [24] proposed the sample-characteristic oversampling technique (SCOTE). It transforms the problem into multiple binary imbalanced problems.

3.2. Data Augmentation Using Data Transformations

The data transformation methods are inspired by data augmentation techniques in computer vision, in which image transformations such as flipping and cropping are often utilized to obtain new samples to enrich the training set. For example, when using vibration signals for the intelligent fault diagnosis of bearings, there are usually two types of input data. The first one is the original vibration signals, which can be directly fed into the machine learning or deep learning model, and the model learns the features of the time series. The other one is images. The vibration signals are first converted into images. This not only enables the utilization of the feature extraction capability of the deep neural network such as CNN for images but also introduces commonly used image augmentation techniques to the field of bearing fault diagnosis.

Raw vibration signals are one-dimensional time series. To construct datasets, it is necessary first to clip time series using the overlapping segmentation method. With the length of the sample and the length of overlap defined, a large number of samples can be obtained. Zhang et al. [25] first proposed this method and verified that the augmented dataset could improve the fault diagnosis accuracy. Kong et al. [26] proposed a novel sparse classification approach to diagnose planetary bearings in which overlapping segmentation is embedded to augment the vibration data. Inspired by image data augmentation, researchers also use similar tricks to enhance the obtained dataset. The most intuitive way is to add Gaussian white noise to the samples. Based on the analysis of the retrieved literature, most of them used this method. Qian et al. [27] first sliced the vibration signal to form a dataset, 25% of which was added with Gaussian noise. Subsequently, the samples were mixed to train their model. Faysal et al. [28] went one step further by proposing a noise-assisted ensemble augmentation technique for 1D time series data. Other commonly used image transformation methods have also been proven effective on time series data, such as translation, rotation, scaling, truncation, and various flipping operations [29,30,31,32,33,34]. Considering the inherent characteristics of vibration signals, it is also an effective method to rearrange the data points of samples. For example, the samples can be equally divided into two parts to form two groups. New samples can subsequently be obtained by randomly recombining the data from the two groups [35]. Ruan et al. [36] proposed a method called signal concatenation to further increase the number of samples. The original samples are divided into several parts, which are augmented, respectively, and concatenated to form new samples finally.

Some researchers also convert vibration signals into images to diagnose bearing faults. One option is to rearrange the time series into a two-dimensional form and represent them as images. Subsequently, commonly used image augmentation techniques such as flipping can be utilized to double the size of the dataset [37]. Another common option is to use signal processing techniques to transform the vibration signal into a time–frequency spectrogram. For example, Yang et al. [38] introduced the image segmentation theory to augment planetary gearbox-bearing fault spectrogram data fed to the subsequent fault diagnostic model. Specifically, the researchers proposed wavelet transform coefficients cyclic demodulation to obtain a 2D spectrogram of the original vibration signal. They divided the spectrogram into small blocks and defined the overlapping length. This generates smaller spectrograms to compose balanced datasets.

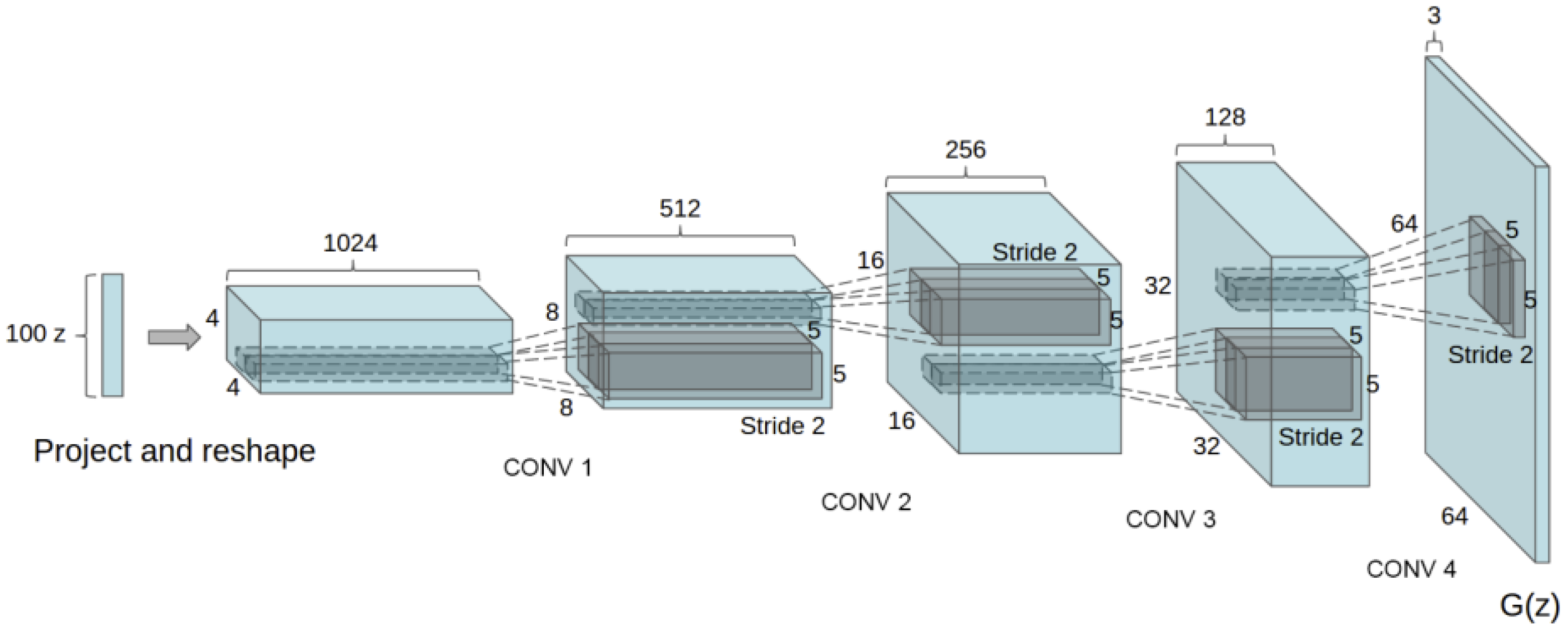
3.3. Data Augmentation Using GANs

According to the purpose of the task, ML/DL models can be generally classified into two categories: discriminative and generative models. Typical discriminative tasks include regression and classification, whereas generative models are widely used to synthesize data. GAN is a kind of generative model. Since it was proposed by Goodfellow et al. [39] in 2014, it has become the most popular method for data augmentation. In contrast to other generative models, such as variational autoencoder (VAE), the idea of adversarial training was introduced in GAN. It consists of two neural networks called discriminator and generator. The structure of a general GAN is shown in Figure 4a.

Generator G is used to generate realistic samples from random noise z. The discriminator D aims to distinguish between real samples x and generated samples $G\left(z\right)$. The adversarial learning of GAN is like a zero-sum game. In the beginning, the discriminator can easily distinguish fake samples from real samples because the samples generated from random noise are also random. However, if the GAN is well trained, the discriminator will no longer be able to judge the authenticity of the samples, and the generator can be used to synthesize realistic samples. Essentially, two data distributions are mapped here, from the distribution of random noise to that of real samples. In the training process, all losses are calculated based on the output of the discriminator. Since the task of the discriminator is to judge the authenticity of the input, it can be regarded as a binary classification problem. Therefore, the binary cross-entropy is used as the loss function. First, the discriminator needs to be optimized while the generator is fixed. If 1 denotes true and 0 denotes false, the optimization objective of the discriminator can be formulated as Equation (1), which means to judge the real samples as true and the generated samples as false. After the discriminator is optimized, the discriminator is fixed and the generator needs to be optimized. The optimization goal of the generator is that the discriminator judges the generated samples as true, which can be formulated as Equation (2).

$$\underset{\mathrm{D}}{max}\mathrm{L}\left(\mathrm{D}\right)={\mathbb{E}}_{\mathrm{x}\sim {\mathrm{p}}_{\mathrm{data}}}[log\mathrm{D}\left(\mathrm{x}\right)]+{\mathbb{E}}_{\mathrm{z}\sim {\mathrm{p}}_{\mathrm{z}}}[log(1-\mathrm{D}\left(\mathrm{G}\left(\mathrm{z}\right)\right))]$$

(1)

$$\underset{G}{min}\mathrm{L}\left(\mathrm{G}\right)={\mathbb{E}}_{\mathrm{z}\sim {\mathrm{p}}_{\mathrm{z}}}[log(1-\mathrm{D}\left(\mathrm{G}\left(\mathrm{z}\right)\right))]$$

(2)

where $D\left(x\right)$ denotes the probability that an original sample is judged to be real data and $D\left(G\right(z\left)\right)$ is the probability that a generated sample is judged to be fake data.

GAN is initially applied to computer vision to augment the image data [40]. However, as mentioned in Section 2.2, GAN was first introduced to bearing fault diagnosis in 2018 [14] and has become a popular research topic in recent years. Wang et al. [41] then used GAN to generate mechanical fault signals to improve the diagnosis accuracy. Section 4 will introduce the improvements and applications of GANs in bearing fault diagnosis in detail.

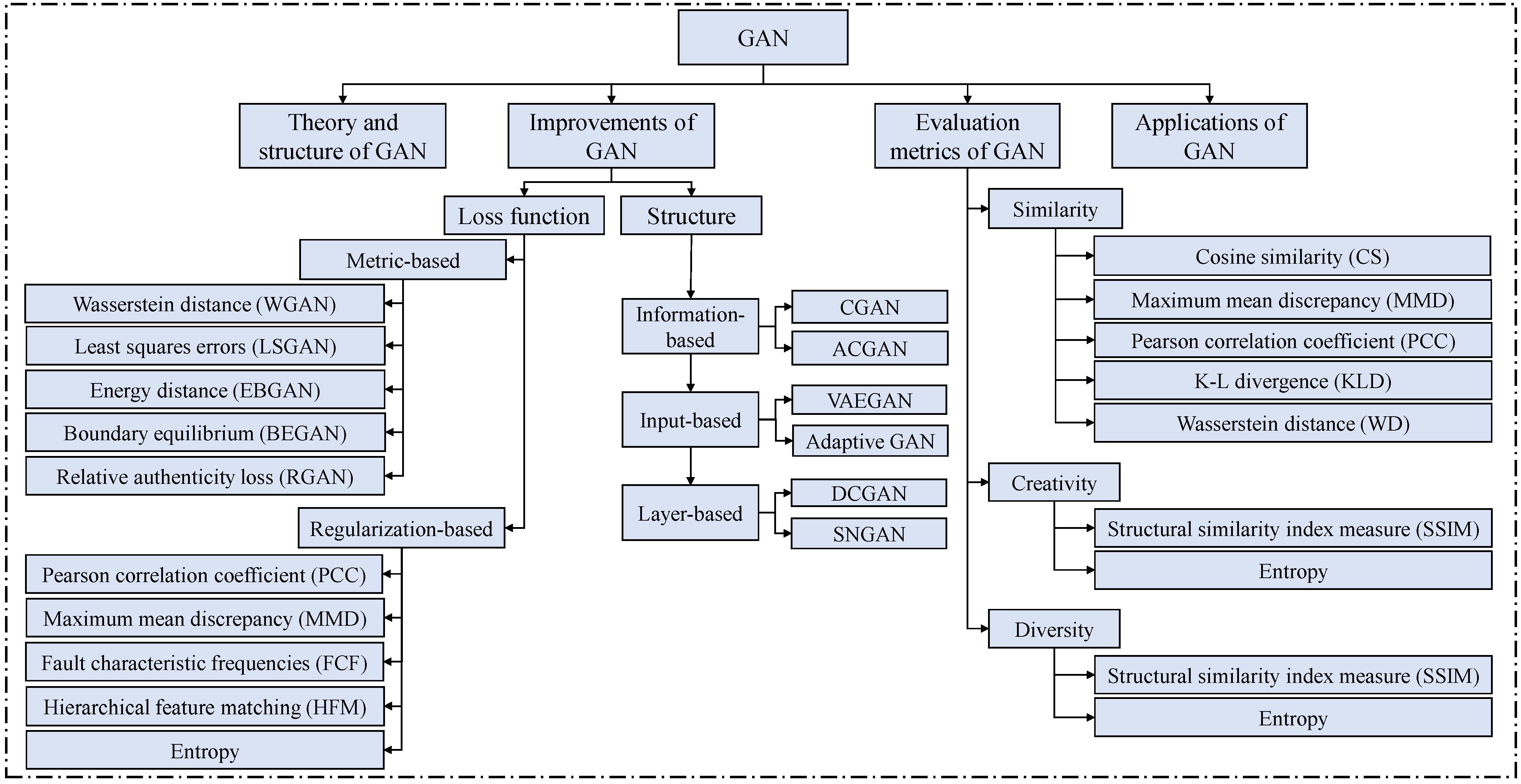
4. Improvements and Applications of GANs in Bearing Fault Diagnosis

The original GAN has three primary problems: unstable convergence, model collapse, and vanishing gradient. To overcome these problems and enhance the quality of sample generation, many variants of GAN have been proposed in recent years. We classify them into two categories: network structure-based improvements and loss function-based improvements. Apart from this, the quality evaluation of the generated samples is a meaningful topic. At the end of this section, the applications of GANs in bearing fault diagnosis are summarized.

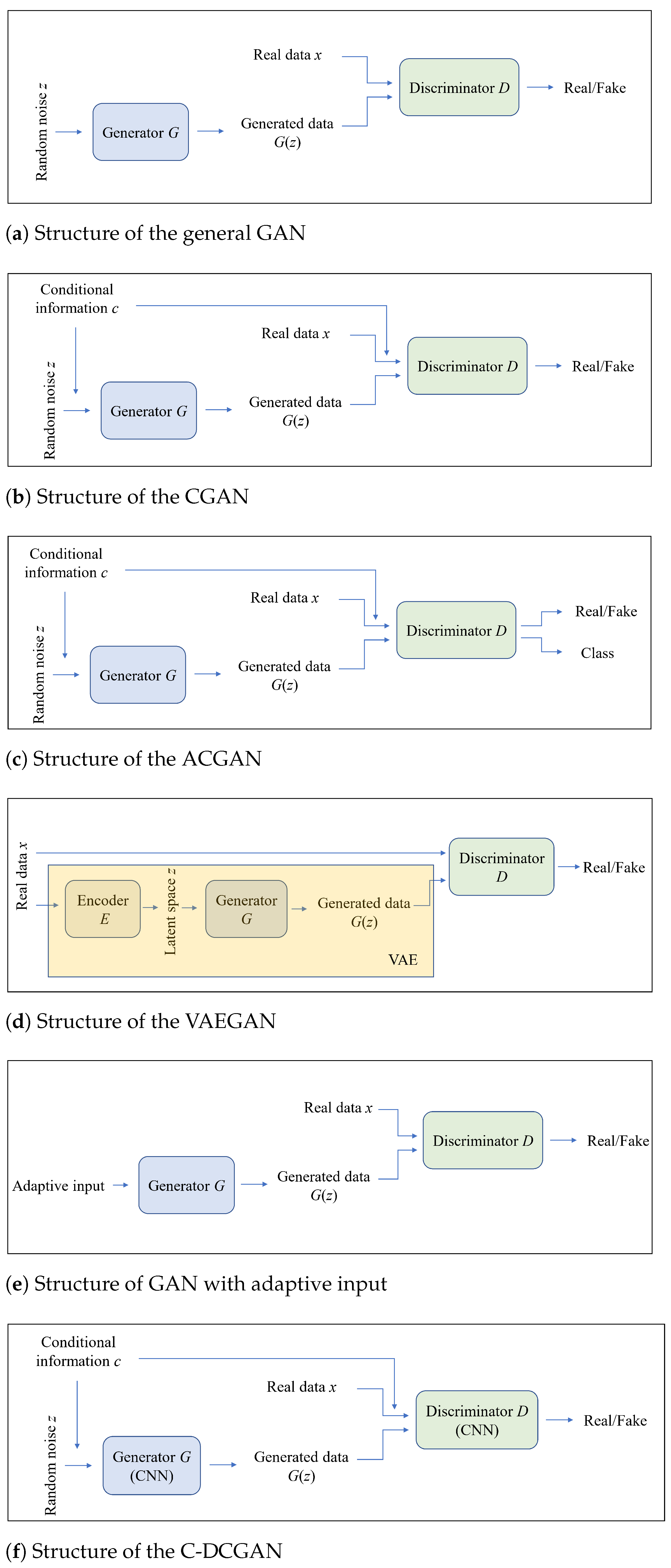
4.1. Improvements in the Network Structure

According to different improvement ideas, we further classify the network structure-based improvements into three categories: information-based improvements, input-based improvements, and layer-based improvements.

4.1.1. Information-Based Improvements

The input to the generator of a general GAN is random noise, which can easily lead to mode collapse. When the mode collapse happens, the GAN’s generator can only produce one or a small subset of the different outputs. To address this problem, Mirza et al. [42] proposed the conditional GAN (CGAN). CGAN adds conditional information to the discriminator and generator of the original GAN. The input to CGAN will be a stitching of conditional information with the original input. This additional information such as category labels can control and stabilize the data generation process. By setting different conditional inputs, the samples of different categories can be generated. The other idea is to improve the discriminator so that it can judge the not only authenticity but also output the class of the samples like a classifier. Auxiliary classifier GAN (ACGAN) introduces an auxiliary classifier to the discriminator, which can not only judge the authenticity of the data but also output the class of the data, thereby improving the stability of the training and the quality of the generated samples [43]. The role of the auxiliary classifier is to predict the category of a sample and pass it to the generator as additional conditional information. ACGAN enables a more stable generation of the realistic samples of a specified category. Both CGAN and ACGAN enhance the performance of the general GAN by providing more information. That is why they are regarded as an information-based structural improvement in this paper. Their structures are presented in Figure 4b,c. The original CGAN and ACGAN were successfully applied to bearing fault diagnosis. Wang et al. [44] utilized CGAN to generate the spectrum samples of vibration signals. The use of category labels as condition information to generate the samples of various categories of bearing faults proved to be effective. In [45], ACGAN was directly utilized to generate 1D vibration signals. Experimental results revealed that generated vibration samples improved the accuracy of the bearing fault diagnostic model from 95% to 98%. Some researchers were inspired by the idea of providing more information by the addition of classifiers or other modules. Zhang et al. [46] designed a multi-modules gradient penalized GAN. A classifier as an additional module was added to the Wasserstein GAN with a gradient penalty (WGAN-GP). In [47] and the generator was integrated with a self-modulation (SM) module, which enables the parameter updating based on both the input data and the discriminator. This makes the convergence of the training faster. These papers demonstrate that the idea of designing and integrating more modules concerning the structure of GAN with the goal of providing more useful information is feasible.

4.1.2. Input-Based Improvements

In the general GAN, random noise is fed into the generator to synthesize realistic samples. This may not be reasonable for specific data distributions. Some researchers have made innovative improvements to the structure of the input of the generator, thereby improving the quality of the generated samples. Larsen et al. [48] combined the VAE and GAN and proposed VAEGAN. VAE is an earlier proposed generative model consisting of an encoder and a decoder. The encoder maps the input data to points in the latent space, which are converted back into points in the original space by the decoder. By learning a latent variable model, VAE can be used to generate more data. In a VAEGAN model, the encoder is used to encode existing data, and the encoded latent vectors are used as input to the generator or decoder instead of the random noise. VAEGAN utilizes the latent variable model of VAE to generate the data and uses the discriminator of GAN to evaluate the authenticity of the generated samples. The advantage of VAEGAN is that it can generate high-quality samples and can operate in the latent variable space, such as performing sample interpolation and other modifications. Figure 4d shows the structure of the VAEGAN. Rathore et al. [49] applied VAEGAN to generate time–frequency spectrograms and balanced the bearing fault dataset. The experiment verified that the generated samples are more reasonable and of higher quality. There are a lot of other alternatives to random noise out there. For example, Zhang et al. [50] proposed an adaptive learning method to update the latent vector instead of sampling from Gaussian distribution, realizing adaptive input instead of random noise, as shown in Figure 4e. By using different distributions to generate the latent vector’s digits, a better combination effect can be produced. Improving the input structure of the discriminator is, likewise, a good starting point. In [51], the input of the discriminator was changed from real data to latent encoding by the encoder. The mutual information between real data and latent encoding was constrained by the proposed variational information technique, which limited the gradient of the discriminator and ensured a more stable training process.

4.1.3. Layer-Based Improvements

Considering CNN’s powerful feature extraction capability, convolutional layers were introduced into a GAN called deep convolutional GAN (DCGAN) and applied to image augmentation [52,53]. The original generator of DCGAN is shown in Figure 5. DCGANs have also proven to be effective in vibration signal augmentation. Luo et al. [54] integrated CGAN and DCGAN into C-DCGAN, as shown in Figure 4f. The augmented data successfully improved the accuracy of the bearing fault diagnosis. Based on the DCGAN, a multi-scale progress GAN (MS-PGAN) framework was designed in [55]. This concatenates multi-DCGANs, which share one generator. Through progressive training, high-scale samples can be generated from low-scale samples. Imposing the spectral normalization (SN) on the layers is another useful trick. Tong et al. [56] proposed a novel auxiliary classifier GAN with spectral normalization (ACGAN-SN) to synthesize the bearing fault data, in which spectral normalization was added to the output of each layer of the discriminator. The introduction of the spectral normalization technique makes the training process more stable.

The three above cases of layer-based improvements reveal that: (1) convolutional neural network can improve the performance of GAN and produce good results in bearing fault data generation; (2) concatenating multiple neural networks can generate high-scale samples of high quality; and (3) proposed layer normalization methods such as spectral normalization are worth trying.

4.2. Improvements in the Loss Function

4.2.1. Metric-Based Improvements

The original GAN uses J-S divergence to measure the distance between real and generated data distributions. However, it has a drawback that J-S divergence is a fixed value if the distance between distributions is too far, and thereby cannot measure how close two distributions are. This causes vanishing gradient in the training process [57]. To solve this problem, Arjovsky et al. [58] proposed Wasserstein GAN, in which J-S divergence was replaced by Wasserstein distance. As a result, the loss function of the generator and the discriminator can be formulated as follows:

$$L_{WGAN}^G=-{\mathbb{E}}_{p_{G\left(z\right)}}\left[D\left(G\left(z\right)\right)\right]$$

(3)

$$L_{WGAN}^D=-{\mathbb{E}}_{p_x}\left[D\left(x\right)\right]+{\mathbb{E}}_{p_{G\left(z\right)}}\left[D\left(G\left(z\right)\right)\right]$$

(4)

where x and $G\left(z\right)$ represent the real and generated data, respectively. $D(.)$ is the probability that the data are judged to be real. Compared to the loss functions of the original GAN, the implementation of the Wasserstein distance discards the operation of logarithms in the loss functions [59].

WGAN has been proven effective in many bearing fault diagnosis studies. Zhang et al. [60] proposed an attention-based feature fusion net using WGAN as the data augmentation part. The experimental results verified the feasibility of the scheme under small sample conditions. In [61], a novel imbalance domain adaption network was presented for rolling bearing fault diagnosis, in which WGAN was embedded. The data imbalance between domains and between fault classes in the target domain was considered. WGAN was used to enhance the target domain datasets. However, the performance of WGAN is still limited because of weight clipping. To overcome this problem, Gulrajani et al. [62] combined WGAN with the gradient penalty strategy (WGAN-GP), which is successful in image augmentation. The difference between WGAN-GP and WGAN is that a regularization term is added to the loss function of the discriminator. The loss function of the generator remains the same.

$$L_{WGAN-GP}^G=L_{WGAN}^G$$

(5)

$$L_{WGAN-GP}^D=L_{WGAN}^D+\lambda L_{gp}$$

(6)

Both WGAN and WGAN-GP use the Wasserstein distance to assess the difference between the generated samples and the training samples, which is superior to the J-S divergence, and WGAN-GP adds a gradient penalty on top of WGAN to eliminate the problem of gradient explosion in the network. The discriminator’s loss function incorporates a gradient penalty in addition to the judgment of real and fake samples, smoothing the generator and decreasing the risk of mode collapse.

Apart from the Wasserstein distance, Mao et al. [63] proposed the least squares GAN (LSGAN), which uses the least squares error to measure the distance between the generated and real samples. The objective functions of the discriminator and generator are as follows:

$$\underset{D}{min}L\left(D\right)={\mathbb{E}}_{x\sim p_x}{(D\left(x\right)-b)}^2+{\mathbb{E}}_{z\sim p_z}{(D\left(G\left(z\right)\right)-a)}^2$$

(7)

$$\underset{G}{min}L\left(G\right)={\mathbb{E}}_{z\sim p_z}{(D\left(G\left(z\right)\right)-c)}^2$$

(8)

Since the discriminator network’s goal is to distinguish between real and fake samples, the generated and real samples are encoded as a and b, respectively. The objective function of the generator replaces a with c, indicating that the discriminator treats the generated samples as real samples. It has been proven that the objective function is equivalent to the Pearson ${\chi }^2$ divergence in a particular case. In [64], LSGAN was used to generate traffic signal images. The results of the comparison experiments show that LSGAN outperforms WGAN and DCGAN in such an application scenario. In [65], Anas et al. reported on a new CT volume registration method, in which LSGAN was employed to learn the 3D dense motion field between two CT scans. After extensive trials and assessments, LSGAN shows higher accuracy than the general GAN in estimating the motion field. LSGAN can alleviate the problem of vanishing gradient during training and generate higher-quality images compared to the general GAN. However, based on our literature research, its application in the field of bearing fault diagnosis was not prevalent. This may be due to the fact that it is not suitable for the generation of bearing fault data. For example, LSGAN shows a worse performance than DCGAN in [66].

Energy-based GAN (EBGAN) [67] introduces an energy function into the discriminator and trains the generator and discriminator by optimizing the energy distance. The discriminator assigns low energy to the real samples and high energy to the fake samples. Usually, the discriminator is a well-trained autoencoder. Instead of judging the authenticity of the input sample, the discriminator calculates its reconstruction score. The loss functions of the discriminator and the generator can be formulated as follows:

$$\mathrm{L}\left(D\right)={\mathrm{E}}_{x\sim P_{\mathrm{data}}}\left[D\left(x\right)+{[m-D\left(G\left(z\right)\right)]}^{+}\right]$$

(9)

$$\mathrm{L}\left(G\right)={\mathrm{E}}_{z\sim P_z}\left[D\left(G\left(z\right)\right)\right]$$

(10)

where m is a positive margin used for the selection of energy functions and ${[·]}^{+}=max(0,·)$. Yang et al. [68] combined EBGAN and ACGAN in their proposed bearing fault diagnosis method under imbalanced data and obtained good sample generation and classification performance.

Boundary equilibrium GAN (BEGAN) [69] is a further improvement on EBGAN. The main contribution is the introduction of the ratio between the autoencoder reconstruction error and the degree of boundary balance of the generator and discriminator to the loss function. The new loss function balances the competition between the generator and the discriminator, resulting in more realistic generated samples. The loss functions of BEGAN can be formulated as follows:

$$\mathrm{L}\left(D\right)={\mathrm{E}}_{x\sim P_{\mathrm{data}}}\left[D\left(x\right)-k_{t}D\left(G\left(z\right)\right)\right]$$

(11)

$$\mathrm{L}\left(G\right)={\mathrm{E}}_{x\sim P_z}\left[(1-D\left(G\left(z\right)\right))\right]$$

(12)

where $k_t$ is a weighting coefficient to balance the performance of the generator and the discriminator.

Relativistic GAN (RGAN) [70] is another well-known variant of GAN, whose primary idea is to turn the discriminator’s output into relative authenticity, i.e., the degree to which the discriminator finds the generated samples to be more realistic than the real ones. RGAN optimizes the model using the relative authenticity loss function and has been demonstrated to converge more easily and be more effective in creating high-quality images. However, RGAN still lacks relevant research in the field of bearing fault diagnosis.

This subsection examines various well-known metric-based improvements for the loss function and their effective applications, particularly in bearing fault diagnosis. The loss functions of the aforementioned GAN variants, as well as the general GAN, are all comparable in that they calculate a certain distance between two distributions, with the optimization goal of minimizing this distance. Much of the literature has verified the validity of the Wasserstein distance in the field of bearing fault diagnosis. However, there are still a number of alternatives that require further research.

4.2.2. Regularization-Based Improvements

Directly applying WGAN-GP to bearing fault diagnosis rarely yields satisfactory results. However, the idea of adding regularizations to the loss function has been proven effective in bearing fault diagnosis. In [71], a new GAN named parallel classification Wasserstein GAN with gradient penalty (PCWGAN-GP) is presented, in which the Pearson loss function was introduced to enhance the performance of the GAN. It can generate the faulty samples of bearings with healthy samples as input. The maximum mean discrepancy (MMD) is a commonly used metric to measure the similarity between domains in transfer learning. Inspired by this, Zheng et al. [55] introduced the MMD to the loss function of WGAN-GP as a new penalty. The experimental results verified the effectiveness of this method in bearing fault sample augmentation. Ruan et al. [72] added the error of fault characteristic frequencies and the results of the fault classifier to the loss function. The improvement in sample quality is evident in the envelope spectrum. In [50,51], the proposed reconstruction module or representation matching module maps the distribution between real and generated data. The calculated difference is sensitive to the data class and can provide additional constraints on the generator. The collected regularizations to the loss function are listed in

Table 1. Regularization to the loss function of various GANs.

Number	Loss	Formulation	Source
1	PCWGAN-GP	$$PC\left({\tilde{x}}_j^k,{\overline{x}}^k\right)=\frac{1}{n}\sum _{j=1}^n\frac{{\sum }_{m=1}^M\left({\tilde{x}}_{j,m}^k-{\tilde{x}}_{j,m}^k\right)\left({\overline{x}}_m^k-{\overline{x}}_m^k\right)}{\sqrt{{\sum }_{m=1}^M{\left({\tilde{x}}_{j,m}^k-{\tilde{x}}_{j,m}^k\right)}^2\sqrt{{\sum }_{m=1}^M{\left({\overline{x}}_m^k-{\overline{x}}_m^k\right)}^2}}}$$	[71]
2	MS-PGAN	$$MM{D}^2\left[D_X,D_Y\right]={∥\frac{1}{x}\sum _{i=1}^{x}f\left(x_i\right)-\frac{1}{y}\sum _{j=1}^{y}f\left(y_i\right)∥}^2$$	[56]
3	FCFE	$$L_{\mathrm{frequency}}=\sum _{i=1}^N\left(\left|M_{\mathrm{real}}^i-M_{\mathrm{fake}}^i\right|+\left|F_{\mathrm{real}}^i-F_{\mathrm{fake}}^i\right|\right)$$	[72]
4	WCGAN-HFM	$$HFM=\sum _l{\omega }_l·\left|D_l(x\mid y)-D_l\left(G(z\mid y)\right)\right|$$	[73]
5	Entropy	$$H\left(G\left(z\right)\right)=E_{z\sim P_z}\left[{∥z-E_n\left(G\left(z\right)\right)∥}^2\right]$$	[74]

(1) M is the dimension of generated samples, ${\tilde{x}}_{j,m}^k$ denotes the $m^{th}$ element in the j-th sample with the category of k, and $\overline{x}$ represents the mean value of x. (2) Maximum mean discrepancy (MMD) measures the similarity between two distributions in transfer learning. The value of $MM{D}^2$ was used as the MMD penalty between the source domain $D_x$ and the target domain $D_y$. (3) N denotes the maximum order of FCF. M stands for the i-th order FCF amplitude from the real and generated sample. F represents the i-th order FCF frequency from the real and generated sample. (4) ${\omega }_l$ is the weighting factor of the l-th layer loss. Hierarchical feature matching (HFM) provides additional information from the perspective of differences between classes. (5) $E_n$ is an encoder with parameters and $E_n\left(G\left(z\right)\right)$ denotes the intermediate layer feature of the generated sample output by the discriminator. The entropy reflects the diversity of generated samples.

.

Adding regularizations to the loss function usually provides more information and constraints, which helps to stabilize the GAN training and improve the quality of the generated samples. On the other hand, knowledge of physics, such as bearing fault mechanisms, can be combined with the loss function of the general GAN, which can not only refine the quality of the generated samples but also make them more interpretable.

4.2.3. Summary

Based on our analysis, there are two kinds of methods to improve the loss function: metric-based improvements and regularization-based improvements. The former is to adopt a new metric to replace the original J-S divergence, thereby more efficiently measuring the similarity between data distributions. The Wasserstein distance is such an excellent example. WGAN and its variants have been used a lot in bearing fault diagnosis. Other GAN variants, such as LSGAN, EBGAN, BEGAN, and RGAN, require more investigation in the field of bearing fault diagnosis. However, proposing entirely new metrics requires advanced mathematical knowledge, which is a challenging work. The improvements in the loss function by adding regularization terms are more popular. Introducing more constraints can effectively stabilize the training of GANs and enable the generation of high-quality samples. The introduction of physical knowledge as a regularization term into GAN has also been shown to be feasible and deserves more research.

4.3. Evaluation of Generated Samples

The samples generated by GANs are not really collected from mechanical equipment. Therefore, to ensure their feasibility as training data, it is necessary to evaluate the quality of the generated samples, which can be considered in three aspects: similarity, creativity, and diversity.

High similarity means that the generated and real data have the most similar distributions possible. This is the most essential requirement for generated data. Based on our analysis of the existing literature, the evaluation methods concerning their similarity can be divided into two categories: qualitative methods and quantitative metrics.

Qualitative methods refer to the comparison of data visualizations, including the time and frequency domains. This method enables an initial evaluation of the similarity between samples. In the time domain, the most intuitive evaluation method is to compare the waveforms of the generated signal and the real signal. Amplitude and peaks should be noticed. In the frequency domain, it is valuable to check the fault characteristic frequencies (FCFs), which are crucial for bearing fault diagnosis [71,72]. In addition, the features extracted from real and generated samples can be compared using the t-distributed stochastic neighbor embedding (t-SNE) technique as a qualitative approach to validate the usability of the generated samples [44,57,71].

To further accurately quantify the similarity, some indicators have been proposed. Cosine similarity (CS) can measure the similarity between two sequences. In [72], cosine similarity was adopted as the time domain similarity metric to evaluate the quality of the generated bearing fault samples. However, a relatively small cosine similarity value can be obtained if the samples are too long. The maximum mean discrepancy (MMD) was initially used to measure the similarity between domains in transfer learning. In [55], it is introduced to measure the similarity between the generated and real samples. In [56,60,71], the correlation between the spectra of real samples and those of generated samples was calculated by the Pearson correlation coefficient (PCC). The K-L divergence and the Wasserstein distance calculate the similarity between data distributions, which can also be used to quantitatively characterize the quality of the generated samples [47,49,56]. Some bearing fault diagnosis schemes first use signal processing techniques such as short-time Fourier transform (STFT) to convert the original vibration signal into a time–frequency spectrogram, and the features are extracted from the spectrograms for subsequent fault diagnosis. Since the GAN is used to directly generate images, it is reasonable to assess the quality of the generated images. In [49], the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) were utilized to investigate the quality of the generated samples. Furthermore, the GAN-test can be conducted to measure the feasibility of the generated data [71]. The real and generated data can be treated as the training and test sets, respectively. The accuracy of the diagnostic network shows the variation between real and generated data. The collected metrics for similarity evaluation are listed in

Table 2. Evaluation metrics for the sample generation quality of GAN.

Number	Metric	Formulation	Source
1	CS	$$cos\theta =\frac{\overrightarrow{m}·\overrightarrow{n}}{|\overrightarrow{m}|·|\overrightarrow{n}|}$$	[72]
2	MMD	$$MMD[F,p,q]=\underset{f\in F}{sup}\left(E_{x\sim p}\left[f\left(x\right)\right]-E_{x\sim q}\left[f\left(x\right)\right]\right)$$	[56]
3	PCC	$$PC{C}_{X,Y}=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}$$	[57,60,71]
4	KLD	$$D_{\mathrm{KL}}(P\parallel Q)=\sum _{x\in \mathcal{X}}P\left(x\right)log\left(\frac{P\left(x\right)}{Q\left(x\right)}\right)$$	[51]
5	WD	$$\mathrm{WD}\left({\mathrm{P}}_1,{\mathrm{P}}_2\right)=\underset{\gamma \sim \left({\mathrm{P}}_1,{\mathrm{P}}_2\right)}{inf}{\mathbb{E}}_{(\mathrm{x},\mathrm{y})\sim \gamma }[\parallel \mathrm{x}-\mathrm{y}\parallel ]$$	[57]
6	PSNR	$$PSNR=10{log}_{10}\left(\frac{{\mathrm{MAX}}_I^2}{{\mathrm{MSE}}^2}\right)$$	[51]
7	SSIM	$$SSIM(x,y)=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}$$	[51]

(1) m and n stand for two time series. (2) F denotes a given set of functions, p and q are two independent distributions, x and y obey p and q, respectively, $sup$ denotes an upper bound, and $f\left(\right)$ denotes a function mapping. (3) X and Y are two variables, ${\sigma }_X$ and ${\sigma }_Y$ are the standard deviations of X and Y, respectively. (4) P and Q are two probability distributions in the same probability space, and X is the relative entropy from Q to P. (5) $P_1$ and $P_2$ are two probability distributions, and $\gamma$ is a joint probability distribution. (6) ${\mathrm{MAX}}_I$ represents the image with the maximum valid value of the pixel in the image, and $\mathrm{MSE}$ is the mean squared error estimated over two images. (7) ${\mu }_x$, ${\mu }_y$, ${\sigma }_x$, ${\sigma }_y$, ${\sigma }_{xy}$ are the mean, standard deviation, and cross-covariances of the x and y. $C_1$, $C_2$, and $C_3$ are the regularization constants.s

.

Creativity and diversity are further requirements for generated data. The former means that the generated signals are not duplicates of the real signals, and the latter requires that the generated signals are not duplicates of each other. In [73], the SSIM and entropy were adopted to quantify the creativity and the diversity of the generated images. Specifically, the SSIM was used to cluster similar generated samples, and the entropy of these clusters reflects their diversity. The entropy can be formulated as follows:

$$\mathrm{Entropy}=-\sum _i^m{p}_{i}log{p}_i$$

(13)

where m is the number of clusters and $p_i$ denotes the probability that the i-th cluster belongs to non-replicated clusters. The duplication occurs when the SSIM is equal to or greater than 0.8. Greater cluster entropy indicates that the generated signals are more diverse. However, there is still a lack of studies evaluating the creativity and diversity of bearing vibration signals.

4.4. Applications of GAN in Bearing Fault Diagnosis

Small sample and data imbalance are two main challenges encountered in data-driven bearing fault diagnosis. In practical engineering, the collected fault data are usually insufficient. On the one hand, machinery and its components are in a healthy status under normal production conditions. On the other hand, they cannot remain faulty for long. Therefore, it is expensive or even impractical to obtain sufficient fault data for the training of diagnostic models. Meanwhile, the probability of various faults, including inner ring faults, outer ring faults, and many other faults, varies due to the inherent characteristics of bearings and different working environments. Therefore, the collected fault data are also unbalanced. The two problems restrict the performance of various ML/DL models and lead to relatively low diagnosis accuracy. An intuitive and widely used solution is to synthesize samples artificially, resulting in a sufficient and balanced dataset. The commonly used data augmentation approaches in bearing fault diagnosis, including traditional oversampling methods and data transformation methods, were covered in previous sections of this paper. As a generative model, one of the most fundamental and important applications of GAN is data augmentation. It is a very promising alternative method for generating bearing fault data. Bearing fault data can be classified into two types based on data dimensions, namely one-dimensional fault data and two-dimensional fault data. The raw vibration signal is one-dimensional time series. GANs are able to directly generate one-dimensional vibration data [45,75]. As the frequency domain of the vibration signal contains a wealth of fault information, in many cases, the raw vibration data are converted from the time domain into the frequency domain. GAN can also be used to generate one-dimensional spectrum data [76,77]. As GAN has its origins in image processing from computer vision, there is no doubt that GAN can also be used to synthesize two-dimensional fault data. One option is to reshape one-dimensional fault data into two-dimensional data [72], while another is to utilize GAN to generate the two-dimensional time–frequency spectrograms of vibration signals [78].

The variety of working conditions is another key issue for data-driven bearing fault diagnosis. Differences in equipment and operational conditions have an impact on the diagnostic model’s generalization performance. GAN can also be applied to transfer learning. Transfer learning refers to the application of a previously trained model to a new task to achieve better performance [79,80]. GAN or the idea of adversarial learning can be integrated into a general transfer learning method to improve the performance of the transfer learning method [27,36,81]. For example, Pei et al. [82] combined WGAN-GP and transfer learning in their proposed rolling bearing fault diagnosis method. Using fault data from only one working condition as the source domain, the fault diagnosis of the target domain under different working conditions is achieved. On the other hand, GAN enables the data transfer between the source and target domains. In [61], Zhu et al. applied adversarial learning to achieve a balance between the data distributions of source and target domain.

From the perspective of application scenarios, promising experimental results have been demonstrated in the two main tasks of bearing fault diagnosis: fault classification and remaining useful life (RUL) prediction. Fault classification is the basic task of fault diagnosis, including the classification of different fault types [74] and the classification of faults of different severity levels [78,83]. To improve the accuracy of bearing RUL prediction, there have also been some studies on the generation of bearing aging data using GANs [84,85,86,87].

In summary, starting from the challenges encountered in practical engineering, GAN can not only be used as a data augmentation technique to address the problem of small sample and data imbalance problems, but can also be applied to transfer learning to improve the ability of models in across-domain diagnosis. Starting from the application scenarios of bearing fault diagnosis, GAN contributes to two major tasks: fault classification and RUL prediction.

5. Conclusions

5.1. Summary

The small sample and data imbalance problems seriously hinder the deployment of DL-based techniques in bearing fault diagnosis. Apart from traditional data augmentation techniques such as oversampling and data transformation, GAN is the most promising method to enable the artificial synthesis of high-quality samples. This paper first reviewed the development of traditional data augmentation methods for bearing fault diagnosis. Subsequently, the recent advances of GANs in bearing fault diagnosis are introduced in detail. Firstly, we divide the improvements of GANs into two primary categories: the improvements in the network structure and the improvements in the loss function. For the former, we further summarized them into three types: information-based, input-based, and layer-based improvements. Likewise, the improvements of loss function are divided into two categories: metric-based improvements and regularization-based improvements. Additionally, we also reviewed the commonly used evaluation methods for generated samples. Finally, we work through the applications of GANs in bearing fault diagnosis. To give an overview of the comparison,

Table 3. Advantages and disadvantages of typical GANs.

Number	Type	Advantages	Disadvantages
1	CGAN	To generate samples with specific attributes such as specific categories.	A large amount of training data with labels are required.
2	ACGAN	With auxiliary classifier, different classes of samples can be generated.	(1) Complex training; (2) Limited quality of generated samples.
3	VAEGAN	The generated samples can be controlled by the autoencoder.	The training is relatively more difficult.
4	DCGAN	The powerful feature extraction capability of CNN is exploited.	More computational resources are required for the training.
5	SNGAN	Exploding and vanishing gradient can be solved effectively.	(1) Slow training speed; (2) Limited diversity of generated samples.
6	WGAN	Wasserstein distance provides a better measure of the difference between distributions.	The training is not stable enough.
7	WGAN-GP	With gradient penalty integrated into WGAN, the stability is improved.	More training time and computational resources.
8	LSGAN	Effectively solves the problems of exploding gradient and vanishing gradient.	Excessive penalization of outliers may lead to a reduction in the diversity of samples being generated.
9	EBGAN	(1) Energy-based loss function allows better interpretability; (2) Improved stability and diversity of sample generation.	(1) Quite complex to implement and train; (2) Prone to mode collapse.
10	BEGAN	Mode collapse can be effectively alleviated.	(1) A relatively complex architecture; (2) Sensitive to hyperparameters.
11	RGAN	With relativistic loss, the quality of sample generation is improved and mode collapse is reduced.	(1) A relatively complex architecture; (2) The relativistic loss is difficult to interpret.

summarizes the advantages and disadvantages of typical GANs, which can be used to guide the choice of GANs under different application scenarios.

5.2. Outlook

•

Explainability from physics

Due to the black-box properties of DL models, the generated samples lack physical interpretability. Based on our literature research, most studies do not take physical knowledge into account in their models. Although there is a large body of literature on physics-guided neural networks [88,89], there is still a lack of research on introducing physical knowledge into GANs. From our point of view, physics-guided GAN can be studied from two perspectives in the field of bearing fault diagnosis. Based on the taxonomy of improvements of GAN in this paper, the first idea belongs to the improvement of the network structure. For example, the bearing fault mechanism model can be integrated into GAN. The second idea aims to improve the loss function by adding physically interpretable regularization terms to the original loss function.

•

Advanced evaluation metrics

To date, the evaluation of the generated samples is not comprehensive. Almost all of the literature we researched only considered the similarity of the generated samples to the real samples. Apart from similarity, the creativity and diversity of the generated samples should be taken into account to achieve a more comprehensive evaluation. More appropriate evaluation metrics deserve further investigation.

•

Application for RUL prediction

Based on our collation of the literature, there are still a number of promising variants or improvements in GAN that have not yet been applied to bearing fault diagnosis, which deserve further research. For the application in bearing fault diagnosis, the majority of reported GAN variants possess the potential to achieve satisfying results, even under imbalanced or small datasets through sample generation. However, concerning RUL prediction, it is quite another matter. In contrast to fault samples, which have obvious features such as different fault characteristic frequencies for different fault types, samples in the aging period do not have such distinct one-to-one features. Therefore, generating aging samples for bearing during the degradation process with GAN remains an open question. Improving the GAN to generate aging samples for RUL prediction under a dataset with limited run-to-failure trajectories is a challenging but rewarding research topic.