Effects of Oil Supply Condition on Spinning–Sliding EHL
Abstract
:1. Introduction
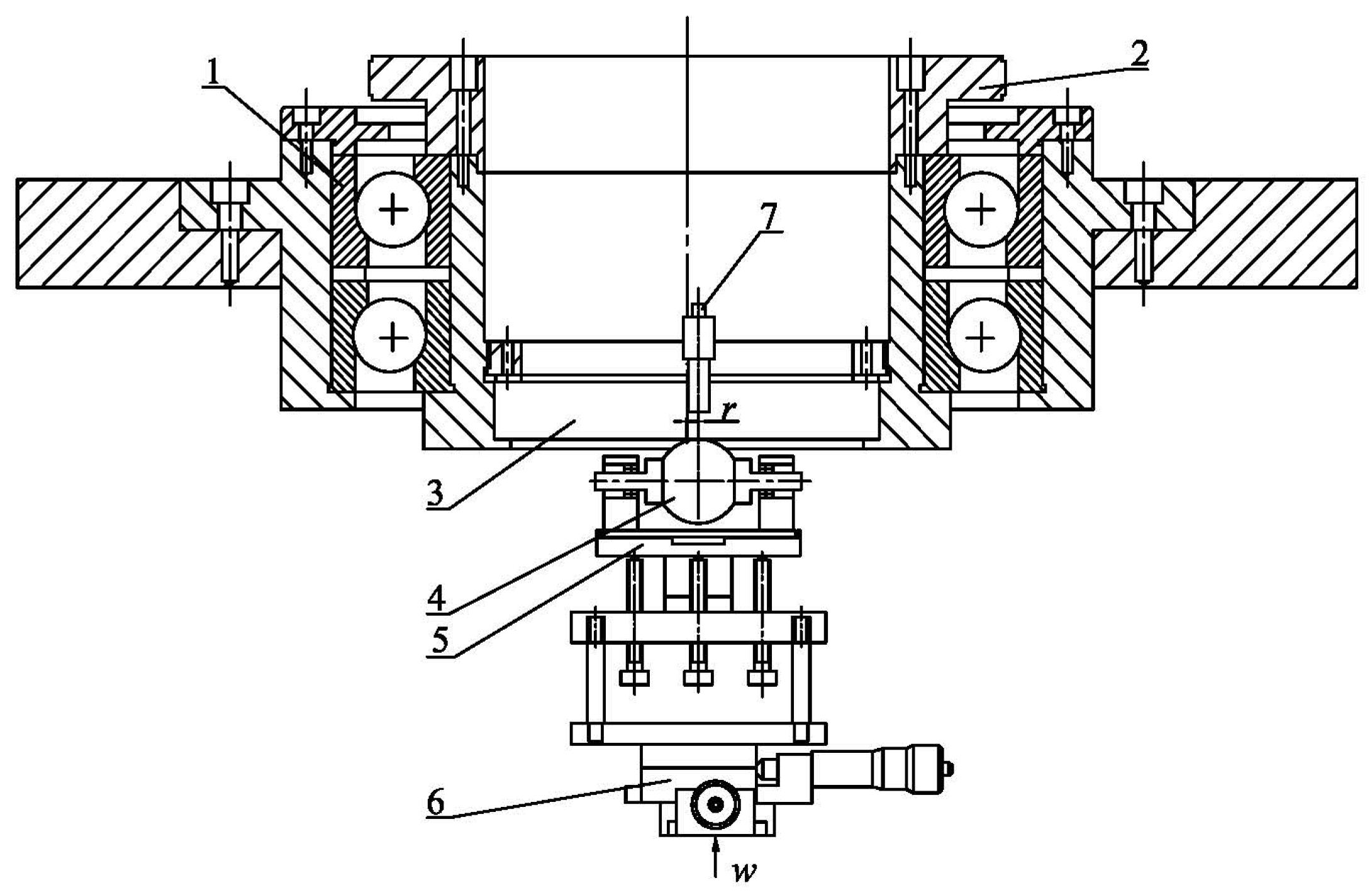
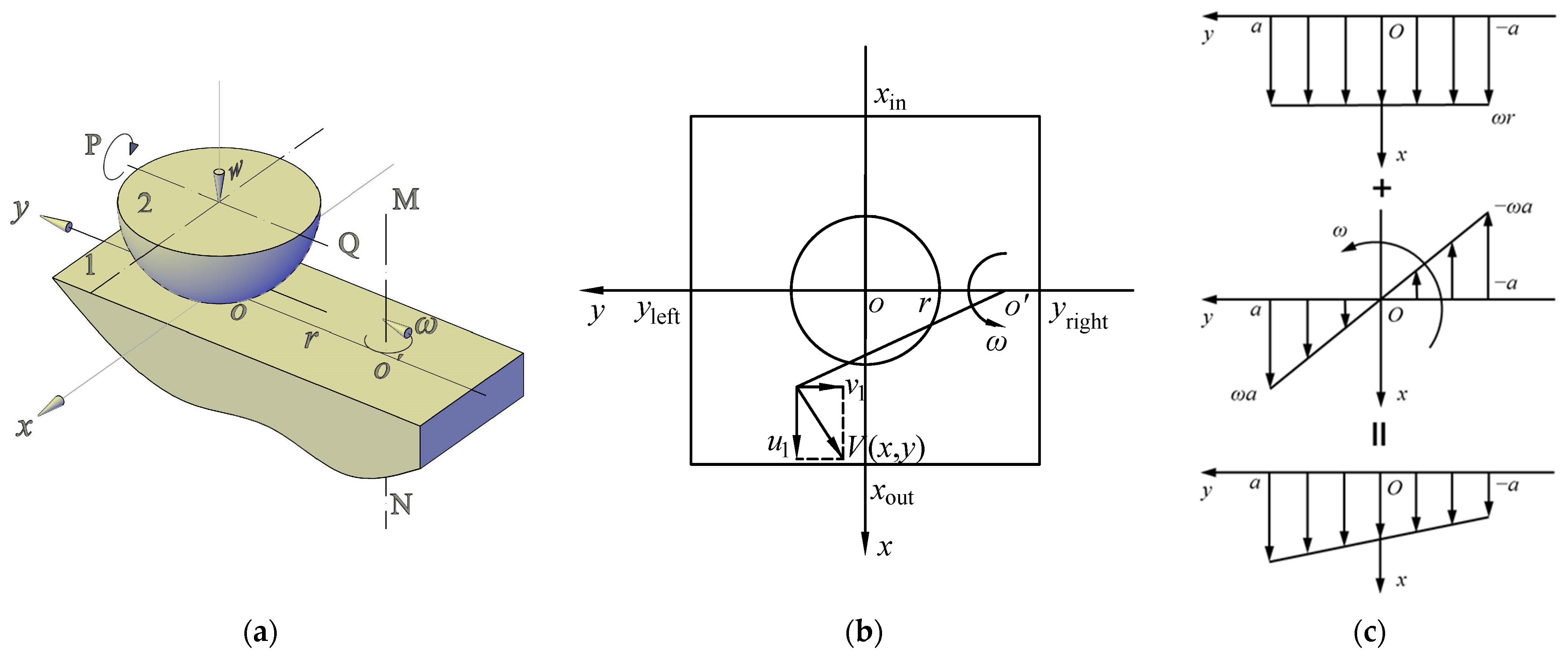
2. Experimental Device and Methods
2.1. Test Rig
2.2. Experimental Material and Condition
2.3. Loading and Velocities
3. Results
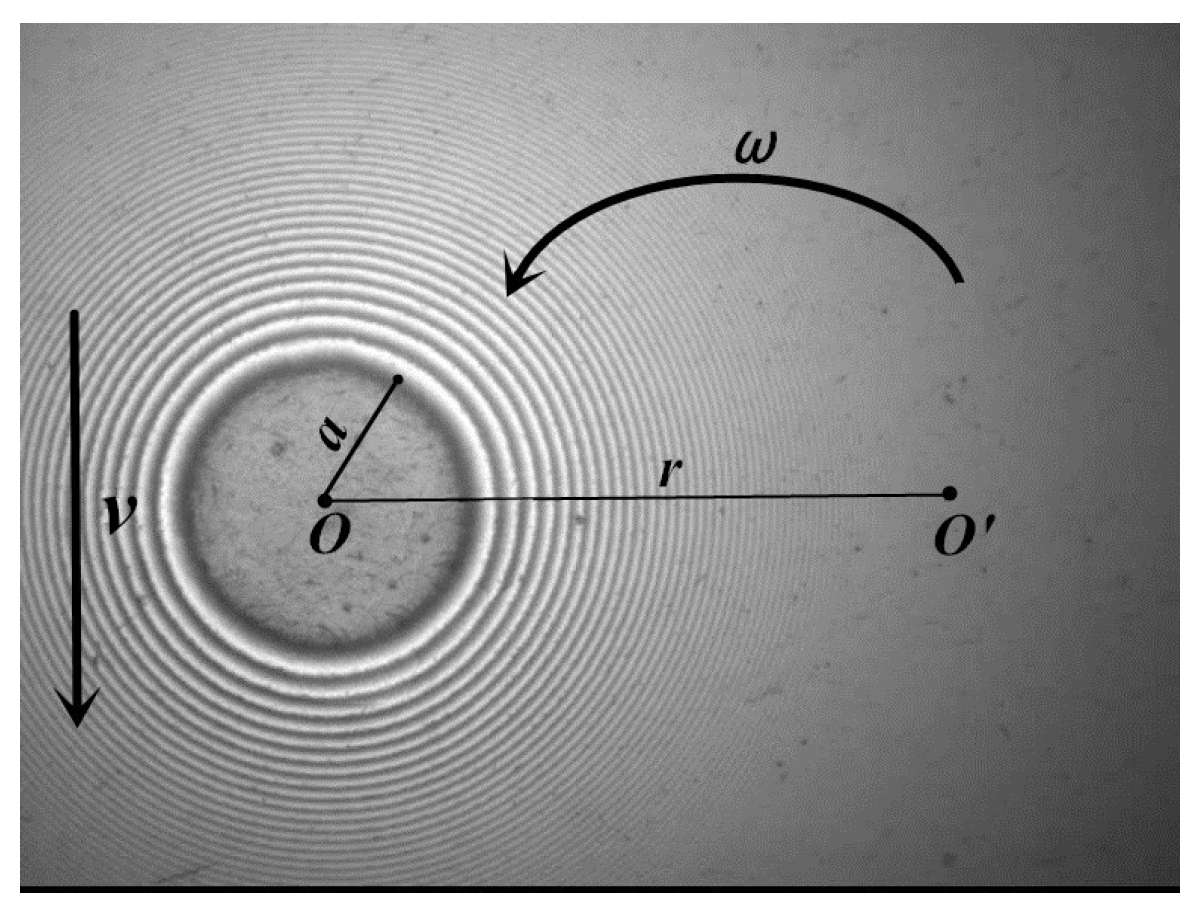
3.1. Preliminary Results of Measurement
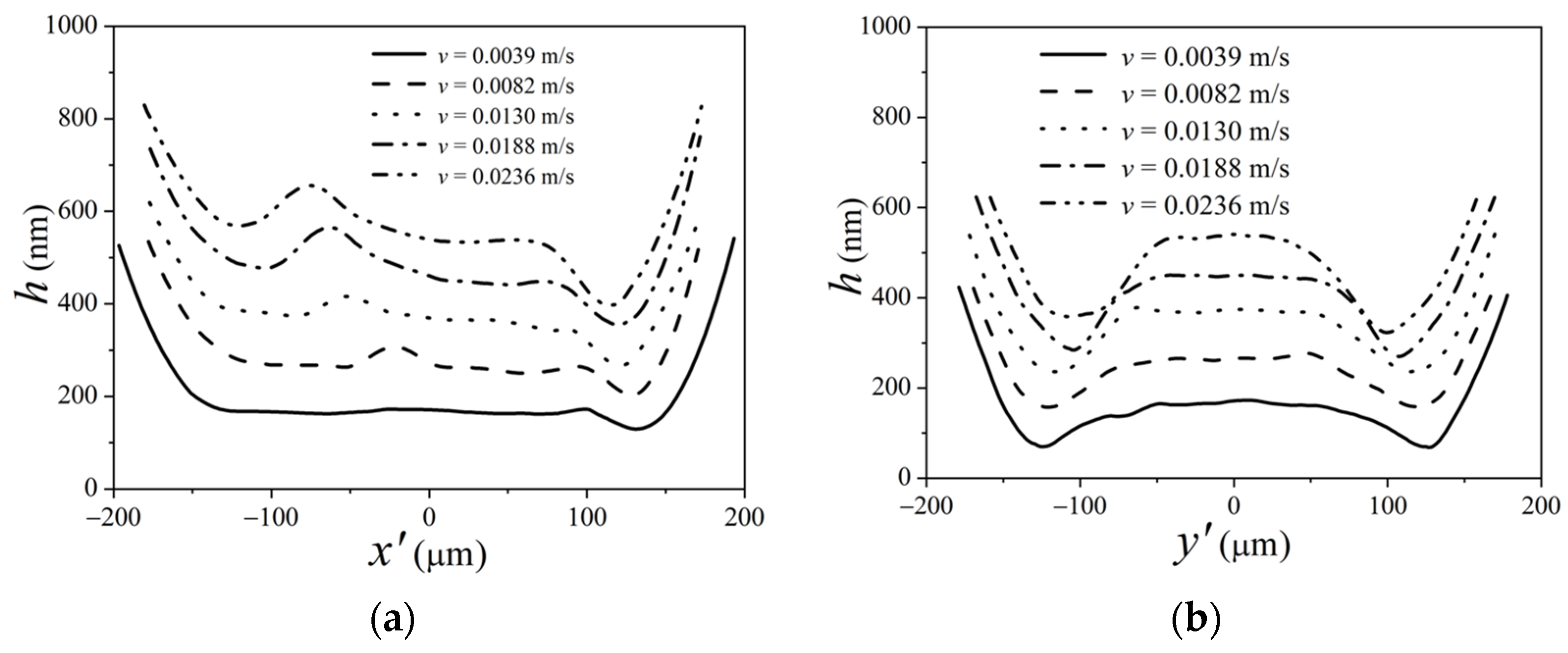
3.2. Effects of Speed and Load under Fully Flooded Condition
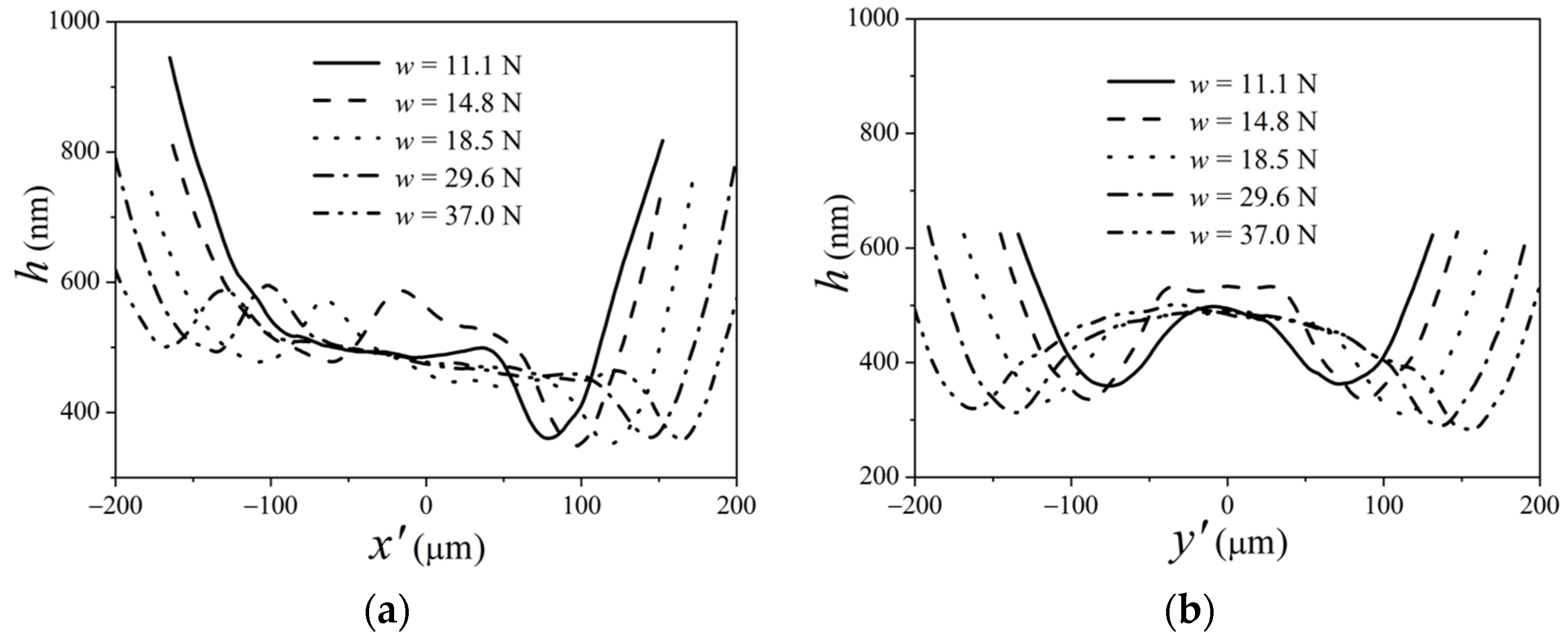
3.3. Effects of the Spinning Factor under Fully Flooded Lubrication
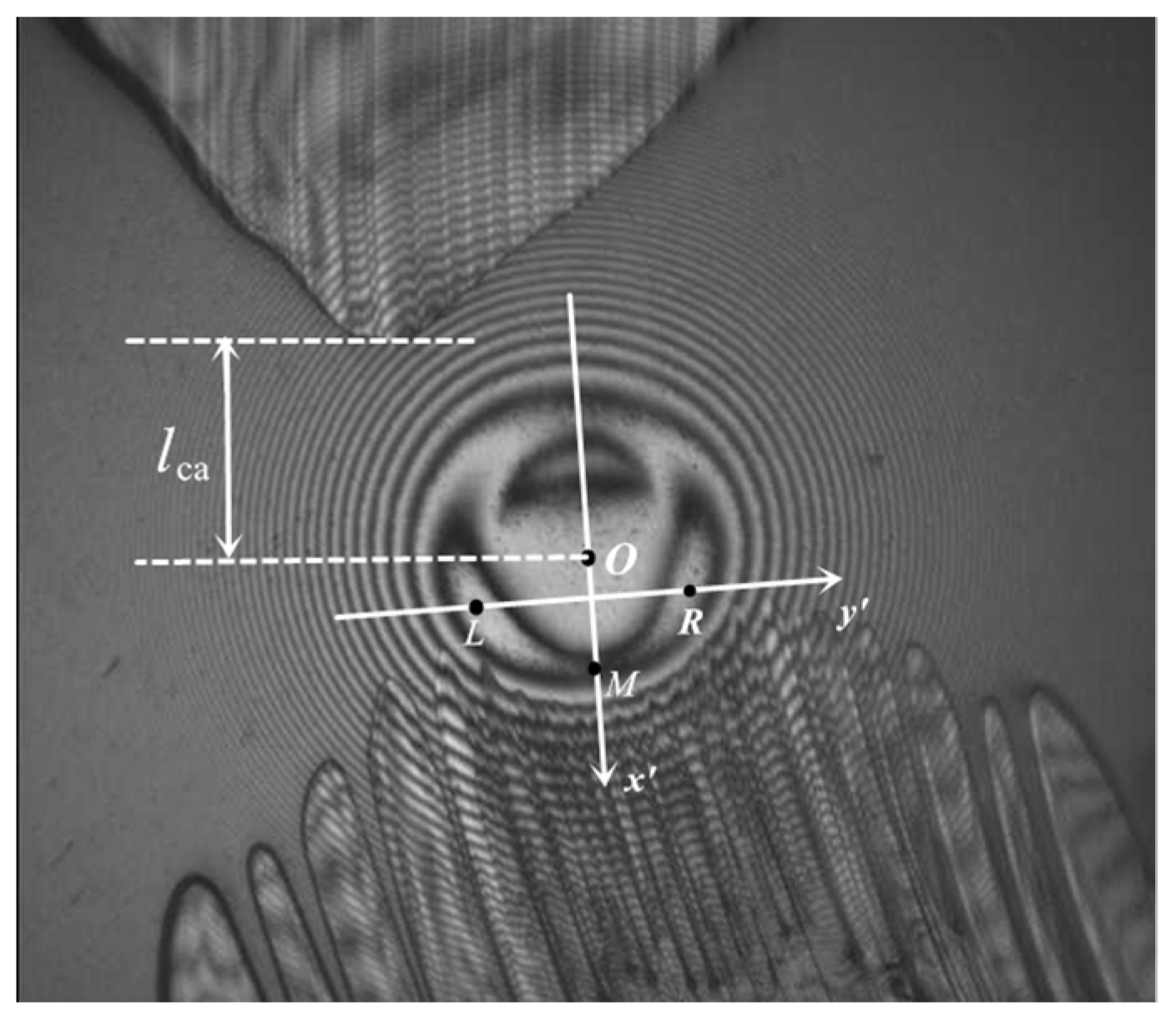
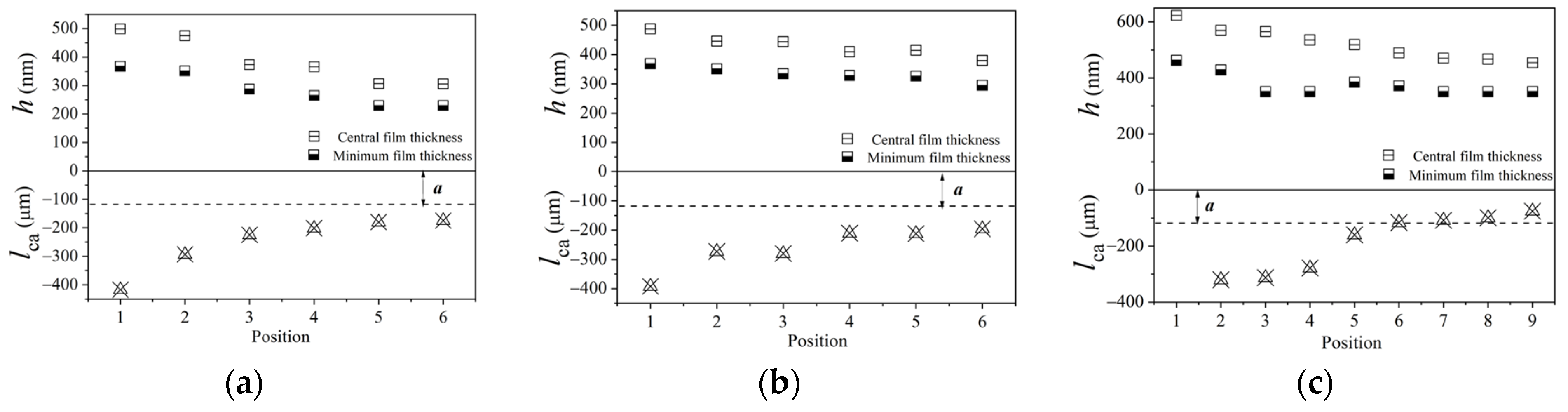
3.4. Effects of Inlet-Starvation Position on Spinning EHL
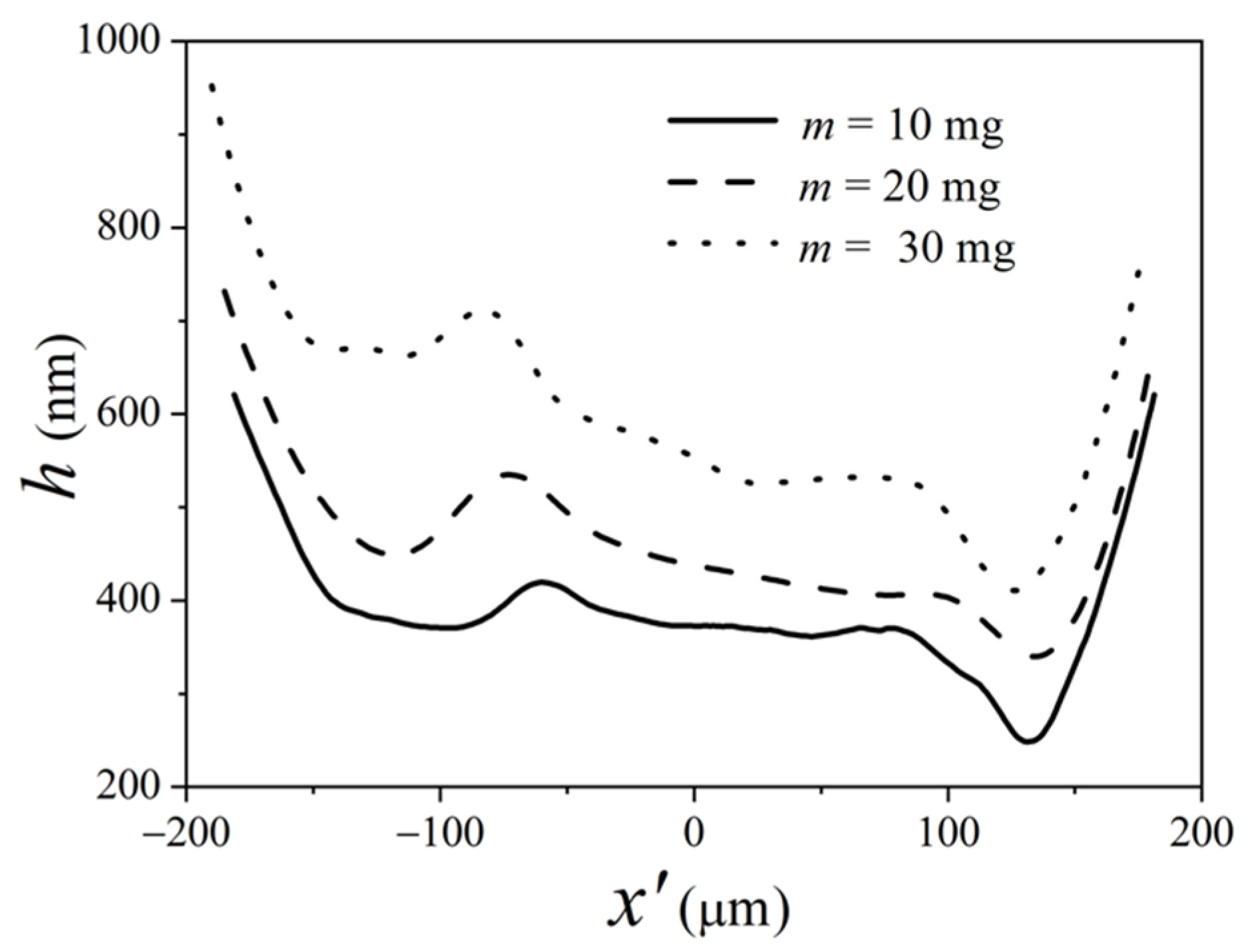
3.5. Effects of Oil-Supply Quantity on Spinning EHL
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, H.S.; Sternlicht, S. A Numerical Solution for the Pressure, Temperature, and Film thickness Between Two Infinitely Long, Lubricated Rolling and Sliding Cylinders, Under Heavy Loads. ASME J. Basic Eng. 1965, 87, 695–707. [Google Scholar] [CrossRef]
- Zhu, D.; Wen, S. A Full Numerical Solution of the Thermal Elastohydrodynamic Lubrication Problem of Elliptic Contact. ASME J. Tribol. 1984, 106, 246–254. [Google Scholar] [CrossRef]
- Yang, P.; Qu, S.; Kaneta, M.; Nishikawa, H. Formation of Steady Dimples in Point TEHL Contacts. ASME J. Tribol. 2001, 123, 42–49. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, M.; Yang, P.; Kaneta, M. Non-Newtonian Thermal Analyses of Point EHL Contacts Using the Eyring Model. ASME J. Tribol. 2005, 127, 70–81. [Google Scholar] [CrossRef]
- Shi, X.; Wang, L.; Mao, Y.; Qin, F. Coupling Study on Dynamics and TEHL Behavior of High-Speed and Heavy-Load Angular Contact Ball Bearing with Spinning. Tribol. Int. 2015, 88, 76–84. [Google Scholar] [CrossRef]
- Miller, S.T.; Parker, R.J.; Zaretsky, E.V. Apparatus for Studying Ball Spinning Friction; NASA Report, NASATN D-2796; National Aeronautics and Space Administration: Washington, DC, USA, 1965.
- Parker, R.J.; Zaretsky, E.V.; Anderson, W.J. Spinning Friction Coefficients with Three Lubricants. ASME J. Lubr. Tech. 1968, 90, 330–335. [Google Scholar] [CrossRef]
- Dietrich, N.W.; Parker, R.J.; Zaretsky, E.V.; Anderson, W.J. Contact Conformity Effects on Spinning Torque and Friction. ASME J. Lubr. Tech. 1969, 68, 308–313. [Google Scholar] [CrossRef]
- Allen, C.W.; Townsend, D.P.; Zaretsky, E.V. Elastohydrodynamic Lubrication of a Spinning Ball in a Nonconforming Groove. ASME J. Lubr. Tech. 1970, 92, 89–95. [Google Scholar] [CrossRef]
- Thorp, N.; Gohar, R. Oil Film Thickness and Shape for a Ball Sliding in a Grooved Raceway. ASME J. Lubr. Tech. 1972, 94, 199–204. [Google Scholar] [CrossRef]
- Johnson, K.L.; Roberts, A.D. Observation of Viscoelastic Behaviour of an Elastohydrodynamic Lubrication Film. Proc. R. Soc. Lond. A Math. Phys. Sci. 1974, 337, 217–242. [Google Scholar]
- Dowson, D.; Taylor, C.M.; Xu, H. Elastohydrodynamic Lubrication of Elliptical Contacts with Pure Spin. Proc. Inst. Mech. Eng. Part C Mech. Eng. Sci. 1993, 207, 83–92. [Google Scholar] [CrossRef]
- Wedeven, L.D.; Evans, D.; Cameron, A. Optical Analysis of Ball Bearing Starvation. ASME J. Lubr. Technol. 1971, 93, 349–353. [Google Scholar] [CrossRef]
- Jiang, P.; Li, X.M.; Guo, F.; Chen, J. Interferometry Measurement of Spin Effect on Sliding EHL. Tribol. Lett. 2009, 33, 161–168. [Google Scholar] [CrossRef]
- Li, X.M. Influence of Spinning on the Rolling EHL Films. Tribol. Int. 2010, 43, 2020–2028. [Google Scholar] [CrossRef]
- Dormois, H.; Fillot, N.; Habchi, W.; Dalmaz, G.; Vergne, P.; Morales-Espejel, G.E.; Ioannides, E. A Numerical Study of Friction in Isothermal EHD Rolling-Sliding Sphere-Plane Contacts with Spinning. J. Tribol. 2010, 132, 021501. [Google Scholar] [CrossRef]
- Liu, X.; Long, T.; Li, X.; Guo, F. Thermal EHL Analysis of the Inner Ring Rib and Roller End in Tapered Roller Bearings with the Carreau Model. Front. Manuf. Technol. 2023, 2, 1029860. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Xie, Y. A Universal Model for Both Flooded and Starved Lubrication Regimes and its Application in Ring-Liner System. Tribol. Trans. 2017, 60, 506–515. [Google Scholar] [CrossRef]
- Colin, F.; Chevalier, F.; Chaomleffel, J.-P.; De Mul, J.; Dalmaz, G. Starved Elastohydrodynamic Lubrication of the Rib-Roller End Contact in Tapered Roller Bearings: Film Thickness, Traction and Moments. In Proceedings of the 24th Leeds-Lyon Symposium on Tribology “Tribology for Energy Conservation”, London, UK, 4–6 September 1997; Tribology Series; Elsevier: Amsterdam, The Netherlands, 1998; Volume 34, pp. 253–263. [Google Scholar]
- Vazquez, A.P. Lubricant Starvation in Elastohydrodynamic Large-Size Spinning Contacts. Ph.D. Thesis, University of Lyon, Lyon, France, 2020. [Google Scholar]
- Vazquez, A.P.; Fillot, N.; Vergne, P.; Philippon, D.; Morales-Espejel, G.E. Influence of Spin on Film Thickness in Elastohydrodynamic Starved Point Contacts. Tribol. Int. 2021, 156, 106825. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Y.; Liu, K. Study on Logarithmic Crowning of Tapered Roller Profile Considering Angular Misalignment. ASME J. Tribol. 2020, 142, 111201. [Google Scholar] [CrossRef]
- Wirsching, S.; Marian, M.; Bartz, M.; Stahl, T.; Wartzack, S. Geometrical Optimization of the EHL Roller Face/Rib Contact for Energy Efficiency in Tapered Roller Bearings. Lubricants 2021, 9, 67. [Google Scholar] [CrossRef]
- Maccioni, L.; Chernoray, V.G.; Mastrone, M.N.; Bohnert, C.; Concli, F. Study of the Impact of Aeration on the Lubricant Behavior in a Tapered Roller Bearing: Innovative Numerical Modelling and Validation Via Particle Image Velocimetry. Tribol. Int. 2022, 165, 107301. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, W.; Zhu, Y.; Yan, K.; Hong, J. Effects of Defect on Roller Raceway Contact State and Friction Torque of Tapered Roller Bearings. ASME J. Tribol. 2020, 142, 111501. [Google Scholar] [CrossRef]
- Gao, P.; Tang, W.; Cui, Y.; Wang, Y.; Mo, G.; Yin, J. Theoretical and Experimental Investigation on Thermal Characteristics of Railway Double-Row Tapered Roller Bearing. Energies 2022, 15, 4217. [Google Scholar] [CrossRef]
- Guo, F.; Wong, P.L. A Wide Range Measuring System for Thin Lubricating form: From Nano to Micro Thickness. Tribol. Lett. 2004, 17, 521–531. [Google Scholar] [CrossRef]
- Guo, F.; Wong, P.L. An Anomalous Elastohydrodynamic Lubrication Film: Inlet Dimple. ASME J. Tribol. 2005, 127, 425–434. [Google Scholar] [CrossRef]
- Cameron, A. The viscosity wedge. ASLE Trans. 1958, 1, 248–253. [Google Scholar] [CrossRef]
- Yagi, K.; Kyogoku, K.; Nakahara, T. Relationship Between Temperature Distribution in EHL Film and Dimple Formation. ASME J. Tribol. 2005, 127, 658–665. [Google Scholar] [CrossRef]
- Yagi, K.; Kyogoku, K.; Nakahara, T. Experimental Investigation of Effects of Slip Ratio on Elastohydrodynamic Lubrication Film Related to Temperature Distribution in Oil Films. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 353–363. [Google Scholar] [CrossRef]
- Qu, S.; Yang, P.; Guo, F. Theoretical Investigation on the Dimple Occurence in the Thermal EHL of Simple Sliding Steeling Steelnce in Contacts. Tribol. Int. 2000, 33, 59–65. [Google Scholar] [CrossRef]
- Yagi, K.; Vergne, P. Abnormal Film Shapes in Sliding Elastohydrodynamic Contacts Lubricated by Fatty Alcohols. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 287–300. [Google Scholar] [CrossRef]
- Nakahara, T.; Yagi, K. Influence of Temperature Distributions in EHL Film on its Thickness under High Slip Ratio Conditions. Tribol. Int. 2007, 40, 632–637. [Google Scholar] [CrossRef]
- Yagi, K.; Vergne, P.; Nakahara, T. In Situ Pressure Measurements in Dimpled Elastohydrodynamic Sliding Contacts by Raman Microspectroscopy. Tribol. Int. 2009, 42, 724–730. [Google Scholar] [CrossRef]
- Yagi, K.; Sugimura, J.; Vergne, P. Rheological Response of Fatty Alcohols in Sliding Elastohydrodynamic Contacts. Tribol. Int. 2012, 49, 58–66. [Google Scholar] [CrossRef]
- Yagi, K.; Kyogoku, K.; Nakahara, T. Mechanism of Dimple Formation under Elastohydrodynamic Conditions. In Tribological Research and Design for Engineering Systems: Proceedings of the 29th Leeds–Lyon Symposium on Tribology, Leeds, UK, 3–6 September 2002; Elsevier: Amsterdam, The Netherlands, 2003; pp. 111–120. [Google Scholar]
- Maruyama, T.; Nakano, K. In Situ Quantification of Oil Film Formation and Breakdown in EHD Contacts. Tribol. Trans. 2018, 61, 1057–1066. [Google Scholar] [CrossRef]
- Maruyama, T.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring of Practical Ball Bearings by Electrical Impedance Method. Tribol. Online 2019, 14, 327–338. [Google Scholar] [CrossRef]







| Lubricant | Dynamic Viscosity (Pa·s) @ 20 °C | Dynamic Viscosity (Pa·s) @ 100 °C | Density (kg·m−3) @ 20 °C | Refractive Index |
|---|---|---|---|---|
| PB950 | 27.5 | 0.201 | 1.497 |
| Load (N) | 10 | 20 | 30 | 40 |
|---|---|---|---|---|
| Theoretical a (μm) | 120 | 149 | 175 | 188 |
| Experimental a (μm) | 122 | 150 | 176 | 188 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Liu, X.; Meng, Q.; Ma, M.; Long, T.; Guo, F. Effects of Oil Supply Condition on Spinning–Sliding EHL. Lubricants 2023, 11, 451. https://doi.org/10.3390/lubricants11100451
Li W, Liu X, Meng Q, Ma M, Long T, Guo F. Effects of Oil Supply Condition on Spinning–Sliding EHL. Lubricants. 2023; 11(10):451. https://doi.org/10.3390/lubricants11100451
Chicago/Turabian StyleLi, Wei, Xiaoling Liu, Qingen Meng, Mingming Ma, Tao Long, and Feng Guo. 2023. "Effects of Oil Supply Condition on Spinning–Sliding EHL" Lubricants 11, no. 10: 451. https://doi.org/10.3390/lubricants11100451
APA StyleLi, W., Liu, X., Meng, Q., Ma, M., Long, T., & Guo, F. (2023). Effects of Oil Supply Condition on Spinning–Sliding EHL. Lubricants, 11(10), 451. https://doi.org/10.3390/lubricants11100451







