Abstract
We present a general approximate analytical solution for the normal contact of layered and functionally graded elastic materials for almost axisymmetric contact profiles. The solution only requires knowledge of the corresponding contact solution for indentation using a rigid cylindrical flat punch. It is based on the generalizations of Barber’s maximum normal force principle and Fabrikant’s approximation for the pressure distribution under an arbitrary flat punch in an inhomogeneous case. Executing an asymptotic procedure suggested recently for almost axisymmetric contacts of homogeneous elastic media results in a simple approximate solution to the inhomogeneous problem. The contact of elliptical paraboloids and indentation using a rigid pyramid with a square planform are considered in detail. For these problems, we compare our results to rigorous numerical solutions for a general (bonded or unbonded) single elastic layer based on the boundary element method. All comparisons show the quality and applicability of the suggested approximate solution. Based on our results, any compact axisymmetric or almost axisymmetric contact problem of layered or functionally graded elastic materials can be reduced asymptotically to the problem of indenting the material using a rigid cylindrical flat punch. The procedure can be used for different problems in tribology, e.g., within the framework of indentation testing or as a tool for the analysis of local features on a rough surface.
1. Introduction
The mechanics of layered [1] and functionally graded [2] elastic materials have received a lot of interest in the framework of modeling tribological properties of, for example, articular cartilage [3], coatings [4], biomaterials [5], or soils [6]. While tribology and the materials science of layered or graded media are vast branches in science with extensive literature studies conducted—see, e.g., the review articles ([7,8,9]) and the references therein—we will focus on the more specific problem of the contact mechanical behavior for these materials. In that regard, one should, however, bear in mind that several tribological phenomena have their origin in the contact mechanical interaction [10].
As the material inhomogeneity severely complicates (or, to put it bluntly, apart from some special cases such as the power-law graded elastic half-space [11], inhibits) an exact closed-form solution of corresponding contact problems, analytical contact solutions of layered materials are often in asymptotic form ([12,13,14,15]). Because of the approximate character of these solutions, their predictions should be checked against rigorous numerical simulations—a step which was significantly simplified recently for the case of a coated elastic half-space, with the publication of a boundary element method (BEM) formulation of the corresponding normal [16] and tangential contact problems [17]. For the respective normal contact, the BEM results were also validated using laboratory experiments for the indentation of hard steel counter-bodies into soft elastic rubber sheets [18].
An ingenious principle to solve contact problems stems from Mossakovskii [19]. It is based on the observation that the incremental difference between two subsequent contact configurations with indentation depths d and d + dd can be understood as an infinitesimal indentation dd using a flat punch, whose planform is given by the contact region at the indentation depth d. Hence, general normal contact can be thought of as a series of incremental flat punch indentations, and therefore, the solution procedure is split into two tasks: the determination of the relation between indentation depth and contact region (which encodes the correct series of flat punches to exactly reproduce the original contact), and the solution of the corresponding flat punch problems.
For the case of axisymmetric indentation of an elastic half-space, both tasks are easily solvable, which leads to the famous solution that is often attributed to Sneddon [20], although it originated a lot earlier [21]. This (exact) axisymmetric solution was generalized some years ago for layered and functionally graded materials [22], albeit in a form where the pressure distribution under a cylindrical flat punch remains unspecified, as it cannot be calculated analytically even in the case of a single homogeneous elastic layer of arbitrary thickness. However, once this pressure distribution has been determined (numerically, e.g., based on the BEM), the corresponding (non-adhesive) normal contact problem of arbitrary axisymmetric convex indenters is solved, as well as all classes of contact problems, which can be reduced to it, e.g., the corresponding adhesive normal contact [23].
Nonetheless, let us, for a moment, turn our attention back to the indentation of a homogeneous elastic half-space. Recently, Popov [24] published an approximate analytical solution for the slightly non-axisymmetric version of this contact problem, which has proven (by comparison with rigorous numerical solutions) to give very satisfactory results. In the follow-up publication [25], the authors thoroughly tested the quality of the suggested approximate analytical solution for contact geometries that are far from axial symmetry and found that it is even well-applicable to indenters with random three-dimensional shapes, e.g., a single asperity of a rough surface.
Popov’s solution rests on two fundaments: On the one hand, Barber’s [26] extremal principle that the contact region at a given indentation depth maximizes a specific integral (which corresponds to the total normal force); and, on the other hand, Fabrikant’s approximation [27] for the pressure distribution under a flat punch of arbitrary (compact) planform. As has been shown very recently by one of the authors of the present manuscript [28], Barber’s principle applies to any elastic normal contact problem (at least, with compact contact regions), which can be thought of as a series of flat punch indentations. That is to say, it also applies to contacts of (sufficiently isotropic) layered or functionally graded materials. On the other hand, the “essence” of Fabrikant’s approximation is to “scale” the axisymmetric pressure distribution under a cylindrical flat punch to the asymmetric arbitrary planform, a procedure which also can be executed very generally if the indented material is sufficiently isotropic. Hence, both fundaments of Popov’s approximate solution for the homogeneous half-space can be generalized for layered or functionally graded materials (albeit in a slightly less rigorous sense, as will be discussed in the manuscript), and it is thus expected the solution itself can be generalized for the application with layered media, as well. This is the aim of the present manuscript. In other words, we extend the approximate reduction in asymmetric elastic contact problems (with compact contact domains) to the respective axisymmetric problem (and, in consequence, to the indentation problem using a rigid cylindrical flat punch, as will be demonstrated)—which was recently suggested and tested thoroughly for homogeneous and power-law graded media—to the application for arbitrary layered or functionally graded materials.
The remainder of the manuscript is organized as follows: In Section 2, we will derive the general approximate solution for the slightly non-axisymmetric normal contact of layered materials, based only on the corresponding cylindrical flat punch solution, the extremal normal force principle, and a newly suggested generalization of Fabrikant’s approximation for layered media. For the convenience of the reader, the derivation of the known axisymmetric solution from the extremal principle (which is indispensable for the understanding of the asymmetric solution) is also shown. The general solution can be significantly simplified in the case of self-similar power-law indenters. In Section 3, we will compare the predictions of the approximate solution with rigorous numerical simulations based on the BEM for the case of a single elastic layer of arbitrary thickness. A short discussion of the method and the obtained results finishes the manuscript.
2. Theory
Let us consider an isotropic, layered, or functionally graded elastic medium, which is indented using a rigid counter-body without friction, as depicted in Figure 1. The layers shall have Young’s moduli Ei and Poisson ratios υi (in the case of a functionally graded material, the change in E(z) and υ(z) is continuous rather than discrete). The rigid indenter shall have the profile f(x,y) in cartesian coordinates, and we control either the indentation depth d or the total normal force F.
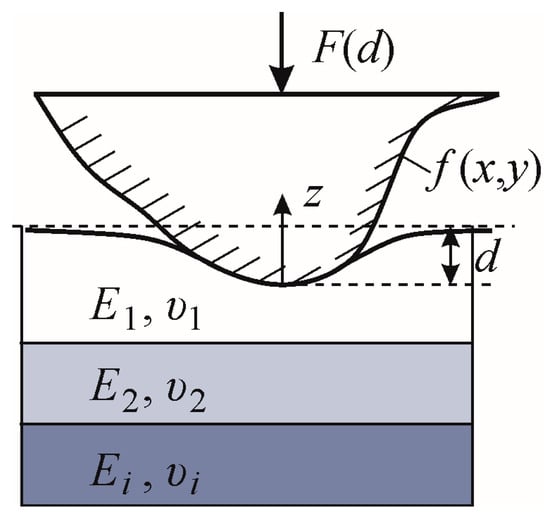
Figure 1.
Indentation of a layered elastic material using a rigid counter-body. Notations are explained in the text.
2.1. Solution for a Cylindrical Flat Punch
For dimensional reasons, we can always write the pressure distribution resulting from the unit indentation of the elastic material using a rigid cylindrical flat punch with radius a in non-dimensional form as
with the radial coordinate r and some length scale l intrinsic to the material, e.g., some layer thickness or grading depth. Depending on the exact form of the vertical inhomogeneity, there might be several more dimensionless quantities involved in the determination of p*, but for the contact problem, these are just constant parameters.
The non-dimensional pressure distribution in Equation (1) must be calculated somehow, e.g., based on the boundary element method (BEM) or with finite elements (FE). However, we will not bother with the details of that calculation and postulate that this non-dimensional distribution is known and tabulated with sufficient precision.
We can also define the universal axisymmetric contact stiffness in non-dimensional form as
This contact stiffness is universal because the incremental difference between two axisymmetric contact configurations is equivalent to an incremental indentation using a rigid flat punch, as has been discussed in the introductory section.
As an illustrative example, in the case of a homogeneous elastic half-space, we have
2.2. Solution for an Axisymmetric Punch
According to Betti’s reciprocal theorem, the total normal force resulting from the indentation using a rigid, smooth axisymmetric indenter at an indentation depth d equals ([29]; [30], p. 52)
Inserting the pressure distribution (1), we obtain
with the transformed profile
As can be seen, T{} denotes a linear operator, specifically the integral transform of the profile, using the flat punch pressure as the integral kernel. Note that β = a/l, i.e., G and g, can be written as explicit functions of a, but for reasons that will become clearer later, we will treat a and β as separate (albeit not independent) variables.
As was shown recently by one of the authors [28], due to the universality of contact stiffness, Barber’s maximum normal force principle—the correct contact domain maximizes the normal force for any given indentation depth—applies to any frictionless normal contact problem with a compact contact domain, that can be thought of as series of incremental flat punch indentations. Hence, the contact radius a can be determined by maximizing the expression (5) with respect to a, and therefore [22],
Note that these are total derivatives, i.e., the dependencies on β must be accounted for.
Up until here, all results have been exact. Let us now turn our attention to the approximate contact solution for an arbitrary convex punch whose shape slightly deviates from rotational symmetry.
2.3. Approximate Solution for Slightly Non-Axisymmetric Profiles
In the case of a general convex punch, the normal force integral resulting from the reciprocity theorem reads ([30], p. 52)
with the contact domain Ω and the corresponding pressure distribution p* for the unit indentation of the inhomogeneous elastic material using a flat punch with that planform. As before, the correct contact domain maximizes the force (8) at any given indentation depth d. However, to constructively apply that principle, we require an expression for the general flat punch pressure distribution p*. For that purpose, let the contour of the domain Ω be given in polar coordinates by the closed curve r = a(φ), and let us assume that the pressure distribution p* can be approximated well enough by the expression
with the known non-dimensional pressure distribution under a cylindrical flat punch.
Equation (9) describes a “Fabrikant-type” approximation. In other words, the pressure distribution under an arbitrary flat punch is assumed to be given approximately by the distribution for a cylindrical punch, scaled to the asymmetric shape of the punch.
However, the important difference to the homogeneous half-space (and, thus, Fabrikant’s original approximation [27]) is the size parameter β, which does not exist for the homogeneous half-space because the latter has no intrinsic length scale, and therefore the contact problem does not exhibit size effects. One may argue that the size parameter also varies over the contour, and therefore, instead of β0, one should use β(φ) as a variable size parameter for the pressure distribution. This, however, would severely complicate the following considerations, and we therefore decided to use the simplified version given in Equation (9). As the final approximate results will be compared with rigorous numerical simulations, anyways, one can dispense with a little mathematical rigor for the sake of the applicability of the analytical results.
Inserting the approximation (9) into the force integral (8), we obtain
with the transformed profile
as in Equation (6). The following procedure for the approximate determination of the contact contour a(φ) operates in analogy to the homogeneous case (see [24] for details) and shall, therefore, only be given briefly.
The maximum principle requires maximizing the force (10) with respect to the contact contour. Let us first maximize the force for a fixed value of a0 by introducing the Lagrange functional
with the Lagrange multiplier λ. The necessary condition for an unconditional extremum of the Lagrange functional leads to the algebraic equation
We can separate the slightly non-symmetric profile into an axisymmetric component and a small non-symmetric deviation,
Accordingly, upon expanding the transformed profile, one obtains
Moreover, the contact area will also be almost axisymmetric,
Equation (13) has exactly the same structure as for the homogeneous half-space. Therefore, we can immediately write, in perfect analogy to the homogeneous solution,
where the prime denotes the first derivative with respect to the first functional argument.
Also, in analogy to the solution for the homogeneous half-space, the normal force (10) simplifies to
which is the same as the axisymmetric result (5).
Hence, maximizing the force (18) with respect to a0 will result in the axisymmetric relation (7) between the indentation depth and the effective contact radius a0, i.e.,
Equations (17)–(19) give a complete, analytic, general, approximate contact solution for the slightly non-symmetric inhomogeneous case, based only on the pressure distribution under a cylindrical flat punch (which gives the integral kernel for the profile transformation f → G).
Note that also the asymmetric pressure distribution p can be calculated by superimposing the flat punch pressure distributions (9) over the whole indentation procedure, i.e., from d = 0 until d = dmax [24].
2.4. Power-Law Indenters
The general asymmetric solution shown above can be simplified considerably if the indenter profile can be written in the self-similar power-law form
where the brackets denote averaging over the polar angle. It is
and therefore, according to Equation (19), the relation between indentation depth and the effective contact radius is given by
and the asymmetric solution follows from Equation (17) as
In the homogeneous case, we have d* = 1, and therefore, of course, the respective known results [25] are recovered.
3. Case Studies
In this section, we will compare our approximate solution to rigorous numerical calculations for the indentation of a single elastic layer with thickness h, resting on a rigid foundation, based on the boundary element method [16]. The corresponding numerical solution for the pressure distribution under a rigid cylindrical flat punch—which is an indispensable prerequisite to the approximate solution—has been provided in the supplementary material of [23].
One may distinguish different boundary conditions between the layer and the rigid foundation: an “unbonded” layer rests on the foundation without (significant) friction, e.g., in the case of delaminated layers, while a “bonded” layer is fixed rigidly to the substrate. Note that for the unbonded layer, only compressive normal stresses can be transmitted to the substrate; in other words, in some configurations, loading of the layer surface could result in loss of contact between the layer and the foundation [31], which corresponds to a receding contact. We will neglect this effect in our analysis; Greenwood & Barber [32], in the framework of indentation of an elastic layer with an infinite-length cylinder, argue that the corresponding tensile stresses (between the layer and its base) necessary to establish contact are too small to significantly alter the contact configuration.
3.1. Contact of an Elliptical Paraboloid with a Single Elastic Layer
First, let us consider the contact with the elliptical quadratic indenter profile
Without loss of generality, we put A < B and define the eccentricity of horizontal indenter cross-sections, e.g.,
In general, the contact domain does not have to be—except for special cases such as the homogeneous half-space—perfectly elliptical. However, we can introduce the “half-axes” of the contact domain as b1 = a(φ = 0) and b2 = a(φ = π/2), and hence the contact eccentricity e as
In Figure 2, the BEM-based numerical results are shown for the difference between the contact eccentricity and the indenter eccentricity as a function of the indenter eccentricity and the logarithmic normalized layer thickness for the indentation of an unbonded elastic layer. The scatter in the contour line with the level 0.002 is due to the finite grid length of the boundary elements. Figure 3 gives the corresponding results based on the general approximate analytical solution developed in the previous section. The agreement between the approximate solution and the rigorous numerical calculations is quite good. Note that the contour line diagrams show a difference between the contact area eccentricity and the indenter eccentricity; i.e., as the contact eccentricity is of the order of 0.1, the error of the contact eccentricity in the approximate solution compared with the rigorous BEM results is less than 10% (and in most parameter ranges significantly less than 10%).
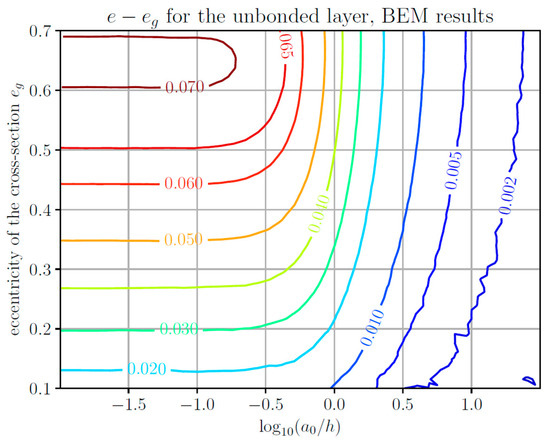
Figure 2.
Contour line diagram of the difference between the contact eccentricity e and the indenter eccentricity eg as a function of the indenter eccentricity and the logarithmic normalized layer thickness, for the contact of an elliptical paraboloid with a single unbonded elastic layer. Numerical results based on the boundary element method (BEM).
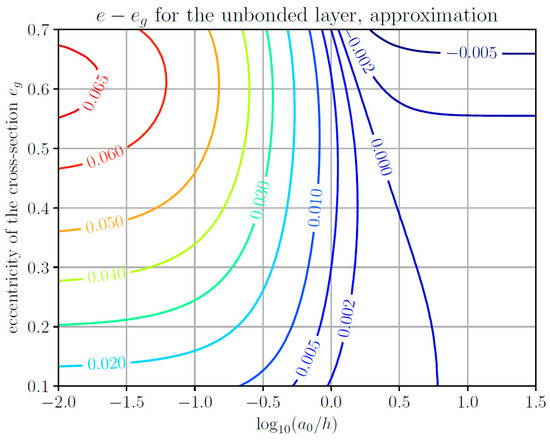
Figure 3.
Contour line diagram of the difference between the contact eccentricity e and the indenter eccentricity eg as a function of the indenter eccentricity and the logarithmic normalized layer thickness, for the contact of an elliptical paraboloid with a single unbonded elastic layer. Approximate analytical solution.
However, for the unbonded layer, the contact eccentricity will never be smaller than the indenter eccentricity. Therefore, slightly negative values for the difference, as in the upper right corner of Figure 3, are unphysical. Also, the half-space solution (at the left edge of both diagrams), according to the numerical simulation, seems to be valid a lot “longer” (until h ≈ 10a0) than estimated by the approximate solution.
Figure 4 (BEM) and Figure 5 (approximate analytical solution) show the results that are analogous to Figure 2 and Figure 3 but for a bonded incompressible layer. The quality of the approximate procedure seems to be a bit worse, which is due to the fact that the material behavior is actually more complicated because of the incompressibility (as the material has to “flow somewhere” if it is pushed by the indenter) than captured by the approximate solution. However, one has to keep in mind that in the diagrams, differences between contact and indenter eccentricities are shown; accordingly, the relative error of the absolute value of contact eccentricity in the approximate solution is still less than 10%.
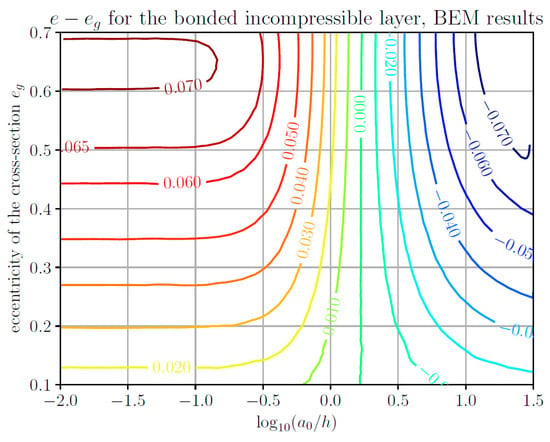
Figure 4.
Contour line diagram of the difference between the contact eccentricity e and the indenter eccentricity eg, as a function of the indenter eccentricity and the logarithmic normalized layer thickness, for the contact of an elliptical paraboloid with a single bonded incompressible elastic layer. Numerical results based on the boundary element method (BEM).
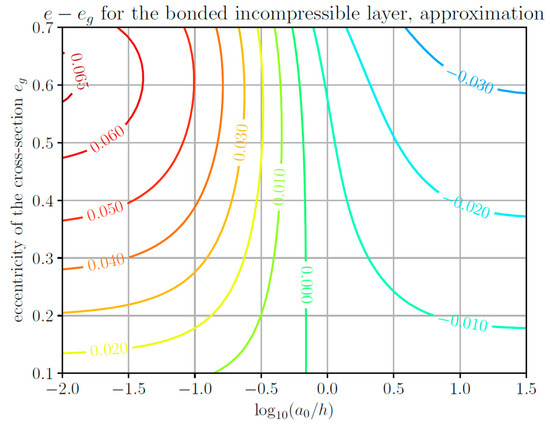
Figure 5.
Contour line diagram of the difference between the contact eccentricity e and the indenter eccentricity eg, as a function of the indenter eccentricity and the logarithmic normalized layer thickness, for the contact of an elliptical paraboloid with a single bonded incompressible elastic layer. Approximate analytical solution.
Let us now turn our attention to the relations between the macroscopic contact quantities, i.e., indentation depth d, normal force F, and average contact radius a0. In Figure 6, the numerical and approximate analytical results are shown for the normalized average contact radius a0/h as a function of the normalized indentation depth for different values of layer thickness in the case of an unbonded layer. Figure 7 presents the corresponding solutions for the total normal force normalized for the maximum value in the case of a homogeneous half-space. The agreement between the approximate analytical procedure and the (rather time-consuming) rigorous numerical calculations is very good.
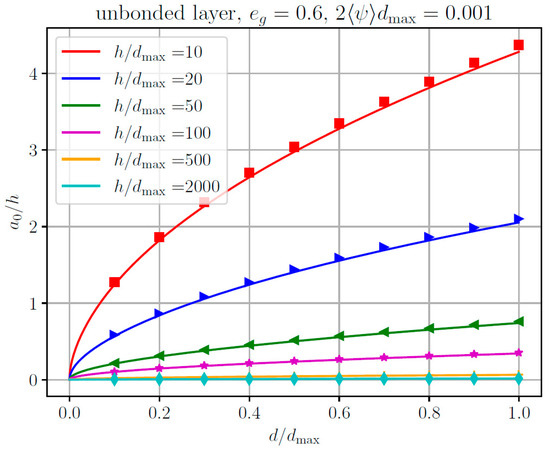
Figure 6.
Normalized average contact radius a0/h as a function of the normalized indentation depth for different values of layer thickness for the contact of an elliptical paraboloid with a single unbonded elastic layer. Lines: approximate analytical solution. Markers: Numerical results based on the boundary element method (BEM).
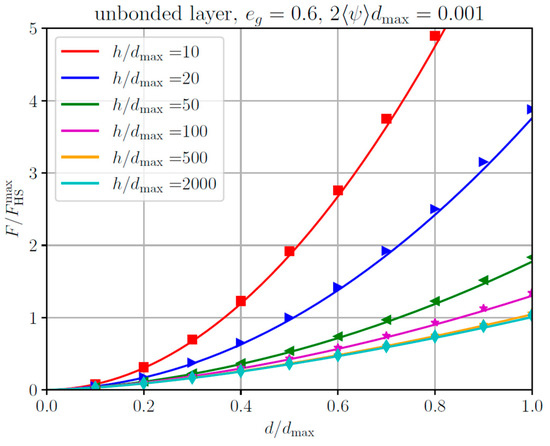
Figure 7.
Total normal force, normalized for the maximum value for the homogeneous half-space, as a function of the normalized indentation depth, for different values of layer thickness, for the contact of an elliptical paraboloid with a single unbonded elastic layer. Lines: approximate analytical solution. Markers: Numerical results based on the boundary element method (BEM).
In Figure 8 and Figure 9, the results analogous to Figure 6 and Figure 7 are shown, but for a bonded incompressible layer. Once again, the agreement between the approximate and numerical solutions is very good.
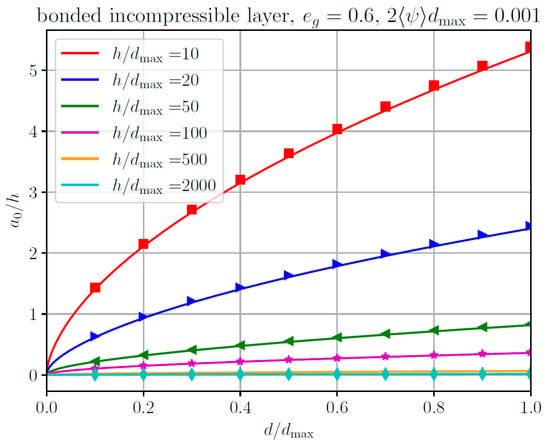
Figure 8.
Normalized average contact radius a0/h as a function of the normalized indentation depth for different values of layer thickness for the contact of an elliptical paraboloid with a single bonded incompressible elastic layer. Lines: approximate analytical solution. Markers: Numerical results based on the boundary element method (BEM).
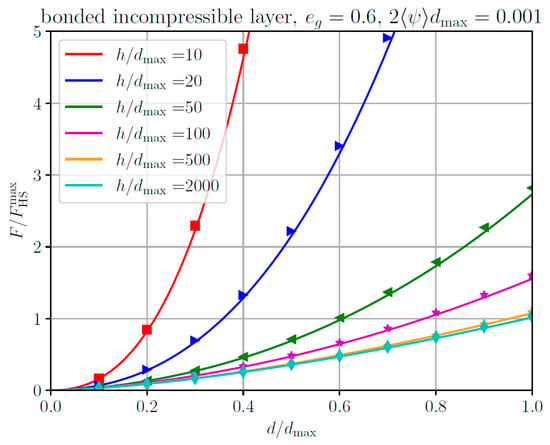
Figure 9.
Total normal force, normalized for the maximum value for the homogeneous half-space, as a function of the normalized indentation depth, for different values of layer thickness, for the contact of an elliptical paraboloid with a bonded incompressible layer. Lines: approximate analytical solution. Markers: Numerical results based on the boundary element method (BEM).
3.2. Indentation of a Single Elastic Layer Using a Rigid Pyramid with Square Planform
As a second example, let us consider the indentation of a single elastic layer using a shallow, rigid pyramid with a square planform. The small inclination angle of the pyramid shall be α. Figure 10 gives comparisons between the approximate solution and BEM-based numerical results for the contact boundary in normalized variables in the case of an unbonded layer (left) and a bonded incompressible layer (right). The prediction of the contact domain by the analytic procedure is very good, except for the sharp corners of the indenter. This is expected because the “Fabrikant-type” approximation (9) can only capture edge-singularities of the pressure distribution (for flat punches that are smooth along the contact boundary); as the stress singularity at the corner is more severe (i.e., of higher order), the contact area is not estimated correctly along the corner of the indenter cross-sections. Interestingly, that effect is smaller for the bonded incompressible layer due to the special (smoother) edge and corner behaviors of the pressure distribution for that material class.
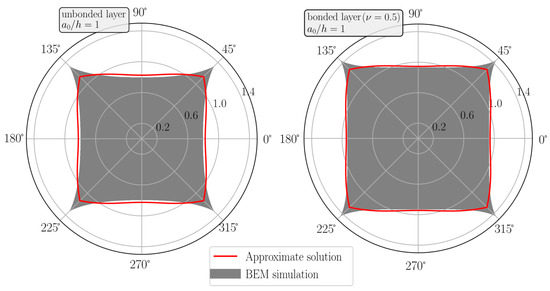
Figure 10.
Normalized contact boundary a(φ) tanα/d for the indentation of a single elastic layer of thickness h = a0 using a shallow, rigid pyramid with square planform. Red line: approximate analytic solution. Grey: contact domain in the BEM simulation. (Left) unbonded layer. (Right) bonded incompressible layer.
Turning to the relations between macroscopic quantities, in Figure 11, the approximate and numerical results are shown for the normalized average contact radius as a function of the normalized indentation depth for different values of layer thickness. As before, the agreement between analytical and numerical calculations is very good.
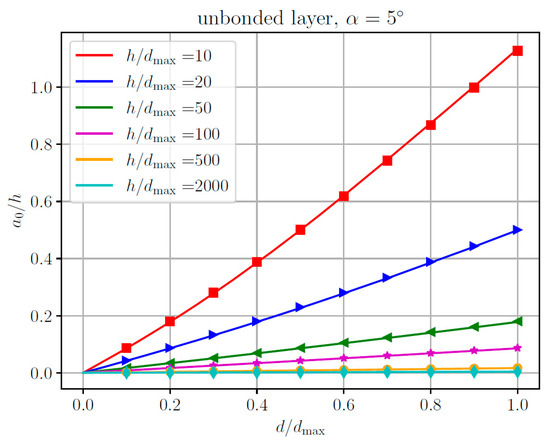
Figure 11.
Normalized average contact radius a0/h as a function of the normalized indentation depth for different values of layer thickness for the indentation of an unbonded elastic layer using a rigid pyramid with square planform and inclination angle α. Lines: approximate analytical solution. Markers: Numerical results based on the boundary element method (BEM).
Figure 12 presents the corresponding solutions for the total normal force, normalized for the maximum value in the case of a homogeneous half-space. Again, the agreement between the suggested approximate analytical solution and the numerical results is almost perfect.
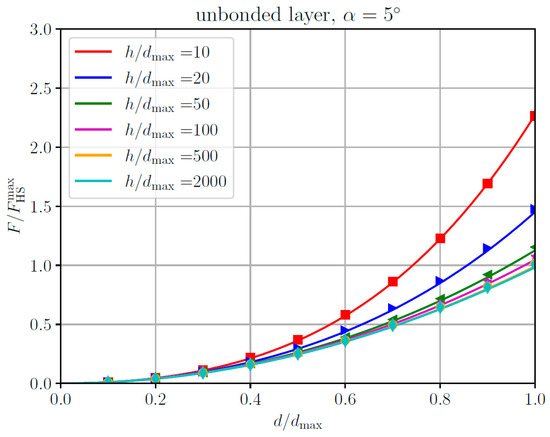
Figure 12.
Total normal force, normalized for the maximum value for the homogeneous half-space, as a function of the normalized indentation depth, for different values of layer thickness, for the indentation of an unbonded elastic layer using a rigid pyramid with square planform and inclination angle α. Lines: approximate analytical solution. Markers: Numerical results based on the boundary element method (BEM).
For reasons of space, we will omit showing the analogous results for the bonded incompressible layer. However, in that case, the agreement between the analytical and numerical calculations is almost perfect.
Finally, it should be noted that, in the case of a thin elastic layer, the material asymptotically behaves similarly to a power-law graded elastic half-space, with the exponent k of the power-law grading given by k = 1 for an unbonded or bonded compressible thin layer, and by k = 3 for a bonded incompressible thin layer. Hence, the corresponding asymptotic contact solutions can be obtained from the general asymptotic contact solution for the indentation of a power-law graded elastic half-space using a slightly non-axisymmetric indenter, which has been published very recently by one of the authors [28].
4. Discussion
We have presented an analytical approximate procedure for the solution of the general (non-symmetric) frictionless normal contact problem (with a compact contact domain) of arbitrary layered functionally graded elastic materials—based only on the solution for the pressure distribution under a rigid cylindrical flat punch indenting the inhomogeneous elastic medium of interest. Thus, the flat punch superposition idea—one of the most powerful tools in analytic contact mechanics—has been extended explicitly to non-homogeneous materials and non-axisymmetric profile geometries. It should be noted that the application of the superposition idea is, generally, not straightforwardly possible for the contact of two elastic bodies if the materials involved exhibit different functional forms of inhomogeneity.
The pressure distribution under a cylindrical flat punch needs to be obtained in the beginning, either using a numerical simulation or from the literature. If one is only interested in the solution of one specific contact problem (and the respective flat solution is not immediately available), it might be debatable whether it is not easier to directly and rigorously solve that problem instead of solving the flat punch problem and constructing an approximate solution for the problem of interest from the flat punch solution. On the other hand, if many contact problems shall be solved for one specific material (e.g., in the context of parameter studies or profile optimization) or the flat punch solution is known, it will speed up the analysis by several orders of magnitude, to only work in the “superposition framework”. In that regard, considering the obvious importance of the flat punch indentation problem, it might be a useful task for future work to create an openly accessible library of flat punch solutions for different types of inhomogeneous materials.
The approximate contact solution presented here is applicable to different tasks in tribology and engineering. It can be used for the fast analysis of macroscopic contacts with complex (or even random) shapes or as a tribological tool for the interaction description of single micro-contacts (“asperities”) in the contact of rough surfaces—with several implications regarding friction and wear [33]. Moreover, the analytic approximate procedure can be used to solve other classes of contact problems, which can be reduced to the elastic normal contact problem, e.g., the viscoelastic contact problem—via the elastic-viscoelastic correspondence principle [34].
Applying the suggested analytic solution, one, however, should be aware of its approximate character. While the macroscopic contact relations, i.e., for the force-indentation curve and, thus, the contact stiffness, seem to be captured extremely well by the analytic solution—at least, for the case studies considered in the present manuscript—local quantities, such as the precise shape of the contact domain, or the contact stress distribution, might differ (slightly) from a rigorous numerical solution of the same problem.
Author Contributions
Conceptualization, E.W.; formal analysis, E.W.; numerical analysis, F.F.; writing—original draft preparation, E.W.; writing—review and editing, E.W. and F.F.; visualization, F.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the German Research Foundation under project number PO 810/66-1.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to Valentin L. Popov for valuable discussions on the topic.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Latin Symbols | |
| a | contact radius; contour of the contact domain in polar coordinates |
| b1, b2 | half-axes of the contact domain |
| A, B | profile constants |
| d | indentation depth |
| d* | short-cut variable |
| dmax | maximum indentation depth |
| e | contact eccentricity |
| eg | eccentricity of horizontal indenter cross-sections |
| E | Young’s modulus |
| E* | effective Young’s modulus |
| f | profile function |
| F | normal force |
| g | derivative of the profile transform G |
| G | transformed profile |
| h | layer thickness |
| k | exponent of the power-law of the elastic grading |
| K | contact stiffness |
| n | exponent of the profile power-law |
| p* | pressure distribution under a cylindrical flat punch with unit indentation depth |
| r | polar radius |
| x, y, z | Cartesian coordinates |
| Greek Symbols | |
| β | non-dimensional layer thickness parameter |
| ν | Poisson ratio |
| κn | stretch factor, corresponding to the exponent n |
| φ | polar angle |
| ψ | angular function |
The index “0” corresponds to the axisymmetric part of a non-axisymmetric variable. A bar over a variable denotes a non-dimensional version of the variable. Brackets denote averaging over the polar angle. A “δ” denotes the deviation of a non-axisymmetric variable from the axisymmetric part.
References
- King, R.B. Elastic analysis of some punch problems for a layered medium. Int. J. Solids Struct. 1987, 23, 1657–1664. [Google Scholar] [CrossRef]
- Suresh, S. Graded materials for resistance to contact deformation and damage. Science 2001, 292, 2447–2451. [Google Scholar] [CrossRef] [PubMed]
- Argatov, I.I. A general solution of the axisymmetric contact problem for biphasic cartilage layers. Mech. Res. Commun. 2011, 38, 29–33. [Google Scholar] [CrossRef]
- Miyoshi, K.; Pohlchuck, B.; Street, K.W.; Zabinski, J.S.; Sanders, J.H.; Voevodin, A.A.; Wu, R.L.C. Sliding wear and fretting wear of diamondlike carbon-based, functionally graded nanocomposite coatings. Wear 1999, 225–229, 65–73. [Google Scholar] [CrossRef]
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional gradients and heterogeneities in biological materials: Design principles, functions, and bioinspired applications. Prog. Mater. Sci. 2017, 88, 467–498. [Google Scholar] [CrossRef]
- Selvadurai, A.P. The Analytical Method in Geomechanics. Appl. Mech. Rev. 2017, 60, 87–106. [Google Scholar] [CrossRef]
- Sathish, M.; Radhika, N.; Saleh, B. A critical review on functionally graded coatings: Methods, properties, and challenges. Compos. B Eng. 2021, 225, 109278. [Google Scholar] [CrossRef]
- Khadem, M.; Penkov, O.V.; Yang, H.-K.; Kim, D.-E. Tribology of multilayer coatings for wear reduction: A review. Friction 2017, 5, 248–262. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, T.; Erdemir, A.; Li, Q. Tribology of two-dimensional materials: From mechanisms to modulating strategies. Mater. Today 2019, 26, 67–86. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Paggi, M.; Popov, V.L. Editorial: Contact Mechanics Perspective of Tribology. Front. Mech. Eng. 2021, 7, 649792. [Google Scholar] [CrossRef]
- Rostovtsev, N.A. On the theory of elasticity of a nonhomogeneous medium. PMM J. Appl. Math. Mech. 1964, 28, 745–757. [Google Scholar] [CrossRef]
- Jaffar, M.J. Asymptotic behaviour of thin elastic layers bonded and unbonded to a rigid foundation. Int. J. Mech. Sci. 1989, 31, 229–235. [Google Scholar] [CrossRef]
- Barber, J.R. Contact problems for the thin elastic layer. Int. J. Mech. Sci. 1990, 32, 129–132. [Google Scholar] [CrossRef]
- Borodich, F.M.; Galanov, B.A.; Perepelkin, N.V.; Prikazchikov, D.A. Adhesive contact problems for a thin elastic layer: Asymptotic analysis and the JKR theory. Math. Mech. Solids 2019, 24, 1405–1424. [Google Scholar] [CrossRef]
- Wu, J.; Ru, C.Q. An analytical solution to the adhesive cylindrical indentation of a compressible elastic thin layer. J. Adhes. 2021, 97, 1291–1309. [Google Scholar] [CrossRef]
- Li, Q.; Pohrt, R.; Lyashenko, I.A.; Popov, V.L. Boundary element method for nonadhesive and adhesive contacts of a coated elastic half-space. Proc. Inst. Mech. Eng. J. J. Eng. Tribol. 2020, 234, 73–83. [Google Scholar] [CrossRef]
- Burger, H.; Forsbach, F.; Popov, V.L. Boundary Element Method for Tangential Contact of a Coated Elastic Half-Space. Machines 2023, 11, 694. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L.; Borysiuk, V. Experimental Verification of the Boundary Element Method for Adhesive Contacts of a Coated Elastic Half-Space. Lubricants 2023, 11, 84. [Google Scholar] [CrossRef]
- Mossakovskii, V.I. Compression of Elastic Bodies under Conditions of Adhesion (Axisymmetric Case). PMM J. Appl. Math. Mech. 1963, 27, 630–643. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Popova, E.; Popov, V.L. Ludwig Föppl and Gerhard Schubert: Unknown classics of contact mechanics. ZAMM Z. Angew. Math. Mech. 2020, 100, e202000203. [Google Scholar] [CrossRef]
- Argatov, I.I.; Heß, M.; Popov, V.L. The extension of the method of dimensionality reduction to layered elastic media. ZAMM Z. Angew. Math. Mech. 2017, 98, 622–634. [Google Scholar] [CrossRef]
- Forsbach, F. A Simple Semi-Analytical Method for Solving Axisymmetric Contact Problems Involving Bonded and Unbonded Layers of Arbitrary Thickness. Machines 2023, 11, 474. [Google Scholar] [CrossRef]
- Popov, V.L. An Approximate Solution for the Contact Problem of Profiles Slightly Deviating from Axial Symmetry. Symmetry 2022, 14, 390. [Google Scholar] [CrossRef]
- Popov, V.L.; Li, Q.; Willert, E. Approximate Contact Solutions for Non-Axisymmetric Homogeneous and Power-Law Graded Elastic Bodies: A Practical Tool for Design Engineers and Tribologists. Friction 2023, 1–16. [Google Scholar] [CrossRef]
- Barber, J.R. Determining the contact area in elastic-indentation problems. J. Strain Anal. Eng. Des. 1974, 9, 230–232. [Google Scholar] [CrossRef]
- Fabrikant, V.I. Flat punch of arbitrary shape on an elastic half-space. Int. J. Eng. Sci. 1986, 24, 1731–1740. [Google Scholar] [CrossRef]
- Willert, E. On Boussinesq’s Problem for a Power-Law Graded Elastic Half-Space on Elliptical and General Contact Domains. Materials 2023, 16, 4364. [Google Scholar] [CrossRef]
- Shield, R.T. Load-Displacement Relations for Elastic Bodies. Z. Angew. Math. Phys. ZAMP 1967, 18, 682–693. [Google Scholar] [CrossRef]
- Barber, J.R. Contact Mechanics; Springer International Publishing AG: Cham, Switzerland, 2018; 585p. [Google Scholar] [CrossRef]
- Filon, L.N.G. On an approximate solution for the bending of a beam of rectangular cross-section under any system of load, with special reference to points of concentrated or discontinuous loading. Proc. R. Soc. Lond. 1902, 70, 491–496. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Barber, J.R. Indentation of an elastic layer by a rigid cylinder. Int. J. Solids Struct. 2012, 49, 2962–2977. [Google Scholar] [CrossRef]
- Milanese, E.; Brink, T.; Aghababaei, R.; Molinari, J.-F. Emergence of self-affine surfaces during adhesive wear. Nat. Commun. 2019, 10, 1116. [Google Scholar] [CrossRef] [PubMed]
- Khazanovich, L. The elastic-viscoelastic correspondence principle for non-homogeneous materials with time translation non-invariant properties. Int. J. Solids Struct. 2008, 45, 4739–4747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).