Simulation Study on the Influence of a Laser Power Change on the Residual Stress of a Laser-Melting RuT300 Valve Seat
Abstract
:1. Introduction
2. Finite Element Simulation Model
2.1. Mesh Model
2.2. Mathematical Model
2.3. Thermophysical Property Parameters of the RuT300 Material
2.4. Parameters of the Laser-Melting Process
3. Results Analysis and Discussion
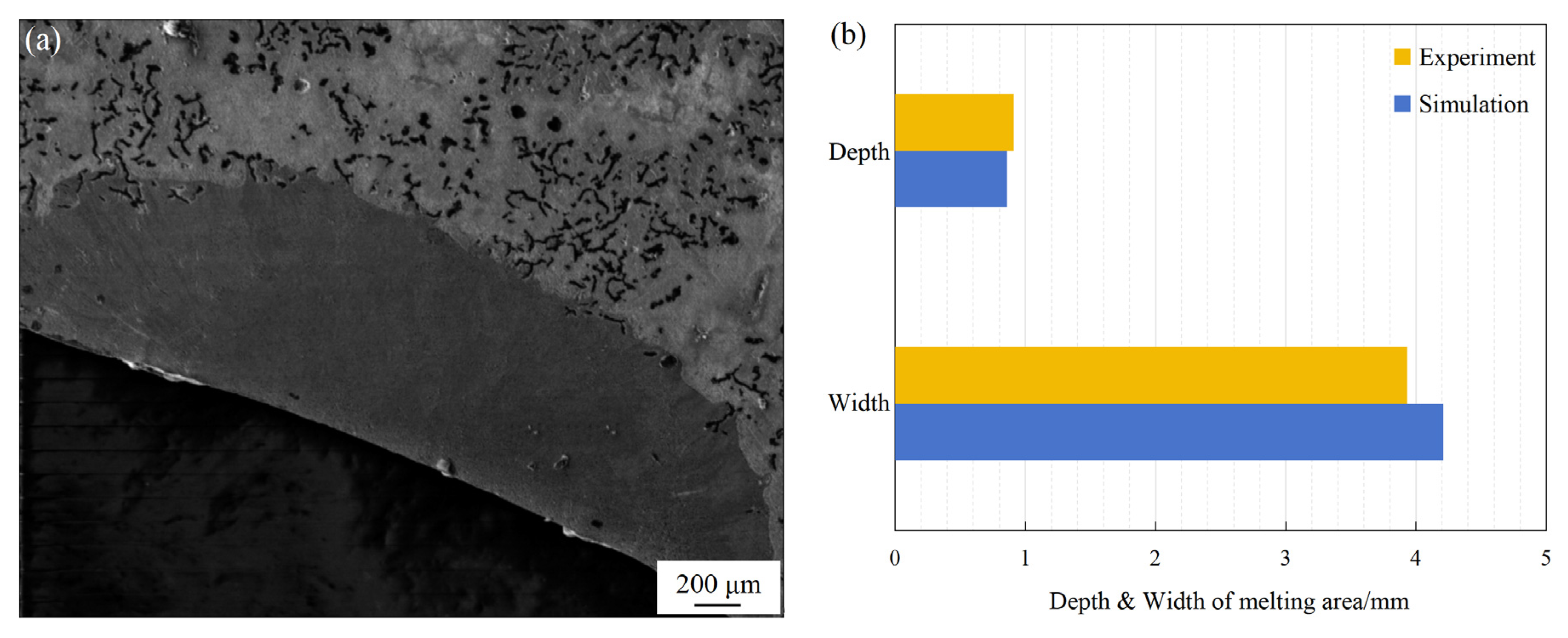
4. Validation of Simulation Results
5. Conclusions
- (1)
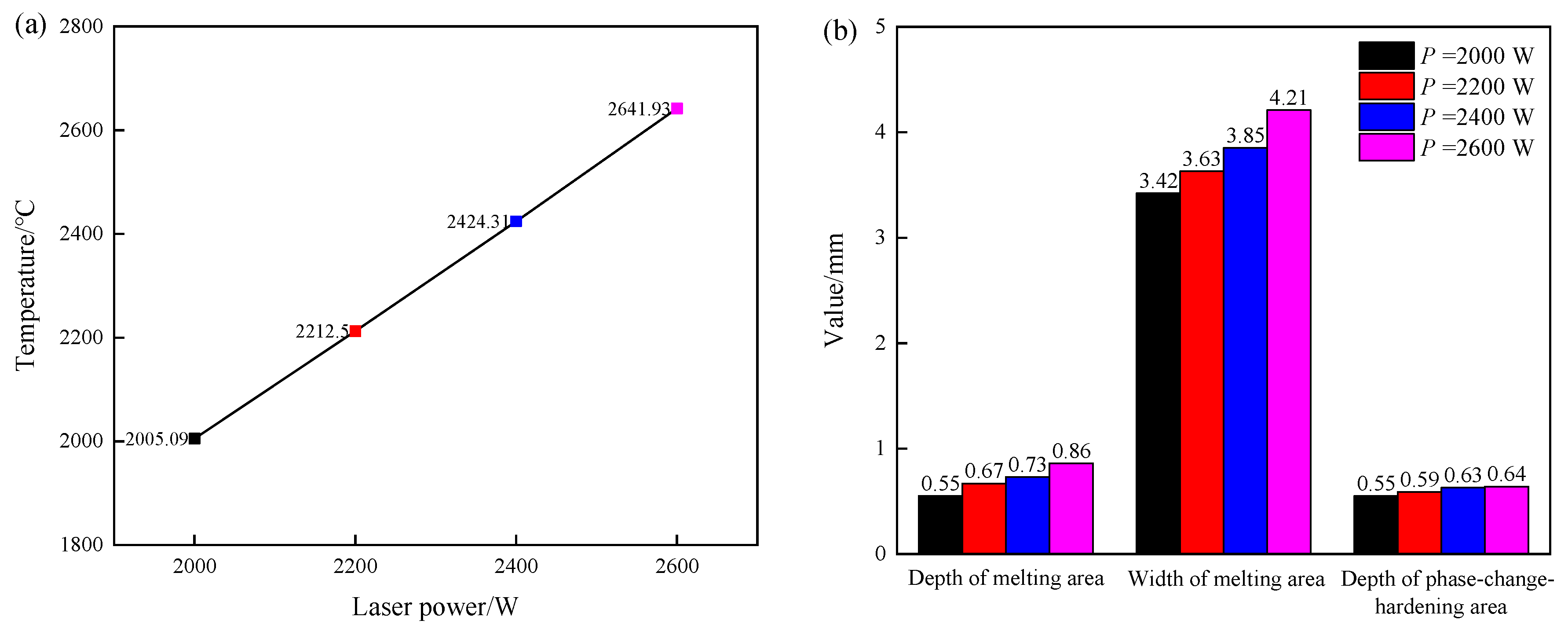
- The laser-melting process could precisely modify the valve seat cone area. Melting and phase-change-hardening areas could be obtained from the surface of the material downwards. With the increase in the laser power, the peak temperature of the molten pool increased almost linearly, and the area of the melting zone and depth of the phase-change-hardening region increased. When the laser power was increased from 2000 to 2600 W, the peak temperature of the laser-melting RuT300 valve seat increased from 2005.09 to 2641.93 °C, the depth of the melting area increased from 0.55 to 0.86 mm, the width of the melting area increased from 3.42 to 4.21 mm, and the depth of the phase-change-hardening area increased from 0.55 to 0.64 mm.
- (2)
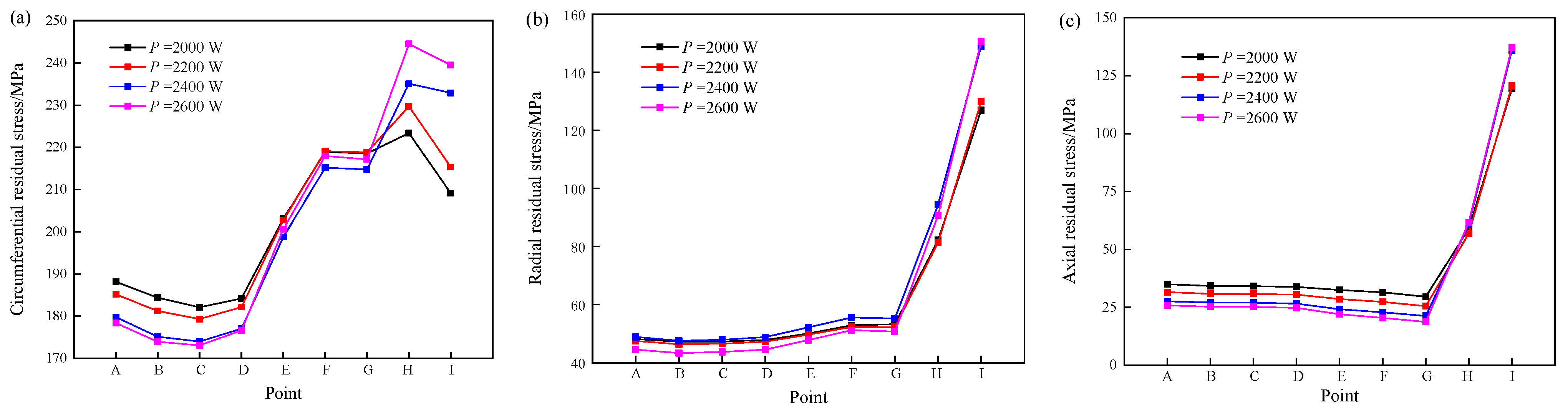
- Due to the influence of the circumferential structure constraint of the valve seat, the circumferential residual tensile stress in the melting area was much higher than in the radial and axial directions. Along the laser scanning direction, the residual stress in the melting area increased as a whole. The temperature of the laser scanning finishing area was greatly increased, resulting in a significant increase in the residual stress in this area, and the highest value of the circumferential residual stress was evident in this area.
- (3)
- The distribution of the valve seat temperature and temperature gradient competed in the contribution of residual stress. As the laser power increased, the circumferential residual stress at the front scanning moment decreased. At the end of the scan, the increase in temperature increased the circumferential residual stress with the increase in laser power. When the laser power was increased from 2000 to 2600 W, the peak circumferential residual stress increased from 224 to 246 MPa.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Pang, J.; Qiu, Y.; Liu, R.; Li, S.; Jing, G.; Xu, C.; Zhang, Z. The high-cycle fatigue fracture mechanism and fatigue strength prediction of compacted graphite iron. Int. J. Fatigue 2022, 161, 106881. [Google Scholar] [CrossRef]
- Qiu, Y.; Pang, J.; Li, S.; Zhang, M.; Zhang, Z. Influence of temperature on the low-cycle fatigue properties of compacted graphite iron. Int. J. Fatigue 2018, 117, 450–460. [Google Scholar] [CrossRef]
- Sun, F. Research on Laser Cladding Integrated Forming Technology of Compacted Graphite Iron; University of Science and Technology Beijing: Beijing, China, 2022. [Google Scholar]
- Qiu, Y.; Pang, J.; Yang, E.; Li, S.; Zhang, Z. Transition of tensile strength and damaging mechanisms of compacted graphite iron with temperature. Mater. Sci. Eng. A 2016, 677, 290–301. [Google Scholar] [CrossRef]
- Qiu, Y.; Pang, J.; Zhang, M.; Zou, C.; Li, S.; Zhang, Z. Influence of temperature on the high-cycle fatigue properties of compacted graphite iron. Int. J. Fatigue 2018, 112, 84–93. [Google Scholar] [CrossRef]
- Qiu, Y.; Pang, J.; Li, S.; Yang, E.; Fu, W.; Liang, M.; Zhang, Z. Influence of thermal exposure on microstructure evolution and tensile fracture behaviors of compacted graphite iron. Mater. Sci. Eng. A 2016, 664, 75–85. [Google Scholar] [CrossRef]
- Lang, T.; Pang, M. Influence of laser power on properties of additive Ni25 layer on valve seat surface. Trans. Mater. Heat Treat. 2022, 43, 120–127. [Google Scholar]
- Chen, Y.; Pang, J.; Li, S.; Zou, C.; Zhang, Z. Damage mechanism and fatigue strength prediction of compacted graphite iron with different microstructures. Int. J. Fatigue 2022, 164, 107126. [Google Scholar] [CrossRef]
- Liu, H.; Yu, G.; He, X.; Li, S.; Zhu, T.; Ning, W.; Zheng, C. Microstructure and mechanical properties of NiCoCrAlY coating on compacted graphite iron by laser cladding. Trans. Mater. Heat Treat. 2015, 36, 171–176. [Google Scholar]
- Pang, M.; Tan, W. Microscopic characteristic analysis and crack suppression of laser-surface remelting of vermicular-graphite cast-iron valve seats. Laser Optoelectron. Prog. 2019, 56, 211402. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H.; Zhou, X.; Zhao, J.; Fu, L.; Liu, W. Laser surface modification technology and research progress. Mater. Rep. 2018, 32, 341–344. [Google Scholar]
- Pang, M.; Tan, W. Effect of preheating temperature on residual stress field of laser melting RuT300 valve seats. Surf. Technol. 2019, 48, 296–301. [Google Scholar]
- Xu, J.; Tan, W.; Hu, Z.; Wang, S.; Zhou, J. Study on tribological properties of laser surface melting 316L stainless steel. Appl. Laser 2022, 42, 129–134. [Google Scholar]
- Qiu, A.; Chen, H.; Song, J.; Cheng, X.; Ding, H.; Zhou, G. Laser melting treatment on NiTi alloy and its biological corrosion properties. Surf. Technol. 2023, 52, 364–371. [Google Scholar]
- Wang, Z.; Hu, Y.; Pang, M. Microstructure and comprehensive properties of laser-melted stainless steel. Laser Optoelectron. Prog. 2021, 58, 1914006. [Google Scholar]
- Bukhari, S.; Husnain, N.; Siddiqui, F.; Anwar, M.; Khosa, A.; Imran, M.; Qureshi, T.; Ahmad, R. Effect of laser surface remelting on Microstructure, mechanical properties and tribological properties of metals and alloys: A review. Opt. Laser Technol. 2023, 165, 109588. [Google Scholar] [CrossRef]
- Castro, R.; Curi, E.; Inacio, L.; Rocha, A.; Pereira, M.; Silva, R.; Pereira, A. Laser remelting of WC-CoCr surface coated by HVOF: Effect on the tribological properties and energy efficiency. Surf. Coat. Technol. 2021, 427, 127841. [Google Scholar] [CrossRef]
- An, Y.; Zheng, S.; Pang, X.; Pu, J. Effect of laser remelting on copper-nickel alloy coating prepared by extreme high-speed laser cladding. J. Manuf. Process. 2023, 95, 497–507. [Google Scholar] [CrossRef]
- Temmler, A.; Pirch, N. Investigation on the mechanism of surface structure formation during laser remelting with modulated laser power on tool steel H11. Appl. Surf. Sci. 2020, 526, 146393. [Google Scholar] [CrossRef]
- Chen, X.; Ge, Y. Simulation of thermal effect of Zr65Al7.5Ni10Cu17.5 amorphous alloy by laser melting. Laer Technol. 2020, 44, 202–205. [Google Scholar]
- Ali, H.; Ghadbeigi, H.; Mumtaz, K. Effect of scanning strategies on residual stress and mechanical properties of selective laser melted Ti6Al4V. Mater. Sci. Eng. A 2018, 712, 175–187. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, W.; Ma, C. Numerical simulation of temperature field in laser surface remelting rare earth magnesium alloy and its corrosion resistance. Hot Work. Technol. 2017, 46, 143–147+154. [Google Scholar]
- Bonek, M.; Śliwa, A.; Mikuła, J. Computer simulation of the relationship between selected properties of laser remelted tool steel surface layer. Appl. Surf. Sci. 2016, 388, 174–179. [Google Scholar] [CrossRef]
- Vastola, G.; Zhang, G.; Pei, Q.; Zhang, Y. Modeling and control of remelting in high-energy beam additive manufacturing. Addit. Manuf. 2015, 7, 57–63. [Google Scholar] [CrossRef]
- Schüßler, P.; Damon, J.; Mühl, F.; Dietrich, S.; Schulze, V. Laser surface hardening: A simulative study of tempering mechanisms on hardness and residual stress. Comput. Mater. Sci. 2023, 221, 112079. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, X.; Ding, N.; Cong, J.; Sun, J.; Jia, Q.; Wang, C. Wear resistance enhancement of QT700-2 ductile iron crankshaft processed by laser hardening. Opt. Laser Technol. 2023, 164, 109519. [Google Scholar] [CrossRef]
- Evdokimov, A.; Jasiewicz, F.; Doynov, N.; Ossenbrink, R.; Michailov, V. Simulation of surface heat treatment with inclined laser beam. J. Manuf. Process. 2022, 81, 107–114. [Google Scholar] [CrossRef]
- Han, X.; Li, C.; Liu, Z.; Chen, X.; Deng, S. Analysis of residual stress distribution characteristics of laser surface hardening based on Voronoi model. Opt. Laser Technol. 2022, 156, 108613. [Google Scholar] [CrossRef]
- Xu, X. Research on Numerical Simulation and Temperature Control Technology of Laser Transformation Hardening; Shandong University: Jinan, China, 2022. [Google Scholar]
- Liverani, E.; Lutey, A.; Ascari, A.; Fortunato, A.; Tomesani, L. A complete residual stress model for laser surface hardening of complex medium carbon steel components. Surf. Coat. Technol. 2016, 302, 100–106. [Google Scholar] [CrossRef]
- Fortunato, A.; Ascari, A.; Orazi, L.; Campana, G.; Cuccolini, G. Numerical evaluation of the reflectivity coefficient in laser surface hardening simulation. Surf. Coat. Technol. 2012, 206, 3179–3185. [Google Scholar] [CrossRef]
- Tobar, M.; Álvarez, C.; Amado, J.; Ramil, A.; Saavedra, E.; Yáñez, A. Laser transformation hardening of a tool steel: Simulation-based parameter optimization and experimental results. Surf. Coat. Technol. 2006, 200, 6362–6367. [Google Scholar] [CrossRef]
- Hu, X.; Xu, Y.; Hu, Y.; Yao, J. Research on laser transformation hardening and simulation model in temperature control mode. Trans. Mater. Heat Treat. 2016, 37, 235–240. [Google Scholar]
- Sun, W.; Li, Y.; Yin, B. Effect of optimizing parameters of laser transformation hardening on 5CrNiMo steel temperature field. J. Tianjin Univ. Technol. 2012, 28, 34–38. [Google Scholar]
- Li, Y.; Li, W. Numerical simulation on welding residual stresses of X80 pipeline girth weld joint. Trans. China Weld. Inst. 2010, 31, 97–100, 104, 118. [Google Scholar]
- GB/T 26655-2011; Compacted (Vermicular) Graphite Iron Castings. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China: Beijing, China, 2012.
- Guo, G.; Ma, H.; Zhang, J. The measurement of thermophysical properties of cast iron and the relationship to its microstructure. Phys. Test. Chem. Anal. (Part A Phys. Test.) 2005, 41, 13–16. [Google Scholar]
- Feng, Z.; Cai, A.; Fan, S.; Cheng, J. Effect of temperature on mechanical properties of vermicular graphite iron. Mod. Cast Iron 2016, 36, 61–64+83. [Google Scholar]




| Parameters | Value | |||||
|---|---|---|---|---|---|---|
| Temperature/℃ | 25 | 400 | 800 (Phase transition temperature [38]) | 1200 (Melting point) | 1600 | 2000 |
| Specific heat capacity/(J·kg−1·K−1) | 465 | 645 | 871 | 938 | 888 | 880 |
| Thermal conductivity/(W·m−1·K−1) | 42.37 | 41.03 | 37.29 | 34.89 | 33.29 | 31.69 |
| Density/(kg·m−3) | 7086 | 7086 | 7086 | 7086 | 7086 | 7086 |
| Elastic modulus/GPa | 145 | 135 | 124 | 80 | 60 | 60 |
| Yield strength/MPa | 240 | 200 | 157 | 20 | 20 | 20 |
| Thermal expansion coefficient/(10−6·°C−1) | 10.6 | 12.5 | 14.5 | 15.7 | 16.1 | 16.5 |
| Poisson’s ratio | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 |
| Parameters | Value | |||
|---|---|---|---|---|
| Laser power/W | 2000 | 2200 | 2400 | 2600 |
| Laser scanning speed/(mm·s−1) | 5 | |||
| Laser spot radius/mm | 1.5 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, W.; Pang, M. Simulation Study on the Influence of a Laser Power Change on the Residual Stress of a Laser-Melting RuT300 Valve Seat. Lubricants 2023, 11, 435. https://doi.org/10.3390/lubricants11100435
Tan W, Pang M. Simulation Study on the Influence of a Laser Power Change on the Residual Stress of a Laser-Melting RuT300 Valve Seat. Lubricants. 2023; 11(10):435. https://doi.org/10.3390/lubricants11100435
Chicago/Turabian StyleTan, Wendan, and Ming Pang. 2023. "Simulation Study on the Influence of a Laser Power Change on the Residual Stress of a Laser-Melting RuT300 Valve Seat" Lubricants 11, no. 10: 435. https://doi.org/10.3390/lubricants11100435
APA StyleTan, W., & Pang, M. (2023). Simulation Study on the Influence of a Laser Power Change on the Residual Stress of a Laser-Melting RuT300 Valve Seat. Lubricants, 11(10), 435. https://doi.org/10.3390/lubricants11100435




