Change in Time of the Value of Dry and Lubricated Friction Coefficients for Surfaces Generated by Different Processing Methods
Abstract
:1. Introduction
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
- -
2. Materials and Methods
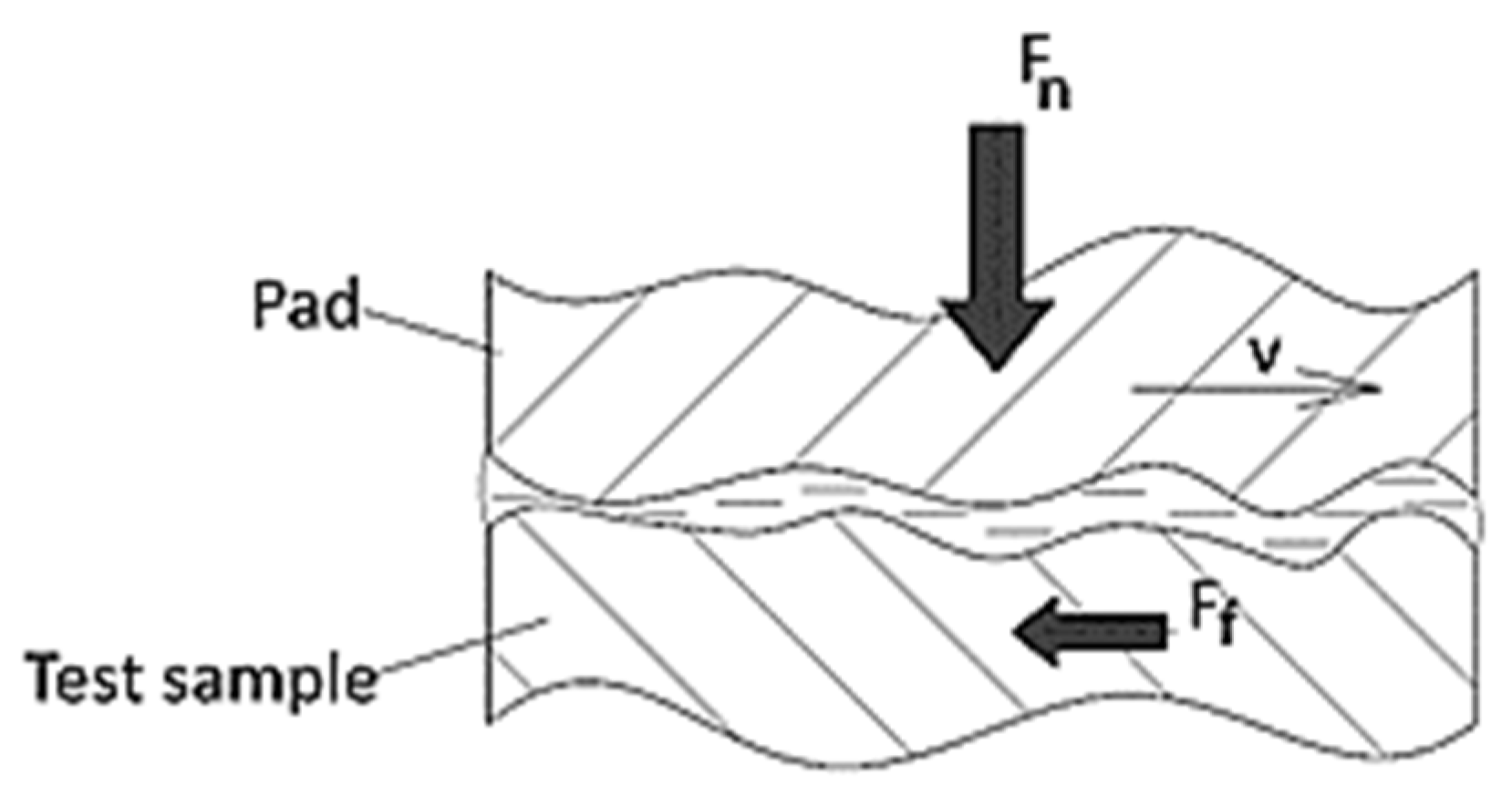
2.1. Lubricated and Dry Friction Considerations for Joints through Cylindrical Surfaces
- The nature, chemical composition, and some physical-mechanical properties of the two materials of the solid bodies (the spindle of a shaft and the bearing) that constitute the joint;
- The dimensions that characterize the two cylindrical surfaces;
- The heights and shapes of the asperities on the two surfaces;
- The presence, nature, and lubrication properties of any solid and liquid lubricants found between the two surfaces;
- The temperature at which the joint operates, both by changing some properties of the lubricants and by the expansion or contraction of the materials of the two parts in contact, thus including the possible change of the type of fit;
- The nature of the contact exerted between the surfaces (continuous and pulsating contacts), etc.
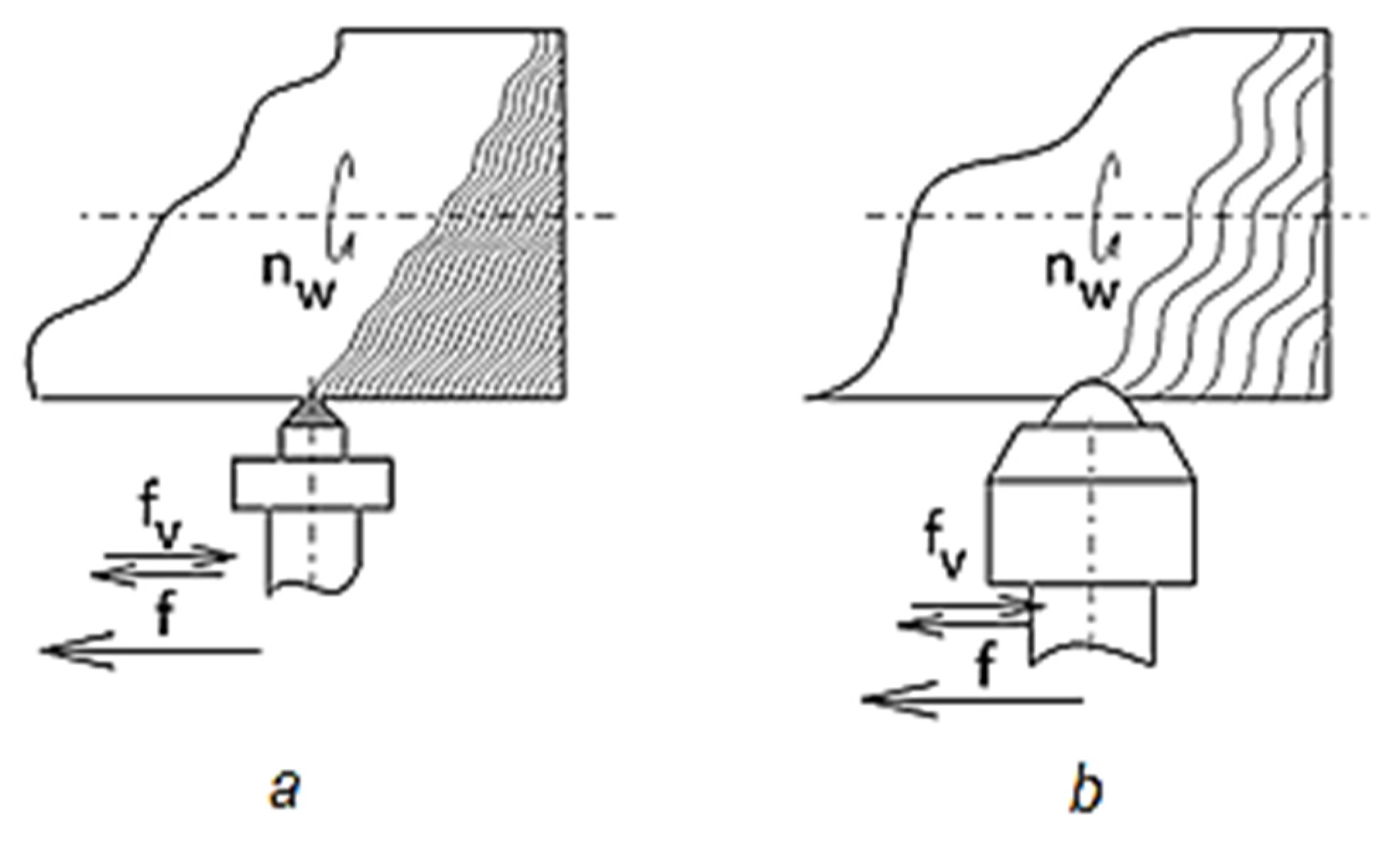
- -
- Microreliefs of the first category (I), when the generated channels do not intersect;
- -
- Microreliefs of the second category (II), when the generated channels are tangent;
- -
- Microreliefs of the third category (III), when the channels partially overlap/intersect, but with the maintenance of some areas that were not affected by the texture generation process;
- -
- Microreliefs of the fourth category (IV), when the overlapping of the channels takes place without maintaining areas of the initial cylindrical surface on which it acts through superficial plastic deformation. It is appreciated that, in this way, it is possible to reach reticular-type surfaces with a geometric appearance of hexagonal, tetragonal, and sinusoidal shapes, etc.
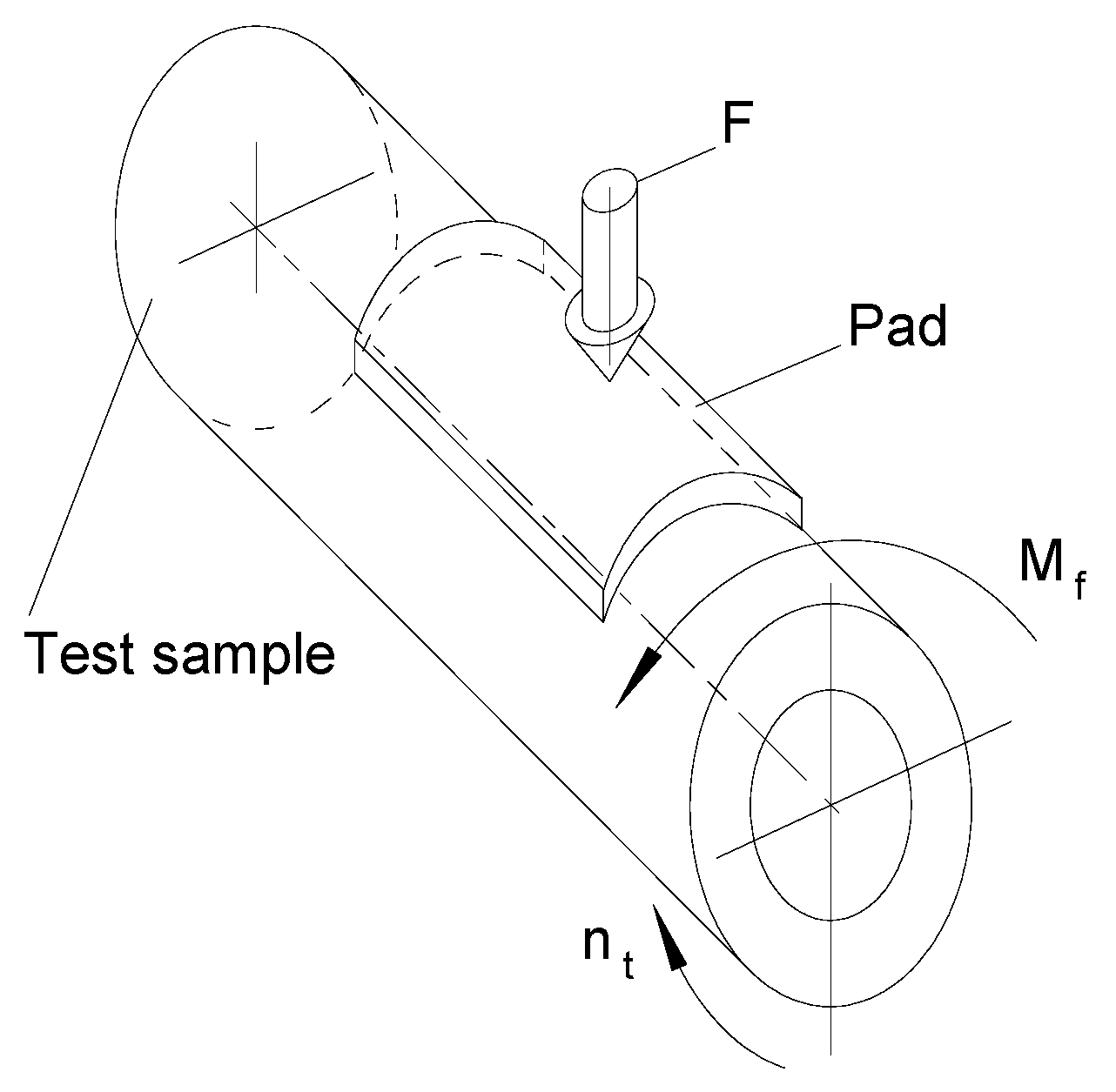
2.2. The Scheme Used for the Experimental Tests
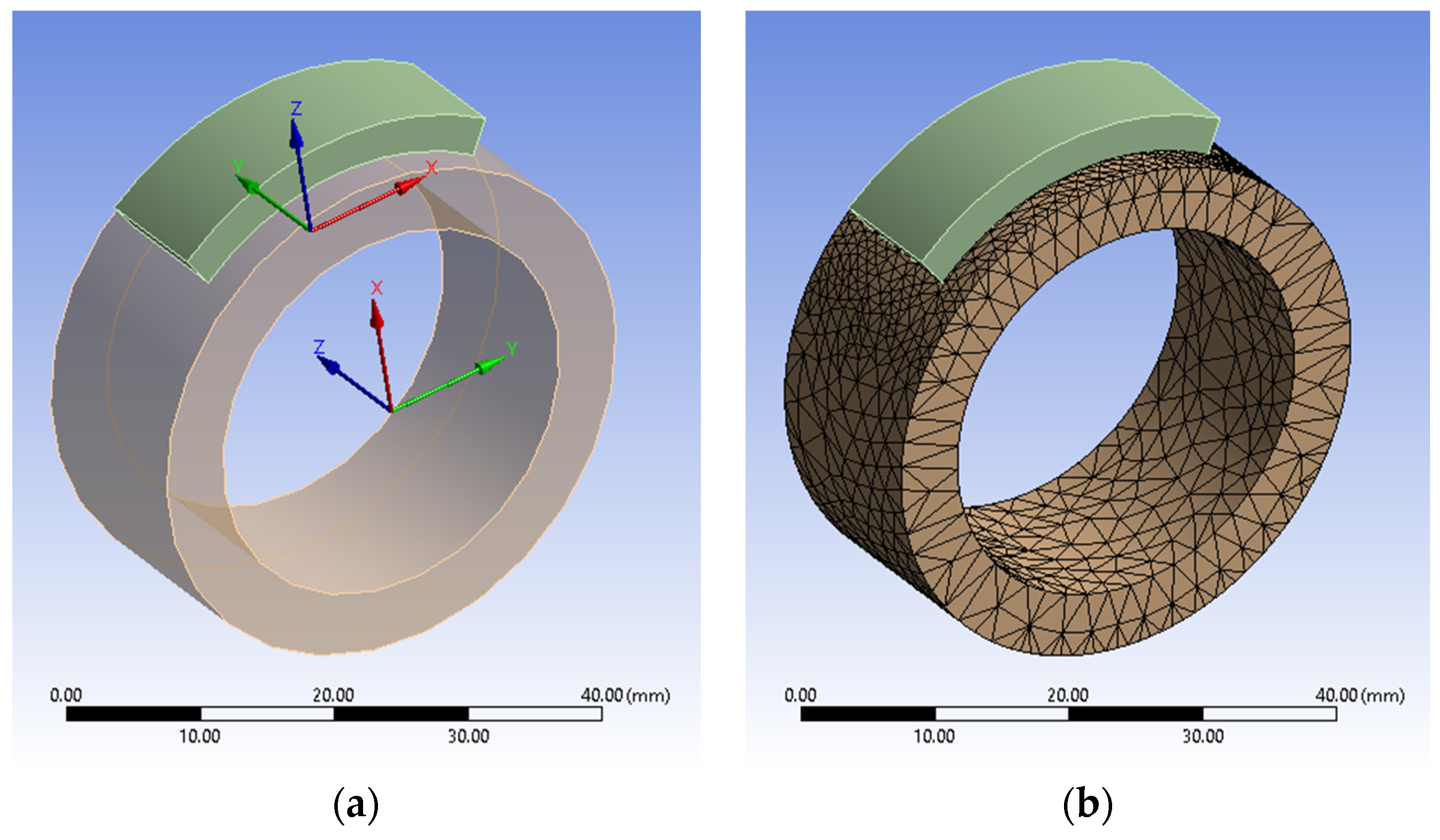
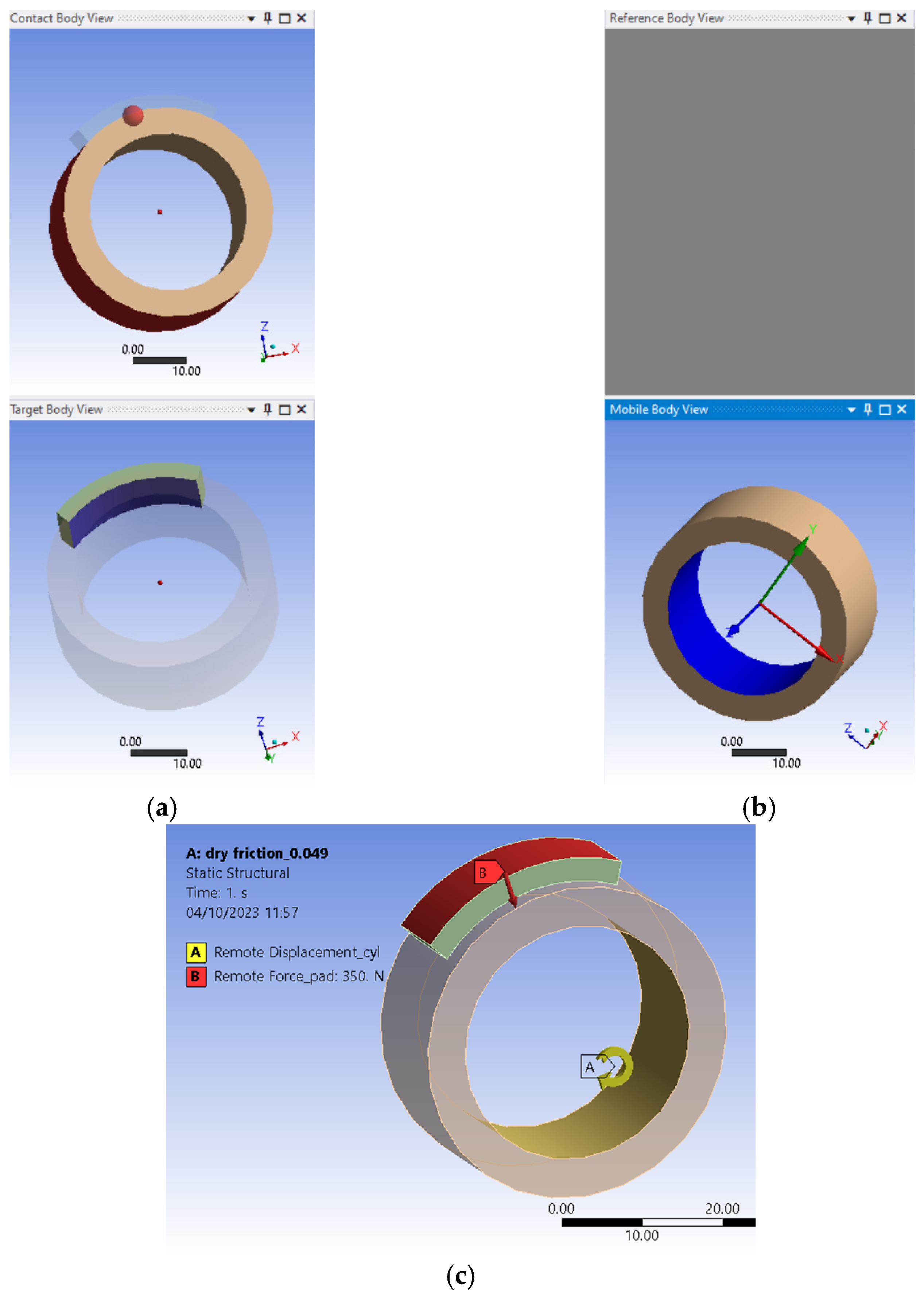
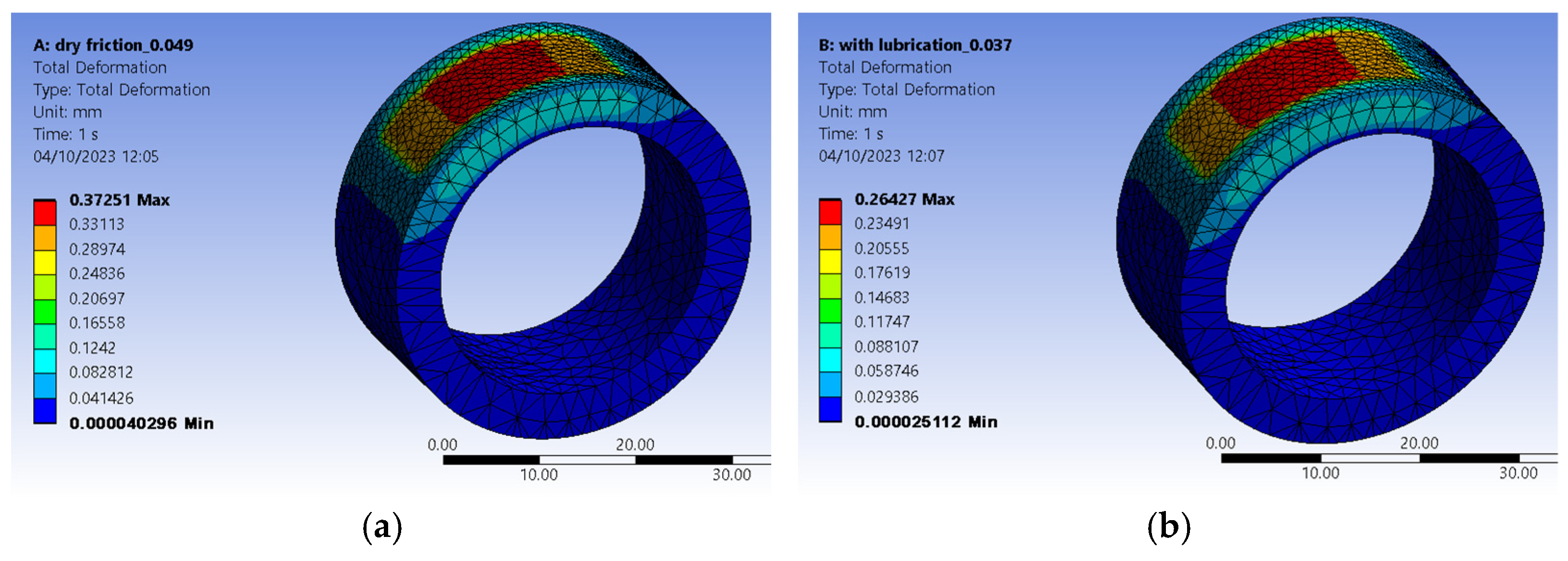
2.3. Analysis by the Finite Element Method of Some Aspects Regarding the Influence Exerted by the Character of Friction and the Final Processing of the Surface on the Magnitude of the Coefficient of Friction
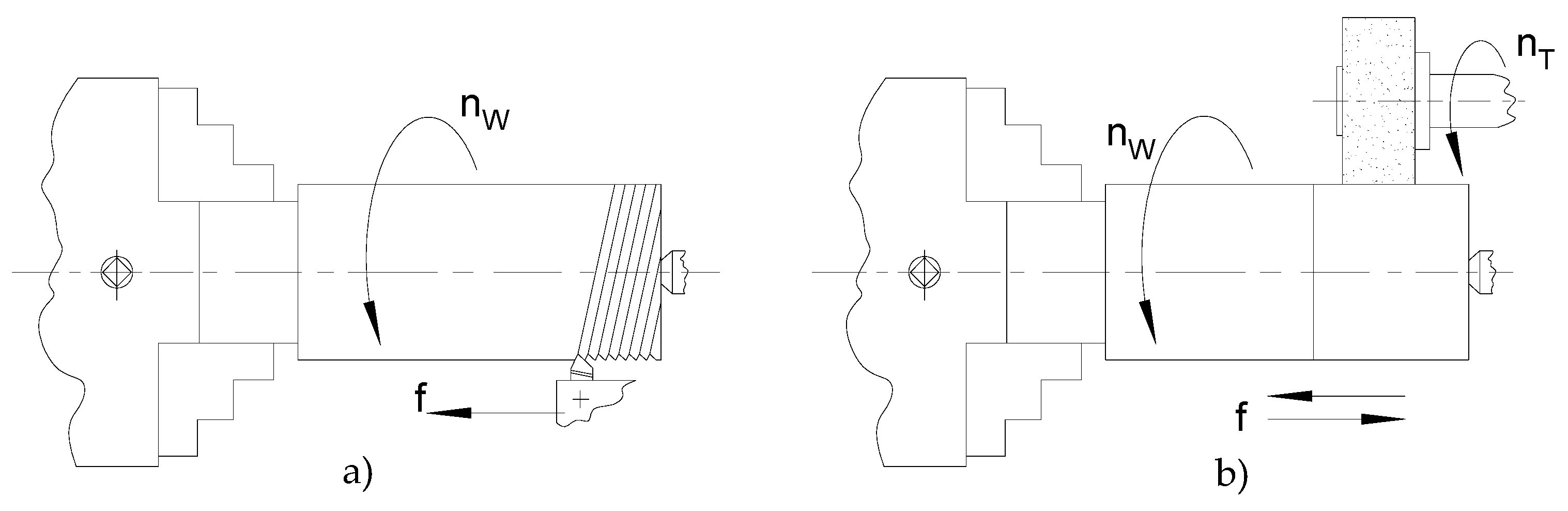
2.4. Planning and Conducting Experimental Tests
- -
- Processing method no. 1: outer cylindrical turning, which led to a value of the roughness parameter Ra = 1.69 µm;
- -
- Processing method no. 2: outer cylindrical grinding, through which a value of the roughness parameter Ra = 0.82 µm was obtained;
- -
- Processing method no. 3: ball burnishing, using a pressing force F = 350 N and a longitudinal feed rate f = 0.059 mm/rev, which led to a value of the roughness parameter Ra = 0.65 µm;
- -
- Processing method no. 4: diamond type smoothing, using a pressing force F = 100 N and a longitudinal feed rate f = 0.059 mm/rev, obtaining a value of the parameter Ra = 0.58 µm;
- -
- Processing method no. 5: ball vibroburnishing, using a longitudinal feed rate f = 0.059 mm/rev, obtaining a type IV microrelief and a value of the roughness parameter Ra = 0.1 µm;
- -
- Processing method no. 6: vibroburnishing type diamond, using a longitudinal feed rate f = 0.059 mm/rev, obtaining a type IV microrelief and a value of the roughness parameter Ra = 0.08 µm;
- -
- Processing method no. 7: ball vibroburnishing, using a longitudinal feed rate f = 0.46 mm/rev and obtaining a type III microrelief;
- -
- Processing method no. 8: diamond-type vibroburnishing, using a longitudinal feed rate f = 0.46 mm/rev and obtaining a type III microrelief;
- -
- Processing method no. 9: ball vibroburnishing, using a longitudinal feed rate f = 0.916 mm/rev and obtaining a type II microrelief;
- -
- Processing method no. 10: diamond tip vibroburnishing, using a longitudinal feed rate f = 0.916 mm/rev and obtaining a type II microrelief;
- -
- Processing method no. 11: ball vibroburnishing, using a longitudinal feed rate f = 1.5 mm/rev and obtaining a type I microrelief;
- -
- Processing method no. 12: ball vibroburnishing, using a longitudinal feed rate f = 1.5 mm/rev and obtaining a type I microrelief;
- -
- Processing method no. 13: ball vibroburnishing, using a longitudinal feed rate f = 0.264 mm/rev and obtaining a type III microrelief;
- -
- Processing method no. 14: ball vibroburnishing, using a longitudinal feed rate f = 0.416 mm/rev and obtaining a type III microrelief.
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marian, M.; Tremmel, S. Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants 2021, 9, 86. [Google Scholar] [CrossRef]
- Costa, H.L.; Schille, J.; Rosenkranz, A. Tailored Surface Textures to Increase Friction—A review. Friction 2022, 10, 1285–1304. [Google Scholar] [CrossRef]
- Li, M.; Shi, W.; Shi, J.; Wang, T.; Shi, L.; Wang, X. Regulation and Control of Wet Friction of Soft Materials Using Surface Texturing: A Review. Friction 2023, 11, 333–353. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Grützmacher, P.G.; Gachot, C.; Costa, H.L. Surface Texturing in Machine Elements—A Critical Discussion for Rolling and Sliding Contacts. Adv. Eng. Mater. 2019, 21, 1900194. [Google Scholar] [CrossRef]
- Hou, Q.; Yang, X.; Cheng, J.; Wang, S.; Duan, D.; Xiao, J.; Li, W. Optimization of Performance Parameters and Mechanism of Bionic Texture on Friction Surface. Coatings 2020, 10, 171. [Google Scholar] [CrossRef]
- Murzin, S.P.; Balyakin, V.; Liedl, G.; Melnikov, A.A.; Fürbacher, R. Improving Tribological Properties of Stainless Steel Surfaces by Femtosecond Laser Irradiation. Coatings 2020, 10, 606. [Google Scholar] [CrossRef]
- Bai, L.; Sun, J.; Zhang, P.; Khan, Z.A. Friction Behavior of a Textured Surface against Several Materials Under Dry and Lubricated Conditions. Materials 2021, 14, 5228. [Google Scholar] [CrossRef] [PubMed]
- Cuao Moreu, C.A.; Maldonado Cortés, D.; Lara Banda, M.d.R.; García Sánchez, E.O.; Zambrano Robledo, P.; Hernández Rodríguez, M.A.L. Surface, Chemical, and Tribological Characterization of an ASTM F-1537 Cobalt Alloy Modified through an Ns-Pulse Laser. Metals 2021, 11, 1719. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, W.; Pawlus, P. Selected Methods and Applications of Anti-Friction and Anti-Wear Surface Texturing. Materials 2021, 14, 3227. [Google Scholar] [CrossRef]
- Bhaumik, S.; Paleu, V.; Chowdhury, D.; Batham, A.; Sehgal, U.; Bhattacharya, B.; Ghosh, C.; Datta, S. Tribological Investigation of Textured Surfaces in Starved Lubrication Conditions. Materials 2022, 15, 8445. [Google Scholar] [CrossRef]
- Marian, M.; Almqvist, A.; Rosenkranz, A.; Fillon, M. Numerical micro-texture optimization for lubricated contacts—A critical discussion. Friction 2022, 10, 1772–1809. [Google Scholar] [CrossRef]
- Wei, Y.; Resendiz, J.; Tomkowski, R.; Liu, X. An Experimental Study of Micro-Dimpled Texture in Friction Control under Dry and Lubricated Conditions. Micromachines 2022, 13, 70. [Google Scholar] [CrossRef]
- Cheng, H.; Zhou, F.; Fei, Z. Dry Friction Properties of Friction Subsets and Angle Related to Surface Texture of Cemented Carbide by Femtosecond Laser Surface Texturing. Coatings 2023, 13, 741. [Google Scholar] [CrossRef]
- Evangelista, I.; Wencel, D.; Beguin, S.; Zhang, N.; Gilchrist, M.D. Influence of Surface Texturing on the Dry Tribological Properties of Polymers in Medical Devices. Polymers 2023, 15, 2858. [Google Scholar] [CrossRef]
- Hao, L.; Meng, Y.; Chen, C. Experimental Investigation on Effects of Surface Texturing on Lubrication of Initial Line Contacts. Lubr. Sci. 2014, 26, 363–373. Available online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/ls.1265 (accessed on 19 September 2023). [CrossRef]
- Sanguedolce, M.; Zekonyte, J.; Alfano, M. Wear of 17-4 PH Stainless Steel Patterned Surfaces Fabricated Using Selective Laser Melting. Appl. Sci. 2021, 11, 9317. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, W.; Liu, Y.; Zhang, H.; Hua, M.; Dong, G.; Tam, H.Y.; Chin, K.S. A Pocket-Textured Surface for Improving the Tribological Properties of Point Contact under Starved Lubrication. Materials 2021, 14, 1789. [Google Scholar] [CrossRef] [PubMed]
- Slavov, S.; Dimitrov, D.; Konsulova-Bakalova, M.; Vasileva, D. Impact of Ball Burnished Regular Reliefs on Fatigue Life of AISI 304 and 316L Austenitic Stainless Steels. Materials 2021, 14, 2529. [Google Scholar] [CrossRef]
- Li, C.; Yang, X.; Wang, S.; Wang, Y.; Lu, C.; Cao, J. Study on Friction and Lubrication Characteristics of Surface with Unidirectional Convergence Texture. Coatings 2019, 9, 780. [Google Scholar] [CrossRef]
- Du, F.; Li, D.; Sa, X.; Li, C.; Yu, Y.; Li, C.; Wang, J.; Wang, W. Overview of Friction and Wear Performance of Sliding Bearings. Coatings 2022, 12, 1303. [Google Scholar] [CrossRef]
- Dzyura, V.; Maruschak, P.; Slavov, S.; Dimitrov, D.; Semehen, V.; Markov, O. Evaluating Some Functional Properties of Surfaces with Partially Regular Microreliefs Formed by Ball-Burnishing. Machines 2023, 11, 633. [Google Scholar] [CrossRef]
- Ren, Y.; Huang, Z.; Wang, Y.; Zhou, Q.; Yang, T.; Li, Q.; Jia, Q.; Wang, H. Friction-Induced Rapid Amorphization in A Wear-Resistant (CoCrNi)88Mo12 Dual-Phase Medium-Entropy Alloy at Cryogenic Temperature. Compos. Part B Eng. 2023, 263, 110833. [Google Scholar] [CrossRef]
- Ye, W.; Xie, M.; Huang, Z.; Wang, H.; Zhou, Q.; Wang, L.; Chen, B.; Wang, H.; Liu, W. Microstructure and Tribological Properties of In-Situ Carbide/CoCrFeNiMn High Entropy Alloy Composites Synthesized by Flake Powder Metallurgy. Tribol. Int. 2023, 181, 108295. [Google Scholar] [CrossRef]
- Mizushima, K.; Suzuki, Y.; Tsuji, T.; Watanabe, T. Deformable fingertip with a friction reduction system based on lubricating effect for smooth operation under both dry and wet conditions. Adv. Robot. 2013, 33, 1–12. [Google Scholar] [CrossRef]
- Leszczyńska-Madej, B.; Madej, M.; Hrabia-Wiśnios, J. Effect of Chemical Composition on the Microstructure and Tribological Properties of Sn-Based Alloys. J. Mater. Eng. Perform. 2019, 28, 4065–4073. [Google Scholar] [CrossRef]
- Zabala, A.; Galdos, L.; Childs, C.; Llavori, I.; Aginagalde, A.; Mendiguren, J.; Saenz de Argandoña, E. The Interaction between the Sheet/Tool Surface Texture and the Friction/Galling Behaviour on Aluminium Deep Drawing Operations. Metals 2021, 11, 979. [Google Scholar] [CrossRef]
- Söderfjäll, M.; Gachot, C. Friction Reduction by Dimple Type Textured Cylinder Liners—An Experimental Investigation. Materials 2023, 16, 665. [Google Scholar] [CrossRef]
- Sun, J.; Bai, L.; Guo, F.; Khan, Z.A. Experimental Study on the Effect of Micro-Texture on EHL Point-Contact Film Thickness Subject to Sliding Conditions. Materials 2022, 15, 7926. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Bie, W.; Zhang, S.; Liu, T. Theoretical and Experimental Study of Friction Characteristics of Textured Journal Bearing. Micromachines 2023, 14, 577. [Google Scholar] [CrossRef] [PubMed]
- Conradi, M.; Drnovšek, A.; Gregorčič, P. Wettability and Friction Control of a Stainless Steel Surface by Combining Nanosecond Laser Texturing and Adsorption of Superhydrophobic Nanosilica Particles. Sci. Rep. 2018, 8, 7457. [Google Scholar] [CrossRef]
- Murzin, S.P.; Balyakin, V.B.; Gachot, C.; Fomchenkov, S.A.; Blokhin, M.V.; Kazanskiy, N.L. Ultraviolet Nanosecond Laser Treatment to Reduce the Friction Coefficient of Silicon Carbide Ceramics. Appl. Sci. 2021, 11, 11906. [Google Scholar] [CrossRef]
- Moldovan, E.R.; Concheso Doria, C.; Ocaña, J.L.; Baltes, L.S.; Stanciu, E.M.; Croitoru, C.; Pascu, A.; Roata, I.C.; Tierean, M.H. Wettability and Surface Roughness Analysis of Laser Surface Texturing of AISI 430 Stainless Steel. Materials 2022, 15, 2955. [Google Scholar] [CrossRef] [PubMed]
- Capilla-González, G.; Martínez-Ramírez, I.; Díaz-Infante, D.; Hernandez-Rodríguez, E.; Alcántar-Camarena, V. Effect of the Ball Burnishing on the Surface Quality and Mechanical Properties of a TRIP Steel Sheet. Int. J. Adv. Manuf. Technol. 2021, 116, 3953–3964. [Google Scholar] [CrossRef]
- Skoczylas, A.; Zaleski, K.; Matuszak, J.; Ciecieląg, K.; Zaleski, R.; Gorgol, M. Influence of Slide Burnishing Parameters on the Surface Layer Properties of Stainless Steel and Mean Positron Lifetime. Materials 2022, 15, 8131. [Google Scholar] [CrossRef]
- Grützmacher, P. Controlling Friction by Multi-Scale Surface Patterning inside and outside the Contact Zone. Ph.D. Thesis, Universitat des Saarlandes, Saarbrucken, Germany, 2019. Available online: https://publikationen.sulb.uni-saarland.de/handle/20.500.11880/28283 (accessed on 19 September 2023).
- Gorohov, V.A. Part Processing by Plastic Deformation; Publishing House Tehnika: Kiev, Ukraine, 1978. [Google Scholar]
- Odintsov, L.G. Better Wear-Resistance of Hydraulic Unit Parts by Vibratory Burnishing. Russ. Eng. J. 1979, 59, 22–24. [Google Scholar]
- Shneider, G. Performance Properties of Parts with Regular Microrelief; Publishing house Mashinostroenie: Leningrad, Russia, 1982. (In Russian) [Google Scholar]
- Berce, P.; Roș, O. Experimental Researches Concerning the Vibroburnishing of the External Cylindrical Surfaces. Mach. Manuf. 1994, 1–2, 86–89. (In Romanian) [Google Scholar]
- Lee, A. In Our Element: What Value for Coefficient of Friction Should I Use in My Calculations. Available online: https://materion.com/about/new-at-materion/in-our-element-what-value-for-coefficient-of-friction-should-i-use-in-my-calculations (accessed on 18 August 2023).
- Nagîț, G.; Slatineanu, L.; Dodun, O.; Mihalache, A.M.; Rîpanu, M.I. Influence of Some Microchanges Generated by Different Processing Methods on Selected Tribological Characteristics. Micromachines 2022, 13, 29. [Google Scholar] [CrossRef] [PubMed]
- Borawski, A. Impact of Operating Time on Selected Tribological Properties of the Friction Material in the Brake Pads of Passenger Cars. Materials 2021, 14, 884. [Google Scholar] [CrossRef] [PubMed]
- Nagîţ, G.; Slătineanu, L.; Dodun, O.; Rîpanu, M.I.; Mihalache, A.M. Surface Layer Microhardness and Roughness after Applying a Vibroburnishing Process. J. Mater. Res. Technol. 2019, 8, 4333–4346. [Google Scholar] [CrossRef]
- Nagîţ, G.; Slătineanu, L.; Merticaru, V.; Rîpanu, M.I.; Mihalache, A.M.; Tăbăcaru, L.; Boca, M. Analysis of a Device for Texturing by Burnishing Using Principles from Axiomatic Design. In Proceedings of the 11th International Conference on Axiomatic Design (ICAD 2017), Iasi, Romania, 13–15 September 2017; Volume 127, p. 01021. [Google Scholar] [CrossRef]
- Nagîț, G.; Braha, V.; Slatineanu, L. Vibration Rolling Device. Romanian Patent 116954, 10 January 1996. Available online: https://worldwide.espacenet.com/patent/search/family/064360902/publication/RO116954B1?q=Nag%C3%AE%C5%A3 (accessed on 20 October 2021).
- Wen, Q.; Liu, M.; Zhang, Z.; Sun, Y. Experimental Investigation into the Friction Coefficient of Ball-on-Disc in Dry Sliding Contact Considering the Effects of Surface Roughness, Low Rotation Speed, and Light Normal Load. Lubricants 2022, 10, 256. [Google Scholar] [CrossRef]
- Hansen, J. Elasto-Hydrodynamic Film Formation in Heavily Loaded Rolling-Sliding Contacts Influence of Surface Topography on the Transition between Lubrication Regimes. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2021. Available online: https://www.diva-portal.org/smash/get/diva2:1527353/FULLTEXT01.pdf (accessed on 19 September 2023).
- Hansen, J.; Björling, M.; Larsson, R. Topography Transformations Due to Running-In of Rolling-Sliding Non-Conformal Contacts. Tribol. Int. 2020, 144, 106126. [Google Scholar] [CrossRef]
- Chou, C.C.; Lin, J.F. Tribological Effects of Roughness and Running-In on Oil-Lubricated Line Contacts. Proc. Inst. Mech. Eng. J J. Eng. Tribol. 1997, 211, 209–222. [Google Scholar] [CrossRef]
- Sakhamuri, M.S.D.; Harvey, T.J.; Vierneusel, B.; Wood, R.J.K. Wear Induced Changes in Surface Topography During Running-In of Rolling-Sliding Contacts. Wear 2023, 522, 204685. [Google Scholar] [CrossRef]


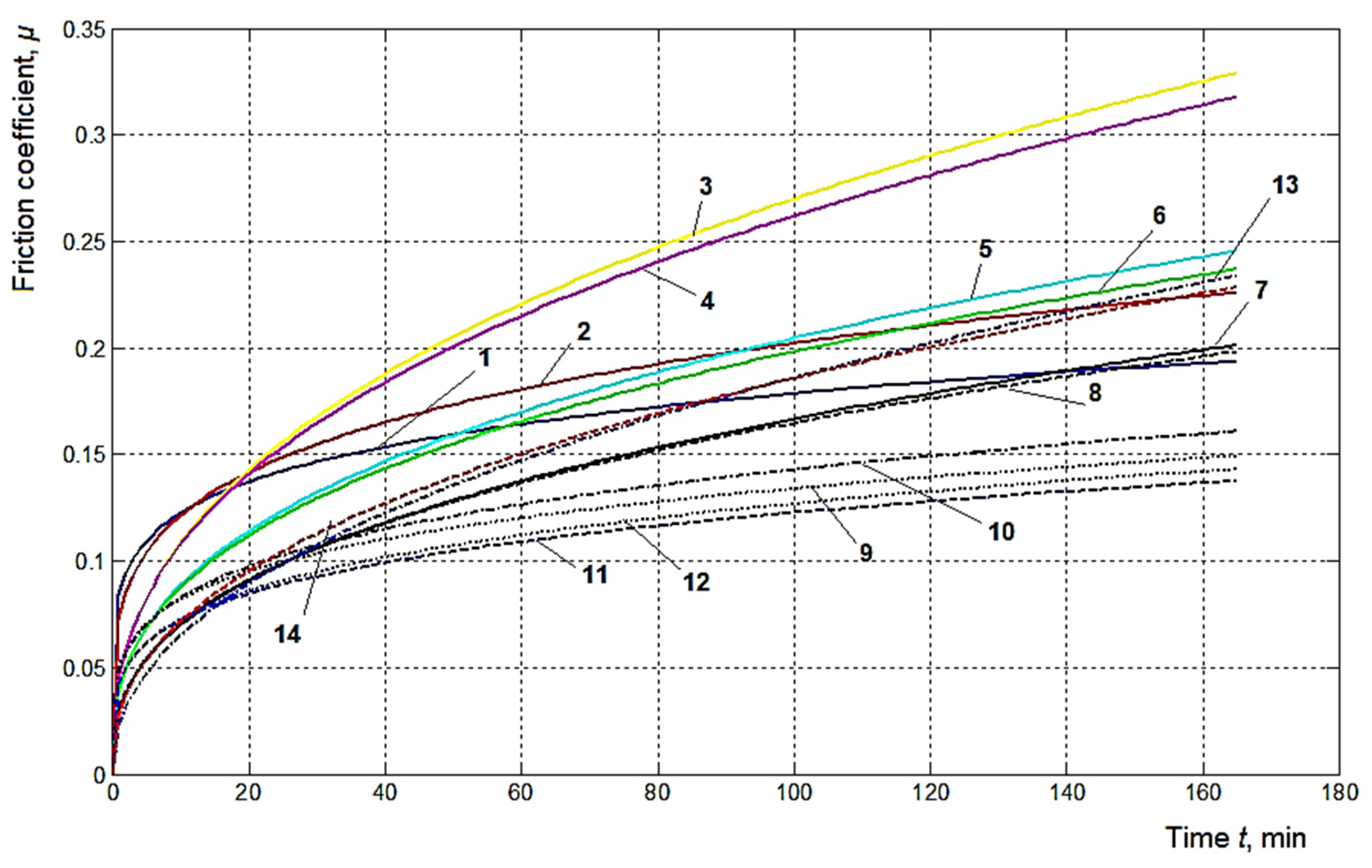
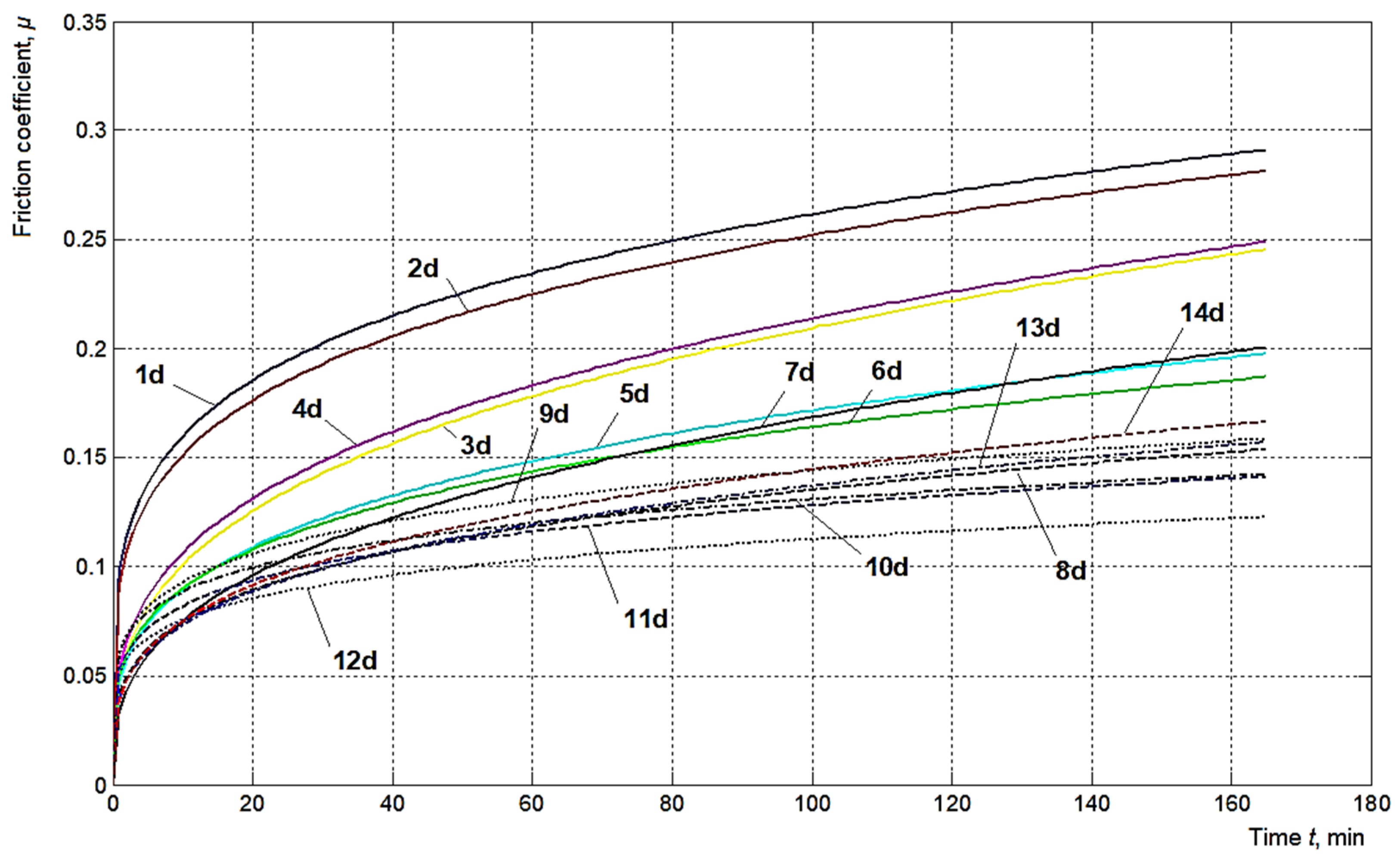
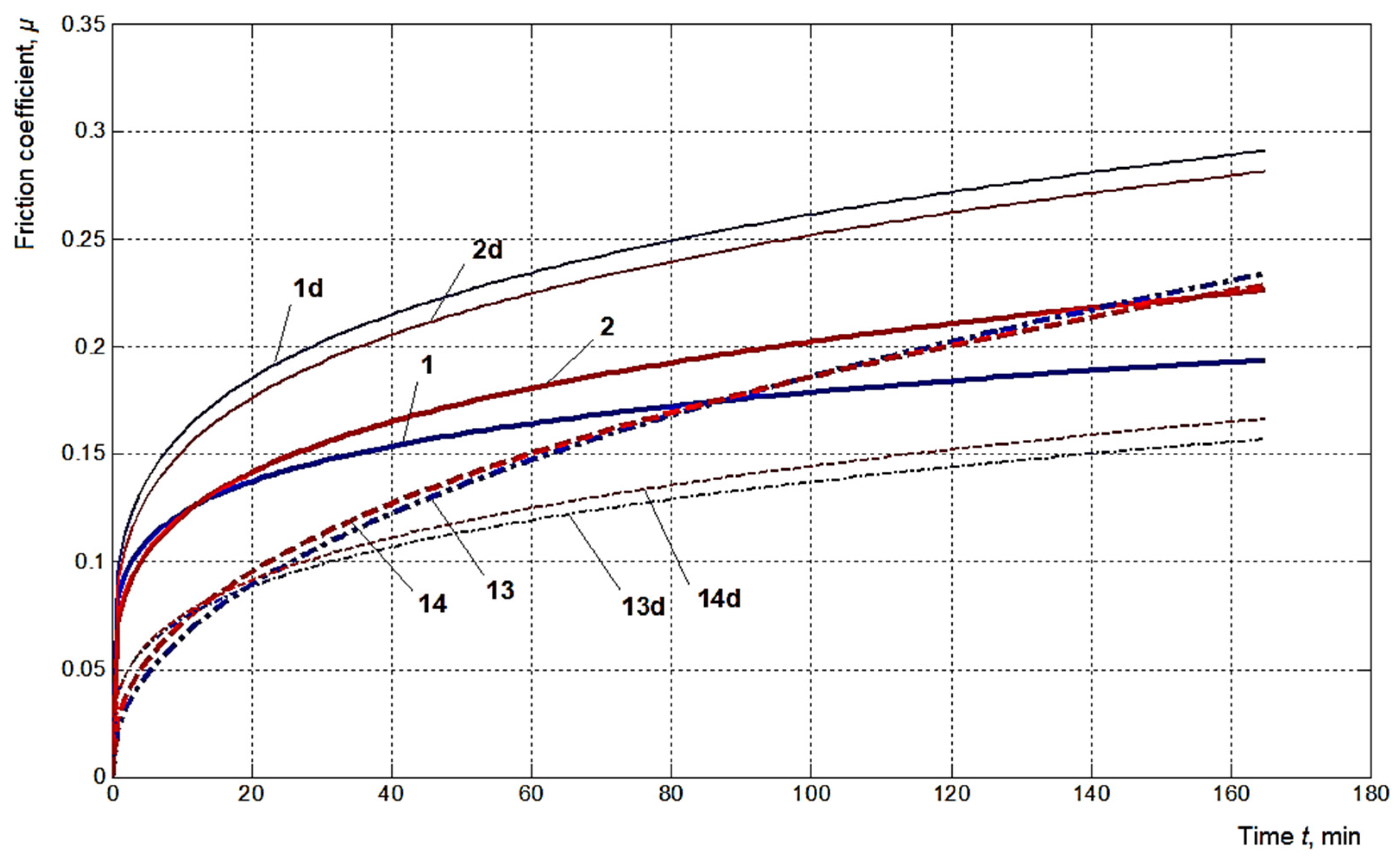
| Test Duration, t, min | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | Final Value/Initial Value Ratio | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The Number of Revolutions Corresponding to a Certain Duration of the Test, in Thousands | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | ||
| Final processing method no. | 1 (turning) | 0.10 | 0.11 | 0.122 | 0.13 | 0.138 | 0.144 | 0.15 | 0.155 | 0.158 | 0.16 | 0.163 | 0.164 | 1.64 |
| 2 (grinding) | 0.092 | 0.104 | 0.113 | 0.123 | 0.131 | 0.136 | 0.141 | 0.146 | 0.149 | 0.152 | 0.153 | 0.155 | 1.684 | |
| 3 (burnishing with ball) | 0.055 | 0.053 | 0.064 | 0.073 | 0.081 | 0.087 | 0.092 | 0.096 | 0.101 | 0.104 | 0.109 | 0.100 | 1.818 | |
| 4 (diamond smoothing) | 0.052 | 0.064 | 0.073 | 0.081 | 0.089 | 0.093 | 0.098 | 0.101 | 0.104 | 0.105 | 0.107 | 0.107 | 2.057 | |
| 5 (ball burnishing) | 0.046 | 0.055 | 0.064 | 0.071 | 0.075 | 0.080 | 0.084 | 0.086 | 0.083 | 0.089 | 0.091 | 0.091 | 1.978 | |
| 6 (diamond tip burnishing) | 0.049 | 0.058 | 0.066 | 0.073 | 0.075 | 0.078 | 0.083 | 0.086 | 0.089 | 0.091 | 0.091 | 0.091 | 1.857 | |
| 7 (ball vibroburnishing) | 0.038 | 0.046 | 0.052 | 0.06 | 0.063 | 0.067 | 0.069 | 0.070 | 0.072 | 0.072 | 0.072 | 0.072 | 1.894 | |
| 8 (diamond tip vibroburnishing) | 0.04 | 0.047 | 0.055 | 0.061 | 0.066 | 0.069 | 0.071 | 0.072 | 0.073 | 0.073 | 0.073 | 0.073 | 1.825 | |
| 9 (ball vibroburnishing) | 0.058 | 0.067 | 0.075 | 0.08 | 0.084 | 0.086 | 0.089 | 0.090 | 0.091 | 0.092 | 0.092 | 0.092 | 1.586 | |
| 10 (diamond tip vibroburnshing) | 0.056 | 0.069 | 0.074 | 0.078 | 0.081 | 0.083 | 0.085 | 0.086 | 0.087 | 0.087 | 0.087 | 0.087 | 1.553 | |
| 11 (ball vibroburnishing) | 0.051 | 0.058 | 0.066 | 0.071 | 0.073 | 0.076 | 0.077 | 0.08 | 0.081 | 0.081 | 0.081 | 0.081 | 1.588 | |
| 12 (diamond tip vibroburnishing) | 0.049 | 0.057 | 0.063 | 0.066 | 0.069 | 0.071 | 0.072 | 0.074 | 0.075 | 0.075 | 0.075 | 0.075 | 1.530 | |
| 13 (ball vibroburnishing) | 0.031 | 0.041 | 0.051 | 0.058 | 0.064 | 0.069 | 0.071 | 0.072 | 0.072 | 0.072 | 0.072 | 0.072 | 2.322 | |
| 14 (ball vibroburnishing) | 0.035 | 0.047 | 0.056 | 0.063 | 0.066 | 0.069 | 0.071 | 0.072 | 0.072 | 0.072 | 0.072 | 0.072 | 2.057 | |
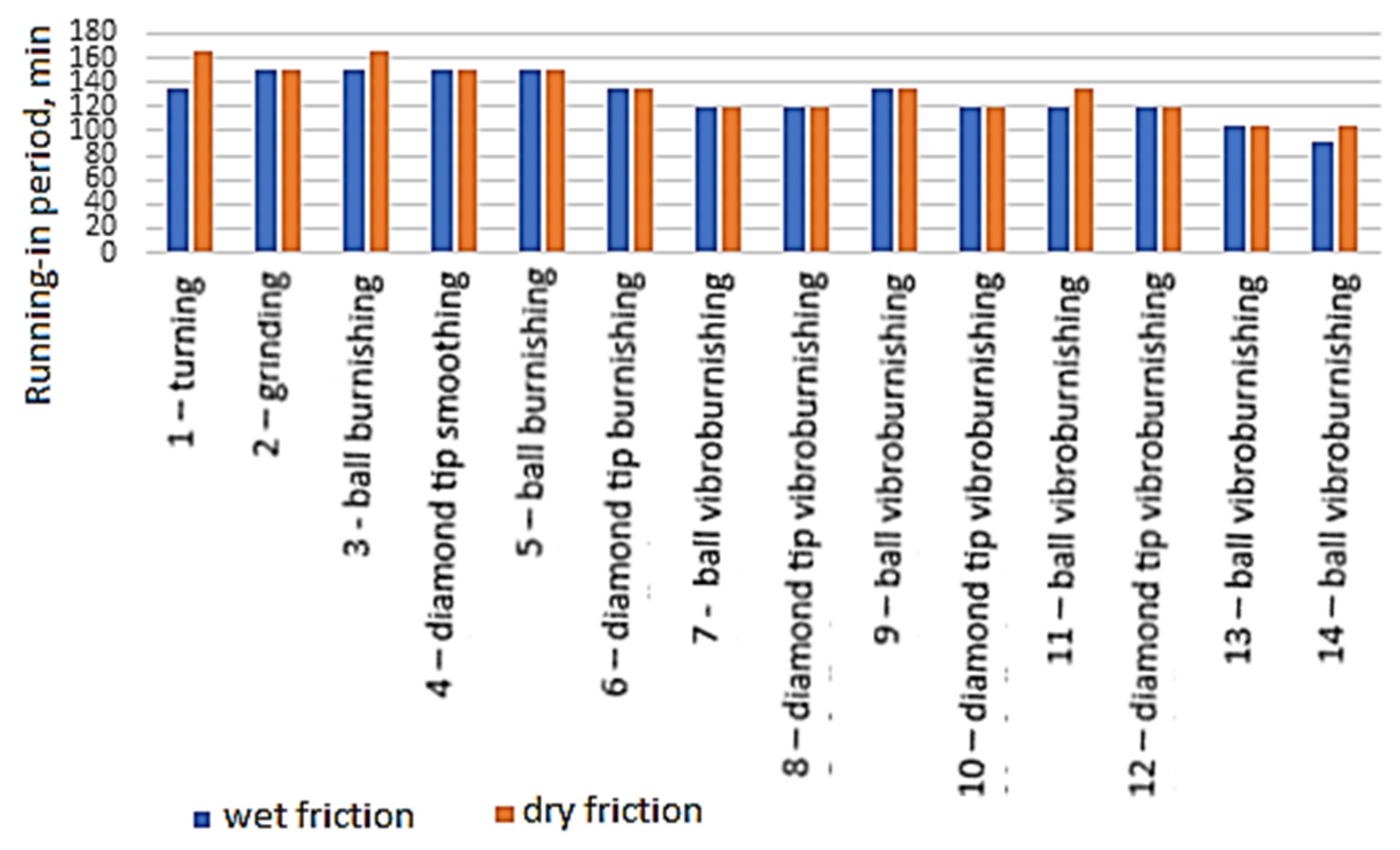
| Test Duration, t, min | 0 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | Final Value/Initial Value Ratio | Estimated Duration of the Running-In Period, Min | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The Number of Revolutions Corresponding to a Certain Duration of the Test, in Thousands | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | |||
| Final processing method no. | 1 (turning) | 0.086 | 0.093 | 0.1 | 0.106 | 0.109 | 0.111 | 0.112 | 0.117 | 0.122 | 0.126 | 0.126 | 0.128 | 1.488 | 135 |
| 2 (grinding) | 0.078 | 0.083 | 0.088 | 0.096 | 0.101 | 0.108 | 0.111 | 0.115 | 0.12 | 0.125 | 0.128 | 0.128 | 1.641 | 150 | |
| 3 (burnishing with ball) | 0.043 | 0.056 | 0.067 | 0.076 | 0.084 | 0.092 | 0.098 | 0.103 | 0.106 | 0.108 | 0.109 | 0.109 | 2.534 | 150 | |
| 4 (diamond smoothing) | 0.042 | 0.055 | 0.076 | 0.077 | 0.084 | 0.091 | 0.096 | 0.102 | 0.104 | 0.106 | 0.108 | 0.108 | 2.571 | 150 | |
| 5 (ball burnishing) | 0.037 | 0.048 | 0.058 | 0.065 | 0.072 | 0.076 | 0.082 | 0.084 | 0.086 | 0.087 | 0.088 | 0.088 | 2.378 | 150 | |
| 6 (diamond tip burnishing) | 0.037 | 0.048 | 0.059 | 0.067 | 0.07 | 0.075 | 0.079 | 0.083 | 0.086 | 0.087 | 0.087 | 0.087 | 2.351 | 135 | |
| 7 (ball vibroburnishing) | 0.028 | 0.037 | 0.044 | 0.052 | 0.058 | 0.062 | 0.066 | 0.067 | 0.068 | 0.068 | 0.068 | 0.068 | 2.428 | 120 | |
| 8 (diamond tip vibroburnishing) | 0.028 | 0.038 | 0.046 | 0.054 | 0.059 | 0.064 | 0.066 | 0.067 | 0.068 | 0.068 | 0.068 | 0.068 | 2.428 | 120 | |
| 9 (ball vibroburnishing) | 0.046 | 0.058 | 0.066 | 0.072 | 0.075 | 0.077 | 0.078 | 0.078 | 0.079 | 0.080 | 0.080 | 0.080 | 1.739 | 135 | |
| 10 (diamond tip vibroburnshing) | 0.044 | 0.055 | 0.065 | 0.072 | 0.075 | 0.078 | 0.079 | 0.079 | 0.080 | 0.080 | 0.080 | 0.080 | 1.818 | 120 | |
| 11 (ball vibroburnishing) | 0.039 | 0.049 | 0.057 | 0.063 | 0.066 | 0.067 | 0.069 | 0.069 | 0.070 | 0.070 | 0.070 | 0.070 | 1.794 | 120 | |
| 12 (diamond tip vibroburnishing) | 0.039 | 0.048 | 0.057 | 0.062 | 0.065 | 0.068 | 0.069 | 0.070 | 0.071 | 0.071 | 0.071 | 0.071 | 1.820 | 120 | |
| 13 (ball vibroburnishing) | 0.02 | 0.03 | 0.039 | 0.047 | 0.053 | 0.058 | 0.061 | 0.061 | 0.061 | 0.061 | 0.061 | 0.061 | 3.05 | 105 | |
| 14 (ball vibroburnishing) | 0.024 | 0.035 | 0.046 | 0.055 | 0.061 | 0.066 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 0.067 | 2.791 | 90 | |
| The Final Processing Method Applied to the Surface No.: | Empirical Mathematical Models for the Time Evolution of the Magnitude of the Friction Coefficient µ | |
|---|---|---|
| Lubricated Friction | Dry Friction | |
| 1 (turning) | µ = 0.084t0.164 | µ = 0.0976t0.214 |
| 2 (grinding) | µ = 0.0728t0.222 | µ = 0.0906t0.222 |
| 3 (burnishing with ball) | µ = 0.0436t0.396 | µ = 0.0484t0.318 |
| 4 (diamond tip smoothing) | µ = 0.0443t0.386 | µ = 0.0527t0.304 |
| 5 (ball burnishing) | µ = 0.0383t0.364 | µ = 0.0466t0.283 |
| 6 (diamond tip burnishing) | µ = 0.0387t0.355 | µ = 0.0493t0.261 |
| 7 (ball vibroburnishing) | µ = 0.0294t0.377 | µ = 0.0336t0.350 |
| 8 (diamond tip vibroburnishing) | µ = 0.0303t0.368 | µ = 0.0412t0.258 |
| 9 (ball vibroburnishing) | µ = 0.0501t0.214 | µ = 0.0598t0.191 |
| 10 (diamond tip vibroburnishing) | µ = 0.0478t0.238 | µ = 0.0598t0.17 |
| 11 (ball vibroburnishing) | µ = 0.0424t0.231 | µ = 0.0522t0.195 |
| 12 (diamond tip vibroburnishing) | µ = 0.0417t0.242 | µ = 0.0508t0.173 |
| 13 (ball vibroburnishing) | µ = 0.0227t0.457 | µ = 0.0392t0.272 |
| 14 (ball vibroburnishing) | µ = 0.0275t0.415 | µ = 0.0389t0.285 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagîț, G.; Mihalache, A.M.; Dodun, O.; Hrițuc, A.; Slătineanu, L.; Merticaru, V. Change in Time of the Value of Dry and Lubricated Friction Coefficients for Surfaces Generated by Different Processing Methods. Lubricants 2023, 11, 436. https://doi.org/10.3390/lubricants11100436
Nagîț G, Mihalache AM, Dodun O, Hrițuc A, Slătineanu L, Merticaru V. Change in Time of the Value of Dry and Lubricated Friction Coefficients for Surfaces Generated by Different Processing Methods. Lubricants. 2023; 11(10):436. https://doi.org/10.3390/lubricants11100436
Chicago/Turabian StyleNagîț, Gheorghe, Andrei Marius Mihalache, Oana Dodun, Adelina Hrițuc, Laurențiu Slătineanu, and Vasile Merticaru. 2023. "Change in Time of the Value of Dry and Lubricated Friction Coefficients for Surfaces Generated by Different Processing Methods" Lubricants 11, no. 10: 436. https://doi.org/10.3390/lubricants11100436
APA StyleNagîț, G., Mihalache, A. M., Dodun, O., Hrițuc, A., Slătineanu, L., & Merticaru, V. (2023). Change in Time of the Value of Dry and Lubricated Friction Coefficients for Surfaces Generated by Different Processing Methods. Lubricants, 11(10), 436. https://doi.org/10.3390/lubricants11100436







