Influence of Nozzle Layouts on the Heat-Flow Coupled Characteristics for Oil-Jet Lubricated Spur Gears
Abstract
1. Introduction
2. Analytical Model
2.1. Kinematics Analysis
2.2. Elastohydrodynamics
2.3. Friction Coefficient and Heat Generation
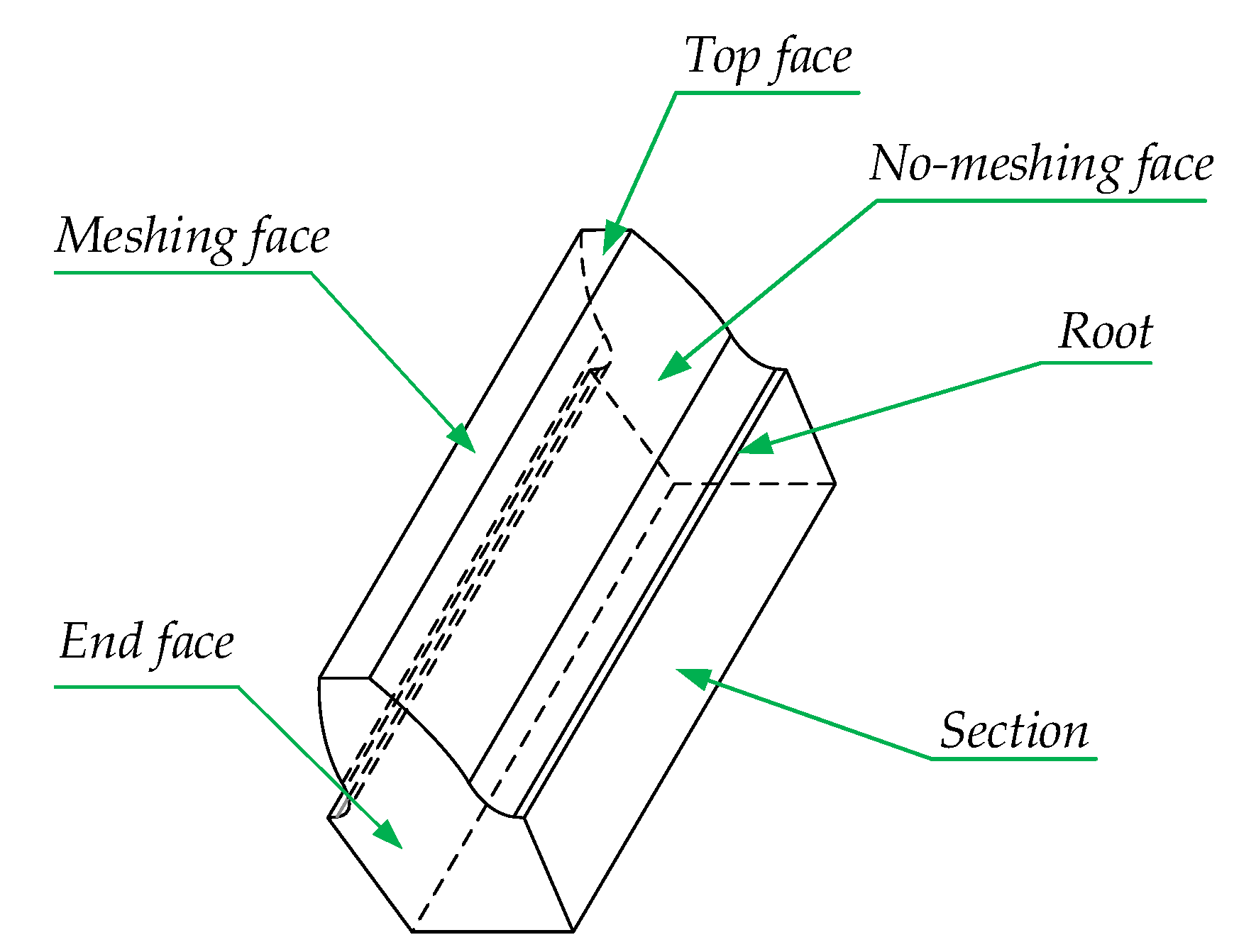
2.4. Heat Exchange
- (1)
- The meshing face
- (2)
- The end faces
- (3)
- Other faces
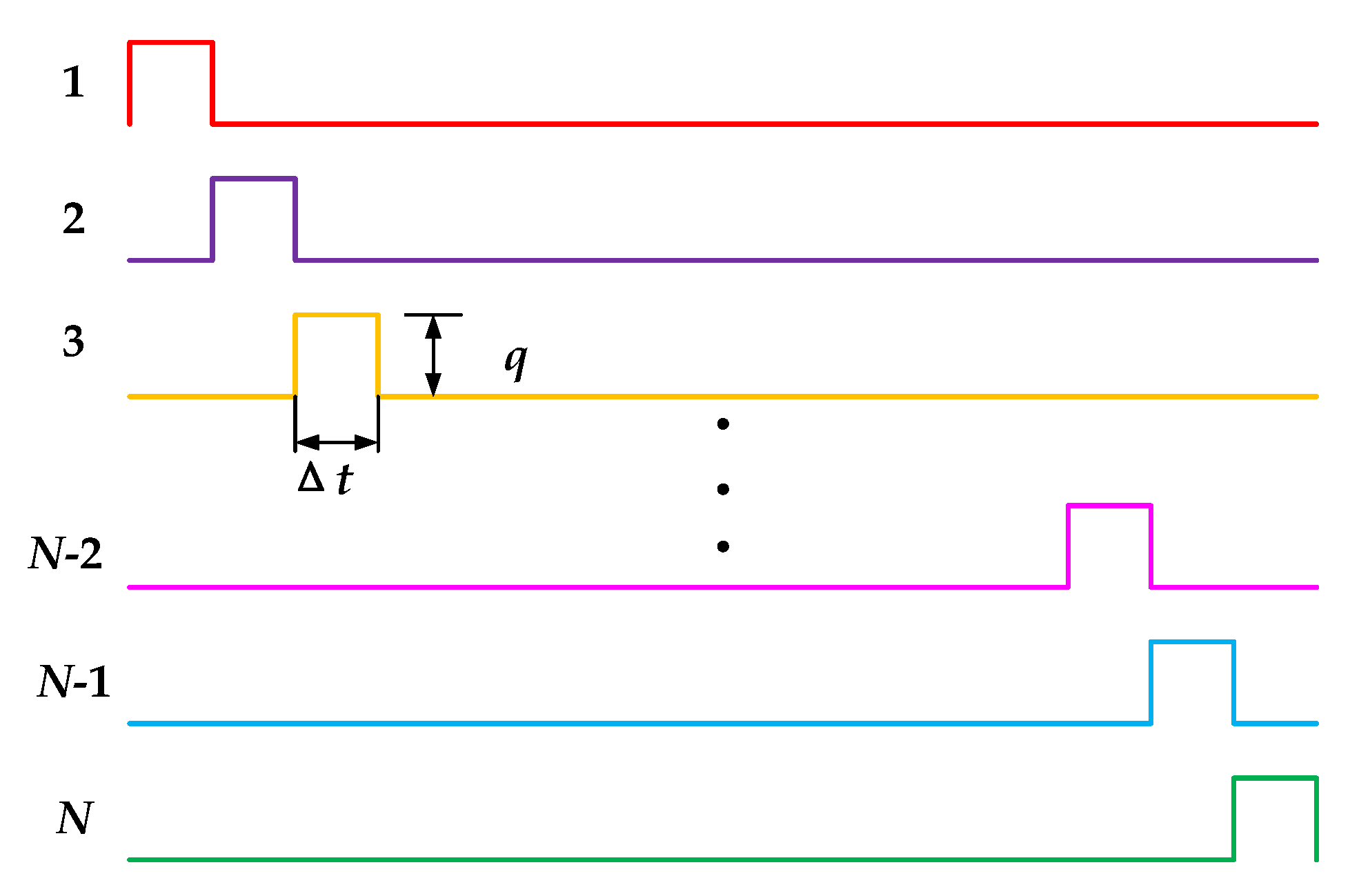
2.5. Temperature Prediction
3. Oil Jet Layout
3.1. Impingement Depth
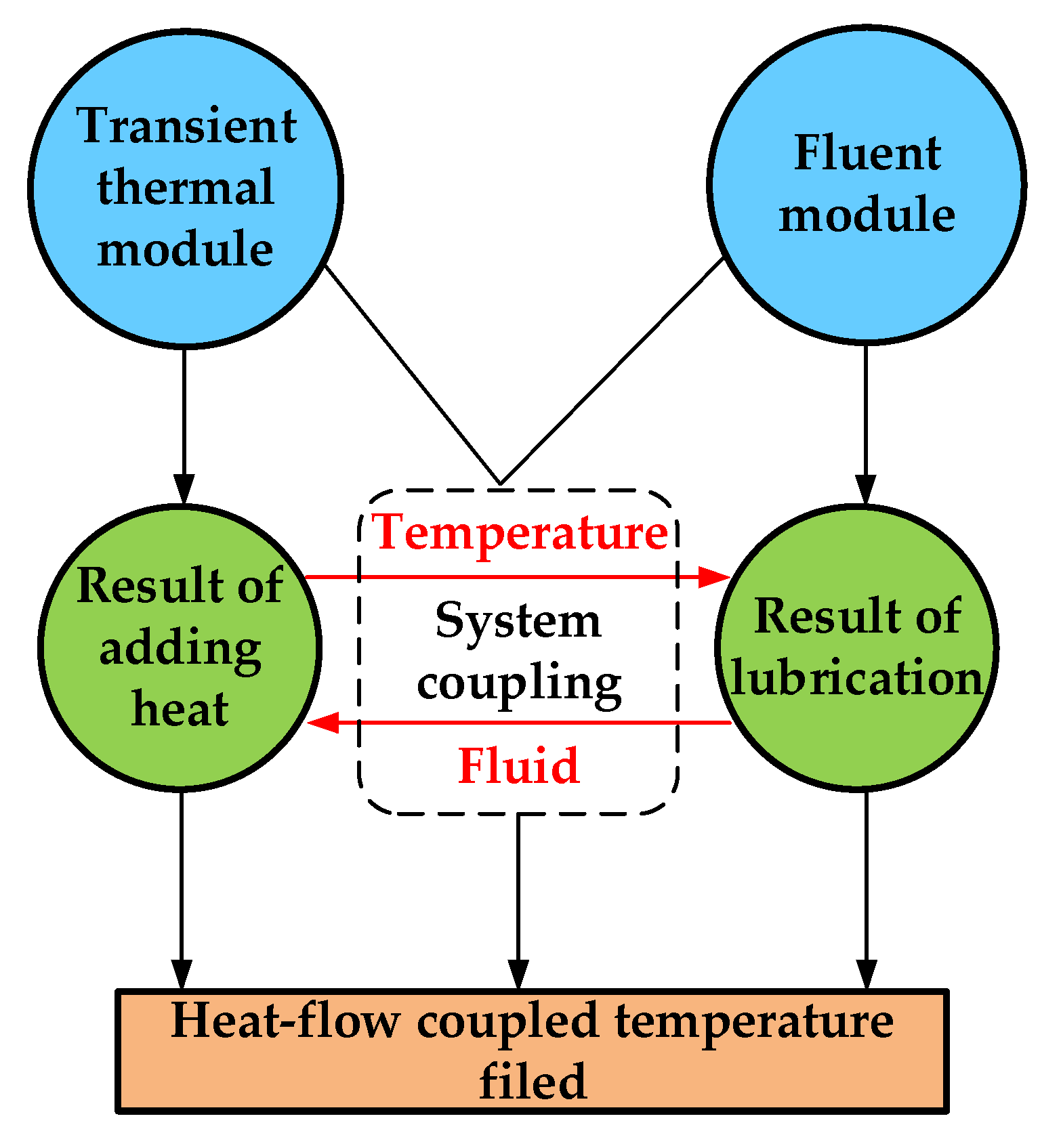
3.2. Finite Element Model
- (1)
- Temperature field
- (2)
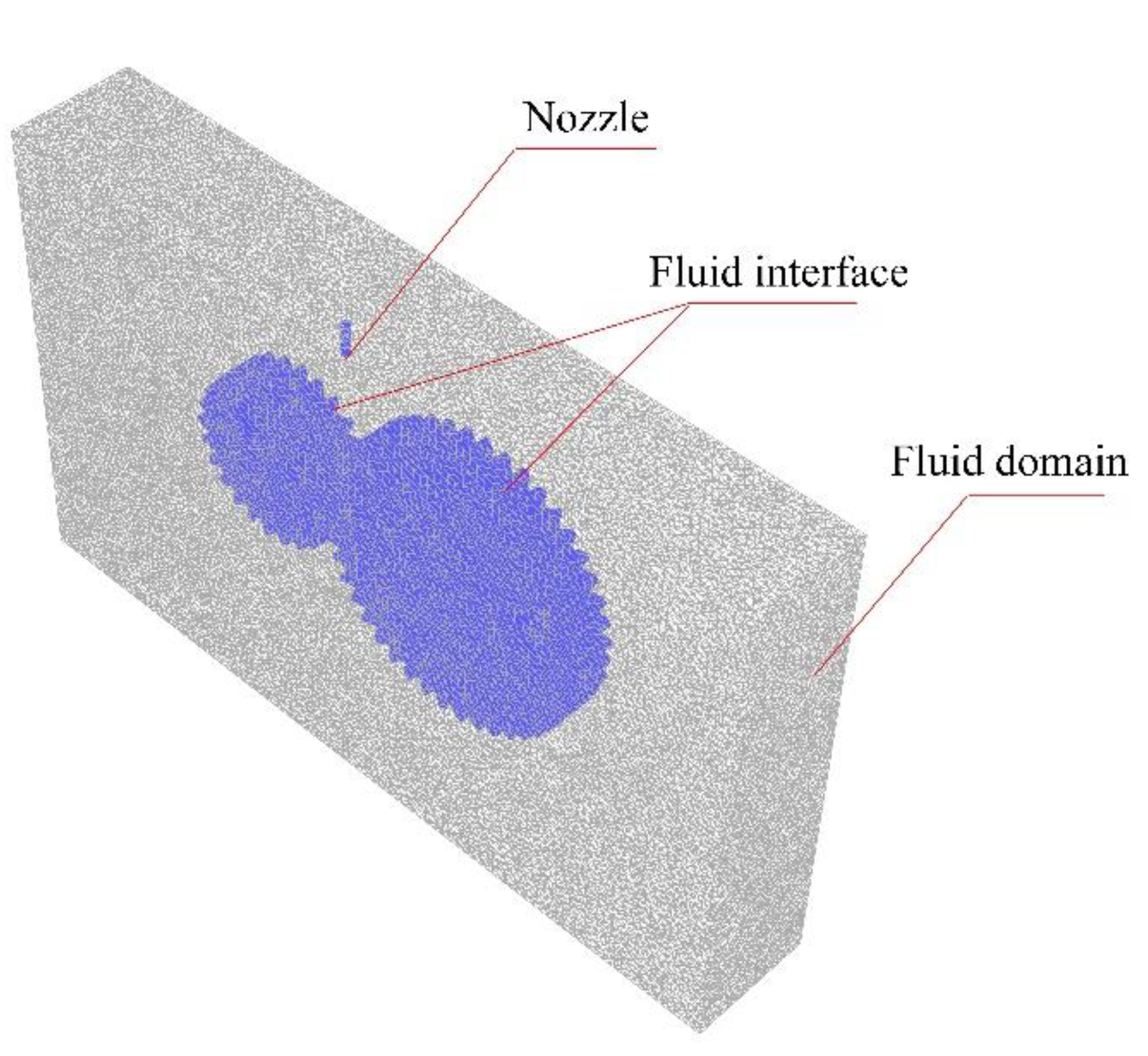
- Fluid field
- (3)
- Boundary conditions
4. Results and Discussion
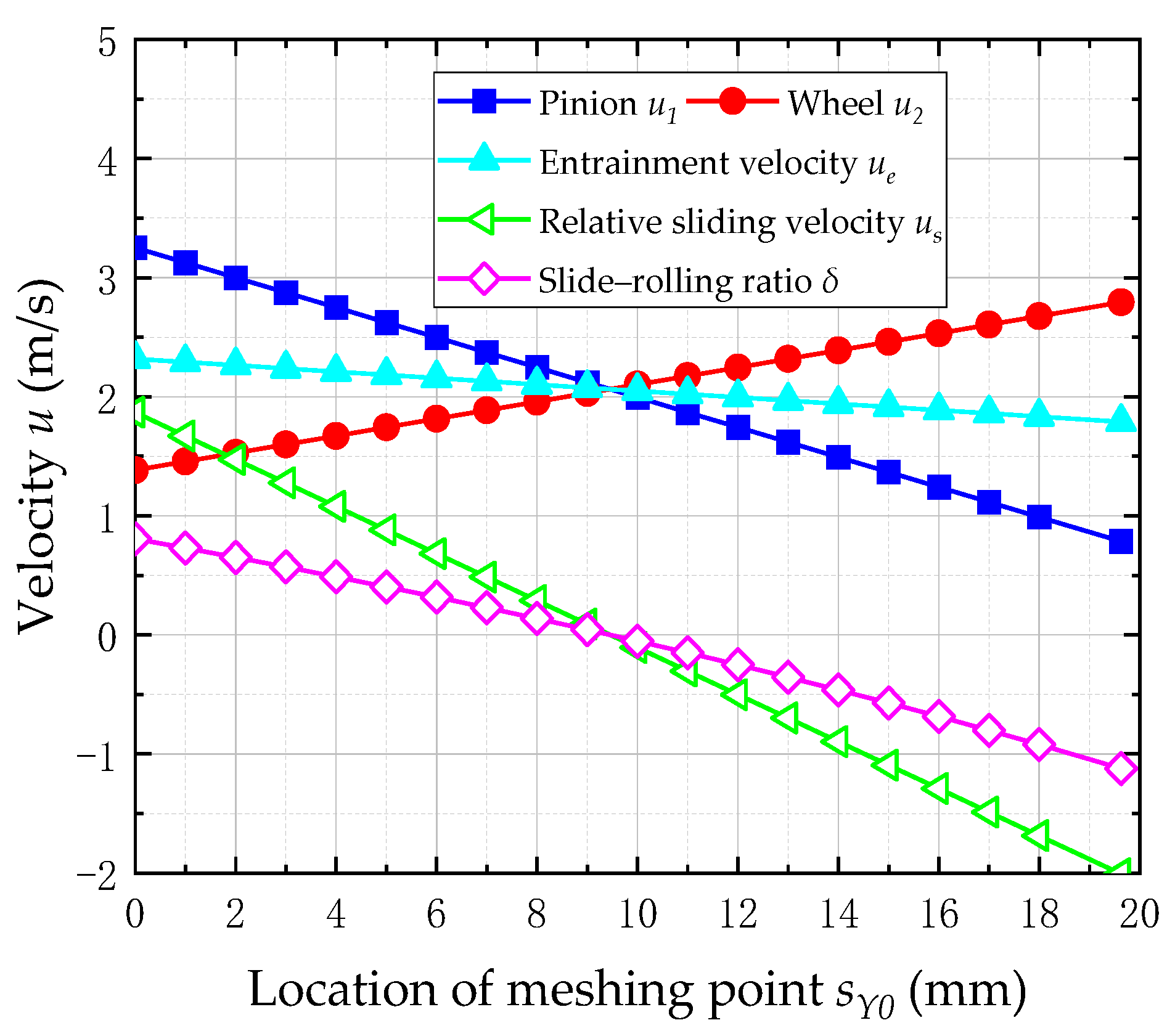
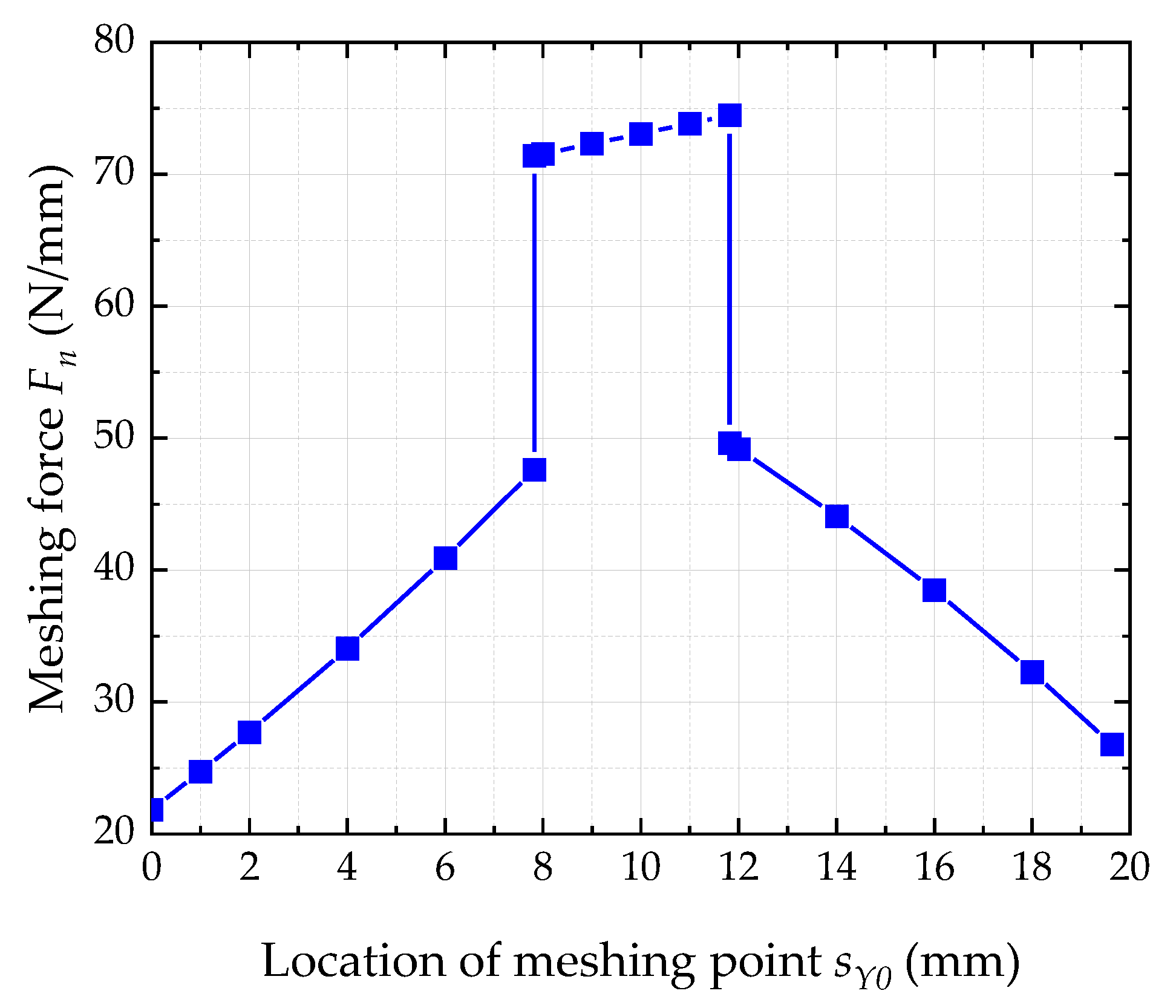
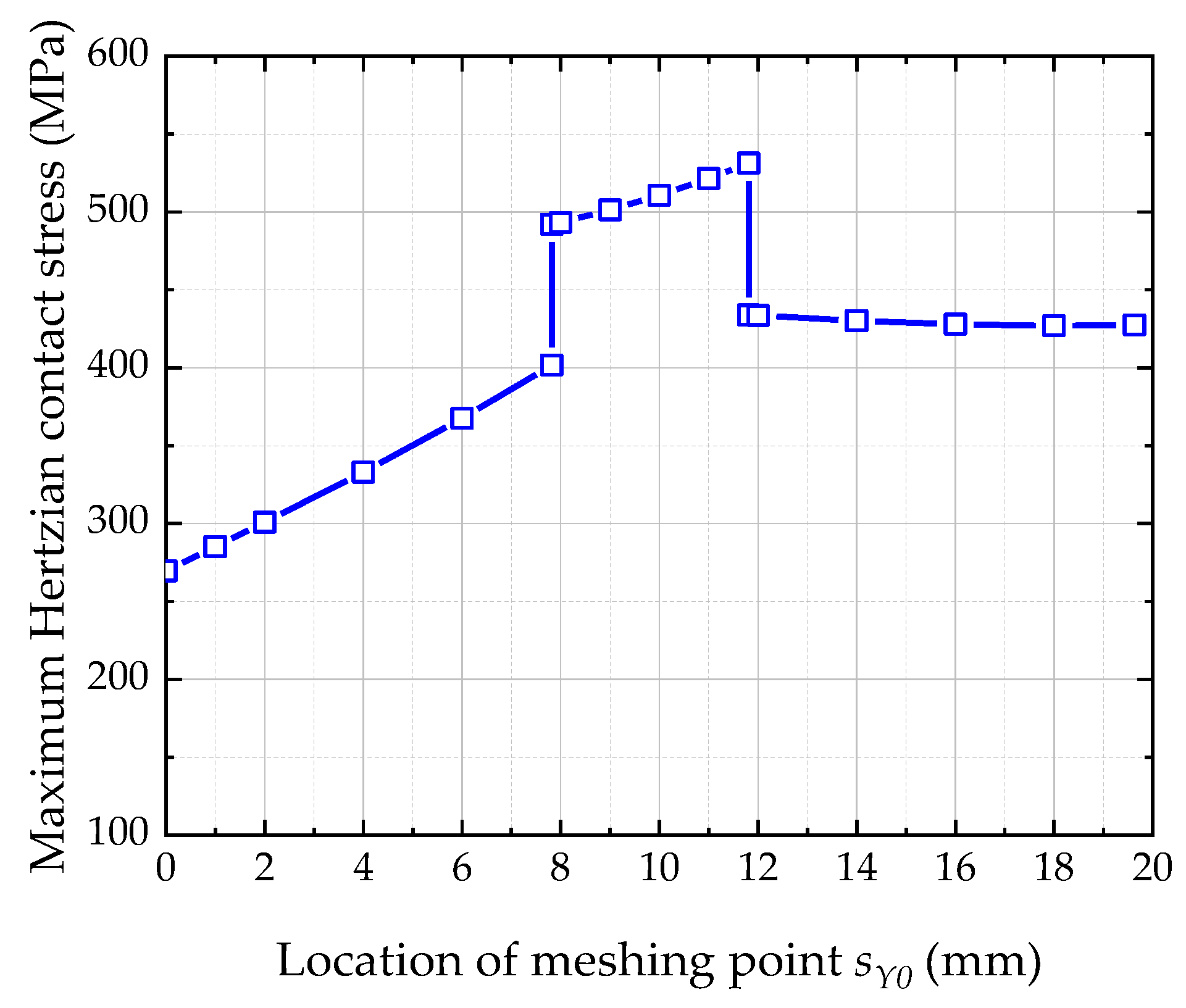
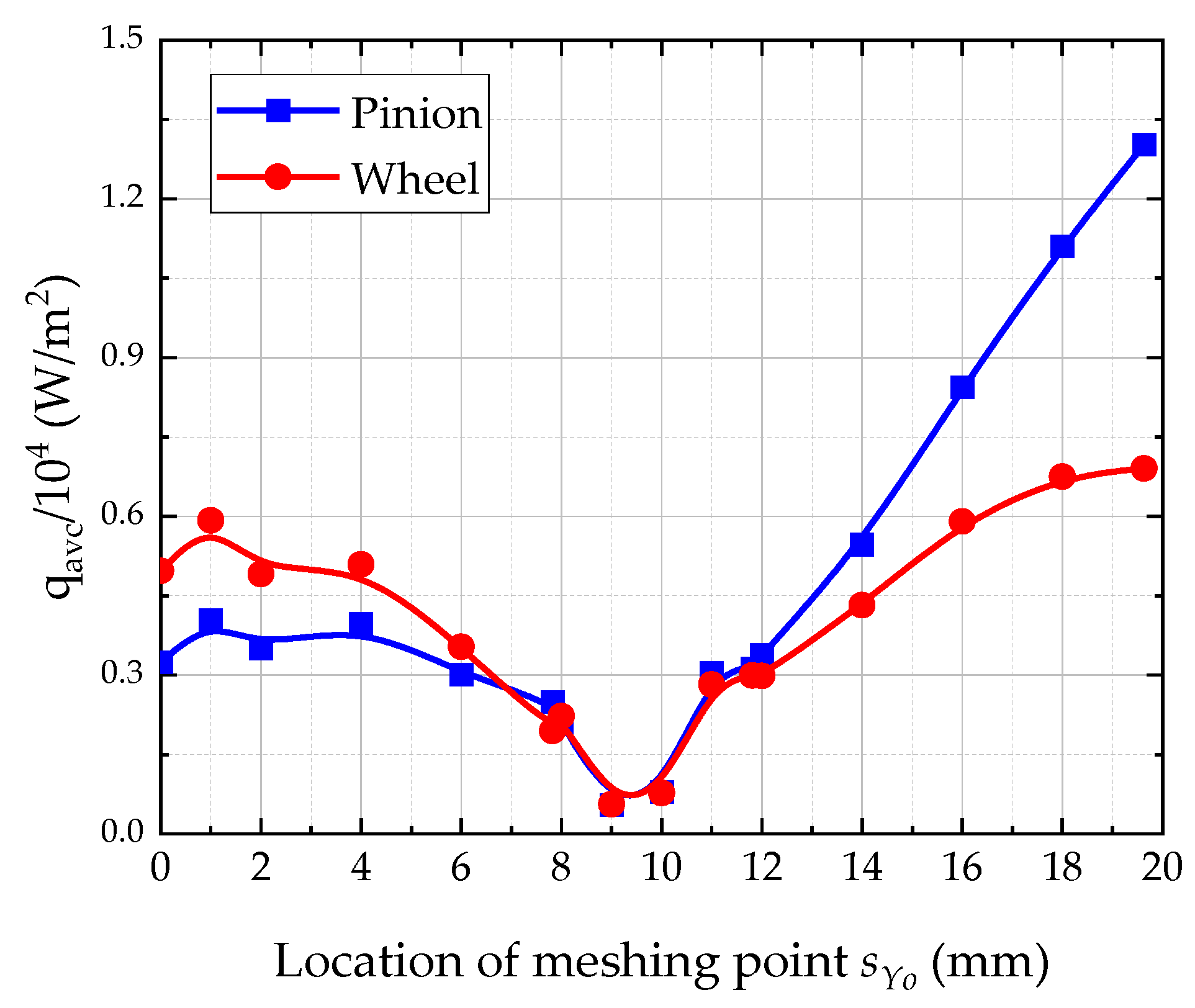
4.1. Numerical Results Analysis
4.2. Bulk Temperature
4.3. Transient Temperature
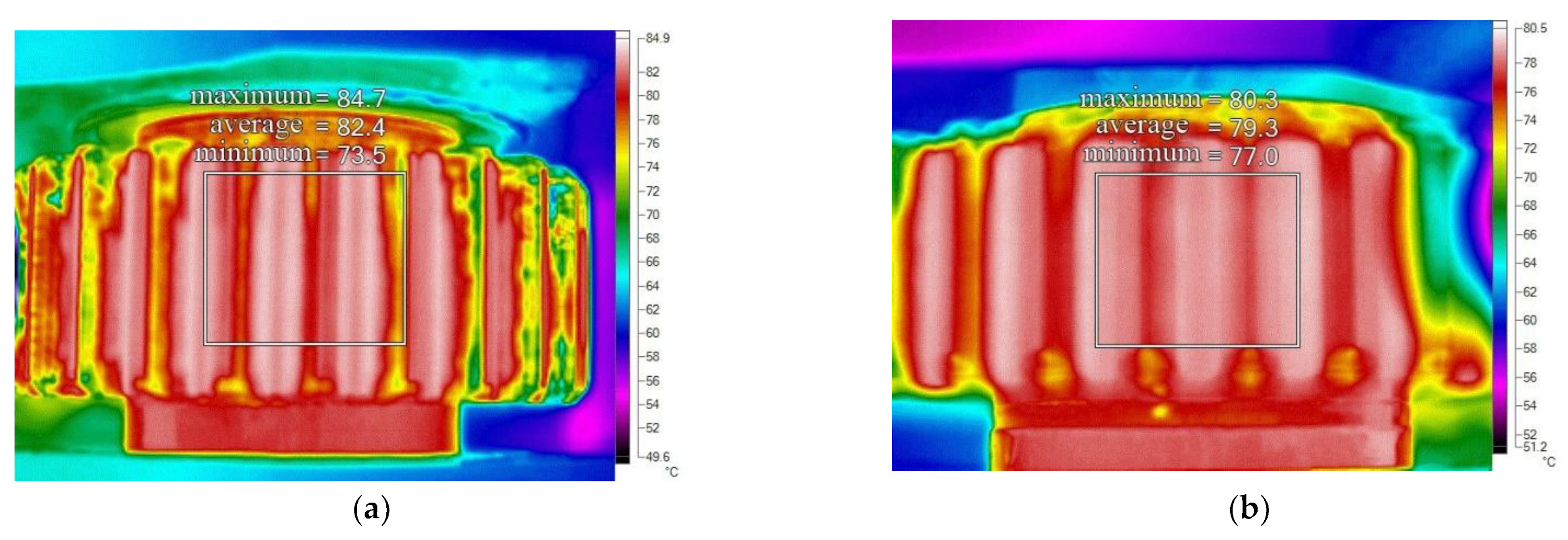
4.4. Verification of Models
- (a)
- For a gear ratio of 1:1, the deviation distance L and oil injection angle β are recommended to be zero. The impact depth increases with an increase in the ratio of the oil jet velocity to the pitch-line velocity, but the speed at which the impact depth changes decreases gradually.
- (b)
- For a gear ratio larger than 1:1, if the deviation distance L and oil injection angle β are equal to zero, the impact depth of the pinion gradually decreases to zero. Due to the unbiased and inclined nozzle, as the gear ratio increases to a certain value, the impact of the lubricating oil on the tooth of the gear begins to be blocked by its previous tooth. In this case, the lubricating oil jet is completely covered by the gear, and the pinion cannot be sprayed by the lubricating oil. Hence, the impact depth of the pinion decreases to zero. Therefore, to ensure the impact depth of the pinion, the deviation distance L and oil injection angle β of the nozzle towards the pinion should be increased with an appropriate increase in the gear ratio, as depicted in Group 3.
5. Conclusions
- (1)
- The transient temperature for spur gears is modeled based on the mixed EHL model and load contact method, and the differences indicate that the impingement depth is closely related to the nozzle layouts. Specifically, the oil jet height H, deviation distance L, and oil injection angle β have enormous influences on the temperature distribution. Furthermore, it reveals that the greater the impact depth, the lower the transient temperature, and the better the lubrication performance.
- (2)
- When the oil nozzle approaches the side of the pinion (deviation distance L > 0, oil injection angle β > 0, e.g., Group 2 in Table 4), the maximum temperature on the gear tooth is lower, which means better lubrication performance. The numerical method can simulate the temperature distribution characteristics of a spur gear pair and provide some recommendations for the design and installation of the nozzle.
- (3)
- Comparisons of the maximum temperature on the gear tooth with the corresponding impingement depth and experimental results indicate that the numerical method on the transient temperature field is accurate and reliable.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Savolainen, M.; Lehtovaara, A. An experimental investigation of scuffing initiation due to axial displacement in a rolling/sliding contact. Tribol. Int. 2018, 119, 688–697. [Google Scholar] [CrossRef]
- Castro, J.; Seabra, J. Influence of mass temperature on gear scuffing. Tribol. Int. 2018, 119, 27–37. [Google Scholar] [CrossRef]
- Massini, D.; Fondelli, T.; Facchini, B.; Tarchi, L.; Leonardi, F. Experimental investigation on power losses due to oil jet lubrication in high speed gearing systems. In Proceedings of the ASME turbo expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 27–29 June 2017. Paper No. GT2017-64703. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, W.; Wei, S.; Song, G. Influence of spin flow on lubricating oil jet-design method of oil spray parameters to high speed spur gears. Tribol. Int. 2015, 92, 290–300. [Google Scholar] [CrossRef]
- Wang, Y.; Song, G.; Niu, W.; Chen, Y. Optimized design of spray parameters of oil jet lubricated spur gears. Tribol. Int. 2018, 120, 149–158. [Google Scholar] [CrossRef]
- Wang, Y.; Song, G.; Niu, W.; Chen, Y. Influence of oil injection methods on the lubrication process of high-speed spur gears. Tribol. Int. 2018, 121, 180–189. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. A numerical solution to the elasto-hydrodynamic problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Yang, P.; Wen, S. A generalized reynolds equation for non-Newtonian thermal elastohydrodynamic lubrication. J. Tribol. 1990, 112, 631–636. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Performance of spur gears considering surface roughness and shear thinning lubricant. J. Tribol. 2008, 130, 021503. [Google Scholar] [CrossRef]
- Majumdar, A.; Tien, C.L. Fractal characterization and simulation of rough surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Castro, J.; Seabra, J. Global and local analysis of gear scuffing tests using a mixed film lubrication model. Tribol. Int. 2008, 41, 244–255. [Google Scholar] [CrossRef]
- Bobach, L.; Beilicke, R.; Bartel, D.; Deters, L. Thermal elastohydrodynamic simulation of involute spur gears incorporating mixed friction. Tribol. Int. 2012, 48, 191–206. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Gao, P. A study of spur gear pitting under EHL conditions: Theoretical analysis and experiments. Tribol. Int. 2016, 94, 146–154. [Google Scholar] [CrossRef]
- Ebner, M.; Yilmaz, M.; Lohner, T.; Michaelis, K.; Höhn, B.R.; Stahl, K. On the effect of starved lubrication on elastohydrodynamic (EHL) line contacts. Tribol. Int. 2018, 118, 515–523. [Google Scholar] [CrossRef]
- Venner, C.H. Multilevel Solution of the EHL Line and Point Contact Problems. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1991. [Google Scholar]
- Fatourehchi, E.; Shahmohamadi, H.; Mohammadpour, M.; Rahmani, R.; Theodossiades, S.; Rahnejat, H. Thermal analysis of an oil jet-dry sump transmission gear under mixed-elastohydrodynamic conditions. J. Tribol. 2018, 140, 051502. [Google Scholar] [CrossRef]
- Fatourehchi, E.; Mohammadpour, M.; Theodossiades, S.; Rahnejat, H. Transient thermal analysis of mixed-elastohydrodynamic contact of high performance transmission in a dry sump environment. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 326–338. [Google Scholar] [CrossRef]
- Rajendhran, N.; Palanisamy, S.; Shyma, A.P.; Venkatachalam, R. Enhancing the thermophysical and tribological performance of gear oil using Ni-promoted ultrathin MoS2 nanocomposites. Tribol. Int. 2018, 124, 156–168. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Prediction of the bulk temperature in spur gears based on finite element temperatureanalysis. ASLE. Trans. 1979, 22, 25–36. [Google Scholar] [CrossRef]
- Handschuh, R.F.; Kicher, T.P. A method for thermal analysis of spiral bevel gears. J. Mech. Des. Trans. ASME 1996, 118, 580–585. [Google Scholar] [CrossRef]
- Shi, Y.; Yao, Y.P.; Fei, J.Y. Analysis of bulk temperature field and flash temperature for locomotive traction gear. Appl. Therm. Eng. 2016, 99, 528–536. [Google Scholar] [CrossRef]
- Li, W.; Tian, J.Y. Unsteady-state temperature field and sensitivity analysis of gear transmission. Tribol. Int. 2017, 116, 229–243. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, W.; Chen, Y.; Wang, T.; Li, G.; Ball, A.D. Investigation into the meshing friction heat generation and transient thermal characteristics of spiral bevel gears. Appl. Therm. Eng. 2017, 119, 245–253. [Google Scholar] [CrossRef]
- Zhang, J.G.; Liu, S.J.; Fang, T. Determination of surface temperature rise with the coupled thermo-elasto-hydrodynamic analysis of spiral bevel gears. Appl. Therm. Eng. 2017, 124, 494–503. [Google Scholar] [CrossRef]
- Akin, L.S.; Townsend, D.P. Into mesh lubrication of spur gears with arbitrary offset oil jet. part 1: For jet velocity less than or equal to gear velocity. ASME J. Mech. Trans. Autom. 1983, 105, 713–718. [Google Scholar] [CrossRef]
- Akin, L.S.; Townsend, D.P. Into mesh lubrication of spur gears with arbitrary offset oil jet. part 2: For jet velocities equal to or greater than gear velocity. ASME J. Mech. Trans. Autom. 1983, 105, 719–724. [Google Scholar] [CrossRef]
- Akin, L.S.; Townsend, D.P. Lubricant jet flow phenomena in spur and helical gears with modified center distances and/or addendums-for out-of-mesh conditions. ASME J. Mech. Trans. Autom. 1985, 107, 24–30. [Google Scholar] [CrossRef]
- Huang, C.H.; Huang, Y.R. An optimum design problem in estimating the shape of perforated pins and splitters in a plate-pin-fin heat sink. Int. J. Therm. Sci. 2021, 170, 107096. [Google Scholar] [CrossRef]
- Dai, Y.; Xu, L.; Zhu, X.; Ouyang, B. Application of an unstructured overset method for predicting the gear windage power losses. Eng. Appl. Comp. Fluid 2021, 15, 130–141. [Google Scholar] [CrossRef]
- Jiang, L.; Lyu, Y.; Zhu, P. Numerical investigation of conjugate heat transfer on a rotating disk under round liquid jet impingement. Int. J. Therm. Sci. 2021, 170, 107097. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, W.; Zhou, H.B.; Zhang, J.; Ma, F.Y. Numerical simulation and optimization of oil jet lubrication for rotorcraft meshing gears. Int. J. Simul. Model 2018, 17, 318–326. [Google Scholar] [CrossRef]
- Dai, Y.; Ma, F.; Zhu, X.; Su, Q.; Hu, X. Evaluation and optimization of the oil jet lubrication performance for orthogonal face gear drive: Modelling, simulation and experimental validation. Energies 2019, 12, 1935. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, Y.; Ma, F.; Ouyang, B. Mathematical modeling and numerical simulation for determining an optimized oil jet layout for spiral bevel gear. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 611–628. [Google Scholar] [CrossRef]
- Ouyang, B.; Ma, F.; Dai, Y.; Zhang, Y. Numerical analysis on heat-flow-coupled temperature field for orthogonal face gears with oil–jet lubrication. Eng. Appl. Comp. Fluid 2021, 15, 762–780. [Google Scholar] [CrossRef]
- Dudley, D.W. Dudley’s Gear Handbook; Tata McGraw-Hill Education: New York, NY, USA, 1991. [Google Scholar]
- Bair, S.; Winer, W.O. A rheological model for elastohydrodynamic contacts based on primary laboratory data. J. Lubr. Technol. 1979, 101, 258–264. [Google Scholar] [CrossRef]
- Zhu, D.; Hu, Y.Z. A computer program package for the prediction of EHL and mixed lubrication characteristics, friction, subsurface stresses and flash temperatures based on measured 3-D surface roughness. Tribol. Trans. 2001, 44, 383–390. [Google Scholar] [CrossRef]
- Hu, Y.Z.; Zhu, D. A full numerical solution to the mixed lubrication in point contacts. J. Tribol. 2000, 122, 1–9. [Google Scholar] [CrossRef]
- Gan, L.; Xiao, K.; Wang, J.; Pu, W.; Cao, W. A numerical method to investigate the temperature behavior of spiral bevel gears under mixed lubrication condition. Appl. Therm. Eng. 2019, 147, 866–875. [Google Scholar] [CrossRef]
- Lienhard, J.H.; Catton, I. Heat transfer across a two-fluid-layer region. ASME J. Heat Transfer. 1986, 108, 198–205. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.J.; Hu, Y. Analysis of influence factor of oil jet lubrication impingement depth of aviation spur gear. J. Mech. Transm. 2017, 41, 23–29. (In Chinese) [Google Scholar] [CrossRef]








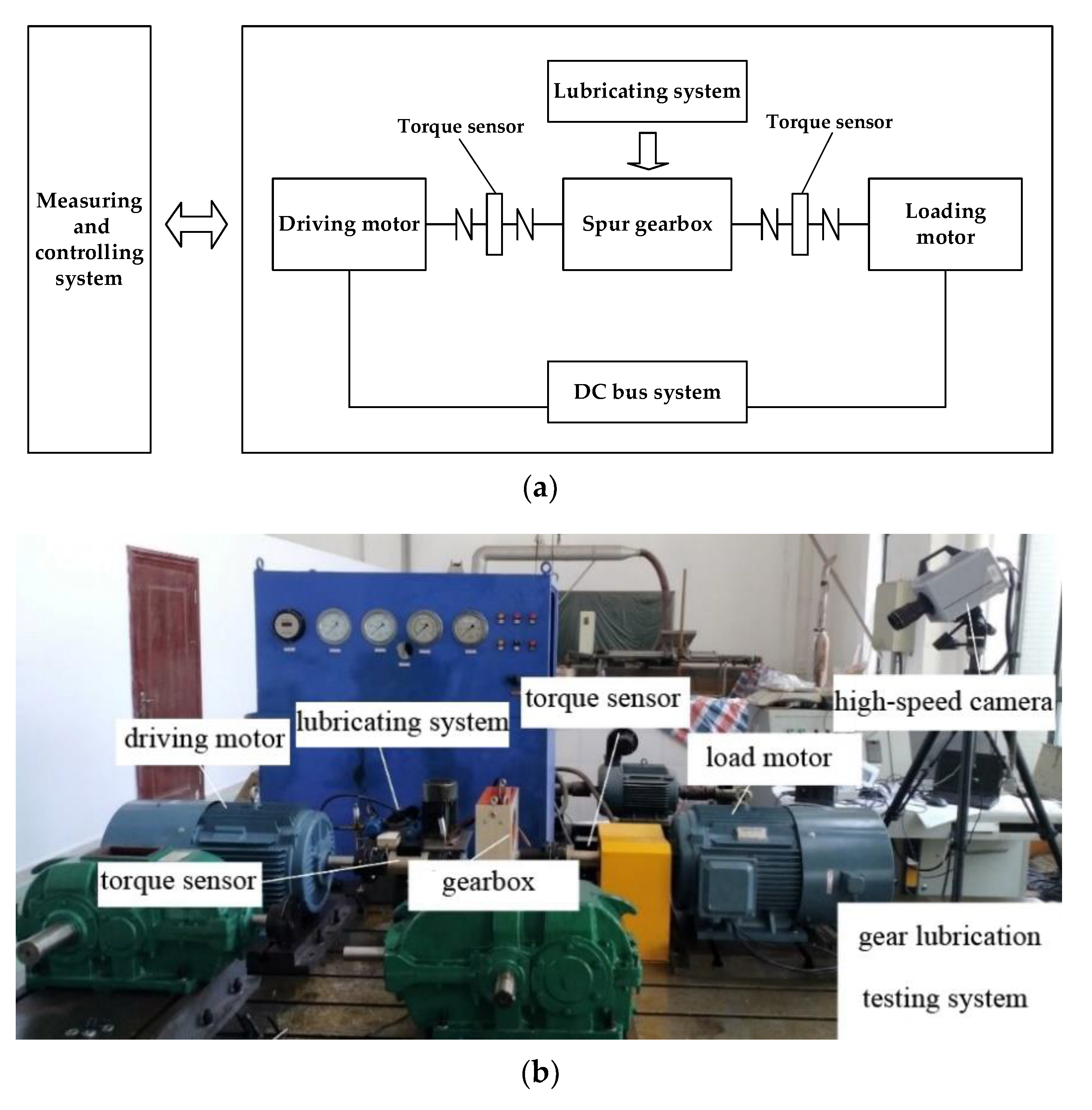

| Temperature (°C) | Thermal Conductivity Coefficient (W/m·°C) | Specific Heat (J/kg·°C) | Density (kg/m3) | Kinematic Viscosity (mm2/s) | Prandtl Number |
|---|---|---|---|---|---|
| 50 | 0.152 | 1910 | 971.2 | 17.4 | 212.34 |
| 100 | 0.146 | 2070 | 970.4 | 5.00 | 68.79 |
| 158 | 0.139 | 2260 | 967.8 | 4.11 | 64.67 |
| Temperature (°C) | Thermal Conductivity Coefficient (W/m·°C) | Specific Heat (J/kg·°C) | Density (kg/m3) | Kinematic Viscosity (mm2/s) | Prandtl Number |
|---|---|---|---|---|---|
| 20 | 2.59 | 1005 | 1.208 | 15.06 | 0.703 |
| 40 | 2.76 | 1005 | 1.128 | 16.96 | 0.699 |
| 60 | 2.90 | 1009 | 1.060 | 18.97 | 0.696 |
| 80 | 3.05 | 1009 | 1.000 | 21.09 | 0.692 |
| Parameter | Value |
|---|---|
| Gear ratio z1/z2 | 24/42 |
| Modulus m/(mm) | 4 |
| Tooth width B/(mm) | 30 |
| Rotation speed of pinion n1/(r/min) | 1500 |
| Output torque T/(Nm) | 200 |
| Group | Oil Jet Height H (mm) | Deviation Distance L (mm) | Oil Injection Angle β (°) | Impingement Depth of Pinion (mm) | Impingement Depth of Gear (mm) |
|---|---|---|---|---|---|
| 1 | 100 | 1.2 | 0 | 0.92198 | 0.29226 |
| 2 | 100 | 8.2 | 5 | 1.1768 | 0 |
| 3 | 100 | 0 | 0 | 0 | 1.2836 |
| Group | Impingement Depth of Pinion (mm) | Experimental Maximum Pinion Temperature (°C) | Numerical Maximum Pinion Temperature (°C) |
|---|---|---|---|
| 1 | 0.92198 | 81.4 | 73.892 |
| 2 | 1.1768 | 77.1 | 69.373 |
| 3 | 0 | 84.7 | 76.896 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Liu, H.; Zhong, J.; Zhu, X.; Dai, Y. Influence of Nozzle Layouts on the Heat-Flow Coupled Characteristics for Oil-Jet Lubricated Spur Gears. Lubricants 2023, 11, 25. https://doi.org/10.3390/lubricants11010025
Yang D, Liu H, Zhong J, Zhu X, Dai Y. Influence of Nozzle Layouts on the Heat-Flow Coupled Characteristics for Oil-Jet Lubricated Spur Gears. Lubricants. 2023; 11(1):25. https://doi.org/10.3390/lubricants11010025
Chicago/Turabian StyleYang, Duan, He Liu, Jianfeng Zhong, Xiang Zhu, and Yu Dai. 2023. "Influence of Nozzle Layouts on the Heat-Flow Coupled Characteristics for Oil-Jet Lubricated Spur Gears" Lubricants 11, no. 1: 25. https://doi.org/10.3390/lubricants11010025
APA StyleYang, D., Liu, H., Zhong, J., Zhu, X., & Dai, Y. (2023). Influence of Nozzle Layouts on the Heat-Flow Coupled Characteristics for Oil-Jet Lubricated Spur Gears. Lubricants, 11(1), 25. https://doi.org/10.3390/lubricants11010025







