Research on the Bearing Sliding Loss Based on Time-Varying Contact Angle between Ball and Raceway

Abstract

Based on the mechanical model, the friction loss between the ball and the raceway along the major axis of the contact ellipse is analyzed. The result shows that this part of the loss accounts for about 13.67% of the overall loss, which is mainly determined by the ball sliding length and cannot be ignored. The effects of the radial force, torque, rotational speed and groove curvature ratio on the sliding are all studied. Compared with other factors, radial force has the greatest influence on the sliding loss. As bearing speed gradually grows, the sliding on the inner raceway gradually increases while it gradually decreases on the outer raceway. Compared to the outer raceway curvature ratio, the sliding length is less sensitive to changes in the curvature ratio of the inner raceway. The paper provides theoretical guidance for the design and application of low-friction bearings.

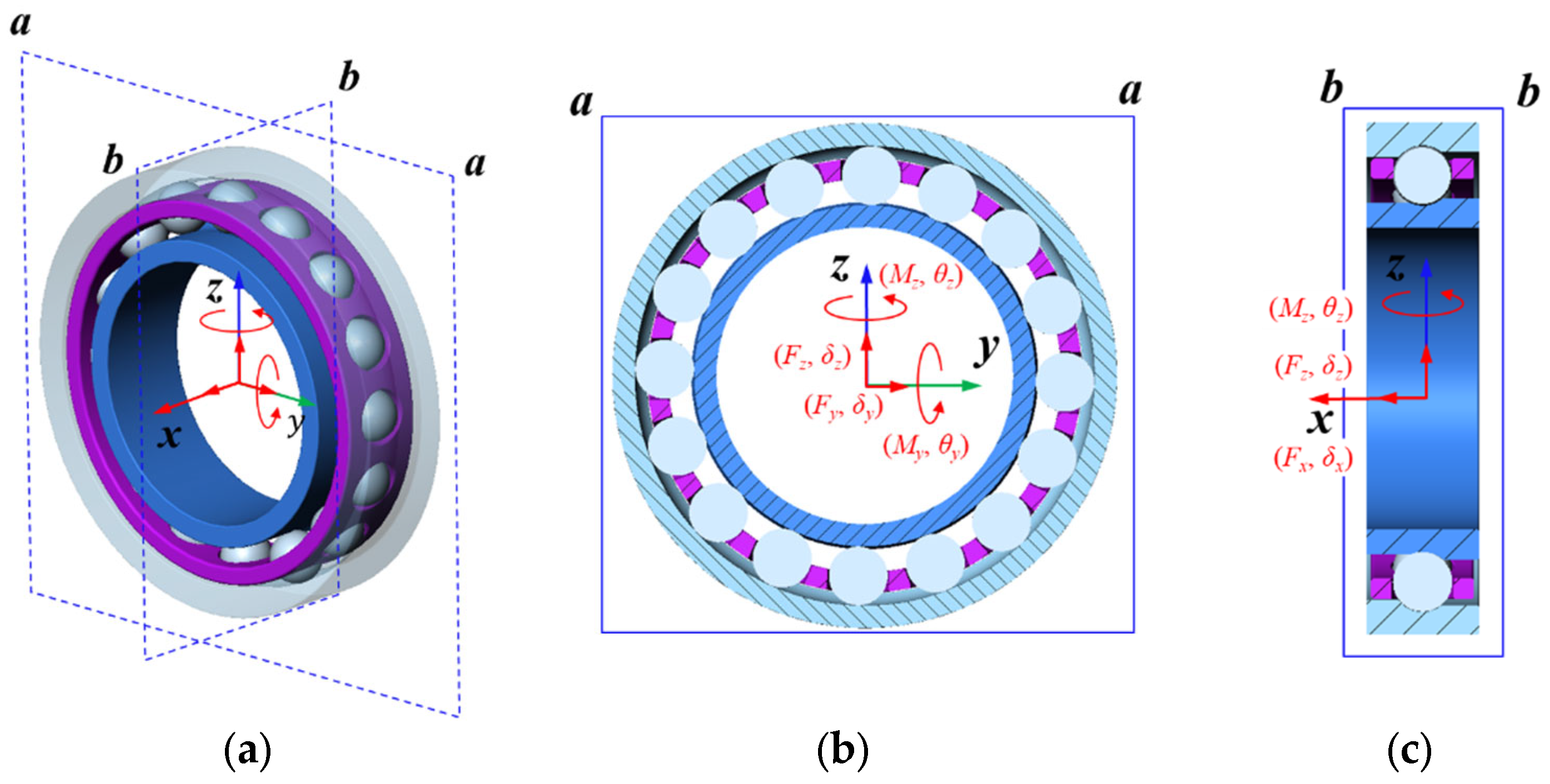
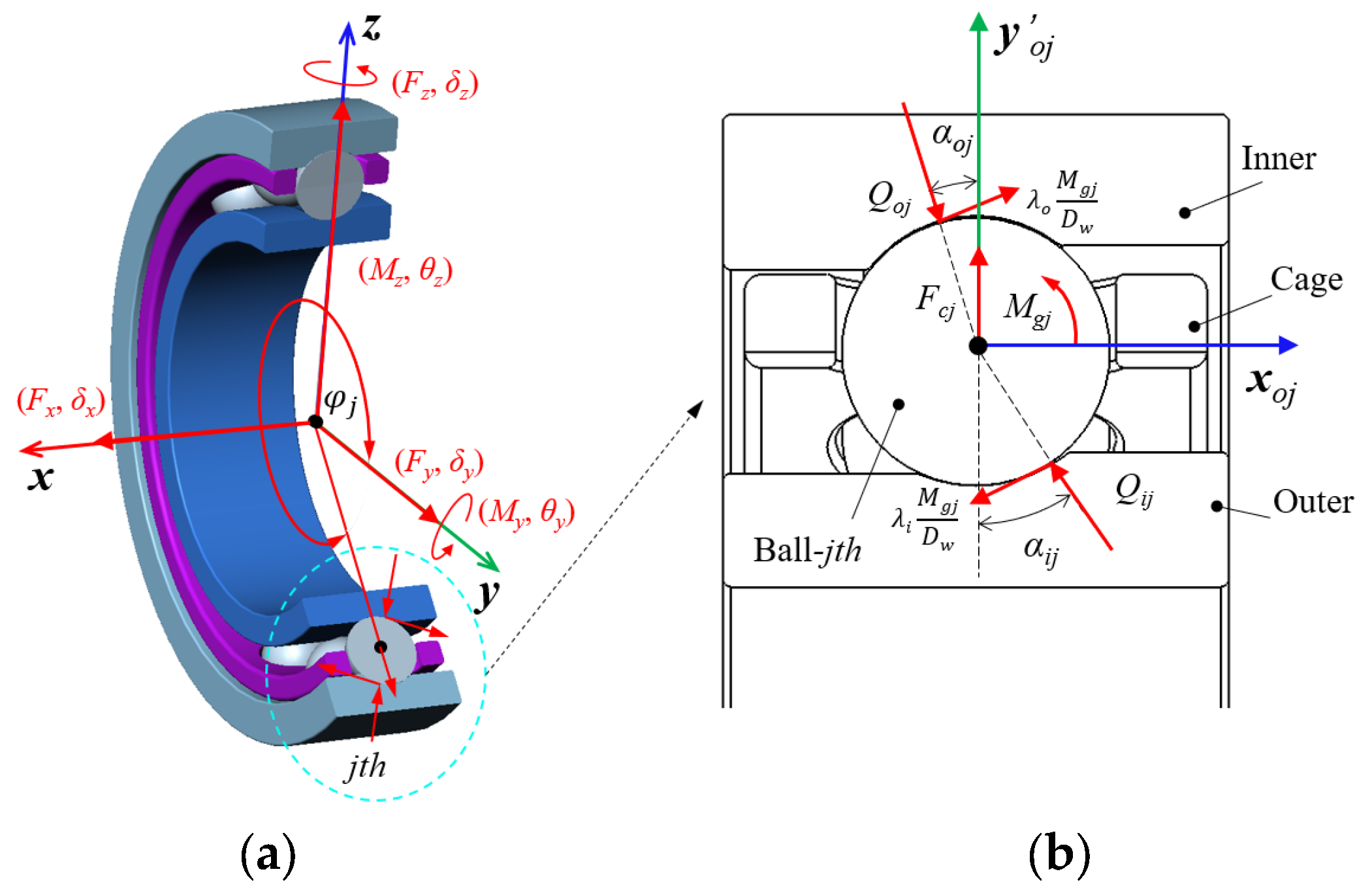
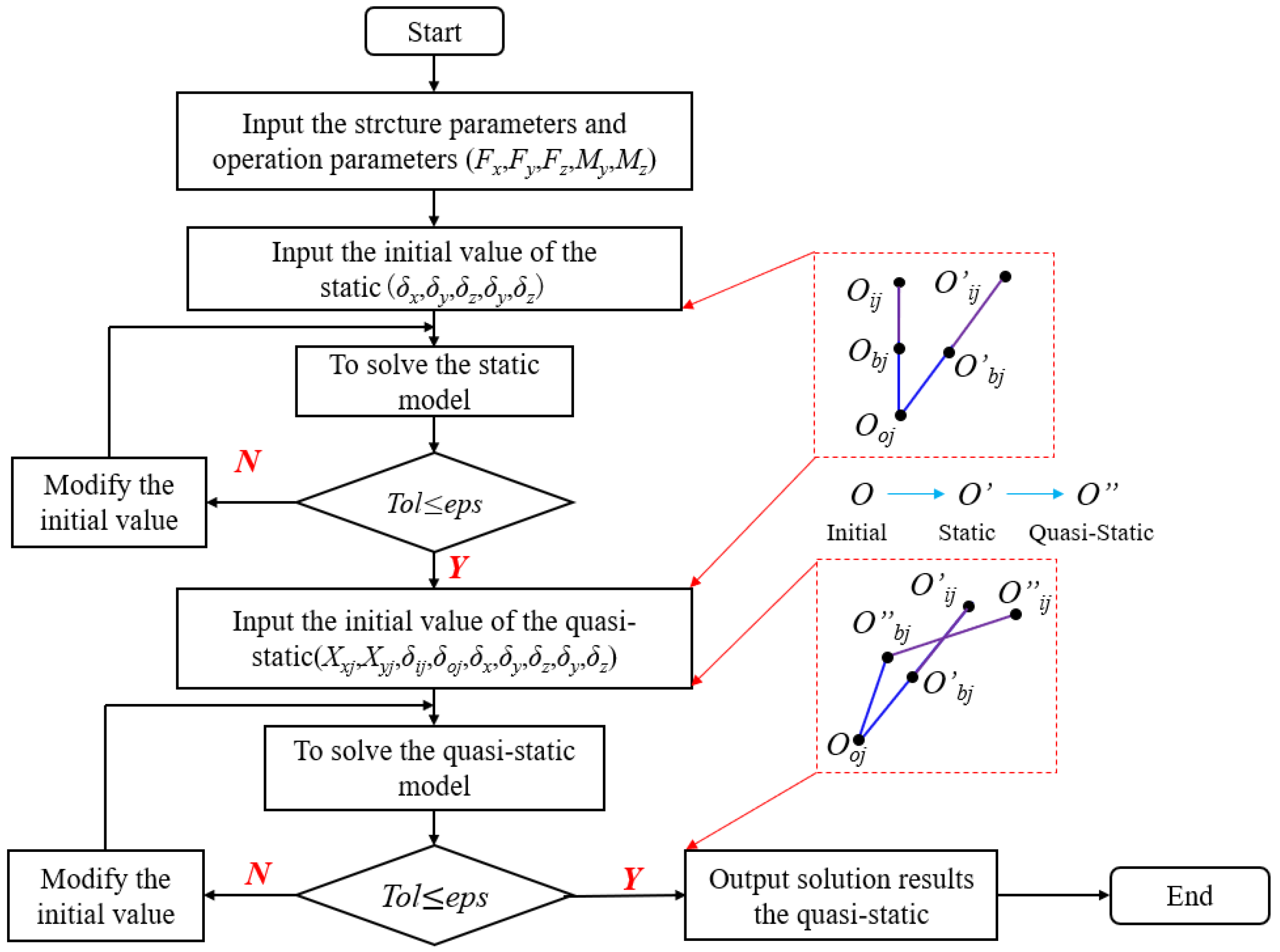
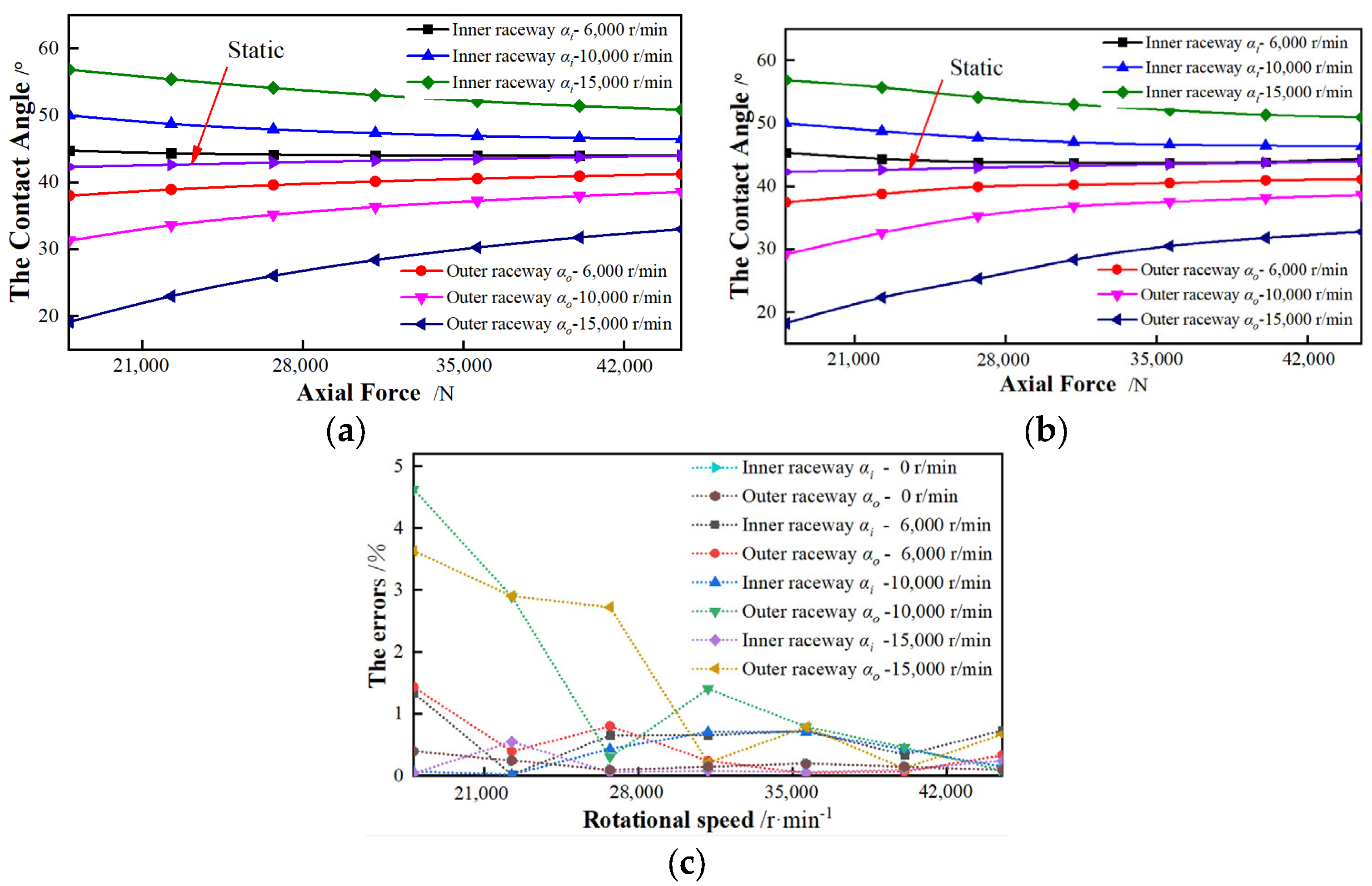
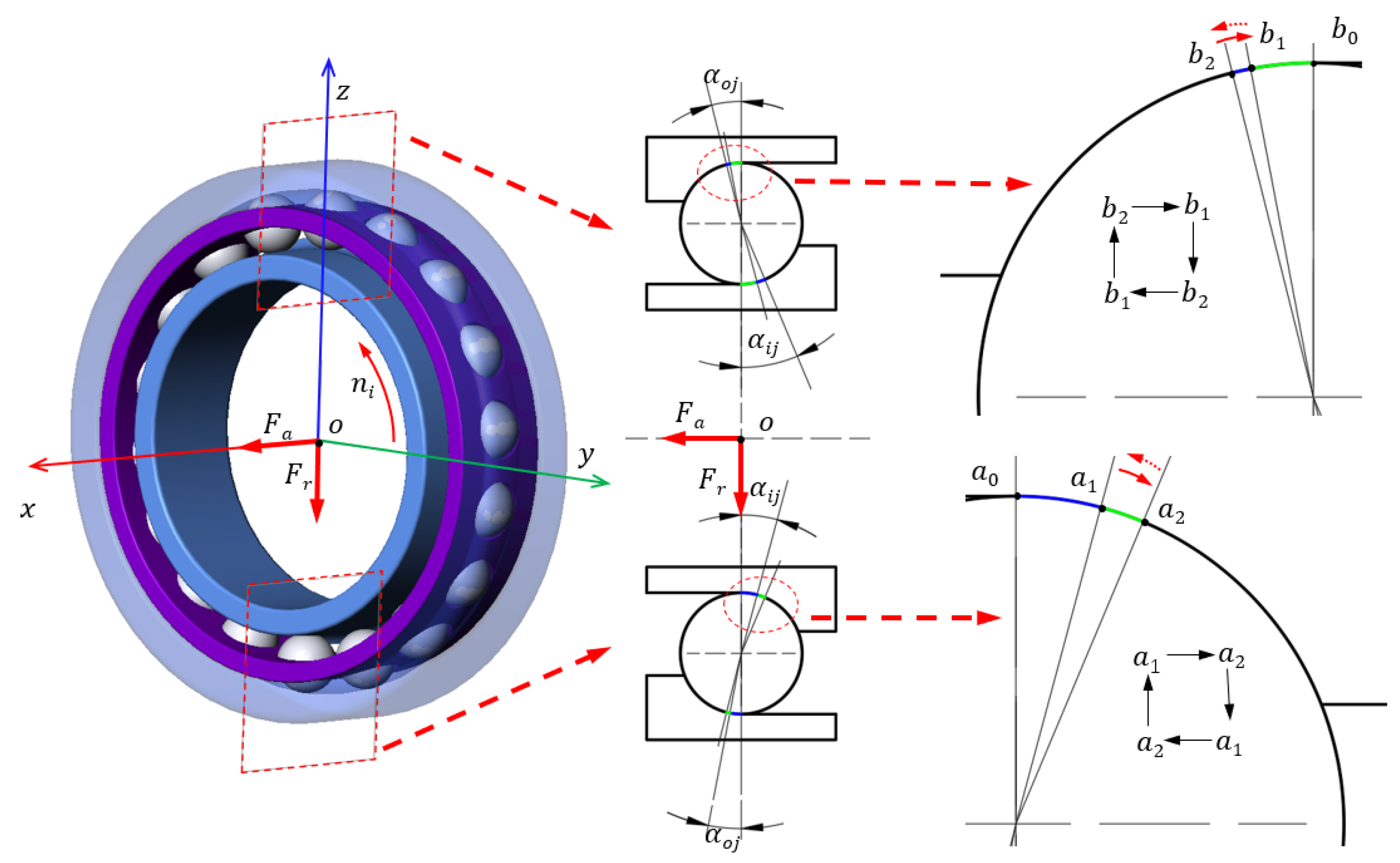
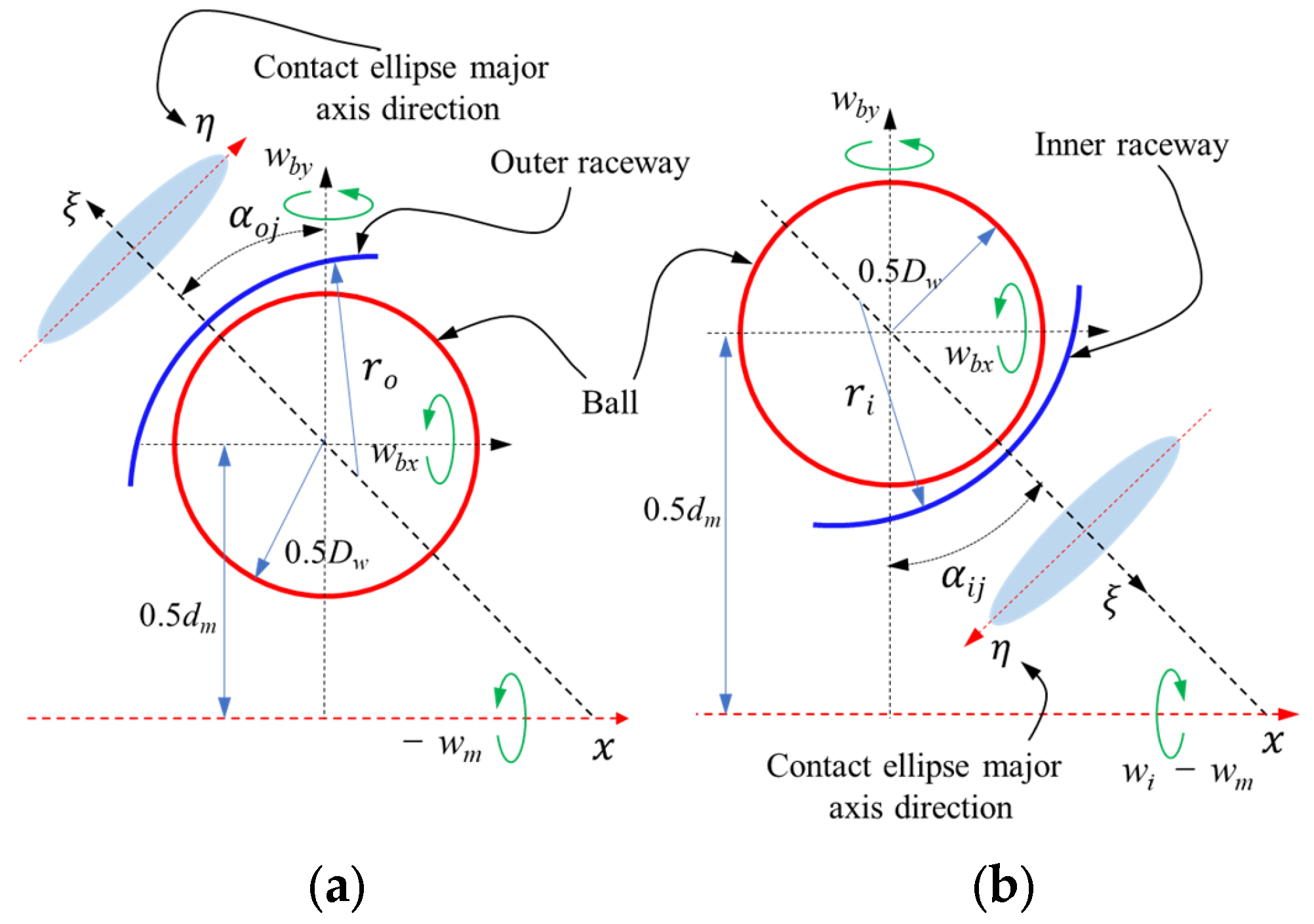
1. Introduction

Owing to the characteristics of low friction and high precision, ball bearings are widely used in rotational systems, such as high-speed motors, precision machine tools and aero engines [1,2]. Regarding the complex internal structure of the bearing, relative motion and force conditions, etc., there are complex tribological behaviors between balls and inner/outer rings, which may cause bearing friction heat and power loss, and even accelerate bearing wear and reduce bearing operation accuracy, etc. [1]. Therefore, the bearing friction phenomenon hinders the further improvement of high-speed bearing performance [3]. Especially with the continuous improvement of energy consumption requirements of rotating equipment, the design of low-friction bearings has become a current research hot topic. It is preferred to analyze the various complex sources of bearing friction, such as the structural constraints, and to reduce their sizes in a targeted manner by improving the structural and external operating conditions. Accurate computation of bearing friction loss, operating in complex motion and force conditions, has become a prerequisite for this research.

Since the middle of the 20th century, the frictional properties of bearing are investigated by few scholars. Under different working conditions, the friction torque of different types of bearings was experimentally tested by Palmgren et al. [4,5]. The empirical formulas of bearing frictional torque were proposed based on the experimental data. However, the friction model by these empirical formulas is mainly suitable for light load and low speed conditions. Besides, the famous bearing company SKF proposed a set of models for calculating bearing frictional torque also based on experimental dates [6]. Compared to the former, the model accuracy has been improved, while it is mainly used for bearings in standard installation and standard load condition. With an experimental method, the influence of the raceway curvature radius on the frictional torque of angular contact ball bearings was experimentally analyzed by Todd et al. [7]. Similarly, Rodionov [8] studied the effects of surface finish quality on bearing friction torque and it showed that, compared with the surface finish quality of rings, the rolling element significantly affected the friction torque. With the development of data processing methods, some new methods were applied to the study of bearing friction torque. Based on statistical correlation theory, the parametric-nonparametric fusion method was used to analyze the bearing friction torque by Xu [9]. By measuring the friction torque, Zhang et al. [10] modeled the data with gray theory to predict bearing friction torque. By summarizing the above work, it can be found that the present friction torque models were all based on experimental methods and dates, and then the overall friction performance of the bearing was investigated. However, the bearing friction torque is actually affected by many factors inside the bearing, such as bearing structural parameters, motion characteristics, load distribution etc. Especially for ball bearing, the ball’s revolution, spin, gyro and other motion forms will affect its friction performance.

Snare, Li and Wang et al. [11,12,13] pointed out that the friction inside the bearing mainly comes from the elastic hysteresis, differential sliding, spinning, and friction agitation. Ye et al. [14] established a simple friction model for bearing in steady state. The differential sliding and spin friction were considered while the complex motion in the contact area was ignored. In order to explore the influence of the movement of the contact area on the friction performance of the bearing, by energy conservation law, the solution results of the mechanical model were used to calculate the friction torque by Deng [15]. The results show that the complex motion of the contact zone, such as balls sliding in the contact zone, has an important impact on the friction loss. On the basis of the above studies, Todd et al. [16] used the micro-slip theory to determine the pure rolling line in the contact zone. Then the frictional resistance was solved by integrating the complex motion of the contact zone. Unfortunately, the friction torque model and mechanical model are unidirectionally coupled, thus the effect of friction torque on bearing internal motion is missing. Houpert et al. [17] analyzed the motion of the contact zone and obtained the pure rolling line between ball and raceway. Then, the integral of the contact zone was calculated to obtain the contact friction. Finally, the bidirectionally coupled friction torque was achieved based on Cao’s quasi-static model [18]. Because of the implementation of bidirectional coupling and the refinement of the contact zone, an obvious change of the friction results was observed. It indicates that the complex contact behavior between bearing components has a significant impact on its total friction loss. Therefore, it is necessary to study the internal friction characteristics of the bearing parts.

For bearing internal friction analysis, the current research mainly focuses on the steady-state friction. That is, the total friction is generated by the complex motion in the contact zone between the bearing parts, such as differential sliding and spin friction, etc. As mentioned earlier, due to the motion of the ball in the ball bearing being particularly special, the friction induced by the revolution is disregarded when the rolling elements move in the circumferential direction. In other words, the current friction calculation mainly considered the motions between the balls and the rings along the contact ellipse minor axis, while the sliding friction along the major axis is ignored [19]. In fact, in conditions of high speed and combined load, the internal forces of the bearing become very complicated. In addition to the friction caused by the gyroscopic torque, the friction generated by the contact angle cannot be neglected. Due to the inconsistent force of each rolling element, the contact angle between the balls and the ring is unequal, which is the main cause of the ball slides along the major axis of the contact ellipse during bearing operation. For instance, the technical report of SKF pointed out that a large variation in contact angle has an impact on the bearing friction [20]. As the ball slides along the major axis of the contact ellipse, the collision force between the cage pocket and the ball increased, which eventually causes the increases of bearing friction. Thus, it is of great significance to investigate the sliding of the rolling element of the bearing along the major axis of the contact zone. In this paper, taking the angular contact ball bearing as the research object, a quasi-static model is established. In condition of the combined load, it is found that the friction caused by the sliding length of the bearing is discussed, such as operating parameters, structural parameters and contact angles.

2. Quasi-Static Model of Ball Bearing

2.1. Establishment of Model

Due to the complex internal structure of angular contact ball bearings, the position relationship among the bearing parts is described. As shown in Figure 1, Figure 1b is the overall structure of an angular contact ball bearing, Figure 1a is a radial sectional view of the bearing, and Figure 1c is an axial sectional view. In Figure 1, the x-axis is defined as the bearing axial direction, and the radial plane is the y-z plane. As a whole, the bearing has five degrees of freedom (δ_x, δ_y, δ_z—movement along the x, y, and z axes, θ_y, θ_z—rotation around the y, z axes). In other words, under the action of load F (F_x, F_y, F_z, M_y, M_z), the bearing may produce a generalized displacement in five directions. When a bearing is used in engineering, the inner ring always rotates and the outer ring is fixed. Therefore, the external load and rotational speed are applied to the inner ring, while the outer ring is limited to six degrees of freedom.

2.1.1. Relative Position Analysis of Bearing Parts

After the ball at the azimuth position φ_j is loaded, its position changes are revealed in Figure 2. Before being loaded, the three points of the curvature center of the inner raceway, the ball center and the curvature center of the outer raceway were collinear and there was no contact deformation. The distance between the curvature center, the inner raceway and the outer can be expressed as follows:

$$l=B\cdot D_w,$$

(1)

where B = f_i + f_o − 1, f_i and f_o are the curvature ratios of the inner raceway and the outer, respectively. D_w represents the ball diameter.

When the load F (F_x, F_y, F_z, M_y, M_z) and rotational speed n_i are applied to the inner ring, the relative positions change among the curvature center of the inner raceway, the ball center and the curvature center of the outer raceway and the three are no longer collinear. As the rotational speed increases, the ball-inner raceway contact angle gradually enlarges, while the contact angle of the ball-outer raceway gradually decreases.

At the azimuth position φ_j, the distance between the curvature center of the inner raceway and the final position of the ball center is written as:

$$d_{ij}=\left(f_i-0.5\right)\cdot D_w+{\delta }_{ij}.$$

(2)

Similarly, the distance of the outer ring is obtained by:

$$d_{oj}=\left(f_o-0.5\right)\cdot D_w+{\delta }_{oj},$$

(3)

where δ_ij is the contact deformation between the ball and the inner raceway while the deformation of the outer is δ_oj.

From Figure 2, the distances between the curvature center of the inner raceway and the outer in the horizontal and vertical directions are calculated as:

$$A_{xj}=B\cdot D_w\cdot \sin {\alpha }^0+B_{xj}$$

(4)

$$A_{yj}=B\cdot D_w\cdot \cos {\alpha }^0+B_{yj},$$

(5)

where α⁰ means the initial contact angle. B_xj and B_yj are the variations of the curvature center of the inner raceway before and after loading on the x-axis and y-axis, respectively, which can be expressed as:

$$B_{xj}={\delta }_x+R_i\cdot {\theta }_y\cdot \sin {\phi }_j+R_i\cdot {\theta }_z\cdot \cos {\phi }_j$$

(6)

$$B_{yj}={\delta }_y\cdot \sin {\phi }_j+{\delta }_z\cdot \cos {\phi }_j,$$

(7)

where δ_x, δ_y, δ_z are the displacements of the inner center relative to the outer center on the x, y, and z axes, respectively. θ_y, θ_z denote the angular displacements around the y and z axes. R_i represents the radius of the inner curvature center, which is determined by:

$$R_i=d_m/2+\left(f_i-0.5\right)\cdot D_w\cdot \cos {\alpha }^0,$$

(8)

where d_m is the pitch diameter of the bearing.

By observing Figure 2, it can be seen that these equilibrium equations, established in the horizontal and vertical directions, contain a larger number of trigonometric functions. Trigonometric functions are known to be unfavorable for numerical iterative solutions because they are periodic functions. However, refer to Jones’s quasi-static model [21]; the new variables X_x and X_y are introduced to eliminate these functions to simplify the solution process. Among them, X_x and X_y denote the distance between the ball center and the inner curvature center in the horizontal and vertical directions, respectively. As shown in Figure 2, The contact angles of the ball at the azimuth position φ_j are written as Equations (9)–(12):

$$\sin {\alpha }_{oj}=\frac{X_{xj}}{\left(f_o-0.5\right)\cdot D_w+{\delta }_{oj}}$$

(9)

$$\cos {\alpha }_{oj}=\frac{X_{yj}}{\left(f_o-0.5\right)\cdot D_w+{\delta }_{oj}}$$

(10)

$$\sin {\alpha }_{ij}=\frac{A_{xj}-X_{xj}}{\left(f_i-0.5\right)\cdot D_w+{\delta }_{ij}}$$

(11)

$$\cos {\alpha }_{ij}=\frac{A_{yj}-X_{yj}}{\left(f_i-0.5\right)\cdot D_w+{\delta }_{ij}}.$$

(12)

In Figure 2, the geometric compatibility equations of the ball at the φ_j azimuth are given as Equations (13) and (14):

$${\left(A_{xj}-X_{xj}\right)}^2+{\left(A_{xj}-X_{xj}\right)}^2+{\left(\left(f_o-0.5\right)\cdot D_w+{\delta }_{oj}\right)}^2=0$$

(13)

$$X_{xj}{}^2+X_{yj}{}^2-{\left(\left(f_o-0.5\right)\cdot D_w+{\delta }_{oj}\right)}^2=0.$$

(14)

2.1.2. Interaction Force of Bearing Parts

Under high-speed operating conditions, the mechanical analysis of bearing components is complicated. The ball is applied to the centrifugal force, causing dissimilar ball-inner and ball-outer contact angles. The friction between the ball and the raceway is caused by the gyroscopic torque. The interaction of the bearing parts is displayed in Figure 3; Figure 3a is the force analysis of the entire bearing while Figure 3b is the j-th ball. When a load F (F_x, F_y, F_z, M_y, M_z) and rotational speed n_i are applied to the inner ring, the corresponding displacement δ (δ_x, δ_y, δ_z, θ_y, θ_z) is generated. At this time, the inner ring is pressed against the ball, and a corresponding contact deformation occurs between them. The gyroscopic torque is generated because of the non-zero contact angle.

By observing Figure 2 and Figure 3, the mechanical equilibrium equations of the ball at the azimuth position φ_j are as follows:

$$Q_{oj}\cdot \cos {\alpha }_{oj}-{\lambda }_o\frac{M_{gj}}{D_w}\cdot \sin {\alpha }_{oj}-Q_{ij}\cdot \cos {\alpha }_{ij}+{\lambda }_i\frac{M_{gj}}{D_w}\cdot \sin {\alpha }_{ij}-F_{cj}=0$$

(15)

$$Q_{oj}\cdot \sin {\alpha }_{oj}+{\lambda }_o\frac{M_{gj}}{D_w}\cdot \cos {\alpha }_{oj}-Q_{ij}\cdot \sin {\alpha }_{ij}-{\lambda }_i\frac{M_{gj}}{D_w}\cdot \cos {\alpha }_{ij}=0,$$

(16)

where Q_i/oj = K_i/oj·δ_i/oj^1.5, K_i/oj is the contact deformation coefficient between the ball and the inner/outer ring, which can be calculated from [22]. λ_i/o represents the inner/outer raceway control coefficient. According to reference [23], if it is inner raceway control, λ_i = 1, λ_o = 1, otherwise it is outer raceway control, λ_i = 0, λ_o = 2.

Besides, the gyroscopic torque and centrifugal force of the ball are calculated with Equations (17) and (18):

$$M_{gj}=J_b\cdot {\left(\frac{w_R}{w_i}\right)}_j\cdot {\left(\frac{w_m}{w_i}\right)}_j\cdot w_i^2\cdot \sin {\beta }_j$$

(17)

$$F_{cj}=0.5\cdot m_b\cdot d_m^2\cdot w_i^2\cdot {\left(\frac{w_m}{w_i}\right)}_j^2,$$

(18)

where J_b is the ball moment of inertia, w_i means the angular velocity of the inner ring, and m_b denotes the ball mass.

According to Jones’ model theory [24], w_m/w_i, w_R/w_i, and tanβ_j are related to the rotation speed and attitude of the ball, which can be expressed as the following formula:

$$\frac{w_m}{w_i}=\frac{1}{1+\left(\frac{\cos {\alpha }_{oj}+\tan \beta \cdot \sin {\alpha }_{oj}}{\cos {\alpha }_{ij}+\tan \beta \cdot \sin {\alpha }_{ij}}\times \frac{1+\gamma \cdot \cos {\alpha }_{oj}}{1-\gamma \cdot \cos {\alpha }_{ij}}\right)}$$

(19)

$$\frac{w_R}{w_i}=\frac{-1}{\left(\frac{\cos {\alpha }_{oj}+\tan \beta \cdot \sin {\alpha }_{oj}}{1+\gamma \cdot \cos {\alpha }_{oj}}+\frac{\cos {\alpha }_{ij}+\tan \beta \cdot \sin {\alpha }_{ij}}{1-\gamma \cdot \cos {\alpha }_{ij}}\right)\cdot \gamma \cdot \cos \beta }$$

(20)

$$\beta =\arctan \left(\frac{\sin {\alpha }_{ij}}{\cos {\alpha }_{ij}+\gamma }\right),$$

(21)

where γ represents the dimensionless constant, γ = D_w/d_m.

Under high-speed operating conditions, the angular contact ball bearing can be regarded as a whole, and the load acting on the bearing should be balanced. In this paper, the inner ring is used as the carrier, and the load applied by the outside should be balanced with the load applied by the ball. The equilibrium equations of the inner can be established:

$$F_x-{\displaystyle \sum _{j=1}^Z\left(Q_{ij}\cdot \sin {\alpha }_{ij}+{\lambda }_i\frac{M_{gj}}{D_w}\cdot \cos {\alpha }_{ij}\right)}=0$$

(22)

$$F_y-{\displaystyle \sum _{j=1}^Z\left(Q_{ij}\cdot \cos {\alpha }_{ij}-{\lambda }_i\frac{M_{gj}}{D_w}\cdot \sin {\alpha }_{ij}\right)}\cos {\phi }_j=0$$

(23)

$$F_z-{\displaystyle \sum _{j=1}^Z\left(Q_{ij}\cdot \cos {\alpha }_{ij}-{\lambda }_i\frac{M_{gj}}{D_w}\cdot \sin {\alpha }_{ij}\right)}\sin {\phi }_j=0$$

(24)

$$M_y-{\displaystyle \sum _{j=1}^Z\left(\left(Q_{ij}\cdot \sin {\alpha }_{ij}+{\lambda }_i\frac{M_{gj}}{D_w}\cdot \cos {\alpha }_{ij}\right)\cdot R_i-{\lambda }_i\cdot f_i\cdot M_{gj}\right)}\sin {\phi }_j=0$$

(25)

$$M_z-{\displaystyle \sum _{j=1}^Z\left(\left(Q_{ij}\cdot \sin {\alpha }_{ij}+{\lambda }_i\frac{M_{gj}}{D_w}\cdot \cos {\alpha }_{ij}\right)\cdot R_i-{\lambda }_i\cdot f_i\cdot M_{gj}\right)}\cos {\phi }_j=0,$$

(26)

where Z means the number of balls.

2.2. Model Solution

The quasi-static model of an angular contact ball bearing is composed of nonlinear equations, including the geometric compatibility Equations (13) and (14) of the ball, the force balance Equations (15) and (16), and the balance equation of the inner ring Equations (22)–(26). The model has 4Z + 5 nonlinear equations and 4Z + 5 unknowns, such as X_xj, X_yj, δ_ij, δ_oj, δ_x, δ_y, δ_z, θ_y, θ_z (j = 1····z). Considering the solution accuracy and efficiency of non-linear equations, the Newton–Raphson iterative algorithm is adopted to solve. Because the initial value affects the accuracy of the iterative algorithm, and a large number of solution parameters is included in this model. The results of the statics model [21] are used as the initial value of the quasi-static and are transferred to the quasi-static model. The solution process of the above model is shown in Figure 4, and the iteration convergence accuracy (eps) sets to 10⁻⁵.

3. Model Verification and Sliding Loss Analysis

3.1. Model Versatility Verification

In this section, the mechanical model established above is verified by comparing the relationship between the force and displacement of the bearing and the contact characteristic. The displacement relation (stiffness) is verified by experiments, and the contact characteristic (contact angle) is compared with the published reference.

3.1.1. The Relationship between Force and Displacement

First, the bearing stiffness test system built by our team was used to verify the mechanical model above. As shown in Figure 5, the inner ring of bearing rotates with the precision mandrel 5 while the outer is fixed. The non-contact axial load is applied to the bearing through the air bearing plate 3, and the displacement sensor 6 and the force sensor 2 are used to test the relative displacement of the inner and outer rings and the axial force. The force and displacement signals are collected through the data acquisition system to measure the axial stiffness of the bearing.

Based on the stiffness test system, the stiffness of a B7008C/P4 angular contact ball bearing is measured. The specific structural parameters of B7008C/P4 are shown in

Table 1. The B7008C/P4 structural parameters.

Parameters	Values
Inner raceway curvature radius ri/mm	4
Outer raceway curvature radius ro/mm	3.79
Ball diameter Dw/mm	7.144
Number of balls Z	19
Pitch diameter dm/mm	54.007
Initial contact angle α0/°	15

. We applied an axial force of 150 N and 300 N respectively, the rotational speed was gradually increased from 100 r/min to 1900 r/min. The change in axial stiffness of the bearing is shown in Figure 6.

By observing Figure 6, it can be seen that the bearing stiffness decreases as the rotational speed increases. This is caused by the change in contact angle due to the variable rotational speed. The axial force has an obvious influence on the bearing stiffness, and the stiffness increases as the axial force grows at the same speed. By comparing the theoretical simulation with the experiment, the errors do not exceed 5%, which proves the model. The errors may be caused by the axial runout of the spindle.

3.1.2. The Contact Characteristic

Second, by comparing the deviation of the solution results of the model with that of Harris et al. [24], the model is proved. A 218 angular contact ball bearing was taken as the research object and the model was solved under given conditions. From reference [24], the initial contact angle of the 218 was 40°, and the rotational speed respectively was set to 6000, 10,000, 15,000 r/min, while the axial force was gradually increased from 17,500 N to 44,500 N since the focus of this study was the contact angle, which was the object of verification. Figure 7 is the result of the comparison.

From Figure 7, the contact angle is greatly affected by the axial force and the rotational speed. The ball-inner raceway contact angle gradually reduces as the axial force increases, while the contact angle of the outer becomes larger. With the increasing rotational speed, the ball-inner raceway contact angle continuously increases and the contact angle of the outer decreases. By comparison, the deviation between the results of this model and the results [24] is within 5%, which is considered to be caused by unit conversion, and the correct and reliable of the model was obtained. The error may be caused by unit conversion.

3.2. Analysis of Sliding Loss Caused by Contact Angle Changes

Based on the model above, the B7008C/P4 bearing is taken as the research object to investigate the sliding. Firstly, the contact characteristics among the bearing components under the combined load are analyzed.

The dynamic characteristics of the 7008 can be obtained by solving the quasi-static model. The constant combined load (F_x = 500 N, F_z = −300 N) and rotational speed (n_i = 10,000 r/min) are considered. The force applied to each ball is not equal because of the radial load, which causes their contact angle values to be different. The variability of the contact angle will cause sliding between the ball and the raceway, as shown in Figure 8.

Owing to the variable of the contact angle, the ball slides along the major axis of the contact ellipse relative to the raceway and the sliding length of the ball relative to the inner raceway at the azimuth position φ_j is:

$$s_{ij}=r_i\cdot \left({\alpha }_{ij}-{\alpha }_{imin}\right).$$

(27)

The sliding length of the ball at this azimuth relative to the outer raceway is:

$$s_{oj}=r_o\cdot \left({\alpha }_{oj}-{\alpha }_{omin}\right),$$

(28)

where α_ij is the contact angle of the ball at the azimuth φ_j with the inner ring and the angle of the ball with the outer is α_ij. α_imin expresses the minimum contact angle of the ball with the inner ring when it runs for a cycle while α_omin means the minimum angle of the ball with the outer ring.

To clearly express the ball information of each azimuth angle, the ball is labeled. The ball mark in the opposite direction to the z axis is designated as 0, where the azimuth angle is 0°. The counterclockwise rotation around the x-axis is specified as the positive direction.

By observing Figure 8 and Figure 9, when the ball azimuth is 0°, the contact angle between the ball and the inner ring or the outer is a minimum. At this location, the contact point between the ball and the inner ring is a₁, and the contact point with the outer ring is b₁. At the azimuth position 180°, the contact angle between the ball and the inner ring or the outer is a maximum. The contact point between the ball and the inner ring at the position is a₂, and the contact point with the outer ring is b₂. When the ball moves from 0° to 180°, the contact angle between the ball and the ring gradually becomes bigger and the contact point between the ball and the ring moves from 1 to 2 along the major axis of the contact ellipse. In contrast, the contact angle between the ball and the ring reduces, when the ball moves from 180° to 360° (0°). The contact point between the ball and the ring moves from 2 to 1 along the major axis of the contact ellipse. In the dynamic operation process, when the ball runs for a week, the contact angle changes cyclically once (from small to large, and then from large to small). The contact point moves back and forth between 1 and 2 points. Figure 9 is the relationship between the change of the contact angle and the sliding length of the ball in a period. Under the working conditions, the maximum sliding length between the ball and the inner ring is 0.6987 mm for 7008, and the maximum sliding length of the outer ring is 0.5381 mm.

During operation, the motion of the bearing parts is shown in Figure 10. Assuming no sliding occurs on the bearing, the driving rotational speed applied by the inner ring only rotates around its own x-axis. Thus, the velocity component of the ball is concentrated in the ellipse contact minor axis direction between the ball and the inner ring, while the component in the major axis direction is smaller under the circumstances. The motion in the minor axis direction is rolling, and the sliding occurs in the major axis direction. Since the rolling friction coefficient is very small, there is little heat generation. However, the sliding friction coefficient is large, and the friction heat is serious. The sliding in major axis direction is the focus of the investigation.

The bearing friction loss above occurs due to sliding caused by changes in the contact angle. The micro-element method is used to calculate the loss. Firstly, the ball is divided into finite parts for a week and the results are added up to obtain the average value, which is expressed as:

$$H=\frac{1}{n}{\displaystyle \sum _{j=1}^{n}F{f}_j}\cdot \frac{\Delta s_j}{\Delta t},$$

(29)

where n means that the operation week of the ball is divided into n stages. Ff_j is the average friction force experienced by the ball in stage j. Δs_j represents the slip increment of the ball in stage j. Δt denotes the time taken to pass stage j for the ball.

For the frictional force Ff_j, assuming ignoring the slight rolling, the sliding is only considered in the major axis direction. Such force can be determined as follows:

$$F{f}_j=\frac{\mu \left(Q_j+Q_{j+1}\right)}{2},$$

(30)

where μ is the sliding friction coefficient, which can be obtained in [25].

Based on the above theory, a combined-loaded bearing (F_x = 500 N, F_z = −300 N, n_i = 10,000 r/min) is solved. Because of the ball sliding along the major axis, the heat generated on the inner raceway is 9.456 W, while the outer is 8.624 W. The integral heating of the bearing obtained by empirical equation [26] is 132.2792 W. The power loss by sliding approximately accounts for 13.67% of the total heat. Ignoring the sliding loss, the results of frictional heat will be seriously affected and the heat generated by the sliding loss is almost proportional to the sliding length of the ball along the major axis direction on the raceway. Thus, the sliding length is taken as the evaluation criterion to investigate the friction, and the effects of working conditions and curvature ratio are analyzed.

4. Results and Discussion

Based on the model in Section 2, a 7008 angular contact ball bearing is taken as the object to be solved. By the sliding length of the ball on the raceway, the friction loss of the bearing with different initial contact angles (15°, 25°) is studied. The efforts of the working conditions and the structural parameters are discussed.

4.1. Radial Loaded Bearing

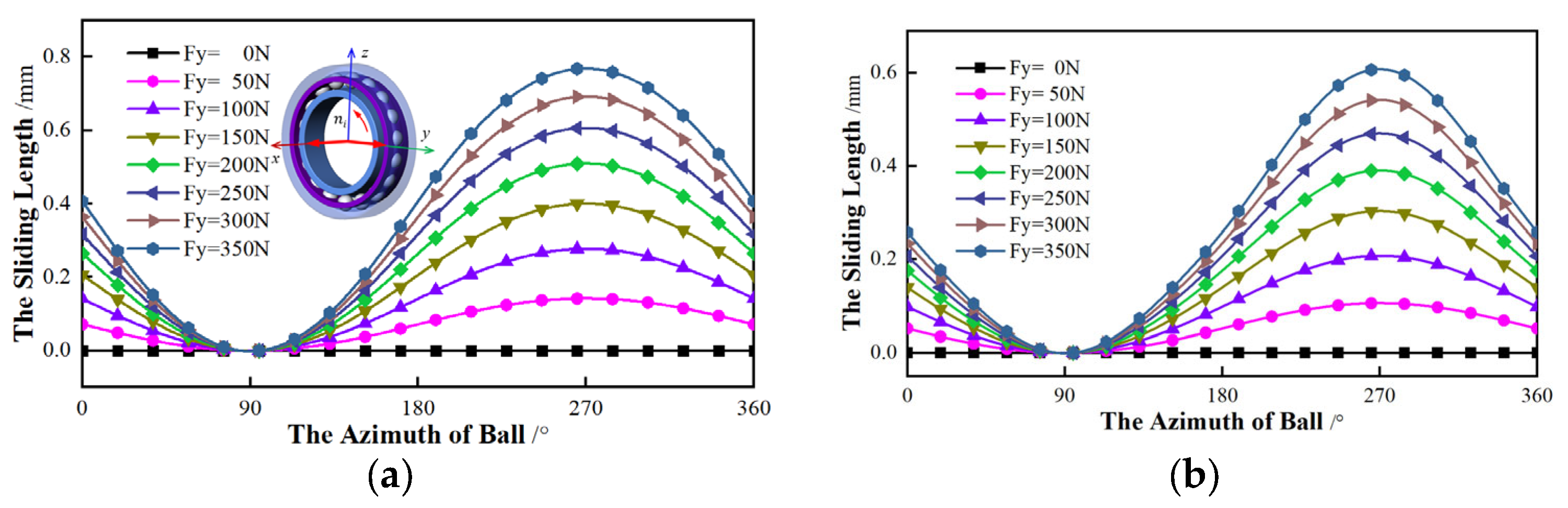
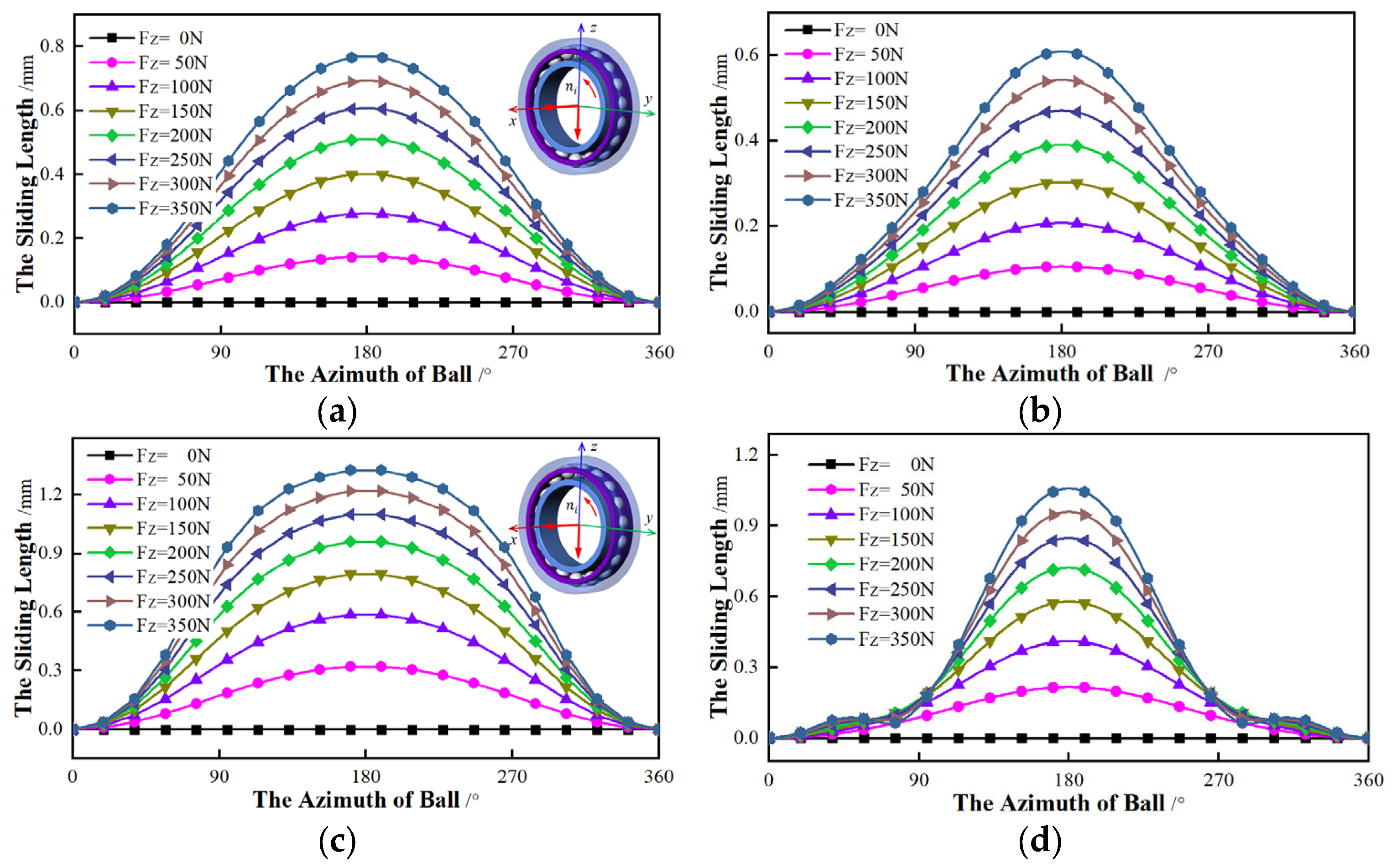
The influence of the radial force on the ball sliding is first studied, including the direction and magnitude. Without the torque (M_y = M_z = 0 N·mm), a constant axial force (F_x = 500 N) and rotational speed (n_i = 10,000 r/min) is considered. By changing the radial force, the trend of sliding with different contact angles is analyzed.

Firstly, the y-axis is applied to the radial force, while the force of the z-axis is 0. With the rising of radial force (F_z) on the y-axis, the sliding length of the ball with different contact angles is shown in Figure 11.

The relationship between the sliding length and the radial force is shown in Figure 9. For bearings with the same initial contact angle, the effect of force is similar. The minimum contact angle (α_min) appears when the ball is 90°, where the sliding length is 0. The maximum contact angle (α_max) is located at the ball azimuth of 270°, which is the largest sliding. As the radial force of F_y grows, the sliding length increases. The variation trend of the sliding is relatively slight when the contact angle of the ball near the α_min or α_max. The friction loss is quite small. On the contrary, the trend is relatively sharp in other positions, and the loss becomes large. As for bearings of different initial contact angles, the azimuth angles of α_min or α_max are the same. However, the sliding trend of the bearing with 25 ° is larger than that of the 15° under the same force, and the friction loss is also greater. When the ball azimuth closes 45° and 135°, the variation of sliding changes rapidly for the inner, while the larger change for outer appears near the azimuth of 225° and 315°. This means there is more friction.

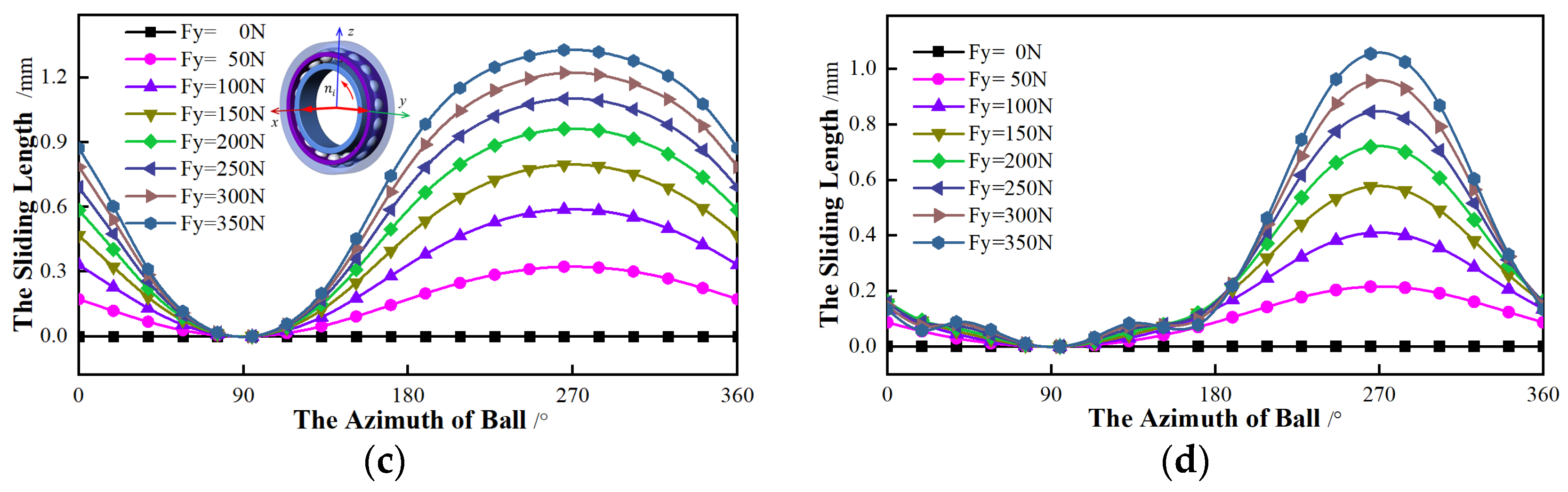
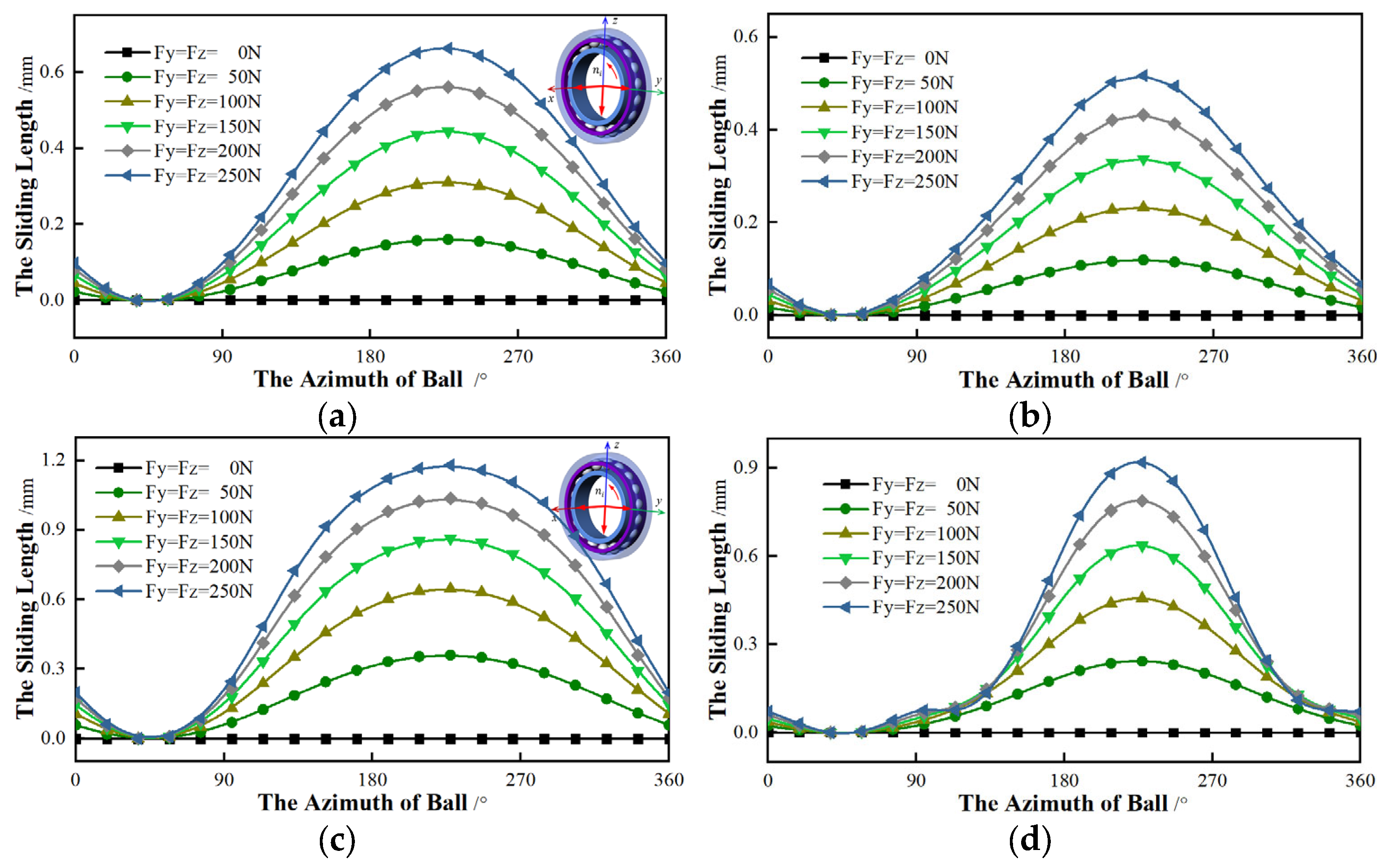
Secondly, setting F_y to 0, the z-axis is applied to the radial force. As shown in Figure 12, the relationship between the sliding with different contact angles and the radial force is analyzed. No matter whether the initial contact angle is 15° or 25°, the α_min appears at the position where the azimuth is 0°, and the azimuth of the α_max is 180°. The other effects of the z-axis are similar to the force applied in the y-axis.

Finally, the y-axis and the z-axis are applied to the radial force at the same time, which is gradually growing. Figure 13 shows the relationship between the radial force and the sliding with different initial contact angles and the radial force. It can be found that, regardless of the initial contact angle, the azimuths of α_min and α_max are constant and the α_min appears at the azimuth of 45°, while the 225° azimuth is the α_max. Other changes have similar effects to the radial force applied to the y-axis or the z-axis individually.

To summarize, the sliding length is only affected by the magnitude of the radial force, independent of its direction. With the increasing of the radial force, the variation trend of sliding is increases. However, the direction of the radial force has an influence on the azimuth angles of α_min and α_max.

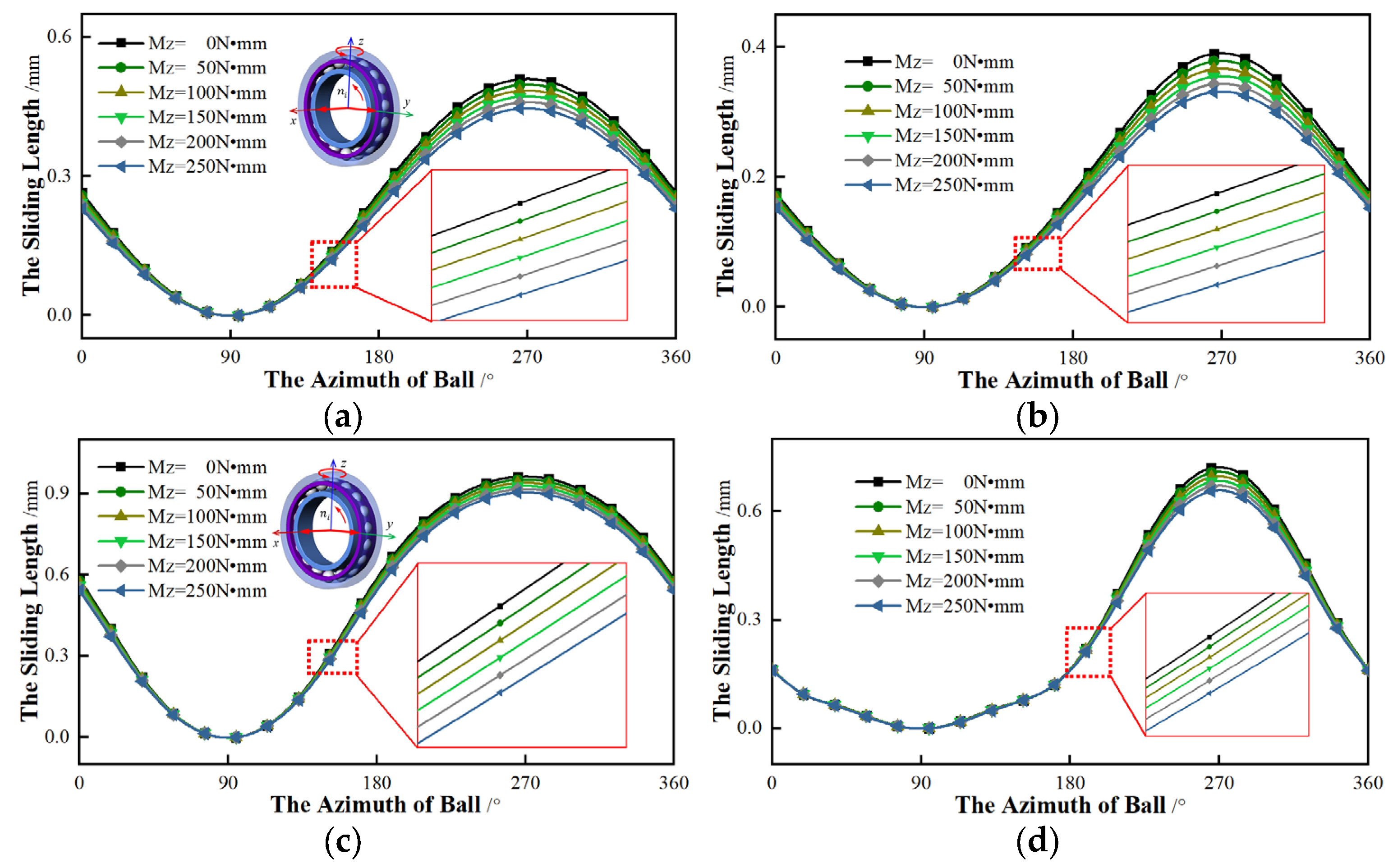
4.2. Torque Component

In this section, the relationship between the torque and the sliding is investigated. The axial force (F_x = 500 N), radial force (F_y = 200 N, F_z = 0 N) and rotational speed (n_i = 10,000 r/min) are constant. The sliding of different initial contact angles is discussed by changing the torque.

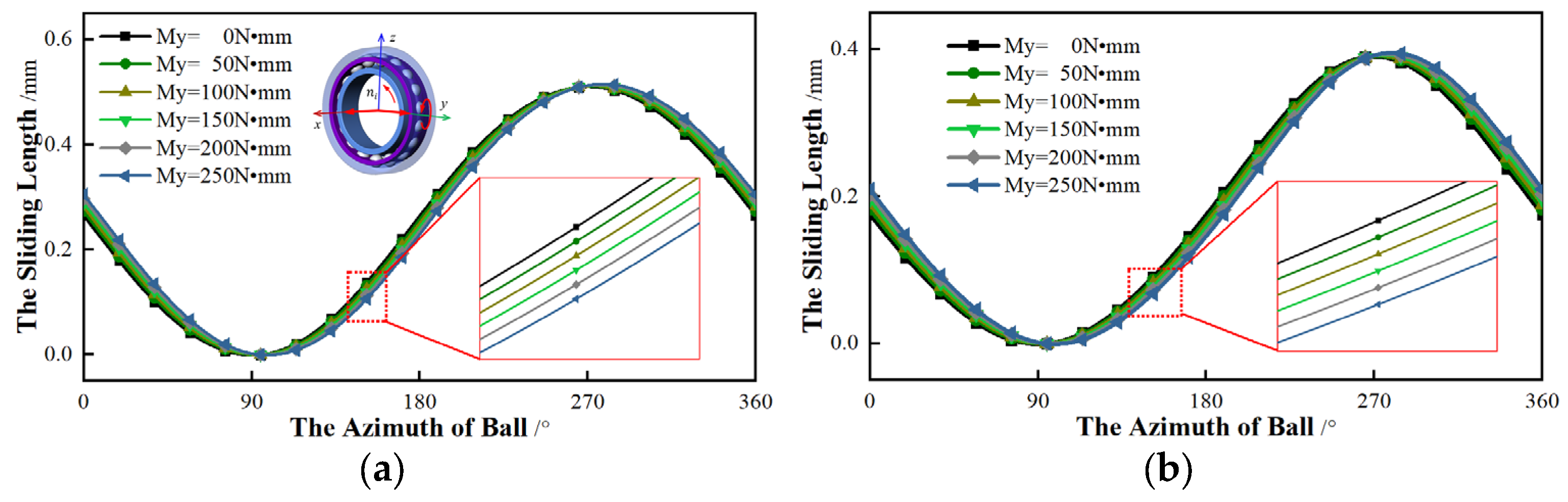
Firstly, the y-axis is only applied to the torque, which increases from 0 N·mm to 250 N·mm. The torque of the z-axis is 0. This means that the radial force and the torque are exerted to the same axis. Figure 14 shows the relationship between the torque and the sliding of different initial contact angles.

From Figure 14, the difference in sliding of different contact angles is small. As the torque component increases, the azimuth angles of α_min and α_max are same and the sliding lengths of different torques are almost equal. Although the sliding rate grows with the increase of torque, the effect is small. For bearings with different initial contact angles, the influence of torque on the sliding is not obvious. The sliding of an initial contact angle of 25 ° is slightly less sensitive to this torque than that of 15 °. From Figure 14, we can see that the total sliding length of a larger initial contact angle is greater than the sliding of a small contact angle.

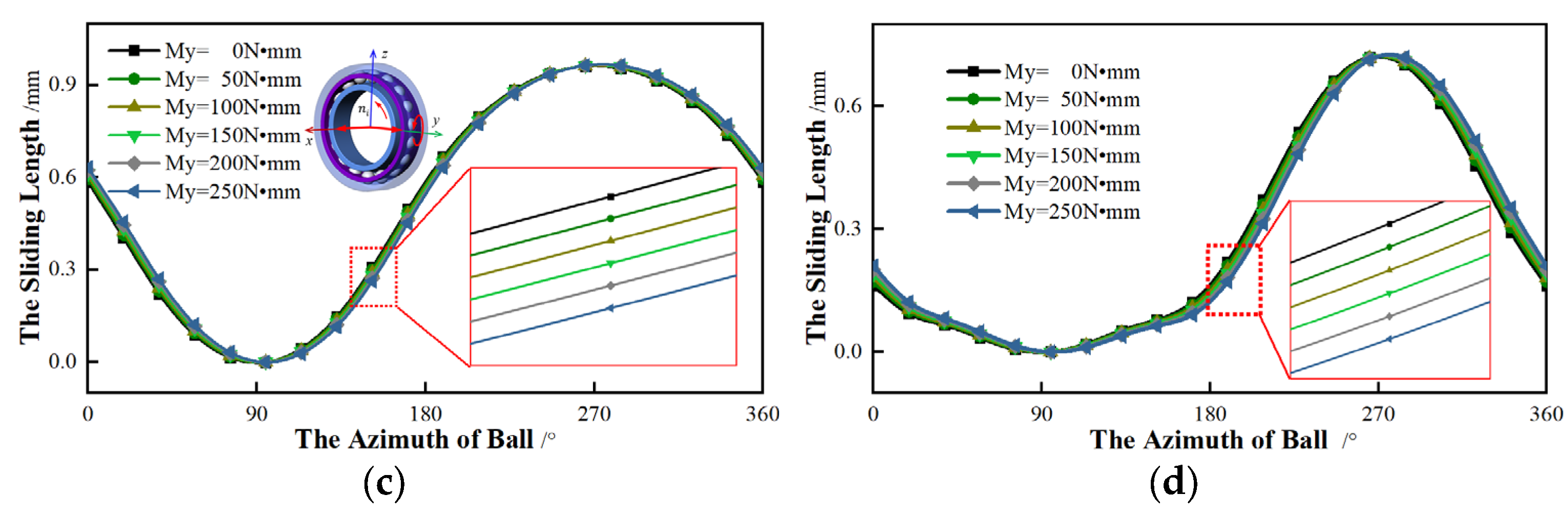
Secondly, the z-axis applied to the torque is considered, which is gradually rising. In other words, the radial force is applied to the y-axis while the z-axis exerts to the torque. The relationship between the torque and the sliding length of different initial contact angles is shown in Figure 15.

As shown in Figure 15, this type of torque has an influence on the sliding length of the bearing with the same initial contact angle. As the torque rises, the sliding length gradually decreases and the azimuth angles of α_min and α_max are constant. As for the variation rate of sliding, it also gradually reduces. With regard to bearings with different initial contact angles, the variation rates are distinct. The rate of bearings with an initial contact angle of 15° is more sensitive to torque than the rate of 25°. However, the total sliding length of the 25° is generally greater than that of the 15°.

In summary, when the torque and radial load are applied to the same axis, the effect of torque on sliding is very weak. On the contrary, applying the torque and radial load to the different axes, the torque has a corresponding effect on the sliding. With the torque increasing, the sliding length gradually lessons. From Figure 14 and Figure 15, regardless of whether the torque and the radial force are on the same axis, the sliding lengths of different initial contact angles are unequal and the sliding with an initial contact angle of 25° is always greater than that of 15°.

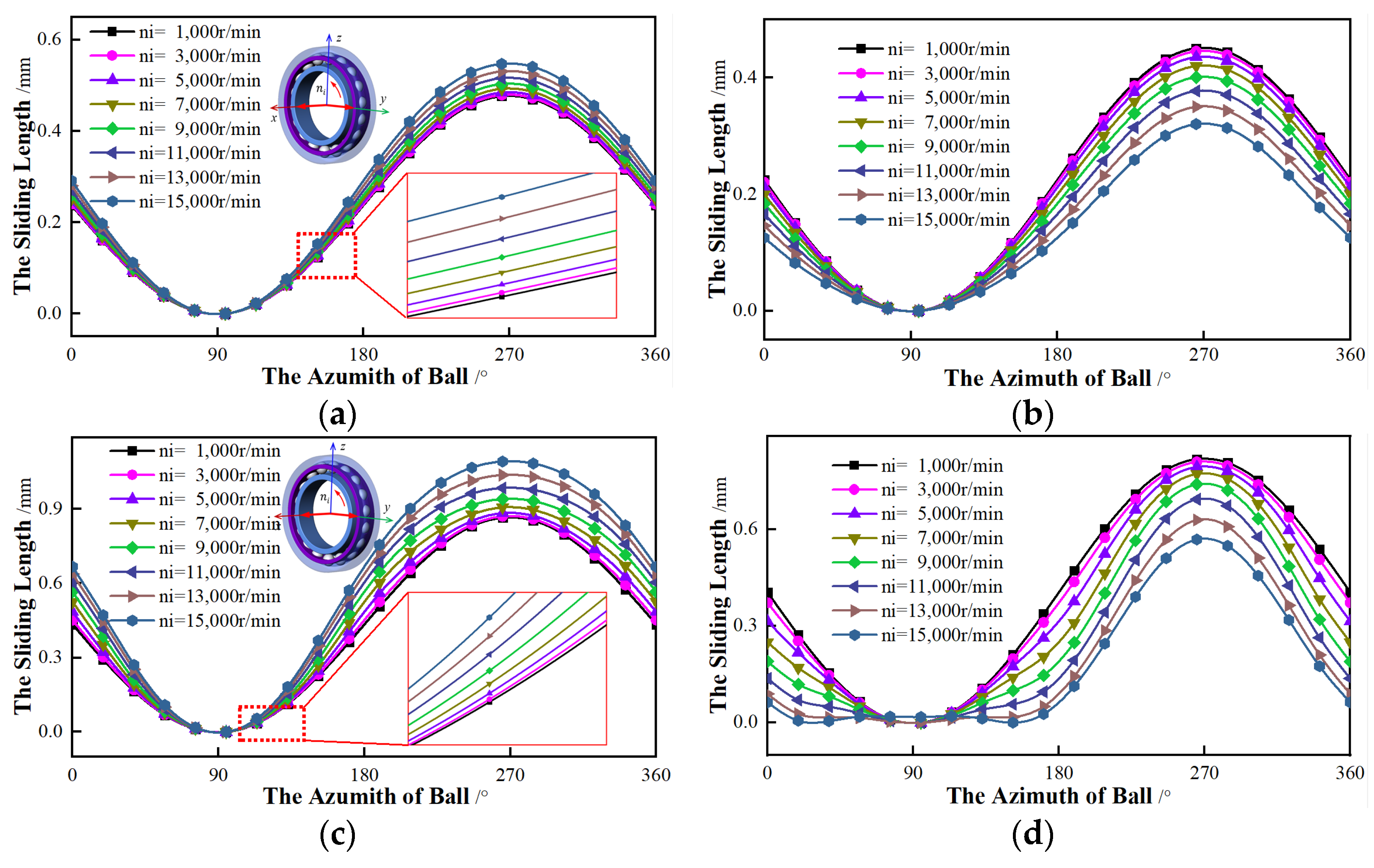
4.3. Rotational Speed Bearings

To reveal the influence of rotational speed on sliding length, speed gradually increases. Regardless of the torque (M_y = M_z = 0 N·mm), the axial force (F_x = 500 N) and the radial force (F_y = 200 N, F_z = 0 N) are considered. Figure 16 shows the relationship between the sliding length and the rotational speed.

Figure 16 shows the curves of the sliding length changing with the rotational speed for the bearing. It can be seen that, as the rotational speed increases, the azimuth angles of α_min and α_max remain unchanged. For the inner ring, the higher the speed, the greater the sliding length, and the faster the variation rate of sliding. On the contrary, with the rising rotational speed, the sliding length of the outer ring reduces and the change rate of outer sliding gradually grows. Compared with the outer ring, the inner ring is more sensitive to the speed. As for the bearing with different initial contact angles, the sliding with an initial contact angle of 25° changes more than that of 15°. Besides, for the bearing with an initial contact angle of 25°, the non-sliding area appears near the α_min.

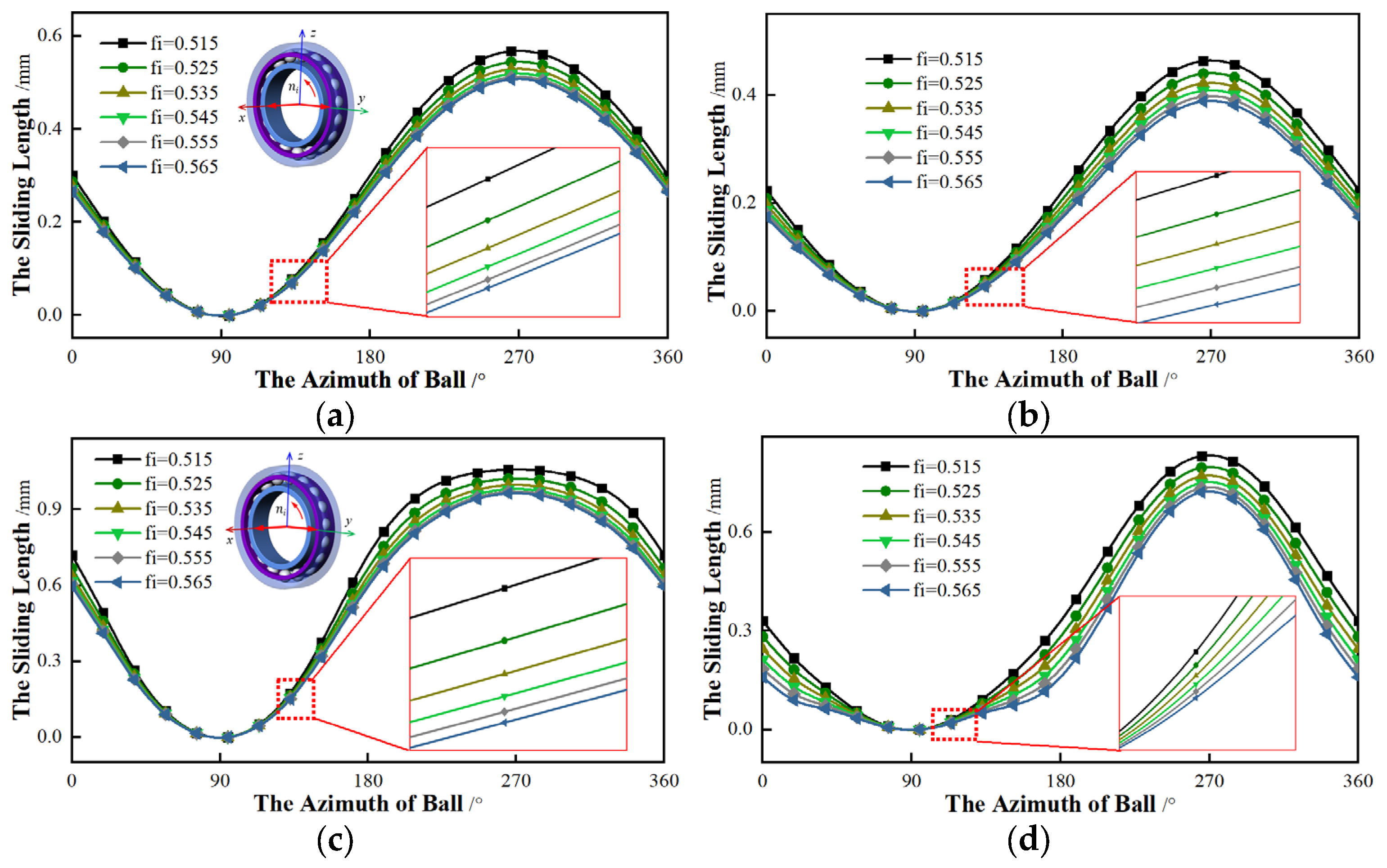
4.4. Groove Curvature Ratio

In addition to working conditions, the structural parameters may also affect the sliding. The curvature ratio of the raceway has an important influence on the friction loss. Ignoring the torque (M_y = M_z = 0 N·mm), a constant combined force (F_x = 500 N, F_y = 200 N, F_z = 0 N) and constant speed (n_i = 10,000 r/min) are applied to the bearings. The effects of the curvature ratio of the raceway on the sliding are investigated.

Firstly, the influence of the curvature ratio of the inner raceway on the sliding is considered. The curvature ratio of the outer raceway is constant (f_o = 0.535), while the ratio of the inner (f_i) gradually increases from 0.515 to 0.565. The relationship between the ratio of the inner and the sliding lengths is shown in Figure 17.

By observing Figure 17, as the curvature ratio of the inner raceway increases, the azimuths of α_min and α_max are constant and the sliding length of rings gradually decreases. However, once the ratio reaches a certain value, the sliding changes will be not obvious. The initial contact angle of the bearing is different, and the influence of the ratio on the sliding is different. The sliding length of a bearing with an initial contact angle of 15° is smaller than that of 25°.

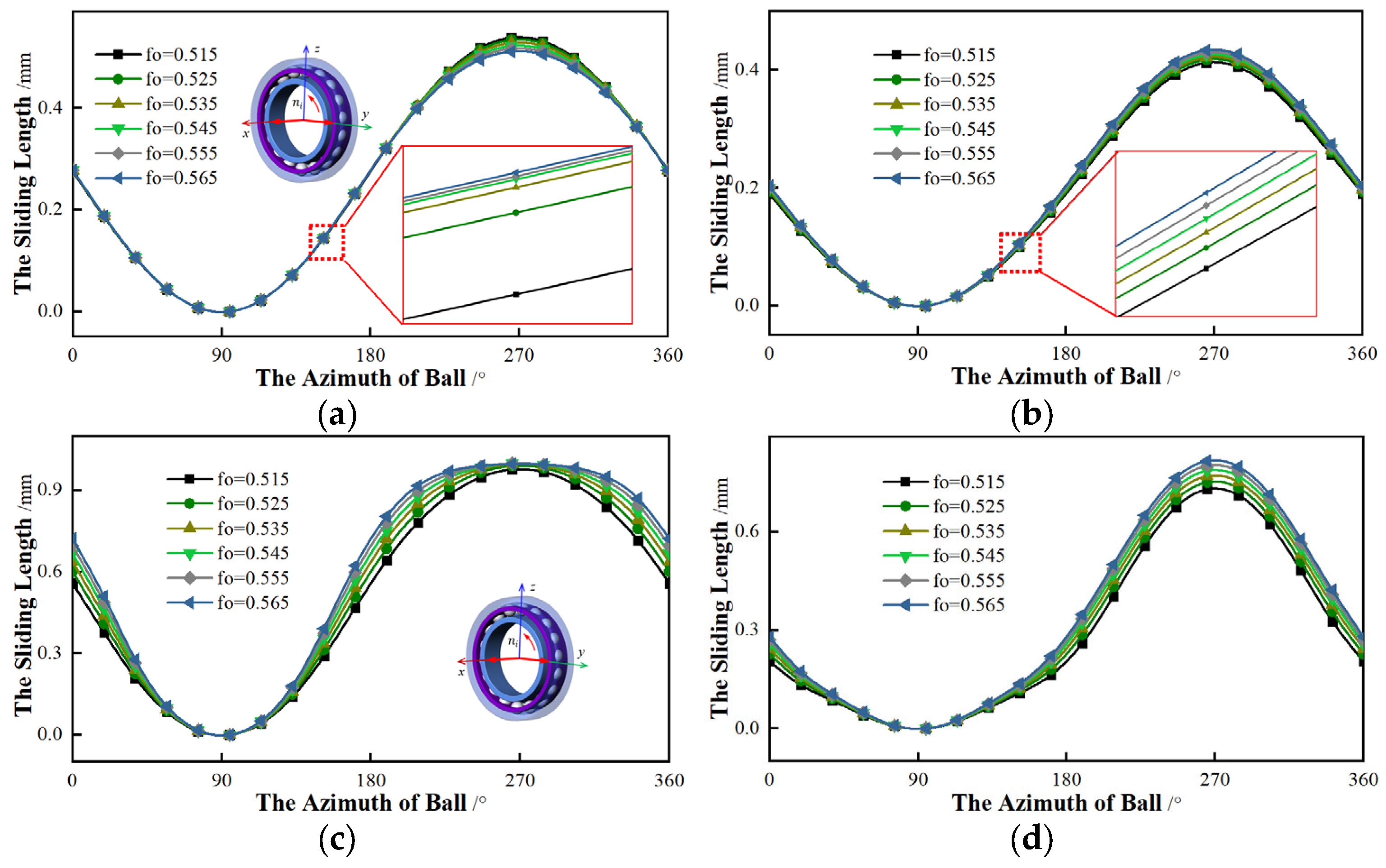
Then the relationship between the curvature ratio of the outer raceway and the sliding is analyzed. Keeping the ratio of the inner constant (f_i = 0.535), the outer ratio (f_o) gradually increases. The influence of the outer ratio on the sliding is presented in Figure 18. The outer ratio has a weak effect on the sliding length, but the overall trend gradually increases. When the outer ratio exceeds a certain value and continues to increase, the sliding length is almost constant. For bearings with different initial contact angles, the effects of the outer ratio on the sliding are disparate. For the bearing with an initial contact angle of 15°, the effect of the outer ratio on sliding is not distinct. However, the outer ratio has a significant impact on the sliding for the bearing with 25°. As the outer ratio increases, not only the sliding length but also the variation rate of the sliding gradually grows.

To summarize, compared with the curvature ratio of the outer raceway, the sliding is more sensitive to the inner ratio. In addition, the larger the inner ratio, the smaller the sliding length. The influence of the outer ratio on the sliding is just the opposite; with an increasing outer ratio, the sliding gradually decreases.

5. Conclusions

Taking the sliding length as the evaluation object, the influences of working conditions and structural parameters on bearing friction are investigated, and the conclusions are as follows:

(1)

The effect of radial force on the sliding length is great. As the radial force rises, the sliding length between the ball and raceway grows, especially with a larger initial contact angle;

(2)

The direction of torque also has an important influence on the sliding length. When the radial force and torque are applied on the same coordinate axis, the magnitude of the torque hardly affects the sliding, while when applied on the different axes, the influence is obvious;

(3)

With the increase of the rotational speed, the sliding between the ball and the inner raceway increases, while the sliding of the outer raceway decreases;

(4)

The curvature ratios of both inner and outer rings affect the sliding, while the influence trend is the opposite. As the ratio increases, the sliding of the inner increases, while that of the outer decreases.