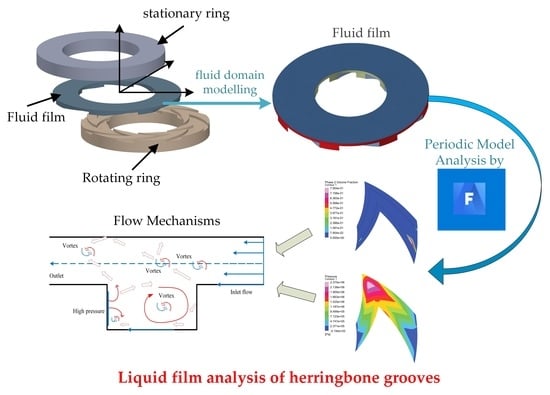
Flow Mechanisms and Lubrication Performance of Water-Lubricated Thrust Bearings with Herringbone Grooves
Abstract
:1. Introduction
2. Governing Equations
2.1. Conservation Equations
2.2. Cavitation Equations
3. Model Analysis
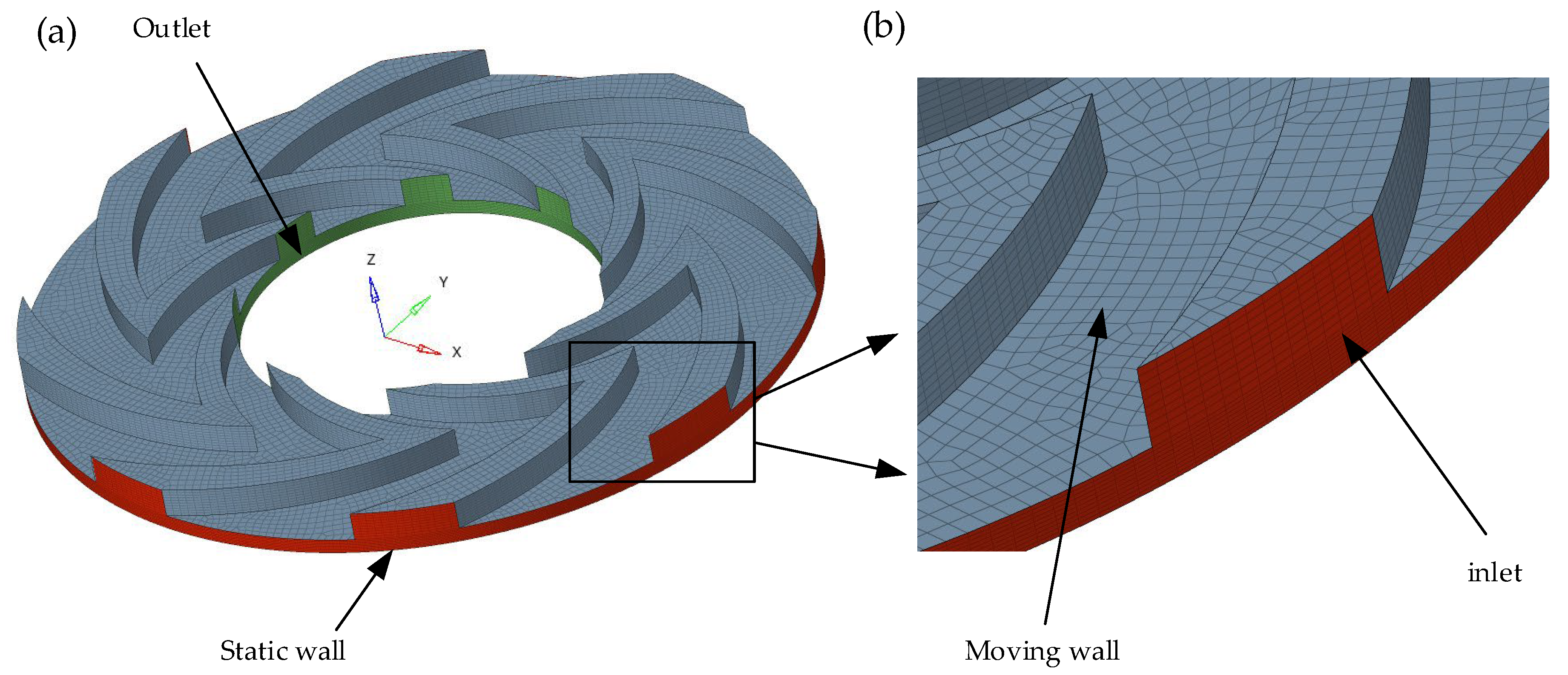
3.1. Geometric Model
3.2. CFD Model
3.3. Viscosity–Temperature Relationship
3.4. Solver Settings
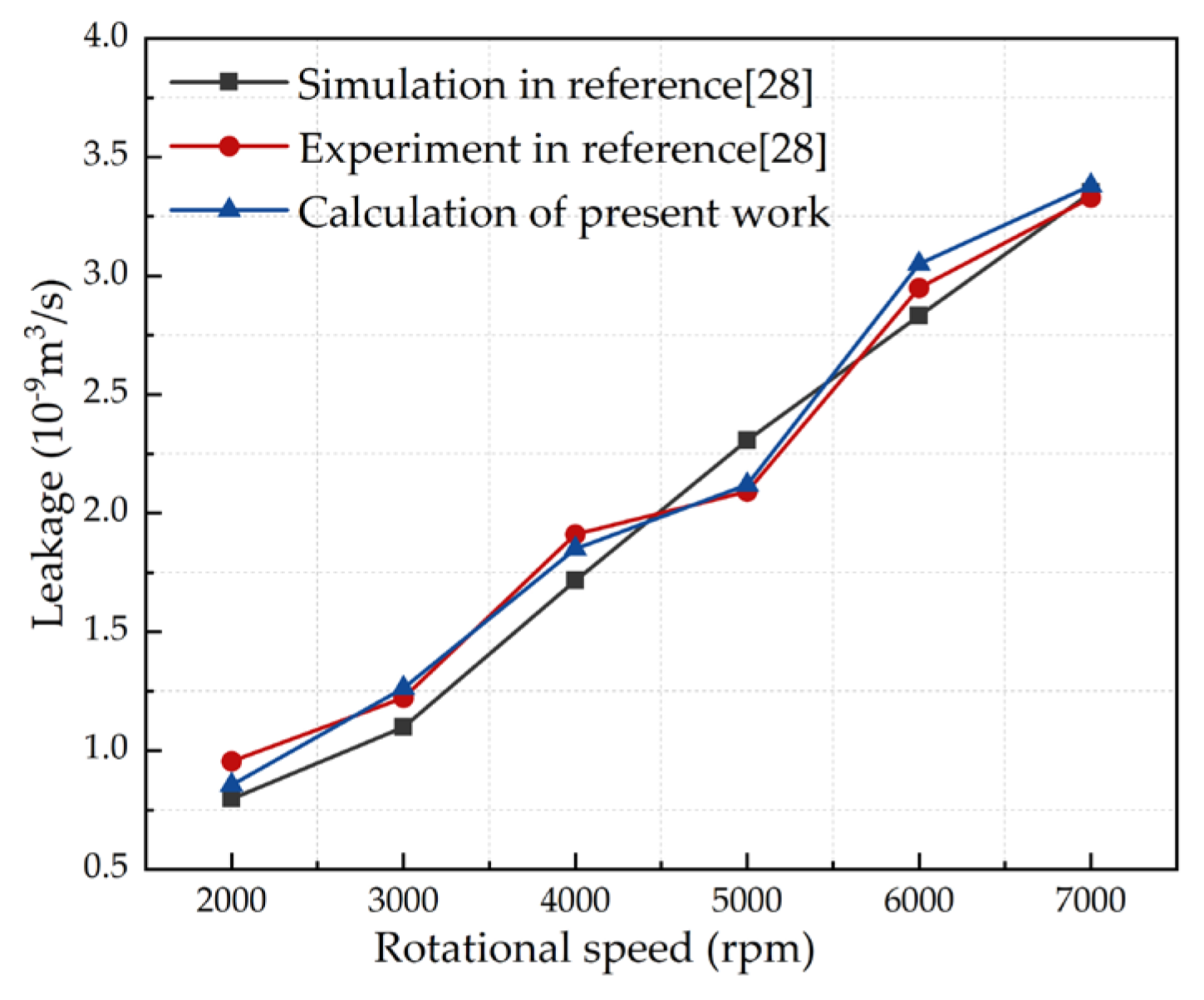
3.5. Verification of the Model
4. Results and Discussion
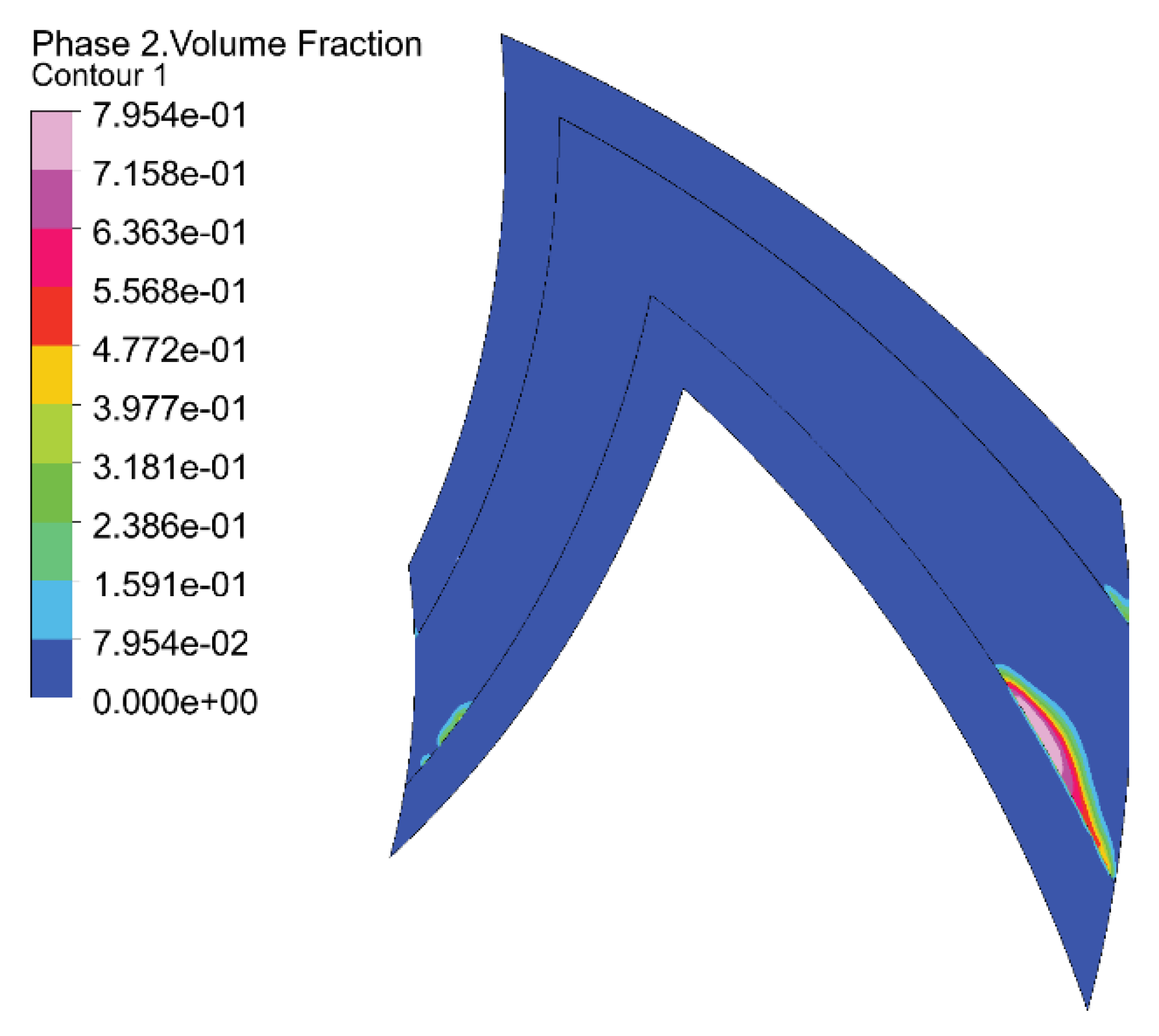
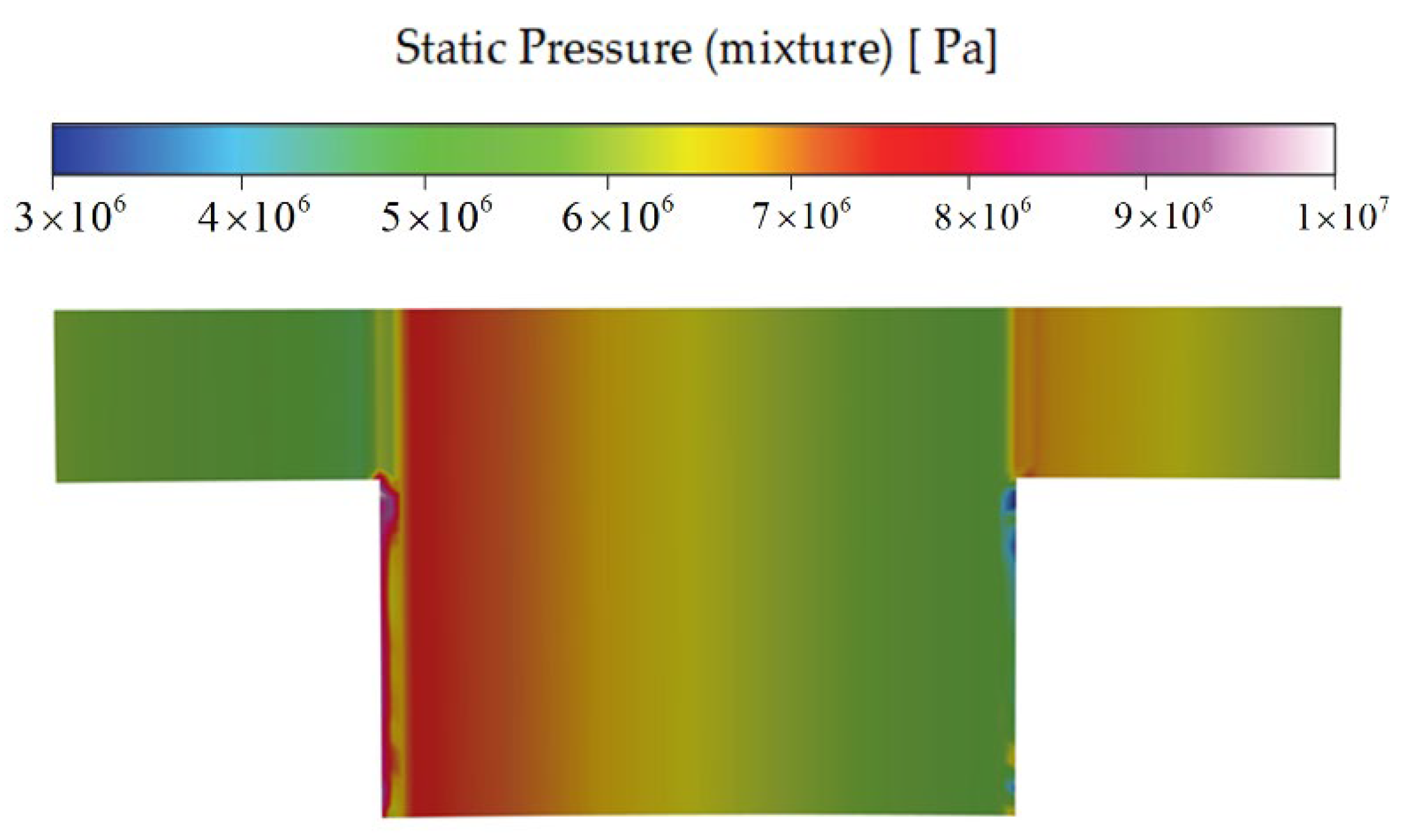
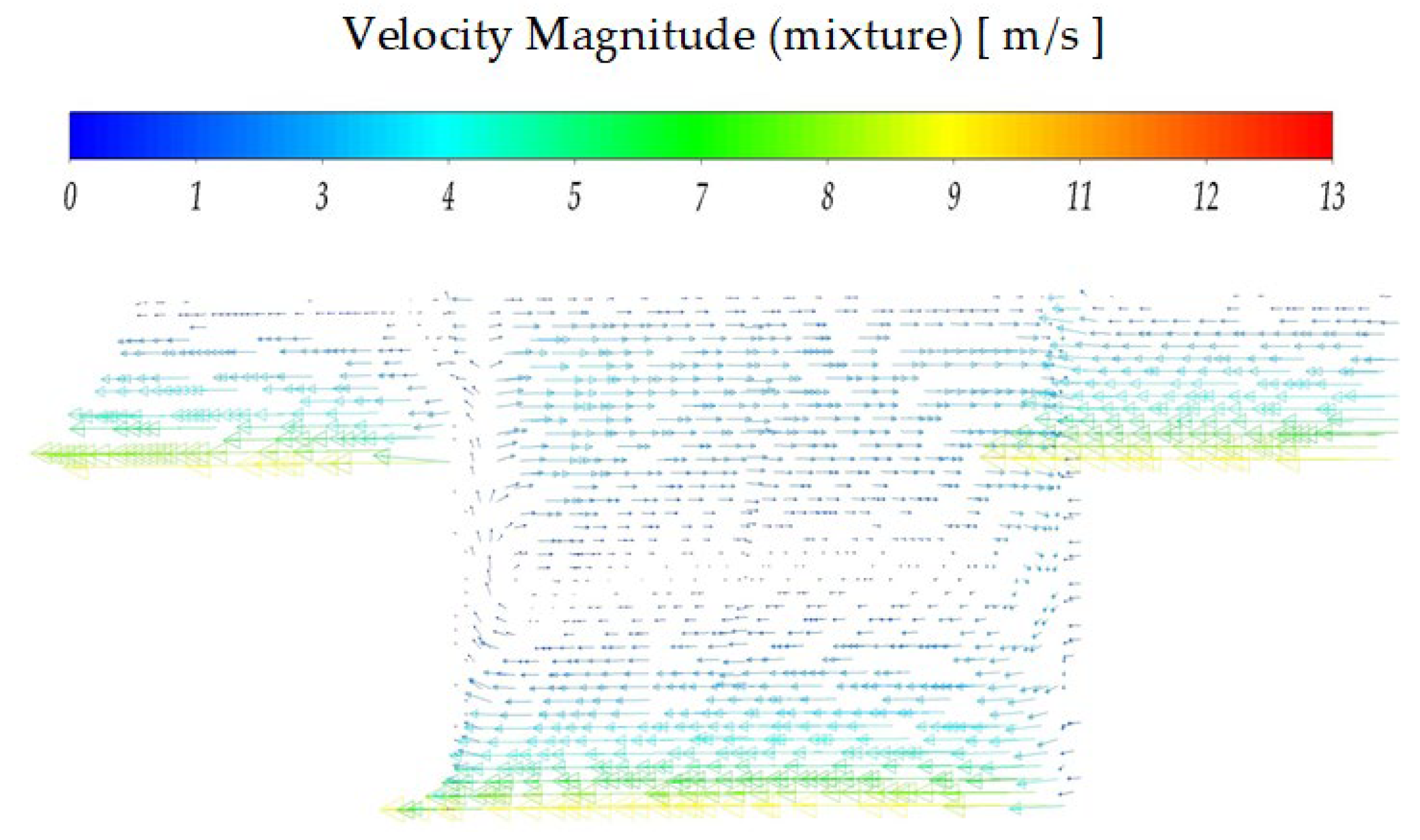
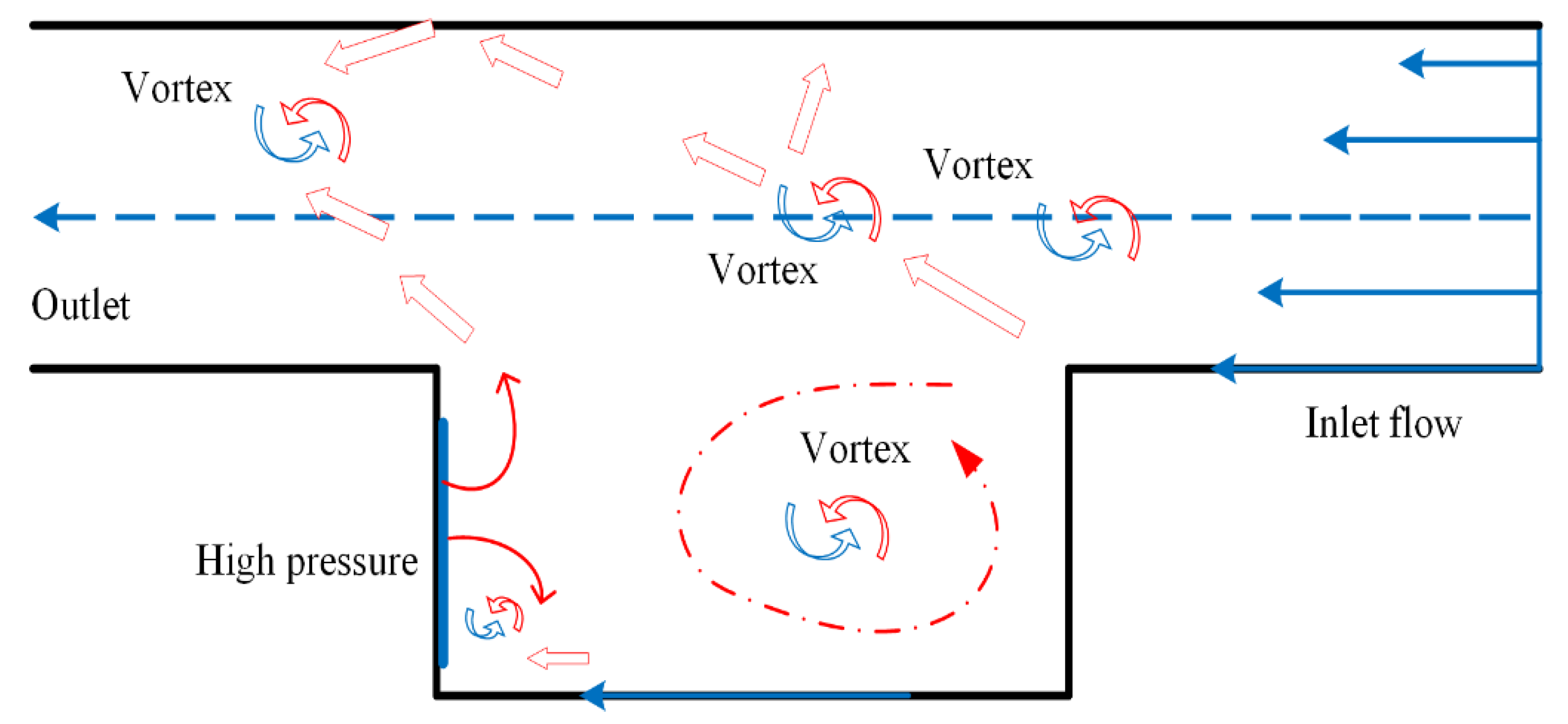
4.1. Liquid Film Flow Mechanism
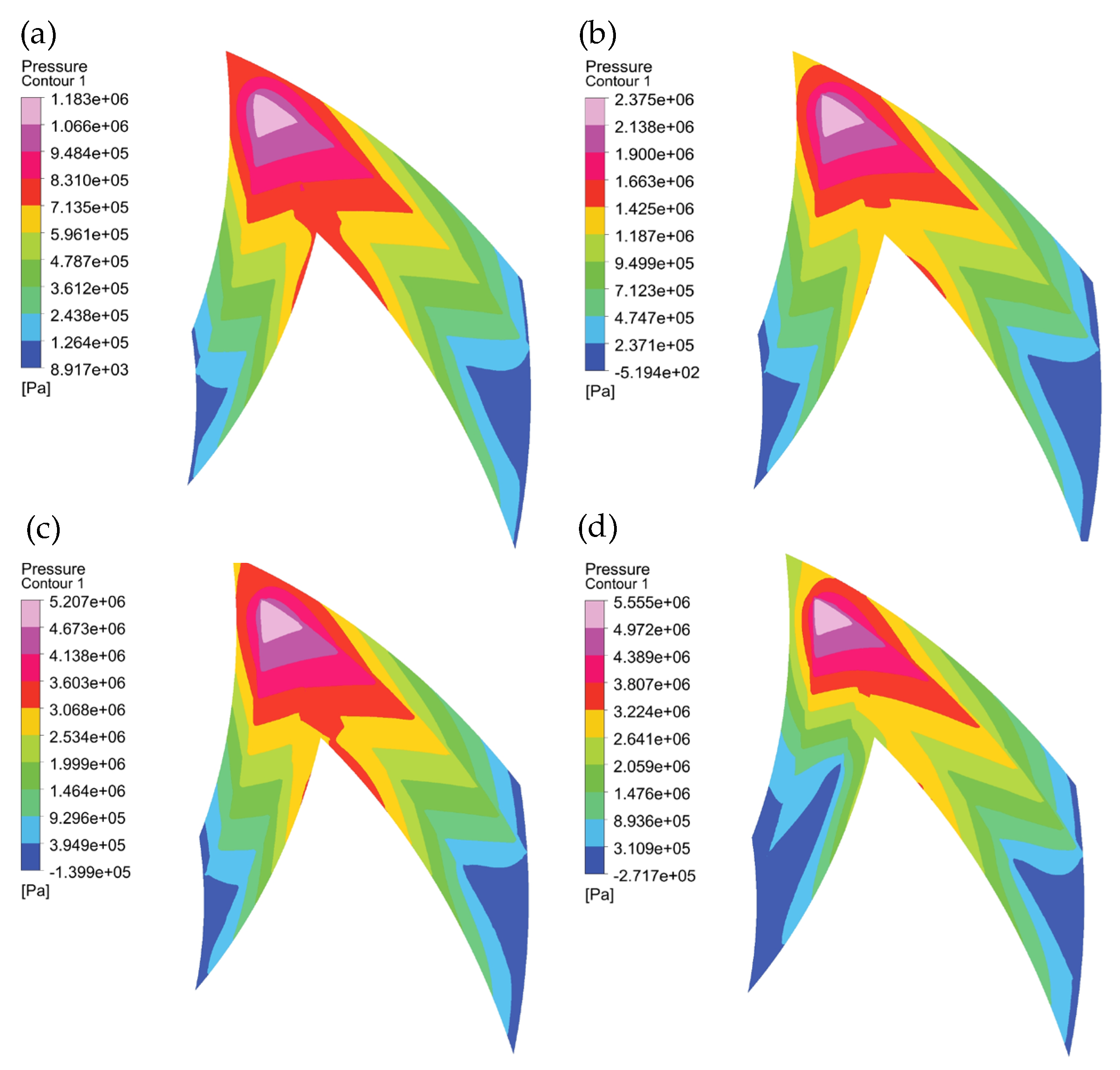
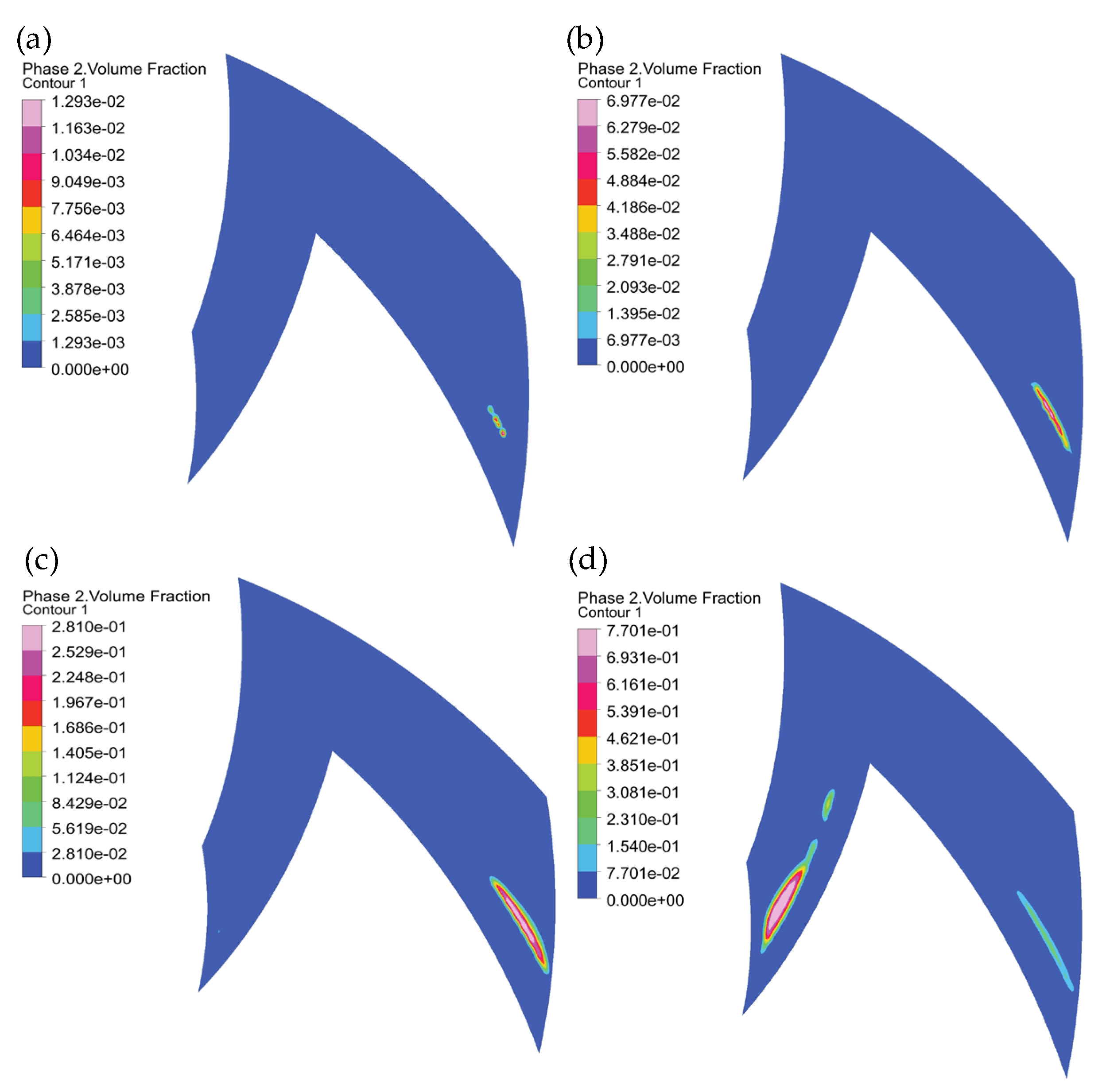
4.2. Influence of Rotational Speed on the Flow Field
4.3. Influence of Structural Parameters on the Flow Field
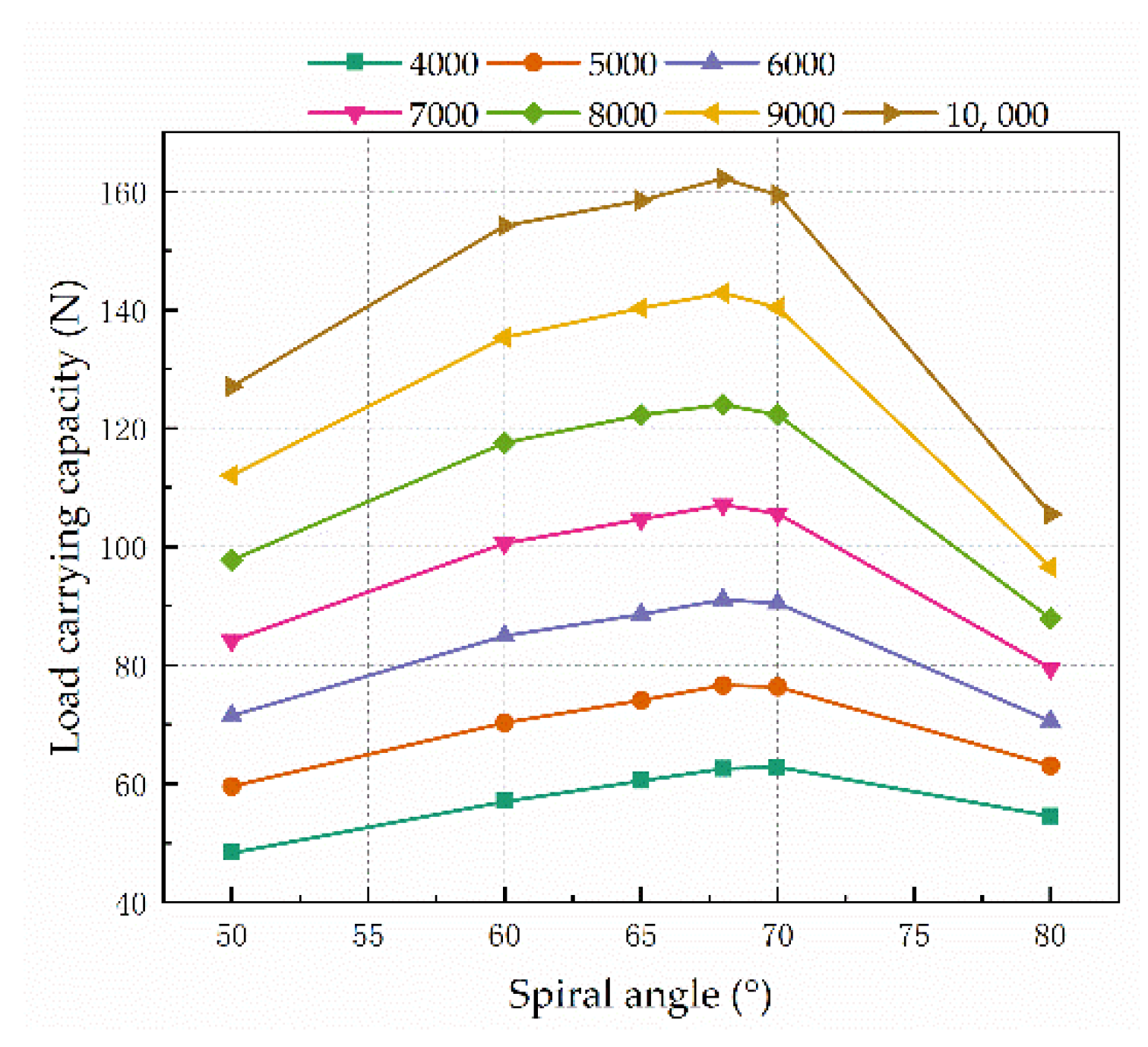
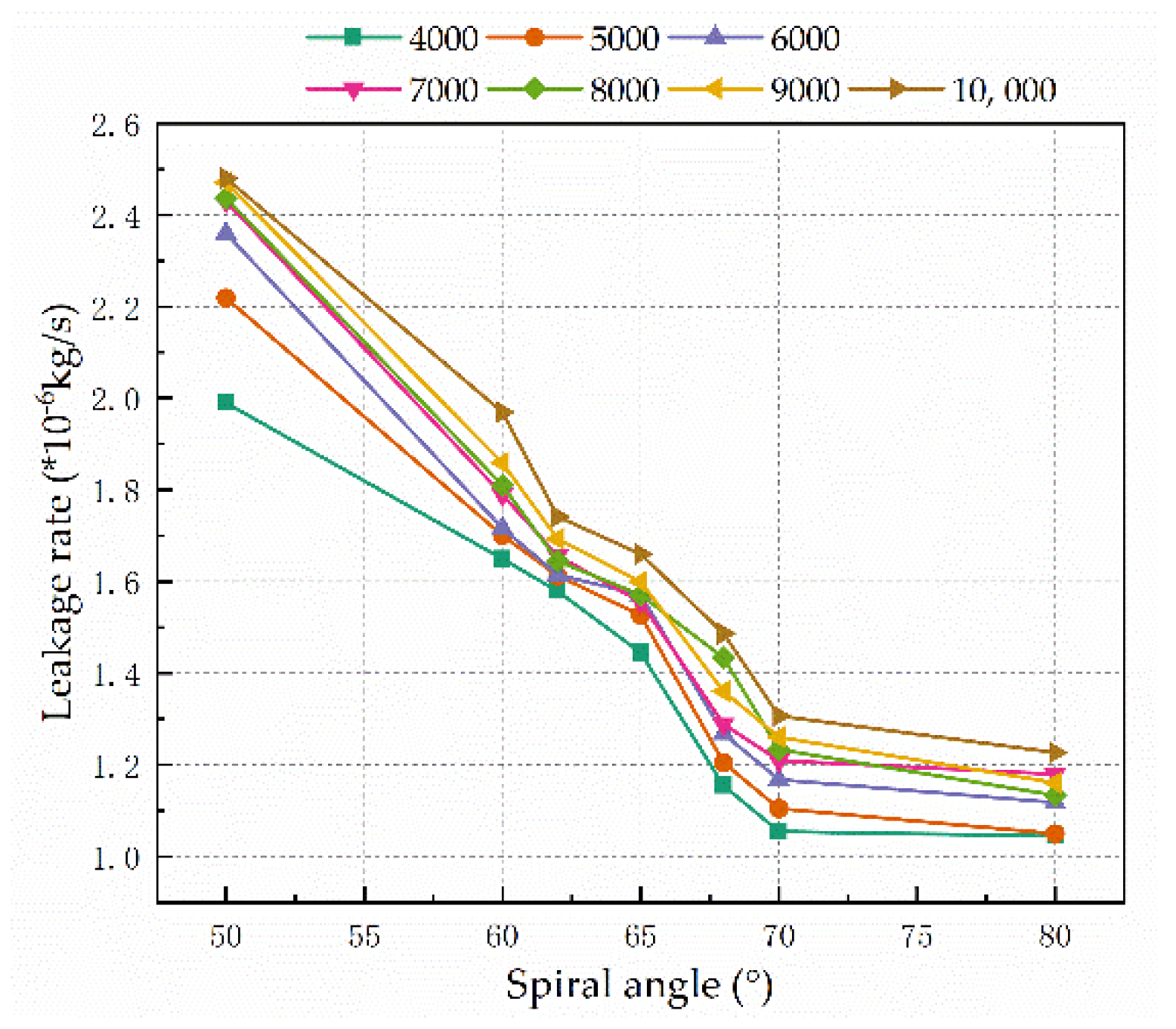
4.3.1. Spiral Angle
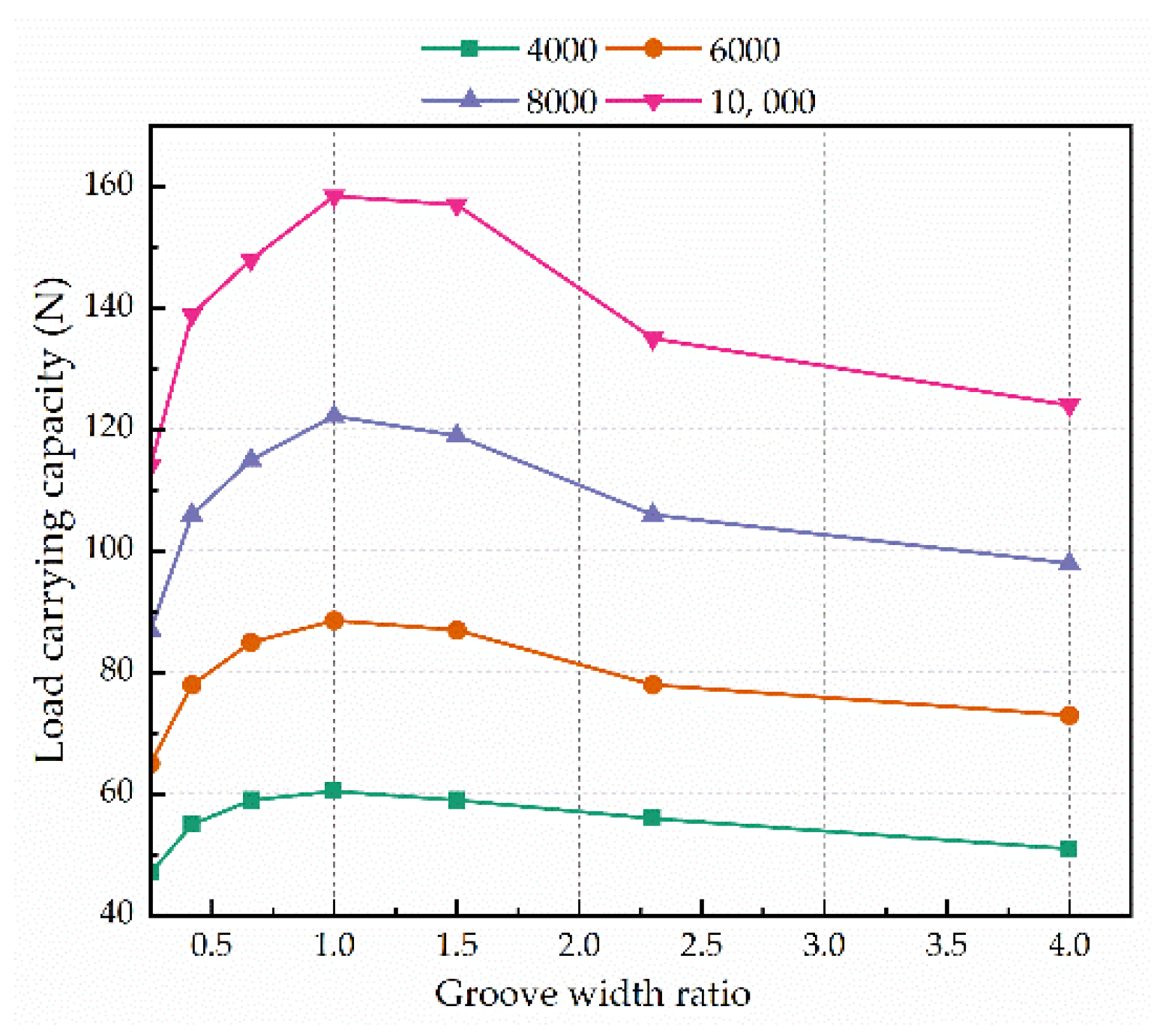
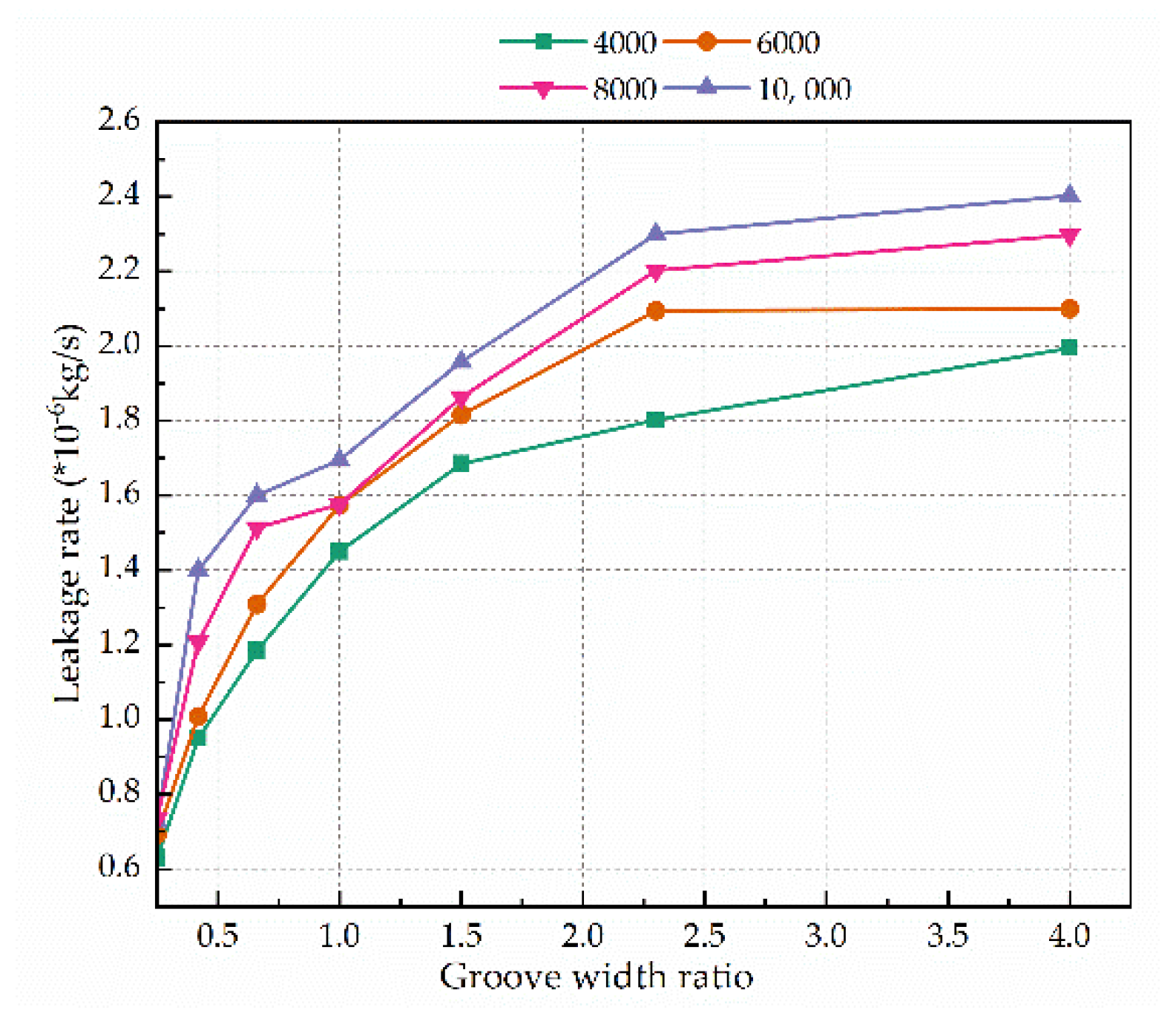
4.3.2. Groove Width Ratio
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.-C.; Lin, J.-T. Numerical study of hydrodynamic herringbone-grooved journal bearings combined with thrust bearings considering thermal effects. J. Mech. 2022, 38, 13–21. [Google Scholar] [CrossRef]
- Yu, Y.; Pu, G.; Jiang, T.; Jiang, K. Discontinuous grooves in thrust air bearings designed with CAPSO algorithm. Int. J. Mech. Sci. 2020, 165, 105197. [Google Scholar] [CrossRef]
- Wagner, P.H.; Van Herle, J.; Schiffmann, J. Theoretical and Experimental Investigation of a Small-Scale, High-Speed, and Oil-Free Radial Anode Off-Gas Recirculation Fan for Solid Oxide Fuel Cell Systems. J. Eng. Gas Turbines Power 2020, 142, 041023. [Google Scholar] [CrossRef]
- Qiao, J.; Zhou, G.; Pu, W.; Li, R.; He, M. Coupling analysis of turbulent and mixed lubrication of water-lubricated rubber bearings. Tribol. Int. 2022, 172, 107644. [Google Scholar] [CrossRef]
- Liu, Q.; Ouyang, W.; Cheng, Q.; Li, J.; Cheng, Q.; Li, R. Influences of bidirectional shaft inclination on lubrication and dynamic characteristics of the water-lubricated stern bearing. Mech. Syst. Signal Process. 2022, 169, 108623. [Google Scholar] [CrossRef]
- Lin, X.; Wang, S.; Jiang, S.; Zhang, S. Thermohydrodynamic Model of Cavitating Flow and Dynamic Characteristic Calculation for High-Speed Water-Lubricated Pump-Out Spiral Groove Bearing. Tribol. Trans. 2020, 63, 736–755. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, S.; Lin, X. Static and dynamic characteristics of high-speed water-lubricated spiral-groove thrust bearing considering cavitating and centrifugal effects. Tribol. Int. 2020, 145, 106159. [Google Scholar] [CrossRef]
- Wang, D.; Mo, J.; Wang, Z.; Chen, G.; Ouyang, H.; Zhou, Z. Numerical study of friction-induced vibration and noise on groove-textured surface. Tribol. Int. 2013, 64, 1–7. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, S.; Shang-Guan, Y. Three-dimensional computational fluid dynamic analysis of high-speed water-lubricated hydrodynamic journal bearing with groove texture considering turbulence. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2021, 235, 2272–2286. [Google Scholar] [CrossRef]
- Guo, Z.; Xie, X.; Yuan, C.; Bai, X. Study on influence of micro convex textures on tribological performances of UHMWPE material under the water-lubricated conditions. Wear 2019, 426–427, 1327–1335. [Google Scholar] [CrossRef]
- Chang, T.; Guo, Z.; Yuan, C. Study on influence of Koch snowflake surface texture on tribological performance for marine water-lubricated bearings. Tribol. Int. 2019, 129, 29–37. [Google Scholar] [CrossRef]
- Feng, H.; Peng, L. Numerical analysis of water-lubricated thrust bearing with groove texture considering turbulence and cavitation. Ind. Lubr. Tribol. 2018, 70, 1127–1136. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Ge, J.; Zhu, W.; Song, P.; Liu, H.; Hao, L.; Tian, W. Analysis of the flow noises of the nuclear main pump caused by the high temperature liquid Sodium in the two-circuit main loop liquid Sodium pump system. Ann. Nucl. Energy 2020, 145, 107550. [Google Scholar] [CrossRef]
- Guenat, E.; Schiffmann, J. Dynamic force coefficients identification on air-lubricated herringbone grooved journal bearing. Mech. Syst. Signal Process. 2020, 136, 106498. [Google Scholar] [CrossRef]
- Guenat, E.; Schiffmann, J. Performance potential of gas foil thrust bearings enhanced with spiral grooves. Tribol. Int. 2019, 131, 438–445. [Google Scholar] [CrossRef]
- Wang, L.; Han, Y.; Tang, D.; Cai, J. Numerical and Experimental Investigations on the Wear Behavior of Water-Lubricated Bearings with Different Materials. Ind. Lubr. Tribol. 2022, 74, 134–143. [Google Scholar] [CrossRef]
- Song, Y.; Gu, C.-W. Development and Validation of a Three-Dimensional Computational Fluid Dynamics Analysis for Journal Bearings Considering Cavitation and Conjugate Heat Transfer. J. Eng. Gas Turbines Power 2015, 137, 122502. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, Z.; Jiang, D.; Gao, G.; Zhang, X. Study of the lubrication performance of water-lubricated journal bearings with CFD and FSI method. Ind. Lubr. Tribol. 2016, 68, 341–348. [Google Scholar] [CrossRef]
- Grando, F.P.; Priest, M.; Prata, A.T. A two-phase flow approach to cavitation modelling in journal bearings. Tribol. Lett. 2006, 21, 233–244. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Q.; Lu, C.; Liang, P. A numerical analysis and experimental investigation of three oil grooves sleeve bearing performance. Ind. Lubr. Tribol. 2019, 71, 181–187. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Z.; Gao, G.; Li, Z. Determination of stiffness coefficients of hydrodynamic water-lubricated plain journal bearings. Tribol. Int. 2015, 85, 37–47. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Y.; He, Q.; Feng, J. Elastohydrodynamic Behavior Analysis of Journal Bearing Using Fluid–Structure Interaction Considering Cavitation. Arab. J. Sci. Eng. 2019, 44, 1305–1320. [Google Scholar] [CrossRef]
- Taghipour, Y.; Akbarzadeh, P.; Moradgholi, F.; Yazdi, M.E. Numerical study of the cavitation effect on plain bearings in constant and variable viscosity states. Meccanica 2021, 56, 2507–2516. [Google Scholar] [CrossRef]
- Chen, H.; Wu, Q.; Xu, C.; Zuo, M. Research on Cavitation Regions of Upstream Pumping Mechanical Seal Based on Dynamic Mesh Technique. Adv. Mech. Eng. 2014, 6, 821058. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.D.; Ma, C.B.; Sun, J.J.; Zhang, Y.Y.; Yu, Q.P. Influence and optimization of groove structure parameters on vaporization characteristics of liquid film mechanical seals based on optimal mass transfer coefficient. Chem. J. 2022, 73, 1147–1156. [Google Scholar]
- Bair, S. A Routine High-Pressure Viscometer for Accurate Measurements to 1 GPa. Tribol. Trans. 2004, 47, 356–360. [Google Scholar] [CrossRef]
- Yang, D.D. Steady Character Research and Software Development of Liquid Film Seal with Herringbone Grooves. Master’s Thesis, China University of Petroleum, Beijing, China, 2016. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201801&filename=1018814320.nh (accessed on 8 July 2022).
- Xie, Z.; Zhang, Y.; Zhou, J.; Zhu, W. Theoretical and experimental research on the micro interface lubrication regime of water lubricated bearing. Mech. Syst. Signal Process. 2021, 151, 107422. [Google Scholar] [CrossRef]
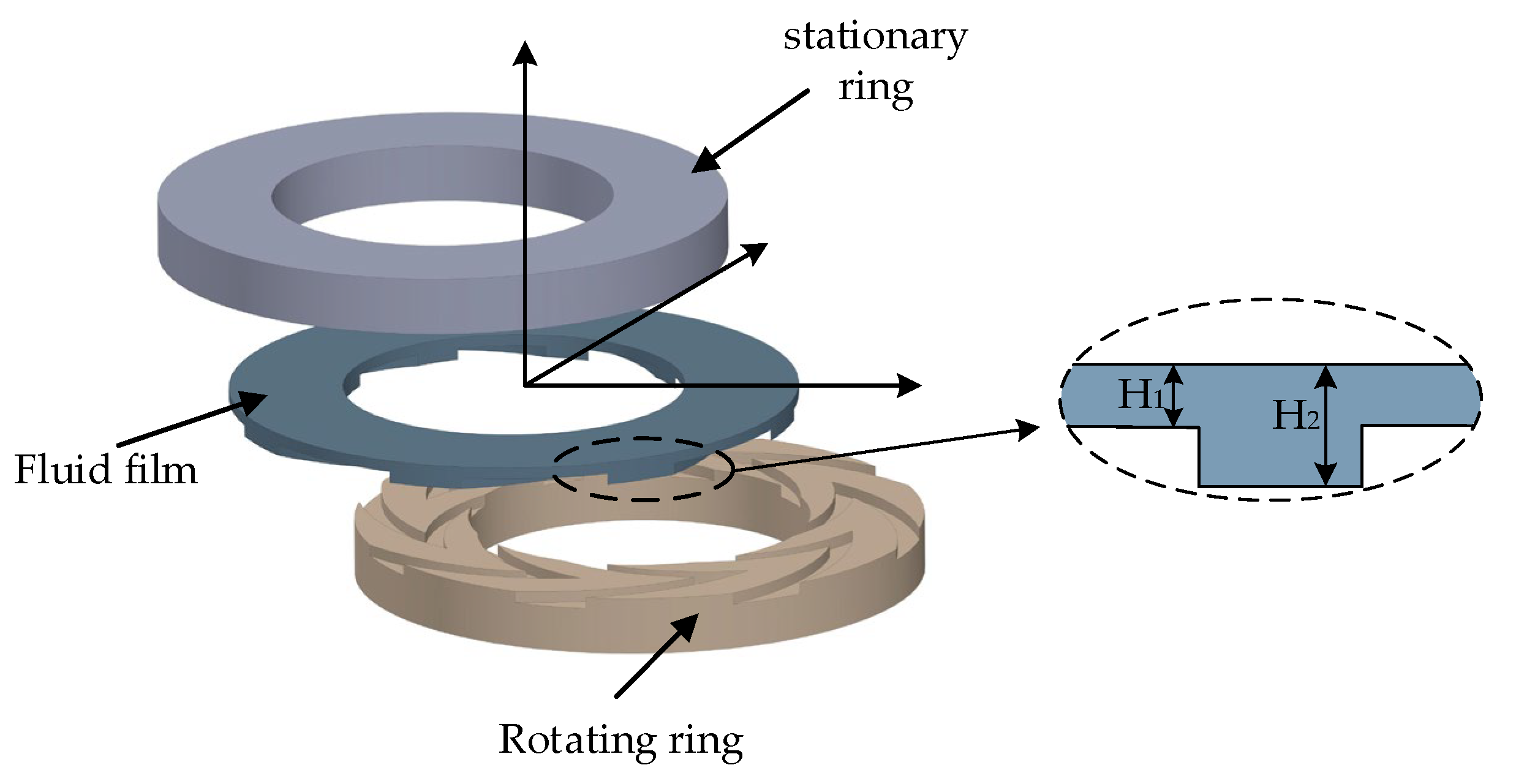
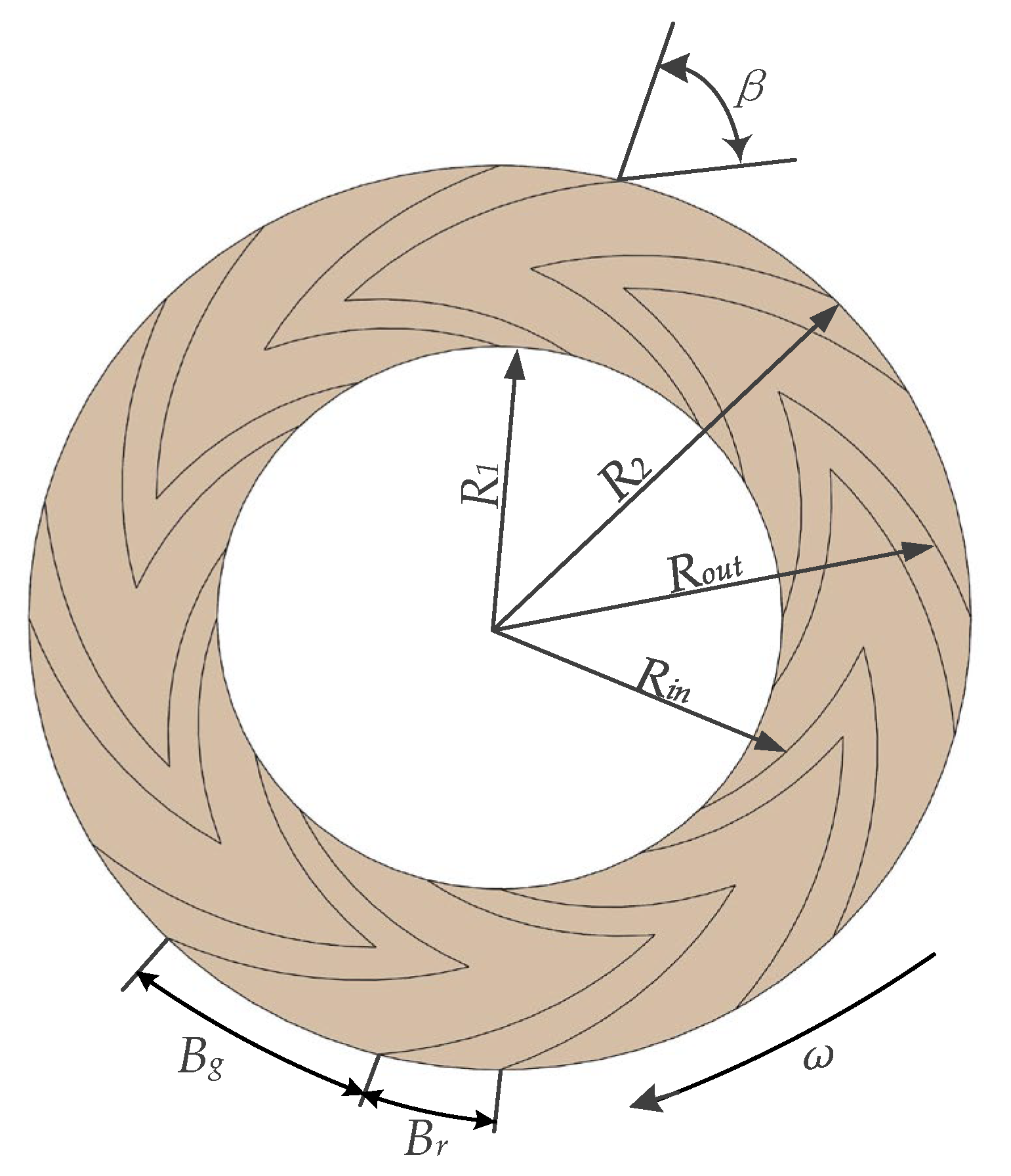
| Parameters | Value |
|---|---|
| Temperature | 300 |
| Groove number | 18 |
| rotational speed | 6000 |
| Spiral groove angle | 65 |
| Inner radius | 15 |
| Outer radius | 20 |
| Pressure inlet | 0.1 |
| Pressure outlet | 0.2 |
| Water film depth | 30 |
| Bearing clearance | 10 |
| Density | 998.2 |
| Viscosity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, H.; Dai, P.; Yan, S.; Wang, F.; Yao, X.; Wang, J.; Zuo, G. Flow Mechanisms and Lubrication Performance of Water-Lubricated Thrust Bearings with Herringbone Grooves. Lubricants 2022, 10, 182. https://doi.org/10.3390/lubricants10080182
Ran H, Dai P, Yan S, Wang F, Yao X, Wang J, Zuo G. Flow Mechanisms and Lubrication Performance of Water-Lubricated Thrust Bearings with Herringbone Grooves. Lubricants. 2022; 10(8):182. https://doi.org/10.3390/lubricants10080182
Chicago/Turabian StyleRan, Haifeng, Peng Dai, Shuping Yan, Fengtao Wang, Xingjia Yao, Jianping Wang, and Guizhong Zuo. 2022. "Flow Mechanisms and Lubrication Performance of Water-Lubricated Thrust Bearings with Herringbone Grooves" Lubricants 10, no. 8: 182. https://doi.org/10.3390/lubricants10080182
APA StyleRan, H., Dai, P., Yan, S., Wang, F., Yao, X., Wang, J., & Zuo, G. (2022). Flow Mechanisms and Lubrication Performance of Water-Lubricated Thrust Bearings with Herringbone Grooves. Lubricants, 10(8), 182. https://doi.org/10.3390/lubricants10080182