Prediction of Remaining Service Life of Rolling Bearings Based on Convolutional and Bidirectional Long- and Short-Term Memory Neural Networks
Abstract
:1. Introduction
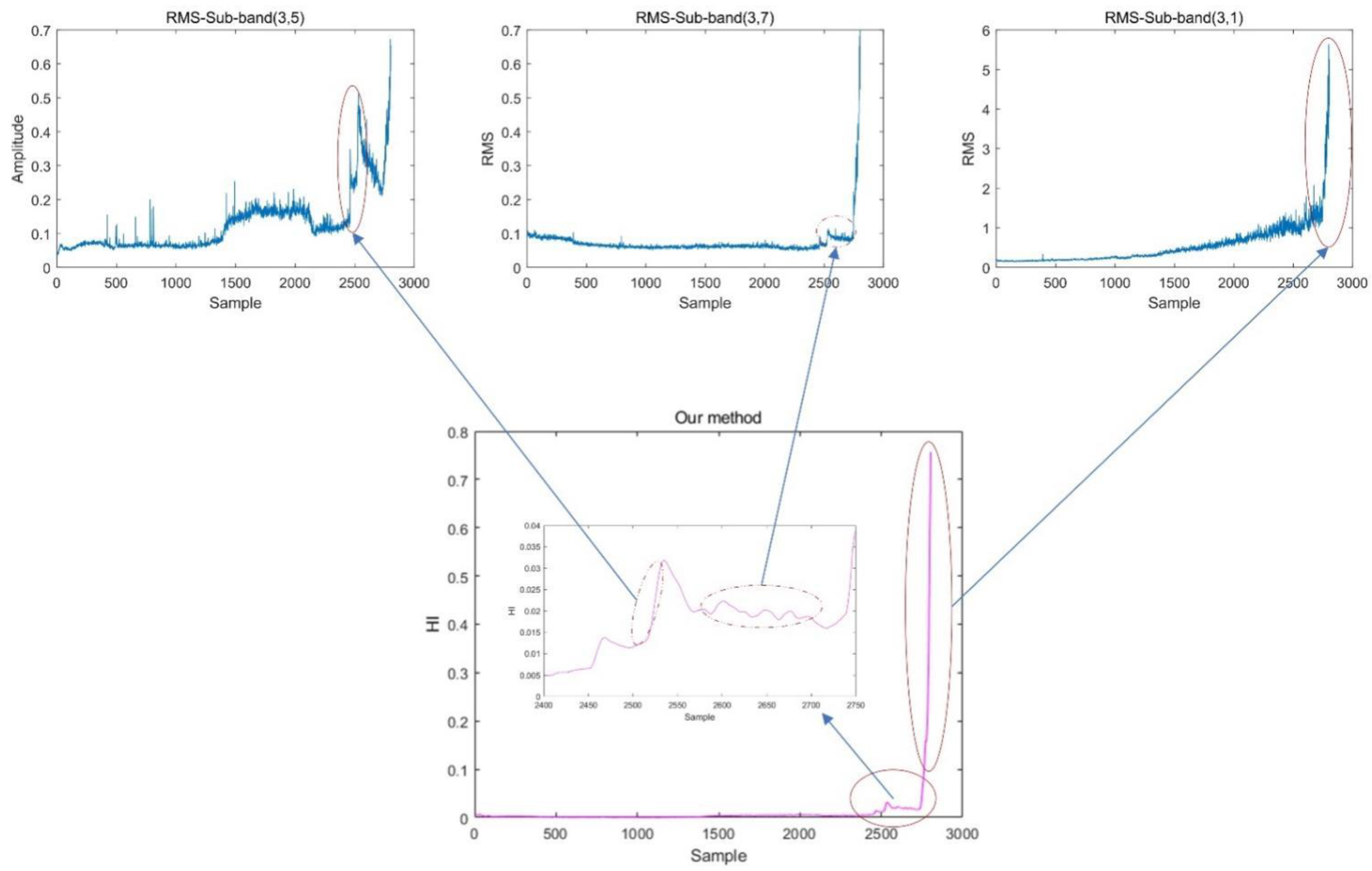
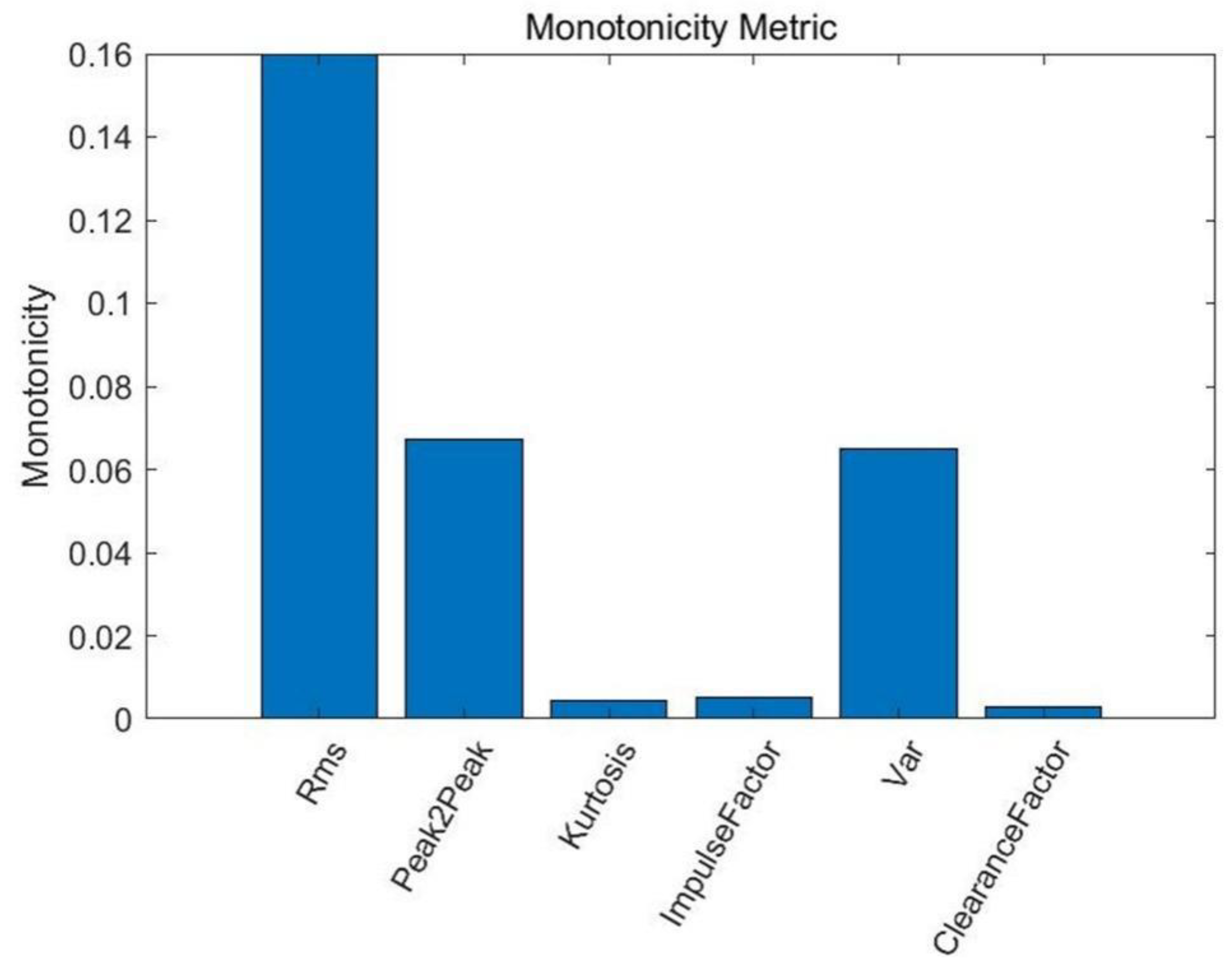
- Discrete wavelet packet transform (DWPT) and principal component analysis (KPCA) were combined to construct new health indicators to solve the labeling problem of RUL prediction. Compared to the life-percentage-style linear HI, this HI can better reflect the bearing degradation trend and retain the time–frequency characteristics of the signal, which is beneficial to the learning of the prediction model.
- A convolutional bidirectional long- and short-term memory neural network (CNN-BiLSTM) was designed for RUL prediction. Convolution can extract signal features from different scales, and combined with the BiLSTM network, the model can take into account both temporal and spatial features of the signal to improve prediction accuracy.
- Experimental data based on rolling bearing dataset were used to verify the effectiveness of the method.
2. Theoretical Background
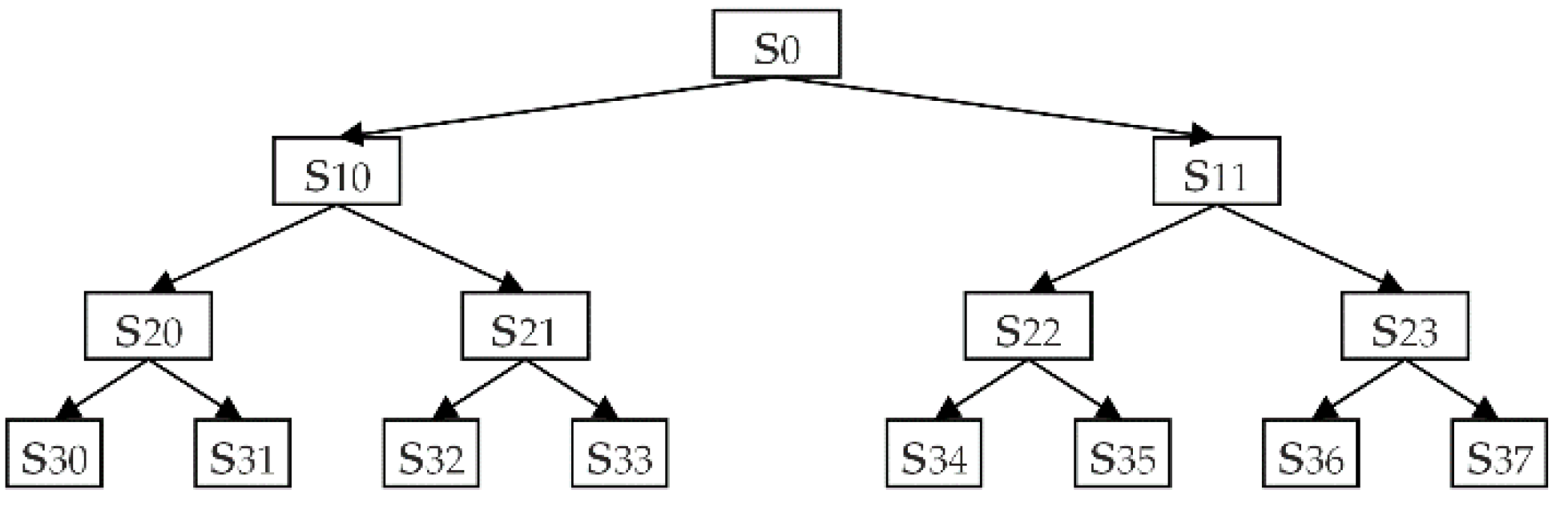
2.1. Discrete Wavelet Packet Transform (DWPT)
2.2. Kernel Principal Component Analysis (KPCA)
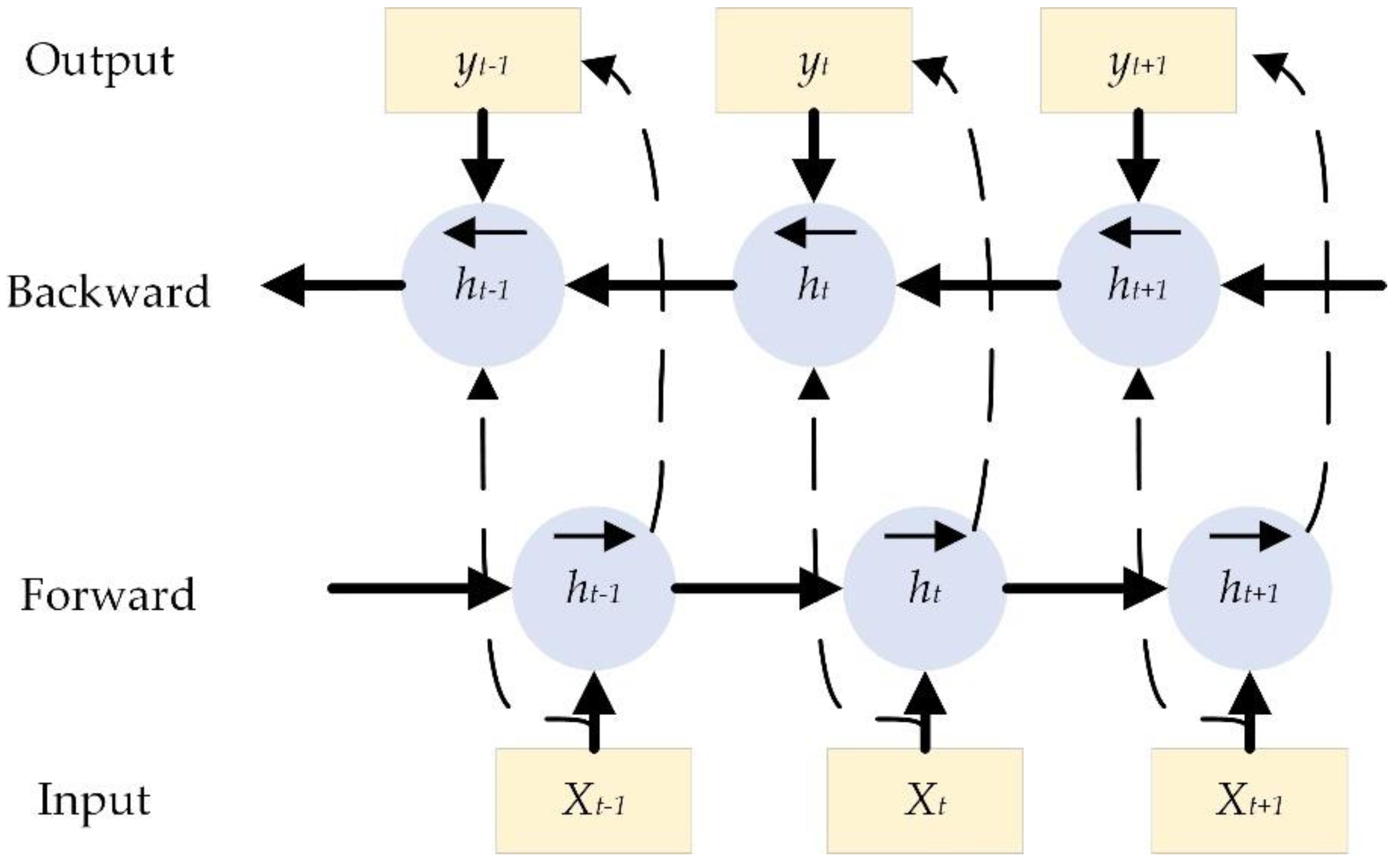
2.3. Bidirectional Long Short-Term Memory Neural Network (BiLSTM)
2.4. Convolutional Neural Network (CNN)
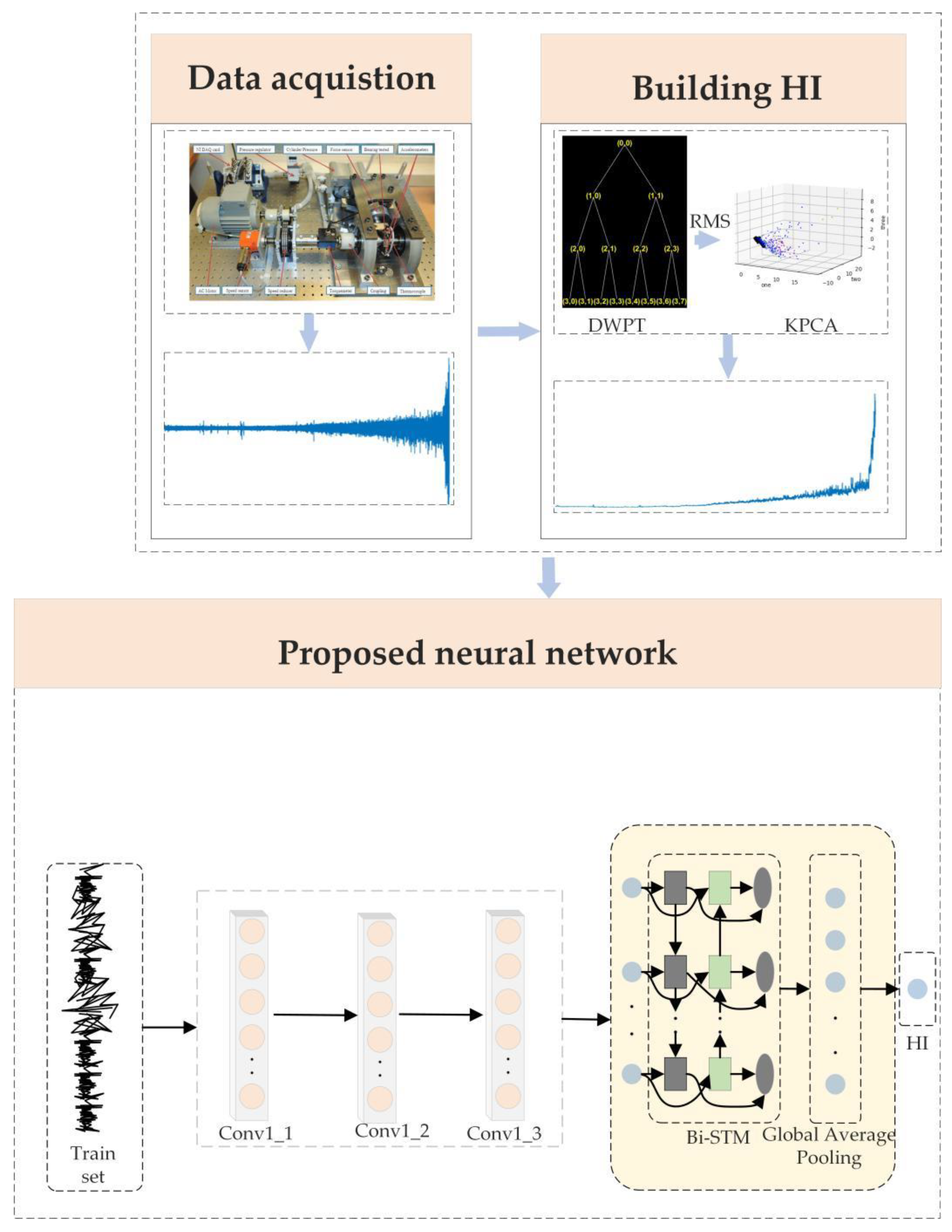
3. The Proposed Framework
- (1)
- Data acquisition: The accelerometers were placed on the horizontal and vertical axes with sampling frequency of 25.6 KHZ, sampling interval of 10 s, and sampling time of 0.1 s. Sampling was performed under three working conditions.
- (2)
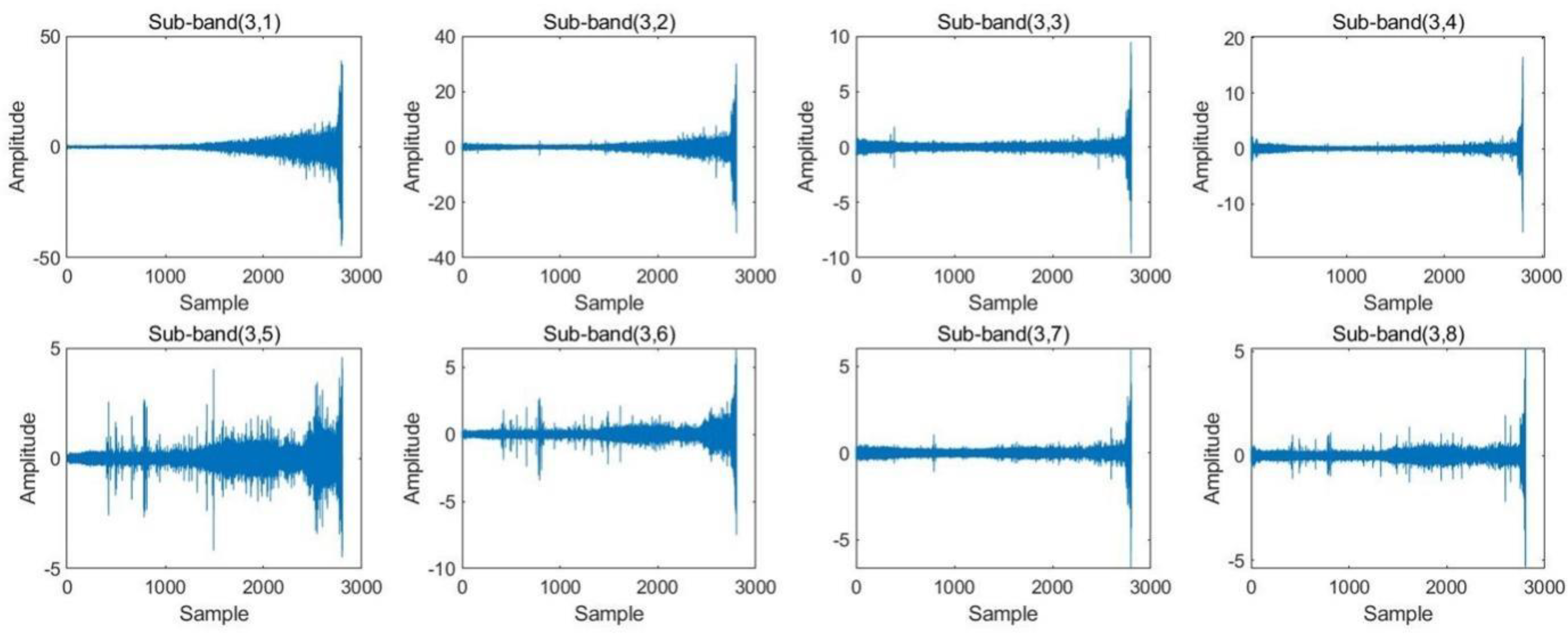
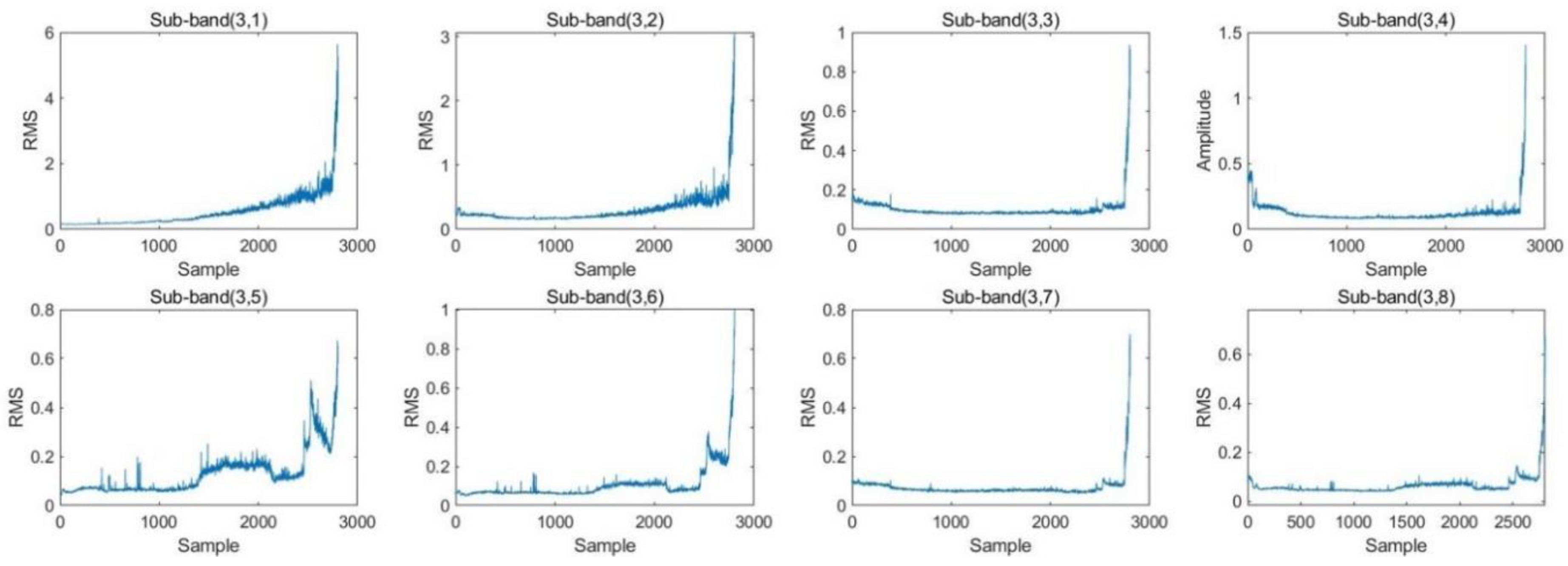
- Building health indicators: The original vibration signal was decomposed into eight sub-bands using DWPT. The sub-bands were reconstructed according to the coefficients, and RMS values were extracted. The multidimensional RMS values were dimensionalized using the KPCA algorithm, and low-dimensional sensitive features were selected as HI and used as training labels for the prediction network.
- (3)
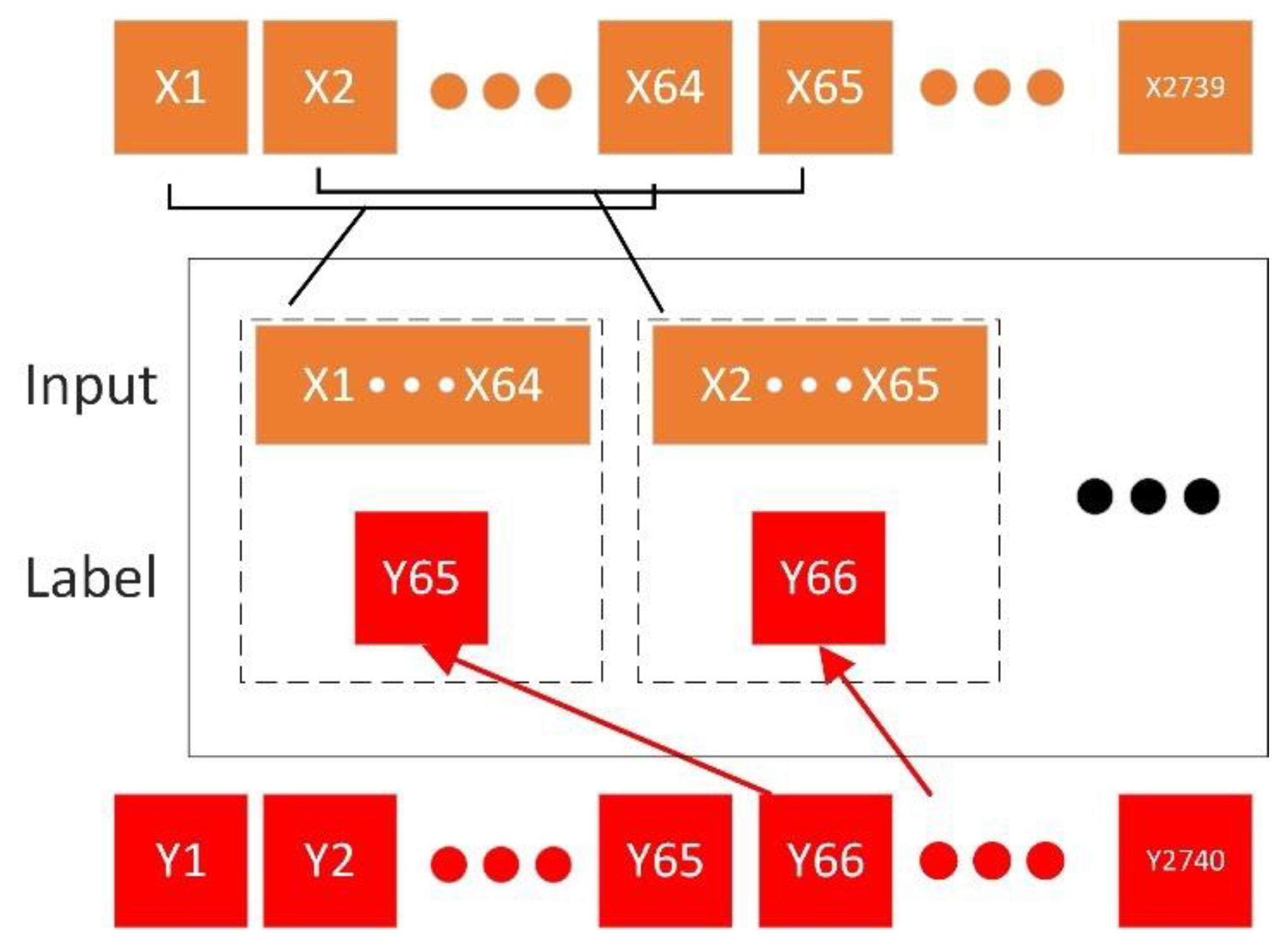
- Proposed neural network: The spatial features of the signal were extracted using a convolutional network followed by a BiLSTM layer to extract temporal features from the forward and reverse directions. The global average pooling layer in the model can pay attention to the overall information, which is conducive to model prediction [35]. The mean square error was used as the loss function, and the optimizer was Adam. The input to the network was RMS at the current moment, and the output was the HI at the future moment.
4. Experiments and Results
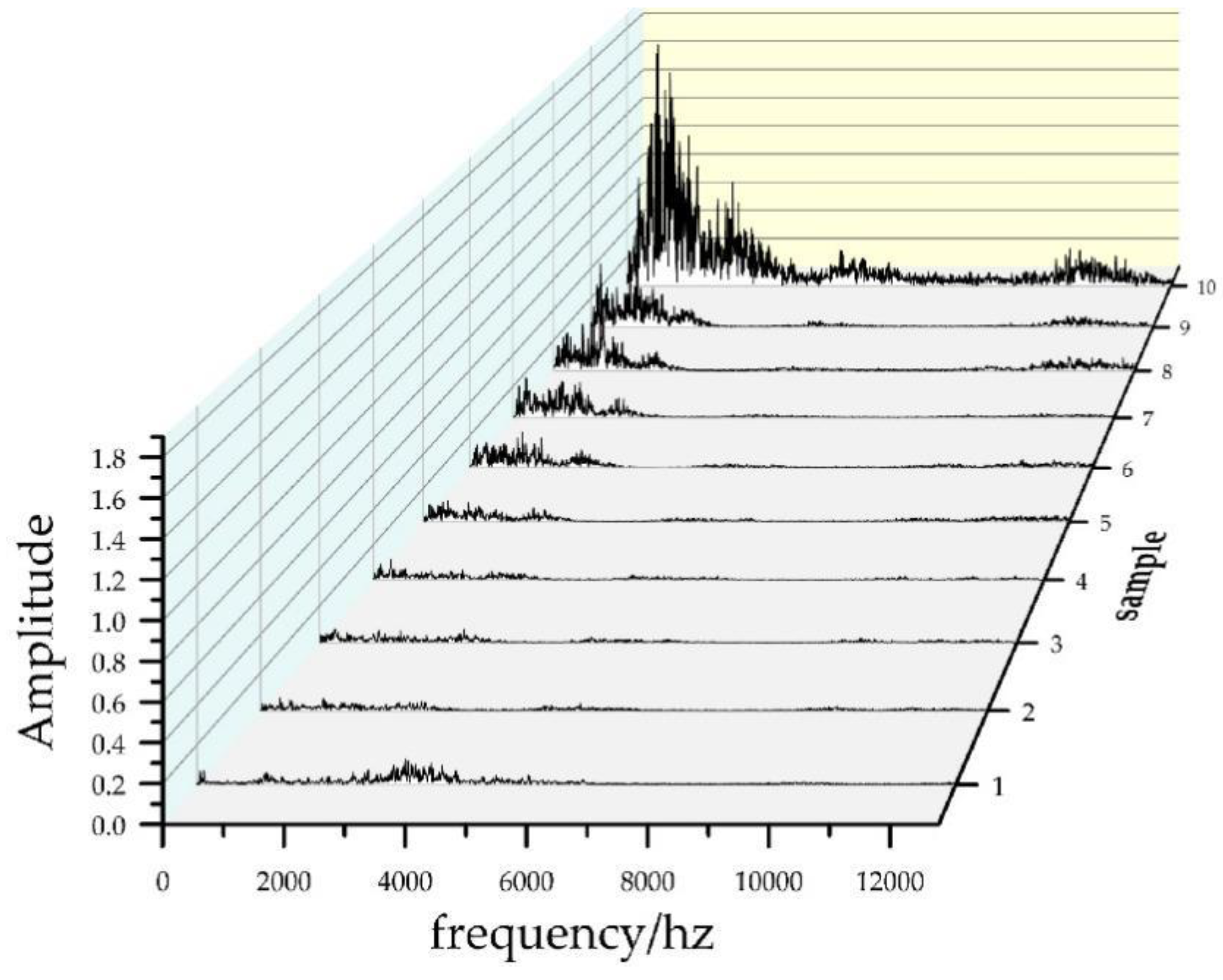
4.1. Data Description
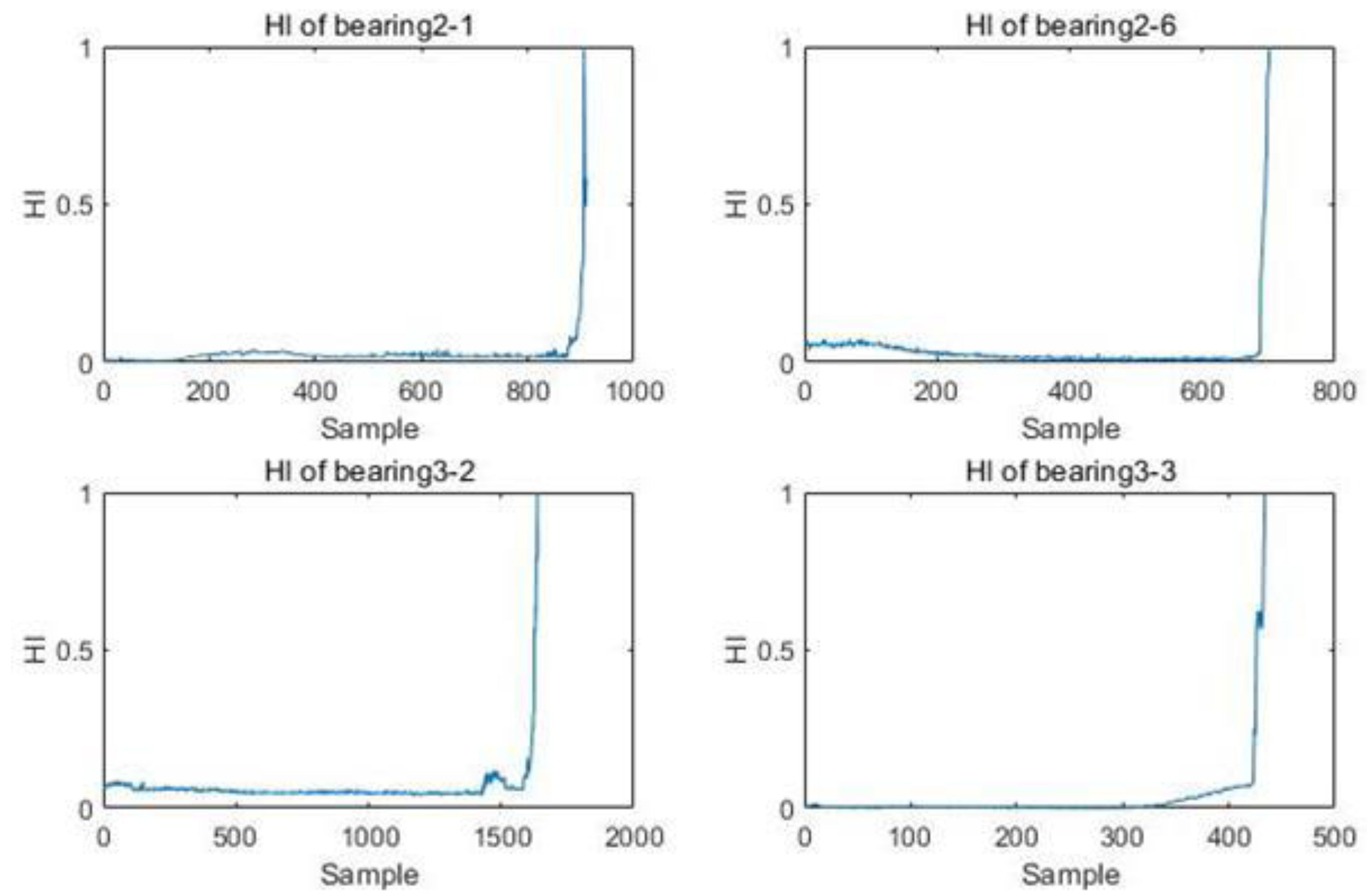
4.2. Construction of Health Indicators
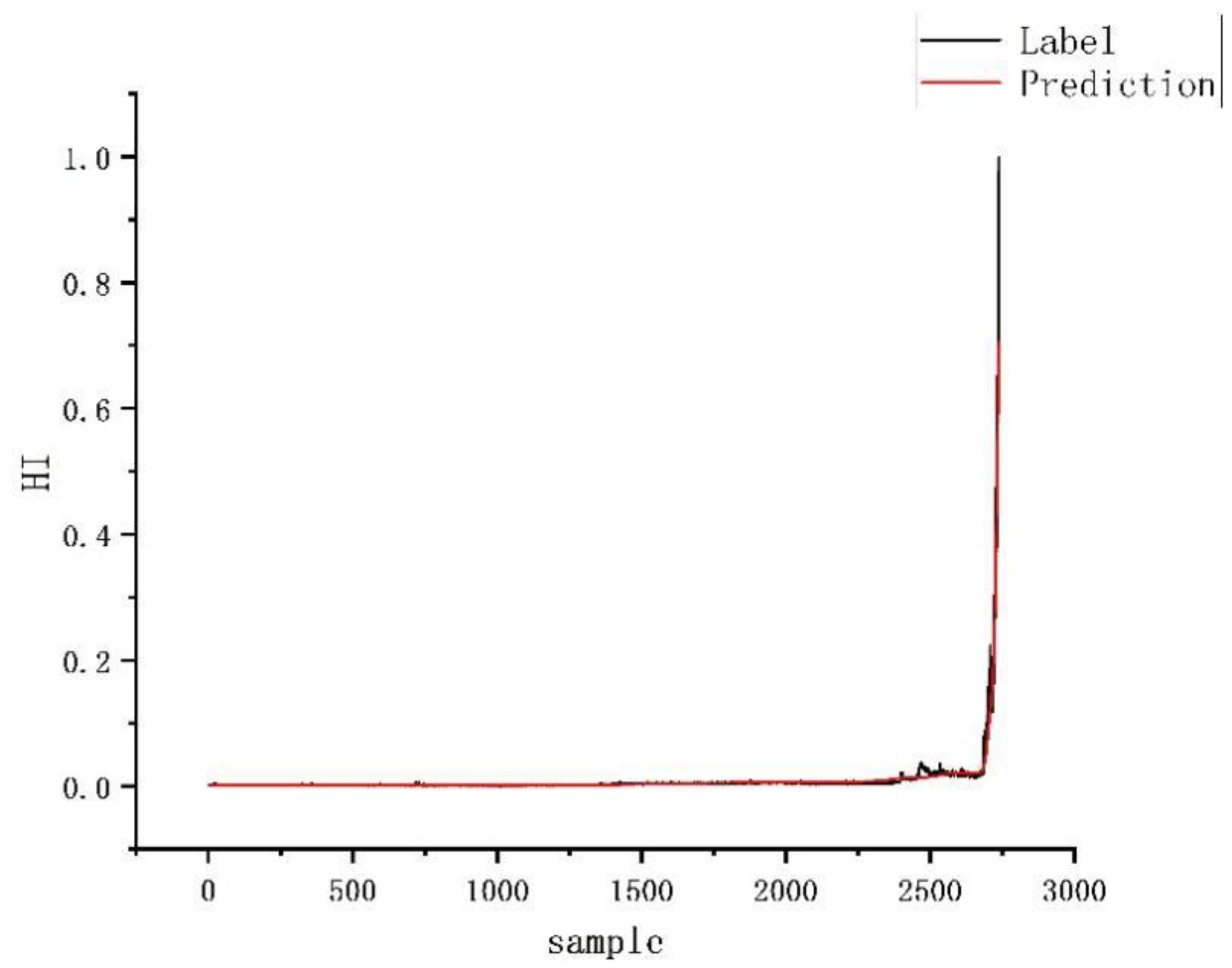
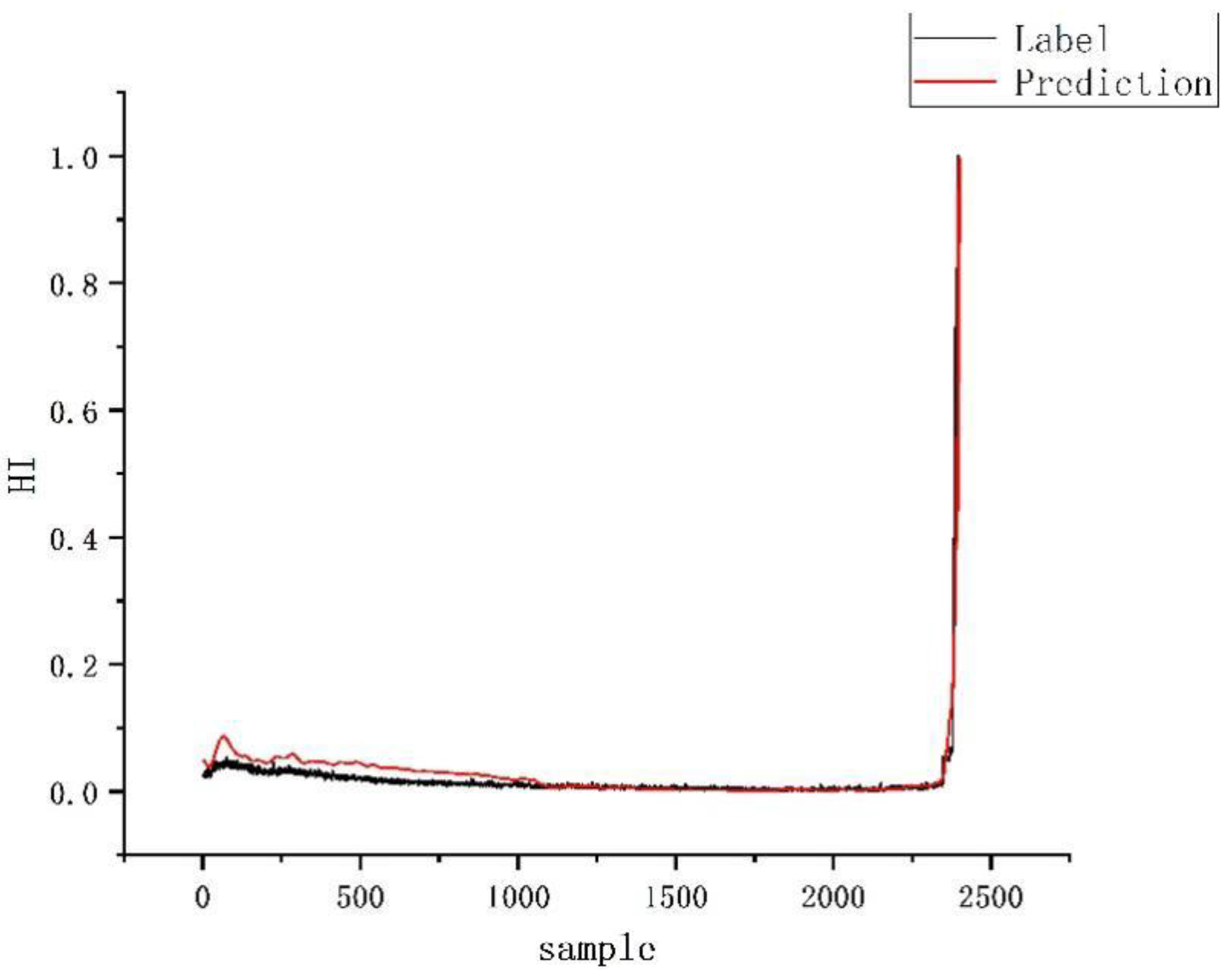
4.3. RUL Prediction
4.3.1. Input Selection
4.3.2. Training and Test of CNN-BiLSTM Model
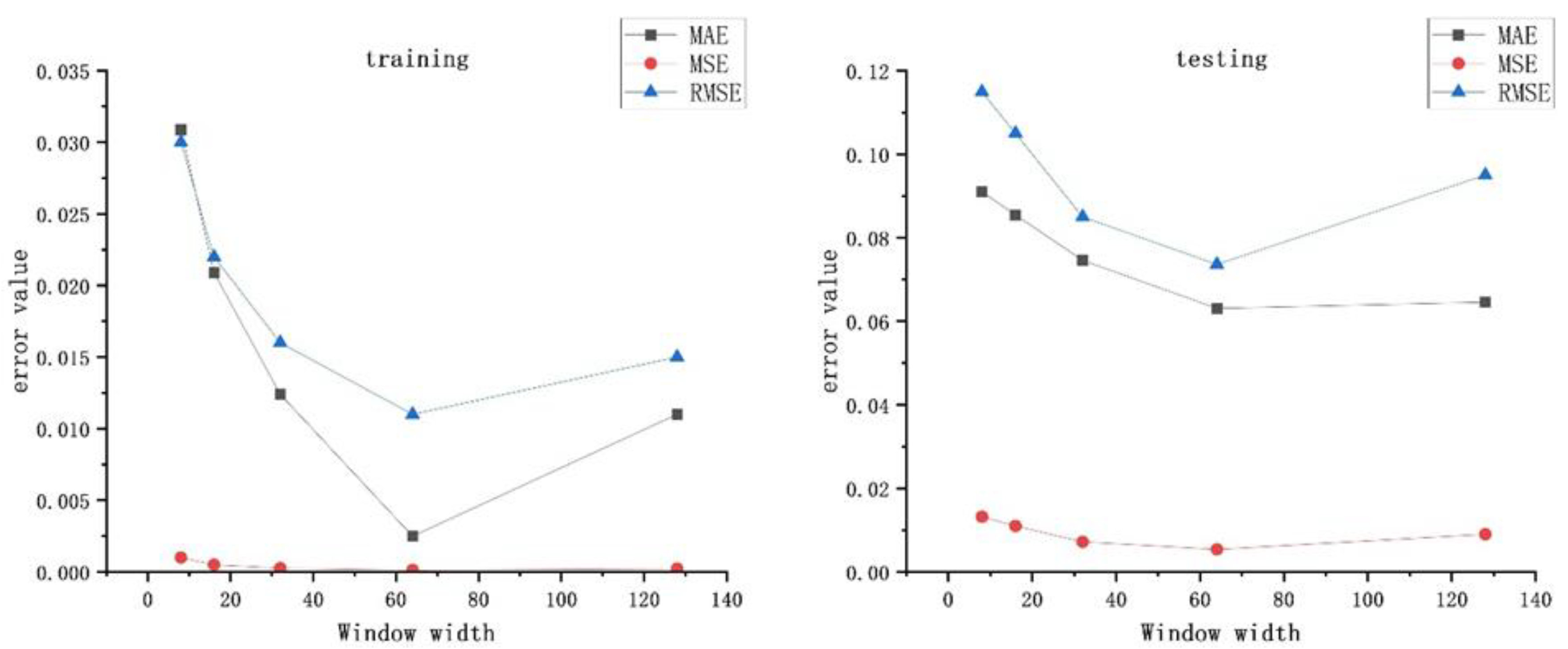
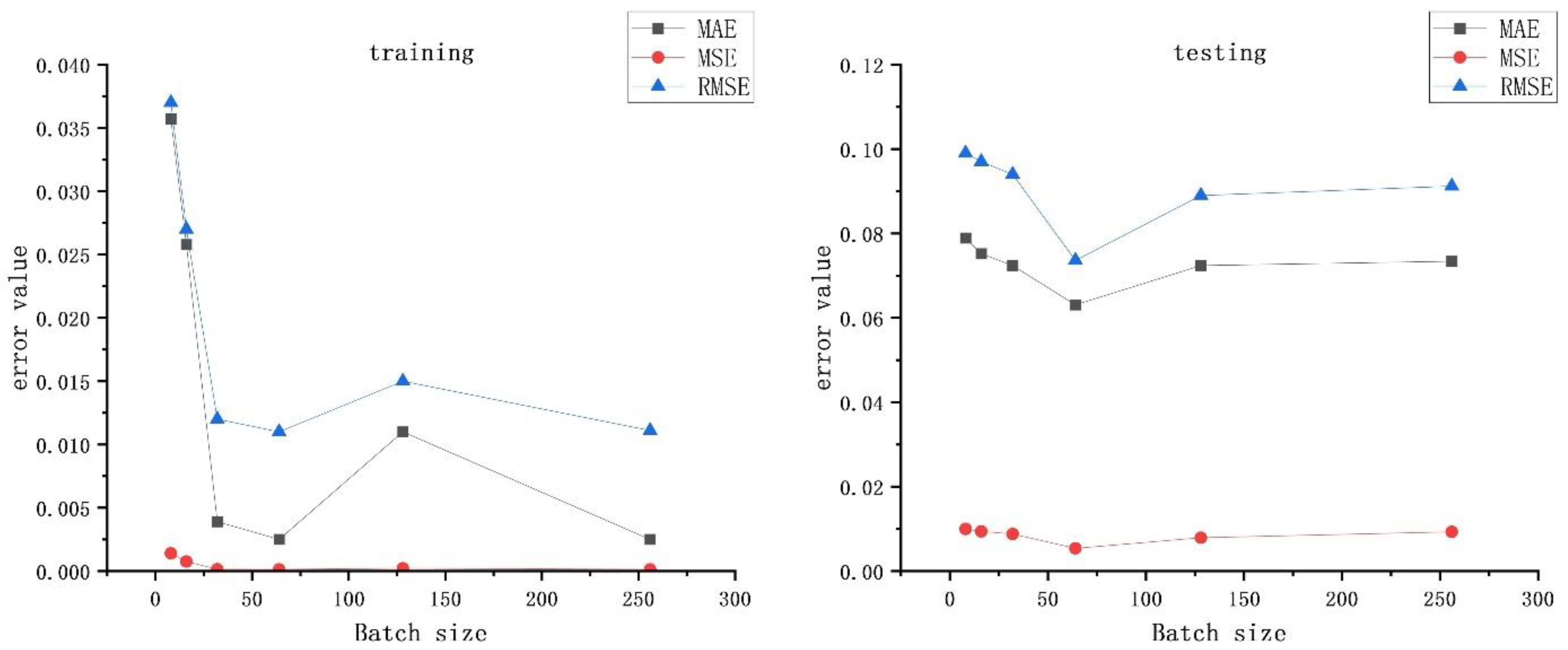
4.3.3. Selection of Hyper Parameters
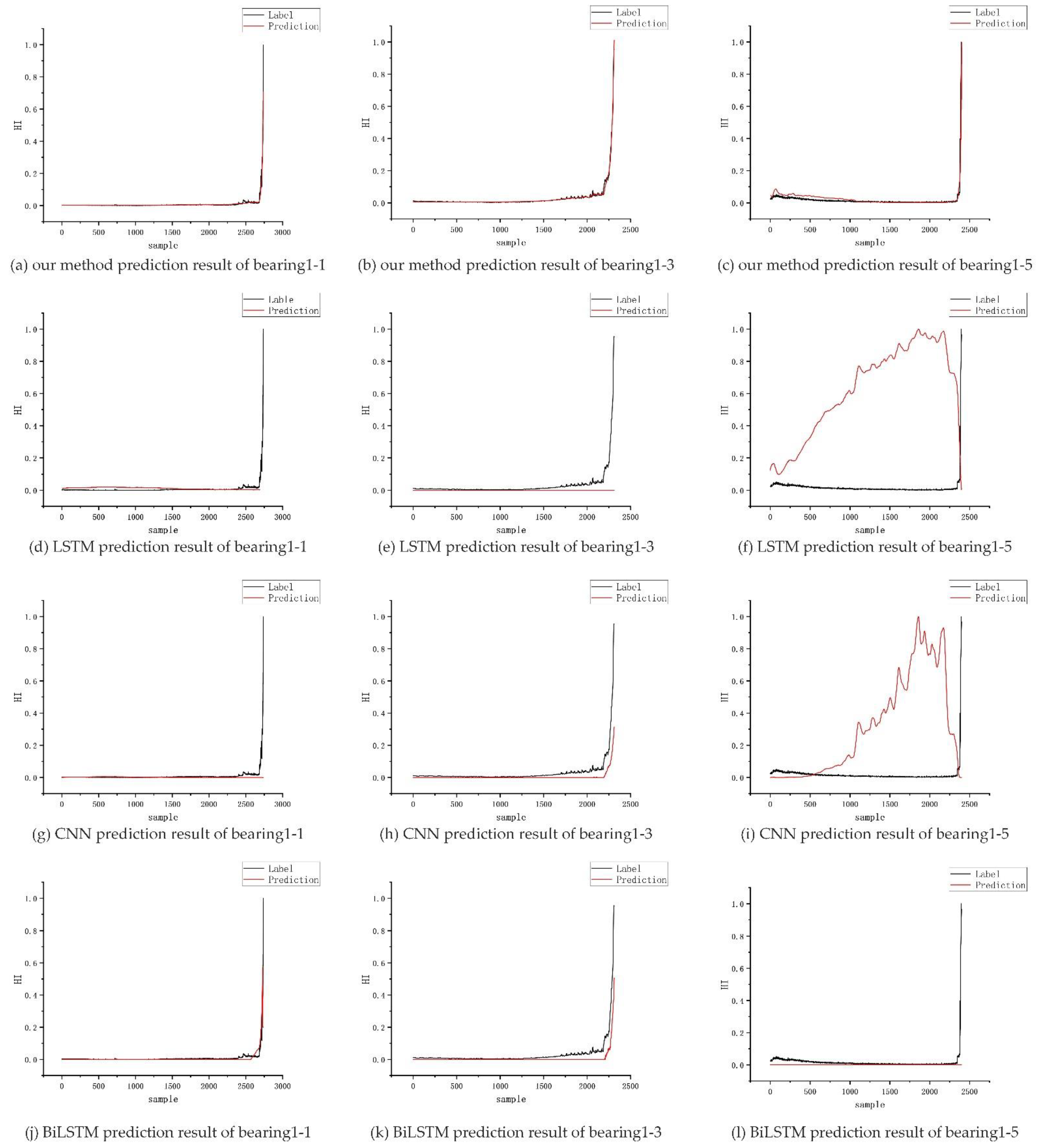
4.3.4. Results of Different Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pech, M.; Vrchota, J.; Bednář, J. Predictive Maintenance and Intelligent Sensors in Smart Factory: Review. Sensors 2021, 21, 1470. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Liu, Y.; Ding, L.; Safian, A.; Liang, X. A New Structured Domain Adversarial Neural Network for Transfer Fault Diagnosis of Rolling Bearings Under Different Working Conditions. IEEE Trans. Instrum. Meas. 2021, 70, 3509013. [Google Scholar] [CrossRef]
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: Shallow and deep learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Kong, X.; Chen, G.; Wang, Q.; Wang, R. Transferable convolutional neural network based remaining useful life prediction of bearing under multiple failure behaviors. Measurement 2021, 168, 108286. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Yan, K.; Zhu, Y.; Hong, J. A Study on Bearing Dynamic Features under the Condition of Multiball–Cage Collision. Lubricants 2022, 10, 9. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Gao, R.X. A multi-time scale approach to remaining useful life prediction in rolling bearing. Mech. Syst. Signal Process. 2017, 83, 549–567. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Duan, S.; Chen, W.; Wang, D.; Fan, Y. SACGNet: A Remaining Useful Life Prediction of Bearing with Self-Attention Augmented Convolution GRU Network. Lubricants 2022, 10, 21. [Google Scholar] [CrossRef]
- Bousdekis, A.; Magoutas, B.; Apostolou, D.; Mentzas, G. Review, analysis and synthesis of prognostic-based decision support methods for condition based maintenance. J. Intell. Manuf. 2018, 29, 1303–1316. [Google Scholar] [CrossRef]
- El-Tawil, K.; Jaoude, A.A. Stochastic and nonlinear-based prognostic model. Syst. Sci. Control Eng. 2013, 1, 66–81. [Google Scholar] [CrossRef] [Green Version]
- Rathore, M.S.; Harsha, S.P. Prognostics Analysis of Rolling Bearing Based on Bi-Directional LSTM and Attention Mechanism. J. Fail. Anal. Prev. 2022, 22, 704–723. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.-V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Mushtaq, S.; Islam, M.M.M.; Sohaib, M. Deep Learning Aided Data-Driven Fault Diagnosis of Rotatory Machine: A Comprehensive Review. Energies 2021, 14, 5150. [Google Scholar] [CrossRef]
- Chen, D.; Qin, Y.; Wang, Y.; Zhou, J. Health indicator construction by quadratic function-based deep convolutional auto-encoder and its application into bearing RUL prediction. ISA Trans. 2021, 114, 44–56. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-H.; Meng, X.-D.; Wei, H.-L.; Chen, L.; Lu, B.-L.; Wang, Z.-H.; Chen, L. A Regularized LSTM Method for Predicting Remaining Useful Life of Rolling Bearings. Int. J. Autom. Comput. 2021, 18, 581–593. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management (PHM’12), Beijing, China, 23–25 May 2012. [Google Scholar]
- Ning, Y.; Wang, G.; Yu, J.; Jiang, H. A Feature Selection Algorithm Based on Variable Correlation and Time Correlation for Predicting Remaining Useful Life of Equipment Using RNN. In Proceedings of the 2018 IEEE Condition Monitoring and Diagnosis (CMD), Perth, Australia, 23–26 September 2018. [Google Scholar]
- Huang, G.; Li, H.; Ou, J.; Zhang, Y.; Zhang, M. A Reliable Prognosis Approach for Degradation Evaluation of Rolling Bearing Using MCLSTM. Sensors 2020, 20, 1864. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Mao, D.; Li, X. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Zhang, X.; Cong, Y.; Yuan, Z.; Zhang, T.; Bai, X. Early Fault Detection Method of Rolling Bearing Based on MCNN and GRU Network with an Attention Mechanism. Shock Vib. 2021, 2021, 6660243. [Google Scholar] [CrossRef]
- Duong, B.P.; Khan, S.A.; Shon, D.; Im, K.; Park, J.; Lim, D.-S.; Jang, B.; Kim, J.-M. A Reliable Health Indicator for Fault Prognosis of Bearings. Sensors 2018, 18, 3740. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Wu, L.; Wang, Z.; Guan, Y. Bearing Remaining Useful Life Prediction Based on Naive Bayes and Weibull Distributions. Entropy 2018, 20, 944. [Google Scholar] [CrossRef] [Green Version]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. Extended Kalman filtering for remaining-useful-life estimation of bearings. IEEE Trans. Ind. Electron. 2015, 62, 1781–1790. [Google Scholar] [CrossRef]
- Zhang, Z.-X.; Si, X.-S.; Hu, C.-H. An Age- and State-Dependent Nonlinear Prognostic Model for Degrading Systems. IEEE Trans. Reliab. 2015, 64, 1214–1228. [Google Scholar] [CrossRef]
- Hu, L.; Hu, N.-Q.; Fan, B.; Gu, F.-S.; Zhang, X.-Y. Modeling the Relationship between Vibration Features and Condition Parameters Using Relevance Vector Machines for Health Monitoring of Rolling Element Bearings under Varying Operation Conditions. Math. Probl. Eng. 2015, 2015, 123730. [Google Scholar] [CrossRef]
- Song, L.; Wang, H.; Chen, P. Vibration-based intelligent fault diagnosis for roller bearings in low-speed rotating machinery. IEEE Trans. Instrum. Meas. 2018, 67, 1887–1899. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Kim, J.; Kim, J.M. Optimal sub-band analysis based on the envelope power Spectrum for effective fault detection in bearing under variable, low speeds. Sensors 2018, 18, 1389. [Google Scholar] [CrossRef] [Green Version]
- Schölkopf, B.; Smola, A.; Mueller, K.-R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Xu, F. Method of fault feature selection and fusion based on poll mode and optimized weighted KPCA for bearings. Measurement 2022, 194, 110950. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Proces. 1997, 45, 2673–2681. [Google Scholar] [CrossRef] [Green Version]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Zhan, Y.; Sun, S.; Li, X.; Wang, F. Combined Remaining Life Prediction of Multiple Bearings Based on EEMD-BILSTM. Symmetry 2022, 14, 251. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Xie, W.; Li, Z.; Xu, Y.; Gardoni, P.; Li, W. Evaluation of Different Bearing Fault Classifiers in Utilizing CNN Feature Extraction Ability. Sensors 2022, 22, 3314. [Google Scholar] [CrossRef]
- Zhang, X.; He, C.; Lu, Y.; Chen, B.; Zhu, L.; Zhang, L. Fault diagnosis for small samples based on attention mechanism. Measurement 2022, 187, 110242. [Google Scholar] [CrossRef]
- Ren, L.; Sun, Y.; Wang, H.; Zhang, L. Prediction of Bearing Remaining Useful Life with Deep Convolution Neural Network. IEEE Access 2018, 6, 13041–13049. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2017, 104, 799–834. [Google Scholar] [CrossRef]
- Yang, F.; Habibullah, M.S.; Zhang, T.; Xu, Z.; Lim, P.; Nadarajan, S. Health Index-Based Prognostics for Remaining Useful Life Predictions in Electrical Machines. IEEE Trans. Ind. Electron. 2016, 63, 2633–2644. [Google Scholar] [CrossRef]
- Lin, P.; Tao, J. A novel bearing health indicator construction method based on ensemble stacked autoencoder. In Proceedings of the 2019 IEEE International Conference on Prognostics and Health Management, San Francisco, CA, USA, 17–20 June 2019. [Google Scholar]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Huang, H.-Z.; Wang, H.-K.; Li, Y.-F.; Zhang, L.; Liu, Z. Support vector machine based estimation of remaining useful life: Current research status and future trends. J. Mech. Sci. Technol. 2015, 29, 151–163. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Xu, J. Degradation Feature Selection for Remaining Useful Life Prediction of Rolling Element Bearings. Qual. Reliab. Eng. Int. 2016, 32, 547–554. [Google Scholar] [CrossRef]
- Han, T.; Pang, J.; Tan, A.C. Remaining useful life prediction of bearing based on stacked autoencoder and recurrent neural network. J. Manuf. Syst. 2021, 61, 576–591. [Google Scholar] [CrossRef]


| Working Condition | Load(N) | Rotation Speed | Dataset |
|---|---|---|---|
| 1 | 4000 | 1800 rpm | Bearing 1-1 (train) |
| Bearing 1-2 (train) | |||
| Bearing 1-3 (test) | |||
| Bearing 1-4 (test) | |||
| Bearing 1-5 (test) | |||
| Bearing 1-6 (test) | |||
| Bearing 1-7 (test) | |||
| 2 | 4200 | 1650 rpm | Bearing 2-1 (train) |
| Bearing 2-2 (train) | |||
| Bearing 2-3 (test) | |||
| Bearing 2-4 (test) | |||
| Bearing 2-5 (test) | |||
| Bearing 2-6 (test) | |||
| Bearing 2-7 (test) | |||
| 3 | 5000 | 1500 rpm | Bearing 3-1 (train) |
| Bearing 3-2 (train) | |||
| Bearing 3-3 (test) |
| Principal Component Serial Number | Contribution Rate | Cumulative Contribution Rate |
|---|---|---|
| 1 | 0.919 | 0.919 |
| 2 | 0.061 | 0.980 |
| 3 | 0.019 | 0.999 |
| Bearing | Monotonicity of RMS | Monotonicity of Proposed HI |
|---|---|---|
| 1-1 | 0.161 | 0.961 |
| 1-2 | 0.102 | 0.962 |
| 1-3 | 0.047 | 0.936 |
| 1-4 | 0.051 | 0.917 |
| 1-5 | 0.101 | 0.959 |
| 1-6 | 0.099 | 0.908 |
| 1-7 | 0.149 | 0.933 |
| 2-1 | 0.087 | 0.915 |
| 2-2- | 0.132 | 0.941 |
| 2-3 | 0.141 | 0.907 |
| 2-4 | 0.097 | 0.913 |
| 2-5 | 0.089 | 0.968 |
| 2-6 | 0.127 | 0.947 |
| 2-7 | 0.152 | 0.903 |
| 3-1 | 0.074 | 0.931 |
| 3-2 | 0.046 | 0.903 |
| 3-3 | 0.047 | 0.933 |
| Model (MSE) | Bearing 1-3 | Bearing 1-4 | Bearing 1-5 | Bearing 1-6 | Bearing 1-7 | Bearing 2-3 | Bearing 2-4 | Bearing 2-5 | Bearing 2-6 | Bearing 2-7 | Bearing 3-3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Proposed | 0.0054 | 0.0031 | 0.007 6 | 0.0044 | 0.0048 | 0.0621 | 0.0091 | 0.0143 | 0.0087 | 0.1026 | 0.0078 |
| CNN | 0.1431 | 0.1101 | 0.1923 | 0.0942 | 0.2721 | 0.0623 | 0.0089 | 0.2641 | 0.3101 | 0.2176 | 0.1739 |
| LSTM | 0.2145 | 0.0671 | 0.2167 | 0.1743 | 0.0074 | 0.1473 | 0.1012 | 0.1149 | 0.2031 | 0.0098 | 0.2147 |
| BiLSTM | 0.0097 | 0.1431 | 0.1016 | 0.2497 | 0.1364 | 0.1824 | 0.2107 | 0.1087 | 0.1047 | 0.4102 | 0.3006 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; Zhao, Y.; Yang, A.; Zhang, H.; Zhang, Z. Prediction of Remaining Service Life of Rolling Bearings Based on Convolutional and Bidirectional Long- and Short-Term Memory Neural Networks. Lubricants 2022, 10, 170. https://doi.org/10.3390/lubricants10080170
Zhong Z, Zhao Y, Yang A, Zhang H, Zhang Z. Prediction of Remaining Service Life of Rolling Bearings Based on Convolutional and Bidirectional Long- and Short-Term Memory Neural Networks. Lubricants. 2022; 10(8):170. https://doi.org/10.3390/lubricants10080170
Chicago/Turabian StyleZhong, Zhidan, Yao Zhao, Aoyu Yang, Haobo Zhang, and Zhihui Zhang. 2022. "Prediction of Remaining Service Life of Rolling Bearings Based on Convolutional and Bidirectional Long- and Short-Term Memory Neural Networks" Lubricants 10, no. 8: 170. https://doi.org/10.3390/lubricants10080170
APA StyleZhong, Z., Zhao, Y., Yang, A., Zhang, H., & Zhang, Z. (2022). Prediction of Remaining Service Life of Rolling Bearings Based on Convolutional and Bidirectional Long- and Short-Term Memory Neural Networks. Lubricants, 10(8), 170. https://doi.org/10.3390/lubricants10080170





