An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers
Abstract
1. Introduction
2. Materials and Methods
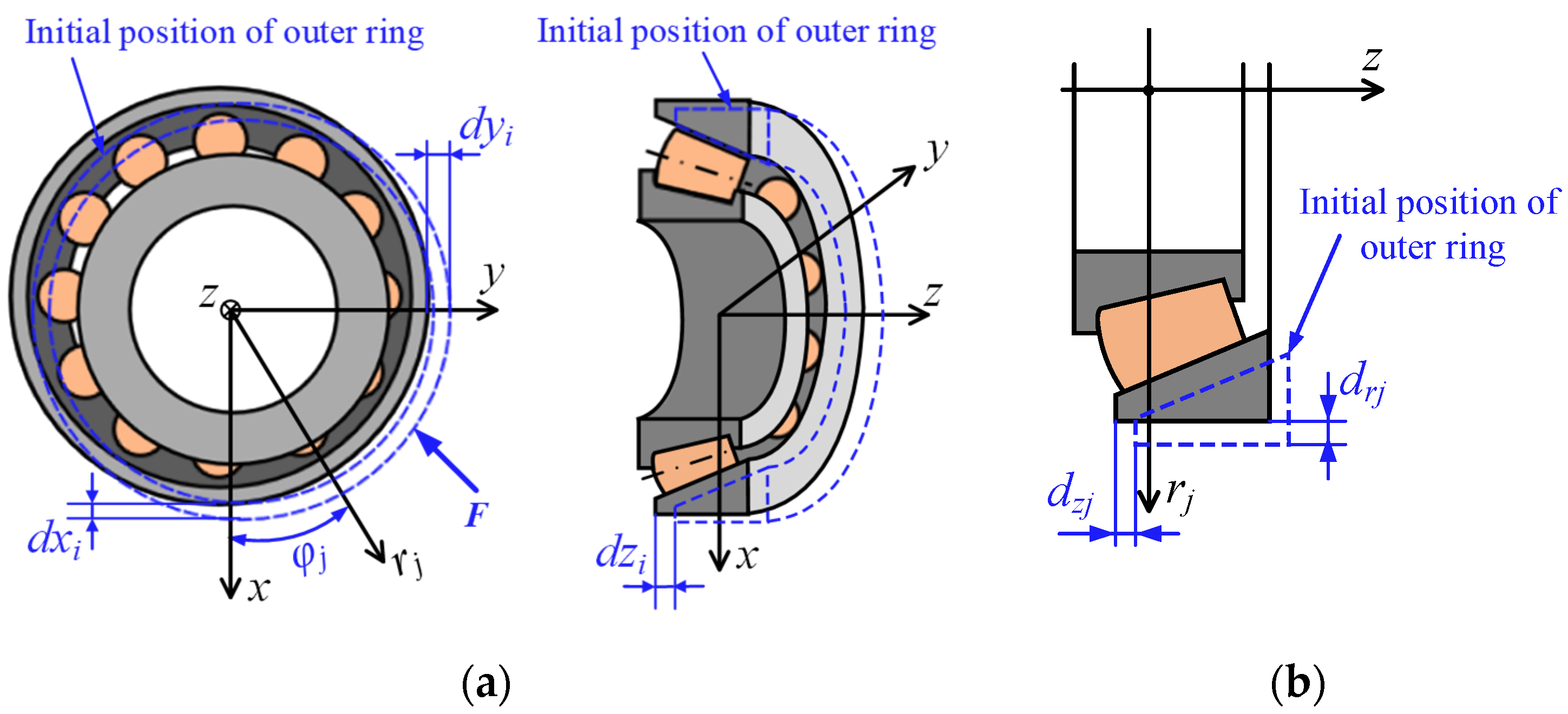
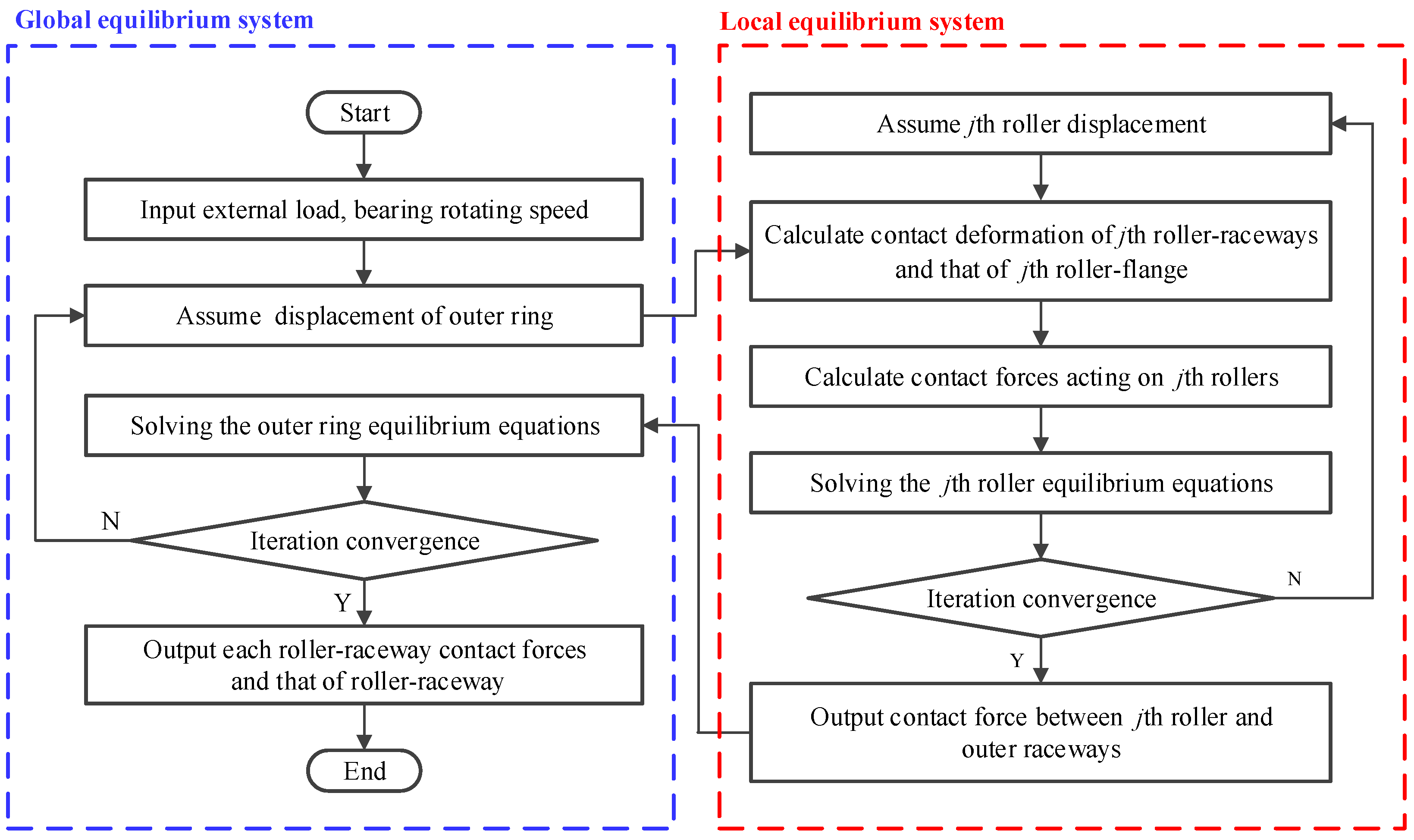
2.1. Quasi-Statics Analysis of TRB Considering the Geometric Homogeneity of Rollers
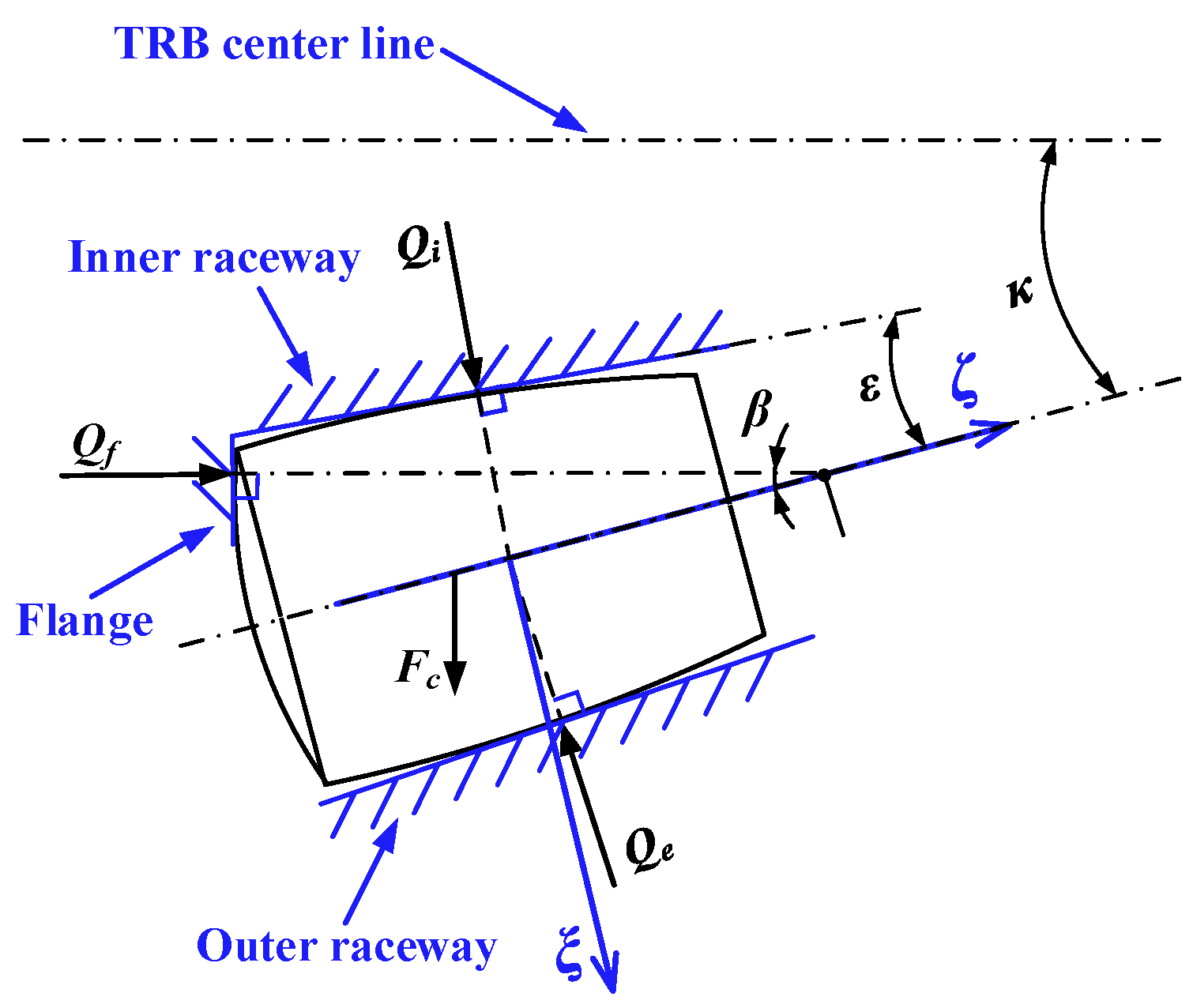
2.2. Friction Torque Analysis of TRBs Considering the Geometric Homogeneity of Rollers
2.3. Geometrical and Material Parameters
3. Results and Discussions
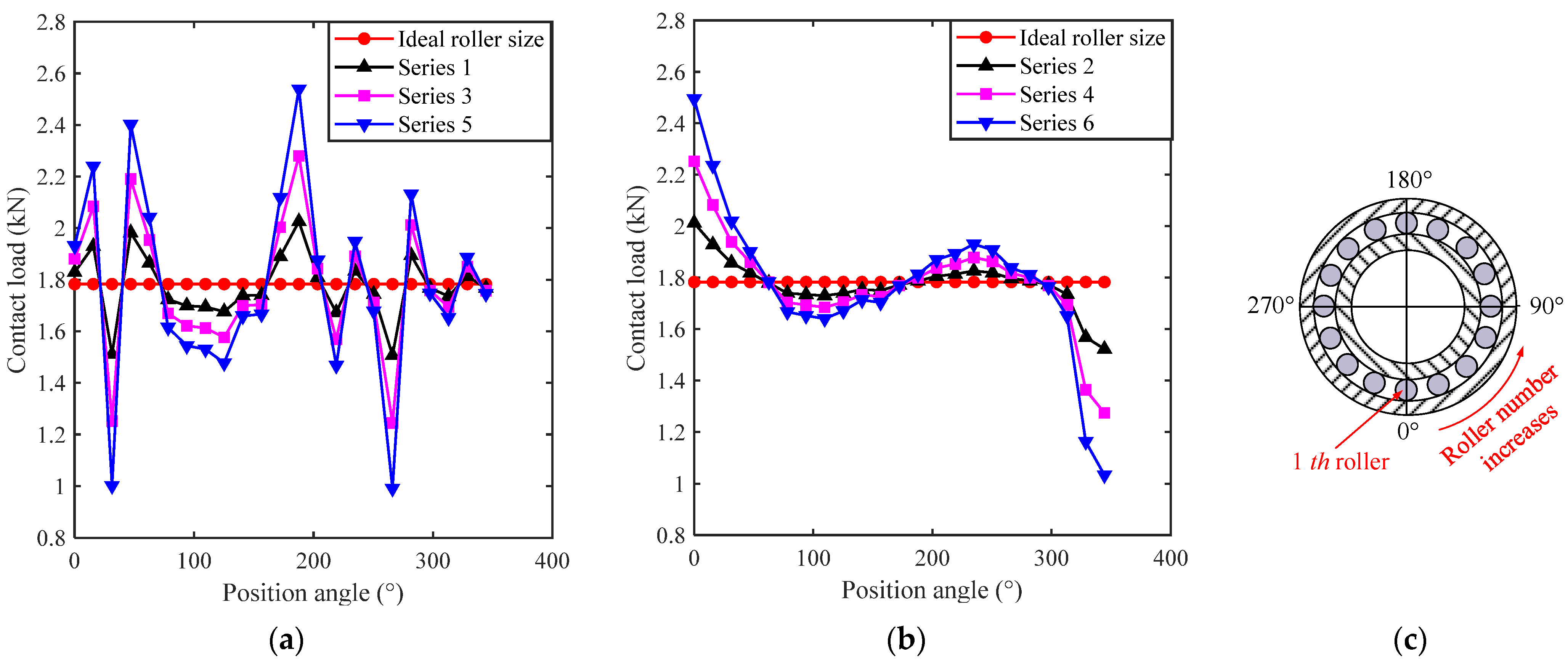
3.1. Effects of the Geometric Homogeneity of Rollers on Contact Force Distribution
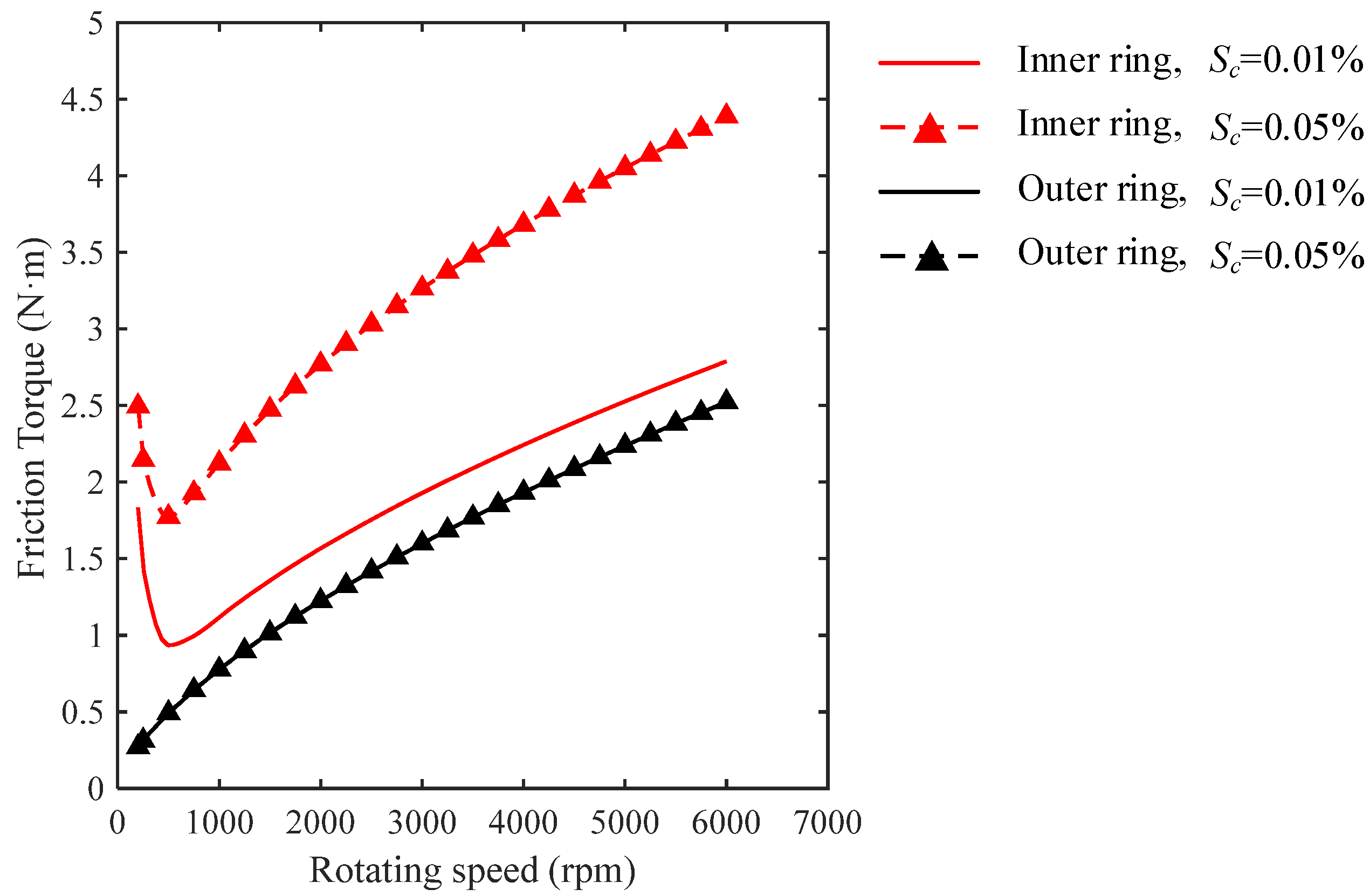
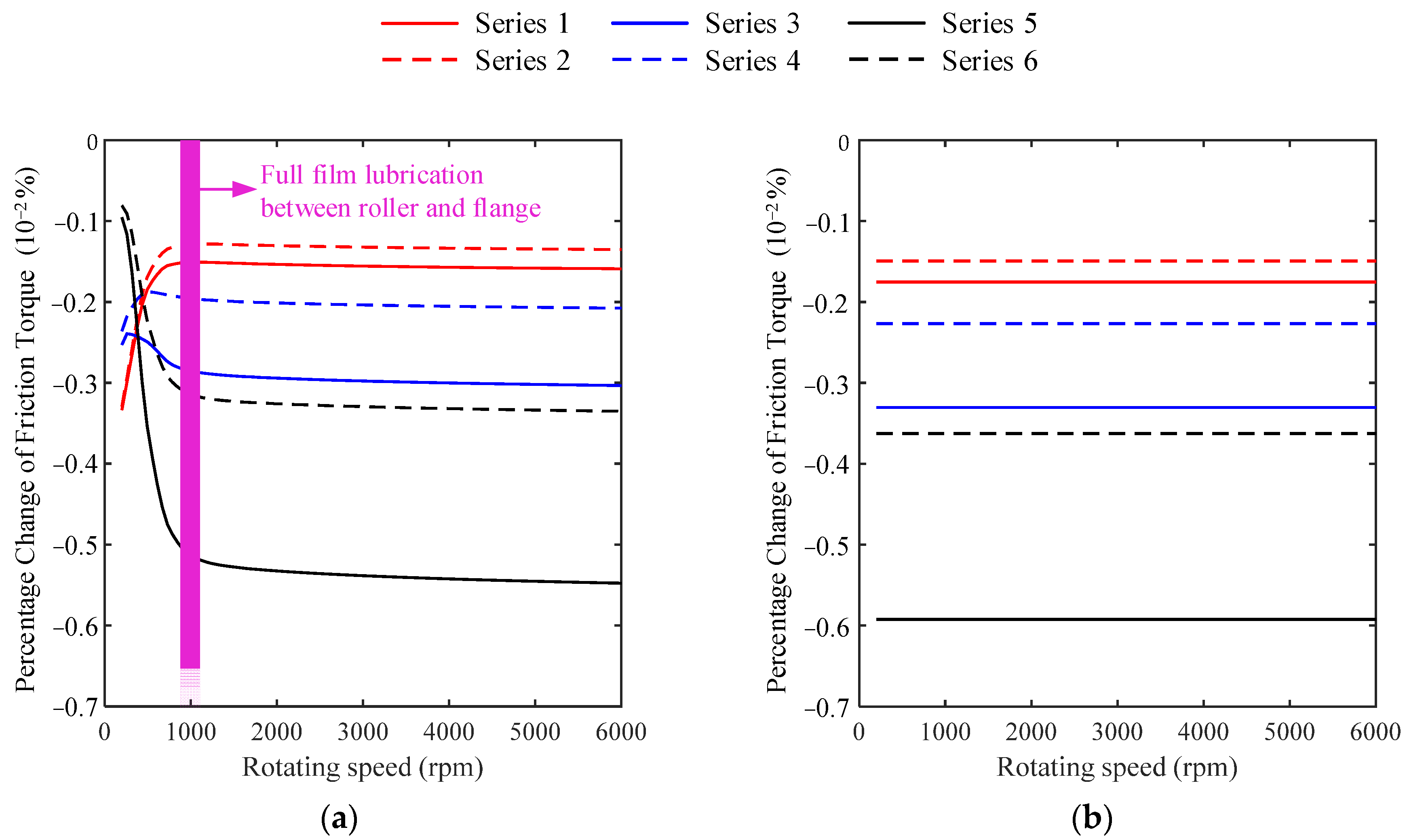
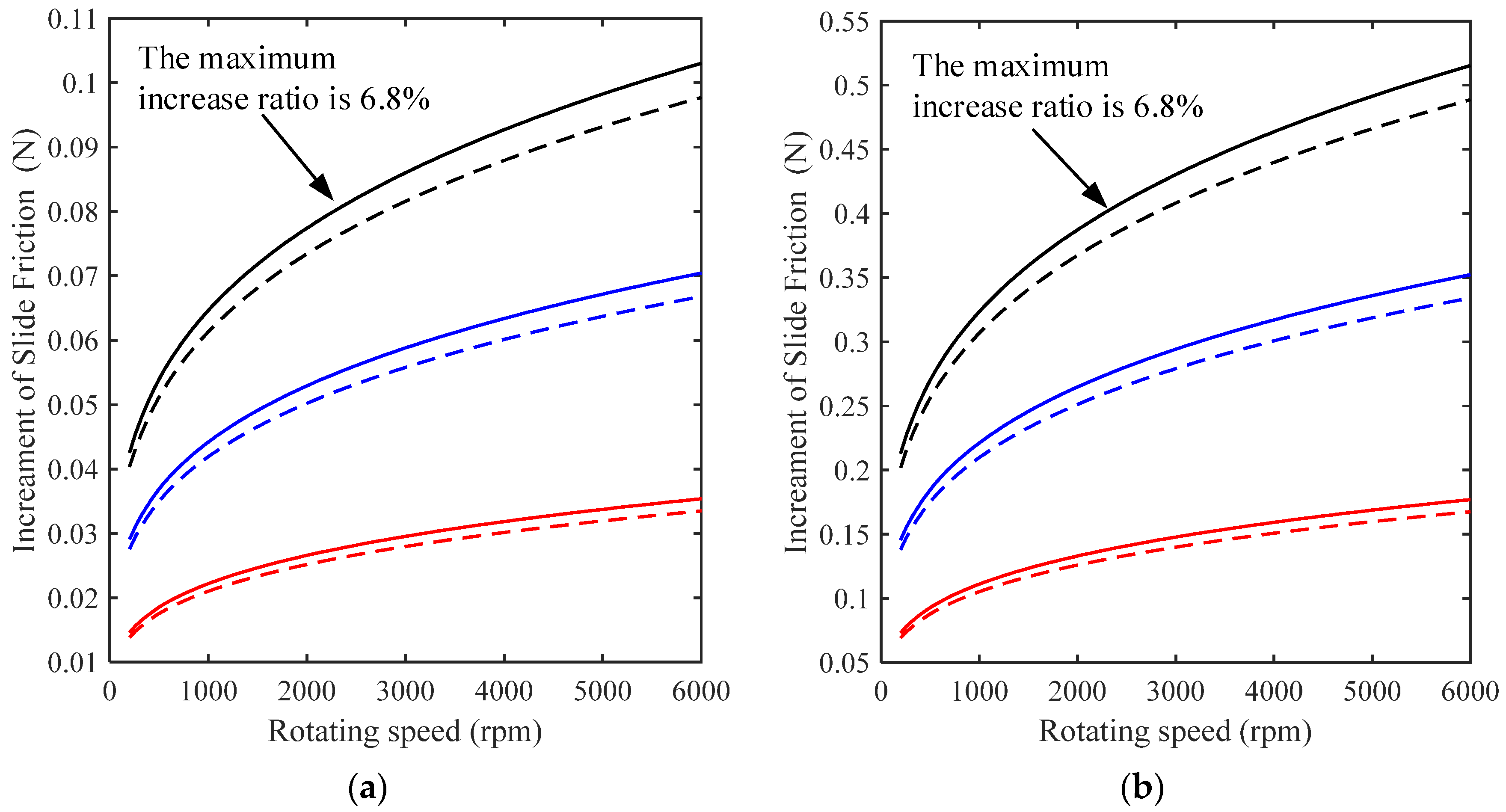
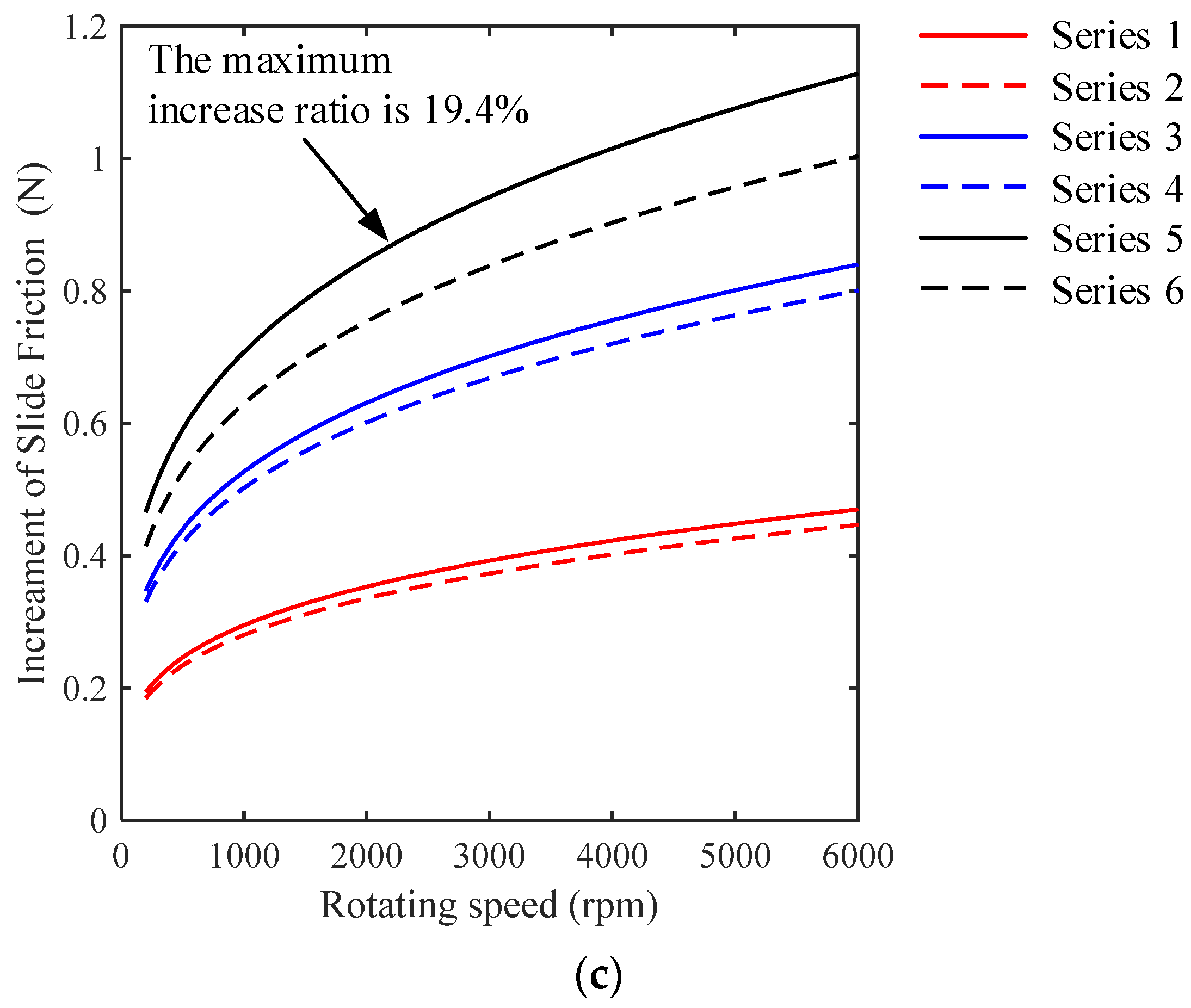
3.2. Effects of the Geometric Homogeneity of Rollers on Friction Force and Torque
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Harris, T.A.; Kotzalas, M.N. Chapter 7: Rolling bearing temperatures. In Advanced Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Witte, D.C. Operating torque of tapered roller bearings. ASLE Trans. 1973, 16, 61–67. [Google Scholar] [CrossRef]
- Karna, C.L. Performance characteristics at the rib roller end contact in tapered roller bearings. ASLE Trans. 1974, 17, 14–21. [Google Scholar] [CrossRef]
- Aihara, S. A new running torque formula for tapered roller bearings under axial load. J. Tribol. 1987, 109, 471–478. [Google Scholar] [CrossRef]
- Zhou, R.S.; Hoeprich, M.R. Torque of Tapered Roller Bearings. J. Tribol. 1991, 113, 590–597. [Google Scholar] [CrossRef]
- SKF. Friction. In General Catalogue 4000; SKF: Gothenburg, Sweden, 2003; Available online: https://imparayaycia.com/SKF%20CATALOGO%20GENERAL.pdf (accessed on 11 July 2022).
- Ma, S.; Zhang, X.; Yan, K.; Zhu, Y.; Hong, J. A Study on Bearing Dynamic Features under the Condition of Multiball–Cage Collision. Lubricants 2022, 10, 9. [Google Scholar] [CrossRef]
- Wu, H.; Liu, J.; Shao, Y. Vibration characteristics of a roller bearing with the waviness error. In Proceedings of the 2019 58th Annual Conference of the Society of Instrument and Control Engineers of Japan, Higashi-Hiroshima, Japan, 10–13 September 2019. [Google Scholar] [CrossRef]
- Savalia, R.; Ghosh, M.K.; Pandey, R.K. Vibration Analysis of Lubricated Angular Contact Ball Bearing of Rigid Rotor Considering Waviness of Ball and Races. Tribol. Online 2008, 3, 322–327. [Google Scholar] [CrossRef][Green Version]
- Nan, G.; Zhang, Y.; Zhu, Y.; Guo, W. Nonlinear dynamics of rotor system supported by bearing with waviness. Sci. Prog. 2020, 103, 003685042094409. [Google Scholar] [CrossRef]
- Aschenbrenner, A.; Schleich, B.; Tremmel, S.; Sandro, W. A variational simulation framework for the analysis of load distribution and radial displacement of cylindrical roller bearings. Mech. Mach. Theory 2020, 147, 103769. [Google Scholar] [CrossRef]
- Deng, S. Analysis on the Friction Torque Fluctuation of Angular Contact Ball Bearings. J. Mech. Eng. 2011, 47, 104. [Google Scholar] [CrossRef]
- Heras, I.; Aguirrebeitia, J.; Abasolo, M. Friction torque in four contact point slewing bearings: Effect of manufacturing errors and ring stiffness. Mech. Mach. Theory 2017, 112, 145–154. [Google Scholar] [CrossRef]
- Halminen, O.; Aceituno, J.F.; Escalona, J.L.; Sopanen, J.; Mikkola, A. A touchdown bearing with surface waviness: Friction loss analysis. Mech. Mach. Theory 2017, 110, 73–84. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y. Modeling of a deep-groove ball bearing with waviness defects in planar multibody system. Multibody Syst. Dyn. 2014, 33, 229–258. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Ding, S.; Pang, R. A time-varying friction moment calculation method of an angular contact ball bearing with the waviness error. Mech. Mach. Theory 2020, 148, 103799. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Z.; Shao, Y. An investigation for the friction torque of a needle roller bearing with the roundness error. Mech. Mach. Theory 2018, 121, 259–272. [Google Scholar] [CrossRef]
- Yao, W.; Yuan, J.; Zhou, F.; Chen, Z.; Zhao, T.; Zhong, M. Trajectory analysis and experiments of both-sides cylindrical lapping in eccentric rotation. Int. J. Adv. Manuf. Technol. 2017, 88, 2849–2859. [Google Scholar] [CrossRef]
- Yuan, J.; Yao, W.; Zhao, P.; Lyu, B.; Chen, Z.; Zhong, M. Kinematics and trajectory of both-sides cylindrical lapping process in planetary motion type. Int. J. Mach. Tools Manuf. 2015, 92, 60–71. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Yan, K.; Wang, F.; Hong, J. A novel method to model effects of natural defect on roller bearing. Tribol. Int. 2018, 122, 169–178. [Google Scholar] [CrossRef]
- Kang, W.; Zhu, Y.; Yan, K.; Ren, Z.; Gao, D.; Hong, J. Research on extracting weak repetitive transients of fault rolling element bearing. ISA Trans. 2021, 123, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Tong, V.; Hong, S. The effect of angular misalignment on the running torques of tapered roller bearings. Tribol. Int. 2016, 95, 76–85. [Google Scholar] [CrossRef]
- Harris, T.A. An analytical method to predict skidding in high speed roller bearings. ASLE Trans. 1966, 9, 229–241. [Google Scholar] [CrossRef]
- Marian, M.; Bartz, M.; Wartzack, S.; Andreas, R. Non-dimensional groups, film thickness equations and correction factors for elastohydrodynamic lubrication: A review. Lubricants 2020, 8, 95. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Chapter 7: Distributions of internal loading in statically loaded bearings. In Essential Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Zhang, Y.; Fang, B.; Kong, L.; Li, Y. Effect of the ring misalignment on the service characteristics of ball bearing and rotor system. Mech. Mach. Theory 2020, 151, 103889. [Google Scholar] [CrossRef]
| Geometrical Characteristics | Value |
|---|---|
| Small diameter of taper roller (mm) | 6.131 |
| Large diameter of taper roller (mm) | 6.846 |
| Length of roller (mm) | 13.66 |
| Number of rollers | 23 |
| Outer raceway angle (rad) | 0.2473 |
| Inner raceway angle (rad) | 0.1949 |
| Roller angle (rad) | 0.0262 |
| Flange angle (rad) | 1.5621 |
| Elasticity modulus (N/mm2) | 2.1 × 105 |
| Poisson’s ratio | 0.278 |
| Roller Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| ΔD (μm) | Series 1 | 0.28 | 0.52 | −0.56 | 0.63 | 0.33 | −0.03 | −0.10 | −0.11 |
| Series 2 | 0.76 | 0.63 | 0.52 | 0.47 | 0.41 | 0.33 | 0.31 | 0.28 | |
| Series 3 | 0.55 | 1.04 | −1.12 | 1.26 | 0.66 | −0.07 | −0.20 | −0.22 | |
| Series 4 | 1.53 | 1.26 | 1.04 | 0.95 | 0.83 | 0.66 | 0.63 | 0.55 | |
| Series 5 | 0.83 | 1.56 | −1.68 | 1.89 | 0.99 | −0.10 | −0.29 | −0.33 | |
| Series 6 | 2.29 | 1.89 | 1.56 | 1.42 | 1.24 | 0.99 | 0.94 | 0.83 | |
| Roller Number | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| ΔD (μm) | Series 1 | −0.15 | 0.01 | 0.03 | 0.41 | 0.76 | 0.23 | −0.10 | 0.31 |
| Series 2 | 0.26 | 0.23 | 0.15 | 0.13 | 0.09 | 0.07 | 0.03 | 0.01 | |
| Series 3 | −0.30 | 0.02 | 0.05 | 0.83 | 1.53 | 0.47 | −0.21 | 0.63 | |
| Series 4 | 0.52 | 0.47 | 0.31 | 0.26 | 0.18 | 0.14 | 0.05 | 0.02 | |
| Series 5 | −0.45 | 0.03 | 0.08 | 1.24 | 2.29 | 0.70 | −0.31 | 0.94 | |
| Series 6 | 0.77 | 0.70 | 0.46 | 0.39 | 0.27 | 0.20 | 0.08 | 0.03 | |
| Roller Number | 17 | 18 | 19 | 20 | 21 | 22 | 23 | ||
| ΔD (μm) | Series 1 | 0.09 | −0.51 | 0.47 | 0.15 | 0.07 | 0.26 | 0.13 | |
| Series 2 | −0.03 | −0.10 | −0.10 | −0.11 | −0.15 | −0.51 | −0.56 | ||
| Series 3 | 0.18 | −1.03 | 0.95 | 0.31 | 0.14 | 0.52 | 0.26 | ||
| Series 4 | −0.07 | −0.20 | −0.21 | −0.22 | −0.30 | −1.03 | −1.12 | ||
| Series 5 | 0.27 | −1.54 | 1.42 | 0.46 | 0.20 | 0.77 | 0.39 | ||
| Series 6 | −0.10 | −0.29 | −0.31 | −0.33 | −0.45 | −1.54 | −1.68 | ||
| Series 1 | Series 2 | Series 3 | Series 4 | Series 5 | Series 6 | |
|---|---|---|---|---|---|---|
| Maximum value (kN) | 2.026 | 2.013 | 2.280 | 2.253 | 2.539 | 2.495 |
| Variance (kN2) | 0.0162 | 0.0096 | 0.0645 | 0.0383 | 0.1441 | 0.0856 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Fan, X.; Wang, J.; Liu, X. An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers. Lubricants 2022, 10, 154. https://doi.org/10.3390/lubricants10070154
Liu Y, Fan X, Wang J, Liu X. An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers. Lubricants. 2022; 10(7):154. https://doi.org/10.3390/lubricants10070154
Chicago/Turabian StyleLiu, Yuwei, Xingyu Fan, Jia Wang, and Xiayi Liu. 2022. "An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers" Lubricants 10, no. 7: 154. https://doi.org/10.3390/lubricants10070154
APA StyleLiu, Y., Fan, X., Wang, J., & Liu, X. (2022). An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers. Lubricants, 10(7), 154. https://doi.org/10.3390/lubricants10070154





