Performance of a New Aeronautic Oil-Guiding Splash Lubrication System
Abstract
:1. Introduction
2. CFD Methodology
2.1. Governing Equation
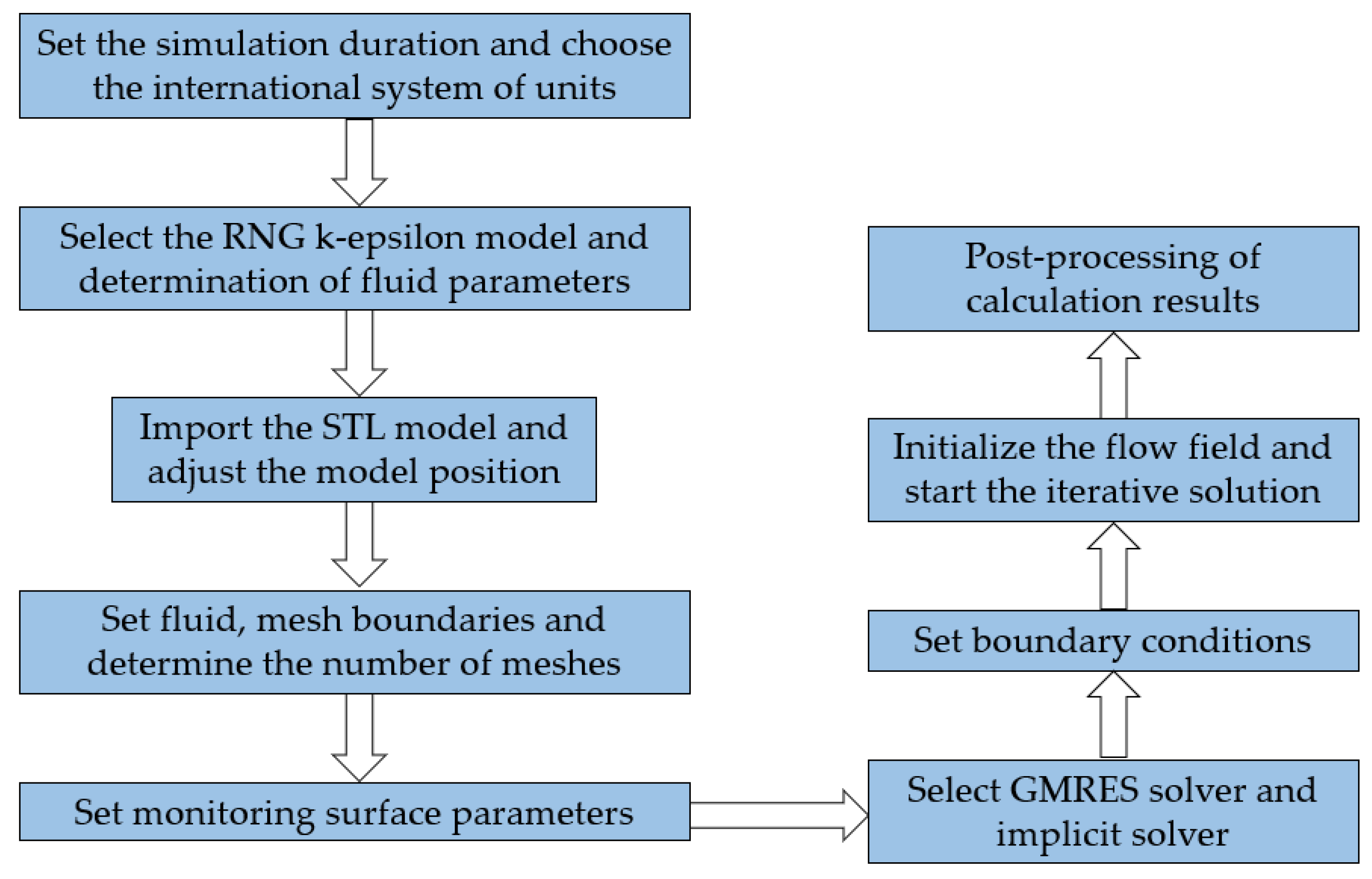
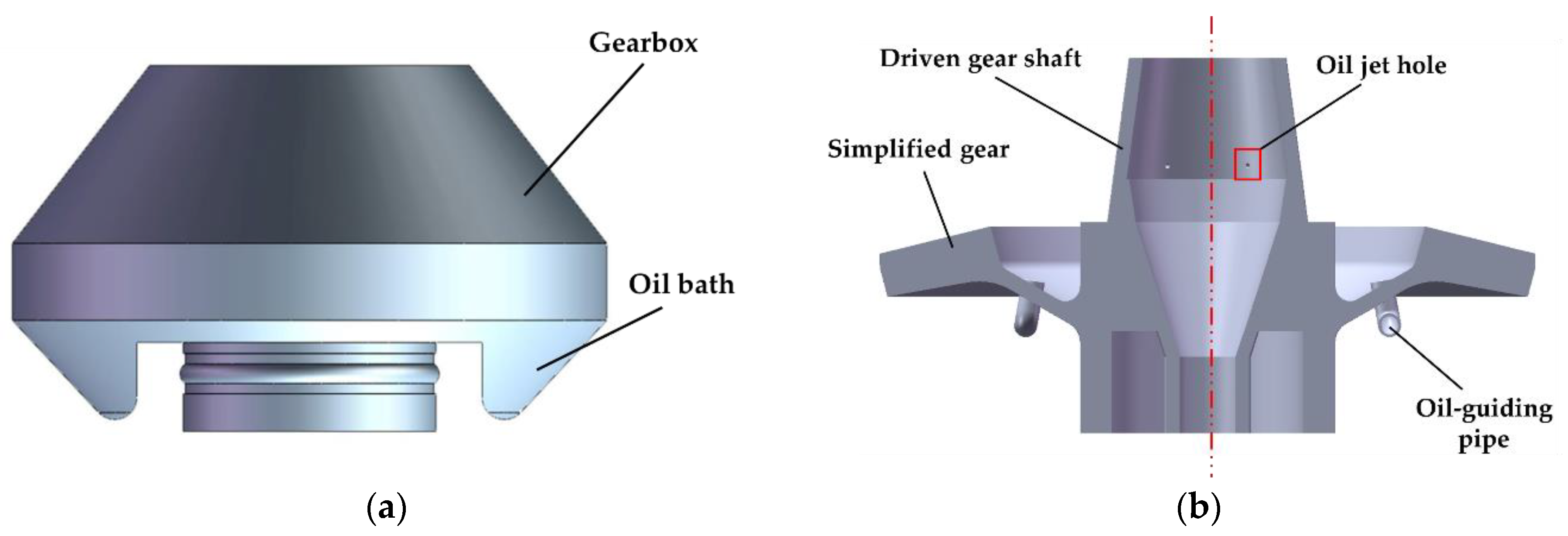
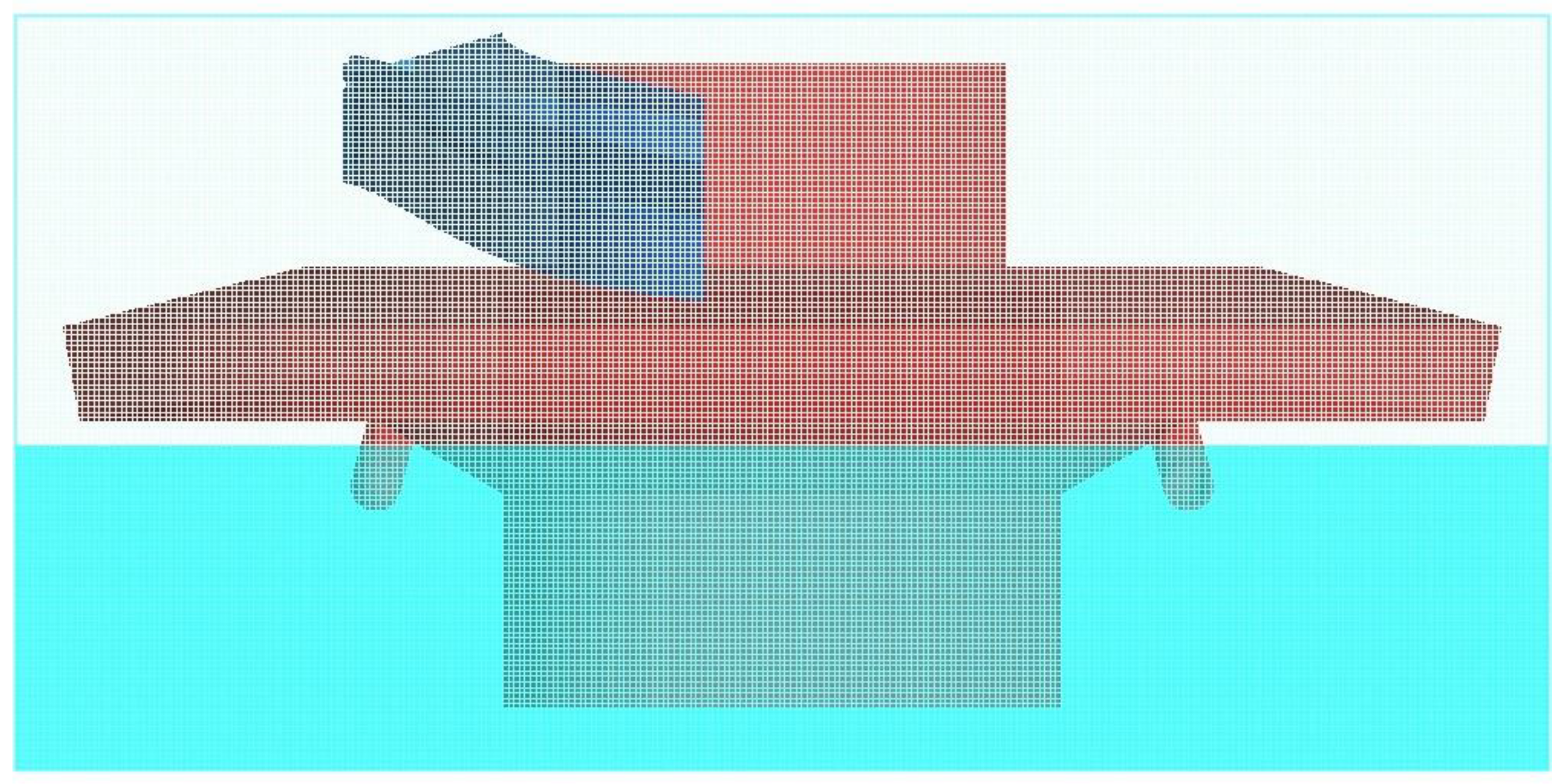
2.2. Numerical Setup and Grids
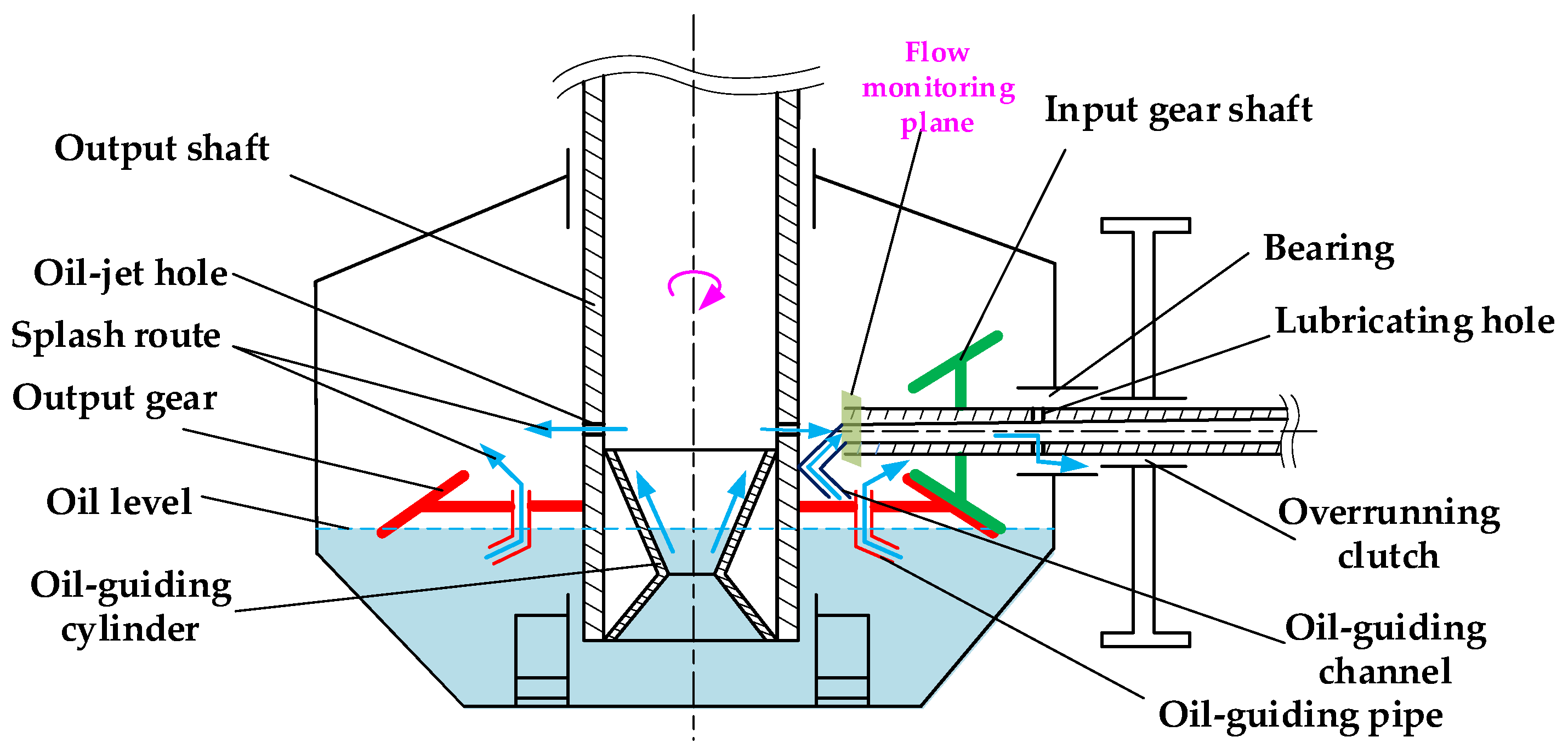
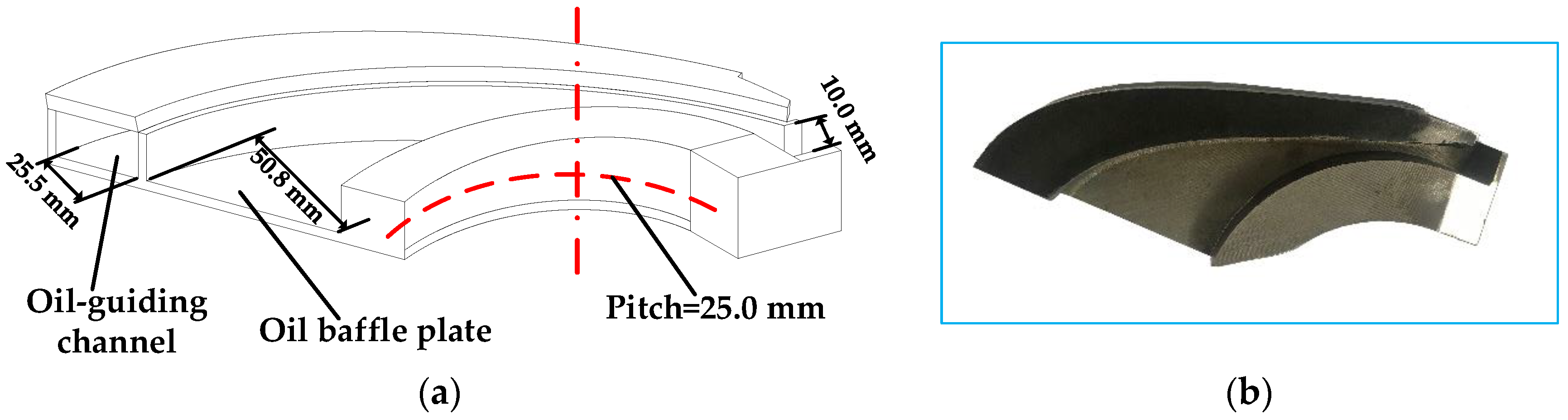
2.2.1. Oil-Guiding Channel
2.2.2. Flow-Monitoring Plane
2.3. CFD Grid Technology
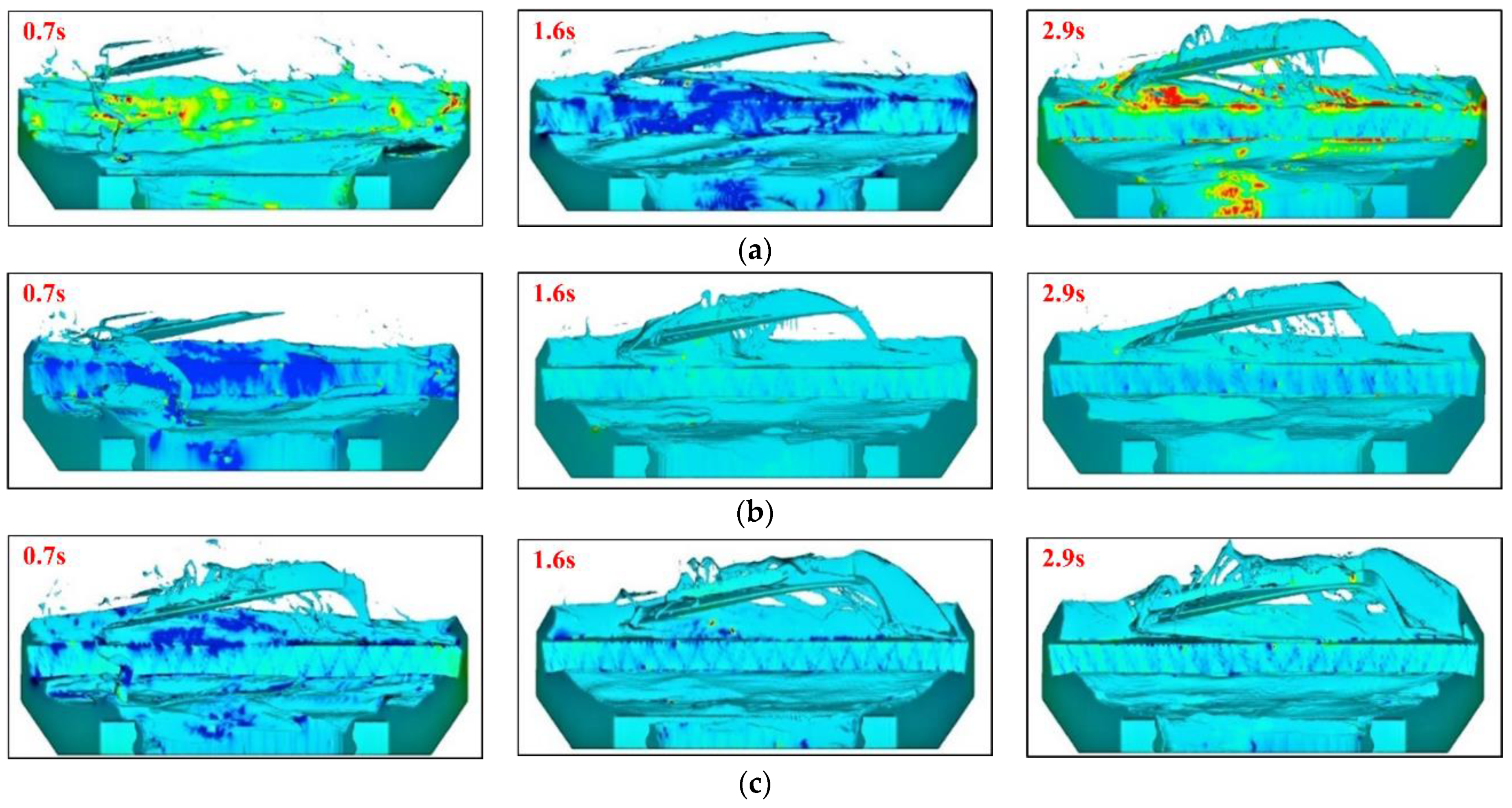
3. Numerical Results
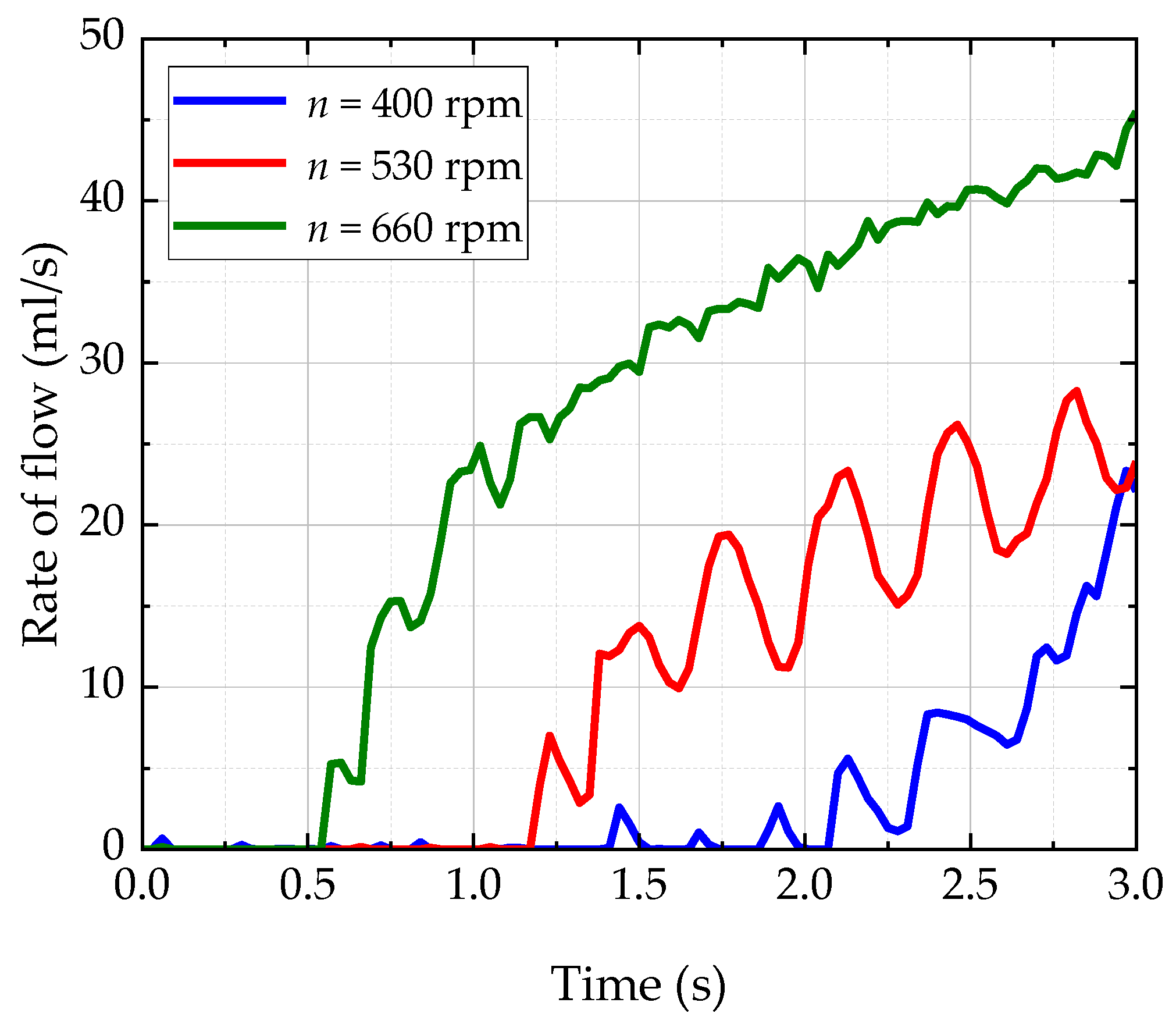
3.1. Rotating Speed
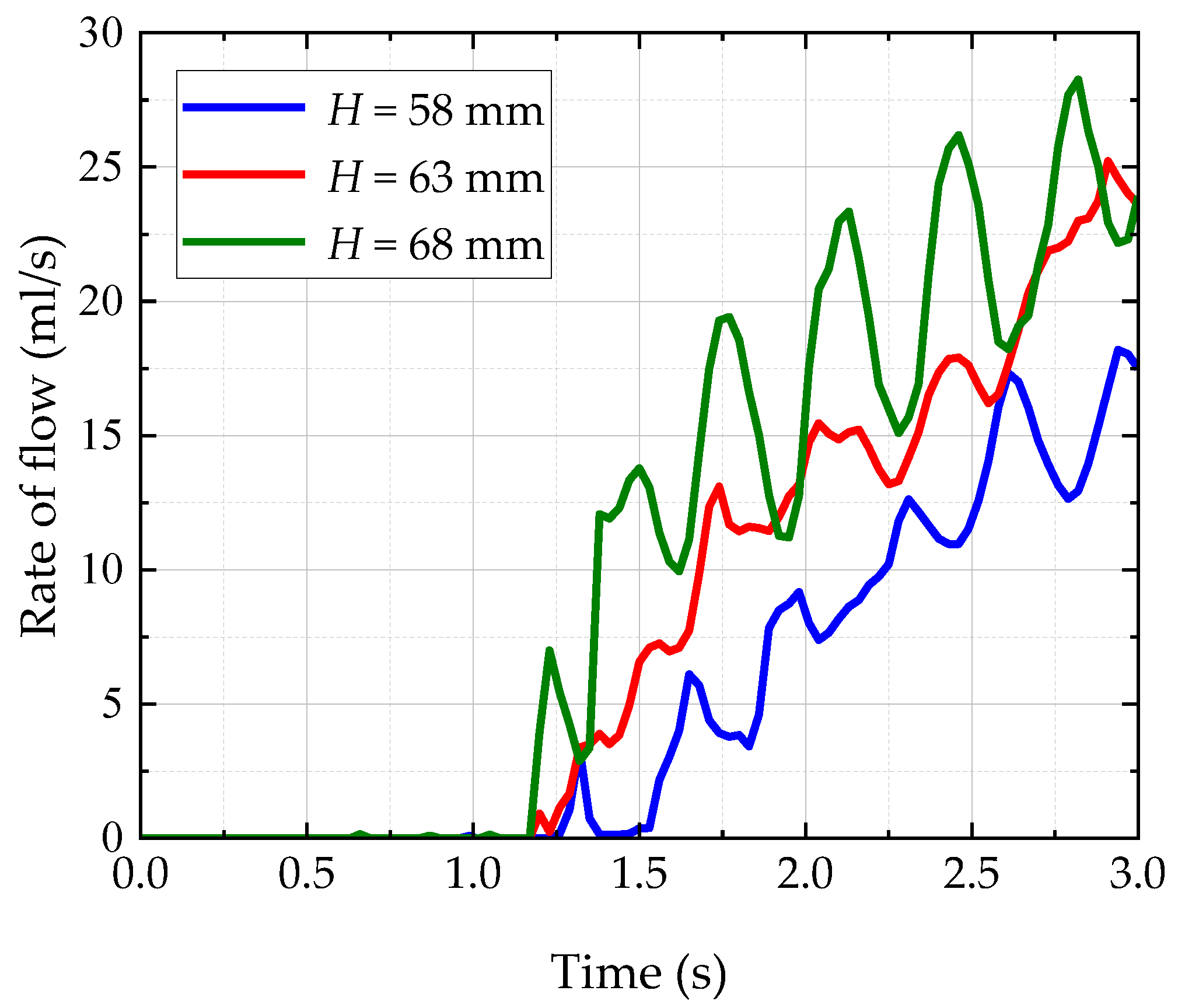
3.2. Oil Bath Depth
4. Experimental Validation
4.1. Test Bench
4.2. Experimental Findings
4.2.1. Rotating Speed
4.2.2. Oil Bath Depth
5. Conclusions
- By leveraging the oil-guiding channel, the oil mass transferred from the gear surface into the channel increases, and then the oil volume collected through the oil-collecting pipe also increases. Specifically, at the rotating speed of 400 rpm, the oil flow rate with the oil-guiding channel in this study exceeds 2.5 mL/s, far more than the experimental data of 0.0017 mL/s, conducted by Yin et al. [27,28]. At the rotating speed of 660 rpm, the oil flow rate with the oil-guiding channel exceeds 22.6 mL/s, much greater than the experimental data of 0.034 mL/s, performed by Yin et al. [27,28]. This shows the oil flow rate is increased by about three orders of magnitude, benefiting from the oil-guiding channel. Therefore, the oil-leading hood can effectively increase the flow rate and improve the lubrication efficiency of the whole lubrication system.
- The flow rate of the oil reaching the oil-jet hole increases with the increase of rotational speed. Increasing the rotational speed, the oil volume through the oil-guiding pipe grows and the splash of oil is stronger. The pipe collects more lubricating oil that passes through the oil-guiding channel, and the increasing rotational speed contributes to the increase of the oil mass, to reach the driving gear.
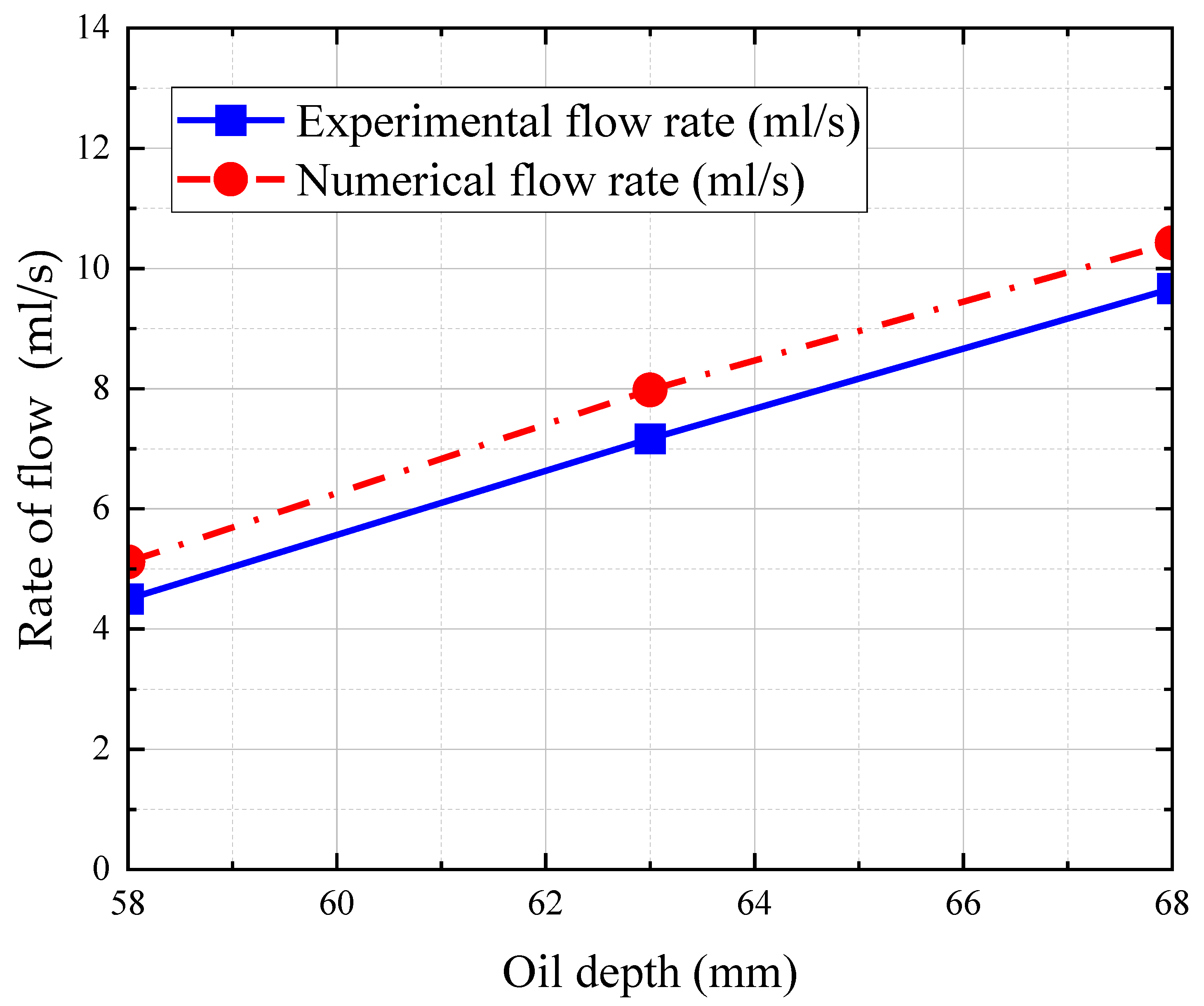
- The flow rate reaching the oil-jet hole increases with the increase of oil depth. When the depth of the oil bath is raised, the oil is churned violently by the spinning gear. So, a deeper oil bath contributes to more oil flowing through the oil-guiding pipe, into the oil-guiding channel. However, too high an oil depth, causing the spiral bevel gear to be immersed in the oil bath, will bring a significant churning power loss.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Concli, F.; Della Torre, A.; Gorla, C.; Montenegro, G. A new integrated approach for the prediction of the load independent power losses of gears: Development of a mesh-handling algorithm to reduce the CFD simulation time. Adv. Tribol. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. Numerical modeling of the power losses in geared transmissions: Windage, churning and cavitation simulations with a new integrated approach that drastically reduces the computational effort. Tribol. Int. 2016, 103, 58–68. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. Numerical modeling of the churning power losses in planetary gearboxes: An innovative partitioning-based meshing methodology for the application of a computational effort reduction strategy to complex gearbox configurations. Lubr. Sci. 2017, 29, 455–474. [Google Scholar] [CrossRef]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Determination of oil distribution and churning power loss of gearboxes by finite volume CFD method. Tribol. Int. 2017, 109, 346–354. [Google Scholar] [CrossRef]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Detailed investigations on the oil flow in dip-lubricated gearboxes by the finite volume CFD method. Lubricants 2018, 6, 47. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Arfaoui, G.; Stanic, M.; Montigny, L.; Jurkschat, T.; Lohner, T.; Stahl, K. Numerical modelling of oil distribution and churning gear power losses of gearboxes by smoothed particle hydrodynamics. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2019, 233, 74–86. [Google Scholar] [CrossRef]
- Gong, R.; Gong, Q.; Che, H.; Zhang, Z. Numerical investigation on churning loss torque and oil distribution of reducer based on lattice boltzmann method. Tribol. Trans. 2021, 64, 968–979. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, Y.; Luo, C.; Feng, L.; Dai, Y. Churning power losses of a gearbox with spiral bevel geared transmission. Tribol. Int. 2019, 129, 398–406. [Google Scholar] [CrossRef]
- Hu, X.; Wang, A.; Li, P.; Wang, J. Influence of dynamic attitudes on oil supply for bearings and churning power losses in a splash lubricated spiral bevel gearbox. Tribol. Trans. 2021, 159, 106951. [Google Scholar] [CrossRef]
- Jiang, Y.; Hu, X.; Hong, S.; Li, P.; Wu, M. Influences of an oil guide device on splash lubrication performance in a spiral bevel gearbox. Tribol. Trans. 2019, 136, 155–164. [Google Scholar] [CrossRef]
- Lu, F.; Wang, M.; Bao, H.; Huang, W.; Zhu, R. Churning power loss of the intermediate gearbox in a helicopter under splash lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 49–58. [Google Scholar] [CrossRef]
- Legrady, B.; Taesch, M.; Tschirschnitz, G.; Mieth, C.F. Prediction of churning losses in an industrial gear box with spiral bevel gears using the smoothed particle hydrodynamic method. Forsch. Im Ing. 2021, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Song, G.; Niu, W.; Chen, Y. Optimized design of spray parameters of oil jet lubricated spur gears. Tribol. Trans. 2018, 120, 149–158. [Google Scholar] [CrossRef]
- Wang, Y.; Song, G.; Niu, W.; Chen, Y. Influence of oil injection methods on the lubrication process of high speed spur gears. Tribol. T. 2018, 121, 180–189. [Google Scholar] [CrossRef]
- Dai, Y.; Ma, F.; Zhu, X.; Su, Q.; Hu, X. Evaluation and optimization of the oil jet lubrication performance for orthogonal face gear drive: Modelling, simulation and experimental validation. Energies 2019, 12, 1935. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, B.; Ma, F.; Dai, Y.; Zhang, Y. Numerical analysis on heat-flow-coupled temperature field for orthogonal face gears with oil–jet lubrication. Eng. Appl. Comp. Fluid 2021, 15, 762–780. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, Y.; Ma, F.; Ouyang, B. Mathematical modeling and numerical simulation for determining an optimized oil jet layout for spiral bevel gear lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 611–628. [Google Scholar] [CrossRef]
- Massini, D.; Fondelli, T.; Facchini, B.; Tarchi, L.; Leonardi, F. High speed visualizations of oil jet lubrication for aero-engine gearboxes. Energy Procedia 2016, 101, 1248–1255. [Google Scholar] [CrossRef]
- Fondelli, T.; Andreini, A.; Da Soghe, R.; Facchini, B.; Cipolla, L. Numerical simulation of oil jet lubrication for high speed gears. Int. J. Aerosp. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Massini, D.; Fondelli, T.; Facchini, B.; Tarchi, L.; Leonardi, F. Experimental investigation on power losses due to oil jet lubrication in high speed gearing systems. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 50886, p. V05BT15A030. [Google Scholar] [CrossRef]
- Keller, M.C.; Braun, S.; Wieth, L.; Chaussonnet, G.; Dauch, T.; Koch, R.; Bauer, H.J. Numerical modeling of oil-jet lubrication for spur gears using smoothed particle hydrodynamics. In Proceedings of the 11th International SPHERIC Workshop, Munich, Germany, 14–16 June 2016; pp. 69–76. [Google Scholar]
- Keller, M.C.; Braun, S.; Wieth, L.; Chaussonnet, G.; Dauch, T.F.; Koch, R.; Bauer, H.J. Smoothed particle hydrodynamics simulation of oil-jet gear interaction1. J. Tribol. ASME 2019, 141, 071703. [Google Scholar] [CrossRef]
- Keller, M.C.; Kromer, C.; Cordes, L.; Schwitzke, C.; Bauer, H.J. CFD study of oil-jet gear interaction flow phenomena in spur gears. Aeronaut. J. 2020, 124, 1301–1317. [Google Scholar] [CrossRef]
- Ambrose, S.; Morvan, H.; Simmons, K. Investigation of oil jet impingement on a rotating gear using lattice boltzman method (LBM). In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 50985, p. V001T01A028. [Google Scholar] [CrossRef]
- Dai, Y.; Liang, C.; Chen, X.; Zhu, X. Numerical analysis for wetting behaviors of an oil jet lubricated spur gear. Lubricants 2022, 10, 17. [Google Scholar] [CrossRef]
- Kromer, C.; von Plehwe, F.C.; Keller, M.C.; Schwitzke, C.; Bauer, H.J. Analytical model for the heat transfer in impingement cooled spur gears. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84058, p. V001T01A023. [Google Scholar] [CrossRef]
- Yin, M.; Xu, L.J.; Dai, Y.; Yang, D.; Zhu, X. Flow characteristics of oil-guiding splash lubrication: Simulation and experiment studies. Int. J. Simul. Model. 2021, 20, 363–374. [Google Scholar] [CrossRef]
- Yin, M.; Chen, X.; Dai, Y.; Yang, D.; Xu, L.; Zhu, X. Numerical and experimental investigation of oil-guiding splash lubrication in light helicopter’s reducers. Aerospace 2021, 8, 345. [Google Scholar] [CrossRef]


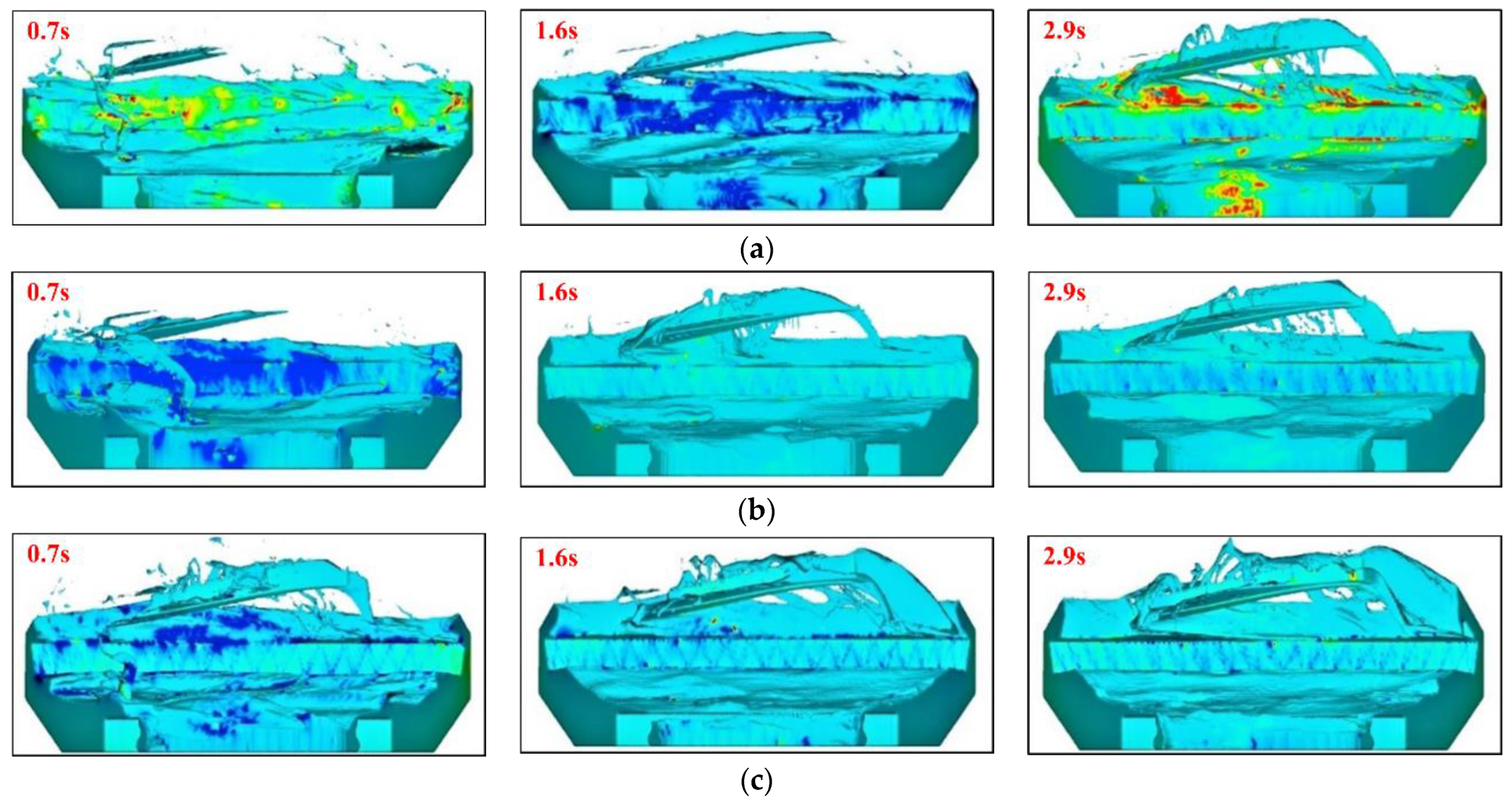




| Rotational Speed n (rpm) | Running Time (s) | Numerical Average Oil Flow Rate (mL/s) |
|---|---|---|
| 400 | 3 | 3.029 |
| 530 | 3 | 10.427 |
| 660 | 3 | 25.332 |
| Oil Depth H (mm) | Running Time (s) | Numerical Average Oil Flow Rate (mL/s) |
|---|---|---|
| 58 | 3 | 5.119 |
| 63 | 3 | 8.177 |
| 68 | 3 | 10.427 |
| Rotational Speed n (rpm) | Running Time (min) | Experimental Flow Rate (mL/s) | Baseline Testing Flow Rate (mL/s) | Numerical Flow Rate (mL/s) | Relative Error |
|---|---|---|---|---|---|
| 400 | 3 | 2.583 | 0.058 | 3.029 | 14.7% |
| 530 | 3 | 9.667 | 0.528 | 10.427 | 7.3% |
| 660 | 3 | 22.667 | 0.556 | 25.332 | 10.5% |
| Oil Depth H (mm) | Running Time (min) | Experimental Flow Rate (mL/s) | Baseline Testing Flow Rate (mL/s) | Numerical Flow Rate (mL/s) | Relative Error |
|---|---|---|---|---|---|
| 58 | 3 | 4.500 | 0.333 | 5.119 | 12.1% |
| 63 | 3 | 7.167 | 0.417 | 8.177 | 12.4% |
| 68 | 3 | 9.667 | 0.528 | 10.427 | 7.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Y.; Chen, X.; Yang, D.; Xu, L.; Zhu, X. Performance of a New Aeronautic Oil-Guiding Splash Lubrication System. Lubricants 2022, 10, 130. https://doi.org/10.3390/lubricants10060130
Dai Y, Chen X, Yang D, Xu L, Zhu X. Performance of a New Aeronautic Oil-Guiding Splash Lubrication System. Lubricants. 2022; 10(6):130. https://doi.org/10.3390/lubricants10060130
Chicago/Turabian StyleDai, Yu, Xi Chen, Duan Yang, Lanjin Xu, and Xiang Zhu. 2022. "Performance of a New Aeronautic Oil-Guiding Splash Lubrication System" Lubricants 10, no. 6: 130. https://doi.org/10.3390/lubricants10060130
APA StyleDai, Y., Chen, X., Yang, D., Xu, L., & Zhu, X. (2022). Performance of a New Aeronautic Oil-Guiding Splash Lubrication System. Lubricants, 10(6), 130. https://doi.org/10.3390/lubricants10060130







