Abstract
The elastohydrodynamic lubrication (EHL) oil film between contact interfaces acts as a spring or damper to reduce wear and vibration for frictional pairs. To analyze the dynamic behaviors of friction pairs in mechanical systems both effectively and accurately, the stiffness and damping parameters under EHL contact states are essential. The presented work develops a numerical model to investigate the EHL stiffness and damping characteristics based on the transient EHL system and elastic contact theory of line contact, in which the stiffness force is separated according to the relationship with approach distance of the contact body established in the steady process, and then the damping can be obtained. The results show that the stiffness force plays an increasingly important role over the applied load conditions while the damping effects is gradually weakened. EHL stiffness is obviously smaller than dry contact stiffness, but the discrepancy is decreasing with the increasing load. Moreover, the higher entrainment velocity, lubricant viscosity and larger curvature radii leads to smaller stiffness and damping. The elastic modulus generates little effect on dynamic characteristics when the load is light while dominates the maximum level of the contact stiffness.
1. Introduction
Elastohydrodynamic lubrication (EHL) line contact is ubiquitous in the key parts and elements of heavy-duty machines, e.g., roller bearings, gears, and cam tappets [1]. The film lubrication state at the contact interface of these components not only determines the tribological performance of the components and mechanisms but also affects their dynamic behaviors. In the conventional sense, the EHL effect of line contact is ignored in the dynamic analysis for these friction pairs in mechanical systems [2], due to the high complexity of modeling and expense of computing. As the lightweight, compact, and high-power density design concepts are becoming mainstream in industrial areas, an increasing number of accurate and efficient dynamics modeling and simulation methods for friction pairs, and thus the whole mechanical system, is desiderated.
In order to embed the EHL effects in the dynamic analysis of complex systems, investigating the stiffness and damping parameters under EHL conditions to replace the traditional dry contact force model is an efficient approach with satisfactory accuracy. In recent years, the evaluation method and the parametric study of stiffness and damping parameters with EHL film considered have drawn broad attention in tribology communities. Nonato [3] assessed the behavior of linear damping approximation of the lubricated contact for point contact and investigated the effects of different loading conditions, to assess the excitation frequency for the dimensionless time domains. Wiegert et al. [4] proposed a reduced dynamic model of EHL line contact, consisting of hydrodynamic and Hertzian force elements. Qin et al. [5] studied the EHL stiffness respectively from three aspects, including the oil film, elastic contact body, and comprehensive stiffness through conducting a numerical analysis with oil pressure and film thickness. Moreover, the simulated results were compared with Hertzian stiffness and then the critical working conditions that can be approximated by dry contact were investigated. Zhang et al. [6] calculated the contact stiffness through Hertzian analytical solution [7] and the Yang-Sun model [8] predicted the oil film stiffness by the empirical EHL film thickness equation and the complete numerical EHL model. Recently, Tsuha et al. [9] introduced linear and nonlinear force models while solving EHL stiffness for finite line contact with four types of profiles considered.
The above investigations are based on steady-state, while the actual operating conditions are mostly high-transient events. Thus, there are some other researchers also focusing on the transient stiffness and damping characteristics during the dynamic process of contact friction pairs. Pei et al. [10] proposed an improved EHL stiffness model based on the transient EHL system for line contact, which combined the surface contact stiffness and oil film stiffness. The analysis results revealed that the stiffness was smaller than that of the conventional Hertz contact and tended to be a constant when the film thickness is thin. Wang et al. [11] showed a numerical method to describe the time-varying stiffness and damping parameters of gears under lubricated conditions. Furthermore, Zhou et al. [12] studied the oil film stiffness both from the normal and tangential directions based on the EHL contact theory with non-Newtonian fluid, and considered and investigated the effects of operating conditions and structure parameters to optimize the stability of the spur gears. Then, based on the above work, Zhou [13] developed an improved novel model, which combined the oil film stiffness and gear tooth contact stiffness both from normal and tangential directions as the comprehensive stiffness in the EHL system. Xiao et al. [14,15] successively investigated the stiffness and damping characteristics of EHL point contact for herringbone gears both in the normal and tangential directions. Moreover, Zhang et al. [16] established the oil film stiffness and damping model under a free vibration working condition with the inertia force considered in the force balance equation. Tsuha et al. [17,18]. also considered the inertia term when balancing the generated oil film force and the applied load in the research on infinite line contact and finite line contact. However, although numerous efforts have been devoted to the stiffness and damping characteristics under the EHL states, most of the existing work concentrates on the steady-state operating conditions and ignores the inertia force. Few researchers are focusing on the highly transient event, e.g., a sudden increasing load condition studied by Hultqvist [19] and Wijnant [20]. Apart from this, the difficulty to study transient EHL contact damping is to separate the stiffness force on the contact process, but few effective methods have appeared with highly transient conditions. In this study, the models of EHL comprehensive stiffness and damping for line contact under a step increased load condition were developed in which a steady-state EHL model was first established to obtain the relationship between the oil film pressure and the approach distance of the contact body, and then the damping parameters calculated in a transient equation for the stiffness force part were separated according to the established relationship. Whereafter, parametric analysis was conducted to investigate the effects of main operating and geometric parameters including the entrainment velocity, the lubricant viscosity, the curvature radius, as well as the elastic modulus of the contact body on the dynamic characteristics.
2. Methodology
The contact surface in engineering practice may be curved in various shapes, in order to simplify the lubricated model, and the EHL line contact pair can be further equivalent to the contact filled with lubricant oil between an equivalent elastic body with curvature radius R, and a semi-infinite rigid plane, as shown in Figure 1.
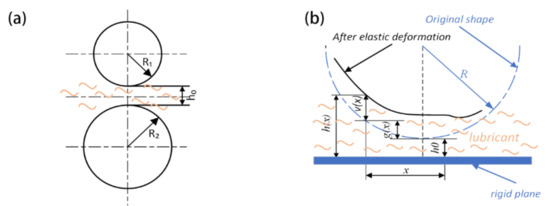
Figure 1.
Representation of line contact model: (a) the equivalent elastic contact bodies; (b) the extended equivalent contact model of line contact.
Assuming that the radius of the original contact body are and , the elastic modulus and the Poisson’s ratio are , , and , , then the radius and elastic modulus of the equivalent body are described as [19]:
2.1. Governing Equation
The time-varying oil film pressure is governed by the Reynolds equation [10], given by:
where on the right of the equation included the wedged effect [21] term that relates to the entrainment velocity , and the squeeze effect term [21] generated by the squeezed oil film with time , , and are oil film pressure and thickness, and are viscosity and density of the lubricant.
The Reynolds boundary condition is applied, expressed as:
where and , respectively, represent the coordinate values of the inlet and outlet on the contact area.
In the line contact pair, when an external load is applied, high oil film pressure is generated in the concentrated contact area. Under this circumstance, the equivalent elastic contact body will be deformed and the oil film thickness is consequently composed of three parts, as shown in Figure 1b, consisting of the geometrical gap between the bodies in central point before the deformation occurs , the structure geometry shape distance of the contact body and the elastic deformation . Then the oil film thickness equation is written as:
It is obvious that , and the elastic deformation is described as a function of the oil film pressure, given by [22]:
where is the additional coordinate in the axis, is a constant in the calculating process.
According to the research of Grubin et al. [23], the rheological properties of the lubricant will be impacted by the high oil film pressure that generated on the contact with the applied load. The density and viscosity of the lubricant changing with the oil film pressure need to be considered in the numerical simulating process. The viscosity–pressure relationship of lubricant is depicted by Roelands [24] formulation, written as Equation (7). The density–pressure relationship described by Dowson and Higginson [25] was utilized to describe the density changes with pressure, according to Equation (8):
where and , respectively, represent the viscosity and density of the lubricant in the atmospheric pressure environment, and is the pressure viscosity index.
To ensure the accuracy of the model, the inertia force term is considered in the force balance equation, which is also one of the main differences from the steady-state EHL problem. The force balance equation is given by:
where is the mass of the equivalent elastic contact body, given as , and , respectively, represent the material density and contact length of the equivalent body, represents the acceleration of the contact body in the normal direction during the contact process, is the applied external load at time step .
The acceleration and velocity in the normal direction is zero while the system is under steady-state [18]. However, in transient loading conditions, the external load changes over time. In order to obtain the transient responses in the time domain, the Newmark-β method is adopted to solve the acceleration and velocity in the normal direction [18]. The time domain is divided into equidistant nodes, and in moment can be expressed as:
where the subscript and represent the calculation moment, is the time step.
2.2. EHL Stiffness and Damping Calculation Models
Because the lubricant is filled between the contact surface, the lubricating oil is continuously compressed when the equivalent contact body moves towards the rigid plane under the action of transient load. Meanwhile, the variation of the transient step-increasing load condition may result in an obvious extrusive effect on the oil film, which will not only affect the distribution of oil pressure and film thickness but also significantly influence the stiffness and damping characteristics of contact pairs. Moreover, since the lubricating oil is generally a viscoelastic fluid, a massless spring-damping system can be considered between two contact bodies in the line contact transient EHL model while analyzing the dynamic responses. A simplified stiffness and damping model of a single degree of freedom is shown in Figure 2.
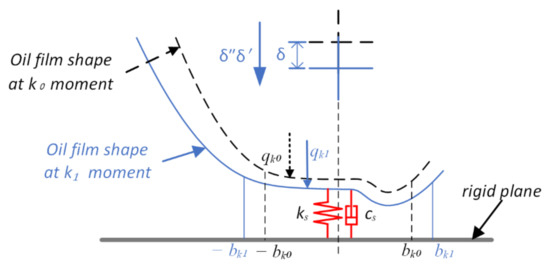
Figure 2.
Representation of film thickness position between two different moments k0 and k1, and the stiffness and damping of EHL line contact.
The approach distance is reflected in the fluctuation of oil film thickness and elastic deformation according to the EHL mechanism. However, the half-width of contact area is determined by the transient external load and changing with the transient conditions, so that the same dimensionless nodes cannot correspond to the actual position between two adjacent moments. Therefore, the average approach distance of all nodes is regarded as the displacement of the elastic body at two adjacent moment, defined as:
where represents the approach distance of the contact body between two adjacent moments, , are the oil film thickness and elastic deformation of node at the last moment, respectively.
In the present work, a steady-state EHL model has been established to obtain the relationship between the oil film pressure and the approach distance of the contact body. Then, the stiffness force can be calculated through the relationship according to the oil film thickness and deformation in the transient model. Finally, the damping force can be evaluated in the single-freedom system equation.
The relationship of force and displacement for an infinite EHL line contact can be approximated as linear according to Tsuha et al. [26], given as:
where denotes the generated oil film force, is EHL stiffness.
Then the stiffness can be calculated in the discrete-time step:
where is the oil film force in the last moment, is the oil film force increment between two adjacent moments.
The transient loading condition results in a compression process in the normal direction, the squeeze velocity and acceleration can be calculated through the approach distance and compression time according to Equations (10) and (11). Then the damping can be obtained through the structural motion equation, written as:
2.3. Numerical Solution
The mathematical model of EHL line contact is composed of several equations, in which the Reynolds equation, the elastic deformation equation, and the lubricant rheology equation have strong nonlinear characteristics and must be solved simultaneously to determine the oil film pressure distribution and film thickness. Moreover, there are more than a dozen orders of magnitude gaps in pressure and thickness, which may cause instability in the numerical calculation system. To optimize the numerical calculating process, the first step is choosing suitable dimensionless parameters to translate the equations to dimensionless form. The following dimensionless parameters are adopted:
where ,, , , , , , and are respectively the dimensionless form of coordinate, oil film pressure, thickness, lubricant density, viscosity, external load, entrainment velocity, and time. In addition, denotes the half-width of the contact area, denotes the maximum pressure according to Hertzian theory [21], expressed as:
The corresponding dimensionless Reynolds equation is shown as:
in which
Meanwhile, the dimensionless film thickness equation can be written as:
The dimensionless form of viscosity-pressure and density-pressure equations can be respectively written as:
Then the dimensionless Reynolds equation is discretized by finite difference method, the dimensionless form of Reynolds equation is differential as:
From the tribological viewpoint, the dynamic characteristics and the distribution of oil film pressure have a strong interaction with each other in transient conditions. Thus, the EHL system and dynamic region are supposed to reach balance simultaneously. In this study, a continuous steady-state condition is supposed before the transient process starts. Therefore, the squeezing effect can be ignored in the first moment because no fluctuation in contact parameters occurs in the previous time and the initial state of oil film can be obtained. Subsequently, the oil film is compressed with the external applied load changing with time. In the numerical calculation process, after assuming the initial distribution and geometrical gap, the oil film thickness and rheology parameters can be calculated. Then, the oil film pressure is updated by solving the discrete dimensionless Reynolds equation. To ensure convergent results, the new pressure needs to satisfy enough precision criteria. As a consequence, the pressure distribution would be adjusted and updated until the criterion is met. Considering the accuracy of the results, it is necessary to verify whether the generated force satisfies the force balance equation with the inertial term in the transient EHL system. If not, the displacement might be updated according to the force relationship until the criterion is satisfied. Consequently, the oil film state and dynamic characteristics can be obtained over the time domain. Finally, EHL stiffness and damping emerged according to the proposed model. The detailed calculation process is shown in Figure 3
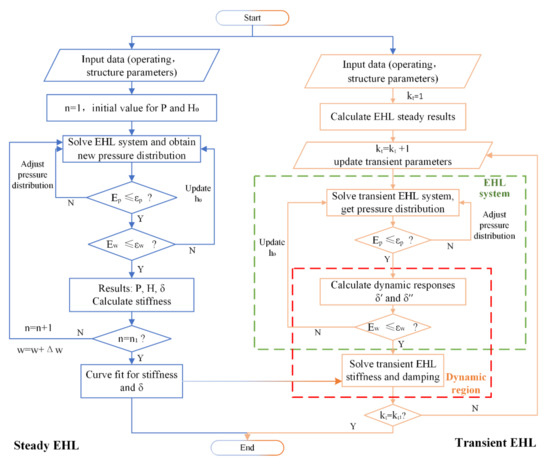
Figure 3.
Flow chart of EHL stiffness and damping calculation process.
The convergence criteria of pressure and force balance at each transient moment are defined as:
where represents oil film pressure in the previous iterative process.
3. Results and Discussion
3.1. Parameter Input and Results
This work aims to study the EHL stiffness and damping characteristics and discuss the effects of main working and structural parameters for line–contact friction pairs through the proposed model. The basic value used in this work are listed as Table 1.

Table 1.
Basic parameters used in the numerical calculation process.
The externally applied load was chosen to be described as a step increasing load that has an increment step to the next moment, similar to the research of Hultqvist [19]. In this way, the external load not only relates to the highly transient event that has a sudden increase but provides convenience for studying stiffness and damping varying with a load while exploring the effects of the researched parameters. The step was decided by the value in the last moment where the applied load increased from to overtime, described as Equation (25) and Figure 4:
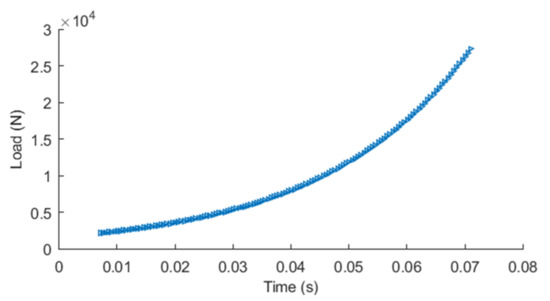
Figure 4.
Transient applied load over time.
Figure 5 shows the EHL contact stiffness and damping results solved by the proposed model via the basic parameters in the above table. The results show similar behavior to the research of Pei et al. [10] and Tsuha [18] that the EHL stiffness increases with the transient increasing load while damping decreases and the trend becomes gradually flat with the load increasing. With the applied load increasing, the lubricant oil film is becoming harder to be compressed for the oil film pressure is gradually increasing with the increasing applied load, resulting the stiffness raised. Meanwhile, the oil film thickness is decreasing with the increasing load, where the viscosity effect of lubricant decreases in extrusion process, leading to decreased damping phenomenon as the load increases. Figure 5a indicates that there is an obvious gap between EHL stiffness and contact stiffness with Johnson theory [2] at light load condition but the gap gradually reduced as the externally applied load increased. The reason is that the lubricant oil film is relatively thicker and pressure is small, resulting in the contact system being easy to be compressed and consequently having a higher discrepancy compared to the results of Johnson model. As the applied load increasing, the oil film thickness is compressed to a very small level while pressure is large. In this case, the lubricant oil film is difficult to compress, and the elastic deformation of the contact body is obvious. Thus, the EHL stiffness gradually approaches the Johnson stiffness when the applied load reaches a higher level. Figure 5b demonstrates that the EHL damping decreases with the increasing load, on the grounds that the gap between the stiffness force and the generated oil film force is gradually narrowing, as shown in Figure 5c, which means the stiffness force plays an increasingly important role in bearing the applied load in heavy load conditions while the damping effects is gradually weakened.
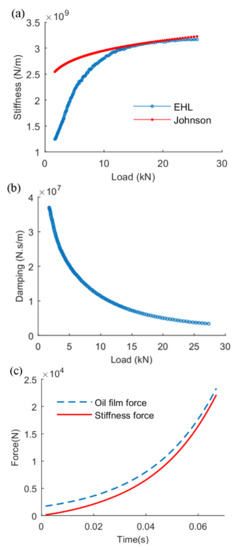
Figure 5.
EHL stiffness and damping of line contact under transient step-increasing loading conditions; (a) The comparison between Johnson stiffness and EHL stiffness, (b) EHL damping, (c) variation of oil film force and stiffness force with time.
3.2. Effects of Entrainment Velocity
Figure 6 plots the variation curves of stiffness and damping coefficients and characteristics of EHL line contact with different entrainment velocities under transient loading conditions. It can be seen in Figure 6a that a higher entrainment velocity might lead to a smaller value of EHL stiffness under the same external load. It is reflected in the dynamic response of approach distance, shown as Figure 6b, which described that a larger value occurs under higher entrainment velocity conditions, implying that the oil film has a weaker load capacity. However, the stiffness under various entrainment velocities reaches a similar level at relatively heavy load conditions. This is because the oil film is thin and the approach distance is dominated by the elastic deformation of the contact body, which alleviates the impact of oil film on stiffness. Figure 6c indicates that higher entrainment velocity corresponds to a smaller damping value in the early period of loading and finally reaches a similar level. When the entrainment velocity becomes larger, the approach distance emerges in the same period and the squeeze velocity becomes larger as well, which results in a smaller damping value, as shown in Figure 6d.
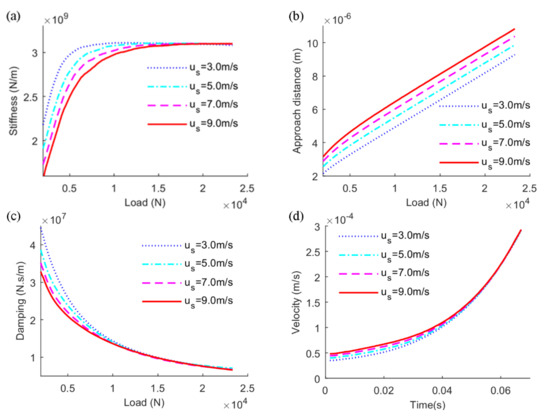
Figure 6.
Effects of entrainment velocity on (a) stiffness, (b) approach distance, (c) damping, (d) squeeze velocity of EHL line contact.
3.3. Effects of Lubricant Viscosity
As the vital factor in the EHL system, the lubricant property parameters significantly affect the lubrication and dynamic performance of the friction pair. Figure 7 describes the effects of lubricant viscosity on dynamic characteristics of EHL line contact. It can be observed that smaller viscosity operating conditions contribute to larger stiffness and damping values at the early loading period, as shown in Figure 7a,c, and tend to be a constant value under heavy load conditions. There is a thicker oil film between the contact surfaces while the viscosity is large, and the contact system is more easily compressed, which leads to a larger approach displacement in Figure 7b, and thus smaller stiffness characteristics. Although the stiffness value is higher at lower level of viscosity, the approach distance of the contact body is smaller. Thus, the stiffness force may play a similar role in bearing the applied load. Whereas the squeeze velocity is lower with smaller viscosity according to Figure 7a, leading to higher damping at lower-level viscosity, as presented in Figure 7c.
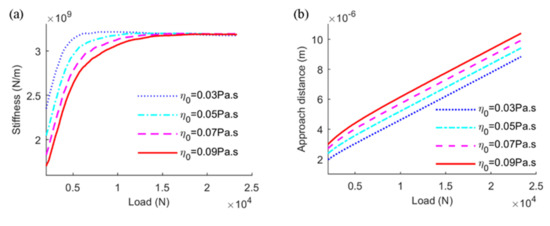
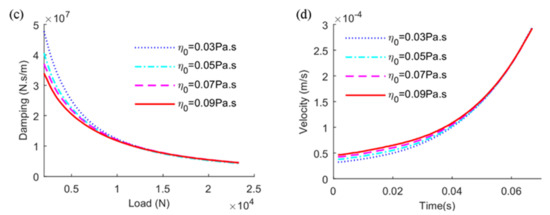
Figure 7.
Effects of lubricant viscosity on (a) stiffness, (b) approach distance, (c) damping, (d) squeeze velocity of EHL line contact.
3.4. Effects of Equivalent Radius
Not only do working condition parameters affect the dynamic characteristics, but the proper structure geometry design of contact bodies will significantly improve the operation performance and extend the service life of the EHL contact system. According to Equation (17), if the manufacturing materials are the same, the half-width of the contact area is directly dominated by the curvature radius of the contact body under a certain external load. Figure 8 shows the effect of equivalent curvature radius along with the transient load. With the curvature radius increasing, there is a wider contact area to enhance the bearing capacity, reflecting a larger film thickness under the same load condition. Therefore, the approach distance is larger with a larger radius, as shown in Figure 8b, because the oil film is easier to be compressed than the contact body in light load applied. As a result, the larger curvature radius corresponds to the smaller stiffness value, as shown in Figure 8a. In this case, more lubricant is easier to compress and larger squeeze velocity is observed (Figure 8d), which corresponds to smaller damping parameters, expressed in Figure 8c.
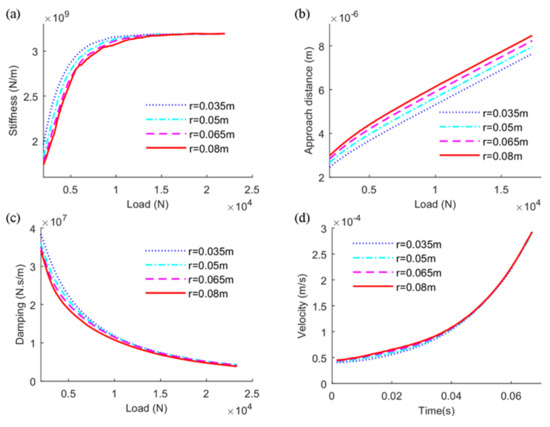
Figure 8.
Effects of equivalent curvature radius on (a) stiffness, (b) approach distance, (c) damping, (d) squeeze velocity of EHL line contact.
3.5. Effects of Elastic Modulus
The elastic modulus of the contact body determines the degree of deformation under the same external applied load. It is necessary to investigate the effect of elastic modulus on the dynamic characteristics, as the elastic deformation is an indispensable term of the film thickness equation under transient state, while the other two terms are related to initial states. As shown in Figure 9a, in contrast to the effect of the aforementioned parameters, a similar stiffness value occurs in the initial loading period with various elastic moduli. Meanwhile, an obvious gap gradually appeared with the increasing applied load and finally reaches an obvious disparity under heavy load conditions. Such a phenomenon can also be explained from the viewpoint of the approach distance. The elastic deformation of contact bodies is not obvious under relatively light external applied load, which brings similar approach distance values, shown as Figure 9b, and small gaps in stiffness, correspondingly. As the load increases, the oil film becomes harder to be compressed and the disparity of elastic deformation becomes clear, which determines the approach distance under heavy load conditions. Consequently, the greater the elastic modulus is, the larger EHL comprehensive stiffness values become. Figure 9c,d show that the elastic modulus generates little influence on damping characteristics.
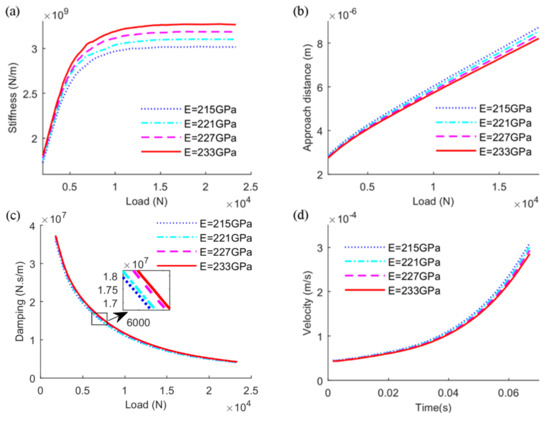
Figure 9.
Effects of elastic modulus on (a) stiffness, (b) approach distance, (c) damping, (d) squeeze velocity of EHL line contact.
4. Conclusions
This work aims to investigate the stiffness and damping characteristics of line contact friction pairs under EHL states. A comprehensive evaluation model is introduced, in which the stiffness force is separated according to the relationship with approach distance established in the steady process, and then the damping force can be obtained. Finally, the effects of operating conditions and structure parameters are investigated and analyzed from the mechanism aspect. From the presented results, a few conclusions can be drawn:
- (1)
- In the aspects of dynamics performance, the stiffness and damping are more sensitive to the lubricating oil film when the applied load is light. The EHL stiffness raises and approaches to the level of Johnson theory while the EHL damping gradually decreases with the increasing applied load for the stiffness force plays an increasingly important role in the contact process over the applied load while the damping effects are gradually weakened.
- (2)
- According to the effects of operating conditions and structural parameters on the lubricating performances and dynamic characteristics, the larger value of entrainment velocity, higher lubricant viscosity, and larger curvature radius of the contact body lead to smaller stiffness and damping values under light load conditions because of the result of the film thickness being thicker and the approach distance being longer.
- (3)
- The effects of elastic modulus on EHL stiffness are increasingly obvious along the applied external load, and they dominate the maximum level of the friction pair, whereas they generate little effect on EHL damping characteristics.
Author Contributions
Conceptualization, C.F., A.Z., and X.M.; methodology, C.F. and A.Z.; software, A.Z.; validation, C.F., A.Z., W.Z., Y.P., and X.M.; formal analysis, A.Z.; investigation, A.Z.; resources, C.F.; data curation, A.Z.; writing—original draft preparation, A.Z.; writing—review and editing, C.F. and Y.P.; visualization, A.Z.; supervision, C.F.; project administration, C.F. and W.Z.; funding acquisition, C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (Grant No.2020YFA0710902), the National Natural Science Foundation of China (Grant No. 51905549, 52130502) and Initial Funding of the Specially appointed Associate Professorship of Central South University, China (Grant No.202045009). This work was also supported by the Fundamental Research Funds for the Central Universities of Central South University (Grant No.2021zzts0684).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, D.; Jane Wang, Q. Elastohydrodynamic Lubrication: A Gateway to Interfacial Mechanics—Review and Prospect. J. Tribol. 2011, 133, 133. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavič, J.; Boltežar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Nonato, F.; Cavalca, K. Investigation on the damping characteristics of elastohydrodynamic lubricated point contacts under dynamic loading. In Proceedings of the 10th International Conference on Vibrations in Rotating Machinery, London, UK, 11–13 September 2012; pp. 503–512. [Google Scholar]
- Wiegert, B.; Hetzler, H.; Seemann, W. A simplified elastohydrodynamic contact model capturing the nonlinear vibration behaviour. Tribol. Int. 2013, 59, 79–89. [Google Scholar] [CrossRef]
- Qin, W.; Chao, J.; Duan, L. Study on stiffness of elastohydrodynamic line contact. Mech. Mach. Theory 2015, 86, 36–47. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Zhu, C.; Song, C.; Li, Z. Influence of lubrication starvation and surface waviness on the oil film stiffness of elastohydrodynamic lubrication line contact. J. Vib. Control. 2018, 24, 924–936. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Yang, D.C.H.; Sun, Z.S. A Rotary Model for Spur Gear Dynamics. J. Mech. Transm. Autom. Des. 1985, 107, 529–535. [Google Scholar] [CrossRef]
- Tsuha, N.A.H.; Cavalca, K.L. Finite line contact stiffness under elastohydrodynamic lubrication considering linear and nonlinear force models. Tribol. Int. 2020, 146, 106219. [Google Scholar] [CrossRef]
- Pei, J.; Han, X.; Tao, Y. An improved stiffness model for line contact elastohydrodynamic lubrication and its application in gear pairs. Ind. Lubr. Tribol. 2020, 72, 703–708. [Google Scholar] [CrossRef]
- Wang, Z.; Pu, W.; Pei, X.; Cao, W. Contact stiffness and damping of spiral bevel gears under transient mixed lubrication conditions. Friction 2022, 10, 545–559. [Google Scholar] [CrossRef]
- Zhou, C.; Xiao, Z.; Chen, S.; Han, X. Normal and tangential oil film stiffness of modified spur gear with non-Newtonian elastohydrodynamic lubrication. Tribol. Int. 2017, 109, 319–327. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Xiao, Z. Stiffness and damping models for the oil film in line contact elastohydrodynamic lubrication and applications in the gear drive. Appl. Math. Model. 2018, 61, 634–649. [Google Scholar] [CrossRef]
- Xiao, Z.; Shi, X. Investigation on stiffness and damping of transient non-Newtonian thermal elastohydrodynamic point contact for crowned herringbone gears. Tribol. Int. 2019, 137, 102–112. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, Z.; Shi, X.; Zhou, C. Oil Film Damping Analysis in Non-Newtonian Transient Thermal Elastohydrodynamic Lubrication for Gear Transmission. J. Appl. Mech. 2018, 85, 85. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Zhu, C.; Liu, M.; Song, C. Oil film stiffness and damping in an elastohydrodynamic lubrication line contact-vibration. J. Mech. Sci. Technol. 2016, 30, 3031–3039. [Google Scholar] [CrossRef]
- Tsuha, N.A.H.; Cavalca, K.L. Stiffness and damping of elastohydrodynamic line contact applied to cylindrical roller bearing dynamic model. J. Sound Vib. 2020, 481, 115444. [Google Scholar] [CrossRef]
- Tsuha, N.A.H.; Nonato, F.; Cavalca, K.L. Stiffness and Damping Reduced Model in EHD Line Contacts. In Proceedings of the 10th International Conference on Rotor Dynamics—IFToMM; Springer: Cham, Switzerland, 2019; pp. 43–55. [Google Scholar]
- Hultqvist, T.; Shirzadegan, M.; Vrcek, A.; Baubet, Y.; Prakash, B.; Marklund, P.; Larsson, R. Elastohydrodynamic lubrication for the finite line contact under transient loading conditions. Tribol. Int. 2018, 127, 489–499. [Google Scholar] [CrossRef]
- Wijnant, Y.H.; Venner, C.H.; Larsson, R.; Eriksson, P. Effects of Structural Vibrations on the Film Thickness in an EHL Circular Contact. J. Tribol. 1999, 121, 259–264. [Google Scholar] [CrossRef]
- Wen, S.; Huang, P. Principles of Tribology; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Huang, P. Numerical Calculation Methods of Elastohydrodynamic Lubrication; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Grubin, A.N. Investigation of the Contact of Machine Components; The Central Mechanical Engineering Research Institute: Moscow, Russia, 1949. [Google Scholar]
- Roeland, C. Correlation Aspect of the Viscosity-Temperature-Pressure Relation of Lubrication Oils. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1966. [Google Scholar]
- Dowson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication; Pergamon: Oxford, UK, 1977. [Google Scholar]
- Tsuha, N.A.H.; Nonato, F.; Cavalca, K.L. Formulation of a reduced order model for the stiffness on elastohydrodynamic line contacts applied to cam-follower mechanism. Mech. Mach. Theory 2017, 113, 22–39. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).