Improving the Endoprosthesis Design and the Postoperative Therapy as a Means of Reducing Complications Risks after Total Hip Arthroplasty
Abstract
:1. Introduction
2. Materials and Methods
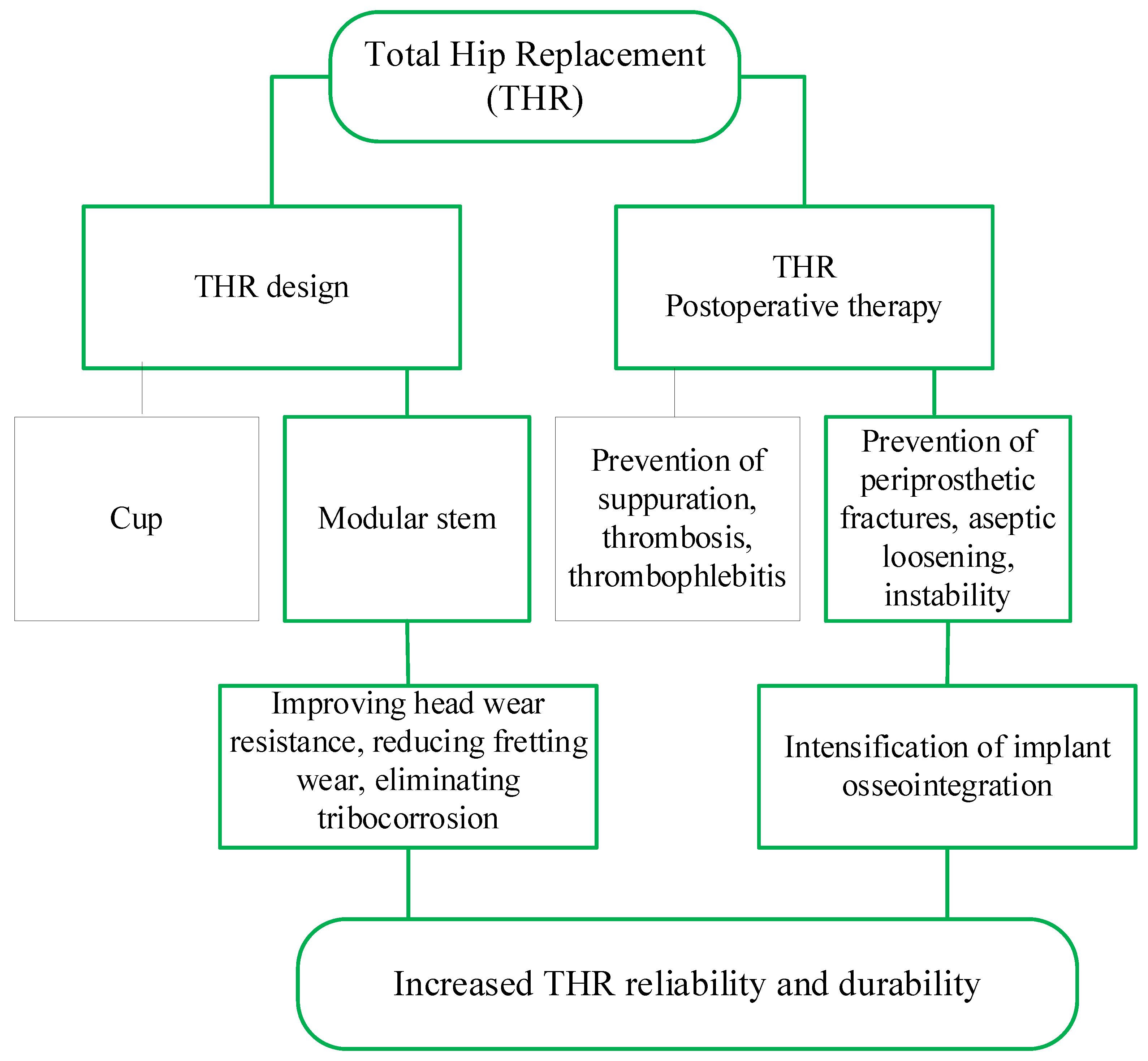
2.1. Constructive and Technological Factors Influencing the Development of Complications after THR
- Intraoperative (fractures of the hip, pelvis, damage to the great vessels, perforation of the femoral canal);
- Early postoperative (suppuration, thrombosis, thrombophlebitis, dislocation of the endoprosthesis head, neuritis, decompensation of concomitant pathology);
- Late postoperative (deep suppuration, periprosthetic fractures, aseptic loosening, instability of implants due to improper planning of the operation or as a result of operation, destruction of the endoprosthesis components).
- Polymers (polytetrafluoroethylene (PTFE), ultra-high molecular weight polyethylene (UHMWPE), cross-linked polyethylene (XLPE), highly cross-linked polyethylene (HXLPE), vitamin E-blended polymers, polyether-ether-ketone (PEEK), poly 2-methacryloyloxyethyl phosphorylcholine (PMPC), polycarbonate-urethane (PCU));
- Metals (Stainless steel, Cobalt-chromium-molybdenum (CoCrMo) alloys, Titanium alloys (Ti-6Al-4V), Zirconium alloy (Zr-2.5Nb));
- Metal alloy surface coatings (Titanium nitride (TiN), Silicon nitride (Si3N4), Diamond-like carbon (DLC), aluminum, nanocrystalline diamond (NCD));
- ceramics (aluminum ceramic, zirconia, zirconia-toughened alumina (ZTA), sapphire).
- hard-on-soft bearings (metal-on-polyethylene (MOP) is a metal femoral head and a polyethylene acetabular liner, ceramic-on-polyethene (COP) is a ceramic femoral head and a polyethylene acetabular liner);
- hard-on-hard bearings (metal-on-metal (MOM), ceramic-on-ceramic (COC), and ceramic-on-metal (COM) is a ceramic femoral head and a metal acetabular liner).
2.2. Mechanobiological Models of Implant Osseointegration
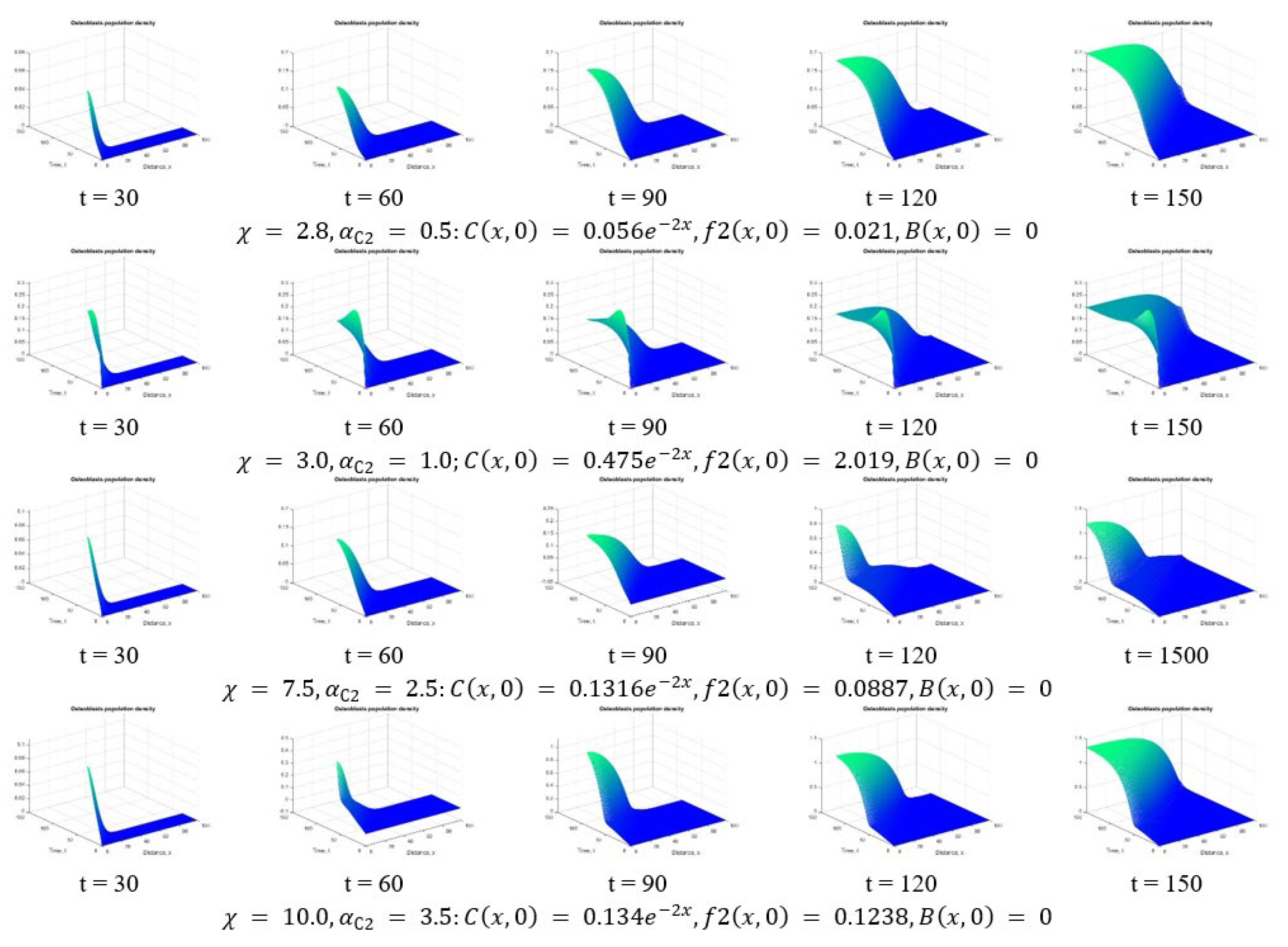
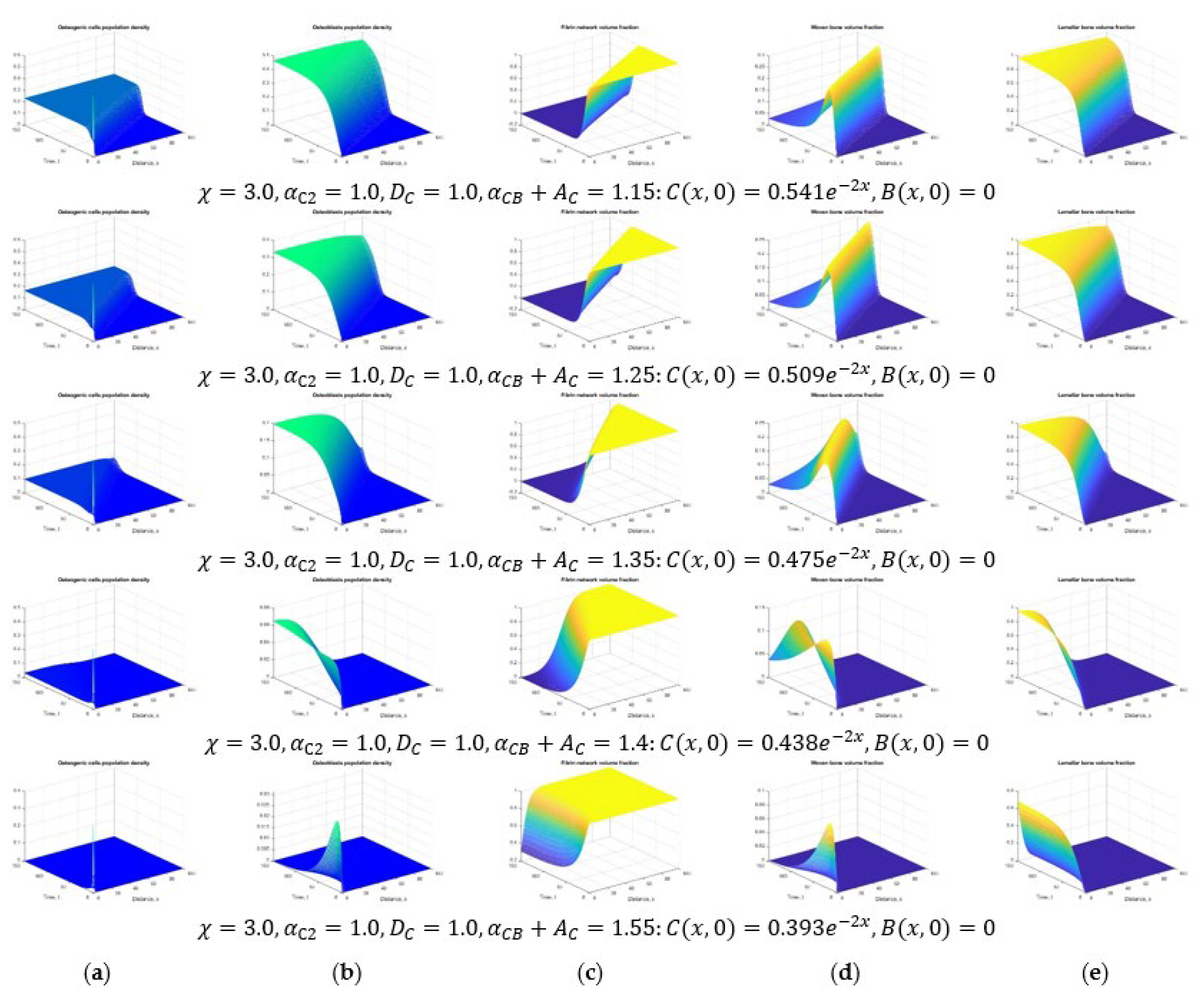
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model state variables | |||
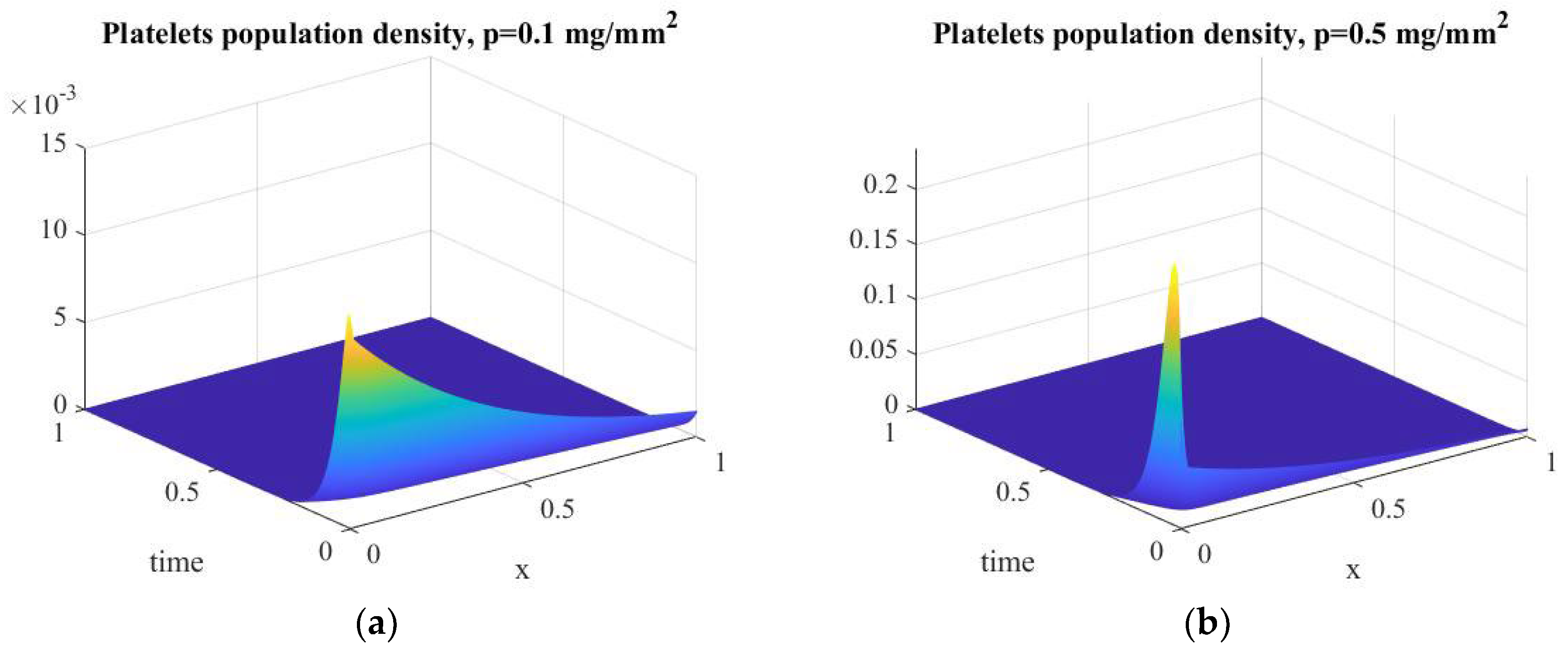
| Platelets population density | |||
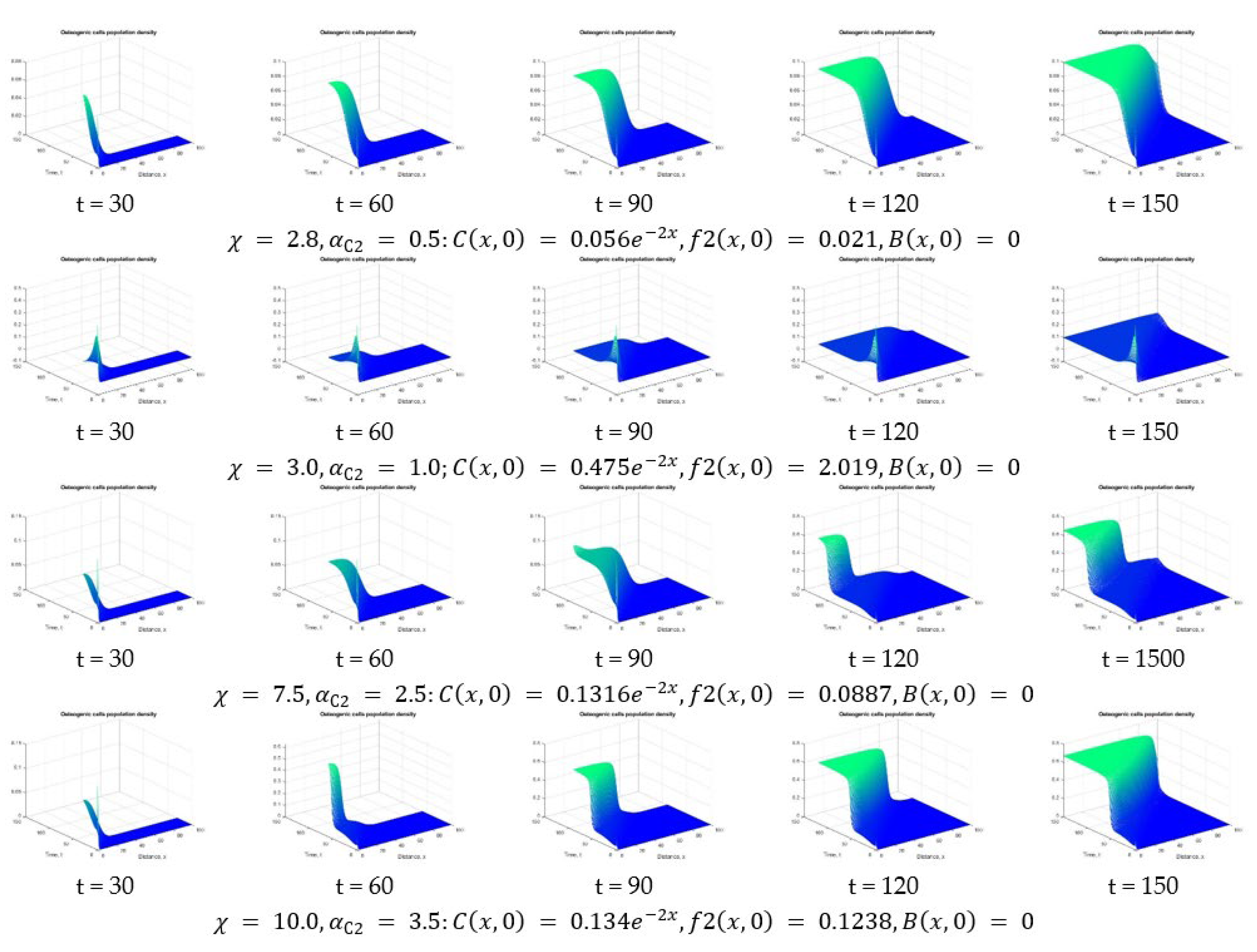
| Osteogenic cells population density | |||
| Osteoblasts population density | |||
| Type 1 growth factors concentration (PDGF, TGF-β) | |||
| Type 2 growth factors concentration (BMP, superfamily TGF-β) | |||
| Fibrin network volume fraction | |||
| Woven bone volume fraction | |||
| Lamellar bone volume fraction) | |||
| Concentration of adsorbed proteins (принимается в зависимoсти oт сoстoяния пoверхнoсти имплантата) | - | ||
| Constant model parameters | |||
| Platelet diffusion coefficient | |||
| Diffusion coefficient of osteogenic cells | |||
| Diffusion coefficient of type 1 growth factors | |||
| Diffusion coefficient of type 2 growth factors | |||
| The coefficient of chemotaxis along gradient of growth factors type 1 | |||
| The coefficient of chemotaxis along gradient of growth factors type 2 | |||
| Linear platelet taxis coefficient | |||
| The coefficient of platelet death due to inflammation | |||
| The coefficient t of natural death of osteogenic cells | |||
| The coefficient of differentiation of osteoblasts into osteocytes | |||
| Natural decay rate of type 1 growth factors | |||
| Natural decay rate of type 2 growth factors | |||
| The coefficient of influence the concentration of adsorbed proteins on the secretion of growth factors of type 1 | |||
| The coefficient of natural secretion of growth factors type 1 | |||
| The coefficient of natural proliferation of osteogenic cells | |||
| The coefficient of enhancing the proliferation of osteogenic cells by growth factors | |||
| The coefficient of influence of growth factors type 1 on the proliferation of osteoblasts | |||
| The coefficient of natural secretion of type 2 growth factors in the environment of osteogenic cells | |||
| The coefficient of natural secretion of type 2 growth factors in the environment of osteoblasts | |||
| The coefficient of influence of type 2 growth factors on bone synthesis | |||
| within one year) | - | - | |
| Additional concentration of adsorbed proteins in the platelet environment | |||
| Additional concentration of type 1 growth factors in the platelet environment | |||
| Additional concentration of type 2 growth factors in the environment of osteogenic cells | |||
| Additional concentration of type 2 growth factors in the environment of osteoblasts | |||
| Additional concentration of growth factors affecting the proliferation of osteogenic cells | |||
| Additional concentration of growth factors affecting the proliferation of osteoblasts | |||
| Additional concentration of type 2 growth factors affecting bone formation | |||
| Limiting cell density | |||
References
- Cieza, A.; Causey, K.; Kamenov, K.; Hanson, S.W.; Chatterji, S.; Vos, T. Global estimates of the need for rehabilitation based on the Global Burden of Disease study 2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet 2021, 396, 2006–2017. [Google Scholar] [CrossRef]
- Popov, V.L.; Poliakov, A.M.; Pakhaliuk, V.I. Synovial Joints. Tribology, Regeneration, Regenerative Rehabilitation and Arthroplasty. Lubricants 2021, 9, 15. [Google Scholar] [CrossRef]
- Mozgovaya, E.E.; Zborovskaya, I.A. Osteoarthritis is the most common joint disease. Med. Her. 2012, 6, 33–40. [Google Scholar]
- Zhang, W.; Doherty, M.; Peat, G.; Bierma-Zeinstra, M.A.; Arden, N.K.; Bresnihan, B.; Herrero-Beaumont, G.; Kirschner, S.; Leeb, B.F.; Lohmander, L.S.; et al. EULAR evidence-based recommendations for the diagnosis of knee osteoarthritis. Ann. Rheum. Dis. 2010, 69, 483–489. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, W.; Doherty, M.; Arden, N.; Bannwarth, B.; Bijlsma, J.; Gunther, K.P.; Hauselmann, H.J.; Herrero-Beaumont, G.; Jordan, K.; Kaklamanis, P.; et al. EULAR evidence based recommendations for the management of hip osteoarthritis: Report of a task force of the EULAR Standing Committee for International Clinical Studies Including Therapeutics (ESCISIT). Ann. Rheum. Dis. 2005, 64, 669–681. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, W.Y.; Song, J.H.; Kim, J.H.; Lee, H.H. Factors Affecting Periprosthetic Bone Loss after Hip Arthroplasty. Hip Pelvis 2021, 33, 53–61. [Google Scholar] [CrossRef]
- Krull, A.; Morlock, M.M.; Bishop, N.E. Factors influencing taper failure of modular revision hip stems. Med. Eng. Phys. 2018, 54, 65–73. [Google Scholar] [CrossRef]
- Bijukumar, D.R.; Segu, A.; Souza, J.C.; Li, X.; Barba, M.; Mercuri, L.G.; Jacobs, J.J.; Mathew, M.T. Systemic and local toxicity of metal debris released from hip prostheses: A review of experimental approaches. Nanomed. Nanotechnol. Biol. Med. 2018, 14, 951–963. [Google Scholar] [CrossRef]
- Liow, M.H.; Kwon, Y.M. Metal-on-metal total hip arthroplasty: Risk factors for pseudotumours and clinical systematic evaluation. Int. Orthop. 2017, 41, 885–892. [Google Scholar] [CrossRef]
- Bijukumar, D.R.; Salunkhe, S.; Morris, D.; Segu, A.; Hall, D.J.; Pourzal, R.; Mathew, M.T. In vitro evidence for cell-accelerated corrosion within modular junctions of total hip replacements. J. Orthop. Res. 2020, 38, 393–404. [Google Scholar] [CrossRef]
- Bijukumar, D.R.; Salunkhe, S.; Zheng, G.; Barba, M.; Hall, D.J.; Pourzal, R.; Mathew, M.T. Wear particles induce a new macrophage phenotype with the potential to accelerate material corrosion within total hip replacement interfaces. Acta Biomater. 2020, 101, 586–597. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, D.W.; Chen, A.F.; Lee, G.C.; Klein, G.R.; Mont, M.A.; Kurtz, S.M.; Taper Corrosion Writing Committee; Cates, H.E.; Kraay, M.J.; Rimnac, C.M. Fretting and Corrosion Damage in Taper Adapter Sleeves for Ceramic Heads: A Retrieval Study. J. Arthroplast. 2017, 32, 2887–2891. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M.; Gilbert, J.L. Compliant interfaces and fretting corrosion of modular taper junctions in total hip implants: The micromechanics of contact. Tribol. Int. 2020, 151, 106437. [Google Scholar] [CrossRef]
- Radzik, B.; Bijukumar, D.; Cheng, K.Y.; Badhe, R.V.; Barba, M.; Mathew, M.T. The role of fretting-frequency on the damage modes of THR modular junction: In-vitro study. Mater. Sci. Eng. C Mater. Biol. Appl. 2021, 126, 112128. [Google Scholar] [CrossRef]
- Royhman, D.; Pourzal, R.; Hall, D.; Lundberg, H.J.; Wimmer, M.A.; Jacobs, J.; Hallab, N.J.; Mathew, M.T. Fretting-corrosion in hip taper modular junctions: The influence of topography and pH levels–An in-vitro study. J. Mech. Behav. Biomed. Mater. 2021, 118, 104443. [Google Scholar] [CrossRef]
- Poliakov, A.; Pakhaliuk, V.; Popov, V. Current Trends in Improving of Artificial Joints Design and Technologies for Their Arthroplasty. Front. Mech. Eng. 2020, 6, 4. [Google Scholar] [CrossRef]
- Goldman, A.H.; Sierra, R.J.; Trousdale, R.T.; Lewallen, D.G.; Berry, D.J.; Abdel, M.P. The Lawrence, D. Dorr surgical techniques & technologies award: Why are contemporary revision total hip arthroplasties failing? An analysis of 2500 cases. J. Arthroplast. 2019, 34, 11–16. [Google Scholar] [CrossRef]
- Polyakov, A.; Pakhaliuk, V.; Kalinin, M.; Kramar, V.; Kolesova, M.; Kovalenko, O. System Analysis and Synthesis of Total Hip Joint Endoprosthesis. Procedia Eng. 2015, 100, 530–538. [Google Scholar] [CrossRef] [Green Version]
- Chethan, K.N.; Shyamasunder Bhat, N.; Zuber, M.; Shenoy, S.B. Finite Element Analysis of Different Hip Implant Designs along with Femur under Static Loading Conditions. J. Biomed. Phys. Eng. 2019, 9, 507–516. [Google Scholar] [CrossRef] [Green Version]
- Chethan, K.N.; Zuber, M.; Shyamasunder Bhat, N.; Shenoy, S.B. Optimized trapezoidal-shaped hip implant for total hip arthroplasty using finite element analysis. Cogent Eng. 2020, 7, 1719575. [Google Scholar] [CrossRef]
- Kenney, C.; Dick, S.; Lea, J.; Liu, J.; Ebraheim, N.A. A systematic review of the causes of failure of revision total hip arthroplasty. J. Orthop. 2019, 16, 393–395. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, A.A.; Bakr, H.M. Updates in biomaterials of bearing surfaces in total hip arthroplasty. Arthroplasty 2021, 3, 32. [Google Scholar] [CrossRef]
- Brown, A.S. Hip New World. ASME Mech. Eng. 2006, 128, 28–33. [Google Scholar] [CrossRef] [Green Version]
- Bhaskar, B.; Arun, S.; Sreekanth, P.; Kanagaraj, S. Biomaterials in total hip joint replacements: The evolution of basic concepts, trends, and current limitations–A review. Trends Biomater. 2016, 5, 175–199. [Google Scholar] [CrossRef]
- Khanna, R.; Ong, J.L.; Oral, E.; Narayan, R.J. Progress in Wear Resistant Materials for Total Hip Arthroplasty. Coatings 2017, 7, 99. [Google Scholar] [CrossRef] [Green Version]
- Bingley, R.; Martin, A.; Manfredi, O.; Nejadhamzeeigilani, M.; Oladokun, A.; Beadling, A.R.; Siddiqui, S.; Anderson, J.; Thompson, J.; Neville, A.; et al. Fretting-corrosion at the modular tapers interface: Inspection of standard ASTM F1875-98. Proc. Inst. Mech. Eng. H 2018, 232, 492–501. [Google Scholar] [CrossRef] [Green Version]
- Corne, P.; De March, P.; Cleymand, F.; Geringer, J. Fretting-corrosion behavior on dental implant connection in human saliva. J. Mech. Behav. Biomed. Mater. 2019, 94, 86–92. [Google Scholar] [CrossRef]
- Geringer, J.; Macdonald, D. Friction/fretting-corrosion mechanisms: Current trends and outlooks for implants. Mater. Lett. 2014, 134, 52–157. [Google Scholar] [CrossRef]
- Hemmerling, K.J.; Weitzler, L.; Bauer, T.W.; Padgett, D.E.; Wright, T.M. Fretting and corrosion of metal liners from modular dual mobility constructs: A retrieval analysis. Bone Jt. J. 2021, 103-B, 1238–1246. [Google Scholar] [CrossRef]
- Fitz, D.W.; Klemt, C.; Chen, W.; Xiong, L.; Yeo, I.; Kwon, Y.-M. Head-Neck Taper Corrosion in Metal-on-Polyethylene Total Hip Arthroplasty: Risk Factors, Clinical Evaluation, and Treatment of Adverse Local Tissue Reactions. J. Am. Acad. Orthop. Surg. 2020, 28, 907–913. [Google Scholar] [CrossRef]
- Fallahnezhad, K.; Feyzi, M.; Ghadirinejad, K.; Hashemi, R.; Taylor, M. Finite element based simulation of tribocorrosion at the head-neck junction of hip implants. Tribol. Int. 2022, 165, 107284. [Google Scholar] [CrossRef]
- McLaughlin, J.R.; Lee, K.R.; Johnson, M.A. Second-generation uncemented total hip arthroplasty: A minimum 20-year follow-up. Bone Jt. Open 2021, 2, 33–39. [Google Scholar] [CrossRef] [PubMed]
- McLaughlin, J.R.; Lee, K.R. Total Hip Arthroplasty with an Uncemented Tapered Femoral Component in Patients Younger than 50 Years of Age: A Minimum 20-Year Follow-Up Study. J. Arthroplast. 2016, 31, 1275–1278. [Google Scholar] [CrossRef] [PubMed]
- Pourzal, R.; Lundberg, H.J.; Hall, D.J.; Jacobs, J.J. What Factors Drive Taper Corrosion? J. Arthroplast. 2018, 33, 2707–2711. [Google Scholar] [CrossRef]
- Pilliar, R.M.; Cameron, H.U.; Macnab, I. Porous surface layered prosthetic devices. Biomed. Eng. 1975, 10, 126–131. [Google Scholar]
- Pilliar, R.M. Powder metal-made orthopedic implants with porous surface for fixation by tissue ingrowth. Clin. Orthop. Relat. Res. 1983, 176, 42–51. [Google Scholar] [CrossRef]
- Pilliar, R.M. Porous-surfaced metallic implants for orthopedic applications. J. Biomed. Mater. Res. 1987, 21, 1–33. [Google Scholar]
- Owen, T.D.; Moran, C.G.; Smith, S.R.; Pinder, I.M. Results of uncemented porous-coated anatomic total hip replacement. J Bone Jt. Surg. Br. 1994, 76, 258–262. [Google Scholar] [CrossRef]
- Diaz-Dilernia, F.; Mansilla, A.M.G.; Forneris, A.A.; Slullitel, P.A.; Zanotti, G.; Comba, F.; Buttaro, F.P.M. Preliminary outcomes of the cementless UNITED hip system for primary total hip arthroplasty at a minimum 2-year follow-up. Eur. J. Orthop. Surg. Traumatol. 2021. [Google Scholar] [CrossRef]
- Kim, Y.H. Long-term results of the cementless porous-coated anatomic total hip prosthesis. J. Bone Jt. Surg. Br. 2005, 87, 623–627. [Google Scholar] [CrossRef]
- Laine, H.J.; Puolakka, T.J.; Moilanen, T.; Pajamäki, K.J.; Wirta, J.; Lehto, M.U. The effects of cementless femoral stem shape and proximal surface texture on ‘fit-and-fill’ characteristics and on bone remodeling. Int. Orthop. 2000, 24, 184–190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swider, P.; Pedrono, A.; Mouzin, O.; Søballe, K.; Bechtold, J.E. Biomechanical analysis of the shear behaviour adjacent to an axially loaded implant. J. Biomech. 2006, 39, 1873–1882. [Google Scholar] [CrossRef] [PubMed]
- Moreo, P.; Perez, M.A.; Garcıa-Aznar, J.M.; Doblare, M. Modelling the mechanical behaviour of living bony interfaces. Comput. Meth. Appl. Mech. Eng. 2007, 196, 3300–3314. [Google Scholar] [CrossRef]
- Ambard, D.; Swider, P. A predictive mechano-biological model of the bone-implant healing. Eur. J. Mech. A-Solids 2006, 25, 927–937. [Google Scholar] [CrossRef] [Green Version]
- Phillips, A.M. Overview of the fracture healing cascade. Injury 2005, 36, S5–S7. [Google Scholar] [CrossRef]
- Gerstenfeld, L.C.; Cullinane, D.M.; Barnes, G.L.; Graves, D.T.; Einhorn, T.A. Fracture healing as a post-natal developmental process: Molecular, spatial, and temporal aspects of its regulation. J. Cell Biochem. 2003, 88, 873–884. [Google Scholar] [CrossRef]
- Tsiridis, E.; Upadhyay, N.; Giannoudis, P. Molecular aspects of fracture healing: Which are the important molecules? Injury 2007, 38, S11–S25. [Google Scholar] [CrossRef]
- Dimitriou, R.; Tsiridis, E.; Giannoudis, P.V. Current concepts of molecular aspects of bone healing. Injury 2005, 36, 1392–1404. [Google Scholar] [CrossRef]
- Vermolen, F.J.; Javierre, E. A Suite of Continuum Models for Different Aspects in Wound Healing. In Bioengineering Research of Chronic Wounds. Studies in Mechanobiology, Tissue Engineering and Biomaterials; Gefen, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 1. [Google Scholar] [CrossRef]
- Sela, M.N.; Badihi, L.; Rosen, G.; Steinberg, D.; Kohavi, D. Adsorption of human plasma proteins to modified titanium surfaces. Clin. Oral Implants Res. 2007, 18, 630–638. [Google Scholar] [CrossRef]
- Nygren, H.; Eriksson, C.; Lausmaa, J. Adhesion and activation of platelets and polymorphonuclear granulocyte cells at TiO2 surfaces. J. Lab. Clin. Med. 1997, 129, 35–46. [Google Scholar] [CrossRef]
- Cheung, A.; Phillips, A.M. Bone morphogenetic proteins in orthopaedic surgery. Current Orthopaedics 2006, 20, 424–429. [Google Scholar] [CrossRef]
- Park, J.Y.; Gemmell, C.H.; Davies, J.E. Platelet interactions with titanium: Modulation of platelet activity by surface topography. Biomaterials 2001, 22, 2671–2682. [Google Scholar] [CrossRef]
- Kikuchi, L.; Park, J.Y.; Victor, C.; Davies, J.E. Platelet interactions with calcium-phosphate-coated surfaces. Biomaterials 2005, 26, 5285–5295. [Google Scholar] [CrossRef] [PubMed]
- Adair, T.H.; Montani, J.P. Angiogenesis. In Overview of Angiogenesis; Morgan & Claypool Life Sciences: San Rafael, CA, USA, 2010; Chapter 1. Available online: https://www.ncbi.nlm.nih.gov/books/NBK53238/ (accessed on 1 December 2021).
- Bikfalvi, A. Angiogenesis. Encyclopedia of Endocrine Diseases; Martini, L., Ed.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 227–233. [Google Scholar] [CrossRef]
- Linkhart, T.A.; Mohan, S.; Baylink, D.J. Growth factors for bone growth and repair: IGF, TGF beta and BMP. Bone 1996, 19 (Suppl. 1), S1–S12. [Google Scholar] [CrossRef]
- Pavlin, D.; Dove, S.B.; Zadro, R.; Gluhak-Heinrich, J. Mechanical loading stimulates differentiation of periodontal osteoblasts in a mouse osteoinduction model: Effect on type I collagen and alkaline phosphatase genes. Calcif. Tissue Int. 2000, 67, 163–172. [Google Scholar] [CrossRef]
- Uto, Y.; Kuroshima, S.; Nakano, T.; Ishimoto, T.; Inaba, N.; Uchida, Y.; Sawase, T. Effects of mechanical repetitive load on bone quality around implants in rat maxillae. PLoS ONE 2017, 12, e0189893. [Google Scholar] [CrossRef] [Green Version]
- Berglundh, T.; Abrahamsson, I.; Lindhe, J. Bone reactions to longstanding functional load at implants: An experimental study in dogs. J. Clin. Periodontol. 2005, 32, 925–932. [Google Scholar] [CrossRef]
- Kuroshima, S.; Yasutake, M.; Tsuiki, K.; Nakano, T.; Sawase, T. Structural and Qualitative Bone Remodeling around Repetitive Loaded Implants in Rabbits. Clin. Implant Dent. Relat. Res. 2015, 17, e699–e710. [Google Scholar] [CrossRef]
- Kitamura, E.; Stegaroiu, R.; Nomura, S.; Miyakawa, O. Biomechanical aspects of marginal bone resorption around osseointegrated implants: Considerations based on a three-dimensional finite element analysis. Clin. Oral Implant. Res. 2004, 15, 401–412. [Google Scholar] [CrossRef]
- Assenza, B.; Scarano, A.; Petrone, G.; Iezzi, G.; Thams, U.; Roman, F.S.; Piattelli, A. Osteoclast activity around loaded and unloaded implants: A histological study in the beagle dog. J. Oral Implantol. 2003, 29, 1–7. [Google Scholar] [CrossRef]
- Puleo, D.A.; Nanci, A. Understanding and controlling the bone-implant interface. Biomaterials 1999, 20, 2311–2321. [Google Scholar] [CrossRef]
- Brunski, J.B. In vivo bone response to biomechanical loading at the bone/dental-implant interface. Adv. Dent. Res. 1999, 13, 99–119. [Google Scholar] [CrossRef] [PubMed]
- Davies, J.E. Understanding peri-implant endosseous healing. J. Dent. Educ. 2003, 67, 932–949. [Google Scholar] [CrossRef] [PubMed]
- Marco, F.; Milena, F.; Gianluca, G.; Vittoria, O. Peri-implant osteogenesis in health and osteoporosis. Micron 2005, 36, 630–644. [Google Scholar] [CrossRef] [PubMed]
- Klein-Nulend, J.; Bacabac, R.G.; Bakker, A.D. Mechanical loading and how it affects bone cells: The role of the osteocyte cytoskeleton in maintaining our skeleton. Eur. Cell Mater. 2012, 24, 278–291. [Google Scholar] [CrossRef]
- Bailón-Plaza, A.; van der Meulen, M.C. A mathematical framework to study the effects of growth factor influences on fracture healing. J. Theor. Biol. 2001, 212, 191–209. [Google Scholar] [CrossRef]
- Geris, L.; Gerisch, A.; Maes, C.; Carmeliet, G.; Weiner, R.; Vander Sloten, J.; Van Oosterwyck, H. Mathematical modeling of fracture healing in mice: Comparison between experimental data and numerical simulation results. Med. Biol. Eng. Comput. 2006, 44, 280–289. [Google Scholar] [CrossRef]
- Moreo, P.; García-Aznar, J.M.; Doblaré, M. Bone ingrowth on the surface of endosseous implants. Part 1: Mathematical model. J. Theor. Biol. 2009, 260, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Moreo, P.; García-Aznar, J.M.; Doblaré, M. Bone ingrowth on the surface of endosseous implants. Part 2: Theoretical and numerical analysis. J. Theor. Biol. 2009, 260, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Korzh, M.O.; Filipenko, V.A.; Radchenko, V.O.; Litvinov, L.A.; Voloshin, O.V.; Sliunin, Y.V.; Timchenko, I.B.; Golukhova, A.G.; Tankut, V.O.; Tankut, O.V. Hip Endoprosthesis. UA Patent 79,551, 25 June 2007. [Google Scholar]
- Massin, P.; Lopes, R.; Masson, B.; Mainard, D. Does Biolox® Delta ceramic reduce the rate of component fractures in total hip replacement? Orthop. Traumatol. Surg. Res. 2014, 100, S317–S321. [Google Scholar] [CrossRef]
- Koch, C.N.; Figgie, M.J.; Figgie, M.P.; Elpers, M.E.; Wright, T.M.; Padgett, D.E. Ceramic Bearings with Titanium Adapter Sleeves Implanted during Revision Hip Arthroplasty Show Minimal Fretting or Corrosion: A Retrieval Analysis. HSS J. 2017, 13, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Bouvet, J.C. Prosthesis Ball Joint. EP Patent 0,406,040, 1991. [Google Scholar]
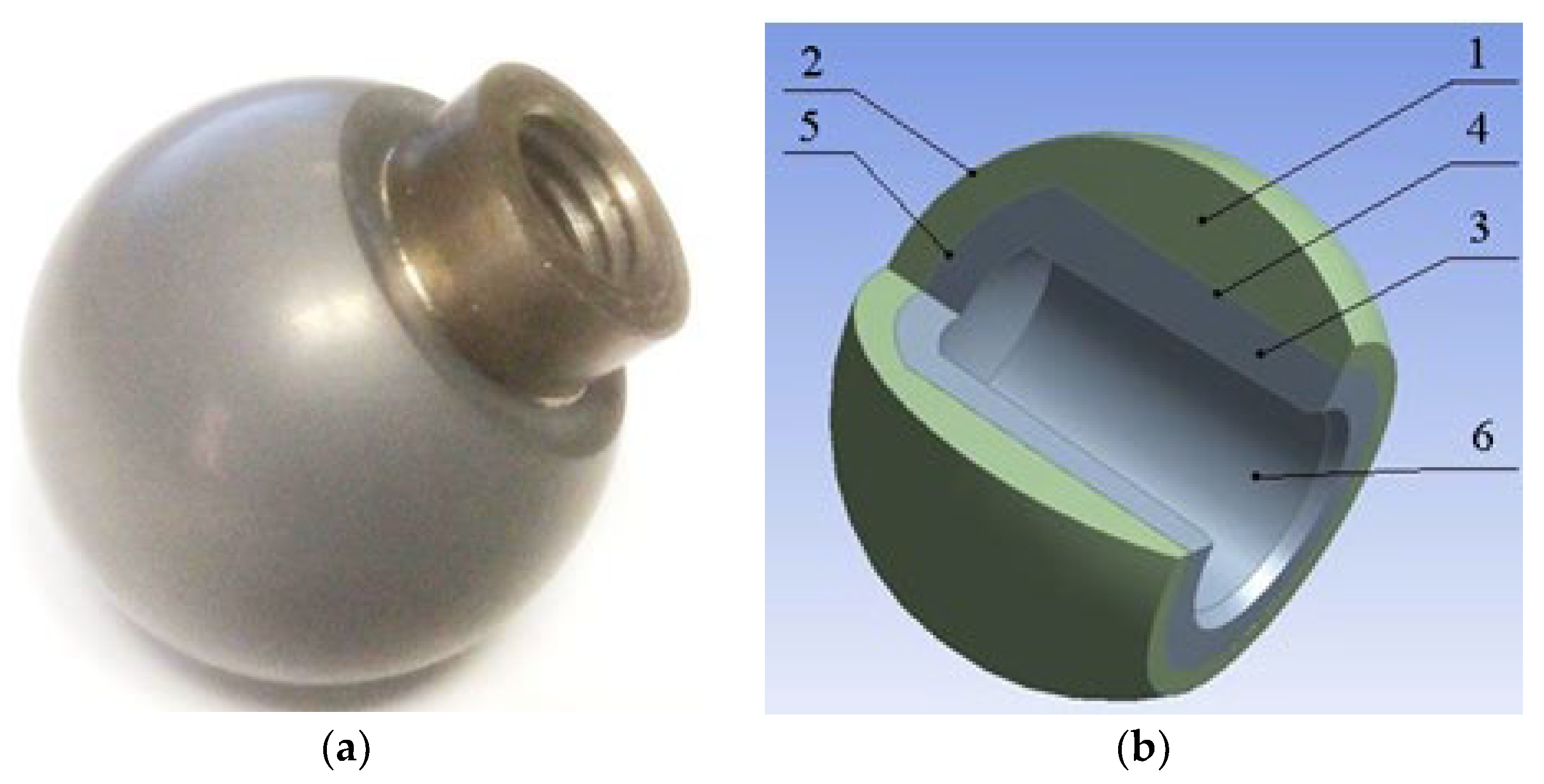
- Pakhaliuk, V.; Poliakov, A.; Fedotov, I. The ceramic modular head improvement in the design of a total hip replacement. Facta Universitatis. Ser. Mech. Eng. 2021, 19, 67–78. [Google Scholar] [CrossRef]
- Kalin, B.A.; Fedotov, I.V.; Sevryukov, O.N.; Pakhalyuk, V.I.; Nemchinov, Y.M.; Ivannikov, A.A.; Suchkov, A.N. Method of soldered connection of alumina ceramic with titanium alloy BT1-0. RU Patent 2,717,446, 23 May 2020. [Google Scholar]
- Carter, D.R.; Blenman, P.R.; Beaupré, G.S. Correlations between mechanical stress history and tissue differentiation in initial fracture healing. J. Orthop. Res. 1988, 6, 736–748. [Google Scholar] [CrossRef] [PubMed]
- Palma, F.D.; Guignandon, A.; Chamson, A.; Lafage-Proust, M.H.; Laroche, N.; Peyroche, S.; Vico, L.; Rattner, A. Modulation of the responses of human osteoblast-like cells to physiologic mechanical strains by biomaterial surfaces. Biomaterials 2005, 26, 4249–4257. [Google Scholar] [CrossRef]
- Raab-Cullen, D.M.; Thiede, M.A.; Petersen, D.N.; Kimmel, D.B.; Recker, R.R. Mechanical loading stimulates rapid changes in periosteal gene expression. Calcif. Tissue Int. 1994, 55, 473–4788. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Hashimoto, F.; Miyamoto, H.; Kanaoka, K.; Miyazaki-Kawashita, Y.; Nakashima, T.; Shibata, M.; Kobayashi, K.; Kato, Y.; Sakai, H. Force-induced osteoclast apoptosis in vivo is accompanied by elevation in transforming growth factor b and osteprotegerin expression. J. Bone Miner. Res. 2000, 15, 1924–1934. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, V.L.; Poliakov, A.M.; Pakhaliuk, V.I. Improving the Endoprosthesis Design and the Postoperative Therapy as a Means of Reducing Complications Risks after Total Hip Arthroplasty. Lubricants 2022, 10, 38. https://doi.org/10.3390/lubricants10030038
Popov VL, Poliakov AM, Pakhaliuk VI. Improving the Endoprosthesis Design and the Postoperative Therapy as a Means of Reducing Complications Risks after Total Hip Arthroplasty. Lubricants. 2022; 10(3):38. https://doi.org/10.3390/lubricants10030038
Chicago/Turabian StylePopov, Valentin L., Aleksandr M. Poliakov, and Vladimir I. Pakhaliuk. 2022. "Improving the Endoprosthesis Design and the Postoperative Therapy as a Means of Reducing Complications Risks after Total Hip Arthroplasty" Lubricants 10, no. 3: 38. https://doi.org/10.3390/lubricants10030038
APA StylePopov, V. L., Poliakov, A. M., & Pakhaliuk, V. I. (2022). Improving the Endoprosthesis Design and the Postoperative Therapy as a Means of Reducing Complications Risks after Total Hip Arthroplasty. Lubricants, 10(3), 38. https://doi.org/10.3390/lubricants10030038







