The Effects of Interval Uncertainties on Dynamic Characteristics of a Rotor System Supported by Oil-Film Bearings
Abstract
1. Introduction
2. Deterministic Modeling and Solution
2.1. Finite Element Modeling of Rotor
2.2. Oil-Film Bearing Model
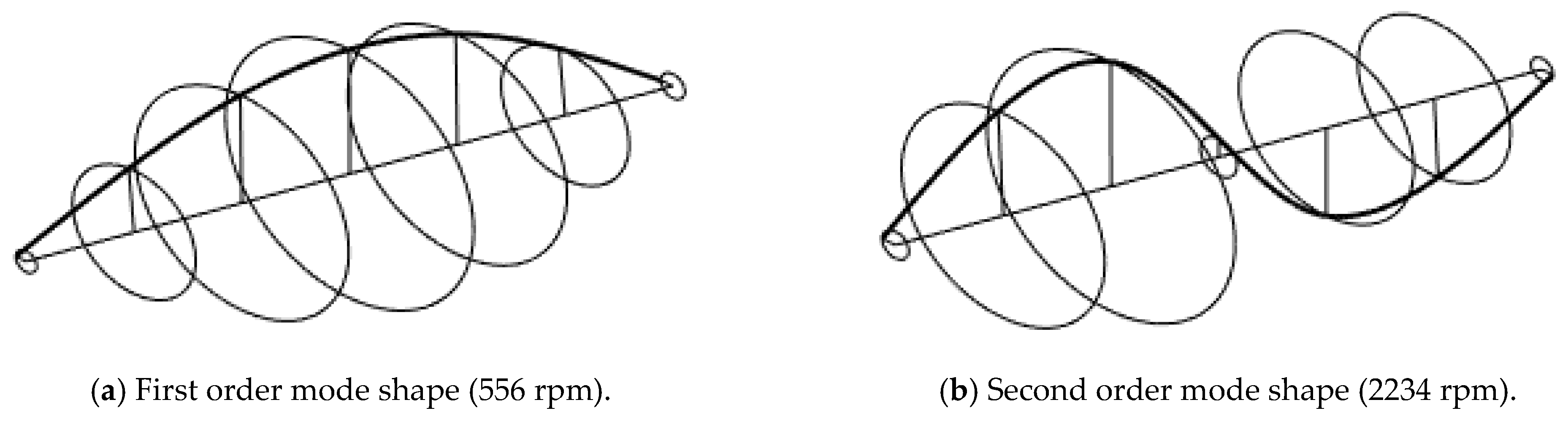
2.3. Dynamic Characteristic Analysis
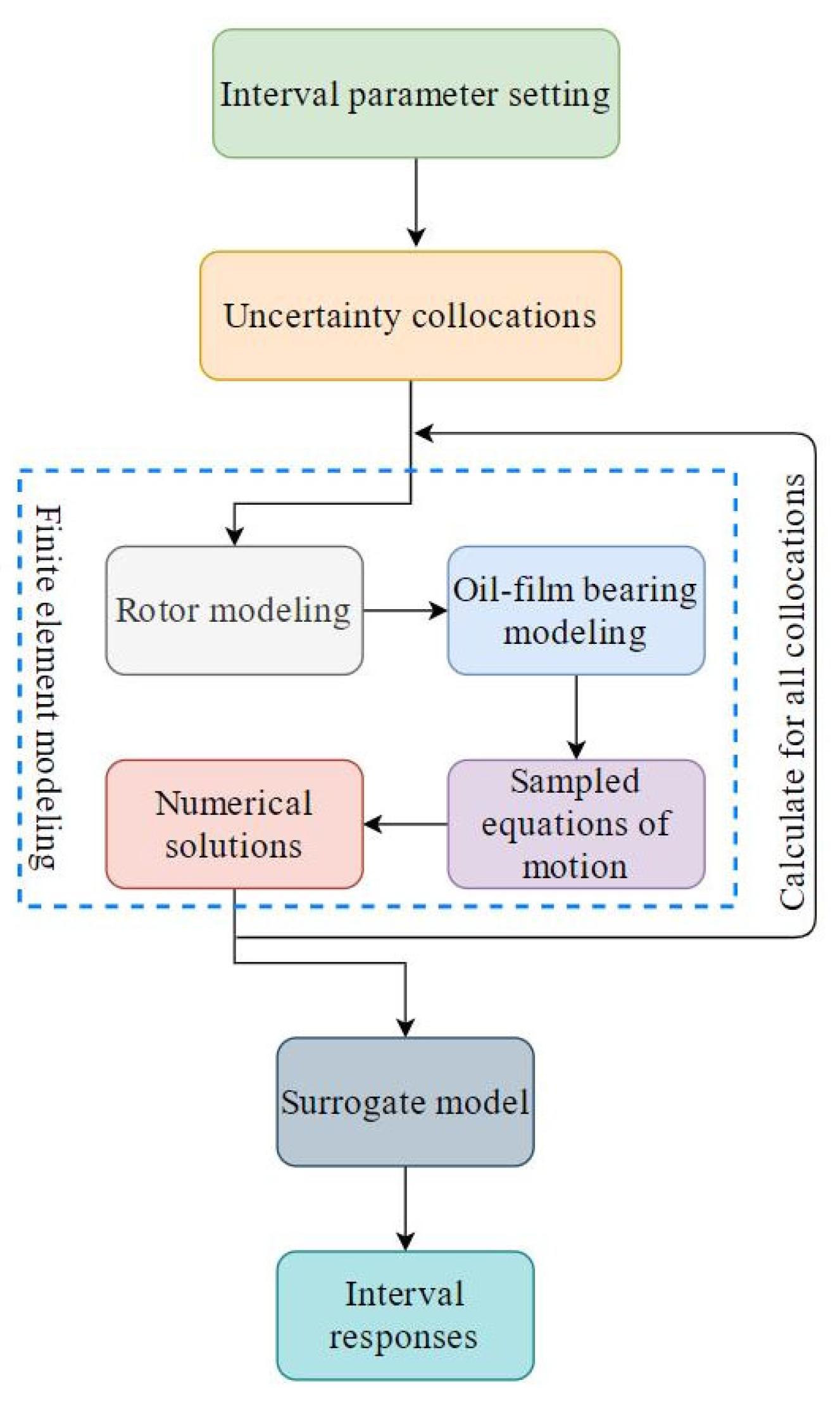
3. Interval Uncertainty Approach
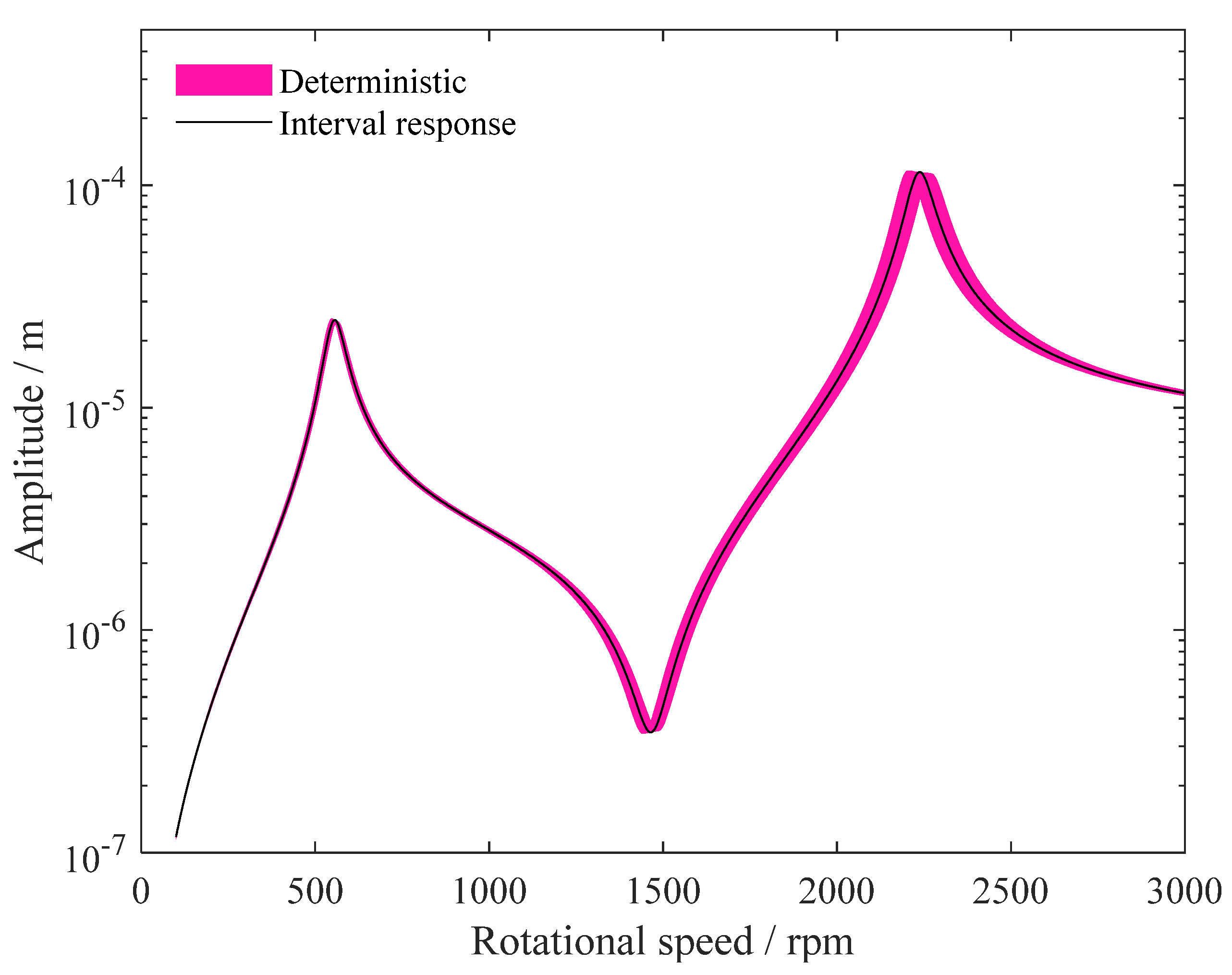
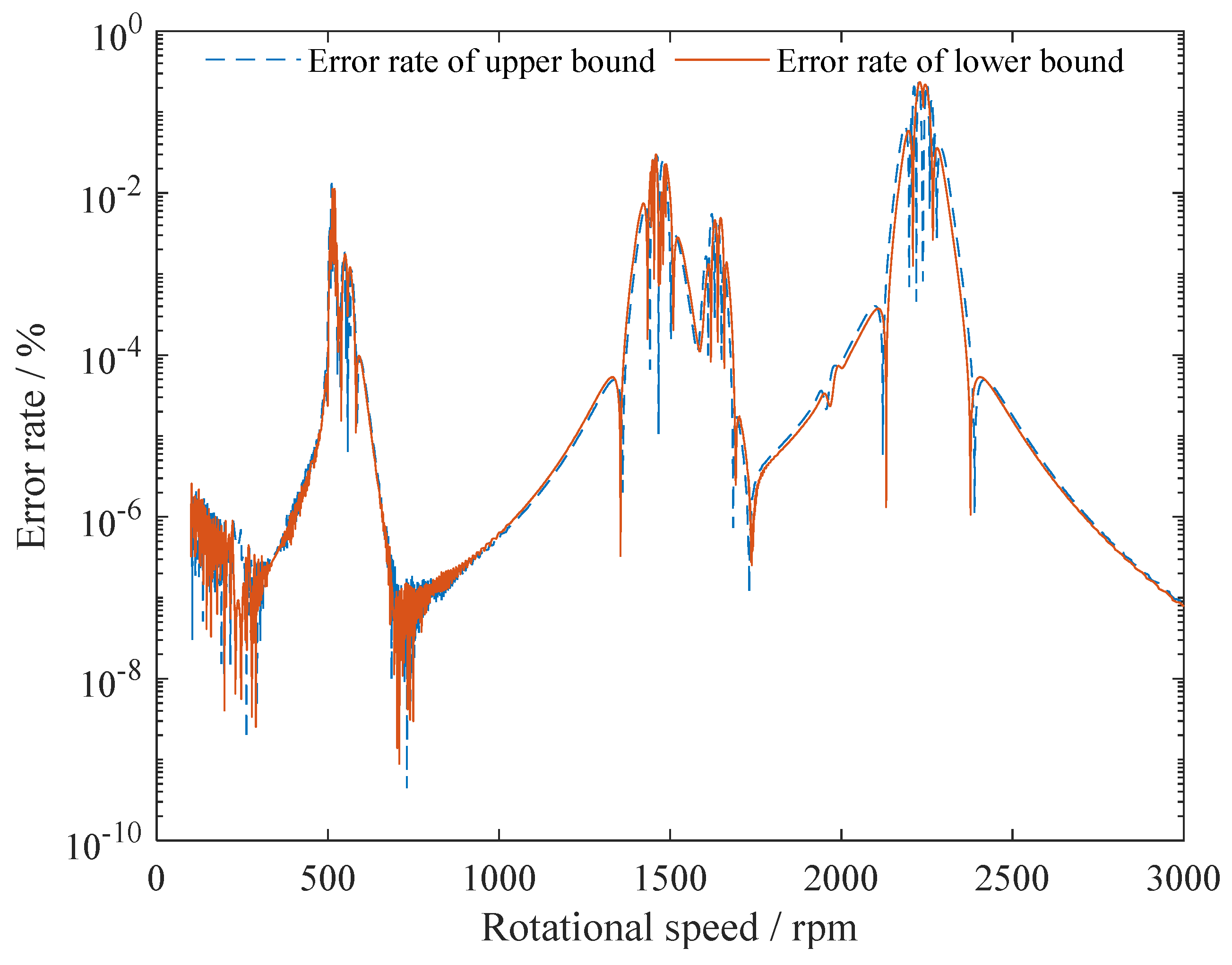
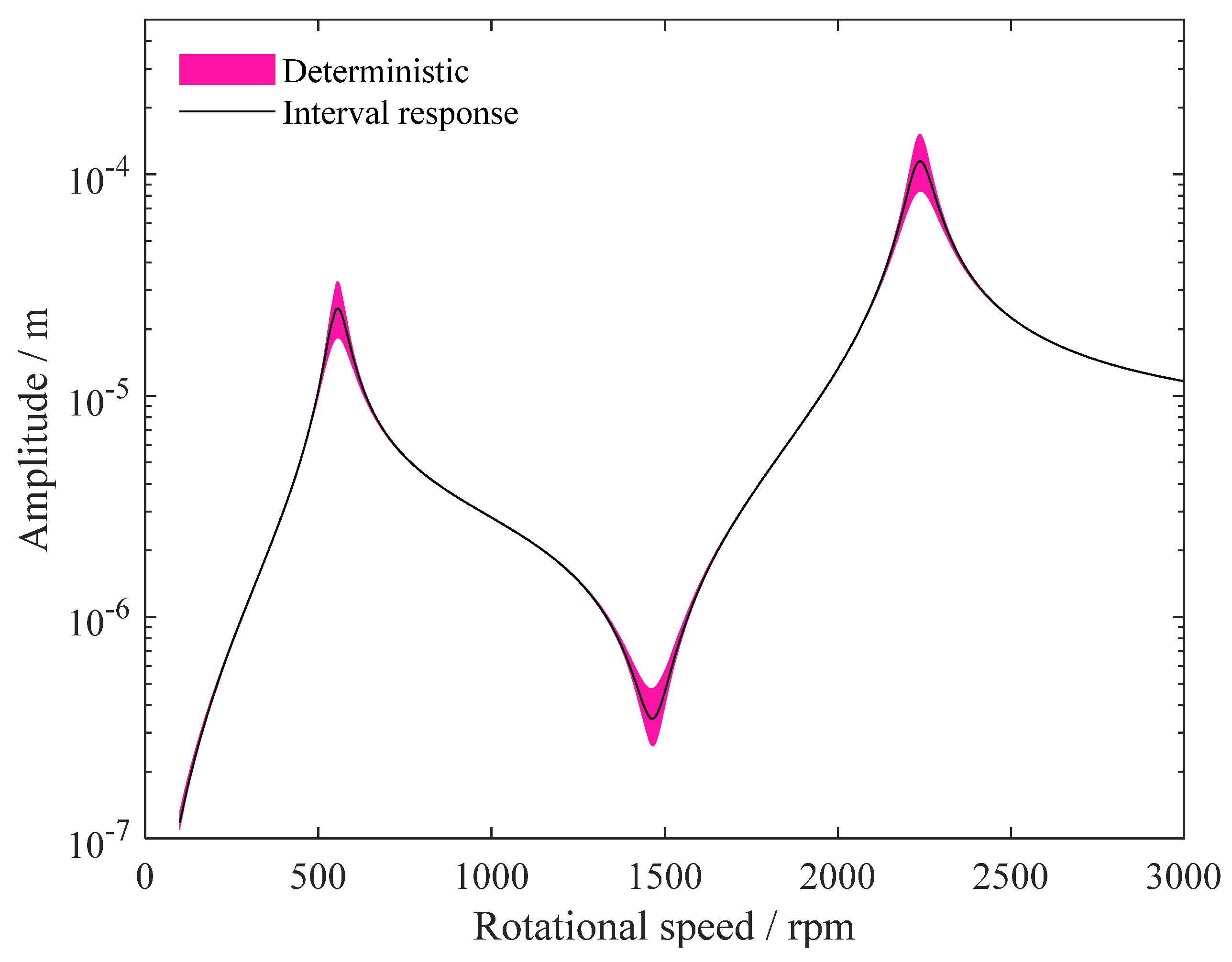
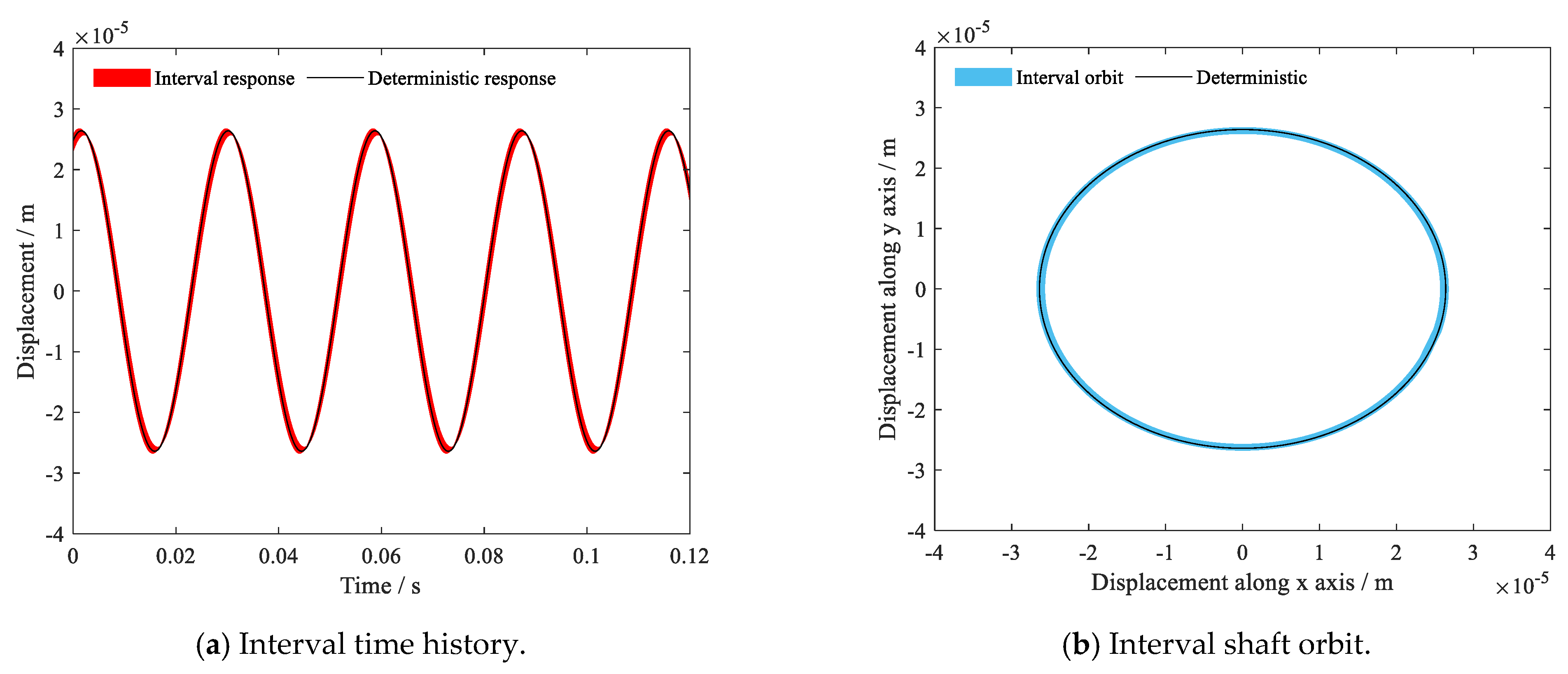
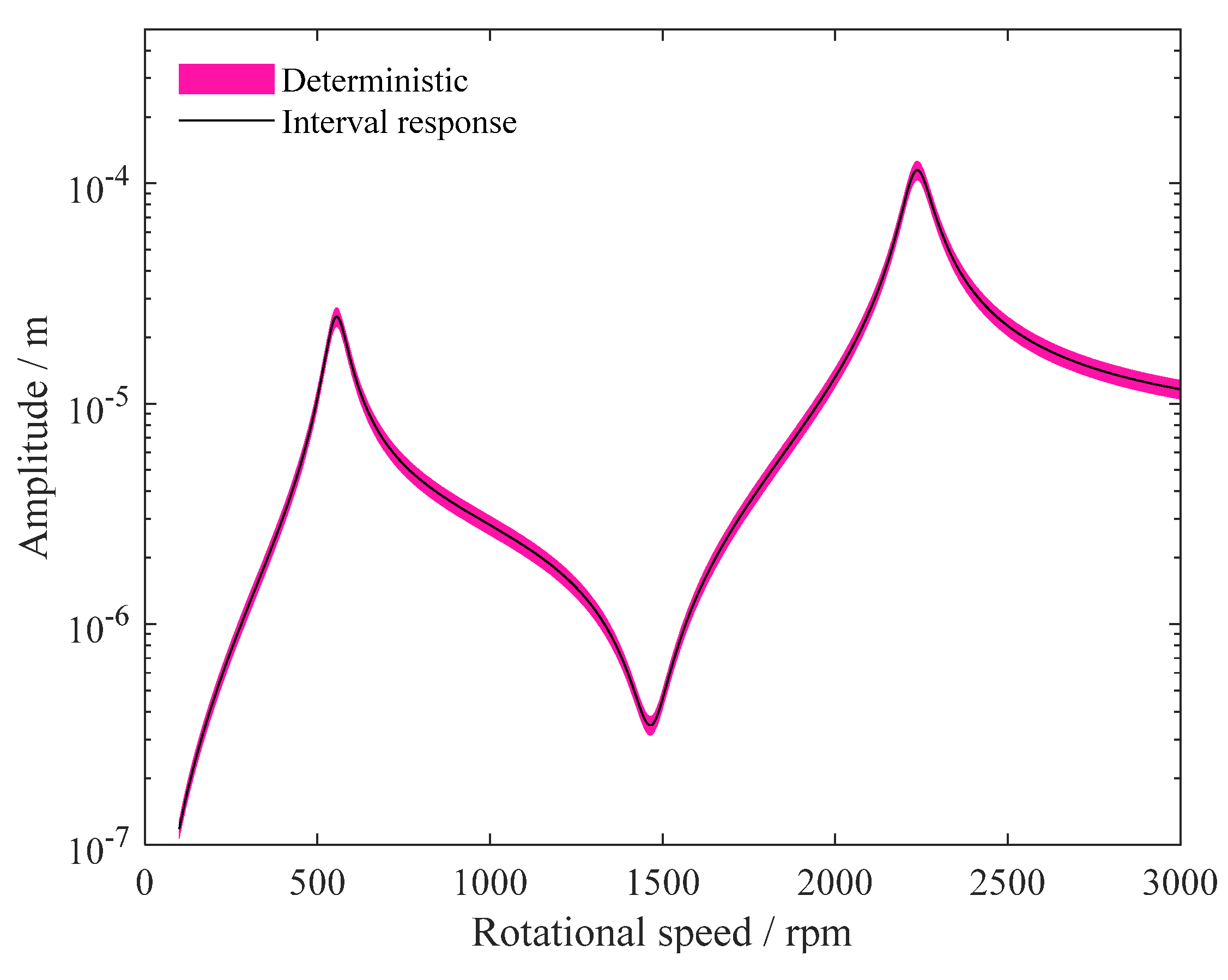
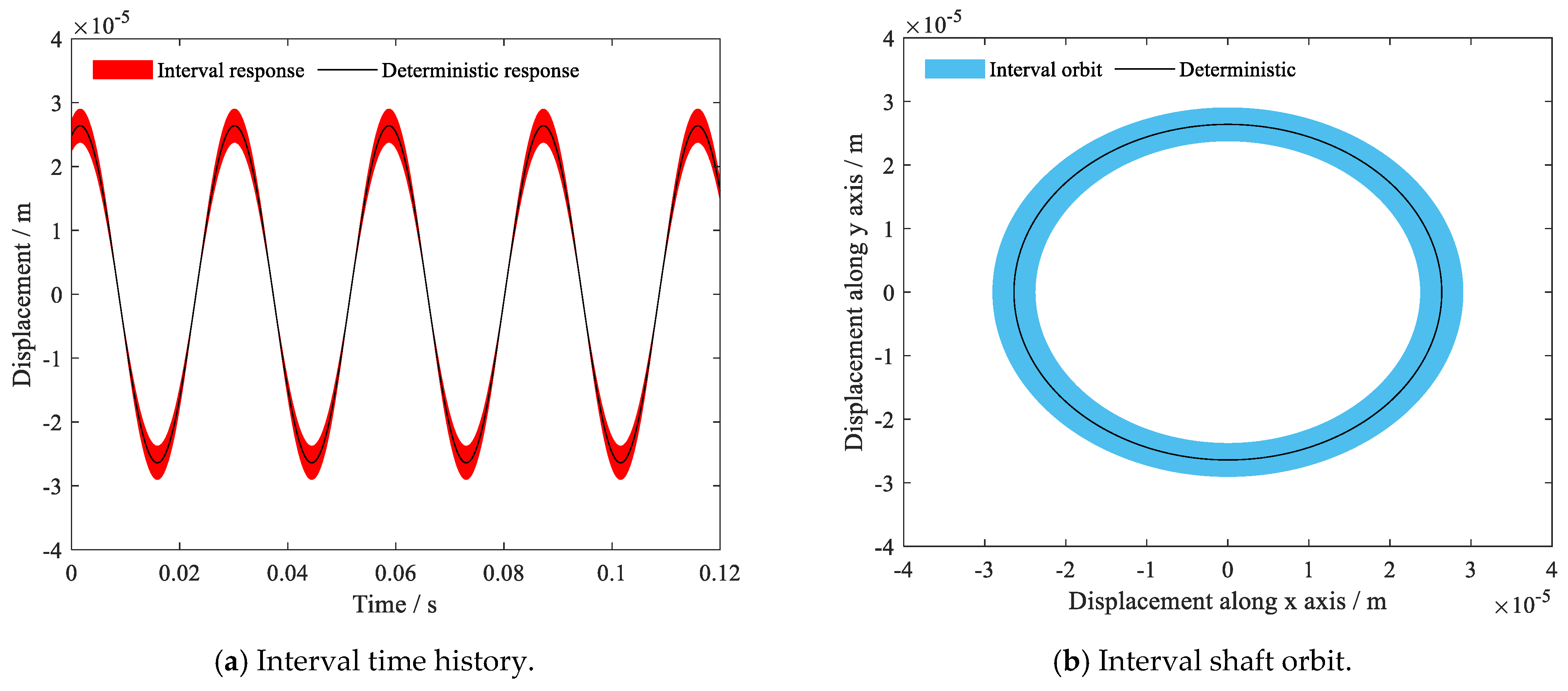
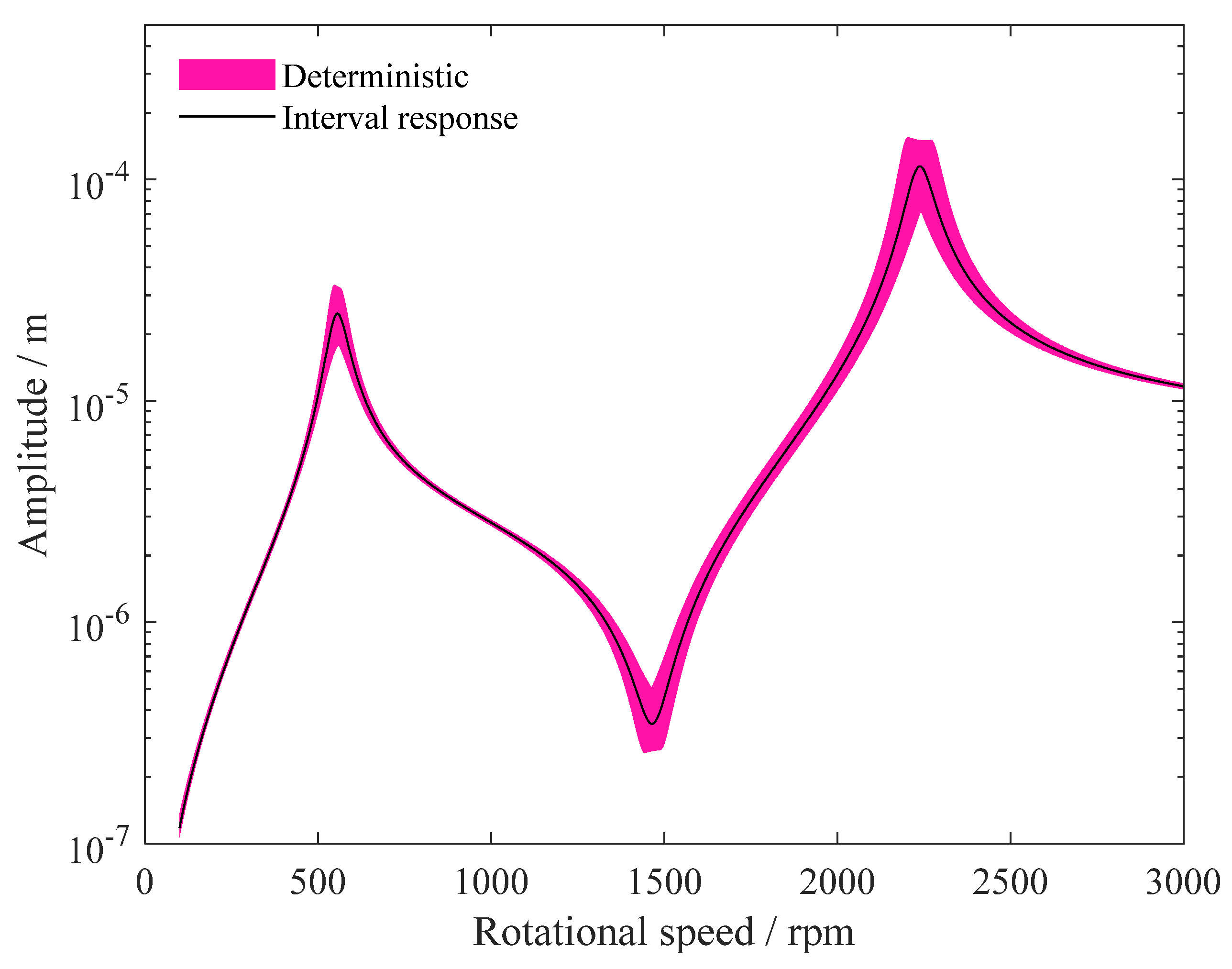
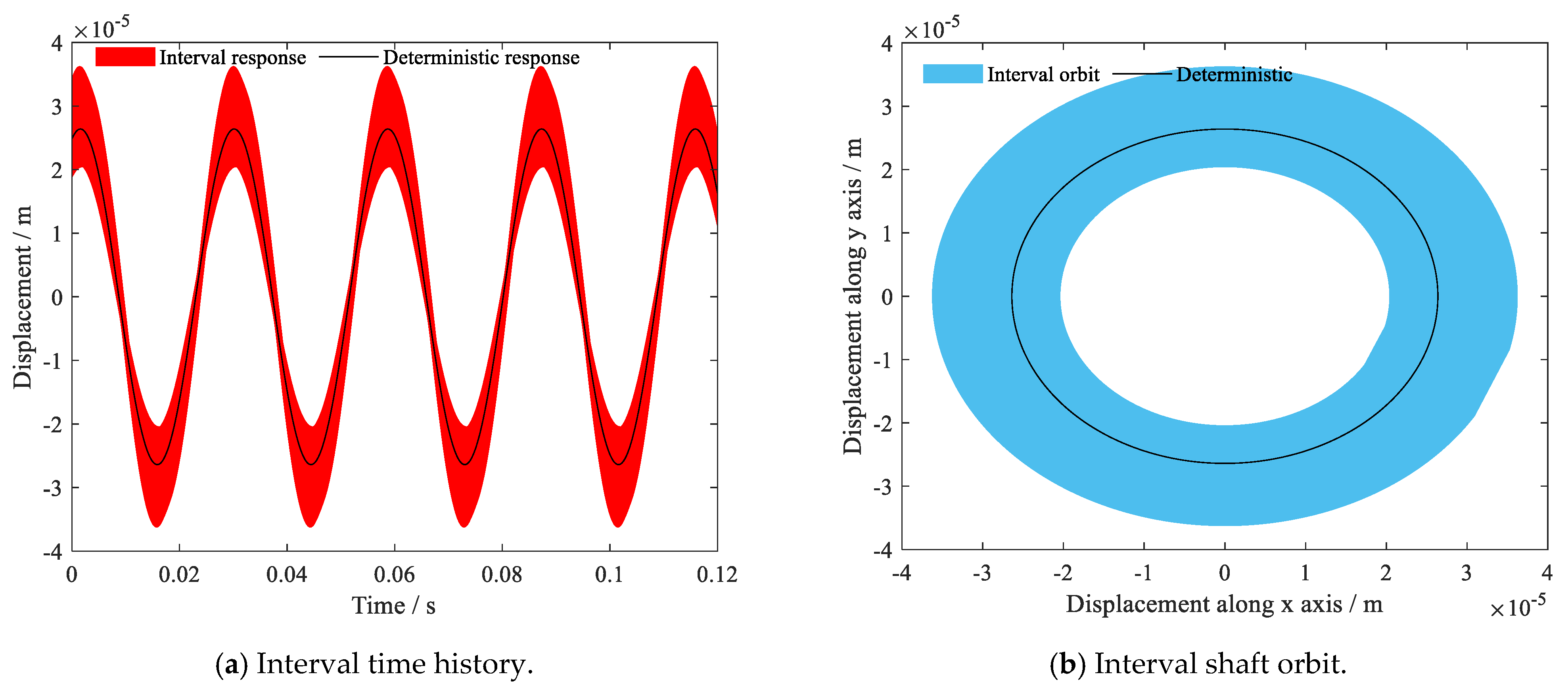
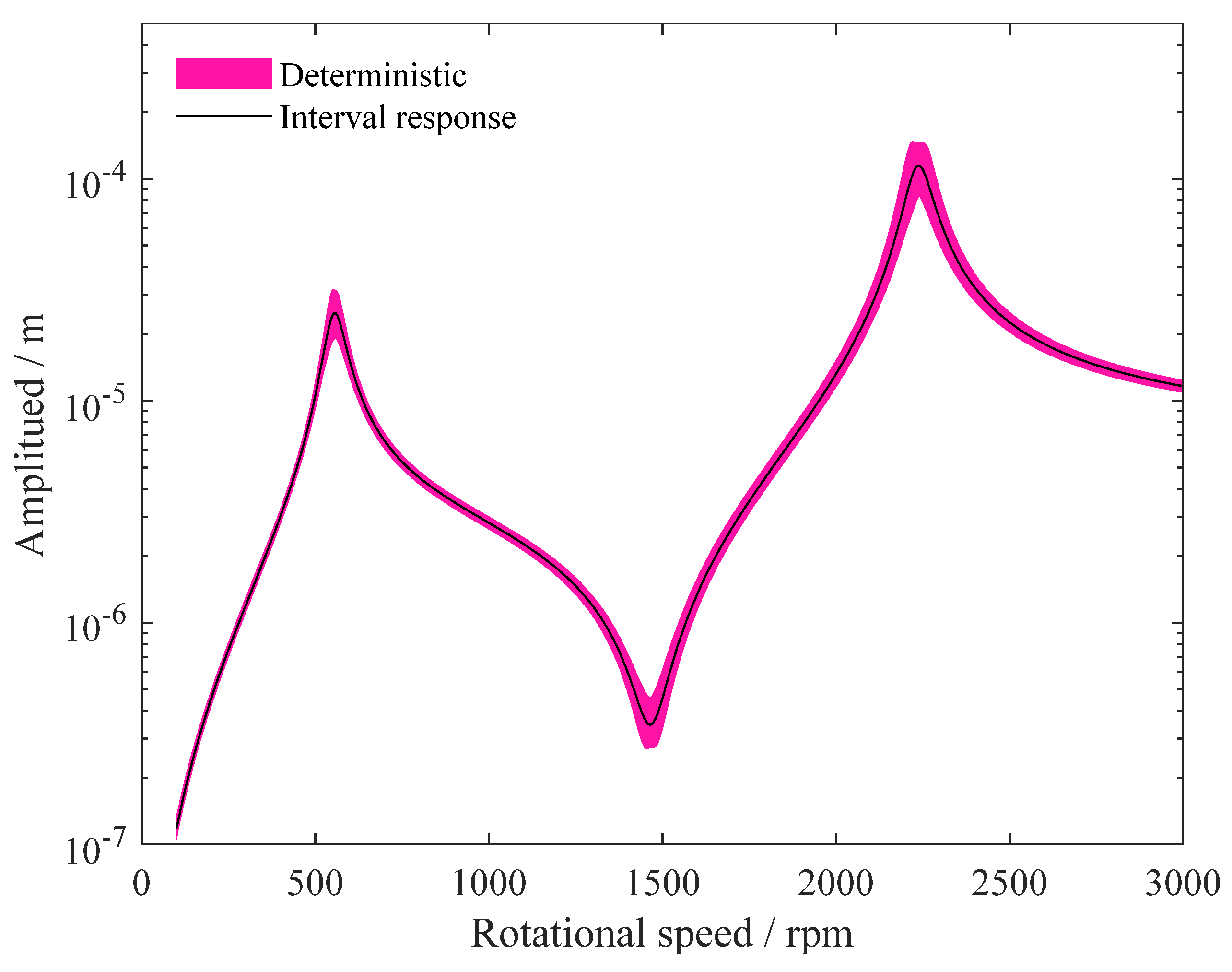
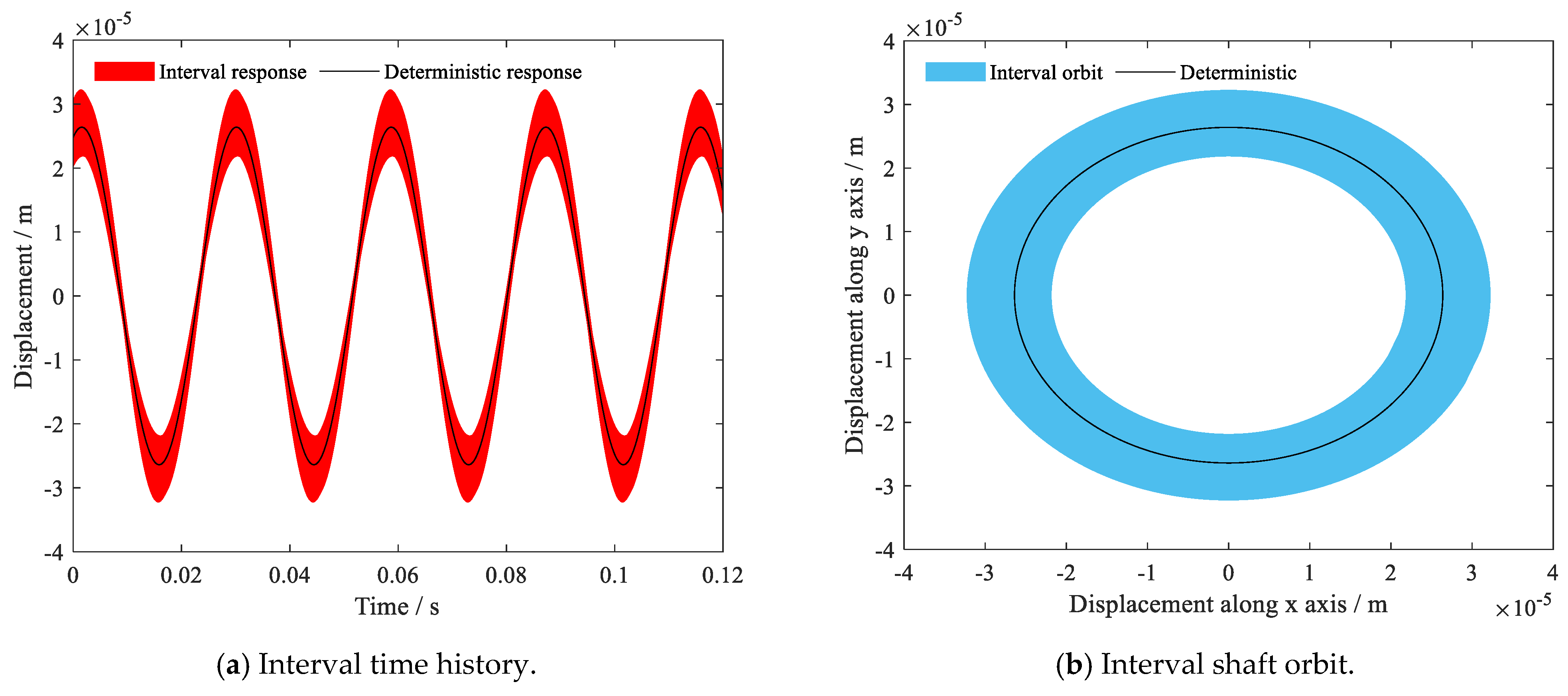
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chasalevris, A.; Louis, J.C. Evaluation of transient response of turbochargers and turbines using database method for the nonlinear forces of journal bearings. Lubricants 2019, 7, 78. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zhang, H.; Chu, F.; Shi, Z.; Gu, F.; Ball, A.D. Modelling non-Gaussian surfaces and misalignment for condition monitoring of journal bearings. Measurement 2021, 174, 108983. [Google Scholar] [CrossRef]
- Dang, P.V.; Chatterton, S.; Pennacchi, P. The effect of the pivot stiffness on the performances of five-pad tilting pad bearings. Lubricants 2019, 7, 61. [Google Scholar] [CrossRef]
- Roy, B.; Dey, S. Machine learning-based performance analysis of two-axial-groove hydrodynamic journal bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2211–2224. [Google Scholar] [CrossRef]
- Xu, B.; Zang, C.; Zhang, G. Intelligent approach to robust design optimization of a rotor system due to its support stiffness uncertainty. Shock Vib. 2020, 2020, 2564679. [Google Scholar] [CrossRef]
- Xiang, G.; Yang, T.; Guo, J.; Wang, J.; Liu, B.; Chen, S. Optimization transient wear and contact performances of water-lubricated bearings under fluid-solid-thermal coupling condition using profile modification. Wear 2022, 502–503, 204379. [Google Scholar] [CrossRef]
- Moustafa, K.A.F. Stability of journal bearing-rotor systems with interval-bearing parameters. J. Vib. Control 1999, 5, 941–953. [Google Scholar] [CrossRef]
- Wale, G.D.; Mba, D. Identifying and minimising uncertainty for experimental journal bearing studies. Int. J. Rotating Mach. 2005, 2005, 591329. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, W.; Ma, J.; Gu, F. Static and dynamic characteristics of journal bearings under uncertainty: A nonprobabilistic perspective. J. Eng. Gas Turbines Power 2022, 144, 071012. [Google Scholar]
- Didier, J.; Sinou, J.J.; Faverjon, B. Study of the non-linear dynamic response of a rotor system with faults and uncertainties. J. Sound Vib. 2012, 331, 671–703. [Google Scholar] [CrossRef]
- Cavalini Jr, A.A.; Lara-Molina, F.A.; Sales, T.d.P.; Koroishi, E.H.; Steffen, V., Jr. Uncertainty analysis of a flexible rotor supported by fluid film bearings. Lat. Am. J. Solids Struct. 2015, 12, 1487–1504. [Google Scholar] [CrossRef]
- Chen, S.; Xiang, G.; Fillon, M.; Guo, J.; Wang, J.; Cai, J. On the tribo-dynamic behaviors during start-up of water lubricated bearing considering imperfect journal. Tribol. Int. 2022, 174, 107685. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.J.; Zhu, W.D.; Lu, K.; Yang, Y.F. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zhu, W.; Lu, K.; Yang, Y. Stochastic analysis of lubrication in misaligned journal bearings. J. Tribol. 2022, 144, 081802. [Google Scholar] [CrossRef]
- Lin, L.; He, M.; Ma, W.; Wang, Q.; Zhai, H.; Deng, C. Dynamic characteristic analysis of the multi-stage centrifugal pump rotor system with uncertain sliding bearing structural parameters. Appl. Sci. 2022, 10, 473. [Google Scholar] [CrossRef]
- Fu, C.; Feng, G.J.; Ma, J.J.; Lu, K.; Yang, Y.F.; Gu, F.S. Predicting the dynamic response of dual-rotor system subject to interval parametric uncertainties based on the non-intrusive metamodel. Mathematics 2020, 8, 736. [Google Scholar] [CrossRef]
- Denimal, E.; Sinou, J.J. Advanced kriging-based surrogate modelling and sensitivity analysis for rotordynamics with uncertainties. Eur. J. Mech.-A/Solids 2021, 90, 104331. [Google Scholar] [CrossRef]
- Stocki, R.; Lasota, R.; Tauzowski, P.; Szolc, T. Scatter assessment of rotating system vibrations due to uncertain residual unbalances and bearing properties. Comput. Assist. Methods Eng. 2017, 19, 95–120. [Google Scholar]
- Fu, C.; Zhu, W.D.; Yang, Y.F.; Zhao, S.B.; Lu, K. Surrogate modeling for dynamic analysis of an uncertain notched rotor system and roles of Chebyshev parameters. J. Sound Vib. 2022, 524, 116755. [Google Scholar] [CrossRef]
- Sun, X.; Sepahvand, K.K.; Marburg, S. Stability analysis of rotor-bearing systems under the influence of misalignment and parameter uncertainty. Appl. Sci. 2021, 11, 7918. [Google Scholar] [CrossRef]
- Garoli, G.Y.; Castro, H.F.d. Analysis of a rotor-bearing nonlinear system model considering fluid-induced instability and uncertainties in bearings. J. Sound Vib. 2019, 448, 108–129. [Google Scholar] [CrossRef]
- Geng, B.; Zuo, Y.; Jiang, Z.; Feng, K.; Wang, C.; Wang, J. A double integral method for quantitative evaluation of influence on thin-walled casing response caused by bearing uncertainties. Chin. J. Aeronaut. 2020, 33, 2372–2381. [Google Scholar] [CrossRef]
- Medina, L.; Ruiz, R.; Di’az, S. A simple approach to determine uncertainty bounds on bearing rotordynamic coefficients identification. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; pp. 1279–1287. [Google Scholar]
- Tauviqirrahman, M.; Jamari, J.; Wicaksono, A.A.; Muchammad, M.; Susilowati, S.; Ngatilah, Y.; Pujiastuti, C. CFD analysis of journal bearing with a heterogeneous rough/smooth surface. Lubricants 2021, 9, 88. [Google Scholar] [CrossRef]
- Da Silva, H.A.P.; Nicoletti, R. Design of tilting-pad journal bearings considering bearing clearance uncertainty and reliability analysis. J. Tribol. 2019, 141, 011703. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, J.; Tian, Z. Stochastic dynamics of a nonlinear misaligned rotor system subject to random fluid-induced forces. J. Comput. Nonlinear Dyn. 2016, 12, 011004. [Google Scholar] [CrossRef]
- Alves, D.S.; Daniel, G.B.; Castro, H.F.d.; Machado, T.H.; Cavalca, K.L.; Gecgel, O.; Dias, J.P.; Ekwaro-Osire, S. Uncertainty quantification in deep convolutional neural network diagnostics of journal bearings with ovalization fault. Mech. Mach. Theory 2020, 149, 103835. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Fu, C.; Xu, Y.D.; Yang, Y.F.; Lu, K.; Gu, F.S.; Ball, A. Response analysis of an accelerating unbalanced rotating system with both random and interval variables. J. Sound Vib. 2020, 466, 115047. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Chen, L.; Luo, Z. A Chebyshev interval method for nonlinear dynamic systems under uncertainty. Appl. Math. Model. 2013, 37, 4578–4591. [Google Scholar] [CrossRef]
- Fu, C.; Zheng, Z.; Zhu, W.; Lu, K.; Yang, Y. Non-intrusive frequency response analysis of nonlinear systems with interval uncertainty: A comparative study. Chaos Solitons Fractals 2022, 165, 112815. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, Z.; Chen, M.; Hong, J. Interval analysis of rotor dynamic response with uncertain parameters. J. Sound Vib. 2013, 332, 3869–3880. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, W.D.; Zheng, Z.L.; Sun, C.Z.; Yang, Y.F.; Lu, K. Nonlinear responses of a dual-rotor system with rub-impact fault subject to interval uncertain parameters. Mech. Syst. Signal Process. 2022, 170, 108827. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Qin, Z.; Ma, L.; Chu, F. Dynamic performance of a novel integral magnetorheological damper-rotor system. Mech. Syst. Signal Process. 2022, 172, 109004. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhu, R.; Han, Q.; Qin, Z.; Chu, F. Modeling approach for flexible shaft-disk-drum rotor systems with elastic connections and supports. Appl. Math. Model. 2022, 106, 402–425. [Google Scholar] [CrossRef]
- Friswell, M.I.; Penny, J.E.; Garvey, S.D.; Lees, A.W. Dynamics of Rotating Machines; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Kornaev, A.V.; Kornaev, N.V.; Kornaeva, E.P.; Savin, L.A. Application of artificial neural networks to calculation of oil film reaction forces and dynamics of rotors on journal bearings. Int. J. Rotating Mach. 2017, 2017, 9196701. [Google Scholar] [CrossRef]
- Cameron, A. Basic Lubrication Theory; Ellis Horwood: Chichester, UK, 1981. [Google Scholar]
- Chasalevris, A.; Dohnal, F. Vibration quenching in a large scale rotor-bearing system using journal bearings with variable geometry. J. Sound Vib. 2014, 333, 2087–2099. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, H.; Lou, S.; Chu, F.; Shi, Z.; Gu, F.; Ball, A.D. Analytical and experimental investigation of vibration characteristics induced by tribofilm-asperity interactions in hydrodynamic journal bearings. Mech. Syst. Signal Process. 2021, 150, 107227. [Google Scholar] [CrossRef]
- Papadopoulos, C.A.; Nikolakopoulos, P.G.; Gounaris, G.D. Identification of clearances and stability analysis for a rotor-journal bearing system. Mech. Mach. Theory 2008, 43, 411–426. [Google Scholar] [CrossRef]
- Fu, C.; Zheng, Z.L.; Zhu, W.D.; Xie, Z.L.; Qin, W.Y.; Lu, K. Nonlinear dynamics of discontinuous uncertain oscillators with unilateral constraints. Chaos 2022, 32, 123112. [Google Scholar] [CrossRef]

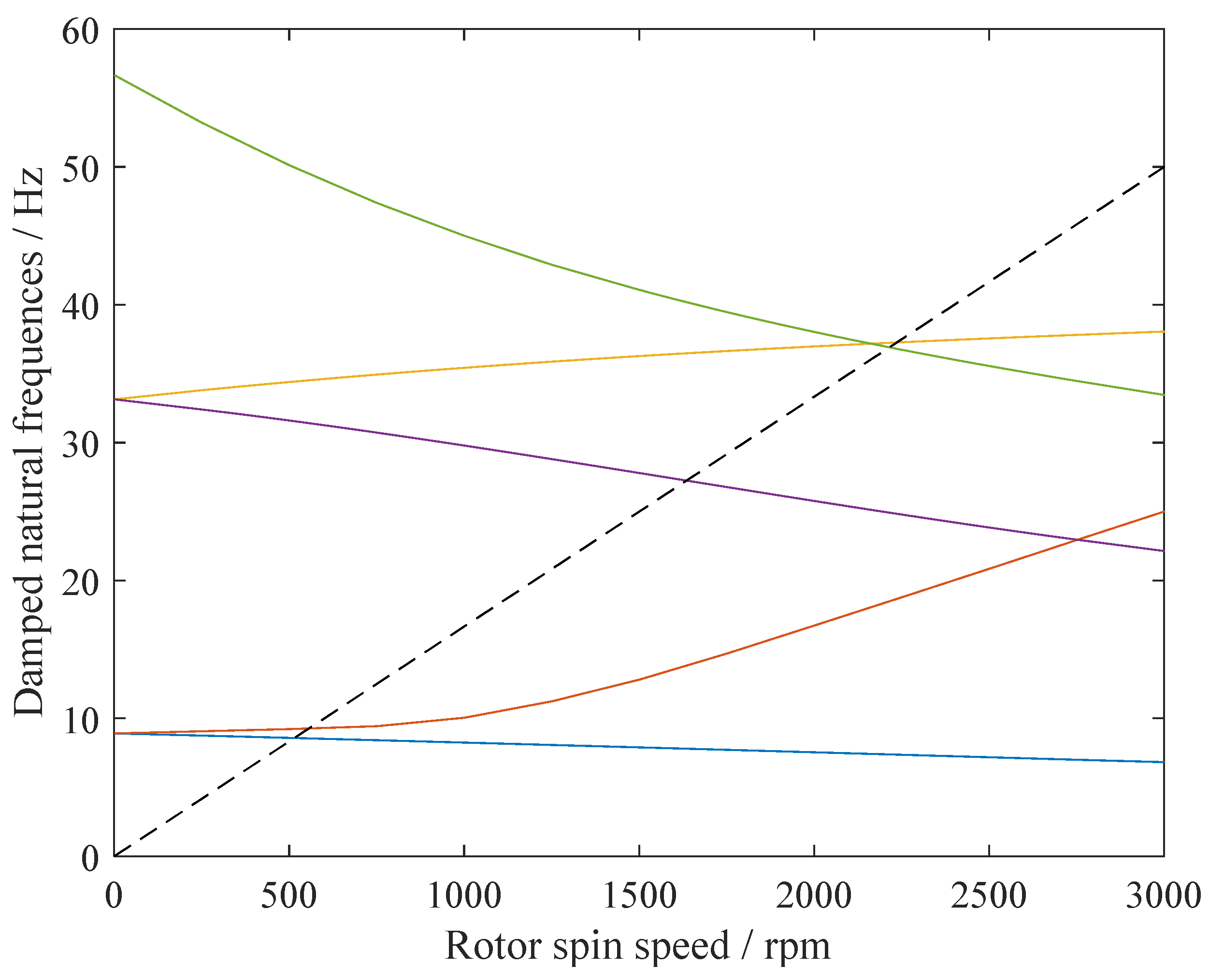

| Name | Value | Name | Value |
|---|---|---|---|
| Length of rotor | 1.5 m | Thickness of disk | 0.07 m |
| Diameter of rotor | 0.05 m | Diameter of disk 1 | 0.06 m |
| Young’s modulus | Diameter of disk 2 | 0.07 m | |
| Lubricant viscosity | 0.1 Pa·s | Unbalance amount | 0.001 kg |
| Bearing length | 0.015 m | Bearing clearance |
| Lower Bound | Upper Bound | |
|---|---|---|
| First critical speed | 551 rpm | 562 rpm |
| Second critical speed | 2219 rpm | 2256 rpm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Fu, C.; Zheng, Z.; Lu, K.; Yang, Y. The Effects of Interval Uncertainties on Dynamic Characteristics of a Rotor System Supported by Oil-Film Bearings. Lubricants 2022, 10, 354. https://doi.org/10.3390/lubricants10120354
Ma J, Fu C, Zheng Z, Lu K, Yang Y. The Effects of Interval Uncertainties on Dynamic Characteristics of a Rotor System Supported by Oil-Film Bearings. Lubricants. 2022; 10(12):354. https://doi.org/10.3390/lubricants10120354
Chicago/Turabian StyleMa, Jiaojiao, Chao Fu, Zhaoli Zheng, Kuan Lu, and Yongfeng Yang. 2022. "The Effects of Interval Uncertainties on Dynamic Characteristics of a Rotor System Supported by Oil-Film Bearings" Lubricants 10, no. 12: 354. https://doi.org/10.3390/lubricants10120354
APA StyleMa, J., Fu, C., Zheng, Z., Lu, K., & Yang, Y. (2022). The Effects of Interval Uncertainties on Dynamic Characteristics of a Rotor System Supported by Oil-Film Bearings. Lubricants, 10(12), 354. https://doi.org/10.3390/lubricants10120354






