Optimization Design of Aerostatic Bearings with Square Micro-Hole Arrayed Restrictor for the Improvement of Stability: Theoretical Predictions and Experimental Measurements
Abstract
1. Introduction
2. Aerostatic Bearing with SMAR Design and Numerical Simulation Method
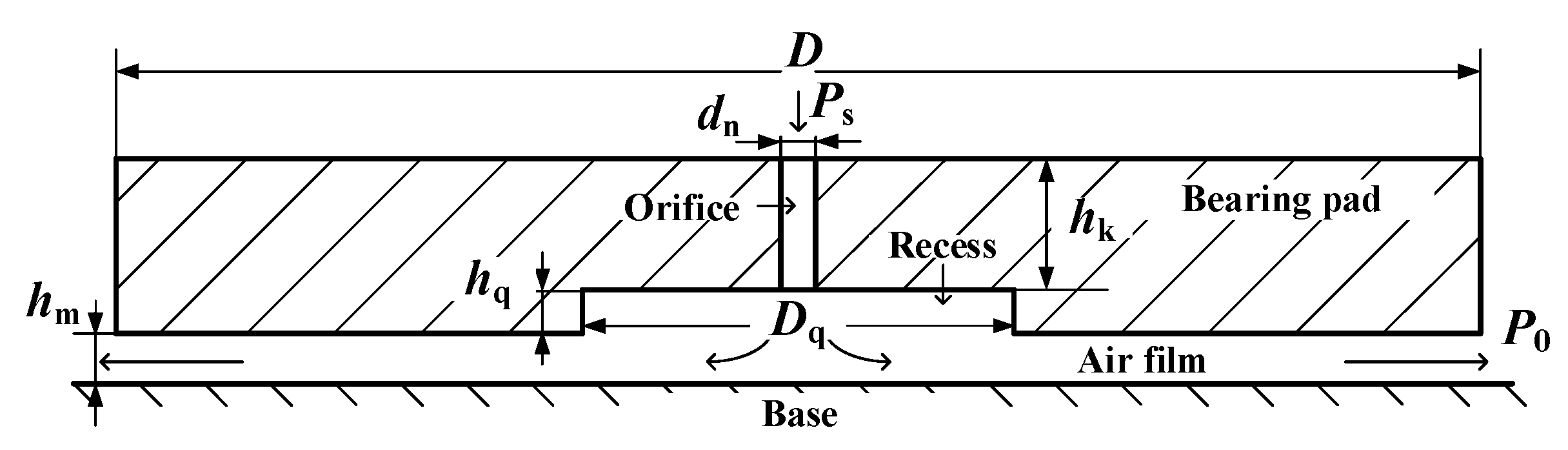
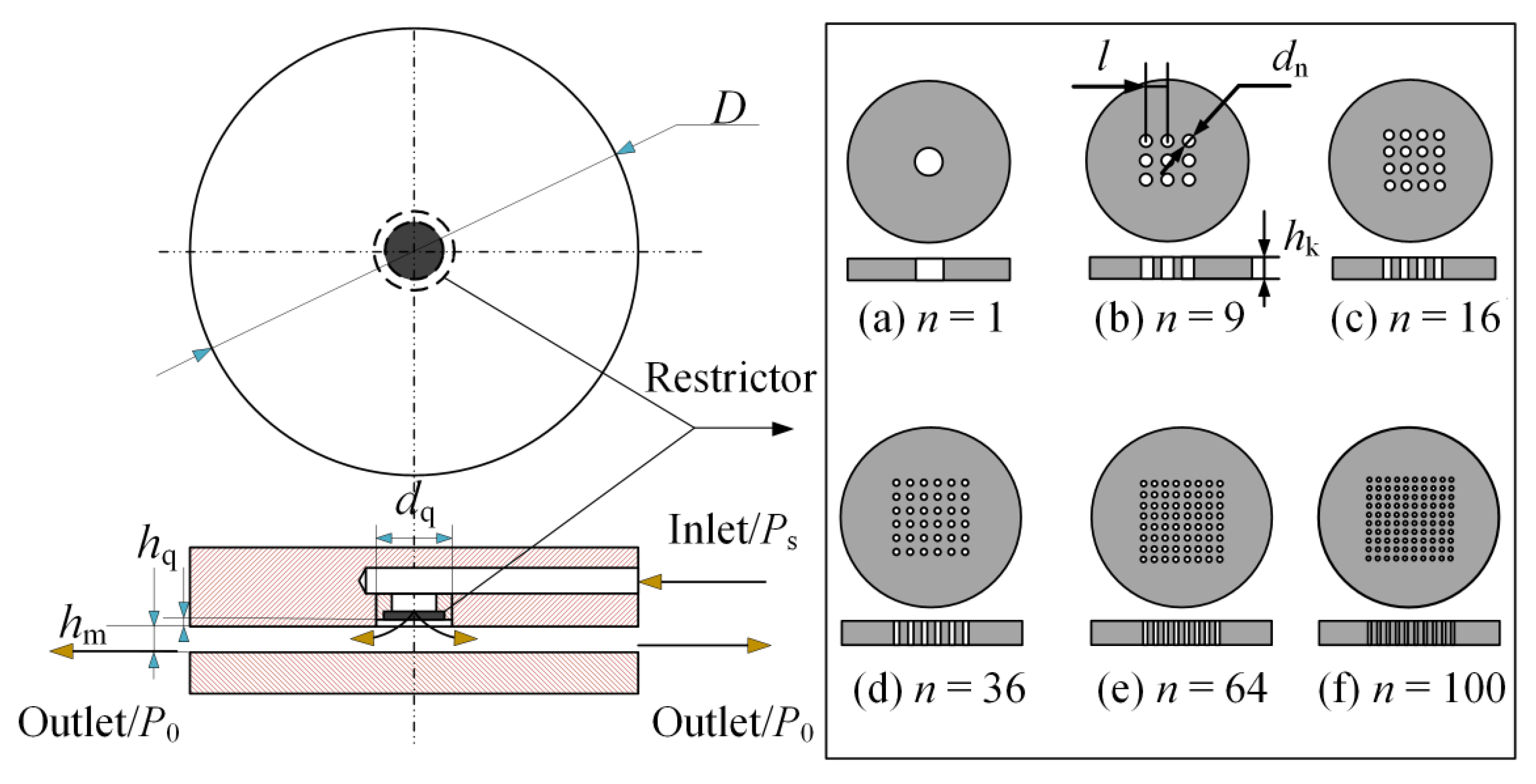
2.1. Design of Aerostatic Bearing with a SMAR
2.2. LES
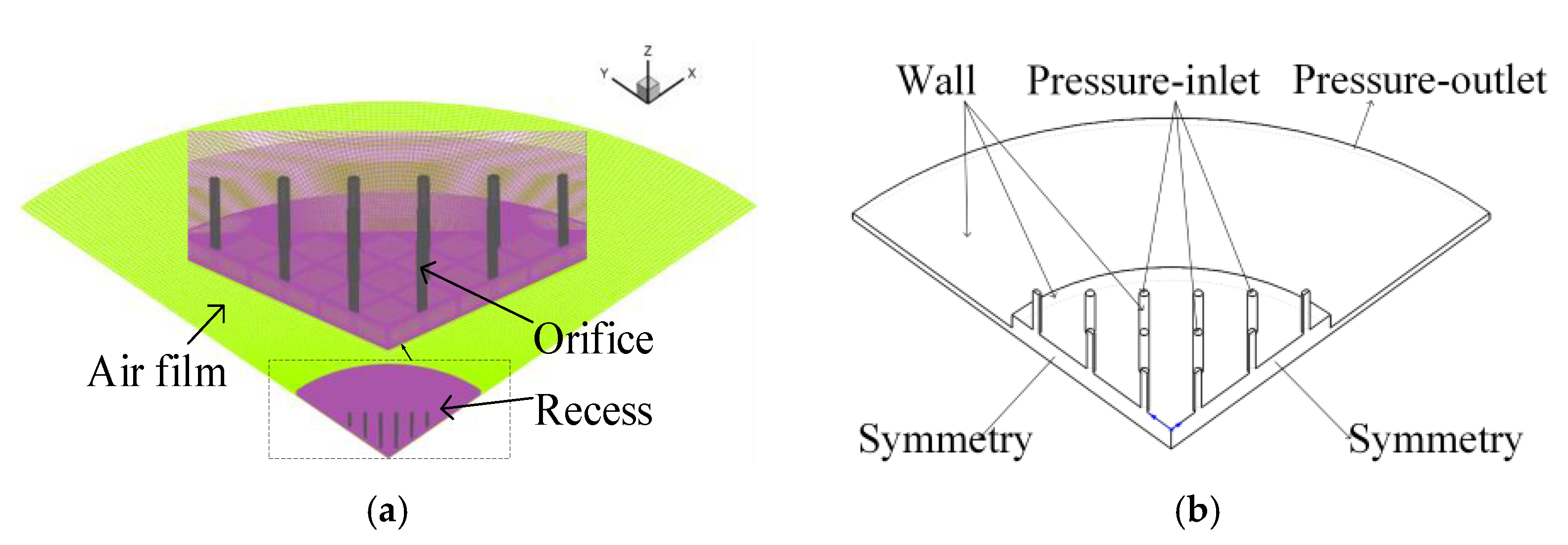
2.3. Computational Mesh and Solution Set
3. Results and Discussion
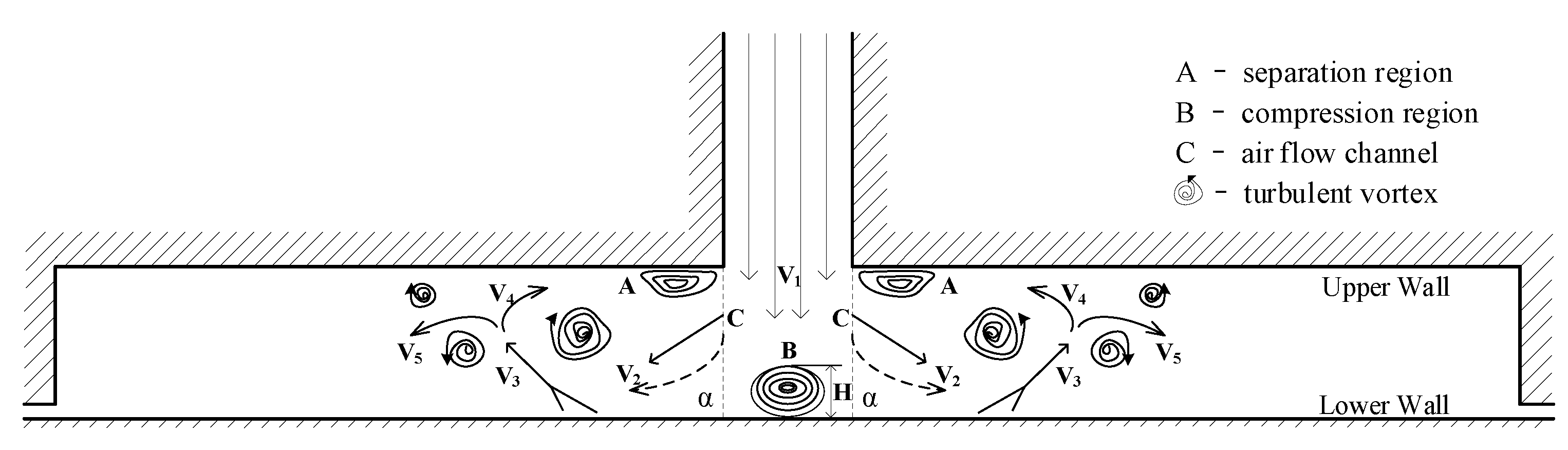
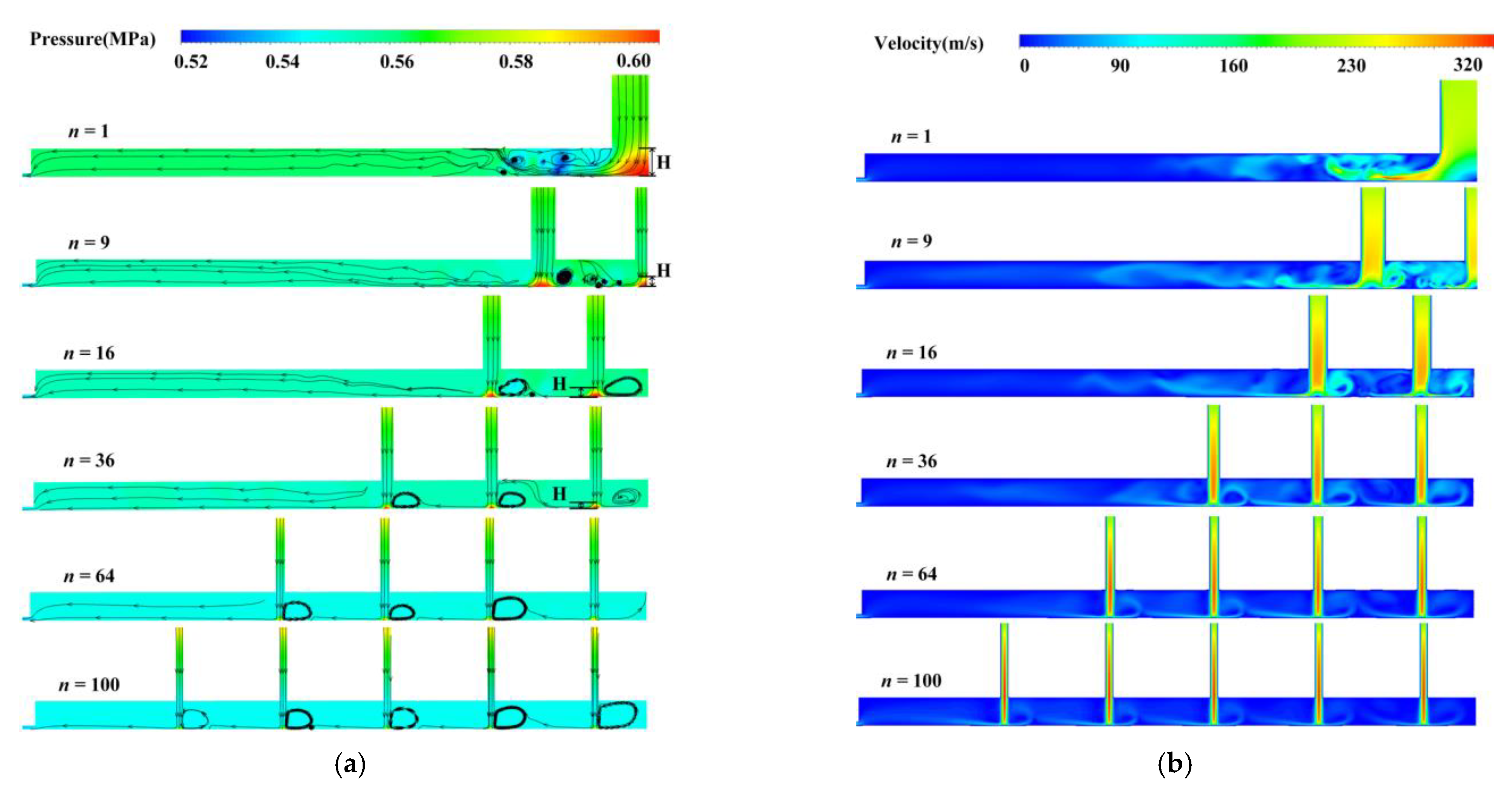
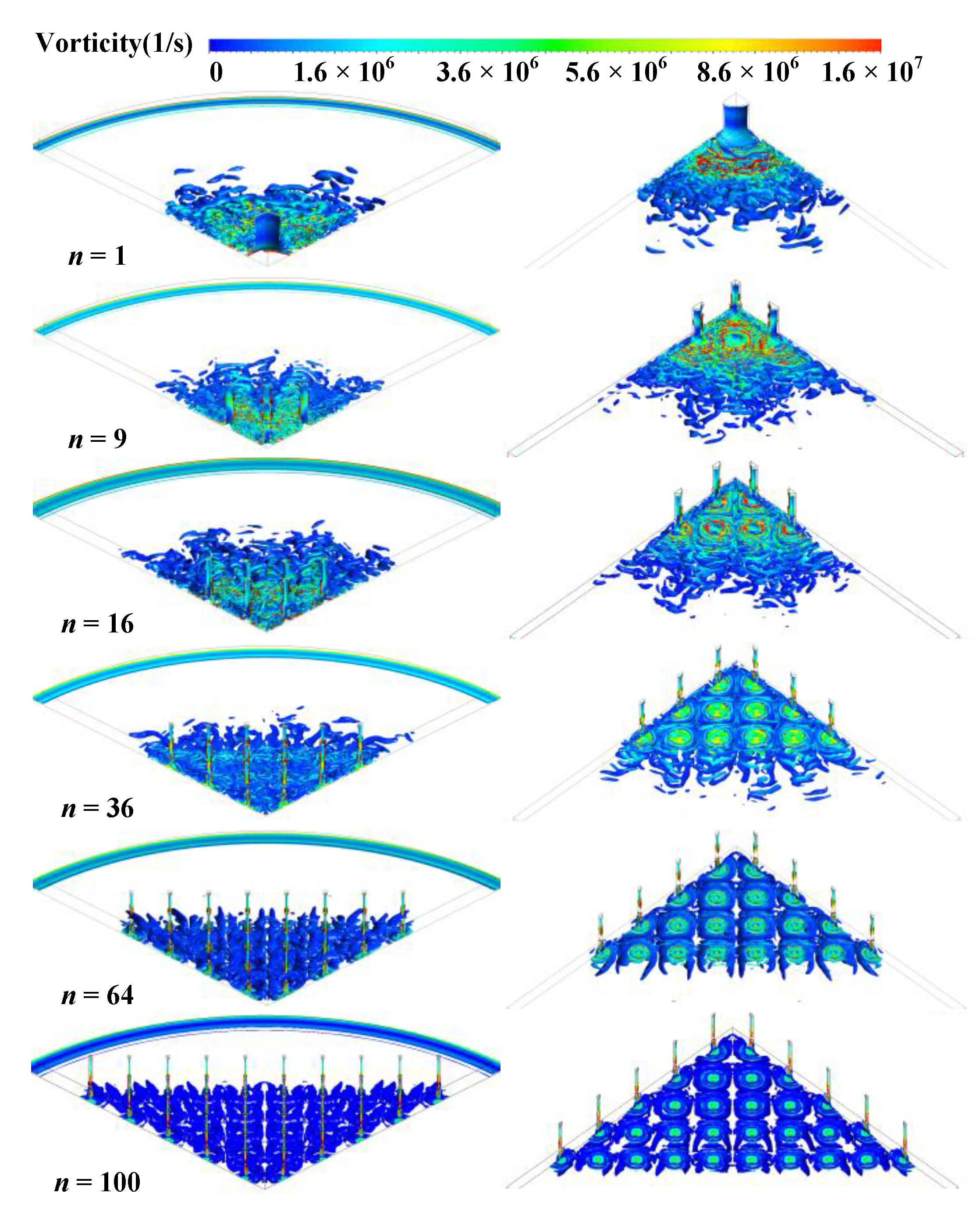
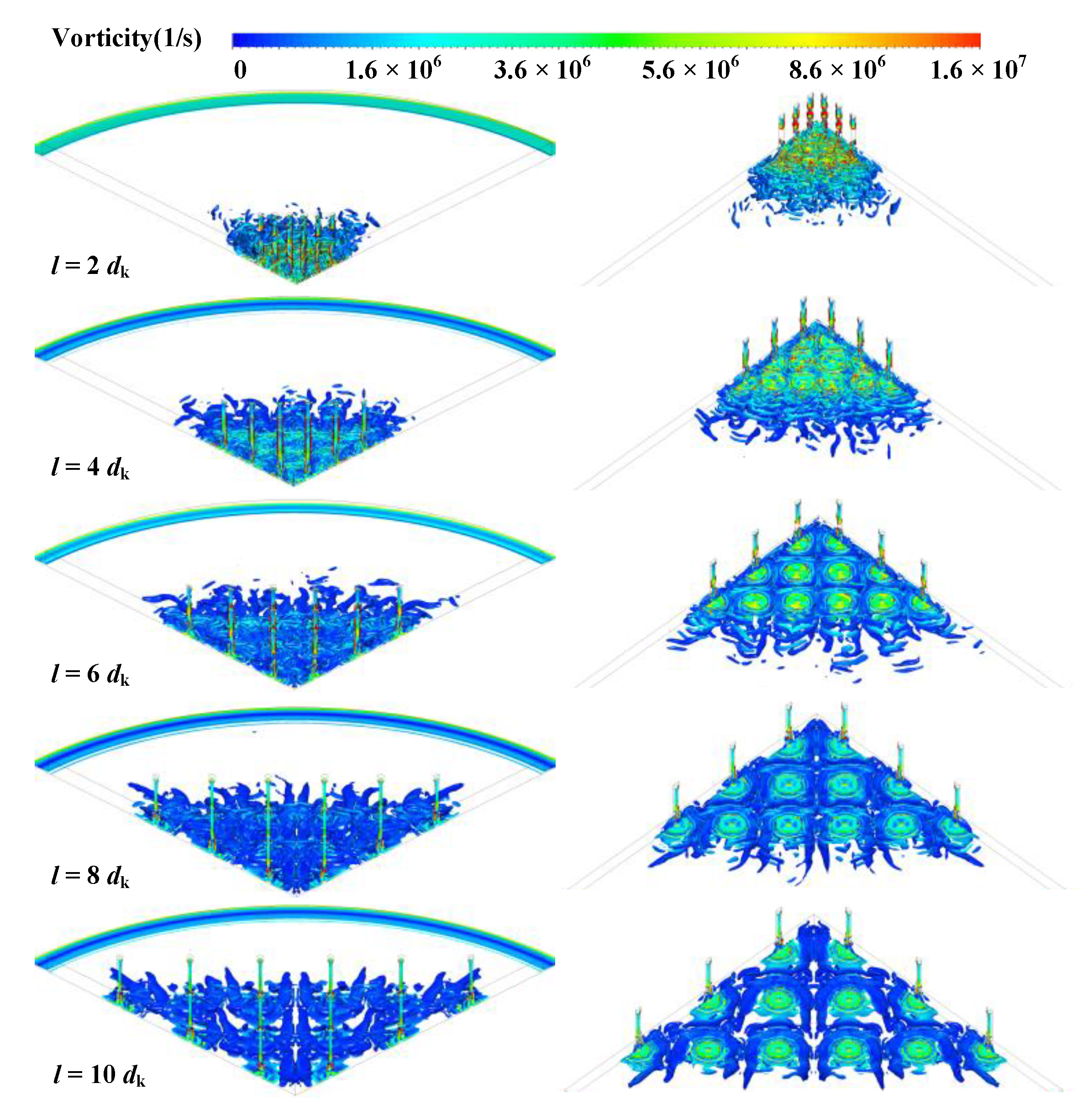
3.1. Turbulent Vortex Formation Mechanism
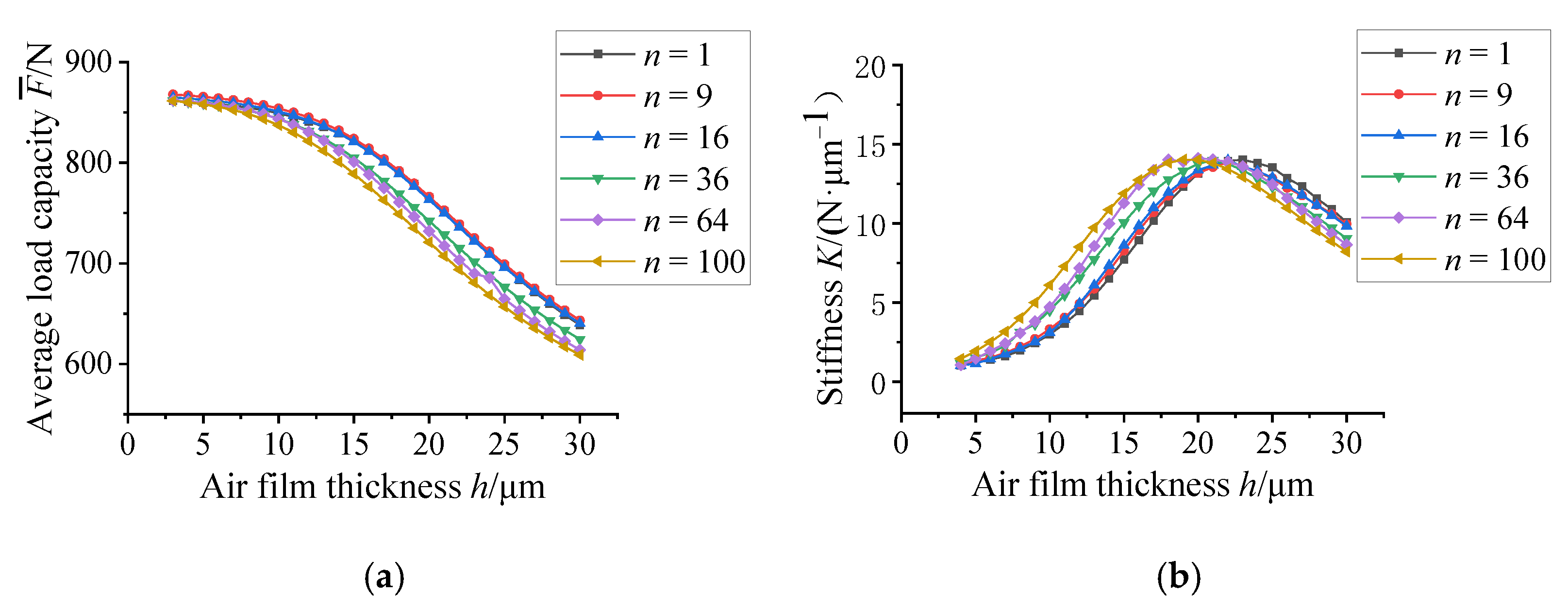
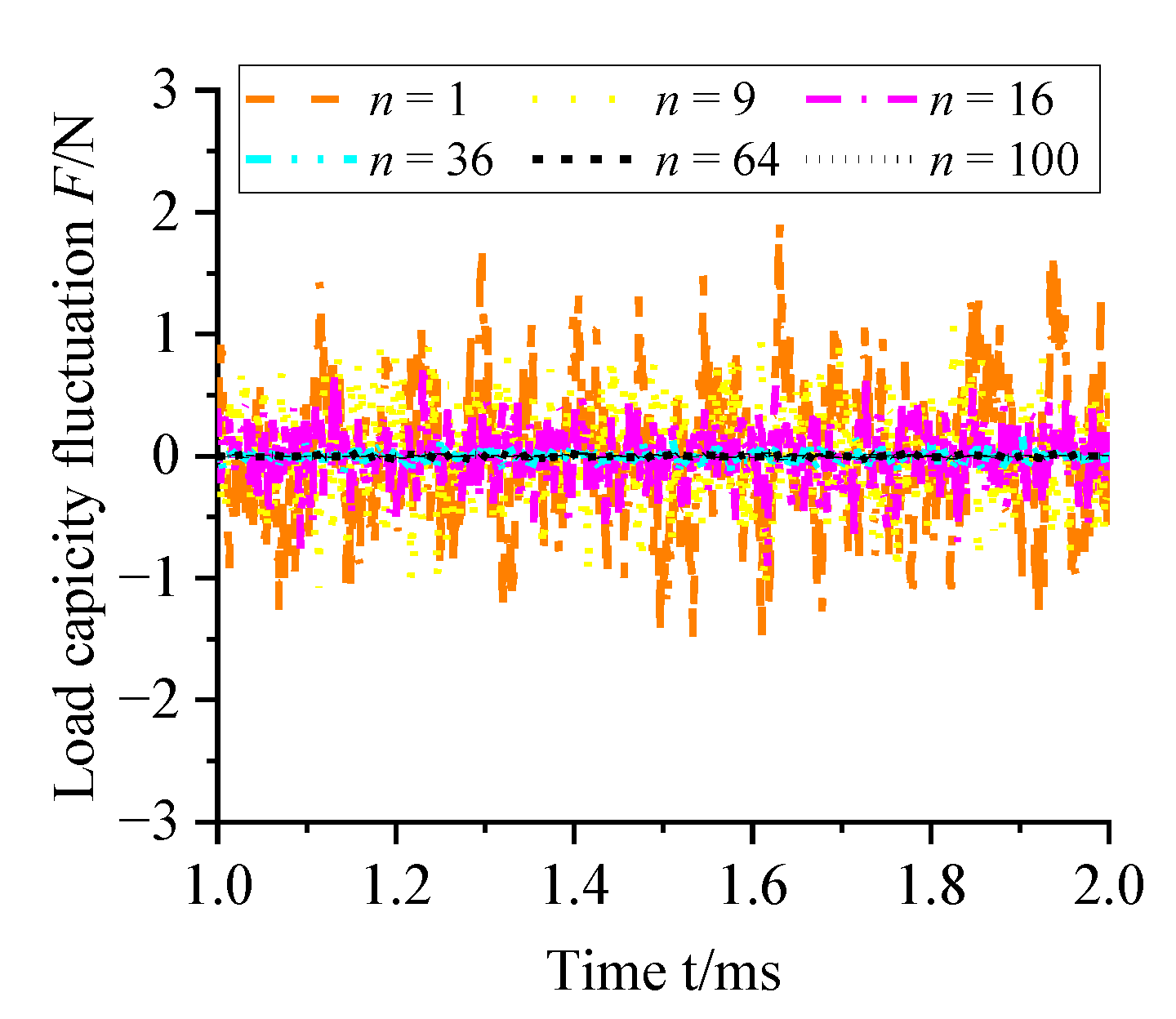
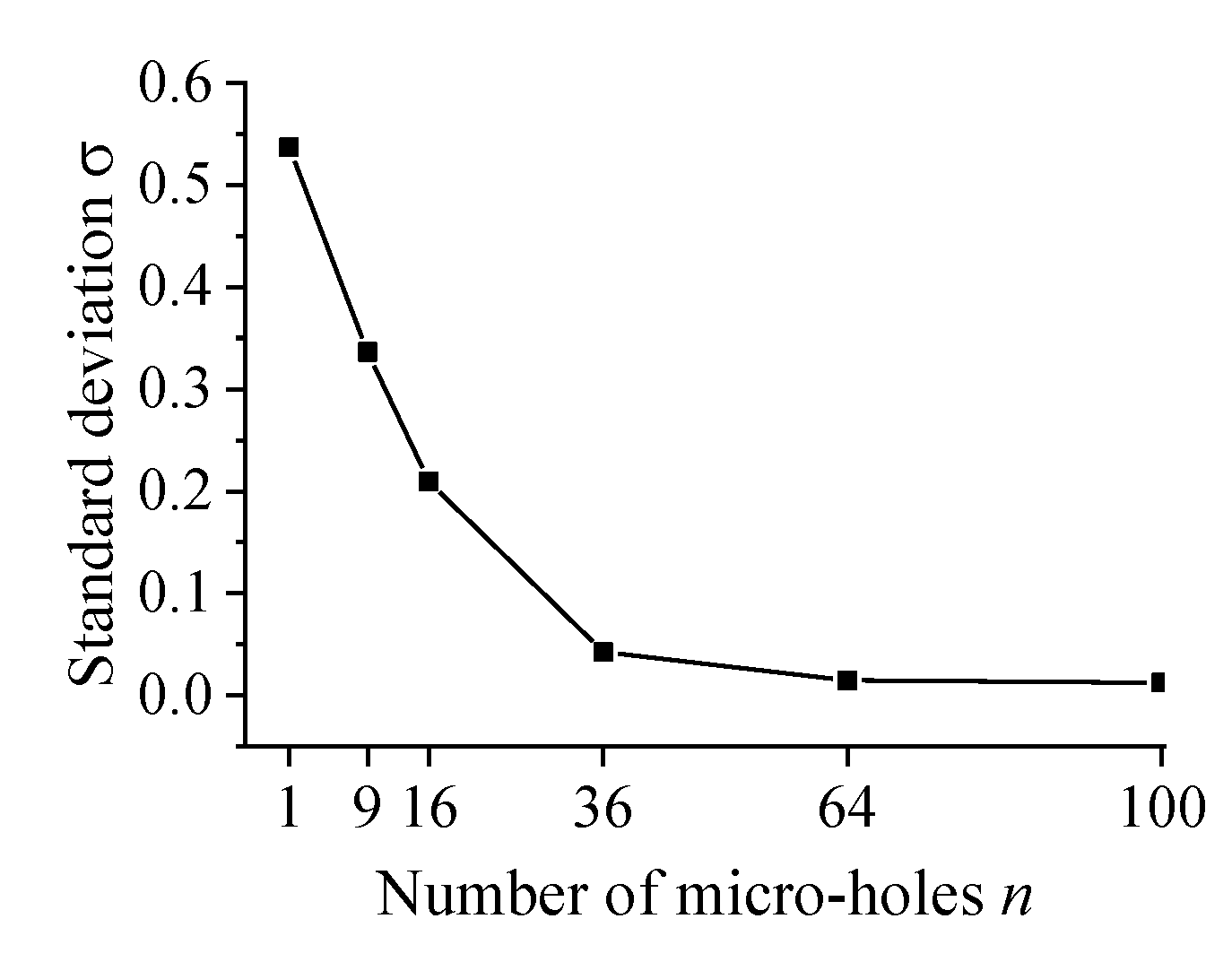
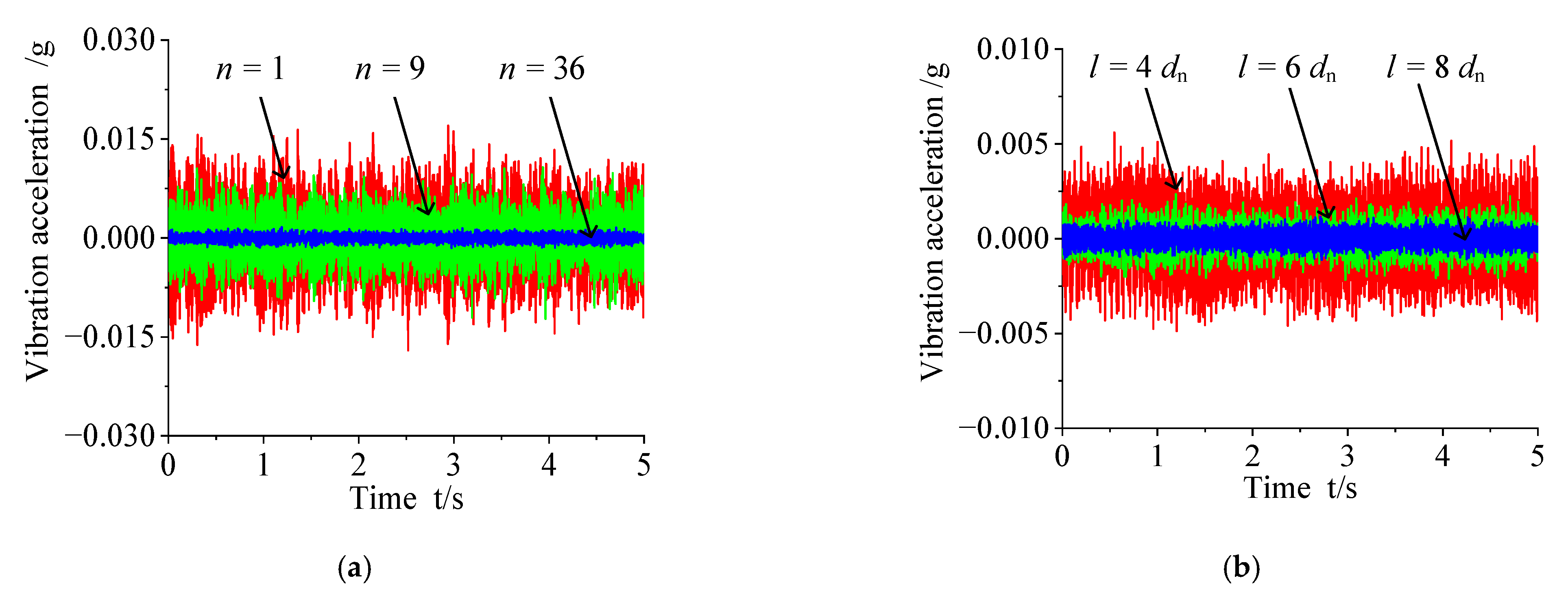
3.2. Effect of the Different Numbers of Micro-Holes on Micro-Vibration Characteristics
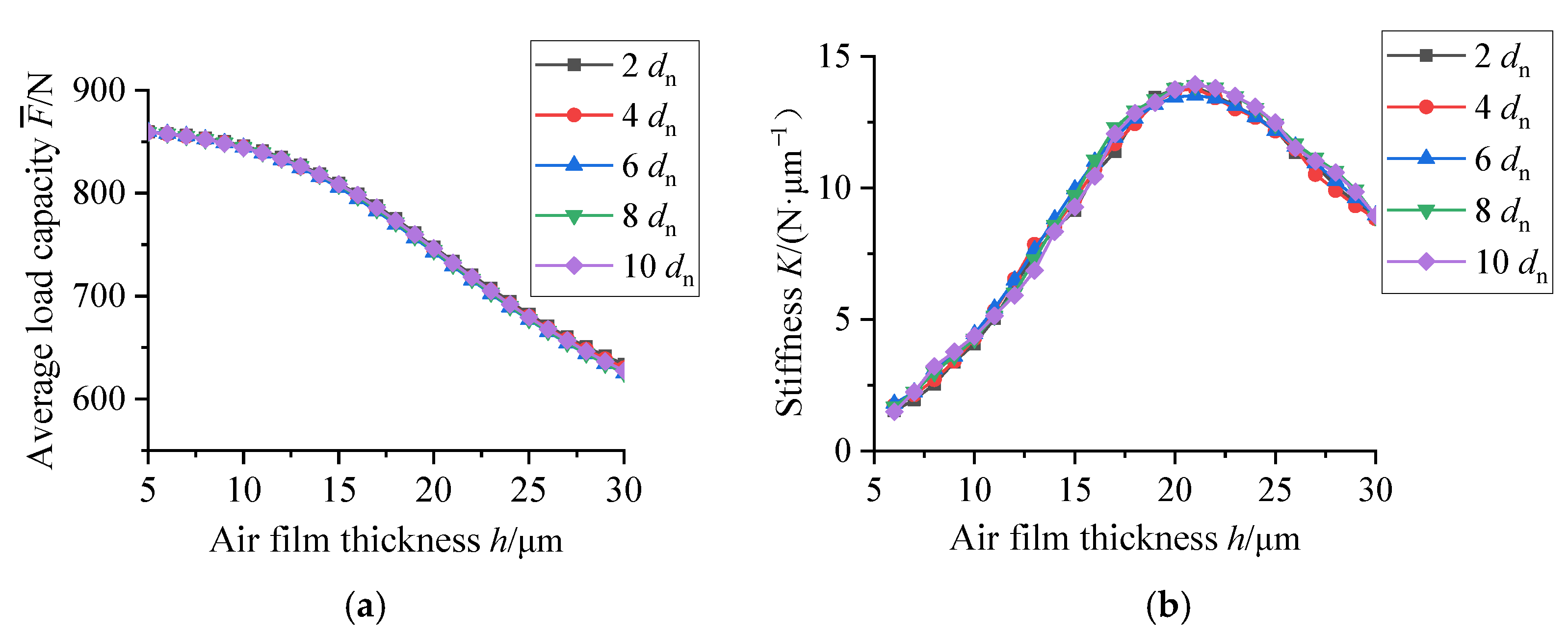
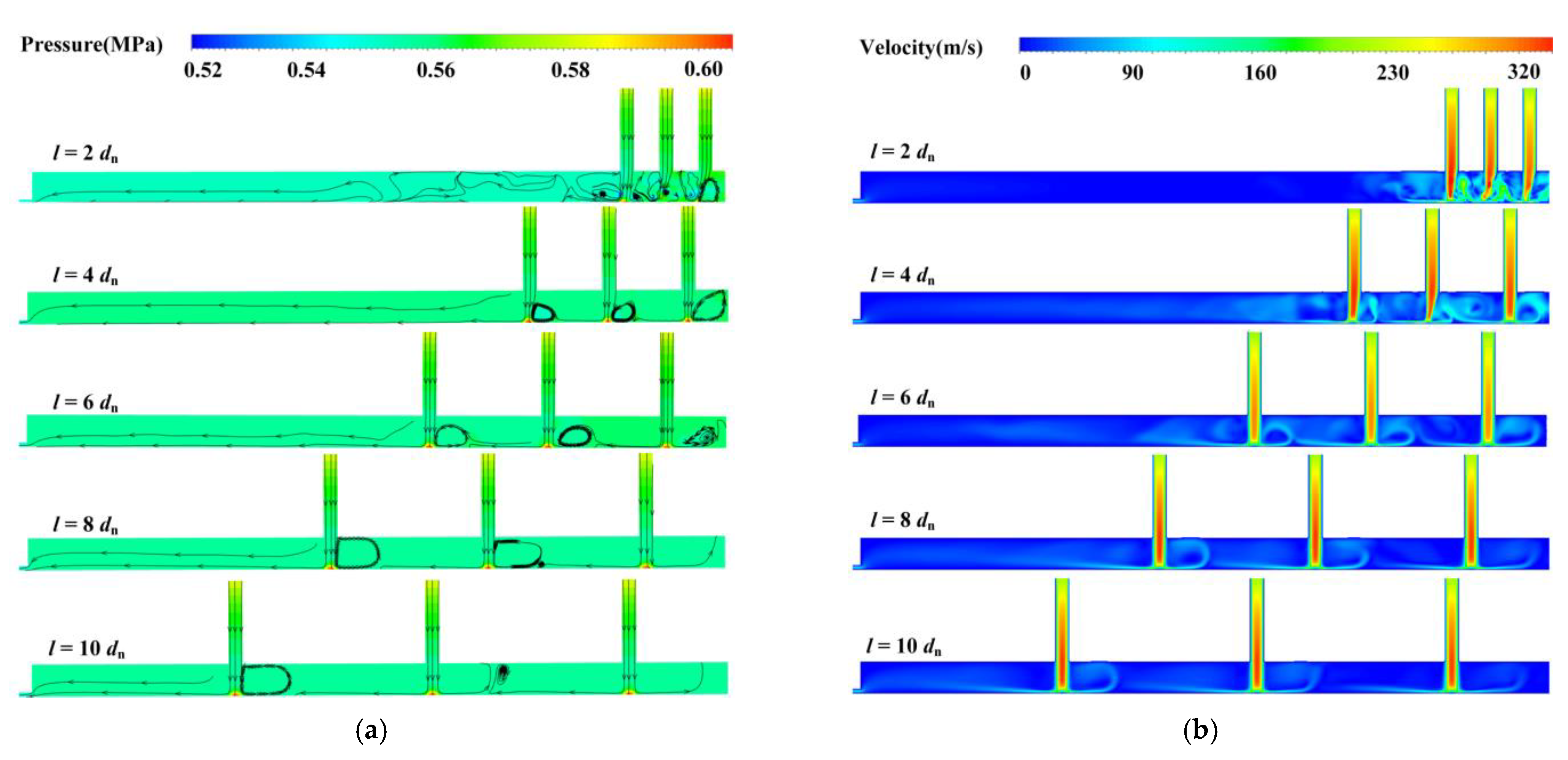
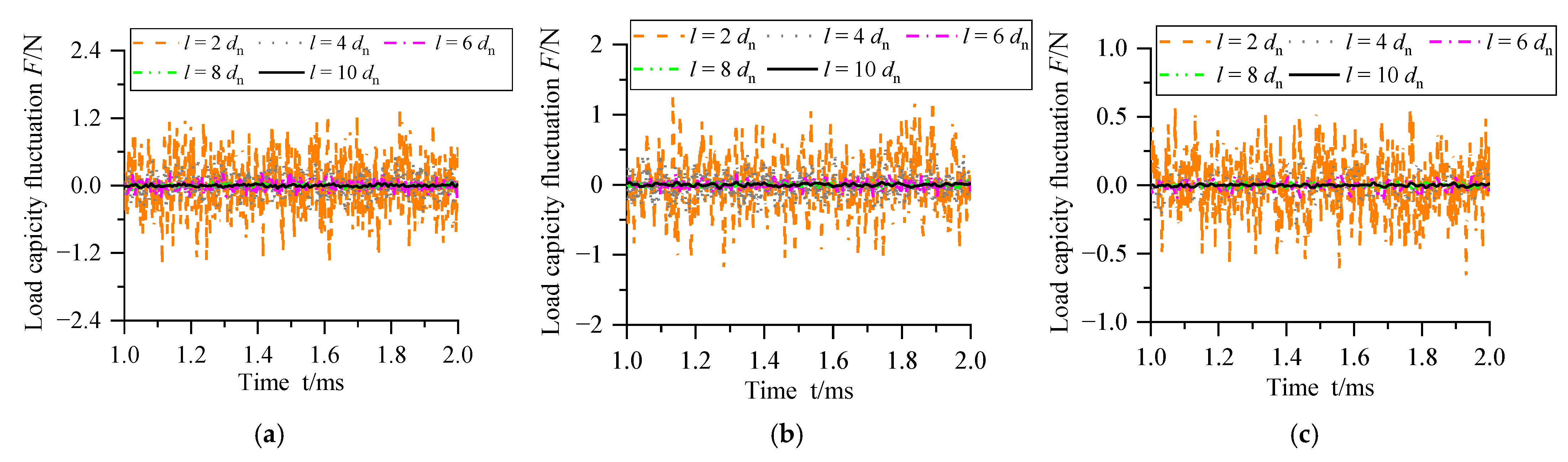
3.3. Effect of the Spacing of Micro-Holes Variation on Micro-Vibration Characteristics
4. Experimental Research
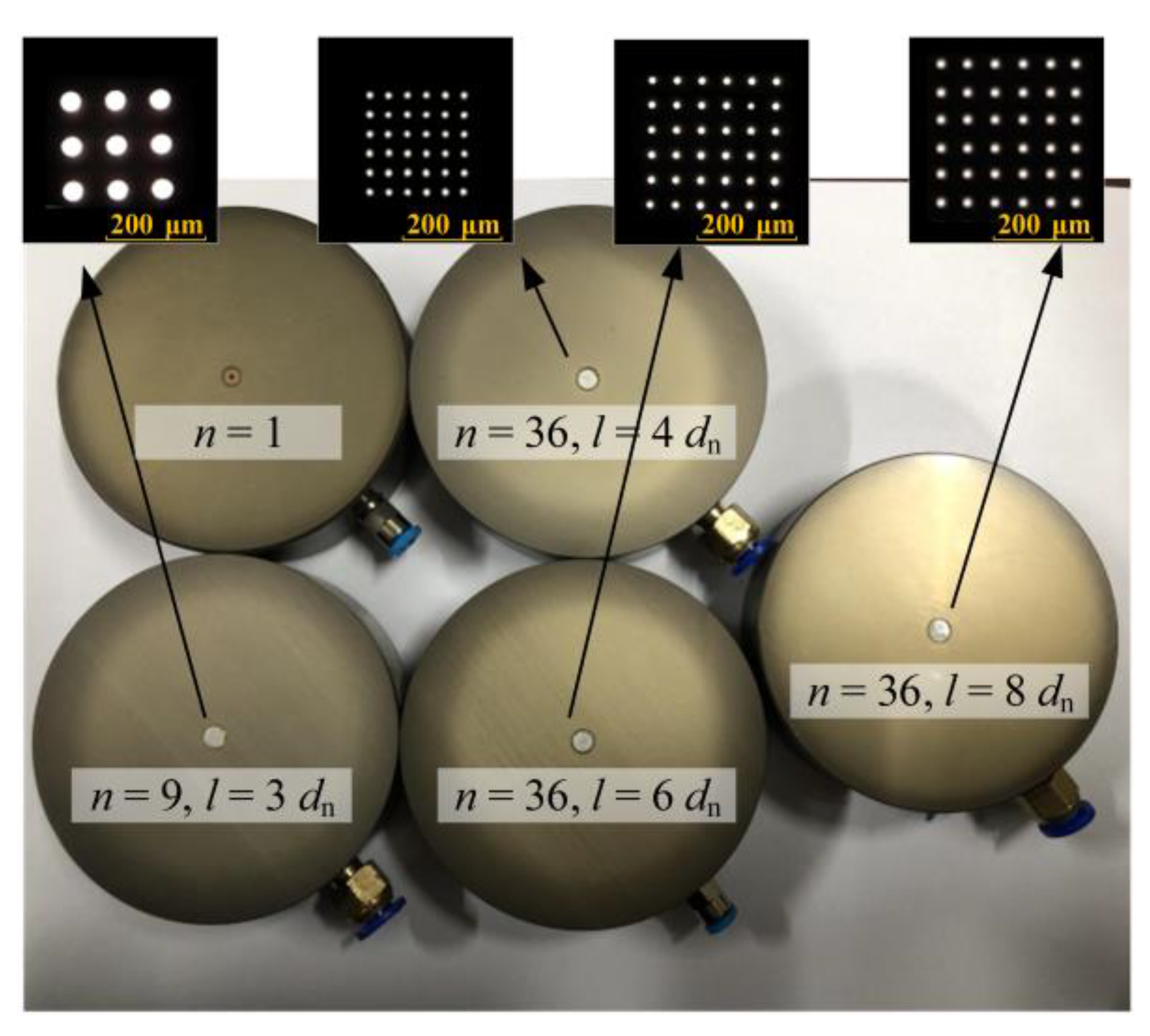
4.1. Manufacturing the Aerostatic Bearing with a SMAR
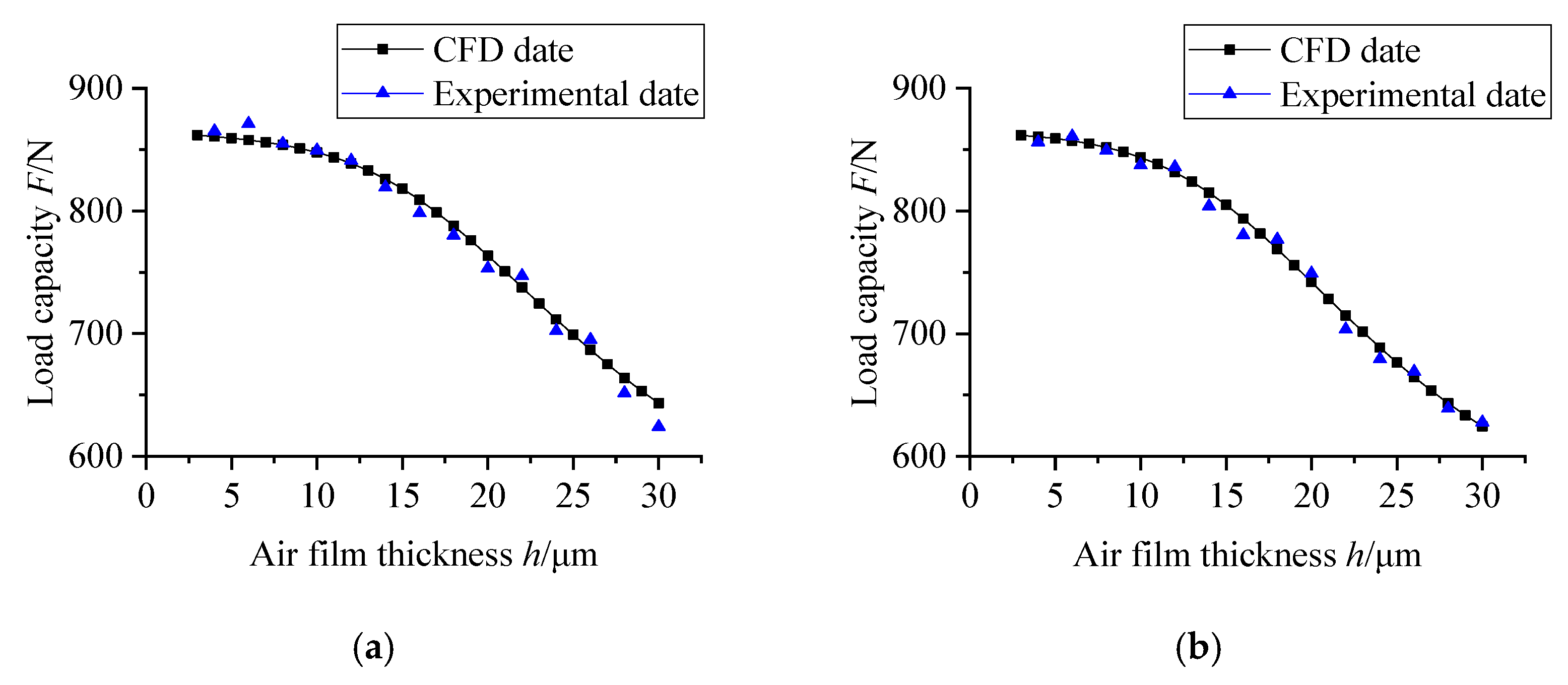
4.2. Load Capacity Testing
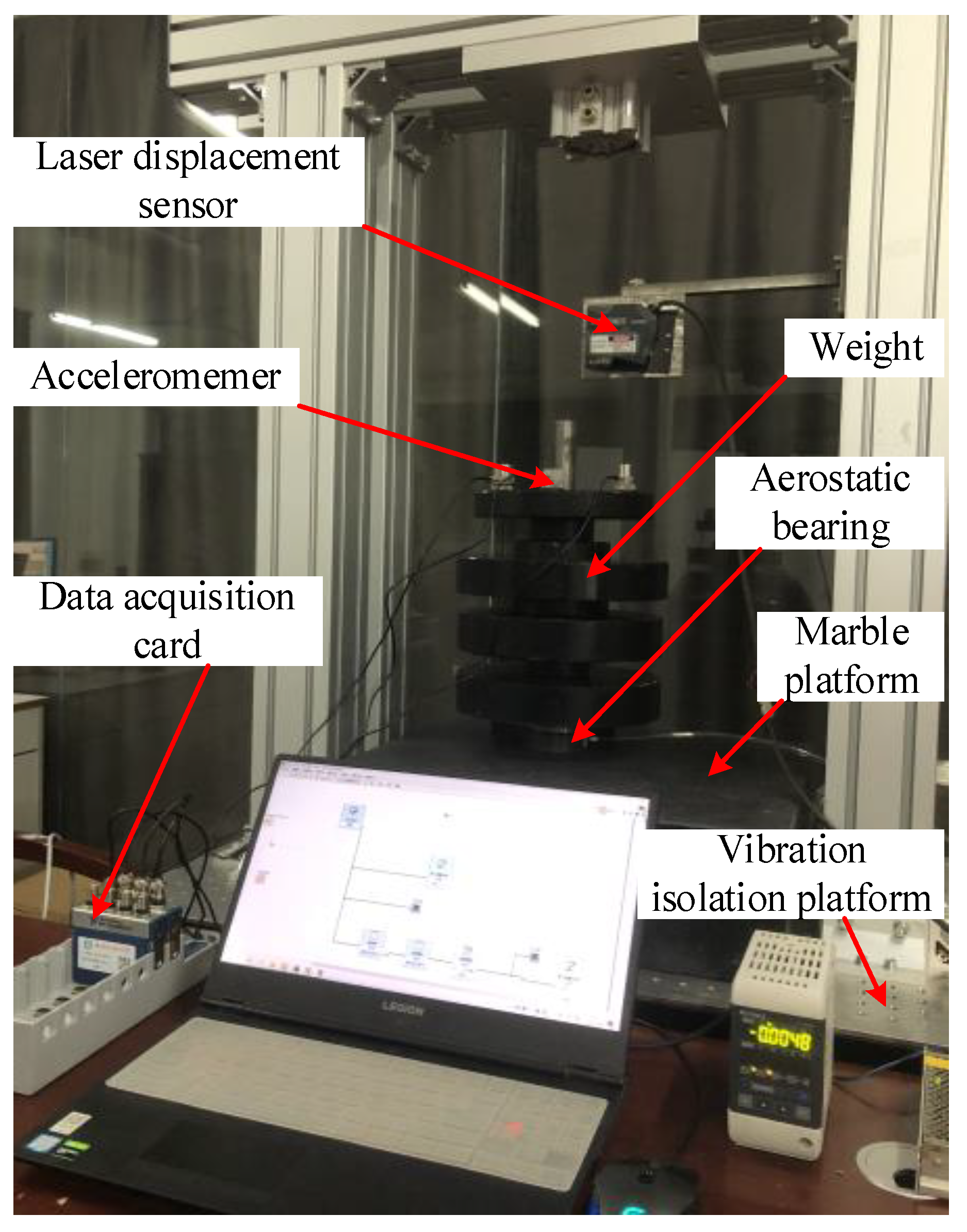
4.3. Micro-Vibration Testing
5. Conclusions
- (1)
- The aerostatic bearing with the SMAR can effectively reduce the micro-vibration characteristics by optimizing the structural parameters, while the load capacity and stiffness basically keep constant when the SMAR keeps essentially the same total restriction area.
- (2)
- Increasing the number of micro-holes can suppress the formation of turbulent vortices near the orifice by reducing the deflection angle α of the airflow and the range of the compression region B. When the number of micro-holes is less than 36, the micro-vibration of the aerostatic bearing decrease remarkably with the increase in the number of micro-holes. When the number of micro-holes is more than 36, the micro-vibration of the aerostatic bearing decreases insignificantly with the increase in the number of micro-holes. However, the micro-hole number should be carefully chosen in optimization design, because of manufacturing cost and possible blockage of the micro-hole.
- (3)
- Increasing the spacing of micro-holes can inhibit the formation of turbulent vortices among the adjacent micro-holes by reducing the interaction of the different airflows from different micro-holes. When the spacing of micro-holes is less than 8dn, the micro-vibration of the aerostatic bearing decreases remarkably with the increase in the spacing of micro-holes. When the spacing of micro-holes is more than 8dn, the micro-vibration of the aerostatic bearing decrease insignificantly with the increase in the spacing of micro-holes. In the optimization design, the larger spacing of micro-holes in the restrictor should be selected to ensure a better micro-vibration suppression effect.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maamari, N.; Krebs, A.; Weikert, S.; Wild, H.; Wegener, K. Stability and dynamics of an orifice based aerostatic bearing with a compliant back plate. Tribol. Int. 2019, 138, 279–296. [Google Scholar] [CrossRef]
- Lu, Z.W.; Zhang, J.A.; Liu, B.; Huang, J. Study on the Gas Film Flow Field and its Influencing Factors at the Outlet of the Orifice of the Aerostatic Bearing. Shock Vib. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Li, W.J.; Wang, G.Q.; Feng, K.; Zhang, Y.C.; Wang, P. CFD-based investigation and experimental study on the performances of novel back-flow channel aerostatic bearings. Tribol. Int. 2022, 165, 107319. [Google Scholar] [CrossRef]
- Otsu, Y.; Somaya, K.; Yoshimoto, S. High-speed stability of a rigid rotor supported by aerostatic journal bearings with compound restrictors. Tribol. Int. 2011, 44, 9–17. [Google Scholar] [CrossRef]
- Gao, Q.; Chen, W.Q.; Lu, L.H.; Huo, D.H.; Cheng, K. Aerostatic bearings design and analysis with the application to precision engineering: State-of-the-art and future perspectives. Tribol. Int. 2019, 135, 1–17. [Google Scholar] [CrossRef]
- Liu, Z.F.; Wang, Y.M.; Cai, L.G.; Zhao, Y.S.; Cheng, Q.; Dong, X.M. A review of hydrostatic bearing system: Researches and applications. Adv. Mech. Eng. 2017, 9, 1–27. [Google Scholar] [CrossRef]
- Chen, Y.S.; Chiu, C.C.; Cheng, Y.D. Influences of operational conditions and geometric parameters on the stiffness of aerostatic journal bearings. Precis. Eng. 2010, 34, 722–734. [Google Scholar] [CrossRef]
- Zheng, Y.Q.; Yang, G.W.; Cui, H.L.; Hou, Y. Pneumatic stability analysis of single-pad aerostatic thrust bearing with pocketed orifice. P. I. Mech. Eng. J-J. Eng. 2019, 234, 1857–1866. [Google Scholar] [CrossRef]
- Wen, Z.P.; Wu, J.W.; Tan, J.B. An adaptive modeling method for multi-throttle aerostatic thrust bearing. Tribol. Int. 2020, 149, 105830. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Chen, X.D.; Chen, H. A hybrid approach to the numerical solution of air flow field in aerostatic thrust bearings. Tribol. Int. 2016, 102, 444–453. [Google Scholar] [CrossRef]
- Kawai, T.; Ebihara, K.; Takeuchi, Y. Improvement of Machining Accuracy of 5-Axis Control Ultraprecision Machining by Means of Laminarization and Mirror Surface Finishing. CIRP Ann. 2005, 54, 329–332. [Google Scholar] [CrossRef]
- Yoshimura, T.; Hanafusa, T.; Kitagawa, T.; Hirayama, T.; Matsuoka, T.; Yabe, H. Clarifications of the mechanism of nano-fluctuation of aerostatic thrust bearing with surface restriction. Tribol. Int. 2012, 48, 29–34. [Google Scholar] [CrossRef]
- Chen, X.D.; He, X.M. The effect of the recess shape on performance analysis of the gas-lubricated bearing in optical lithography. Tribol. Int. 2006, 39, 1336–1341. [Google Scholar] [CrossRef]
- Li, Y.F.; Yin, Y.H.; Yang, H.; En, L.X.; Mo, J.; Cui, H.L. Modeling for optimization of circular flat pad aerostatic bearing with a single central orifice-type restrictor based on CFD simulation. Tribol. Int. 2017, 109, 206–216. [Google Scholar]
- Zhu, J.C.; Chen, H.; Chen, X.D. Large eddy simulation of vortex shedding and pressure fluctuation in aerostatic bearings. J. Fluid Struct. 2013, 40, 42–51. [Google Scholar] [CrossRef]
- Aoyama, T.; Kakinuma, Y.; Kobayashi, Y. Numerical and Experimental Analysis for the Small Vibration of Aerostatic Guideways. CIRP Ann. 2006, 55, 419–422. [Google Scholar] [CrossRef]
- Gao, S.Y.; Cheng, K.; Chen, S.J.; Ding, H.; Fu, H.Y. CFD based investigation on influence of orifice chamber shapes for the design of aerostatic thrust bearings at ultra-high speed spindles. Tribol. Int. 2015, 92, 211–221. [Google Scholar] [CrossRef]
- Chen, X.D.; Chen, H.; Zhu, J.C.; Jiang, W. Vortex suppression and nano-vibration reduction of aerostatic bearings by arrayed microhole restrictors. J. Vib. Control 2016, 23, 842–852. [Google Scholar] [CrossRef]
- Feng, K.; Wang, P.; Zhang, Y.J.; Hou, W.J.; Li, W.J.; Wang, J.W.; Cui, H.L. Novel 3-D printed aerostatic bearings for the improvement of stability: Theoretical predictions and experimental measurements. Tribol. Int. 2021, 163, 107149. [Google Scholar] [CrossRef]
- Lentini, L.; Moradi, M.; Colombo, F. A Historical Review of Gas Lubrication: From Reynolds to Active Compensations. Tribol. Ind. 2018, 40, 165–182. [Google Scholar] [CrossRef][Green Version]
- Eleshaky, M.E. CFD investigation of pressure depressions in aerostatic circular thrust bearings. Tribol. Int. 2009, 42, 1108–1117. [Google Scholar] [CrossRef]
- Gao, W.; Arai, Y.; Shibuya, A.; Kiyono, S.; Park, C.H. Measurement of multi-degree-of-freedom error motions of a precision linear air-bearing stage. Precis. Eng. 2006, 30, 96–103. [Google Scholar] [CrossRef]
- Li, L.Q.; Lou, J.L.; Nishikawa, H.; Luo, H. Reconstructed discontinuous Galerkin methods for compressible flows based on a new hyperbolic Navier-Stokes system. J. Comput. Phys. 2021, 427, 110058. [Google Scholar] [CrossRef]
- Li, L.Q.; Lou, J.L.; Luo, H.; Nishikawa, H. High-Order Hyperbolic Navier-Stokes Reconstructed Discontinuous Galerkin Method. In Proceedings of the AIAA Scitech 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Kabir, H.; Aghdam, M.M. A robust Bézier based solution for nonlinear vibration and post-buckling of random checkerboard graphene nano-platelets reinforced composite beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A generalized 2D Bézier-based solution for stress analysis of notched epoxy resin plates reinforced with graphene nanoplatelets. Thin Wall Struct. 2021, 169, 108484. [Google Scholar] [CrossRef]
- Li, Y.T.; Zhao, J.Y.; Zhu, H.X.; Lin, Y.X. Numerical analysis and experimental study on the microvibration of an aerostatic thrust bearing with a pocketed orifice-type restrictor. Proc. Inst. Mech. Eng. J. Eng. Tribol. 2014, 229, 609–623. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modeling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 2002, 34, 349–374. [Google Scholar]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Ann. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Zhu, J.C.; Chen, H.; Chen, X.D. Numerical Simulation of the Turbulent Flow in Ultra-Precision Aerostatic Bearings. Adv. Mat. Res. 2013, 680, 417–421. [Google Scholar] [CrossRef]



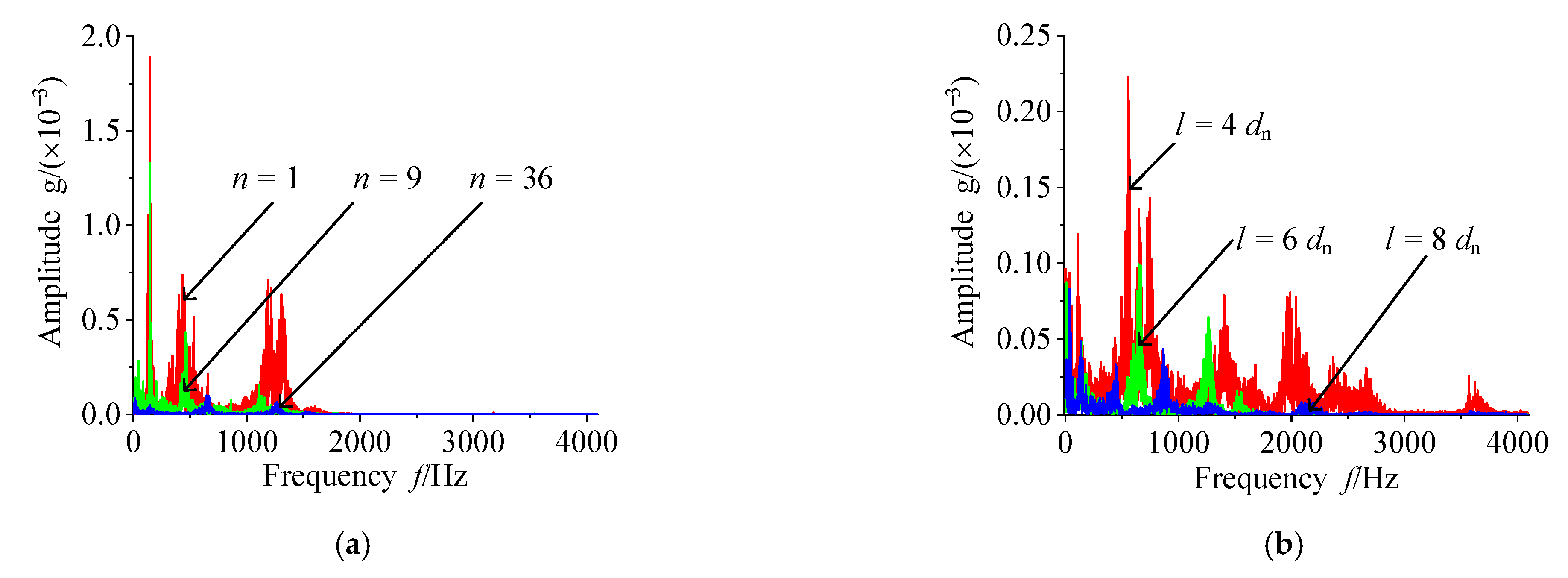
| Parameter Variables | Value | |||||
|---|---|---|---|---|---|---|
| Number of micro-holes n | 1 | 9 | 16 | 36 | 64 | 100 |
| Orifice diameter dn/mm | 0.3 | 0.1 | 0.075 | 0.05 | 0.0375 | 0.03 |
| spacing of micro-holes l/mm | 0.1~1.0 | |||||
| Inlet pressure Ps/MPa | 0.5~0.6 | |||||
| Air film thickness hm/μm | 5~30 | |||||
| Outlet pressure P0/MPa | 0.1 | |||||
| Mesh | Recess | Orifice | Air film | Total Number | Fluctuations of Load Capacity F(N) | Standard Deviation σ | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| δmin | δmax | δmin | δmax | δmin | δmax | |||||
| Coarse | 1.26 | 1590 | 30.25 | 103.15 | 1267 | 9825 | 1.6 | 2084581 | 0.38 | 0.049 |
| Fine | 0.58 | 632 | 0.7 | 3423926 | 0.39 | 0.051 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Lu, J.; Luo, Q.; Li, G.; Yin, X. Optimization Design of Aerostatic Bearings with Square Micro-Hole Arrayed Restrictor for the Improvement of Stability: Theoretical Predictions and Experimental Measurements. Lubricants 2022, 10, 295. https://doi.org/10.3390/lubricants10110295
Yu P, Lu J, Luo Q, Li G, Yin X. Optimization Design of Aerostatic Bearings with Square Micro-Hole Arrayed Restrictor for the Improvement of Stability: Theoretical Predictions and Experimental Measurements. Lubricants. 2022; 10(11):295. https://doi.org/10.3390/lubricants10110295
Chicago/Turabian StyleYu, Puliang, Jiong Lu, Qiang Luo, Guanghui Li, and Xianxiong Yin. 2022. "Optimization Design of Aerostatic Bearings with Square Micro-Hole Arrayed Restrictor for the Improvement of Stability: Theoretical Predictions and Experimental Measurements" Lubricants 10, no. 11: 295. https://doi.org/10.3390/lubricants10110295
APA StyleYu, P., Lu, J., Luo, Q., Li, G., & Yin, X. (2022). Optimization Design of Aerostatic Bearings with Square Micro-Hole Arrayed Restrictor for the Improvement of Stability: Theoretical Predictions and Experimental Measurements. Lubricants, 10(11), 295. https://doi.org/10.3390/lubricants10110295




