Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing
Abstract
1. Introduction
1.1. Research Objectives
- The creation of a numerical algorithm for the automated creation of a bearing parametrized model with recesses for lubrication of different geometries and filling schemes to solve and process the numerical solution results.
- An evaluation of the influence of recesses with a lubricant on the structure performance.
- The identification of quantitative and qualitative patterns of frictional contacts of the bearing steel elements with an anti-friction layer, taking into account the recesses with a lubricant.
1.2. Problem Context and Description
2. Materials and Methods
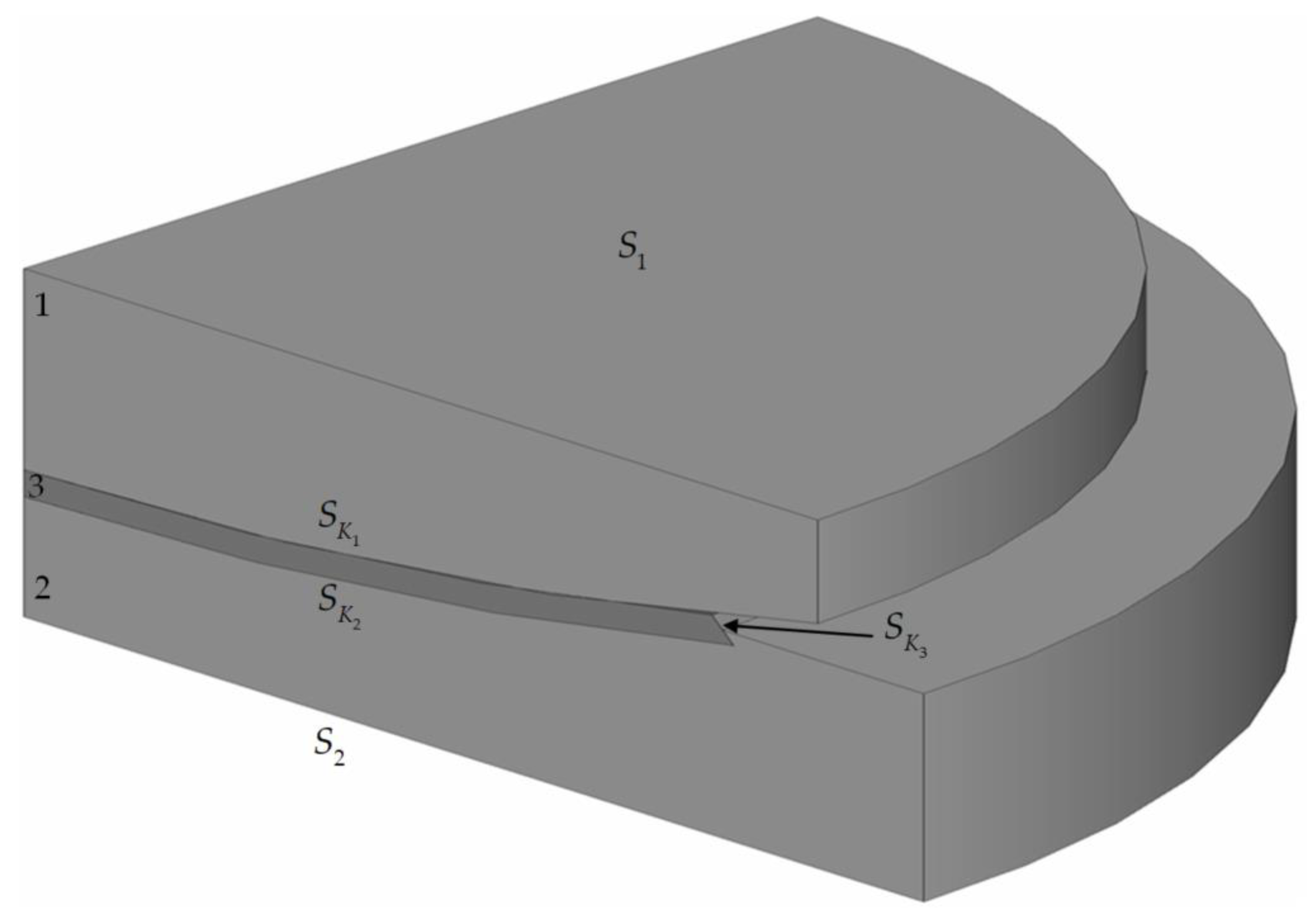
2.1. Model
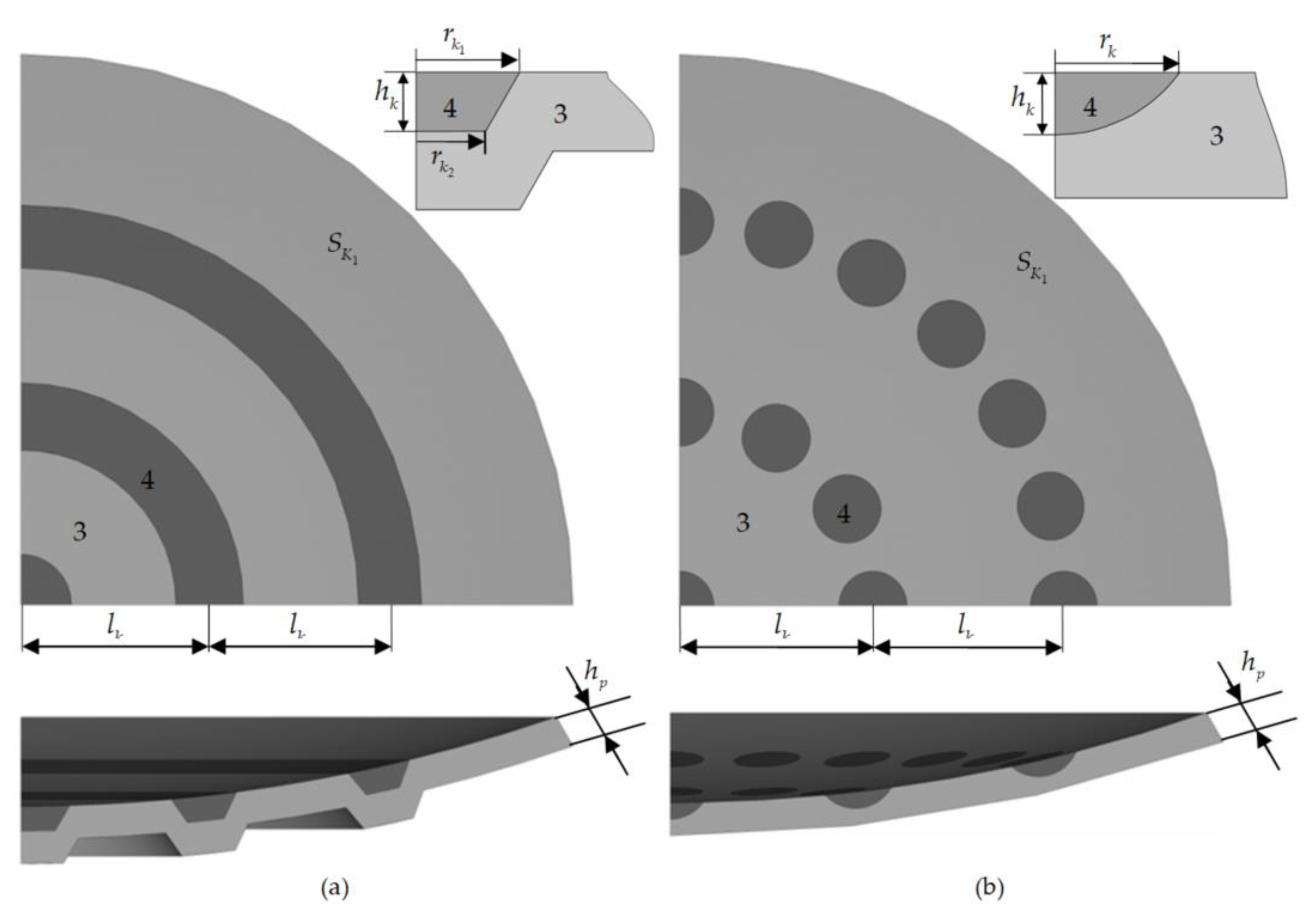
- A comparison of the contact deformation of the bearings with different geometric configurations of lubricant recesses (the annular grooves and spherical holes) using the same arrangement and number of rows of recesses in the polymer sliding layer (three rows of recesses).
- An analysis of the influence of the arrangement of the lubricant recesses on the deformation behaviour of the structure using the example of a spherical well with a constant number of three rows of recesses.
- An analysis of the influence of the arrangement of filling the anti-friction layer with lubricant recesses (a change in the number of recess rows) on the nature of the deformation of the bearing as a whole and the parameters of the contact areas in particular.
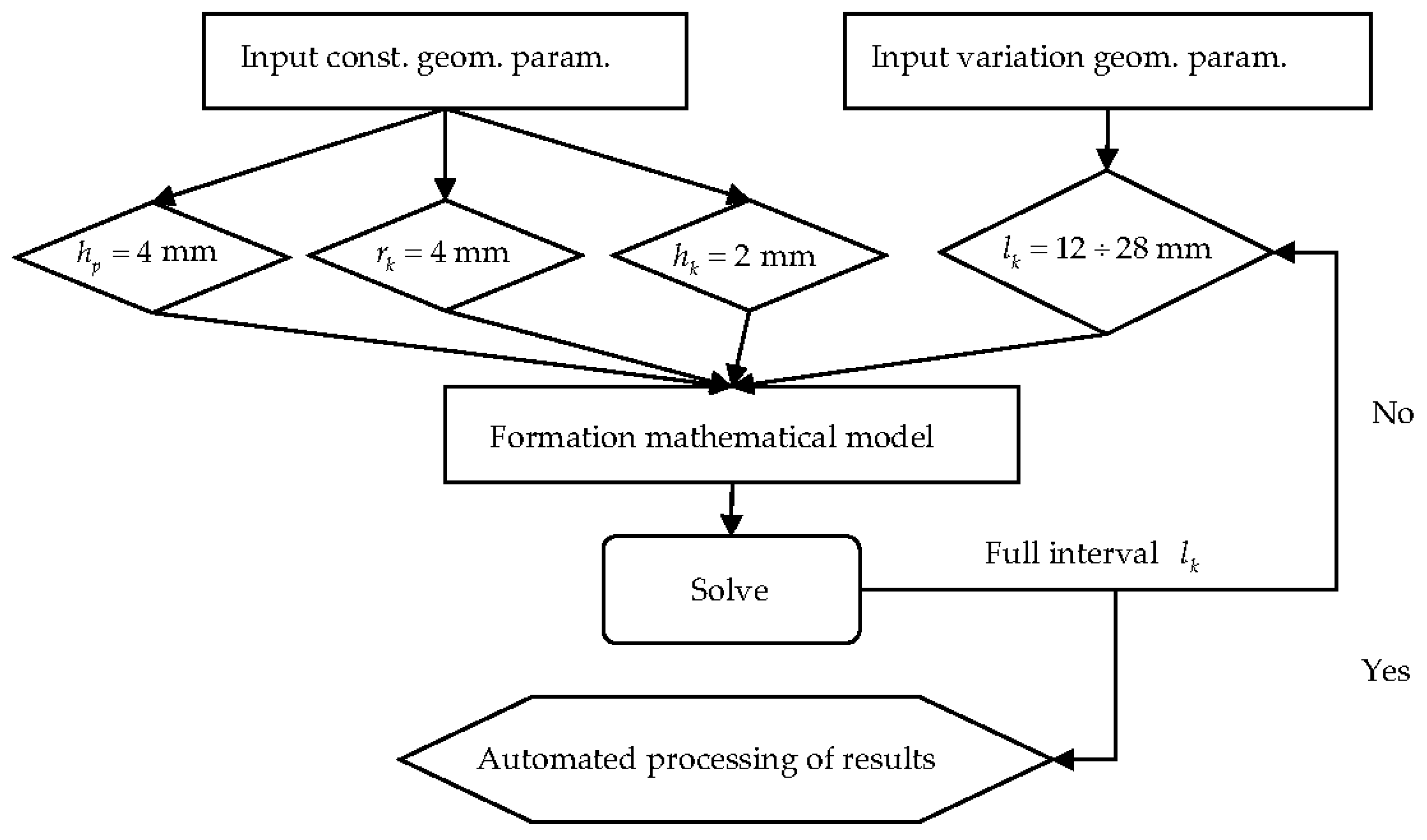
2.2. Scheme of the Computational Experiments
2.3. Materials
2.4. Finite Element Model and Contact Elements
- -
- The average contact pressure in the full adhesion areas of the contact surface was 7.3% lower on average;
- -
- The average contact tangential stress in the full adhesion areas of the contact surface was higher by 0.3–1.8 MPa;
- -
- A more uniform distribution of contact parameters across the sliding surface.
3. Discussion
3.1. Limitation Statement
- -
- A constant coefficient of friction of 0.04 was taken from the manufacturer’s data on the bridge bearings;
- -
- A simplified model of the lubricant’s behaviour as a low compressible body without viscoplasticity;
- -
- The sliding material model is, in the first approximation, elastoplastic;
- -
- A quarter of the structure was modelled so that the horizontal load of the bridge span could not be introduced into the system;
- -
- The ambient temperature was constant at 23 °C.
- -
- An analysis of the operation of the structure under experimentally obtained friction coefficients [18];
- -
- A refinement of the mathematical model of lubricant (viscoelasticity) and anti-friction (viscoelasticity) materials;
- -
- An extension of research to a wide temperature range (−60 °C to +60 °C);
- -
- The introduction of horizontal and dynamic loads;
- -
- An analysis of the influence of geometrical features of lubricant pits;
- -
- The determination of manufacturing requirements for the bridge bearing, in particular, to increase the durability of the bridge span as a whole.
3.2. About the Materials
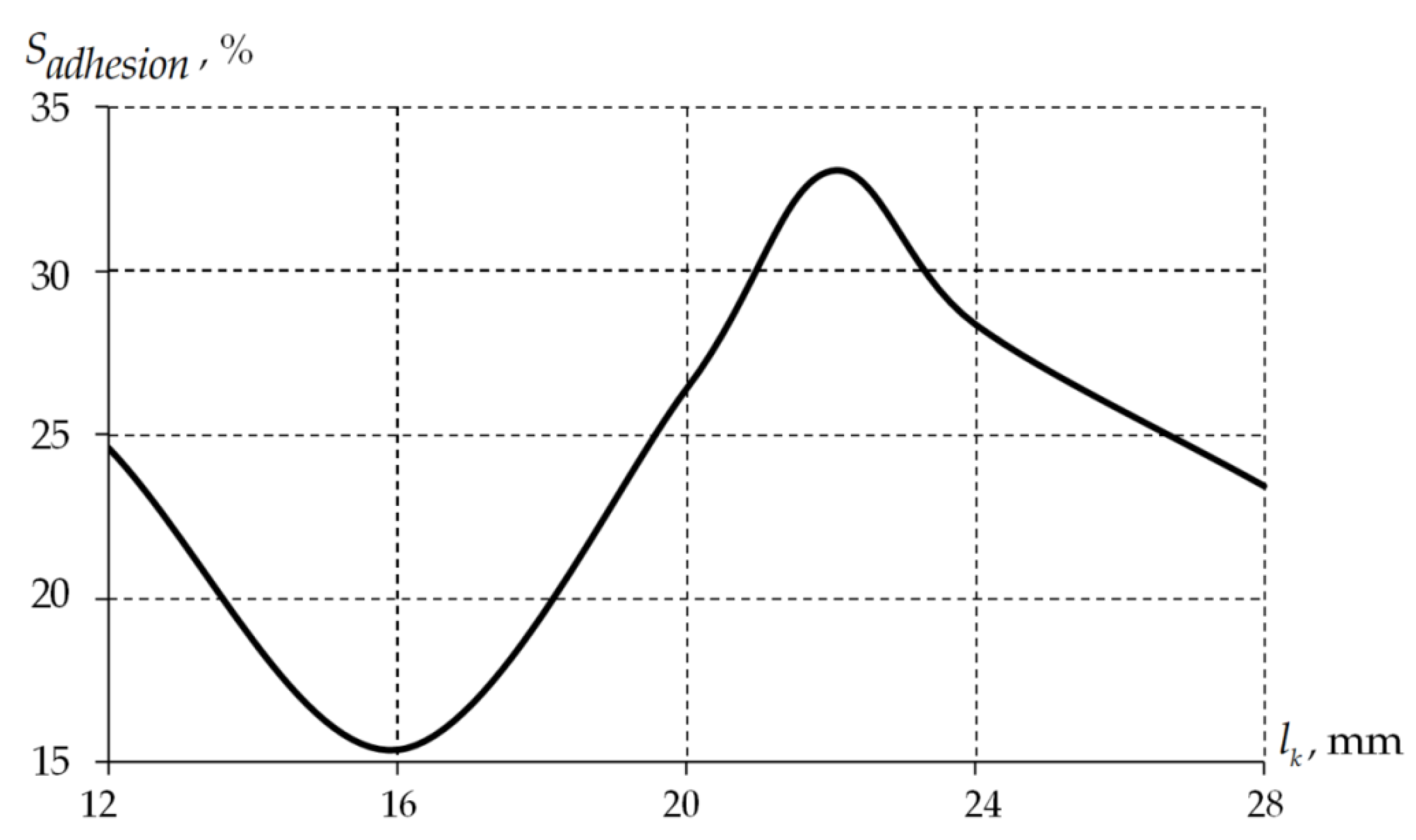
3.3. About the Geometric Parameters
4. Conclusions
- -
- A more uniform distribution of contact parameters across the sliding surface;
- -
- Plastic strain rates in the layer , displacements along the normal to the sliding layer face , and settlements of the bearing lower than in the structure with annular grooves for lubrication;
- -
- A simplified manufacturing process for the bottom steel plate due to the lack of additional cut-outs for the layer with annular grooves.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| boundary condition surfaces; | |
| contact surfaces; | |
| thickness anti-friction layer; | |
| row spacing; | |
| maximum depth; | |
| upper radius; | |
| lower radius; | |
| radius spherical hole; | |
| volume of lubrication from the spherical holes; | |
| volume of lubrication from the grooves; | |
| contact pressure; | |
| contact friction stress; | |
| plastic strain; | |
| normal displacements to the end-face of the sliding layer; | |
| sliding layer compresses; | |
| adhesion area; | |
| average contact pressure in the adhesion area; | |
| average contact pressure in the sliding area; | |
| average contact friction stress in the adhesion area; | |
| average contact friction stress in the sliding area. |
References
- Shapovalov, V.V.; Sladkovsky, A.; Erkenov, A.C. Actual problems of modern tribotechnology and ways of solution. Bull. High. Educ. Establ. Mech. Eng. 2015, 658, 64–75. [Google Scholar] [CrossRef]
- Shapovalov, V.V.; Ryabysh, D.A.; Areshjan, G.A. Technology for monitoring current states of mechanical systems. Vestn. RGUPS 2021, 82, 67–74. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L.; Xie, G.; Li, Z.; Chen, H.; Gong, H.; Xu, W.; Guo, D.; Luo, J. A review on tribology of polymer composite coatings. Friction 2021, 9, 429–470. [Google Scholar] [CrossRef]
- Deng, H.; Zhu, P.; Hu, C.; He, T. Study on dynamic lubrication characteristics of the external return spherical bearing pair under full working conditions. Machines 2022, 10, 107. [Google Scholar] [CrossRef]
- Boldyrev, Y.Y. A radial two-sector gas bearing with maximum load capacity. Math. Model. Comput. Simul. 2020, 12, 510–518. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P. Influence analysis of the antifriction layer materials and thickness on the contact interaction of spherical bearings elements. Lubricants 2022, 10, 30. [Google Scholar] [CrossRef]
- Fetisov, A.S.; Babin, A.Y.; Tyurin, V.O. Experimental stand for research of journal bearing lubricated by magnetoreological liquid. Lect. Notes Mech. Eng. 2020, 1, 1263–1270. [Google Scholar] [CrossRef]
- Cheng, Z.; Huang, K.; Xiong, Y.; Sang, M. Dynamic analysis of a high-contact-ratio spur gear system with localized spalling and experimental validation. Machines 2022, 10, 154. [Google Scholar] [CrossRef]
- Timofeev, G.A.; Tsukanov, O.N. Analysis of contact stresses in cylindric-bevel gears at the synthesis stage in generalizing parameters. Vestn. Mashinostroeniya 2020, 4, 41–47. [Google Scholar] [CrossRef]
- Velicu, R.G.; Lates, M.T.; Gavrila, C.C. Frictional losses of polyamides mounted on tensioning guides in contact with chains. Materials 2020, 15, 1345. [Google Scholar] [CrossRef]
- Manzhirov, A.V.; Kazakov, K.E. Modeling of the contact interaction between a nonuniform foundation and rough punch. Math. Model. Comput. Simul. 2018, 10, 314–321. [Google Scholar] [CrossRef]
- Meshcheryakova, A.R.; Goryacheva, I.G. Stress state of elastic bodies with an intermediate layer in rolling contact with slip. Phys. 2021, 24, 441–450. [Google Scholar] [CrossRef]
- Arutyunyan, A.M.; Fedotenkov, G.V. Transient contact interaction of a rigid die and elastic half-space with a cavity. Probl. Strength Plast. 2021, 83, 87–100. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Nicola, L. Incipient sliding of adhesive contacts. Friction 2022, 10, 963–976. [Google Scholar] [CrossRef]
- Myshkin, N.K.; Goryacheva, I.G.; Grigoriev, A.Y.; Kavaliova, I.N.; Makhovskaya, Y.Y. Contact interaction in precision tribosystems. J. Frict. Wear 2020, 41, 191–197. [Google Scholar] [CrossRef]
- Decrozant-Triquenaux, J.; Pelcastre, L.; Prakash, B.; Hardell, J. Influence of lubrication, tool steel composition, and topography on the high temperature tribological behaviour of aluminium. Friction 2021, 9, 155–168. [Google Scholar] [CrossRef]
- Dastani, H.; Botto, D.; Glorioso, M. Experimental and numerical investigation of contact parameters in a dovetail type of blade root joints. Appl. Sci. 2021, 11, 12008. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskih, A.A.; Pankova, A.P. Numerical analysis of the spherical bearing geometric configuration with antifriction layer made of different materials. PNRPU Mech. Bull. 2020, 4, 15–26. [Google Scholar] [CrossRef]
- Bourago, N.G.; Kukudzhanov, V.A. Review of contact algorithms. Mech. Solids 2005, 40, 35–71. [Google Scholar]
- Burago, N.G.; Nikitin, I.S.; Nikitin, A.D. Algorithms for calculating contact problems in the solid dynamics. Smart Innov. Syst. Technol. 2020, 173, 185–198. [Google Scholar] [CrossRef]
- Niemierko, A. Modern bridge bearings and expansion joints for road bridges. Transp. Res. Procedia 2016, 14, 4040–4049. [Google Scholar] [CrossRef]
- Rajczyk, J.; Rajczyk, M.; Lazarev, Y.; Rajczyk, P.; Kirillova, D. Elastomer bearing modification for efficient design. Lect. Notes Civ. Eng. 2020, 70, 715–726. [Google Scholar] [CrossRef]
- Liu, T.; Yu, O.; Fan, J.; Peng, Z.; Wang, E. Concrete spherical joint contact stress distribution and overturning moment of swing bridge. Structures 2020, 28, 1187–1195. [Google Scholar] [CrossRef]
- Guo, J.; Geng, T.; Yan, H.; Du, L.; Zhang, Z.; Sun, C. Implementation of a load sensitizing bridge spherical bearing based on low-coherent fiber-optic sensors combined with neural network algorithms. Sensors 2021, 21, 37. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Han, G.; Qi, X.; Du, J.; Lin, C.; Shu, L. A Hybrid Machine Learning Model for Demand Prediction of Edge-Computing-Based Bike-Sharing System Using Internet of Things. IEEE Internet Things J. 2020, 7, 7345–7356. [Google Scholar] [CrossRef]
- Chong, H.F.; Ng, D.W.K. Development of IoT device for traffic management system. In Proceedings of the 14th IEEE Student Conference on Research and Development: Advancing Technology for Humanity (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2016. [Google Scholar] [CrossRef]
- Karasev, O.I.; Krivtsova, A.O. Assessment of the level of metropolitan cities transport system development. Stat. Econ. 2019, 16, 22–31. [Google Scholar] [CrossRef]
- Abdallah, A.M.; Atadero, R.A.; Ozbek, M.E. A state-of-the-art review of bridge inspection planning: Current situation and future needs. J. Bridge Eng. 2022, 27, e0001812. [Google Scholar] [CrossRef]
- Sangiorgio, V.; Nettis, A.; Uva, G.; Pellegrino, F.; Varum, H.; Adam, J.M. Analytical fault tree and diagnostic aids for the preservation of historical steel truss bridges. Eng. Fail. Anal. 2022, 133, 105996. [Google Scholar] [CrossRef]
- Sengsri, P.; Kaewunruen, S. Additive manufacturing meta-functional composites for engineered bridge bearings: A review. Constr. Build. Mater. 2020, 262, 120535. [Google Scholar] [CrossRef]
- Sahu, A.R.; Behera, S.; Mukharjee, B.B.; Mondal, S. Parametric study on dynamic responses of stiffened sandwich composite bridge deck panel. J. Eng. Appl. Sci. 2022, 69, 30. [Google Scholar] [CrossRef]
- Schuler, H.; Muller, M. Fatigue measurements in an existing highway concrete bridge. Sensors 2022, 22, 2868. [Google Scholar] [CrossRef] [PubMed]
- Contiu, M.; Chiocel, D.M.; Cretu, D.; Botis, M.F. A Step-by-Step Probabilistic Seismic Soil–Structure Interaction Analysis with Ground Motion Incoherency for a Bridge Pier on Bored Pile Foundations. Appl. Sci. 2022, 12, 1828. [Google Scholar] [CrossRef]
- Schapery, R.A. Elastomeric Bearing Sizing Analysis Part 1: Spherical Bearing. Int. J. Solids Struct. 2018, 152–153, 118–139. [Google Scholar] [CrossRef]
- Heggade, V.N. Bearings & Their Configurations Within Bridge System. Bridge Struct. Eng. 2013, 43, 23–35. [Google Scholar]
- Adamov, A.A.; Kamenskikh, A.A.; Strukova, V.I. Influence of geometry and configuration of the spherical sliding layer of bridge bearings on the structure working capacity. Comput. Contin. Mech. 2021, 14, 289–299. [Google Scholar] [CrossRef]
- Kamenskih, A.A.; Trufanov, N.A. Regularities interaction of elements contact spherical unit with the antifrictional polymeric interlayer. J. Frict. Wear 2015, 36, 170–176. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, W.S.; Yoo, Y. Friction Properties of Solid Lubricants with Different Multiwalled Carbon Nanotube Contents. Materials 2022, 15, 4054. [Google Scholar] [CrossRef]
- Kamenskih, A.A.; Trufanov, N.A. Numerical analysis of the stress state of a spherical contact system with an interlayer of antifriction material. Comput. Contin. Mech. 2013, 6, 54–61. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Zdorovets, M.V. Effect of doping of Ce4+/3+ on optical, strength and shielding properties of (0.5−x)TeO2-0.25MoO-0.25Bi2O3-xCeO2 glasses. Mater. Chem. Phys. 2021, 263, 124444. [Google Scholar] [CrossRef]
- Kozlovskiy, A.L.; Zdorovets, M.V. Synthesis, structural, strength and corrosion properties of thin films of the type CuX (X = Bi, Mg, Ni). J. Mater. Sci. Mater. Electron. 2019, 30, 11819–11832. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Algarou, N.A.; Slimani, Y.; Sadaqat, A.; Baykal, A.; Manikandan, A.; Trukhanov, S.V.; Trukhanov, A.V.; Ercan, I. Investigation of exchange coupling and microwave properties of hard/soft (SrNi0.02Zr0.01Fe11.96O19)/(CoFe2O4)x nanocomposites. Mat. Today Nano 2022, 18, 100186. [Google Scholar] [CrossRef]
- Trukhanov, S.; Kostishyn, V.; Panina, L.; Turchenko, V.; Kazakevich, I.; Trukhanova, E.; Natarov, V.; Balagurov, A. Thermal evolution of exchange interactions in lightly doped barium hexaferrites. J. Magn. Magn. Mater. 2017, 426, 554–562. [Google Scholar] [CrossRef]
- Zhumatayeva, I.Z.; Kenzhina, I.E.; Kozlovskiy, A.L.; Zdorovets, M.V. The study of the prospects for the use of Li0.15Sr0.85TiO3 ceramics. J. Mater. Sci. Mater. Electron. 2020, 31, 6764–6772. [Google Scholar] [CrossRef]
- Darwish, M.A.; Zubar, T.I.; Kanafyev, O.D.; Zhou, D.; Trukhanova, E.L.; Trukhanov, S.V.; Trukhanov, A.V.; Henaish, A.M. Combined Effect of Microstructure, Surface Energy, and Adhesion Force on the Friction of PVA/Ferrite Spinel Nanocomposites. Nanomaterials 2022, 12, 1998. [Google Scholar] [CrossRef] [PubMed]
- Balyakin, V.B.; Khatipov, S.A.; Pilla, C.K. Experimental studies of tribotechnical characteristics of radiation-modified polytetrafluoroethylene to use in rotor supports. J. Frict. Wear 2015, 36, 346–349. [Google Scholar] [CrossRef]
- Smolyanskii, A.S.; Politova, E.D.; Koshkina, O.A.; Arsentyev, M.A.; Kusch, P.P.; Moskvitin, L.V.; Slesarenko, S.V.; Kiryukhin, D.P.; Trakhtenberg, L.I. Structure of polytetrafluoroethylene modified by the combined action of γ-radiation and high temperatures. Polymers 2021, 13, 3678. [Google Scholar] [CrossRef]
- Oyabu, H.; Fujikura, S.; Hai, N.M.; Takeuchi, S.; Nakajima, A. Behavior of bridge superstructure model with double spherical sliding bearing under live load. Lect. Notes Civ. Eng. 2021, 101, 353–539. [Google Scholar] [CrossRef]
- Allmaier, H. Increase Service Life for Rail Wheel Bearings—A Review of Grease Lubrication for This Application. Lubricants 2022, 10, 36. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, P.; Lin, J.; Gao, X. Rheological and tribological properties of lithium grease and polyurea grease with different consistencies. Coatings 2022, 12, 527. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P.; Strukova, V.I. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants 2022, 10, 207. [Google Scholar] [CrossRef]

| Maximum Number of Well Holes | ||||||
|---|---|---|---|---|---|---|
| 12 | 16 | 20 | 22 (Standard) | 24 | 28 | |
| 3 | + | + | + | + | + | + |
| 4 | – | + | – | – | – | – |
| 5 | + | – | – | – | – | – |
| Parameter | Bearing Pars with Different Geometries of Lubricant Recesses | |
|---|---|---|
| Annular Grooves | Spherical Holes | |
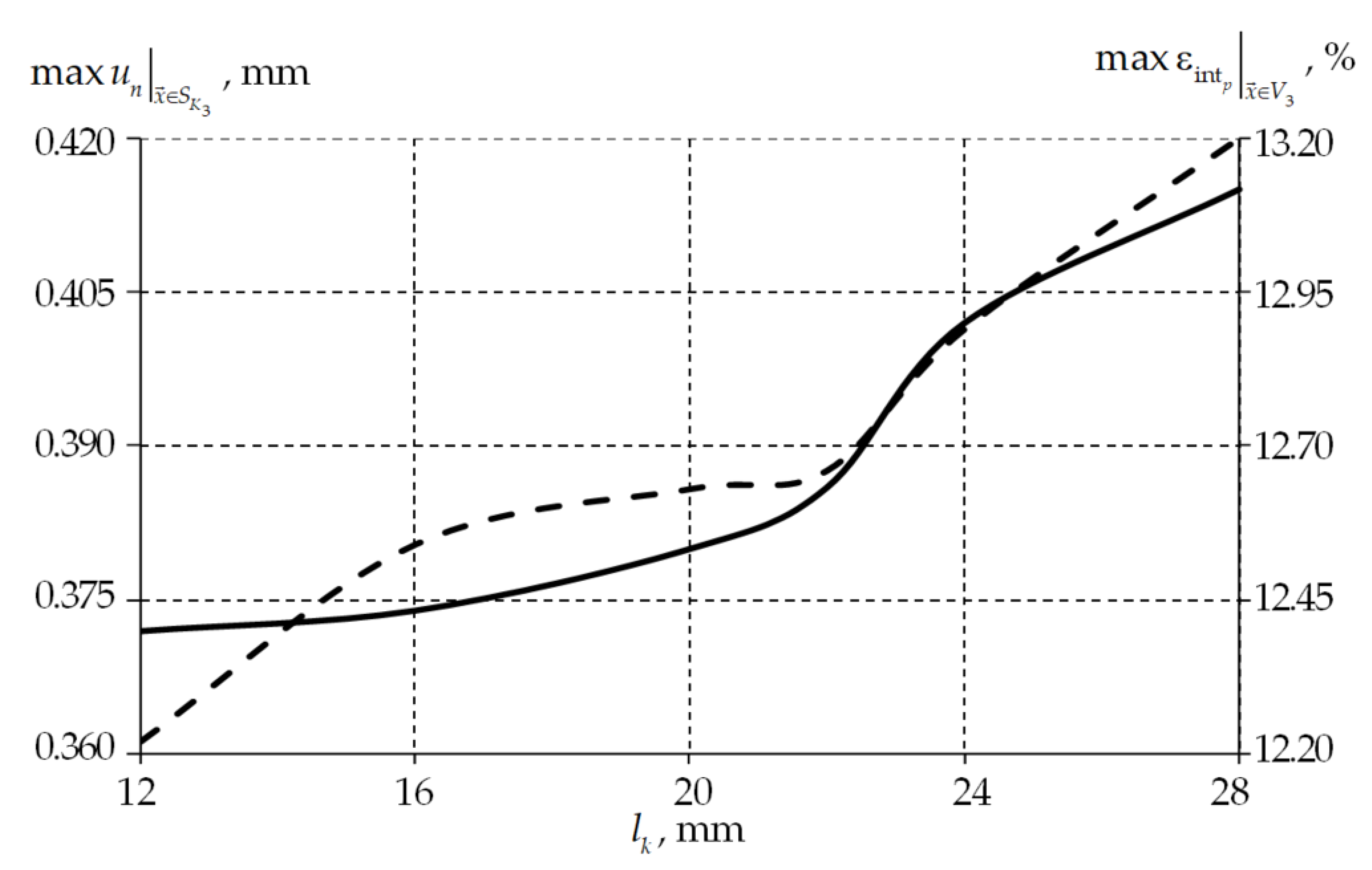
| , % | 23.10 | 12.66 |
| , mm | 0.555 | 0.386 |
| , mm | 0.130 | 0.109 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Spherical Holes | Annular Grooves | |||||
| Arrangement 1 | Arrangement 2 | |||||
| 12 | 16 | 22 (Standard) | 12 | 16 | 22 | |
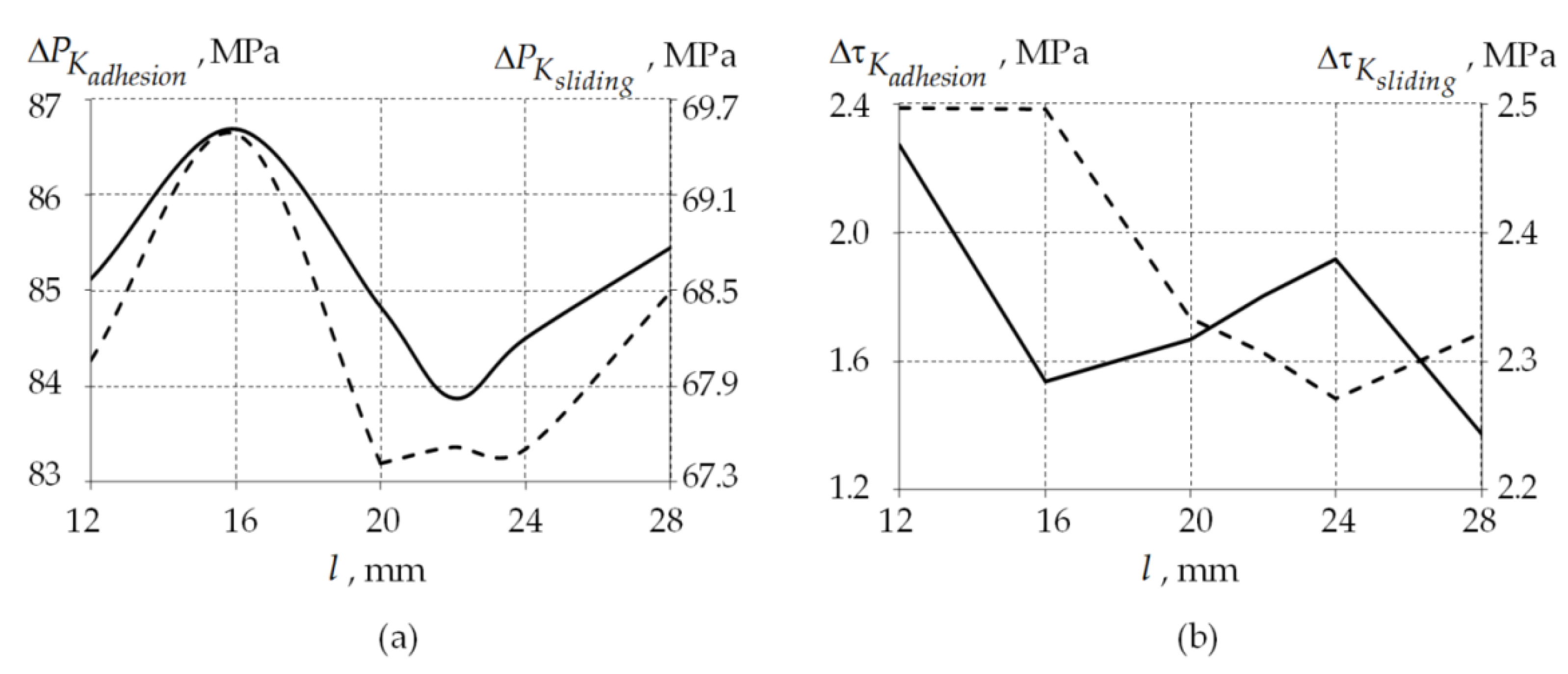
| , % | 24.59 | 15.42 | 33.02 | 15.69 | 15.62 | 22.07 |
| , MPa | 85.12 | 86.68 | 83.87 | 85.69 | 86.07 | 92.41 |
| , MPa | 2.27 | 1.54 | 1.81 | 1.85 | 1.49 | 1.19 |
| , MPa | 68.07 | 69.49 | 67.52 | 69.43 | 69.50 | 69.29 |
| , MPa | 2.49 | 2.49 | 2.31 | 2.19 | 2.29 | 2.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nosov, Y.O.; Kamenskikh, A.A. Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing. Lubricants 2022, 10, 283. https://doi.org/10.3390/lubricants10110283
Nosov YO, Kamenskikh AA. Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing. Lubricants. 2022; 10(11):283. https://doi.org/10.3390/lubricants10110283
Chicago/Turabian StyleNosov, Yuriy O., and Anna A. Kamenskikh. 2022. "Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing" Lubricants 10, no. 11: 283. https://doi.org/10.3390/lubricants10110283
APA StyleNosov, Y. O., & Kamenskikh, A. A. (2022). Influence Analysis of Lubricant Recesses on the Working Capacity of the Bridge Span Spherical Bearing. Lubricants, 10(11), 283. https://doi.org/10.3390/lubricants10110283





