Abstract
In this work, we have presented a detailed analysis of the event horizon of regular black holes (BHs) in modified gravity known as MOG, the so-called regular MOG BH. The motion of neutral particles around the BH has also been explored. The test particle motion study shows that the positive (negative) values of the MOG parameter mimic the spin of a rotating Kerr BH, providing the same values for the innermost stable pro-grade (retrograde) orbits of the particles in the range of the spin parameter . The efficiency of energy release from the accretion disk by the Novikov–Thorne model has been calculated, and the efficiency was shown to be linearly proportional to the increase of the MOG parameter . Moreover, we have developed a new methodology to test gravity theories in strong-field regimes using precision data from twin-peaked quasiperiodic oscillations (QPOs) of objects calculating possible values of upper and lower frequencies. However, it is obtained that the positive MOG parameter can not mimic the spin of Kerr BHs in terms of the same QPO frequencies. We have provided possible ranges for upper and lower frequencies of twin-peak QPOs with the ratio of the upper and lower frequencies of 3:2 around regular MOG BHs in the different models. Moreover, as an example, we provide detailed numerical analysis of the QPO of GRS 1915+105 with the frequencies and . It is shown that the central BH of the QPO object can be a regular MOG BH when the value of the parameter is and shines in the orbits located at the distance from the central BH. It is also shown that the orbits where QPOs shine are located near the innermost stable circular orbit (ISCO) of the test particle. The correlation between the radii of ISCO and the QPO orbits is found, and it can be used as a new theoretical way to determine ISCO radius through observational data from the QPOs around various compact objects.
1. Introduction
The vicinity of the astrophysical BHS being a compact gravitating object may serve as a laboratory for testing the gravity theories in the strong-field regime. The test of gravity theories through X-ray observation of stellar mass (3–30 ) and supermassive (up to ) has been carried out by numerous authors (see, e.g., [1]). Other ways of testing the gravity in the strong-field regime are through detection of gravitational waves by LIGO/VIRGO [2] and image of supermassive BHs at the Event Horizon Telescope (EHT) [3,4].
The first spherical symmetric vacuum solution within the general relativity describing the non-rotating BH with total mass M has been obtained by Schwarzschild in 1916 [5]. Later, Reissner and Nordström independently found the solution describing electrically charged BH [6,7]. The fundamental problem of these and other exact solutions of the field equations in general relativity in the presence of the singularity at the center of the BH, which can not be resolved by the concept of classical theory. Rotating, electric and magnetic regular BH solutions obtained by coupling general relativity to nonlinear electrodynamics obeying the singularity problem and physical properties of the BHs such as thermodynamics, thermal stability and possible phase transition, QNMs and photon motions are studied in, e.g., refs. [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Regular BHs in modified gravity have been investigated in [24].
The spacetime around BHs is strongly curved, leading to the formation of an event horizon, which is a surface bounding the region of spacetime unobservable by the external observer. Depending on the central BH, the spacetime geometry near the horizon differs from each other. The geometrical structure of the spacetime can be determined by the motion of the particles in the vicinity of the BH [25,26,27,28,29,30,31]. The existence of a magnetic field around BH also alters the particle motion resulting in the chaotic dynamics [32,33,34,35,36].
The existence of dark energy and dark matter in the Universe has been proven by several observations (e.g., the galactic rotation curves and the accelerated expansion of the Universe, etc.), which can be explained by introducing the cosmological constant in the cosmological solutions of general relativity and hidden mass as cold dark matter so-called standard cold dark matter (CDM) cosmological model. However, general relativity modifications try to explain such phenomena by the intrinsic effects of the extended theories of gravity. One of such modifications is the so-called Scalar-Tensor-Vector Gravity (STVG) proposed by Moffat [37]. The theory has been applied to galaxy rotation curves [38,39], BH shadow [40,41], supernovae [42] and gravitational lensing in plasma and vacuum environment [43,44]. Non-rotating and rotating BH solutions in MOG (known as Schwarzschild–MOG and Kerr–MOG ones, respectively) have been obtained in [40]. The role of the MOG field on plasma magnetospheric radiation from rotating magnetized relativistic stars and magnetized particles motion around gravitating compact objects have also been discussed in refs. [45,46].
Another interesting phenomenon appearing while studying the dynamics of test particles, especially circular orbits around a compact gravitating object, is related to QPOs. These objects are detected in the X-ray radiation of microquasars which contains a BH surrounded by a star. The matter flow from the star to companion BH creates the accretion disc and the system starts to irradiate in the X-ray diapason due to strong friction of the matter near the ISCO [47]. The study of QPO is very important since it is related to astrophysical processes happening in the close environment of the BH. QPOs are useful for testing both accretion matter physics and the nature of gravitational interaction in the strong-field regime. Accretion disc surrounding BH as a source of QPO in different models has been widely discussed in the literature [48,49,50,51,52,53,54,55,56,57]. Particularly, various models explaining the qualitative behaviour of the QPO including disc-seismic models, hot-spot models, warped disk models, and resonance models have been proposed [50,58,59,60]. Here, we analyze the twin peak QPOs observed in X-ray sources thin the MOG model.
In the present work, we have studied dynamics of test particles and twin peak QPOs around regular MOG BHs based on the idea of whether the regular BH in MOG can show similar effects as rotating Kerr BHs on generations of the same QPO frequencies. This work is organized as follows: In Section 2, we have focused on the analysis of the properties of geometry around regular MOG BH. In Section 3, we have investigated the dynamics of electrically neutral test particles. Section 4 is devoted to studying fundamental frequencies, and in Section 5 we have provided astrophysical applications of the studies of fundamental frequencies of test particles to the analysis of twin peak QPOs in different models. Finally, in Section 6 we summarize the obtained main results.
Throughout the paper, the space-like signature is selected for the spacetime, and the geometrized system of units is used where (however, for an astrophysical application the speed of light and the Newtonian gravitational constant are written explicitly in our expressions). The Latin indices run from 1 to, 3 and the Greek ones from 0 to 3.
2. The Spacetime Properties
Action in MOG (STVG) has three additional terms on top of the standard Einstein–Hilbert action [37]:
where are actions of massive vector field, scalar fields and pressureless matter, respectively. Vs are potentials and is a kinetic term for field with . is a scalar field responsible for a strength of the interaction between matter and gravity, is the gravitational source charge and where is the matter energy-momentum tensor, is density of the pressureless matter and with where is a Newtonian gravitational constant.
Field equations are given by [37]:
By coupling the field equations of MOG to nonlinear electromagnetic field, a regular BH solution can be obtained [61].
The spacetime around the regular MOG BH can be described by the following line element [40,62].
with
where M is the total mass of the BH, is the so-called MOG parameter being responsible for the modified gravity. The metric takes the form of the Schwarzschild solution when and as the metric reflects flat spacetime effects. There are several constraints for the parameter obtained by Moffat et al. using the different astronomical observational data. For example, in ref. [24] authors have shown that MOG plays the role of dark matter providing the same gravitational redshift with the MOG parameter based on the data from X-ray band observations of the galactic cluster Abel 1689. Analysing the data from the gravitational wave events GW150914 and GW151226, the authors of ref. [63] have obtained the values of the MOG parameter in the range . It has been shown in ref. [64] that the effect of MOG near the Sgr A* is weak and the upper limit of the parameter takes the value . Another constraint for MOG parameter as has been obtained using the observational data on the image of M87 event horizon [65]. The analysis of observational data from rotation curves of the nearby galaxies has allowed getting constraint on the upper value of MOG parameter as [38]. The upper limit for the MOG parameter for the millisecond pulsars J2145-0750, J0024-7204D, and J0024-7204H, has been found as 1.6011, 3.06528, and 0.9747, respectively, have been recently obtained in our previous paper [45].
Now we explore the event horizon properties of the regular MOG BH governed by the lapse function (8) with nonvanishing MOG parameter . Generally, the radius of the event horizon of a BH is defined in a standard way imposing or, equivalently, by solving the equation with respect to r. We get a quite complicated form of expression for the radius of outer and inner horizons denoted with and signs, respectively, in the following form:
where
and are corresponding to radius of outer (+) and inner (-) horizons.
The dependence of the radii of (outer and inner) event horizons for the different values of is shown in Figure 1. One can see from the figure that the inner and outer horizons coincide each other at the critic value of the MOG parameter.
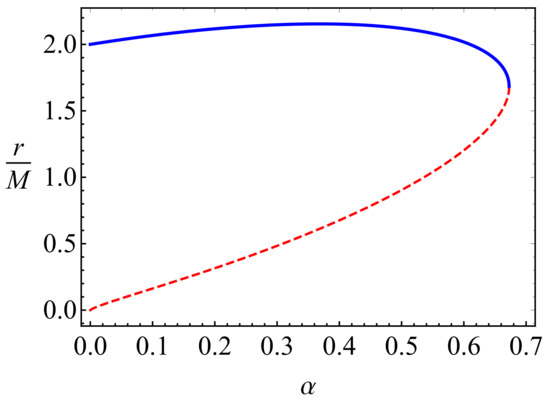
Figure 1.
Dependence of event horizon radii from MOG parameter. Solid blue line represents outer horizon and red dashed one is for inner horizon.
At the extreme values of the MOG parameter, the two horizons coincide. The minimum value of the outer horizon can be easily found by the following system of equations and solving them with respect to r and
where the prime () denotes derivative along radial coordinate. One may solve the equations of the system with respect to the MOG parameter and the radial coordinate, r which implies the critical value of the MOG parameter and minimum value of the outer horizon. Then we have 1.68119 and 0.67276.
If the value of MOG parameter exceeds the critical one, no BH can be formed.
Now we explore the radial profiles of the lapse function (8) for the different values of the MOG parameter.
Figure 2 shows the dependence of outer and inner horizons of regular MOG BHs from the MOG parameters. One can see that the values of outer and inner horizons match when MOG parameter takes the critical value. Consequently, we may conclude the follows:
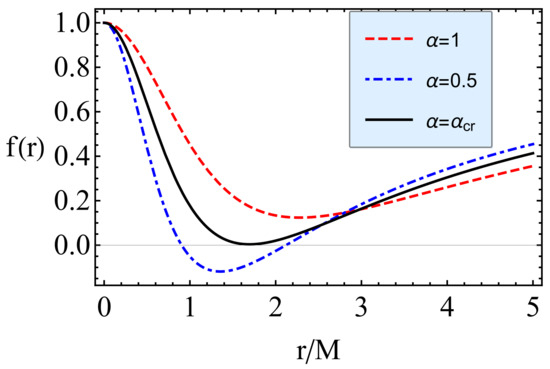
Figure 2.
Dependence of lapse function from the radial coordinate for the different values of the MOG parameters .
- In the case when two event horizons do exist: inner and outer ones;
- In the case when there are no event horizons;
- If we have extreme regular MOG BH and the two horizons coincide (see Figure 2).
3. Test Particle Motion
In this section, we will perform a detailed analysis of dynamics of test particles around regular MOG BH described by the metric (7).
3.1. Equation of Motion
The Lagrangian for neutral test particles with mass m can be expressed in the standard form,
where m is the mass of the particle. Then integrals of motion corresponding to Killing symmetries of the spacetime are read
where and are specific energy and specific angular momentum of the particle, respectively. One can govern the equations of motion for test particles through the normalization condition
where takes the values 0 and for massless and massive particles, respectively.
For electrically neutral, massive test particles’ motion is governed by timelike geodesics of the spacetime (7) and the equations of motion can be derived using Equation (12). Taking into account Equation (11), one may obtain the equations of motion in the separated and integrable form,
where is the Carter constant corresponding to the total angular momentum.
Restricting the motion of test particles to the plane with and (that is justified by the conservation of the angular momentum), the Carter constant takes the form . Then the equation of the radial motion can be expressed in the form
where the effective potential of the motion of test particles reads
Now we consider the conditions for the circular motion, corresponding to zero radial velocity and acceleration . Then one may obtain the radial profiles of the specific angular momentum and specific energy for circular orbits at the equatorial plane () in the following form
Figure 3 illustrates the radial profiles of the specific energy and angular momentum. One can see that the presence of the MOG parameter causes the increase of the specific angular momentum, the energy decreases. Moreover, the distance corresponding to minimum values of the energy and angular momentum goes outward of the central BH with the increase of the MOG parameter.
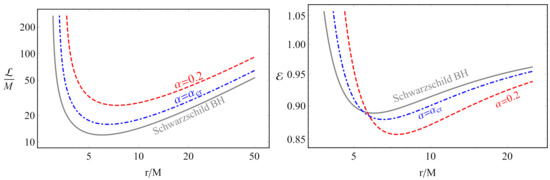
Figure 3.
Radial dependence of specific angular momentum (left panel) and energy (right panel) for circular orbits for different values of MOG parameter.
3.2. Stable Circular Orbits
The radius of ISCOs for particles around BHs can be defined by the solution of the condition with respect to the radial coordinate:
It is impossible to find the exact solutions of Equation (20), however, the limit of the solution at the critical value of MOG parameter can be obtained numerically in the following form
It shows that ISCO radius of test particles around Regular MOG BHs with the critic value of the parameter matches ISCO of the particles in prograde orbits around Kerr BH with the spin parameter . This fact allows to compare the effects of the MOG and spin parameters on ISCO radius and may be used for the estimation of MOG parameter using the observational data for accretion discs.
3.3. Regular MOG BH versus Kerr BH: The Same ISCO
In this subsection, we will carry on our detailed analysis on comparison of effects of the spin parameter of rotating Kerr BH and MOG field on ISCO radius of the test particles. In theoretical studies and astrophysical measurements of ISCO radius of test particles, a problem of indistinguishability of different gravity effects may appear. In most cases BHs are considered as rotational Kerr BHs, however, other some types of static BHs can provide similar gravitational effects on ISCO radius as rotating BH [66,67,68,69]. In such cases, it is quite difficult to distinguish the difference of gravitational effects of the two different types of BHs. Due to this reason, in this subsection we will investigate how the MOG parameter can cover the gravitational effects of spin of Kerr BH providing the same ISCO radius for test particles mimicking each other and show possible cases of distinguishable values of the MOG and spin parameters which can not cover the gravitational effects of each other.
The ISCO radius of test particles in retrograde and prograde orbits around Kerr BH can be expressed as [70]
where the notations,
Figure 4 shows ISCO radius as a function of the MOG and the spin parameters of the regular MOG and Kerr BHs, respectively. We provide the figure in order to see how the MOG parameter can mimic the spin parameter of rotating Kerr BHs providing the same values to the ISCO radius. It is seen that the spin and MOG parameters can provide the same ISCO radius to test particles around the Kerr and regular MOG BHs, at their values in the range () vs. () and () vs. (). That means the effects of positive (negative) MOG and negative (positive) spin parameters are the same on ISCO radius of test particles, at the above-mentioned range of the parameters. Moreover, one can see that the negative (positive) values of spin parameter and positive (negative) values of MOG parameter increases (decreases) the ISCO radii.
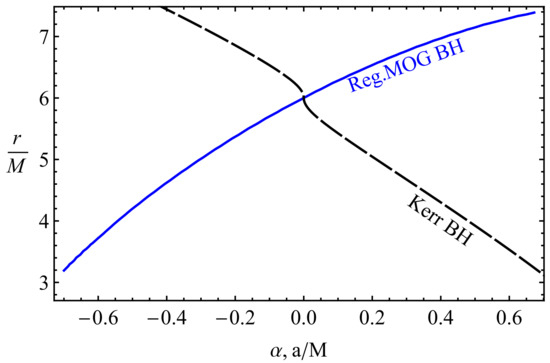
Figure 4.
Dependence of ISCO radius of test particles from the MOG parameter of regular MOG BHs and the spin of rotating Kerr BHs.
Figure 5 shows the relation between MOG and spin parameters for the same values of ISCO radii. It is clear that one cannot fully mimic the spin of Kerr BH by the effects of MOG parameter, since prograde and retrograde motions require different values of MOG parameter. The numerical results show that the MOG parameter can mimic the spin parameter in the range of when its values .
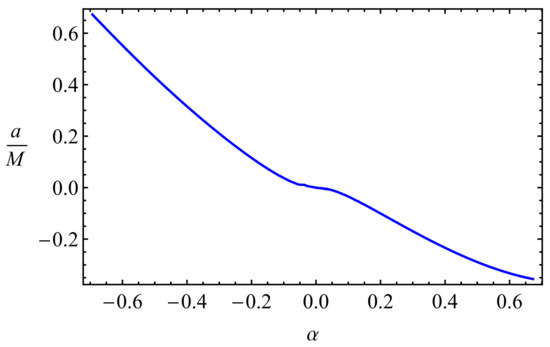
Figure 5.
The degeneracy graph between spin and MOG parameters providing the same ISCO radius.
3.4. The Energy Extraction Efficiency
Keplerian accretion around an astrophysical BH is explained by Novikov and Thorn as geometrically thin disks [71]. The efficiency of energy extraction process in the accretion disk around a BH is the maximum energy which matter falling in to the central BH from the disk extracts as radiation energy. The efficiency of the accretion of the particle can be calculated using the following standard expression
where is the energy of the particle at the ISCO which is characterized by the ratio of the binding energy (BH-particle system) and rest energy of test particle, and it can be calculated using the energy of the particles given by Equation (19) at ISCO.
The effects of MOG parameter on the efficiency of the accretion of the test particle around regular BHs in MOG is presented in Figure 6. One can see that efficiency grows linearly with the increase of MOG parameter and gives maximum about 15% in the range of the parameter .
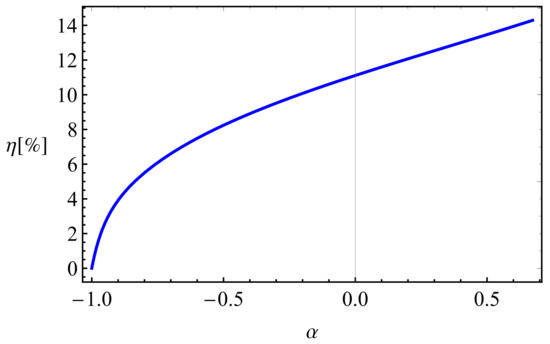
Figure 6.
Dependence of energy extraction efficiency from the MOG parameter .
3.5. Regular MOG BH versus Kerr BH: The Same Energy Efficiency
Here we provide additional astrophysical application of performed study on the efficiency of energy release from accretion disk around regular MOG BH which is proportional to the measurable total bolometric luminosity of the whole of the accretion disk, (where stands for the falling rate of accreting matter in to the central BH) [72,73]. Our main purpose is to explore whether the MOG parameter can show the similar gravitational effect on the efficiency as well as the spin of Kerr BH. The expression for the energy efficiency from accretion disk of Kerr BH reads [70]
where and .
It is possible to get a relation between the energy efficiency and the Kerr spin parameter by substituting Equation (22) into Equation (24), then finally using the expression for energy efficiency given by Equation (6).
In Figure 7, we present degeneracy values of spin and MOG parameters providing the same energy efficiency of energy release from co- and counter-rotating accretion disk. One can conclude from the graph is presented in Figure 7 and numerical analysis that the MOG parameter can mimic the spin up to for retrograde orbits, and the limit for prograde orbits is .
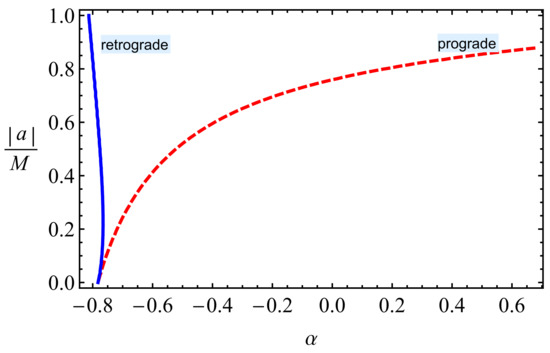
Figure 7.
The same graph as presented in Figure 5 but providing the same values of energy efficiency.
4. Fundamental Frequencies
The fundamental frequencies of test particles orbiting regular MOG BHs are studied. It can help to be one of the simplest models to explain QPOs observed around BHs.
4.1. Keplerian Frequency
The angular velocity of test particles measured by an observer located at infinity, called the Keplerian frequency, is given by
For better understanding of the QPO frequencies it is convenient to express them in Hertz units as,
where we insert the speed of light and the Newtonian gravitational constant
Alternately, the expression for the Keplerian frequency in the spacetime of a static BH, which gives the same results, is given by
For the regular BHs it takes the form,
4.2. Harmonic Oscillations
In this section, we investigate small perturbations of the orbital motion in radial and vertical directions, where and are a radial and an angular coordinates in which the effective potential takes its extreme value.
Expanding the effective potential into power series of the perturbations and up to the second order we get the following
The first term equals to zero at limited motion of the particles characterized by the energetic boundary conditions given as and , and we have . Second, third and sixth terms of the expansion given in Equation (28) vanish due to the conditions . The next two terms, being proportional to the second-order derivatives of the effective potential concerning the coordinates r and . The equation of motion is obtained by replacing the derivatives to the affine parameter with the time derivative, as in Euler–Lagrange equations. Finally, we can get equations for displacements and in the following form
where and are, respectively, the radial and vertical angular frequencies measured by a distant observer, defined as
The radial dependence of the Keplerian frequencies of test particles around regular MOG BH is shown in Figure 8 with comparison to pure Schwarzschild BH. One can see that the existence of the MOG parameter causes an increase (decrease) of frequencies of Keplerian orbits (the maximum frequencies of radial oscillations). Moreover, at large distances, the effect of MOG (STVG) field on the frequencies vanishes.
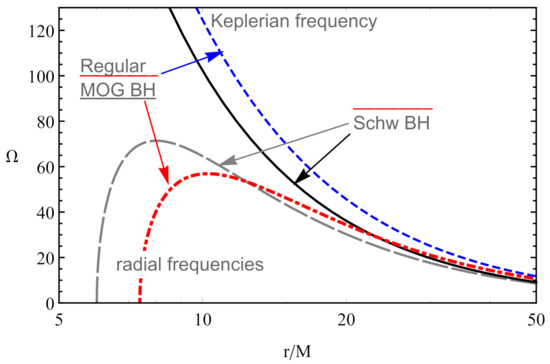
Figure 8.
Keplerian and radial frequencies of test particles around RMOG BH as a function of the radial coordinate . The unit of the frequency is given in Hz.
5. Astrophysical Applications
From an astrophysical point of view, QPOs are one of the mysterious objects which explanations of their existence are strongly model-dependent. The physics of QPOs in the Keplerian orbits are dependent on vertical and radial oscillations of test particles along stable orbits around BHs. On the other hand, they can play a role as a testing tool of dominated gravity theories in spacetime around BHs. In most literature, where detailed QPO data analyse are provided, the central BHs considered as a rotating Kerr BH [50]. However, other BHs in alternative theories of gravity can pretend to be the object providing the same QPO frequencies in twin-peaked models. In such cases, when another static BH alternates the Kerr one, in other words, it is impossible to distinguish the rotating Kerr BH and static BH of alternative gravity by theoretical analysis of data from QPOs. Thus, in this section, we aimed to explore a new way of providing such analyses, which help to determine the relations between possible values of upper and lower frequencies of twin-peak QPOs around regular MOG BHs. Then, one can compare the results with the results in Schwarzchild and Kerr BHs in various models of twin-peak QPOs [50]. Moreover, another actual astrophysical issue connected with the determination of ISCO radius around BHs, which can be the inner edge of the accretion disk around a BH.
Here, we investigate the relation between the possible values of lower and upper frequencies of twin-peak low and high-frequency QPOs around a BH in possible values of the BH parameters, in the various QPO models which are, namely, relativistic precession (RP) model where the upper and lower frequencies of the twin peaked QPOs are and , respectively, [74], the epicyclic resonance (ER) model (the frequencies for ER2, ER3, ER4 , ; , , and , , respectively), [75] and warped disc (WD) model (, ) [76,77]. Below we show the relation for the above-considered models for testing the modified gravity effects on twin-peak QPOs with the ratio of 3:2.
Figure 9 illustrates the relationship between upper and lower frequencies of twin-peak QPOs for the different models of BHs and QPOs. In the numerical calculations, we have assumed for stellar-mass BHs with the value of its mass of . In this figure, we have also provided analysis of the QPO GRS 1915+105 [49,60,78] with upper and lower frequencies and Hzs, respectively, and the total mass . Here we are interested in whether MOG can help to explain the appearance of the object. Performed analysis shows that one can explain it by only the RP model, values of the MOG parameter dominated around gravitating compact objects is in the distance from the centre of the BH . Other models show that the value of the parameter around the object is . According to the WD and ER2-4 models, the QPO object GRS 1915+105 can not be regular MOG BH, but the RP model indicates it could be with the parameter approximately . One may also see from this figure that the MOG parameter can not mimic the spin of Kerr BHs providing the same QPO frequencies.
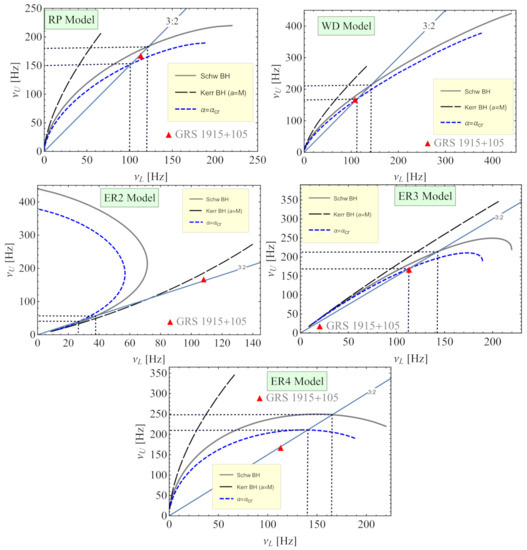
Figure 9.
Relations between the frequencies of upper and lower peaks of twin-peak QPO objects in the RP, WD and ER2-4 models. The red triangle symbol implies a twin-peak QPO object called GRS 1915+105 with the upper and lower frequency relation 3:2.
Moreover, using analyses of the models, we are interested in the possible range of upper and lower frequencies for twin-peak QPOs around the regular MOG BH with 3:2 frequency ratios. We have found the following results with the help of numerical calculations summarized in the following Table 1:

Table 1.
The range of upper and lower frequencies of twin peak QPOs from the RMOG BHs in different QPOs models.
The provided table may help to distinguish (recognizing) the central object of a new detected twin peak QPO object with the frequency ratio of 3:2. The importance of such analyses is connected to determine the different theories of gravity that can cause to existence of the same twin-peak QPO objects at the corresponding values of their parameters.
Here, we are interested in another issue related to the distance from the centre of the BH to an orbit where the QPO generate by test particles in geodesic motion. As an example, we investigate the distance from the central BH to the QPO around object GRS 1915+105.
We shown the range of orbits where the QPO GRS J1915-105 could observe in Figure 10 with a light blue-coloured area in the RP model. One can see from the figure that the increase of the MOG parameter shrinks the range, while the orbits where the QPO object could shine go outwards as ISCO grows.
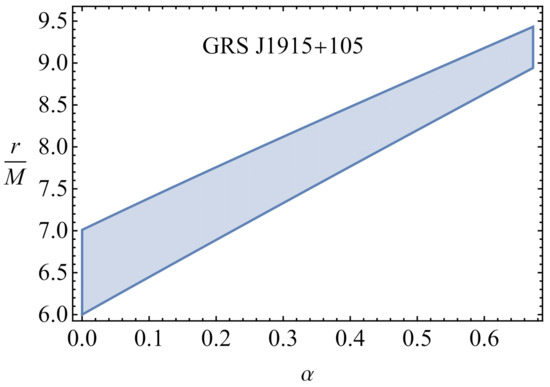
Figure 10.
The range of orbits where the QPO around object GRS J1915-105 can shine as a function of MOG parameter.
Here, we also plan to determine the relationship between this distance and MOG parameters for the given ratio of upper and lower frequencies 3:2, 4:3, and 5:4. For this, we first set the following equations
Using contour plots of these equations, one can get the relation illustrating the equation in a given QPO model.
We show the distance from the regular MOG BH to the positions of twin-peaked QPOs with the upper and lower frequencies’ ratios 3:2, 4:3 and 5:4 in Figure 11 in RP, WD and ER2-4 models. It can be seen from the figure that as the MOG parameter becomes bigger, the position of the QPO goes outwards from the central BH due to the gravitational behaviour of the MOG field. The QPO orbits locate at further distances than ISCO. Moreover, there is a correlation between the distance and ISCO radius that if the ISCO radius increases the distance also increases proportionally. The orbits where QPOs with the ratios 4:3 and 5:4 are located closer than the QPO location with the ratio 3:2. That means the performed study of the QPO distance may use as a new theoretical tool for determining the values of ISCO radius in measurements of twin frequencies of the QPOs. In other words, finding the location of QPO orbits helps to evaluate the ISCO radius. Since practically they are approximately equal to each other. However, only in the ER2 model, ISCO and the QPO orbits are located far from each other, and the correlation does not play a role well.
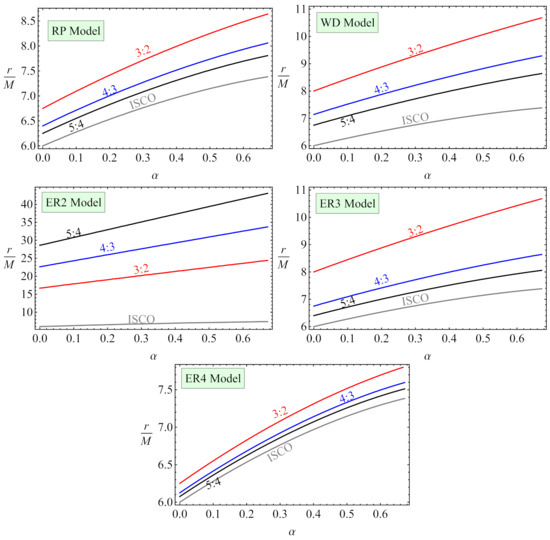
Figure 11.
The radius of orbits where twin peak QPOs are located with the ratios 3:2, 4:3, and 5:4 in RP, WD, and ER3-4 models and ISCO radius as function of MOG parameter.
Finally, one can conclude that the intensity of radiation from the oscillations of particles is higher near ISCO, due to stronger gravitational field. It is seen that due to the presence of the MOG field, the orbits of QPOs shift farther from ISCO and higher frequency ratio orbits shift more and are overall located on larger distances.
6. Conclusions
In the present work, we have studied the properties of the spacetime and event horizon of regular BH in MOG gravity. It has shown that the increase of the MOG parameter causes the decrease of scalar invariants of the spacetime of the BH such as Ricci scalar, square of Riemann tensor and Kretschmann scalar.
We have also explored the motion of neutral particles and obtained that positive (negative) values of the MOG parameter causes the increase (decrease) of ISCO radius. We have shown similar effects of the MOG parameter on ISCO radius with the effect spin of Kerr BH and how the MOG parameter can mimic the spin of Kerr BH, providing the same values for the ISCO radius of test particles. The energy efficiency of accretion disk by the model of Novikov and Thorne has also been investigated. We found that the efficiency exceeds 15 %. The fact is that the bolometric luminosity of the accretion disk around BHs is proportional to the energy efficiency and the rate of falling matter into the central object. We have also been interested in whether the MOG parameter mimics the spin of Kerr BH in providing the same value for the luminosity by assuming the same mass rate falling into the BHS. We have shown that the mimic range of the spin parameter at the MOG parameter .
Moreover, we have developed a new methodology that helps to test parameters of gravity theories in strong-field regime using precision observational data from twin-peak QPO objects constructing diagrams for their upper and lower frequencies. We can see that possible values for upper and lower frequencies of QPOs can generate around Schwarzschild, Kerr and regular MOG BHs in RP, WD and ER models. It is shown that regular MOG BHs can not mimic rotating Kerr BHs providing the same frequencies of upper and lower peaks of twin QPOs with positive values of the MOG parameter. Numerical analysis for the twin peak QPO object called GRS 1915+105 with the frequencies and show that the central BH of the QPO can be regular MOG BH when MOG parameter and the resonance oscillations generate at the distances from the central BH.
Finally, we have provided possible ranges for upper and lower frequencies of twin-peak QPOs with the ratio of the upper and lower frequencies 3:2 around regular MOG BHs in the different models. We have also interested in the study of the orbits of twin peak QPOs with the ratio 3:2, 4:3, and 5:4 and the range where the QPO object GRS 1915+105 is generated. We have shown that the orbits/range are located near the innermost stable circular orbits (ISCO). Likewise, we have also found that there is a correlation between the radii of ISCO and the QPO orbits. Furthermore, we have concluded that the performed study of the QPO distance may play a role new theoretical tool for determining the values of ISCO radius using data from astrophysical observations of twin peak QPOs, which is an important issue in relativistic astrophysics.
Author Contributions
J.R.: Ideas; formulation or evolution of overarching research goals and aims. Application of statistical, mathematical, computational, and other formal techniques to analyze or synthesize study data. Development or design of methodology; creation of models. Conducting a research and investigation process, specifically performing the experiments, or data/evidence collection. Preparation, creation and/or presentation of the published work, specifically writing the initial draft (including substantive translation). Preparation, creation and/or presentation of the published work by those from the original research group, specifically critical review, commentary or revision—including pre- or post-publication stages. P.T.: Application of statistical, mathematical, computational, and other formal techniques to analyze or synthesize study data. Preparation, creation and/or presentation of the published work, specifically writing the initial draft (including substantive translation). A.A.: Verification, whether as a part of the activity or separate, of the overall replication/reproducibility of results/experiments and other research outputs. Over sight and leadership responsibility for there search activity planning and execution, including mentorship external to the core team. Preparation, creation and/or presentation of the published work by those from the original research group, specifically critical review, commentary or revision—including pre- or post-publication stages. B.A.: Management and coordination responsibility for the research activity planning and execution. Provision of study materials, reagents, materials, patients, laboratory samples, animals, instrumentation, computing resources, or other analysis tools. Oversight and leadership responsibility for the research activity planning and execution, including mentorship external to the core team. M.K.: Conducting a research and investigation process, specifically performing the experiments, or data/evidence collection. Management activities to annotate (produce metadata), scrub data and maintain research data (including software code, where it is necessary for interpreting the data itself) for initial use and later re-use. All authors have read and agreed to the published version of the manuscript.
Funding
Ministry of Innovative Development of the Republic of Uzbekistan: MRB-AN-2019-29.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research is supported by Grants of the Uzbekistan Ministry for Innovative Development, NT-01 of the Abdus Salam International Centre of Theoretical Physics. A.A. acknowledges the support from Chinese academy of sciences through PIFI foundation. J.R. thanks ERASMUS+ project 608715-EPP-1-2019-1-UZ-EPPKA2-JP (SPACECOM).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bambi, C. Testing black hole candidates with electromagnetic radiation. Rev. Mod. Phys. 2017, 89, 025001. [Google Scholar] [CrossRef]
- Vogt, R. The U.S. LIGO Project. In Proceedings of the Sixth Marcel Grossman Meeting on General Relativity, Kyoto, Japan, 23–29 June 1991; Sato, H., Nakamura, T., Eds.; World Scientific: Singapore, 1992; pp. 244–266. [Google Scholar]
- Akiyama, K. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. 2019, 875, L6. [Google Scholar] [CrossRef]
- Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinchen Theorie. Sitzungsberichte Der KöNiglich PreußIschen Akad. Der Wiss. 1916, 92, 189–196. [Google Scholar]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Der Phys. 1916, 355, 106–120. [Google Scholar] [CrossRef]
- Nordström, G. On the Energy of the Gravitation field in Einstein’s Theory. K. Ned. Akad. Van Wet. Proc. Ser. B Phys. Sci. 1918, 20, 1238–1245. [Google Scholar]
- Bardeen, J.M. Kerr Metric Black Holes. Nature 1970, 226, 64. [Google Scholar] [CrossRef]
- Bahrami Asl, B.; Hendi, S.H.; Sajadi, S.N. Complexity Conjecture of Regular Electric Black Holes. arXiv 2021, arXiv:2102.12515. [Google Scholar]
- Hendi, S.H.; Sajadi, S.N.; Khademi, M. Physical properties of a regular rotating black hole: Thermodynamics, stability, and quasinormal modes. Phys. Rev. D 2021, 10, 064016. [Google Scholar] [CrossRef]
- Hayward, S.A. Energy and entropy conservation for dynamical black holes. Phys. Rev. D 2004, 70, 104027. [Google Scholar] [CrossRef]
- Dymnikova, I.; Korpusik, M. Thermodynamics of Regular Cosmological Black Holes with the de Sitter Interior. Entropy 2011, 13, 1967–1991. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Regular rotating electrically charged black holes and solitons in non-linear electrodynamics minimally coupled to gravity. Class. Quantum Gravity 2015, 32, 165015. [Google Scholar] [CrossRef]
- Toshmatov, B.; Bambi, C.; Ahmedov, B.; Stuchlík, Z.; Schee, J. Scalar perturbations of nonsingular nonrotating black holes in conformal gravity. Phys. Rev. D 2017, 96, 064028. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Ahmedov, B. Rotating black hole solutions with quintessential energy. Eur. Phys. J. Plus 2017, 132, 98. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Comment on “Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics”. Phys. Rev. Lett. 2000, 85, 4641. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Ahmedov, B. Comment on “Construction of regular black holes in general relativity”. Phys. Rev. D 2018, 98, 028501. [Google Scholar] [CrossRef]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlík, Z. Rotating regular black hole solution. Phys. Rev. D. 2014, 89, 104017. [Google Scholar] [CrossRef]
- Toshmatov, B.; Abdujabbarov, A.; Stuchlík, Z.; Ahmedov, B. Quasinormal modes of test fields around regular black holes. Phys. Rev. D 2015, 91, 083008. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Circular geodesic of Bardeen and Ayon-Beato-Garcia regular black-hole and no-horizon spacetimes. Int. J. Mod. Phys. D 2015, 24, 50020. [Google Scholar] [CrossRef]
- Schee, J.; Stuchlík, Z. Gravitational lensing and ghost images in the regular Bardeen no-horizon spacetimes. JCAP 2015, 6, 48. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Schee, J.; Ahmedov, B. Electromagnetic perturbations of black holes in general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2018, 97, 084058. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlík, Z.; Ahmedov, B. Electromagnetic perturbations of black holes in general relativity coupled to nonlinear electrodynamics: Polar perturbations. Phys. Rev. D 2018, 98, 085021. [Google Scholar] [CrossRef]
- Moffat, J.W.; Zhoolideh Haghighi, M.H. Modified gravity (MOG) and the Abell 1689 cluster acceleration data. Eur. Phys. J. Plus 2017, 132, 417. [Google Scholar] [CrossRef]
- Jawad, A.; Ali, F.; Jamil, M.; Debnath, U. Dynamics of Particles Around a Regular Black Hole with Nonlinear Electrodynamics. Commun. Theor. Phys. 2016, 66, 509. [Google Scholar] [CrossRef]
- Hussain, S.; Jamil, M. Timelike geodesics of a modified gravity black hole immersed in an axially symmetric magnetic field. Phys. Rev. D 2015, 92, 043008. [Google Scholar] [CrossRef]
- Babar, G.Z.; Jamil, M.; Lim, Y.K. Dynamics of a charged particle around a weakly magnetized naked singularity. Int. J. Mod. Phys. D 2016, 25, 1650024. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef]
- Majeed, B.; Jamil, M. Dynamics and center of mass energy of colliding particles around black hole in f(R) gravity. Int. J. Mod. Phys. D 2017, 26, 1741017. [Google Scholar] [CrossRef]
- Zakria, A.; Jamil, M. Center of mass energy of the collision for two general geodesic particles around a Kerr–Newman-Taub-NUT black hole. J. High Energy Phys. 2015, 2015, 147. [Google Scholar] [CrossRef]
- Brevik, I.; Jamil, M. Black holes in the turbulence phase of viscous rip cosmology. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950030. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M.; Jing, J. Chaotic motion of particles in the accelerating and rotating black holes spacetime. J. High Energy Phys. 2016, 2016, 82. [Google Scholar] [CrossRef]
- Hashimoto, K.; Tanahashi, N. Universality in chaos of particle motion near black hole horizon. Phys. Rev. D 2017, 95, 024007. [Google Scholar] [CrossRef]
- Dalui, S.; Majhi, B.R.; Mishra, P. Presence of horizon makes particle motion chaotic. Phys. Lett. B 2019, 788, 486–493. [Google Scholar] [CrossRef]
- Han, W. Chaos and dynamics of spinning particles in Kerr spacetime. Gen. Relativ. Gravit. 2008, 40, 1831–1847. [Google Scholar] [CrossRef][Green Version]
- De Moura, A.P.S.; Letelier, P.S. Chaos and fractals in geodesic motions around a nonrotating black hole with halos. Phys. Rev. E 2000, 61, 6506–6516. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar tensor vector gravity theory. JCAP 2006, 2006, 004. [Google Scholar] [CrossRef]
- Moffat, J.W.; Rahvar, S. The MOG weak field approximation and observational test of galaxy rotation curves. Mon. Not. R. Astron. Soc. 2013, 436, 1439–1451. [Google Scholar] [CrossRef]
- Moffat, J.W. Modified gravity black holes and their observable shadows. Eur. Phys. J. C 2015, 75, 130. [Google Scholar] [CrossRef]
- Moffat, J.W. Black holes in modified gravity (MOG). Eur. Phys. J. C 2015, 75, 175. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. Rotational velocity curves in the Milky Way as a test of modified gravity. Phys. Rev. D 2015, 91, 043004. [Google Scholar] [CrossRef]
- Wondrak, M.F.; Nicolini, P.; Moffat, J.W. Superradiance in modified gravity (MOG). JCAP 2018, 2018, 021. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. The bending of light and lensing in modified gravity. Mon. Not. R. Astron. Soc. 2009, 397, 1885–1892. [Google Scholar] [CrossRef]
- Atamurotov, F.; Abdujabbarov, A.; Rayimbaev, J. Weak gravitational lensing Schwarzschild-MOG black hole in plasma. Eur. Phys. J. C 2021, 81, 118. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Tadjimuratov, P. Can modified gravity silence radio-loud pulsars? Phys. Rev. D 2020, 102, 024019. [Google Scholar] [CrossRef]
- Haydarov, K.; Rayimbaev, J.; Abdujabbarov, A.; Palvanov, S.; Begmatova, D. Magnetized particle motion around magnetized Schwarzschild-MOG black hole. Eur. Phys. J. C 2020, 80, 399. [Google Scholar] [CrossRef]
- Bambi, C.; Cárdenas-Avendaño, A.; Dauser, T.; García, J.A.; Nampalliwar, S. Testing the Kerr Black Hole Hypothesis Using X-Ray Reflection Spectroscopy. Astrophys J. 2017, 842, 76. [Google Scholar] [CrossRef]
- Rezzolla, L.; Yoshida, S.; Zanotti, O. Oscillations of vertically integrated relativistic tori-I. Axisymmetric modes in a Schwarzschild space-time. Mon. Not. R. Astron. Soc. 2003, 344, 978–992. [Google Scholar] [CrossRef]
- Török, G.; Kotrlová, A.; Srámková, E.; Stuchlík, Z. Confronting the models of 3:2 quasiperiodic oscillations with the rapid spin of the microquasar GRS 1915+105. Astron. Astrophys. 2011, 531, A59. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Models of quasi-periodic oscillations related to mass and spin of the GRO J1655-40 black hole. Astron. Astrophys. 2016, 586, A130. [Google Scholar] [CrossRef]
- Šrámková, E.; Török, G.; Kotrlová, A.; Bakala, P.; Abramowicz, M.A.; Stuchlík, Z.; Goluchová, K.; Kluźniak, W. Black hole spin inferred from 3:2 epicyclic resonance model of high-frequency quasi-periodic oscillations. Astron. Astrophys. 2015, 578, A90. [Google Scholar] [CrossRef][Green Version]
- Kotrlová, A.; Šrámková, E.; Török, G.; Stuchlík, Z.; Goluchová, K. Super-spinning compact objects and models of high-frequency quasi-periodic oscillations observed in Galactic microquasars. II. Forced resonances. Astron. Astrophys. 2017, 607, A69. [Google Scholar] [CrossRef][Green Version]
- Stuchlík, Z.; Kotrlová, A.; Török, G. Resonant radii of kHz quasi-periodic oscillations in Keplerian discs orbiting neutron stars. Astron. Astrophys. 2011, 525, A82. [Google Scholar] [CrossRef]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Possible signature of the magnetic fields related to quasi-periodic oscillations observed in microquasars. Eur. Phys. J. C 2017, 77, 860. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kotrlová, A.; Török, G. Multi-resonance orbital model of high-frequency quasi-periodic oscillations: Possible high-precision determination of black hole and neutron star spin. Astron. Astrophys. 2013, 552, A10. [Google Scholar] [CrossRef]
- Kološ, M.; Shahzadi, M.; Stuchlík, Z. Quasi-periodic oscillations around Kerr-MOG black holes. Eur. Phys. J. C 2020, 80, 133. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Rezzolla, L.; Yoshida, S.; Maccarone, T.J.; Zanotti, O. A new simple model for high-frequency quasi-periodic oscillations in black hole candidates. Mon. Not. R. Astron. Soc. 2003, 344, L37–L41. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. HF QPOs in the neutron star binary system XTE J1701-462 fitted by the model of oscillating string loops. In Proceedings of the RAGtime 14–16: Workshops on Black Holes and Neutron Stars, Opava, Czech Republic, 11–19 October 2014; pp. 243–255. [Google Scholar]
- Stuchlík, Z.; Kološ, M. Mass of intermediate black hole in the source M82 X-1 restricted by models of twin high-frequency quasi-periodic oscillations. Mon. Not. R. Astron. Soc. 2015, 451, 2575–2588. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Mureika, J.R.; Moffat, J.W.; Faizal, M. Black hole thermodynamics in MOdified Gravity (MOG). Phys. Lett. B 2016, 757, 528–536. [Google Scholar] [CrossRef]
- Moffat, J.W. LIGO GW150914 and GW151226 gravitational wave detection and generalized gravitation theory (MOG). Phys. Lett. B 2016, 763, 427–433. [Google Scholar] [CrossRef]
- Rahvar, S.; Moffat, J.W. Propagation of electromagnetic waves in MOG: Gravitational lensing. Mon. Not. R. Astron. Soc. 2019, 482, 4514–4518. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. Masses and shadows of the black holes Sagittarius A* and M87* in modified gravity. Phys. Rev. D 2020, 101, 024014. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Figueroa, M.; Stuchlík, Z.; Juraev, B. Test particle orbits around regular black holes in general relativity combined with nonlinear electrodynamics. Phys. Rev. D 2020, 101, 104045. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Rayimbaev, J.; Turimov, B.; Atamurotov, F. Dynamics of magnetized particles around 4-D Einstein Gauss–Bonnet black hole. Phys. Dark Universe 2020, 30, 100715. [Google Scholar] [CrossRef]
- Juraeva, N.; Rayimbaev, J.; Abdujabbarov, A.; Ahmedov, B.; Palvanov, S. Distinguishing magnetically and electrically charged Reissner-Nordström black holes by magnetized particle motion. Eur. Phys. J. C 2021, 81, 70. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Rayimbaev, J.; Atamurotov, F.; Ahmedov, B. Magnetized Particle Motion in γ-Spacetime in a Magnetic Field. Galaxies 2020, 8, 76. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon & Breach: New York, NY, USA, 1973; pp. 343–450. [Google Scholar]
- Bian, W.H.; Zhao, Y.H. Accretion Rates and the Accretion Efficiency in AGNs. PASJ 2003, 55, 599–603. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Rayimbaev, J.; Ahmedov, B. Test particles dynamics around deformed Reissner-Nordström black hole. Phys. Rev. D 2020, 102, 124078. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M.; Morsink, S.M. Correlations in the Quasi-periodic Oscillation Frequencies of Low-Mass X-Ray Binaries and the Relativistic Precession Model. Astrophys. J. 1999, 524, L63–L66. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Kluźniak, W. A precise determination of black hole spin in GRO J1655-40. Astron. Astrophys. 2001, 374, L19–L20. [Google Scholar] [CrossRef]
- Kato, S. Resonant Excitation of Disk Oscillations by Warps: A Model of kHz QPOs. Publ. Astron. Soc. Jpn. 2004, 56, 905–922. [Google Scholar] [CrossRef]
- Kato, S. Frequency Correlation of QPOs Based on a Resonantly Excited Disk-Oscillation Model. Publ. Astron. Soc. Jpn. 2008, 60, 889. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Vrba, J. Epicyclic Oscillations around Simpson–Visser Regular Black Holes and Wormholes. Universe 2021, 7, 279. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).