Abstract
Local scale covariance posits that no privileged length scales should appear in the fundamental equations of local, Minkowskian physics—why should nature have scale, but not position preferences?—yet, they clearly do. A resolution is proposed wherein scale covariance is promoted to the status of Poincaré covariance, and privileged scales emerge as a result of ‘scale clustering’, similarly to the way privileged positions emerge in a translation covariant theory. The implied ability of particles to ‘move in scale’ has recently been shown by the author to offer a possible elegant solution to the missing matter problem. For cosmology, the implications are: (a) a novel component of the cosmological redshift, due to scale-motion over cosmological times; (b) a radically different scenario for the early universe, during which the conditions for such scale clustering are absent. The former is quantitatively analyzed, resulting in a unique cosmological model, empirically coinciding with standard Einstein–de-Sitter cosmology, only in some non-physical limit. The latter implication is qualitatively discussed as part of a critique of the conceptual foundations of CDM which ignores scale covariance altogether.
1. Introduction
For over a millennium, astronomers agreed on an observationally sound cosmological model which was founded on the premise that humans are at the center of the universe. They have since become much more modest with the inclusion of translation covariance as a fundamental principle in physics, but without treating scale covariance on equal footing, the primitive sin of anthropocentrism will not be fully atoned. Indeed, physics currently suffers from a manifest anthropocentric bias wherein the very small and very large are described using completely different, incompatible languages (quantum vs. classical), with ‘small’ and ‘large’ being defined relative to the scale of some (not particularly impressive) biological species.
Scale covariance is just as natural a symmetry as translation covariance: a fundamental description of nature should not include a privileged length scale, just like it should not include a privileged position; Both ought to appear as attributes of specific solutions rather than of the equations. However, this is not only a philosophically appealing principle. Speculating from astronomical measurements, what is happening elsewhere in the vast cosmos is pointless without the assumption of translation covariance. Equally pointless is any attempt at extrapolating terrestrial physics to scales much larger or smaller than our native scale, unless our description of nature is scale-covariant. Take Maxwell’s equations in vacuum as an example. All Maxwell knew was certain relations between the electric and magnetic fields, experimentally deduced by Faraday on scales of a few centimeters. Extrapolating those to the scale at which light is allegedly propagating was sound only because Maxwell’s equations are scale-free. This, however, is not the case with all physical theories ever proposed to describe matter: Schrödinger’s equation, Dirac’s, and the Standard Model are not scale-covariant in any reasonable sense of the term, let alone the sense in which they are translation- or Poincaré-covariant. Consequently, the findings at CERN and elsewhere on earth regarding the nature of matter, probing exactly of all possible scales, are of very limited value for astronomy, as any of an infinite number of new interactions between known matter could dominate on such large scales, and infinitely, many new stable particles—small-scale extensions of the Standard Model—could be contemplated. In other words, if local physics is not constrained by scale covariance, then with enough ‘epicycles’—modified gravity, exotic dark matter, quintessence, inflaton, etc.—any observational tension can and will be resolved. Moreover, if cosmology is decoupled from terrestrial physics, there will inevitably come a time when the inhabitants of Terra would stop financing this field. The encouraging finding reported in this paper is that the unique cosmological model respecting local scale covariance has no tunable parameters, already passes major tests, and predicts concrete deviations from CDM, even with regard to the late universe.
Our solution to the non-covariance problem, then, is to ‘simply’ represent matter in a manifestly scale-covariant form (minimally coupling its dynamical fields to gravity and adding the resultant action to the Einstein–Hilbert action). Once all physical objects of interest, gauges included, are represented this way, the result of any measurement can, in principle, be obtained. A unique cosmological model then follows by imposing a natural condition regarding the (observed) scale ‘selected’ by particles—a constraint on the space of solutions adding to standard large-scale spatial homogeneity—coinciding with Einstein–de-Sitter cosmology only in some non-physical limit. ‘Radical conservatism’, then, defying standard cosmology.
Granted that astronomy is mostly about the collection and interpretation of electromagnetic signals, the representation of matter ought to be sufficiently realistic to account for the emission and absorption of such signals. Einstein’s skepticism notwithstanding [1], the author’s [2,3] Extended Charge Dynamics (ECD) appears to be capable of doing so, and for the sake of completeness, we elaborate on this point in the discussion (Section 4). Nevertheless, the results obtained rely little on the specifics of ECD and mostly on the general characteristics of any scale-covariant representation of matter supporting electromagnetism and are therefore valuable in their own right.
Finally, “scale covariance/invariance” is a massively overloaded term in the context of cosmology, appearing in the literature countless times. Perhaps closest in spirit to ours are those models stemming from Weyl’s geometry, which extends Riemann’s diffeomorphism symmetry group with local rescaling of the metric ([4,5,6,7,8] being a very partial but representative list). While prima facie sharing our lack-of-absolute-local-scale philosophy, the actual gravitational theories imply otherwise. Weyl’s scale factor multiplying the Einstein’s metric becomes a spacetime dependent ratio between measurements based on ‘gravitational gauges’ and ‘material gauges’. Not surprisingly, the formal structure of those theories coincides with various varying-G or (‘Machian’) varying-particle-mass theories. In contrast, our approach is non-geometrical from the outset. As in previous papers by the author, it directly addresses the ‘elephant in the lab’: any measurement—not only length/time measurements—refers to a measured object and a gauge, both made of matter, yet that matter’s representation is currently incomplete at best (see discussion, Section 4). In fact, we see general covariance as a necessary condition for a consistent representation of matter and EFE—an integral part of such a representation ([9] Section 1). It follows that insofar as ‘teleportation’ of a physicist and his lab across spacetime can be given a consistent meaning—which is not always the case—his reports regarding local physics, local gravity included, would not change. Local scale covariance, then, is just another constraint imposed on a representation of matter for the reasons given above.
2. Scale Covariance and Its Conflict with the Equivalence Principle
Scale covariance is a symmetry of a physical theory in Minkowski’s spacetime (not to be confused with Weyl invariance). For concreteness, classical electrodynamics (CE) will serve as an archetype of a scale-covariant physical theory (there are good reasons to believe that this choice is more than a toy model; see Section 4). By CE, we mean a concrete realization of its two obvious pillars, referred to as the basic tenets of CE, which are: Maxwell’s equations in the presence of a conserved 1 source due to all particles (labeled by a)
with the antisymmetric Faraday tensor, and local ‘Lorentz force equation’
with the symmetric ‘matter’ e-m tensor associated with particle a. Defining the canonical tensor
we obtain from (1) and (4) Poynting’s theorem
Summing (3) over a and adding to (5), we obtain the local energy-momentum (e-m) conservation
and, purely by the symmetry and conservation of , also generalized angular momentum conservation
A concrete realization of the basic tenets of CE is scale-covariant if the following is a symmetry 2 for any
with any parameter of the realization unchanged. The exponent of is referred to as the scaling dimension of a density which, by definition, is 0 for the parameters of the realization. For , (8) is just the CPT transformation. Extending (8) to all therefore combines the two symmetries.
When shifting to a different scale, the electric charge of a particle, whether elementary or composite, does not change by virtue of scale invariance of electric charge . In contrast, the scaling dimension of the particle’s magnetic dipole moment is 1 and hence scale-dependent. If, further, the particle is sufficiently isolated then, since the electromagnetic field in its neighborhood is dominated by its electric current, one can associate the global e-m tensor P (6) in that neighborhood with the particle (or particles in the case of a composite), referring to it as . The particle’s self-energy (or mass), , incorporating also the electromagnetic self-energy (which must be a finite quantity in a well-defined CE), therefore has scaling dimension , while its three-dimensional angular momentum, , is scale-invariant. Note that these quantities’ scaling dimensions coincide with their familiar length dimensions, thus giving meaning to the latter which is independent of the concept of a ‘system of units’.
2.1. The Zero Point Field and Broken Scale Covariance
The reason why most physicists do not consider the lack of scale covariance a problem is, probably, that nature does appear to single out privileged scales. All Hydrogen atoms around us, for example, have a common Bohr radius. However, all such atoms also have the same position (on cosmological scales), and this does not imply translation covariance is not a symmetry of the equations describing Hydrogen atoms. It does mean, nonetheless, that for scale covariance to be compatible with observations, some dynamical process must exist in the universe, causing all Hydrogen atoms to ‘cluster in scale’, similarly to the way gravity induces spatial clustering.
Continuing the above analogy, for matter to cluster in space, its position must be able to change. Likewise, for it to cluster in scale, its scale, viz., in (8), must be able to change. As such a ‘motion in scale’ must still respect local e-m conservation, and given the scaling dimension, , of self-energy, for a particle moving towards larger scales, there must be a net imbalance between its advanced and retarded self-fields, favoring the latter. This is a direct consequence of applying Stokes theorem to e-m conservation (6) (see, e.g., Equation (100) in [2]). Likewise, for a particle moving towards smaller scales, the imbalance must favor its advanced field 3. In [2] (Section 3.3), it is shown why such a time-dependent, particle-specific ‘selection’ of radiation field is not only consistent with the basic tenets, but even appears to be mandated by them. Note the contrast to some Brans–Dicke-type or Machian theories [10,11,12], which can also be interpreted as implying ‘motion in scale’ of some sort. Those introduce a new ‘cosmic field’, having no convincing observational justification, which uniformly scales the masses of all particles (equivalently, the gravitational constant)—parameters of a scale non-covariant theory.
The total electromagnetic field at a point x in empty spacetime, containing both advanced and retarded components of such scale-moving particles lying on the light-cone of x, will be referred to as the zero-point-field (ZPF) at x, a name borrowed from Stochastic Electrodynamics (SED) [13], although it does not represent the very same entity. In particular, our ZPF is not some global homogeneous solution of Maxwell’s equations. Instead, it is a byproduct of different particles exchanging e-m in the spirit of action-at-a-distance electrodynamics [14,15].
Scale clustering and the nature of the ZPF are both discussed in greater detail in [9], but for the purpose of the current paper, the following natural assumption would suffice: All stable particles in the universe are in some state of (mutual) ‘energetic equilibrium’ such that their time-averaged self-energy is constant—in the usual empirical sense, to be made more precise in Section 3.1. This entails the appearance of parameters of non-zero scaling dimensions in the equations of physics, which are the exact counterparts of some fixed coordinate value, , appearing in the equations of a ‘spontaneously broken’ translation covariant equation, viz., in an effective description incorporating the specific solution responsible for (such as the c.o.m. of the earth–moon system in the equations describing the tide). Furthermore, just like the result of any calculation associated with a measurement, it must not depend on the value of nor on the values of such scale non-scalars. Constants which are scale-scalars, on the other hand, are the counterparts of fixed coefficients, defining the equations.
Notable scale scalars are c, ℏ, and e, but different triplets define empirically distinct physics only if their respective are distinct. Besides particle masses, of scaling dimensions , the relevant non-scalars arise in linearized gravity. Now, gravity in general and, strictly speaking, also linearized gravity, is by no means a Minkowskian theory, on equal footing with CE. However, for the purpose of the current paper, the two can be partially merged by writing CE in a generally covariant form and retaining only the leading order in the metric perturbation (of the Minkowskian metric). The standard result entails the appearance of two non-scalars in linearized Einstein’s equations, seen as a spin-2 Minkowskian theory: and , of scaling dimension 2 and , respectively (the meaning of ‘P’, standing for ‘Proper’, will transpire in the sequel), when the metric perturbation is treated as a scale-scalar. We shall see that those will indeed not appear in the final result of our calculations.
2.2. The Slim Equivalence Principle
Using CE to express matter in cosmology requires first that it be consistently fused with GR. This is done by expressing flat spacetime CE in an arbitrary coordinate system via the use of a ‘metric’ . The resulting equations are supplemented by Einstein’s field equations (see [9] for this different take on general covariance)
with P the generally covariant CE e-m tensor, and the expression for the Ricci tensor in terms of the metric, (signature ), and its derivatives:
Note that G and in (9) are just a couple of (dimensionless) numbers (in the case of ECD, G can be set to 1 without loss of generality, as it can be absorbed into rescaled ECD fields and constants). In contrast, their Minkowsikian counterparts, and , being scale non-scalars, cannot have definite values, and their values in a given system of units are to be read from a CE solution describing a gravitating system and the relevant gauges.
The basic tenets (1)–(3) become their obvious generally covariant extensions. In particular, by the antisymmetry of F, Maxwell’s equations simplify to
while covariant e-m conservation reads
with . From (10)(a) and the antisymmetry of , one obtains as a consistency condition, generalizing (2). Using the same construction as in appendix D of [2], one can then show that if a coordinate system exists for which is slowly varying over the extent of the particle, then (11) implies that the path of the ‘center of the particle’, (given a clear meaning there), is described by the geodesic equation
with ‘dot’ standing for the derivative with respect to any parametrization, s, of . From (12), we see that along , from which follows , the proper-time differential.
Einstein’s equivalence principle states that, around any spacetime point, x, a local coordinate system, y, exists for which and . The geodesic equation at x, expressed in the y coordinates, then has the form . It follows that, to the extent the above special form of the geodesic equation implies free fall, and insofar as the second derivatives of the metric are negligible, the Minkowskian form of CE locally holds true in a freely falling frame. We shall dub this simple consequence of the tensorial nature of and its Minkowskian signature the slim equivalence principle.
However, Einstein went a step beyond the slim equivalence principle. Mesmerized by the mathematical similarity between GR and Riemannian geometry, , or rather the coordinate-invariant interval is endowed with a selective metrical role, involving space/time measurements 4. This addition conflicts with CE’s scale covariance, which prohibits assigning a priori metrical meaning to coordinate intervals. We are therefore forced to use directly the definition of a measurement: The result of any measurement is some dimensionless number extracted solely from the e-m tensor. For example, a standard length gauge is represented by some compact region in space, occupied by a relatively higher energy density. The length of an elongated object in standard length units, likewise occupying some compact region in space, is just the number of standard gauges exactly fitting the object and similarly with the object’s other physical attributes, such as mass, luminosity, etc. We shall be very explicit about this procedure in Section 3.1.
3. The Friedmann Model for a Scale-Covariant-CE Universe
The overall framework used in this section is the so-called Friedmann model, i.e., we seek a solution of EFE (9)
for some fictitious metric
representing a maximally symmetric space (we have restricted ourselves for the time being to the flat space case, ). On the r.h.s. of (13) is a similarly fictitious, -independent e-m tensor which, in turn, is assumed to represent the coarse-grained matter distribution
with K a normalized kernel. The time in (14), denoted also by , is known as the conformal time, and the reader is warned to keep that in mind, as the standard equations of cosmology will take a somewhat unusual form. The ‘tilde pseudo tensors’ and are therefore involved in dynamical changes on cosmological time scales, while the fluctuations around them are only relevant on much smaller scales.
The three-tensor must be invariant under rotations so as to respect the isotropy of space. For the same reason, the vector, , must vanish, leaving us with
with and arbitrary functions of (conformal) time alone. Note that both are merely components of the e-m tensor at this stage, whose relation to concrete observations will have to await Section 3.2—a complication entailed by the slimness of our equivalence principle.
The pseudo tensor incorporates two distinct contributions: electromagnetic, due to the ZPF, and one from matter, i.e., from regions of non-vanishing mechanical e-m T. In the case of the ZPF, the tracelessness of and necessitate
Inside matter itself, we have also a contribution from T, spoiling the tracelessness of . For non-relativistic matter, the usual form shall be used
but it is instructive to re-derive (18) in our unusual context: Multiplying e-m conservation (6) by and integrating by parts over a region in three-space, we get
By pulling out of the integral on the r.h.s. of (19), ‘equation-of-state’ (18) follows when is the momentum density of a collection of non-relativistic, ‘on-shell’, and (at most) locally interacting particles, in which case a particle’s momentum is just its mass times its c.o.m.’s velocity. The r.h.s. of (19) is then just twice the kinetic energy of all particles (and always less than ). In the early universe—we shall later argue—this is no longer the case. The and in matter-dominated regions must then be calculated separately for the electromagnetic component of , and for , with a result which, in general, could be different from (18). Given the large uncertainty in the amount of matter in the universe, it is even conceivable that some such out-of-scale-equilibrium/off-shell matter is also present in the current epoch of the universe, possibly rendering a cosmological constant redundant. This appealing possibility, however, will not be explored in the current paper.
A mixture of ZPF and ordinary, non-relativistic matter, with a ratio , is therefore represented by an ‘equation-of-state’ for (16)
We shall later see that must be non-trivially time-dependent.
To leading order in the fluctuations, covariant e-m conservation (11) implies the same equation for :
with and the Christoffel symbol derived from the metric (14). This implies
in general, and in particular for & (but not individually for ZPF or matter components thereof). If we wish to include electromagnetic contribution, , of origin other than the ZPF, which is not interacting (significantly) with matter (coming from, say, the CMB, whose associated electromagnetic field can be assumed to superpose incoherently with that of the ZPF), then its equation-of-state, (17), and (21) readily integrates 5 to .
Finally, Equation (13) for provides the first Friedmann equation 6 for
with subscript ‘A’ standing for current (Astronomer’s) values.
3.1. The Cosmological Redshift
Matter in the universe, even if contributing negligibly to the coarse-grained e-m , is indispensable in two complementary senses. First, without matter, there are no astronomical objects and no equipment to observe them—the latter mandated by the slimness of our equivalence principle. Second, without matter, there is no ZPF; from the discussion in Section 2.1, it follows that matter and the ZPF are just different facets of the same physical entity.
We shall represent (the centers of) particles in the universe by a collection of world-lines, , which is compatible with the time-independent homogeneity of . Such world-lines must be those of comoving particles, viz., have the form , so as to respect the above compatibility condition at any time. By virtue of derived from the metric (14) vanishing, those are indeed the world-lines of ‘freely falling’ particles. Mach’s vague principle is thereby given a concrete meaning, as the world-line of a fixed spatial coordinates triplet, belonging to a local frame which is rotating relative to the local comoving frame, will no longer solve the geodesic Equation (12).
Next, we wish to investigate the observational consequences of a gradual change in the intensity of the ZPF over cosmological time scales—a consequence of (21) and (22). The main challenge we face is in the need to give meaning to a comparison of properties of matter at distinct conformal times, without resorting to ‘universal gauges’ at every point in the universe, manifested in the (full) equivalence principle. Instrumental to our analysis is the following postulate of scale equilibrium: For any given particle species, elementary or composite, there exists a fixed ratio between the (average) energy density of the particle at x and . By the symmetry of a Friedman model and the assumption of scale-clustering (Section 2.1), within each constant- slice, all such particles should have a common density. However, that the above ratio is -independent, viz., that the ‘average vacuum energy density’ sets the standard for energy density 7 is more subtle, and although it can be motivated further, we only expect it to emerge as an approximation in a rigorous analysis, incorporating also the fluctuations in the density of matter and its phase transitions over cosmological time scales.
As a first example, we analyze a primary observable in cosmology, known as the luminosity distance of an isotropically radiating astronomical object,
Above, , referred to as the proper flux, is the measured energy-flux in terms of some energy-flux standard, as determined by an astronomer with (fixed) coordinates (the spatial part ) at conformal-time , and L is the object’s total power, or luminosity, as would have been determined by the astronomer, had the remote astronomical object been ‘teleported’ to earth (or the astronomer to the object) from its point in spacetime (‘S’ for source/star/supernova...) with the retarded conformal-time, , where
Defining the proper distance, , between two points at a given conformal-time as the minimal number of local length gauges exactly fitting between them, the homogeneity of space implies
with depending on the choice of standard length gauge and on time. Since null geodesics satisfy , a wave of sufficiently high-frequency, , viz., , retains its wavelength in the x coordinates. Given the definition of the redshift, z,
Equation (25) then implies that a standard length gauge, when teleported to an earlier conformal time, measures a larger coordinates interval by a factor , i.e.,
or, equivalently,
The proper-flux of a distant object can be computed either classically, via Poynting’s theorem, or by resorting to the language of ‘photons’, with identical results (that the concept of a photon is compatible with a CE ontology is shown in [16] and in greater detail in [9]). The former, somewhat longer derivation, appears in Appendix A. In the case of photons, (26) leads to
(This standard expression can be found in virtually any textbook on GR, but there, the proper-distance derived from the metric is being used). The first term in (29) is just the luminosity, L (as determined, e.g., by an astronomer near ) divided by the surface area of a sphere with proper radius , over which the emitted photons are distributed. The second term involves our slim equivalence principle, namely, the assumption that the proportionality constant relating the measured energy and frequency of a photon, both having scaling dimension , is the same at and , hence one power of , and that the rate at which photons penetrate the sphere of radius r, on which earth resides, is diminished by another such factor 8. Plugging (29) in (23) gives
Expression (30), coinciding with that of standard cosmology, implies other commonalities: Using (27), the observed angular diameter of a sphere with proper diameter D is the standard
with the so-called angular diameter distance. Using (30), the sphere’s surface brightness, , has the usual dependence. Both relations apply also in the case of .
To test our cosmological model against observations, we still need to express r in (30) as a function of z or, equivalently, z as a function of . To this end, we change coordinates to the local Minkowskian frame at both and , implying there. In these new coordinates, the previously identical coordinate extent of a single wave cycle transforms as , and the value of the ZPF density as . We thus arrive at two (locally) Minkowskians frames, with length gauges whose representations are related by a scale transformation (8) for some . Our postulate of scale equilibrium, combined with the scaling dimension of energy density, , readily gives the ratio between the local coordinate extents, ℓ, of the length gauges
Combined with the transformation of , the definition of the redshift, (26), gives
To make contact with standard cosmological terminology, we take the derivative of (27) with respect to at . The derivative of z (at ) is computed using (32),
The (locally) exponential expansion implied by (33) (even for a constant ) is misleading due to the non-physical nature of the conformal time . To see its physical content, we proceed as follows. Denoting by the coordinate interval spanned by a comoving standard length-gauge, and (33) imply the shrinkage
By our slim equivalence principle, this must also be true for the conformal-time interval between two consecutive ticks of a comoving physical clock and, in particular, of a ‘light clock’—two parallel mirrors, separated by a single standard length gauge, with light ray bouncing in between (this choice respects our implicit choice). It can then be easily shown that the growth rate of with respect to the time, , shown by a comoving light-clock (our counterpart of the cosmological time in standard cosmology), satisfies
Choosing , (25) mandates . Setting in (35) and dividing by , (27) then implies that, in our model, corresponding to the usual z-dependent Hubble parameter, viz., (in conformal time), is , where
The extra (z + 1) above, reflecting the different time standards of A and S, could have been deduced also from (25) and (28). Combining with (32) and (35) then gives an important relation
which, with (30), gives
with the locally inferred, dimensionful Hubble’s constant. Equation (35) can be naively interpreted as either an expansion of the universe, a collective shrinkage of matter, or both—neither will be truly adequate.
To fully define a cosmological model, we still need to specify a third equation, complementing (21) and (22) in determining the three unknown functions of : . It should be clear that the ratio is a quantity which, in principle, can be derived from the underlying physics. Specifically, insofar as our postulate of scale equilibrium holds true, each particle can be seen as a standard length gauge undergoing a shrinkage (34). From our postulate of scale equilibrium, the effect this has on is deduced by taking a large coordinate volume and calculating the resulting differential change in the part of that volume taken by matter, with the obvious result
Cosmic scale phase transitions of matter would only have a marginal influence on the validity of (40), but in the early universe (40) is completely invalid; see Section 4.
Eliminating between (40) and (41) gives
Next, we extend our model to curved spaces, using the metric
where k is any non-vanishing real. By virtue of the spatial part also describing a homogeneous space, the previous flat space results can essentially be copy-pasted, with only three differences. First, in (25) applies only in the local Cartesian coordinates, where effectively equals r; the proper distance then becomes the number of standard length gauges exactly fitting along a geodesic curve connecting and at , making this number an extremum with respect to small deformations of the curve. Second, the r.h.s. of (22) receives a term . Third, in the expression of (30), for the luminosity distance, . To arrive at these results, one only needs to decompose the previous teleportation operation into two commuting stages: spatial, using the three metric, and the previous, temporal stage, implementing some local scale transformation by a factor .
As a concrete example for the above procedure, consider the observational signature of a standard ruler. A transverse comoving ruler of length ℓ is defined as two mutually close comoving points of equal r, measured by a local observer to have a proper separation equal to . To compute its observed angular size, , we decompose its teleportation to its location in spacetime, , into two commuting stages. In the first, the three-metric in the observer’s hyper-surface is used to move the ruler from the origin to . Making standard use of the spatial part of the metric (43), the angular separation of the ruler’s end-points is calculated to be . Then, temporally teleporting the ruler to the retarded conformal time increases by a factor which is dropped out by the definition of a comoving standard ruler. As null geodesics in our coordinates x satisfy , is clearly the measured angular size of the ruler. With (31) we then get , which is the expression for the angular size also in standard cosmology.
Standard rulers ‘pointing at us’ have their observational signature in the redshift difference between their end points. Repeating the above procedure, the spatial teleportation stage gives a coordinate separation . After temporally teleporting to the retarded time, (38) readily gives a redshift difference , again, formally coinciding with standard cosmology.
3.2. Comparison with Observations
The slimness of our equivalence principle necessitates prudence in associating the dynamical variables of the model with observations. We have already seen that to convert a coordinate difference to proper distance, one must divide the former by the coordinate extent, , of a standard length gauge. Similarly, to convert to the corresponding measurement, one must divide it by the numerical value of the energy-density associated with a standard energy-density gauge, expressed in local x-coordinates—call it . Now, the postulate of scale equilibrium tells us that . It then follows from (40) that the proper (viz., measured) density behaves as , which is the standard, purely geometrical expression for (non-relativistic) matter density. Similarly, (32) gives the standard . The fluctuations, , representing objects in the universe, must also be divided by before being compared with the fluctuations at a different surface. Using the transformation rule of standard gauges (as defined at the end of Section 2), it can then easily be shown that the measured (“Proper”) values of and (and of the speed-of-light ) as deduced by a local observer from linearized/Newtonian gravity, are teleportation invariant, viz., just some numbers which depend on the choice of standard gauges being teleported.
The above scheme for coping with scale covariance is sufficient if one is interested in the reports of future and past generations of astronomers relative to ours, but it cannot provide the proportionality constants, and , without explicitly representing the gauges as CE solutions. This fact restricts the reports of present-day astronomers using our model to dimensionless quantities only which, by their nature, do not depend on such proportionality constants. Whether knowingly or not, this is a restriction cosmologists tend to take upon themselves anyhow.
As the ultimate result must be dimensionless, rather than expressing it as a combination of independent dimensionful quantities, one may as well do the same with a maximal set of independent dimensionless quantities. Besides experiment-specific dimensionless quantities, such as angles, redshifts, or luminosity ratios, there are only five such independent quantities: (where , etc.); the baryonic and radiation ‘density parameters’, respectively,
where in our dark-matter-free model. Note indeed the absence of and .
The remaining two dimensionless parameters could be k and , but a more conventional choice would be:
with the current Hubble distance.
The baryonic density parameter, is directly determined from the ‘count’ of baryonic matter. The figure published by the Planck collaboration, , is consistent with the direct count. Nonetheless, given that just a couple of years ago, the direct count gave only half this value, the Planck figure should better be viewed as a lower bound, and with a much larger uncertainty. The radiation parameter is currently negligible, .
Our related dark-matter model ([9] and Section 4) must be further advanced in order to provide independent stringent bounds on but those will most likely be on the order of 1. As for , all model-independent bounds on its value are consistent with . Finally, as the Hubble distance is so much larger than the size of galaxies, any value of which is not absurdly large is compatible with observations involving local gravitation.
Moving to actual observations, there are two primary ways of determining the relative values of the luminosity distance, , at different redshifts (or equivalently, by (31), of or ), using either standard candles, primarily type Ia supernovae, or the so-called transverse BAO standard ruler [17]. Comparing the relative values of the Hubble distance, , makes use of the line-of-sight BAO ruler. Note that the ‘ruler’s length’, ℓ, and the ‘candle’s luminosity’, L, do not appear in such relative distances.
To compute our model’s and , one propagates backwards in (from ) the three dynamical variables, , and , via the system (21), (22) and (40), with , , and as initial conditions, arriving via (32) and (42) at and , respectively, which is used to express in terms of z. For astronomers to currently see a redshift (rather than blueshift), must be a monotonically increasing function in the current epoch of the universe, further taken to be positive. Like in standard cosmology, the map from our model’s seven 9 variables and constants to the five (current, dimensionless) observable parameters, implies a two-dimensional parameter degeneracy.
Normalizing both distances by for convenience, in the regime , our model reduces to standard (Einstein–de-Sitter) cosmology. This is so because, in such regime, . Substituting in (32) , using (40), viz., , and solving for gives
as in standard, conformal time cosmology (when ). From (38) then follows that the luminosity distance (30) has the standard z-dependence.
The above coincidence certainly does not imply that the principle of scale covariance is invalid in a negligible-ZPF universe. It does explain, nonetheless, why complete disregard for such a fundamental principle—assumed, of course, to be respected by nature—could have resulted in a cosmological model which is not in severe conflict with observations.
It appears, then, that consistency with observations requires but, remarkably, our model comes close to reproducing the CDM curves already at (Figure 1). This relatively small value of is further mandated by our associated dark-matter model, which is briefly discussed in Section 4 next.
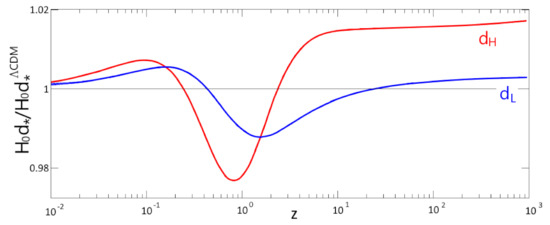
Figure 1.
Normalized distances relative to their, similarly normalized, CDM curves (, , ), for model’s parameters: , , , (). Such small deviations from CDM would become noticeable soon, when CHIME starts singing.
In the regime, spacetime becomes effectively Minkowskian on large enough scales. To wit, since in this regime , we get in (32) and a vanishing (42), implying the vanishing of . This regime is relevant to the far future where indeed vanishes asymptotically, but the de-Sitter (future conformal-) singularity implies the divergence of in (42), and the vanishing of necessarily comes with the divergence of . A nearly balanced battle of infinities ends with an eternally increasing—in terms of proper-time (36)—unbounded , viz., a ‘big-rip’ scenario. Note, nonetheless, that once all standard gauges are ripped apart, teleportation becomes ill-defined; hence, the predictions of our model, as is, are meaningless (as in the case of the very early universe which is discussed below).
4. Discussion: Towards a Full-Fledged Scale-Covariant Cosmology
Why challenge the concordance model? Despite being experimentally rather sound, CDM rests on shaky conceptual foundations. Moreover, recent precise measurements have begun revealing ‘cracks’ in its alleged experimental integrity, with only epicyclic repairs in sight. In this section, we elaborate on its shortcomings, showing how a full-fledged, scale-covariant cosmological model would be conceptually much sounder. In future publications, we intend to propose natural-to-the-model fixes to the said experimental cracks. As scale covariance is a symmetry of (the representation of) matter, the discussion below would necessarily spill into particle physics and its shaky conceptual foundations which, in turn, must involve QM’s. This brings us back to the point made in the introduction, regarding the anthropocentric scale bias of current physics as a whole.
- The Standard Model of particle physics on which CDM is based is not scale-covariant.
One can either reject the principle of scale covariance (few would) or else declare SM, hence also CDM, fundamentally wrong. There is no middle way. On the other hand, making use of scale-covariant CE to represent matter might (rightfully) appear farfetched. Nevertheless, there are good reasons to believe otherwise. First, as explained in great detail in [2], CE means different things to different people. If point-charges CE is meant, then CE is simply ill-defined due to the classical self-force problem. If it is some concrete, well-defined realization of the basic tenets, then there is currently only one such proposal (to the author’s best knowledge) dubbed extended charge dynamics (ECD) (first appearing in [3] and then fine-tuned and related to the classical self-force problem in [2]), and that realization is indeed scale-covariant in the sense of symmetry (8). Second, as can be expected, a formally conserved Noether current associated with scale covariance exists for ECD, implying, among others, that the scale/mass of a particle is conserved, which conflicts with our assumption that particles can ‘move in scale’. This assumption is not some model-specific curiosity but rather a generic feature of any scale-covariant theory in which particles acquire their observed mass dynamically. Remarkably, the associated ECD charge can ‘leak’ into singularities around which ECD charges are centered (appendix of [2]). This is a peculiarity not shared by the (integrable and conserved) ECD e-m tensor or electric current, both similarly diverging.
There are further reasons to not outright dismiss CE in its ECD realization, on the grounds of being an unrealistic representation of matter. In the cases of a single relativistic charge and multiple interacting non-relativistic charges, ECD has been shown [16] to be a plausible ontology underlying the statistical description of Dirac’s and Schrödinger’s equations, respectively. There are also positive indications [9] that ECD may be the ontology in the subatomic domain, and that ‘scale transitions’ are routinely observed in the associated experiments (but evidently not interpreted as such). At the very least, ECD is a proof-of-concept for the embedding of (scale non-covariant) particle physics in a scale-covariant framework.
- The representation of matter in CDM mixes incompatible classical and quantum notions.
Our coarse-grained ‘tilde tensors’, and , appearing in (13), are both finite classical quantities. In contrast, the fundamental representation of matter in CDM uses QM (QFT). To get a similar categorial equality between the right and left sides of EFE, one takes the expectation value of the quantum field associated with the e-m tensor, with respect to some ‘universal wave-function’, , allegedly encoding the matter content of the universe. Now, in standard QM, the expectation value of an operator represents certain repeated measurements associated with it, averaged over an ensemble represented by the wave-function. As there is only a single universe, it is therefore unclear what that expectation value stands for and how to treat the fluctuations around it, let alone who is doing the measurement. What is worse is that even the ‘shut-up-and-calculate’ approach cannot be implemented in this case, for two reasons: First, the usual infinity subtraction schemes do not work even in an empty universe, viz., ; the VEV of the energy density is both highly ambiguous and manifestly incompatible with cosmological observations [18] (The situation in SED is no better—the SED ZPF is a meaningless infinity. Indeed, the vacuum e-m tensor must be proportional to —the only Lorentz invariant tensor—and yet have a vanishing trace—a contradiction). Second, SM is the result of fitting twenty or so parameters 10 against data streaming from particle accelerators, such as scattering probabilities, life-times, etc., which has not proven itself yet outside this narrow context. The first time it was confronted with a phenomenon which could not have been tested in accelerators—the so-called neutrino oscillation phenomenon—it completely collapsed. Moreover, even in that narrow context, the very notion of a quantum field is not even necessary (as it is in classical field theories). SM can be formulated entirely as an algebraic structure involving Feynman diagrams or path-integrals 11.
- CDM relies on the existence of dark-matter which hitherto evaded direct detection.
Of the two leading contenders in the missing matter challenge—dark-matter and modified gravity—the former is a clear favorite. The l.h.s. of Einstein’s equations (the “marble wing”) is the simplest nontrivial equation for , fully consistent and experimentally well-tested (albeit in a limited domain), whereas the r.h.s. (the “cheap wood wing”) is a mess—see the previous bullet. However, dark-matter theorists make no attempt to rebuild the r.h.s. from marble, sticking to the familiar, phenomenological role of the e-m tensor, endlessly adjusting its properties to conform with new observations. In contrast, ECD’s ‘marblization’ of the r.h.s. results in the e-m tensor of ‘visible matter’ containing a ‘transparent part’, allegedly mistaken for dark-matter. This further explains why ordinary and dark contributions to the e-m tensor are on the same order.
The strongest, most direct support for dark-matter comes from the dynamics of galaxies and clusters. The explanation of those within our model is that, as in action-at-a-distance electrodynamics [14,15], the ZPF at any point in empty space is due to the sum of individual fields, each “adjunct” to specific particles, implying that the ZPF in the neighborhood of galaxies and clusters should be stronger than the coarse-grained average . This ultra-low-density, transparent component of the e-m tensor, when integrated over galactic scales, creats an illusion of ‘dark-matter’ whose distribution is determined by that of baryonic matter (see [9] for details). In [9,16], we argue that also when moving in the opposite direction in scale, towards the microscopic, the effects of such a feeble ZPF become consequential and are allegedly at the heart of virtually any quantum phenomenon.
Cold dark-matter further plays a critical role in the large-scale structure formation, according to CDM. Our dark-matter model possibly provides a substitute in the form of a stronger feed-forward amplification of matter clustering: as matter falls into a relatively matter-dense region, it also increases the surrounding ‘ZPF halo’. This energy halo warps space, inducing a MOND like, viz., long (-er than ) range potential which, in turn, increases the attraction basin of the over-dense region.
Finally, cold-dark matter is absolutely essential for CDM to be compatible with the observed heights of the acoustic peaks. Although not yet fully analyzed, the associated ‘dark-matter’ model [9] qualitatively agrees with these observations: The dominance of the first peak is due to the same feed-forward mechanism, mentioned above in the context of large-scale structure formation. The second peak is initially strongly suppressed, in comparison, by the deep potential well created by ‘dark-matter’. The third peak therefore sees no such deep well, and so on (note that in the early universe, ; hence, the expansion is effectively as in CDM). However, as advocated in the introduction, the assumption that beyond the surface-of-last-scattering (s.o.l.s), terrestrial baryonic physics still applies, even if true, is highly speculative (in fact, the earliest direct evidence for baryonic matter is from cosmic dawn, at ). Nevertheless, as the electric charge of a particle is identically conserved, the idea that the origin of the CMB’s anisotropy is plasma oscillation is both plausible and compatible with an epoch in which matter was not yet (fully) baryonic, but more ‘jet like’. The ‘jets’ referred to are those charged particles seen in particle detectors just before they ‘morph’ into metastable particles. Those, we hypothesize, are just ECD solutions out of scale-equilibrium (with the ZPF), resulting from the trauma of the collision—solutions which do not represent known particles only with a time-varying scale. Likewise, the ‘hyper trauma’ of the big-bang (see below) has left matter out of equilibrium with the ZPF, but in a much deeper sense: The ZPF itself is out of equilibrium, hence the much longer time it took matter to attain a meta-stable equilibrium with it, compared with that measured in particle detectors. Recalling from Section 2.1 the role of the ZPF, as a middleman for e-m exchange between particles, matter and the ZPF are just different facets of a single entity—if one is unstable then so must be the other. As the matter–ZPF entity gradually attained its present-day equilibrium, scaling symmetry (8)—its CPT discrete subgroup included—became spontaneously broken. Baryonic matter dominating the universe then introduced a privileged local scale and an imbalance between matter and antimatter—two concepts which only apply to matter in scale equilibrium.
- CDM requires inflation.
Preceding the primordial plasma oscillation, according to CDM’s popular extension, is cosmic inflation. That hypothetical epoch is incompatible with scale covariance, ill-defined by its quantum nature (as discussed above), and invokes yet another form of energy—the inflaton.
An alleged triumph of inflation theory is its prediction of scale-invariant and Gaussian density perturbations of matter, seeding the plasma oscillation. Now, Gaussian noise is perhaps the most ubiquitous form of noise, so a greater challenge would be to derive a cosmological model predicting a non-Gaussian spectrum (roughly quoting Neil Turok). As for scale invariance, this is just what the scale-free epoch preceding entails; the only spectrum retaining its form under a scale transformation, , is a (non-integrable) power law, , for some .
Inflation theory is appended to CDM in order to solve the latter’s flatness and horizon problems. As is, the horizon problem would plague also our model, but also as is, our model is inapplicable to the early universe. As discussed following (18), in the conjectured, scale-free epoch of matter, there are many possible alternatives to (18) (or its relativistic counterpart) for which there is no horizon problem.
The flatness problem (formulated in terms of (47) as the notion of critical density is inapplicable in our case) is that for to nearly vanish, it must be much more so—unnaturally more so—in the early universe. One can argue that this is not really a problem as, both in our model and in CDM, ultimately becomes much smaller than it has ever been, including today, so large relative variations in could be just nature’s preference. However, for those who do not, our model can alleviate their unease, since comparing the values of at two distinct times is only meaningful so long as teleportation is well-defined. When the universe was in its scale-free epoch, possibly not much earlier than , standard length gauges took a completely different form if it at all existed. It is therefore possible that the largest, well-defined relative value was still big, but not fantastically so.
Finally, lest the reader protest that the previous discussion is meaningless without entering the uncharted realm of quantum gravity, we mention that by ‘relieving from its metrical duty’ via the slimness of our equivalence principle, the conceptual difficulties with quantum gravity disappear; space and time no longer have any meaning other than that which is related to the readings of clocks and other gauges. Quantum gravity then becomes just the statistical description of a classical, generally covariant e-m tensor (see [16] for the flat spacetime case). Now, it is true that the coarse graining operation, , in our Friedmann model, is closely related to the ensemble average operation which is used [16] to establish CE as a plausible ontology underlying QM’s statistical content, and that therefore quantum gravity could be helpful, if not essential, in determining . This extra knowledge, however, would boil down to a modified equation-of-state with regard to which we have pled ignorance.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Classical Derivation of the Luminosity Distance
By direct substitution, one can show that for an arbitrary function f, the following ansatz satisfies covariant e-m conservation (11) for the metric (14):
Being traceless and locally propagating at light-speed, it is an immediate suspect for the e-m tensor associated with a spherical electromagnetic pulse, readily generalizing to via in the denominator. However, a perfectly spherically symmetric electromagnetic wave cannot exist; the closest there is to it is an incoherent superposition of plane-waves with random polarizations, creating a statistically spherical symmetry. Plugging, therefore, into Maxwell’s Equation (10), a single such linearly polarized, plane-wave ansatz
results in . Consistency with (A1) mandates which, indeed, solves the equation.
Up to some constant which depends on the choice of standard gauges, converting (A1) to the proper-canonical tensor amounts to dividing it by the local (note that being a local ratio between two quantities of the same type, the ratio can be taken in any coordinate system). Taking some point, , along the null geodesic connecting and , the following is then evidently true:
where is r (24) with there. Letting approach , and using (28), we have
independently of (equivalently, ). Implicit in (A4) is our assumption that the astronomer’s luminosity measurement, L, of a teleported copy of S, equals to the luminosity reported by that astronomer, had he been teleported to . Plugging (A4) into (A3), we obtain
Combined with (25) and (32) finally gives (29):
Notes
| 1 | The antisymmetry of F implies that solutions of Maxwell’s equations exist for a conserved source only. |
| 2 | Transformation (8) is a formal symmetry of point-charges CE, written in a manifestly scale-covariant form [2,3]. |
| 3 | The most general (sensible) radiation field generated by a particle’s electric current, j, is given by
More accurately, the above two equations do not uniquely define K, but the remaining freedom can be shown to translate to a gauge transformation . |
| 4 | Much later work incorporated this addition of Einstein into the formalism of GR by ‘dotting the commas’ in the flat, scale non-covariant matter Lagrangian, which introduces into it a dependence on and its first derivatives. Insofar as that representation is realistic, the slim equivalence principle then implies that coordinates do have a metrical meaning which is consistent with the privileged length scale introduced by matter. Note that, in the early days of GR, in the absence of even a candidate for such representation, Einstein’s addition had to appear as a postulate. |
| 5 | Our definition (16) of contains an extra relative the usual one. In Section 3.2, we recover the standard observable. |
| 6 | The second (...order) Friedmann equation, , together with the first, gives (21), which is therefore exact, despite being only the leading order term in the fluctuations of (the exactly covariantly conserved) P. The reason for this is that is formally equivalent to the e-m tensor of a perfect fluid in a symmetric space. |
| 7 | This is implicit in standard cosmology, when the cosmological constant is seen as the fixed vacuum energy density. See, however, Section 4. |
| 8 | This follows from the ‘conservation of photons’: In the x coordinates, as in flat spacetime, the number of photons penetrating a sphere of radius R per oscillation of the pulse is independent of R. A non-vanishing z only means that the astronomer considers a unit oscillation as a longer period by a factor , compared with an observer at S. |
| 9 | This includes G, as it appears in tandem with in (22). In standard cosmology, the corresponding map is 6-to-4, and the degeneracy is removed by the choice of units and by setting either or to 1. |
| 10 | Twenty parameters is a generous figure. Combining all the published and unpublished attempts to parameterize accelerators data, the community of high-energy physicists acted as a giant neural network trained against the data. That network had thousands of parameters, of which only twenty turned out significant. |
| 11 | The one place where a quantum field appears necessary and gives correct predictions (modulo some dubious infinity subtractions which, at any rate, are inapplicable in the case of the universe as a whole) is in the case of the Casimir force, which can be explained and derived much more directly as a Van der Waals force. |
References
- Lehmkuhl, D. General relativity as a hybrid theory: The genesis of Einstein’s work on the problem of motion. Stud. Hist. Philos. Sci. B 2019, 67, 176–190. [Google Scholar] [CrossRef] [Green Version]
- Knoll, Y. Quantum mechanics as a solution to the classical self-force problem. arXiv 2018, arXiv:0902.4606. [Google Scholar]
- Knoll, Y.; Yavneh, I. Scale covariant physics: A ‘quantum deformation’ of classical electrodynamics. J. Phys. A 2010, 43, 055401. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Long Range Forces and Broken Symmetries. Proc. R. Soc. Lond. A 1973, 333, 403–418. [Google Scholar]
- Canuto, V.; Adams, P.J.; Hsieh, S.H.; Tsiang, E. Scale-covariant theory of gravitation and astrophysical applications. Phys. Rev. D 1977, 16, 1643. [Google Scholar] [CrossRef]
- Canuto, V.; Hsieh, S.H.; Adams, P.J. Scale-covariant theory of gravitation and astrophysical applications. Phys. Rev. Lett. 1977, 39, 429. [Google Scholar] [CrossRef]
- Maeder, A. An alternative to the ΛCDM model: The case of scale invariance. Astrophys. J. 2017, 834, 194. [Google Scholar] [CrossRef] [Green Version]
- Wesson, P.S. Scale-invariant gravity: A simple formulation. Astron. Astrophys. 1981, 102, 45–52. [Google Scholar]
- Knoll, Y. Dark Matter as Variations in the Electromagnetic Zero-Point Field Induced by Baryonic Matter. Symmetry 2020, 12, 1534. [Google Scholar] [CrossRef]
- Wetterich, C. Universe without expansion. Phys. Dark Univ. 2013, 4, 184–187. [Google Scholar] [CrossRef] [Green Version]
- Jain, P. A Flat Spacetime Model of the Universe. Mod. Phys. Lett. A 2012, 27, 1250201. [Google Scholar] [CrossRef] [Green Version]
- Narlikar, J.; Arp, H. Flat spacetime cosmology—A unified framework for extragalactic redshifts. Astrophys. J. 1993, 405, 51–56. [Google Scholar] [CrossRef] [Green Version]
- de la Pena, L.; Cetto, A.M. The Quantum Dice: An Introduction to Stochastic Electrodynamics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wheeler, J.A.; Feynman, R.P. Interaction with Absorber as the Mechanism of Radiation. Rev. Mod. Phys. 1945, 17, 157–181. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Feynman, R.P. Classical Electrodynamics in Terms of Direct Interparticle Action. Rev. Mod. Phys. 1949, 21, 425–433. [Google Scholar] [CrossRef] [Green Version]
- Knoll, Y. Quantum mechanics as a statistical description of classical electrodynamics. Found. Phys. 2017, 47, 959, Erratum in arXiv 2019, arXiv:1804.00509. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational probes of cosmic acceleration. Phys. Rep. 2013, 530, 87–255. [Google Scholar]
- Jérôme, M. Everything you always wanted to know about the cosmological constant problem (but were afraid to ask). Comptes Rendus Phys. 2012, 13, 566–665. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).