Abstract
In the presence of a thermal medium or an external electro-magnetic field, neutrinos can interact with photon, mediated by the corresponding charged leptons (real or virtual). The effect of a medium or an electromagnetic field is two-fold—to induce an effective vertex and to modify the dispersion relations of all the particles involved to render the processes kinematically viable. It has already been noted that, in a medium, neutrinos acquire an effective charge, which in the standard model of electroweak interaction comes from the vector type vertex of weak interaction. On the other hand, in a magnetized plasma, the axial vector part also starts contributing to the effective charge of a neutrino. This contribution corresponding to the axial vector part in the interaction Lagrangian is denoted as the axial polarisation tensor. In this note, we outline the calculation of the axial polarization tensor to odd and even powers in . We further show its gauge invariance properties. Finally, we infer upon the zero external momentum limit of this axial polarisation tensor.
1. Introduction
Neutrinos are of significant importance because of the observable imprints they leave on astrophysical or cosmological observables through their interactions. These imprints are related to their mass, charge, dipole moment, etc. These are generally unexplainable through a standard model of particle physics. In a cosmological context, they play a significant role in the synthesis of primordial light elements [1,2], modifying the power spectrum of cosmic microwave background (CMB) anisotropies [3] and in the large scale clustering of matter in the universe [4]. They contribute to many physical processes involving electromagnetic interactions (many of them involve astrophysical situations [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]), a list of them and the origin of the same can be found in [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95]. In this note, we would rather consider the astrophysical part of it.
To understand neutrino-astrophysics, we need to understand the physics of the models that dictate neutrino behaviour. To have predictable power, such models should be re-normalizable. To have a re-normalizable model of the physics of elementary particles, the tree level interactions are protected from being realised in nature. Thus, at the tree level, neutrinos do not couple to photon in the standard model of particle physics, and this coupling can only take place at a loop level, mediated by the fermions and gauge bosons. This coupling can give birth to off-shell photons only, since, for on-shell particles, the processes like and are restrained kinematically. Only in the presence of a medium can all the particles be on shell as there the dispersion relation of the photon changes, giving the much required phase space for the reactions. Intuitively, when a neutrino moves inside a thermal medium composed of electrons and positrons, they interact with these background particles. The background electrons and positrons themselves have interaction with the electromagnetic fields, and this fact gives rise to an effective coupling of the neutrinos to the photons. Under these circumstances, the neutrinos may acquire an “effective electric charge” through which they interact with the ambient plasma.
Finite neutrino charge at the tree level is however possible with the introduction of gauge bosons with an extra U’(1) symmetry [86,87,88]. As a result, neutrinos can acquire an intrinsic charge and turn out to be a Dirac particle.
Whatever may be the source of electric charge of neutrino (induced or intrinsic), neutrino–photon interactions have many far reaching consequences in this universe. To provide an example, because of in-medium neutrino–photon interaction, the supernova explosions are realized in nature. It is highly possible that the neutrinos actually dump a fraction of their energy inside an exploding star during its stellar evolution. For instance, during a type II supernovae collapse [12], neutrinos are produced deep inside the proto-neutron star surge out, carrying an effective energy whose order of magnitude estimate is ∼ erg/s. It is conjectured that the neutrinos deposit some fraction (ranging between 1 to 10%) of its total energy during the explosion through different kinds of neutrino electromagnetic interactions, e.g, , , , to name a few. It is important to note here that all of these processes are of order (where is the four Fermi coupling constant). However, the amount of energy dumped by these mechanisms to the mantle of the proto-neutron star seems to be barely sufficient to blow the outer part of the same. The celebrated paper of [15] could account for erg of energy release by hydrodynamic processes taking place in a nuclear media. The supernova shock wave was found to get stalled in respective computer simulations. Hence, neutrino-mediated processes were invoked so as to revive the shock wave, so that there can be a delayed shock revival. However, this attempt was not entirely successful [16].
However, inside a star, a nonzero magnetic field would be present owing to different hydrodynamics induced dynamo mechanisms. It is usually conjectured that this magnetic field of the supernova-progenitor—when compressed to the size of the neutron star—during the Super Nova (SN) type II explosion, its strength can reach up to or more in most of the regions of the nascent proto-neutron star. This follows due to the conservation of surface magnetic field of the SN precursor. The symbol m denotes the mass of electron. In addition, in the rest of this paper, we would refer to field strengths of this magnitude as critical field strength . Given the possibility of strong field generation in proto-neutron star, it is worth investigating their role of interaction in a magnetized media. This would help in understanding if the magnetic field induced effects can account for the release of erg of energy in a super nova type II explosion—that is, to find out if the strong magnetic field induced contributions can exceed the same due to unmagnetized ones by the desired orders of magnitude. This happens to be one of our objectives of this work.
Apart from this, there are several high energy processes in astrophysics that are in need of some explanation for asymmetric energy transfer. This happens to be an extra motivation to this investigation. To provide an example, during gamma ray burst, a prompt gamma ray flash from the optically thick environment of the progenitor has been noticed in many GRB events and are found to be anisotropic in their distribution in space and too fast in their temporal appearance to point to the existence of a class of feebly charged weakly interacting particles at the source [17].
Other examples where explanations using asymmetric processes can be useful—which are explosions in magnetars [18] accompanied by associated jets [20] and the presence of unexplained anomalous drift- velocity that newly born pulsars are found to be accompanied with [23]. Ideally, in a symmetric SN explosion, the associated newly born neutron star should be stationary. However, they are seen to be born with some velocity—usually referred to in the literature as pulsar kicks. Since the presence of a field breaks the rotational symmetry for a system, it thus makes a good choice to look for signatures of the same while studying neutrino electromagnetic interactions in a magnetized media.
1.1. Intrinsic Charge of Neutrino
We have introduced the origin of neutrino charge in the Introduction. They happen to be (i) intrinsic () in their origin and can be accounted for from studies beyond the standard model of elementary particle physics, (ii) medium induced neutrino effective charge () owing its existence to in-medium effects upon standard model left-handed neutrinos. The second one gets contributions to itself coming from the vector vertex of neutrino- interaction (denoted as ), and the axial vertex of interaction (denoted as ). The second one is realised in nature only in the presence of magnetized matter (medium).
1.2. Induced Charge of Neutrino
In this paper, we concentrate upon the effective neutrino photon interaction vertex coming from the axial vector part of the interaction. From there, we estimate the effective charge of the neutrino (in a magnetised medium). We name the axial contribution in the effective neutrino photon Lagrangian as the axial polarisation tensor , which we will define in the next section. We discuss the physical situations where the axial polarisation tensor arises, then show how it affects the physical processes. The effective charge of the neutrino has been calculated previously by many authors, the induced charge calculated in the references [82,83,84,85] and the intrinsic charge in [86,87,88,89,90,91,92,93]. Any discussion about the origin and magnitude of a very fundamental entity–intrinsic neutrino charge , both experimental and theoretical, deserves special attention. Since that is not the main focus of our work, we will refrain from any such attempt here, except attempts to compare their magnitude obtained in various terrestrial laboratory conditions with that of obtained for different background media. This particular attempt is made to keep free from medium induced contributions. At the end, we would like to mention that any analysis on the estimates of from experimental and astrophysical observations is yet to be performed to the best of our knowledge and understanding.
The plan of the paper is as follows. We start with Section 2 which deals with the formalism through which the physical importance of is appreciated. In Section 3, the general form factor analysis of “axial polarisation tensor” on the basis of symmetry arguments is provided. In Section 4, we show the fermion propagator in a magnetised medium, and, using the same, explicitly write down in the rest frame of the medium. In the next section, i.e., Section 5, we show the formal proof of gauge invariance of . In Section 6, we calculate the effective electric charge from the expression of the axial polarisation tensor odd in even in as well as even in odd in . In Section 7, we discuss our results and conclude by touching upon the physical relevance of our work. Section 8 covers an outlook on future perspectives. In the Appendix A, we outline the construction of the basis tensors for from 4-vectors, having appropriate CPT transformation properties. We follow the natural system of units in which .
2. Formalism
In this work, we consider neutrino momenta that are small compared to the masses of the W and Z bosons. We can, therefore, neglect the momentum dependence in the W and Z propagators, which is justified if we are performing a calculation to the leading order in the Fermi constant, . In this limit, four-fermion interaction is given by the following effective Lagrangian:
where and f are the neutrino and the corresponding lepton fields, respectively. In Equation (1), and are the weak vector and axial vector coupling strengths, respectively. For electron Z boson vertex,
where the first terms in and are the contributions from the W exchange diagram and the second one from the Z exchange diagram. Here, is the Weinberg angle (where ) and is the four Fermi coupling constant (, where is the proton mass).
With this interaction Lagrangian, we can write down the matrix element for the Cherenkov amplitude as
where is the photon polarisation tensor, and Z is the wave function renormalisation factor inside a medium. The term is defined as
which looks exactly like the photon polarisation tensor, but doesn’t have the same interpretation here. The symbol e in Equation (5) represents the coupling constant for the U(1) gauge field (). The momentum labels of the propagators can be understood from the corresponding Feynman diagram (Figure 1). Henceforth, we would call it the polarisation tensor. is defined as
which we call the axial polarisation tensor. Both the polarisation tensor and the axial polarisation tensor are obtained by calculating the Feynman diagram given in Figure 1 drawn in a four-Fermi-limit.
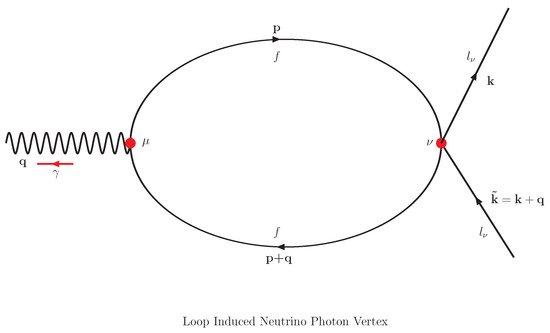
Figure 1.
One-loop diagram for the effective electromagnetic vertex of the neutrino in the limit of infinitely heavy W and Z masses.
The off-shell electromagnetic vertex function is defined in such a way that, for on-shell neutrinos, the amplitude is given by:
where k is the photon momentum. Here, is the the neutrino spinor and stands for the electromagnetic vector potential. In general, would depend on k and the characteristics of the medium. With our effective Lagrangian, the vertex is given by
Charge radius of a neutrino can be obtained from the vertex function given by Equation (8). This observable in general should be gauge independent, UV finite and a renormalisation group invariant.
On the other hand, the neutrino charge radius can also be estimated using an effective field theory approach. It was performed in [95] from the coefficients of a four fermion effective field theory that was constructed from the current–current co-relators involving neutrinos and other standard model fermions, after integrating out the heavy degrees of freedom. In this approach, the energy scale of the coefficients are extrapolated to the mass of the electron to relate them to the charge radius of neutrino. The effective charge we are evaluating is related to the charge radius. Given the expression for one, it is possible to find the same for the other, from the expression of the previous one. The physical situation considered in this work is substantially different from that of [95] because of the presence of magnetic field and the medium. They belong to two different paradigms so we will not deal with it here any further.
The effective charge of the neutrinos is defined in terms of the vertex function by the following relation [82,83]:
For massless Weyl spinors, this definition can be cast into the form:
where is the helicity of the fermions in the external line. Since we do not consider the right-handed neutrino, we therefore choose . Before going to estimate neutrino-charge in various situations, we would like to state that this induced neutrino charge vanishes in vacuum. This statement is true in general for any number of physical dimensions ’d’ and in any gauge parameter [96,97].
While discussing about , it should be remembered that it has two vertices, one is axial vector vertex and the other one is a vector vertex; The current conservation relation for the electromagnetic vertex is obeyed in the form,
which also happens to be the current conservation condition.
In order to calculate the Cherenkov amplitude or the effective charge of the neutrinos inside a medium, we have to calculate . The formalism thus discussed is a general one, and we extend the calculations previously done based on this formalism to the case where we have a constant background magnetic field in addition to a thermal medium. In doing so, we give the full expression of in a magnetised medium and explicitly show its gauge invariance. We also comment on the effective charge contribution from the axial polarisation part.
Discussing about the effective charge of the neutrinos in a medium, the way we have done, it should be mentioned that, although it is interesting to find it theoretically, it is not the “charge” with which the neutrinos couple with a magnetic field. From the definition of the electromagnetic vertex as given in Equation (7) and the definition of charge in Equation (9), it is clear that we are interested to find the coupling of the photon field with and not . The magnetic interaction will come from the term , but we will see at the end of the calculation that no exists in the limit , , whereby we cannot speak of any possible interaction of the neutrinos with the external static uniform magnetic field.
3. General Analysis
We start this section with a discussion on the possible tensor structure and form factor analysis of , based on the symmetry of the interaction. To begin with, we note that in the vacuum should vanish. This follows from the following arguments. In vacuum, the available vectors and tensors at hand are the following:
The two point axial-vector correlation function can be expanded in a basis, constructed out of tensors , , and vector . Given the parity structure of the theory, it is impossible to construct a tensor of rank two using and . Thus, the only available tensor (with the right parity structure) we have at hand is . The other vector needed to make it a tensor of rank two is . As we contract with , , since is completely antisymmetric tensor of rank four, the corresponding term vanishes.
On the other hand, in a medium, we have an additional vector , i.e., the velocity of the centre of mass of the medium. Therefore, the polarisation tensor can be expanded in terms of form factors along with the new tensors constructed out of and the ones we already had in the absence of a medium as
Here,
with
In the rest frame of the medium, the four velocity is given by . It is easy to see that the longitudinal projector is not zero in the limit , and is also not zero in the above-mentioned limit. This fact is responsible for giving nonzero contribution to the effective charge of neutrinos.
It has already been mentioned that, in a medium, we have another extra four vector and hence it is possible to construct the axial polarisation tensor of rank two, out of , , , i.e, that would verify the Ward identity for the two point function. An explicit calculation of verifies the tensor structure of it as predicted here. It is worth noting that this contributes to the Cherenkov amplitude, but not to the effective electric charge of the neutrinos since, for charge calculation, we have to put the index . In the rest frame, only exists that forces the totally antisymmetric tensor to vanish.
In a constant background magnetic field in addition to the ones mentioned in Equation (12), one has the freedom of having other extra vectors and tensors (to first order in field strength), such as
along with
Explicit evaluation of the axial polarisation tensor, in a constant background magnetic field, is (however, the metric used by the authors in references mentioned is different from that of us) [98,99],
where , and . According to the notation used in Equation (20), and . Lastly, and are functions of . It is easy to note that, in consonance with the general parity structure of the theory, the basis tensors for this case are , and . The most general tensorial structure including medium and field effects can be obtained using the four-vectors provided in the Appendix A of this text.
We would like to digress a little and point out that the polarization operator given in Equation (20) can be obtained from a fermion triangle diagram having one axial current and two vector currents when one of the vector current carries the momentum that is ultra soft. It has been shown in Ref. [100] that this diagram won’t admit any radiative corrections due to various non-renormalisation theorems.
4. One Loop Calculation of the Axial Polarisation Tensor
Since we investigate the case with a background magnetic field, without any loss of generality, it can be taken to be in the z-direction. We denote the magnitude of this field by . Ignoring first the presence of the medium, the electron propagator in such a field can be written down following Schwinger’s approach [101,102,103]:
where and G are as given below:
where
and we have used
and m is electron mass. To make the expressions transparent, we specify our convention in the following way:
Of course, in the range of integration indicated in Equation (21), s is never negative and hence equals s. In the presence of a background medium, the above propagator is now modified to [104]:
where
and
for a fermion propagator, such that
Here, contains the distribution function for the fermions and the anti-fermions:
denotes the Fermi–Dirac distribution function:
and is the step function given by:
Here, the centre of mass four velocity of the medium is u, in the rest frame, it looks like (in units .) , , when T is the temperature and is the chemical potential.
4.1. The Expression for in Thermal Medium and in the Presence of a Background Uniform Magnetic Field
The axial polarisation tensor is expressed as
Leaving out the vacuum contribution (the contribution devoid of any thermal effects) and the contributions with two thermal factors, we are left with
The vacuum part has already been done in [98] and the thermal part is related with pure absorption effects in the medium, which we are leaving out for the time being.
4.2. to Even and Odd Orders in the Magnetic Field
We calculate to even and odd orders in the external magnetic field and call them and . The reason for doing this is that the two contributions have different properties as far as their dependence on medium is concerned, a topic which will be discussed in the concluding section. Calculating the traces, we obtain
and
Here,
which contain the information about the distribution functions. In addition, it should be noted that, in our convention,
If we concentrate on the rest frame of the medium, then . Thus, the distribution function does not depend on the spatial components of p. In this case, we can write the expressions of and using the relations derived earlier [105] inside the integral sign, as
and get
and
The symbol signifies that the above relations are not proper equations, and the equality holds only inside the momentum integrals in Equation (34).
5. Gauge Invariance
5.1. Gauge Invariance for to Even Orders in the External Field
The axial polarisation tensor even in the external field is given by
Using Equation (44) in the rest frame of the medium, we have
Here, throughout, we have omitted terms such as , since, by the application of Equation (39), we have
which is zero. After rearranging the terms appearing in Equation (48), and by the application of Equations (39) and (40), we arrive at the expression
Because of the presence of terms like and if we contract by , it vanishes.
5.2. Gauge Invariance for to Odd Orders in the External Field
The axial polarisation tensor odd in the external field is given by
where is given by Equation (45). The general gauge invariance condition in this case
can always be written down in terms of the following two equations:
where is that part of where the index can take the values 0 and 3 only. Similarly, stands for the part of , where can take the values 1 and 2 only. contains , which, from Equation (45), is as follows:
and contains , which is
Equations (52) and (53) implt that one should have the following relations satisfied,
and
Out of the two above equations, Equation (56) can be verified easily since
Now, we look at Equation (57). We explicitly consider the case (the case leads to similar results). For ,
Apart from the small convergence factors,
where we have defined the parameters
From the last two equations, we can write
which implies
The equation above is valid in the sense that both sides of it actually act upon , where
The above equation can also be written as
Transforming to , variables and, using the above equation, we can write the parametric integrations (integrations over s and ) on the left-hand side of Equation (57) as
where
The integration over the and variables in Equation (68) can be represented as
Here, the second step follows from the first one as the first integrand containing the function vanishes at both limits of the integration. The remaining integral is now only a function of and is even in . However, in Equation (68), we have sitting, which makes the the integrand odd under integration in the left-hand side of Equation (57), as is an even function in . Thus, the integral as it occurs in the left-hand side of Equation (57) vanishes as expected, yielding the required result shown in Equation (52).
6. Effective Charge
Now, we concentrate on the neutrino effective charge. From the outset, it is to be made clear that we are only calculating the axial contribution to the effective charge (in a forthcoming publication, we will comment on the vector contribution to the effective charge of the neutrino [106,107]). We can now write the full expression of the axial polarisation tensor as
where and are given by Equations (45) and (44) in the rest frame of the medium.
6.1. Effective Charge to Odd Orders in External Field
In the limit when the external momentum tends to zero, only two terms survive from . Denoting , we obtain
The other terms turn out to be zero in this limit. The above equation shows that, except the exponential functions, the integrand is free of the perpendicular components of momenta. This implies that we can integrate out the perpendicular component of the loop momentum. Upon performing the Gaussian integration over the perpendicular components and taking the limit , we obtain
It is worth noting that the s integral gives
and the integral gives
Using the above results in Equation (72) and using the delta function constraint, we arrive at
In deriving Equation (75), pieces proportional to in the numerator were neglected. Now, if one makes the substitution, and sets , one arrives at
Here, are the functions , and , as given in Equation (31), which are nothing but the Fermi–Dirac distribution functions of the particles and the antiparticles in the medium. The new term is defined as follows:
and it can be expanded for small external momenta in the following way:
where . Noting that
one can use this expansion in Equation (76), to arrive at:
The expression for when expanded in the powers of the external momentum is given by
up to first order terms in the external momentum . In the expression above, in units where .
6.1.1. Effective Charge for
In the limit, when , one can use the following expansion,
Now, using Equation (80) in Equation (78), we get
The first term vanishes by symmetry of the integral, but the second term is finite and thus we get:
To perform the momentum integration, use of the following integral transform turns out to be extremely convenient
Identifying with and as (since the square root opens up), one can easily perform the Gaussian integration without any difficulty. The result is:
Performing the u integration, the axial part of the effective charge of neutrino, being called (the subscript a in is to denote the axial vector vertex origin of the same)—in the limit of —turns out to be
Here, is the angle between the neutrino three momentum and the background magnetic field . The superscript on denotes that we are calculating the axial contribution of the effective charge. is the modified Bessel function (of the second kind) of order one (for this function, ), which sharply falls off as we move away from the origin in the positive direction. Recall that is the axial coupling constant of the electron in the loop as already mentioned in Section 2. However, as the temperature tends to zero, Equation (85) seems to blow up because of the presence of , but would damp its growth as , hence the result remains finite.
The factor of is the contribution of the magnetic field and along with are the contributions from the medium effects of the background magnetized media. The constant is related to the mass of W and Z bosons and is the helicity of the neutrino spinors.
6.1.2. Effective Charge for
Here, we would try to estimate neutrino effective charge when and . We would like to emphasise that the last condition should be strictly followed, i.e., temperature . Using Equations (78) and (79), we would obtain
Neglecting m in the expression in , we would obtain
The same can also be written as
The expression for the effective charge then turns out to be
It can be seen from the expression above that only left-handed Weyl neutrinos acquire induced charge. The expressions for in the limit of and can further be cast, after expressing and substituting the values of the physical constant , in the following forms, for :
and the same for :
It should be noted that Equation (91) goes to zero as . For a sufficiently dense medium, when and low temperature, can be as close to unity. For example, when 10 MeV, and and , the may turn out to be the order of electric charge e.
6.2. Effective Charge at Even Order in the External Field and Their Coupling with the Magnetic Fields
From the part of , which is even in the external fields, we see from Equation (49) that
which shows that to even orders in the external field will vanish when , . This implies that there will be no contribution to the effective neutrino charge from the sector which is even in the powers of . Can the neutrinos that are propagating in a magnetised plasma couple with the classical magnetic field? The situation is a little bit subtle here, as the vertex of the neutrinos with the dynamical photons do get changed here due to the presence of the magnetic field, but this change cannot induce any electromagnetic form factor responsible for coupling of the neutrinos with any magnetic field. In order to find the effective charge of the neutrinos which couples them with time independent magnetic field, one should look for (as given in Equation (7)) the ’s, where . A magnetic field in the z-direction is given by a gauge where , are both non zero, or one of them is nonzero. Thus, to calculate the charge that is essential for the neutrino current to couple with a magnetic field, one has to put the index in Equation (70) and take the limit , and see which component of exists in the pre-mentioned momentum limit. For the odd part, we see from Equation (45) that
which goes to zero as the photon momentum tends to zero. By the same argument, it follows that, for , there is vanishing contribution. Thus, it shows that there is no effective magnetic coupling from the odd part. For the even part, it is seen from Equation (44) that only survives, and is given by
which vanishes in the limit when the external momentum goes to zero. Thus, from this, we can say that has no contribution for any charge of the neutrinos which can couple them with the magnetic field.
7. Conclusions
In our analysis, we have calculated the contributions to to odd and even orders in the external constant magnetic field. The main reason for doing so is the fact that and , the axial polarisation tensors to odd and even powers in , have different dependence on the background matter. Pieces proportional to even powers in are proportional to , an odd function of the chemical potential. On the other hand, pieces proportional to odd powers in depend on , and are even in and, as a result, it survives in the limit . Equations (90) and (91) corroborate this observation. The underlying theory, being a theory of weak interaction, violates parity but preserves CP and CPT. The same can be verified from the C, P and T transformation properties of Equations (35) and (36). We have estimated the field dependent part of the induced neutrino effective charge from odd and even contribution of .
The leading order estimate of that follows from our work can be grouped into two categories: (i) non degenerate and (ii) highly degenerate . The complete estimate of belonging to the first class can be approximated by keeping the leading order effects in () for , and it turns out to be
The same belonging to the second class can similarly be estimated for as
For Weyl neutrinos, one can notice that only left-handed neutrinos contribute to the effective charge provided the angle between neutrino momentum and the magnetic field is less than . We would like to point out that the neutrino charge for dependent part has turned out to be direction-dependent—a result that is expected because of the presence of magnetic field that breaks the isotropy of the system.
For the sake of completeness, we next provide the estimate of the same originating from the unmagnetized medium; the same is
where is the Debye radius. This result was originally obtained in [82,83,85].
A magnitude wise comparison of neutrino charge owing to the vector vertex contribution from unmagnetized medium and that owing to axial vector vertex contribution from magnetized medium would reveal why, in some environments, energy transfer mechanism is isotropic and in some of the same is anisotropic. For instance, if we make a comparison of the induced charge that neutrinos acquire in SNII, white dwarves and red-giants with the same that neutrinos acquire in the environment of GRB, Magnetar or astrophysical objects having jets associated with strong magnetic fields, we shall see that the size of in the latter dominates over of the former.
Having the limiting expressions of neutrino charge for different physical situations, it makes sense to compare the contributions and determine the dominant one. Using the limiting expressions, the ratio of the neutrino axial charge in magnetized medium to that in unmagnetized medium for and turns out to be
and, in the degenerate limit, it is
Notable points in these two expressions are the appearance of in the ratio and the appearance of the factor . Thus, for and , the axial induced neutrino charge can dominate over that due to unmagnetized or weakly magnetized media. Thus, in a strongly magnetized media, neutrino induced high energy processes are likely to introduce anisotropy in the physical processes taking place in astrophysical situations e.g., GRB, magnetar and anisotropic distribution of isolated moving pulsars with initial kick. This is what was one of the motivating issues behind this investigation, laid out in the Introduction section of this work.
In view of the investigations being carried out to find the intrinsic charge of neutrino, the induced charge of the same due to an unmagnetised medium acquires some importance—the reason being the presence of an ambient plasma of varying density all over the universe that can contribute to the intrinsic charge as the terrestrial and celestial experiments are being performed. For that purpose, we have considered three astrophysical objects (i) type-II supernovae ( = 350 MeV, MeV), red giant (400 keV and 10 keV) and white dwarf (500 keV and keV) [108]. The estimates of the induced charges are:
To complete the comparison of the induced charges, we provide the estimate of induced neutrino electric charge coming from axial vertex contribution next. The limiting expression of the same is found in Equation (96). Assuming an old pulsar (age years, K and fermi momentum (100 MeV) [109], the for this case for left handed neutrinos turns out to be
when the angle () between the neutrino momentum and the ambient magnetic field tends to zero. For a very conservative estimate of , the induced charge would be of the order of .
There are several laboratory based studies available in the literature that tried to put a bound on neutrino effective charge. This charge can be intrinsic or induced . Out of these, for an intergalactic field and for G were obtained from time of flight estimate from SN-1987A in [110], was obtained in [111] from a SLAC electron beam dump experiment, and was obtained in [112] demanding charge neutrality of the universe. The limits in terrestrial laboratory based experiments were found to be significantly larger in size—for instance, estimates of the same in scattering experiments performed in reactor based experiments dedicated for measuring neutrino effective charge as was explored in [38,81] and in the TEXONO reactor based experiment [113,114,115]. The reactor limit on neutrino charge as was reported in [113] happened to be with 90% C.L. (considering the Debye length for Ge detector to be 0.68 m).
On the other hand, the induced charge reported in [85,116] is due to medium effects in astrophysical situations. This induced charge is not due to any intrinsic property of neutrinos and hence can vary from situation to situation. Their estimates can be best verified through consistency checks of various medium dependent processes.
However, the medium induced charge has an important role in establishing the intrinsic charge of neutrino. Because the terrestrial experiments aiming to find are contaminated with medium effects, the induced charge would add on to the intrinsic charge, thus affecting the conclusions. For instance, many body effects of Ge used in determining in TEXONO experiments [113,114,115] enter in the estimates of through the Debye radius. On the other hand, even in the absence of , there will be a contributing factor due to loop and medium effects (entering through Debye length). This factor should be sub-dominant. Our estimates show that, for charge-neutral neutrinos, the contribution to the effective neutrino charge is of the order of , which is twelve orders less than reported in [113,114,115] from these experiments. If we consider the effect of atmospheric plasma at standard temperature and pressure, it turns out to be , which is also way beyond the recognisable contribution compared to the results reported in [113,114,115].
8. Outlook
In this work, we have explored the physical implication of medium induced neutrino effective charge for celestial as well as terrestrial events. We have found many situations where their effect can be substantial. However, in addition to what we have discussed, there are other issues of beyond the standard model physics that can be connected to the same. For example, existence of non-zero mass for neutrino [117,118] indicates a beyond the standard model issue involved in the neutrino sector. Similarly, the existence of various electromagnetic properties of neutrinos like charge, etc., if confirmed, can be considered as a consequence of the physics beyond the standard model. However, in order to indicate the corrections appearing from beyond the standard model physics, one needs to quantify the same appearing from medium induced effects. In this paper, a small step was taken in that direction. More about it will be communicated elsewhere.
Author Contributions
A.K.G. has contributed in conceptualization, and writing of the original draft, V.S. has contributed in methodology, supervision and investigation involved in preparation of the draft, D.S. has contributed in software, Investigation and verification, A.C. has contributed in software, visualisation and verification. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Existing policy has been followed for both the institutions.
Informed Consent Statement
Every author has given their consent for this work and the conclusions.
Data Availability Statement
The work in this text is theoretical; therefore, no data are available for this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Structure of Axial Polarization Tensor
The axial polarization tensor given by Equation (70) can be expressed in terms of the form factors and basis tensors constructed out of:
following [119,120], where , , and are normalization constants given by
Here, the variable, . The same for vacuum part of was done in [106]. The medium induced part can be constructed keeping the CP symmetry of and the ward identity of at the electromagnetic vertex . More about it will be conveyed in a separate communication.
References
- Raffelt, G.G. Stars as Laboratories for Fundamental Physics; University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of General Theory of Relativity; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Winberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Dolgov, A.D. Cosmological Implications of Neutrinos. Surv. High Energy Phys. 2002, 17, 91–114. [Google Scholar] [CrossRef][Green Version]
- Llamas-Bugarin, A.; Gutierrez-Rodriguez, A.; Gonzalez-Sanchez, A.; Hernandez-Ruiz, M.A.; Espinoza-Garrido, A.; Chubikalo, A. Stellar energy loss rates beyond the standard model. Eur. Phys. J. Plus 2020, 135, 481. [Google Scholar] [CrossRef]
- Raffelt, G.G. Astrophysics probes of particle physics. Phys. Rept. 2000, 333, 593. [Google Scholar] [CrossRef]
- Raffelt, G.G. New bound on neutrino dipole moments from globular-cluster stars. Phys. Rev. Lett. 1990, 64, 2856. [Google Scholar] [CrossRef]
- Viaux, N.; Catelan, M.; Stetson, P.B.; Raffelt, G.G.; Redondo, J.; Valcarce, A.A.R. Particle-physics constraints from the globular cluster M5: Neutrino dipole moments. Astron. Astrophys. 2013, 558, A12. [Google Scholar] [CrossRef]
- Arceo-Díaz, S.; Schröder, K.P.; Zuber, K.; Jack, D. Constraint on the magnetic dipole moment of neutrinos by the tip-RGB luminosity in ω-Centauri. Astropart. Phys. 2015, 70, 1. [Google Scholar] [CrossRef]
- Giunti, C.; Kouzakov, K.; Li, Y.F.; Lokhov, A.; Studenikin, A.; Zhou, S. Electromagnetic neutrinos in laboratory experiments and astrophysics. Annalen Phys. 2016, 528, 198. [Google Scholar] [CrossRef]
- Grimus, W.; Maltoni, M.; Schwetz, T.; Tortola, M.A.; Valle, J.W.F. Constraining Majorana neutrino electromagnetic properties from the LMA-MSW solution of the solar neutrino problem. Nucl. Phys. B 2003, 648, 376–396. [Google Scholar] [CrossRef][Green Version]
- Cooperstein, J. Neutrinos in supernovae. Phys. Rep. 1988, 163, 95. [Google Scholar] [CrossRef]
- Bethe, H.A. Supernova mechanisms. Rev. Mod. Phys. 1990, 62, 801. [Google Scholar] [CrossRef]
- Bludman, S.; Feng, D.H.; Gaisser, T.; Pittel, S. The Physics of Supernovae. Phys. Rep. 1995, 256, 1. [Google Scholar]
- Bethe, H.A.; Wilson, J.R. Revival of a stalled supernova shock by neutrino heating. Astroph. J. 1985, 295, 14. [Google Scholar] [CrossRef]
- Janka, H.T. Neutrino emission from Supernovae. In Handbook of Supernovae; Alsabti, A., Murdin, P., Eds.; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-21845-8. [Google Scholar]
- Yamazaki, R.; Toma, K.; Ioka, K.; Nakamura, T. Tail emission of prompt gamma-ray burst jets. MNRAS 2006, 369, 311. [Google Scholar] [CrossRef][Green Version]
- Bernardini, M.G. Gamma-ray bursts and magnetars: Observational signatures and predictions. JHEAP 2015, 7, 64. [Google Scholar] [CrossRef]
- Wijers, R. The burst, the burster and its lair. Nature 1998, 393, 13. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts and relativistic jets. Phys. Rep. 2015, 561, 1. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Li, G. Cumulative Parity Violation in Supernovae. Phys. Rev. Lett. 1998, 80, 3694. [Google Scholar] [CrossRef]
- Hines, D.; Peer, A. Physics of Gamma-Ray Bursts Prompt Emission. Adv. Astron. 2015, 2015, 907321. [Google Scholar]
- Arzoumanian, Z.; Chernoffs, D.F.; Corder, J.M. The velocity distribution of isolated radio pulsars. Astrophys. J. 2002, 568, 289. [Google Scholar] [CrossRef]
- Balaji, S.; Ramirez-Quezada, M.; Zhou, Y.-L. CP violation and circular polarisation in neutrino radiative decay. J. High Energy Phys. 2020, 4, 178. [Google Scholar] [CrossRef]
- Grigoriev, A.; Kupcheva, E.; Ternov, A. Neutrino spin oscillations in polarized matter. Phys. Lett. B 2019, 797, 135861. [Google Scholar] [CrossRef]
- Abdi, M.; Mohammadi, R.; Xue, S.-S.; Zarei, M. Distinguishing Dirac from Majorana neutrinos in a microwave cavity. arXiv 2004, arXiv:1909.01536. [Google Scholar]
- Fujikawa, K.; Shrock, R. The Magnetic Moment of a massive neutrino and neutrino spin rotation. Phys. Rev. Lett. 1980, 45, 963. [Google Scholar] [CrossRef]
- Nowakowski, M.; Paschos, E.A.; Rodriguez, J.M. All electromagnetic form-factors. Eur. J. Phys. 2005, 26, 545. [Google Scholar] [CrossRef]
- Wong, T.H.; Li, H.B. Neutrino magnetic moments. Mod. Phys. Lett. A 2005, 20, 1103. [Google Scholar] [CrossRef]
- Balantekin, A.B. Neutrino magnetic moment. AIP Conf. Proc. 2006, 847, 128. [Google Scholar]
- Giunti, C.; Studenikin, A. Neutrino electromagnetic properties. Phys. Atom.Nucl. 2009, 72, 2089. [Google Scholar] [CrossRef]
- Studenikin, A. Neutrino magnetic moment: A window to new physics. Nucl. Phys. Proc. Suppl. 2009, 188, 220. [Google Scholar] [CrossRef]
- Broggini, C.; Giunti, C.; Studenikin, A. Electromagnetic properties of neutrinos. Adv. High Energy Phys. 2012, 2012, 459526. [Google Scholar] [CrossRef]
- Akhmedov, E. Majorana neutrinos and other Majorana particles: Theory and experiment. arXiv 2014, arXiv:1412.3320. [Google Scholar]
- Giunti, C.; Studenikin, A. Neutrino electromagnetic interactions: A window to new physics. Rev. Mod. Phys. 2015, 87, 531. [Google Scholar] [CrossRef]
- Studenikin, A. Status and perspectives of neutrino magnetic moments. J. Phys. Conf. Ser. 2016, 718, 062076. [Google Scholar]
- Studenikin, A. Electromagnetic properties of neutrinos: Three new phenomena in neutrino spin oscillations. EPJ Web Conf. 2016, 125, 04018. [Google Scholar] [CrossRef]
- Beda, A.G.; Brudanin, V.B.; Egorov, V.G.; Medvedev, D.V.; Pogosov, V.S.; Shirchenko, M.V. The results of search for the neutrino magnetic moment in GEMMA experiment. Adv. High Energy Phys. 2012, 2012, 350150. [Google Scholar] [CrossRef]
- Agostini, M.; Borexino Collaboration. Limiting neutrino magnetic moments with Borexino Phase-II solar neutrino data. Phys. Rev. D 2017, 96, 091103. [Google Scholar] [CrossRef]
- Bell, N.F.; Cirigliano, V.; Ramsey-Musolf, M.J.; Vogel, P.; Wise, M.B. How magnetic is the Dirac neutrino? Phys. Rev. Lett. 2005, 95, 151802. [Google Scholar] [CrossRef] [PubMed]
- Bell, N.F.; Gorchtein, M.; Ramsey-Musolf, M.J.; Vogel, P.; Wang, P. Model independent bounds on magnetic moments of Majorana neutrinos. Phys. Lett. B 2006, 642, 377. [Google Scholar] [CrossRef]
- Studenikin, A. New bounds on neutrino electric millicharge from limits on neutrino magnetic moment. Europhys. Lett. 2014, 107, 21001, Erratum in Europhys. Lett. 2014, 107, 39901. [Google Scholar] [CrossRef]
- Gninenko, S.; Krasnikov, N.; Rubbia, A. New limit on milicharged particles from reactor neutrino experiments and the PVLAS anomaly. Phys. Rev. D 2007, 75, 075014. [Google Scholar] [CrossRef]
- Zyla, P.A. Partice Data Group. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar]
- Studenikin, A.I.; Tokarev, I. Millicharged neutrino with anomalous magnetic moment in rotating magnetized matter. Nucl. Phys. B 2014, 884, 396. [Google Scholar] [CrossRef]
- Bernabeu, J.; Papavassiliou, J.; Binosi, D. The neutrino charge radius in the presence of fermion masses. Nucl. Phys. B 2005, 716, 352. [Google Scholar]
- Kouzakov, K.A.; Studenikin, A.I. Electromagnetic properties of massive neutrinos in low-energy elastic neutrino-electron scattering. Phys. Rev. D 2017, 95, 055013. [Google Scholar] [CrossRef]
- Cisneros, A. Effect of neutrino magnetic moment on solar neutrino observations. Astrophys. Space Sci. 1971, 10, 87. [Google Scholar] [CrossRef]
- Studenikin, A. Neutrinos in electromagnetic fields and moving media. Phys. Atom. Nucl. 2004, 67, 993. [Google Scholar] [CrossRef]
- Studenikin, A. Neutrino in magnetic fields: From the first studies to the new effects in neutrino oscillations. arXiv 2004, arXiv:0407010. [Google Scholar]
- Kartavtsev, A.; Raffelt, G.G.; Vogel, H. Neutrino propagation in media: Flavor-, helicity-, and pair correlations. Phys. Rev. D 2015, 91, 125020. [Google Scholar] [CrossRef]
- Studenikin, A. Neutrino spin and spin-flavour oscillations in transversally moving or polarized matter. J. Phys. Conf. Ser. 2017, 888, 012221. [Google Scholar] [CrossRef]
- Gouvea, A.; Shalgar, S. Effect of transition magnetic moments on collective supernova neutrino oscillations. J. Cosmol. Astropart. Phys. 2012, 1210, 027. [Google Scholar] [CrossRef]
- Gouvea, A.; Shalgar, S. Transition magnetic moments and collective neutrino oscillations: Three-flavor effects and detectability. J. Cosmol. Astropart. Phys. 2013, 1304, 018. [Google Scholar] [CrossRef]
- Kosmas, T.S. Non-standard neutrino-nucleus interactions. In Proceedings of the Invited Talk in Neutrinos and Dark Matter in Nuclear Physics 2015 (NDM-15), Jyvaskyla, Finland, 1–5 June 2015. [Google Scholar]
- Schechter, J.; Valle, J.W.F. Majorana neutrinos and magnetic fields. Phys. Rev. D 1981, 24, 1883, Erratum in 1982, D2, 283. [Google Scholar] [CrossRef]
- Shrock, R.E. Electromagnetic properties and decays of Dirac and Majorana neutrinos in a general class of gauge theories. Nucl. Phys. B 1982, 206, 359. [Google Scholar] [CrossRef]
- Kayser, B. Majorana Neutrinos and their Electromagnetic Properties. Phys.Rev. D 1982, 26, 1662. [Google Scholar] [CrossRef]
- Nieves, J.F. Electromagnetic properties of majorana neutrinos. Phys. Rev. D 1982, 26, 3152. [Google Scholar] [CrossRef]
- Beacom, J.F.; Vogel, P. Neutrino magnetic moments, flavor mixing, and the superKamiokande solar data. Phys. Rev. Lett. 1999, 83, 5222–5225. [Google Scholar] [CrossRef]
- Papoulias, D.; Kosmas, T. Neutrino transition magnetic moments within the non-standard neutrino–nucleus interactions. Phys. Lett. B 2015, 747, 454–459. [Google Scholar] [CrossRef]
- Beringer, J. Review of Particle Physics (RPP). Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
- Tortola, M. Constraining neutrino magnetic moment with solar and reactor neutrino data. PoS AHEP 2003, 2003, 022. [Google Scholar]
- Kosmas, T.S.; Miranda, O.G.; Papoulias, D.K.; Tortola, J.W.F. Probing neutrino magnetic moments at the Spallation Neutron Source facility. Phys. Rev. D 2015, 92, 013011. [Google Scholar] [CrossRef]
- Wong, H. A Search of Neutrino Magnetic Moments with a High-Purity Germanium Detector at the Kuo-Sheng Nuclear Power Station. Phys. Rev. D 2007, 75, 012001. [Google Scholar] [CrossRef]
- Wong, H.T.; Li, H.-B.; Lin, S.-T. Enhanced sensitivities for the searches of neutrino magnetic moments through atomic ionization. Phys. Rev. Lett. 2010, 105, 061801. [Google Scholar] [CrossRef]
- Deniz, M. Measurement of Neutrino-Electron Scattering Cross-Section with a CsI(Tl) Scintillating Crystal Array at the Kuo-Sheng Nuclear Power Reactor. Phys. Rev. D 2010, 81, 072001. [Google Scholar] [CrossRef]
- Vogel, P.; Engel, J. Neutrino electromagnetic form-factors. Phys. Rev. D 1989, 39, 3378. [Google Scholar] [CrossRef]
- Miranda, O.G. Constraining the neutrino magnetic moment with anti- neutrinos from the sun. Phys. Rev. Lett. 2004, 93, 051304. [Google Scholar] [CrossRef]
- Miranda, O.G.; Rashba, T.I.; Rez, A.I.; Valle, J.W.F. Enhanced solar anti-neutrino flux in random magnetic fields. Phys. Rev. D 2004, 70, 113002. [Google Scholar] [CrossRef]
- Barranco, J.; Miranda, O.; Rashba, T. Improved limit on electron neutrino charge radius through a new evaluation of the weak mixing angle. Phys. Lett. B 2008, 662, 431. [Google Scholar] [CrossRef][Green Version]
- Hirsch, M.; Nardi, E.; Restrepo, D. Bounds on the tau and muon neutrino vector and axial vector charge radius. Phys. Rev. D 2003, 67, 033005. [Google Scholar] [CrossRef]
- Bernabeu, J.; Cabral-Rosetti, L.; Papavassiliou, J.; Vidal, J. On the charge radius of the neutrino. Phys. Rev. D 2000, 62, 113012. [Google Scholar] [CrossRef]
- Simon, E. SICANE: A Detector array for the measurement of nuclear recoil quenching factors using a monoenergetic neutron beam. Nucl. Instrum. Meth. A 2003, 507, 643. [Google Scholar] [CrossRef]
- Barranco, J. Constraining non-standard interactions in nu/e e or anti- nu/e e scattering. Phys. Rev. D 2006, 73, 113001. [Google Scholar] [CrossRef]
- Barranco, J.; Miranda, O.; Rashba, T. Low energy neutrino experiments sensitivity to physics beyond the Standard Model. Phys. Rev. D 2007, 76, 073008. [Google Scholar] [CrossRef]
- Miranda, O.; Nunokawa, H. Non standard neutrino interactions. arXiv 2015, arXiv:1505.06254. [Google Scholar]
- Giunti, C.; Kouzakov, K.A.; Li, Y.F.; Lokhov, A.V.; Studenikin, A.I.; Zhou, S. Electromagnetic neutrinos in terrestrial experiments and astrophysics. arXiv 2015, arXiv:1506.05387. [Google Scholar]
- Kosmas, T.; Vergados, J.; Civitarese, O.; Faessler, A. Study of the muon number violating mu to e conversion in a nucleus by using quasiparticle RPA. Nucl. Phys. A 1994, 570, 637. [Google Scholar] [CrossRef]
- Kosmas, T.S. Exotic μ−→e− conversion in nuclei: Energy moments of the transition strength and average energy of the outgoing e−. Nucl. Phys. A 2001, 683, 443. [Google Scholar] [CrossRef]
- Beda, A.; Brudanin, V.; Egorov, V.; Medvedev, D.; Pogosov, V. Gemma experiment: The results of neutrino magnetic moment search. Phys. Part Nucl. Lett. 2013, 10, 139. [Google Scholar] [CrossRef]
- Nieves, J.F.; Pal, P.B. Induced charge of neutrinos in a medium. Phys. Rev. D 1994, 49, 1398. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Pal, P.B. Massive neutrinos in Physics and Astrophysics. In World Scientific Lecture Notes in Physics; World Scientific: Singapore, 1998; p. 60. [Google Scholar]
- Oraevsky, V.N.; Semikoz, V.B.; Smorodinsky, Y.A. Polarization Loss and Induced Electric Charge of Neutrinos in Plasmas. JETP Lett. 1986, 43, 709. [Google Scholar]
- Altherr, T.; Salati, P. The electric charge of neutrinos and plasmon decay. Nuc. Phys. B 1994, 421, 662. [Google Scholar] [CrossRef][Green Version]
- Babu, K.S.; Mohapatra, R.N. Quantization of electric charge from anomaly constraints and a Majorana neutrino. Phys. Rev. D 1990, 41, 271. [Google Scholar] [CrossRef]
- Foot, R.; Joshi, G.C.; Lew, H.; Volkas, R. Charge quantization in the standard model and some of its extentations. Mod. Phys. Lett. A 1990, 5, 2721. [Google Scholar] [CrossRef]
- Foot, R.; Lew, H.; Volkas, R. Electric-charge quantization. J. Phys. G Nucl. Part. Phys. 1993, 19, 361. [Google Scholar] [CrossRef]
- Davidson, S.; Hannestad, S.; Raffelt, G. Updated bounds on milli-charged particles. J. High Energy Phys. 2000, 5, 003. [Google Scholar] [CrossRef]
- Geng, C.Q.; Marshak, R.E. Uniqueness of quark and lepton representations in the standard model from the anomalies viewpoint. Phys. Rev. D 1989, 39, 693. [Google Scholar] [CrossRef] [PubMed]
- Minahan, J.A.; Ramond, P.; Warner, R.C. Comment on anomaly cancellation in the standard model. Phys. Rev. D 1990, 41, 715. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Gastmans, R.; Lautrup, B. Static quantities in Weinberg’s model of weak and electromagnetic interactions. Nucl. Phys. B 2002, 46, 319. [Google Scholar] [CrossRef]
- Gross, D.; Jackiw, R. Effect of Anomalies on Quasi-Renormalizable Theories. Phys. Rev. D 1972, 6, 477. [Google Scholar] [CrossRef]
- Monyonko, N.M.; Reid, J.H. What is the charge radius of the neutrino? Prog. Theor. Phys. 1985, 73, 3. [Google Scholar] [CrossRef]
- Hill, R.J.; Tomalak, O. On the effective theory of neutrino-electron and neutrino-quark interactions. Phys. Lett. B 2020, 805, 135466. [Google Scholar] [CrossRef]
- Lucio Martinez, J.L.; Rosado, A.; Zepeda, A. Neutrino charge in the linear Rξ gauge. Phys. Rev. D 1983, 29, 7. [Google Scholar]
- Dvornikov, M.; Studenikin, A. Electric charge and magnetic moment of a massive neutrino. Phys. Rev. D 2004, 69, 073001. [Google Scholar] [CrossRef]
- DeRaad, L.L., Jr.; Milton, K.A.; Hari, N.D. Photon decay into neutrinos in a strong magnetic field. Phys. Rev. D 1976, 14, 3326. [Google Scholar] [CrossRef]
- Ioannisian, A.N.; Raffelt, G.G. Cherenkov radiation by massless neutrinos in a magnetic field. Phys. Rev. D 1997, 55, 7038. [Google Scholar] [CrossRef]
- Vainshtein, A. Perturbative and non perturbative renormalisation of anomalous quark triangles. Phys. Lett. B 2003, 569, 187–193. [Google Scholar] [CrossRef]
- Schwinger, J. On gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664. [Google Scholar] [CrossRef]
- Tsai, W.Y. Modified electron propagation function in strong magnetic fields. Phys. Rev. D 1974, 10, 1342. [Google Scholar] [CrossRef]
- Dittrich, W. Effective Lagrangians at finite temperatures. Phys. Rev. D 1979, 19, 2385. [Google Scholar] [CrossRef]
- Elmfors, P.; Grasso, D.; Raffelt, G. Neutrino dispersion in magnetized media and spin oscillations in the early universe. Nucl. Phys. B 1996, 479, 3. [Google Scholar] [CrossRef]
- Ganguly, A.K.; Konar, S.; Pal, P.B. Faraday effect: A field theoretical point of view. Phys. Rev. D 1999, 60, 105014. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Ganguly, A.K. Axial-vector-vector amplitude and neutrino effective charge in a magnetized medium. Phys. Rev. D 2003, 68, 053011. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Ganguly, A.K.; Konar, S. Neutrinos interactions in a magnetized medium. Phys. Rev. D 2001, 65, 013007. [Google Scholar] [CrossRef]
- Bellac, M.L. Thermal Field Theory; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Ofengeim, D.D.; Zyuzin, D.A. Thermal spectrum and neutrino cooling rate of the vela pulsar. Particles 2018, 1, 194–202. [Google Scholar] [CrossRef]
- Barbiellini, G.; Coeeoni, G. Electric charge of the neutrinos from SN1987A. Nature 1987, 329, 21. [Google Scholar] [CrossRef]
- Davidson, S.; Campbell, B.; Bailey, D.C. Limits on particles of small electric charge. Phys. Rev. D 1991, 43, 2314. [Google Scholar] [CrossRef]
- Caprini, C.; Ferreira, P.G. Constraints on the electrical charge asymmetry of the universe. J. Cosmol. Astropart. Phys. 2005, 2, 006. [Google Scholar] [CrossRef]
- Chen, J.-W.; Chi, H.-C.; Li, H.-B.; Liu, C.-P.; Singh, L.; Wong, H.-T.; Wu, C.L.; Wu, C.-P. Constraints on millicharged neutrinos via analysis of data from atomic ionisations with germanium detectors at sub-keV sensitivities. Phys. Rev. D 2014, 90, 011301(R). [Google Scholar] [CrossRef]
- Chen, J.W.; Chi, H.C.; Huang, K.N.; Li, H.B.; Liu, C.P.; Singh, L.; Wong, H.T.; Wu, C.L.; Wu, C.P. Constraining neutrino electromagnetic properties by germanium detectors. Phys. Rev. D 2015, 91, 013005. [Google Scholar] [CrossRef]
- Kosmas, T.S.; Miranda, O.G.; Papoulias, D.K.; Tortola, M.; Valle, J.W.F. Sensitivities to neutrino electromagnetic properties at the TEXONO experiment. Phys. Lett. B 2015, 750, 459. [Google Scholar] [CrossRef]
- Raffelt, G.G. Limits on neutrino electromagnetic properties—An update. Phys. Rep. 1999, 320, 319. [Google Scholar] [CrossRef]
- Fukuda, Y.; Super-Kamiokande Collaboration. Evidence for oscillations for atmospheric neutrinos. Phys. Rev. Lett. 1998. [Google Scholar] [CrossRef]
- Ahmad, Q.R.; SNO Collaboration. Measurement of the Rate of νe + d → p + p + e− interactions produced by 8B solar neutrinos at the sudbury neutrino observatory. Phys. Rev. Lett. 2001, 87, 071301. [Google Scholar] [CrossRef] [PubMed]
- Chaubey, A.; Jaiswal, M.K.; Ganguly, A.K. Exploring scalar-photon interactions in energetic astrophysical events. Phys. Rev. D 2020, 102, 123029. [Google Scholar] [CrossRef]
- Ganguly, A.K.; Jain, P.; Mandal, S. Photon and axion oscillation in a magnetized medium: A general treatment. Phys. Rev. D 2009, 79, 115014. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).