A Possible Quasi-Periodic Oscillation in the X-ray Emission of 3C 120
Abstract
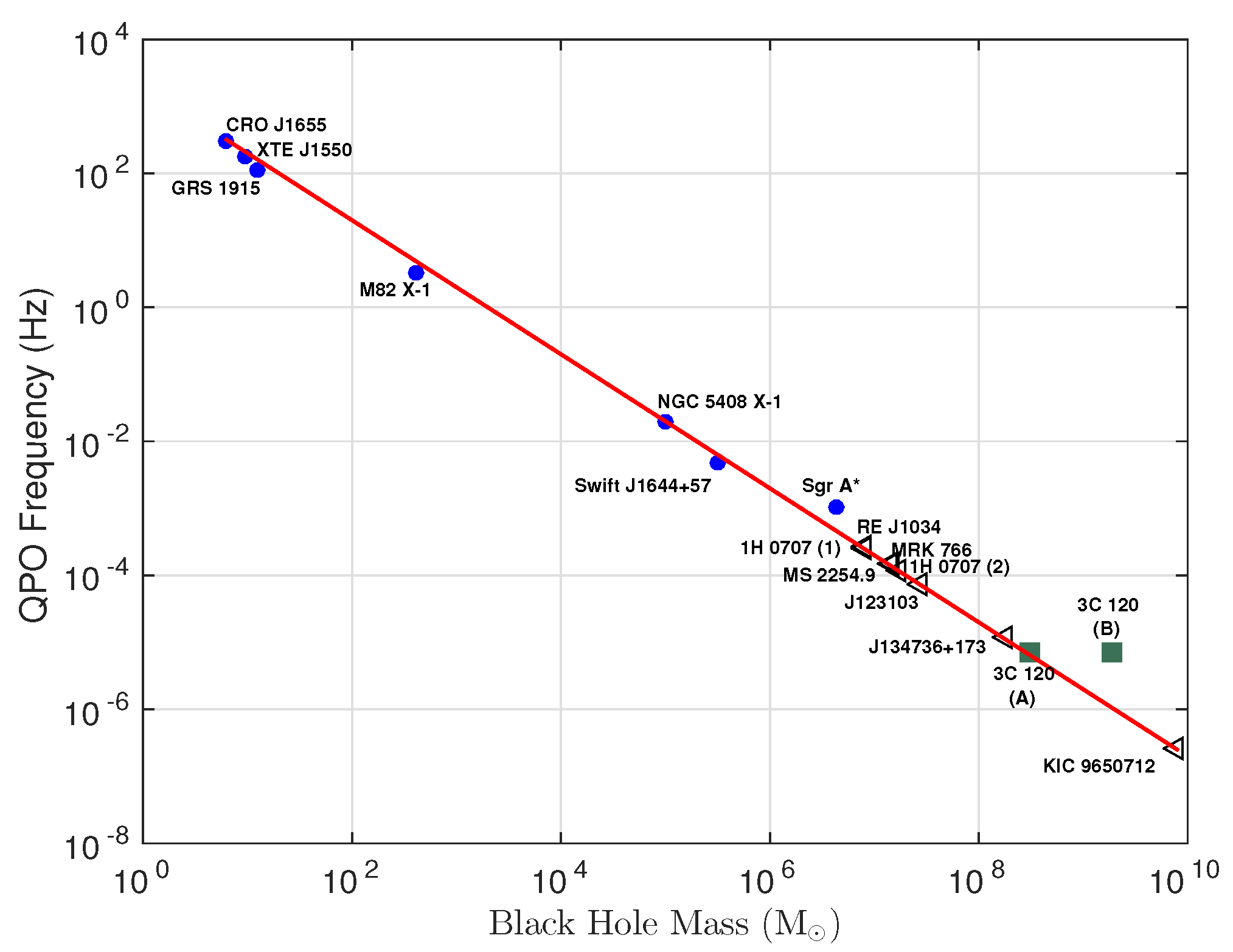
1. Introduction
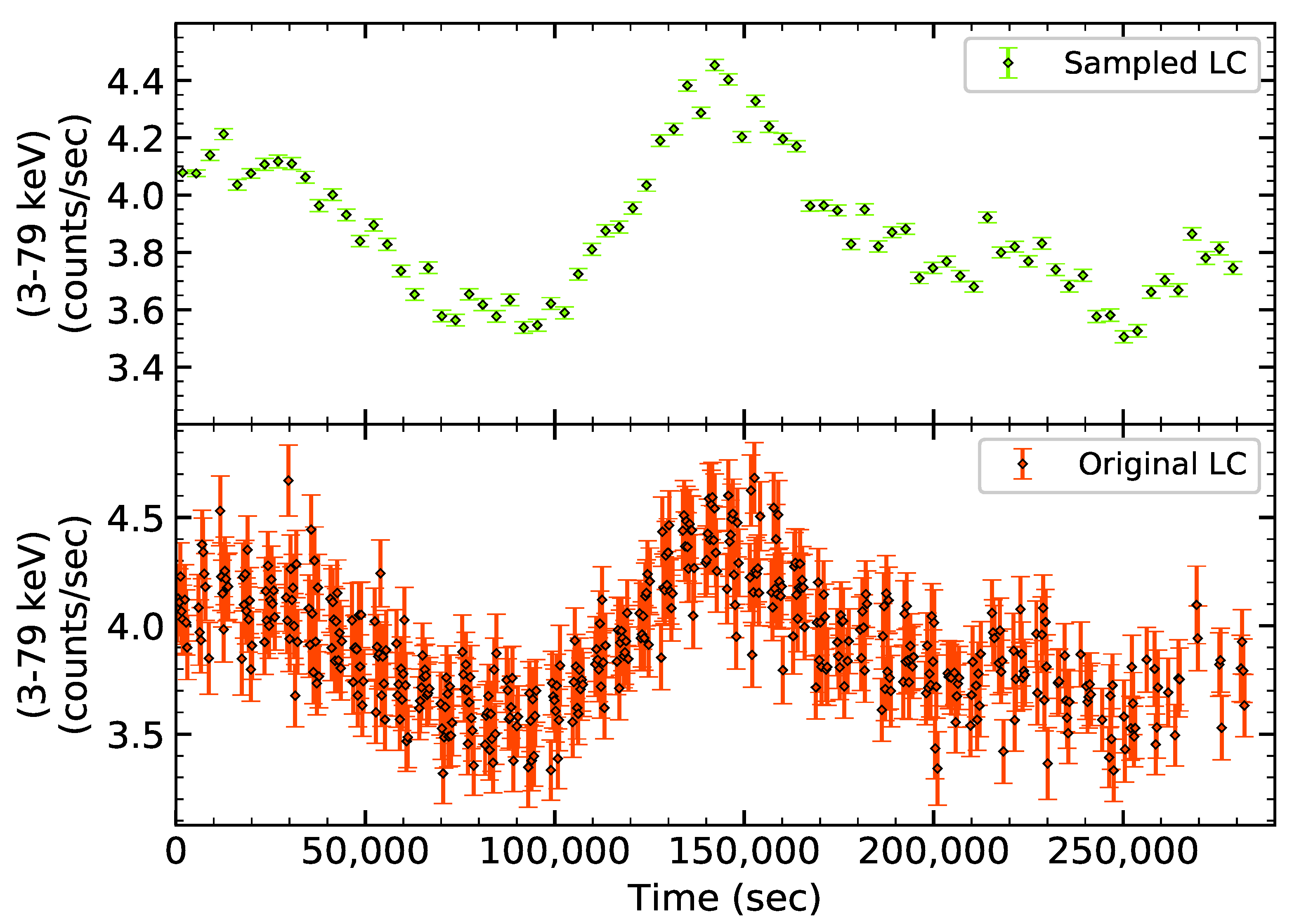
2. NuSTAR Observations and Data Analysis
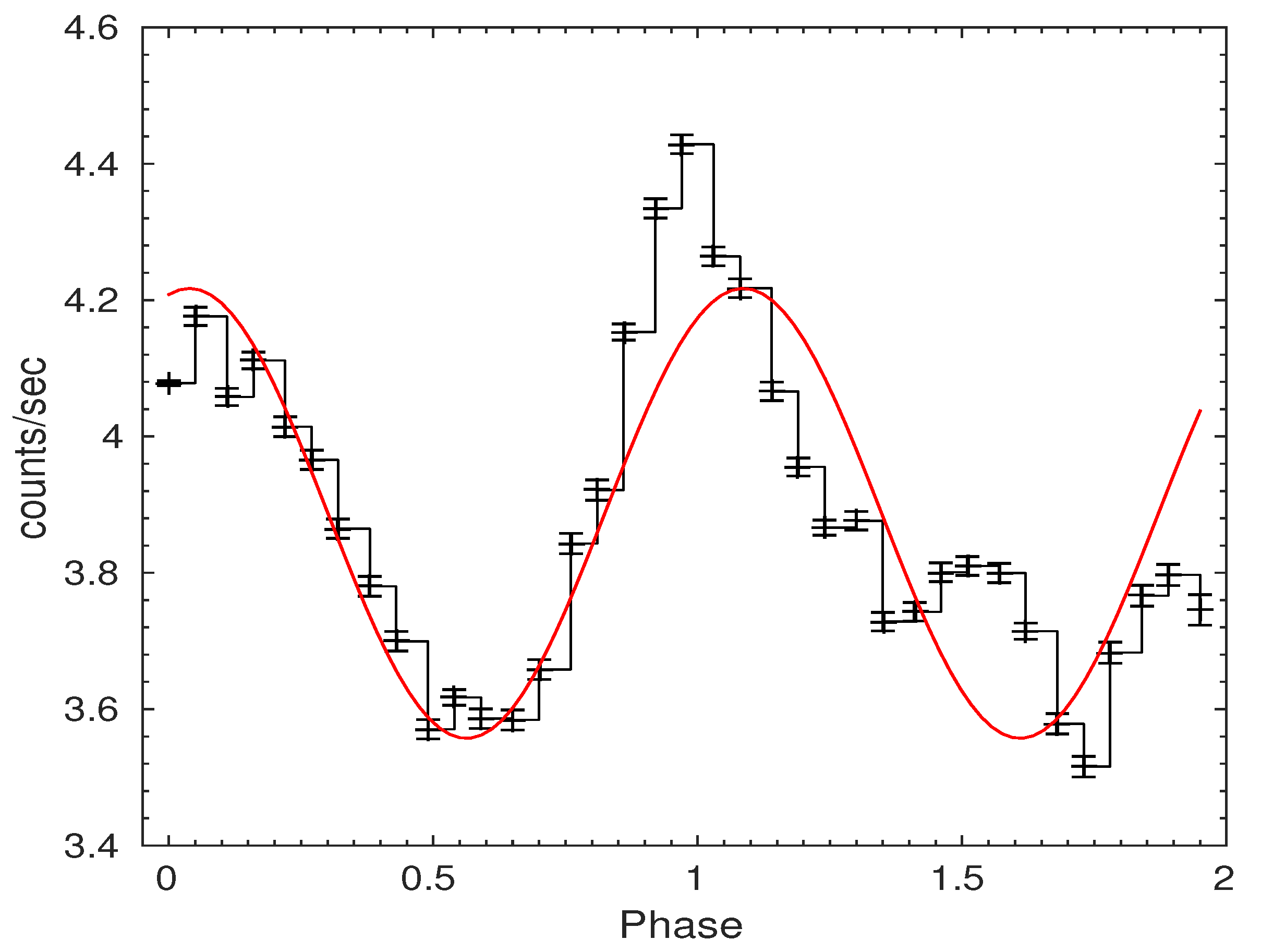
3. Analysis and Results
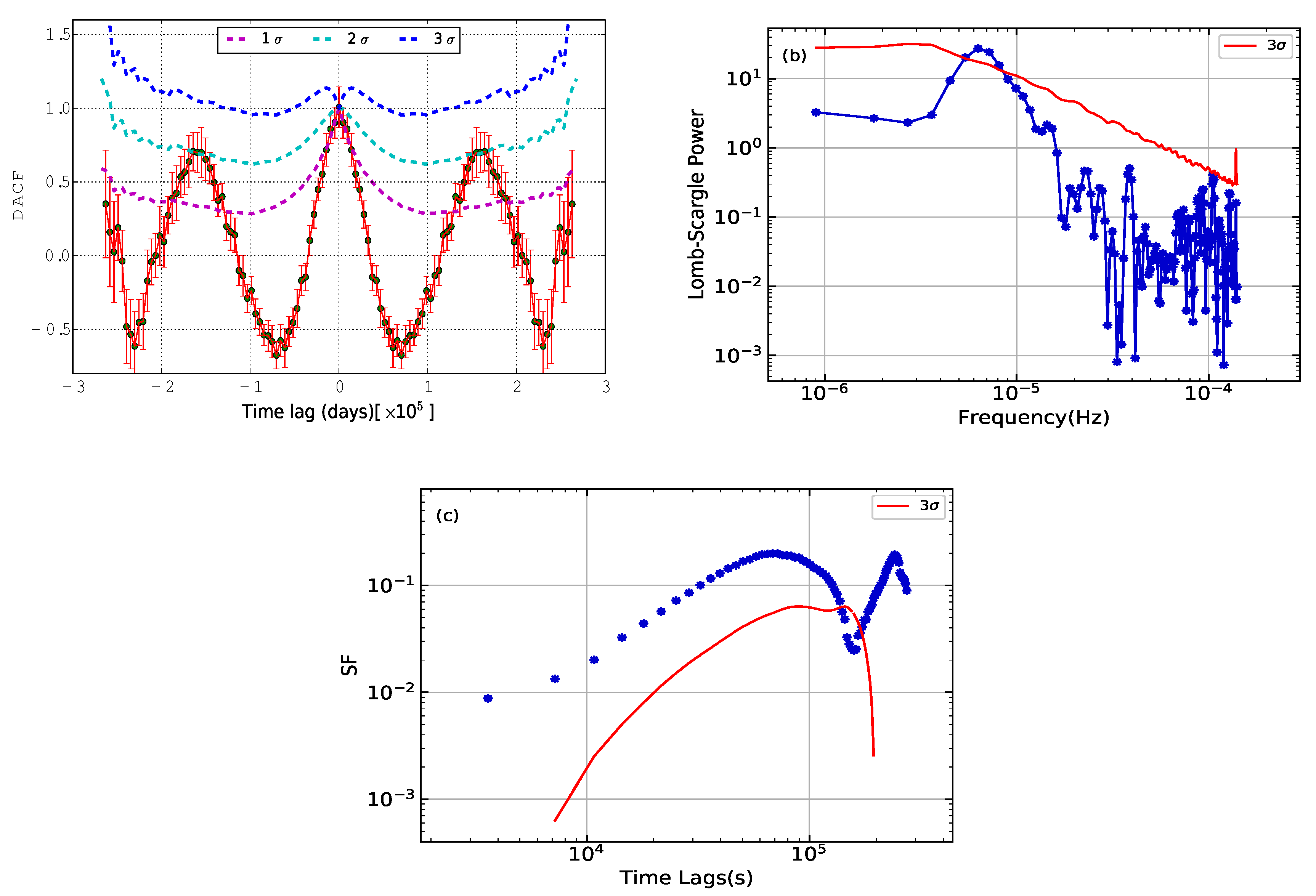
3.1. Discrete Correlation Function
3.2. Lomb–Scargle Periodogram
3.3. Structure Function
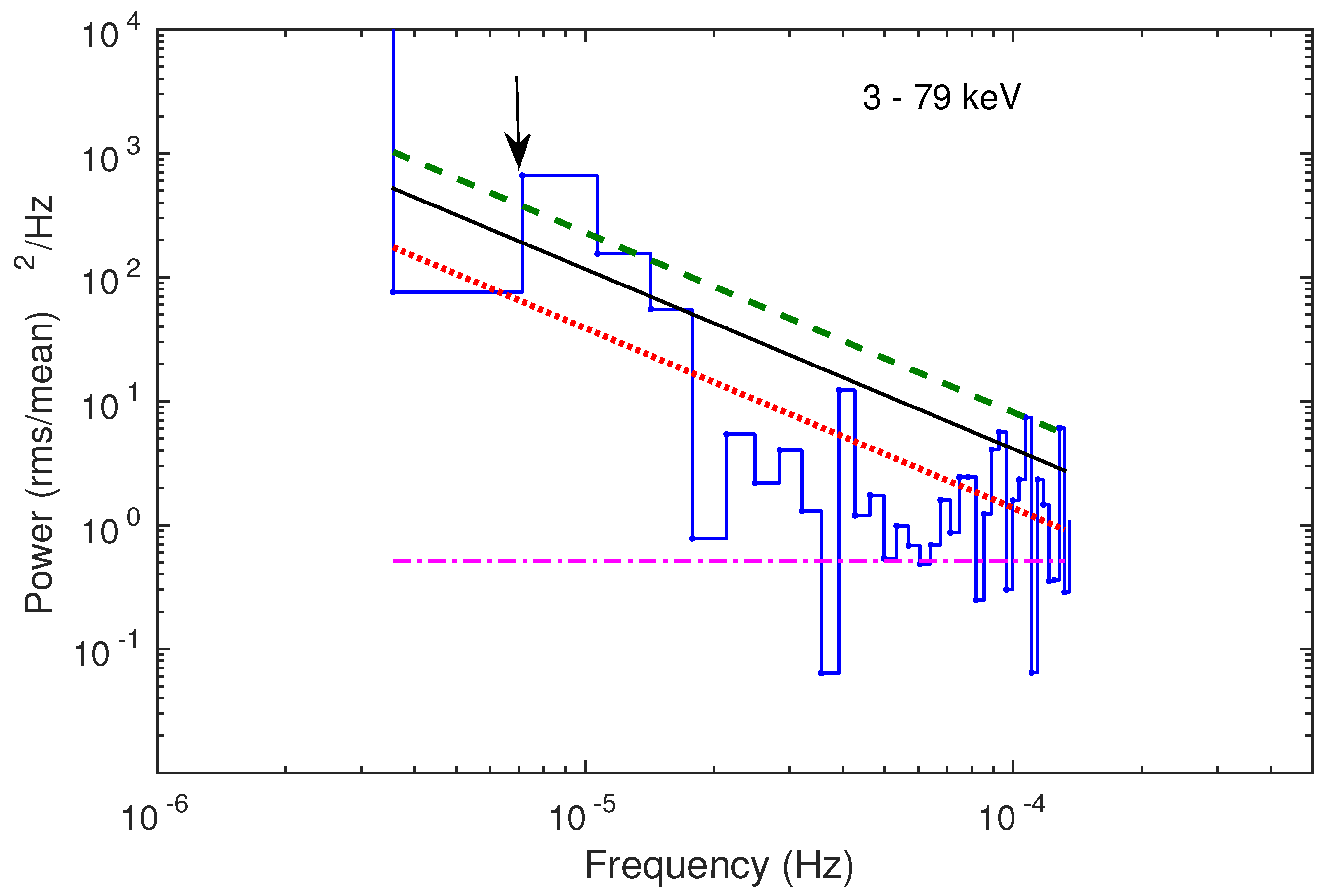
3.4. Power Spectral Density
3.5. Significance and Uncertainty Estimation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Theory of Extragalactic Radio Sources. Rev. Mod. Phys. 1984, 56, 255–351. [Google Scholar] [CrossRef]
- Shakura, N.I.; Sunyaev, R.A. Reprint of 1973A&A....24..337S. Black Holes in Binary Systems. Obs. Appearance. Astron. Astrophys. 1973, 500, 33–51. [Google Scholar]
- Blandford, R.D.; Königl, A. Relativistic Jets as Compact Radio Sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Blandford, R.; Meier, D.; Readhead, A. Relativistic Jets from Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2019, 57, 467–509. [Google Scholar] [CrossRef]
- Wagner, S.J.; Witzel, A. Intraday Variability In Quasars and BL Lac Objects. Annu. Rev. Astron. Astrophys. 1995, 33, 163–198. [Google Scholar] [CrossRef]
- Hovatta, T.; Lindfors, E. Relativistic Jets of Blazars. New Astron. Rev. 2019, 87, 101541. [Google Scholar] [CrossRef]
- Mushotzky, R.F.; Done, C.; Pounds, K.A. X-ray Spectra and Time Variability of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 1993, 31, 717. [Google Scholar] [CrossRef]
- Pahari, M.; McHardy, I.M.; Mallick, L.; Dewangan, G.C.; Misra, R. Detection of the High-Energy Cut-off from the Seyfert 1.5 Galaxy NGC 5273. Mon. Not. R. Astron. Soc. 2017, 470, 3239–3248. [Google Scholar] [CrossRef]
- Tortosa, A.; Marinucci, A.; Matt, G.; Bianchi, S.; La Franca, F.; Ballantyne, D.R.; Boorman, P.G.; Fabian, A.C.; Farrah, D.; Fuerst, F.; et al. Broad-Band X-ray Spectral Analysis of the Seyfert 1 Galaxy GRS 1734-292. Mon. Not. R. Astron. Soc. 2017, 466, 4193–4200. [Google Scholar]
- Rani, P.; Stalin, C.S. Measurement of Coronal Properties of Seyfert Galaxies from NuSTAR’s Hard X-ray Spectrum. J. Astrophys. Astron. 2018, 39, 15. [Google Scholar] [CrossRef]
- Gierliński, M.; Middleton, M.; Ward, M.; Done, C. A Periodicity of 1hour in X-ray Emission from the Active Galaxy RE J1034+396. Nature 2008, 455, 1. [Google Scholar] [CrossRef]
- Espaillat, C.; Bregman, J.; Hughes, P.; Lloyd-Davies, E. Wavelet Analysis of AGN X-ray Time Series: A QPO in 3C 273? Astrophys. J. 2008, 679, 182–193. [Google Scholar] [CrossRef]
- An, T.; Baan, W.A.; Wang, J.-Y.; Wang, Y.; Hong, X.-Y. Periodic Radio Variabilities in NRAO 530: A Jet-Disc Connection? Mon. Not. R. Astron. Soc. 2013, 434, 3487–3496. [Google Scholar] [CrossRef]
- Xie, G.Z.; Yi, T.F.; Li, H.Z.; Zhou, S.B.; Chen, L.E. Periodicity Analysis of the Radio Curve of PKS 1510-089 and Implications for Its Central Structure. Astron. J. 2008, 135, 2212–2216. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Villata, M.; Aller, H.D.; Aller, M.F.; Heidt, J.; Kurtanidze, O.M.; Lanteri, L.; Maesano, M.; Massaro, E.; Montagni, F.; et al. Optical and Radio Variability of the BL Lacertae Object <ASTROBJ>AO 0235+16</ASTROBJ>: A Possible 5-6 Year Periodicity. Astron. Astrophys. 2001, 377, 396–412. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Dotti, M.; Treves, A. Quasi-Periodicities at Year-like Timescales in Blazars. Astron. J. 2016, 151, 54. [Google Scholar] [CrossRef]
- Bhatta, G.; Stawarz, Ł.; Ostrowski, M.; Markowitz, A.; Akitaya, H.; Arkharov, A.A.; Bachev, R.; Benítez, E.; Borman, G.A.; Carosati, D.; et al. Multifrequency Photo-Polarimetric WEBT Observation Campaign on the Blazar S5 0716+714: Source Microvariability and Search for Characteristic Timescales. Astrophys. J. 2016, 831, 92. [Google Scholar] [CrossRef]
- Lachowicz, P.; Czerny, B.; Abramowicz, M.A. Wavelet Analysis of MCG-6-30-15 and NGC 4051: A Possible Discovery of QPOs in 2:1 and 3:2 Resonance. arXiv 2006, arXiv:astro-ph/0607594. [Google Scholar]
- Rani, B.; Wiita, P.J.; Gupta, A.C. Nearly Periodic Fluctuations in the Long-Term X-ray Light Curves of the Blazars AO 0235+164 and 1ES 2321+419. Astrophys. J. 2009, 696, 2170–2178. [Google Scholar] [CrossRef]
- Zhang, P.-F.; Yan, D.-H.; Zhou, J.-N.; Fan, Y.-Z.; Wang, J.-C.; Zhang, L. A γ-Ray Quasi-Periodic Modulation in the Blazar PKS 0301-243? Astrophys. J. 2017, 845, 82. [Google Scholar] [CrossRef]
- Warner, B.; Woudt, P.A.; Pretorius, M.L. Dwarf Nova Oscillations and Quasi-Periodic Oscillations in Cataclysmic Variables - III. A New Kind of Dwarf Nova Oscillation, and Further Examples of the Similarities to X-ray Binaries. Mon. Not. R. Astron. Soc. 2003, 344, 1193–1209. [Google Scholar] [CrossRef][Green Version]
- Zhou, X.-L.; Yuan, W.; Pan, H.-W.; Liu, Z. Universal Scaling of the 3:2 Twin-Peak Quasi-Periodic Oscillation Frequencies With Black Hole Mass and Spin Revisited. Astrophys. J. 2015, 798, L5. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, P.; Yan, J.; Fan, Y.; Liu, Q. An X-ray Periodicity of ∼1.8 Hr in Narrow-Line Seyfert 1 Galaxy Mrk 766. Astrophys. J. 2017, 849, 9. [Google Scholar] [CrossRef]
- Homan, J.; Wijnands, R.; van der Klis, M.; Belloni, T.; van Paradijs, J.; Klein-Wolt, M.; Fender, R.; Méndez, M. Correlated X-ray Spectral and Timing Behavior of the Black Hole Candidate XTE J1550-564: A New Interpretation of Black Hole States. Astrophys. J. 2001, 132, 377–402. [Google Scholar] [CrossRef]
- Strohmayer, T.E. Discovery of a Second High-Frequency Quasi-Periodic Oscillation from the Microquasar GRS 1915+105. Astrophys. J. 2001, 554, L169–L172. [Google Scholar] [CrossRef]
- Remillard, R.A.; McClintock, J.E. X-ray Properties of Black-Hole Binaries. Annu. Rev. Astron. Astrophys. 2006, 44, 49–92. [Google Scholar] [CrossRef]
- Mangalam, A.V.; Wiita, P.J. Accretion Disk Models for Optical and Ultraviolet Microvariability in Active Galactic Nuclei. Astrophys. J. 1993, 406, 420. [Google Scholar] [CrossRef]
- Camenzind, M.; Krockenberger, M. The Lighthouse Effect of Relativistic Jets in Blazars. A Geometric Originof Intraday Variability. Astron. Astrophys. 1992, 255, 59–62. [Google Scholar]
- Gopal-Krishna; Wiita, P.J. Swinging Jets and the Variability of Active Nuclei. Astron. Astrophys. 1992, 259, 109–117. [Google Scholar]
- Burbidge, E.M. Redshifts of Thirteen Radio Galaxies. Astrophys. J. 1967, 149, L51. [Google Scholar] [CrossRef]
- Grier, C.J.; Peterson, B.M.; Pogge, R.W.; Denney, K.D.; Bentz, M.C.; Martini, P.; Sergeev, S.G.; Kaspi, S.; Minezaki, T.; Zu, Y.; et al. Reverberation Mapping Results for Five Seyfert 1 Galaxies. Astrophys. J. 2012, 755, 60. [Google Scholar] [CrossRef]
- Harris, D.E.; Hjorth, J.; Sadun, A.C.; Silverman, J.D.; Vestergaard, M. X-ray Emission from the Radio Jet in 3C 120. Astrophys. J. 1999, 518, 213–218. [Google Scholar] [CrossRef][Green Version]
- Halpern, J.P. X-ray Spectrum and Variability of 3C 120. Astrophys. J. 1985, 290, 130–135. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; et al. Fermi Large Area Telescope Observations of Misaligned Active Galactic Nuclei. Astrophys. J. 2010, 720, 912–922. [Google Scholar] [CrossRef]
- Rani, P.; Stalin, C.S. Coronal Proerties of the Seyfert 1 Galaxy 3C 120 with NuSTAR. Astrophys. J. 2018, 856, 120. [Google Scholar] [CrossRef]
- Harrison, F.A.; Craig, W.W.; Christensen, F.E.; Hailey, C.J.; Zhang, W.W.; Boggs, S.E.; Stern, D.; Cook, W.R.; Forster, K.; Giommi, P.; et al. The Nuclear Spectroscopic Telescope Array (NuSTAR) High-Energy X-ray Mission. Astrophys. J. 2013, 770, 103. [Google Scholar] [CrossRef]
- Edelson, R.A.; Krolik, J.H. The Discrete Correlation Function: A New Method for Analyzing Unevenly Sampled Variability Data. Astrophys. J. 1988, 333, 646. [Google Scholar] [CrossRef]
- Stalin, C.S.; Kawabata, K.S.; Uemura, M.; Yoshida, M.; Kawai, N.; Yanagisawa, K.; Shimizu, Y.; Kuroda, D.; Nagayama, S.; Toda, H. Simultaneous MITSuME g’RCIC Monitoring of S5 0716+714. Mon. Not. R. Astron. Soc. 2009, 399, 1357–1366. [Google Scholar] [CrossRef]
- McQuillan, A.; Mazeh, T.; Aigrain, S. Stellar Rotation Periods of the Kepler Objects of Interest: A Dearth of Close-in Planets around Fast Rotators. Astrophys. J. 2013, 775, L11. [Google Scholar] [CrossRef]
- Sandrinelli, A.; Covino, S.; Treves, A.; Holgado, A.M.; Sesana, A.; Lindfors, E.; Ramazani, V.F. Quasi-Periodicities of BL Lacertae Objects. Astron. Astrophys. 2018, 615, A118. [Google Scholar] [CrossRef]
- Agarwal, A.; Mihov, B.; Andruchow, I.; Cellone, S.A.; Anupama, G.C.; Agrawal, V.; Zola, S.; Slavcheva-Mihova, L.; Özdönmez, A.; Ege, E.; et al. Multi-Band Behaviour of the TeV Blazar PG 1553+113 in Optical Range on Diverse Timescales. Flux and Spectral Variations. Astron. Astrophys. 2021, 645, A137. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in Astronomical Time Series Analysis. II. Statistical Aspects of Spectral Analysis of Unevenly Spaced Data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Press, W.H.; Rybicki, G.B. Fast Algorithm for Spectral Analysis of Unevenly Sampled Data. Astrophys. J. 1989, 338, 277. [Google Scholar] [CrossRef]
- VanderPlas, J.T. Understanding the Lomb-Scargle Periodogram. Astrophys. J. 2018, 236, 16. [Google Scholar] [CrossRef]
- Simonetti, J.H.; Cordes, J.M.; Heeschen, D.S. Flicker of Extragalactic Radio Sources at Two Frequencies. Astrophys. J. 1985, 296, 46–59. [Google Scholar] [CrossRef]
- Agarwal, A.; Cellone, S.A.; Andruchow, I.; Mammana, L.; Singh, M.; Anupama, G.C.; Mihov, B.; Raj, A.; Slavcheva-Mihova, L.; Özdönmez, A.; et al. Multiband Optical Variability of 3C 279 on Diverse Time-Scales. Mon. Not. R. Astron. Soc. 2019, 488, 4093–4105. [Google Scholar] [CrossRef]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On Characterizing the Variability Properties of X-ray Light Curves from Active Galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271–1284. [Google Scholar] [CrossRef]
- Vaughan, S. A Simple Test for Periodic Signals in Red Noise. Astron. Astrophys. 2005, 431, 391–403. [Google Scholar] [CrossRef]
- Agarwal, A.; Mohan, P.; Gupta, A.C.; Mangalam, A.; Volvach, A.E.; Aller, M.F.; Aller, H.D.; Gu, M.F.; Lähteenmäki, A.; Tornikoski, M.; et al. Core Shift Effect in Blazars. Mon. Not. R. Astron. Soc. 2017, 469, 813–840. [Google Scholar] [CrossRef]
- Papadakis, I.E.; Lawrence, A. Quasi-Periodic Oscillations in X-ray Emission from the Seyfert Galaxy NGC5548. Nature 1993, 361, 233–236. [Google Scholar] [CrossRef]
- Press, W.H. Flicker Noises in Astronomy and Elsewhere. Comments Astrophys. 1978, 7, 103–119. [Google Scholar]
- Goyal, A. Blazar Variability Power Spectra from Radio up to TeV Photon Energies: Mrk 421 and PKS 2155-304. Mon. Not. R. Astron. Soc. 2020, 494, 3432–3448. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On Generating Power Law Noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Zhang, P.; Zhang, P.; Liao, N.; Yan, J.; Fan, Y.; Liu, Q. Two Transient X-ray Quasi-Periodic Oscillations Separated by an Intermediate State in 1H 0707-495. Astrophys. J. 2018, 853, 193. [Google Scholar] [CrossRef]
- Lin, D.; Irwin, J.A.; Godet, O.; Webb, N.A.; Barret, D. A 3.8 Hr Periodicity from an Ultrasoft Active Galactic Nucleus Candidate. Astrophys. J. 2013, 776, L10. [Google Scholar] [CrossRef]
- Alston, W.N.; Parker, M.L.; Markevičiūtė, J.; Fabian, A.C.; Middleton, M.; Lohfink, A.; Kara, E.; Pinto, C. Discovery of an ∼2-h High-Frequency X-ray QPO and Iron KαReverberation in the Active Galaxy MS 2254.9-3712. Mon. Not. R. Astron. Soc. 2015, 449, 467–476. [Google Scholar] [CrossRef]
- Carpano, S.; Jin, C. Discovery of a 23.8 h QPO in the Swift Light Curve of XMMU J134736.6+173403. Mon. Not. R. Astron. Soc. 2018, 477, 3178–3184. [Google Scholar] [CrossRef]
- Blundell, K.M.; Beasley, A.J.; Bicknell, G.V. A Relativistic Jet in the Radio-Quiet Quasar PG 1407+263. Astrophys. J. 2003, 591, L103–L106. [Google Scholar] [CrossRef][Green Version]
- Czerny, B.; Elvis, M. Constraints on Quasar Accretion Disks from the Optical/Ultraviolet/Soft X-ray Big Bump. Astrophys. J. 1987, 321, 305. [Google Scholar] [CrossRef]
- Fanali, R.; Caccianiga, A.; Severgnini, P.; Della Ceca, R.; Marchese, E.; Carrera, F.J.; Corral, A.; Mateos, S. Studying the Relationship between X-ray Emission and Accretion in AGN Using the XMM-Newton Bright Serendipitous Survey. Mon. Not. R. Astron. Soc. 2013, 433, 648–658. [Google Scholar] [CrossRef]
- Pal, M.; Dewangan, G.C.; Misra, R.; Pawar, P.K. X-ray/UV Variability and the Origin of Soft X-ray Excess Emission from II Zw 177. Mon. Not. R. Astron. Soc. 2016, 457, 875–886. [Google Scholar] [CrossRef][Green Version]
- Chakrabarti, S.K.; Wiita, P.J. Spiral Shocks in Accretion Disks As a Contributor to Variability in Active Galactic Nuclei. Astrophys. J. 1993, 411, 602. [Google Scholar] [CrossRef]
- Smith, K.L.; Mushotzky, R.F.; Boyd, P.T.; Wagoner, R.V. Evidence for an Optical Low-Frequency Quasi-Periodic Oscillation in the Kepler Light Curve of an Active Galaxy. Astrophys. J. 2018, 860, L10. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Becerra Gonzalez, J.; Bellazzini, R.; et al. Multiwavelength Evidence for Quasi-Periodic Modulation in the Gamma-Ray Blazar PG 1553+113. Astrophys. J. Lett. 2015, 813, L41. [Google Scholar] [CrossRef]
- Caproni, A.; Abraham, Z.; Motter, J.C.; Monteiro, H. Jet Precession Driven by a Supermassive Black Hole Binary System in the BL Lac Object PG 1553+113. Astrophys. J. 2017, 851, L39. [Google Scholar] [CrossRef]
- Abraham, Z. Jet Precession in Binary Black Holes. Nat. Astron. 2018, 2, 443–444. [Google Scholar] [CrossRef]
- Sahakyan, N.; Zargaryan, D.; Baghmanyan, V. On the Gamma-Ray Emission from 3C 120. Astron. Astrophys. 2015, 574, A88. [Google Scholar] [CrossRef][Green Version]
- Tanaka, Y.T.; Doi, A.; Inoue, Y.; Cheung, C.C.; Stawarz, L.; Fukazawa, Y.; Gurwell, M.A.; Tahara, M.; Kataoka, J.; Itoh, R. Six Years of Fermi-LAT and Multi-Wavelength Monitoring of the Broad-Line Radio Galaxy 3c 120: Jet Dissipation At Sub-Parsec Scales from the Central Engine. Astrophys. J. Lett. 2015, 799, L18. [Google Scholar] [CrossRef]
- Wiita, P.J. Active Galactic Nuclei. I. Observations and Fundamental Interpretations. Phys. Rep. 1985, 123, 117–213. [Google Scholar] [CrossRef]
- Gupta, A.C.; Srivastava, A.K.; Wiita, P.J. Periodic Oscillations in the Intra-Day Optical Light Curves of the Blazar S5 0716+714. Astrophys. J. 2009, 690, 216–223. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophys. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Pan, H.-W.; Yuan, W.; Yao, S.; Zhou, X.-L.; Liu, B.; Zhou, H.; Zhang, S.-N. Detection of a Possible X-ray Quasi-Periodic Oscillation in the Active Galactic Nucleus 1H 0707-495. Astrophys. J. Lett. 2016, 819, L19. [Google Scholar] [CrossRef]
- Lohfink, A.M.; Reynolds, C.S.; Jorstad, S.G.; Marscher, A.P.; Miller, E.D.; Aller, H.; Aller, M.F.; Brenneman, L.W.; Fabian, A.C.; Miller, J.M.; et al. An X-ray View of the Jet Cycle in the Radio-Loud AGN 3C120. Astrophys. J. 2013, 772, 83. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarwal, A.; Rani, P.; Prince, R.; Stalin, C.S.; Anupama, G.C.; Agrawal, V. A Possible Quasi-Periodic Oscillation in the X-ray Emission of 3C 120. Galaxies 2021, 9, 20. https://doi.org/10.3390/galaxies9020020
Agarwal A, Rani P, Prince R, Stalin CS, Anupama GC, Agrawal V. A Possible Quasi-Periodic Oscillation in the X-ray Emission of 3C 120. Galaxies. 2021; 9(2):20. https://doi.org/10.3390/galaxies9020020
Chicago/Turabian StyleAgarwal, Aditi, Priyanka Rani, Raj Prince, C. S. Stalin, G. C. Anupama, and Vipul Agrawal. 2021. "A Possible Quasi-Periodic Oscillation in the X-ray Emission of 3C 120" Galaxies 9, no. 2: 20. https://doi.org/10.3390/galaxies9020020
APA StyleAgarwal, A., Rani, P., Prince, R., Stalin, C. S., Anupama, G. C., & Agrawal, V. (2021). A Possible Quasi-Periodic Oscillation in the X-ray Emission of 3C 120. Galaxies, 9(2), 20. https://doi.org/10.3390/galaxies9020020





