Abstract
The Dirac electron is considered as a particle-like solution consistent with its own Kerr–Newman (KN) gravitational field. In our previous works we considered the regularized by López KN solution as a bag-like soliton model formed from the Higgs field in a supersymmetric vacuum state. This bag takes the shape of a thin superconducting disk coupled with circular string placed along its perimeter. Using the unique features of the Kerr–Schild coordinate system, which linearizes Dirac equation in KN space, we obtain the solution of the Dirac equations consistent with the KN gravitational and electromagnetic field, and show that the corresponding solution takes the form of a massless relativistic string. Obvious parallelism with Heisenberg and Schrödinger pictures of quantum theory explains remarkable features of the electron in its interaction with gravity and in the relativistic scattering processes.
1. Introduction
One of the main points of confrontation between gravity and quantum theory is the structure of elementary particles, which are considered in quantum theory as structureless, like a point-like electron in Dirac theory, but must be represented as an extended field model in configuration space for compatibility with the stress-energy tensor of Einstein’s equations.
A revolutionary step towards unification quantum with gravity was taken in superstring theory, which represented particles as extended strings. Gravitational black holes (BH) have been considered as candidates for elementary particles repeatedly since 1980, and since the 1990s, they have also attracted attention in the theory of superstrings.
However, as one of its founders, John Schwartz, noted, “... Since 1974, superstring theory has ceased to be regarded as particle physics...” and “... a realistic model of elementary particles still seems a distant dream ...” [1].
Meanwhile, a renewed interest to relationships between black holes and elementary particles has been obtained recently in the works [2,3,4,5].
Formation of BHs is related with gravitational effect of frame-dragging. In the rotating Kerr–Newman BH solution, with parameters corresponding to spin, mass, and Kerr’s rotational parameter a of elementary particle, spin creates a giant over-rotating dragging of space, which is directed along the direction of rotation, leading to a new important effect, the formation of the closed Wilson loop, which never was used in particle physics before.
In contrast to considered earlier cases of the Schwarzschild or Reissner–Nordström gravity, the characteristic scale of the KN gravity essentially increases because it is determined by the radius of the Kerr singular ring:
which corresponds to the reduced Compton wave length of the particle.
This fact, established already in the first models of an electron based on the Kerr geometry [6,7,8,9,10,11,12] was remarkable because it was known, but was not timely estimated as one of the first evidences of the correspondence between KN particle and quantum theory.
The gigantic ratio between the spin and mass values for elementary particles in KN geometry violated the generally accepted concept of the weakness of gravity, based on the earlier estimations of gravitational radius of the Schwarzschild solution:
The gravitational field of an electron, corresponding to the Kerr–Newman solution, has singular ring which changes topology of space at the Compton distance.
In 1968, Carter obtained that the Kerr–Newman (KN) solution for a charged and rotating black hole (BH) has a gyromagnetic ratio – just as that of the Dirac electron [6]. It gave rise to the study of the electron model based on the KN solution, see [6,7,8,9,10,11,12,13,14] and so on.
It should be noted that the KN electron model is not actually a black hole because taking the parameters of KN solution in correspondence with parameters of an electron, mass charge e, and angular momentum we obtain the relation which shows that the rotation parameter a is so large, that all horizons of the BH solution disappear. There appears the Kerr singular ring (see Figure 1), which was hidden earlier behind the horizon of the KN solution. This ring forms a type of door that opens the way to another sheet of Kerr space. The space becomes two-sheeted, having the basic background and some kind of mirror Alice world behind the Kerr ring.
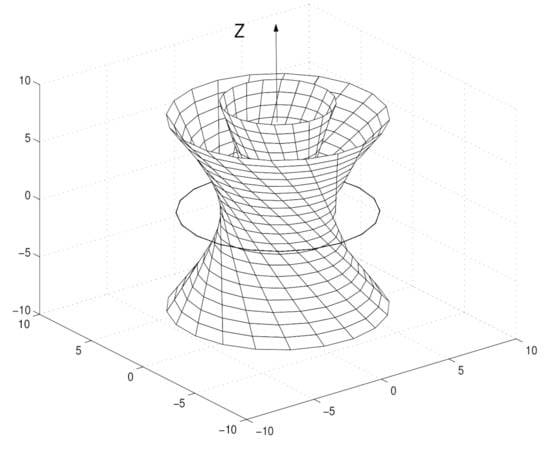
Figure 1.
Kerr congruence and Kerr singular ring generated by null congruence .
In previous papers [15,16,17], we developed the line started by W. Israel [8], who suggested to truncate the second sheet of the Kerr geometry along the disk spanned by the Kerr singular ring. After analysis of the Israel source by Hamity [9], a modified disk-like source was suggested by C. López [10] as an ellipsoidal vacuum bubble–a thin shell covering the Kerr singular ring and matching with the external KN solution.
In the works [15,16,17], we considered a generalization of the López model, in which the KN bubble was formed from the Higgs field in a superconducting vacuum state. The thin shell of bubble was replaced by a domain-wall solution, which was described by the Landau–Ginzburg (LG) supersymmetric model of phase transition. Domain wall (DW) was interpolated between the superconducting (and supersymmetric) internal vacuum state and the external exact gravitational KN solution.
The obtained, by the C.López bubble source of the KN geometry [10] (see Figure 2) was presented in our works as a supersymmetric and superconducting bag model. The reason for interpretation of the KN source as a bag model, was their ability to be elastic and deformable under influence of external conditions, which was known from the behavior of the well-known MIT and SLAC bag models [18,19]. It was assumed also that bags are similar to strings and can turn into strings under strong deformations [20,21].
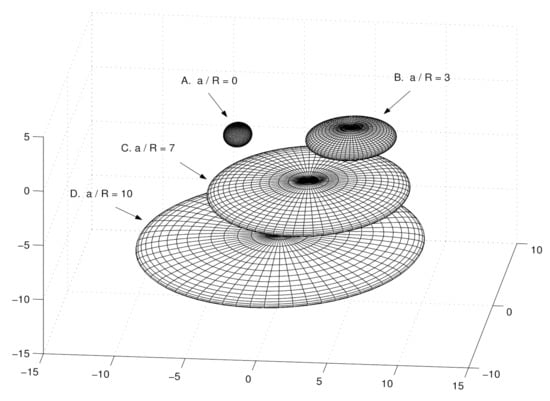
Figure 2.
Disk-like source of the regularized solution of Kerr–Newman (KN) as a bag model. Deformation of the disk at different ratios of parameters and For , the disk is very thin, and corresponds to the fine structure const.
Meanwhile, one feature of the KN bag significantly distinguishes it from the MIT and SLAC bag models–the usual bag models form a cavity in superconductor, while the KN bag must have an internal superconducing state. This feature was the source of problems that forced us to use a supersymmetric LG field model of the phase transition [22,23,24,25,26]. The use of supersymmetry becomes necessary since the simpler non-supersymmetric LG models cannot provide concentration of the Higgs field inside of the bag model and lead typically to the opposite configuration of the bag as a cavity in a superconducting matter. This problem was discussed in detail in [15,16], and will not be discussed here as the goal here is different–to get the consistent with gravity solutions of the Dirac equations.
However, attention will be paid to the important result obtained in the letter [17]–the disk-like source of the KN solution turns out to be two-sided, and has an antiDW-side along with the DW surface, and the presence of this DW-antiDW (breather) structure is essential for the solutions of Dirac equations discussed here.
Our task here is to obtain a self-consistent solution of the Dirac equation embedded in the proper gravitational and electromagnetic field of the electron corresponding to the Kerr–Newman solution. By solving this problem, we obtain that the Kerr–Schild coordinate system is unique, in the sense that it allows us to use -matrices of the auxiliary Minkowski space, where the Dirac equations in proper gravitational and electromagnetic field are linearized.
We obtain that solutions of the Dirac equations take the form of a massless relativistic string based on an orientifold structure discussed in previous works [27].
2. Kerr–Schild Geometry and Structure of KN Solution
Specific feature of the Kerr–Schild approach is the use of the auxiliary Minkowski space (signature ), with Cartesian coordinates
In these coordinates, the metric of the KN solutions is [7]:
where is a flat metric of the auxiliary Minkowski space, and H is the scalar function, which for the KN solution takes the form:
The KN vector potential is given as:
The field forms a principal null congruence (PNC), shown in Figure 1. In terms of BH geometry, this field shows a local direction of dragging the frame, that in the case of overrotating HB solutions produces closed Wilson lines surrounding the source of KN geometry, see Figure 3.
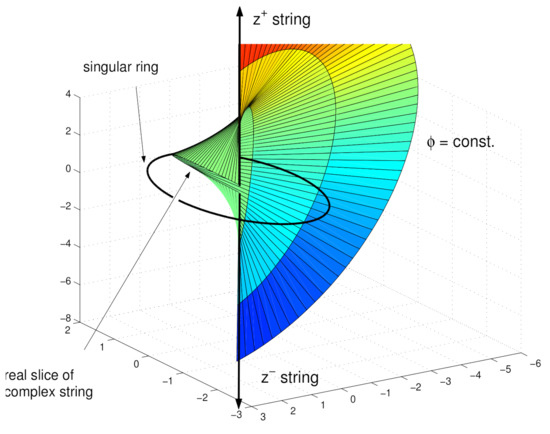
Figure 3.
Deformations of the Kerr coordinate caused by dragging of space in angular direction near the Kerr singular ring.
Kerr’s congruence can be represented as an electromagnetic radiation which propagates (with twist) from infinity towards the Kerr ring, penetrates it, and by coming out on the other sheet of the Kerr geometry goes out again to infinity. In Cartesian coordinates , the form shows local direction of frame-dragging.
In the Kerr coordinates PNC, is presented in [7] by the form:
The relation between the Cartesian coordinates and Kerr’s angular coordinates is the following:
The incoming PNC is directed to the Kerr ring. Rays lying in an equatorial plane () focus on the Kerr singular ring. Other incoming rays, passing trough the ring, turn into out-going rays propagating on another (say “negative”) sheet of the Kerr space. Thus, the Kerr solution in the KS form describes two different sheets of space-time with two different congruences:
and two different metrics:
on the same Minkowski background Working with outgoing Kerr field corresponding to retarded potentials, we choose sign plus in (8), and by following [7] we take
The Kerr theorem:
Kerr theorem defines two fields of PNC, and in terms of Penrose’s twistor theory [28,29,30]. Kerr theorem presents two complex analytic solutions of the equation:
where F is a quadratic holomorphic function of the projective twistor coordinates: and
are the null Cartesian coordinates of the auxiliary Minkowski space
In the class of quadratic in Y functions the Kerr theorem gives two analytic solutions of Equation (10), which correspond to two projective spinor coordinates:
which are antipodically conjucate:
and the corresponding Weyl spinors and define two antipodal fields of the principal null directions:
3. Shape of the KN Bag Model and Wilson Loop
The López boundary of the bubble, where the KN space can be matched continuously with the flat internal metric is unambiguously determined by the Kerr–Schild metric form (3), as the surface where Setting we obtain:
that gives us the “classical” electron radius.
Since r is the Kerr radial coordinate, we obtain that the bag boundary represents indeed an oblate ellipsoidal surface–a thin disk of the radius which is about the reduced Compton wave length, and the thickness of the disk which is equal to a classical electron radius. One sees that the degree of oblateness of the disk is , which corresponds to the fine structure constant
Therefore, the Kerr–Newman spin parameter a leads to a strong deformation of the shape of the bag model, and this deformation of the bag leads to the appearance of a relativistic string at the sharp edge of the KN disk (see Figure 4).
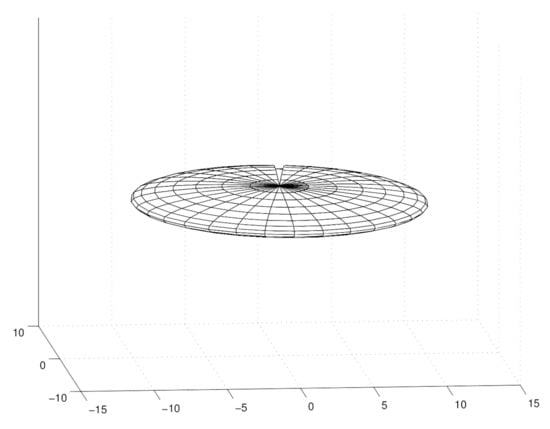
Figure 4.
Disk-like shape of the Kerr–Newman bag model. Border of the superconducting bag ends with Wilson loop forming a closed circular string.
The existence of this string is evidenced by the Wilson loop of the vector potential placed along border of the bag, which was obtained first in [31] and then discussed in [15,32,33].
From (5) and (6) we obtain that the vector-potential of the regularized KN solution takes its maximal value in the equatorial plane () at the bag border ,
This potential is tangent to the bag border and for the fixed time it forms the closed Wilson loop so that the loop integral gives the following incursion of the potential:
Integration gives and using relation we obtain:
Definiteness of the phase incursion requires and (18) leads to quantum condition
4. String Structure and Superficial Currents on the Border of KN Bag
4.1. Scattering Process and Orientation of the Kerr Disk
On the initially two-sheeted KN space-time, the directed in future vortex field of the Kerr congruence formed an in-going field on the negative sheet of the Kerr space where it was directed towards the Kerr singular ring. Penetrating through the ring, this field continues analytically on the second sheet turning into an out-going field, where another coordinate system is used (7).
Although, in the regularized KN solution the passage to the sheet is closed, consideration of the analog of this sheet is relevant in the scattering process when we observe the in-going field incident on the source of the KN solution before the scattering, and then the signal reflected in the scattering process in the form of an out-going field.
In contrast to the case with the negative sheet of the Kerr solution, in this case we use the same Kerr’s coordinate system (7) for both in-going and out-going fields, in which we do a replacement of getting an equivalent coordinate transformation for the in-going field on
compatible with metric:
and with in-going Kerr congruence
This process shows that disk-like source of the KN field has two faces: one from the side of the in-going fields and the other from the side of the out-going fields These two sides are related with a reverse sign of the disk rotation and change the orientation angle for the incoming field.
The corresponding string-like structure was suggested in [27] as an orientifold string. This string forms the Kerr’s light-like world-sheet containing only the left modes on the fundamental interval For a static picture of the Kerr disk at the orientifold string is formed as a parity operator which covers the string world sheet twice: the first time on interval and the second time on interval in the opposite direction.
The full orientifold world-sheet is formed as a folded string on the doubled interval and contains the sum of the left and right modes
The orientifold string is a left-right symmetric in static representation, which in quantum theory is called as Heisenberg picture, however the symmetry is broken on the rotating disk.
4.2. Surface Currents Caused by Wilson Loop, Higgs Phases, and Stringy Parametrization
The Kerr–Newman solution demonstrates an intrinsic connection to string theory. The role of the string is played by the singular ring of the Kerr solution [12,13]. A regularized version of this string occurs at the sharp edge of the disk-like boundary of the ellipsoidal bag forming the regular source of the Kerr–Newman solution (see Figure 5).
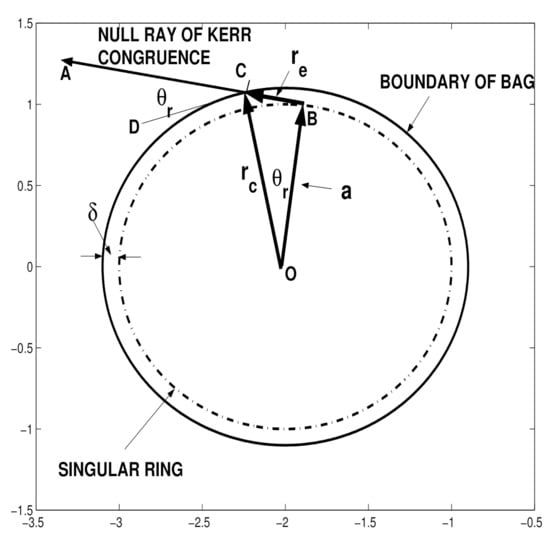
Figure 5.
KN disk as a carrier of the orientifold string in the static picture. Kinematic relations in the equatorial plane of the KN disk. The shown out-going light-like beam of the Kerr congruence is tangent to th Kerr singular ring and crosses the edge of the disk at angle .
As is known, the Higgs field model coincides with the Landau–Ginzburg (LG) model for a phase transition in a superconducting medium [34]. Similarly, the supersymmetric Higgs model is described by a supersymmetric (or generalized) Landau–Ginzburg (LG) model [22,25].
The corresponding supersymmetric bag model is formed by the domain wall (DW), which separates the external gravitational field KN from the flat inner space filled with the supersymmetric vacuum of the Higgs field.
Although the consistent description of this phase transition requires a supersymmetric scheme of a phase transition with several chiral fields [15,16,17], the simple LG field model with one chiral field can describe each separate process of the phase transition with the creation of superficial currents on the boundary of the bag. Corresponding Lagrangian with one Higgs fields is [34],
where are covariant derivatives with vector-potencial , and
where is the v.e.v. of the Higgs field .
The superconducting vacuum state of the Higgs field inside the Bag leads to equations:
which shows that inside the superconductor current is pushed out, and equations:
show that the current must be concentrated on a surface layer with a depth of penetration ,35]). Inside the superconductor, potential must be eaten by phase of the Higgs field according to (24).
The potential of the KN field (5) increases near the bag boundary, and takes maximum in the equatorial plane, near the bag boundary
According to the Wess–Zumino model, the supersymmetric QED is described by two Higgs fields and [36], and Equation (24) allow us to connect two phases of the Higgs fields and with two boundaries of the KN bag model and which were obtained in the double-face structure of the KN disk [17], related with congruences and and forming a DW-AntiDW structure, know also as a “breather” [37].
Integration of the LG Equation (24) for the superficial currents related with the out-going phase of the Higgs field, placed on the boundary gives while for the in-going Higgs phase, placed on the boundary we obtain where the change in the sign by the transition was also taken into account.
Therefore, on the boundary we obtain the potential and on the boundary – the potential
Applying these solutions to the out-going vector field on the boundary which is dragged by gravitational field of the Kerr congruence, forming the closed Wilson loop on the border we obtain:
(1) Incursion of the potential along the loop is controlled by the Higgs phase and integration of the equations gives:
(2) Similarly, the out-going potential acting on the boundary gives:
and therefore, the phases of the Higgs fields and behave like parametrization of the left and right modes of a relativistic string, see [17,33].
The formation of a Wilson loop around a singular ring is a characteristic feature of the string models where the string tension mechanism is formed by a tube of force lines [38].
The singular ring of the Kerr solution is formed of two light-like lines, “left” and “right”, controlled by the conjugate phases and and the existence of “right” and “left” excitation modes is an indispensable condition for the formation of a string as a world sheet. A string described by only one mode, say the right one, turns into world line that depends on only one parameter. For this reason, a simple light -like Kerr’s singular ring does not form a world sheet, and strictly speaking is not a string, but a world line. The KN string is formed as the ’orientifold’ string [27] consisting of two half-modes acting sequentially in time, in correspondence with the DW-AntiDW field model of the KN source considered in [17], i.e., forming an oscillating solution of the type ‘breather’ [37].
5. The Dirac Equations for an Electron Interacting with Its Own Gravitational and Electromagnetic Field
We come to the main part of our consideration–the solutions of the Dirac equations for fermionic string which emerge on the border of the regularized KN disk interacting with the consistent gravitational and electromagnetic KN field.
We see that our analysis unavoidably leads us to the typical features of the quantum considerations: The importance of the separable analysis of the Heisenberg and Schrödinger pictures, the corresponding state vectors, unitary transformation, plane waves, and the scattering process.
5.1. The KN Disk-Like Source as an Electron in the Heisenberg Picture
The KN gravitational field can only be consistent with one of two types of the Kerr congruence, either in-going or out-going [39], and the out-going variantwas chosen as it is consistent with the retarded electromagnetic fields.
Out-going Kerr congruence:
propagates from the both sides of the disk and towards direction The in-going congruence:
propagates from towards the disk and focus at the both sides of the disk and
The transition from the out-going picture to in-going is connected with the replacement that in the coordinate transformation (7) corresponds to the replacement changing in the direction of rotation and in orientation angle
The Kerr disk is located at the scattering boundary which corresponds to the state vector in the Heisenberg picture. Orientation of the disk is changed under transition from to and the string on the border of KN disk acquires the properties of the orientifold string with two faces and
The regularized Kerr’s disk has a finite thickness , which is determined by the physics of a scattering process.
The role of the equations of motion in the Heisenberg picture is played by the Dirac equations.
5.2. Uniqueness of the Kerr–Schild coordinates
The Dirac equation in the Kerr–Newman gravitational field was studied in many works, in particular in [40,41,42,43,44,45,46]. The freedom of choice for a coordinate system is an important aspect of general relativity. However, in the case of the Kerr–Newman solution for the over-rotating gravitational and electromagnetic field, the Kerr–Schild coordinate system plays an exceptional role, greatly simplifying the problem under consideration.
The association with the Kerr–Schild space coordinates of the auxiliary Minkowski space or the equivalent null coordinates (11), allows one to represent the Maxwell and Dirac equations in a form that formally coincides with their form in the flat Minkowski space.
In particular, the electromagnetic KN field is represented in [7] by the self-dual complex tensor:
where is completely skew-symmetric and equal to when
The system of Maxwell equations takes in this case the form:
and since the determinant of the Kerr–Schild metric is:
see for example [7], solutions of the Maxwell Equations (30) written in the tetrad form [7],
coincide with the corresponding solutions in the flat auxiliary Minkowski space expressed in the null Cartesian coordinates (11), see pp. 6, 7 in [7]. In particular, these solutions create the electromagnetic field (7.8) and the stationary vector-potential (7.7) of [7], which corresponds to expressions (5) and (6).
Considering the Dirac equation in the KN gravitational field regularized by the López boundary (15), we get a cut off of the Kerr singular ring, and also the additional suppression of the gravitational field by the condition , leading to an almost flat space on the boundary of the KN disk.
In this case, for the Dirac operator in the weak gravitational field, we can start in the first approximation from the Dirac equation in the nearly flat Minkowski space-time with Cartesian coordinates and the constant -matrices of the flat Minkowski space. Denoting these matrices as we can estimate our deviations by using the convenient formula of the work: [43]
where
In the result, since in the Kerr–Schild coordinate system we have we obtain that and the initial substitution turns out to be exact.
We obtain that the description of the KN solution in the Kerr–Schild coordinate system is the unique in that it leads to linearization of both electromagnetic and Dirac equations in accordance with the gravitational background of the KN solution.
5.3. The Dirac Equations in the Weyl Representation
The Dirac equations in the Weyl representation decompose into two equations:
where and or
The Wilson loop potential acts on both - boundaries (faces) of the KN disk.
In the considered earlier analogous physical model of the rotating KN disk-like source, the in-going and out-going Kerr congruences are controlled by two related phases of the Higgs field, and the momentum of the string solution must be completed by an "internal" angular momentum of two semi-strings associated with rotation of the KN disk under its evolution in time,
According (14), the spinors and have different helicities with respect to helicity operator and the Weyl spinor is aligned with out-going direction while the spinor is aligned with in-going direction The sign of is already taken into account in Dirac Equations (35) and (36).
In the same time, the both vector fields of the Wilson lines are out-going and, being emanated from the boundaries and they are related with spinors of different chirality. As a result, the electromagnetic contribution from Wilson line should change the sign in Equation (36).
The spinor string is formed of two semi-strings of opposite helicities and which have the unique common point corresponding to the point where the orientation of the string changes,
Integrating the Ginzburg–Landau equations for the out-going phase of the Higgs field and we obtained which for gives The corresponding vector potential is
For the boundary , we have the opposite sign of charge, which corresponds to the Wess–Zumino supersmmetric QED model, and also corresponds to the integration of the BPS equations considered in [17]. The change of orientation, is accompanied by the potential of the Wilson line in the form
To simplify notations we will omit further the index K in the Kerr angular coordinate
5.4. The Dirac Equations in the Heisenberg Picture for
Taking the Weyl representation for -matrices, we can write the Dirac equations in the Heisenberg picture for
Setting with and we obtain the Dirac equations in the rest frame,
where and are normalized spinors and I is unit matrix.
for any and the first equation is identically satisfied when:
and the second equation is identically satisfied when:
Spinors are normalized as
In the Heisenberg picture presenting the KN string at fixed time we have:
(1) The spinor string which is a massless half-string, created by the out-going light-like directions and emanated from Wilson’s counter placed at and also the one more massless half-string, created by the out-going light-like directions emanated from Wilson’s counter placed at
(2) The spinor string representing the second massless half-string, created by the in-going light-like directions towards the Wilson counter placed at .
Since is everywhere, for exclusion of singular point where the opposite directed semi-strings are joined, both half-strings are massless and do not interact, except for point where and the mass term is presented as a delta-function
The potential at the end of the out-going semi-string is:
and the potential at the end of the in-going semi-string, turns out to be the same, Thus, the potential difference between the ends of the semi-strings in the static Heisenberg picture is zero.
In the Weyl representation for matrices , the out-going and in-going fields are ordered in time, and the fields with negative frequencies do not arise.
5.5. The Schrödinger Picture, Plane Waves, and String in the Kerr–Schild Coordinates
In the Schrödinger picture the plane waves and Kerr–Schild coordinates are described by wave function [47]:
where and
The spinor satisfies the Dirac equations:
In the rest system, functions and are connected by unitary transformation where is the Hamiltonian of the system.
We consider as the operator acting on a state vector in the static Heisenberg picture, while the plane wave:
represents the state vector in the dynamic Schrödinger picture.
When the semi-strings are joined,
In the Schrödinger picture the string turns out to be asymmetric:
the semi-string covering the interval gives and
the semi-string covering the interval gives
The potential at the end point of the out-going semi-string is while the potential of the in-going semi-string at the end point is
We note that this potential difference corresponds to the Josephson effect in superconducting junctions, where the voltage is determined by the rotation of the Higgs phase.
Although in Heisenberg picture, the electron represents a string about the Compton size (or Wilson Loop) surrounding the Kerr–Newman disk, this is a static picture corresponding to the shape of the string at a fixed time The electron is an ultra-relativistic object, and external observer (including other particles) perceives the electron in the Schrödinger picture, or in the interaction representation where the wave function of the electron is multiplied by unitary factor
The consistency with gravity Compton radius of an electron is not its effective scattering radius, and the people working in the high energy physics perceive it as an ultra-small tornado that can work like a scalpel.
6. Conclusions
This analysis shows that, following pioneering works by Carter, Israel, and López, the Dirac electron could be described as an over-rotating KN gravitating BH solution described by the Dirac equations interacting with its proper gravitational and electromagnetic field in the Kerr–Schild coordinate system.
Such a description is important both from the point of view of the unification gravity with quantum theory, and from the point of view of the nonperturbative model of the extended electron based on the Higgs mechanism of the spontaneously broken gauge theory.
This treatment shows that the existing theories and models of elementary particles are at least incomplete, and do not take into account a number of important effects associated with the gravitational process of the frame-dragging in the spinning gravitational space-time, in particular, the strong influence of the gravitationally-induced Wilson loop in the over-rotating Kerr–Newman gravitational field.
The main new lessons that this model provides are as follows:
1. The gravitational field of an electron can be described in theHeisenberg picture by the regularized Kerr–Newman solution, which distorts space on the Compton scale, increasing the usually accepted zone of influence of gravity by about 22 orders of magnitude;
2. The supersymmetric Higgs model (Landau–Ginzburg field model) separates gravitational field of the electron from its flat core, resolving the known conflict between gravity and quantum theory without changing Einstein’s equations;
3. The regularized nonperturbative electron model takes the shape of a superconducting disk formed from the Higgs field in a supersymmetric vacuum state.
4. The Kerr-Schild coordinates linearize the Dirac and Maxwell equations on the KN background, playing an exceptional role in the formation of the nonperturbative disk-like image of the electron in the Heisenberg picture;
5. The Dirac equations consistent with the KN gravitational field take a stringy form, generating the circular currents at the boundary of a nonperturbative bag model.
The fact that the core of an electron takes the form of a relativistic string in the Heisenberg picture is important, since it can explain its gravitational interaction on the Compton scale, while having the ultra-relativistic stringy nature, the electron can exhibit strongly different features in the Schrödinger picture and in the interaction representation, which may explain the properties of the electron known from scattering experiments, where it exhibits the seemingly point-like structure.
When this paper was finished, the works by Ahmed Alharthy and Vladimir V. Kassandrov [48] were found, which overlaps with the main theme of this work. The work by these authors is interesting and based on the old works by F.Edjo Ovono, V. Kassandrov, and Ya. Terletsky, which develops the works and ideas of Natan Rosen [49]. Although it seems that these works are far from the KN electron model, we find that the introduced Rosen scalar potential is a prototype of the considered in our work Higgs field.
Funding
This research was supported by Fundamental Research NSI RAS N 11407/15.1/2020, see http://www.ibtrae.ac.ru/contents/352/, accessed on 16 March 2021.
Acknowledgments
I would like to thank first of all our colleagues in Nuclear Safety Institute, L.V. Matveev, Yu.N. Obukhov, P.S. Kondratenko, and V.N. Ponomariov, whose permanent discussions supported the author in the process of searching for the truth.
Conflicts of Interest
The author declares no conflict of interest.
References
- Schwarz, J. The Early History of String Theory and Supersymmetry, CALT-68-2858. arXiv 2012, arXiv:1201.0981. [Google Scholar]
- Arkani-Hamed, N.; Huang, Y.; O’Connell, D. Kerr Black Holes as Elementary Particles. J. High Energ. Phys. 2020, 46, 1–12. [Google Scholar] [CrossRef]
- Schmekel, B.S. Quasi-Local Energy of a Charged Rotating Object Described by the Kerr-Newman Metric. Phys. Rev. D 2019, 100, 124011. [Google Scholar] [CrossRef]
- Burinskii, A. Spinning Particle as Kerr–Newman “Black Hole”. Phys. Part Nuclei Lett. 2020, 17, 724. [Google Scholar] [CrossRef]
- Burinskii, A. The Kerr–Newman Black Hole Solution as Strong Gravity for Elementary Particles. Gravit. Cosmol. 2020, 26, 87. [Google Scholar] [CrossRef]
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef]
- Debney, G.C.; Kerr, R.P.; Schild, A. Solutions of the Einsein and Einstein-Maxwell Equations. J. Math. Phys. 1969, 10, 1842. [Google Scholar] [CrossRef]
- Israel, W. Source of the Kerr metric. Phys. Rev. D 1970, 2, 641. [Google Scholar] [CrossRef]
- Hamity, V. An interior of the Kerr metric. Phys. Lett. A 1986, 56, 77. [Google Scholar] [CrossRef]
- López, C.A. Extended model of the electron in general relativity. Phys. Rev. D 1984, 30, 313. [Google Scholar] [CrossRef]
- Grön, O. New derivation of López’s source of the Kerr-Newman field. Phys. Rev. D 1985, 32, 1588. [Google Scholar] [CrossRef]
- Burinskii, A.Y. Microgeons with spin. Sov. Phys. JETP 1974, 39, 193. [Google Scholar]
- Ivanenko, D.D.; Burinskii, A.Y. Gravitational strings in the models of elementary particles. Izv. Vuz. Fiz. 1975, 5, 135. [Google Scholar] [CrossRef]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment of the Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385. [Google Scholar] [CrossRef]
- Burinskii, A. Gravitating lepton bag model. JETP Zh. Eksp. Teor. Fiz. 2015, 148, 228. [Google Scholar] [CrossRef][Green Version]
- Burinskii, A. Stability of the lepton bag model based on the Kerr-Newman solution. JETP Zh. Eksp. Teor. Fiz. 2015, 148, 937. [Google Scholar] [CrossRef]
- Burinskii, A. Source of the Kerr-Newman solution as a supersymmetric domain-wall bubble: 50 years of the problem. Phys. Lett. B 2016, 754, 99. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. New extended model of hadrons. Phys. Rev. D 1974, 9, 3471. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Chanowitz, M.S.; Drell, S.D.; Weinstein, M.; Yan, T.M. Heavy quarks and strong binding: A field theory of hadron structure. Phys. Rev. D 1974, 11, 1094. [Google Scholar]
- Giles, R.C. Semiclassical dynamics of the “SLAC bag”. Phys. Rev. D 1976, 70, 1670. [Google Scholar] [CrossRef]
- Johnson, K.; Thorn, C.B. Stringlike solutions of the bag model. Phys. Rev. D 1976, 13, 1934. [Google Scholar] [CrossRef]
- Fendley, P.; Mathur, S.; Vafa, C.; Warner, N.P. Integrable Deformations and Scattering Matrices for the N=2 Supersymmetric Discrete Series. Phys. Lett. B 1990, 243, 257. [Google Scholar] [CrossRef]
- Abraham, E.R.C.; Townsend, P.K. Intersecting extended objects in supersymmetric field theories. Nucl. Phys. B 1991, 351, 313. [Google Scholar] [CrossRef]
- Cvetic, M.; Quevedo, F.; Rey, S.J. Target space duality and stringy domain walls. Phys. Rev. Lett. 1991, 67, 1836. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Losev, A.; Shifman, M. BPS saturated solitons in N=2 two-dimensional theories on RxS (domain walls in theories with compactified dimensions). Phys. Rev. D 2000, 61, 085005. [Google Scholar] [CrossRef]
- Chibisov, B.; Shifman, M. BPS-saturated walls in supersymmetric theories. Phys. Rev. D 1997, 56, 7990. [Google Scholar]
- Burinskii, A. Orientifold D-String in the Source of the Kerr Spinning Particle. Phys. Rev. D 2003, 68, 105004. [Google Scholar] [CrossRef]
- Penrose, R. Twistor Algebra. J. Math. Phys. 1967, 8, 345. [Google Scholar] [CrossRef]
- Burinskii, A. Wonderful Consequences of the Kerr Theorem. Grav. Cosmol. 2005, 11, 301. [Google Scholar]
- Burinskii, A. Complex Kerr geometry and nonstationary Kerr solutions. Phys. Rev. D 2003, 67, 124024. [Google Scholar] [CrossRef]
- Burinskii, A. Kerr-Newman electron as spinning soliton. Int. J. Mod. Phys. A 2014, 29, 1450133. [Google Scholar] [CrossRef]
- Burinskii, A. Source of the Kerr-Newman solution as a gravitating bag model: 50 years of the problem of the source of the Kerr solution. Int. J. Mod. Phys. A 2016, 31, 1641002. [Google Scholar] [CrossRef]
- Burinskii, A. Features of spinning gravity in particle physics: supersymmetric core of the Kerr-Newman electron. J. Phys. Conf. Ser. 2019, 1275, 012031. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Olesen, P. Vortex-line models for dual strings. Nucl. Phys. B 1973, 61, 45. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media (Volume 8 of A Course of Theoretical Physics); Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Wess, J.; Bagger, J. Supersymmetry and Supergravity; Princeton University Press: Princeton, NJ, USA, 1983. [Google Scholar]
- Lomdahl, P.S.; Olsen, O.H.; Samuelsen, M.R. Breather—kink-antikink-pair conversion in the driven sine-Gordon system. Phys. Rev. A 1984, 29, 350. [Google Scholar] [CrossRef]
- Zwiebach, B. A First Course in String Theory; Massachusetts Institute of Technology: Cambridge, MA, USA, 2009. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation, Part 3; W. H. Freeman: San Francisco, CA, USA, 2000; ISBN 978-0-7167-0344-0. [Google Scholar]
- Einstein, S.; Finkelstein, R. Lorentz covariance and the Kerr-Newman geometry. Phys. Rev. D 1977, 15, 2721. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: London, UK, 1992. [Google Scholar]
- Adler, R.J.; Bazin, M.; Schiffer, M.M. Introduction to General Relativity, 2nd ed.; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Finster, F. Local U(2,2) Symmetry in Relativistic Quantum Mechanics. J. Math. Phys. 1998, 39, 6276. [Google Scholar] [CrossRef][Green Version]
- Finster, F.; Smoller, J.; Yau, S.-T. Particlelike solutions of the Einstein-Dirac equations, gr-qc/9801079. Phys. Rev. D 1999, 59, 104020. [Google Scholar] [CrossRef]
- Finster, F.; Smoller, J.; Yau, S.-T. Non-Existence of Time-Periodic Solutions of the Dirac Equation in a Reissner-NordstrEom Black Hole Background. J. Math. Phys. 2000, 41, 2173. [Google Scholar] [CrossRef]
- Burinskii, A. Emergence of the Dirac Equation in the Solitonic Source of the Kerr Spinning Particle. Grav. Cosmol. 2014, 21, 28. [Google Scholar] [CrossRef][Green Version]
- Akhiezer, A.I.; Berestetskii, V.B. Quantum Electrodynamics; Interscience Publishers: Geneva, Switzerland, 1965. [Google Scholar]
- Alharthy, A.; Kassandrov, V. On a Crucial Role of Gravity in the Formation of Elementary Particles. Universe 2020, 6, 193. [Google Scholar] [CrossRef]
- Rosen, N. A field theory of elementary particles. Phys. Rev. 1939, 55, 94. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).