Abstract
Noncommutative-like model (NC-like) is an interesting alternative inspired by string theory to understand and describe the velocity rotation curves of galaxies without the inclusion of dark matter particles. In a natural way, a Gaussian density profile emerges and is characterized by a parameter , called the NC-like parameter. Hence we aim to confront the NC-like model with a galaxy sample of the Spitzer Photometry and Accurate Rotation Curves (SPARC) catalog to constrain the model parameters and compare statistically with the Einasto density profile using the Akaike and Bayesian information criteria. According to our results, some galaxies prefer the NC-like over the Einasto model while others do not support NC-like.
PACS:
04.50.Kd; 98.10.+z; 97.20.Vs
1. Introduction
Nowadays, dark matter (DM) is one of the most elusive components in modern astrophysics and cosmology, observed in several phenomena, from rotation curves in galaxy dynamics [1] to large scale structure in the Universe [2,3,4]. Additionally, DM is confirmed in the Cosmic Microwave Background Radiation (CMB) [4], having percentages around ∼ of the total components. Moreover, the addition of a cold dark matter component and its analysis with computational simulations is in agreement with the knowledge of structure formation at large scales and the observed distribution of structures [5,6].
The assumption of a DM halo generates the stability of the galactic structure and a compatibility with the observed velocity rotation at large radius. Thus, the corresponding rotation velocities of the galaxies can be described by several empirical density profiles, based for example, on N-body simulations like the Navarro-Frenk-White (NFW) [7] profile or by phenomenological models such as pseudo isothermal (PISO) [8], Burkert [9], Einasto [10], scalar field dark matter (SFDM) [11], among others [12]. However, each of these models has its advantages and disadvantages (See for example in Refs. [13,14], where the halo profiles are more dense and more pronounced than those inferred observationally), proving that there is not yet a definitive model.
Despite the amount of empirical models proposed in recent years, the microscopic nature of DM is still a mystery. In literature, many mechanisms have been proposed in order to explain DM and its possible relation with the density profiles in galaxies and also with the large scale structure. For instance, supersymmetric models related to weak interacting massive particles (WIMPS) are the most accepted candidates by the scientific community to explain DM, due to their advantages in the standard model of particles (SM) or in quantum gravity like string theory [15,16]. However, several interesting alternatives have emerged, for example: SFDM as in the case of axions [17,18] or ultralight scalar fields [19,20,21]; or even extensions to General Relativity (GR) like theories [22], brane-world models [23,24,25,26,27,28], etc.
Another possibility to explain the rotation curves of galaxies comes from noncommutativity (NC) models [29]. The idea emerges from string theory, based on the assumption of NC space-time coordinates, obtaining a new type of gauge theory via the Seiberg-Witten map [30]. In this sense, one of the most common examples of NC comes from quantum mechanics in two dimensions in where are encoded the new commutation relations via the coordinate operators. Therefore, many studies have been done in order to constrain the NC parameter, obtaining values approximately equal to the Planck length [31] or even Trans-Planckian. Hence, based on these hypotheses, a Gaussian distribution of minimal width may be used instead of a Dirac-delta function (The Dirac-delta function help to describe a point-like structure in the standard case of quantum field theory). In fact, this change is also motivated when the amplitude between two states with different mean position is estimated using the Feynman path integral [32,33].
On the other hand, as the NC modifies the energy-momentum tensor presented in GR, the smeared objects described by a Gaussian distribution may be used to study macroscopic systems such as black holes [34,35,36], in which is presented a form of NC model to alleviate singularities (In this context it is shown how the Ricci scalar at zero radius, is a function of the NC-like parameter in the form [34], presenting no divergences) as well as issues of galactic dynamics (rotation curves) [29], the latter of which will be the focus of our study.
In this sense, inspired by the study of Rahaman et al. [29], where they suggest that a density profile inspired by NC could produce the same intragalactic dynamics as a DM profile (called hereafter NC-like). The idea behind this is as follows: assume the DM halo is replaced by a Gaussian density profile, arising from NC effects smearing out the density of a central compact body. This new profile is then parameterized by a central density as well as a length-scale that emerges from NC effects at the quantum level. In fact, this model could be expected to provide a good fit, as its functional form could be reproduced by an Einasto density profile in the appropriate limit. Moreover, because of the smoothness shape of a Gaussian around the central region, the study of the NC-like model is also motivated by the results found in [37] which suggests that the central density of the galaxies flattens out, forming a core. In this vein, we propose a robust statistical study through the current Spitzer Photometry and Accurate Rotation Curves (SPARC) sample [38] by performing a Markov Chain Monte Carlo (MCMC) analysis. In particular, we constrain the associated free parameters and improve the statistical test using Akaike and Bayesian information criteria (There are other alternatives to compare models statistically such as Bridge Criterion [39]) to compare the NC-like model with the Einasto density profile due to its similarity with the NC-like density.
We organize this paper as follows: in Section 2 we present the rotation velocity of NC-like and Einasto, through the density profile associated for each model. In Section 3 we present the Bayesian MCMC analysis of NC-like and Einasto performed through a galaxy sample provided by SPARC. Finally, in Section 4 we discuss the results obtained and the viability of using NC in other astrophysical or cosmological studies.
In what follows, we work in units in which , unless explicitly written.
2. Noncommutative-Like and Einasto Rotation Velocity
This section presents the DM profiles associated to NC theory and the phenomenological Einasto density profile with the aim to confront them with observational rotation curves of galaxies.
We start considering V as the sum of the velocities of the disk (), gas (), and the halo (). In other words
where is the stellar mass-to-light ratio, which is in general a function of r and in this work it is considered as a free parameter. While the first two terms are given by observations, the latter will be described by the two density profiles studied below.
Hence, the rotation velocity at Newtonian level is related to the effective potential and is given for the halo as
where is its mass within a radius r, obtained through the integral
where is associated to the halo density profile, where in our case will be for NC-like and Einasto profiles.
2.1. Noncommutativity-Like Density Profile
For the NC-like case, the density profile is given by [40,41]
where is the central density at , not presenting divergences (If in this vein it is not necessary, extend the region in the form as Ref. [29] suggests) and it is defined as , being M the halo mass and is a characteristic length of the model, and being the free parameters which will be constrained by observations and it is assumed that is a constant term (A variable function, implies additional hypotheses that generates unnecessary complications and interpretations). We remark that the density profile presented in Equation (4) is inspired by NC, expecting that is constrained to be of the order of kiloparsec, being an emergent variable of noncommutative microscopic quantities.
2.2. Einasto Density Profile
As it was mentioned before, the NC-like model is a particular case of Einasto’s model given by [42]
The is the radius where the density profile has a slope and is the local density at that radius; the parameter n is known as Einasto index which describes the shape of the density profile.
From Equations (2) and (3), the following form of the rotation velocity is
where
is the incomplete gamma function. Notice that when we recover the functional form of Equation (5).
In order to compare both profiles, it is convenient to compare the densities at a same point, hence the NC density in the core is related to in Einasto case, and the smear parameter corresponds to . One disadvantage of Einasto profile is that it has more free parameters than the NC-like model which implies a better fit with galaxies rotation curves.
3. Data Samples and Fits
In this section we describe the procedure to constrain phase-space of the model parameter using a rotation curve sample collected in the SPARC catalog [38]. We model the RC distribution of the galaxies as the sum of the stellar disk, gas, and a spherical dark component. Both disk and gas component are provided by this catalog and the latter are the NC-like or Einasto’s models presented in Equations (5) and (7) respectively.
To test both DM models NC-like and Einasto, we select a subset of nine of the new general catalog (NGC) galaxies of low surface brightness (LSB) listed in Table 1 which satisfy the following conditions: the galaxy contains at least 10 data points to avoid an overfitting, the last point must be measured at kpc as a measurement of the galaxy size, and the galaxies do not contain a bulk component as this component affects mainly the central region (The elected subsample of galaxies does not contain any special relation that could benefit one or another theory). Based on MCMC method implemented in lmfit package [43], after initially discarding 400 chains (burn-in) to stabilize the steps, a total of chains is generated to explore the confidence region of the parameter space, and for NC-like and Einasto respectively. Additionally, we consider flat priors on the region: densities ( or ): , radius ( or ):kpc, and . The best fit values of the parameters are obtained by maximizing the likelihood function , where

Table 1.
For Noncommutative-like (NC) model, from left to right: Name of low surface brightness (LSB) galaxies of the Spitzer Photometry and Accurate Rotation Curves (SPARC), the reduced , energy density, , parameter, and is the DM mass within a radius which the density is (200 times the critical density of the universe).
In the above expression, is the observed velocity and its corresponding uncertainty at the radial distance and is the theoretical velocity.
Table 1 and Table 2 present the best fit values with their uncertainties at () confidence level (CL) for NC-like and Einasto respectively. Additionally, it is listed the reduced defined as , where N is the total number of data points and p is the number of free model parameters. To compare the results of these models, we present for the Einasto case, the density evaluated at and as an equivalent to parameter . Figure 1 presents the best fits for NC-like (dashed line) and Einasto (solid line) profile over total velocity data, the disk (star markers) and gas (circle markers) components. Furthermore, we estimate the halo mass within a radius for each model (shown in the last column of the Table 1 and Table 2), i.e., the mass contained in a radius in which the density is 200 times the critical density of the universe. We find consistent values using Einasto model to those obtained by [37,38] within , except for NGC3726, NGC3867 which are deviated at , respectively. When we compare our best fit values, we find consistent values within , for and respectively and deviations up to for the Einasto index except for NGC2366, NGC2403, and NGC3198 which obtain deviations larger than .

Table 2.
For Einasto model, from left to right: Name of LSB galaxies of the SPARC catalog under study, the reduced , the density at , , the spectral index n, parameter, and is the dark matter (DM) mass within a radius in which the density is (200 times the critical density of the universe). The values in parentheses in the last column are those halo mass reported in [38].
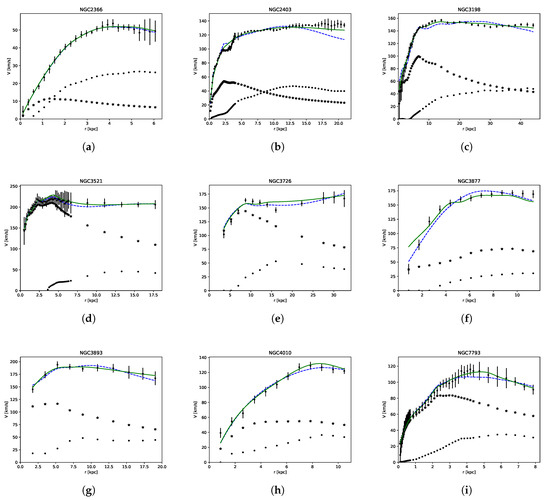
Figure 1.
Best fit of NC-like (dashed line) and Einasto (solid line) profiles over galaxy rotation velocity data (points with error bars), disk velocity (star markers), and gas velocity (circle markers). The total rotation velocity is obtained from Equation (1).
To improve a statistical comparison of both models, we use the corrected Akaike information criterion (AICc) [44,45,46] defined as and the Bayesian information criterion (BIC) [47] defined as . In the previous expressions, k is the size of the parameter space and N is the number of data points. The model with lower values of AICc and BIC is the one preferred by the data. In this context, the difference between the AICc value of a given model and the best one is denoted as . If , both models are supported by the data equally, if the data still support the given model but less than the preferred one. A value of indicates that the data does not support the given model. In contrast, ΔBIC gives the evidence against a candidate model over the best model, which is the one with lower BIC value. Then, a yield of suggests that there is no evidence against the candidate model. A value within indicates that there is modest evidence against the candidate model. A strong evidence against the candidate model happens when , and a stronger evidence against is whether . According to our AIC results shown in Table 3, the galaxies NGC2366, NGC3893, and NGC4010 prefer both models equally, the galaxies NGC3521, NGC3726, and NGC7793 prefer NC-like over Einasto, and the galaxy NGC3877 does not support Einasto. Only the galaxies NGC2403 and NGC3198 do not support NC-like. Based on BIC, our results indicate that the galaxies NGC3893 and NGC4010 do not suggest a evidence against any model. The galaxies NGC2366 and NGC3726 suggest a modest evidence against Einasto model but a strong evidence using NGC3521 and NGC3877. In contrast, the sample NGC7793 gives a modest evidence against NC but a stronger evidence is observed using NGC2403 and NGC3198.

Table 3.
Akaike information criterion (AIC) and Bayesian information criterion (BIC) for NC-like and Einasto. ΔAIC (ΔBIC) yield value is the difference between AIC (BIC) model values of AIC for each galaxy.
Furthermore, Figure 2 displays the comparison of the space , obtained by fitting the NGC2366, NGC3726, and NGC3893. These contours show consistent values for within up to confidence level (CL) value in which the NC-like model is recovered from Einasto. The contours represent and CL respectively. On the other hand, we also present in Figure 3 the correlations between and for both models which is observed as uncorrelated between them, when Einasto is considered and also the uncertainties are considerable larger than these obtained using NC-like because the Einasto model has one more free parameter than NC-like. In this panel, contours at and are included.
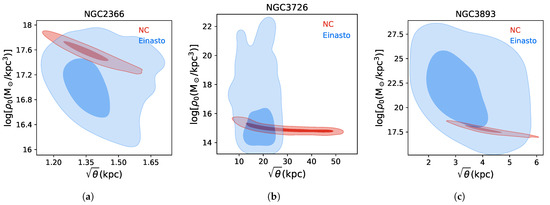
Figure 2.
Contours at 1 and 2 CL of NGC2366, NGC3521 and NGC7793 for NC-like and Einasto profiles in the parameters: central density and , (). The corresponding mean value of the spectral index in the Einasto model is . Darker region represents and lighter region is .
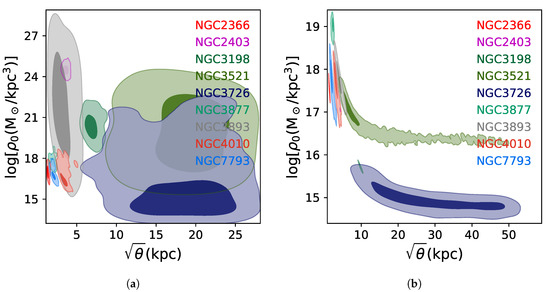
Figure 3.
Correlation of the parameter model ( and or ) for: Einasto (a) and NC-like (b). Darker region represent and lighter region is .
4. Discussion
This manuscript was devoted to the comparison of the well-known Einasto density profile to describe DM halos at galactic scale with a particular profile obtained when the Einasto index is and named as NC-like. The NC-like model is motivated by the idea of a noncommutative space-time coming from string theory. Then, the strategy followed was to confront the total rotation curve using both models with a sample of galaxies provided by SPARC catalog [38] by performing a Bayesian MCMC procedure. To model the rotation curves, we considered the gas, disk, and dark components; the latter corresponds to NC-like or Einasto model and the first two are provided by data. According to our results, for some galaxies (NGC3521, NGC3726, and NGC7793) we found a better preference of the NC-like over Einasto model but other galaxies (NGC2403 and NGC3198) do not support NC. Although the galaxies NGC2366, NGC3893, and NGC4010 prefer both models equally, NC-like has the advantage that it allows one to obtain best fitting values with an uncertainty lower than those obtained by Einasto because the parameter is fixed. We compare the contours obtained for NGC3521, NGC3726, and NGC7793 at and showing consistent regions because the Einasto indexes obtained are in agreement with the value for NC-like. Additionally, from Table 1 and Table 2, we conclude that masses in NC and Einasto are at the same order of magnitude, some Einasto masses are even larger than the NC case. At least for the case (Einasto case), both masses are in good agreement. Indeed, this result is expected because NC could be considered as a particular case of Einasto density profile.
From the results presented in Table 1 we can observe that NC length is not an invariant quantity and therefore is not a fundamental structure. However, it is expected that the factor is constructed by quantum cells that emerge from NC theory. The presence of the density profile (Equation (4)) in galaxies is the emergence of noncommutative quantum properties of space-time and may be an indirect evidence of the granular structure. It is important to remark that we are hypothesizing about the quantum structure and the mathematical support is not the aim of the present paper.
This work motivates further studies with more statistics and includes new observables to allow for the discrimination between the NC-like model and others (Einasto, piso, etc.) and also to find correlations between NC properties and the characteristic of the galaxies, see for instance [11,37]. Note that a joint analysis does not strengthen our results, since the parameters are not invariant and they depend on characteristics such as the size of the galaxy. Additionally, it could be interesting to perform a statistical test to compare the NC-like model with other densities using alternative criteria such as Bridge criterion presented in [39]. Finally, we expect that accumulative terms of NC-like can have macroscopic repercussions that might be explored as a possible solution to fundamental problems like dark matter or dark energy, having always in mind that the NC-like profile has theoretical foundations of great importance and repercussion.
Author Contributions
J.J.A.-F. and A.H.-A. implemented the software and developed the data analysis, M.A.G.-A. proposed the idea and developed the theoretical foundations. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited.
Acknowledgments
We thank the anonymous referees for thoughtful remarks and suggestions. A.H.A. thanks SNI-México for partial financial support. M.A.G.-A. acknowledges support from SNI-México, CONACyT research fellow, CONICYT REDES (190147), COZCyT and Instituto Avanzado de Cosmología (IAC).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sofue, Y.; Rubin, V. Rotation curves of spiral galaxies. Annu. Rev. Astron. Astrophys. 2001, 39, 137–177. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Phys. 2012, 524, 507–534. [Google Scholar] [CrossRef]
- Diaferio, A. From the vacuum to the universe. In Proceedings of the Symposium, Innsbruck, Austria, 19–20 October 2007; pp. 71–85. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters, Planck. Astron. Astrophys. 2020, 641. [Google Scholar] [CrossRef]
- Springel, V.; White, S.; Jenkins, A.; Frenk, C.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.; Fattahi, A.; Navarro, J.; Bower, R.; Crain, R.; Vecchia, C.; Furlong, M.; Helly, J.; Jenkins, A.; et al. The APOSTLE simulations: Solutions to the Local Group’s cosmic puzzles. Mon. Not. R. Astron. Soc. 2016, 457, 1931–1943. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Begeman, K.G.; Broeils, A.H.; Sanders, R.H. Extended rotation curves of spiral galaxies: Dark haloes and modified dynamics. Mon. Not. R. Astron. Soc. 1991, 294, 523–537. [Google Scholar] [CrossRef]
- Burkert, A. The Structure of Dark Matter Halos in Dwarf Galaxies. Astrophys. J. Lett. 1995, L25. [Google Scholar] [CrossRef]
- Einasto, J. On the Construction of a Composite Model for the Galaxy and on the Determination of the System of Galactic Parameters. Trudy Inst. Astrofiz. Alma-Ata 1965, 87, 87–100. [Google Scholar]
- Hernández-Almada, A.; García-Aspeitia, M.A. Multistate scalar field dark matter and its correlation with galactic properties. Int. J. Mod. Phys. D 2017, 27, 1850031. [Google Scholar] [CrossRef]
- Dehnen, W. A family of potential-density pairs for spherical galaxies and bulges. Mon. Not. Roy. Astron. Soc. 1993, 265, 250–256. [Google Scholar] [CrossRef]
- Subramanian, K.; Cen, R.; Ostriker, J. The structure of dark matter halos in hierarchical clustering theories. ApJ 2000, 538, 528–542. [Google Scholar] [CrossRef]
- Gentile, G.; Salucci, P.; Klein, U.; Vergani, D.; Kalberla, P. The cored distribution of dark matter in spiral galaxies. Mon. Not. R. Astron. Soc. 2004, 351, 903–922. [Google Scholar] [CrossRef]
- Horava, P.; Witten, E. Eleven-dimensional supergravity on a manifold with boundary. Nucl. Phys. 1996, B475, 94–114. [Google Scholar] [CrossRef]
- Horava, P.; Witten, E. Heterotic and Type I string dynamics from eleven dimensions. Nucl. Phys. 1996, B460, 506–524. [Google Scholar] [CrossRef]
- Lee, J.-W.; Koh, I.-G. Galactic halos as boson stars. Phys. Rev. 1996, D53, 2236–2239. [Google Scholar] [CrossRef]
- Barranco, J.; Bernal, A. Self-gravitating system made of axions. Phys. Rev. 2011, D83, 043525. [Google Scholar] [CrossRef]
- Urena-Lopez, L.A.; Matos, T. New cosmological tracker solution for quintessence. Phys. Rev. 2000, D62, 081302. [Google Scholar] [CrossRef]
- Rodríguez-Meza, M.A. Study of rotation curves of spiral galaxies with a scalar field dark matter model. Aip Conf. Proc. 2012, 1473, 74. [Google Scholar] [CrossRef]
- Robles, V.H.; Lora, V.; Matos, T.; Sánchez-Salcedo, F.J. Evolution of a dwarf satellite galaxy embedded in a scalar field dark matter halo. Astrophys. J. 2015, 810, 99. [Google Scholar] [CrossRef]
- Martins, C.F.; Salucci, P. Analysis of rotation curves in the framework of Rn gravity. Mon. Not. R. Astron. Soc. 2007, 381, 1103–1108. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to Compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Maartens, R.; Koyama, K. Brane-World Gravity. Living Rev. Relativ. 2010, 13, 5. [Google Scholar] [CrossRef]
- Garcia-Aspeitia, M.A.; Rodriguez-Meza, M.A. Constraining brane tension using rotation curves of galaxies. arXiv 2015, arXiv:1509.05960. [Google Scholar] [CrossRef]
- Garcia-Aspeitia, M.A.; Hernandez-Almada, A.; Magaña, J.; Amante, M.H.; Motta, V.; Martínez-Robles, C. Brane with variable tension as a possible solution to the problem of the late cosmic acceleration. Phys. Rev. D 2018, 97, 101301. [Google Scholar] [CrossRef]
- García-Aspeitia, M.A.; Magaña, J.; Hernández-Almada, A.; Motta, V. Probing dark energy with braneworld cosmology in the light of recent cosmological data. Int. J. Mod. Phys. D 2017, 27, 1850006. [Google Scholar] [CrossRef]
- Rahaman, F.; Kuhfittig, P.K.F.; Chakraborty, K.; Usmani, A.A.; Ray, S. Galactic rotation curves inspired by a noncommutative-geometry background. Gen. Rel. Grav. 2012, 44, 905–916. [Google Scholar] [CrossRef][Green Version]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. JHEP 1999, 9, 032. [Google Scholar] [CrossRef]
- Romero, J.M.; Vergara, J.D. The Kepler Problem and Noncommutativity. Mod. Phys. Lett. 2003, A18, 1673–1680. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E. Feynman path integral on the non-commutative plane. J. Phys. 2003, A36, L467–L471. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E. UV divergence-free QFT on noncommutative plane. J. Phys. Math. Gen. 2003, 36, L517–L521. [Google Scholar] [CrossRef]
- Nicolini, P. Noncommutative black holes, the final appeal to quantum gravity: A review. Int. J. Mod. Phys. 2009, A24, 1229–1308. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A.; Nicolini, P. Non-commutative geometry inspired higher-dimensional charged black holes. Phys. Lett. B 2009, 670, 449–454. [Google Scholar] [CrossRef]
- Ansoldi, S.; Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired charged black holes. Phys. Lett. B 2007, 645, 261–266. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. A Comprehensive Catalog of Dark Matter Halo Models for SPARC Galaxies. Astrophys. J. Suppl. Ser. 2020, 247, 31. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass model for 175 disk galaxies with SPITZER photometry and accurate rotation curves. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Ding, J.; Tarokh, V.; Yang, Y. Bridging AIC and BIC: A New Criterion for Autoregression. IEEE Trans. Inf. Theory 2018, 64, 4024–4043. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E. Lorentz invariance, unitarity in UV-finite of QFT on noncommutative spacetime. J. Phys. 2004, A37, 7169–7178, (Erratum). [Google Scholar] [CrossRef]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. 2006, B632, 547–551. [Google Scholar] [CrossRef]
- Einasto, J. Kinematics and Dynamics of Stellar Systems. Trudy Inst. Astrofiz. Alma-Ata 1965, 51, 87. [Google Scholar]
- Newville, M.; Stensitzki, T.; Allen, D.B.; Rawlik, M.; Ingargiola, A.; Nelson, A. Lmfit: Non-Linear Least-Square Minimization and Curve-Fitting for Python. June 2016. Available online: https://ui.adsabs.harvard.edu/abs/2016ascl.soft06014N (accessed on 5 March 2021).
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Sugiura, N. Further analysts of the data by akaike’ s information criterion and the finite corrections. Commun. Stat. Theory Methods 1978, 7, 13–26. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).