On the Modeling of Algol-Type Binaries
Abstract
1. Introduction
2. Paths through the Hertzsprung Russell Diagram (HRD)
3. Tidal Interaction
4. Liberal Evolution
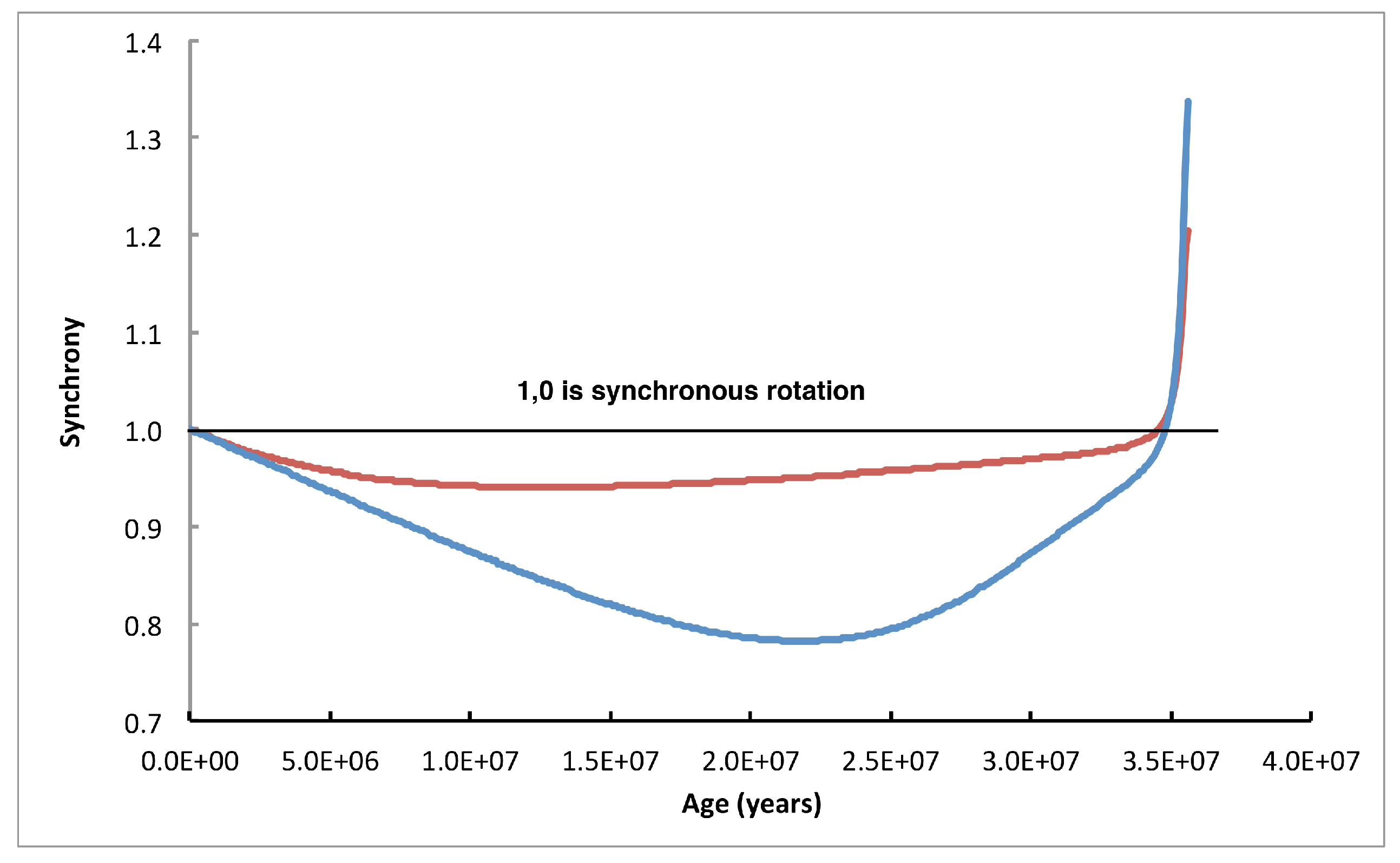
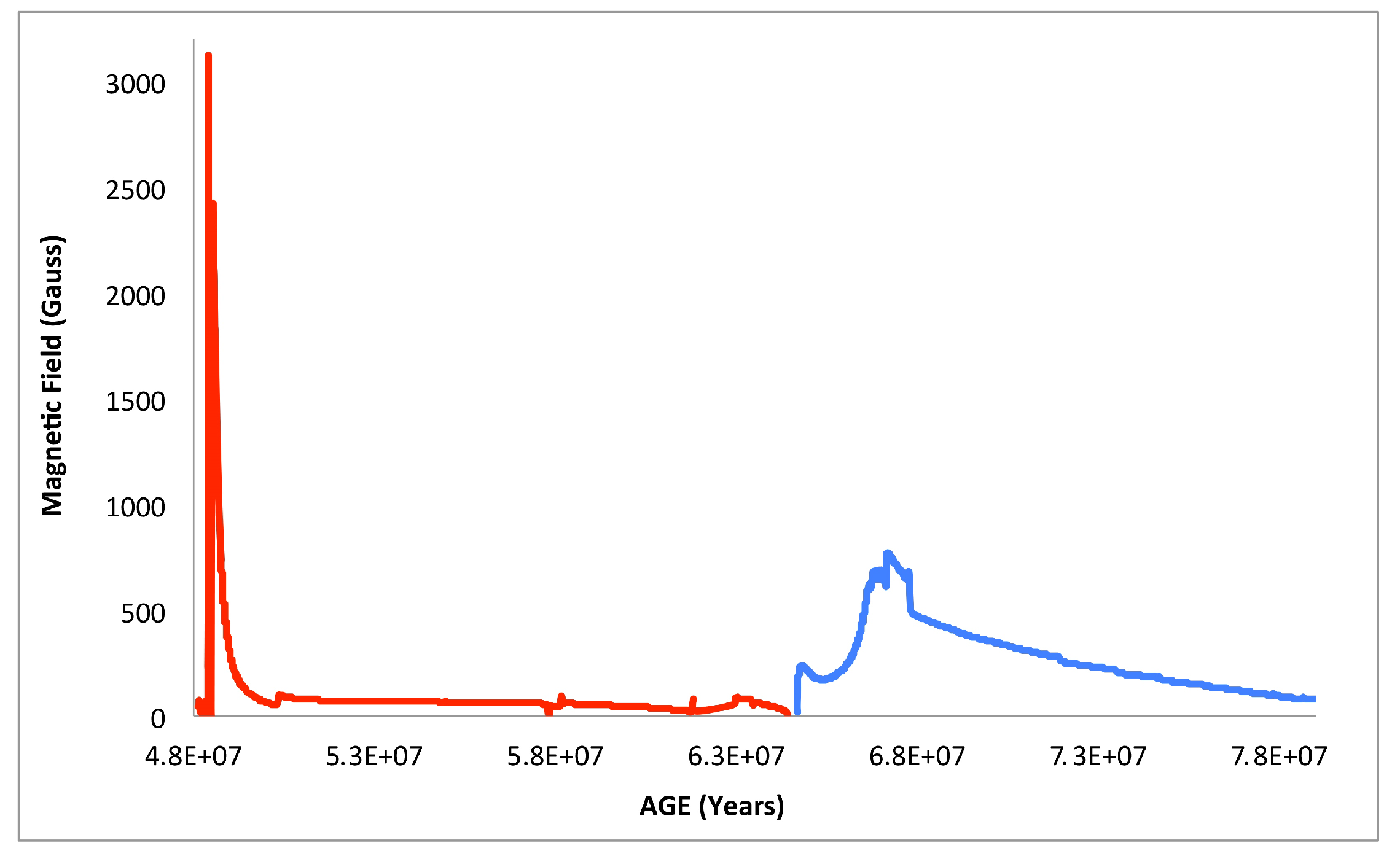
5. Magnetic Braking
5.1. Generation of the Magnetic Field of the Gainer
5.2. Extent of the Shell
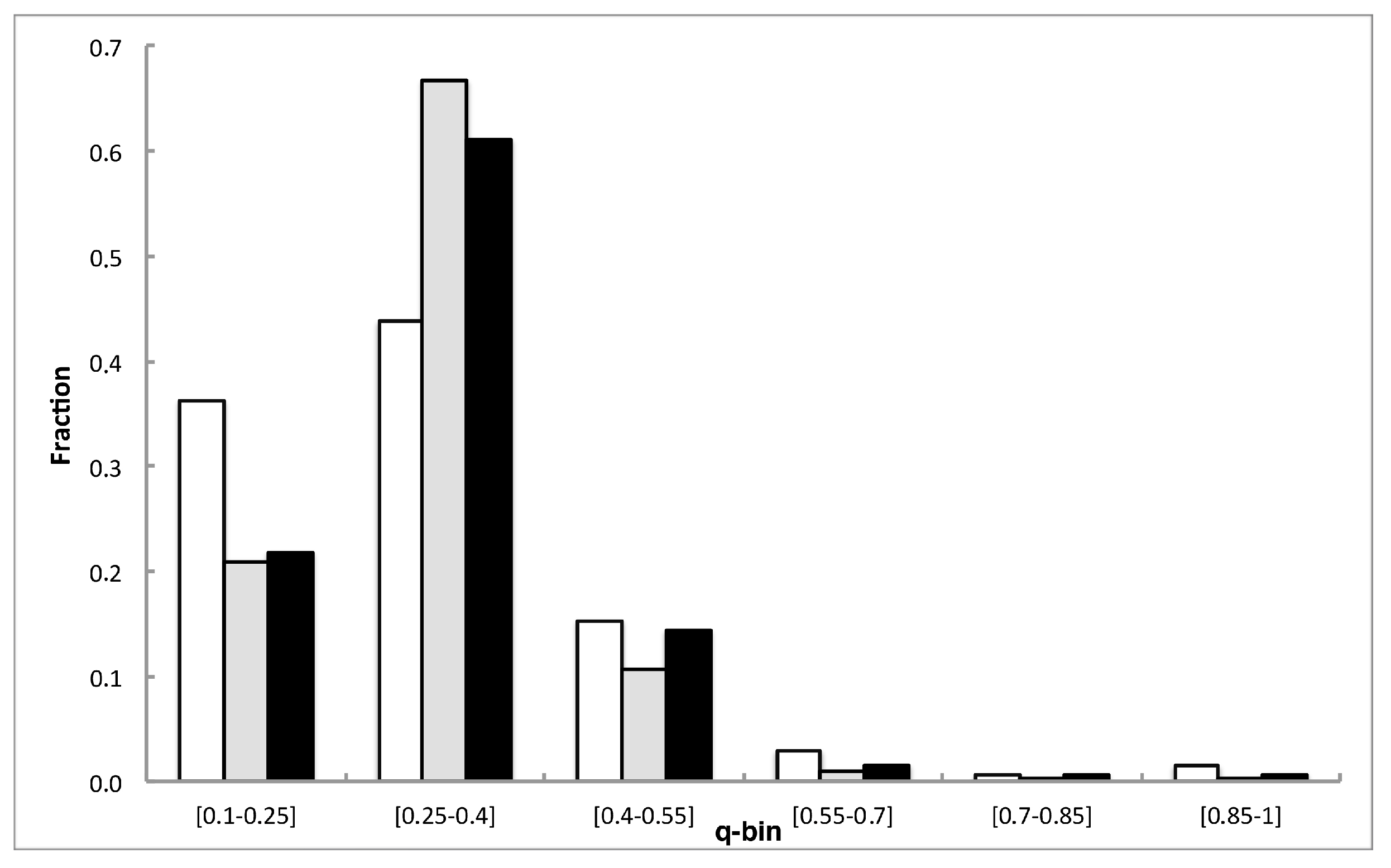
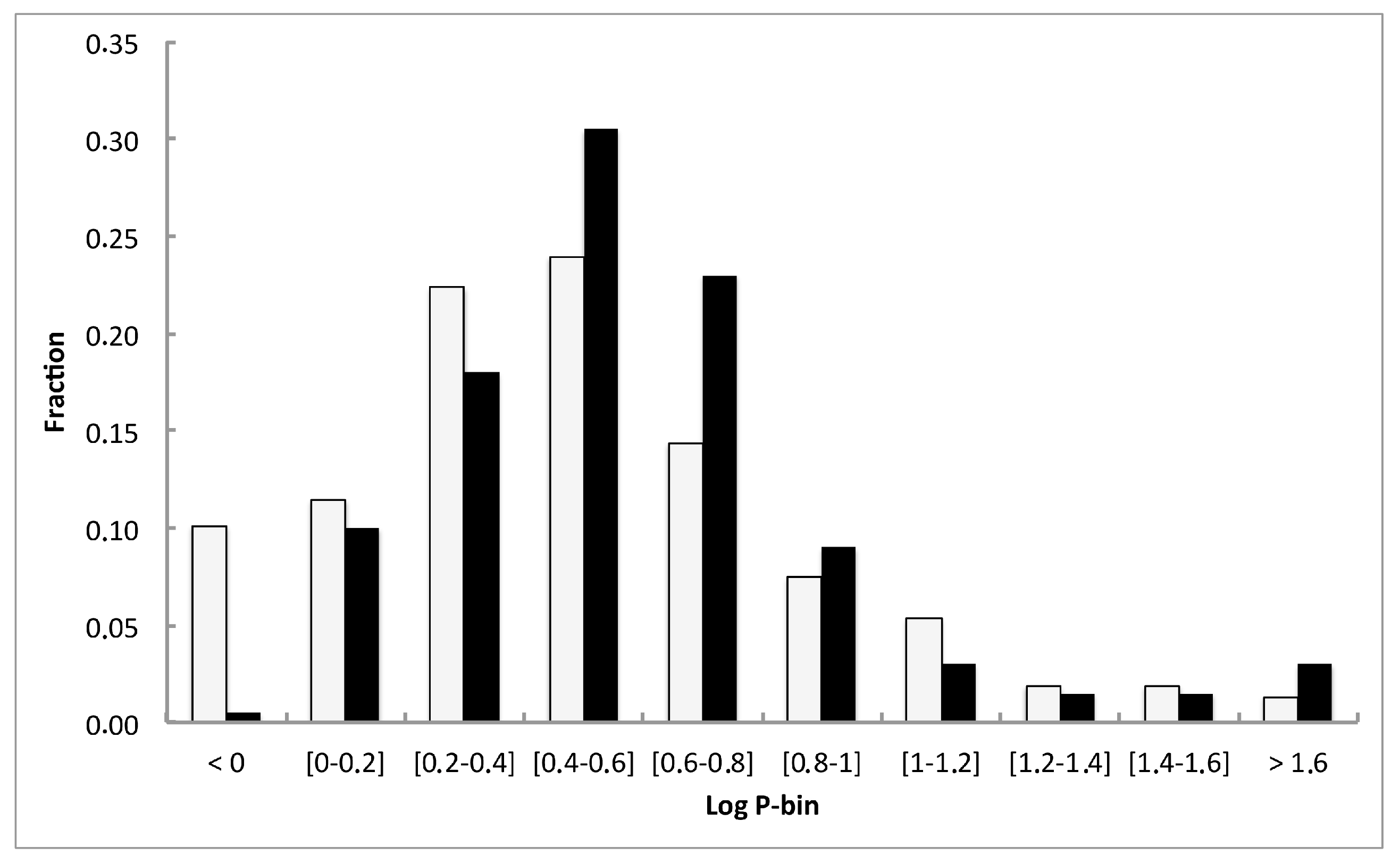
6. Calculated Cases
- The observed equatorial velocities of 16 Algol-systems are very well confirmed by theory (R < 0.1).
- Seventeen more Algols can be considered andl explained by the theory (R ∈ [0.11–0.35]).
- No systems were found with R ∈ [0.36–0.49].
- Seven other Algol-systems are weakly reproduced by the theory (R ∈ [0.50–0.90]).
- Only one Algol (U CrB) is badly reproduced by the theory (R > 0.90).
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paczynski, B. Evolution of Close Binaries I. Acta Astron. 1966, 16, 231–247. [Google Scholar]
- Paczynski, B. Evolution of Close Binaries IV. Acta Astron. 1967, 17, 193–206. [Google Scholar]
- Paczynski, B. Evolution of Close Binaries V. Acta Astron. 1967, 17, 355–378. [Google Scholar]
- Kippenhahn, R.; Weigert, A. Entwicklung in engen Doppelsternsystemen I. ZA 1967, 65, 251–273. [Google Scholar]
- Tutukov, A.; Yungelson, L. Evolution of close binaries with mass loss from the system. Nauchnye Informatsii 1971, 20, 86–93. [Google Scholar]
- Tutukov, A. Evolution of Close Binaries. In Fundamental Problems in the Theory of Stellar Evolution, Proceedings of the Symposium, Kyoto, Japan, 22–25 July 1980; Reidel Publishing Co.: Dordrecht, The Netherlands, 1981; pp. 137–153. [Google Scholar]
- Eggleton, P. Evolutionary Processes in Binary and Multiple Stars, 1st ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Nelson, C.; Eggleton, P. A Complete Survey of Case A Binary Evolution with Comparison to Observed Algol-type Systems. Astrophys. J. 2001, 552, 664–678. [Google Scholar] [CrossRef]
- Song, H.; Maeder, A.; Meynet, G.; Huang, Q.; Ekström, S.; Granada, A. Close-binary evolution I. Astron. Astrophys. 2013, 556, A100. [Google Scholar] [CrossRef]
- Song, H.; Meynet, G.; Maeder, A.; Ekström, S.; Eggenberger, P.; Georgy, C.; Qin, Y.; Fragos, T.; Soerensen, M.; Barblan, F.; et al. Close-binary evolution II. Astron. Astrophys. 2018, 609, A3. [Google Scholar] [CrossRef]
- Van Rensbergen, W.; De Greve, J.P.; De Loore, C.; Mennekens, N. Spin-up and hot spots can drive mass out of a binary. Astron. Astrophys. 2008, 487, 1129–1138. [Google Scholar] [CrossRef]
- Van Rensbergen, W.; De Greve, J.P.; Mennekens, N.; Jansen, K.; De Loore, C. Mass loss out of close binaries. Case A Roche lobe overflow. Astron. Astrophys. 2010, 510, A13. [Google Scholar] [CrossRef]
- Van Rensbergen, W.; De Greve, J.P.; Mennekens, N.; Jansen, K.; De Loore, C. Mass loss out of close binaries. The formation of Algol-type systems completed with case B RLOF. Astron. Astrophys. 2011, 528, A16. [Google Scholar] [CrossRef]
- Van Rensbergen, W.; De Greve, J.P. Accretion disks in Algols, Progenitors and evolution. Astron. Astrophys. 2016, 592, A151. [Google Scholar] [CrossRef][Green Version]
- Van Rensbergen, W.; De Greve, J.P. Magnetic braking at work in binaries. Astron. Astrophys. 2020, 642, A183. [Google Scholar] [CrossRef]
- Budding, E.; Erdem, A.; Cicek, C.; Bulut, I.; Soydugan, F.; Soydugan, E.; Bakis, V.; Demircan, O. Catalogue of Algol type binary stars. Astron. Astrophys. 2004, 417, 263–268. [Google Scholar] [CrossRef]
- Zavala, R.; Hummel, C.; Boboltz, D.; Ojha, R.; Shaffer, D.; Tycner, C.; Richards, M.; Hutter, D. The Algol Triple System Spatially resolved at Optical Wavelengths. Astrophys. J. Lett. 2010, 715, L18, Erratum in 2017, 843, L44. [Google Scholar] [CrossRef]
- Packet, P. On the spin-up of the Mass Accreting Component in a Close Binary System. Astron. Astrophys. 1981, 102, 17–19. [Google Scholar]
- Darwin, G. On the Secular Changes in the Elements of the Orbit of a Satellite Revolving about a Tidally Distorted Planet. Philos. Trans. R. Soc. Lond. 1880, 171, 713–891. [Google Scholar]
- Wellstein, S. Präsupernovaentwicklung Enger Massereicher Doppelsternsysteme. Ph.D. Thesis, Potsdam University, Potsdam, Germany, 2001. [Google Scholar]
- Hurley, J.; Tout, C.; Pols, O. Evolution of binary stars and the effect of tides on binary populations. Mon. Not. R. Astron. Soc. MNRS 2002, 329, 897–928. [Google Scholar] [CrossRef]
- Hut, P. Tidal evolution in close binary systems. Astron. Astrophys. 1981, 99, 126–140. [Google Scholar]
- Hilditch, R. An Introduction to Close Binary Stars; Cambridge University Press: Cambridge, UK, 2001; pp. 152–154. [Google Scholar]
- Zahn, J.P. Tidal Friction in Close Binary Stars. Astron. Astrophys. 1977, 57, 383–394. [Google Scholar]
- Tassoul, J.L. Stellar Rotation; Cambridge University Press: Cambridge, UK, 2000; pp. 214–228. [Google Scholar]
- Peters, G.; Polidan, R. Evidence for a high temperature accretion region in Algol-type binary systems. Astrophys. J. 1984, 283, 745–759. [Google Scholar] [CrossRef]
- Salpeter, E. The Luminosity Function and Stellar Evolution. Astrophys. J. 1955, 121, 161–167. [Google Scholar] [CrossRef]
- Van Rensbergen, W.; De Loore, C.; Jansen, K. Evolution of interacting binaries with a B type primary at birth. Astron. Astrophys. 2006, 446, 1071–1079. [Google Scholar] [CrossRef][Green Version]
- Popova, E.; Tutukov, A.; Yungelson, L. Study of Physical Properties of Spectroscopic Binary Stars. Astrophys. Space Sci. 1982, 88, 55–80. [Google Scholar] [CrossRef]
- Van Hamme, W.; Wilson, R. Rotation Statistics of Algol-type binaries and Results on RY Geminorum, RW Monocerotis and RW Tauri. Astron. J. 1990, 100, 1982–1993. [Google Scholar] [CrossRef]
- Miller, B.; Budaj, J.; Richards, M. Revealing the Nature of Algol Disks through Optical and UV Spectroscopy, Synthetic Spectra and Tomography of TT Hya. Astrophys. J. 2007, 656, 1075–1091. [Google Scholar] [CrossRef][Green Version]
- Glazunova, L.; Yushcenko, A.; Tsymbal, V.; Mkrtichian, D.; Lee, J.; Kang, Y.; Valyavin, G.; Lee, B. Rotational Velocities of the Components of 23 Binaries. Astrophys. J. 2008, 135, 1736–1745. [Google Scholar] [CrossRef][Green Version]
- Dervisoglu, A.; Tout, C.; Ibanglu, C. Spin angular momentum evolution of the long-period Algols. Mon. Not. R. Astron. Soc. MNRS 2010, 406, 1071–1083. [Google Scholar]
- Vink, J.; De Koter, A.; Lamers, H. Mass-loss predictions for O and B stars as a function of metallicity. Astron. Astrophys. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- De Jager, C.; Nieuwenhuyzen, H.; Van der Hucht, K. Mass Loss Rates in the Hertzsprung-Russell Diagram. Astron. Astrophys. Suppl. Ser. 1988, 72, 259–289. [Google Scholar]
- Spruit, H. Dynamo action of differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Dominis, D.; Mimica, P.; Pavlovski, K.; Tamajo, E. In between β Lyrae and Algol: The Case Of V356 Sgr. ApSS 2005, 296, 189–192. [Google Scholar]


| System | obs | obs | obs | R obs | Reference-Observations |
|---|---|---|---|---|---|
| Progenitor | calc | calc | calc | R calc | Initial Period Progenitor |
| Very good | Agreement | R ≤ 0.1 | |||
| Per | 3.70 | 0.81 | 52.51 | 0.00 | Dervisoglu et al. [33] |
| 3.41 + 1.1 | 3.69 | 0.82 | 50.04 | 0.00 | 1.146250 |
| HS Hya | 2.47 | 0.70 | 45.41 | 0.01 | Glazunova et al. [32] |
| 2.37 + 0.8 | 2.47 | 0.70 | 78.97 | 0.00 | 1.18912 |
| KO Aql | 2.53 | 0.55 | 41.92 | 0.02 | Dervisoglu et al. [33] |
| 2.28 + 0.8 | 2.53 | 0.55 | 50.33 | 0.01 | 1.27150 |
| CW Eri | 2.59 | 0.74 | 33.28 | −0.01 | Glazunova et al. [32] |
| 2.23 + 1.1 | 2.59 | 0.74 | 48.22 | 0.01 | 1.30138 |
| ZZ Boo | 3.43 | 0.96 | 9.51 | −0.02 | Glazunova et al. [32] |
| 2.59 + 1,8 | 3.49 | 0.90 | 48.19 | 0.01 | 1.5 |
| AU Mon | 5.93 | 1.18 | 126.32 | 0.25 | Dervisoglu et al. [33] |
| 4.16 + 3.00 | 5.93 | 1.19 | 104.87 | 0.22 | 2.005 |
| Y Psc | 2.80 | 0.70 | 38.05 | 0.00 | Dervisoglu et al. [33] |
| 2.3 + 1,2 | 2.80 | 0.70 | 47.58 | 0.03 | 1.34865 |
| WW Cyg | 2.10 | 0.60 | 41.01 | 0.03 | Dervisoglu et al. [33] |
| 1.5 + 1.2 | 2.10 | 0.60 | 51.35 | 0.06 | 1.138 |
| V505 Sgr | 2.68 | 1.23 | 102.56 | 0.05 | Dervisoglu et al. [33] |
| 2.71 + 1.2 | 2.67 | 1.24 | 107.85 | 0.08 | 1.23198 |
| TX UMa | 4.76 | 1.18 | 63.62 | 0.04 | Dervisoglu et al. [33] |
| 4.24 + 1.7 | 4.75 | 1.19 | 71.78 | 0.00 | 1.44948 |
| XY Cet | 5.30 | 0.94 | 84.05 | 0.07 | Glazunova et al. [32] |
| 5.04 + 1.2 | 5.09 | 1.14 | 72.46 | 0.02 | 1.55429 |
| SZ Psc | 3.00 | 0.77 | 9.26 | −0.03 | Glazunova et al. [32] |
| 2.47 + 1.3 | 3.00 | 0.77 | 44.38 | 0.03 | 1.4765 |
| RZ Cas | 2.10 | 0.74 | 87.65 | 0.06 | Dervisoglu et al. [33] |
| 2.14 + 0.7 | 2.10 | 0.74 | 62.93 | 0.00 | 1.33437 |
| U Cep | 3.57 | 1.86 | 437.37 | 0.87 | Dervisoglu et al. [33] |
| 3.33 + 2.1 | 3.56 | 1.87 | 488.95 | 0.95 | 2.13447 |
| UV Psc | 1.86 | 0.77 | 70.81 | 0.01 | Glazunova et al. [32] |
| 2.03 + 0.6 | 1.86 | 0.77 | 105.78 | −0.09 | 1.3999 |
| AI Dra | 2.37 | 1.09 | 86.90 | −0.06 | Van Hamme & Wilson [30] |
| 2.36 + 1.1 | 2.36 | 1.10 | 85.71 | 0.04 | 1.18128 |
| Good | Agreement | R ∈ [0.11–0.35] | |||
| CD Tau | 2.5 | 1.0 | 20.91 | 0.00 | Glazunova et al. [32] |
| 1.9 + 1.6 | 2.5 | 1.0 | 77.27 | 0.11 | 1.91047 |
| AT Peg | 2.50 | 1.21 | 84.51 | 0.01 | Dervisoglu et al. [33] |
| 2.61 + 1.1 | 2.49 | 1.22 | 121.86 | 0.12 | 1.3406 |
| TV Cas | 3.78 | 1.53 | 80.48 | −0.03 | Dervisoglu et al. [33] |
| 3.21 + 2.1 | 3.77 | 1.54 | 117.86 | 0.12 | 1.14467 |
| RW Tau | 2.43 | 0.55 | 94.00 | 0.18 | Van Hamme & Wilson [30] |
| 2.18 + 0.8 | 2.43 | 0.55 | 50.13 | 0.02 | 1.24613 |
| VZ Hya | 2.52 | 0.89 | 19.90 | 0.00 | Glazunova et al. [32] |
| 2.01 + 1.4 | 2.52 | 0.89 | 107.24 | 0.17 | 1.47042 |
| X Tri | 2.43 | 1.21 | 50.00 | −0.16 | Van Hamme & Wilson [30] |
| 2.44 + 1.2 | 2.43 | 1.21 | 93.42 | 0.02 | 0.98383 |
| Z Vul | 5.39 | 2.26 | 135.02 | 0.18 | Van Hamme & Wilson [30] |
| 5.65 + 2.0 | 5.36 | 2.28 | 142.71 | 0.00 | 3.07536 |
| IM Aur | 2.38 | 0.77 | 139,76 | 0.20 | Van Hamme & Wilson [30] |
| 2.35 + 0.8 | 2.38 | 0.77 | 70.04 | 0.00 | 1.15531 |
| System | obs | obs | obs | R obs | Reference-Observations |
|---|---|---|---|---|---|
| Progenitor | calc | calc | calc | R calc | Initial Period Progenitor |
| Good | Agreement (continued) | R ∈ [0.11–0.35] | |||
| DL Vir | 2.18 | 1.06 | 121.00 | 0.20 | Van Hamme & Wilson [30] |
| 2.44 + 0.8 | 2.17 | 1.07 | 136.81 | 0.00 | 2.18242 |
| Lib | 4.76 | 1.67 | 68.85 | −0.09 | Van Hamme & Wilson [30] |
| 3.93 + 2.5 | 4.75 | 1.69 | 113.16 | 0.12 | 1.23263 |
| Tau | 7.19 | 1.87 | 90.96 | 0.05 | Van Hamme & Wilson [30] |
| 6.36 + 2.7 | 7.15 | 1.88 | 177.83 | 0.26 | 1.89745 |
| V356 Sgr | 10.40 | 2.80 | 212,81 | 0.37 | Glazunova et al. [32] |
| 8.7 + 6 | 10.90 | 2.64 | 118.34 | 0.14 | 1.86560 |
| TW Dra | 1.70 | 0.80 | 37.09 | −0.02 | Dervisoglu et al. [33] |
| 1.5 + 1.0 | 1.70 | 0.80 | 121.51 | 0.23 | 2.092 |
| RX Gem | 4.40 | 0.80 | 157.60 | 0.38 | Dervisoglu et al. [33] |
| 3.0 + 2.2 | 4.40 | 0.80 | 298.59 | 0.69 | 1.85226 |
| TW And | 1.68 | 0.32 | 31.64 | 0.01 | Glazunova et al. [32] |
| 1.4 + 0.6 | 1.68 | 0.32 | 155.42 | 0.32 | 1.08976 |
| W Del | 2.01 | 0.42 | 30.00 | 0.03 | Van Hamme & Wilson [30] |
| 1.53 + 0.9 | 2.01 | 0.42 | 169.80 | 0.36 | 1.10746 |
| SW Cyg | 2.50 | 0.50 | 197.47 | 0.46 | Dervisoglu et al. [33] |
| 2.1 + 0.9 | 2.50 | 0.50 | 73.25 | 0.13 | 1.32299 |
| Weak | Agreement | R ∈ [0.5–0.90] | |||
| TT Hya | 2.77 | 0.63 | 168.93 | 0.44 | Miller et al. ([31]) |
| 2.0 + 1.4 | 2.77 | 0.63 | 482.24 | 1.00 | 1.68341 |
| RY Per | 6.24 | 1.69 | 214.60 | 0.39 | Dervisoglu et al. [33] |
| 4.45 + 3.40 | 6.22 | 1.63 | 556.23 | 0.99 | 1.98167 |
| RS Cep | 2.83 | 0.41 | 170.23 | 0.33 | Dervisoglu et al. [33] |
| 2.04 + 1.2 | 2.83 | 0.41 | 412.17 | 0.99 | 1.32215 |
| AD Her | 2.90 | 0.90 | 143.79 | 0.31 | Dervisoglu et al. [33] |
| 2.7 + 1.1 | 2.90 | 0.91 | 382.61 | 1.00 | 6.6282 |
| RY Gem | 2.66 | 0.24 | 70.53 | 0.14 | Glazunova et al. [32] |
| 2.35 + 0.55 | 2.61 | 0.24 | 376.12 | 0.87 | 1.12077 |
| TU Mon | 12.6 | 2.7 | 153.02 | 0.18 | Dervisoglu et al. [33] |
| 11.5 + 4.3 | 12.09 | 2.74 | 621.52 | 0.98 | 1.75065 |
| U Sge | 4.45 | 1.65 | 76.00 | 0.04 | Dervisoglu et al. [33] |
| 3.4 + 2.7 | 4.44 | 1.66 | 446.87 | 0.86 | 1.72982 |
| No | Agreement | R > 0.90 | |||
| U CrB | 6.78 | 2.87 | 60.59 | 0.04 | Van Hamme & Wilson [30] |
| 5.25 + 4.4 | 6.76 | 2.88 | 533.20 | 0.99 | 2.06346 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Rensbergen, W.; de Greve, J.-P. On the Modeling of Algol-Type Binaries. Galaxies 2021, 9, 19. https://doi.org/10.3390/galaxies9010019
van Rensbergen W, de Greve J-P. On the Modeling of Algol-Type Binaries. Galaxies. 2021; 9(1):19. https://doi.org/10.3390/galaxies9010019
Chicago/Turabian Stylevan Rensbergen, Walter, and Jean-Pierre de Greve. 2021. "On the Modeling of Algol-Type Binaries" Galaxies 9, no. 1: 19. https://doi.org/10.3390/galaxies9010019
APA Stylevan Rensbergen, W., & de Greve, J.-P. (2021). On the Modeling of Algol-Type Binaries. Galaxies, 9(1), 19. https://doi.org/10.3390/galaxies9010019




