Radio Constraints of Dark Matter: A Review and Some Future Perspectives
Abstract
1. Introduction
2. Radio Emissions Due to Dark Matter Annihilation
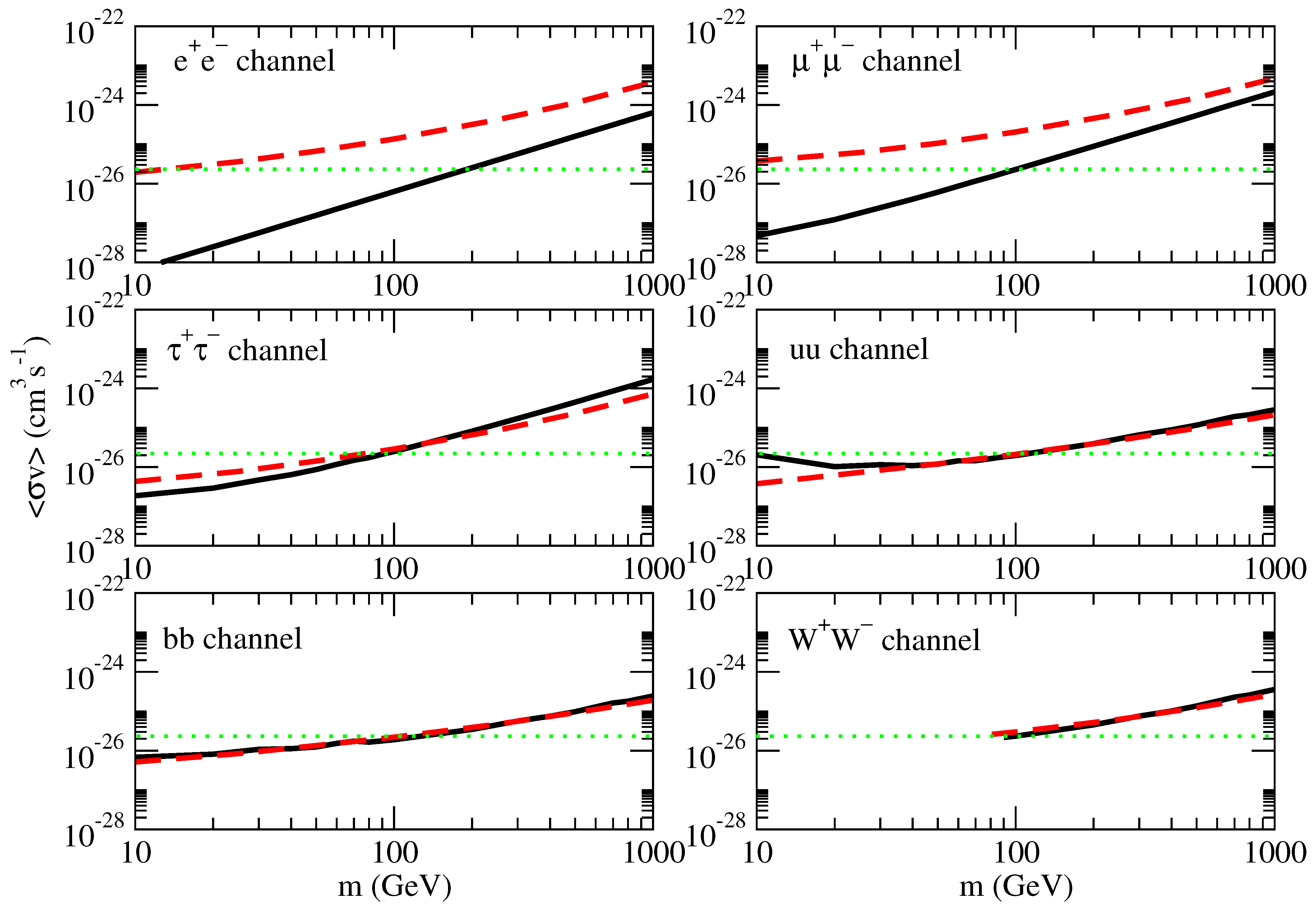
3. Results
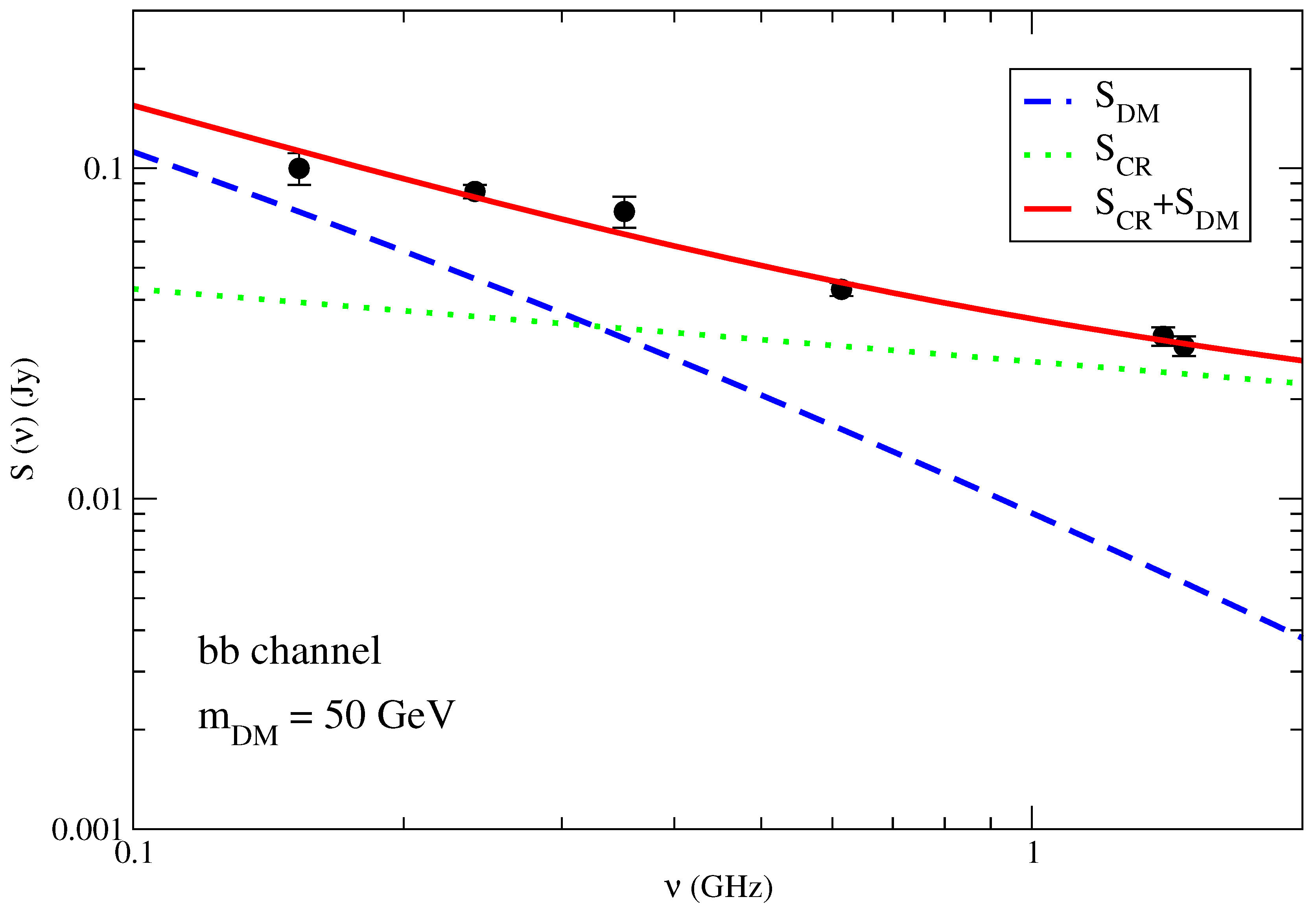
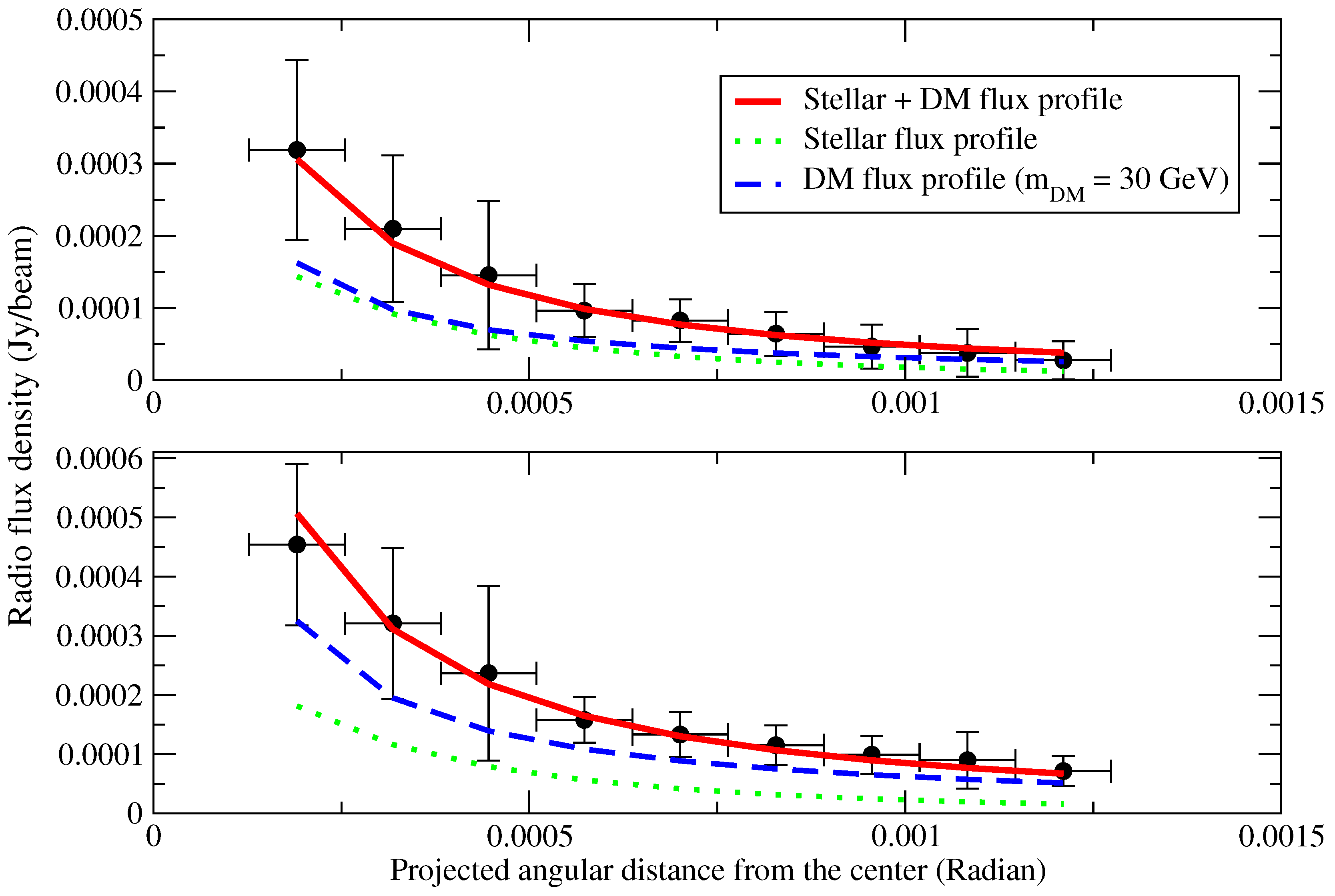
3.1. Galaxies
3.2. Galaxy Clusters
4. Future Perspectives
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bertone, G.; Bozorgnia, N.; Kim, J.S.; Liem, S.; McCabe, C.; Otten, S.; de Austri, R.R. Identifying WIMP dark matter from particle and astroparticle data. J. Cosmol. Astropart. Phys. 2018, 3, 26. [Google Scholar] [CrossRef]
- Calore, F.; Cholis, I.; McCabe, C.; Weniger, C. A tale of tails: Dark matter interpretations of the Fermi GeV excess in light of background model systematics. Phys. Rev. D 2015, 91, 063003. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Lovellette, M.N.; Fermi-LAT Collaboration. Searching for dark matter annihilation from Milky Way dwarf spheroidal galaxies with six years of Fermi Large Area Telescope data. Phys. Rev. Lett. 2015, 115, 231301. [Google Scholar]
- Daylan, T.; Finkbeiner, D.P.; Hooper, D.; Linden, T.; Portillo, S.K.N.; Rodd, N.L.; Slatyer, T.R. The characterization of the gamma-ray signal from the central Milky Way: A case for annihilating dark matter. Phys. Dark Uni. 2016, 12, 1. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Keeley, R.E. Bright gamma-ray Galactic Center excess and dark dwarfs: Strong tension for dark matter annihilation despite Milky Way halo profile and diffuse emission uncertainties. Phys. Rev. D 2016, 93, 083514. [Google Scholar] [CrossRef]
- Albert, A.; Fermi-LAT, DES Collaborations. Searching for dark matter annihilation in recently discovered Milky Way satellites with Fermi-Lat. Astrophys. J. 2017, 834, 110. [Google Scholar] [CrossRef]
- Chan, M.H.; Leung, C.H. Ruling out dark matter interpretation of the galactic GeV excess by gamma-ray data of galaxy clusters. Sci. Rept. 2017, 7, 14895. [Google Scholar] [CrossRef]
- Aguilar, M.; Alberti, G.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Anderhub, H.; Arruda, L.; Azzarello, P.; Bachlechner, A.; et al. First result from the Alpha Magnetic Spectrometer on the International Space Station: Precision measurement of the positron fraction in primary cosmic rays of 0.5–350 GeV. Phys. Rev. Lett. 2013, 110, 141102. [Google Scholar] [CrossRef]
- Ambrosi, G.; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bertucci, B.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; et al. Direct detection of a break in the teraelectronvolt cosmic-ray spectrum of electrons and positrons. Nature 2017, 552, 63. [Google Scholar]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; Barrin, L.; et al. Towards understanding the origin of cosmic-ray positrons. Phys. Rev. Lett. 2019, 122, 041102. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M. Origin of the DAMPE 1.4 TeV peak. Mon. Not. R. Astron. Soc. 2019, 486, L85. [Google Scholar] [CrossRef]
- Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; Bottacini, E.; et al. Characterizing the population of pulsars in the inner Galaxy with the Fermi-Large Area Telescope. arXiv 2017, arXiv:1705.00009. [Google Scholar]
- Bartels, R.; Hooper, D.; Linden, T.; Mishra-Sharma, S.; Rodd, N.L.; Safdi, B.R.; Slatyer, T.R. Comment on “Characterizing the population of pulsars in the Galactic bulge with the Fermi large area telescope”. Phys. Dark Univ. 2018, 20, 88. [Google Scholar] [CrossRef]
- Blasi, P.; Olinto, A.V.; Tyler, C. Detecting WIMPs in the microwave sky. Astropart. Phys. 2003, 18, 649. [Google Scholar] [CrossRef][Green Version]
- Aloisio, R.; Blasi, P.; Olinto, A.V. Neutralino annihilation at the galactic centre revisited. J. Cosmol. Astropart. Phys. 2004, 5, 7. [Google Scholar] [CrossRef][Green Version]
- Tasitsiomi, A.; Siegal-Gaskins, J.M.; Olinto, A.V. Gamma-ray and synchrotron emission from neutralino annihilation in the Large Magellanic Cloud. Astropart. Phys. 2004, 21, 637. [Google Scholar] [CrossRef][Green Version]
- Baltz, E.A.; Wai, L. Diffuse inverse Compton and synchrotron emission from dark matter annihilations in galactic satellites. Phys. Rev. D 2004, 70, 023512. [Google Scholar] [CrossRef]
- Borriello, E.; Cuoco, A.; Miele, G. Radio constraints on dark matter annihilation in the galactic halo and its substructures. Phys. Rev. D 2009, 79, 023518. [Google Scholar] [CrossRef]
- Siffert, B.B.; Limone, A.; Borriello, E.; Longo, G.; Miele, G. Radio emission from dark matter annihilation in the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2011, 410, 2463. [Google Scholar] [CrossRef]
- Natarajan, A.; Peterson, J.B.; Voytek, T.C.; Spekkens, K.; Mason, B.; Aguirre, J.; Willman, B. Bounds on dark matter properties from radio observations of Ursa Major II using the Green Bank Telescope. Phys. Rev. D 2013, 88, 083535. [Google Scholar] [CrossRef]
- Cholis, I.; Hooper, D.; Linden, T. A critical reevaluation of radio constraints on annihilating dark matter. Phys. Rev. D 2015, 91, 083507. [Google Scholar] [CrossRef]
- Regis, M.; Colafrancesco, S.; Profumo, S.; de Blok, W.J.G.; Massardi, M.; Richter, L. Local Group dSph radio survey with ATCA (III): Constraints on particle dark matter. J. Cosmol. Astropart. Phys. 2014, 10, 016. [Google Scholar] [CrossRef]
- Natarajan, A.; Aguirre, J.E.; Spekkens, K.; Mason, B.S. Green Bank Telescope constraints on dark matter annihilation in Segue I. arXiv 2015, arXiv:1507.03589. [Google Scholar]
- Regis, M.; Richter, L.; Colafrancesco, S. Dark matter in the Reticulum II dSph: A radio search. J. Cosmol. Astropart. Phys. 2017, 07, 025. [Google Scholar] [CrossRef]
- Chan, M.H. Relieving tensions related to the dark matter interpretation of the Fermi-LAT data. Galaxies 2018, 6, 92. [Google Scholar] [CrossRef]
- Vollmann, M.; Heesen, V.; Shimwell, T.W.; Hardcastle, M.J.; Brüggen, M.; Sigl, G.; Röttgering, H.J.A. Radio constraints on dark matter annihilation in Canes Venatici I with LOFAR. Mon. Not. R. Astron. Soc. 2020, 496, 2663. [Google Scholar] [CrossRef]
- Egorov, A.E.; Pierpaoli, E. Constraints on dark matter annihilation by radio observations of M31. Phys. Rev. D 2013, 88, 023504. [Google Scholar] [CrossRef]
- Chan, M.H. Revisiting the constraints on annihilating dark matter by the radio observational data of M31. Phys. Rev. D 2016, 94, 023507. [Google Scholar] [CrossRef]
- Chan, M.H.; Cui, L.; Liu, J.; Leung, C.S. Ruling out ∼100–300 GeV thermal relic annihilating dark matter by radio observation of the Andromeda galaxy. Astrophys. J. 2019, 872, 177. [Google Scholar] [CrossRef]
- Borriello, E.; Longo, G.; Miele, G.; Paolillo, M.; Siffert, B.B.; Tabatabaei, F.S.; Beck, R. Searching for dark matter in Messier 33. Astrophys. J. 2010, 709, L32. [Google Scholar] [CrossRef]
- Chan, M.H. Constraining annihilating dark matter by radio data of M33. Phys. Rev. D 2017, 96, 043009. [Google Scholar] [CrossRef]
- Chan, M.H. A possible signature of annihilating dark matter. Mon. Not. R. Astron. Soc. 2018, 474, 2576. [Google Scholar] [CrossRef]
- Chan, M.H. A new target object for constraining annihilating dark matter. Astrophys. J. 2017, 844, 9. [Google Scholar] [CrossRef]
- Colafrancesco, S.; Profumo, S.; Ullio, P. Multi-frequency analysis of neutralino dark matter annihilations in the Coma cluster. Astron. Astrophys. 2006, 455, 21. [Google Scholar] [CrossRef]
- Storm, E.; Jeltema, T.E.; Profumo, S.; Rudnick, L. Constraints on dark matter annihilation in clusters of galaxies from diffuse radio emission. Astrophys. J. 2013, 768, 106. [Google Scholar] [CrossRef]
- Colafrancesco, S.; Marchegiani, P.; Beck, G. Evolution of darak matter halos and their radio emissions. J. Cosmol. Astrophys. Phys. 2015, 2, 032. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M. Fitting dark matter mass with the radio continuum spectral data of the Ophiuchus cluster. Phys. Dark Uni. 2019, 26, 100355. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M.; Ng, C.-Y.; Leung, C.S. Constraining annihilating dark matter mass by the radio continuum spectral data of a high-redshift galaxy cluster. Astrophys. J. 2020, 900, 126. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M. A possible radio signal of annihilating dark matter in the Abell 4038 cluster. Mon. Not. R. Astron. Soc. 2021, 500, 5583. [Google Scholar] [CrossRef]
- Fornengo, N.; Lineros, R.; Regis, M.; Taoso, M. Possibility of a dark matter interpretation for the excess in isotropic radio emission reported by ARCADE. Phys. Rev. Lett. 2011, 107, 271302. [Google Scholar] [CrossRef]
- Cirelli, M.; Corcella, G.; Hektor, A.; Hütsi, G.; Kadastik, M.; Panci, P.; Raidal, M.; Sala, F.; Strumia, A. PPPC 4 DM ID: A poor particle physicist cookbook for dark matter indirect detection. J. Cosmol. Astropart. Phys. 2011, 3, 051. [Google Scholar] [CrossRef]
- Atoyan, A.M.; Aharonian, F.A.; Völk, H.J. Electrons and positrons in the galactic cosmic rays. Phys. Rev. D 1995, 52, 3265. [Google Scholar] [CrossRef] [PubMed]
- Strong, A.W.; Moskalenko, I.V. Propagation of cosmic-ray nucleons in the Galaxy. Astrophys. J. 1998, 509, 212. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Cosmic ray nuclei, antiprotons and gamma rays in the galaxy: A new diffusion model. J. Cosmol. Astropart. Phys. 2008, 10, 18. [Google Scholar] [CrossRef]
- Kissmann, R. PICARD: A novel code for the Galactic Cosmic Ray propagation problem. Astropart. Phys. 2014, 55, 37. [Google Scholar] [CrossRef]
- Maurin, D. USINE: Semi-analytical models for Galactic cosmic-ray propagation. Comp. Phys. Comm. 2020, 247, 106942. [Google Scholar] [CrossRef]
- Kar, A.; Mitra, S.; Mukhopadhyaya, B.; Choudhury, T.R. Heavy dark matter particle annihilation in dwarf spheroidal galaxies: Radio signals at the SKA telescope. Phys. Rev. D 2020, 101, 023015. [Google Scholar] [CrossRef]
- Profumo, S.; Ullio, P. Particle Dark Matter: Observations, Models and Searches; Bertone, G., Ed.; Cambridge University Press: Cambridge, UK, 2010; Chapter 27. [Google Scholar]
- Bertone, G.; Cirelli, M.; Strumia, A.; Taoso, M. Gamma-ray and radio tests of the e± excess from DM annihilations. J. Cosmol. Astropart. Phys. 2009, 3, 009. [Google Scholar] [CrossRef]
- Ullio, P.; Valli, M. A critical reassessment of particle dark matter limits from dwarf satellites. J. Cosmol. Astropart. Phys. 2016, 7, 025. [Google Scholar] [CrossRef]
- Steigman, G.; Dasgupta, B.; Beacom, J.F. Precise relic WIMP abundance and its impact on searches for dark matter annihilation. Phys. Rev. D 2012, 86, 023506. [Google Scholar] [CrossRef]
- Sommerfeld, A. Öber die Beugung und Bremsung der Elektronen. Ann. Der Phys. 1931, 403, 257. [Google Scholar] [CrossRef]
- Feldman, D.; Liu, Z.; Nath, P. PAMELA positron excess as a signal from the hidden sector. Phys. Rev. D 2009, 79, 063509. [Google Scholar] [CrossRef]
- Kim, H.; Hong, J.-P.; Shin, C.S. A map of the non-thermal WIMP. Phys. Lett. B 2017, 768, 292. [Google Scholar] [CrossRef]
- Visinelli, L. (Non-)thermal production of WIMPs during Kination. Symmetry 2018, 10, 546. [Google Scholar] [CrossRef]
- Choi, K.-Y.; Kang, S.K.; Kim, J. Non-thermal WIMP baryogenesis. Phys. Lett. B 2018, 782, 657. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A universal density profile from hierarchical clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Chen, Y.; Reiprich, T.H.; Böhringer, H.; Ikebe, Y.; Zhang, Y.-Y. Statistics of X-ray observables for the cooling-core and non-cooling core galaxy clusters. Astron. Astrophys. 2007, 466, 805. [Google Scholar] [CrossRef]
- Molinè, A.; Sànchez-Conde, M.A.; Palomares-Ruiz, S.; Prada, F. Characterization of subhalo structural properties and implications for dark matter annihilation signals. Mon. Not R. Astron. Soc. 2017, 466, 4974. [Google Scholar] [CrossRef]
- Sànchez-Conde, M.A.; Prada, F. The flattening of the concentration-mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271. [Google Scholar] [CrossRef]
- Sofue, Y. Dark halos of M31 and the Milky Way. Pub. Astron. Soc. Jpn. 2015, 67, 75. [Google Scholar] [CrossRef]
- Gießübel, R.; Beck, R. The magnetic field structure of the central region in M31. Astron. Astrophys. 2014, 571, A61. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Vacca, V.; Loi, F.; Girardi, M.; Gastaldello, F.; Giovannini, G.; Feretti, L.; Paladino, R.; Carretti, E.; et al. Sardinia Radio Telescope observations of Abell 194. The intra-cluster magnetic field power spectrum. Astron. Astrophys. 2017, 603, A122. [Google Scholar] [CrossRef]
- Kunz, M.W.; Schekochihin, A.A.; Cowley, S.C.; Binney, J.J.; Sanders, J.S. A thermally stable heating mechanism for the intracluster medium: Turbulence, magnetic fields and plasma instabilities. Mon. Not. R. Astron. Soc. 2011, 410, 2446. [Google Scholar] [CrossRef]
- Hooper, D.; Finkbeiner, D.P.; Dobler, G. Possible evidence for dark matter annihilations from the excess microwave emission around the center of the Galaxy seen by the Wilkinson Microwave Anisotropy Probe. Phys. Rev. D 2007, 76, 083012. [Google Scholar] [CrossRef]
- Carlson, E.; Hooper, D.; Linden, T.; Profumo, S. Testing the dark matter origin of the WMAP-Planck haze with radio observations of spiral galaxies. J. Cosmol. Astropart. Phys. 2013, 7, 026. [Google Scholar] [CrossRef]
- Regis, M.; Ullio, P. Multiwavelength signals of dark matter annihilations at the Galactic center. Phys. Rev. D 2008, 78, 043505. [Google Scholar] [CrossRef]
- Wechakama, M.; Ascasibar, Y. Multimessenger constraints on dark matter annihilation into electron-positron pairs. Mon. Not. R. Astron. Soc. 2014, 439, 566. [Google Scholar] [CrossRef]
- Gondolo, P.; Silk, J. Dark matter annihilation at the Galactic Center. Phys. Rev. Lett. 1999, 83, 1719. [Google Scholar] [CrossRef]
- Fields, B.D.; Shapiro, S.L.; Shelton, J. Galactic Center gamma-ray excess from dark matter annihilation: Is there a black hole spike? Phys. Rev. Lett. 2014, 113, 151302. [Google Scholar] [CrossRef]
- Egorov, A.E.; Gaskins, J.M.; Pierpaolo, E.; Pietrobon, D. Dark matter implications of the WMAP-Planck Haze. J. Cosmol. Astropart. Phys. 2016, 3, 060. [Google Scholar] [CrossRef][Green Version]
- Gießübel, R.; Heald, G.; Beck, R.; Arshakian, T. Polarized synchrotron radiation from the Andromeda galaxy M31 and background sources at 350 MHz. Astron. Astrophys. 2013, 559, A27. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M. Constraining the annihilating dark matter mass by the radio continuum spectral data of the NGC4214 galaxy. Phys. Rev. D 2020, 102, 063017. [Google Scholar] [CrossRef]
- Fang, K.; Linden, T. Cluster mergers and the origin of the ARCADE-2 excess. J. Cosmol. Astropart. Phys. 2016, 10, 004. [Google Scholar] [CrossRef]
- Kehayias, J.; Kephart, T.W.; Weiler, T.J. The excess radio background and fast radio transients. J. Cosmol. Astropart. Phys. 2015, 10, 053. [Google Scholar] [CrossRef][Green Version]
- Fairbairn, M.; Grothaus, P. Note on the dark matter explanation of the ARCADE excess and AMS data. Phys. Rev. D 2014, 90, 127302. [Google Scholar] [CrossRef]
- Evoli, C.; Morlino, G.; Blasi, P.; Aloisio, R. AMS-02 beryllium data and its implication for cosmic ray transport. Phys. Rev. D 2020, 101, 023013. [Google Scholar] [CrossRef]
- Fang, K.; Bi, X.-J.; Yin, P.-F. DAMPE proton spectrum indicates a slow-diffusion zone in the nearby ISM. Astrophys. J. 2020, 903, 69. [Google Scholar] [CrossRef]
- Beck, G. An excess of excesses examined via dark matter radio emissions from galaxies. J. Cosmol. Astropart. Phys. 2019, 8, 019. [Google Scholar] [CrossRef]
- Gao, L.; Frenk, C.S.; Jenkins, A.; Springel, V.; White, S.D.M. Where will supersymmetric dark matter first be seen? Mon. Not. R. Astron. Soc. 2012, 419, 1721. [Google Scholar] [CrossRef]
- Dolag, K.; Schindler, S.; Govoni, F.; Feretti, L. Correlation of the magnetic field and the intra-cluster gas density in galaxy clusters. Astron. Astrophys. 2001, 378, 777. [Google Scholar] [CrossRef]
- Jaffe, W.J. Origin and transport of electrons in the halo radio source in the Coma cluster. Astrophys. J. 1977, 212, 1. [Google Scholar] [CrossRef]
- Rephaeli, Y. Spatial distribution of Compton-produced X-ray flux from rich and regular clusters of galaxies. Astrophys. J. 1977, 212, 608. [Google Scholar] [CrossRef]
- Rephaeli, Y. Relativistic electrons in the intracluster space of clusters of galaxies: The hard X-ray spectra and heating of the gas. Astrophys. J. 1979, 227, 364. [Google Scholar] [CrossRef]
- Dennison, B. Formation of radio halos in clusters of galaxies from cosmic-ray protons. Astrophys. J. 1980, 239, L93. [Google Scholar] [CrossRef]
- Keshet, U.; Loeb, A. Using radio halos and minihalos to measure the distributions of magnetic fields and cosmic rays in galaxy clusters. Astrophys. J. 2010, 722, 737. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts - I. Mon. Not. R. Astron. Soc. 1978, 182, 147. [Google Scholar] [CrossRef]
- Malkov, M.A.; Drury, L.O. Nonlinear theory of diffusive acceleration of particles by shock waves. Rep. Prog. Phys. 2001, 64, 429. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Sievers, A.; Thiemann, H. The diffuse radio emission from the Coma cluster. Astron. Astrophys. 1987, 182, 21. [Google Scholar]
- Thierbach, M.; Klein, U.; Wielebinski, R.R. The diffuse radio emission from the Coma cluster at 2.675 GHz and 4.85 GHz. Astron. Astrophys. 2003, 397, 53. [Google Scholar] [CrossRef]
- Brunetti, G.; Setti, G.; Feretti, L.; Giovannini, G. Particle reacceleration in the Coma cluster: Radio properties and hard X-ray emission. Mon. Not. R. Astron. Soc. 2001, 320, 365. [Google Scholar] [CrossRef]
- Enßlin, T.A.E.; Gopal-Krishna. Reviving fossil radio plasma in clusters of galaxies by adiabatic compression in environmental shock waves. Astron. Astrophys. 2001, 366, 26. [Google Scholar] [CrossRef]
- Enßlin, T.A.E.; Brüggen, M. On the formation of cluster radio relics. Mon. Not. R. Astron. Soc. 2002, 331, 1011. [Google Scholar] [CrossRef]
- van Weeren, R.J.; de Gasperin, F.; Akamatsu, H.; Brüggen, M.; Feretti, L.; Kang, H.; Stroe, A.; Zandanel, F. Diffuse radio emission from galaxy clusters. Space Sci. Rev. 2019, 215, 16. [Google Scholar] [CrossRef]
- Murgia, M.; Eckert, D.; Govoni, F.; Ferrari, C.; Pandey-Pommier, M.; Nevalainen, J.; Paltani, S. GMRT observations of the Ophiuchus galaxy cluster. Astron. Astrophys. 2010, 514, A76. [Google Scholar] [CrossRef]
- Macario, G.; Venturi, T.; Intema, H.T.; Dallacasa, D.; Brunetti, G.; Cassano, R.; Giacintucci, S.; Ferrari, C.; Ishwara-Chandra, C.H.; Athreya, R. 153 MHz GMRT follow-up of steep-spectrum diffuse emission in galaxy clusters. Astron. Astrophys. 2013, 551, A141. [Google Scholar] [CrossRef]
- Kale, R.; Dwarakanath, K.S. Multi-frequency studies of radio relics in the galaxy clusters A4038, A1664, and A786. Astrophys. J. 2012, 744, 46. [Google Scholar] [CrossRef]
- Brown, A.M.; Lacroix, T.; Lloyd, S.; Hm, C.B.; Chadwick, P. Understanding the γ-ray emission from the globular cluster 47 Tuc: Evidence for dark matter? Phys. Rev. D 2018, 98, 041301. [Google Scholar] [CrossRef]
- Cholis, I.; Linden, T.; Hooper, D. A robust excess in the cosmic-ray antiproton spectrum: Implications for annihilating dark matter. Phys. Rev. D 2019, 99, 103026. [Google Scholar] [CrossRef]
- Storm, E.; Jeltema, T.E.; Splettstoesser, M.; Profumo, S. Synchrotron emission from dark matter annihilation: Predictions for constraints from non-detections of galaxy clusters with new radio surveys. Astrophys. J. 2017, 839, 33. [Google Scholar] [CrossRef]
- Bartels, R.; Storm, E.; Weniger, C.; Calore, F. The Fermi-LAT GeV excess as a tracer of stellar mass in the Galactic bulge. Nat. Astron. 2018, 2, 819. [Google Scholar] [CrossRef]
- Chan, M.H.; Yeung, C.F.; Cui, L.; Leung, C.S. Analysing the radio flux density profile of the M31 galaxy: A possible dark matter interpretation. Mon. Not. R. Astron. Soc. 2021, 501, 5692–5696. [Google Scholar]
- Battye, R.A.; Garbrecht, B.; McDonald, J.I.; Pace, F.; Srinivasan, S. Dark matter axion detection in the radio/mm waveband. Phys. Rev. D 2020, 102, 023504. [Google Scholar] [CrossRef]
- Graham, P.W.; Irastorza, I.G.; Lamoreaux, S.K.; Lindner, A.; van Bibber, K.A. Experimental searches for the axion and axion-like particles. Ann. Rev. Nucl. Part. Sci. 2015, 65, 485. [Google Scholar] [CrossRef]
- Caputo, A.; Garay, C.P.; White, S.J. Looking for axion dark matter in dwarf spheroidal galaxies. Phys. Rev. D 2018, 98, 083024. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, M.H. Radio Constraints of Dark Matter: A Review and Some Future Perspectives. Galaxies 2021, 9, 11. https://doi.org/10.3390/galaxies9010011
Chan MH. Radio Constraints of Dark Matter: A Review and Some Future Perspectives. Galaxies. 2021; 9(1):11. https://doi.org/10.3390/galaxies9010011
Chicago/Turabian StyleChan, Man Ho. 2021. "Radio Constraints of Dark Matter: A Review and Some Future Perspectives" Galaxies 9, no. 1: 11. https://doi.org/10.3390/galaxies9010011
APA StyleChan, M. H. (2021). Radio Constraints of Dark Matter: A Review and Some Future Perspectives. Galaxies, 9(1), 11. https://doi.org/10.3390/galaxies9010011



