Signatures of Lorentz Violation in Continuous Gravitational-Wave Spectra of Ellipsoidal Neutron Stars
Abstract
1. Introduction
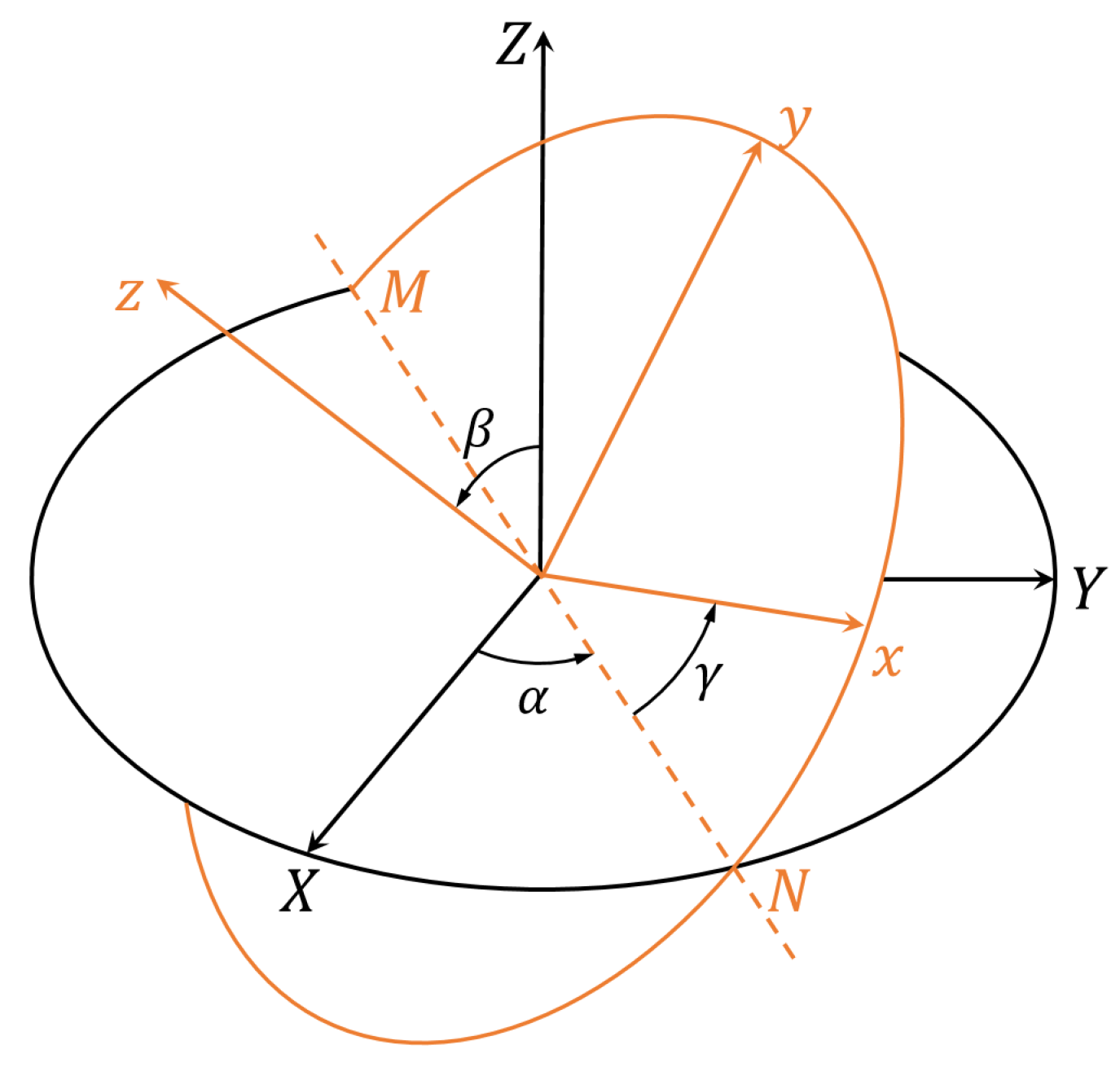
2. Theoretical Basics
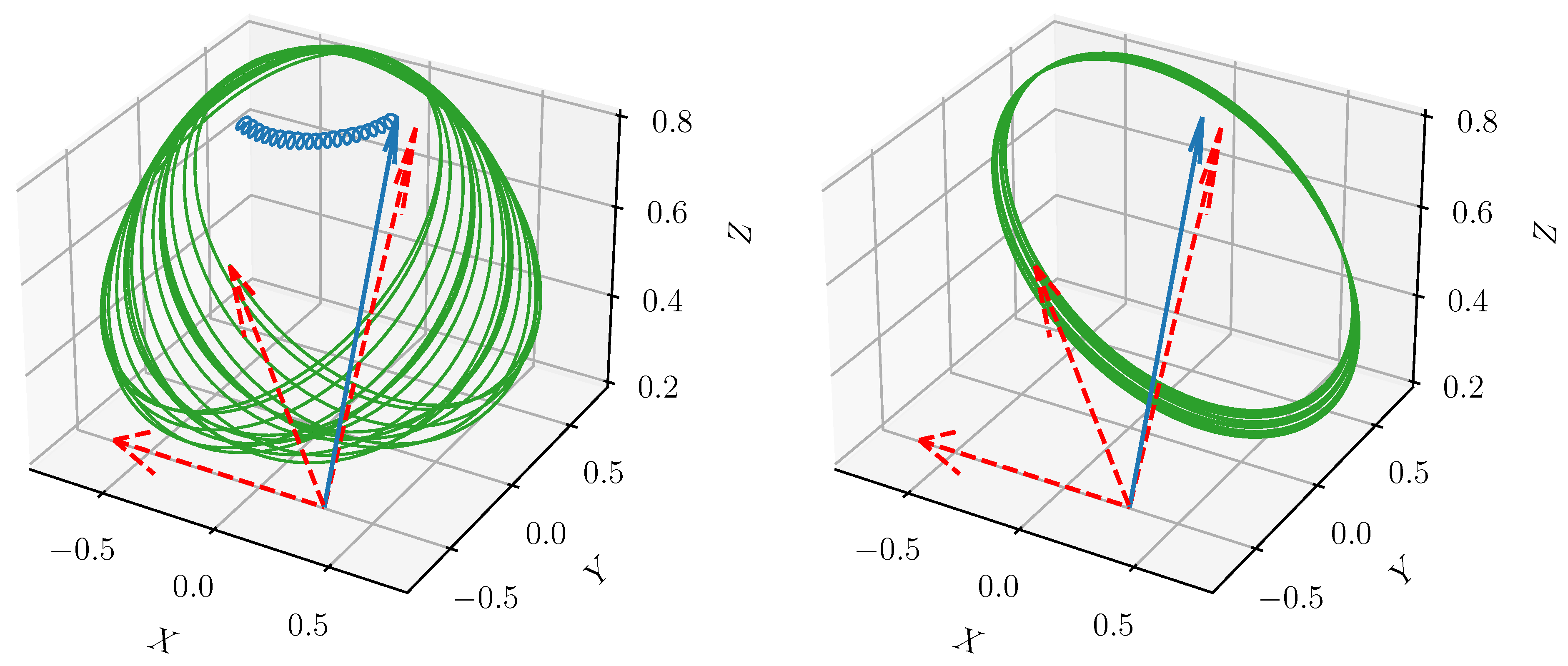
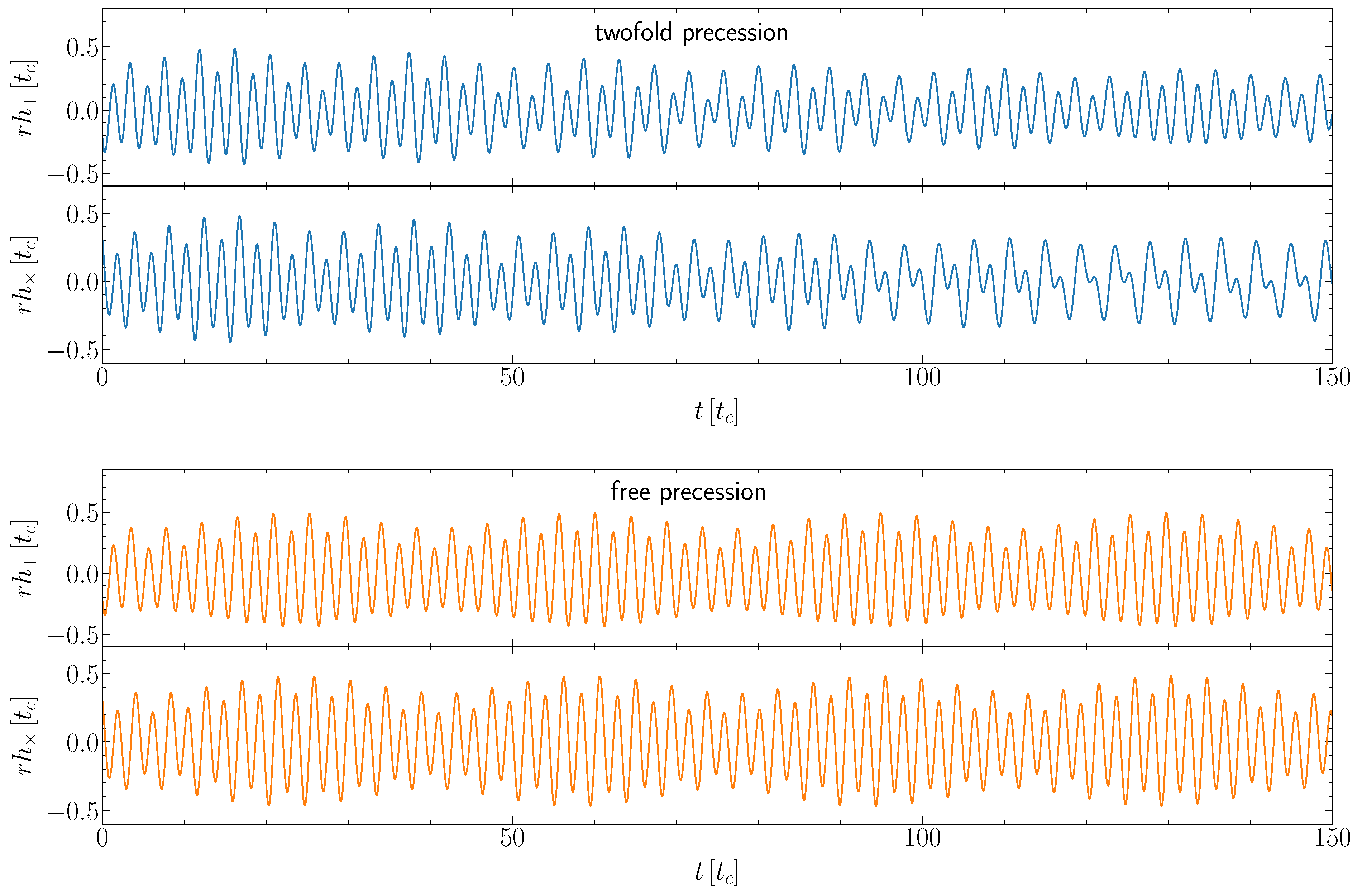
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Corda, C. Interferometric detection of gravitational waves: The definitive test for General Relativity. Int. J. Mod. Phys. D 2009, 18, 2275–2282. [Google Scholar] [CrossRef]
- Mirshekari, S.; Yunes, N.; Will, C.M. Constraining Generic Lorentz Violation and the Speed of the Graviton with Gravitational Waves. Phys. Rev. D 2012, 85, 024041. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Testing local Lorentz invariance with gravitational waves. Phys. Lett. B 2016, 757, 510–514. [Google Scholar] [CrossRef]
- Shao, L. Combined search for anisotropic birefringence in the gravitational-wave transient catalog GWTC-1. Phys. Rev. D 2020, 101, 104019. [Google Scholar] [CrossRef]
- Liu, X.; He, V.F.; Mikulski, T.M.; Palenova, D.; Williams, C.E.; Creighton, J.; Tasson, J.D. Measuring the speed of gravitational waves from the first and second observing run of Advanced LIGO and Advanced Virgo. Phys. Rev. D 2020, 102, 024028. [Google Scholar] [CrossRef]
- Xu, R.; Zhao, J.; Shao, L. Neutron Star Structure in the Minimal Gravitational Standard-Model Extension and the Implication to Continuous Gravitational Waves. Phys. Lett. B 2020, 803, 135283. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760–6774. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecký, V.A. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 2002, 66, 056005. [Google Scholar] [CrossRef]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Bailey, Q.G.; Kostelecký, V.A. Signals for Lorentz violation in post-Newtonian gravity. Phys. Rev. D 2006, 74, 045001. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11–31. [Google Scholar] [CrossRef]
- Zimmermann, M.; Szedenits, E. Gravitational waves from rotating and precessing rigid bodies: Simple models and applications to pulsars. Phys. Rev. D 1979, 20, 351–355. [Google Scholar] [CrossRef]
- Zimmermann, M. Gravitational waves from rotating and precessing rigid bodies. 1. general solutions and computationally useful formulas. Phys. Rev. D 1980, 21, 891–898. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO O2 data. Phys. Rev. D 2019, 100, 024004. [Google Scholar] [CrossRef]
- Covas, P.B.; Sintes, A.M. First all-sky search for continuous gravitational-wave signals from unknown neutron stars in binary systems using Advanced LIGO data. Phys. Rev. Lett. 2020, 124, 191102. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A. Results from the first all-sky search for continuous gravitational waves from small-ellipticity sources. Phys. Rev. Lett. 2020, 125, 171101. [Google Scholar] [CrossRef]
- Papa, M.A.; Ming, J.; Gotthelf, E.V.; Allen, B.; Prix, R.; Dergachev, V.; Eggenstein, H.B.; Singh, A.; Zhu, S.J. Search for Continuous Gravitational Waves from the Central Compact Objects in Supernova Remnants Cassiopeia A, Vela Jr., and G347.3–0.5. Astrophys. J. 2020, 897, 22. [Google Scholar] [CrossRef]
- Steltner, B.; Papa, M.; Eggenstein, H.B.; Allen, B.; Dergachev, V.; Prix, R.; Machenschalk, B.; Walsh, S.; Zhu, S.; Kwang, S. Einstein@Home all-sky search for continuous gravitational waves in LIGO O2 public data. arXiv 2020, arXiv:2009.12260. [Google Scholar]
- Zhang, Y.; Papa, M.A.; Krishnan, B.; Watts, A.L. Search for Continuous Gravitational Waves from Scorpius X-1 in LIGO O2 Data. Astrophys. J. Lett. 2021, 906, L14. [Google Scholar] [CrossRef]
- Xu, R.; Gao, Y.; Shao, L. Precessions of Spheroidal Stars under Lorentz Violation and Observational Consequences. arXiv 2020, arXiv:2012.01320. [Google Scholar]
- Van Den Broeck, C. The Gravitational wave spectrum of non-axisymmetric, freely precessing neutron stars. Class. Quant. Grav. 2005, 22, 1825–1840. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, L.; Xu, R.; Sun, L.; Liu, C.; Xu, R.X. Triaxially-deformed Freely-precessing Neutron Stars: Continuous electromagnetic and gravitational radiation. Mon. Not. Roy. Astron. Soc. 2020, 498, 1826–1838. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics; Butterworth-Heinemann: Oxford, UK, 1976. [Google Scholar] [CrossRef]
- Poisson, E.; Will, C.M. Gravity: Newtonian, Post-Newtonian, Relativistic; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Lebovitz, N.R. The Potentials and the Superpotentials of Homogeneous Ellipsoids. Astrophys. J. 1962, 136, 1037. [Google Scholar] [CrossRef]
- Owen, B.J. Maximum elastic deformations of compact stars with exotic equations of state. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef]
- Goldreich, P. Neutron Star Crusts and Alignment of Magnetic Axes in Pulsars. Astrophys. J. Lett. 1970, 160, L11. [Google Scholar] [CrossRef]
- Jones, D.; Andersson, N. Gravitational waves from freely precessing neutron stars. Mon. Not. Roy. Astron. Soc. 2002, 331, 203. [Google Scholar] [CrossRef]
- Zanazzi, J.; Lai, D. Electromagnetic Torques, Precession and Evolution of Magnetic Inclination of Pulsars. Mon. Not. Roy. Astron. Soc. 2015, 451, 695–704. [Google Scholar] [CrossRef][Green Version]
- Gao, Y.; Shao, L. Precession of triaxially deformed neutron stars. arXiv 2020, arXiv:2011.04472. [Google Scholar]
| 1 | Relativistic corrections are reasonably characterized by the compactness of the body, which is about for a NS. |

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Gao, Y.; Shao, L. Signatures of Lorentz Violation in Continuous Gravitational-Wave Spectra of Ellipsoidal Neutron Stars. Galaxies 2021, 9, 12. https://doi.org/10.3390/galaxies9010012
Xu R, Gao Y, Shao L. Signatures of Lorentz Violation in Continuous Gravitational-Wave Spectra of Ellipsoidal Neutron Stars. Galaxies. 2021; 9(1):12. https://doi.org/10.3390/galaxies9010012
Chicago/Turabian StyleXu, Rui, Yong Gao, and Lijing Shao. 2021. "Signatures of Lorentz Violation in Continuous Gravitational-Wave Spectra of Ellipsoidal Neutron Stars" Galaxies 9, no. 1: 12. https://doi.org/10.3390/galaxies9010012
APA StyleXu, R., Gao, Y., & Shao, L. (2021). Signatures of Lorentz Violation in Continuous Gravitational-Wave Spectra of Ellipsoidal Neutron Stars. Galaxies, 9(1), 12. https://doi.org/10.3390/galaxies9010012





