Gravitational Measurements in Higher Dimensions
Abstract
1. Introduction
- Large extra dimensions, mostly motivated by the ADD model, by Arkani-Hamed, Dimopoulos, and Dvali, together with Antoniadis in Refs. [3,4,5] to solve the hierarchy problem in which the difference between the standard model interactions and GR manifests itself, notably in their dissimilar coupling strengths. While the electromagnetic, weak and strong forces differ by just six orders of magnitude, the gravitational interaction falls apart by a further thirty-three orders.
- Warped extra dimensions, such as those proposed by the Randall–Sundrum (RS) model [6], in which our observable universe is modeled as a four-dimensional hyper surface, known as the 3-brane, embedded in a five dimensional space, are usually called the bulk. The novel idea of the Brane world is that all the gauge interactions, described by the Standard Model, are confined to live in the 3-brane while the gravitational interaction can spread into the fifth dimension of the space.
- Universal extra dimensions, proposed and first studied in Ref. [7]; assume, at variance with the ADD and RS approaches, that all fields propagate universally in extra dimensions.
2. Schwarzschild Black Hole in Higher Dimensions
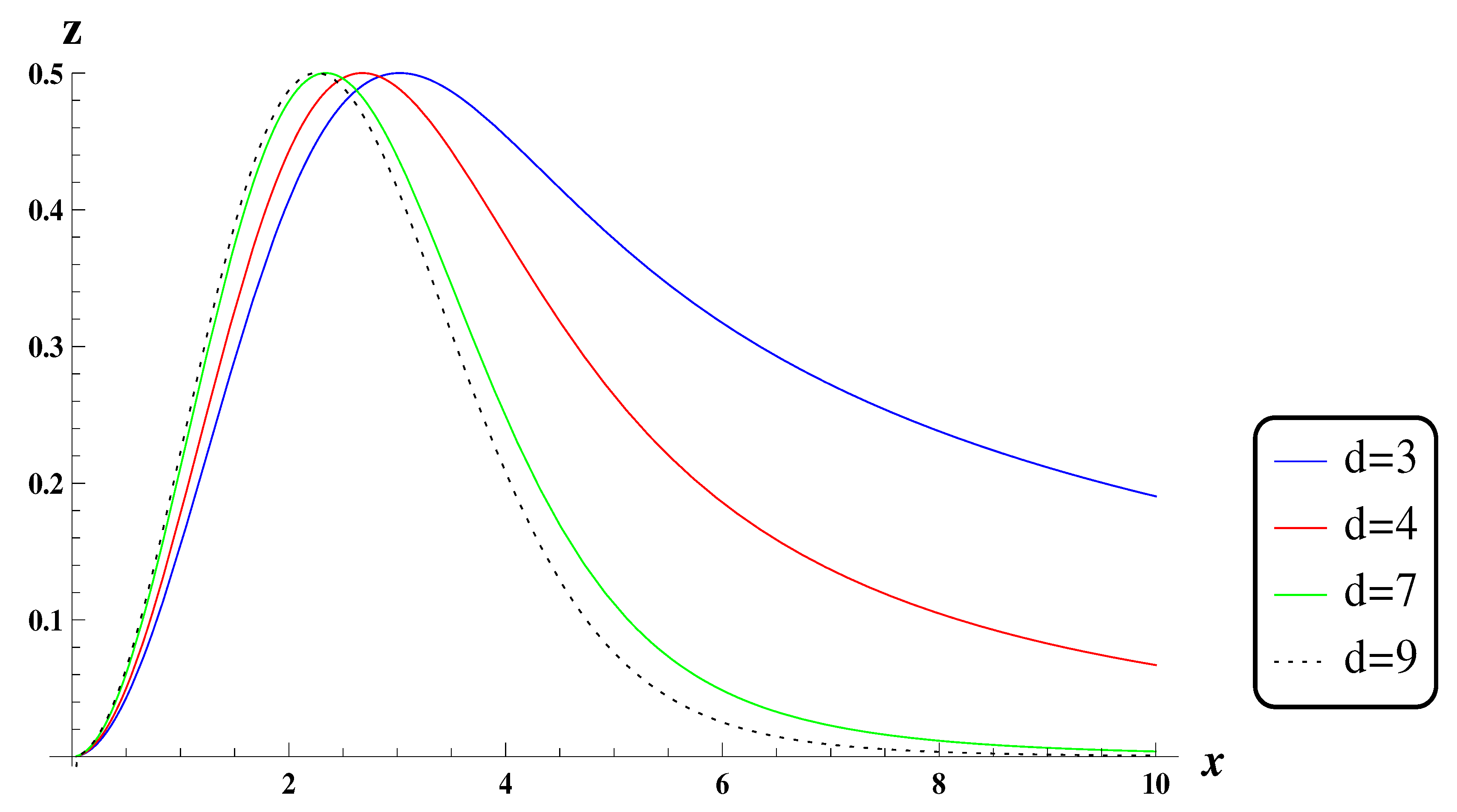
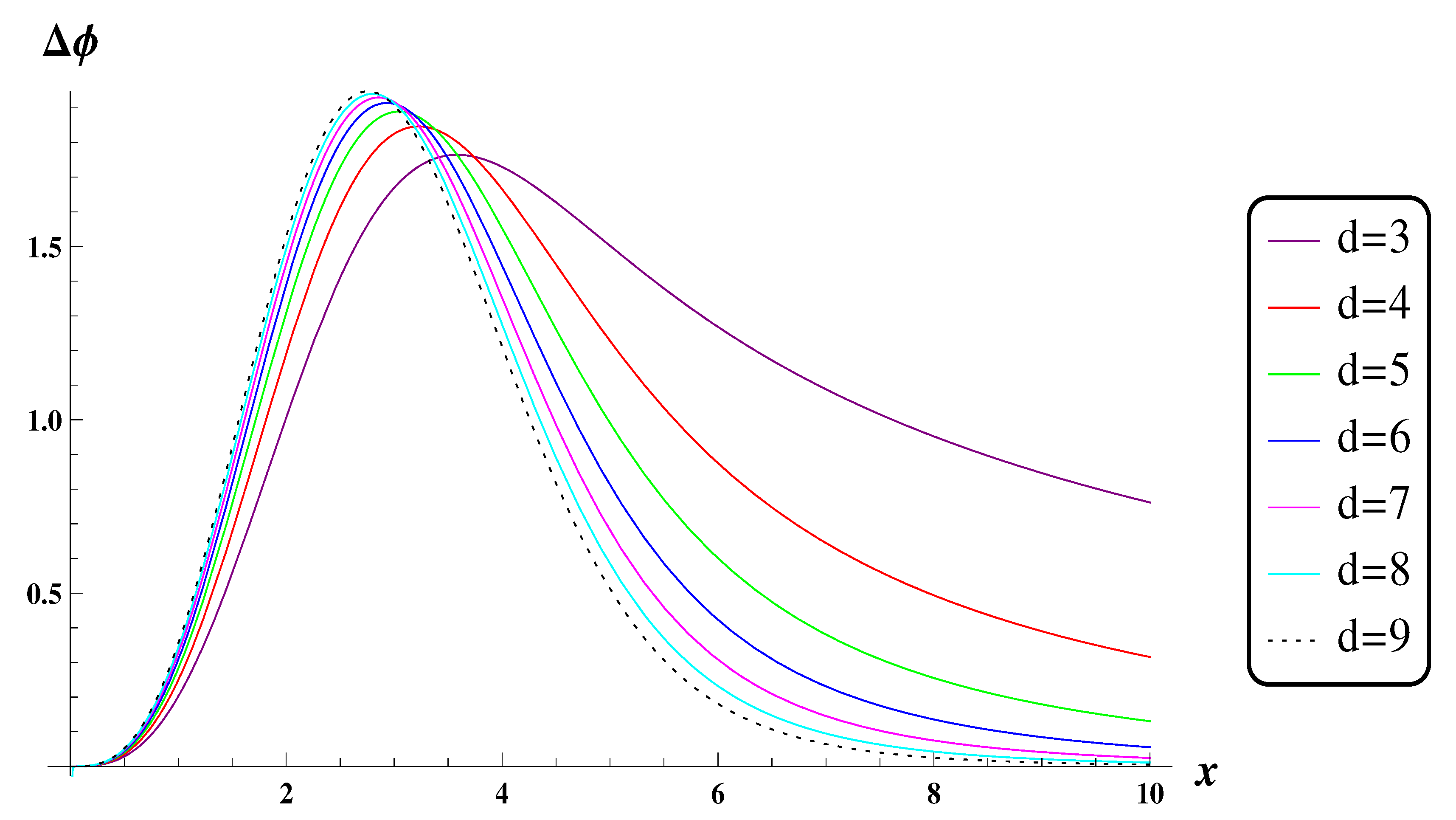
3. Gravitational Effects in Higher Dimensions
4. Gravitational Effects in Higher Dimensional Non-Commutative Spaces
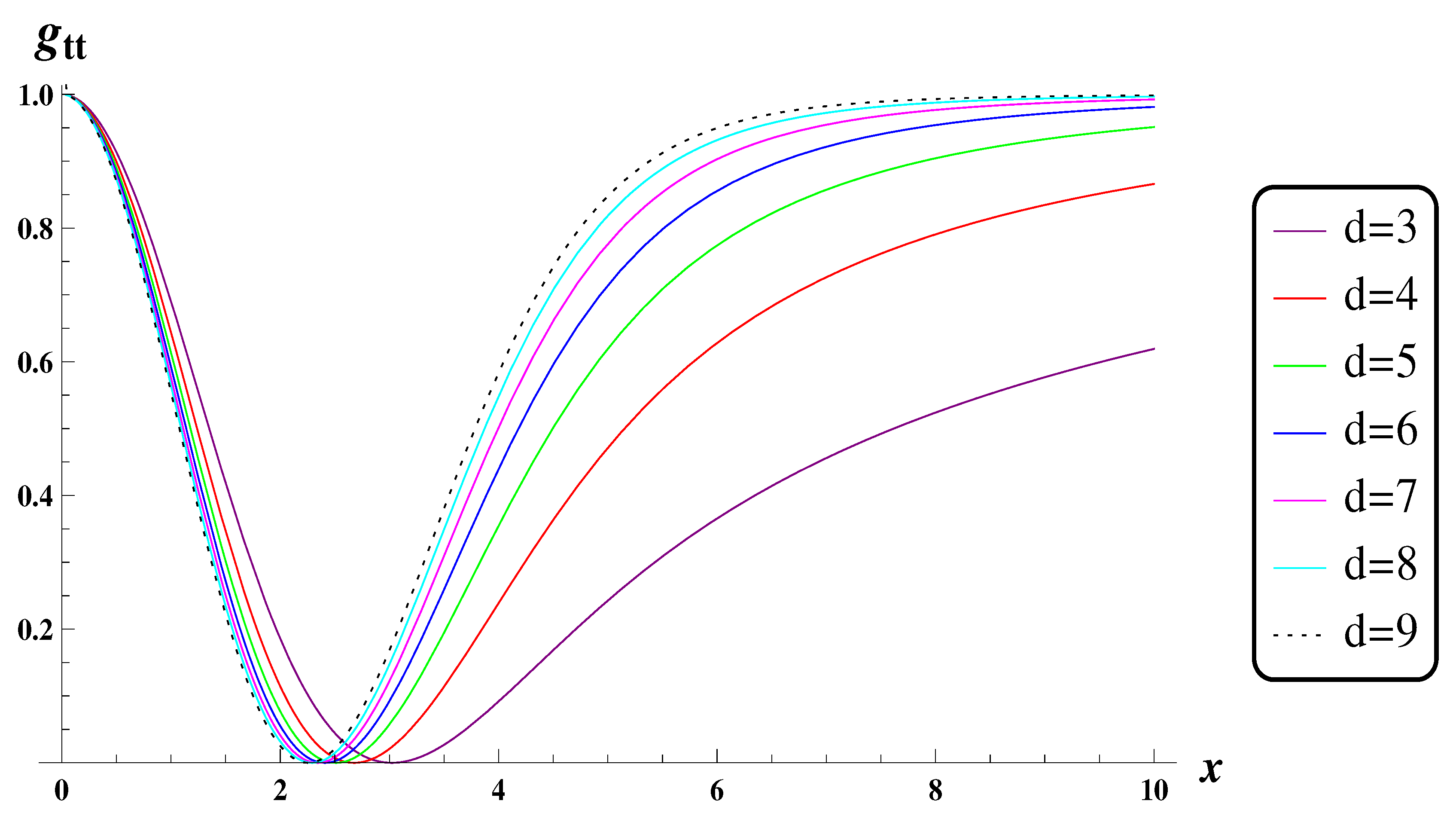
- For , there are two distinct horizons shown by the green curve in Figure 7. By increasing M, i.e., for , the inner horizon shrinks to zero, while the outer horizon approaches the Schwarzschild value .
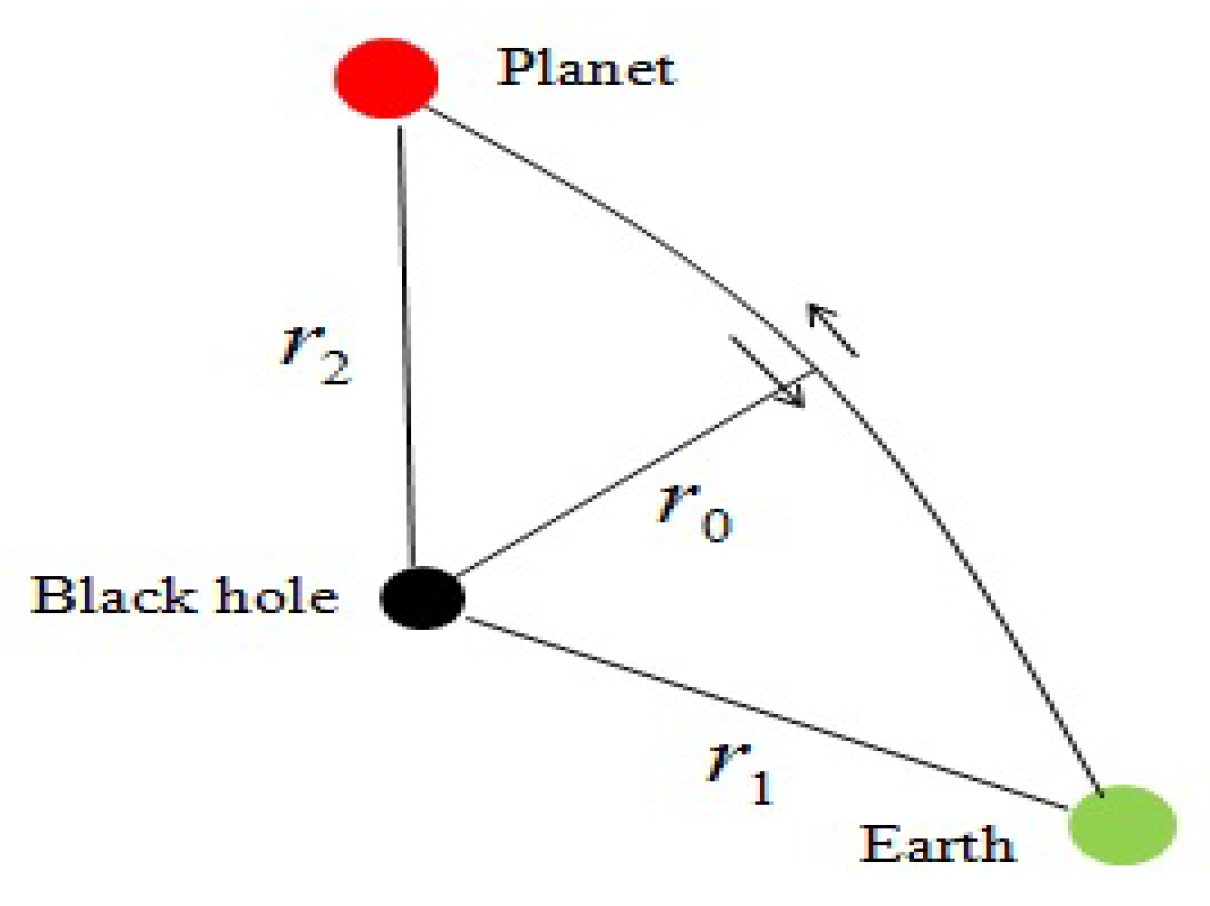
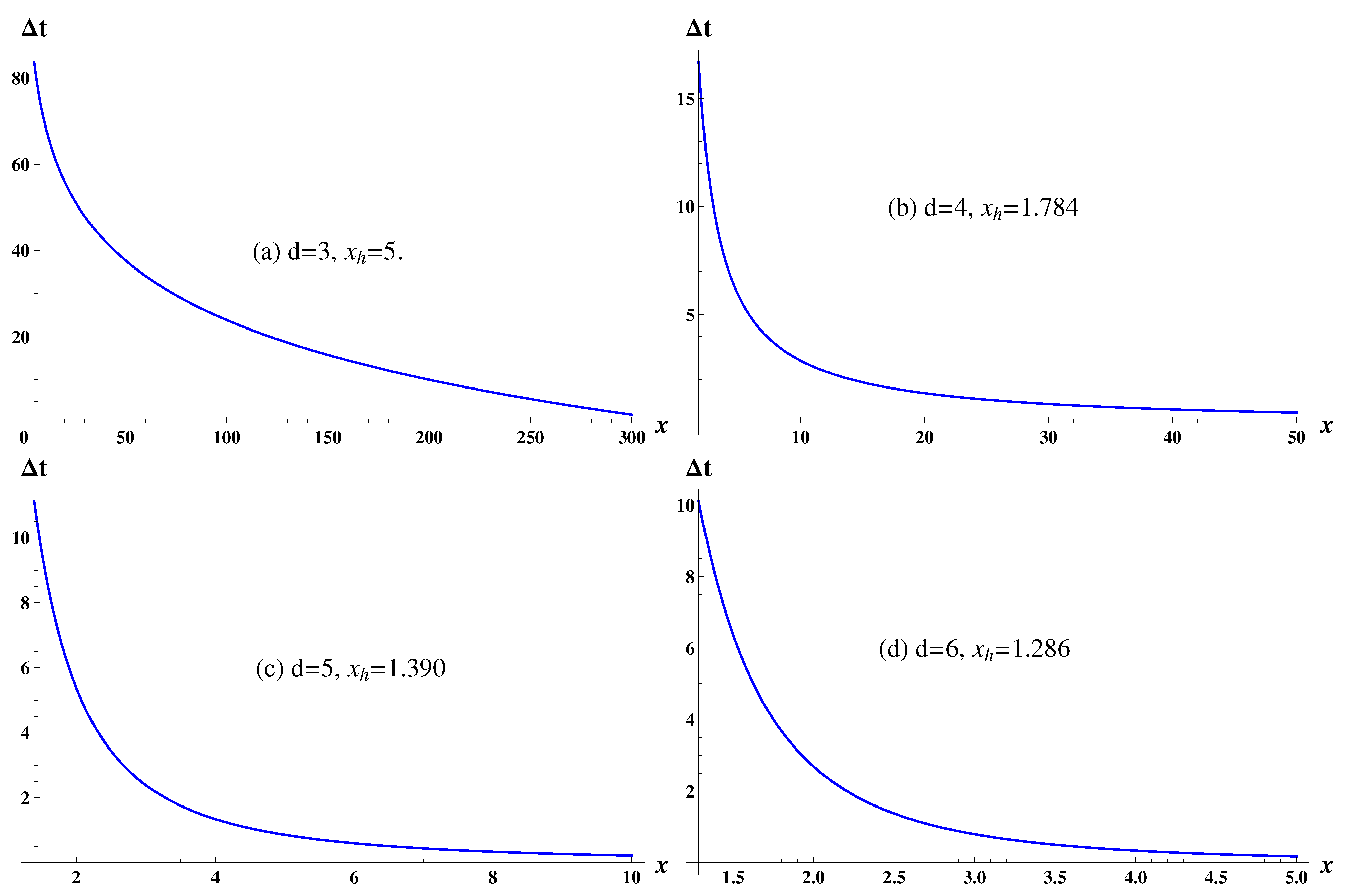
4.1. Gravitational Measurements
4.2. Determination of Lower Bounds
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCS | Coordinate Coherent State |
| GR | General Relativity |
| GPS | Global Positioning Systems |
| LIGO | Laser Interferometer Gravitational-Wave Observatory |
| NC | Non-Commutative |
| RN | Reisnner-Nordstrom |
References
- Kaluza, T. Zum Unitätsproblem der Physik. Int. J. Mod. Phys. D 2018, 27, 1870001. [Google Scholar] [CrossRef]
- Klein, O. Quantentheorie und funfdimensionale Relativititstheorie. Z. Phys. 1926, 37, 895. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef]
- Appelquist, T.; Cheng, H.C.; Dobrescu, B.A. Bounds on universal extra dimensions. Phys. Rev. D 2001, 64, 035002. [Google Scholar] [CrossRef]
- Giddings, S.B.; Thomas, S.D. High-energy colliders as black hole factories: The End of short distance physics. Phys. Rev. D 2002, 65, 056010. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Emparan, R. String balls at the LHC and beyond. Phys. Lett. B 2002, 526, 393. [Google Scholar] [CrossRef][Green Version]
- Nagano, M.; Watson, A.A. Observations and implications of the ultrahigh-energy cosmic rays. Rev. Mod. Phys. 2000, 72, 689. [Google Scholar] [CrossRef]
- Emparan, R.; Masip, M.; Rattazzi, R. Cosmic rays as probes of large extra dimensions and TeV gravity. Phys. Rev. D 2002, 65, 064023. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Landsberg, G.L. Black holes at the LHC. Phys. Rev. Lett. 2001, 87, 161602. [Google Scholar] [CrossRef] [PubMed]
- Cheung, K.M. Black hole production and large extra dimensions. Phys. Rev. Lett. 2002, 88, 221602. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.L.; Shapere, A.D. Black hole production by cosmic rays. Phys. Rev. Lett. 2002, 88, 021303. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Feng, J.L.; Goldberg, H.; Shapere, A.D. Black holes from cosmic rays: Probes of extra dimensions and new limits on TeV scale gravity. Phys. Rev. D 2002, 65, 124027. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. [LIGO Scientific and Virgo Collaborations], Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. [LIGO Scientific and Virgo Collaborations], GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. [LIGO Scientific and VIRGO Collaborations], GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. [LIGO Scientific and Virgo Collaborations], Binary Black Hole Mergers in the first Advanced LIGO Observing Run. Phys. Rev. X 2016, 6, 041015. [Google Scholar]
- Pound, R.V.; Rebka, G.A. Apparent Weight of Photons. Phys. Rev. Lett. 1960, 4, 337. [Google Scholar] [CrossRef]
- Dyson, F.W.; Eddington, A.S.; Davidson, C. A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29. Phil. Trans. R. Soc. Lond. A 1920, 220, 291. [Google Scholar]
- Peebles, P.J.E. Probing general relativity on the scales of cosmology. In Proceedings of the 17th International Conference on General Relativity and Gravitation (GR17), Dublin, Ireland, 18–24 July 2004. [Google Scholar]
- Song, Y.S.; Dore, O. A step towards testing general relativity using weak gravitational lensing and redshift surveys. JCAP 2009, 0903, 025. [Google Scholar] [CrossRef][Green Version]
- Fomalont, E.B.; Sramek, R.A. Measurements of the Solar Gravitational Deflection of Radio Waves in Agreement with General Relativity. Phys. Rev. Lett. 1976, 36, 1475. [Google Scholar] [CrossRef]
- Fomalont, E.; Kopeikin, S.; Lanyi, G.; Benson, J. Progress in Measurements of the Gravitational Bending of Radio Waves Using the VLBA. Astrophys. J. 2009, 699, 1395. [Google Scholar] [CrossRef]
- Bull, P. Extending cosmological tests of General Relativity with the Square Kilometre Array. Astrophys. J. 2016, 817, 26. [Google Scholar] [CrossRef]
- Rusin, D.; Kochanek, C.S.; Falco, E.E.; Keeton, C.R.; McLeod, B.A.; Impey, C.D.; Lehár, J.; Muñoz, J.A.; Peng, C.Y.; Rix, H.W. The Evolution of a mass-selected sample of early-type field galaxies. Astrophys. J. 2003, 587, 143. [Google Scholar] [CrossRef][Green Version]
- Reyes, R.; Mandelbaum, R.; Seljak, U.; Baldauf, T.; Gunn, J.E.; Lombriser, L.; Smith, R.E. Confirmation of general relativity on large scales from weak lensing and galaxy velocities. Nature 2010, 464, 256. [Google Scholar] [CrossRef]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef]
- Amenomori, M. [Tibet AS-gamma], Anisotropy and Corotation of Galactic Cosmic Rays. Science 2006, 314, 439–443. [Google Scholar] [CrossRef]
- Takamoto, M.; Hong, F.L.; Higashi, R.; Katori, H. An optical lattice clock. Nature 2005, 435, 321–324. [Google Scholar] [CrossRef]
- Ashby, N. Relativity in the Global Positioning System. Living Rev. Rel. 2003, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. JHEP 1999, 9909, 032. [Google Scholar] [CrossRef]
- Ardalan, F.; Arfaei, H.; Sheikh-Jabbari, M.M. Noncommutative geometry from strings and branes. JHEP 1999, 9902, 016. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Living Rev. Rel. 2013, 16, 5. [Google Scholar] [CrossRef] [PubMed]
- Connes, A.; Douglas, M.R.; Schwarz, A.S. Noncommutative geometry and matrix theory: Compactification on tori. JHEP 1998, 9802, 003. [Google Scholar] [CrossRef]
- Fatollahi, A.H.; Hajirahimi, M. Noncommutative Black-Body Radiation: Implications On Cosmic Microwave Background. EPL 2006, 75, 542. [Google Scholar] [CrossRef][Green Version]
- Zhang, B.; Cai, Q.Y.; Zhan, M.S.; You, L. Noncommutative information is revealed from Hawking radiation as tunneling. EPL 2011, 94, 20002. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized spacetime. Phys. Rev. 1947, 71, 38. [Google Scholar] [CrossRef]
- Doplicher, S.; Fredenhagen, K.; Roberts, J.E. The Quantum structure of spacetime at the Planck scale and quantum fields. Commun. Math. Phys. 1995, 172, 187. [Google Scholar] [CrossRef]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. B 2006, 632, 547. [Google Scholar] [CrossRef]
- Ansoldi, S.; Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired charged black holes. Phys. Lett. B 2007, 645, 261. [Google Scholar] [CrossRef]
- Alavi, S.A. Reissner-Nordstrom black hole in noncommutative spaces. Acta Phys. Polon. B 2009, 40, 2679. [Google Scholar]
- Rizzo, T.G. Noncommutative Inspired Black Holes in Extra Dimensions. JHEP 2006, 0609, 021. [Google Scholar] [CrossRef]
- Nozari, K.; Mehdipour, S.H. Noncommutative Inspired Reissner-Nordstrom Black Holes in Large Extra Dimensions. Commun. Theor. Phys. 2010, 53, 503. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A.; Nicolini, P. Non-commutative geometry inspired higher-dimensional charged black holes. Phys. Lett. B 2009, 670, 449. [Google Scholar] [CrossRef]
- Gingrich, D.M. Noncommutative geometry inspired black holes in higher dimensions at the LHC. JHEP 2010, 1005, 022. [Google Scholar] [CrossRef]
- Calmet, X. Cosmological constant and noncommutative spacetime. EPL 2007, 77, 19902. [Google Scholar] [CrossRef]
- Alavi, S.A.; Nasseri, F. Running of the spectral index in noncommutative inflation. Int. J. Mod. Phys. A 2005, 20, 4941. [Google Scholar] [CrossRef]
- Pramanik, S.; Das, S.; Ghosh, S. Noncommutative extension of AdS–CFT and holographic superconductors. Phys. Lett. B 2015, 742, 266. [Google Scholar] [CrossRef]
- Zeng, X.X.; Liu, X.M.; Liu, W.B. Holographic thermalization in noncommutative geometry. Phys. Lett. B 2015, 744, 48. [Google Scholar] [CrossRef][Green Version]
- Pramanik, S.; Ghosh, S. AdS-CFT Correspondence in Noncommutative background, related thermodynamics and Holographic Superconductor in Magnetic Field. Gen. Rel. Grav. 2019, 51, 7. [Google Scholar] [CrossRef]
- Nicolini, P.; Spallucci, E. Noncommutative geometry inspired wormholes and dirty black holes. Class. Quantum Gravity 2010, 27, 015010. [Google Scholar] [CrossRef]
- Liang, J.; Liu, B. Thermodynamics of noncommutative geometry inspired BTZ black hole based on Lorentzian smeared mass distribution. EPL 2012, 100, 30001. [Google Scholar] [CrossRef]
- Ghosh, S.G. Noncommutative geometry inspired Einstein–Gauss–Bonnet black holes. Class. Quantum Gravity 2018, 35, 085008. [Google Scholar] [CrossRef]
- Wei, S.W.; Cheng, P.; Zhong, Y.; Zhou, X.N. Shadow of noncommutative geometry inspired black hole. JCAP 2015, 1508, 004. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.W.; Park, Y.J. Thermodynamics and evaporation of the noncommutative black hole. JHEP 2007, 0702, 012. [Google Scholar] [CrossRef]
- Nozari, K.; Akhshabi, S. Orbits of particles in noncommutative Schwarzschild spacetime. EPL 2007, 80, 20002. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R.; Samanta, S. Noncommutative Black Hole Thermodynamics. Phys. Rev. D 2008, 77, 124035. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R.; Modak, S.K. Noncommutative Schwarzschild Black Hole and Area Law. Class. Quantum Gravity 2009, 26, 085010. [Google Scholar] [CrossRef]
- Miao, Y.G.; Xu, Z.M. Thermodynamics of noncommutative high-dimensional AdS black holes with non-Gaussian smeared matter distributions. Eur. Phys. J. C 2016, 76, 217. [Google Scholar] [CrossRef]
- Tanaka, Y.; Nandra, K.; Fabian, A.C.; Inoue, H.; Otani, C.; Dotani, T.; Hayashida, K.; Iwasawa, K.; Kii, T.; Makino, F.; et al. Gravitationally Redshifted Emission Implying an Accretion Disk and Massive Black Hole in the Active Galaxy MCG:-6-30-15. Nature 1995, 375, 659. [Google Scholar] [CrossRef]
- Yaqoob, T.; George, I.M.; Turner, T.J.; Nandra, K.; Ptak, A.; Serlemitsos, P.J. A peculiar emission line feature in the X-ray spectrum of the quasar pks 0637-752. Astrophys. J. Lett. 1998, 505, L87. [Google Scholar] [CrossRef]
- Connell, P.; Frolov, V.P. Ray-tracing in four and higher dimensional black holes: An Analytical approximation. Phys. Rev. D 2008, 78, 024032. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Frame-dragging and bending of light in Kerr and Kerr-(anti) de Sitter spacetimes. Class. Quantum Gravity 2005, 22, 4391–4424. [Google Scholar] [CrossRef]
- Briet, J.; Hobill, D. Determining the Dimensionality of Spacetime by Gravitational Lensing. arXiv 2008, arXiv:0801.3859. [Google Scholar]
- Bin-Nun, A.Y. Lensing By Sgr A* as a Probe of Modified Gravity. Phys. Rev. D 2010, 82, 064009. [Google Scholar] [CrossRef]
- Pardo, K.; Fishbach, M.; Holz, D.E.; Spergel, D.N. Limits on the number of spacetime dimensions from GW170817. JCAP 2018, 1807, 048. [Google Scholar] [CrossRef]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 208. [Google Scholar] [CrossRef]
- Karimabadi, M.; Alavi, S.A.; Yekta, D.M. Non-commutative effects on gravitational measurements. Class. Quantum Gravity 2020, 37, 8. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636. [Google Scholar] [CrossRef]
- Myers, R.C. Stress tensors and Casimir energies in the AdS / CFT correspondence. Phys. Rev. D 1999, 60, 046002. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black Holes in Higher Dimensional spacetimes. Ann. Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Scardigli, F.; Casadio, R. Generalized uncertainty principle, extra dimensions and holography. Class. Quantum Gravity 2003, 20, 3915. [Google Scholar] [CrossRef]
- Nouicer, K. Black holes thermodynamics to all order in the Planck length in extra dimensions. Class. Quantum Gravity 2007, 24, 5917. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. Black Holes in Higher Dimensions. Living Rev. Rel. 2008, 11, 6. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108–1118. [Google Scholar] [CrossRef]
- Scardigli, F.; Casadio, R. Gravitational tests of the Generalized Uncertainty Principle. Eur. Phys. J. C 2015, 75, 425. [Google Scholar] [CrossRef]
- Liddle, A.R.; Green, A.M. Cosmological constraints from primordial black holes. Phys. Rept. 1998, 307, 125–131. [Google Scholar] [CrossRef]
- Sato-Polito, G.; Kovetz, E.D.; Kamionkowski, M. Constraints on the primordial curvature power spectrum from primordial black holes. Phys. Rev. D 2019, 100, 063521. [Google Scholar] [CrossRef]
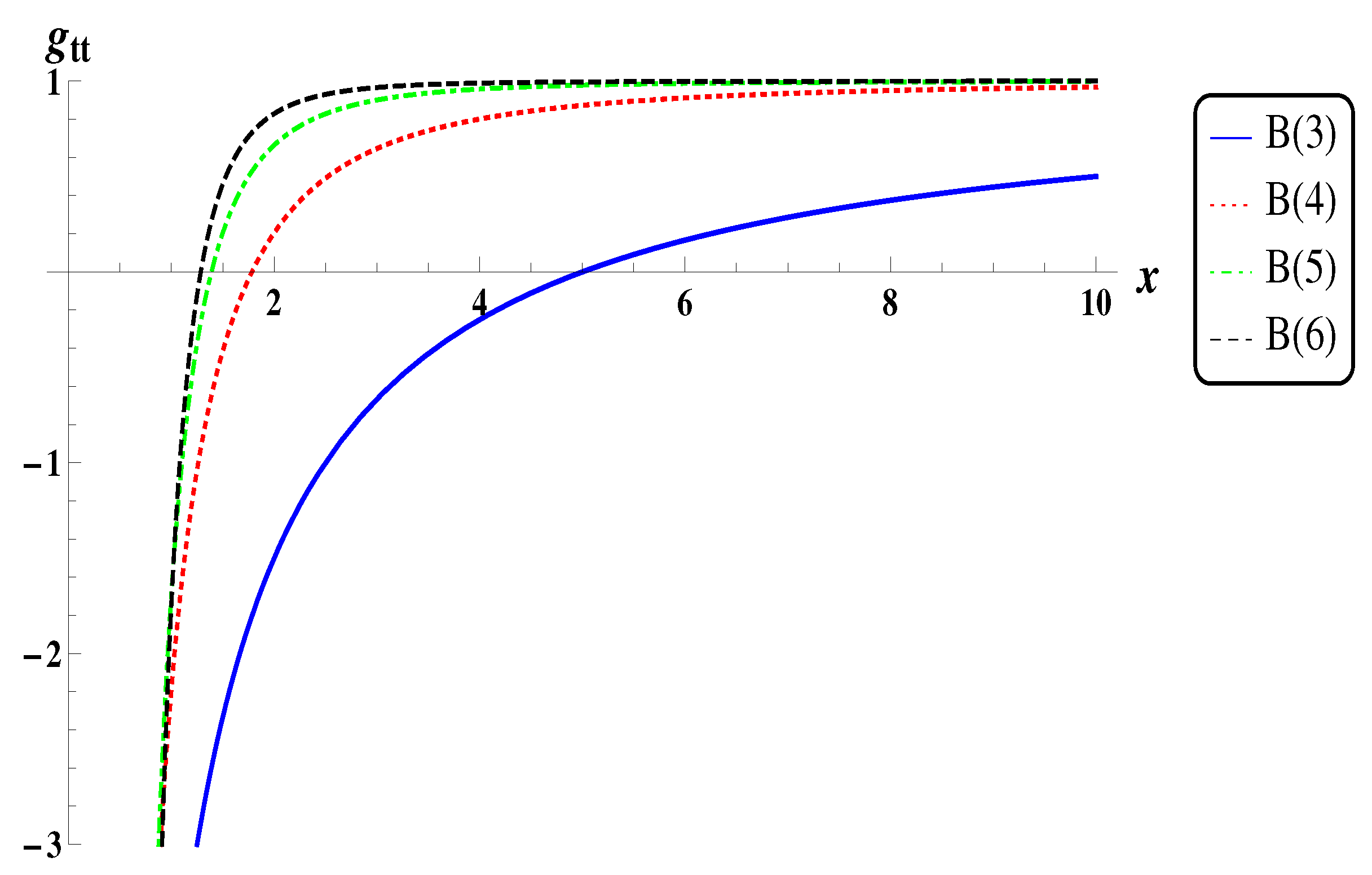
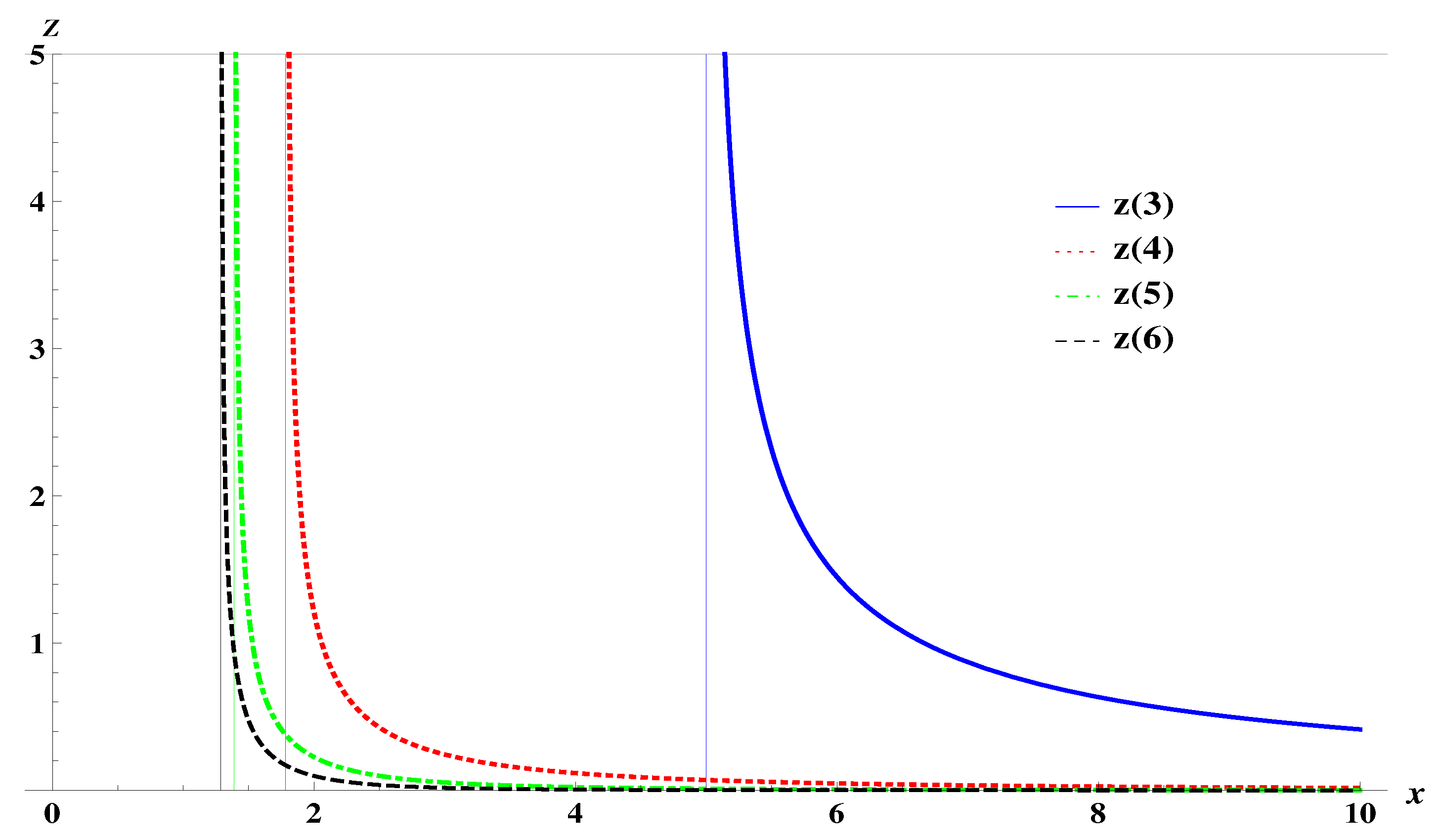
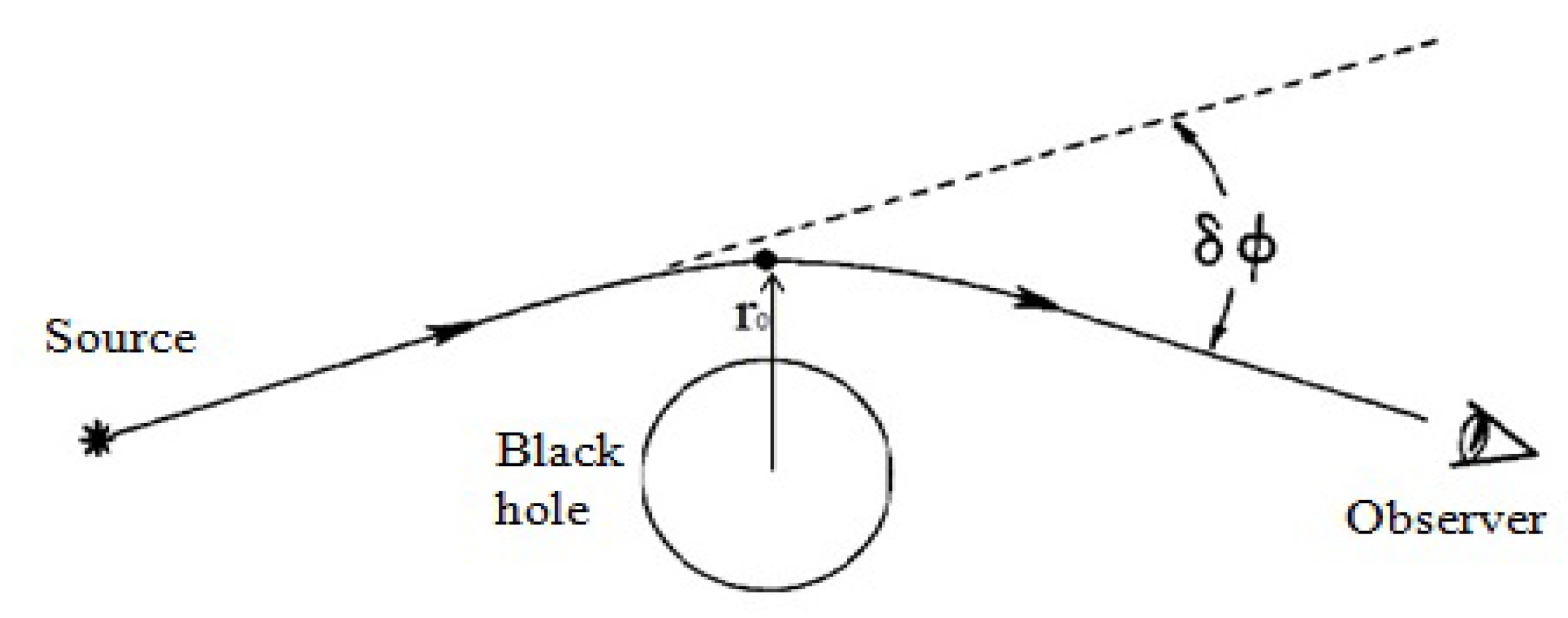
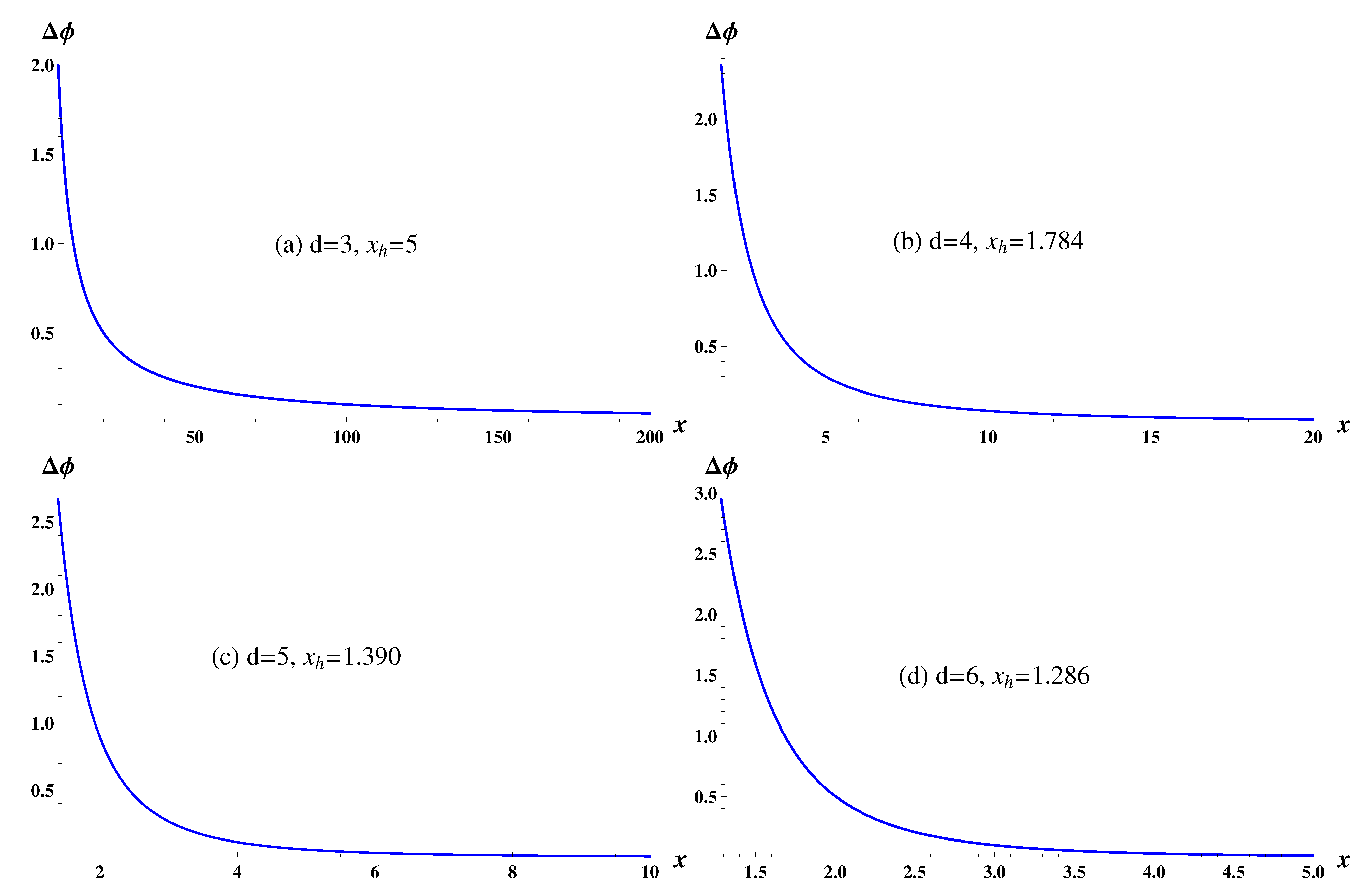

| d | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| d | ||
|---|---|---|
| 4 | 2.68 | |
| 5 | 2.51 | |
| 6 | 2.41 | |
| 7 | 2.34 | |
| 8 | 2.29 | |
| 9 | 2.26 |
| d | M(kg) |
|---|---|
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yekta, D.M.; Alavi, S.A.; Karimabadi, M. Gravitational Measurements in Higher Dimensions. Galaxies 2021, 9, 4. https://doi.org/10.3390/galaxies9010004
Yekta DM, Alavi SA, Karimabadi M. Gravitational Measurements in Higher Dimensions. Galaxies. 2021; 9(1):4. https://doi.org/10.3390/galaxies9010004
Chicago/Turabian StyleYekta, Davood Mahdavian, Seyed Aliasghar Alavi, and Majid Karimabadi. 2021. "Gravitational Measurements in Higher Dimensions" Galaxies 9, no. 1: 4. https://doi.org/10.3390/galaxies9010004
APA StyleYekta, D. M., Alavi, S. A., & Karimabadi, M. (2021). Gravitational Measurements in Higher Dimensions. Galaxies, 9(1), 4. https://doi.org/10.3390/galaxies9010004





