Numerical Simulations of Jets from Active Galactic Nuclei
Abstract
1. Introduction
2. Observations and Theoretical Models
2.1. Models of Jet Formation
2.2. Parsec-Scale Jets and Superluminal Radio Sources
2.3. Kiloparsec-Scale Jets
2.4. AGN Jets in the Cosmological Context
3. Simulations of Jet Formation
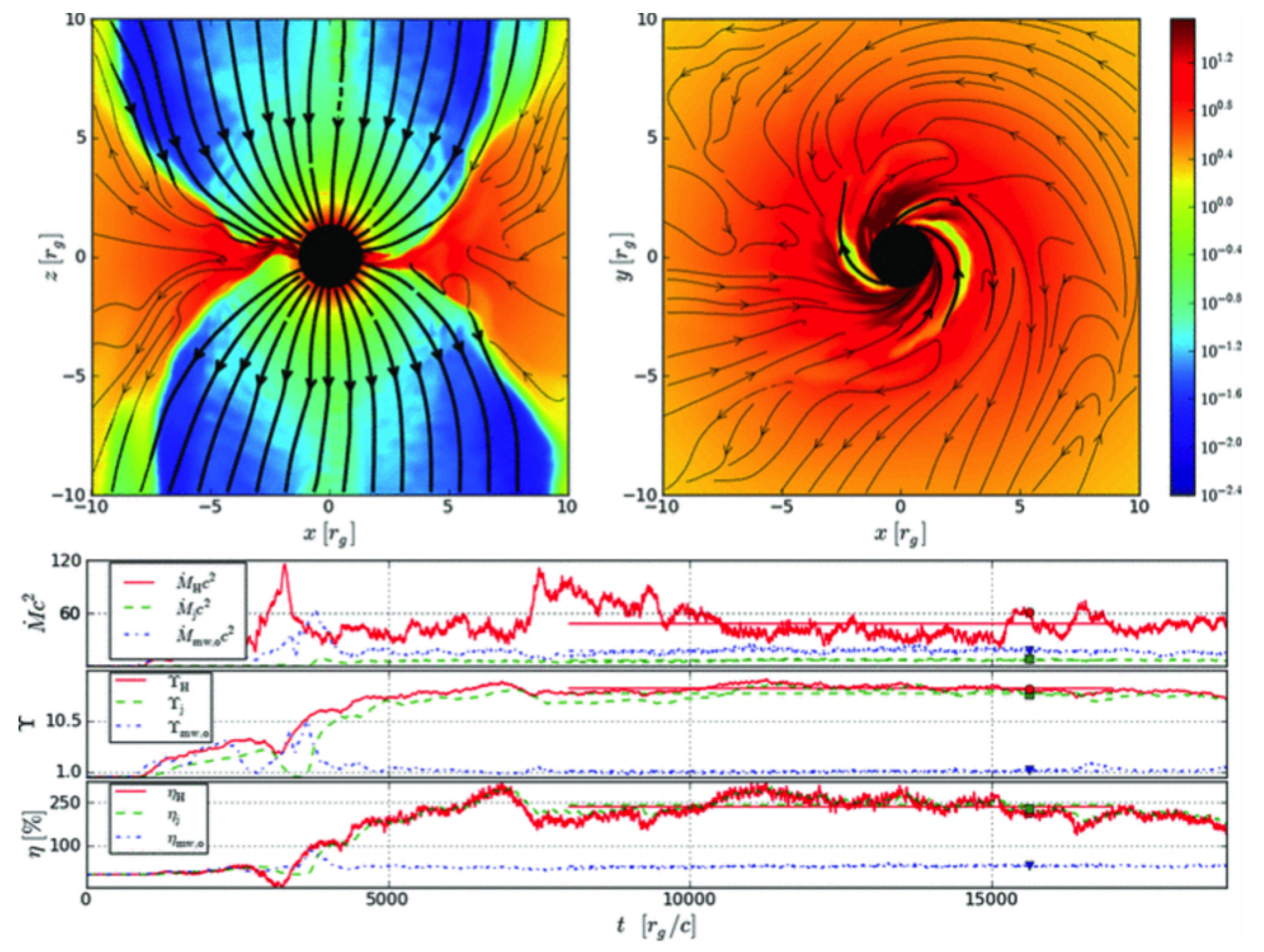
3.1. Jet Formation Mechanisms on the Test Bench
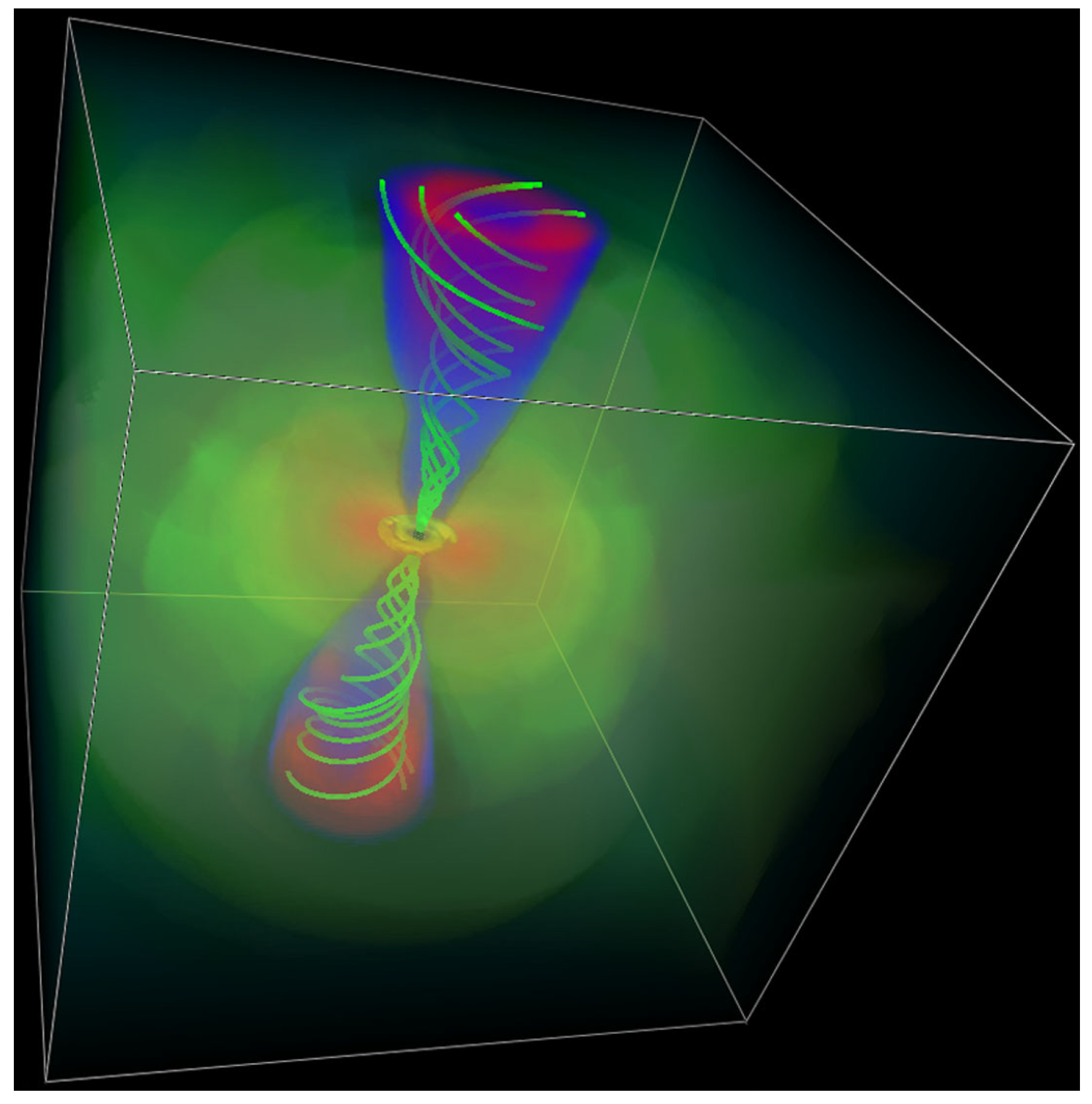
3.2. Long-Term Simulations of Jet Formation
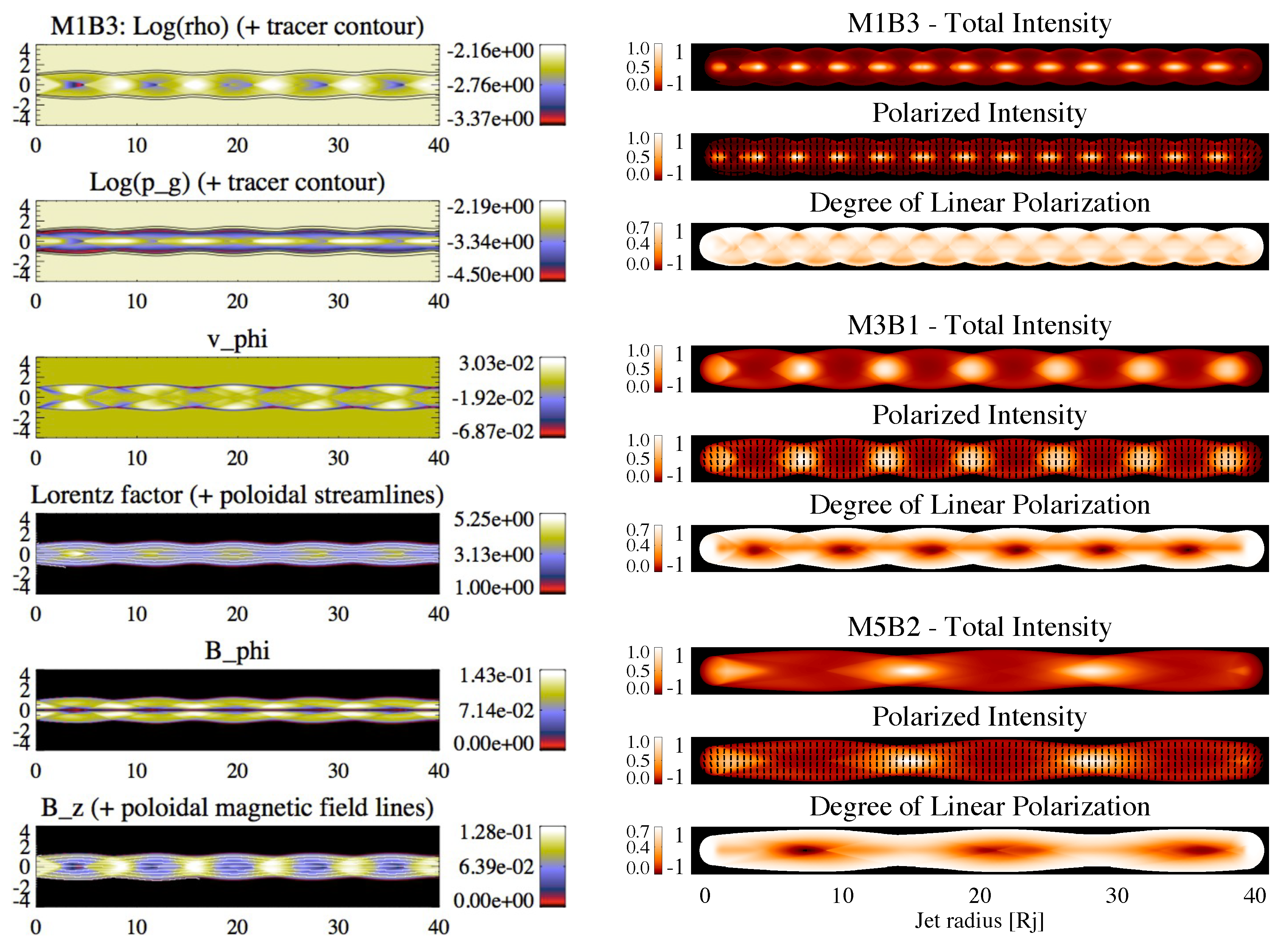
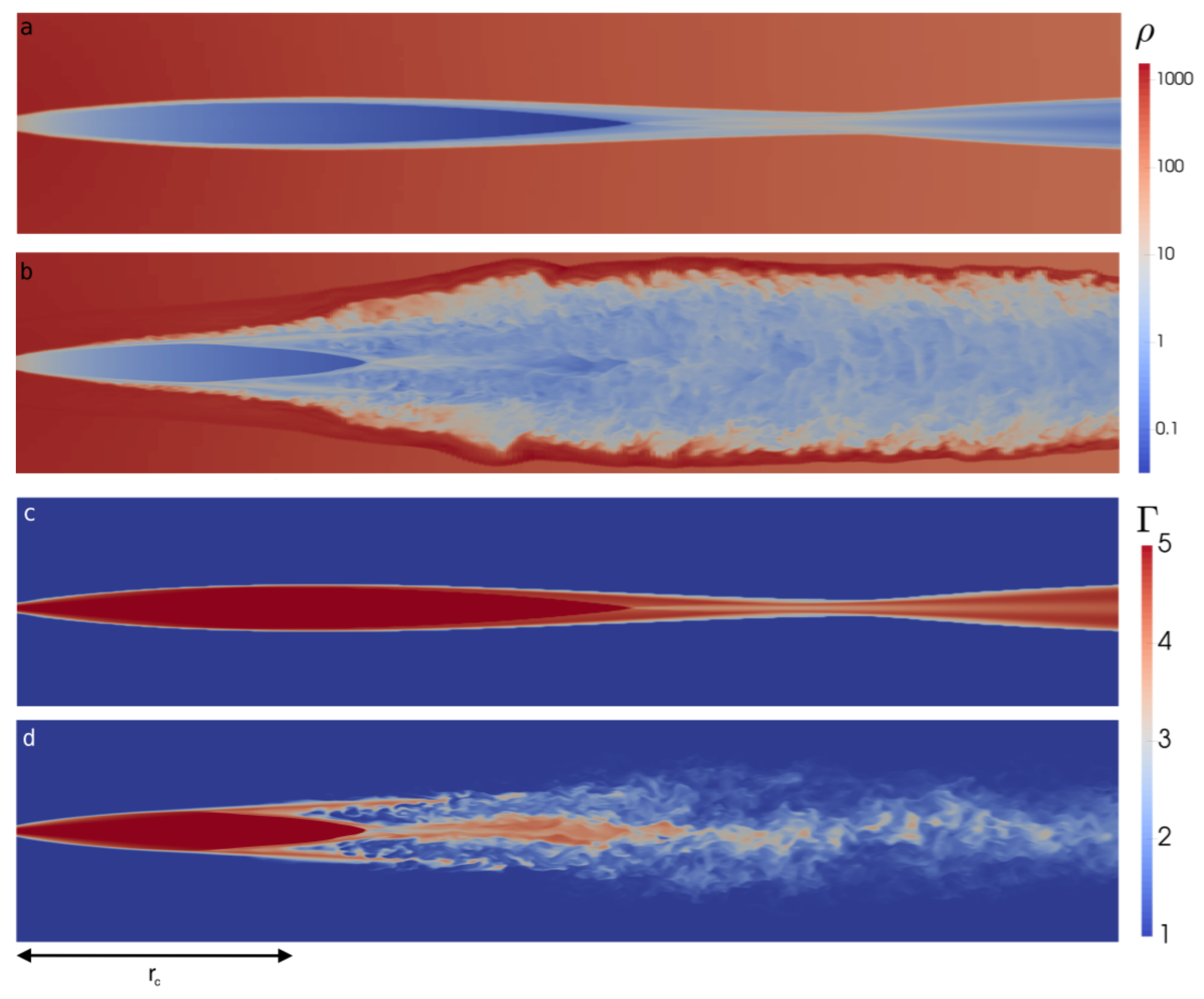
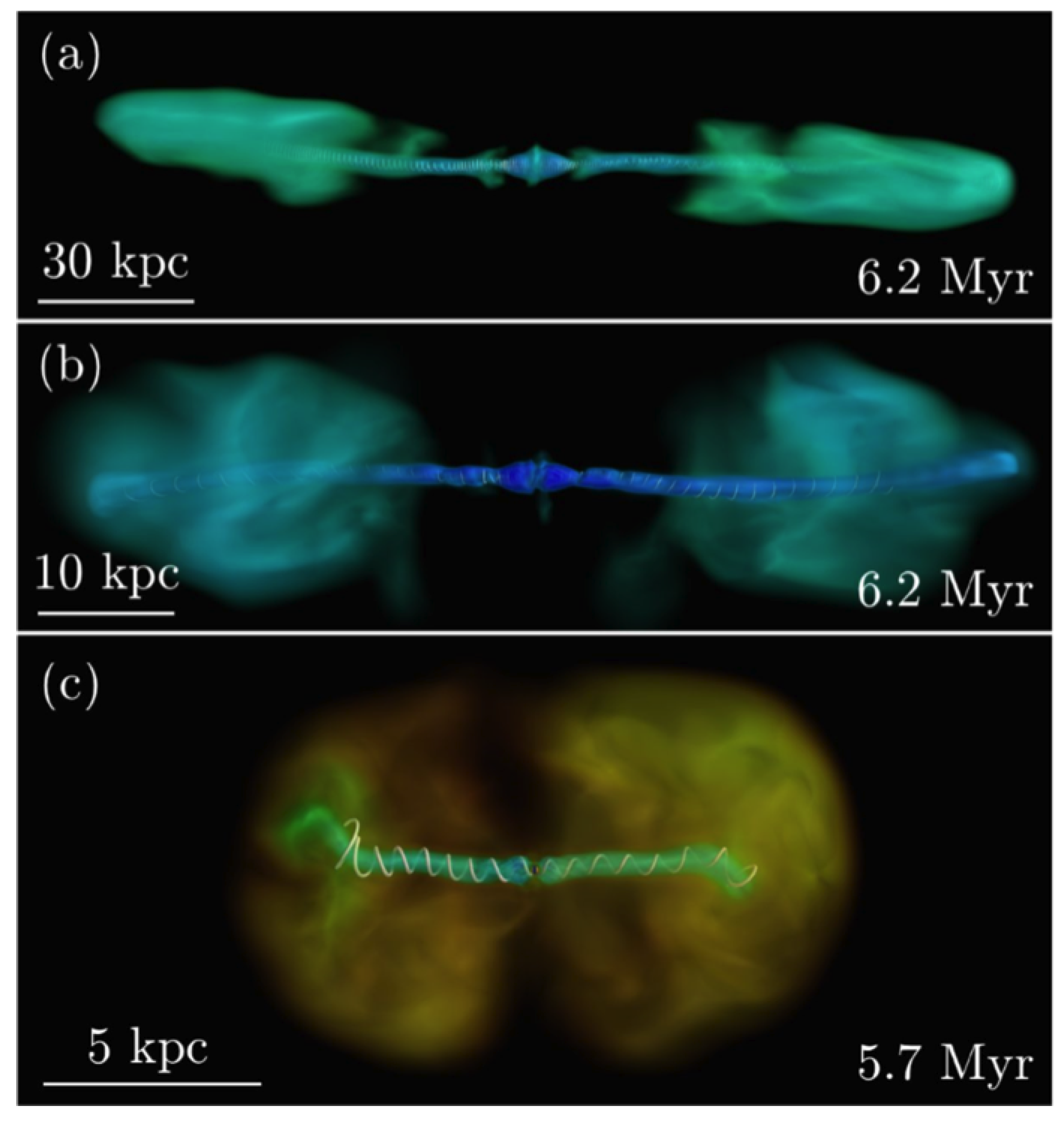
3.3. Current-Driven Kink Instability and Magnetic Energy Dissipation
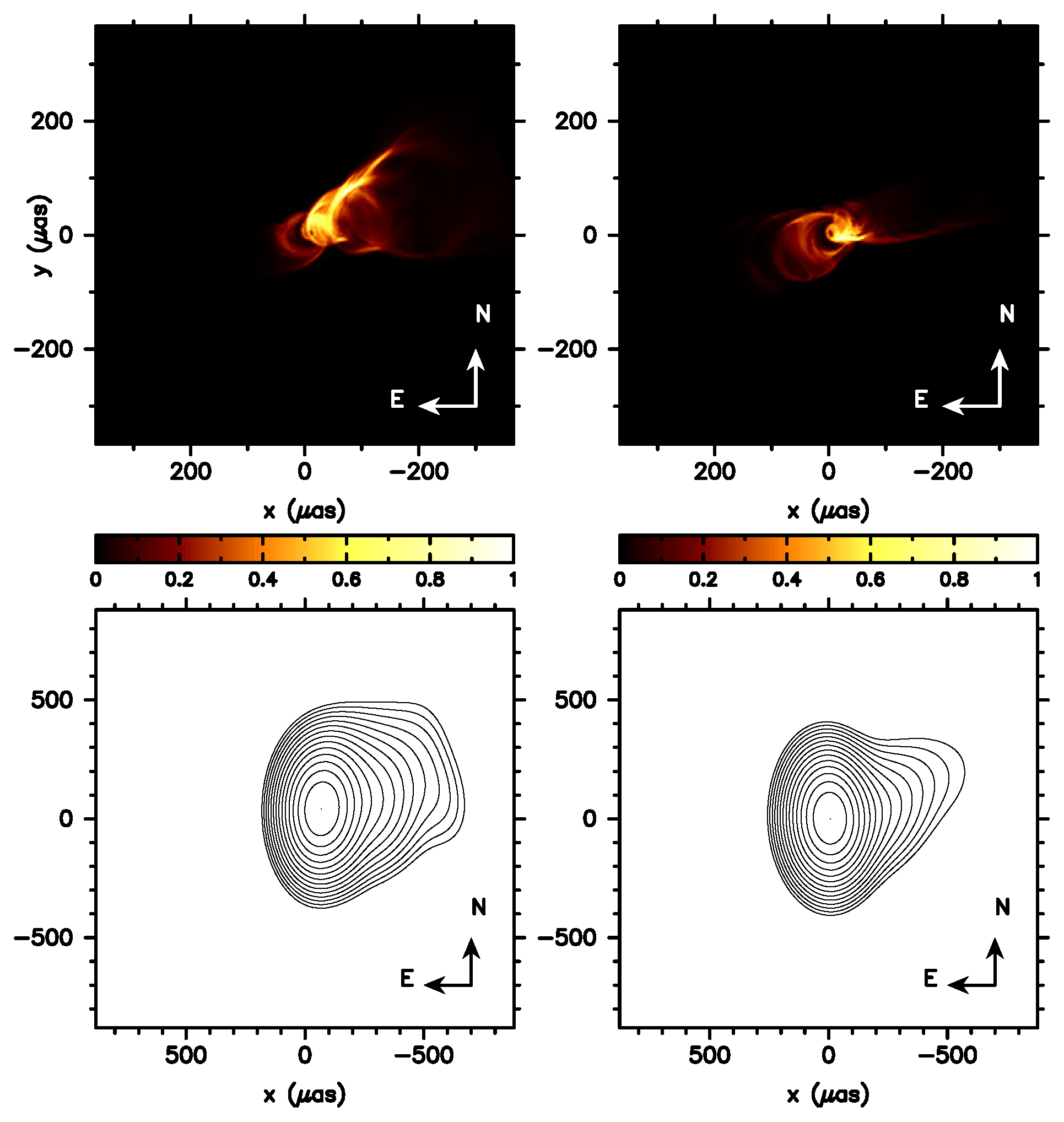
3.4. General Relativistic Radiative Transfer Simulations
4. Simulations of Jets at Parsec and Subparsec Scales
4.1. (Magneto-)Hydrodynamical Simulations
4.2. Instabilities
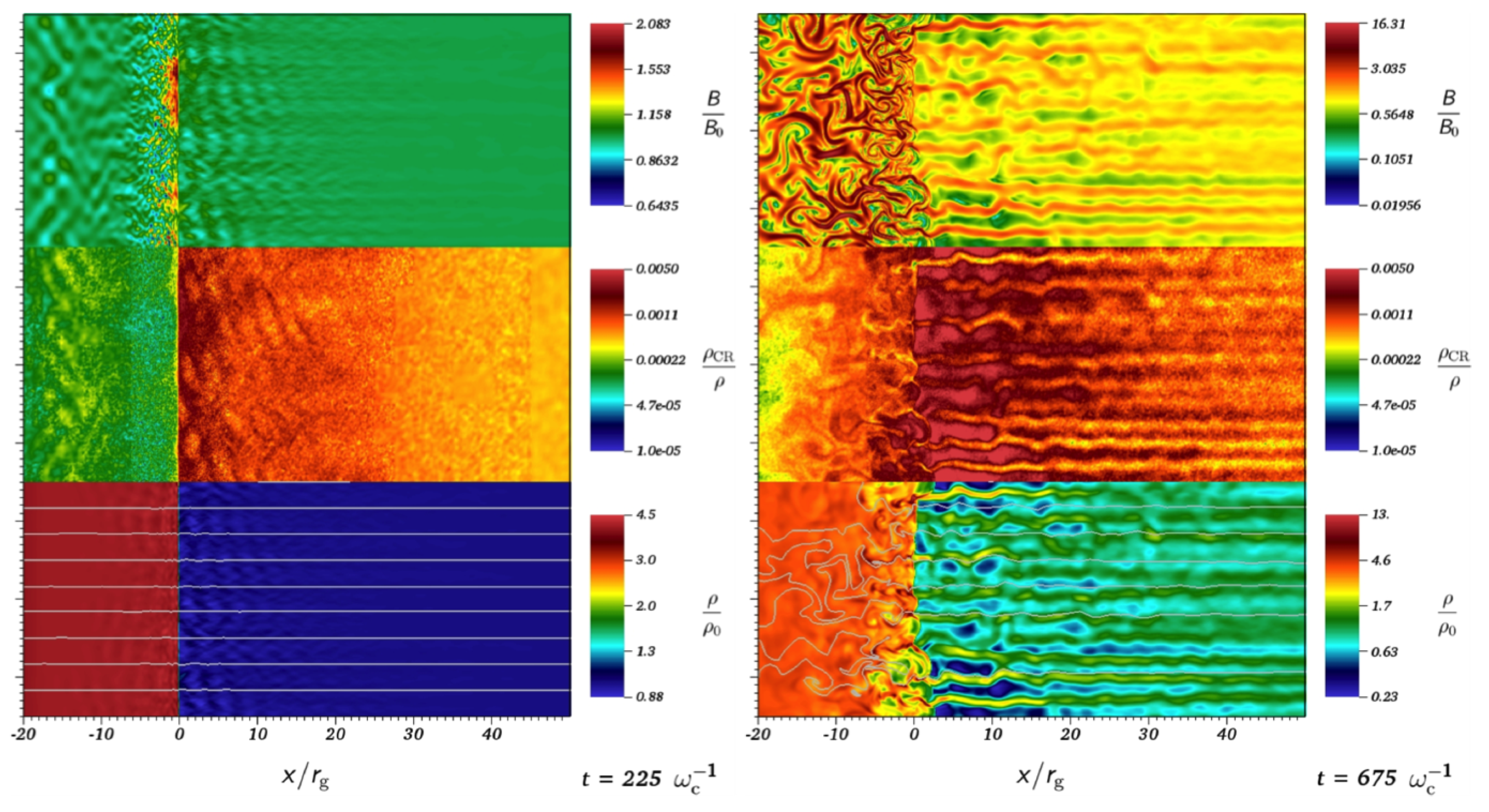
4.3. Microphysics
5. Simulations of Kiloparsec-Scale Jets
5.1. Morphology and Dynamics of kpc-Jets
5.2. Large-Scale Simulations of kpc-Jets and the FR I/FR II Dichotomy
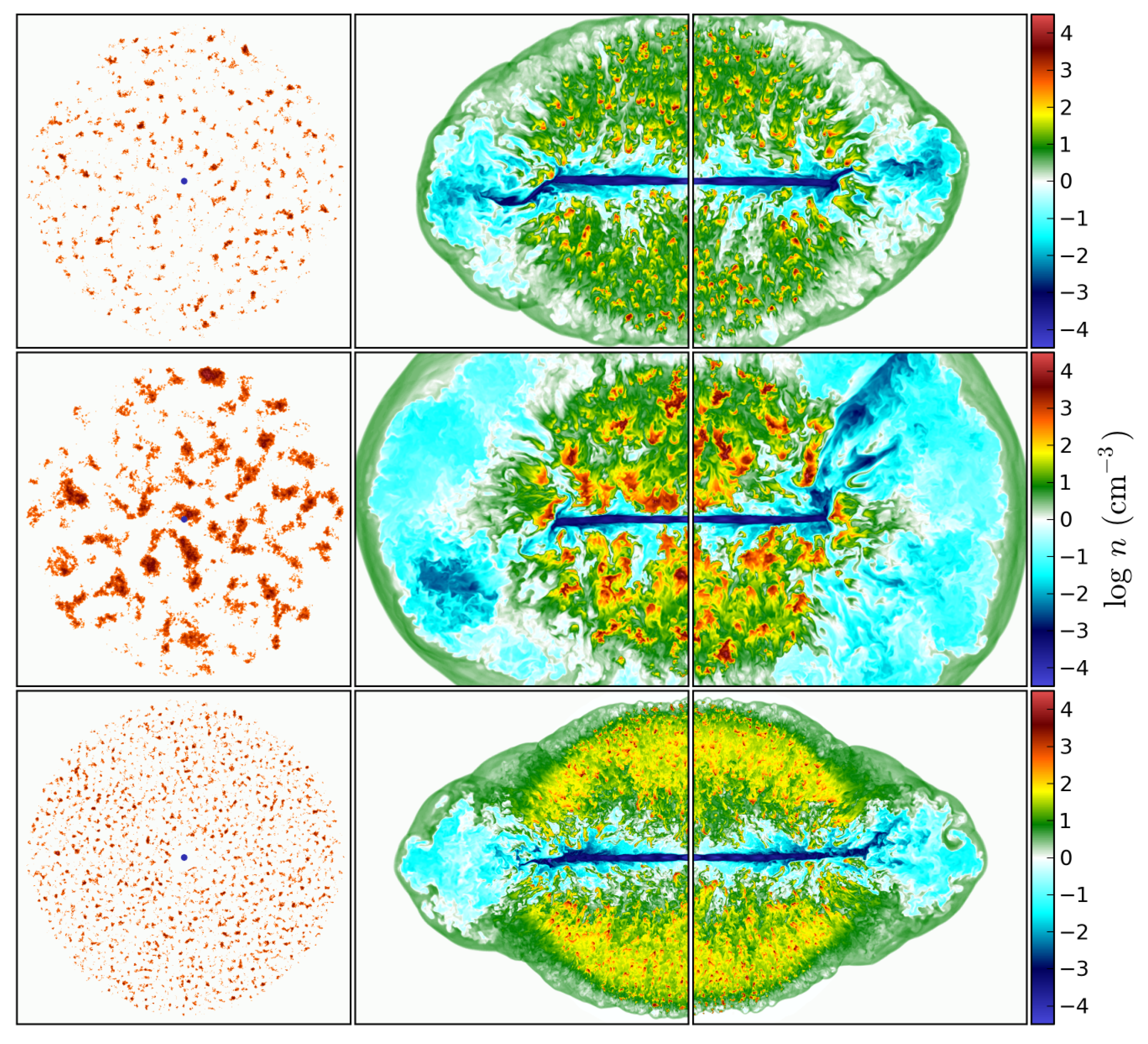
5.3. AGN Feedback
6. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Norman, M.L.; Winkler, K.-H.A.; Smarr, L.; Smith, M.D. Structure and dynamics of supersonic jets. Astron. Astrophys. 1982, 113, 285–302. [Google Scholar]
- Scheuer, P.A.G. Models of extragalactic radio sources with a continuous energy supply from a central object. Mon. Not. R. Astron. Soc. 1974, 166, 513–528. [Google Scholar] [CrossRef]
- Blandford, R.D.; Rees, M.J. A ’twin-exhaust’ model for double radio sources. Mon. Not. R. Astron. Soc. 1974, 169, 395–415. [Google Scholar] [CrossRef]
- Hawley, J.F.; Fendt, C.; Hardcastle, M.; Nokhrina, E.; Tchekhovskoy, A. Disks and Jets. Gravity, Rotation and Magnetic Fields. Space Sci. Rev. 2015, 191, 441–469. [Google Scholar] [CrossRef]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Theory of extragalactic radio sources. Rev. Mod. Phys. 1984, 56, 255–351. [Google Scholar] [CrossRef]
- Leahy, J.P. Interpretation of large scale extragalactic jets. In Beams and Jets in Astrophysics; Hughes, P.A., Ed.; Cambridge University Press: Cambridge, UK, 1991; pp. 100–186. ISBN 0 521 33576 0. [Google Scholar]
- Böttcher, M.; Harris, D.E.; Krawczynski, H. Relativistic Jets from Active Galactic Nuclei; Wiley-VCH: Weinheim, Germany, 2012; ISBN 978-3-527-41037-8. [Google Scholar]
- Martí, J.M.; Müller, E. Grid-based Methods in Relativistic Hydrodynamics and Magnetohydrodynamics. Living Rev. Comput. Astrophys. 2015, 1. [Google Scholar] [CrossRef] [PubMed]
- Font, J.A. Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity. Living Rev. Relativ. 2008, 11. [Google Scholar] [CrossRef]
- Lovelace, R.V.E. Dynamo model of double radio sources. Nature 1976, 262, 649–652. [Google Scholar] [CrossRef]
- Blandford, R.D. Accretion disc electrodynamics—A model for double radio sources. Mon. Not. R. Astron. Soc. 1976, 176, 465–481. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Chiueh, T.; Begelman, M.C. Electromagnetically driven relativistic jets—A class of self-similar solutions. Astrophys. J. 1992, 394, 459–471. [Google Scholar] [CrossRef]
- Vlahakis, N.; Königl, A. Relativistic Magnetohydrodynamics with Application to Gamma-Ray Burst Outflows. I. Theory and Semianalytic Trans-Alfvénic Solutions. Astrophys. J. 2003, 596, 1080–1103. [Google Scholar] [CrossRef]
- Vlahakis, N.; Königl, A. Magnetic Driving of Relativistic Outflows in Active Galactic Nuclei. I. Interpretation of Parsec-Scale Accelerations. Astrophys. J. 2004, 605, 656–661. [Google Scholar] [CrossRef]
- Beskin, V.S.; Nokhrina, E.E. The effective acceleration of plasma outflow in the paraboloidal magnetic field. Mon. Not. R. Astron. Soc. 2006, 367, 375–386. [Google Scholar] [CrossRef]
- Lyubarsky, Y. Asymptotic Structure of Poynting-Dominated Jets. Astrophys. J. 2009, 698, 1570–1589. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Hirotani, K.; Takahashi, M.; Nitta, S.-Y.; Tomimatsu, A. Accretion in a Kerr black hole magnetosphere—Energy and angular momentum transport between the magnetic field and the matter. Astrophys. J. 1992, 386, 455–463. [Google Scholar] [CrossRef]
- Komissarov, S.S. Central Engines: Acceleration, Collimation and Confinement of Jets. In Relativistic Jets from Active Galactic Nuclei; Böttcher, M., Harris, D.E., Krawczynski, H., Eds.; Wiley-VCH: Weinheim, Germany, 2012; pp. 3–16. ISBN 978-3-527-41037-8. [Google Scholar]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817. [Google Scholar] [CrossRef]
- Fish, V.L.; Akiyama, K.; Bouman, K.L.; Chael, A.; Johnson, M.; Doeleman, S.; Blackburn, L.; Wardle, J.; Freeman, W. The Event Horizon Telescope Collaboration. Observing—And Imaging—Active Galactic Nuclei with the Event Horizon Telescope. Galaxies 2016, 4, 54. [Google Scholar] [CrossRef]
- Lister, M.L.; Cohen, M.H.; Homan, D.C.; Kadler, M.; Kellermann, K.I.; Kovalev, Y.Y.; Ros, E.; Savolainen, T.; Zensus, J.A. MOJAVE: Monitoring of jets in Active Galactic Nuclei with VLBA experiments. VI. Kinematic analysis of a complete sample of blazar jets. Astron. J. 2009, 138, 1874–1892. [Google Scholar] [CrossRef]
- Blandford, R.D.; Königl, A. Relativistic Jets as Compact Radio Sources. Astrophys. J. 1979, 232, 34–48. [Google Scholar] [CrossRef]
- Rees, M.J. Appearance of Relativistically Expanding Radio Sources. Nature 1966, 211, 468–470. [Google Scholar] [CrossRef]
- Marscher, A.P.; Gear, W.K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. Astrophys. J. 1985, 298, 114–127. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; Gómez, J.L.; Aller, M.F.; Teräsranta, H.; Lister, M.L.; Stirling, A.M. Observational evidence for the accretion-disk origin for a radio jet in an active galaxy. Nature 2002, 417, 625–627. [Google Scholar] [CrossRef] [PubMed]
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, R.; Marscher, A.P.; Jorstad, S.G.; Markowitz, A.; Rivers, E.; Rothschild, R.E.; McHardy, I.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; et al. Connection between the accretion disk and jet in the radio galaxy 3C 111. Astrophys. J. 2011, 734. [Google Scholar] [CrossRef]
- Cawthorne, T.V.; Jorstad, S.G.; Marscher, A.P. Evidence for Recollimation Shocks in the Core of 1803+784. Astrophys. J. 2013, 772. [Google Scholar] [CrossRef]
- Daly, R.A.; Marscher, A.P. The gasdynamics of compact relativistic jets. Astrophys. J. 1988, 334, 539–551. [Google Scholar] [CrossRef]
- Asada, K.; Nakamura, M. The Structure of the M 87 Jet: A Transition from Parabolic to Conical Streamlines. Astrophys. J. 2012, 745. [Google Scholar] [CrossRef]
- Boccardi, B.; Krichbaum, T.P.; Bach, U.; Mertens, F.; Ros, E.; Alef, W.; Zensus, J.A. The stratified two-sided jet of Cygnus A. Acceleration and collimation. Astron. Astrophys. 2016, 585. [Google Scholar] [CrossRef]
- Nagai, H.; Haga, T.; Giovannini, G.; Doi, A.; Orienti, M.; D’Ammando, F.; Kino, M.; Nakamura, M.; Asada, K.; Hada, K.; Giroletti, M. Limb-brightened Jet of 3C 84 Revealed by the 43 GHz Very-Long-Baseline-Array Observation. Astrophys. J. 2014, 785. [Google Scholar] [CrossRef]
- Mertens, F.; Lobanov, A.P.; Walker, R.C.; Hardee, P.E. Kinematics of the jet in M 87 on scales of 100–1000 Schwarzschild radii. Astron. Astrophys. 2016, 595. [Google Scholar] [CrossRef]
- Lobanov, A.P.; Zensus, J.A. A Cosmic Double Helix in the Archetypical Quasar 3C 273. Science 2001, 294, 128–131. [Google Scholar] [CrossRef] [PubMed]
- Gabuzda, D.C.; Vitrishchak, V.M.; Mahmud, M.; O’Sullivan, S. Radio circular polarization produced in helical magnetic fields in eight active galactic nuclei. Mon. Not. R. Astron. Soc. 2008, 384, 1003–1014. [Google Scholar] [CrossRef]
- Homan, D.C.; Lister, M.L.; Aller, H.D.; Aller, M.F.; Wardle, J.F.C. Full Polarization Spectra of 3C 279. Astrophys. J. 2009, 696, 328–347. [Google Scholar] [CrossRef]
- Potter, W.J.; Cotter, G. New constraints on the structure and dynamics of black hole jets. Mon. Not. R. Astron. Soc. 2015, 453, 4070–4088. [Google Scholar] [CrossRef]
- Böttcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-detected Blazars. Astrophys. J. 2013, 768. [Google Scholar] [CrossRef]
- The MAGIC Collaboration. The blazar TXS 0506+056 associated with a high-energy neutrino: Insights into extragalactic jets and cosmic ray acceleration. Astrophys. J. 2018, 863. [Google Scholar] [CrossRef]
- Laing, R.A. Magnetic fields in extragalactic radio sources. Astrophys. J. 1981, 248, 87–104. [Google Scholar] [CrossRef]
- Asada, K.; Inoue, M.; Uchida, Y.; Kameno, S.; Fujisawa, K.; Iguchi, S.; Mutoh, M. A Helical Magnetic Field in the Jet of 3C 273. Publ. Astron. Soc. Jpn. 2002, 54, L39–L43. [Google Scholar] [CrossRef]
- Hovatta, T.; Lister, M.L.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kovalev, Y.Y.; Pushkarev, A.B.; Savolainen, T. MOJAVE: Monitoring of Jets in Active Galactic Nuclei with VLBA Experiments. VIII. Faraday Rotation in Parsec-scale AGN Jets. Astron. J. 2012, 144. [Google Scholar] [CrossRef]
- Zamaninasab, M.; Savolainen, T.; Clausen-Brown, E.; Hovatta, T.; Lister, M.L.; Krichbaum, T.P.; Kovalev, Y.Y.; Pushkarev, A.B. Evidence for a large-scale helical magnetic field in the quasar 3C 454.3. Mon. Not. R. Astron. Soc. 2013, 436, 3351–3356. [Google Scholar] [CrossRef]
- Fanaroff, B.L.; Riley, J.M. The morphology of extragalactic radio sources of high and low luminosity. Mon. Not. R. Astron. Soc. 1974, 167, 31P–36P. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Relativistic models and the jet velocity field in the radio galaxy 3C 31. Mon. Not. R. Astron. Soc. 2002, 336, 328–352. [Google Scholar] [CrossRef]
- Carilli, C.L.; Barthel, P.D. Cygnus A. Astron. Astrophys. Rev. 1996, 7, 1–54. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H. Systematic properties of decelerating relativistic jets in low-luminosity radio galaxies. Mon. Not. R. Astron. Soc. 2014, 437, 3405–3441. [Google Scholar] [CrossRef]
- Bridle, A.H.; Hough, D.H.; Lonsdale, C.J.; Burns, J.O.; Laing, R.A. Deep VLA Imaging of Twelve Extended 3CR Sample. Astron. J. 1994, 108, 766–820. [Google Scholar] [CrossRef]
- Ledlow, M.J.; Owen, F.N. 20 CM VLA Survey of Abell Clusters of Galaxies. VI. Radio/Optical Luminosity Functions. Astron. J. 1996, 112, 9–22. [Google Scholar] [CrossRef]
- Baan, W.A. Fluid jets in radio sources. Astrophys. J. 1980, 239, 433–444. [Google Scholar] [CrossRef]
- Bicknell, G.V. A model for the surface brightness of a turbulent low Mach number jet. I—Theoretical development and application to 3C 31. Astrophys. J. 1984, 286, 68–87. [Google Scholar] [CrossRef]
- De Young, D.S. Emission line regions and stellar associations in extended extragalactic radio sources. Nature 1981, 293, 43–44. [Google Scholar] [CrossRef]
- Komissarov, S.S. Mass-Loaded Relativistic Jets. Mon. Not. R. Astron. Soc. 1994, 269, 394–402. [Google Scholar] [CrossRef]
- Fabian, A.C. Observational Evidence of Active Galactic Nuclei Feedback. Ann. Rev. Astron. Astrophys. 2012, 50, 455–489. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Fabian, A.C. Investigating AGN heating in a sample of nearby clusters. Mon. Not. R. Astron. Soc. 2006, 373, 959–971. [Google Scholar] [CrossRef]
- Rafferty, D.A.; McNamara, B.R.; Nulsen, P.E.J.; Wise, M.W. The Feedback-regulated Growth of Black Holes and Bulges through Gas Accretion and Starbursts in Cluster Central Dominant Galaxies. Astrophys. J. 2006, 652, 216–231. [Google Scholar] [CrossRef]
- Nulsen, P.E.J.; Hambrick, D.C.; MacNamara, B.R.; Rafferty, D.; Bîrzan, L.; Wise, M.W.; David, L.P. The Powerful Outburst in Hercules A. Astrophys. J. 2005, 625, L9–L12. [Google Scholar] [CrossRef]
- Simionescu, A.; Roediger, E.; Nulsen, P.E.J.; Brüggen, M.; Forman, W.R.; Böhringer, H.; Werner, N.; Finoguenov, A. The large-scale shock in the cluster of galaxies Hydra A. Astron. Astrophys. 2009, 495, 721–732. [Google Scholar] [CrossRef]
- McNamara, B.R.; Nulsen, P.E.J.; Wise, M.W.; Rafferty, D.A.; Carilli, C.; Sarazin, C.L.; Blanton, E.L. The heating of gas in a galaxy cluster by X-ray cavities and large-scale shock fronts. Nature 2005, 433, 45–47. [Google Scholar] [CrossRef]
- Gitti, M.; O’Sullivan, E.; Giacintucci, S. Cavities and Shocks in the Galaxy Group HCG 62 as Revealed by Chandra, XMM-Newton, and Giant Metrewave Radio Telescope Data. Astrophys. J. 2010, 714, 758–771. [Google Scholar] [CrossRef]
- Koide, S.; Shibata, K.; Kudoh, T. General Relativistic Magnetohydrodynamic Simulations of Jets from Black Hole Accretions Disks: Two-Component Jets Driven by Nonsteady Accretion of Magnetized Disks. Astrophys. J. 1998, 495, L63–L66. [Google Scholar] [CrossRef]
- Koide, S.; Shibata, K.; Kudoh, T. Relativistic Jet Formation from Black Hole Magnetized Accretion Disks: Method, Tests, and Applications of a General RelativisticMagnetohydrodynamic Numerical Code. Astrophys. J. 1999, 522, 727–752. [Google Scholar] [CrossRef]
- Nishikawa, K.-I.; Richardson, G.; Koide, S.; Shibata, K.; Kudoh, T.; Hardee, P.; Fishman, G.J. A General Relativistic Magnetohydrodynamic Simulation of Jet Formation. Astrophys. J. 2005, 625, 60–71. [Google Scholar] [CrossRef]
- Koide, S.; Meier, D.L.; Shibata, K.; Kudoh, T. General Relativistic Simulations of Early Jet Formation in a Rapidly Rotating Black Hole Magnetosphere. Astrophys. J. 2000, 536, 668–674. [Google Scholar] [CrossRef]
- Koide, S.; Shibata, K.; Kudoh, T.; Meier, D.L. Extraction of Black Hole Rotational Energy by a Magnetic Field and the Formation of Relativistic Jets. Science 2002, 295, 1688–1691. [Google Scholar] [CrossRef] [PubMed]
- Komissarov, S.S. Observations of the Blandford-Znajek process and the magnetohydrodynamic Penrose process in computer simulations of black hole magnetospheres. Mon. Not. R. Astron. Soc. 2005, 359, 801–808. [Google Scholar] [CrossRef]
- Lasota, J.-P.; Gourgoulhon, E.; Abramowicz, M.; Tchekhovskoy, A.; Narayan, R. Extracting black-hole rotational energy: The generalized Penrose process. Phys. Rev. D 2014, 89, 024041. [Google Scholar] [CrossRef]
- Koide, S. Relativistic Outflow Magnetically Driven by Black Hole Rotation. Astrophys. J. 2004, 606, L45–L48. [Google Scholar] [CrossRef]
- Komissarov, S.S. General relativistic magnetohydrodynamic simulations of monopole magnetospheres of black holes. Mon. Not. R. Astron. Soc. 2004, 350, 1431–1436. [Google Scholar] [CrossRef]
- Komissarov, S.S. Direct numerical simulations of the Blandford-Znajek effect. Mon. Not. R. Astron. Soc. 2001, 326, L41–L44. [Google Scholar] [CrossRef]
- Komissarov, S.S. Electrodynamics of black hole magnetospheres. Mon. Not. R. Astron. Soc. 2004, 350, 427–448. [Google Scholar] [CrossRef]
- McKinney, J.C.; Gammie, C.F. A Measurement of the Electromagnetic Luminosity of a Kerr Black Hole. Astrophys. J. 2004, 611, 977–995. [Google Scholar] [CrossRef]
- De Villiers, J.-P.; Hawley, J.F.; Krolik, J.H. Magnetically Driven Accretion Flows in the Kerr Metric. I. Models and Overall Structure. Astrophys. J. 2003, 599, 1238–1253. [Google Scholar] [CrossRef]
- Hirose, S.; Krolik, J.H.; De Villiers, J.-P.; Hawley, J.F. Magnetically Driven Accretion Flows in the Kerr Metric. II. Structure of the Magnetic Field. Astrophys. J. 2004, 606, 1083–1097. [Google Scholar] [CrossRef]
- De Villiers, J.-P.; Hawley, J.F.; Krolik, J.H.; Hirose, S. Magnetically Driven Accretion in the Kerr Metric. III. Unbound Outflows. Astrophys. J. 2005, 620, 878–888. [Google Scholar] [CrossRef]
- McKinney, J.C. General relativistic magnetohydrodynamic simulations of the jet formation and large-scale propagation from black hole accretion systems. Mon. Not. R. Astron. Soc. 2006, 368, 1561–1582. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Barkov, M.V.; Vlahakis, N.; Königl, A. Magnetic acceleration of relativistic active galactic nucleus jets. Mon. Not. R. Astron. Soc. 2007, 380, 51–70. [Google Scholar] [CrossRef]
- McKinney, J.C.; Blandford, R.D. Stability of relativistic jets from rotating, accreting black holes via fully three-dimensional magnetohydrodynamic simulations. Mon. Not. R. Astron. Soc. 2009, 394, L126–L130. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C. Prograde and retrograde black holes: whose jet is more powerful? Mon. Not. R. Astron. Soc. 2012, 423, L55–L59. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astron. Soc. 2012, 423, 3083–3117. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Ruzmaikin, A.A. The Accretion of Matter by a Collapsing Star in the Presence of a Magnetic Field. Astrophys. Space Sci. 1974, 28, 45–59. [Google Scholar] [CrossRef]
- Narayan, R.; Igumenshchev, I.V.; Abramowicz, M.A. Magnetically Arrested Disk: An Energetically Efficient Accretion Flow. Publ. Astron. Soc. Jpn. 2003, 55, L69–L72. [Google Scholar] [CrossRef]
- Mckinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. Alignment of Magnetized Accretion Disks and Relativistic Jets with Spinning Black Holes. Science 2013, 339, 49–52. [Google Scholar] [CrossRef] [PubMed]
- Liska, M.; Tchekhovskoy, A.; Ingram, A.; van der Klis, M.; Markoff, S. Formation of precessing jets by tilted black hole discs in 3D general relativistic MHD simulations. Mon. Not. R. Astron. Soc. 2018, 474, L81–L85. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.; Nishikawa, K.-I. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Magnetized Spine-Sheath Relativistic Jets. Astrophys. J. 2007, 662, 835–850. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.-I.; Hardee, P.E. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of Current-Driven Instability. I. Instability of a Static Column. Astrophys. J. 2009, 700, 684–693. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.; Nishikawa, K.-I. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability with a Sub-Alfvénic Jet: Temporal Properties. Astrophys. J. 2011, 734. [Google Scholar] [CrossRef]
- Mizuno, Y.; Lyubarsky, Y.; Nishikawa, K.-I.; Hardee, P.E. Three-dimensional Relativistic Magnetohydrodynamic Simulations of Current-driven Instability. III. Rotating Relativistic Jets. Astrophys. J. 2012, 757. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.E.; Nishikawa, K.-I. Spatial Growth of the Current-driven Instability in Relativistic Jets. Astrophys. J. 2014, 784. [Google Scholar] [CrossRef]
- Singh, C.B.; Mizuno, Y.; de Gouveia Dal Pino, E.M. Spatial Growth of Current-driven Instability in Relativistic Rotating Jets and the Search for Magnetic Reconnection. Astrophys. J. 2016, 824. [Google Scholar] [CrossRef]
- Porth, O. Three-dimensional structure of relativistic jet formation. Mon. Not. R. Astron. Soc. 2013, 429, 2482–2492. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability in blazars: jets in a jet. Mon. Not. R. Astron. Soc. 2009, 395, L29–L33. [Google Scholar] [CrossRef]
- Lyubarski, Y. A New Mechanism for Dissipation of Alternating Fields in Poynting-dominated Outflows. Astrophys. J. 2010, 725, L234–L238. [Google Scholar] [CrossRef]
- O’Neill, S.M.; Beckwith, K.; Begelman, M.C. Local simulations of instabilities in relativistic jets—I. Morphology and energetics of the current-driven instability. Mon. Not. R. Astron. Soc. 2012, 422, 1436–1452. [Google Scholar] [CrossRef]
- Dexter, J.; McKinney, J.C.; Markoff, S.; Tchekhovskoy, A. Transient jet formation and state transitions from large-scale magnetic reconnection in black hole accretion discs. Mon. Not. R. Astron. Soc. 2014, 440, 2185–2190. [Google Scholar] [CrossRef]
- Singh, C.B.; Garofalo, D.; de Gouveia Dal Pino, E.M. Magnetic reconnection and Blandford-Znajek process around rotating black holes. Mon. Not. R. Astron. Soc. 2018, 478, 5404–5409. [Google Scholar] [CrossRef]
- Quian, Q.; Fendt, C.; Vourellis, C. Jet Launching in Resistive GR-MHD Black Hole-Accretion Disk Systems. Astrophys. J. 2018, 859. [Google Scholar] [CrossRef]
- Mościbrodzka, M. Modeling Polarized Emission from Black Hole Jets: Application to M 87 Core Jet. Galaxies 2017, 5, 54. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C.; Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444–457. [Google Scholar] [CrossRef]
- Gold, R.; McKinney, J.C.; Johnson, M.D.; Doeleman, S.S. Probing the Magnetic Field Structure in Sgr A* on Black Hole Horizon Scales with Polarized Radiative Transfer Simulations. Astrophys. J. 2017, 837. [Google Scholar] [CrossRef]
- O’ Riordan, M.; Pe’er, A.; McKinney, J.C. Observational Signatures of Mass-loading in Jets Launched by Rotating Black Holes. Astrophys. J. 2018, 853. [Google Scholar] [CrossRef]
- Broderick, A.E.; Tchekhovskoy, A. Horizon-scale Lepton Acceleration in Jets: Explaining the Compact Radio Emission in M 87. Astrophys. J. 2015, 809. [Google Scholar] [CrossRef]
- Mościbrodzka, M.; Falcke, H.; Shiokawa, H. General relativistic magnetohydrodynamical simulations of the jet in M 87. Astron. Astrophys. 2016, 586. [Google Scholar] [CrossRef]
- Wilson, M.J. Steady relativistic fluid jets. Mon. Not. R. Astron. Soc. 1987, 226, 447–454. [Google Scholar] [CrossRef]
- Dubal, M.R.; Pantano, O. The steady-state structure of relativistic magnetic jets. Mon. Not. R. Astron. Soc. 1993, 261, 203–221. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.; Marscher, A.P.; Ibáñez, J.M.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. 1995, 449, L19–L21. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.; Marscher, A.P.; Ibáñez, J.M.; Alberdi, A. Hydrodynamical Models of Superluminal Sources. Astrophys. J. 1997, 482, L33–L36. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Falle, S.A.E.G. Simulations of Superluminal Radio Sources. Mon. Not. R. Astron. Soc. 1997, 288, 833–848. [Google Scholar] [CrossRef]
- Mioduszewski, A.J.; Hughes, P.A.; Duncan, G.C. Simulated VLBI Images from Relativistic Hydrodynamic Jet Models. Astrophys. J. 1997, 476, 649–665. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marscher, A.P.; Alberdi, A.; Martí, J.M.; Ibáñez, J.M. Subparsec Polarimetric Radio Observations of 3C 120: A Close-up Look at Superluminal Motion. Astrophys. J. 1998, 499, 221–226. [Google Scholar] [CrossRef]
- Aloy, M.A.; Gómez, J.L.; Ibáñez, J.M.; Martí, J.M.; Müller, E. Radio Emission from Three-dimensional Relativistic Hydrodynamic Jets: Observational Evidence of Jet Stratification. Astrophys. J. 2000, 528, L85–L88. [Google Scholar] [CrossRef] [PubMed]
- Agudo, I.; Gómez, J.L.; Martí, J.M.; Ibáñez, J.M.; Marscher, A.P.; Alberdi, A.; Aloy, M.A.; Hardee, P.E. Jet Stability and the Generation of Superluminal and Stationary Components. Astrophys. J. 2001, 549, L183–L186. [Google Scholar] [CrossRef]
- Aloy, M.A.; Martí, J.M.; Gómez, J.L.; Agudo, I.; Müller, E.; Ibáñez, J.M. Three-dimensional Simulations of Relativistic Precessing Jets Probing the Structure of Superluminal Sources. Astrophys. J. 2003, 585, L109–L112. [Google Scholar] [CrossRef]
- Perucho, M.; Agudo, I.; Gómez, J.L.; Kadler, M.; Ros, E.; Kovalev, Y.Y. On the nature of an ejection event in the jet of 3C 111. Astron. Astrophys. 2008, 489, L29–L32. [Google Scholar] [CrossRef]
- Wehrle, A.E.; Piner, B.G.; Unwin, S.C.; Zook, A.C.; Xu, W.; Marscher, A.P.; Teräsranta, H.; Valtaoja, E. Kinematics of the Parsec-Scale Relativistic Jet in Quasar 3C 279: 1991–1997. Astrophys. J. Suppl. Ser. 2001, 133, 297–320. [Google Scholar] [CrossRef]
- Kadler, M.; Ros, E.; Perucho, M.; Kovalev, Y.Y.; Homan, D.C.; Agudo, I.; Kellermann, K.I.; Aller, M.F.; Aller, H.D.; Lister, M.L.; Zensus, J.A. The Trails of Superluminal Jet Components in 3C 111. Astrophys. J. 2008, 680, 867–884. [Google Scholar] [CrossRef]
- Fromm, C.M.; Perucho, M.; Porth, O.; Younsi, Z.; Ros, E.; Mizuno, Y.; Zensus, J.A.; Rezzolla, L. Jet-torus connection in radio galaxies. Relativistic hydrodynamics and synthetic emission. Astron. Astrophys. 2018, 609. [Google Scholar] [CrossRef]
- Broderick, A.E.; McKinney, J.C. Parsec-scale Faraday Rotation Measures from General Relativistic Magnetohydrodynamic Simulations of Active Galactic Nucleus Jets. Astrophys. J. 2010, 725, 750–773. [Google Scholar] [CrossRef]
- Porth, O.; Fendt, C.; Meliani, Z.; Vaidya, B. Synchrotron Radiation of Self-collimating Relativistic Magnetohydrodynamic Jets. Astrophys. J. 2011, 737. [Google Scholar] [CrossRef]
- Jorstad, S.G.; Marscher, A.P.; Lister, M.L.; Stirling, A.M.; Cawthorne, T.V.; Gear, W.K.; Gómez, J.L.; Stevens, J.A.; Smith, P.S.; Forster, J.R.; Robson, E.I. Polarimetric Observations of 15 Active Galactic Nuclei at High Frequencies: Jet Kinematics from Bimonthly Monitoring with the Very Long Baseline Array. Astron. J. 2005, 130, 1418–1465. [Google Scholar] [CrossRef]
- Lister, M.L.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kellermann, K.I.; Kovalev, Y.Y.; Pushkarev, A.B.; Richards, J.L.; Ros, E.; Savolainen, T. MOJAVE. X. Parsec-scale Jet Orientation Variations and Superluminal Motion in Active Galactic Nuclei. Astron. J. 2013, 146. [Google Scholar] [CrossRef]
- Cohen, M.H.; Meier, D.L.; Arshakian, T.G.; Homan, D.C.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Richards, J.L.; Savolainen, T. Studies of the Jet in Bl Lacertae. I. Recollimation Shock and Moving Emission Features. Astrophys. J. 2014, 787. [Google Scholar] [CrossRef]
- Mizuno, Y.; Gómez, J.L.; Nishikawa, K.-I.; Meli, A.; Hardee, P.E.; Rezzolla, L. Recollimation Shocks in Magnetized Relativistic Jets. Astrophys. J. 2015, 809. [Google Scholar] [CrossRef]
- Martí, J.M.; Perucho, M.; Gómez, J.L. The Internal Structure of Overpressured, Magnetized, Relativistic Jets. Astrophys. J. 2016, 831. [Google Scholar] [CrossRef]
- Fuentes, A.; Gómez, J.L.; Martí, J.M.; Perucho, M. Total and Linearly Polarized Synchrotron Emission from Overpressured Magnetized Relativistic Jets. Astrophys. J. 2018, 860. [Google Scholar] [CrossRef]
- Martí, J.M.; Perucho, M.; Gómez, J.L.; Fuentes, A. Recollimation shocks in relativistic jets. Int. J. Mod. Phys. D 2018, 27. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Porth, O.; Lyutikov, M. Stationary relativistic jets. Comput. Astrophys. Cosmol. 2015, 2. [Google Scholar] [CrossRef]
- Porth, O.; Komissarov, S.S. Causality and stability of cosmic jets. Mon. Not. R. Astron. Soc. 2015, 452, 1089–1104. [Google Scholar] [CrossRef]
- Fromm, C.; Porth, O.; Younsi, Z.; Mizuno, Y.; de Laurentis, M.; Olivares, H.; Rezzolla, L. Radiative Signatures of Parsec-Scale Magnetised Jets. Galaxies 2017, 5, 73. [Google Scholar] [CrossRef]
- Shepherd, M.C. Difmap:An Interactive Program for Synthesis Imaging. ASP Conf. Ser. 1997, 125, 77–84. [Google Scholar]
- Högbom, J.A. Aperture Synthesis with a Non-Regular Distribution of Interferometer Baselines. Astron. Astrophys. Suppl. Ser. 1974, 15, 417–426. [Google Scholar]
- Hardee, P.E. The stability of astrophysical jets. Proc. Int. Astron. Union 2011, 275, 41–49. [Google Scholar] [CrossRef]
- Owen, F.N.; Hardee, P.E.; Cornwell, T.J. High-resolution, high dynamic range VLA images of the M 87 jet at 2 centimeters. Astrophys. J. 1989, 340, 698–707. [Google Scholar] [CrossRef]
- Lobanov, A.; Hardee, P.; Eilek, J. Internal structure and dynamics of the kiloparsec-scale jet in M 87. New Astron. Rev. 2003, 47, 629–632. [Google Scholar] [CrossRef]
- Hardee, P.E.; Eilek, J.A. Using Twisted Filaments to Model the Inner Jet in M 87. Astrophys. J. 2011, 735. [Google Scholar] [CrossRef]
- Lobanov, A.P.; Krichbaum, T.P.; Witzel, A.; Kraus, A.; Zensus, J.A.; Britzen, S.; Otterbein, K.; Hummel, C.A.; Johnston, K. VSOP imaging of S5 0836+710: A close-up on plasma instabilities in the jet. Astron. Astrophys. 1998, 340, L60–L64. [Google Scholar]
- Perucho, M.; Lobanov, A.P. Physical properties of the jet in 0836+710 revealed by its transversal structure. Astron. Astrophys. 2007, 469, L23–L26. [Google Scholar] [CrossRef]
- Perucho, M.; Kovalev, Y.; Lobanov, A.P.; Hardee, P.E.; Agudo, I. Anatomy of Helical Extragalactic Jets: The Case of S5 0836+710. Astrophys. J. 2012, 749. [Google Scholar] [CrossRef]
- Perucho, M.; Martí-Vidal, I.; Lobanov, A.P.; Hardee, P.E. S5 0836+710: An FR II jet disrupted by the growth of a helical instability? Astron. Astrophys. 2012, 545. [Google Scholar] [CrossRef]
- Perucho, M.; Lobanov, A.P.; Martí, J.M.; Hardee, P.E. The role of Kelvin-Helmholtz instability in the internal structure of relativistic outflows. The case of the jet in 3C 273. Astron. Astrophys. 2006, 456, 493–504. [Google Scholar] [CrossRef]
- Walker, R.C.; Benson, J.M.; Unwin, S.C.; Lystrup, M.B.; Hunter, T.R.; Pilbratt, G.; Hardee, P.E. The Structure and Motions of the 3C 120 Radio Jet on Scales of 0.6-300 Parsecs. Astrophys. J. 2001, 556, 756–772. [Google Scholar] [CrossRef]
- Walker, R.C.; Hardee, P.E. The implications of helical patterns in 3C 120. New Astron. Rev. 2003, 47, 645–647. [Google Scholar] [CrossRef]
- Hardee, P.E.; Walker, R.C.; Gómez, J.L. Modeling the 3C 120 Radio Jet from 1 to 30 Milliarcseconds. Astrophys. J. 2005, 620, 646–664. [Google Scholar] [CrossRef]
- Cohen, M.H.; Meier, D.L.; Arshakian, T.G.; Clausen-Brown, E.; Homan, D.C.; Hovatta, T.; Kovalev, Y.Y.; Lister, M.L.; Pushkarev, A.B.; Richards, J.L.; Savolainen, T. Studies of the Jet in Bl Lacertae. II. Superluminal Alfvén Waves. Astrophys. J. 2015, 803. [Google Scholar] [CrossRef]
- Perucho, M.; Hanasz, M.; Martí, J.M.; Sol, H. Stability of hydrodynamical relativistic planar jets. I. Linear evolution and saturation of Kelvin-Helmholtz modes. Astron. Astrophys. 2004, 427, 415–429. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Hanasz, M. Stability of hydrodynamical relativistic planar jets. II. Long-term nonlinear evolution. Astron. Astrophys. 2004, 427, 431–444. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Hanasz, M. Nonlinear stability of relativistic sheared planar jets. Astron. Astrophys. 2005, 443, 863–881. [Google Scholar] [CrossRef]
- Perucho, M.; Hanasz, M.; Martí, J.M.; Miralles, J.A. Resonant Kelvin-Helmholtz modes in sheared relativistic flows. Phys. Rev. E 2007, 75, 056312. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Cela, J.M.; Hanasz, M.; de La Cruz, R.; Rubio, F. Stability of three-dimensional relativistic jets: implications for jet collimation. Astron. Astrophys. 2010, 519. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L. THC: A new high-order finite-difference high-resolution shock-capturing code for special-relativistic hydrodynamics. Astron. Astrophys. 2102, 547. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L. Universality and Intermittency in Relativistic Turbulent Flows of a Hot Plasma. Astrophys. J. 2013, 766. [Google Scholar] [CrossRef]
- Zrake, J.; MacFadyen, A.I. Spectral and Intermittency Properties of Relativistic Turbulence. Astrophys. J. 2013, 763. [Google Scholar] [CrossRef]
- Zhang, W.; MacFadyen, A.; Wang, P. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of the Kelvin-Helmholtz Instability: Magnetic Field Amplification by a Turbulent Dynamo. Astrophys. J. 2009, 692, L40–L44. [Google Scholar] [CrossRef]
- Beckwith, K.; Stone, J.M. A Second-order Godunov Method for Multi-dimensional Relativistic Magnetohydrodynamics. Astrophys. J. Suppl. Ser. 2011, 193. [Google Scholar] [CrossRef]
- Zrake, J.; MacFadyen, A.I. Numerical Simulations of Driven Relativistic Magnetohydrodynamic Turbulence. Astrophys. J. 2012, 744. [Google Scholar] [CrossRef]
- Matsumoto, J.; Masada, Y. Two-dimensional Numerical Study for Rayleigh-Taylor and Richtmyer-Meshkov Instabilities in Relativistic Jets. Astrophys. J. 2013, 772. [Google Scholar] [CrossRef]
- Toma, K.; Komissarov, S.S.; Porth, O. Rayleigh-Taylor instability in two-component relativistic jets. Mon. Not. R. Astron. Soc. 2017, 472, 1253–1258. [Google Scholar] [CrossRef]
- Matsumoto, J.; Aloy, M.A.; Perucho, M. Linear theory of the Rayleigh-Taylor instability at a discontinuous surface of a relativistic flow. Mon. Not. R. Astron. Soc. 2017, 472, 1421–1431. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Komissarov, S.S. Reconfinement and loss of stability in jets from active galactic nuclei. Nat. Astron. 2018, 2, 167–171. [Google Scholar] [CrossRef]
- Meliani, Z.; Keppens, R. Transverse stability of relativistic two-component jets. Astron. Astrophys. 2007, 475, 785–789. [Google Scholar] [CrossRef]
- Meliani, Z.; Keppens, R. Decelerating Relativistic Two-Component Jets. Astrophys. J. 2009, 705, 1594–1606. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Komissarov, S.S. Relativistic centrifugal instability. Mon. Not. R. Astron. Soc. 2018, 475, L125–L129. [Google Scholar] [CrossRef]
- Millas, D.; Keppens, R.; Meliani, Z. Rotation and toroidal magnetic field effects on the stability of two-component jets. Mon. Not. R. Astron. Soc. 2017, 470, 592–605. [Google Scholar] [CrossRef]
- Heavens, A.F.; Drury, L.O. Relativistic shocks and particle acceleration. Mon. Not. R. Astron. Soc. 1988, 235, 997–1009. [Google Scholar] [CrossRef]
- Sironi, L.; Petropoulou, M.; Giannios, D. Relativistic jets shine through shocks or magnetic reconnection? Mon. Not. R. Astron. Soc. 2015, 450, 183–191. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780. [Google Scholar] [CrossRef]
- Zakamska, N.L.; Begelman, M.C.; Blandford, R.D. Hot Self-Similar Relativistic Magnetohydrodynamic Flows. Astrophys. J. 2008, 679, 990–999. [Google Scholar] [CrossRef]
- Anantua, R.; Blandford, R.D.; Tchekhovskoy, A. Multiwavelength Observations of Relativistic Jets from General Relativistic Magnetohydrodynamic Simulations. Galaxies 2018, 6, 31. [Google Scholar] [CrossRef]
- Jones, T.W.; Ryu, D.; Engel, A. Simulating Electron Transport and Synchrotron Emission in Radio Galaxies: Shock Acceleration and Synchrotron Aging in Axisymmetric Flows. Astrophys. J. 1999, 512, 105–124. [Google Scholar] [CrossRef]
- Micono, M.; Zurlo, N.; Massaglia, S.; Ferrari, A.; Melrose, D.B. Diffusive shock acceleration in extragalactic jets. Astron. Astrophys. 1999, 349, 323–333. [Google Scholar]
- Tregillis, I.L.; Jones, T.W.; Ryu, D. Simulating Electron Transport and Synchrotron Emission in Radio Galaxies: Shock Acceleration and Synchrotron Aging in Three-dimensional Flows. Astrophys. J. 2001, 557, 475–491. [Google Scholar] [CrossRef]
- Mimica, P.; Aloy, M.A.; Agudo, I.; Martí, J.M.; Gómez, J.L.; Miralles, J.A. Spectral Evolution of Superluminal Components in Parsec-Scale Jets. Astrophys. J. 2009, 696, 1142–1163. [Google Scholar] [CrossRef]
- Fromm, C.M.; Perucho, M.; Mimica, P.; Ros, E. Spectral evolution of flaring blazars from numerical simulations. Astron. Astrophys. 2016, 588. [Google Scholar] [CrossRef]
- Vaidya, B.; Mignone, A.; Bodo, G.; Rossi, P.; Massaglia, S. A Particle Module for the PLUTO Code. II. Hybrid Framework for Modeling Nonthermal Emission from Relativistic Magnetized Flows. Astrophys. J. 2018, 865. [Google Scholar] [CrossRef]
- Sironi, L.; Keshet, U.; Lemoine, M. Relativistic Shocks: Particle Acceleration and Magnetization. Space Sci. Rev. 2015, 191, 519–544. [Google Scholar] [CrossRef]
- Kagan, D.; Sironi, L.; Cerutti, B.; Giannios, D. Relativistic Magnetic Reconnection in Pair Plasmas and Its Astrophysical Applications. Space Sci. Rev. 2015, 191, 545–573. [Google Scholar] [CrossRef]
- Nishikawa, K.-I.; Frederiksen, J.T.; Nordlund, Å.; Mizuno, Y.; Hardee, P.E.; Niemiec, J.; Gómez, J.L.; Pe’er, A.; Duţan, I.; Meli, A.; et al. Evolution of Global Relativistic Jets: Collimations and Expansion with kKHI and the Weibel Instability. Astrophys. J. 2016, 820. [Google Scholar] [CrossRef]
- Nishikawa, K.-I.; Mizuno, Y.; Niemiec, J.; Kobzar, O.; Pohl, M.; Gómez, J.L.; Duţan, I.; Pe’er, A.; Frederiksen, J.; Nordlund, Å.; et al. Microscopic Processes in Global Relativistic Jets Containing Helical Magnetic Fields. Galaxies 2016, 4, 38. [Google Scholar] [CrossRef]
- Bai, X.-N.; Caprioli, D.; Sironi, L.; Spitkovsky, A. Magnetohydrodynamic-particle-in-cell Method for Coupling Cosmic Rays with a Thermal Plasma: Application to Non-relativistic Shocks. Astrophys. J. 2015, 809. [Google Scholar] [CrossRef]
- Van Marle, A.J.; Casse, F.; Markowith, A. On magnetic field amplification and particle acceleration near non-relativistic astrophysical shocks: particles in MHD cells simulations. Mon. Not. R. Astron. Soc. 2018, 473, 3394–3409. [Google Scholar] [CrossRef]
- Mignone, A.; Bodo, G.; Vaidya, B.; Mattia, G. A Particle Module for the PLUTO Code. I. An Implementation of the MHD-PIC Equations. Astrophys. J. 2018, 859. [Google Scholar] [CrossRef]
- Smith, M.D.; Norman, M.L.; Winkler, K.-H.A.; Smarr, L. Hotspots in radio galaxies—A comparison with hydrodynamic simulations. Mon. Not. R. Astron. Soc. 1985, 214, 67–85. [Google Scholar] [CrossRef]
- Burns, J.O.; Norman, M.L.; Clarke, D.A. Numerical models of extragalactic radio sources. Science 1991, 253, 522–530. [Google Scholar] [CrossRef] [PubMed]
- Van Putten, M.H.P.M. A two-dimensional relativistic (Gamma = 3.25) jet simulation. Astrophys. J. 1993, 408, L21–L23. [Google Scholar] [CrossRef]
- Martí, J.M.; Müller, E.; Ibáñez, J.M. Hydrodynamical simulations of relativistic jets. Astron. Astrophys. 1994, 281, L9–L12. [Google Scholar]
- Duncan, G.C.; Hughes, P.A. Simulations of relativistic extragalactic jets. Astrophys. J. 1994, 436, L119–L122. [Google Scholar] [CrossRef]
- Martí, J.M.; Müller, E.; Font, J.A.; Ibáñez, J.M. Morphology and Dynamics of Highly Supersonic Relativistic Jets. Astrophys. J. 1995, 448, L105–L108. [Google Scholar] [CrossRef]
- Martí, J.M.; Müller, E.; Font, J.A.; Ibáñez, J.M.; Marquina, A. Morphology and Dynamics of Relativistic Jets. Astrophys. J. 1997, 479, 151–163. [Google Scholar] [CrossRef]
- Rosen, A.; Hughes, P.A.; Duncan, G.C.; Hardee, P.E. A Comparison of the Morphology and Stability of Relativistic and Nonrelativistic Jets. Astrophys. J. 1999, 516, 729–743. [Google Scholar] [CrossRef]
- Monceau-Baroux, R.; Keppens, R.; Meliani, Z. The effect of angular opening on the dynamics of relativistic hydro jets. Astron. Astrophys. 2012, 545. [Google Scholar] [CrossRef]
- Aloy, M.A.; Ibáñez, J.M.; Martí, J.M. High-Resolution Three-dimensional Simulations of Relativistic Jets. Astrophys. J. 1999, 523, L125–L128. [Google Scholar] [CrossRef]
- Hughes, P.A.; Miller, M.A.; Duncan, G.C. Three-dimensional Hydrodynamic Simulations of Relativistic Extragalactic Jets. Astrophys. J. 2002, 572, 713–728. [Google Scholar] [CrossRef]
- Choi, E.; Wiita, P.J.; Ryu, D. Hydrodynamic Interactions of Relativistic Extragalactic Jets with Dense Clouds. Astrophys. J. 2007, 655, 769–780. [Google Scholar] [CrossRef]
- Koide, S.; Nishikawa, K.-I.; Mutel, R.L. A Two-dimensional Simulation of Relativistic Magnetized Jet. Astrophys. J. 1996, 463, L71–L74. [Google Scholar] [CrossRef]
- Nishikawa, K.-I.; Koide, S.; Sakai, J.-I.; Christodoulou, D.M.; Sol, H.; Mutel, R.L. Three-Dimensional Magnetohydrodynamic Simulations of Relativistic Jets Injected along a Magnetic Field. Astrophys. J. 1997, 483, L45–L48. [Google Scholar] [CrossRef]
- Koide, S. A Two-dimensional Simulation of a Relativistic Jet Bent by an Oblique Magnetic Field. Astrophys. J. 1997, 478, 66–69. [Google Scholar] [CrossRef]
- Nishikawa, K.-I.; Koide, S.; Sakai, J.-I.; Christodoulou, D.M.; Sol, H.; Mutel, R.L. Three-dimensional Magnetohydrodynamic Simulations of Relativistic Jets Injected into an Oblique Magnetic Field. Astrophys. J. 1998, 498, 166–169. [Google Scholar] [CrossRef]
- Komissarov, S.S. Numerical simulations of relativistic magnetized jets. Mon. Not. R. Astron. Soc. 1999, 308, 1069–1076. [Google Scholar] [CrossRef]
- Mignone, A.; Massaglia, S.; Bodo, G. Relativistic MHD Simulations of Jets with Toroidal Magnetic Fields. Space Sci. Rev. 2005, 121, 21–31. [Google Scholar] [CrossRef]
- Keppens, R.; Meliani, Z.; van der Holst, B.; Casse, F. Extragalactic jets with helical magnetic fields: Relativistic MHD simulations. Astron. Astrophys. 2008, 486, 663–678. [Google Scholar] [CrossRef]
- Leismann, T.; Antón, L.; Aloy, M.A. Relativistic MHD simulations of extragalactic jets. Astron. Astrophys. 2005, 436, 503–526. [Google Scholar] [CrossRef]
- Begelman, M.C.; Cioffi, D.F. Overpressured cocoons in extragalactic radio sources. Astrophys. J. 1989, 345, L21–L24. [Google Scholar] [CrossRef]
- Falle, S.A.E.G. Self-similar jets. Mon. Not. R. Astron. Soc. 1991, 250, 581–596. [Google Scholar] [CrossRef]
- Kaiser, C.R.; Alexander, P. A self-similar model for extragalactic radio sources. Mon. Not. R. Astron. Soc. 1997, 286, 215–222. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Falle, S.A.E.G. The large-scale structure of FR-II radio sources. Mon. Not. R. Astron. Soc. 1998, 297, 1097–1108. [Google Scholar] [CrossRef]
- Clarke, D.A.; Harris, D.E.; Carilli, C.L. Formation of cavities in the X-ray emitting cluster gas of Cygnus A. Mon. Not. R. Astron. Soc. 1997, 284, 981–993. [Google Scholar] [CrossRef]
- Zanni, C.; Bodo, G.; Rossi, P.; Massaglia, S.; Durbala, A.; Ferrari, A. X-ray emission from expanding cocoons. Astron. Astrophys. 2003, 402, 949–962. [Google Scholar] [CrossRef]
- Krause, M. Very light jets II: Bipolar large scale simulations in King atmospheres. Astron. Astrophys. 2005, 431, 45–64. [Google Scholar] [CrossRef]
- Tregillis, I.L.; Jones, T.W.; Ryu, D. Synthetic Observations of Simulated Radio Galaxies. I. Radio and X-Ray Analysis. Astrophys. J. 2004, 601, 778–797. [Google Scholar] [CrossRef]
- Gaibler, V.; Krause, M.; Camenzind, M. Very light magnetized jets on large scales—I. Evolution and magnetic fields. Mon. Not. R. Astron. Soc. 2009, 400, 1785–1802. [Google Scholar] [CrossRef]
- Huarte-Espinosa, M.; Krause, M.; Alexander, P. 3D magnetohydrodynamic simulations of the evolution of magnetic fields in Fanaroff-Riley class II radio sources. Mon. Not. R. Astron. Soc. 2011, 417, 382–399. [Google Scholar] [CrossRef]
- Hardcastle, M.J.; Krause, M.G.H. Numerical modelling of the lobes of radio galaxies in cluster environments—II. Magnetic field configuration and observability. Mon. Not. R. Astron. Soc. 2104, 441, 1482–1499. [Google Scholar] [CrossRef]
- Scheck, L.; Aloy, M.A.; Martí, J.M.; Gómez, J.L.; Müller, E. Does the plasma composition affect the long-term evolution of relativistic jets? Mon. Not. R. Astron. Soc. 2002, 331, 615–634. [Google Scholar] [CrossRef]
- Mignone, A.; Rossi, P.; Bodo, G.; Ferrari, A.; Massaglia, S. High-resolution 3D relativistic MHD simulations of jets. Mon. Not. R. Astron. Soc. 2010, 402, 7–12. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Laing, R.A.; Hardee, P.E. On the deceleration of Fanaroff-Riley Class I jets: Mass loading by stellar winds. Mon. Not. R. Astron. Soc. 2014, 441, 1488–1503. [Google Scholar] [CrossRef]
- Rossi, P.; Mignone, A.; Bodo, G.; Massaglia, S.; Ferrari, A. Formation of dynamical structures in relativistic jets: The FR I case. Astron. Astrophys. 2008, 488, 795–806. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M. A numerical simulation of the evolution and fate of a Fanaroff-Riley type I jet. The case of 3C 31. Mon. Not. R. Astron. Soc. 2007, 382, 526–542. [Google Scholar] [CrossRef]
- Krause, M.; Alexander, P.; Riley, J.; Hopton, D. A new connection between the jet opening angle and the large-scale morphology of extragalactic radio sources. Mon. Not. R. Astron. Soc. 2012, 427, 3196–3208. [Google Scholar] [CrossRef]
- Massaglia, S.; Bodo, G.; Rossi, P.; Capetti, S.; Mignone, A. Making Faranoff-Riley I radio sources. I. Numerical hydrodynamic 3D simulations of low-power jets. Astron. Astrophys. 2016, 596. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Bromberg, O. Three-dimensional relativistic MHD simulations of active galactic nuclei jets: Magnetic kink instability and Fanaroff–Riley dichotomy. Mon. Not. R. Astron. Soc. 2016, 461, L46–L50. [Google Scholar] [CrossRef]
- Yates, P.M.; Shabala, S.S.; Krause, M.G.H. Observability of intermittent radio sources in galaxy groups and clusters. Mon. Not. R. Astron. Soc. 2018, 480, 5286–5306. [Google Scholar] [CrossRef]
- Böhringer, H.; Voges, W.; Fabian, A.C.; Edge, A.C.; Neumann, D.M. A ROSAT HRI study of the interaction of the X-ray-emitting gas and radio lobes of NGC 1275. Mon. Not. R. Astron. Soc. 1993, 264, L25–L28. [Google Scholar] [CrossRef]
- Fabian, A.C. Cooling Flows in Clusters of Galaxies. Ann. Rev. Astron. Astrophys. 1994, 32, 277–318. [Google Scholar] [CrossRef]
- Churazov, E.; Brüggen, M.; Kaiser, C.R.; Böhringer, H.; Forman, W. Evolution of Buoyant Bubbles in M87. Astrophys. J. 2001, 554, 261–273. [Google Scholar] [CrossRef]
- Quilis, V.; Bower, R.G.; Balogh, M.L. Bubbles, feedback and the intracluster medium: Three-dimensional hydrodynamic simulations. Mon. Not. R. Astron. Soc. 2001, 328, 1091–1097. [Google Scholar] [CrossRef]
- Reynolds, C.S.; Heinz, S.; Begelman, M.C. The hydrodynamics of dead radio galaxies. Mon. Not. R. Astron. Soc. 2002, 332, 271–282. [Google Scholar] [CrossRef]
- Sijacki, D.; Springel, V.; Di Matteo, T.; Hernquist, L. A unified model for AGN feedback in cosmological simulations of structure formation. Mon. Not. R. Astron. Soc. 2007, 380, 877–900. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.; Nelson, D.; Hernquist, L. Introducing the Illustris Project: Simulating the coevolution of dark and visible matter in the Universe. Mon. Not. R. Astron. Soc. 2014, 444, 1518–1547. [Google Scholar] [CrossRef]
- Dubois, Y.; Devriendt, J.; Slyz, A.; Teyssier, R. Self-regulated growth of supermassive black holes by a dual jet-heating active galactic nucleus feedback mechanism: Methods, tests and implications for cosmological simulations. Mon. Not. R. Astron. Soc. 2012, 420, 2662–2683. [Google Scholar] [CrossRef]
- Dubois, Y.; Peirani, S.; Pichon, C.; Devriendt, J.; Gavazzi, R.; Welker, C.; Volonteri, M. The HORIZON-AGN simulation: Morphological diversity of galaxies promoted by AGN feedback. Mon. Not. R. Astron. Soc. 2016, 463, 3948–3964. [Google Scholar] [CrossRef]
- Bîrzan, L.; Rafferty, D.A.; McNamara, B.R.; Wise, M.W.; Nulsen, P.E.J. A Systematic Study of Radio-induced X-Ray Cavities in Clusters, Groups, and Galaxies. Astrophys. J. 2004, 607, 800–809. [Google Scholar] [CrossRef]
- Reynolds, C.S. Jets and AGN feedback. In Relativistic Jets from Active Galactic Nuclei; Böttcher, M., Harris, D.E., Krawczynski, H., Eds.; Wiley-VCH: Weinheim, Germany, 2012; pp. 369–394. ISBN 978-3-527-41037-8. [Google Scholar]
- Yang, H.-Y.K.; Reynolds, C.S. How AGN Jets Heat the Intracluster Medium—Insights from Hydrodynamic Simulations. Astrophys. J. 2016, 829. [Google Scholar] [CrossRef]
- Yang, H.-Y.K.; Reynolds, C.S. Interplay Among Cooling, AGN Feedback, and Anisotropic Conduction in the Cool Cores of Galaxy Clusters. Astrophys. J. 2016, 818. [Google Scholar] [CrossRef]
- Martizzi, D.; Quataert, E.; Faucher-Ciguère, C.A.; Fielding, D. Simulations of Jet Heating in Galaxy Clusters: Successes and Challenges. Mon. Not. R. Astron. Soc. 2019, 483, 2465–2486. [Google Scholar] [CrossRef]
- Ruszkowski, M.; Yang, H.-Y.K.; Reynolds, C.S. Cosmic-Ray Feedback Heating of the Intracluster Medium. Astrophys. J. 2017, 844. [Google Scholar] [CrossRef]
- Ehlert, K.; Weinberger, R.; Pfrommer, C.; Pakmor, R.; Springel, V. Simulations of the dynamics of magnetized jets and cosmic rays in galaxy clusters. Mon. Not. R. Astron. Soc. 2018, 481, 2878–2900. [Google Scholar] [CrossRef]
- Heinz, S.; Brüggen, M.; Young, A.; Levesque, E. The answer is blowing in the wind: simulating the interaction of jets with dynamic cluster atmospheres. Mon. Not. R. Astron. Soc. 2006, 373, L65–L69. [Google Scholar] [CrossRef]
- Morsony, B.J.; Heinz, S.; Brüggen, M.; Ruszkowski, M. Swimming against the current: Simulations of central AGN evolution in dynamic galaxy clusters. Mon. Not. R. Astron. Soc. 2010, 407, 1277–1289. [Google Scholar] [CrossRef]
- Mendygral, P.J.; Jones, T.W.; Dolag, K. MHD Simulations of Active Galactic Nucleus Jets in a Dynamic Galaxy Cluster Medium. Astrophys. J. 2012, 750. [Google Scholar] [CrossRef]
- Bourne, M.A.; Sijacki, D. AGN jet feedback on a moving mesh: Cocoon inflation, gas flows and turbulence. Mon. Not. R. Astron. Soc. 2017, 472, 4707–4735. [Google Scholar] [CrossRef]
- Hitomi Collaboration. The quiescent intracluster medium in the core of the Perseus cluster. Nature 2016, 535, 117–121. [Google Scholar] [CrossRef] [PubMed]
- Perucho, M.; Quilis, V.; Martí, J.M. Intracluster Medium Reheating by Relativistic Jets. Astrophys. J. 2011, 743. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Quilis, V.; Ricciardelli, E. Large-scale jets from active galactic nuclei as a source of intracluster medium heating: Cavities and shocks. Mon. Not. R. Astron. Soc. 2014, 445, 1462–1481. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Quilis, V. Long-term FRII jet evolution: Clues from three-dimensional simulations. Mon. Not. R. Astron. Soc. 2018. [Google Scholar] [CrossRef]
- Perucho, M.; Martí, J.M.; Quilis, V.; Borja-Lloret, M. Radio mode feedback: Does relativity matter? Mon. Not. R. Astron. Soc. 2017, 471, L120–L124. [Google Scholar] [CrossRef]
- English, W.; Hardcastle, M.J.; Krause, M.G.H. Numerical modelling of the lobes of radio galaxies in cluster environments—III. Powerful relativistic and non-relativistic jets. Mon. Not. R. Astron. Soc. 2016, 461, 2025–2043. [Google Scholar] [CrossRef]
- Gaibler, V. Positive and negative feedback by AGN jets in high-redshift galaxies. Astron. Nachr. 2014, 335, 531–536. [Google Scholar] [CrossRef]
- Wagner, A.Y.; Bicknell, G.V.; Umemura, M. Galaxy-scale AGN feedback - theory. Astron. Nachr. 2016, 337, 167–174. [Google Scholar] [CrossRef]
- Gaibler, V.; Khochfar, S.; Krause, M.; Silk, J. Jet-induced star formation in gas-rich galaxies. Mon. Not. R. Astron. Soc. 2012, 425, 438–449. [Google Scholar] [CrossRef]
- Wagner, A.Y.; Bicknell, G.V.; Umemura, M. Driving Outflows with Relativistic Jets and the Dependence of Active Galactic Nucleus Feedback Efficiency on Interstellar Medium Inhomogeneity. Astrophys. J. 2012, 757. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martí, J.-M. Numerical Simulations of Jets from Active Galactic Nuclei. Galaxies 2019, 7, 24. https://doi.org/10.3390/galaxies7010024
Martí J-M. Numerical Simulations of Jets from Active Galactic Nuclei. Galaxies. 2019; 7(1):24. https://doi.org/10.3390/galaxies7010024
Chicago/Turabian StyleMartí, José-María. 2019. "Numerical Simulations of Jets from Active Galactic Nuclei" Galaxies 7, no. 1: 24. https://doi.org/10.3390/galaxies7010024
APA StyleMartí, J.-M. (2019). Numerical Simulations of Jets from Active Galactic Nuclei. Galaxies, 7(1), 24. https://doi.org/10.3390/galaxies7010024



