Progress in Multi-Wavelength and Multi-Messenger Observations of Blazars and Theoretical Challenges

Abstract

This review provides an overview of recent advances in multi-wavelength and multi-messenger observations of blazars, the current status of theoretical models for blazar emission, and prospects for future facilities. The discussion of observational results will focus on advances made possible through the Fermi Gamma-Ray Space Telescope and ground-based gamma-ray observatories (H.E.S.S., MAGIC, VERITAS), as well as the recent first evidence for a blazar being a source of IceCube neutrinos. The main focus of this review will be the discussion of our current theoretical understanding of blazar multi-wavelength and multi-messenger emission, in the spectral, time, and polarization domains. Future progress will be expected in particular through the development of the first X-ray polarimeter, IXPE, and the installation of the Cherenkov Telescope Array (CTA), both expected to become operational in the early to mid 2020s.

1. Introduction

Blazars are the class of jet-dominated, radio-loud active galactic nuclei (AGN) whose relativistic jets point close to our line of sight. Due to this viewing geometry, all emissions from a region moving with Lorentz factor $\mathsf{\Gamma }\equiv {(1-{\beta }_{\mathsf{\Gamma }}^2)}^{-1/2}$, where ${\beta }_{\mathsf{\Gamma }}$c is the jet speed, along the jet, at an angle ${\theta }_{\mathrm{obs}}$ with respect to our line of sight, will be Doppler boosted in frequency by a factor $\delta ={\left(\mathsf{\Gamma }[1-{\beta }_{\mathsf{\Gamma }}cos{\theta }_{\mathrm{obs}}]\right)}^{-1}$ and in bolometric luminosity by a factor ${\delta }^4$ with respect to quantities measured in the co-moving frame of the emission region. Any time scale of variability in the co-moving frame will be observed shortened by a factor ${\delta }^{-1}$. These effects make blazars the brightest $\gamma$-ray sources in the extragalactic sky (e.g., [1]), exhibiting variability, in extreme cases, on time scales down to just minutes (e.g., [2,3,4,5]).

The broad-band continuum (radio through $\gamma$-ray) spectral energy distributions (SEDs) of blazars are typically dominated by two broad, non-thermal radiation components. The low-frequency component, from radio through optical/UV (in some cases, X-rays) is generally agreed to be synchrotron emission from relativistic electrons in the jet, as evidenced by the measurement of significant, variable linear polarization in the radio (e.g., [6]) and optical (e.g., [7]) wavebands. For the high-energy (X-ray through $\gamma$-ray) SED component, both leptonic (high-energy emission dominated by electrons and/or electron-positron pairs) and hadronic (high-energy emission dominated by ultrarelativistic protons) models are being considered (for a comparative discussion of both types of models with application to a sample of $\gamma$-ray blazas see, e.g., [8], and for a general review of emission models of relativistic jet sources, see, e.g., [9]).

The population of blazars consists of flat-spectrum radio quasars (FSRQs) and BL Lac objects, the latter distinguishing themselves by (nearly) featureless optical spectra with emission-line equivalent widths $EW<5$Å. An alternative classification based on the broad-emission-line luminosity (rather than EW) was proposed by [10]. The featureless optical continuum spectra of BL Lac objects often makes it difficult or impossible to determine their redshift. A more physical distinction between different blazar classes might be on the basis of the location of their SED peak frequencies. Low-synchrotron peaked blazars (LSP) are defined by having a synchrotron peak frequency ${\nu }_{\mathrm{sy}}<{10}^{14}$ Hz, intermediate-synchrotron peaked blazars (ISP) have ${10}^{14}\mathrm{Hz}\le {\nu }_{\mathrm{sy}}<{10}^{15}$ Hz, while high-synchrotron peaked blazars (HSPs) have ${\nu }_{\mathrm{sy}}>{10}^{15}$ Hz [11]. Most HSP and ISP blazars have been classified as BL Lac objects based on their optical spectra, while the LSP class contains both FSRQs and low-frequency-peaked BL Lac objects.

In leptonic models, the high-energy emission is produced by Compton scattering of soft (IR–optical–UV) target photon fields by relativistic electrons. Target photon fields can be the co-spatially produced synchrotron radiation (synchrotron self-Compton or SSC; see, e.g., [12]) or external radiation fields, such as those from the accretion disk (e.g., [13]), the broad-line region (e.g., [14]) a dusty, infrared-emitting torus (e.g., [15]), or synchrotron emission from other, slower or faster moving regions of the jet, such as a slow sheath surrounding the highly relativistic spine in a radially stratified jet (e.g., [16]) or another (slower/faster) jet component in a decelerating jet flow (e.g., [17]). Even though in leptonic models the radiation output is dominated by electrons and/or pairs, it is generally believed that the jets also contain non- or mildly-relativistic protons. Due to their much larger mass, they will not contribute significantly to the radiative output, but they may still carry a significant (if not dominant) fraction of the momentum and kinetic power of the jet (see, e.g., [18]).

In hadronic models for blazar emission, it is assumed that protons are accelerated to ultra-relativistic energies so that they can dominate the high-energy emission through proton-synchrotron radiation (e.g., [19,20]) or through photo-pion production (e.g., [21,22]), with subsequent pion decay leading to the production of ultra-high-energy photons and pairs (and neutrinos!). These ultra-relativistic secondary electrons/positrons lose their energy quickly due to synchrotron radiation. Both these synchrotron photons and the initial ${\pi }^0$ decay photons have too high energy to escape $\gamma \gamma$ absorption in the source, thus initiating synchrotron-supported pair cascade. This typically leads to very broad emerging $\gamma$-ray spectra, typically extending into the X-ray regime (e.g., [23]).

This review will provide, in Section 2, an overview of recent observational highlights on blazars across the electromagnetic spectrum, including aspects of flux and polarization variability, as well as multi-messenger aspect, especially the recent likely identification of the blazar TXS 0506+056 as a source of very-high-energy neutrinos detected by IceCube. Necessarily, this review will need to focus on recent highlights for a few selected topics, also biased by the author’s scientific interests. However, a balanced and fair review of relevant works on the selected topics is attempted.

Section 3 summarizes recent developments on the theory side, with a view towards inferences from these recent observational highlights. Section 4 prospects for future multi-wavelength and multi-messenger observations, especially towards addressing the following questions, where the author believes that major breakthroughs are possible through dedicated blazar observations within the next decade:

• What is the matter composition of blazar jets, and what is the dominant particle population responsible for the high-energy emission? Answering this question will allow major progress concerning physics of jet launching and loading, and the mode of acceleration of relativistic particles in jets.
• What is the structure of magnetic fields in the high-energy emission region and their role in the acceleration of relativistic particles? The answer to this question will aid in understanding the physics of jet collimation and stability and provide further clues to the physics of ultra-relativistic particle acceleration (magnetic reconnection vs. shocks vs. shear layers, …)
• Where along the jet is high-energy and very-high-energy $\gamma$-ray emission predominantly produced? Different observational results currently point towards different answers (sub-pc vs. 10s of pc from the central black hole). The confident localization of the blazar $\gamma$-ray emission region will further constrain plausible radiation mechanisms and could possibly hint at beyond-the-standard-model physics (if evidence suggests that $\gamma \gamma$ absorption in the radiation field of the broad line region is suppressed below standard expectations).

Throughout the text, physical quantities are parameterized with the notation $Q={10}^x{Q}_x$ in c.g.s. units.

2. Recent Observational Highlights

This section summarizes highlights of recent multi-wavelength and multi-messenger observations of blazars, focusing on results directly probing the high-energy emission region, which tends to be optically thick to radio wavelengths. Radio observations typically probe the larger-scale (pc-scale and larger) structure of jets and will not be discussed in this review. For recent reviews of radio observations of blazar jets, the reader is referred to, e.g., [24,25,26,27].

2.1. Flux Variability

Blazars are characterized by their significant variability across the entire electromagnetic spectrum, on all time scales ranging from years down to minutes. In addition to the very short variability time scales, a major challenge for our understanding of the optical through $\gamma$-ray emission is the fact that the variability patterns in different wavelength bands do not show a consistent behaviour of correlation (or non-correlation).

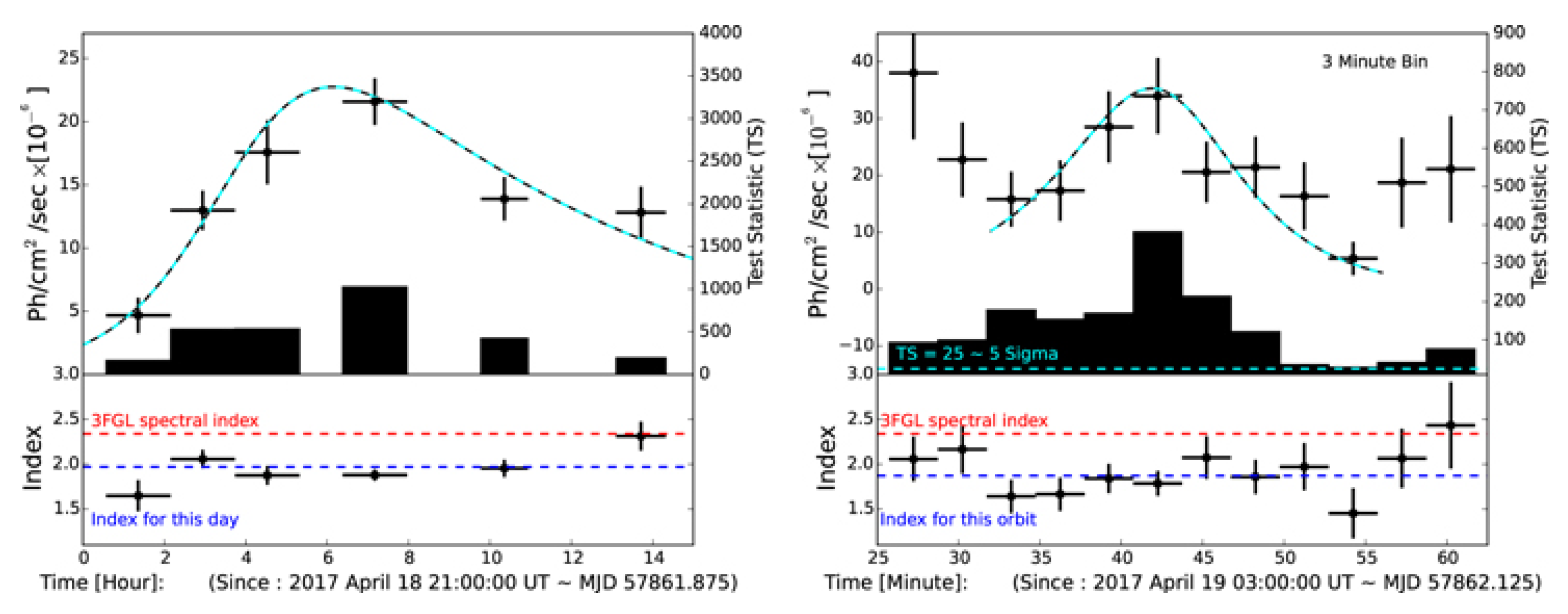
2.1.1. Minute-Scale Variability

The shortest variability time scales, down to minutes, have been found in very-high-energy $\gamma$-ray observations using ground-based Imaging Atmospheric Cherenkov Telescope (IACT) facilities (H.E.S.S., MAGIC, VERITAS). They were first identified in HSP blazars, such as PKS 2155-304 [2] and Mrk 501 [3], but later also in LSP blazars, namely the prototypical BL Lac object BL Lacertae [5] and the FSRQ PKS 1222+21 [4]. Remarkably, sub-hour very-high-energy (VHE) $\gamma$-ray variability was also seen by MAGIC in IC 310 [28], which, based on its large-scale radio structure had been classified as a radio galaxy, in which case relativistic beaming effects would be inefficient. However, its broadband SED and variability behaviour suggest a blazar-like orientation of the inner jet, as is probably also the case for the H.E.S.S.-detected radio galaxy PKS 0625-35 [29].

Rapid variability has also been seen at GeV energies with Fermi-LAT, although the limited photon statistics (because of the ∼${10}^5$ times smaller collection area of Fermi-LAT compared to IACTs) typically limits the time scales to ≳hours (e.g., [30,31]). Note, however, that minute-scale GeV variability has been detected with Fermi-LAT during the giang $\gamma$-ray outburst of 3C 279 in June 2015 [32] and, more recently, at $4.7\sigma$ significance during the exceptional long-term outburst of the FSRQ CTA 102 in 2016–2017 (see Figure 1 [33]).

Due to causality arguments, the observed variability time scale $t_{\mathrm{var}}^{\mathrm{obs}}$ imposes a limit on the size R of the emission region,

$$R\le c{t}_{\mathrm{var}}^{\mathrm{obs}}\frac{\delta }{1+z}=1.8\times {10}^{14}\left(\frac{t_{\mathrm{var}}^{\mathrm{obs}}}{5\min }\right){\delta }_1.$$

(1)

The observed $\gamma$-ray flux, modulo Doppler boosting, implies a luminosity, which can be translated into a lower limit on the photon energy density in the emission region, using the size constraint from Equation (1). Since there is, so far, no evidence for internal $\gamma \gamma$ absorption on the co-spatially produced low-energy (IR–X-ray) radiation field in the MeV–GeV $\gamma$-ray emission of blazars, the emission region must be optically thin to this process. This then implies a lower limit on the Doppler factor. $\gamma$-ray photons in the GeV regime interact primarily with target photons that are observed in the X-ray regime. Assuming an observed X-ray spectrum with an energy spectral index ${\alpha }_X$ and an integrated flux $F_{0-1}$ in the range $E_0$ to $E_1$ (corresponding to normalized energies ${ϵ}_{0,1}\equiv E_{0,1}/\left[m_e{c}^2\right]$), the limit on the Doppler factor can be derived as [34,35]

$$\delta \ge {\left({10}^{3{\alpha }_X}\frac{{\sigma }_T{d}_L^2}{3m_e{c}^4{t}_{\mathrm{var}}^{\mathrm{obs}}}{F}_{0-1}\frac{1-{\alpha }_X}{{ϵ}_1^{1-{\alpha }_X}-{ϵ}_0^{1-{\alpha }_X}}{[1+z]}^{2{\alpha }_X}{E}_{GeV}^{{\alpha }_X}\right)}^{\frac{1}{4+2{\alpha }_X}}.$$

(2)

where $E_{GeV}$ is the maximum photon energy (in units of GeV) out to which there is no evidence for a spectral break due to $\gamma \gamma$ absorption (typically of the order of ∼10–100 GeV in the case of most Fermi blazars), $d_L$ is the luminosity distance, and ${\sigma }_T$ is the Thomson cross section. In the case of the 5-min variability observed in a few blazars, this, in fact, implies minimum Doppler factors of $\delta$≳ 50 [36]. Such values are much higher than the Doppler factors of $\delta \sim 10$ typically inferred from superluminal motion speeds observed in radio Very Long Baseline Interferometry (VLBI) monitoring observations of blazars (e.g., [37,38])—a problem sometimes referred to as the Doppler-factor crisis [39]. Various suggested model solutions to this problem will be discussed in Section 3.1.

2.1.2. Multiwavelength Correlations

Another major challenge to our current understanding of the physical processes in blazar $\gamma$-ray emission regions is the fact that multi-wavelength variability patterns are sometimes correlated, sometimes not, among different wavelength bands. Even within the same object, the correlated/uncorrelated variability behaviour changes between different observation periods. Most blazar emission scenarios ascribe the entire IR–$\gamma$-ray emission to one single dominant emission region (single-zone models). In this case, one would naturally expect all radiating particles to be subject to the same acceleration and cooling mechanisms. As the radiative cooling time scales of particles are energy-dependent (scaling as $t_{\mathrm{cool}}\propto {\gamma }^{-1}$ for synchrotron radiation and Thomson scattering), variability patterns at different energies are expected to show time delays, but still be correlated. In fact, if an observed time delay between the variability patterns at two frequencies $E_1=E_{1,keV}$ keV and $E_2=E_{2,keV}$ keV is related to different radiative cooling time scales of synchrotron-emitting electrons radiating at those energies, this can be used to place a lower limit on the magnetic field [40]. If electron cooling is dominated by synchrotron and Compton cooling in the Thomson regime, a synchrotron time delay ${\tau }_{1,2}\equiv {\tau }_h$ hr translates into a lower limit on the magnetic field of

$$B\gtrsim 0.9{\tau }_h^{-2/3}{\delta }^{-1/3}{(1+k)}^{-2/3}{\left(E_{1,keV}^{-1/2}-E_{2,keV}^{-1/2}\right)}^{2/3}\mathrm{G}$$

(3)

where $k=L_{\mathrm{C}}/L_{\mathrm{sy}}$ is the Compton dominance parameter of the SED. Such arguments have, in several cases, constrained the magnetic fields in the emission regions of blazars to be of the order of B≳ 1 G (e.g., [41]).

In the case of LSP blazars, leptonic single-zone emission models predict the optical synchrotron emission and GeV (Compton) $\gamma$-ray emission to be produced by electrons of approximately the same energy. The optical and $\gamma$-ray light curves are therefore expected to be closely correlated with very small time lags. In the case of HSP blazars, the same type of correlation is expected to exist between X-rays and VHE $\gamma$-rays. Such a close correlation is often observed, but there are also many examples in which the correlation is absent. The most striking cases are the so-called “orphan flares”, in which either $\gamma$-ray flares occur with no visible counterpart in the synchrotron component ((e.g., [42,43]), or synchrotron (IR–optical–X-ray) flares without $\gamma$-ray counterpart.

A remarkable and unusual case of an orphan flare was detected by H.E.S.S. from the FSRQ 3C 279 on 27–28 January 2018 [44]. H.E.S.S. observations had been triggered by a Fermi-LAT detected GeV $\gamma$-ray flare of 3C 279 around 16 January 2018. While H.E.S.S. did not detect the source around the time of the Fermi-LAT flare, a significant detecton (∼11$\sigma$) resulted with a delay of ∼11 days with respect to the GeV flare (see Figure 2). Also the optical (e.g., from the Steward Observatory Blazar Monitoring Program1) and X-ray (e.g., Swift-XRT2) light curves showed no renewed activity at the time of the H.E.S.S. VHE flare detection. Such orphan flares appear to strongly argue against simple single-zone emission models, and possible alternatives will be discussed in Section 3.1.

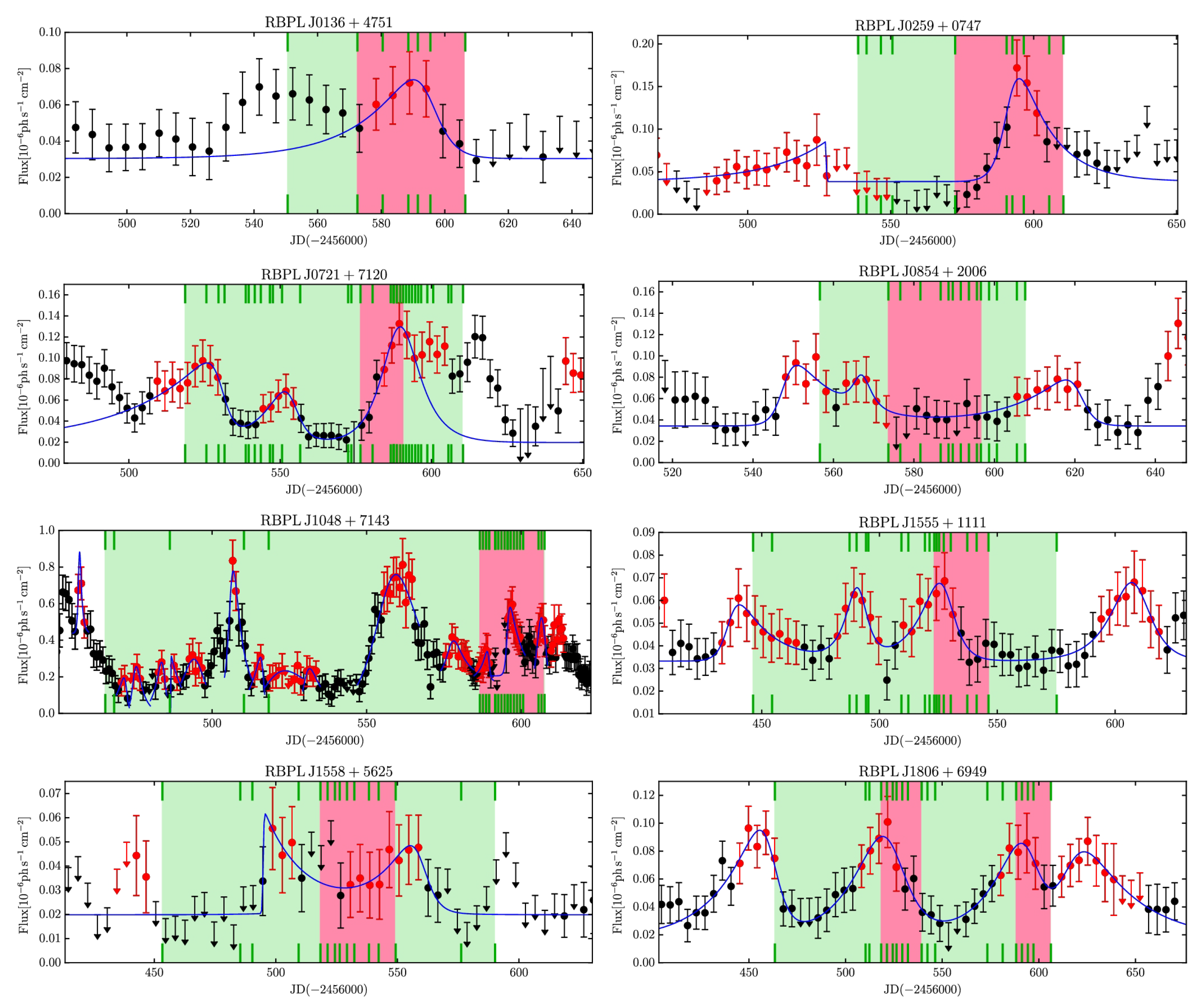
2.1.3. Periodicities?

AGN activity is often associated with recent galaxy mergers (e.g., [45,46,47,48]). If this is true, then one might expect binary supermassive black hole (SMBH) systems, instead of a single SMBH, to be present in the centers of at least some AGN. The orbital modulation as well as Lense-Thirring precession of the dominant accretion disk (and likely also the jet), might then lead to periodic or quasi-periodic modulations of the multi-wavelength emissions of blazars. However, the only case in which quasi-periodicity, likely related to the presence of a binary SMBH system, is clearly established, is the BL Lac object OJ 287, where a dominant SMBH of ∼ a few $\times {10}^9{M}_{\odot }$ appears to be in a ∼12 year orbit with a smaller SMBH, which intercepts the primary accretion disk twice per orbit [49,50,51].

Given the long time lines of many (especially optical and radio) blazar monitoring campaigns and the now ∼10 years of operations of Fermi, continuous $\gamma$-ray and well-sampled multi-wavelength light curves now exist for a large number of blazars, allowing for efficient searches for periodicities on yearly time scales. The most promising candidate for such periodicities appears to be the BL Lac object PG 1553+113, where a period of ∼2.2 years has been identified in Fermi-LAT and multi-wavelength data [52], possibly including secondary “twin peaks” symmetrically spaced around the main peaks [53]. A systematic search for periodicities in Fermi-LAT blazar light curves by [54], however, finds no significant evidence for periodicities beyond 95% confidence in any of the 10 sources studied, including PG 1553+113. Thus, one may conclude that the question concerning periodicities and the existence of binary SMBHs in blazars (beyond the case of OJ 287) is still controversial.

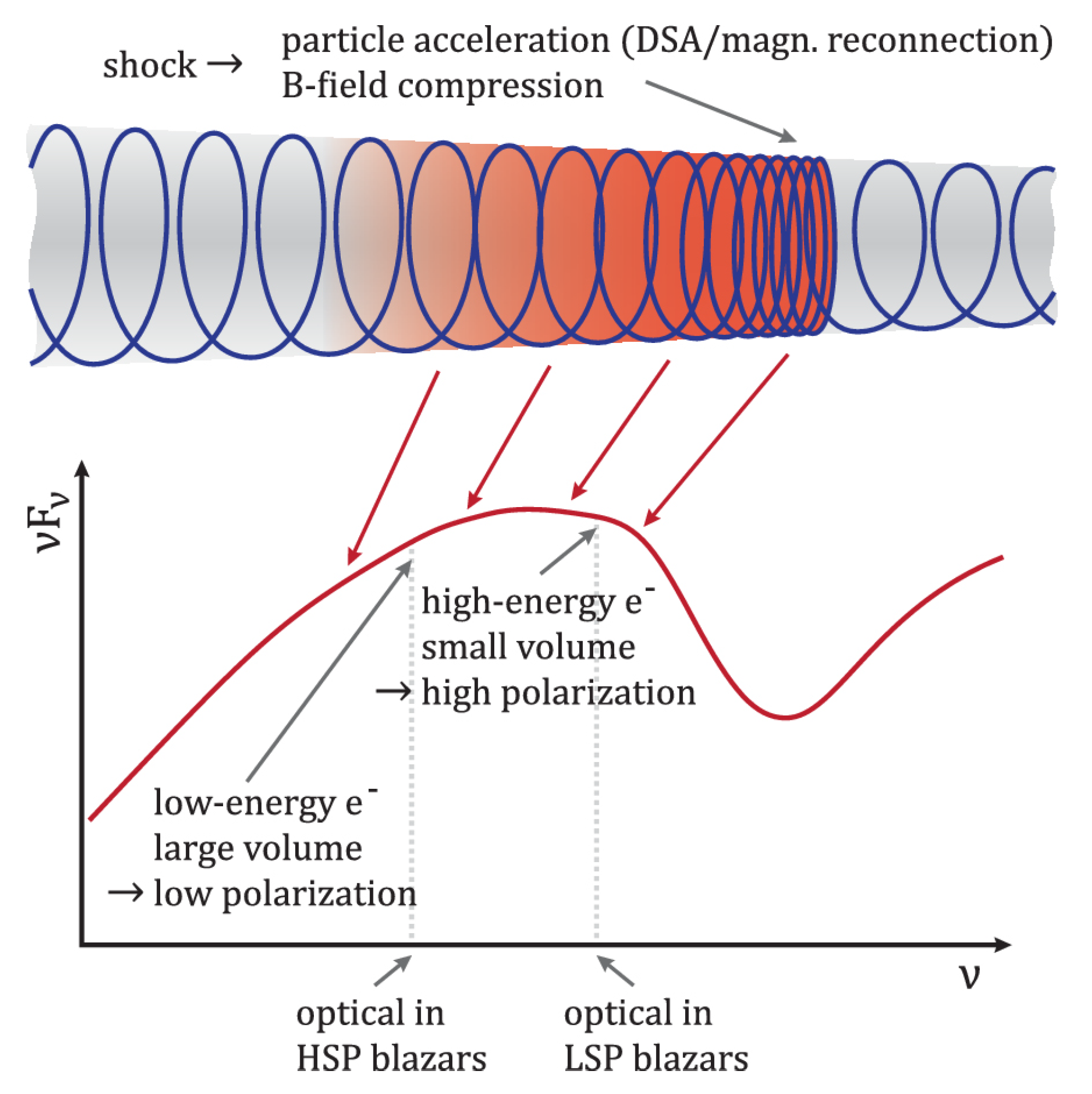
2.2. Polarization—Variability

The radio through optical emission from blazars has long been known to be polarized with significant variability both in the degree of polarization ($\mathsf{\Pi }$) and the polarization angle (PA). In this review, we will focus on optical polarization measurements, as those might be the best probes of the magnetic field structure in the high-energy emission region. The optical polarization in blazars varies from virtually unpolarized sources/states to highly polarized states with polarization degrees of $\mathsf{\Pi }\lesssim 50$% (e.g., [55]). In addition to photopolarimetric and spectropolarimetric monitoring of blazars by, e.g., the Steward Observatory blazar monitoring program, a systematic study of the polarization variability of a large sample of blazars was performed with the RoboPol polarimeter3 on the 1.3 m telescope of the Skinakas Observatory [56].

The average degree of polarization has been found to be systematically larger for $\gamma$-ray loud blazars compared to $\gamma$-ray quiet ones [57], which is likely due to the fact that $\gamma$-ray loud blazars appear more strongly Doppler boosted and thus more strongly synchrotron dominated in the optical spectrum. The average degree of optical polarization systematically decreases as a function of increasing synchrotron peak frequency within the RoboPol sample [57]. This may be attributed to the fact that in LSP blazars, the optical range is at or near the peak of the synchrotron emission, thus reflecting freshly accelerated electrons in a presumably very confined region in the jet, while in HSP blazars, optical-synchrotron-emitting electrons have already cooled substantially and are most likely distributed over a larger portion of the jet (see Figure 3).

While the PAs in blazars typically exhibit erratic small-angle variations, they occasionally undergo systematic PA swings exceeding 180${}^{\circ }$, typically over the course of a few days [58,59,60]. These PA swings are often associated with $\gamma$-ray and multi-wavelength flares. A central goal of the RoboPol project was a systematic study of such PA swings in a large sample of blazars [7,56,61,62,63,64]. Key results of this study were that (a) PA rotations do not occur in all blazars, but whether a blazar shows PA rotations or not does not appear to depend on its sub-class (FSRQ/BL Lac object/LSP/HSP) or its average fractional polarization [7], and (b) PA rotations are statistically correlated with $\gamma$-ray flares detected by Fermi-LAT, while the reverse is not true, i.e., not all Fermi-LAT flares in a blazar showing PA rotations are actually associated with such a rotation ([63] see Figure 4). Notably, also, there does not appear to be a preferred direction of PA rotations, i.e., PA swings can occur in either direction in any given object.

The observations of such PA variability, and especially the PA swings, have spurred a large number of theoretical works attempting to explain them. They will be discussed in Section 3.2.

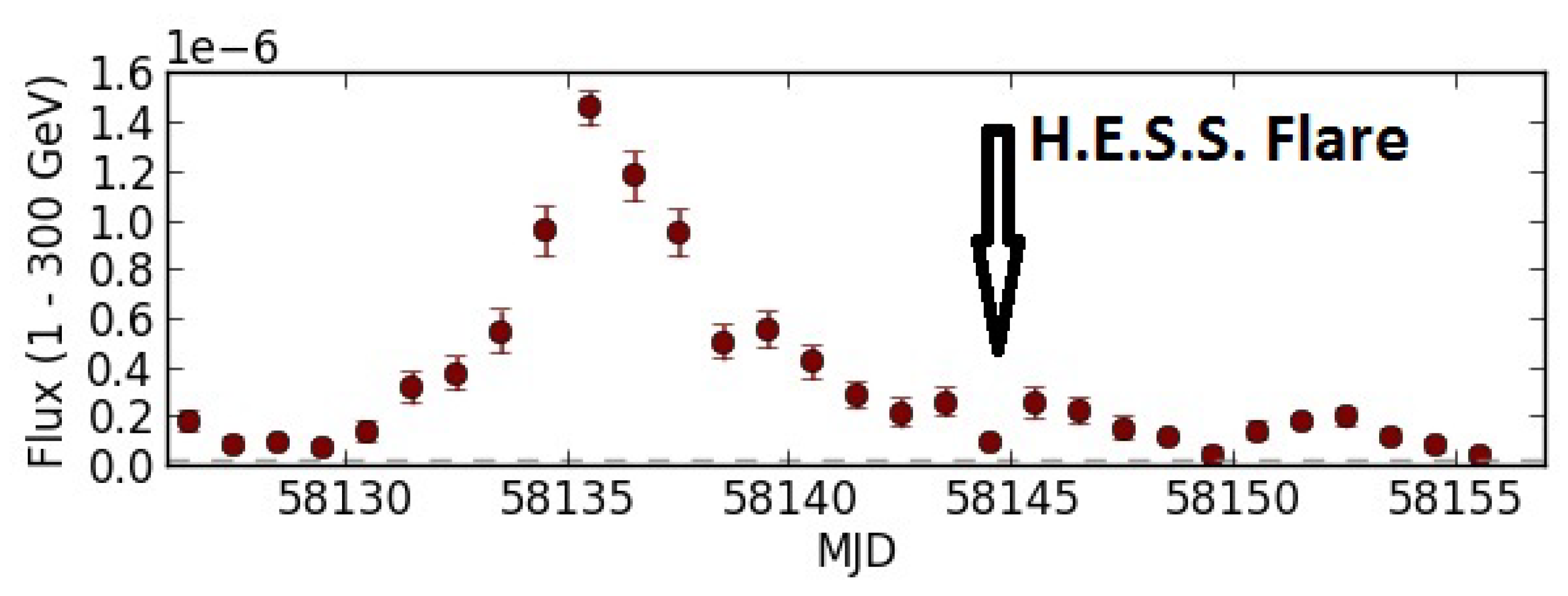
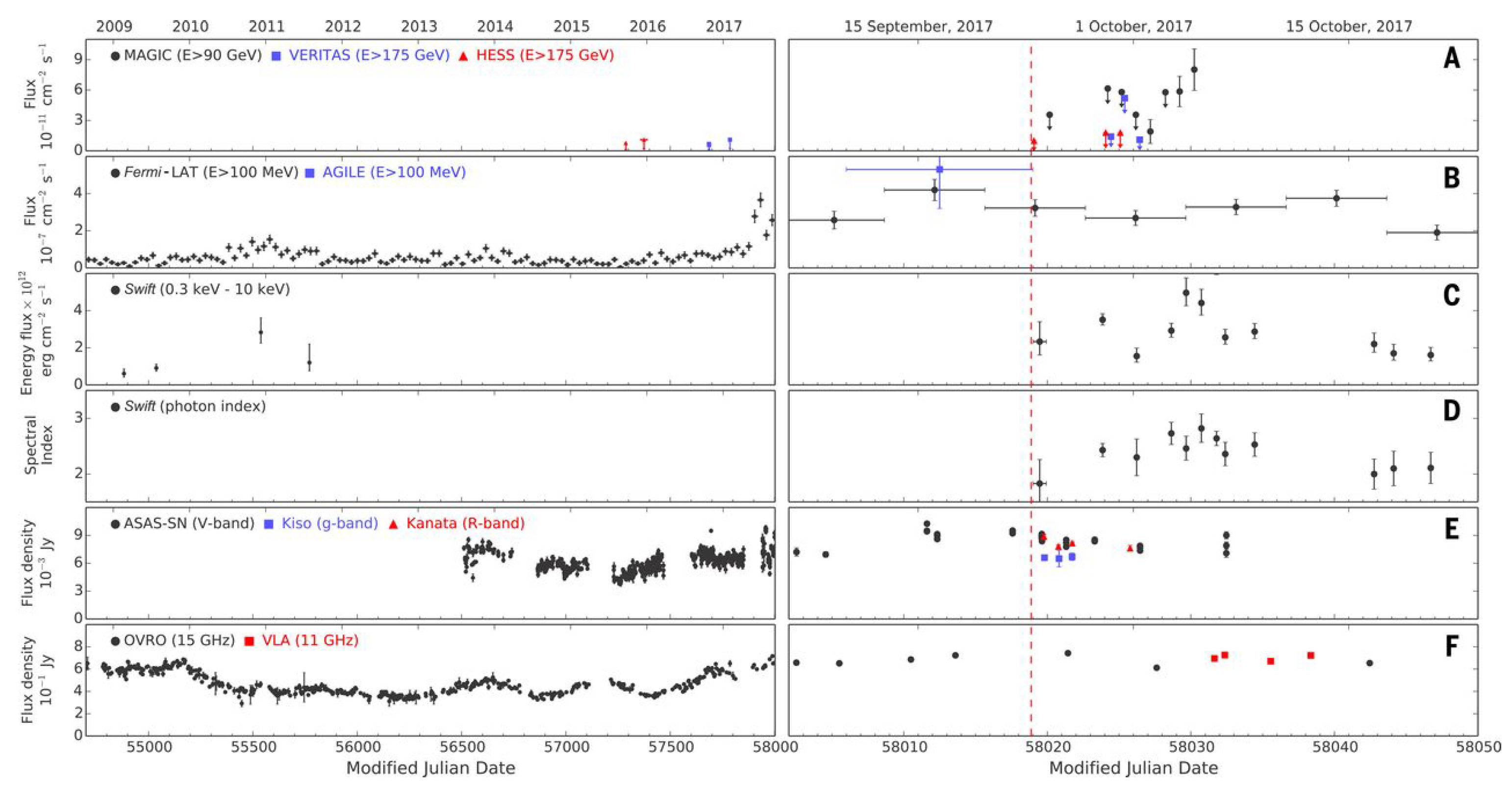
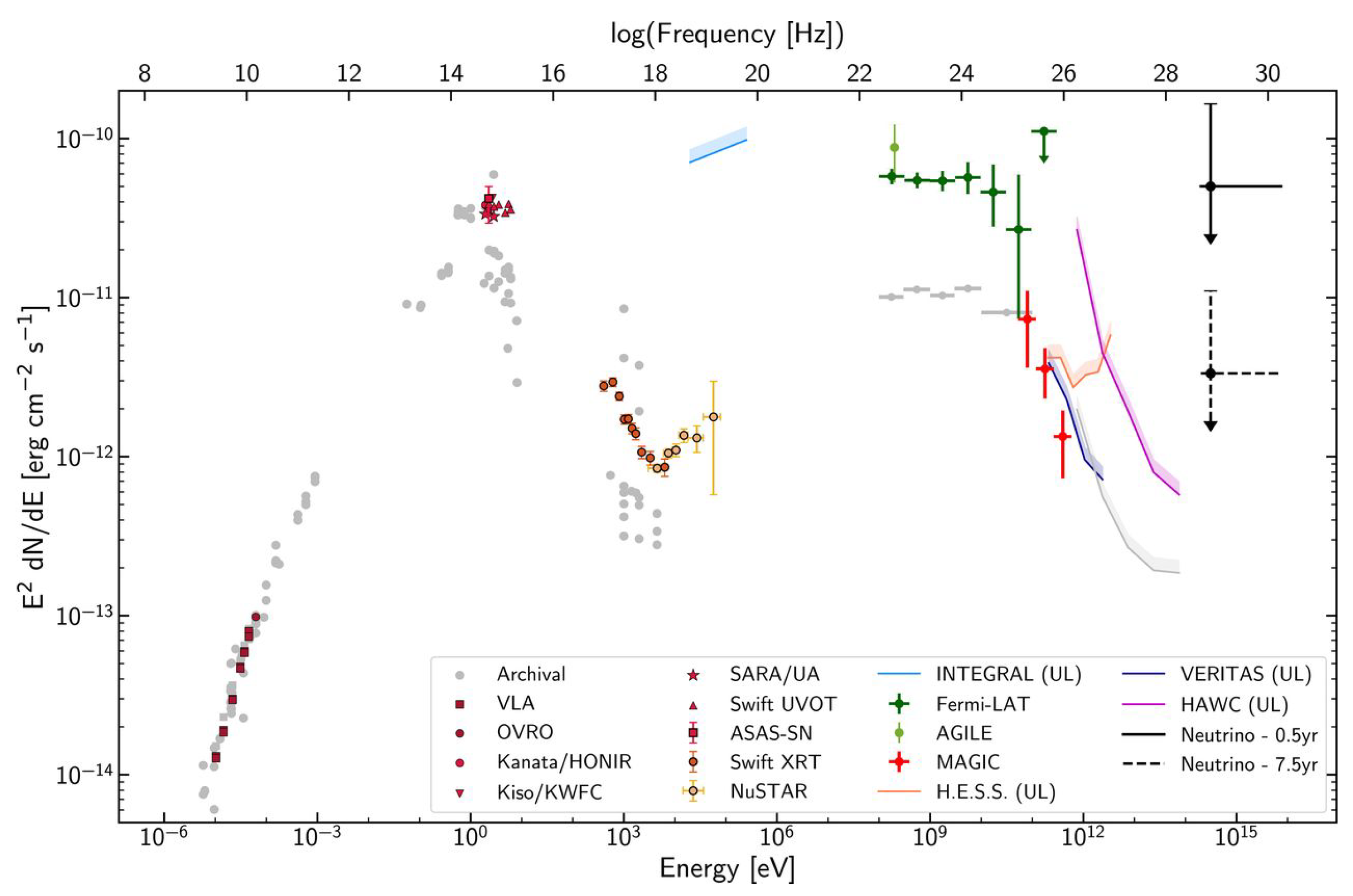
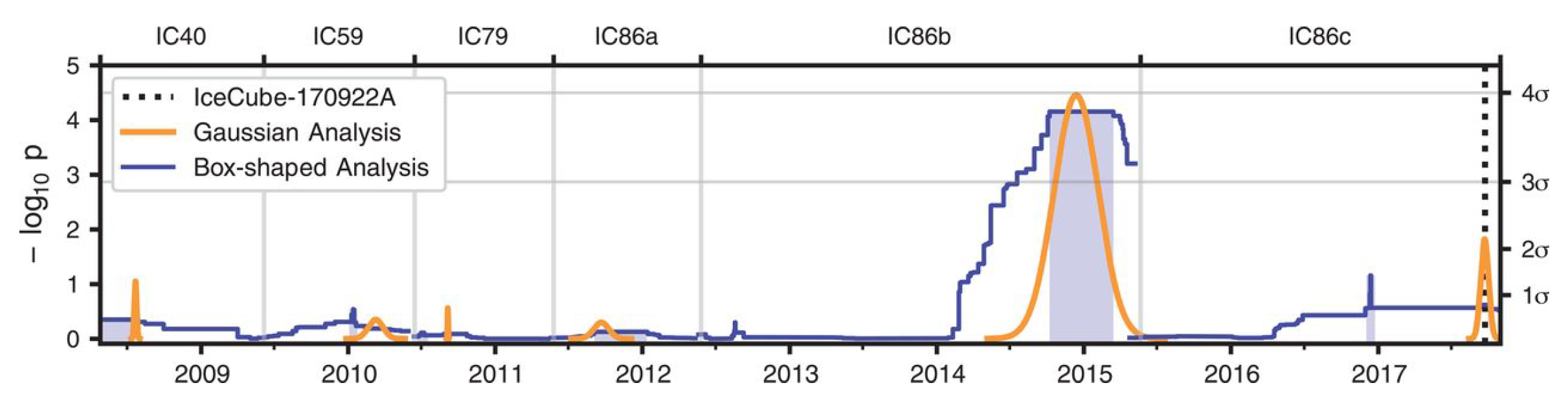
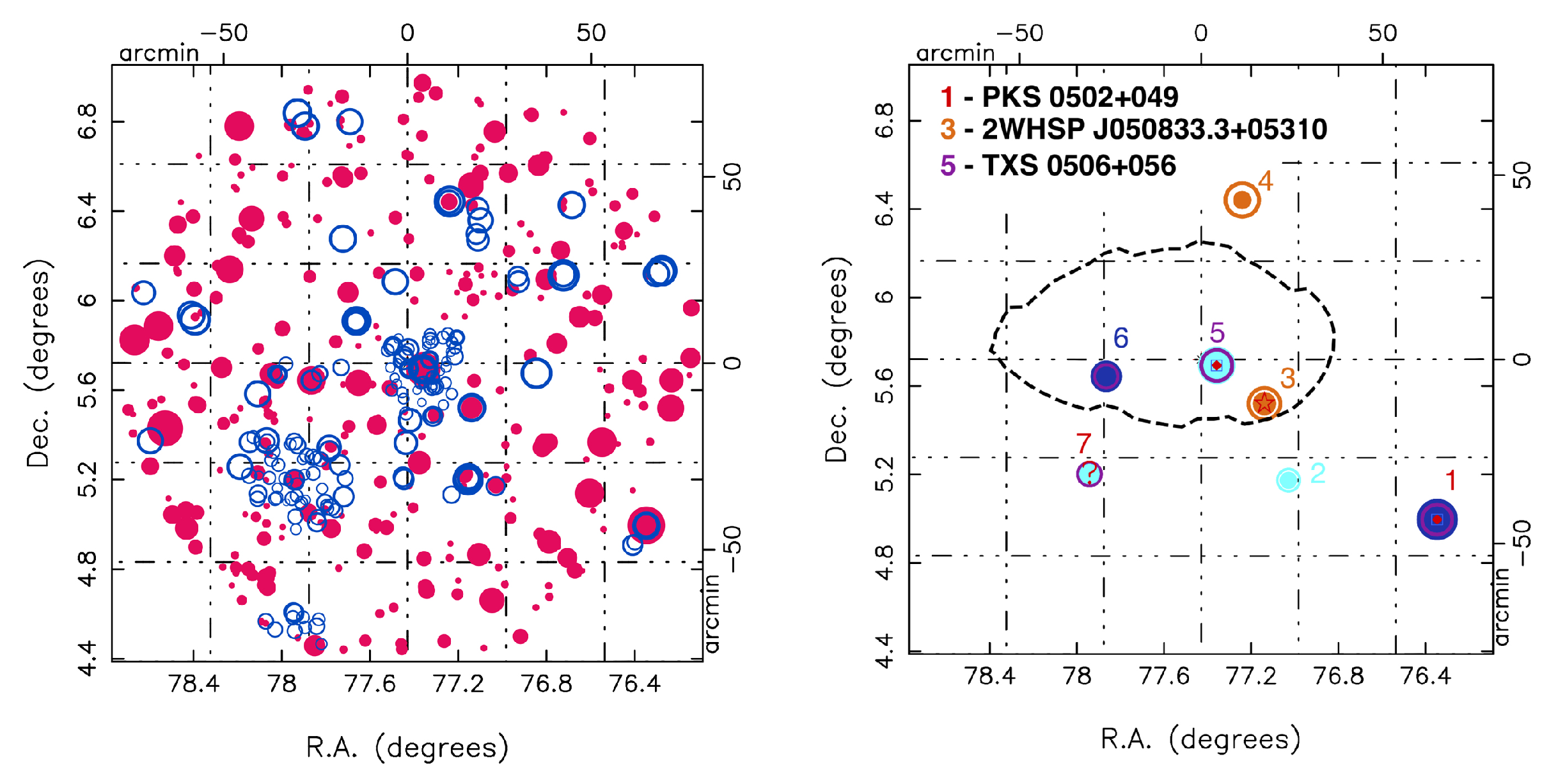
2.3. Multi-Messenger Observations—Neutrinos

The past few years (2015–2018) marked the birth of multi-messenger astronomy, with the first direct detection of gravitational waves from a binary-black-hole merger [65], the first confirmed multi-messenger detection of gravitational waves from a binary-neutron-star merger and the associated short gamma-ray burst [66], and the first strong hint for a blazar as the source of astrophysical high-energy neutrinos [67,68].

The jets of AGN have long been considered a prime candidate for the sites of acceleration of high-energy cosmic rays and the production of high-energy neutrinos, as detected by IceCube [69,70]. Such neutrino emission is expected in hadronic models for the $\gamma$-ray emission from blazars (e.g., [21,23,71,72,73,74,75]). However, until 2017, all searches for electromagnetic counterparts of the IceCube astrophysical neutrinos remained inconclusive (e.g., [76,77]), except for the identification of the blazar PKS B1424-418 as the possible source of the PeV IceCube neutrino event HESE-35 (aka “Big Bird”), which was detected during an extended multi-wavelength outburst of the blazar in 2012–2013 [78].

This picture changed with the detection of the ∼290 TeV neutrino IceCube-170922A from a direction consistent with the blazar TXS 0506+056 [67] on 22 September 2017. The blazar was in an extended GeV $\gamma$-ray flaring state in September–October 2017 (see Figure 5), as detected by Fermi-LAT, and was subsequently also detected in VHE $\gamma$-rays by MAGIC. This single neutrino, however, only had a ∼50% likelihood of actually being of astrophysical origin (due to its moderate energy), thus, by itself, providing only marginal evidence for the association. Furthermore, being only one single event, it allowed for the calculation of only flux upper limits (see Figure 6). In an archival search for additional neutrino events from the direction of TXS 0506+056, however, the IceCube collaboration found evidence for an excess of $13\pm 5$ astrophysical high-energy muon-neutrinos from that location during an extended ∼5 month long period in 2014–2015 [68], henceforth termed the “neutrino flare” (see Figure 7). This provided the first strong hint for TXS 0506+056 being a source of high-energy neutrinos, and allowed for the first calculation of a measured high-energy neutrino flux from an astrophysical source, corresponding to an all-flavour fluence (after correcting for neutrino oscillations) of ${4.2}_{-1.4}^{+2.0}\times {10}^{-3}$ erg cm${}^{-2}$ with a spectrum between 32 TeV and 3.6 PeV fitted by a power-law with spectral index $\gamma =2.1\pm 0.3$.

Most notably, the $\gamma$-ray and multi-wavelength flux of TXS 0506+056 during the time of this neutrino flare showed no evidence of enhanced activity. Note, however, that [79] identified a nearby blazar, PKS 0502+049, which was in a $\gamma$-ray flaring state for several weeks before and after the 2014–2015 neutrino flare (see Figure 8), but disfavour this source as the potential counterpart of IceCube-170922A as it was not flaring during the neutrino flare, but TXS 0506+056 was in a historical hard-spectrum (but low-flux) state at that time. The substantial body of theoretical developments spurred by this association will be discussed in Section 3.3.

3. Theoretical Developments

This section summarizes some of the most recent developments in the modeling and interpretation of the multi-wavelength and multi-messenger emission from blazars, specifically addressing the observational highlights described in the previous section. For a general review of leptonic and hadronic blazar emission models, see, e.g., [8,34,80].

3.1. Models of Flux Variability

As elaborated in Section 2.1, observed blazar variability patterns pose at least two major challenges to currently existing blazar radiation models: (a) the rapid, minute-scale ($\gamma$-ray) variability, and (b) the inconsistent cross-correlation patterns, with emission in different wavelength bands being sometimes correlated, sometimes not, including occurrences of orphan flares. This section will provide a brief overview over various blazar variability models currently “on the market”, discussing how they may have the potential to address the issues mentioned in the preivous section.

3.1.1. Causes of Variability

Variability of blazar emission can, in principle, be caused in a variety of ways, by which different models may be classified:

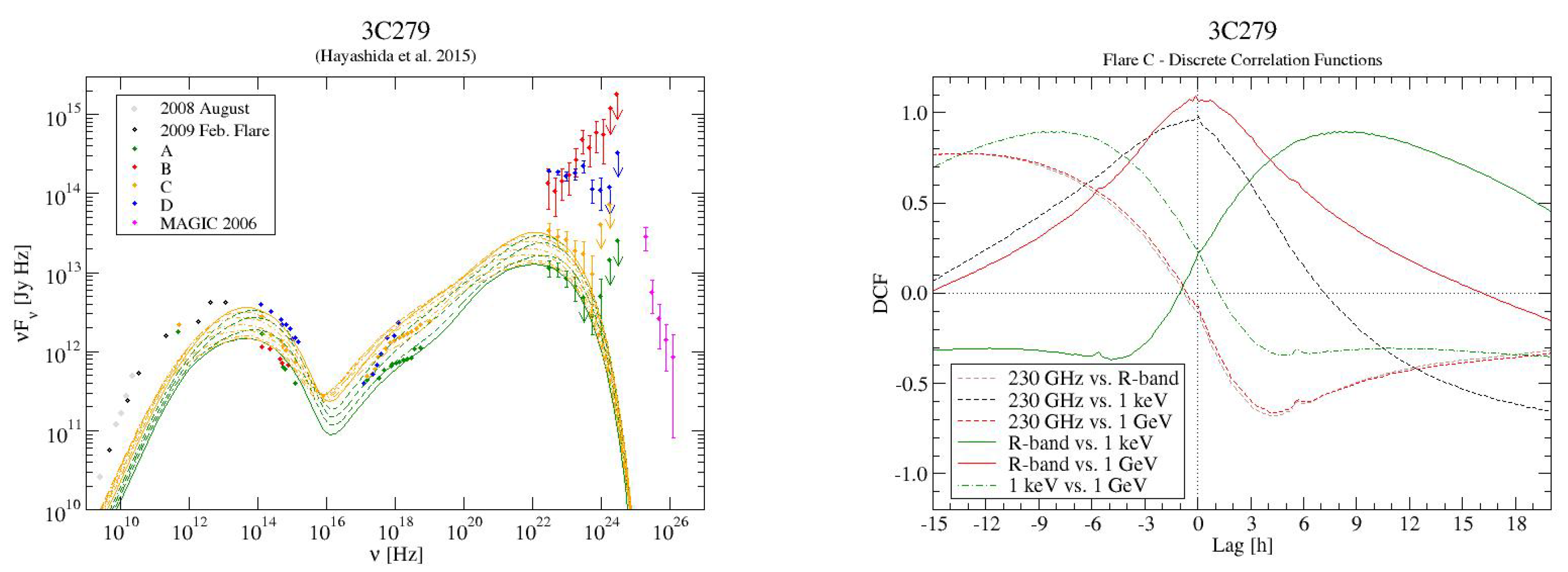
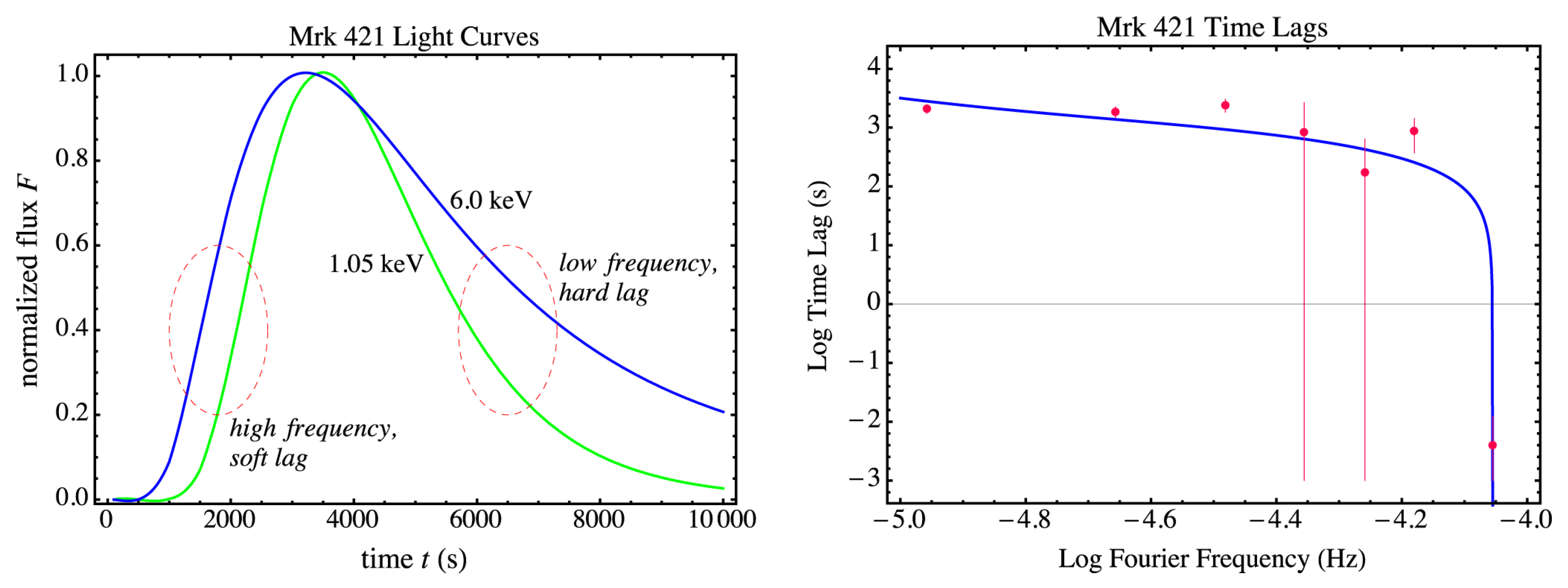
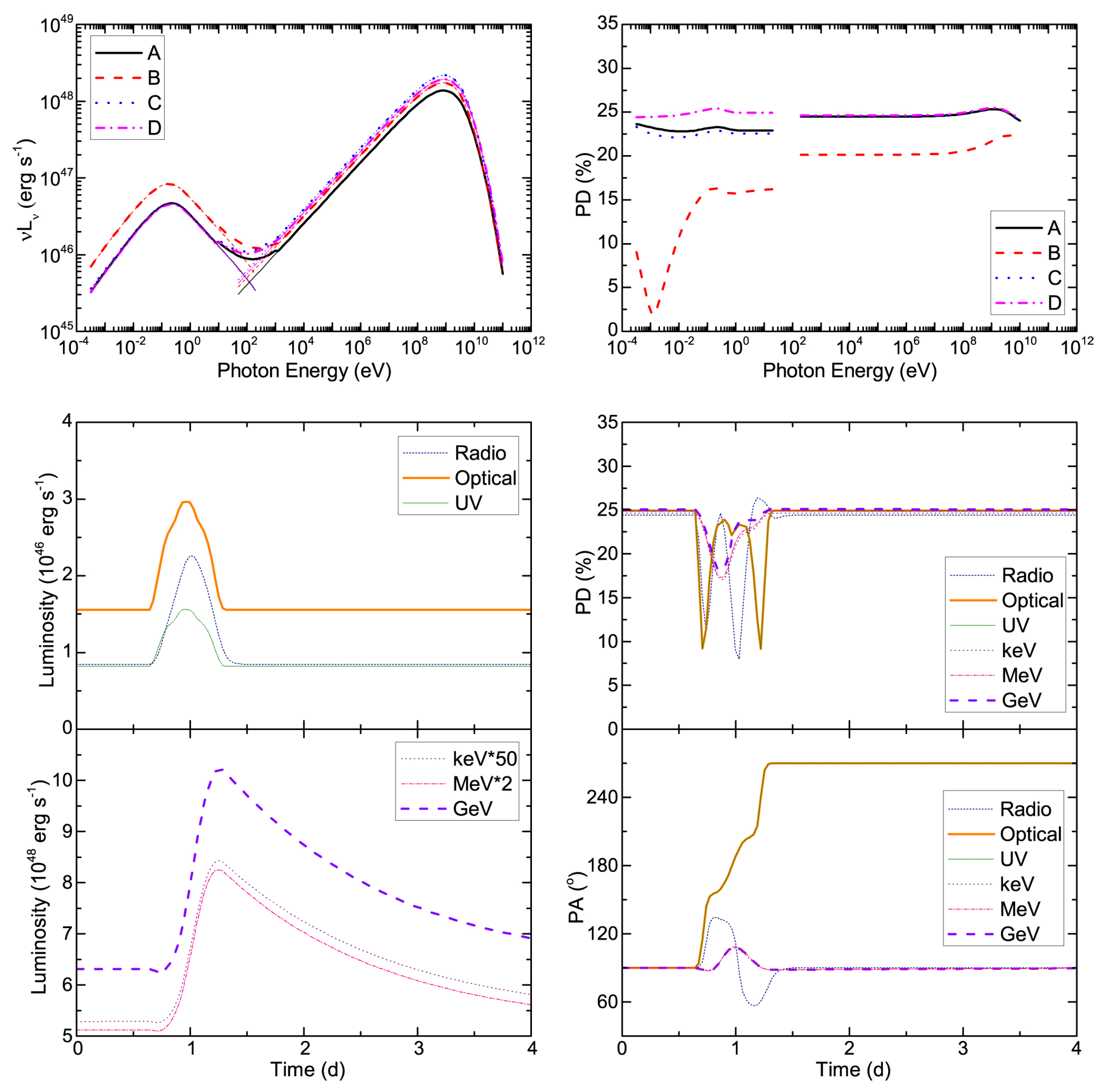
• Shock-in-jet models: In these models (also termed “internal shock models”) inhomogeneities in the jet flow produce mildly relativistic shocks travelling through the (relativistically moving) jet plasma, leading to the acceleration of particles, most plausibly through Diffusive Shock Acceleration (DSA; see, e.g., [81,82,83,84,85]). The shock-in-jet model for blazars was first suggested in the seminal work by Marscher & Gear [86], and subsequently refined in a large number of works, mostly in the framework of leptonic emission scenarios (e.g., [87,88,89,90,91,92,93,94,95,96,97,98]).
  In shock-in-jet models, particle acceleration occurs in a single region around the shock, equally affecting all radiating particles (leptonic or hadronic). Thus, these models generally predict correlated multi-wavelength variability with inter-band time lags reflecting energy-dependent electron (or proton) cooling (and/or acceleration) time scales (e.g., [87]). In the case of a leptonic emission scenario, for FSRQs, the optical and GeV $\gamma$-ray emissions are produced by electrons of similar energies and therefore are expected to be correlated with close to zero time lag. Radio and X-rays are produced by lower-energy electrons, expected to exhibit a delayed response compared to the optical and $\gamma$-ray emissions. Figure 9 shows an example resulting from a shock-in-jet simulation representing a multiwavelength flare of the FSRQ 3C 279 (flare C from [30]), where the radio and X-ray emissions are expected to lag behind the optical and VHE $\gamma$-ray emissions by ∼10 h. In the case of HSP blazars, the X-ray and $\gamma$-ray emissions are expected to be closely correlated, with GeV $\gamma$-ray and optical emissions lagging behind the X-ray and VHE variations.
  Uncorrelated variability amongst the two SED components could be achieved, in the framework of shock-in-jet models, with the assumption of the emission from the dominant shock being strongly synchrotron- or high-energy (Compton in leptonic models) dominated, enhancing the quiescent emission from the larger-scale jet only in a narrow frequency band (e.g., [99,100]). Alternatively, in a hadronic shock-in-jet scenario, vastly different acceleration time scales of electrons and protons might give the impression of uncorrelated variability due to the long time delay between the radiation components produced by electrons and protons (e.g., see [101] Figure 10).
  Shock-in-jet models naturally assume that the shock affects the entire cross section of the jet, with a radius of typically $R_{\perp }\sim {10}^{15}$–${10}^{16}$ cm. As discussed in Section 2.1, this constrains the variability time scale to $t_{\mathrm{var}}\gtrsim R_{\perp }(1+z)/\left(\delta c\right)\sim 9R_{\perp ,16}(1+z)/{\delta }_1$ hours, which is very difficult to reconcile with minute-scale variability, unless a very small jet cross section and/or a very large Doppler factor are assumed.
  It is well known that the formation of strong shocks and efficient particle acceleration at shocks is suppressed in the presence of a dominant magnetic field (e.g., [102]). The low magnetizations ($u_B/u_e\sim 0.1$–${10}^{-3}$) typically inferred from broadband SED modeling of blazars (see, e.g., [8,103]) therefore seem to support the hypothesis of shocks being the dominant particle acceleration sites in blazars.
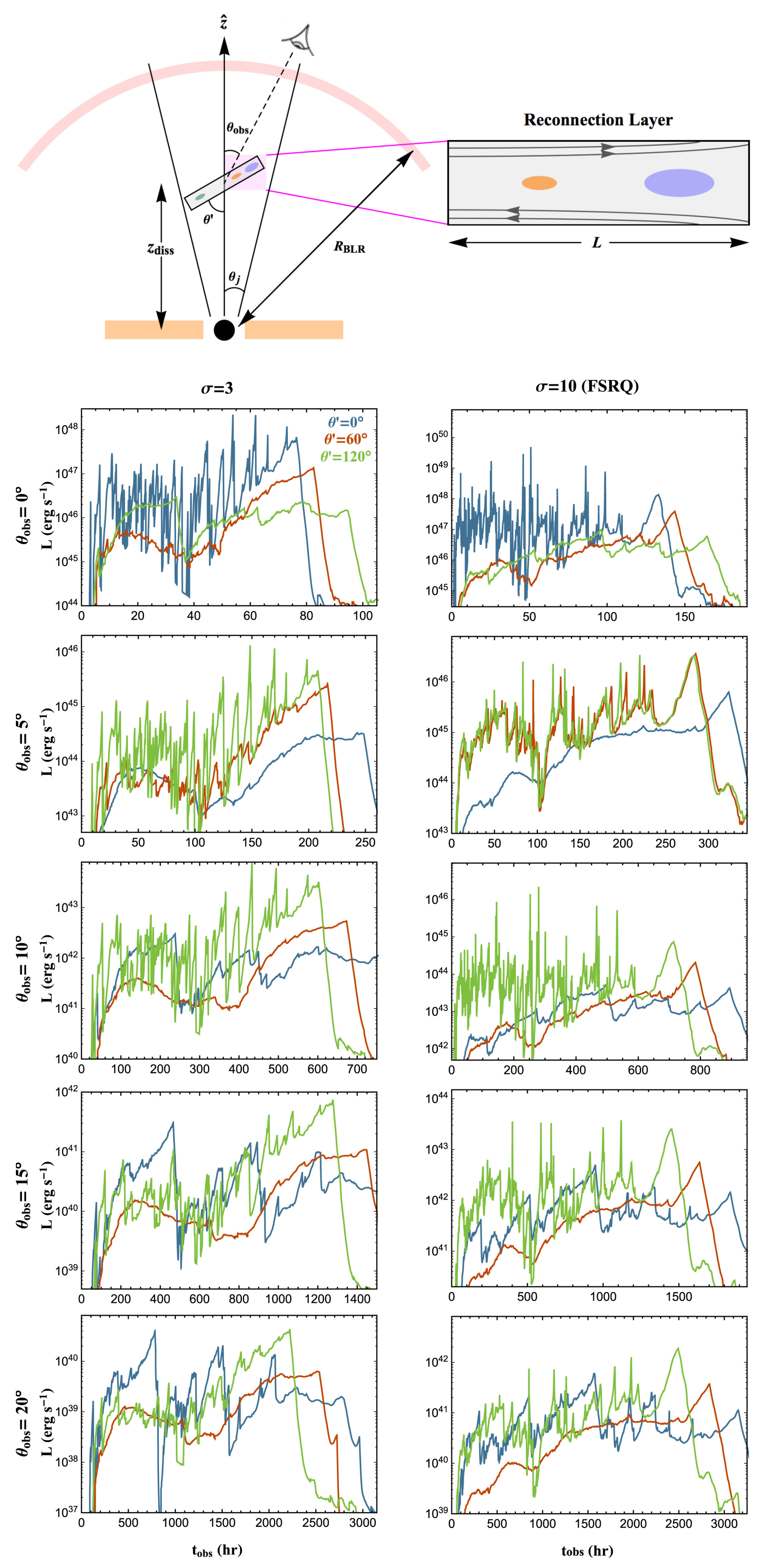
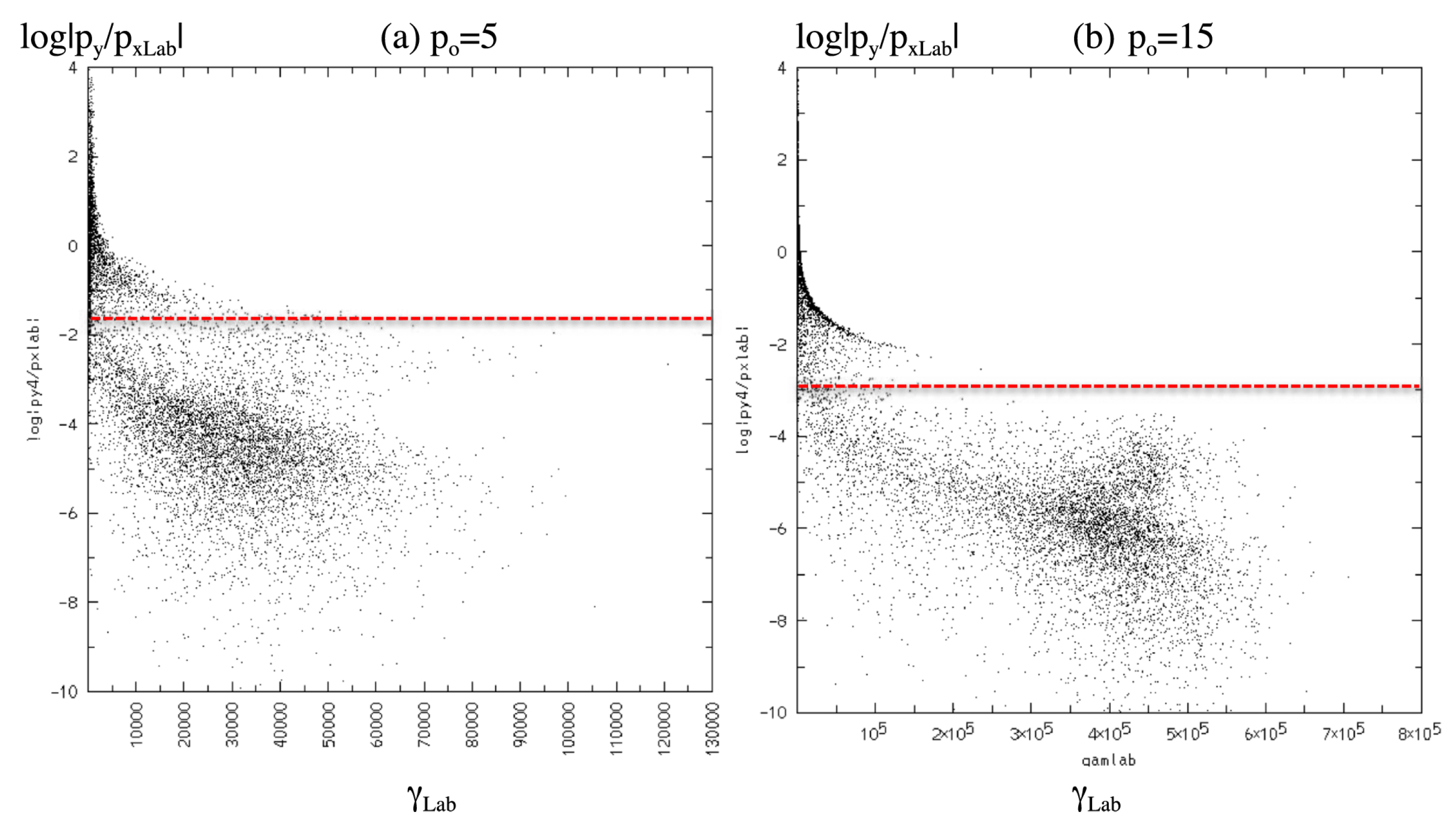
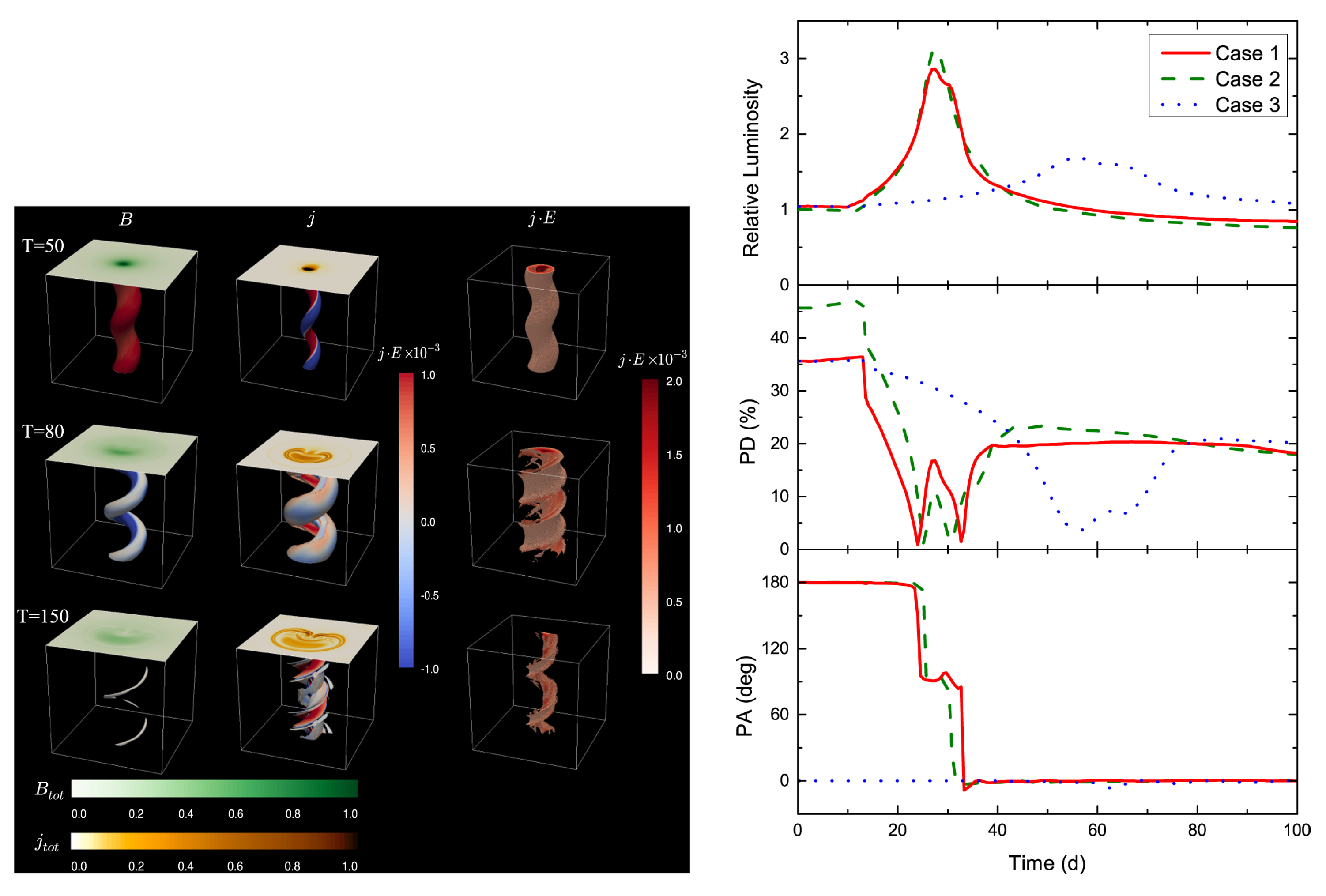
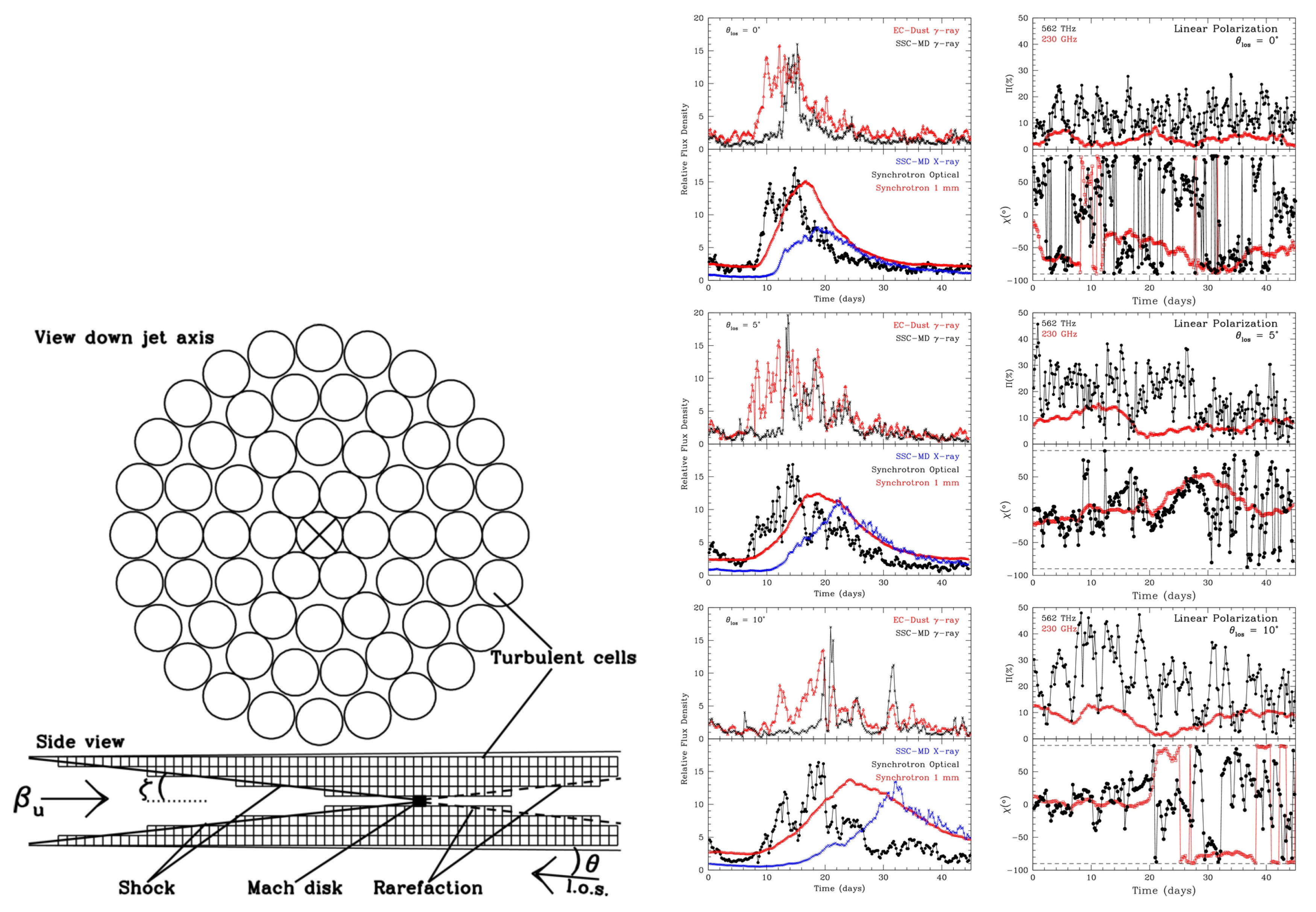
• Turbulence/Magnetic Reconnection: The relativistic flows of AGN jets are likely to develop turbulence, which may trigger magnetic reconnection. This has been studied in a large number of works in recent years (e.g., [104,105,106,107,108]). It has been shown that magnetic reconnection produces hard power-law spectra of relativistic electrons, $n_e\left(\gamma \right)\propto {\gamma }^{-p}$, including spectral indices approaching a value of 1 (e.g., [109]), which, however, is also achievable with oblique relativistic, but still subluminal shocks [85].
  In view of the minute-scale variability problem discussed in Section 2.1, magnetic-reconnection models are particularly appealing as they provide the possibility to produce small-scale ultrarelativistic flows within the reconnection region, the so-called “jets-in-a-jet” scenario [110,111,112]. The resulting ultrarelativistic bulk motion of small plasmoids provides additional Doppler boosting, resulting in very short, bright flares. With modest magnetization ($\sigma \sim$ a few), this model is capable of producing the observed fast (minute-scale) variability (see [110,112,113,114,115] Figure 11) without requiring ultrarelativistic ($\mathsf{\Gamma }\gg 10$) bulk motions of the entire jet material.
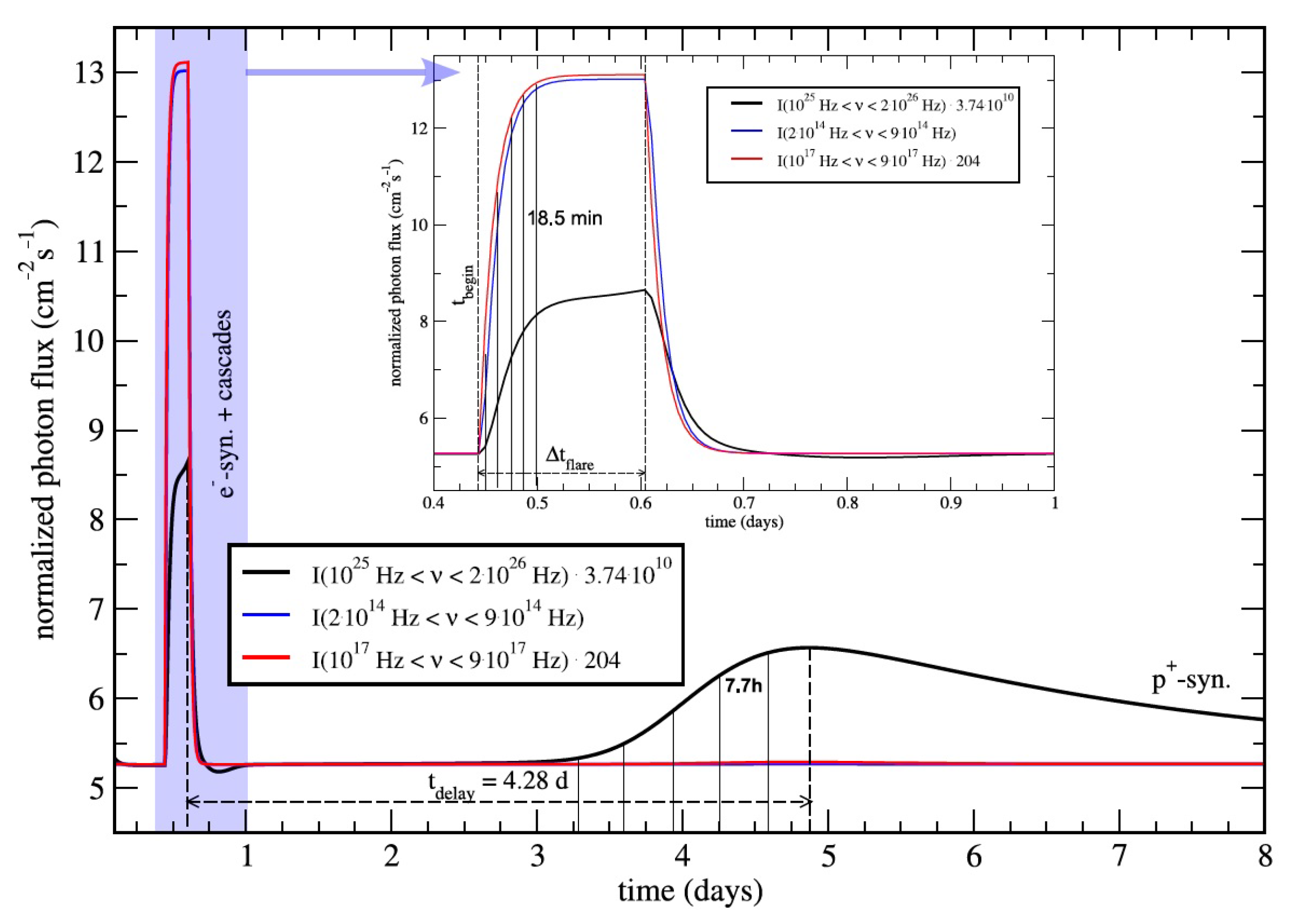
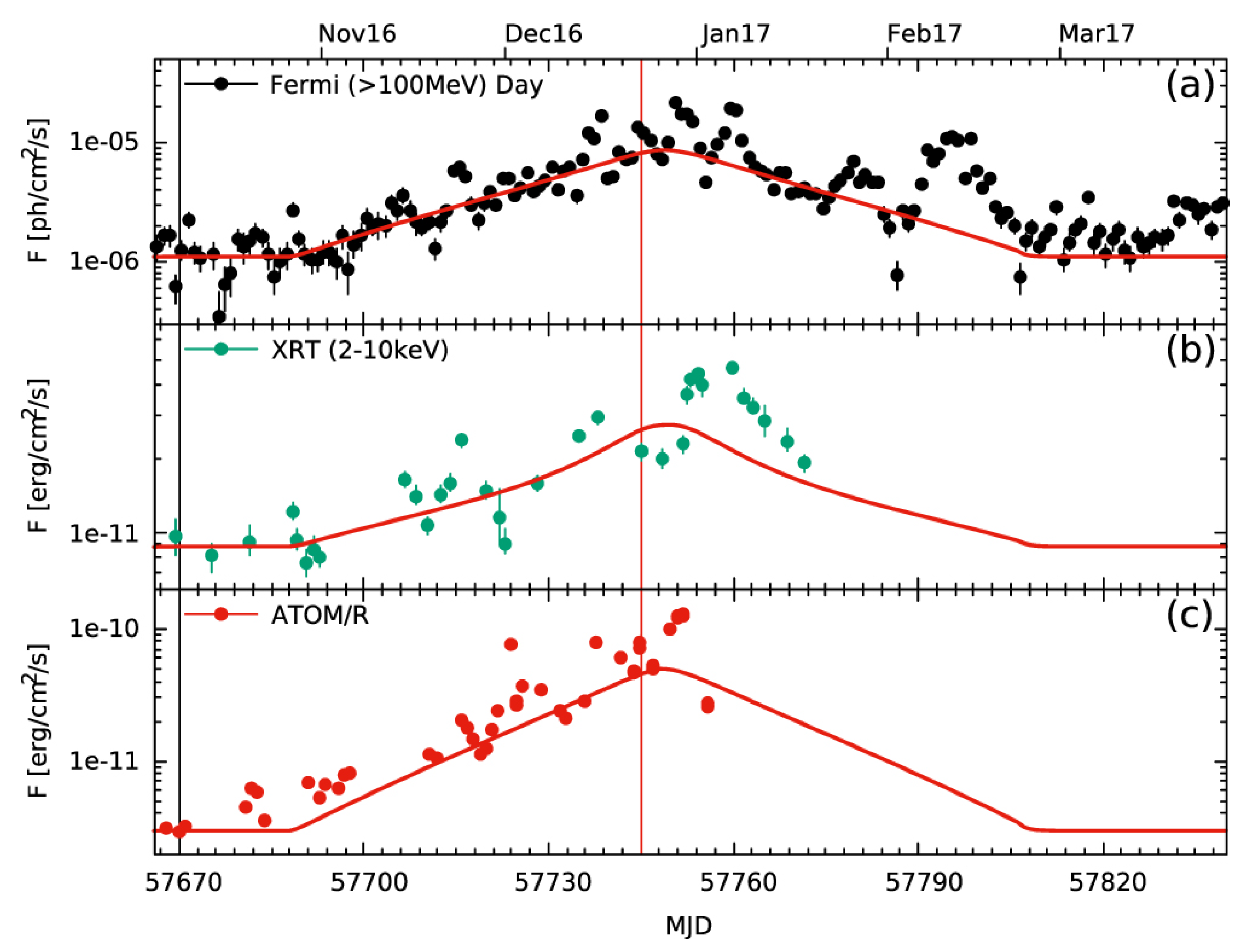
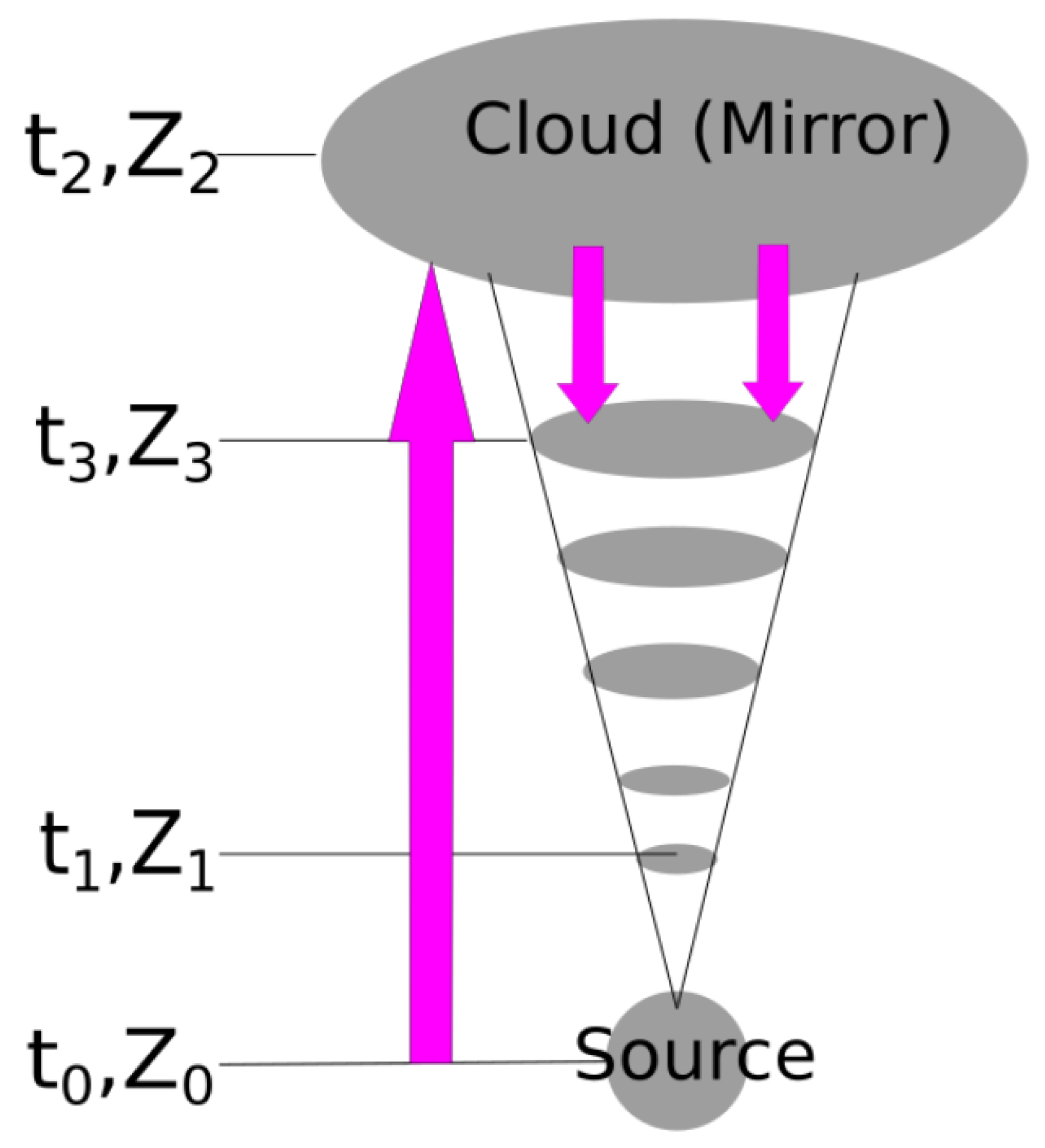
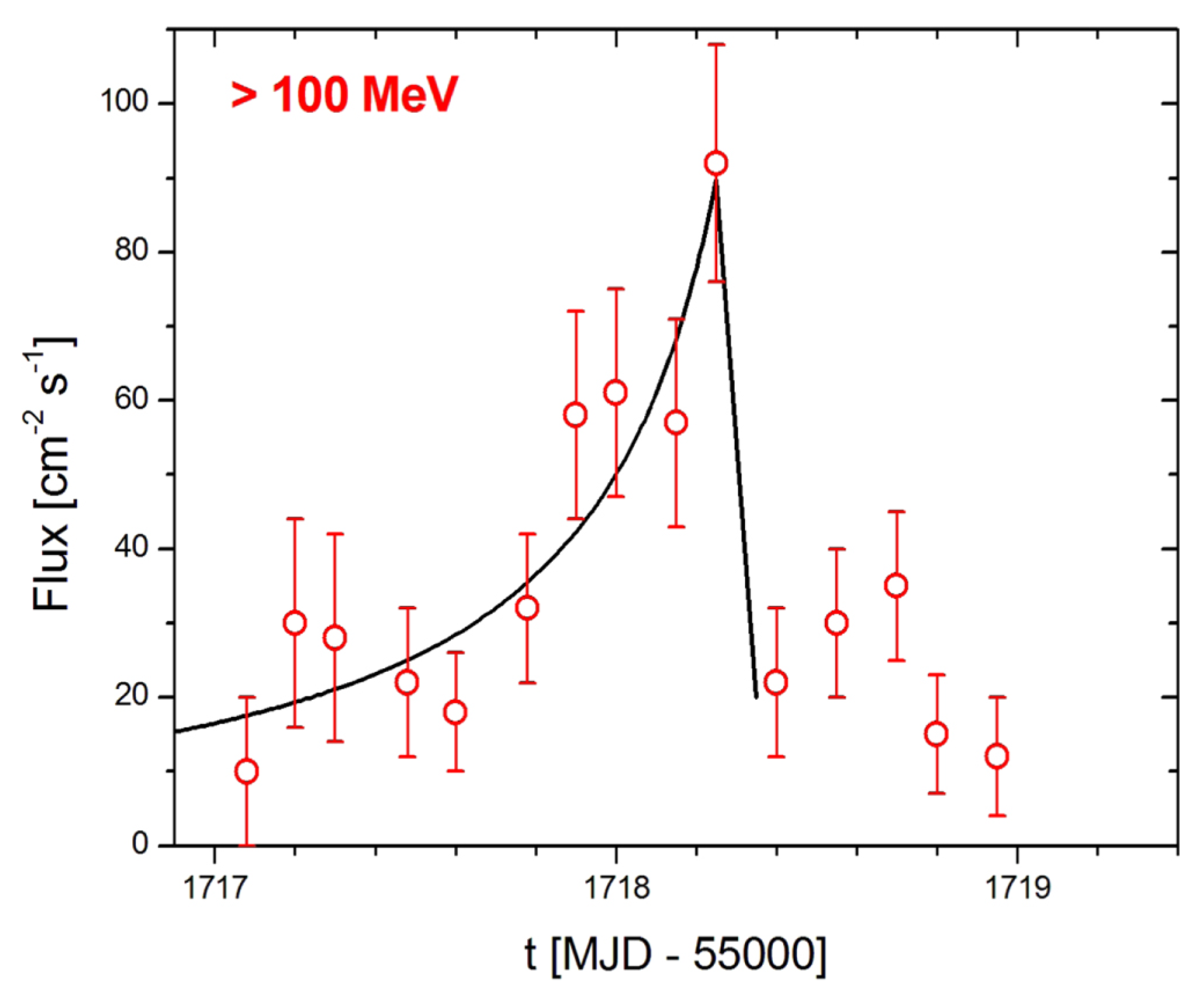
• External Sources of Variability: Another class of models attributes variability to interactions of the jet (or the high-energy emission region within the jet) with matter external to the jet, either by direct collisions or by means of radiative interactions.
  Examples of the former models include jet–star/cloud collision models (e.g., [116,117,118,119,120]), where the jet interacts with and (at least partially) disrupts a star or a gas cloud, leading to the formation of a strong shock with subsequent particle acceleration. The natural duration of flares in such a scenario is expected to be of the order of the crossing time of the cloud or star through the jet, typically of the order of days to weeks or months. For example, a model of cloud ablation by a blazar jet has recently been proposed by [121] to model the ∼4 months long giant multi-wavelength outburst of the FSRQ CTA 102 in 2016–2017, see Figure 12. Note that [119] argue that a jet-star interaction may also produce rapid, minute-scale variability due to the acceleration of fragments of the stellar envelope to ultra-relativistic bulk speeds.
  Variability models based on radiative interactions of the jet with external medium include, in particular, synchrotron mirror models, in which the synchrotron emission produced within the jet is reflected off an external obstacle (the “mirror”, which could, e.g., be a cloud of the Broad Line Region or a stationary feature within the jet) (e.g., [122,123] see Figure 13). It thereby appears as an intense target photon field either for Compton scattering (leptonic models—see Figure 14) or p$\gamma$ pion producton (hadronic models) for a short time around the passage of the high-energy emission region by the mirror. A hadronic synchrotron mirror model has been proposed by [122] to explain the orphan TeV flare of 1ES 1959+650. The reflected synchrotron X-ray emission in this case would be an inefficient target for Compton scattering due to Klein-Nishina suppression, leaving p$\gamma$ interactions off relativistic protons as the dominant signature of the mirror process.
  Into the same category falls the “Ring of Fire” model by [124,125], in which the high-energy emission region passes a stationary external source of seed photons for Compton scattering and which has also been proposed as a model for “orphan flares” [125].
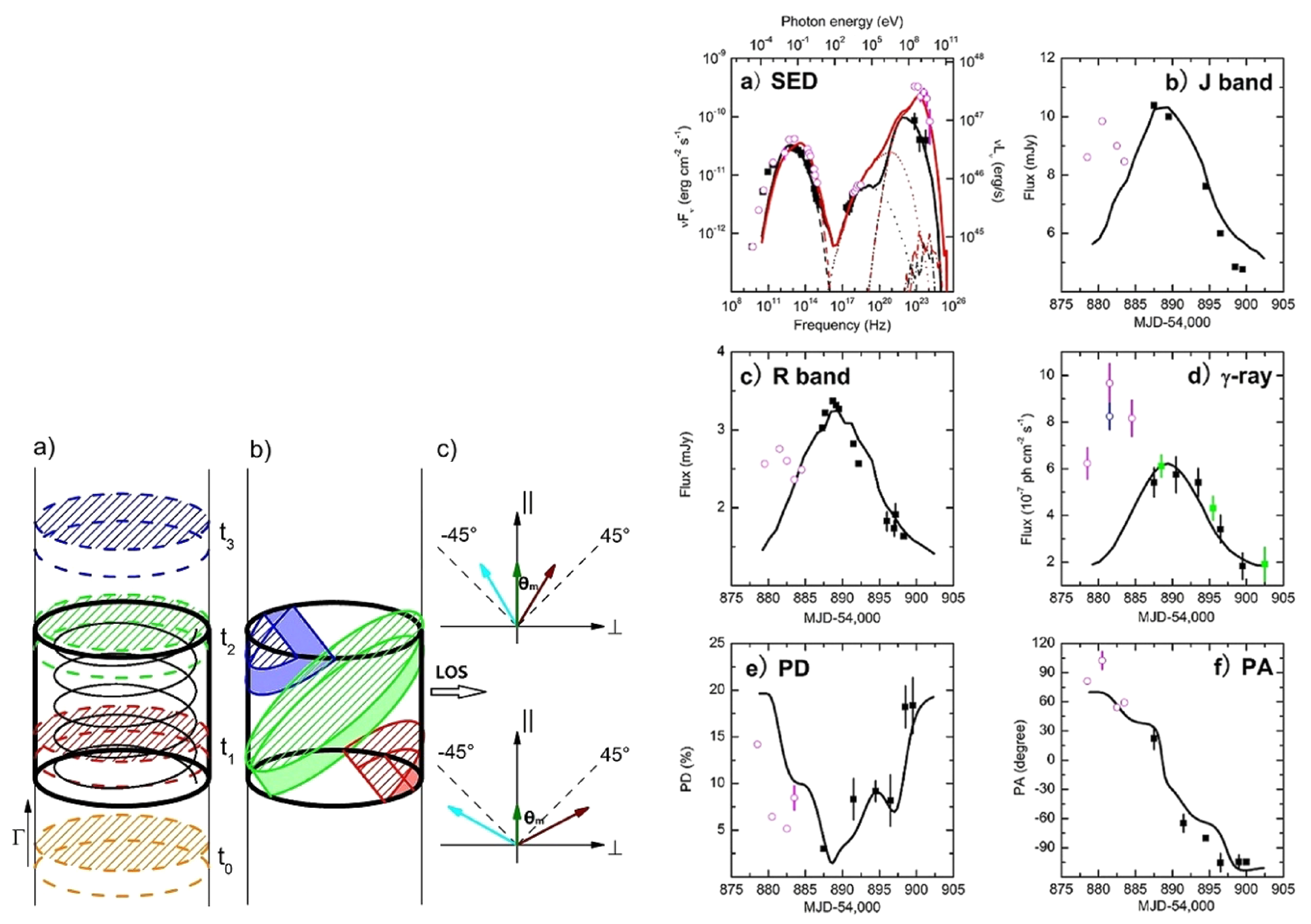
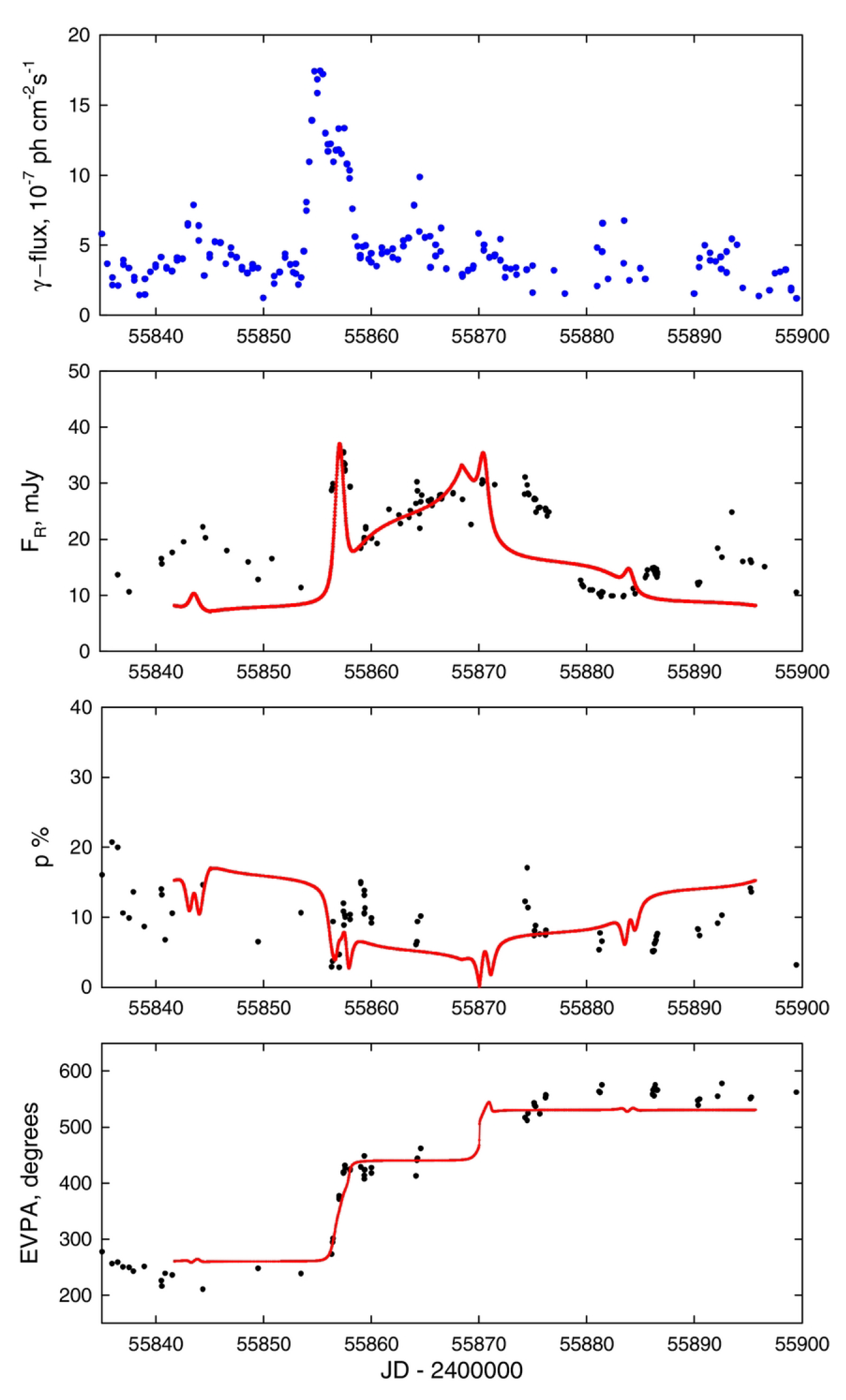
• Geometric Models: Variability models based on bending or helical jets invoke a change of the viewing geometry as the dominant source of variability, due to a change in the Doppler factor (e.g., [126,127,128,129,130]). Bending or helical jet structures are often observed in radio VLBI monitoring (e.g., [131]). Models based on Doppler-factor variability typically predict correlated, almost acromatic variability, except for a small shift in frequency by the changing Doppler factor, unless one assumes that different portions of the electromagnetic spectrum are not produced co-spatially and may be affected by different Doppler-factor variations (e.g., [129]). Such models have also had some success in reproducing optical polarization variability, as discussed further in the next sub-section.
  Another class of models that may be categorized as geometric invokes particle acceleration triggered by the kink instability in jets (e.g., [132,133]). In these models, variability is caused by particle acceleration due to magnetic energy dissipation in the development of the instability, which is expected to be accompanied by significant changes in the polarization signatures, as discussed further below.

3.1.2. Numerical Approaches

Modeling of blazar variability requires the time-dependent treatment of both the distributions of relativistic particles and the radiation fields in the emission region. In leptonic models, the relevant particle populations are only the electrons (and positrons, which are usually not distinguished from electrons, as they cool and radiate identically, and pair annihilation is irrelevant for highly relativistic electrons); in hadronic models, in principle, electrons/positrons need to be evolved simultaneously with ultrarelativistic protons, pions, and muons. In almost all models currently available in the literature, the particle momentum distributions are assumed to be isotropic in the rest frame of the high-energy emission region. This is a critical simplifying assumption which makes the models tractable, as one needs to keep track only of the particles’ energy distributions (in one dimension), and current models based on isotropic particle distributions have met with significant success in representing SEDs and variability patterns of blazars. However, realistically, neither relativistic shock acceleration (e.g., [85]) nor particle acceleration at relativistic shear layers [134] appear to produce isotropic particle distributions in any frame. In particular, [134] have shown that relativistic shear layer acceleration produces highly beamed particle distributions in the direction of the shear flow, possibly leading to much more strongly beamed radiation patterns than the standard $1/\mathsf{\Gamma }$ scaling resulting from relativistic aberration of emission produced isotropically in an emission region moving at Lorentz factor $\mathsf{\Gamma }$ (see Figure 15).

An interesting contribution to the discussion about anisotropy of particle distributions was published by [135]. These authors argue that gygoresonant pitch-angle scattering, which might isotropize accelerated particles in the emission region, is effective only out to some isotropization energy ${\gamma }_{\mathrm{iso}}$, typically much smaller than the break energy ${\gamma }_b$ due to inefficient acceleration and/or escape. Particles with ${\gamma }_e>{\gamma }_b$ are expected to move primarily along the magnetic field and will therefore not contribute to synchrotron emission. However, particles in the range ${\gamma }_{\mathrm{iso}}<{\gamma }_e<{\gamma }_b$ may still efficiently contribute to Compton scattering. This removes the need for strongly sub-equipartition magnetic fields, which contradict the paradigm of dynamically important B-fields in the jets of AGN.

Accepting the isotropic particle distribution approximation, as done in most of the current literature, the evolution of particle energy distributions is usually done by means of an isotropic Fokker-Planck equation of the form (see, e.g., [136,137,138,139,140,141,142,143] for leptonic models, and [71,101,144,145] for hadronic models):

$$\frac{\partial n_i(\gamma ,t)}{\partial t}=Q_i(\gamma ,t)-\frac{\partial }{\partial \gamma }\left(\dot{\gamma }{n}_i[\gamma ,t]\right)-\frac{n_i(\gamma ,t)}{t_{\mathrm{esc}}}+\frac{\partial }{\partial \gamma }\left(D\left[\gamma \right]\frac{\partial n_i[\gamma ,t]}{\partial \gamma }\right)-\frac{n_i(\gamma ,t)}{\gamma t_{\mathrm{decay}}}.$$

(4)

Here, i indicates the particle species (electrons/positrons, protons, pions, muons). $Q_i(\gamma ,t)$ is an injection term, which is often used to describe rapid particle acceleration, such as first-order Fermi acceleration. This is because the first-order Fermi acceleration time scale increases with energy as $t_{\mathrm{acc},1}\propto {\gamma }^{\alpha }$, typically with $\alpha \ge 1$, while radiative cooling time scales (at least for synchrotron and Compton scattering) scale as $t_{\mathrm{cool}}\propto {\gamma }^{-1}$. Thus, for energies below the maximum energy where $t_{\mathrm{acc},1}\left({\gamma }_{\max }\right)=t_{\mathrm{cool}}\left({\gamma }_{\max }\right)$, typically $t_{\mathrm{acc}}<<t_{\mathrm{cool}}$. Thus, first-order fermi acceleration is well approximated by an instantaneous injection term. Depending on particle species, $Q_i(\gamma ,t)$ may also include pair production by $\gamma \gamma$ absorption and particle production through the decay of pions or muons, thus directly coupling to the evolution of those parent particles. The term $\dot{\gamma }$ describes systematic energy losses or gains (if not already included in $Q_i$), in particular radiative losses. $t_{\mathrm{esc}}$ is the (possibly energy-dependent) escape time scale. The fourth term on the right-hand side describes diffusion in momentum space, leading to second-order Fermi acceleration where $D\left(\gamma \right)$ is the momentum diffusion coefficient. The last term describes the decay of unstable particles (pions, muons).

For a self-consistent solution, in the case of hadronic models, the Fokker-Planck Equation (4) for all species have to be solved simultaneously, along with the radiation transfer problem (see below). The most efficient way to achieve stable numerical solutions to Equation (4) is through implicit Crank-Nichelson schemes (e.g., [88,146]).

There are two main approaches to solving the radiation transfer problem in most blazar emission codes. Most commonly employed are direct solutions to a photon continuity equation of the form

$$\frac{\partial n_{\mathrm{ph}}\left(ϵ\right)}{\partial t}=\frac{4\pi j_{ϵ}}{ϵm_e{c}^2}-{\alpha }_{ϵ}c{n}_{\mathrm{ph}}\left(ϵ\right)-\frac{n_{\mathrm{ph}}\left(ϵ\right)}{t_{\mathrm{esc}}}.$$

(5)

Here, $ϵ=h\nu /\left(m_e{c}^2\right)$ is the dimensionless photon energy, $j_{ϵ}$ is the emissivity due to the various radiation mechanisms, ${\alpha }_{ϵ}$ is the absorption coefficient, primarily due to synchrotron self-absorption and $\gamma \gamma$ absorption (wich then feeds back into the electron/positron Fokker-Planck equation through pair production), and $t_{\mathrm{esc}}$ is the photon escape time scale. Such schemes are typically numerically inexpensive, but they are appropriate only for very simple (typically homogeneous, one-zone) geometries. There are, however, a few attempts to apply such schemes also to inhomogeneous multi-zone models, in particular shock-in-jet [91,92] and extended-jet [147,148,149] models.

An alternative method to solve the radiation transfer problem is through Monte-Carlo simulations (e.g., [88,89,97,98,150]). Such schemes are much more flexible in terms of geometries, they allow straightforward time-tagging of photons and polarization-dependent ray tracing [97,98]. However, time-dependent multi-zone simulations quickly become extremely time consuming due to the large number of photons that need to be tracked in order to achieve meaningful photon statistics.

An innovative new approach to solving time-dependent particle and photon evolution in blazar models has been developed by [151,152,153]. These authors solve the Fokker-Planck and radiation transfer equations in Fourier space and re-convert them into observable light curves and cross correlations. With this approach, it was, for the first time, feasible to model Fourier-frequency-dependent time lags between hard and soft X-rays, as observed from Mrk 421 (see Figure 16).

3.2. Multi-Wavelength Polarization Modeling

In this section, various models advanced to explain the large-angle optical PA swings in flaring blazars, as well as predictions for future high-energy polarimeters will be discussed.

3.2.1. Optical polarization Angle Swings

The large-angle optical PA rotations associated with multi-wavelength flares discussed in Section 2.2 have spurred a large number of theoretical works to interpret these events. The large degree of optical polarization is a clear indication that the non-thermal emission is synchrotron radiation in partially ordered magnetic fields. A non-thermal synchrotron spectrum with energy index $\alpha =(p-1)/2$, where p is the underlying non-thermal electron spectral index, can be maximally polarized by a degree of

$${\mathsf{\Pi }}_{\max }=\frac{p+1}{p+7/3}=\frac{\alpha +1}{\alpha +5/3}$$

(6)

in the case of a perfectly ordered magnetic field. For typical spectral indices of $p\sim 2$–3, this corresponds to ∼70%–75% polarization. The observed degree of optical polarization is typically in the range ${\mathsf{\Pi }}_o\sim$ a few percent—30%, this indicates that the magnetic fields in the optical emission regions must be partially ordered. Changes in the PA then likely indicate a change in the orientation of the magnetic field with respect to our line of sight. This can be either an intrinsic change in a (more or less) straight jet, or it can indicate a change of the jet orientation with respect to the line of sight. Alternatively, PA variations may be the result of stochastic processes in a turbulent jet environment. All of these possibilities will be discussed in more detail below.

Intrinsic magnetic field changes may be caused through magnetic-field compression in a shock. Models based on shock propagation in a jet pervaded by a magnetic field have been advanced, in particular, by [96,97,98]. Here, the finite transverse light travel time plays a crucial role in producing PA swings. Ref. [97] have used such a model to self-consistently explain SEDs, multi-wavelength light curves, and PA and $\mathsf{\Pi }$ variations, including a ∼180${}^{\circ }$ PA rotation, in the FSRQ 3C279, as observed by [58] (see Figure 17). A potential drawback of such a model is that a single shock passage predicts swings of at most 180${}^{\circ }$. Thus, rotations by multiples of 180${}^{\circ }$ would require a succession of multiple shocks. Furthermore, assuming that the helicity of the magnetic field structure does not change in the same object between different observation periods, such rotations are predicted to occur always in the same direction, which is contrary to observations. Thus, while this model has been very successful in explaining some PA rotations associated with multi-wavelength flares, it can likely not be applied to all.

Models along similar lines involve magnetic-field re-structuring and particle energization through the kink instability [132,133] (see Figure 18). This process will also lead to flaring activity, with the strength of flares depending on the initial magnetization, correlated with PA swings. In this model, as with the internal-shock model, the unit of PA rotations is 180${}^{\circ }$, also expected to occur always in the same direction.

Alternatively, PA swings may result from a change in the jet orientation, such as assumed in the helical-jet model (e.g., [59,126,127,128,129,130,155]). In particular, ref. [126,127] modelled the optical flux and polarization variability of S5 0716+71 and CTA 102, respectively (see Figure 19). Such models have been successful in representing flux and polarization variability in some cases. However, also here the direction of the rotations is expected to be pre-determined by the helicity of the jet (and B-field structure) and thus not changing for a given object. Also, as discussed in Section 3.1, at least in their simplest form, they predict essentially achromatic multi-wavelength variability, which is rarely observed.

Finally, stochastic polarization variability may result from turbulent environments in the jet. In  particular, ref. [156] developed a “Turbulent Extreme Multi-Zone” (TEMZ) model in which different turbulent cells in the jet are characterized by different magnetic-field orientations. The summed radiation of a large number of such turbulent cells will result in a (normally small) residual polarization with stochastically varying direction. This model has successfully reproduced stochastic polarization and flux variations in blazars (see Figure 20) and may occasionally also lead to large-angle PA swings. It naturally accounts for changing directions of PA swings in the same object and has also been used to model circular radio polarization from the inner jet regions of blazars [157]. However, due to the stochasticity of both flux and polarization variations, large-angle PA swings are expected to be very rare, and such swings are not expected to correlate systematically with multi-wavelength flares, as observed by the RoboPol experiment [63].

3.2.2. High-Energy Polarization

As will be discussed in more detail below in Section 4, there are currently great prospects for future detections of high-energy (X-ray and $\gamma$-ray) polarization from blazars. Thus, it is timely to consider model predictions of such high-energy polarization. In addition to synchrotron radiation, also Compton scattering may induce polarization, but only in the case of scattering off non-relativistic electrons (see, e.g., [158]). Inverse-Compton scattering by relativistic electrons does not induce polarization, but reduces the degree of polarization of a polarized target photon field by at least ∼1/2 (e.g., [159]).

Detailed predictions for the X-ray and $\gamma$-ray polarization in blazars have been made by [160] (see Figure 21). In the case of leptonic models, the X-ray emission in blazars is generally dominated by either synchrotron (in HSPs) or SSC emission (in ISPs and LSPs) and thus expected to be polarized. The $\gamma$-ray emission in LSP (and ISP) blazars is usually dominated by Compton scattering of external radiation fields by relativistic electrons and, thus, unpolarized, whereas in HSP blazars, it is usually modelled as being due to SSC emission, thus exhibiting a low, but non-zero, degree of polarization. In hadronic models, the high-energy emission is dominated by synchrotron emission of either protons or secondary pairs from photo-pion production and subsequent cascades, and thus expected to be polarized with a similar degree of polarization as the optical. High-energy polarization can thus be used as a diagnostic between leptonic and hadronic models.

A first attempt at a time-dependent, multi-zone hadronic model with polarization-dependent radiation transfer has been published by [161]. The model is applicable in a parameter regime in which the high-energy emission is dominated by proton synchrotron radiation, as appears to be preferred, at least for most LSPs when fitted with hadronic models (e.g., [8,162]). Ref. [161] shows that, in such a hadronic scenario, even though optical PA swings may be produced by a shock in a jet with a helical magnetic field, similar PA swings are not expected in the X-ray and $\gamma$-ray polarization (see Figure 22). This is because of the much longer radiative cooling time of protons responsible for the X-ray and $\gamma$-ray emission, which therefore occupy a much larger active volume than the optical-synchrotron emitting primary electrons, so that the effect of the shock on the magnetic field orientation is less pronounced for the proton synchrotron emission. Consequently, the X-ray and $\gamma$-ray PA is expected to remain relatively stable even during a shock-induced flare, which significantly improves the chances of experimental detection of such polarization.

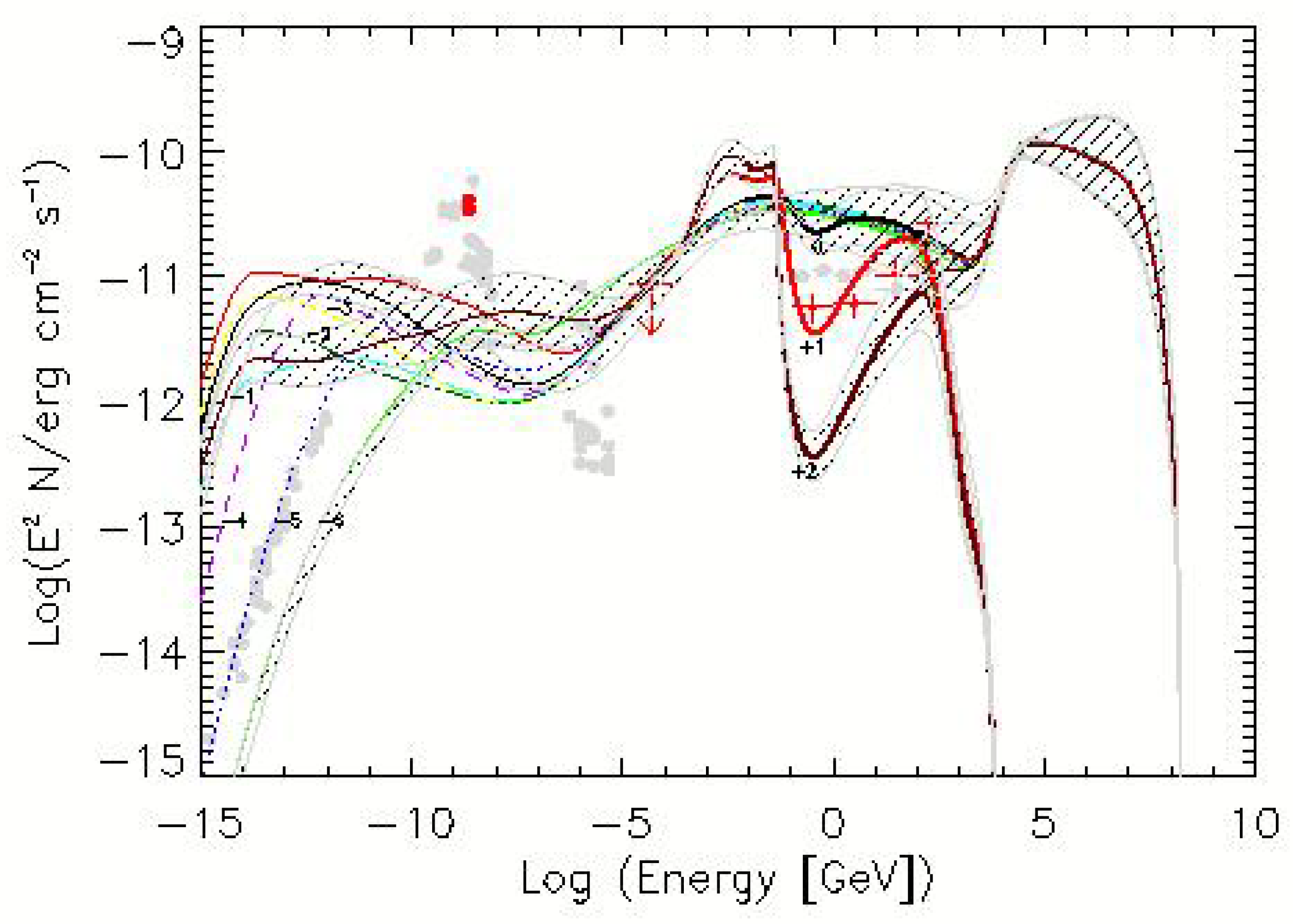
3.3. Models of Neutrino Emission from Blazars

Blazars have long been considered a prime candidate for the source of at least part of the VHE neutrinos detected by IceCube (e.g., [21,23,71,72,73,74,75,163,164,165,166,167]). In hadronic models of blazars, protons are accelerated to sufficiently high energies to produce $\gamma$-ray emission via proton synchrotron radiation and/or photo-pion production, $p+\gamma \to p+{\pi }^o$, $p+\gamma \to n+{\pi }^{+}$, or higher-order processes with multi-pion production, followed by pion decay, ${\pi }^{\pm }\to {\mu }^{\pm }+{\nu }_{\mu }\left(\overline{{\nu }_{\mu }}\right)$ and muon decay, ${\mu }^{\pm }\to e^{\pm }+\overline{{\nu }_{\mu }}\left({\nu }_{\mu }\right)+{\nu }_e\left(\overline{{\nu }_e}\right)$. In typical AGN jet environments, photo-pion production is expected to be significantly more efficient than hadro-nuclear (i.e., proton-proton) interactions. Therefore, almost all works on neutrino production in AGN work on the basis of photo-pion production (see, however, hadro-nuclear emission models for neutrino production in AGN by [168,169]). Usually, $p\gamma$ interactions are strongly dominated by single-pion production through the ${\mathsf{\Delta }}^{+}$ resonance at an energy of $E_{{\mathsf{\Delta }}^{+}}=1232$ MeV, in which case each photo-pion interaction results in the production of 3 neutrinos, each carrying an average energy of ∼5% of the proton energy,

$$E_{\nu }^{\prime }\approx 0.05E_p^{\prime }$$

(7)

where the prime indicates quantities in the rest frame of the emission region, in which the interactions are assumed to take place. Interaction at the ${\mathsf{\Delta }}^{+}$ resonance energy requires that the photon ($E_{\gamma }^{\prime }$) and proton energies obey the relation for the center-of-momentum energy squared, s,

$$s\approx E_{\gamma }^{\prime }{E}_p^{\prime }\approx E_{{\mathsf{\Delta }}^{+}}^2$$

(8)

Hence, combining Equations (7) and (8), one finds that the production of IceCube neutrinos of energies $E_{\nu }=\delta E_{\nu }^{\prime }=100E_{14}$ TeV requires protons of energy

$$E_p^{\prime }\approx 200E_{14}/{\delta }_1\mathrm{TeV}$$

(9)

and target photons of energy

$$E_{\gamma }^{\prime }\gtrsim 1.6{\delta }_1/E_{14}\mathrm{keV}.$$

(10)

Hence, first, while the sources of IceCube neutrinos must be able to accelerate protons to ∼EeV energies, they are not necessarily the sources of ultra-high-energy cosmic rays (UHECRs, with energies $E_{\mathrm{UHECR}}>{10}^{19}$ eV). Second, Equation (10) indicates that, for efficient IceCube neutrino production, an intense target photon field at X-ray energies (in the co-moving frame of the emission region) is required. Note that the co-moving primary-electron-synchrotron radiation field in all blazars (especially, LSP and ISP blazars) peaks at much lower energies than required by Equation (10). Therefore, photo-hadronic blazar models utilizing the co-moving synchrotron radiation fields typically produce very hard IceCube neutrino spectra, peaking significantly above the IceCube energy range (see, e.g., [170]).

Further constraints on the photo-hadronic scenario to produce both high-energy $\gamma$-rays and PeV neutrinos stem from the fact that the target photon field for photo-pion production also acts to absorb any co-spatially produced $\gamma$-rays via $\gamma \gamma$ absorption. The $p\gamma$ cross section is several orders of magnitude smaller than the $\gamma \gamma$ absorption cross section. Efficient $p\gamma$ neutrino (and $\gamma$-ray) production requires that the optical depth for relativistic protons to interact with the target photon field, ${\tau }_{p\gamma }\sim 1$, which then implies that the optical depth of the emission region to ∼ GeV photons is ${\tau }_{\gamma \gamma }\sim 310{\tau }_{p\gamma }\gg 1$ (e.g., [171]). Thus, any $\gamma$-rays produced co-spatially with IceCube neutrinos, are expected to be strongly absorbed and initiate electromagnetic cascades, whose energy will ultimately escape the emission region in the optical – UV – X-ray regime.

This led several authors (e.g., [172,173,174]) to conclude that if blazars are the sources of (at least some) IceCube neutrinos, their $\gamma$-ray emission is likely to be dominated by leptonic processes, and no correlation between $\gamma$-ray and neutrino emissions is necessarily expected. Instead, the unavoidable cascade emission from photo-hadronic processes in blazar jets is expected to leave an imprint in the X-ray emission from blazars, which may be a better indicator of neutrino-production activity than $\gamma$-rays.

This conclusion is further corroborated by detailed studies of electromagnetic cascades initiated by photo-hadronic neutrino-production processes in blazar jet environments by [171]. Ref. [171] investigated possible regimes of electromagnetic cascades based on the energetics requirements to produce the neutrino flux from TXS 0506+056 during the 2014–2015 neutrino flare, and found that a synchrotron-supported cascade regime can be ruled out, as the cascades violate observational constraints (see Figure 23). Further considering the nature of the target photon field, they found that there is only a narrow range of parameters not violating observational constraints, requiring a $p\gamma$ UV–soft X-ray target photon field external to the jet (stationary in the AGN rest frame) and a kinetic luminosity in protons near the Eddington limit of the central black hole in TXS 0506+056. The nature of the required UV–soft X-ray target photon field remains unclear, but could possibly be related to a radially structured jet (spine-sheath, see [175,176]), or a radiatively inefficient accretion flow [177].

To conclude, photo-hadronic PeV neutrino production in blazar jets is not necessarily correlated with $\gamma$-ray activity (but rather X-ray activity), and due to the expected high $\gamma \gamma$ opacity of the required $p\gamma$ target photon fields, $\gamma$-rays in neutrino-producing blazars are likely to be dominated by leptonic processes, likely not spatially coincident with the site of neutrino production.

4. Future Prospects

The next decade will witness the start of operations of several new ground- and space-based astronomy facilities. Of particular relevance to blazar research will be, in the author’s opinion, the Cherenkov Telescope Array (CTA [178]) and the Imaging X-ray Polarimetry Explorer (IXPE, [179]), while ground-based radio and optical flux and polarimetry monitoring projects will continue, and hopefully the Fermi Gamma-Ray Space Telescope and the Neil Gehrels Swift X-Ray Observatory will continue to provide all-sky GeV $\gamma$-ray monitoring and flexible X-ray coverage to blazar observations, respectively, for several years to come. KM3NeT [180,181] and planned upgrades to IceCube (IceCube-Gen2] [182,183]) and the Lake Baikal neutrino detector [184] will greatly improve our view of the neutrino sky and hopefully provide a definitive answer whether blazars are PeV neutrino sources. If selected, future missions such as the All-sky Medium Energy Gamma-ray Observatory (AMEGO, [185]) would also provide a boost to the study of blazars.

4.1. The Cherenkov Telescope Array

CTA4 will be the next-generation ground-based Cherenkov Telescope facility, consisting of ∼100 Cherenkov telescopes of three different sizes at two sites, one in the nothern hemisphere (La Palma, Canary Islands, Spain), and one in the southern hemisphere (Paranal/ESO, Chile). It will improve on the sensitivity of current IACT facilities by about an order of magnitude and extend the observable energy range to ∼20 GeV–∼300 TeV. The current schedule foresees CTA to be operational by 2024. In addition to key science projects conducted by the CTA Consortium, CTA observing time will be open to community through a competitive proposal process. For an in-depth discussion of the science potential and key science projects to be conducted with the CTA, see [186]. Highlights of progress that CTA promises for blazar studies, include:

• Short-term variability: The ∼10-fold improved sensitivity of CTA compared to currently operating IACT facilities will allow for the study of blazar variability on short time-scales. In the case of the brightest flares, variability down to sub-minute time-scales could, in principle, be detected, if present. Already the ∼5 min. variability observed in a few cases is severely challenging current blazar models, as discussed in Section 3.1. If blazars do indeed show significant variability on sub-minute time scales, this would call for a profound paradigm shift concerning our understanding of $\gamma$-ray emission from blazars.
  The detection of minute-scale variability strongly suggests a location of the emission region close to the central black hole, at a distance of the order $r\sim 2{\mathsf{\Gamma }}^{2}c{t}_{\mathrm{var}}\sim 3.6\times {10}^{14}{\mathsf{\Gamma }}_1^2{t}_{\mathrm{var},\min }$ cm. Even for bulk Lorentz factors of order $\mathsf{\Gamma }\sim 100$, this would normally be within the Broad Line Region (BLR) of an FSRQ. Thus, in the case of FSRQs (such as PKS 1222+216, from which sub-hour variability has been seen), it would be very difficult to avoid $\gamma \gamma$ absorption by the BLR radiation field (e.g., [187,188,189,190]). Thus, such detections either require exotic physics to suppress $\gamma \gamma$ absorption within the BLR (e.g., [191,192]), or a mechanism to produce very compact emission regions along the jet at ∼$pc$ distances from the central black hole.
  The improved sensitivity will also enable the detection of short-term variability in fainter $\gamma$-ray-detected AGN, including mis-aligned blazars (seen as radio galaxies) and narrow-line Seyfert-1 galaxies, some of which also appear to show blazar-like properties (e.g., [193,194]). Thus, we will be able to study whether sub-hour variability is a property of only a few blazars, or whether it is a common phenomenon among $\gamma$-ray emitting radio-loud AGN.
• Detailed $\gamma$-ray spectral studies: The improved sensitivity and extended energy range of CTA compared to current IACTs will enable detailed $\gamma$-ray spectral studies with substantial overlap in energy with the Fermi-LAT. Potential spectral features due to $\gamma \gamma$ absorption in the BLR or dust torus radiation fields of the AGN are expected to arise in the ∼10–100 GeV regime (e.g., [190]), i.e., just in the transition region between the energy ranges of Fermi-LAT and IACTs. Currently, the study of spectral features in this regime, beyond simple exponential cut-offs or similar smooth spectral shapes (see, e.g., [195]), is complicated by the fact that a high-quality Fermi-LAT spectrum, for most blazars, typically requires exposures of (at least) several days, during which the source is likely to show substantial variability. On the other hand, IACTs perform short, pointed observations of at most a few hours per night. Thus, any spectral features in this overlap energy range may well be an artifact of the often vastly different integration times in the GeV and TeV regimes. The substantial energy overlap between Fermi-LAT (up to $\lesssim 100$ GeV) and CTA ($\gtrsim 20$ GeV) will enable to proper flux cross-calibration of the two instruments and allow for a detailed study of spectral features in the overlap region, at least in cases where observations do not indicate significant variability over the course of the joint observations. The identification of BLR $\gamma \gamma$ absorption features would provide a key diagnostic for the location of the $\gamma$-ray emission region and, thus, the region where relativistic particles are accelerated to >TeV energies. The location of the particle acceleration region would provide strong clues towards the nature of the acceleration mechanism.
  It has also been suggested (e.g., [196]) that hadronic emission processes might lead to detectable spectral features in the multi-TeV spectra of blazars due to separate spectral components from muon and pion synchrotron emission and photo-pion induced pair cascades. Such features may be detectable, at least for nearby blazars, with the CTA. If they are systematically identified in a sample of blazars, they might provide a “smoking-gun” signature of hadronic processes and point to blazars as sources of high-energy cosmic rays.

4.2. High-Energy Polarimetry

The Imaging X-Ray Polarimetry Explorer (IXPE)5 has been selected by NASA for launch in (or after) 2020 as the first dedicated high-energy polarimetry mission. It will provide X-ray polarimetry in the 2–8 keV X-ray regime and has the capacity to detect X-ray polarization from bright blazars within a few hours of observations. In the $\gamma$-ray regime, the proposed AMEGO6 mission promises to perform, for the first time, polarimetry in the MeV regime.

X-ray polarimetry of HSP blazars, where the X-ray emission is electron-synchrotron dominated, would probe the degree of ordering and dominant direction of magnetic fields in the high-energy emission region. When compared to simultaneous optical polarimetry, this will allow for test of the co-spatiality of X-ray and optical emission in HSPs and for a comparison of the respective emission region sizes. As the optical emission in HSPs originates from lower-energy electrons than the X-ray emission, one would expect the X-ray emission region to be more confined near the particle acceleration site, likely embedded in a more highly ordered magnetic field than in the, presumably much larger, optical emission site. A significantly higher degree of polarization in X-rays compared to optical would then be expected. Such results will allow us to study the spatial dependence of turbulence in the jet and discriminate between different particle acceleration mechanisms, such as diffusive shock acceleration and magnetic reconnection.

In ISP/LSP blazars, the X-rays are likely produced by synchrotron self-Compton (SSC) emission in leptonic emission scenarios, or by proton synchrotron and cascade synchrotron emission in hadronic scenarios. Thus, if X-ray polarimetry reveals a degree of polarization of the order of the optical polarization in ISPs/LSPs, this would be a strong indication of hadronic emission [160].

Along the same lines, as disussed in Section 3.2, if $\gamma$-ray polarimetry by AMEGO shows significant (of the order of the optical degree of polarization) MeV polarization, hadronic emission scenarios will be strongly favoured, thus identifying blazars as (at least) PeV proton accelerators and likely sources of IceCube neutrinos.

As the optical polarization of blazars is known to be variable, at least on daily time scales, both in degree and angle of polarization, one might expect that the same holds true for X-ray and $\gamma$-ray polarization. Given that, for the X-ray fainter LSP sources, IXPE might require integration times of days to weeks, PA changes during the exposure might destroy any intrinsic polarization signal, unless data analysis techniques can be developed to account for a changing PA during the exposure, such as using the PA evolution observed in the optical, as a template for the IXPE analysis. However, as shown by [161], if PA rotations are produced by a straight shock-in-jet model with a helical magnetic field, the anticipated high degree of polarization in a hadronic model might be measurable without the expectation of a significant PA change.

4.3. Future Neutrino Detectors

KM3NeT7 is the next-generation neutrino telescope, to be built at three sites at the bottom of the Mediterranean Sea. It will improve on the sensitivity of IceCube by more than an order of magnitude and might therefore provide the statistics to identify individual sources of neutrinos confidently. In addition, major upgrades are planned to the existing IceCube detector at the South Pole (IceCube-Gen2)8 and to the neutrino detector in Lake Baikal9.

If blazars are identified systematically as a source of neutrinos by future neutrino observatories, it would prove their nature as cosmic-ray proton accelerators (up to at least PeV energies). However, as discussed in Section 3.3, a correlation with GeV–TeV $\gamma$-ray emission is not expected if the neutrinos are produced via photo-pion production. As there is no expected constrain on the $\gamma \gamma$ opacity in the case of hadro-nuclear neutrino production, a correlation between neutrino emission and $\gamma$-ray activity may therefore hint towards this neutrino production channel. Joint KM3NeT neutrino detections and $\gamma$-ray monitoring with Fermi-LAT and CTA will allow us to establish or refute such a correlation and thus constrain the mechanism of neutrino production.

5. Summary and Conclusions

The past few years have seen many observational discoveries on blazars, among which this article highlights a few, such as the rapid variability at GeV and TeV energies, down to just a few minutes; large-angle optical polarization-angle rotations, found to be systematically correlated with $\gamma$-ray and multi-wavelength flares, and a strong hint of the blazar TXS 0506+056 as a source of IceCube neutrinos.

Minute-scale blazar variability severely challenges existing models for blazar emission, possibly indicating the prominence of small-scale structures due to magnetic reconnection. Polarization-decline seem to hint towards the presence of helical magnetic field structures, possibly, but not necessarily, associated with a changing viewing angle. The possible TXS 0506+056 + IceCube neutrino association provides a hint towards hadronic particle acceleration in blazars. However, a careful study of photo-pion neutrino production suggests that a direct correlation between $\gamma$-ray activity and neutrino emission is not necessarily expected, and the cascade emission going in tandem with $p\gamma$ neutrino production is likely to show up more prominently in X-rays than in $\gamma$-rays.

Future observations by the CTA will allow for a more sensitive exploration of minute-scale VHE $\gamma$-ray variability in blazars, potentially invalidating the current blazar emission paradigm. IXPE and possibly AMEGO promise the first X-ray (and $\gamma$-ray) polarimetry results, which will aid in testing the co-spatiality of optical and X-ray emissions and provide further diagnostics for hadronic vs. leptonic emission scenarios. When analysing future IXPE observations of blazars, special care has to be taken to account for possible PA rotations of the X-ray polarization, which might mirror those seen in the optical.

On the multi-messenger side, the future KM3NeT will greatly improve the statistics of astrophysical PeV neutrinos and promises the clear identification of a source class (or multiple source classes), possibly including blazars. This would provide conclusive proof of PeV proton acceleration in AGN jets, but does not necessarily point towards the origin of ultra-high-energy cosmic-rays in AGN.