Planetary Nebulae Shaped by Common Envelope Evolution

Abstract

The morphologies of planetary nebula have long been believed to be due to wind shaping processes in which a “fast wind” from the central star impacts a previously ejected envelope. It is assumed that asymmetries existing in the “slow wind” envelope would lead to inertial confinement, shaping the resulting interacting wind flow. We present new results demonstrating the effectiveness of Common Envelope Evolution (CEE) at producing aspherical envelopes which, when impinged upon by a spherical fast stellar wind, produce highly bipolar, jet-like outflows. We have run two simple cases using the output of a single PHANTOM SPH CEE simulation. Our work uses the Adaptive Mesh Refinement code AstroBEAR to track the interaction of the fast wind and CEE ejecta allows us to follow the morphological evolution of the outflow lobes at high resolution in 3-D. Our two models bracket low and high momentum output fast winds. We find the interaction leads to highly collimated bipolar outflows. In addition, the bipolar morphology depends on the fast wind momentum injection rate. With this dependence comes the initiation of significant symmetry breaking between the top and bottom bipolar lobes. Our simulations, though simplified, confirm the long-standing belief that CEE can plan a major role in PPN and PN shaping. These simulations are intended as an initial exploration of the post-CE/PPN flow patterns that can be expected from central source outflows and CE ejecta.

1. Introduction

Planetary nebulae (“PN”) are formed via gas ejected from highly evolved stars starting within a few thousand years before their final state as white dwarfs. The interaction between a fast wind ejected during the post-Asymtotic Giant Branch (post-AGB) evolutionary state of the star and the previously ejected AGB slow material drives both Pre-PN (“PPN”) and mature PN [1]. Given the bipolar nature of many PPN and PN, a “Generalized Interacting Stellar Wind” model has long been thought to be a dominant mechanism for understanding their shaping. The Interacting Stellar Winds model began with the seminal work of [2] who proposed that fast, line driven winds from the hot Central Star of a PN (CSPN) expanding at velocities of order v_f ~ 1000 km/s would drive shocks into the heavy and slowly expanding AGB wind ejected earlier (v_f ~ 10 km/s). The bright rims of PN were then the ionized shells of swept up AGB material. The generalization of this model, to explain aspherical PN, began with suggestions by [1,3] in which they proposed that slow AGB winds could include a pole-to-equator density contrast. Once a spherical fast wind begins impinging on this aspherical slow wind, “inertial confinement” leads the resulting shocks to take on the elliptical or bipolar configurations. In this Generalized Interacting Stellar Wind model (GISW), the run from mildly elliptical PN to strongly bipolar “butterfly” shaped nebula depends on the pole-to-equator density contrast in the AGB slow wind (e = ρ_p/ρ_e) and its aspherical morphology. Analytic solutions [3] and later simulations [4,5,6] verified the ability of the GISW model to capture observed PN morphologies. With time, other shaping processes have been considered including the role of magnetic fields [7,8], clumps [9] and the possibility that the fast wind was already collimated in the form of jets [10]. In addition, new observations indicated that much of the shaping process for PN may actually occur before the central star heats up enough to produce ionizing radiation (the post-AGB/PPN phases [11]). While this recognition, along with the other mechanisms such as MHD, have contributed greatly to the understanding of PN shaping, the GISW model often remains in the background. For example, MHD models may still require a strong pole to equator density contrast to produce certain kinds of wasp-waisted nebula. Thus, in spite of the evolution of PN shaping studies since Kwok, Balick and Icke’s initial ground-breaking studies, the existence of a pre-existing toroidal density distribution still figures centrally in our understanding of the PN shaping process.

Of course, the assumption of a toriodal circumstellar slow wind has always begged the question of its formation. While single star models for the production of a pole-to-equator density contrast have been proposed [12], most of these rely on degrees of rotation that have proven difficult to obtain for slow rotating AGB stars. Thus binary stars have been seen as essential to modeling PN shaping for some time. Early work of Livio and Soker [13,14] provided key insights into how binary interactions could produce aspherical circumstellar environments. More recent 3-D simulation work has shown how even detached binary interactions can produce fertile ground for PPN shaping [15].

Throughout the extensive discussion of the role that binary stars may play in creating PN, Common Envelope Evolution (CEE) has long been seen as a primary means for generating AGB environments with a high pole to equator density contrast [16]. Common Envelope Evolution occurs when a more compact companion plunges into the envelope of an RGB or AGB star [17]. The release of gravitational energy during the rapid orbital decay is expected to unbind some, or all, of the AGB envelope, creating an expanding toroidal flow that can then serve as the aspherical slow wind for GISW models. The ability to calculate CEE out to the point where the expanding envelope could serve as input for GISW models has, in the past, been hampered by the complexity of CEE 3-D flows. Over the last decade, however, a number of new simulation platforms have been developed for CEE including smooth particle methods and fixed grid [18], AMR mesh methods [19,20] as well as moving mesh methods [21].

In this contribution, we take on the problem of PPN evolution from CEE systems by combining a SPH CEE simulation with an AMR grid-based wind interaction simulation. Our goal in these initial studies is to map out the basic flow patterns emerging from GISW interactions with CEE initial conditions, using fully 3-D, high-resolution simulations.

2. Model and Methods

Our simulations begin with the output of CEE models calculated using the SPH code PHANTOM. The model tracks a binary system with a M₁ = 0.88${\mathrm{M}}_{\odot }$ primary and M₂ = 0.6${\mathrm{M}}_{\odot }$ companion. The envelope of the primary holds M_1,e = 0.48${\mathrm{M}}_{\odot }$ of mass. Thus, there is approximately 1.1${\mathrm{M}}_{\odot }$ in the two stellar cores that will eventually form a tight binary or merged object. From the simulations, the final separation of the binary has stabilized at approximately R = 20${\mathrm{R}}_{\odot }$ (for more details on the simulation including the EOS used, see [22,23].

The results in terms of 3-D flow variable distributions then become the initial conditions for our AstroBEAR AMR simulation (for details of the AstroBEAR AMR multi-physics code see [24]). The numerical results from the SPH simulation (density, 3-D velocity and temperature) are then sampled at regularized points in a grid. This grid of points is then mapped onto an Eulerian mesh appropriate for an AMR simulation. The sampling occurs at the highest level of a 7 level AMR tree and is then restricted using the AMR tolerances for gradients within the flow to the less resolved grids in the AMR hierarchy. The base grid of the mesh has a physical dimension of (1000${\mathrm{R}}_{\odot }$)³ and the 7th level grid has a physical dimension of (7.8${\mathrm{R}}_{\odot }$)³. The simulation domain is cropped to (16,000${\mathrm{R}}_{\odot }$)² × (128,000${\mathrm{R}}_{\odot }$). The origin of the simulation is set at the center of the domain.

After reading in the original SPH data and mapping it to the Eulerian mesh, a point particle with mass 1 M_o is placed at the grid origin. The point particle’s gravity is imposed on the gas, however, the self-gravity of the gas is not considered. A spherical inner “wind” boundary is created around the point particle with r = 46.9R_sun (spanning 6 of finest mesh cells). The fast wind conditions are injected into the grid through this boundary. Note that the binary orbit at the end of the SPH CE simulation fits within this wind boundary region. Thus, we do not resolve the binary’s evolution any further or consider its effect on the fast wind that is considered a spherical outflow in our models.

After preparing the AMR grid with the SPH CEE conditions, we allow for a quiescent period of evolution where the CEE ejecta is simply allowed to expand for some time before the fast wind is initiated. We do this to allow the expanding CE flow to relax on the grid. We note that while we do not include self-gravity in the calculation, our tests during the quiescent period show no significant morphological evolution of the CE ejecta during this time. The most important feature of the quiescent period is that some innermost CE material falls back onto the inner boundary condition (which during this period is set to allow for infall). The fast wind is then turned on instantaneously. For the fast wind interaction with the CE ejecta we used a polytropic index of γ = 5/3. In fact, cooling is likely too important in these flows, however, for these initial experiments we chose to explore the fundamental hydrodynamic response of the wind/CE interactions. We ran two different models for the fast wind: a low and a high momentum flux case. We have listed both types of condition in

Table 1. Parameters for Runs.

	Case A: High Momentum Flux	Case B: Low Momentum Flux
ρFW (g cm−3)	1.0 × 10−11	5.0 × 10−13
VFW (km s−1)	300	300
Quiescent Phase Δt (days)	500	6000
Mass Loss Rate (${\mathrm{M}}_{\odot }$ y−1)	6.4 × 10−4	3.2 × 10−5
TFW (oak)	30,000	30,000

.

Our simulations occurred just a few years after the onset of the CEE. At this point, the nature of the central object driving the central outflow was quite uncertain. It could have been a wind from a disk surrounding either the the core of the primary [25] or the secondary [26] or It could have also been a magnetically powered flow from the primary via a Poynting–Flux driven “magnetic tower” [27]. Thus, linking this immediate post-CE flow to the radiative flux driving single post-AGB stars is only one of a number of possibilities. Most importantly, however, are the results of [11] which showed that many PPN showed “momentum excesses” in their outflows that were orders of magnitude above what stellar photons could provide. Thus, it is particularly unlikely that the central outflow is a “standard” post-AGB radiative driven wind. Note that the timescales for the launching of the outflow in the Bujarrabal et al. study were generally shown to be t_l ~ 100 year. This, along with the measured mass in their flows, implies that brief periods (or order a 100 years or less) with mass loss rates of 10⁻⁵ or 10⁻⁴ solar masses/year may not be uncommon in PPN flows. Note that this “momentum excess” problem has only been strengthened by results since the 2001 paper. It has been the motivation for a number of MHD driving models for the winds of post-CE objects.

3. Results

In the GISW model, two shocks formed as the fast wind interacted with the previously deposited slow-moving material. An outer shock, facing radially outward from the central wind source, was created as slow wind material was accelerated and swept up via the driving action of the interior fast wind. In addition, an inner shock formed facing back to the wind source via the deceleration of the fast wind. The inner shock converts wind kinetic energy into thermal energy of post-shock fast wind material. If both the fast and slow wind are spherical, the two shocks will be spherical. If, however, the slow wind is aspherical, the inner shock takes on a convex semi-elliptical shape. This distortion of the inner shock is important because radial fast wind streamlines no longer encounter the shock normally but instead strike it at an angle. Streamlines passing through a shock at an acute angle are refracted away from the shock normal. In this way, an aspherical slow wind in GISW models lead to a “shock focused inertial confinement” of the fast wind producing well-collimated jets [5]. The stronger the pole to equator contrast in the slow wind, the more effective is the shock focusing of fast wind material into bipolar jets.

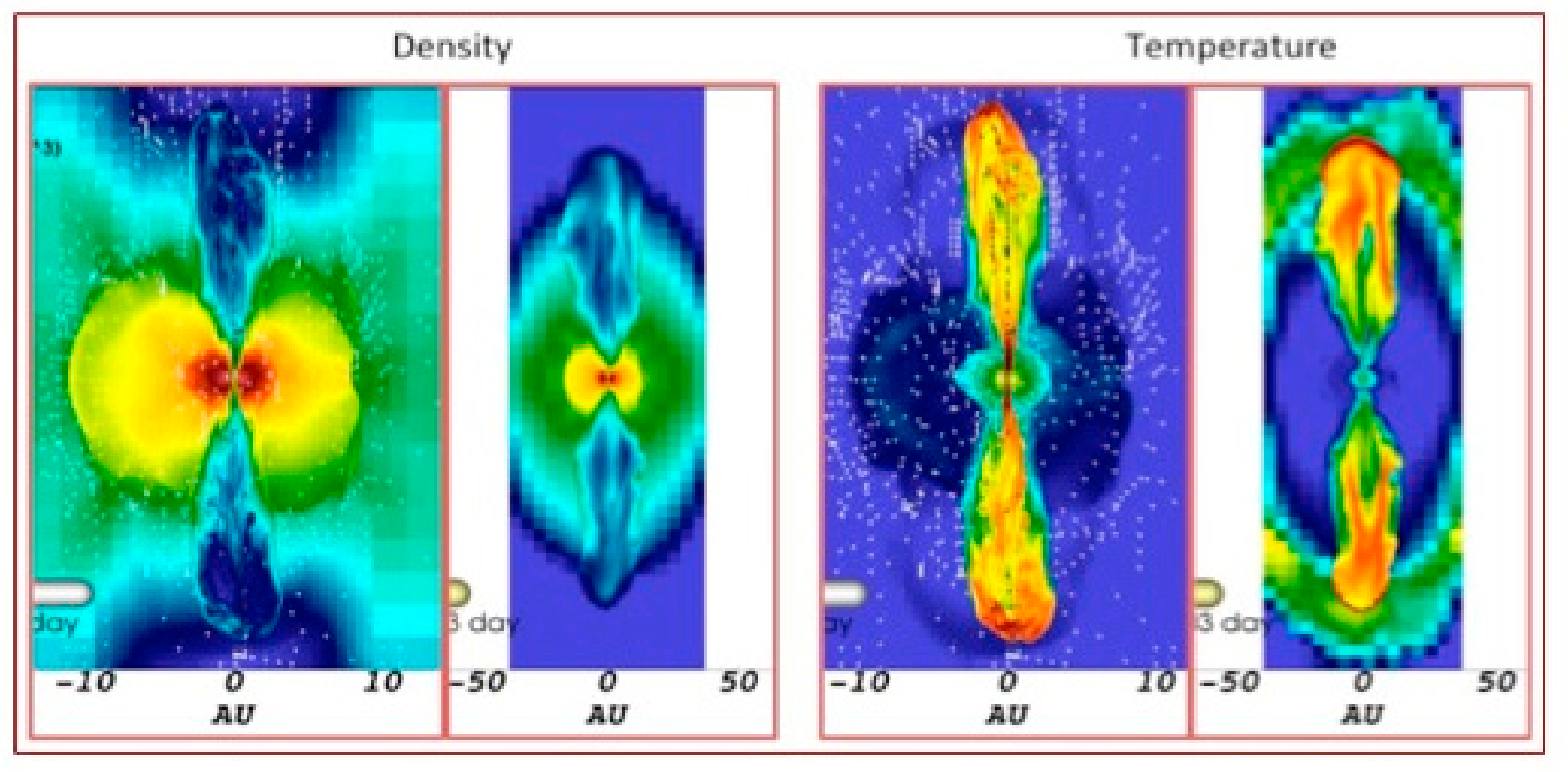
• Model A: In Figure 1 we show slices of the X-Z plane from our AMR AstroBEAR simulation taken at two different times. The first slice is taken 780 days after the initialization of the fast wind and the second is taken at 1600 days.

We first note that the CEE ejecta began with a high pole to equator density contrast (e > 100) and a “cored apple” morphology. During the quiescent evolution of the CEE ejecta, we did not observe this morphology to change significantly. Once the fast wind began, we saw that the high densities of the CEE led to strong inertial confinement in which the momentum injection via the fast wind was unable to move ejecta material in the equatorial direction. In the polar regions, however, fast wind material was able to drive through the ejecta, leading to two highly collimated shocked wind flows which, together, created an overall bipolar outflow.

Consideration of the flow at t = 780 days shows that the lobes are essentially hollow, bounded externally by shocked, swept up CEE ejecta and filled internally with low density shocked fast wind material. The shocked fast wind leads, as one would expect, to high temperatures (T ~ 10⁶ K) in the lobe interiors.

As the lobes expand, their basic morphology remains relatively steady with a length to radius ratio of order L_lobe/R_lobe ~ 7. What is noteworthy, however, is the difference between the upper and lower lobes in the two time slices. We emphasize that the flows associated with CEE are inherently and fully 3-D. In particular, the binary star’s movement through the CE gas sets up strong shearing shocks that lead to KH instabilities which drive local regions of turbulence. The complexity of the flows after repeatedly being shocked by the subsequent driving of unstable modes during each orbit creates local flow patterns that does not need to be axi-symmetric or top-bottom symmetric. We note that such perturbations are seen not just in SPH simulations but also in AMR grid-based simulations ([19], Figure 4, [28], Figure 1). We note that while it’s possible that the initial perturbations driving instabilities may have numerical seeds, the development of turbulent, non-symmetric local flow conditions is to be expected.

Because the evolution of the CE ejecta need not respect top/bottom symmetry relative to the orbital plane, it presents a different environment for fast wind interaction above and below the equatorial regions. Thus, we see the details of density and temperature inhomogeneities in the top and bottom lobes differing significantly. This natural cause of symmetry breaking in the two lobes holds great promise in explaining the rich morphologies seen in high-resolution images of PNe.

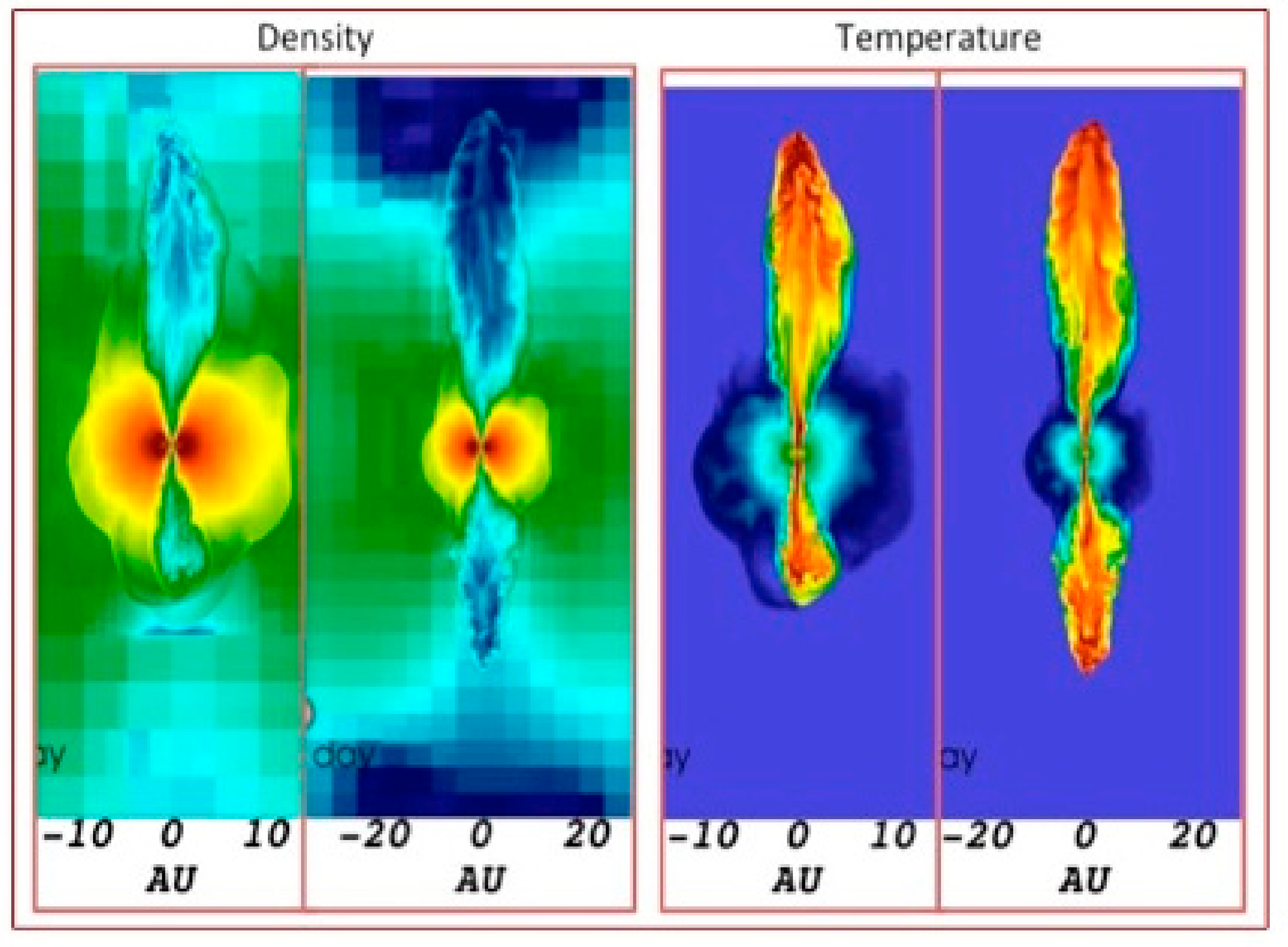
• Model B: In Figure 2, we show slices from a simulation with a fast wind momentum injection rate that is 20 times lower than Model A. In this model, it takes considerable time for the bipolar lobes to work their way out of the aspherical CEE ejecta as it is demonstrated by the time at which the two sets of images are taken (t = 6440 and 6770 days, respectively). The two times shown are relatively close, as compared to what was shown in Model A. This is because before t = 6440, the lobes have yet to break out from the central regions of the CEE ejecta. Once the lobes escape the central regions, they begin a rapid expansion in the z-direction (as defined by the binary orbital angular momentum vector).

What is most noteworthy for this model is the strong asymmetry between the top and bottom lobes. While Model A showed differences in details of density/temperature inhomogeneities, Model B provides evidence for a very different evolutionary history between the two lobes. While the top lobe has advanced to almost Z = 60 AU from the central source, the bottom lobe has only made it to Z = 40 AU. Inspection of the evolution of the Model B shows that the difference between the top and bottom lobe lies in sensitivity to the wind interaction in the CEE polar “channels” (the cored-apple structures in density). In the low momentum case, shocked fast wind accumulates in central regions of CEE ejecta. Inhomogeneities in the “walls” of the CEE ejecta, which are not symmetric about the equatorial plane, lead to the shocked fast wind being becoming trapped/diverted in local density pockets in the lower half of the domain compared to the upper half. Thus, while the shocked fast wind is capable of pushing through the upper CEE channel to form an extended bipolar lobe, the fast wind in the lower channel is blocked for some time. By the time it escapes from the lower channel to form a jet, it significantly lags behind the upper lobe. As discussed above, these global scale asymmetries in the outflow result from local scale asymmetries in the “cored apple” region of the CE ejecta which acts as a nozzle or funnels for collimating the spherical wind into a collimated, bipolar outflow.

Note that the combination of the temperature and density maps show that once they form, the lobes are, just as in Model A, composed of high temperature, low density shocked fast wind material.

4. Conclusions

Using the full CEE simulations as input, we have performed AMR simulations that track the interaction of a fast wind from a central source (the compact binary) and a strongly aspherical CEE ejecta. We find that CEE ejecta provides the strong aspherical density environment needed in classic GISW models to produce strongly bipolar outflows such as those seen in some PPN and PN. Thus, our models confirm and extend the original emphasis on CEE in PN shaping.

We note that one significant new result is the ability of full 3-D CEE models to drive symmetry breaking in GISW bipolar outflows. Our models not only show the differences between top and bottom lobes in terms of inhomogeneous, but they also showed a difference in the size and extent of the upper and lower lobe. If this result continues to be obtained in a more detailed and extensive modeling, then it may offer a natural explanation for objects like OH231+8+04.2 and other highly asymmetric bipolar nebulae.

Finally we note that 2-D fixed grid studies of this problem have recently been completed by [29] using a different set of CE inputs. These results along with the work discussed here show that the field is finally in a position to calculate the PN morp ${\mathrm{R}}_{\odot }$ hologies directly from models of the evolution of ejecta from the host binary star system.