Long-Term Stability of Chemical Spots and Reasons for the Period Variations in Ap Star CU Vir
Abstract
1. Introduction
2. Observational Data
2.1. Spectroscopy
2.2. Calculation of Rotational Phases
3. Doppler Imaging
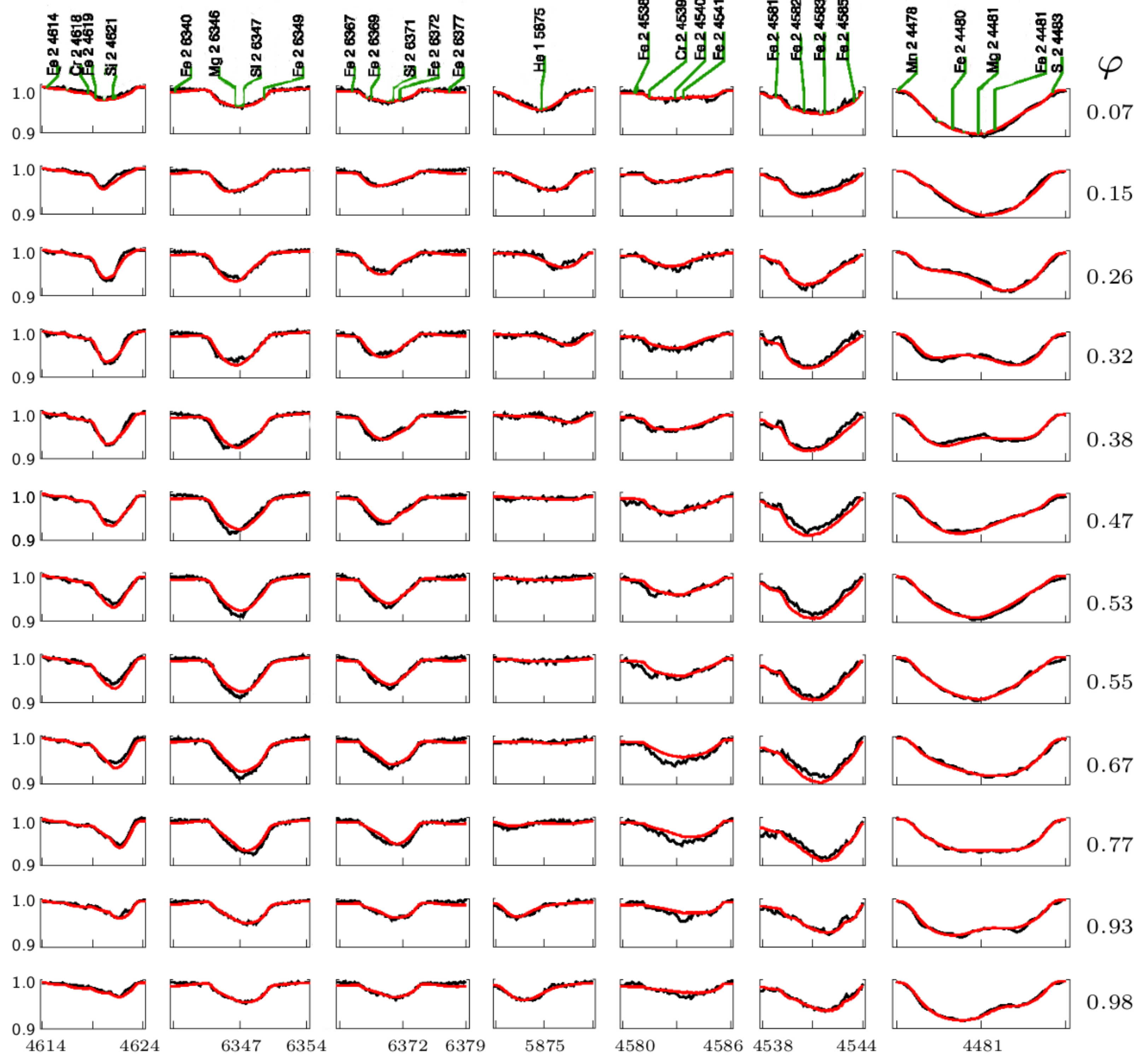
3.1. Technique
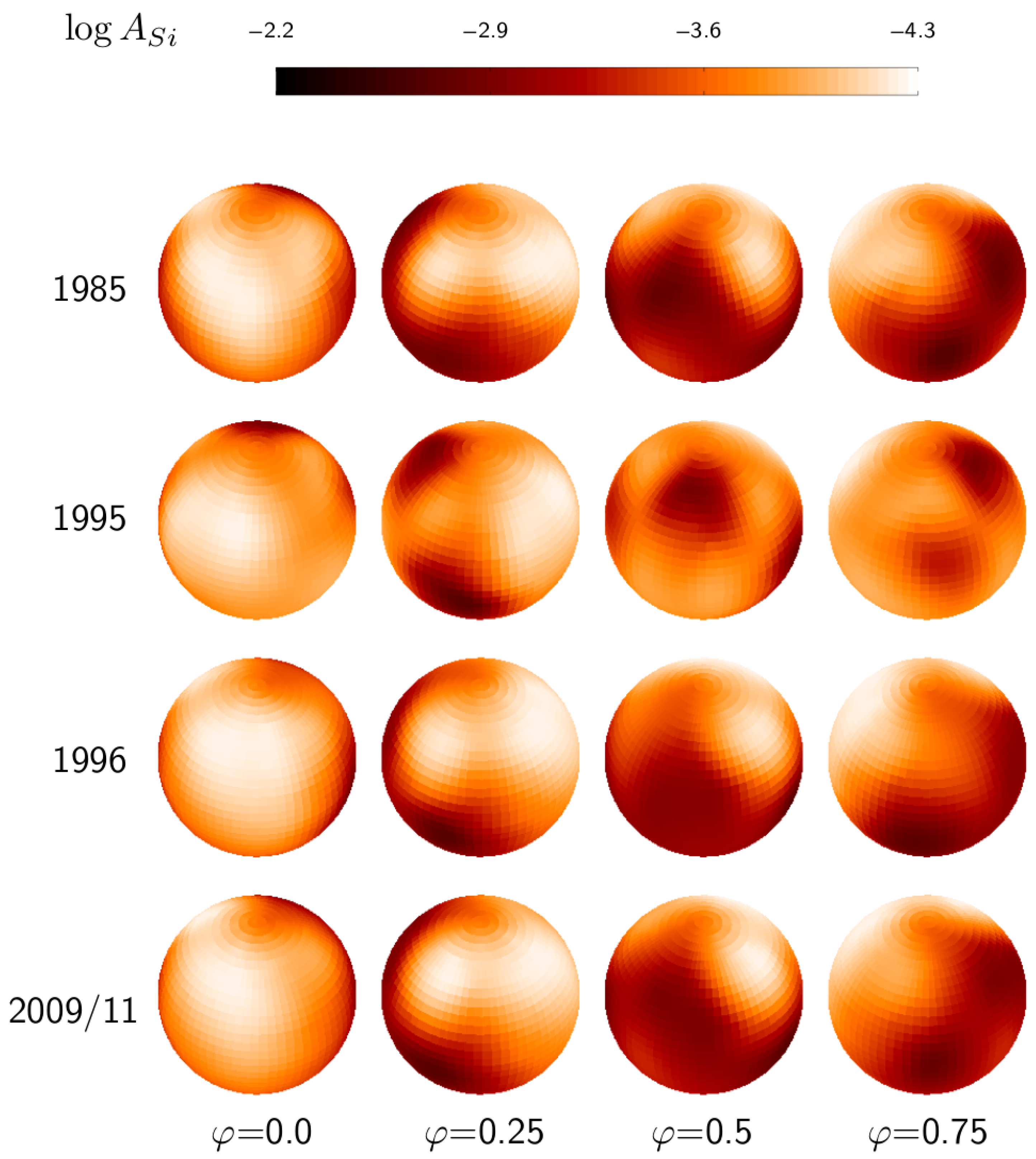
3.2. Silicon Spots in 1985–2011
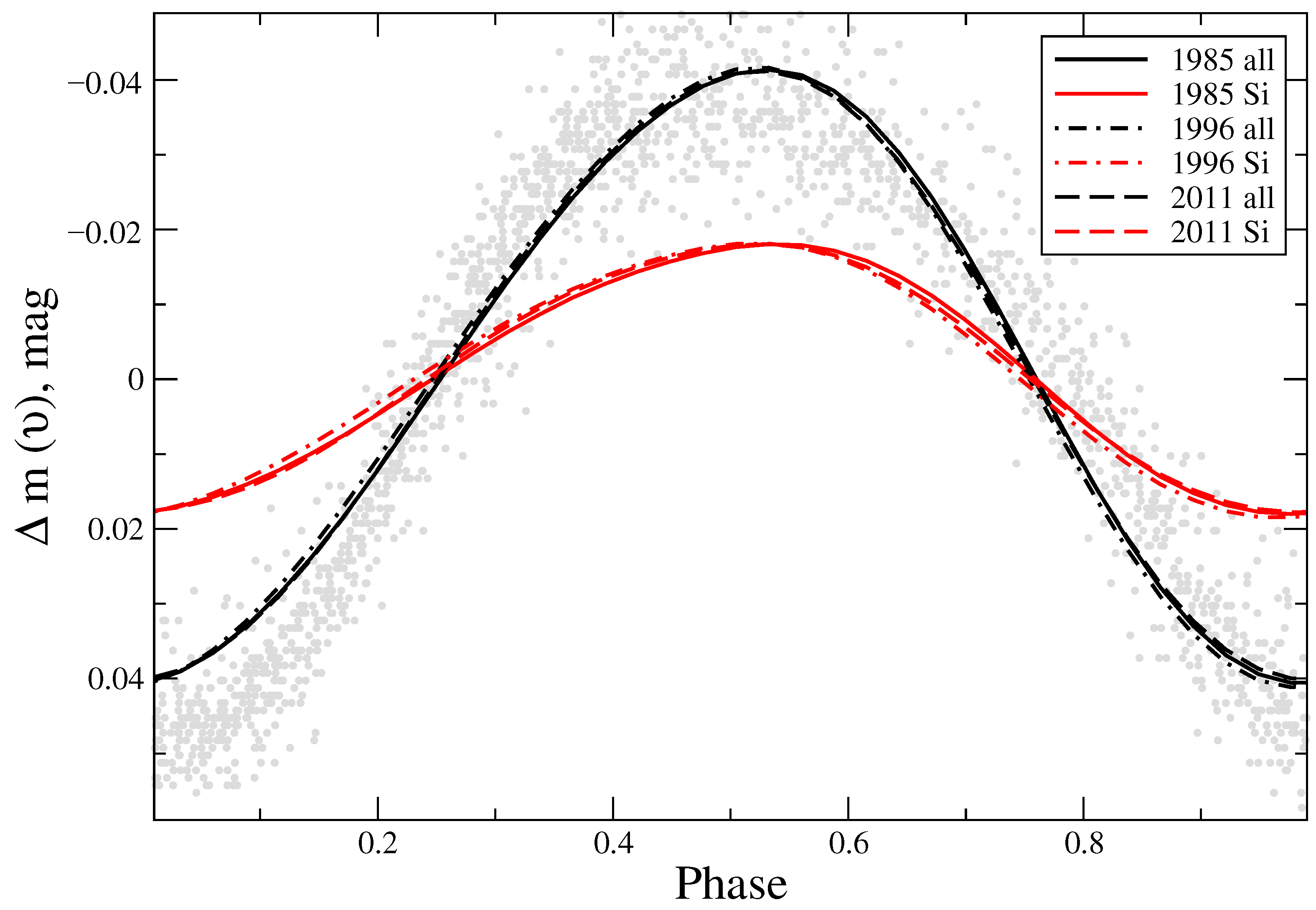
3.3. Light Curves in 1985–2011
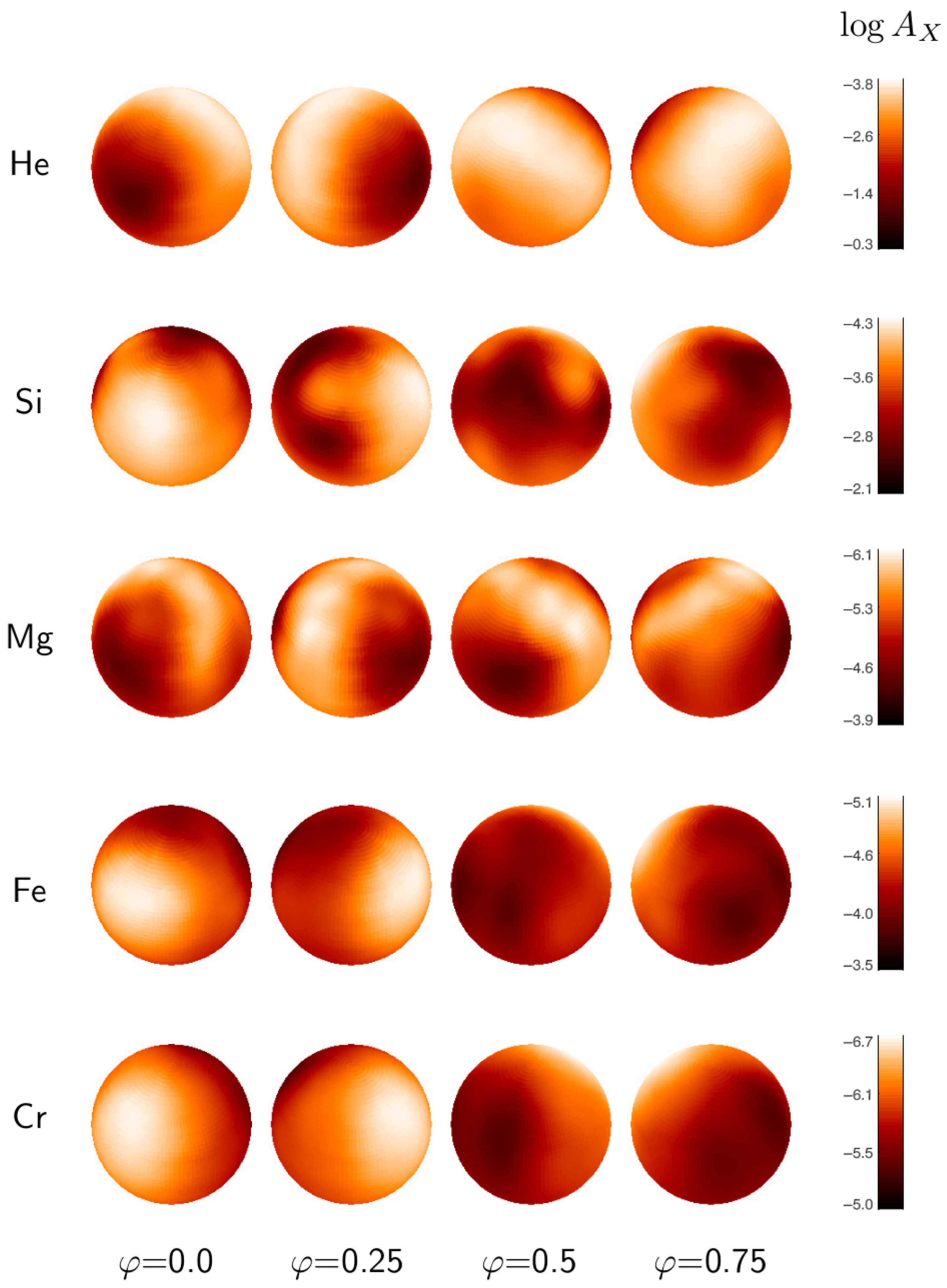
3.4. Multi-Element DI
3.4.1. Helium
3.4.2. Magnesium
3.4.3. Silicon
3.4.4. Iron
3.4.5. Chromium
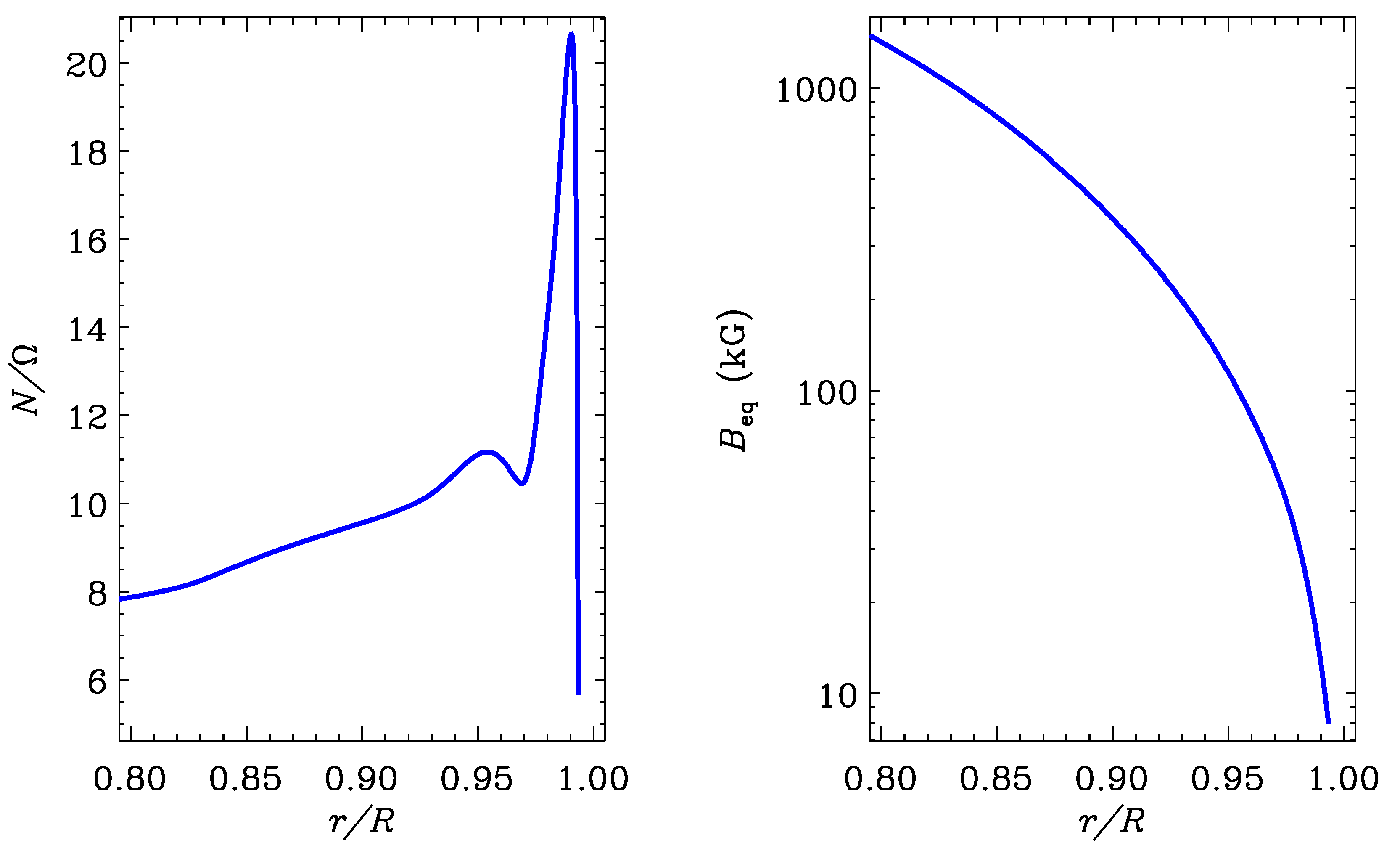
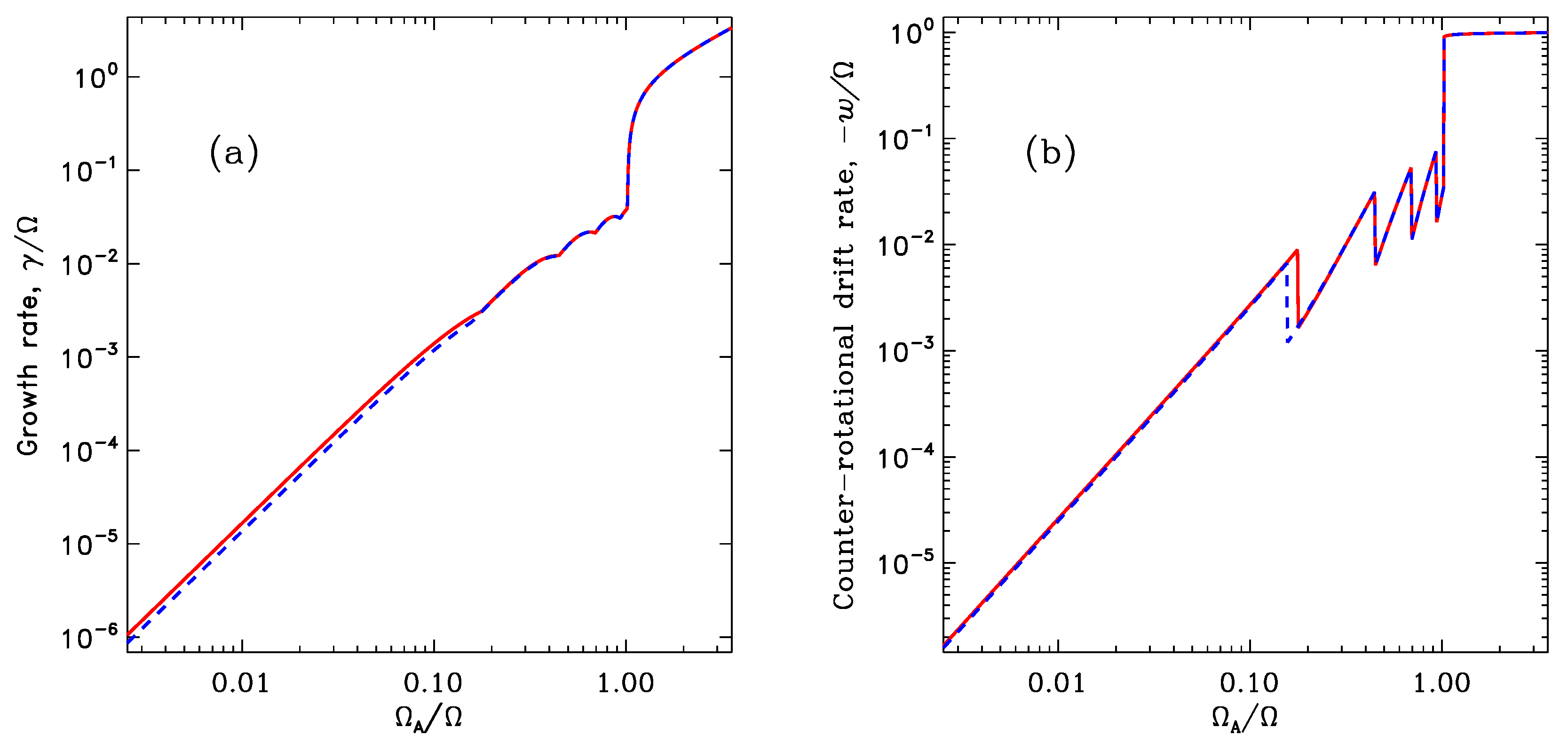
4. Tayler Instability of Magnetic Field in CU Vir
5. Discussion
5.1. Surface-Abundance Distributions in CU Vir and Their Stability
5.2. Period Changes and Longitudinal Drift of Magnetic and Abundance Structures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DI | Doppler Imaging |
| ZDI | Zeeman–Doppler Imaging |
| LTE | Local Thermodynamic Equilibrum |
Appendix A. List of Elements and Lines Used for DI
| Element | Line, Å | , eV | Comment | ||
|---|---|---|---|---|---|
| Si ii | 4621.4182 | 12.525 | −0.540 | −3.860 | bl. Fe ii, Cr ii |
| 4621.6960 | 12.525 | −1.680 | −3.860 | ||
| 4621.7216 | 12.525 | −0.380 | −3.860 | ||
| 5041.0240 | 10.0664 | 0.150 | −5.170 | bl. Fe ii, Ni ii | |
| 5055.9841 | 10.0739 | 0.512 | −5.170 | bl. Fe ii, Ni ii, atm. | |
| 5056.3165 | 10.0739 | −0.679 | −5.170 | ||
| 6347.1087 | 8.1210 | 0.000 | −5.680 | bl. Fe ii, Mg ii, : −0.17 dex | |
| 6347.1329 | 13.9351 | −1.721 | −2.810 | : −0.3 dex | |
| 6347.1973 | 13.9351 | −1.567 | −2.810 | : −0.3 dex | |
| 6371.3714 | 8.1210 | −0.320 | −5.680 | bl. Fe ii, : −0.3 dex | |
| He i | 4471.4690 | 20.9641 | −2.198 | −3.690 | bl. Fe ii, Ti ii |
| 4471.4730 | 20.9641 | −1.028 | −3.690 | ||
| 4471.4730 | 20.9641 | −0.278 | −3.690 | ||
| 4471.4850 | 20.9641 | −1.028 | −3.690 | ||
| 4471.4880 | 20.9641 | −0.548 | −3.690 | ||
| 4471.6820 | 20.9642 | −0.898 | −3.690 | ||
| 5875.5990 | 20.9641 | −1.511 | −4.720 | w.bl.atm. | |
| 5875.6140 | 20.9641 | −0.341 | −4.720 | ||
| 5875.6150 | 20.9641 | 0.409 | −4.720 | ||
| 5875.6250 | 20.9641 | −0.341 | −4.720 | ||
| 5875.6400 | 20.9641 | 0.139 | −4.720 | ||
| 5875.9660 | 20.9642 | −0.211 | −4.720 | ||
| Fe ii | 4515.3330 | 2.8441 | −2.537 | −6.530 | bl. Ca ii |
| 4520.2180 | 2.8067 | −2.600 | −6.530 | bl. Mn ii | |
| 4522.6276 | 2.8441 | −2.189 | −6.530 | bl. S ii | |
| 4541.5156 | 2.8555 | −2.927 | −6.530 | ||
| 4582.8296 | 2.8441 | −3.130 | −6.530 | ||
| 4583.8292 | 2.8067 | −1.940 | −6.530 | ||
| 4583.9912 | 2.7043 | −3.840 | −6.540 | ||
| Cr ii | 4554.9880 | 4.0712 | −1.282 | −6.540 | bl. Fe ii, Ba ii |
| 4558.6500 | 4.0734 | −0.449 | −6.540 | bl. Fe ii | |
| 4558.7830 | 4.0735 | −2.530 | −6.540 | ||
| 4588.1990 | 4.0712 | −0.826 | −6.560 | ||
| 4589.9010 | 4.0722 | −2.660 | −6.560 | ||
| Mg ii | 4481.1260 | 8.8637 | 0.740 | −4.70 | bl. Fe ii, Mn ii, Al iii |
| 4481.1500 | 8.8637 | −0.560 | −4.70 | ||
| 4481.3250 | 8.8637 | 0.590 | −4.70 |
| 1 |
References
- Deutsch, A.J. A New Spectrum Variable of Short Period, HD 124224. Astrophys. J. 1952, 116, 536. [Google Scholar] [CrossRef]
- Kochukhov, O.; Lüftinger, T.; Neiner, C.; Alecian, E.; MiMeS Collaboration. Magnetic field topology of the unique chemically peculiar star CU Virginis. Astron. Astrophys. 2014, 565, A83. [Google Scholar] [CrossRef]
- Krivoseina, A.A.; Ryabchikova, T.A.; Khokhlova, V.L. Distribution of SI on the Surface of the Silicon Ap-Star Cu-Virginis and Interpretation of the Lightcurves in the Vby Bands. Nauchnye Informatsii 1980, 43, 70. [Google Scholar]
- Hatzes, A.P. Mapping the Surface Distribution of Elements on Ap-Stars Using the Maximum Entropy Method. In Proceedings of the IAU Colloq. 138: Peculiar versus Normal Phenomena in A-type and Related Stars, Trieste, Italy, 6–10 July 1993. [Google Scholar]
- Hatzes, A.P. Doppler imaging of the silicon distribution on CUVir: Evidence for a decentred magnetic dipole? Mon. Not. R. Astron. Soc. 1997, 288, 153–160. [Google Scholar] [CrossRef][Green Version]
- Kuschnig, R.; Ryabchikova, T.A.; Piskunov, N.E.; Weiss, W.W.; Gelbmann, M.J. Multi element Doppler imaging of AP stars. I. He, Mg, Si, CR and Fe surface distribution for CU Virginis. Astron. Astrophys. 1999, 348, 924–932. [Google Scholar][Green Version]
- Krtička, J.; Mikulášek, Z.; Lüftinger, T.; Shulyak, D.; Zverko, J.; Žižňovský, J.; Sokolov, N.A. Modelling of the ultraviolet and visual SED variability in the hot magnetic Ap star CU Virginis. Astron. Astrophys. 2012, 537, A14. [Google Scholar] [CrossRef]
- Krtička, J.; Mikulášek, Z.; Henry, G.W.; Janík, J.; Kochukhov, O.; Pigulski, A.; Leto, P.; Trigilio, C.; Krtičková, I.; Lüftinger, T.; et al. HST/STIS analysis of the first main sequence pulsar CU Virginis. Astron. Astrophys. 2019, 625, A34. [Google Scholar] [CrossRef]
- Mikulášek, Z.; Semenko, E.; Paunzen, E.; Hümmerich, S.; North, P.L.; Bernhard, K.; Krtička, J.; Janík, J. HD 60431, the CP2 star with the shortest rotational period. Physical parameters and period analysis. Astron. Astrophys. 2022, 668, A159. [Google Scholar] [CrossRef]
- Semenko, E.; Romanyuk, I.; Yakunin, I.; Kudryavtsev, D.; Moiseeva, A. Spectropolarimetry of magnetic Chemically Peculiar stars in the Orion OB1 association. Mon. Not. R. Astron. Soc. 2022, 515, 998–1011. [Google Scholar] [CrossRef]
- Pyper, D.M.; Ryabchikova, T.; Malanushenko, V.; Kuschnig, R.; Plachinda, S.; Savanov, I. An abrupt decrease in the rotational period of the chemically peculiar magnetic star CU Virginis. Astron. Astrophys. 1998, 339, 822–830. [Google Scholar]
- MacDonald, J.; Natan, T.; Petit, V.; Kochukhov, O.; Shultz, M.E. Using ZDI maps to determine magnetic forces and torques at the photospheres of early-type stars. Mon. Not. R. Astron. Soc. 2024, 530, 2840–2851. [Google Scholar] [CrossRef]
- Mikulášek, Z.; Krtička, J.; Henry, G.W.; Janík, J.; Zverko, J.; Žižňovský, J.; Zejda, M.; Liška, J.; Zvěřina, P.; Kudrjavtsev, D.O.; et al. Surprising variations in the rotation of the chemically peculiar stars CU Virginis and V901 Orionis. Astron. Astrophys. 2011, 534, L5. [Google Scholar] [CrossRef]
- Trigilio, C.; Leto, P.; Umana, G.; Leone, F.; Buemi, C.S. A three-dimensional model for the radio emission of magnetic chemically peculiar stars. Astron. Astrophys. 2004, 418, 593–605. [Google Scholar] [CrossRef]
- Trigilio, C.; Leto, P.; Umana, G.; Buemi, C.S.; Leone, F. The radio lighthouse CU Virginis: The spin-down of a single main-sequence star. Mon. Not. R. Astron. Soc. 2008, 384, 1437–1443. [Google Scholar] [CrossRef]
- Das, B.; Chandra, P. Ultra-wideband, Multiepoch Radio Study of the First Discovered “Main-sequence Radio Pulse Emitter” CU Vir. Astrophys. J. 2021, 921, 9. [Google Scholar] [CrossRef]
- Pyper, D.M.; Stevens, I.R.; Adelman, S.J. An update on the rotational period of the magnetic chemically peculiar star CU Virginis. Mon. Not. R. Astron. Soc. 2013, 431, 2106–2110. [Google Scholar] [CrossRef]
- Pyper, D.M.; Adelman, S.J. Newly Discovered Period Changes in Two mCP Stars and Updates for Previously Published Stars. Publ. Astron. Soc. Pac. 2020, 132, 024201. [Google Scholar] [CrossRef]
- Pyper, D.M.; Adelman, S.J. Light Curve Changes and Possible Precession in mCP Stars. Publ. Astron. Soc. Pac. 2021, 133, 084203. [Google Scholar] [CrossRef]
- Mikulášek, Z.; Krtička, J.; Henry, G.W.; Janík, J.; Pigulski, A. Towards Comprehension of the Variability of the mCP Star CU Virginis. Phys. Magn. Stars 2019, 518, 125. [Google Scholar] [CrossRef]
- Stȩpień, K. On a mechanism of an abrupt change of period of CU Virginis. Astron. Astrophys. 1998, 337, 754–756. [Google Scholar]
- Kochukhov, O.; Adelman, S.J.; Gulliver, A.F.; Piskunov, N. Weather in stellar atmosphere revealed by the dynamics of mercury clouds in α Andromedae. Nat. Phys. 2007, 3, 526–529. [Google Scholar] [CrossRef]
- Hubrig, S.; Savanov, I.; Ilyin, I.; González, J.F.; Korhonen, H.; Lehmann, H.; Schöller, M.; Granzer, T.; Weber, M.; Strassmeier, K.G.; et al. The magnetic field and the evolution of element spots on the surface of the HgMn eclipsing binary ARAur. Mon. Not. R. Astron. Soc. 2010, 408, L61–L65. [Google Scholar] [CrossRef]
- Korhonen, H.; González, J.F.; Briquet, M.; Flores Soriano, M.; Hubrig, S.; Savanov, I.; Hackman, T.; Ilyin, I.V.; Eulaers, E.; Pessemier, W. Chemical surface inhomogeneities in late B-type stars with Hg and Mn peculiarity. I. Spot evolution in HD 11753 on short and long time scales. Astron. Astrophys. 2013, 553, A27. [Google Scholar] [CrossRef][Green Version]
- Prvák, M.; Krtička, J.; Korhonen, H. The nature of the photometric variability of HgMn stars: A test of simulated light curves of φ Phe against the TESS data. Mon. Not. R. Astron. Soc. 2020, 492, 1834–1840. [Google Scholar] [CrossRef]
- Urpin, V. Chemical spots and oscillatory diffusion modes in magnetic stars. Astron. Nachrichten 2016, 337, 633. [Google Scholar] [CrossRef]
- Krtička, J.; Mikulášek, Z.; Henry, G.W.; Kurfürst, P.; Karlický, M. Torsional oscillations and observed rotational period variations in early-type stars. Mon. Not. R. Astron. Soc. 2017, 464, 933–939. [Google Scholar] [CrossRef]
- Takahashi, K.; Langer, N. Standing torsional Alfvén waves as the source of the rotational period variation in magnetic early-type stars. Astron. Astrophys. 2025, 696, A129. [Google Scholar] [CrossRef]
- Potravnov, I.S.; Kitchatinov, L.L. Tayler instability of magnetic field as the possible reason for the period changes in Ap star 56 Ari. Astron. Rep. 2025, 69, 500. [Google Scholar] [CrossRef]
- Shore, S.N.; Adelman, S.J. Magnetic fields and diffusion processes in peculiar A stars. II. Precession and the oblique rotator model. Astrophys. J. 1976, 209, 816–820. [Google Scholar] [CrossRef]
- Petit, P.; Louge, T.; Théado, S.; Paletou, F.; Manset, N.; Morin, J.; Marsden, S.C.; Jeffers, S.V. PolarBase: A Database of High-Resolution Spectropolarimetric Stellar Observations. Publ. Astron. Soc. Pac. 2014, 126, 469. [Google Scholar] [CrossRef]
- Donati, J.F.; Semel, M.; Carter, B.D.; Rees, D.E.; Collier Cameron, A. Spectropolarimetric observations of active stars. Mon. Not. R. Astron. Soc. 1997, 291, 658–682. [Google Scholar] [CrossRef]
- Pakhomov, Y.; Potravnov, I.; Ryabchikova, T. Light variability from UV to near-infrared in Ap star CU Vir induced by chemical spots. Galaxies 2025, 13, 97. [Google Scholar] [CrossRef]
- Piskunov, N.; Kochukhov, O. Doppler Imaging of stellar magnetic fields. I. Techniques. Astron. Astrophys. 2002, 381, 736–756. [Google Scholar] [CrossRef]
- Piskunov, N.E.; Rice, J.B. Techniques for Surface Imaging of Stars. Publ. Astron. Soc. Pac. 1993, 105, 1415. [Google Scholar] [CrossRef]
- Piskunov, N. Doppler imaging. Phys. Scr. Vol. T 2008, 133, 014017. [Google Scholar] [CrossRef]
- Shulyak, D.; Tsymbal, V.; Ryabchikova, T.; Stütz, C.; Weiss, W.W. Line-by-line opacity stellar model atmospheres. Astron. Astrophys. 2004, 428, 993–1000. [Google Scholar] [CrossRef]
- Ryabchikova, T.; Piskunov, N.; Kurucz, R.L.; Stempels, H.C.; Heiter, U.; Pakhomov, Y.; Barklem, P.S. A major upgrade of the VALD database. Phys. Scr. 2015, 90, 054005. [Google Scholar] [CrossRef]
- Pakhomov, Y.; Potravnov, I.; Romanovskaya, A.; Ryabchikova, T. Modeling the TESS Light Curve of Ap Si Star MX TrA. Universe 2024, 10, 341. [Google Scholar] [CrossRef]
- Mashonkina, L. Non-local thermodynamic equilibrium line formation for Si I-II-III in A-B stars and the origin of Si II emission lines in ι Her. Mon. Not. R. Astron. Soc. 2020, 493, 6095–6108. [Google Scholar] [CrossRef]
- Spruit, H.C. Differential rotation and magnetic fields in stellar interiors. Astron. Astrophys. 1999, 349, 189–202. [Google Scholar] [CrossRef]
- Cowling, T.G. On the Sun’s general magnetic field. Mon. Not. R. Astron. Soc. 1945, 105, 166. [Google Scholar] [CrossRef]
- Moss, D. Magnetic Fields in the Ap and Bp Stars: A Theoretical Overview. Magn. Fields Across-Hertzsprung-Russell Diagr. 2001, 248, 305. [Google Scholar]
- Bogomazov, A.I.; Tutukov, A.V. Merging of components in close binaries: Type Ia supernovae, massive white dwarfs, and Ap stars. Astron. Rep. 2009, 53, 214–222. [Google Scholar] [CrossRef]
- Schneider, F.R.N.; Ohlmann, S.T.; Podsiadlowski, P.; Röpke, F.K.; Balbus, S.A.; Pakmor, R.; Springel, V. Stellar mergers as the origin of magnetic massive stars. Nature 2019, 574, 211–214. [Google Scholar] [CrossRef]
- Tayler, R.J. The adiabatic stability of stars containing magnetic fields-I.Toroidal fields. Mon. Not. R. Astron. Soc. 1973, 161, 365. [Google Scholar] [CrossRef]
- Pitts, E.; Tayler, R.J. The adiabatic stability of stars containing magnetic fields. IV - The influence of rotation. Mon. Not. R. Astron. Soc. 1985, 216, 139–154. [Google Scholar] [CrossRef]
- Spruit, H.C. Dynamo action by differential rotation in a stably stratified stellar interior. Astron. Astrophys. 2002, 381, 923–932. [Google Scholar] [CrossRef]
- Arlt, R.; Rüdiger, G. Magnetic fields of Ap stars as a result of the Tayler instability. Astron. Nachrichten 2011, 332, 70–76. [Google Scholar] [CrossRef]
- Rüdiger, G.; Kitchatinov, L.L. The kink-type instability of toroidal stellar magnetic fields with thermal diffusion. Geophys. Astrophys. Fluid Dyn. 2010, 104, 273–285. [Google Scholar] [CrossRef][Green Version]
- Kitchatinov, L.L.; Potravnov, I.S.; Nepomnyashchikh, A.A. Longitudinal drift of Tayler instability eigenmodes as a possible explanation for super-slowly rotating Ap stars. Astron. Astrophys. 2020, 638, L9. [Google Scholar] [CrossRef]
- Kitchatinov, L.; Rüdiger, G. Stability of toroidal magnetic fields in rotating stellar radiation zones. Astron. Astrophys. 2008, 478, 1–8. [Google Scholar] [CrossRef]
- Kitchatinov, L.L. Stability of toroidal magnetic fields in the radiation zone of a star. Astron. Rep. 2008, 52, 247–255. [Google Scholar] [CrossRef]
- Goossens, M.; Biront, D.; Tayler, R.J. Additional Results for Unstable Stratified Toroidal Magnetic Fields in Stars. Astrophys. Space Sci. 1981, 75, 521–526. [Google Scholar] [CrossRef]
- Denissenkov, P.A.; Pinsonneault, M. A Revised Prescription for the Tayler-Spruit Dynamo: Magnetic Angular Momentum Transport in Stars. Astrophys. J. 2007, 655, 1157–1165. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. 2011, 192, 3. [Google Scholar] [CrossRef]
- Potravnov, I.; Piskunov, N.; Ryabchikova, T. Secular stability of surface abundance structures in the rapidly rotating Ap star 56 Ari. Astron. Astrophys. 2024, 689, A111. [Google Scholar] [CrossRef]
- Parker, E.N. The Instability of a Horizontal Magnetic Field in an Atmosphere Stable Against Convection. Astrophys. Space Sci. 1979, 62, 135–142. [Google Scholar] [CrossRef]
- Hughes, D.W.; Weiss, N.O. Double-diffusive convection with two stabilizing gradients: Strange consequences of magnetic buoyancy. J. Fluid Mech. 1995, 301, 383–406. [Google Scholar] [CrossRef]

| HJD | Phase (P20) | Phase (M19) | HJD | Phase (P20) | Phase (M19) |
|---|---|---|---|---|---|
| 1985 (Lick) | 1996 (CrAO) | ||||
| 2446101.905 | 0.913 | 0.874 | 2449470.295 | 0.895 | 0.833 |
| 2446101.925 | 0.952 | 0.912 | 2449470.320 | 0.943 | 0.881 |
| 2446101.973 | 0.042 | 0.005 | 2449496.344 | 0.920 | 0.859 |
| 2446102.016 | 0.126 | 0.087 | 2450134.603 | 0.658 | 0.606 |
| 2446102.063 | 0.217 | 0.177 | 2450174.451 | 0.184 | 0.132 |
| 2446102.989 | 0.995 | 0.956 | 2450191.418 | 0.769 | 0.716 |
| 2446132.900 | 0.439 | 0.400 | 2450210.412 | 0.244 | 0.193 |
| 2446132.965 | 0.564 | 0.525 | 2450233.317 | 0.232 | 0.181 |
| 2446133.020 | 0.670 | 0.631 | 2450233.358 | 0.311 | 0.260 |
| 2446133.069 | 0.764 | 0.725 | 2450233.454 | 0.495 | 0.444 |
| 2446133.887 | 0.335 | 0.296 | 2450253.303 | 0.615 | 0.563 |
| 2446133.960 | 0.475 | 0.436 | 2450253.363 | 0.730 | 0.679 |
| 1995 (OHP) | 2450254.311 | 0.551 | 0.499 | ||
| 2449798.489 | 0.172 | 0.115 | 2450255.275 | 0.402 | 0.351 |
| 2449798.622 | 0.427 | 0.371 | 2450255.289 | 0.428 | 0.377 |
| 2449799.434 | 0.986 | 0.930 | 2450255.305 | 0.459 | 0.408 |
| 2449799.575 | 0.257 | 0.201 | 2009/11 (PdM) | ||
| 2449799.612 | 0.328 | 0.272 | 2454902.517 | 0.151 | 0.09 |
| 2449800.410 | 0.861 | 0.805 | 2454904.485 | 0.930 | 0.869 |
| 2449800.502 | 0.037 | 0.981 | 2454905.554 | 0.984 | 0.922 |
| 2449800.599 | 0.224 | 0.168 | 2454906.487 | 0.774 | 0.714 |
| 2449801.412 | 0.785 | 0.729 | 2454909.493 | 0.548 | 0.487 |
| 2449802.415 | 0.711 | 0.655 | 2454935.487 | 0.468 | 0.407 |
| 2449803.438 | 0.676 | 0.620 | 2454935.523 | 0.537 | 0.476 |
| 2449804.444 | 0.601 | 0.552 | 2454945.486 | 0.670 | 0.610 |
| 2449804.468 | 0.654 | 0.598 | 2455292.589 | 0.261 | 0.203 |
| 2449806.413 | 0.389 | 0.333 | 2455596.718 | 0.322 | 0.269 |
| 2449806.435 | 0.431 | 0.375 | 2455657.510 | 0.070 | 0.017 |
| 2449806.452 | 0.464 | 0.408 | 2455690.479 | 0.385 | 0.333 |
| 2449806.469 | 0.497 | 0.441 | |||
| 2449806.484 | 0.525 | 0.469 | |||
| 2449806.500 | 0.556 | 0.500 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Potravnov, I.; Ryabchikova, T.; Kitchatinov, L.; Pakhomov, Y. Long-Term Stability of Chemical Spots and Reasons for the Period Variations in Ap Star CU Vir. Galaxies 2025, 13, 90. https://doi.org/10.3390/galaxies13040090
Potravnov I, Ryabchikova T, Kitchatinov L, Pakhomov Y. Long-Term Stability of Chemical Spots and Reasons for the Period Variations in Ap Star CU Vir. Galaxies. 2025; 13(4):90. https://doi.org/10.3390/galaxies13040090
Chicago/Turabian StylePotravnov, Ilya, Tatiana Ryabchikova, Leonid Kitchatinov, and Yuri Pakhomov. 2025. "Long-Term Stability of Chemical Spots and Reasons for the Period Variations in Ap Star CU Vir" Galaxies 13, no. 4: 90. https://doi.org/10.3390/galaxies13040090
APA StylePotravnov, I., Ryabchikova, T., Kitchatinov, L., & Pakhomov, Y. (2025). Long-Term Stability of Chemical Spots and Reasons for the Period Variations in Ap Star CU Vir. Galaxies, 13(4), 90. https://doi.org/10.3390/galaxies13040090






