Wind and Eruptive Mass Loss near the Eddington Limit

Abstract

Luminous, hot, massive stars can lose mass both through quasi-steady winds driven by line-scattering of the star’s continuum luminosity, and through transient eruptions identified as Luminous Blue Variables (LBVs). This paper compares and contrasts the processes involved in steady vs. eruptive mass loss, with an emphasis on their dependence on the star’s proximity to the classical Eddington limit. For winds, I examine the role of the iron opacity bump in initiating a quasi-continuum-driven outflow, which can induce atmospheric turbulence in O-stars, an envelope inflation cycle in LBVs, or enhanced wind mass loss in WR stars. In contrast, the giant eruptions of eruptive LBVs like $\eta$ Carinae require a sudden addition of energy to the stellar envelope, like that which can occur from stellar mergers. The positive net energy imparted to a substantial fraction (>10%) of the stellar mass leads to sudden ejection that closely follows an analytic exponential similarity solution. Moreover, the rapid rotation and enhanced luminosity of the post-merger star drive a super-Eddington wind that. Due to equatorial gravity darkening, this wind is stronger over the poles, sculpting a bipolar structure in the ejected mass, consistent with observations of $\eta$ Carinae’s Homunculus nebula.

1. Introduction

As summarized in Figure 1, stars can lose mass through steady wind outflows, giant eruptions, and supernova explosions. The annotations summarize their respective properties, showing that the mass loss from the pressure-driven solar wind is very small compared to the radiatively driven winds from massive, luminous OB and Wolf–Rayet (WR) stars. Such massive stars generally end their lives as core collapse supernovae, but in addition to their strong winds, such stars can undergo episodes of eruptive mass loss, known as ‘eruptive Luminous Blue Variables’ (eLBVs). The next section (Section 2) reviews the driving of solar and stellar winds, while the following section (Section 3) summarizes how eruptive mass loss can be triggered by energy addition to the stellar envelope1, including, for example, through stellar mergers, which can provide a basis for understanding the famous eLBV $\eta$ Carinae and its associated Homunculus nebula. The final section (Section 4) concludes with a summary of the key points of this contribution. The overall goal is to summarize the current understanding of key physical principles behind wind and eruptive mass loss; readers interested in a more comprehensive literature review may consult Davidson [1], Weis and Bomans [2], and the references therein.

2. Basic Stellar Wind Theory

2.1. Polytropic Winds

For a spherical steady-state ($\partial /\partial t=0)$ wind outflow with mass loss rate $\dot{M}=4\pi \rho v{r}^2$ set by the density $\rho$ and speed v at any local radius r, the advective acceleration depends on the local balance between competing forces, taken here to include the local gravitational acceleration $GM/r^2$ associated with stellar mass M and the radial gradient in pressure P,

$$v{\displaystyle \frac{dv}{dr}}=-{\displaystyle \frac{GM}{r^2}}-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{dP}{dr}}$$

(1)

If one assumes a polytropic relation between pressure and density, $P\sim {\rho }^{\gamma }$, Equation (1) can be integrated to yield a simple “Bernoulli” relation between specific forms for kinetic energy, gravitational energy, and gas enthalpy,

$${\displaystyle \frac{v^2}{2}}-{\displaystyle \frac{GM}{r}}+{\displaystyle \frac{\gamma }{\gamma -1}}{\displaystyle \frac{P}{\rho }}=B_n,$$

(2)

where $B_n$ is known as the “Bernoulli constant”. Using mass continuity to cast the enthalpy purely in terms of speed and radius, Figure 2 plots the radial variation of speed for select values of the polytropic index $\gamma$. The red curve shows results for the standard isothermal solar wind, with $\gamma =1.01\approx 1$. The blue curve shows that an accelerating wind solution also holds for $\gamma =4/3$, which corresponds to optically thick radiation-dominated gas. The horizontal dashed line shows that for the transition case $\gamma =3/2$, the flow speed is actually just a constant, while for even large $\gamma$ values, including the standard adiabatic case $\gamma =5/3$, only decelerating solutions are possible, including the case of an adiabatic cooling flow, shown here by the black curve.

2.2. Flux-Driven Scalings

The winds of hot, luminous, massive stars are often described as “radiation-pressure-driven”, but in most all cases, the winds are not sufficiently optically thick enough to cast radiation in terms of a nearly isotropic pressure. Instead, it is the radiative flux, set at a given radius by the luminosity $F=L/4\pi r^2$, that drives the outflow through interaction with a flux-weighted mean opacity ${\kappa }_F$, producing an associated outward radiative acceleration $g_{rad}={\kappa }_{F}F/c$. Since this has the same inverse-square radial dependence as gravity, it is convenient to cast it in terms of an Eddington ratio

$${\mathsf{\Gamma }}_F\equiv g_{rad}/g={\kappa }_{F}L/\left(4\pi GMc\right),.$$

(3)

Ignoring for simplicity the relatively unimportant gas pressure (thus effectively assuming the limit of vanishing sound speed), the equation of motion can now be cast as

$$v{\displaystyle \frac{dv}{dr}}=({\mathsf{\Gamma }}_F-1){\displaystyle \frac{GM}{r^2}}.$$

(4)

For the simple case of a constant Eddington factor, integration from the nearly static stellar surface radius R gives the simple velocity law

$$v\left(r\right)=v_{\infty }{(1-R/r)}^{1/2},$$

(5)

where the terminal flow speed scales as $v_{\infty }=\sqrt{{\mathsf{\Gamma }}_F-1}{v}_{esc}$, where $v_{esc}\equiv \sqrt{2GM/R}$ is the surface escape speed.

If we multiply the equation of motion (4) by the mass loss rate $\dot{M}\equiv 4\pi \rho v{r}^2$, we find that we can cast the wind momentum in terms of a star’s radiative momentum $L/c$ times an associated wind optical depth ${\tau }_F\equiv {\int }_R^{\infty }{\kappa }_F\rho dr$,

$$\dot{M}{v}_{\infty }={\tau }_F{\displaystyle \frac{L}{c}}{\displaystyle \frac{{\mathsf{\Gamma }}_F-1}{{\mathsf{\Gamma }}_F}}.$$

(6)

Optically thin OB winds thus generally have $\dot{M}{v}_{\infty }<L/c$, while optically thick WR winds can have $\dot{M}{v}_{\infty }>L/c$.

Using the fact that ${\mathsf{\Gamma }}_F=1+v_{\infty }^2/v_{esc}^2$, Equation (6) can be rearranged to give a constraint on the associated total kinetic and gravitational energy of the outflow,

$$\dot{M}{\displaystyle \frac{v_{\infty }^2+v_{esc}^2}{2}}={\tau }_{F}L{\displaystyle \frac{v_{\infty }}{2c}}.$$

(7)

Since this can never exceed the source luminosity, we must require ${\tau }_F<2c/v_{\infty }$, representing a kind of “photon tiring” limit. More simply, for a given base luminosity L from the underlying star, the maximum mass loss rate that can be lifted to escape from the surface radius R of a star with mass M is

$${\dot{M}}_{max}\equiv {\displaystyle \frac{L}{GM/R}}.$$

(8)

We can then define a “photon tiring parameter” $m\equiv \dot{M}/{\dot{M}}_{max}$ that characterizes how close a given mass loss rate $\dot{M}$ is to this fundamental energy limit.

To summarize, a sustained stellar wind requires both ${\mathsf{\Gamma }}_F>1$ and $m<1$.

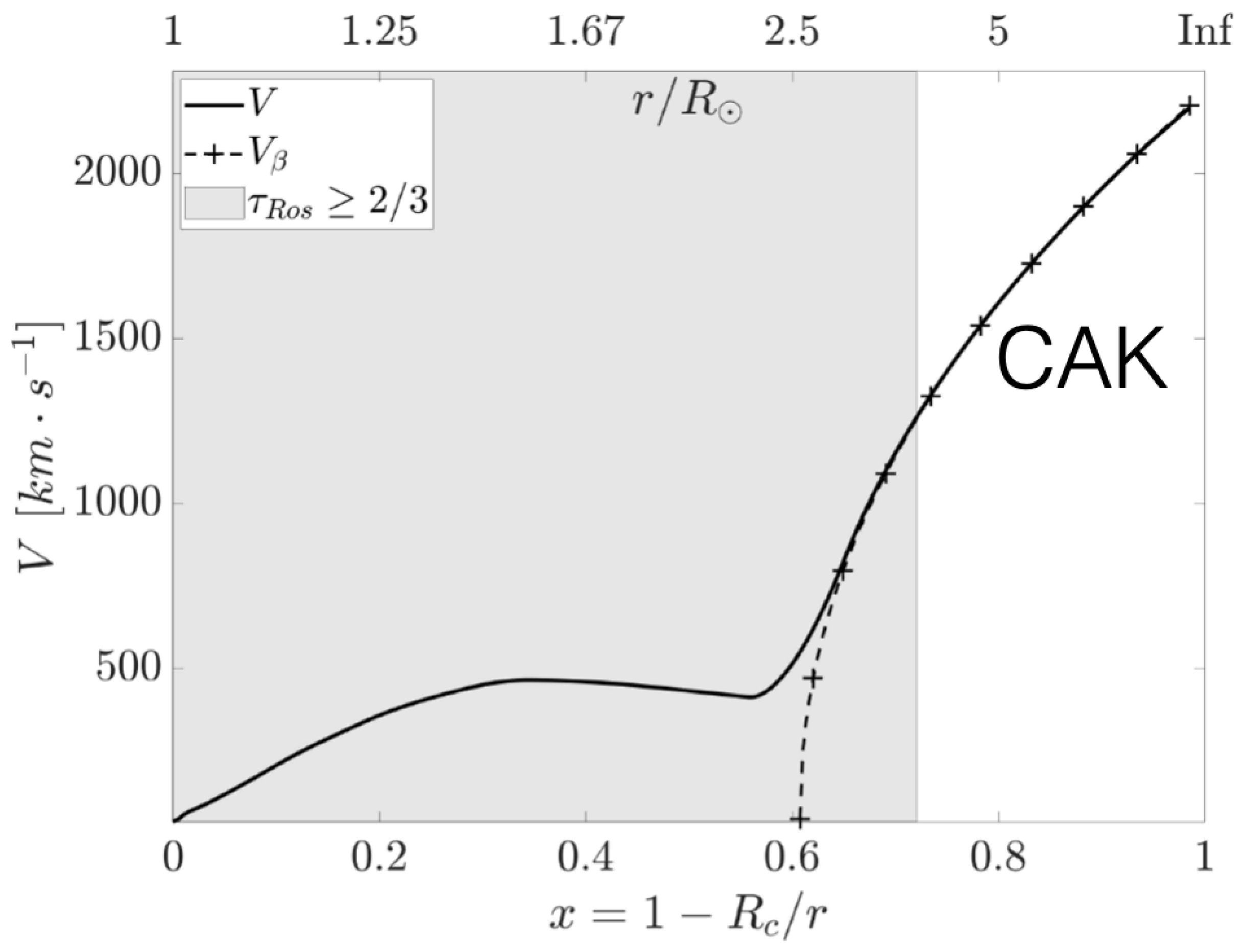
2.3. Line-Driven Scalings

In general, deriving the flux-weighted opacity ${\kappa }_F$ can be quite challenging. But for the key case that the wind opacity comes from bound–bound line transitions in heavy minor ions, the pioneering work by Castor, Abbott, and Klein (1975; hereafter CAK) [3] applied Sobolev line-transfer models to derive local expressions for ${\kappa }_F$ and the associated line acceleration. Gayley (1995) [4] defined a cumulative line opacity $\overline{Q}={\kappa }_{lines}/{\kappa }_e$ scaled by electron scattering opacity ${\kappa }_e$, with typical values of $\overline{Q}\approx 1000$. For a CAK power-law ensemble of lines with index $\alpha$, the Eddington ratio line-acceleration can be written in terms of the standard electron scattering Eddington factor ${\mathsf{\Gamma }}_e\equiv {\kappa }_{e}L/\left(4\pi GMc\right)$,

$${\mathsf{\Gamma }}_{line}={\displaystyle \frac{\overline{Q}{\mathsf{\Gamma }}_e}{{\left(\overline{Q}{t}_e\right)}^{\alpha }}},$$

(9)

where $t_e\equiv {\kappa }_e\rho c/(dv/dr)$ represents the Sobolev optical depth of a line with an electron scattering opacity. Its presence in the denominator of ${\mathsf{\Gamma }}_{line}$ reflects line-desaturation effects that regulate line driving and leads to the characteristic CAK mass loss rate. The associated tiring parameter scales as

$$m_{line}={\displaystyle \frac{v_{esc}^2}{2c^2}}{\left({\displaystyle \frac{\overline{Q}{\mathsf{\Gamma }}_e}{1-{\mathsf{\Gamma }}_e}}\right)}^{-1+1/\alpha }.$$

(10)

The speed ratio factor is $<{10}^{-5}$, while for $\alpha =2/3$ and ${\mathsf{\Gamma }}_e=0.5$, the parenthesis factor is of order 100, implying that $m_{line}\lesssim 0.001$. Thus, even with $v_{\infty }\approx 3v_{esc}$, the total kinetic and potential energy of such winds is typically less than a percent of the radiative luminosity, implying that photon tiring effects are quite negligible for line-driven OB winds. However, next we see that, for more optically thick outflows, such photon tiring effects can become significant, and ultimately even set a fundamental limit on the possible mass loss rate.

2.4. Continuum Initiation of WR Winds

Wolf–Rayet (WR) stars have mass loss rates that can be an order of magnitude higher than OB winds of a similar luminosity. Building on previous considerations of the potential role of the iron opacity bump on the envelopes of WR stars [5,6], recent work by Poniatowski et al. (2021) [7] explored how such a stronger mass loss can be initiated by this iron opacity bump. In this case, the flux-weighted opacity is approximated by the Rosseland mean, as tabulated by the OPAL opacity project. This is the result of the cumulative effect of a multitude of iron lines; but their strong overlap means this opacity is treated as if it were a continuum process, without the desaturation effects central to CAK line driving. However, as shown in Figure 3, once this iron bump fades in the inner wind, the CAK line driving with such desaturation takes over to drive the outflow to escape. The net effect is to enhance the mass loss rate of WR stars by an order of magnitude compared to OB stars of a comparable luminosity; the associated wind optical depths can thus be of order $\tau \sim 10$, producing modest photon tiring effects with $m\approx 0.1$.

For lower-luminosity OB stars, the iron bump can induce a failed outflow that, in multi-dimensional models, leads to strong, supersonic turbulence in the surface layers, greatly complicating the initiation of their line-driven wind outflows [8].

2.5. Super-Eddington Continuum-Driven Winds

If stellar envelopes have a combined increase in opacity $\kappa$ and/or luminosity L (e.g., from energy deposition by waves [9]) that causes a super-Eddington condition $\mathsf{\Gamma }>1$ beyond some radius R, this can induce a continuum-driven outflow, with a mass loss that now can readily approach the photon tiring limit, $m\lesssim 1$. Such flows can be sufficiently dense and optically thick that their driving can now indeed be characterized in terms of the gradient of radiation pressure, which for standard gray medium scales is $P_r\approx \tau F/c$. Moreover, the analysis by Owocki, Townsend, and Quataert (2017; hereafter OTQ) [10] shows that this optical thickness scales with the product of the wind parameters $m\mathsf{\Gamma }$ through

$$\tau \approx m\mathsf{\Gamma }{\displaystyle \frac{c}{v_{esc}}},$$

(11)

where $v_{esc}=\sqrt{2GM/R}$ is the escape speed from the onset radius R. The ratio of advective flux of radiation to the usual diffusive flux is thus given by

$${\displaystyle \frac{P_r{v}_{esc}}{F}}=m\mathsf{\Gamma }.$$

(12)

As long as $m\mathsf{\Gamma }\ll 1$, the advective flux is negligible, and the above picture of a radiative-flux-driven flow holds; but if $m\mathsf{\Gamma }\gtrsim 1$, the flow solution is better described as radiation-pressure-driven, as described in Section 2.1 and illustrated in Figure 2, with the index now being $\gamma =4/3$ for a radiation-dominated fluid. The associated radiative enthalpy is given by $h_r=4P_r/\rho$, with the flow solution given by Equation (2) (cast in scaled form by OTQ Equation (37)).

OTQ illustrates the transition between these flux-driven vs. enthalpy-driven limits by deriving full flow solutions for various assumed values for m and $\mathsf{\Gamma }$. For a given $\mathsf{\Gamma }$,the maximum tiring is set by $m_{max}=1-1/\mathsf{\Gamma }$, corresponding to the maximum mass loss rate, given by

$${\dot{M}}_{max}={\displaystyle \frac{4\pi Rc}{\kappa }}(\mathsf{\Gamma }-1)=0.0012{\displaystyle \frac{M_{\odot }}{yr}}{\displaystyle \frac{R}{R_{\odot }}}{\displaystyle \frac{{\kappa }_e}{\kappa }}(\mathsf{\Gamma }-1).$$

(13)

For hot massive supergiants with $R>100 R_{\odot }$, we see that even modest super-Eddington parameters $\mathsf{\Gamma }>2$ could drive mass loss rates $M_{max}>0.1 M_{\odot }$/yr that far exceed what is possible from line driving.

OTQ also shows that the wind terminal speed scales as

$$v_{\infty }=v_{esc}\sqrt{{\displaystyle \frac{(1-m)\mathsf{\Gamma }-1}{m\mathsf{\Gamma }+1}}},$$

(14)

which for $m\mathsf{\Gamma }\ll 1$ reduces to the standard result $v_{\infty }=v_{esc}\sqrt{\mathsf{\Gamma }-1}$, as given by Equation (5) above.

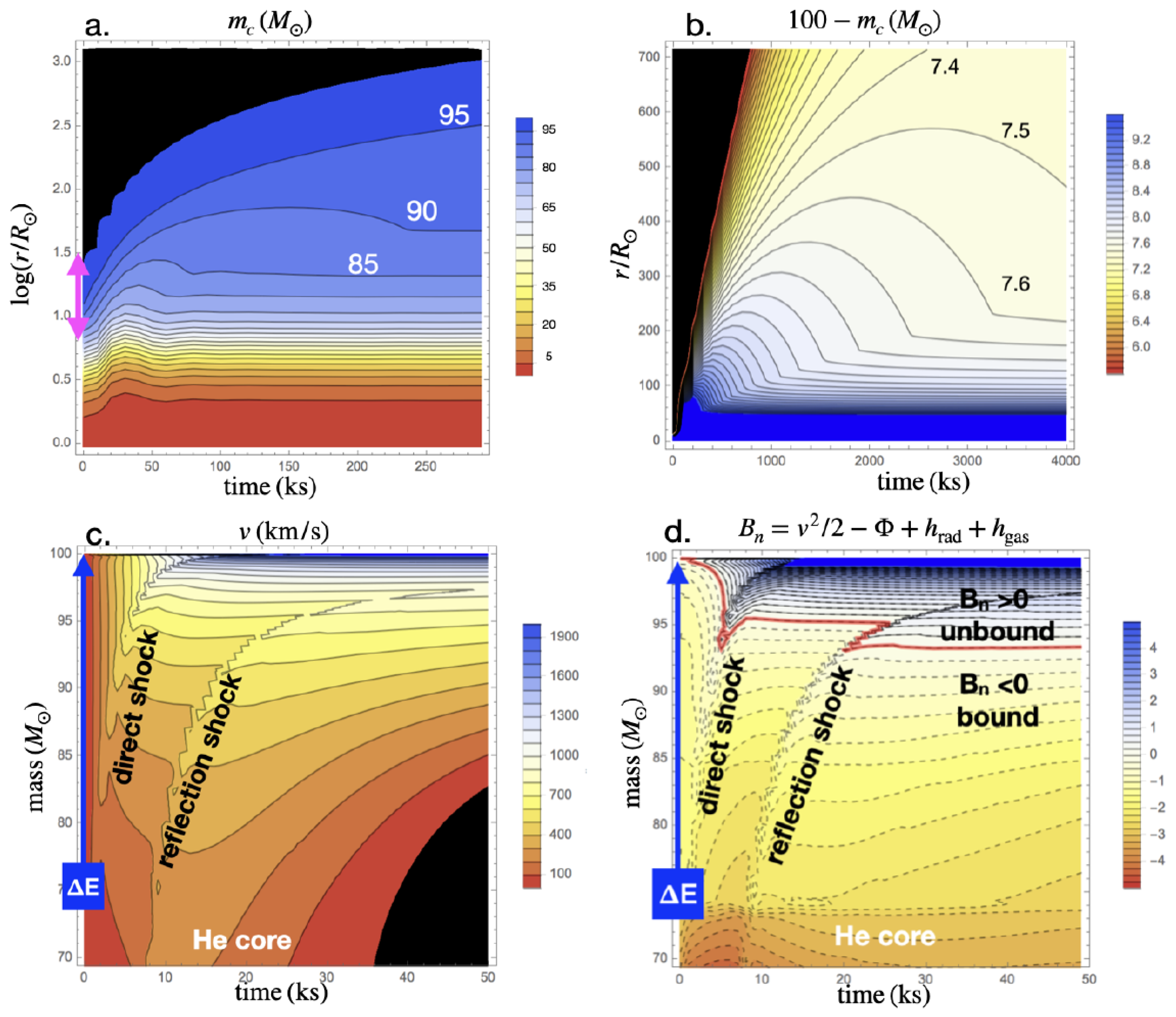
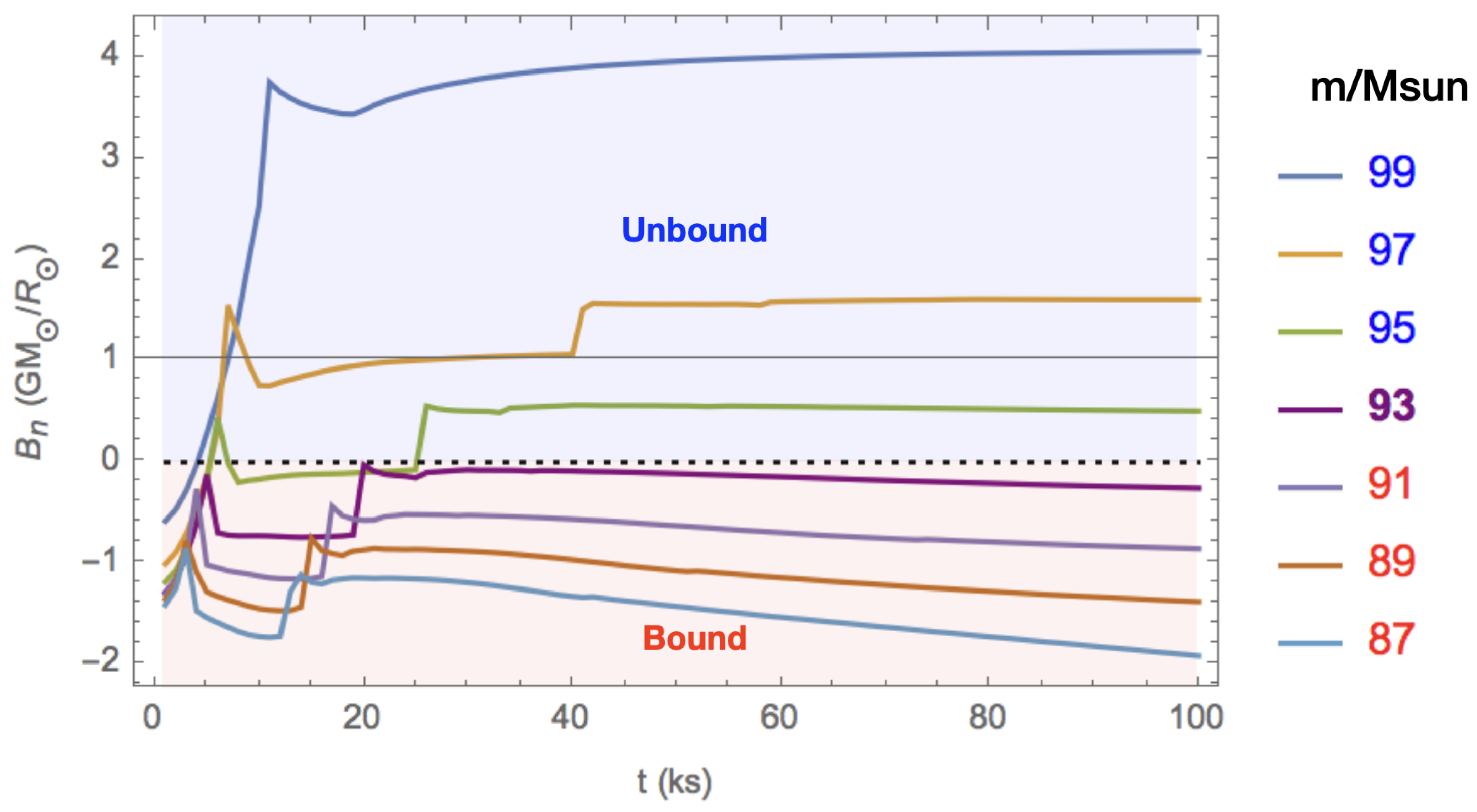
3. Eruptive Mass Loss

3.1. Energy Requirement for eLBV Mass Ejection

To complement the above discussion on the initiation of steady winds, let us next review the processes for initiating mass loss in an observational class of luminous, massive stars known as “eruptive Luminous Blue Variables” (eLBVs). These have properties that are intermediate between steady solar and stellar winds and the explosive mass ejection of core-collapse supernovae (SNe). In the latter, the energy generated by core collapse deposits sufficient energy into the overlying stellar envelope to blow it completely from the star, over an initial dynamical timescale of seconds, and with ejecta speeds that can approach $0.1$c.

The giant eruptions seen from eLBVs have properties intermediate between winds and SNe. While their initiation may be sudden, their evolution can extend over years or even decades, much longer than a dynamical timescale, but generally short compared with a thermal relaxation timescale of the erupting star. The mass fraction ejected can be up to 10–20% of the stellar, much less than the full envelope ejection of SNe, but much larger than even the cumulative mass loss of stellar winds. Unlike the fixed terminal speed of winds, the eLBV ejecta speed can have a broad range, extending from a faster, low density leading edge to a bulk of mass that just barely escapes the star’s gravity.

A promising paradigm is to consider such eLBV eruptions as arising from a quite sudden addition of energy to the star’s envelope, which, unlike the explosive addition of SNe, is only a fraction $f<1$ of the envelope binding energy [11]. Such energy addition could arise from tidal dissipation from a close companion [12,13], or, as we detail below, from the eventual merger with such a companion [14].

Figure 4 shows results for 1D hydrodynamical simulations of the response when energy that is a fraction $f=1/2$ of the stellar binding energy is added to the outer 25 $M_{\odot }$ of a 100 $M_{\odot }$ star, as indicated by the arrow along the left axes of the panels. In terms of fluid parcels defined by their mass coordinate from the surface, the contours show the time response of the total “Bernoulli” specific energy,

$$B_n\equiv {\displaystyle \frac{v^2}{2}}-{\mathsf{\Phi }}_{grav}+h,$$

(15)

where v is the flow speed, ${\mathsf{\Phi }}_{grav}$ is the gravitational potential, and h is the total specific enthalpy from gas and radiation; in terms of gas density and gas and radiation pressure, this is given by

$$h={\displaystyle \frac{\frac{5}{2}{P}_{gas}+4P_{rad}}{\rho }}={\displaystyle \frac{5}{2}}{\displaystyle \frac{kT}{\mu }}+{\displaystyle \frac{4a_{rad}{T}^4}{3\rho }},$$

(16)

with $a_{rad}$ being the radiation constant and $\mu$ being the mean molecular weight of the gas.

Note how the initial energy addition induces a pair of direct and shock fronts that propagate toward the surface, heating the gas there so that the increased enthalpy makes the total Bernoulli energy positive for the upper $\sim 7 M_{\odot }$ from the surface. The result is an outward expansion of the stellar envelope, with the positive energy mass parcels with $M<7.4 M_{\odot }$ escaping completely from the star, while the negative energy mass parcels with $M>7.5 M_{\odot }$ eventually falling back onto the star. For the noted selected values of mass parcels, Figure 5 plots the time evolution of the Bernoulli quantity, marking in blue unbound parcels with $B_n>0$, and in red bound material with $B_n<0$.

As shown in Figure 6, the ejecta’s variations in time t and radius r for the velocity v and density $\rho$ are quite well fit by similarity forms in the variable $r/t\approx v$. Specifically, the scaled density follows a simple exponential decline $\rho t^3\sim exp(-r/v_{o}t)$. This exponential similarity leads to analytic scaling relations for total ejecta mass $\Delta M$ and kinetic energy $\Delta K$ that agree well with the hydrodynamical simulations, with the specific-energy-averaged speed related to the exponential scale speed $v_o$ through $\overline{v}=\sqrt{2\Delta K/\Delta M}=\sqrt{12}{v}_o$, and a value comparable to the star’s surface escape speed, $v_{esc}$.

Unlike the fixed terminal speed $v_{\infty }$ of a stellar wind, a small amount of material can be ejected at very high speeds, >5000 km/s. But, like stellar winds, gravity still plays a central role in controlling the mass and speed of the outflow, through the ratio of the added energy to the gravitational binding energy. This is distinct from the standard SNe explosion, for which the added energy essentially overwhelms the gravitational binding of the envelope, leading to explosion speeds of order 0.1c.

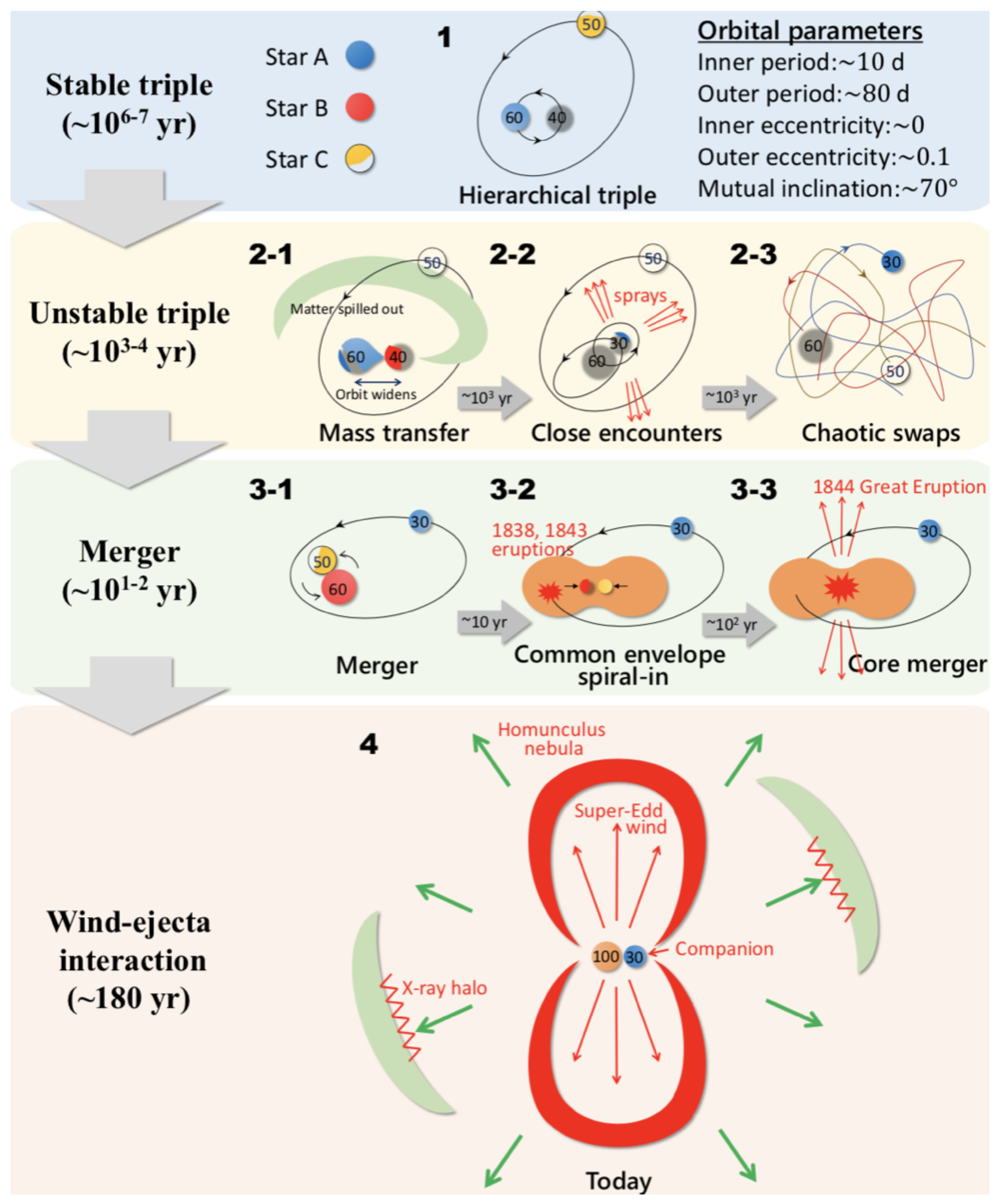
3.2. Merger Model for $\eta$ Carinae

The 1840’s giant eruption of $\eta$ Carinae is perhaps the most prominent and extreme example of an eLBV, with the estimated $10-20M_{\odot }$ ejected mass forming the bipolar ‘Homunculs’ nebula (shown in the 3rd image in Figure 1). Two key challenges are understanding the energy source powering the eruption and the causes of the bipolar form. $\eta$ Carinae is known to have a massive companion in an eccentric ($ϵ\approx 0.9$) orbit with a period ∼5.5 yr.

Figure 7 summarizes a model by Hirai et al. (2021) [14], in which an original triple system (phase 1) becomes unstable due to mass exchange (phase 2), leading to swaps and close encounters that result in a series of random ejecta that, today, are observed with source times extending back several centuries. Eventually, orbital decay of the innermost pair leads to a merger (phase 3), powering the 1840’s giant eruption. The enhanced luminosity and rapid rotation of the post-merger star (phase 4) drives a strong, bipolar, super-Eddington wind that sculpts the compressed Homunculus nebula seen today.

4. Concluding Summary

Let us conclude with a summary of the key points of this contribution.

• Radiation-driven winds from hot, luminous, massive stars, with spectral-type OB and WR, can have mass loss rates up to billion times the gas-pressure-driven solar wind.
• Although often characterized as radiation-pressure-driven, their driving is more accurately described by the interaction of the star’s radiative flux with opacity, set by bound–bound line transitions of minor ions, as originally developed by CAK [3].
• The stronger mass loss of WR stars may result from an initiation by the iron opacity bump, which can be treated as a continuum process. As this bump fades, the line desaturation in the expanding wind allows for transition to standard CAK line-driving that propels the outer wind.
• Both OB and WR winds are energetically inefficient, characterized by a "photon-tiring" fraction $m<0.1$.
• Winds driven fully by continuum opacity can approach the fundamental tiring limit $m<1$. For $m\mathsf{\Gamma }>1$, such winds are sufficiently optically thick for radiation advection to exceed the diffusive flux, which leads to a true radiation-pressure-driven flow that can be characterized in terms of the Bernoulli solution with polytropic index $\gamma =4/3$.
• Sudden energy addition into the outer stellar envelope can induce a positive Bernouil energy in the outer layers, causing them to be unbound, with a similarity form $v=r/t$ for velocity, and a “exponential” similarity form for density. This represents an underlying connection to the above Bernoulli solution for steady, continuum-driven winds.
• The giant eruption in the famous eLBV $\eta$ Carinae may have been induced by the merger of two stars within a dynamically unstable triple system. The rapid rotation and high luminosity of the merger star leads to a super-Eddington wind that is strongest over the poles, which can then sculpt the mass ejection into a bipolar form, seen as the Homunculus nebula.